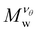Molecular dynamics study of the swelling and osmotic properties of compact nanogel particles†
Alexandros
Chremos
 *a,
Jack F.
Douglas
*a,
Jack F.
Douglas
 b,
Peter J.
Basser
a and
Ferenc
Horkay
b,
Peter J.
Basser
a and
Ferenc
Horkay
 *a
*a
aSection on Quantitative Imaging and Tissue Sciences, Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health, Bethesda, MD 20892, USA. E-mail: alexandros.chremos@nih.gov
bMaterials Science and Engineering Division, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA. E-mail: horkayf@mail.nih.gov
First published on 15th August 2022
Abstract
Owing to their great importance in materials science and other fields, we investigate the solution and osmotic properties of uncharged compact nanogel particles over a wide range of solvent quality and particle concentration by molecular dynamics (MD) simulations. We characterize the osmotic pressure by estimating the second and third virial coefficients, and by extension, we identify the θ-point where the second virial coefficient vanishes. Calculations of the structure factor indicate that these particles are similar to macrogels in that the particle-like scattering profile disappears at moderate concentrations. We also find that improving the solvent quality enhances the spatial segmental uniformity, while significant heterogeneous structure arises near the θ-point. Well below the θ-point where the second osmotic virial coefficient vanishes, these heterogeneous structures become less prevalent as the particles tend to collapse. We also investigate the degree of swelling and structure of compact nanogel particles with a variable excluded volume interaction and gel particle concentration. The osmotic modulus and the scaling exponents in good and θ-point conditions of these gels are characteristic of interacting randomly branched polymers, i.e., “lattice animals”.
I. Introduction
Nanogel particles are typically, but not always, hydrogel materials with a high capacity for swelling in water, depending on the extent of cross-linking and polymer excluded interactions within and between them.1–3 They are increasingly becoming essential building blocks of modern (bio)-manufacturing,4–6 because they are often highly bio-compatible, due to their hydrophilic nature. The high loading capacity for guest molecules and their unique physical properties offer distinct advantages over other types of nanomaterials for biomedical applications. Moreover, they are highly customizable since they can be composed of a variety of naturally occurring or synthetic polymers, and their size, softness, and degradability can be fine-tuned by varying the chemical composition. For example, nanogel particles can be designed to exhibit multi-stimuli responsiveness in targeted therapy of cancer7 or to provide targeted delivery of short interfering RNA (siRNAs), a gene-regulating tool to increase the efficacy of chemotherapy drugs.8 Owing to the growing number of applications of nanogel particles, there is a need to understand these particles better to enable optimization of their properties for specific applications.While nanogel particles are predominately being used as targeted drug-delivery vehicles, nanogel particles have been also used in bacterial bio-production,9 as self-healing materials,10 in enhanced oil recovery,11 coatings12,13 and sensors.14 Another emerging role of nanogel particles is by embedding them within a polymer network to improve performance for the desired application. Specifically, the articular cartilage of the knee and hip exhibits compromised load-bearing capacity when its compressive resistance is reduced. Moreover, articular cartilage experiences large-amplitude repetitive loading during walking or jumping, so a rapid recovery of the bulk tissue is crucial to normal function. Deviation from the physiological material performance in articular cartilage is associated with degenerative conditions such as osteoarthritis.15–18 Recently, Horkay and Basser19 have utilized nanogel particles to develop a synthetic composite hydrogel that mimics functional properties of articular cartilage.19 As a prerequisite to studying composite gels, it is prudent to develop descriptions of the two primary components, the network and the nanogel particles. In this paper, we study the swelling and osmotic properties of compact nanogel particles in dilute and concentrated solutions in the absence of a polymer matrix. The inclusion of the polymer matrix is integral for creating the composite gel model, but it also increases the complexity of the model. We plan for this to be the subject of a subsequent paper. It is then essential to understand the behavior of the nanogel particles in the absence of a polymer matrix as the natural step toward our goal.
Our previous study of polymers having a network topology indicated that the apparent exponents describing the mass scaling of these polymers under good solvent conditions generally depend on the density of branch points in the network and the fraction of bonds cut in the network.20,21 This led us to define two distinct general classes of networks. First, the ‘ideal’ or ‘compact nanogel particles’ have a network topology defined by a lattice-like structure, resulting in a more symmetric particle-like geometry. Second, the ‘open nanogel particles’ have a polymer network that is highly defective so that the polymer network forms an anisotropic fractal-like structure. The mass scaling of the ‘open gels’ was found to conform rather well with randomly branched polymers (‘lattice animals’), but the situation was found to be more complicated for the perfect nanogel particles whose size did not seem to conform with the expectations of randomly branched polymers.21 In particular, the apparent mass scaling exponents describing the average size of these nanogel particles depended on the mesh spacing in the network. The radius of gyration mass scaling exponent when the mesh size was small was found to be consistent with that for the swollen linear chains composing the network in isolation (ν ≈ 0.588) with increasing M while the apparent exponent was found to be near (ν ≈ 1/3) with increasing branched points in each direction. An examination of the structure factor of these closed gel nanoparticles exhibits a mass scaling similar to self-avoiding linear polymers at high scattering wavevector. However, a cross-over to a wavevector scaling is consistent with a higher effective fractal dimension at larger length scales.20,21 It is apparent from these observations that the structures simulated cannot be described as being ‘fractal’ objects, but they are rather hybrid structures having properties in common to fractals, epitomized by linear polymer chains, and symmetric particles having uniform density. It is difficult from the limited size simulations to deduce the asymptotic mass scaling in the limit of large polymer mass from the study of individual network polymer chains, but additional insights into these mass scaling characteristics can be obtained from the study of the swelling of these structures as solvent quality is varied and from the concentration dependence of the osmotic pressure under variable solvent conditions. We will show that there are slow cross-over effects on the ν exponent, as found even in linear polymer chains when the polymers are semi-flexible, suggesting there is an appreciable rigidification of polymer network when the mesh spacing is small.
This paper studies the swelling and osmotic properties of compact nanogel particles in dilute and concentrated solutions. We have already developed methods for generating nanogel particles, and we have studied the structure and conformational properties in athermal dilute solutions.20,21 We use these methods to construct gels composed of nanogel particles and characterize their structure, osmotic pressure, and osmotic modulus. In addition, we estimate the virial coefficients of compact nanogel particles and compare them with star polymer solutions. We also investigate the influence of solvent quality on the degree of swelling in both dilute and concentrated nanogel particle concentrations.
The paper is organized as follows. Section II contains details of the simulation model and methods. The results are presented in Section III, where we investigate the influence of solvent quality in the swelling of nanogel particles in dilute and concentrated solutions. We also investigate the scattering profiles of these gels and the calculate the osmotic modulus. Finally, we draw our conclusions in Section IV.
II. Methods and models
We employ a bead-spring model suspended in an implicit solvent, in which we have adapted a model developed previously for studying the swelling behavior of linear polymer chains in solution. All the nanogel particles are assigned the same mass m, size σ, and strength of interaction ε; we set ε and σ as the units of energy and length.The expression describing the non-bonded interactions operating between all pairs of beads contains three terms. First we write the purely repulsive Weeks–Chandler–Andersen (WCA) potential,22 which is a Lennard-Jones potential cut and shifted at the position of the minimum, rmin = 21/6σ:
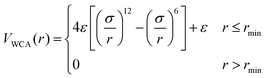 | (1) |
To represent the attractive interactions, the WCA potential is shifted in the range 0 ≤ r ≤ rmin by a square-well (SW) potential,
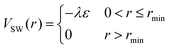 | (2) |
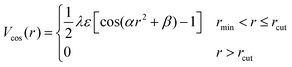 | (3) |
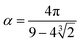 and
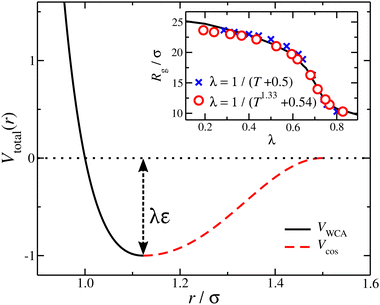
and 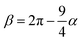 . The final non-bonded potential is V(r) = VWCA + VSW(r) + Vcos(r), see Fig. 1. The parameter λ controls the depth of the potential well at r = rmin, and provides a convenient measure of the solvent quality. In a good solvent, the effective bead–bead interactions are purely repulsive; this corresponds to λ = 0. In a poor solvent, the bead–bead interactions are attractive, and this behavior can be modeled with λ = 1; the parameter λ also corresponds roughly to the Lennard-Jones potential well, which has been used frequently in the past in coarse-grained modeling of neutral polymers both in solution and in the melt.24,25
. The final non-bonded potential is V(r) = VWCA + VSW(r) + Vcos(r), see Fig. 1. The parameter λ controls the depth of the potential well at r = rmin, and provides a convenient measure of the solvent quality. In a good solvent, the effective bead–bead interactions are purely repulsive; this corresponds to λ = 0. In a poor solvent, the bead–bead interactions are attractive, and this behavior can be modeled with λ = 1; the parameter λ also corresponds roughly to the Lennard-Jones potential well, which has been used frequently in the past in coarse-grained modeling of neutral polymers both in solution and in the melt.24,25
In simple models of uncharged polymer solutions, a variable excluded volume interaction strength is normally described theoretically by the ratio of the strength of the nearest–neighbor interaction (e.g., the depth of a square potential) divided by temperature as in the classical Flory–Huggins theory of polymer solutions and polymers in the melt state where the the dimensionless energetic well-depth parameter (normally denoted as χ) is estimated from fitting the model calculations based on such idealized intermolecular potentials to experiment.26 It is well-known that this approach must often be modified by adding a constant “entropic” term to the χ interaction parameter so that the T dependence is more complicated than indicated by the original Flory–Huggins theory neglecting monomer and solvent structure, as well as the topology and bending rigidity of the molecules. A general, albeit complex extension of the Flory–Huggins model has been developed which addresses these specific monomer effects27,28 which explains this more complex temperature phenomenology of polymer–polymer interactions under high polymer polymer concentrations where mean field theory reasonably applies. Correspondingly, we may expect some deviation from the simple dependence of solvent quality on the ratio λε/T that one may infer from the Lennard-Jones or the square-well like potential alone. We address this complication in describing the reduced interaction strength so that obtain a unified description of the variation of solvent quality by varying either λ or T.
The benefit of using the depth of the potential interaction instead of T for the control of the solvent quality is that a wider range of “solvent quality” can be explored by molecular dynamics simulation. A “map” between the λ and T can be constructed by matching an appropriate quantity, here we used the radius of gyration for a nanogel particle, see inset of Fig. 1. A first order approximation results in λ = (T + 0.5)−1, which evidently athermal solvents having λ → 0 require T → ∞; an improved description is found with λ = (T1.33 + 0.54)−1. In other words, athermal or very “good” solvents require high temperature values that are prohibited in a molecular dynamics simulation. Moreover, high temperature simulations of some complexity models, such as polymers, have the potential of not sampling appropriately the configurational space due to deviation between the configurational temperature and thermodynamic temperature.29 The segments along a chain are connected with their neighbors via a stiff harmonic spring, VH(r) = k(r − l0)2, where l0 = 0.99σ is the equilibrium length of the spring, and k = 2000ε/σ2 is the spring constant.
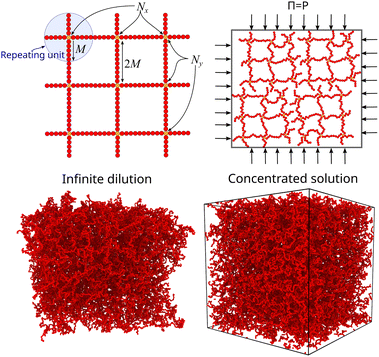
A perfect compact gel that is composed of star polymers placed in a square or in a cubic lattice and with two or more of their free ends bonded with the free ends of the neighboring stars, the number of branched points (or star polymers) in each direction is labeled as Nx, Ny, and Nz, see Fig. 2.20 The repeating structural unit of the polymer network studied here is a branched structure that is identical to a regular star polymer. Other polymeric structures and/or other lattices could be utilized but these are out of the scope of the current study. A regular star polymer has a core particle, which is connected with the free end of f chains (or arms) composed of M segments. Thus, the total number of interaction centers per star polymer is Mw,star = fM + 1. The molecular mass of a nanogel particle is Mw = (NxNyNz)Mw,star. We use the quantity Nb to characterize the number of branched points in each direction. We focus on nanogel particles having Nb = Nx = Ny = Nz. Every star polymer unit at the interior of the nanogel is fully bonded with its neighbors and thus the only dangling polymer chains are located at the exterior of the nanogel structure. Nanogel particles are randomly placed in a simulation box without overlaps. For highly dilute conditions, we consider a single nanogel particle in a simulation box several times larger than the size of the nanogel particle. For concentrated solutions, we considered a small number of nanogel particles ranging from one to eight. Unless stated otherwise, we mainly focus on compact nanogel particles having Nb = 10, f = 4, and M = 25.
The systems in dilute concentrations were equilibrated at constant temperature kBT/ε = 1.0, maintained by a Nosé-Hoover thermostat. In concentrated solutions, the systems were equilibrated at constant temperature kBT/ε = 1.0 and constant pressure maintained by a Nosé-Hoover thermostat and barostat. Typical simulations equilibrate for 5000τ and data is accumulated over a 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ interval, where τ = σ(m/ε)1/2 is the MD time unit; the time step used was Δt/τ = 0.005.
000τ interval, where τ = σ(m/ε)1/2 is the MD time unit; the time step used was Δt/τ = 0.005.
The osmotic pressure of the system is calculated from the virial equation Π = ρkT + W/V, where the internal virial W is calculated from the sum of a pair virial function w(rij) = rijdU(rij)/drij. Due to the presence of non-vanishing intra-molecular contributions, a small constant is added in Π to ensure that the correct limit is reached at vanishing small segmental densities.
III. Results and discussion
We first discuss the two main approaches to identifying the θ-point in compact nanogel particles MD simulations where the second virial coefficient vanishes. The first approach involves taking advantage of the invariance of the mass scaling of the size of the polymer, and the second approach uses the virial equation to estimate the second virial. Once the θ-point is identified, then we develop a universal description for the size of the compact nanogel particles. Following this analysis, we calculate the form factor and structure factor for these structures and characterize the structure of these gels as the θ-point is approached. Finally, we utilize our model of compact nanogel particles to estimate the osmotic modulus over a wide range of molecular characteristics and solvent conditions.A. Compact nanogel particles in super-dilute concentrations
We initiate our discussion on the swelling of compact nanogel particles in super-dilute concentrations. We define the segmental density ρ =NgelMw/V, where Ngel is the number of nanogel particles and V is the volume of the simulation box. We note the local segmental density inside the nanogel particle ρgel = Mw/Vnanogel, where Vnanogel is the volume occupied by nanogel particle, does not decrease towards vanishing small values as ρ → 0 due to the polymer crosslinking. For the purposes of the current study, we assume that the volume of the nanogel particle is approximately,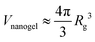 .
.
At high temperatures, polymer chains in solution30–32 and, by extension, the gels,33 swell due to the dominance of repulsive interactions, while at low temperatures, the polymer chains collapse because the attractive interactions dominate over the repulsive interactions resulting in chain collapse conformations. At intermediate temperatures, near the θ-temperature where attractive interactions compensate the repulsive inter-polymer interactions, the chains adopt nearly ‘ideal’ conformations because the attractive and repulsive interaction contributions cancel each other, but the scaling of the polymer size under this ideal condition depends on polymer topology, in general. Linear chain melts and concentrated solutions have practically ideal chain conformations between monomers because the surrounding chains almost completely screen the interactions between the monomers.
There are two main approaches to identifying the θ-temperature for a polymeric system. The first one takes advantage of the size mass invariance that polymers exhibit at the θ-temperature, provided one knows the Flory exponent, νθ appropriate to the kind of polymer involved. The approach is relatively straightforward, requiring the estimation of the size of the polymer at different solvent quality solvents and molecular masses. The radius of gyration Rg is typically used as a measure of polymer size for this purpose. As the temperature of the system is increased, the polymer (assuming that it is neutral) will swell. This type of calculation is repeated for polymers of different molecular masses. The θ-temperature can be identified by the location where 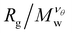 remains fixed for all molecular masses. The advantage of this approach is that it is relatively straightforward to implement computationally. However, its disadvantage is that it requires a priori knowledge of νθ, which cannot be assumed to be the same as polymers having a linear topology and this definition does not generally coincide with the condition at which the second virial coefficient vanishes for finite-sized polymers. The second approach is the estimation of θ-temperature by the calculation of the second virial, and we will discuss this approach in Subsection IIIC.
remains fixed for all molecular masses. The advantage of this approach is that it is relatively straightforward to implement computationally. However, its disadvantage is that it requires a priori knowledge of νθ, which cannot be assumed to be the same as polymers having a linear topology and this definition does not generally coincide with the condition at which the second virial coefficient vanishes for finite-sized polymers. The second approach is the estimation of θ-temperature by the calculation of the second virial, and we will discuss this approach in Subsection IIIC.
The scaling regions are clearly distinguishable in Fig. 3. In the first region 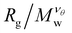 increases as Mw increases corresponding to a good solvent regime, and in the second region
increases as Mw increases corresponding to a good solvent regime, and in the second region 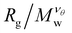 decreases as Mw increases corresponding to a poor solvent regime. In between these two regimes all
decreases as Mw increases corresponding to a poor solvent regime. In between these two regimes all 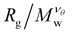 curves for different values of Mw cross, suggesting that
curves for different values of Mw cross, suggesting that 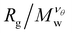 becomes independent of Mw variation. This crossover point defines the θ-point. Additionally, our high fidelity results provide a clear identification of a single point where
becomes independent of Mw variation. This crossover point defines the θ-point. Additionally, our high fidelity results provide a clear identification of a single point where 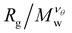 remains invariant of Mw corresponding to λθ ≈ 0.7, see Fig. 3. While the same mass scaling exponents for each solvent quality condition are found in both linear chains and our compact nanogel particles, the location of the θ-point is significantly different; for linear chains, λθ,chains = 0.646. The branched nature of the polymer network evidently also influences the θ-point.
remains invariant of Mw corresponding to λθ ≈ 0.7, see Fig. 3. While the same mass scaling exponents for each solvent quality condition are found in both linear chains and our compact nanogel particles, the location of the θ-point is significantly different; for linear chains, λθ,chains = 0.646. The branched nature of the polymer network evidently also influences the θ-point.
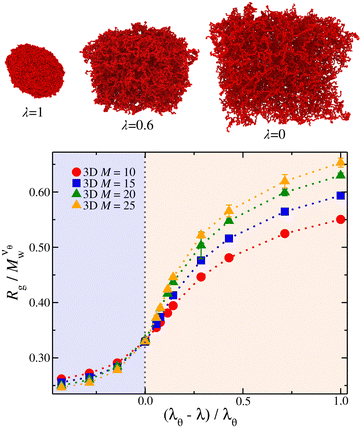
Knowledge of the conditions at which the θ-conditions emerge provide an important reference point to describe the changes in the size of a polymer over the variation of the solvent quality. There is no rigorous theory for the swelling of these networks, and we first offer a highly simplified mean field model of the swelling of the polymer networks. Inspired by previous modeling of the swelling of polymer brushes and gels;34 The basic idea is that the extent of polymer swelling ultimately saturates, and we model the swelling by a tanh function which varies sigmoidally and inherently exhibits this saturation tendency. Indeed, we find Rg/Rg,q for that compact nanogel particle having M and variable Nb follows this empirical functional form rather well. In particular, Rg/Rg,θ for compact nanogel particles can be described by the empirical functional form,
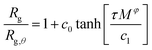 | (4) |
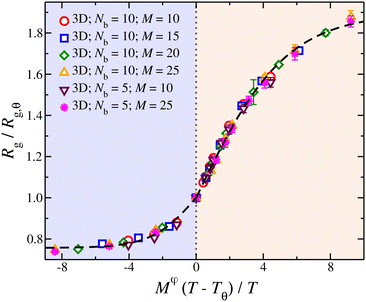 | ||
| Fig. 4 Average radius of gyration, Rg, of isolated compact nanogel particles normalized by Rg at θ-point, as a function of the reduced temperature, τ = (T − Tθ)/T and chain length, M, scaled with an exponent φ. The highlighted regions outline the good solvent conditions for τ > 0 and poor solvent conditions for τ < 0. The uncertainty estimates correspond to two standard deviations. The dashed line is a fit of eqn (4) and the values of the parameters are presented in Table 1. | ||
| Parameter | τ > 0 | τ <0 |
|---|---|---|
| c 0 | 0.89 | 0.24 |
| c 1 | 5.31 | 2.64 |
| φ | 0.8 | 0.8 |
In Fig. 5, we show a comparison to the first order renormalization group expression for Rg2/Rg,θ2,35,36
| Rg2/Rg,q2 = (1 +z/u*)(2ν − 2νθ)/φ[1 + b(z/u*)/(1 + z/u*)] | (5) |
There has been some disagreement about which model is most appropriate in describing random networks which arise in a wide range of physical problems. We note that Parisi40 and Cates41 have made arguments favoring the properties of the first type of network model. Numerical simulations of random surfaces having a free boundary in three dimensions42,43 appear to closely accord with ν in three dimensions being exactly 1/2 under self-avoiding conditions, as suggested for our network polymer simulations (Fig. 5).
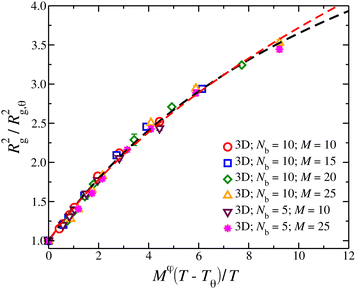 | ||
| Fig. 5 Average square radius of gyration, Rg2, of isolated compact nanogel particles normalized by Rg2 at θ-point, as a function of the reduced temperature, τ = (T − Tθ)/T and chain length, M, scaled with an exponent φ. The dashed line is a fit of eqn (5) with ν = 1/2 (black line) and ν = 0.588 (red line). The uncertainty estimates correspond to two standard deviations. | ||
The crossover function for the swelling of the nanogel particles in eqn (5) provides a reasonable reduction of a swelling data and interpolates between the mass scaling before for the nanogel particles in the good solvent limit where Rg scales as Rg ∼ M1/2 and the observations of the present paper for nanogel particles at their θ-point where Rg,q scales as, Rg,q ∼ M0.4. We should note that in a previous paper we initially estimated the exponent ν for the closed gel polymers to have a value consistent with linear polymer chains in a good solvent (ν = 0.588), but we now appreciate the uncertainties in this type of exponent estimation for the inherently limited size of the polymeric structures that we can simulate. Accordingly, we can obtain some insight into this apparent exponent by considering the crossover expression eqn (5) with ν assumed to equal our former estimate, i.e., ν = 0.588. We see in Fig. 5 that this exponent also describes our swelling data for smaller values of z, but the cross-over curve is better described by ν = 1/2 for large z. Minimally, this underscores the uncertainty in the estimation of ν and to the need for further investigation of this quantity for much larger networks. Similar trends were observed in the formation of clusters of branched polymers.44 Below we approach this problem from another direction through the scaling of the osmotic pressure with polymer concentration where we find compelling evidence for ν = 1/2 in a good solvent from the scaling of the osmotic pressure of solutions of these polymers in the semi-dilute concentration regime. At any rate, the extension of the linear chain RG crossover description of chain swelling to network polymers seems promising, and we plan to develop this type of crossover description further in the future.
Continuum perturbative models of polymers with excluded volume interactions should only apply for relatively high mass polymers under conditions where chain semi-flexibility and other effects related to the detailed functional form of the pair interaction does not influence the asymptotic scaling.45–47 Even short random flight polymer chains do not closely resemble Gaussian chains because of short range correlations and chain semi-flexibility makes the approach to this asymptotic scaling slower. The limitations of the two parameter model of polymer excluded volume observed for linear polymers should apply also to randomly branched polymers; see discussion in ESI.†
B. Size of nanogel particles in concentrated solutions
Now that we understand the swelling behavior of compact nanogel particles under infinite dilution conditions, we focus on concentrated solutions where the nanogel particles fill the interstitial space resembling a mesh of polymer chains. Similar to linear polymer solutions, we can define three characteristic concentration regimes: (i) the dilute solution, in which the individual polymers do not overlap, (ii) the semi-dilute solution where polymers are strongly overlapping but the volume fraction of polymers are still small, and (iii) the concentrated solutions. The crossover between dilute and semi-dilute regimes is typically defined by the overlap concentration defined as ρ/ρ* = 1, where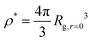 .
.
The nanogel particles exhibit two distinct behaviors. In dilute solutions ρ/ρ* < 0.2, we find Rg/Rg,r=0 ≈ 1 meaning that in these dilute concentrations the size of the nanogel is not concentration dependent. Above the threshold ρ/ρ* ≈ 0.2, we find a sharp crossover to a power-law Rg/Rg,r=0 ∼ (ρ/ρ*)−μ, where μ ≈ 1/3, see Fig. 6. This scaling exponent provides information on how the nanogel particle's size changes once each particle starts to interact with each neighbors in solution. An effect that has been observed in polymer solutions, the corresponding exponent is μ ≈ 0.12 for linear chain,48μ ≈ 0.29 for ring polymers,48 and μ ≈ 0.22 for single-chain nanoparticles solutions.49 The starting point in understanding this effect is based on the observation that the conformational properties of linear polymer chains in a melt are essentially the same as those for ‘unperturbed’ chains without excluded volume interactions, consistent with arguments given by Flory.50 Freed and Edwards51 theoretically explained this behavior from the screening of excluded volume interactions with increasing polymer concentration and it has been confirmed by Small Angle Neutron Scattering (SANS) with labeled linear chains.52 For nanogel particles, at concentrations where we observe this emergence of Rg/Rg,r=0 ∼ (ρ/ρ*)−1/3 scaling, the interstitial space is filled by the nanogel particles. This is consistent with recent modeling of dense microgels suspensions.53 Thus any volume changes (δV) are correlated by changes in the size of the nanogel particle, suggesting δV ∼ ρ−1 ∼ Rg3. This behavior is observed for all the solvent quality range as seen Fig. 6. The exponent in nanogel particles is much larger than in the case of linear chains but closer to ring polymers.
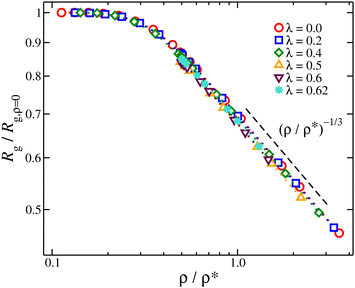 | ||
Fig. 6 Average radius of gyration normalized by its value of infinite dilution, Rg/Rg,ρ=0 as a function of the reduced segmental density, ρ/ρ*, where 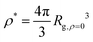 . . | ||
C. Osmotic pressure and second virial coefficients of compact nanogel particles
The osmotic pressure Π can be estimated from the virial coefficients in the virial equation, a formulation developed by McMillan and Mayer.54,55 For a monodisperse polymer solution, the compressibility factor Z can be expanded in powers of ρ,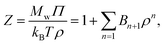 | (6) |
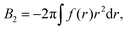 | (7) |
To estimate the virial coefficients, we consider the virial expansion for ρ as power series in terms of a reduced concentration that is defined in terms of the second virial coefficient.56,62,63 In particular, we have,
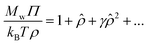 | (8) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) = ρMwB2. Concentrated polymer solutions and gels exhibit similar osmotic pressure behavior at the high concentrations where packing interactions of the polymers becomes predominant and we correspondingly hypothesize that this universality also applies in the semi-dilute regime between the dilute and concentrated regimes. In particular, we hypothesize that eqn (8) applies as an approximation to both polymer solutions of different architectures and polymer gels.
= ρMwB2. Concentrated polymer solutions and gels exhibit similar osmotic pressure behavior at the high concentrations where packing interactions of the polymers becomes predominant and we correspondingly hypothesize that this universality also applies in the semi-dilute regime between the dilute and concentrated regimes. In particular, we hypothesize that eqn (8) applies as an approximation to both polymer solutions of different architectures and polymer gels.
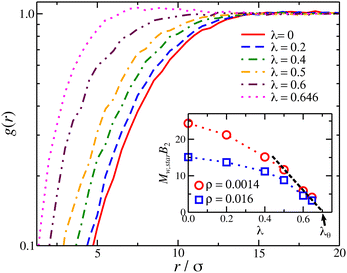
The θ-temperature or solvent is defined when the temperature and/or solvent results in B2 = 0,64,65 requiring the evaluation of the integral in eqn (7) at ρ → 0. This calculation can be done analytically for simple models like hard spheres and square well potential, but it becomes challenging, requiring extensive computation/sampling resources, with increasing the complexity of the molecular architecture. There are a few studies of the estimation of the second virial of different polymers having molecular topology near the θ-point than in the good solvent conditions, such as stars47,66,67 and rings68,69 that offer some insight into this problem. We calculate the pair-correlation of the center-of-mass of star polymers in dilute solutions, see Fig. 7, and by utilizing g(r) =e−u(r)/kT, we obtain the concentration-dependent second virial by eqn (7). We note that by doing this calculation in a polymer solution, we effectively mimic the experimental difficulties in estimating B2 solely based on the interaction of two particles/polymers. We minimize this problem by repeating the process by reducing the polymer concentration and identifying the second virial by extrapolating to ρ → 0, see inset of Fig. 7. As we decrease the solvent quality (increasing λ), the adjustment needed by extrapolating to ρ → 0 becomes smaller. Moreover, the dependence of B2 in our star solution model as a function of λ suggest that λθ,star ≈ 0.7. This value corresponds to a lower θ-temperature than linear chains, consistent with experimental observations of the star and ring68,70 polymers. Now that we have determined the values of B2 at different quality solvents, we use them to compact nanogel particles composed of star polymers.
The osmotic pressure of compact nanogel particles is presented in Fig. 8. We find that the osmotic pressure of both systems (gels and star polymer solutions) in the high-density regime are in agreement even though we used the same value for B2 in both cases. This agreement confirms our initial hypothesis that these two systems exhibit approximately the same osmotic behavior at high densities. The deviation is expected at lower densities because the nanogel particles cease to behave as a unified macrogel structure or a star polymer solution. Another consequence of our assumption is that λθ,gel = λθ,star ≈ 0.7, which is in agreement with our estimation of the θ-point by the Rg mass scaling as we discussed above. In the case of star polymer solutions, Tθ in gels is also expected to be lower than in linear chains.
 | ||
| Fig. 8 Compressibility factor, Mw,starΠ/ρ, for compact nanogel particles (dotted lines) and star polymer solutions (symbols), as a function of B2Mwρ for different values of solvent quality parameter, λ. The cases of hard spheres based on the Carnahan-Starling,71 flexible chains,72 and randomly branched structures56 are also presented. | ||
D. Structure factor
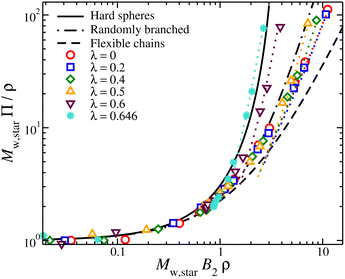
To probe the structure of nanogel particles, we focus on calculating the spatial correlations between the polymer segments. The structure factor, S(q), is a suitable property for this purpose and describes the mean correlations in the positions of a collection of point particles distributed in space.73S(q) is defined55 as: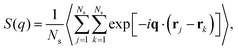 | (9) |
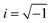 , q = |q| is the wave number, rj is the position of particle j, 〈〉 denote the time average, and Ns is the total number of polymer segments defined as Ns = NxNyNz (fM + 1).
, q = |q| is the wave number, rj is the position of particle j, 〈〉 denote the time average, and Ns is the total number of polymer segments defined as Ns = NxNyNz (fM + 1).
The scattering profiles generated by our model can be described by the following functional form,
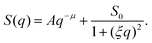 | (10) |
The heterogeneous structure formation resulting in a steep upturn in S(q) is captured in the first term. Both parameters are A and μ are fitting parameters, where μ describes the fractal nature of the clusters formed at length scales larger than the size of the polymer chains and typically, in experiments, the scaling exponent μ is found to be in the range 2 to 5.74 In polymer systems, clustering often plays an important role, however, large clusters do not contribute significantly to the thermodynamics of the solution but strongly modify the scattering spectrum in the low-q range.74 The second term, given by Ornstein–Zernike expression75 (Lorentzian function), captures the local structure and interactions between the polymer chains composing the nanogel structure. The parameter ξ is a ‘correlation length’ that describes that local packing of the chain segments and S0 is the estimated height of the plateau in the absence of heterogeneous structure formation. We emphasize that eqn (10) is phenomenological and we are following common experimental practice in defining the correlation length as prescribed by eqn (10).
At highly dilute concentrations of compact nanogel particles, the form factor P(q) is typically described by the “fuzzy sphere” model,76 in which the particles are described by a dense homogeneous core and an outer loose corona.77–79 At length scales larger than the size of the nanogel particle, there is a sharp increase in P(q) that results in P(q → 0)→ Mw. At length scales near Rg, and sufficiently high values of Nb > 5, there is a primary scattering peak characteristic of particle-like scattering. A power-law behavior is observed at high q-values corresponding to the fractal nature of the polymer chains. We proposed an extension to the fuzzy sphere model to improve the description of the scattering profile at higher q-values, for more details see ref. 20. A typical example of S(q) data for a nanogel particle and a fit to the “extended fuzzy sphere model” is presented in Fig. 9(a).
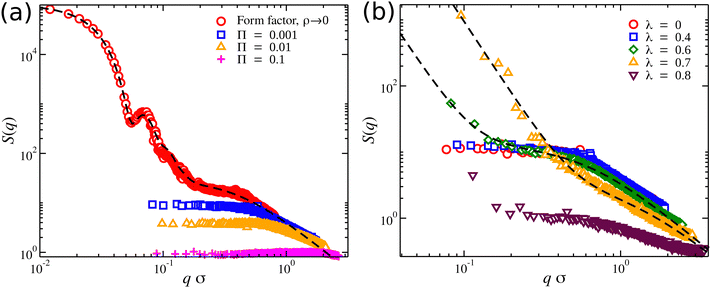 | ||
| Fig. 9 Structure factor S(q) of nanogel particles at different conditions. (a) Athermal solvent (λ = 0) at different osmotic pressures Π; the form factor (dashed line) of an isolated nanogel particle is also presented along with a fit to the “extended fuzzy sphere” model.20 (b) Different solvent qualities at osmotic pressure Π = 0.0001; the dashed lines are fits with eqn (10). | ||
The scattering features of an isolated nanogel particle disappear in concentrated solutions of nanogel particles because the interface surrounding the nanogel particles vanishes once the nanogel particles start to interpenetrate. In other words, the scattering features of nanogel particles become indistinguishable at moderate and high concentrations of these particles. In the athermal solvents, the polymer segments are relatively uniformly spatially distributed and fill the space resulting in a plateau at lower q-values in S(q), see Fig. 9(a). The height of this plateau is often in experiments extrapolated to q = 0 to determine the S(q = 0) value, which provides information about the long-range density fluctuations. In equilibrium, S(0) = kTρκT, where κT is the isothermal compressibility (we will discuss more about κT below). The height of this plateau decreases with an increase in Π. At Π ≈ 0.1, the structure factor becomes equal to unity over a wide range of length scales (qσ < 1), and this is analogous to an ideal gas that exhibits S(q) = 1 for all q. In other words, there is a pressure threshold where the gel effectively loses its structural features.
Near the θ-point, the chains in the nanogel structure begin to shrink and partially ‘collapse’. This effect creates denser regions in the gel structure than an assumed homogeneous spatial segmental distribution. The contrast between these denser regions, which occur randomly within the gel structure, and the voids (regions in which there are no gel segments) results in the formation of heterogeneous structures. This is evident in the structure factor profiles at low-q regime, where a clustering term Sc(q) = Aq−μ is needed to describe the emergence of this behavior. The emergence of clusters/heterogeneous structure formation has been observed experimentally.80 The heterogeneous structures become more dominant because the collapsed structures increase in size as the solvent quality worsens (increasing λ) below but near the θ-point, λθ < λ ≈ 0.7. Eventually, these collapsed structures increase in size and start to merge as the solvent quality worsens, λ > 0.7. Moreover, any voids in the gel structure shrink, resulting in a more homogeneous and dense structure. An increase in the osmotic pressure reduces the impact of heterogeneous structure formation in S(q). We note that the influence of the solvent quality is also expected to influence the scaling exponent in the high q-regime in S(q) scattering profiles.81 For linear chains and other regular polymers, it is expected to scale as S(q) ∼ q1/ν. For the chains in the nanogel particles, we find that S(q) ∼ q−1.3 for λ < 0.7, suggesting that the chains are significantly stretched.
E. Osmotic modulus
The osmotic modulus, K, is defined as the inverse of isothermal compressibility, κT,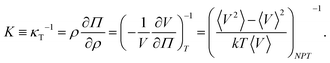 | (11) |
We find that for concentrated solutions, the osmotic modulus of the nanogel particles scales with ρ for the whole range of osmotic pressures. As the osmotic pressure increases, the material's resistance to volumetric changes increases with ρ raised to a scaling exponent that describes the fractal distribution of polymer segments in the gel structure. It is established in experiments and in theory that K ∼ ρδ, where δ = 3ν/(3ν − 1) corresponding to δ = 9/4 for ν = 0.588 and δ = 3 for ν = 1/2.75,82,83 Alternative functional forms for osmotic modulus based on empirical observations have been developed.56,84,85 Linear chain solutions under good solvent conditions exhibit K ∼ ρ9/4 as expected. However, in our nanogel particle solutions, the scaling exponent was found to be K ∼ ρ3 in good solvent, see Fig. 10. This highlights the difference in the fractal nature of the gel from that of linear chain solution. We also note that the experimental procedure of gelation through the cross-linking of long linear chains may lead to the formation of gel structures in which the chains are trapped in a non-equilibrium state where the linear chain scaling of the osmotic modulus is apparently preserved. Recent measurements of polymers cross-linked to form a solution network have shown a tendency to exhibit the osmotic scaling exponents of the parent linear polymer chains. It has been observed that diffusion of randomly branched polymers and the viscosity of branched polymer solutions in which the branched polymers are formed from polymerizing oligomers in solution can be quite different from solutions in which the branched polymers are formed by cross-linking high molecular mass polymers.86,87 There is evidently a ‘memory effect’ of the conditions of cross-linking that requires further investigation. The fractal nature of our gel model is also apparent in our solutions of network polymers. In particular, we find a scaling exponent of K ∼ ρ6 near the θ-point, suggesting νθ ≈ 2/5, which is in agreement with our previous calculations on Rg mass scaling. This scaling exponent is expected to increase further in the poorer solvent conditions but is not expected to change with the variation of the chain length, see Fig. 10. However, the range of K for the same range of Π was significantly different. Longer chains provide the gel with a wider range of K variation. The gel can initiate its resistance to volumetric changes at lower segmental densities and reach higher values of K at higher segmental densities.
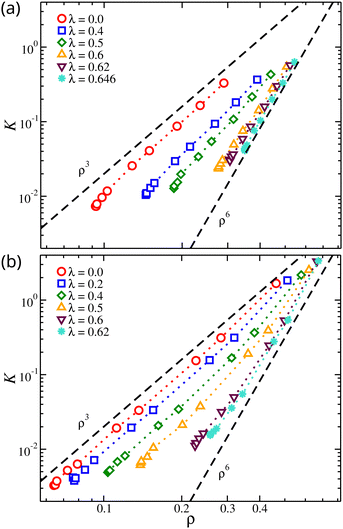 | ||
| Fig. 10 Osmotic modulus, K, of compact nanogel particles as a function of segmental density, ρ. Results for different solvent qualities are also presented. The dashed lines are guides for the eye. | ||
To evaluate these predictions, we examine the elastic modulus G of poly(vinyl acetate)/isopropyl alcohol gels as a function of the polymer volume fraction. The elastic modulus defines the elastic pressure that contracts the gel while the osmotic pressure expands it. The shear moduli of osmotically deswollen gel samples at constant temperature exhibited a scaling exponent of 1/3 with the polymer concentration in both good and θ-solvents, see Fig. 11.88 At equilibrium and an excess amount of solvent, the elastic pressure balances the osmotic pressure, suggesting that the scaling trends found in osmotic modulus will be expected in elastic modulus. The elastic modulus of poly(vinyl acetate)/isopropyl alcohol gels presented in Fig. 11 confirms the predictions for the scaling exponents of our model.
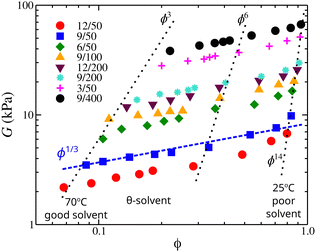 | ||
| Fig. 11 Elastic modulus of poly(vinyl acetate)/isopropyl alcohol gels as a function of the polymer volume fraction, ϕ. The dotted lines approximately correspond to isotherms with a temperature range is (from left to right) 70 °C, 60, 55 °C, 52 °C (identified as the θ-temperature), 50 °C, 45 °C, 37 °C, 30 °C, and 25 °C. Samples are identified by their polymer concentration at the time of introduction of crosslinks and with their degree of crosslinking; for example, 12/50 means that the concentration of PVA solution at which the crosslinks were introduced was 12 mass% and the degree of crosslinking was 50. For more details see ref. 88. | ||
IV. Conclusions
We investigated the structure and osmotic properties of polymer gels composed of compact nanogel particles over a wide range of solvent qualities by molecular dynamics simulations with a bead-spring model. We characterized the osmotic pressure changes in the gel by estimating the second virial coefficients. Moreover, we identified the conditions at which the θ-point emerges. We found that the location of θ-point is the same in both dilute and concentrated conditions, however, the θ-point occurred at a lower temperature than linear chains. Based on the location of the θ-point, we developed an empirical master curve to describe the swelling of the nanogel particles in dilute concentrations. Even at small values of osmotic pressures, the nanogel particles fill the interstitial space so that the particle-like scattering is no longer apparent at moderate concentrations. We also find that improving the solvent quality enhances spatial segmental uniformity in an average sense, while significant heterogeneous structure formation occurs near the θ-point. Well below the θ-point, these heterogeneous structures start to diminish as the gels have nearly collapsed at high osmotic pressures. We also investigate the degree of swelling and structure of compact nanogel particles with the variation of solvent quality at both infinite dilution and concentrated conditions. Finally, we calculated the osmotic modulus and the scaling exponents in good and θ-point conditions found are characteristic of lattice animals.37 These findings provide useful guidelines for the design of gels and a better understanding of the role of gels in biological function.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Intramural Research Program of the NICHD, NIH.References
- J. P. Rolland, B. W. Maynor, L. E. Euliss, A. E. Exner, G. M. Denison and J. M. DeSimone, Direct fabrication and harvesting of monodisperse, shape-specific nanobiomaterials, J. Am. Chem. Soc., 2005, 127, 10096–10100 CrossRef CAS PubMed
.
- X. Zhang, S. Malhotra, M. Molina and R. Haag, Micro-and nanogels with labile crosslinks-from synthesis to biomedical applications, Chem. Soc. Rev., 2015, 44, 1948–1973 RSC
.
- K. S. Soni, S. S. Desale and T. K. Bronich, Nanogels: An overview of properties, biomedical applications and obstacles to clinical translation, J. Controlled Release, 2016, 240, 109–126 CrossRef CAS PubMed
.
- K. Y. Lee and D. J. Mooney, Hydrogels for tissue engineering, Chem. Rev., 2001, 101, 1869 CrossRef CAS PubMed
.
- R. Langer and D. A. Tyrrell, Designing materials for biology and medicine, Nature, 2004, 428, 487 CrossRef CAS PubMed
.
- S. Lv, D. M. Dudek, Y. Cao, M. M. Balamurali, J. Gosline and H. Li, Designed biomaterials to mimic the mechanical properties of muscles, Nature, 2010, 465, 69 CrossRef CAS PubMed
.
- N. Morinloto, X. P. Qiu, F. M. Winnik and K. Akiyoshi, Dual stimuli-responsive nanogels by self-assembly of polysaccharides lightly grafted with thiol-terminated poly(Nisopropylacrylamide) chains, Macromolecules, 2008, 41, 5985–5987 CrossRef
.
- E. B. Dickerson, W. H. Blackburn, M. H. Smith, L. B. Kapa, L. A. Lyon and J. F. McDonald, Chemosensitization of cancer cells by siRNA using targeted nanogel delivery, BMC Cancer, 2010, 10, 10 CrossRef PubMed
.
- P. Srisawat, M. Higuchi-Takeuchi, R. Honda, T. Shirai, A. Kondo and Y. Hoshino,
et al., Engineered nanogel particles enhance the photoautotrophic biosynthesis of polyhydroxyalkanoate in marine photosynthetic bacte, ACS Sustainable Chem. Eng., 2022, 10, 4133–4142 CrossRef CAS
.
- G. V. Kolmakov, K. Matyjaszewski and A. C. Balazs, Harnessing labile bonds between nanogel particles to create self-healing materials, ACS Nano, 2009, 3, 885–892 CrossRef CAS PubMed
.
- T. Liang, J. Hou, M. Qu, M. Zhao and I. Raj, High-viscosity α-starch nanogel particles to enhance oil recovery, RSC Adv., 2020, 10, 8275–8285 RSC
.
- A. M. Atta, H. A. Al-Lohedan and K. A. Al-Haddad, Epoxy coating with embedded self-healing networks formed by nanogel particles, RSC Adv., 2016, 6, 41229–41238 RSC
.
- D. Keskin, G. Zu, A. M. Forson, L. Tromp, J. Sjollema and P. van Rijn, Nanogels: A novel approach in antimicrobial delivery systems and antimicrobial coatings, Bioact. Mater., 2021, 6, 3634–3657 CrossRef CAS PubMed
.
- W. Wu, N. Mitra, E. C. Yan and S. Zhou, Multifunctional hybrid nanogel for integration of optical glucose sensing and self-regulated insulin release at physiological pH, ACS Nano, 2010, 4, 4831–4839 CrossRef CAS PubMed
.
- J. A. Buckwalter, H. J. Mankin and A. J. Grodzinsky, Articular cartilage and osteoarthritis, Instr. Course Lect., 2005, 54, 465 Search PubMed
.
- A. D. Pearle, R. F. Warren and S. A. Rodeo, Basic science of articular cartilage and osteoarthritis, Clin. Sports Med., 2005, 24, 1–12 CrossRef PubMed
.
- J. Martel-Pelletier, C. Boileau, J. P. Pelletier and P. J. Roughley, Cartilage in normal and osteoarthritis conditions, Best Pract. Res., Clin. Rheumatol., 2008, 22, 351–384 CrossRef CAS PubMed
.
- D. Heinegard and T. Saxne, The role of the cartilage matrix in osteoarthritis, Nat. Rev. Rheumatol., 2011, 7, 50–56 CrossRef PubMed
.
- F. Horkay and P. J. Basser, Composite hydrogel model of cartilage predicts its load-bearing ability, Sci. Rep., 2020, 10, 1–7 CrossRef PubMed
.
- A. Chremos, J. F. Douglas and F. Horkay, Structure and conformational properties of ideal nanogel particles in athermal solutions, J. Chem. Phys., 2021, 155, 134905 CrossRef CAS PubMed
.
- A. Chremos, J. F. Douglas and F. Horkay, Influence of network defects on the conformational structure of nanogel particles: From “closed compact” to “open fractal” nanogel particles, J. Chem. Phys., 2022, 156, 094903 CrossRef CAS
.
- J. D. Weeks, D. Chandler and H. C. Andersen, Role of repulsive forces in determining the equilibrium structure of simple liquids, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS
.
- M. O. Steinhauser, A molecular dynamics study on universal properties of polymer chains in different solvent qualities. Part I. A review of linear chain properties, J. Chem. Phys., 2005, 122, 094901 CrossRef PubMed
.
- A. Chremos, E. Glynos, V. Koutsos and P. J. Camp, Adsorption and self-assembly of linear polymers on surfaces: A computer simulation study, Soft Matter, 2008, 5, 637–645 RSC
.
- A. Chremos, E. Glynos, V. Koutsos and P. J. Camp, Adsorption of star polymers: Computer simulations, Soft Matter, 2010, 6, 1483–1493 RSC
.
- A. Chremos, A. Nikoubashman and A. Z. Panagiotopoulos, Flory–Huggins parameter chi, from binary mixtures of Lennard-Jones particles to block copolymer melts, J. Chem. Phys., 2014, 140, 054909 CrossRef PubMed
.
- J. Dudowicz, K. F. Freed and J. F. Douglas, New patterns of polymer blend miscibility associated with monomer shape and size asymmetry, J. Chem. Phys., 2002, 116, 9983–9996 CrossRef CAS
.
- J. Dudowicz, K. F. Freed and J. F. Douglas, Beyond Flory–Huggins theory: New classes of blend miscibility associated with monomer structural asymmetry, Phys. Rev. Lett., 2002, 88, 095503 CrossRef PubMed
.
- B. D. Butler, G. Ayton, O. G. Jepps and D. J. Evans, Configurational temperature: Verification of Monte Carlo simulations, J. Chem. Phys., 1998, 109, 6519–6522 CrossRef CAS
.
- W. R. Krigbaum and D. O. Geymer, Thermodynamics of polymer solutions. The polystyrene-cyclohexane system near the Flory theta temperature, J. Am. Chem. Soc., 1959, 81, 1859–1868 CrossRef CAS
.
- A. Y. Grosberg and D. V. Kuznetsov, Single-chain collapse or precipitation? Kinetic diagram of the states of a polymer solution, Macromolecules, 1993, 26, 4249–4251 CrossRef CAS
.
- X. Wang and C. Wu, Light-scattering study of coil-to-globule transition of a poly(N-isopropylacrylamide) chain in deuterated water, Macromolecules, 1999, 32, 4299–4301 CrossRef CAS
.
- F. A. Escobedo and J. J. de Pablo, Simulation and theory of the swelling of athermal gels, J. Chem. Phys., 1997, 106, 793–810 CrossRef CAS
.
- A. Karim, J. F. Douglas, F. Horkay, L. J. Fetters and S. K. Satija, Comparative swelling of gels and polymer brush layers, Phys. B, 1996, 143, 221 Search PubMed
.
- J. F. Douglas and K. F. Freed, Renormalization and the two-parameter theory, Macromolecules, 1984, 23, 2344–2354 CrossRef
.
- K. F. Freed and J. F. Douglas, Comparison between Borel resummation and renormalization group descriptions of polymer expansion, J. Chem. Phys., 1988, 88, 2764–2768 CrossRef CAS
.
- J. F. Douglas, Swelling and growth of polymers, membranes, and sponges, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 2677–2689 CrossRef CAS
. The scaling exponent ν for polymer without excluded volume is ν = 1/4 and it is not equivalent to branched polymers at their θ-point or having screened excluded volume interactions where ν ≈ 2/5. “Percolation clusters” are branched polymers with screened excluded volume interactions.
- E. Guth and M. James, Elastic and thermoelastic properties of rubber like materials, Ind. Eng. Chem., 1941, 33, 624 CrossRef CAS
.
- M. James and E. Guth, Statistical thermodynamics of rubber elasticity, J. Chem. Phys., 1953, 21, 1039 CrossRef
.
- G. Parisi, Hausdorff dimensions and gauge theories, Phys. Lett., 1979, 81B, 357 CrossRef CAS
.
- M. E. Cates, The Liouville field theory of random surfaces: When is the bosonic string a branched polymer?, EPL, 1998, 7, 719 CrossRef
.
- U. Glaus, Monte Carlo simulation of self-avoiding surfaces in three dimensions, Phys. Rev. Lett., 1996, 56, 1996 CrossRef PubMed
.
- U. Glaus and T. L. Einstein, On the universality class of planar self-avoiding surfaces with fixed boundary, J. Phys. A, 1987, 20, L105 CrossRef
.
- E. V. Patton, J. A. Wesson, M. Rubinstein, J. C. Wilson and L. E. Oppenheimer, Scaling properties of branched polyesters, Macromolecules, 1989, 22, 1946–1959 CrossRef CAS
.
- H. Yamakawa, On the theory of the second virial coefficient for polymer chains, Macromolecules, 1992, 25, 1912–1916 CrossRef CAS
.
- B. J. Cherayil, J. F. Douglas and K. F. Freed, Effect of residual interactions on polymer properties near the theta point, J. Chem. Phys., 1985, 83, 5293–5310 CrossRef CAS
.
- B. J. Cherayil, J. F. Douglas and K. F. Freed, Effect of residual interactions on polymer properties near the theta point. II. Higher moments and comparison with Monte Carlo calculations, J. Chem. Phys., 1987, 87, 3089–3098 CrossRef CAS
.
- S. Y. Reigh and D. Y. Yoon, Concentration dependence of ring polymer conformations from Monte Carlo simulations, ACS Maro Lett., 2013, 2, 296–300 CrossRef CAS PubMed
.
- A. J. Moreno, F. L. Verso, A. Arbe, J. A. Pomposo and J. Colmenero, Concentrated solutions of single-chain nanoparticles: A simple model for intrinsically disordered proteins under crowding conditions, J. Phys. Chem. Lett., 2016, 7, 838–844 CrossRef CAS PubMed
.
-
P. J. Flory, Statistical Mechanics of Chain Molecules, Interscience, New York, 1969 Search PubMed
.
- K. F. Freed and S. F. Edwards, Polymer viscosity in concentrated solutions, J. Chem. Phys., 1974, 61, 3626–3633 CrossRef CAS
.
- M. Daoud, J. P. Cotton, B. Farnoux, G. Jannink, G. Sarma and H. Benoit,
et al., Solutions of flexible polymers. Neutron experiments and interpretation, Macromolecules, 1975, 8, 804–818 CrossRef CAS
.
- S. V. Nikolov, A. Fernandez-Nieves and A. Alexeev, Behavior and mechanics of dense microgel suspensions, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27096–27103 CrossRef CAS PubMed
.
- W. G. McMillan and J. E. Mayer, The statistical thermodynamics of multicomponent systems, J. Chem. Phys., 1945, 13, 276 CrossRef CAS
.
-
J. P. Hansen and I. R. McDonald, Theory of simple liquids, Academic Press, Cambridge, 2006 Search PubMed
.
- T. Aberle and W. Burchard, Universality in behaviour of branched macromolecules in semidilute solutions, Comput. Theor. Polym. Sci., 1997, 7, 215–225 CrossRef CAS
.
- S. Vafaei, B. Tomberli and C. G. Gray, McMillan–Mayer theory of solutions revisited: Simplifications and extensions, J. Chem. Phys., 2014, 141, 154501 CrossRef PubMed
.
- W. Burchard, Particle scattering factors of some branched polymers, Macromolecules, 1977, 10, 919 CrossRef CAS
.
- P. J. Flory and W. R. Krigbaum, Statistical mechanics of swelling of network structures, J. Chem. Phys., 1950, 18, 1086 CrossRef CAS
.
- W. Gobush, K. Sole and W. H. Stockmayer, Statistical mechanics of random-flight chains. V Excluded volume expansion and second virial coefficient for linear chains of varying shape, J. Chem. Phys., 1974, 60, 12 CrossRef CAS
.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke and J. Allgaier,
et al., Star polymers viewed as ultrasoft colloidal particles, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS
.
- I. Noda, N. Kato, T. Kitano and M. Nagasawa, Thermodynamic properties of moderately concentrated solutions of linear polymers, Macromolecules, 1981, 14, 668–676 CrossRef CAS
.
- T. Yasuda, N. Sakumichi, U. I. Chung and T. Sakai, Universal equation of state describes osmotic pressure throughout gelation process, Phys. Rev. Lett., 2020, 125, 267801 CrossRef CAS PubMed
.
- P. J. Flory, The statistical thermodynamics of multicomponent systems, J. Chem. Phys., 1949, 7, 303 CrossRef
.
- H. A. G. Chermin and J. W. Kennedy, The statistical thermodynamics of multicomponent systems, Macromolecules, 1972, 5, 655–656 CrossRef CAS
.
- J. Batoulis and K. Kremer, Residual 3-body interactions of a θ-polymer, EPL, 1988, 7, 683 CrossRef CAS
.
- S. Huissmann, R. Blaak and C. N. Likos, Star polymers in solvents of varying quality, Macromolecules, 2009, 42, 2806–2816 CrossRef CAS
.
- J. Roovers, Dilute-solution properties of ring polystyrenes, J. Polym. Sci., 1985, 23, 1117–1126 CAS
.
- A. Takano, Y. Kushida, Y. Ohta, K. Masuoka and Y. Matsushita, The second virial coefficients of highly-purified ring polystyrenes in cyclohexane, Polymer, 2009, 50, 1300–1303 CrossRef CAS
.
- J. Roovers and P. M. Toporowski, Synthesis of high molecular weight ring polystyrenes, Macromolecules, 1983, 16, 843–849 CrossRef CAS
.
- N. F. Carnahan and K. E. Starling, Equation of state for nonattracting rigid spheres, J. Chem. Phys., 1969, 51, 635 CrossRef CAS
.
-
P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, 1953 Search PubMed
.
-
K. Mortensen, Structural studies of polymer systems using smallangle neutron scattering, in Advanced functional molecules and polymers processing and spectroscopy, ed. H. Nalwa, Overseas Publishers Association, 2001, pp. 223–269, vol. 2 Search PubMed
.
- F. Horkay and B. Hammouda, Small-angle neutron scattering from typical synthetic and biopolymer solutions, Colloid Polym. Sci., 2008, 286, 611–620 CrossRef CAS
.
-
P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, 1979 Search PubMed
.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids, J. Chem. Phys., 2004, 120, 6197 CrossRef CAS PubMed
.
- N. Gnan, L. Rovigatti, M. Bergman and E. Zaccarelli,
In silico synthesis of microgel particles, Macromolecules, 2017, 50, 8777–8786 CrossRef CAS PubMed
.
- S. Bergmann, O. Wrede, T. Huser and T. Hellweg, Super-resolution optical microscopy resolves network morphology of smart colloidal microgels, Phys. Chem. Chem. Phys., 2018, 20, 5074–5083 RSC
.
- A. J. Moreno and F. L. Verso, Computational investigation of microgels: Synthesis and effect of the microstructure on the deswelling behavior, Soft Matter, 2018, 14, 7083–7096 RSC
.
- A. M. Hecht, F. Horkay, S. Mallam and E. Geissler, Scattering properties of polymer gels at the theta temperature, Macromolecules, 1992, 25, 6915–6920 CrossRef CAS
.
- S. Goossen, A. R. Bras, W. P. A. Wischnewski, M. D. Richter, M. Rubinstein and J. Roovers,
et al., Influence of the solvent quality on ring polymer dimensions, Macromolecules, 2015, 48, 1598–1605 CrossRef CAS PubMed
.
- E. Geissler, A. M. Hecht, F. Horkay and M. Zrinyi, Compressional modulus of swollen polyacrylamide networks, Macromolecules, 1988, 21, 2594–2599 CrossRef CAS
.
- F. Horkay, A. M. Hecht and E. Geissler, The effects of cross-linking on the equation of state of a polymer solution, J. Chem. Phys., 1989, 91, 2706–2711 CrossRef CAS
.
- G. Merkle, W. Burchard, P. Lutz, K. F. Freed and J. Gao, Osmotic pressure of linear, star, and ring polymers in semidilute solution. A comparison between experiment and theory, Macromolecules, 1993, 26, 2736–2742 CrossRef CAS
.
- G. Galinsky and W. Burchard, Starch fractions as examples for nonrandomly branched macromolecules. 2. Behavior in the semidilute region, Macromolecules, 1996, 29, 1498–1506 CrossRef CAS
.
- J. E. Martin, J. Wilcoxon and D. Adolf, Critical exponents for the sol–gel transition, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 1803 CrossRef CAS PubMed
.
- J. A. M. Smit, J. A. P. P. Van Dijk, M. G. Mennen and M. Daoud, Polymer size exponents of branched dextrans, Macromolecules, 1992, 25, 3585–3590 CrossRef CAS
.
- M. Zrinyi and F. Horkay, On the elastic modulus of swollen gels, Polymer, 1987, 28, 1139–1143 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00681b |
| This journal is © The Royal Society of Chemistry 2022 |