 Open Access Article
Open Access ArticleDirect observation of narrow electronic energy band formation in 2D molecular self-assembly†
Jack
Hellerstedt‡
 ab,
Marina
Castelli‡
ab,
Anton
Tadich
c,
Antonija
Grubišić-Čabo
ab,
Marina
Castelli‡
ab,
Anton
Tadich
c,
Antonija
Grubišić-Čabo
 a,
Dhaneesh
Kumar
ab,
Benjamin
Lowe
ab,
Spiro
Gicev
d,
Dionysios
Potamianos
e,
Maximilian
Schnitzenbaumer
e,
Pascal
Scigalla
e,
Simiam
Ghan
f,
Reinhard
Kienberger
e,
Muhammad
Usman
d and
Agustin
Schiffrin
a,
Dhaneesh
Kumar
ab,
Benjamin
Lowe
ab,
Spiro
Gicev
d,
Dionysios
Potamianos
e,
Maximilian
Schnitzenbaumer
e,
Pascal
Scigalla
e,
Simiam
Ghan
f,
Reinhard
Kienberger
e,
Muhammad
Usman
d and
Agustin
Schiffrin
 *ab
*ab
aSchool of Physics and Astronomy, Monash University, Clayton Victoria 3800, Australia. E-mail: agustin.schiffrin@monash.edu
bARC Centre of Excellence in Future Low-Energy Electronics Technologies, Monash University, Clayton Victoria 3800, Australia
cAustralian Synchrotron, 800 Blackburn Road, Clayton Victoria 3168, Australia
dCentre for Quantum Computation and Communication Technology, School of Physics, The University of Melbourne, Parkville Victoria 3010, Australia
ePhysik-Department, Technische Universität München, 85748 Garching, Germany
fChair for Theoretical Chemistry, Catalysis Research Center, Technical University of Munich, Lichtenbergstraße 4, D-85747 Garching, Germany
First published on 17th August 2022
Abstract
Surface-supported molecular overlayers have demonstrated versatility as platforms for fundamental research and a broad range of applications, from atomic-scale quantum phenomena to potential for electronic, optoelectronic and catalytic technologies. Here, we report a structural and electronic characterisation of self-assembled magnesium phthalocyanine (MgPc) mono and bilayers on the Ag(100) surface, via low-temperature scanning tunneling microscopy and spectroscopy, angle-resolved photoelectron spectroscopy (ARPES), density functional theory (DFT) and tight-binding (TB) modeling. These crystalline close-packed molecular overlayers consist of a square lattice with a basis composed of a single, flat-adsorbed MgPc molecule. Remarkably, ARPES measurements at room temperature on the monolayer reveal a momentum-resolved, two-dimensional (2D) electronic energy band, 1.27 eV below the Fermi level, with a width of ∼20 meV. This 2D band results from in-plane hybridization of highest occupied molecular orbitals of adjacent, weakly interacting MgPc's, consistent with our TB model and with DFT-derived nearest-neighbor hopping energies. This work opens the door to quantitative characterisation – as well as control and harnessing – of subtle electronic interactions between molecules in functional organic nanofilms.
1 Introduction
Organic molecular films adsorbed on surfaces have shown remarkable versatility as platforms for fundamental scientific research with potential for applications in nanoelectronic devices,1–4 catalysis,5 and optoelectronics.6,7 It is therefore essential to understand – and ultimately control – the interplay between morphology and electronic structure of such surface-supported molecular systems, from the dilute to many-layer limit.8 For instance, when adsorbed on a metal, the characterisation of such overlayers can shed light on possible interactions that could occur with metal interconnects in prospective electrical input/readout devices based on organic molecules.In particular, metallated tetrapyrrole molecules such as metal-phthalocyanines (M-Pc)9,10 – with their robust and flexible planar π-conjugated ligand coordinated with a central metal atom – allow for versatile on-surface self-assembling into functional ordered 2D superlattices, including crystalline monolayers (ML),11–14 bilayers (2L)15,16 and beyond. Their electronic properties can be tuned by the selection of the metal centre, peripheral functional groups (influencing intermolecular and molecule-surface interactions, and steering the self-assembly) and the underlying substrate.10 These compounds can be used as functional materials for, e.g., catalysis,17 photovoltaics,18 light-emitting devices,19 nanoelectronics20 and sensing.21 A relevant example is magnesium phthalocyanine (MgPc), which is a part of the chlorophyll molecule responsible for photosynthesis in bioorganisms22,23 and has potential for light-harvesting and light-emitting technologies.24,25 The frontier electronic structure of neutral, isolated MgPc consists of a single highest occupied molecular orbital (HOMO) and two degenerate lowest unoccupied molecular orbitals (LUMOs), separated by 1.4 eV; both HOMO and LUMOs have strong dominant contributions from phthalocyanine (Pc) ligand states.26
Here, we focus on the morphology and electronic structure of the MgPc ML and 2L self-assembly on the weakly interacting Ag(100) surface, studied via low-temperature scanning tunneling microscopy (STM) and spectroscopy (STS), non-contact atomic force microscopy (ncAFM) and angle-resolved photoelectron spectroscopy (ARPES), and supported by density functional theory (DFT) and tight-binding (TB) modeling. While MgPc on Ag(100) has been investigated recently by STM, STS and ncAFM in the dilute few-molecule regime,26 ordered mono-to few-layers on this surface have not yet been studied to our knowledge, in particular via ARPES. The latter has allowed for determining the momentum-resolved, near-Fermi, electronic band structure of molecular crystals,27,28 as well as crystalline molecular multilayers29,30 and monolayers adsorbed on metal surfaces.31–34 In these systems composed of non-covalently bonded π-conjugated molecules, direct (e.g., π-stacking) or indirect (e.g., mediated by molecule-surface interactions) intermolecular hybridisation gives rise to significant bandwidths, on the order of 100 meV up to 1 eV. There have been indications of a narrow bandwidth (<20 meV) energy dispersion resulting from direct intermolecular hybridisation in a 2D molecular self-assembly on a weakly interacting metal; however, such narrow band structure has not been clearly resolved nor quantitatively modeled.35 In the case where molecule–molecule interactions can be omitted, ARPES of 2D self-assembled molecular monolayers can retrieve the real-space morphology of molecular orbitals (MOs) via orbital tomography,36–39 also providing information on molecule-surface charge transfer and energy level alignment.40–42
In this work, we resolve, via ARPES measurements at room temperature, the narrow bandwidth (∼20 meV) electronic energy dispersion resulting from in-plane inter-HOMO hybridization within a 2D self-assembled ML of MgPc on Ag(100).
2 Results & discussion
2.1 Morphology of MgPc ML and 2L on Ag(100): STM, ncAFM
MgPc deposited onto Ag(100) held at room temperature forms well-ordered, self-assembled ML molecular films. Fig. 1a and b shows STM topographic images of the saturated ML, with a close-packed arrangement of MgPc. For bias voltages (Vbias) far below the Fermi level (Fig. 1a) MgPc molecules are imaged as cross shapes, characteristic of their gas-phase structure (overlaid ball-and-stick model), with subtle chiral intermolecular features between adjacent isoindole units, similar to previous studies of M-Pc's in the dilute limit.44 For Vbias closer to the Fermi level (Fig. 1b), the appearance of MgPc is altered, with increased intensity at the peripheral isoindole units, and with more pronounced chiral intermolecular features (red dashed ellipse). These chiral intermolecular features hint towards some degree of intermolecular electronic hybridisation.26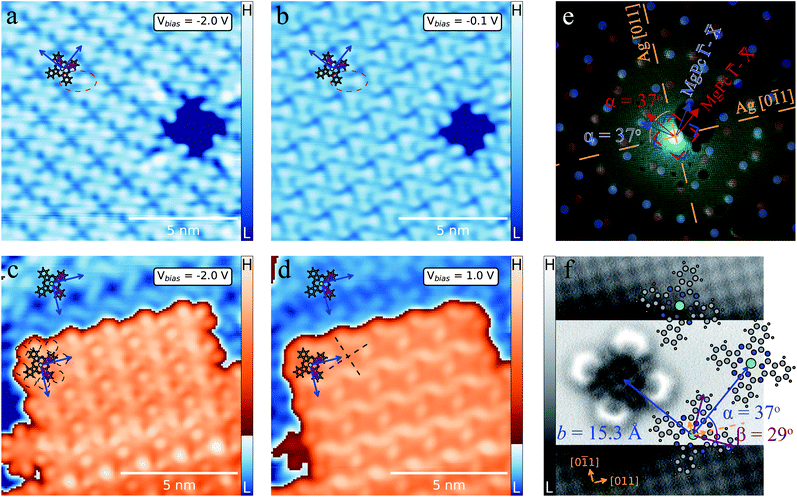 | ||
| Fig. 1 MgPc monolayer (ML) and bilayer (2L) self-assemblies on Ag(100). (a)–(d) STM topographies of ML [It = 100 pA, Vbias = −2 V (a) and Vbias = −0.1 V (b)] and 2L [It = 100 pA, Vbias = −2 V (c) and Vbias = 1 V (d)] with MgPc chemical structure superimposed (grey: carbon; blue: nitrogen; white: hydrogen; green: magnesium). Blue arrows: unit cell vectors b1 and b2 of 2D square molecular lattice (lattice constant: b = ‖b1‖ = ‖b2‖ = 1.53 ± 0.02 nm). Violet arrows: MgPc isoindole axes. (e) LEED pattern (electron energy: 25.5 eV) of MgPc ML. Orange dashed lines: Ag(100) high-symmetry directions. Superimposed blue and red dots correspond to LEEDPat43 simulation for MgPc arrangement within ML, consistent with STM data (with ±37° angle between MgPc self-assembly and Ag(100) high-symmetry directions). Dashed blue and red squares: Brillouin zone boundaries of equivalent, mirror-symmetric MgPc ML configurations. LEED image with no annotation available in Fig. S5 of ESI.† (f) Constant-height ncAFM image of single MgPc, including Ag(100) atomic resolution for MgPc registration [STM setpoint: Vbias = 1.5 mV, It = 10 pA on MgPc; Vbias = 1.5 mV, It = 220 pA on Ag(100)], with superimposed MgPc chemical structure consistent with ML MgPc arrangement given by STM (a) and (b) and LEED (e). MgPc isoindole axes (violet) and MgPc superlattice unit cell vectors (blue) are rotated by 29° and 37°, respectively, relative to Ag(100) unit cell vectors (orange arrows). | ||
When increasing the amount of molecules deposited on the surface at room temperature, a second crystalline layer (2L) of close-packed MgPc adheres to the ML, as shown in Fig. 1c and d. We estimated that the room temperature sticking coefficient on the ML is ∼2.5 times smaller than on bare Ag(100). Via Fourier analysis over large-scale STM topographies, we determined that both the ML and 2L consist of a square lattice with a lattice constant b = 1.53 ± 0.02 nm, consistent with previous studies of planar M-Pc self-assemblies.11,45 Our STM imaging reveals the molecules in the 2L have their symmetry axes (defined by opposite isoindole units; violet arrows in Fig. 1) rotated by ∼5° with respect to those in the ML.
Similar to Fig. 1a, ML MgPc's appear as chiral crosses (we attribute the significant differences in ML MgPc imaging between Fig. 1a and c to a different STM tip). STM imaging of the 2L MgPc's is qualitatively different, with a double lobe structure at the end of each isoindole unit (black dashed circles, Fig. 1c), reminiscent of the HOMO morphology of other M-Pc's adsorbed on insulating layers.46 At positive Vbias = 1 V (Fig. 1d), 2L molecules are imaged with significant apparent height at the Pc ring periphery, with an apparent depression at their Mg centre, and with two orthogonal nodal planes along the isoindole–isoindole axes (black dashed lines in Fig. 1d). Similar STM topographies [e.g., measured on a decoupling layer,46 and on Ag(100) for dilute MgPc's26] have been attributed to the doubly degenerate LUMOs of neutral gas-phase M-Pc's. This is again qualitatively different from Vbias = 1 V imaging of MgPc in the ML. From these variations in bias-dependent STM imaging, we infer that the electronic properties of ML and 2L differ qualitatively, indicating some degree of interactions between MgPc and Ag(100) for the ML, consistent with the dilute case.26
Low-energy electron diffraction (LEED) characterization of the ML (Fig. 1e) revealed the orientation of the MgPc ML superlattice relative to the underlying Ag(100) surface, with two mirror-symmetric ML configurations (red and blue markers, determined using LEEDPat43) with square unit cell vectors rotated by α = ±37° with respect to the Ag(100) high-symmetry orientations. The real-space ML MgPc arrangement corresponding to this LEED pattern is shown in the overlaid ball-and-stick chemical structure in Fig. 1f, consistent with STM imaging in Fig. 1a–d. The ratio between the Ag(100) and MgPc ML lattice constants, 0.189 ± 0.013, determined from STM measurements, agrees reasonably with the value 0.2 inferred from LEED measurements and corresponding LEEDPat simulation in Fig. 1e. Via atomically and sub-molecularly resolved ncAFM imaging (tip functionalised with carbon monoxide molecule; see Methods), we determined the atomic registration of a single MgPc with respect to the Ag(100) lattice (Fig. 1f), with the MgPc isoindole–isoindole axes (violet arrows) rotated by 29° relative to the Ag(100) unit cell vectors. This orientation of single MgPc relative to Ag(100) is the same as in the ML (as inferred from the combination of single MgPc STM, and ML STM and LEED), and is consistent with previous studies of M-Pc's on Ag(100).45,47 From these STM, LEED and ncAFM data, we can express MgPc ML unit cell vectors b1 and b2 relative to Ag(100) unit cell vectors a1 and a2:
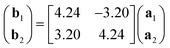 | (1) |
2.2 Electronic structure: STS, photoelectron spectroscopy (PES)
To gain insight into the electronic properties of MgPc ML and 2L, we performed dI/dV STS and ARPES measurements (Fig. 2; see Methods). The dI/dV spectrum (normalised by I/V) acquired at a peripheral isoindole site of an isolated molecule (for reference; Fig. 2a) shows two main features at −1.4 V and −0.1 V, associated with the HOMO and LUMOs, respectively (i.e., here the LUMOs are populated due to substrate-to-molecule electron transfer26,44). The normalised dI/dV spectrum recorded on an equivalent Pc ligand site for the ML shows similar electronic features at similar energies (indicated by vertical solid grey lines in Fig. 2a).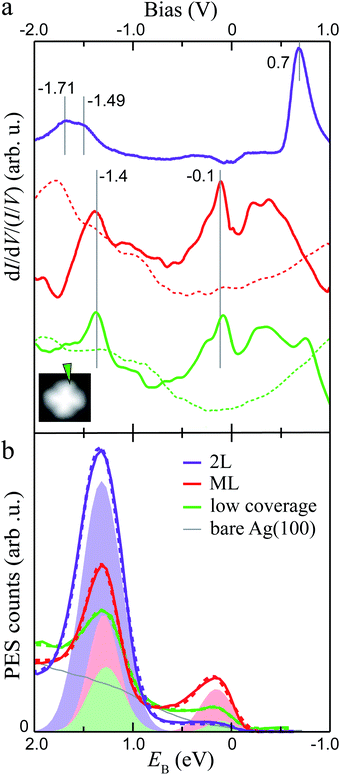 | ||
Fig. 2 Electronic structure of dilute, ML and 2L MgPc coverages on Ag(100). (a) Normalised dI/dV/(I/V) STS spectra acquired at peripheral isoindole site, for isolated molecule (green; setpoint: It = 3 nA, Vbias = −2 V), ML (red; It = 1 nA, Vbias = 1 V), and 2L (purple; It = 100 pA, Vbias = 1.5 V). Spectra for isolated MgPc and ML were subtracted by bare Ag(100) reference (dashed curves). Inset: STM image (It = 10 pA, Vbias = −2 V) of isolated MgPc with spectroscopy location indicated by arrow. ML and 2L spectra were acquired at equivalent locations. (b) Momentum-integrated photoelectron spectra (PES; solid curves) as a function of binding energy EB for coverages indicated in legend. Angle-resolved PES (ARPES) spectra were acquired for in-plane wavevectors k‖ along [011] (![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ) direction of Ag(100), and integrated for ‖k‖‖ ∈ [1.35, 1.85] Å−1. Each spectrum was rescaled by an arbitrary factor to make them directly visible and comparable with each other. Integrated PES curves were fitted (dashed curves) with a Shirley background48 and Gaussian peaks (shaded areas: one for 2L, two for low coverage and ML) to account for MgPc HOMO and populated LUMOs. ) direction of Ag(100), and integrated for ‖k‖‖ ∈ [1.35, 1.85] Å−1. Each spectrum was rescaled by an arbitrary factor to make them directly visible and comparable with each other. Integrated PES curves were fitted (dashed curves) with a Shirley background48 and Gaussian peaks (shaded areas: one for 2L, two for low coverage and ML) to account for MgPc HOMO and populated LUMOs. | ||
For the 2L, the normalised dI/dV spectrum differs significantly, with a broad electronic resonance centred at ∼−1.6 V and a sharp resonance at +0.7 V. The broad feature at negative bias exhibits a double peak structure, one at −1.71 and one at −1.49 V. By comparison to the ML, we attribute the peak closest to the Fermi level to the HOMO (−1.49 eV, consistent with STM topography at negative bias, Fig. 1c), and the peak at −1.71 eV to the HOMO−1.49 We attribute the resonance at +0.7 V to the LUMOs, again consistent with the STM topography (Fig. 1d). Note that this peak associated with the LUMOs has an asymmetric shape, with an elongated tail at higher energies, consistent with vibronic replica, as seen in general for molecules on insulating substrates.50–52 In this 2L case, the first layer acts as a decoupling layer, hindering electron transfer from Ag(100) to second layer molecules, resulting in unoccupied LUMOs above the Fermi level. This is consistent with the lower HOMO energy (in comparison to the sub-ML and ML cases), the latter being indicative of a higher ionization energy and lower hole stabilization energy, arguably due to decreased electronic screening by the (more distant) underlying metal and to the neutral charge state of the second layer MgPc's.
Fig. 2b shows PES spectra for sub-ML, ML and 2L coverages of MgPc, resulting from ARPES measurements [i.e., photoelectron count intensity, I(k‖, EB) = I(kx, ky, EB), as a function of in-plane wavevector k‖ and binding energy EB] integrated for ‖k‖‖ ∈ [1.35, 1.85] Å−1 along the [011] (![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ) direction of the underlying Ag(100). For sub-ML and ML coverages, we fitted these spectra with a Shirley background48 and two Gaussian peaks whose magnitudes increase with MgPc coverage, indicating their molecular origin. The binding energy positions of these peaks are EB ≈ 1.27 and 0.10 eV (sub-ML), and 1.29 and 0.15 eV (ML). For the 2L, the PES spectrum was fitted with a Shirley background and only one Gaussian peak at EB ≈ 1.31 eV, with no observable peak near EB = 0 (i.e., Fermi level). These PES peaks, including the vanishing of the near-Fermi peak for the 2L, are directly comparable to the negative-bias (i.e., occupied states) STS peaks in Fig. 2a. We therefore attribute the high EB PES peak to the MgPc HOMO (observable for coverages between sub-ML to 2L) and the low EB peak (observable from dilute to ML coverages) to the (populated) MgPc LUMOs.
) direction of the underlying Ag(100). For sub-ML and ML coverages, we fitted these spectra with a Shirley background48 and two Gaussian peaks whose magnitudes increase with MgPc coverage, indicating their molecular origin. The binding energy positions of these peaks are EB ≈ 1.27 and 0.10 eV (sub-ML), and 1.29 and 0.15 eV (ML). For the 2L, the PES spectrum was fitted with a Shirley background and only one Gaussian peak at EB ≈ 1.31 eV, with no observable peak near EB = 0 (i.e., Fermi level). These PES peaks, including the vanishing of the near-Fermi peak for the 2L, are directly comparable to the negative-bias (i.e., occupied states) STS peaks in Fig. 2a. We therefore attribute the high EB PES peak to the MgPc HOMO (observable for coverages between sub-ML to 2L) and the low EB peak (observable from dilute to ML coverages) to the (populated) MgPc LUMOs.
We speculate that the differences in assignment of the HOMO position of the 2L could be due to the larger sampling area and sampling depth of the photoelectron experiment compared to the STS measurement. It is likely that ML areas contribute to the signal, as well as the 1st layer of the 2L due to the sampling depth. These contributions would shift the overall signal to lower binding energy, as observed here. These differences between PES and STS are comparable to other previously reported results.53–56
2.3 Electronic structure: ARPES constant binding energy (CBE) maps
Having assigned the near-Fermi and high-EB PES features in Fig. 2 to MgPc populated LUMOs (sub-ML to ML cases) and HOMO (sub-ML to 2L), respectively, we acquired ARPES constant binding energy (CBE) maps, I(kx, ky, EB = const), for EB = 0.1 (related to the ML populated LUMOs) and 1.2 eV (related to the ML and 2L HOMO) [Fig. 3; see ESI Fig. S1† for clean Ag(100)].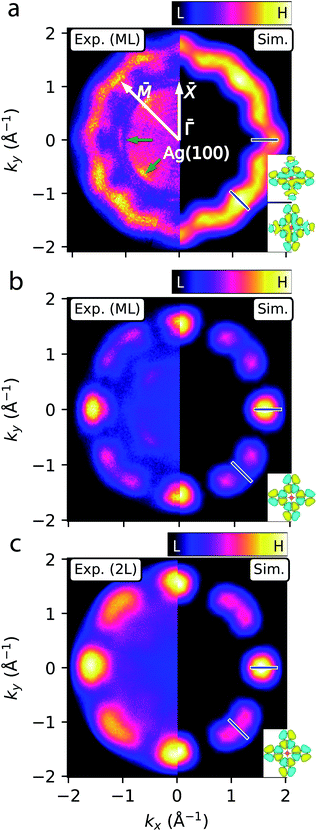 | ||
| Fig. 3 ARPES constant binding energy (CBE) maps of MgPc ML and 2L on Ag(100). (a)–(c) Experimental (kx < 0) and simulated (kx > 0) CBE maps of ML at EB = 0.1 eV [LUMO; (a)], and of ML (b) and 2L (c) at EB = 1.2 eV (HOMO). Experimental CBE maps correspond to integration within ∼0.15 eV-window around chosen binding energy. White arrows indicate Ag(100) high symmetry directions. Green arrows indicate Ag sp-band features.57,58 Blue bars denote wavevectors k‖ considered in subsequent fit analysis (Fig. 4). Insets: DFT-calculated gas-phase LUMOs (a) and HOMO (b) and (c) isosurfaces (charge density 5 × 10−3 Å−3; cyan/yellow: positive/negative wavefunction) used for simulations. | ||
The CBE map for the ML at EB = 0.1 eV (left of Fig. 3a, corresponding to the populated LUMOs) shows a wavy ring with a reciprocal space radius of ∼1.7 Å−1, with 12 oscillations and 4-fold rotational symmetry, consistent with the symmetry of the system. This CBE map is comparable to previous studies of FePc on Ag(100).11 The wavy ring is not observed for the CBE map of bare Ag(100) at the same energy (ESI Fig. S1†); it is related to electronic states of the MgPc self-assembly, with the mean ‖k‖‖ radius associated with the characteristic real-space separation between MgPc orbital lobes.34 We simulated this CBE map59 by using the DFT-calculated gas-phase MgPc LUMOs (Fig. 3a, right side), and by accounting for the 4-fold rotational symmetry of the system and for the ∼29° angle (based on our ncAFM measurements, Fig. 1f) between MgPc isoindole–isoindole and Ag(100) crystalline axes. The subtle experimental features at ‖k‖‖ ≈ 1 Å−1 (green arrows in Fig. 3a) are given by the highly dispersive57,58 Ag sp-bands (ESI Fig. S1†). The experimental CBE map of the ML at the HOMO binding energy (EB = 1.2 eV) is shown in Fig. 3b (left). This map is characterised by 4-fold rotationally symmetric lobes located along the Ag(100) ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) axes, each surrounded by two features of lesser intensity. Similarly to the case of the LUMOs, we simulated this CBE map (right) by using the DFT-calculated gas-phase MgPc HOMO. The strong qualitative agreement between simulations and experimental observations confirms that the STS and PES near-Fermi and large-EB features (Fig. 2) of the ML are related, respectively, to the populated MgPc LUMOs and HOMO. This agreement also indicates that the morphology of these MOs remain relatively unperturbed by the adsorption on Ag(100). For the 2L (Fig. 3c), the experimental HOMO-related CBE map (left) is reproduced by reducing the angle between MgPc isoindole–isoindole and Ag(100) axes to 26.5°, reasonably consistent with STM observations (∼24°, Fig. 1).
axes, each surrounded by two features of lesser intensity. Similarly to the case of the LUMOs, we simulated this CBE map (right) by using the DFT-calculated gas-phase MgPc HOMO. The strong qualitative agreement between simulations and experimental observations confirms that the STS and PES near-Fermi and large-EB features (Fig. 2) of the ML are related, respectively, to the populated MgPc LUMOs and HOMO. This agreement also indicates that the morphology of these MOs remain relatively unperturbed by the adsorption on Ag(100). For the 2L (Fig. 3c), the experimental HOMO-related CBE map (left) is reproduced by reducing the angle between MgPc isoindole–isoindole and Ag(100) axes to 26.5°, reasonably consistent with STM observations (∼24°, Fig. 1).
2.4 Electronic structure: ARPES energy distribution curves (EDCs)
We further acquired ARPES energy distribution curves (EDCs) to investigate possible electronic intermolecular interactions26,31,33,35 affecting the electronic properties of the MgPc film, as suggested by Fig. 1. Fig. 4a and b shows ARPES intensity, I(EB, k‖), as a function of EB, for k‖ along the Ag(100)![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and
and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) orientations, for the ML. These ARPES maps include remnants of the Ag sp-band (green arrows, corresponding to those in Fig. 3a); see ESI Fig. S2† for EDCs of bare Ag(100). In addition to these substrate sp-band features, we observe a diffuse background, as well as broad features at EB ≈ 0 and 1.2 eV throughout the k‖-range. The latter (in particular for ‖k‖‖ ∈ [∼1.3, ∼1.9] Å−1; white boxes in Fig. 4a and b) are related to the CBE maps in Fig. 3, and are attributed to the MgPc populated LUMOs and HOMO, respectively.
orientations, for the ML. These ARPES maps include remnants of the Ag sp-band (green arrows, corresponding to those in Fig. 3a); see ESI Fig. S2† for EDCs of bare Ag(100). In addition to these substrate sp-band features, we observe a diffuse background, as well as broad features at EB ≈ 0 and 1.2 eV throughout the k‖-range. The latter (in particular for ‖k‖‖ ∈ [∼1.3, ∼1.9] Å−1; white boxes in Fig. 4a and b) are related to the CBE maps in Fig. 3, and are attributed to the MgPc populated LUMOs and HOMO, respectively.
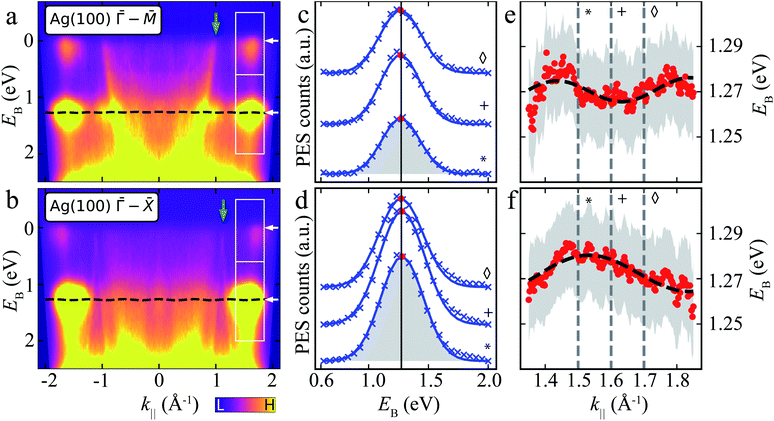 | ||
Fig. 4 ARPES energy distribution curves (EDCs) of MgPc ML on Ag(100). (a) and (b) ARPES signal intensity, I(EB, k‖), for k‖ along Ag(100) ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) (a) and (a) and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (b) orientations. White boxes: k‖ and EB ranges related to LUMOs (upper) and HOMO (lower). White arrows indicate average EB-positions of LUMO and HOMO features. Green arrows: Ag sp-band features (related to green arrows in Fig. 3a). Black dashed line: tight-binding HOMO-related energy dispersion for full k‖-range [using same fitted parameters as in (e) and (f)]. Data symmetrized with respect to k‖ = 0 due to non-normal incidence of UV beam, i.e., I(EB, k‖) = I(EB, −k‖) (see Methods). (c) and (d) ARPES intensity, I(EB, k‖), as a function of EB for different k‖ [related to HOMO; lower boxes in (a) and (b)] along Ag(100) (b) orientations. White boxes: k‖ and EB ranges related to LUMOs (upper) and HOMO (lower). White arrows indicate average EB-positions of LUMO and HOMO features. Green arrows: Ag sp-band features (related to green arrows in Fig. 3a). Black dashed line: tight-binding HOMO-related energy dispersion for full k‖-range [using same fitted parameters as in (e) and (f)]. Data symmetrized with respect to k‖ = 0 due to non-normal incidence of UV beam, i.e., I(EB, k‖) = I(EB, −k‖) (see Methods). (c) and (d) ARPES intensity, I(EB, k‖), as a function of EB for different k‖ [related to HOMO; lower boxes in (a) and (b)] along Ag(100) ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) (c) and (c) and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (d) orientations. Curves offset for clarity. Blue crosses: experimental data (Shirley background subtracted); blue curves: single Gaussian peak fit (shaded grey area); red dots: fit Gaussian peak energy positions; black vertical line: average Gaussian peak energy position. Symbols match curves to k‖ values indicated by grey vertical dashed lines in (e) and (f). (e) and (f) Energy positions of HOMO-related fit Gaussian peak as a function of k‖ along Ag(100) (d) orientations. Curves offset for clarity. Blue crosses: experimental data (Shirley background subtracted); blue curves: single Gaussian peak fit (shaded grey area); red dots: fit Gaussian peak energy positions; black vertical line: average Gaussian peak energy position. Symbols match curves to k‖ values indicated by grey vertical dashed lines in (e) and (f). (e) and (f) Energy positions of HOMO-related fit Gaussian peak as a function of k‖ along Ag(100) ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) (e) and (e) and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (f) orientations (red dots). Grey shaded regions: standard error of Gaussian peak fit energy position plus kBT (T = 293 K, accounting for room temperature thermal broadening). Dashed black curve: fit resulting from single-band tight-binding model. Note that the room temperature thermal broadening does not affect the energy position of the HOMO-related peaks in (c) and (d), and hence has no influence on the single-band tight-binding model fitting. See ESI Fig. S4† for data related to LUMOs. (f) orientations (red dots). Grey shaded regions: standard error of Gaussian peak fit energy position plus kBT (T = 293 K, accounting for room temperature thermal broadening). Dashed black curve: fit resulting from single-band tight-binding model. Note that the room temperature thermal broadening does not affect the energy position of the HOMO-related peaks in (c) and (d), and hence has no influence on the single-band tight-binding model fitting. See ESI Fig. S4† for data related to LUMOs. | ||
We fit I(EB, k‖) for EB ∈ [∼0.6, ∼2] eV related to the HOMO, for k‖ ∈ [∼1.3, ∼1.9] Å−1 (Fig. 4c and d; see ESI Fig. S4† for data related to LUMO) with a single Gaussian peak and a Shirley background.48 Here, we focus on a specific k‖ range, since the data for smaller k‖ are dominated by the remnant Ag(100) features (which include Umklapp scattering of the sp-band by the MgPc layer).13,60,61 The fit Gaussian full-width-at-half-maximum is ∼401 ± 6 meV (resulting from the combination of instrument energy resolution, molecule–substrate hybridization and thermally excited vibrational modes), consistent with comparable studies of noble-metal-supported molecular layers,11,62,63 and in contrast to narrower MO peaks observed on, e.g., graphite.64
At first sight, the EB position of the HOMO Gaussian peak (red dots) does not seem to vary significantly with k‖, with an average EB = 1.27 eV. However, a more careful look suggests a subtle EB position variation of this HOMO peak with k‖ (Fig. 4e and f).
To address whether this HOMO EB position variation is physical, we considered a single site (single band) nearest-neighbour tight-binding model (TB) for the MgPc ML square lattice (Fig. 1), where we assumed that intermolecular hybridization leads to dispersion of the HOMO eigenenergy:
| E(kx, ky) = E0 + 2t[cos(kx·b) + cos(ky·b)]. | (2) |
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) (Fig. 4e) and
(Fig. 4e) and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (Fig. 4f) directions with E(kx, ky) in Eqn (2). We considered variables kx and ky in the reference frame of the MgPc ML lattice [which is rotated with respect to the Ag(100) high-symmetry directions; Fig. 1], with fitting parameters t, b, and angle α between MgPc ML and Ag(100) unit cell vectors. We constrained t to be identical, and α to have a maximum variation of ±5°, for E(kx, ky) along both the Ag(100)
(Fig. 4f) directions with E(kx, ky) in Eqn (2). We considered variables kx and ky in the reference frame of the MgPc ML lattice [which is rotated with respect to the Ag(100) high-symmetry directions; Fig. 1], with fitting parameters t, b, and angle α between MgPc ML and Ag(100) unit cell vectors. We constrained t to be identical, and α to have a maximum variation of ±5°, for E(kx, ky) along both the Ag(100) ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and
and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) directions; we did not constrain b for E(kx, ky) along these two directions (Fig. 4e and f). For
directions; we did not constrain b for E(kx, ky) along these two directions (Fig. 4e and f). For ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) (
(![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) , respectively), we obtained a best fit for t = −2.5 ± 0.2 meV, b = 15.46 (14.48) ± 0.05 Å and α = 39° (43°) ± 2°. These structural values are in very good agreement with the LEED and scanning probe microscopy (SPM) analysis in Fig. 1, which yielded b = 15.3 Å and α = 37°. The fit value t = −2.5 ± 0.2 meV corresponds to a bandwidth BW = 8|t| = 20 ± 1.6 meV.
, respectively), we obtained a best fit for t = −2.5 ± 0.2 meV, b = 15.46 (14.48) ± 0.05 Å and α = 39° (43°) ± 2°. These structural values are in very good agreement with the LEED and scanning probe microscopy (SPM) analysis in Fig. 1, which yielded b = 15.3 Å and α = 37°. The fit value t = −2.5 ± 0.2 meV corresponds to a bandwidth BW = 8|t| = 20 ± 1.6 meV.
In particular, the fact that this fit yields, for both Ag(100) directions ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and
and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) , values of b and α that are very close to those measured experimentally, validates the simple nearest-neighbor TB picture, and compellingly demonstrates that the small dispersion of EB observed in Fig. 4 as a function of k‖ is physical and results from inter-HOMO hybridisation.
, values of b and α that are very close to those measured experimentally, validates the simple nearest-neighbor TB picture, and compellingly demonstrates that the small dispersion of EB observed in Fig. 4 as a function of k‖ is physical and results from inter-HOMO hybridisation.
If we consider the DFT-calculated gas-phase HOMO (inset Fig. 3b), the MgPc ML structural properties determined by SPM/LEED measurements (Fig. 1), and an effective Coulomb interaction26 Hamiltonian 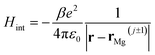 between two nearest-neighbor MgPc's in the ML (where β ≈ 5.9 is a unitless constant that determines the strength of the interaction and rMg(j±1) is the position vector of the nearest-neighbor MgPc), the calculated value for t is ∼10−5 eV. The calculated value of t (for the DFT-calculated gas-phase HOMO) becomes substantial, on the order of a few meV's (i.e., consistent with experiment), when the ML lattice constant is reduced by ∼2 Å (i.e., by ∼10%). Based on a previous study,26 this can be explained by electronic hybridization between MgPc and underlying metal, which can lead to the spatial extension of ΨHOMO(r): this spatially extended ΨHOMO(r) increases inter-HOMO overlap, resulting in an observed t ≈ 2.5 meV which is two orders of magnitude larger than that calculated for the DFT-derived gas-phase HOMO (∼10−5 eV).
between two nearest-neighbor MgPc's in the ML (where β ≈ 5.9 is a unitless constant that determines the strength of the interaction and rMg(j±1) is the position vector of the nearest-neighbor MgPc), the calculated value for t is ∼10−5 eV. The calculated value of t (for the DFT-calculated gas-phase HOMO) becomes substantial, on the order of a few meV's (i.e., consistent with experiment), when the ML lattice constant is reduced by ∼2 Å (i.e., by ∼10%). Based on a previous study,26 this can be explained by electronic hybridization between MgPc and underlying metal, which can lead to the spatial extension of ΨHOMO(r): this spatially extended ΨHOMO(r) increases inter-HOMO overlap, resulting in an observed t ≈ 2.5 meV which is two orders of magnitude larger than that calculated for the DFT-derived gas-phase HOMO (∼10−5 eV).
The CBE maps and corresponding simulations (Fig. 3) provide a precise way of determining the MgPc adsorption orientation relative to the underlying Ag(100) substrate (significantly more precisely than by SPM), and corroborate the attribution of STS features in Fig. 2a the HOMO and LUMOs.26 These simulations, based on gas-phase DFT-calculated MOs, show that the HOMO and LUMO morphologies remain (at least qualitatively) relatively unaltered by the adsorption, and similar between ML and 2L. The latter suggests weaker intermolecular interactions36,37 compared to instances involving stronger (direct) molecule–molecule (e.g., via π-stacking27,28) or (indirect) molecule–substrate–molecule hybridization.31,33,34,66 These latter cases31–34,53,63,66–69 involve frontier MOs and bandwidths BW ≈ 100 meV and above. Conversely, our results here on the MgPc ML show that subtle in-plane intermolecular hybridization occurs between fully occupied HOMOs, which interact non-covalently and lie well below the Fermi level and the frontier populated LUMOs. The observation of the resulting, narrow-BW, k-dependent energy dispersion is enabled by the non-degeneracy of the HOMO (well isolated in energy from other MOs), and by the k-resolution capability of ARPES, even with experimental energy resolutions and kBT similar to or larger than BW. In contrast, we claim that the detection of such narrow band by STS (Fig. 2b) is hindered by the k-integration and HOMO energy broadening due to hybridization between molecule and metal surface.
We acquired ARPES data similar to Fig. 4 for the MgPc 2L (ESI Fig. S3†). Fitting of the 2L EDCs with Eqn (2) yielded, for ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) (
(![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) , respectively), t = −5.2 ± 0.2 meV (corresponding to bandwidth 40 meV), b = 15.18 (16.0) ± 0.05 Å and α = 33° (28°) ± 2°, again consistent with the experimental structural data (Fig. 1). That is, the bandwidth of the HOMO-related energy dispersion for the 2L seems to be twice that for the ML, which could be explained by some degree of interlayer π-stacking.
, respectively), t = −5.2 ± 0.2 meV (corresponding to bandwidth 40 meV), b = 15.18 (16.0) ± 0.05 Å and α = 33° (28°) ± 2°, again consistent with the experimental structural data (Fig. 1). That is, the bandwidth of the HOMO-related energy dispersion for the 2L seems to be twice that for the ML, which could be explained by some degree of interlayer π-stacking.
An interpretation of the LUMO-related near-Fermi features in the ARPES EDCs (Fig. 4a and b) based on the simple TB model is hampered by the LUMO two-fold degeneracy,26 which would arguably give rise to two narrow bands within an energy window significantly smaller than the energy resolution of our ARPES measurements (Methods). See ESI† for more details. Resolving such LUMO-related energy dispersions would require a significantly better energy resolution (e.g., low-temperature ARPES).
3 Conclusions
We have directly observed and quantitatively characterised the formation of a narrow electronic energy band in a 2D molecular self-assembly on a metal, MgPc on Ag(100), with a bandwidth of ∼20 meV for the ML and ∼40 meV for the 2L. This subtle energy dispersion is the result of weak in-plane intermolecular hybridization between filled MOs, lying >1 eV below the Fermi level, which interact non-covalently. These weak intermolecular interactions don't significantly perturb the morphology of these MOs (Fig. 3), while still giving rise to a well-defined (albeit narrow) energy dispersion. Remarkably, our room temperature ARPES measurements (supported by structural LEED and low-temperature SPM characterisation) are able to resolve (in k-space) such narrow energy dispersion, despite a bandwidth that is significantly smaller than the effective ARPES energy resolution; this is enabled by the wavevector sensitivity of ARPES. Our work confirms the involvement of the underlying metal surface in the intermolecular interactions and electronic hybridization, enhancing the latter in this case via molecule-surface hybridization.26 Our results highlight an intermediate regime in intermolecular and molecule-surface hybridization, bonding and band structure formation, with characteristic energy scales of ∼10 meV, between the extremes of, on the one hand, conventional covalent or strong non-covalent (e.g. hydrogen-70) bonding (∼0.1–1 eV), and, on the other hand, isolated non-interacting molecules. Our study offers pathways for band structure engineering in organic nanomaterials, with tuning of intermolecular hybridisation via tailoring of molecular functional groups, size and symmetries, and via choice of supporting substrates.4 Experimental & theoretical methods
4.1 Sample preparation
For all measurements, MgPc molecules (Sigma Aldrich) were deposited in ultrahigh vacuum (UHV) from the gas phase (sublimation temperature: 340 °C) onto a clean Ag(100) surface (Mateck GmbH) maintained at room temperature. The Ag(100) was prepared by repeated cycles of Ar+ sputtering and annealing (450 °C). Base pressure was below ∼3 × 10−9 mbar during molecular depositions.4.2 Scanning probe microscopy (SPM)
Scanning tunneling microscopy (STM) and dI/dV spectroscopy (STS), and non-contact atomic force microscopy (ncAFM) were performed using a Createc LT-STM system, at base temperature 4.6 K in UHV (∼1 × 10−10 mbar) with an Ag-terminated Pt/Ir tip. Topographic STM images were acquired in constant-current mode. dI/dV STS spectra were obtained by averaging multiple I(V) curves and subsequent numerical derivation; spectra were normalised by (I/V) to minimise tunneling transmission effects and emphasise spectroscopic features far away from the Fermi level.71,72 The ncAFM measurements were performed73 with the Pt/Ir tip functionalized with a carbon monoxide (CO) molecule at its apex. Such tip functionalisation was achieved by dosing CO gas into the UHV chamber (∼5 × 10−8 mbar for ∼10 s) with the Ag(100) temperature <10 K, placing the tip above a CO molecule on bare Ag(100) surface with a bias voltage of 3 mV, and approaching the tip toward the surface (feedback off) until the tunneling current reaches ∼5 nA and then decreases suddenly due to a CO molecule being picked-up. After CO functionalization, ncAFM frequency-shift mapping was done with a qPlus tuning fork in frequency modulation mode (f0 ≈ 29 kHz, Q ≈ 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, K ≈ 1.8 kN m−1, 50 pm oscillation amplitude). Atomic registration of MgPc (Fig. 1f) was achieved by changing the tip-sample distance during the ncAFM scan to resolve both surface atoms and molecule features. No post-processing filtering was applied to the ncAFM image in Fig. 1f. All reported bias voltages were applied to the sample.
000, K ≈ 1.8 kN m−1, 50 pm oscillation amplitude). Atomic registration of MgPc (Fig. 1f) was achieved by changing the tip-sample distance during the ncAFM scan to resolve both surface atoms and molecule features. No post-processing filtering was applied to the ncAFM image in Fig. 1f. All reported bias voltages were applied to the sample.
4.3 Photoelectron spectroscopy
Photoelectron spectroscopy experiments were performed with a helium lamp photon source (Scienta Omicron VUV5K, Ephoton = 21.22 eV, unpolarized) and a toroidal electron-energy analyzer74 at the Soft X-ray Beamline of the Australian Synchrotron, at room temperature, on sub-ML, ML and 2L MgPc/Ag(100) samples prepared in UHV following the same protocols as for the STM, STS and ncAFM experiments (see above). Structural properties of these samples were checked via low-energy electron diffraction (LEED; Fig. 1e), showing very homogeneous molecular coverages for both ML and 2L samples.The intrinsic energy resolution of the detector was ∼150 meV, resulting from thermal broadening and intrinsic contributions from analyser and photon source. This was established through prior measurement of the Fermi edge width of a clean sputtered gold foil at room temperature. The photon incident angle relative to sample surface normal is ∼45°. The surface normal is always contained in the measurement slit plane; for a given azimuthal orientation of the sample ϕ (with respect to the measurement plane of the analyser), the analyzer simultaneously records emitted photoelectrons over the entire range of polar angles i.e. θ ∈ [−90°, +90°] (see Fig. 1 of Ules et al.34). The UV beam spot on the sample is elongated due to the incidence angle, with a size on the order of ∼1 mm in length. Because of this relatively large and elongated beam spot, and the molecular coverage homogeneity revealed by LEED, we have not proceeded with systematic PES measurements at different sample locations.
The reported k‖ = ‖k‖‖ = ‖kx![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + kyŷ‖ values (kx = k‖
+ kyŷ‖ values (kx = k‖![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ; ky = k‖
ϕ; ky = k‖![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) were calculated using instrument specific packages provided by the beamline. The kinetic energy of the photoelectrons is related to their vacuum wavevector k by:
ϕ) were calculated using instrument specific packages provided by the beamline. The kinetic energy of the photoelectrons is related to their vacuum wavevector k by:
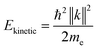 | (3) |
The electron binding energies (with respect to the Fermi energy) EB are related to the measured kinetic energy by the usual relation:
| Ekinetic = hν − EB − φs | (4) |
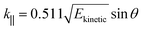 | (5) |
The presented ARPES energy distribution curves (e.g., Fig. 4a and b) are symmetrized with respect to k‖ = 0. That is, the data showed for positive values of k‖ are the same as those showed for negative values of k‖, symmetric with respect to k‖ = 0. This symmetrization compensates for the asymmetric photoemission intensity given by the non-normal incidence of the UV beam, and allows for a better signal-to-noise ratio of our data and for a more reliable fit of these data based on the single-band tight-binding model.
The k‖-integrated photoelectron spectra in Fig. 2b have arbitrary units, with each spectrum rescaled by an arbitrary factor such as to make them directly visible and comparable with each other.
4.4 Density functional theory
Density functional theory (DFT) calculations were performed for gas-phase MgPc using the SIESTA75 simulation tool with periodic boundary conditions, Troullier–Martins norm-conserving pseudopotentials, and the RPBE exchange-correlation76 functional with van der Waals corrections (Grimme's method).77 Kohn–Sham orbitals were represented by a DZP basis set with an energy shift of 0.01 Ry. The total electron charge density was represented on a real space grid corresponding to a mesh cut-off of 300 Ry.4.5 CBE simulations
Analysis of experimental CBE maps (Fig. 3) was done following Puschnig et al.36 These experimental maps were compared with simulations performed with software by Brandstetter et al.59 (Fig. 3), using DFT-calculated gas-phase MgPc orbitals (see above) as inputs, using the ‘toroid’ polarization factor setting, unpolarized light, and the kinetic energies of the respective scans (HOMO: 15.5 eV; LUMO: 16.65 eV; k resolution: 0.03 Å−1). The simulated CBE map for the ML two-fold degenerate LUMOs (Fig. 3a) was obtained by adding the k-maps generated for each LUMO.Author contributions
J. H., M. C., A. L. T., A. G.-C., D. K., B. L., A. S. performed the photoelectron spectroscopy experiments at the Australian Synchrotron. J. H., M. C., D. K., D. P., M. S., P. S. performed the scanned probe microscopy (STM, ncAFM) experiments. S. G. (both), M. U. performed the numerical simulations. R. K., A. S. conceived and developed the research theme. All authors contributed to the interpretation of the data, analysis, and composition of this manuscript.Conflicts of interest
The authors have no conflicts to declare.Acknowledgements
A. S. acknowledges support from the Australian Research Council (ARC) Future Fellowship Scheme (FT150100426) and from the Australia-Germany Joint Research Cooperation Scheme (project “Ultrafast charge dynamics in light-harvesting materials”). M. C. acknowledges support from the Monash Centre of Atomically Thin Materials (MCATM). J. H., M. C., D. K. and B. L. acknowledge the ARC Centre of Excellence in Future Low-Energy Electronics Technologies (FLEET). M. S., P. S. and R. K. acknowledge support from the funding program “Programm Projektbezogener Personenaustausch Australien 2017” (project 57319274, “Ultrafast charge dynamics in light-harvesting materials”). D. P. acknowledges support from the European Union's Horizon 2020 Research and Innovation Program under the Marie Skłodowska-Curie grant agreement no. 641789. The computational resources for this work were provided by the National Computing Infrastructure (NCI) and Pawsey Supercomputing Center through National Computational Merit Allocation Scheme (NCMAS). Part of this research was undertaken on the soft X-ray beamline at the Australian Synchrotron, a part of ANSTO.References
- Y. Q. Wen, Y. L. Song, G. Y. Jiang, D. B. Zhao, K. Ding, W. F. Yuan, X. Lin, H. J. Gao, L. Jiang and D. B. Zhu, Adv. Mater., 2004, 16, 2018–2021 CrossRef CAS.
- Organic Nanomaterials, ed. T. Torres and G. Bottari, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2013 Search PubMed.
- S. Casalini, C. A. Bortolotti, F. Leonardi and F. Biscarini, Chem. Soc. Rev., 2017, 46, 40–71 RSC.
- P. T. Mathew and F. Fang, Engineering, 2018, 4, 760–771 CrossRef CAS.
- I. O. Benítez, B. Bujoli, L. J. Camus, C. M. Lee, F. Odobel and D. R. Talham, J. Am. Chem. Soc., 2002, 124, 4363–4370 CrossRef PubMed.
- H. Hoppe and N. S. Sariciftci, J. Mater. Res., 2004, 19, 1924–1945 CrossRef CAS.
- S. Forrest, IEEE J. Sel. Top. Quantum Electron., 2000, 6, 1072–1083 CAS.
- Molecular Self-Assembly in Nanoscience and Nanotechnology, ed. A. Kilislioğlu and S. Karakuş, InTech, 2017 Search PubMed.
- W. Auwärter, D. Écija, F. Klappenberger and J. V. Barth, Nat. Chem., 2015, 7, 105–120 CrossRef PubMed.
- J. M. Gottfried, Surf. Sci. Rep., 2015, 70, 259–379 CrossRef CAS.
- V. Feyer, M. Graus, P. Nigge, M. Wießner, R. Acres, C. Wiemann, C. Schneider, A. Schöll and F. Reinert, Surf. Sci., 2014, 621, 64–68 CrossRef CAS.
- E. Annese, J. Fujii, I. Vobornik and G. Rossi, J. Phys. Chem. C, 2011, 115, 17409–17416 CrossRef CAS.
- F. C. Bocquet, L. Giovanelli, P. Amsalem, L. Petaccia, D. Topwal, S. Gorovikov, M. Abel, N. Koch, L. Porte, A. Goldoni and J.-M. Themlin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 241407 CrossRef.
- P. Amsalem, L. Giovanelli, J. M. Themlin and T. Angot, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235426 CrossRef.
- Y. Wang, J. Kröger, R. Berndt and W. Hofer, Angew. Chem., Int. Ed., 2009, 48, 1261–1265 CrossRef CAS PubMed.
- T. G. Gopakumar, T. Brumme, J. Kröger, C. Toher, G. Cuniberti and R. Berndt, J. Phys. Chem. C, 2011, 115, 12173–12179 CrossRef CAS.
- A. B. Sorokin, Chem. Rev., 2013, 113, 8152–8191 CrossRef CAS PubMed.
- M. V. Martínez-Díaz, G. de la Torre and T. Torres, Chem. Commun., 2010, 46, 7090 RSC.
- H. Xu, R. Chen, Q. Sun, W. Lai, Q. Su, W. Huang and X. Liu, Chem. Soc. Rev., 2014, 43, 3259–3302 RSC.
- G. de la Torre, C. G. Claessens and T. Torres, Chem. Commun., 2007, 2000–2015 RSC.
- F. I. Bohrer, C. N. Colesniuc, J. Park, M. E. Ruidiaz, I. K. Schuller, A. C. Kummel and W. C. Trogler, J. Am. Chem. Soc., 2009, 131, 478–485 CrossRef CAS PubMed.
- T. Masuda, Photosynth. Res., 2008, 96, 121–143 CrossRef CAS PubMed.
- M.-S. Liao and S. Scheiner, J. Chem. Phys., 2001, 114, 9780–9791 CrossRef CAS.
- N. Peltekis, B. N. Holland, S. Krishnamurthy, I. T. McGovern, N. R. J. Poolton, S. Patel and C. McGuinness, J. Am. Chem. Soc., 2008, 130, 13008–13012 CrossRef CAS PubMed.
- J. Elemans, R. van Hameren, R. Nolte and A. Rowan, Adv. Mater., 2006, 18, 1251–1266 CrossRef CAS.
- M. Castelli, J. Hellerstedt, C. Krull, S. Gicev, L. C. L. Hollenberg, M. Usman and A. Schiffrin, Small, 2021, 17, 2005974 CrossRef CAS PubMed.
- F. Bussolotti, J. Yang, T. Yamaguchi, K. Yonezawa, K. Sato, M. Matsunami, K. Tanaka, Y. Nakayama, H. Ishii, N. Ueno and S. Kera, Nat. Commun., 2017, 8, 173 CrossRef CAS PubMed.
- S.-i. Machida, Y. Nakayama, S. Duhm, Q. Xin, A. Funakoshi, N. Ogawa, S. Kera, N. Ueno and H. Ishii, Phys. Rev. Lett., 2010, 104, 156401 CrossRef PubMed.
- G. Koller, S. Berkebile, M. Oehzelt, P. Puschnig, C. Ambrosch-Draxl, F. P. Netzer and M. G. Ramsey, Science, 2007, 317, 351–355 CrossRef CAS PubMed.
- H. Yamane and N. Kosugi, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 61–67 CrossRef CAS.
- M. Wießner, J. Ziroff, F. Forster, M. Arita, K. Shimada, P. Puschnig, A. Schöll and F. Reinert, Nat. Commun., 2013, 4, 1514 CrossRef PubMed.
- M. G. Betti, P. Gargiani, R. Frisenda, R. Biagi, A. Cossaro, A. Verdini, L. Floreano and C. Mariani, J. Phys. Chem. C, 2010, 114, 21638–21644 CrossRef CAS.
- D. Lüftner, S. Weiß, X. Yang, P. Hurdax, V. Feyer, A. Gottwald, G. Koller, S. Soubatch, P. Puschnig, M. G. Ramsey and F. S. Tautz, Phys. Rev. B, 2017, 96, 125402 CrossRef.
- T. Ules, D. Lüftner, E. M. Reinisch, G. Koller, P. Puschnig and M. G. Ramsey, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155430 CrossRef.
- H. Yamane and N. Kosugi, J. Phys. Chem. C, 2018, 122, 26472–26479 CrossRef CAS.
- P. Puschnig, S. Berkebile, A. J. Fleming, G. Koller, K. Emtsev, T. Seyller, J. D. Riley, C. Ambrosch-Draxl, F. P. Netzer and M. G. Ramsey, Science, 2009, 326, 702–706 CrossRef CAS PubMed.
- V. Feyer, M. Graus, P. Nigge, G. Zamborlini, R. Acres, A. Schöll, F. Reinert and C. Schneider, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 125–131 CrossRef CAS.
- G. Di Santo, T. Miletić, M. Schwendt, Y. Zhou, B. M. Kariuki, K. D. M. Harris, L. Floreano, A. Goldoni, P. Puschnig, L. Petaccia and D. Bonifazi, J. Phys. Chem. C, 2021, 125, 24477–24486 CrossRef CAS PubMed.
- S. Weiß, D. Lüftner, T. Ules, E. M. Reinisch, H. Kaser, A. Gottwald, M. Richter, S. Soubatch, G. Koller, M. G. Ramsey, F. S. Tautz and P. Puschnig, Nat. Commun., 2015, 6, 8287 CrossRef PubMed.
- T. G. Boné, A. Windischbacher, M. S. Sättele, K. Greulich, L. Egger, T. Jauk, F. Lackner, H. F. Bettinger, H. Peisert, T. Chassé, M. G. Ramsey, M. Sterrer, G. Koller and P. Puschnig, J. Phys. Chem. C, 2021, 125, 9129–9137 CrossRef PubMed.
- M. Hollerer, D. Lüftner, P. Hurdax, T. Ules, S. Soubatch, F. S. Tautz, G. Koller, P. Puschnig, M. Sterrer and M. G. Ramsey, ACS Nano, 2017, 11, 6252–6260 CrossRef CAS PubMed.
- X. Yang, L. Egger, J. Fuchsberger, M. Unzog, D. Lüftner, F. Hajek, P. Hurdax, M. Jugovac, G. Zamborlini, V. Feyer, G. Koller, P. Puschnig, F. S. Tautz, M. G. Ramsey and S. Soubatch, J. Phys. Chem. Lett., 2019, 10, 6438–6445 CrossRef CAS PubMed.
- K. E. Hermann and M. A. Van Hove, LEEDPat, 2014, http://www.fhi-berlin.mpg.de/KHsoftware/LEEDpat/index.html Search PubMed.
- A. Mugarza, R. Robles, C. Krull, R. Korytár, N. Lorente and P. Gambardella, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–13 CrossRef.
- A. Mugarza, N. Lorente, P. Ordejón, C. Krull, S. Stepanow, M. L. Bocquet, J. Fraxedas, G. Ceballos and P. Gambardella, Phys. Rev. Lett., 2010, 105, 30–33 CrossRef PubMed.
- C. Uhlmann, I. Swart and J. Repp, Nano Lett., 2013, 13, 777–780 CrossRef CAS PubMed.
- F. Chen, X. Chen, L. Liu, X. Song, S. Liu, J. Liu, H. Ouyang, Y. Cai, X. Liu, H. Pan, J. Zhu and L. Wang, Appl. Phys. Lett., 2012, 100, 081602 CrossRef.
- S. Hüfner, Photoelectron Spectroscopy, Springer, Berlin, Heidelberg, 2003 Search PubMed.
- M. Zhao, F. Almarzouqi, E. Duverger, P. Sonnet, G. Dujardin and A. J. Mayne, Phys. Chem. Chem. Phys., 2018, 20, 19507–19514 RSC.
- X. H. Qiu, G. V. Nazin and W. Ho, Phys. Rev. Lett., 2004, 92, 206102 CrossRef CAS PubMed.
- N. A. Pradhan, N. Liu and W. Ho, J. Phys. Chem. B, 2005, 109, 8513–8518 CrossRef CAS PubMed.
- G. V. Nazin, S. W. Wu and W. Ho, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 8832–8837 CrossRef CAS PubMed.
- H. Yamane, A. Carlier and N. Kosugi, Mater. Chem. Front., 2018, 2, 609–614 RSC.
- L. Gao, W. Ji, Y. B. Hu, Z. H. Cheng, Z. T. Deng, Q. Liu, N. Jiang, X. Lin, W. Guo, S. X. Du, W. A. Hofer, X. C. Xie and H.-J. Gao, Phys. Rev. Lett., 2007, 99, 106402 CrossRef CAS PubMed.
- C. Baldacchini, C. Mariani, M. G. Betti, L. Gavioli, M. Fanetti and M. Sancrotti, Appl. Phys. Lett., 2006, 89, 152119 CrossRef.
- E. Tsiper, Z. Soos, W. Gao and A. Kahn, Chem. Phys. Lett., 2002, 360, 47–52 CrossRef CAS.
- R. Courths, V. Bachelier and S. Hüfner, Solid State Commun., 1981, 38, 887–889 CrossRef CAS.
- E. D. Hansen, T. Miller and T.-C. Chiang, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 1871–1875 CrossRef CAS.
- D. Brandstetter, X. Yang, D. Lüftner, F. S. Tautz and P. Puschnig, Comput. Phys. Commun., 2021, 263, 107905 CrossRef CAS.
- J. Anderson and G. J. Lapeyre, Phys. Rev. Lett., 1976, 36, 376–379 CrossRef CAS.
- L. Giovanelli, F. C. Bocquet, P. Amsalem, H.-L. Lee, M. Abel, S. Clair, M. Koudia, T. Faury, L. Petaccia, D. Topwal, E. Salomon, T. Angot, A. A. Cafolla, N. Koch, L. Porte, A. Goldoni and J.-M. Themlin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035413 CrossRef.
- D. Lüftner, M. Milko, S. Huppmann, M. Scholz, N. Ngyuen, M. Wießner, A. Schöll, F. Reinert and P. Puschnig, J. Electron Spectrosc. Relat. Phenom., 2014, 195, 293–300 CrossRef PubMed.
- F. Evangelista, A. Ruocco, R. Gotter, A. Cossaro, L. Floreano, A. Morgante, F. Crispoldi, M. G. Betti and C. Mariani, J. Chem. Phys., 2009, 131, 174710 CrossRef CAS PubMed.
- S. Kera, H. Yamane, I. Sakuragi, K. K. Okudaira and N. Ueno, Chem. Phys. Lett., 2002, 364, 93–98 CrossRef CAS.
- M. Newville, T. Stensitzki, D. B. Allen and A. Ingargiola, LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python, 2014, https://zenodo.org/record/11813#.YvIe3HZByF4 Search PubMed.
- M. Wießner, J. Kübert, V. Feyer, P. Puschnig, A. Schöll and F. Reinert, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 075437 CrossRef.
- N. Koch, A. Vollmer, I. Salzmann, B. Nickel, H. Weiss and J. P. Rabe, Phys. Rev. Lett., 2006, 96, 156803 CrossRef CAS PubMed.
- H. Yamane and N. Kosugi, Phys. Rev. Lett., 2013, 111, 086602 CrossRef PubMed.
- H. Yamane and N. Kosugi, J. Chem. Phys., 2014, 141, 224701 CrossRef PubMed.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- H. J. Zandvliet and A. van Houselt, Annu. Rev. Anal. Chem., 2009, 2, 37–55 CrossRef CAS PubMed.
- A. Schiffrin, M. Capsoni, G. Farahi, C.-G. Wang, C. Krull, M. Castelli, T. Roussy, K. A. Cochrane, Y. Yin, N. V. Medhekar, M. Fuhrer, A. Q. Shaw, W. Ji and S. A. Burke, ACS Nano, 2018, 12, 6545–6553 CrossRef CAS PubMed.
- L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, Science, 2009, 325, 1110–1114 CrossRef CAS PubMed.
- A. Tadich, J. Riley, E. Huwald, R. Leckey, T. Seyller, L. Ley, R. Garrett, I. Gentle, K. Nugent and S. Wilkins, AIP Conf. Proc., 2010, 943–946 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00385f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |
