Following the crystal growth of anthradithiophenes through atomistic molecular dynamics simulations and graph characterization

Abstract

While organic semiconductors (OSC) offer distinctive features for several electronic and optical technologies, questions remain as to how the chemistries of the molecular building blocks impact material nucleation and growth and the resulting solid-state packing arrangements that are critical to semiconductor performance. Here we demonstrate a combined molecular dynamics (MD) simulation and graph characterization approach to follow the crystallization of anthradithiophene (ADT), a rigid, π-conjugated molecule used in OSC. Notably, ADT presents particular challenges as molecular synthesis leads to two isomeric structures wherein the sulfur atoms are syn or anti with respect to each other. Using our combined approach, we demonstrate how these molecular-scale differences impact the nucleation and growth of crystallites, starting from the gas phase through a condensed liquid (melt) to the solid state. The resulting systems, which are comprised of several crystalline/aggregate regions, are then thermally annealed, with the resulting thermal properties showing good consistency with experiment. The computational framework discussed here provides opportunities for robust and fast examination of the dynamics of the nucleation and growth of crystalline OSC.

---

Design, system, application

Organic semiconductors (OSC) offer distinctive features for several electronic and optical technologies. However, questions remain as to how the chemistries of the molecular building blocks impact material nucleation and growth and the resulting solid-state packing arrangements that are critical to semiconductor performance. In this work we develop and deploy a combined molecular dynamics (MD) simulations and graph characterization approach to examine the crystallization of rigid, π-conjugated molecules. In particular, we study the crystallization of anthradithiophenes, which offer the challenge that the molecular synthesis results in two isomers. We demonstrate that the combined computational approach can distinguish how the modest deviations in molecular structure impact crystallization. While this is an initial demonstration of the combined approach, it is a first step towards the development of high-throughput computational methods to explore crystallization in molecular organic semiconductors.

I. Introduction

The last several decades have witnessed molecular organic semiconductors (OSC) move from academic curiosity to implementation in demonstrative technologies to entering the consumer goods space at a massive scale in the form of organic light-emitting displays (OLED) and radio-frequency identification (RFID) tags.^1–11 While an ultimate goal of OSC is to print the active semiconducting layer,^12–23 this has yet to be realized on large scales due to difficulties in reproducibility and active-layer morphologies that are not conducive to optimal device performance. Hence, current OSC manufacturing relies on chemical vapor deposition, wherein ultra-pure materials are evaporated, transported, and condensed as a thin film on a target surface within a vacuum environment.

There has been a longstanding effort to understand how the molecular chemistry of the OSC building blocks and processing methods impact the nucleation, growth, and order – including designs to either increase or suppress crystallization – of the resulting thin film.^24–37 From a modeling perspective, exploring these connections requires combinations of techniques that cover multiple length and temporal scales, with atomistic and coarse-grained molecular dynamics (MD), kinetic Monte Carlo, and microscopic thermodynamics models being developed for these purposes.^30,38–48 While these modeling investigations are non-trivial, they can provide physically meaningful insight into these processes at experimentally relevant scales.

While the above methods have allowed the community to successfully explore and understand the interplay between nucleation, growth, and order, our ability to simulate increasingly larger systems outstrips the ability to comprehensively analyze the large datasets produced. Specifically, while the capability to simulate MD simulations has increased enormously over the last few decades, approaches to analyze this data have advanced at a slower pace. Framing molecular quantities of interest as graph constructs^49,50 allows leveraging powerful graph algorithms that exhibit excellent computational complexity,⁵¹ scale very well to large systems, and are agnostic to dimensionality and number of components.⁵² Additionally, very efficient implementations of graph algorithms (tailored for various compute architectures) are widely available,⁵³ thus democratizing⁵⁴ the ability to use these constructs for downstream analyses of large datasets, even on desktop computers. Finally, recent work has also shown that a diverse array of atomistic features (representing, for instance, correlations, shape/size/orientation distributions, topology) can be framed as graph features of the 3D data.^55–57

Building on previous investigations of the molecular-scale phase transitions of rigid anthradithiophene (ADT) chromophores upon heating, where our focus was on understanding the effects of molecular structure and chemical substitution on thermally induced phase transitions,⁵⁸ we now endeavor to understand the reverse process, cooling molecular gases and observing the transformation of the ADT morphology as it progresses from gas to condensate to solid. Using a highly parameterized version of the OPLS-AA force field, we undertake fully atomistic MD simulations of the anti (sulfur atoms are on the opposite sides of the π-conjugated backbone) and syn (sulfur atoms are on the same side of the π-conjugated backbone) ADT (Fig. 1), as the varied positions of the sulfur atoms can lead to modified solid-state packings and properties for OSC derived from this core.^58–65 While ADT continue to attract considerable attention as OSC building blocks, we are particularly interested in these systems as their unsubstituted forms pack in the herringbone motif found across the OSC literature, making the study of the nucleation and growth transferable to other systems of interest, and that understanding how the slight variations in molecular chemistry noted above impact nucleation and growth can provide insights to improve chromophore design for controllable materials growth. We model nucleation, crystallization, and morphology differences between synADT and antiADT consistent with experimental observations, and observe the nucleation of ordered domains from within the disordered amorphous phase that ultimately results in a herringbone crystalline morphology. The development and deployment of graph constructs allows fast evaluation and exploration of molecular alignment and grain boundary formation. The methods presented here provide a framework upon which additional simulations can be performed to further explore the dynamics of nucleation and the growth of crystalline phases within organic molecular crystals.

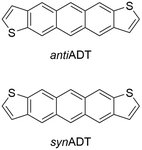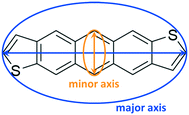
Fig. 1 Chemical structures of the anti- (antiADT) and syn- (synADT) forms of anthradithiophenes (ADT).

II. Computational methods

Force field preparation

All MD simulations were performed with the GROMACS 2016 software suite^66,67 using a highly parameterized version of the OPLS-AA (optimized potentials for liquid simulations – all atom) force field^68,69 for all intra- and intermolecular interaction parameters. As in our previous report, the thiophene force field parameters of Schwarz and co-workers⁷⁰ were used for the bonded interactions. Atom-centered partial charges were calculated using density functional theory (DFT) at the B3LYP/6-31G(d,p) level within the Charge Model 5 (CM5) framework using the Gaussian 16 software suite.⁷¹ We refer interested readers to our previous publication⁵⁸ for more in-depth discussion on force field validation for both single-molecule and bulk simulations. All MD simulations used a leap-frog integrator with 1 fs time step at temperatures above 850 K or 2 fs time step for temperatures below 850 K. For NVT (constant number, N, volume, V, and temperature, T) simulations a velocity rescaling thermostat with a temperature coupling time of 0.1 ps was used. For NPT (constant number, N, pressure, P, and temperature, T) simulations a Parrinello–Rahman barostat with 2.0 ps pressure coupling constant and velocity rescaling thermostat with 0.1 temperature coupling constant were used. An isotropic compressibility of 4.5 × 10⁻⁵ bar was applied. Periodic boundary conditions were applied to all simulations with a spherical cutoff of 1.4 nm for short-range van der Waals (vdW) interactions while long-range electrostatic interactions are treated via particle-mesh Ewald (PME) with 1.4 nm cutoff. The LINCS (LINear Constraint Solver) algorithm was used to constrain intramolecular bonds, angles, and dihedrals in an effort to reduce computation time without sacrificing accuracy.

Initial simulation system generation

Supercells containing either 1600 antiADT or 2000 synADT were created from the bulk crystal structures as reported by Mamada and co-workers.⁷² These systems were equilibrated at a temperature of 113 K and 1 bar of pressure to replicate the conditions at which the experimental crystal structures were obtained. Initial equilibration simulations consisted one NVT and two NPT steps. An initial NPT simulation with a Berendsen⁷³ barostat was used to obtain reasonable atomic velocities before the more physically meaningful Parrinello–Rahman⁷⁴ barostat was applied. After initial equilibration simulated annealing was used to heat the systems from 113 K to 1200 K at a rate of 40 K ns⁻¹ followed by an additional NPT equilibration for 2 ns and NVT equilibration for 10 ns. At this point a well-behaved, disperse molecular gas is obtained that is used as the starting point for all subsequent condensation simulations.

Annealing simulations

Starting with the disperse molecular gas, each simulation box was treated with six additional simulation stages: two cooling, two equilibration, and two re-heating. The initial NPT cooling stage cooled the systems from 1200 K to 850 K at a rate of 10 K ns⁻¹ for 35 ns; a higher rate resulted in system instability. The second NPT cooling stage cooled the systems from 850 K to 300 K at a rate of 20 K ns⁻¹ for 27.5 ns. Both NPT cooling stages used a velocity-rescaling thermostat and Parrinello–Rahman barostat with 0.1 ps and 2.0 ps couplings, respectively.

Upon condensation and following the cooling steps, the simulation boxes were allowed to equilibrate for 10 ns within both NPT and NVT ensembles. The NPT equilibration occurred first to allow for the system pressure and simulation box dimensions to stabilize. NPT equilibration used a Parrinello–Rahman barostat and velocity-rescaling thermostat with reference pressure of 1.0 bar. NVT equilibration used a velocity-rescaling thermostat. Final crystalline packing parameters for distance and angles were taken from various points through each of these equilibration simulations.

Lastly, each simulation box was reheated to determine the impact of crystallite (grain) boundaries and disorder on the simulated melting points. These were run as a mirror of the cooling simulations with the first simulation step an NPT annealing simulation from 300 K to 850 K at a rate of 20 K ns⁻¹. The second step continued the heating within the NPT ensemble from 850 K to 1000 K at a rate of 10 K ns⁻¹. Example GROMACS molecular dynamics parameter (MDP) files and force field parameters are available in the ESI.†

The PLUMED 2.6 plugin was used for part of the crystallinity analysis.^75–77 Two collective variables (CV) were used to define crystallinity descriptor: i) SMAC,⁷⁸ which differentiates solids and liquids based on relative molecular orientation vectors within a given range of intermolecular distance distributions, and ii) CC1, a modified CV by Parrinello and co-workers that accounts for the largest connected cluster through depth first search clustering in addition to the calculated SMAC.⁷⁹ Parameters for defining the CV, including crystal intermolecular distances and vector angles, were determined using the Gromacs_rdf and Plumed INTERMOLECULARANGLES functions.

Graph-based analysis of structural features and ordering

To quantify the evolution of crystallinity and formation of orientated domains, we first recast the 3D molecular information into an equivalent graph. We refer the interested reader to works from Wodo and co-workers^55,56 for a detailed description of the approach. Briefly, each ADT molecule is represented as a node of a graph. Each node is associated with two node features, which encode the major and minor axis along which the ADT molecule is oriented (Fig. 2): The major axis is chosen to be along the long-axis of the molecule, running between (syn-/anti-) the two thiophene rings, while the minor axis is perpendicular to the major axis, running along the short-axis of the molecule. In addition, each node also stores its position in 3D space.

Fig. 2 Pictorial representation of the definitions of the ADT major and minor axes.

To define a graph from the above set of nodes, we construct neighborhoods for each of these nodes. Nodes (or equivalent ADT molecules) that are within a specified distance from each other are assigned to be neighbors. Thus, neighboring nodes are connected with an edge. This data structure of nodes and associated edges constitutes the graph.

The representation of the atomistic data as an equivalent graph enables efficient downstream analysis. Specifically, in this work, we use the graph construct to first find the number of ‘connected components’⁵¹ in the system and how the number (and size) of components vary with time. Appropriately defined connected components of the graph are equivalent to the aggregates that form during crystallization. Further analysis in the context of our system is presented in the Results and discussion. The connected components provide quantitative insights into the initiation and growth of aggregates. For example, we identify initiation sites through initial formation of aggregates. Then, we analyze each aggregate to see (i) how the aggregate grows in time – both in terms of number fraction as well as volume fraction of the total system, and (ii) how crystallinity of each aggregate varies with time. We quantify crystallinity by considering the orientation alignment between adjacent ADT molecules of an aggregate. This orientation alignment is quantified through (i) the angle between the long axis of the two molecules θ, and (ii) the angle between two planes that pass through the two molecules, representing the rotation across molecules ϕ. Identification of aggregates and crystals becomes a trivial exercise by framing it as a graph feature.

III. Results and discussion

Cooling of molecular gas to liquid

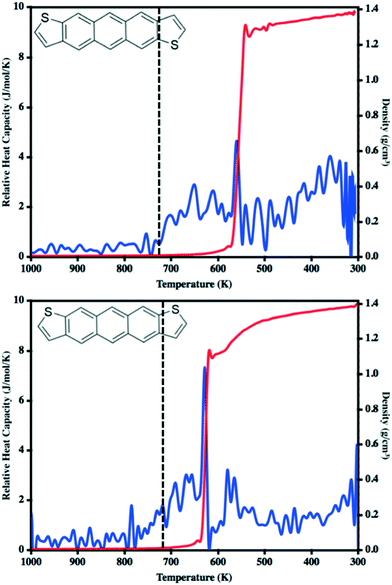
In our previous work to understand the thermal transitions that occur in syn and antiADT,⁵⁸ we performed annealing simulations wherein simulation cells, created from the respective experimental unit cells, were slowly heated and the overall density and heat capacity were captured for each snapshot. Even though the rate of heating that we used was slow from the point-of-view of MD, it is fast compared to what is obtained in experiment. Thus, we observed superheating that resulted in melting points much higher than what was observed in experiment. However, if we introduced vacancies/defects or surfaces (through slab models), wherein additional opportunities for disorder and entropy come into play, we obtained melting points in excellent agreement with experiment at computationally reasonable heating rates. Since our initial goal is to observe the condensation of a disperse molecular gas to a liquid, the issues we previously experienced with nucleation should not be an issue as each molecule may act as a nucleation site. In a manner reverse to that used to model the melting process, we cool an equilibrated molecular gas at an initial rate of 10 K ns⁻¹ before switching to 20 K ns⁻¹ for most of the annealing process.

The relative heat capacity and density of synADT and antiADT are shown in Fig. 3 over the range of 1000 K to 300 K. For both systems there is an initial gradual rise in the heat capacities at approximately 725 K that represents the initial formation of stable aggregates with liquid characteristics. As the systems further cool, there are drastic changes in density and heat capacity at 570 K for antiADT and 640 K for synADT that represent the agglomeration of all ADT globules within the simulation boxes to a single liquid phase. That the formation of the liquid phase does not agree with the experimental melting point is not surprising due to the velocities of each molecule within the simulation box and the need for a collision event to occur within the simulation box for any molecule to stick to another. If the simulation were held at a given temperature below the vaporization temperature for a sufficient length of time, similar behavior would also be observed, although over a much longer simulation time window.

Fig. 3 Relative heat capacity (blue) and simulation box density (red) of antiADT (top) and synADT (bottom) as the system is cooled from 1000 K to 300 K. The experimental melting points of the antiADT (725 K) and synADT (720 K) are highlighted with dashed, black lines.

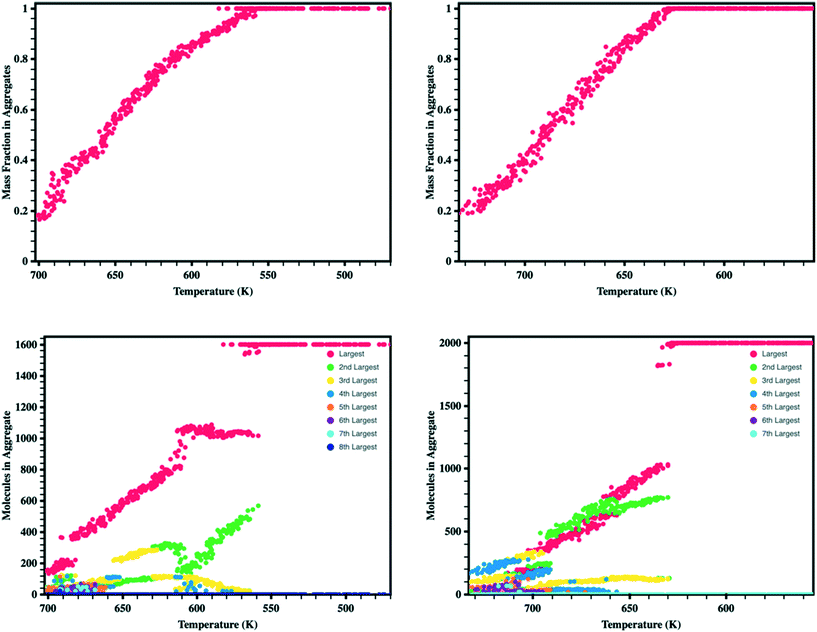
Looking more closely at the behavior of each molecule within the simulation boxes, we extracted the portion of all molecules that are free versus in aggregates (defined as collection of at least four ADT molecules that form a neighborhood, i.e., within a specified distance to each other) as the simulation box is cooled (Fig. 4). We note a linear relationship between the fraction of the total mass in the aggregates and temperature, which is in part associated with the cooling rates used in this work.⁴³ During the initial stages of aggregation, several aggregates are present that interact with free molecules and other aggregates. As the temperature continues to drop, the energy available and, therefore, probability for molecules to remove themselves from an aggregate reduces leading to the formation of larger aggregates.^80–82 Additionally, aggregates begin to interact and combine to form even larger aggregates such that by the time synADT reaches 630 K there is only a single aggregate present, while antiADT takes considerably longer to reach this point at 550 K. Note that these initial aggregates (liquid droplets) do not display internal order and instead represent a fully disordered amorphous phase.

Fig. 4 (Top) Fraction of total simulation mass present within aggregates versus free molecules for antiADT (left) and synADT (right). (Bottom) Total number of molecules within the largest aggregates present within the simulation boxes prior to aggregates coalescing. Note differing X-axis scales for antiADT and synADT due to aggregate formation initiating at different temperatures (Fig. 1).

Liquid to crystalline transition

Upon the initial formation of pre-nucleates there is relatively low order within the condensed phase resulting in a fully amorphous simulation box. However, as the temperature of the simulation further reduces and the internal energy of individual molecules equilibrates, local regions of order begin to develop at various nucleation sites within the amorphous bulk. This behavior is further highlighted in Fig. 5 where the number of molecules present within ordered crystalline aggregates is presented versus simulation temperature; data points are colored by the size of the crystalline aggregate in which they reside. Crystalline order is defined as those molecules whose long axis is aligned to within ±10°.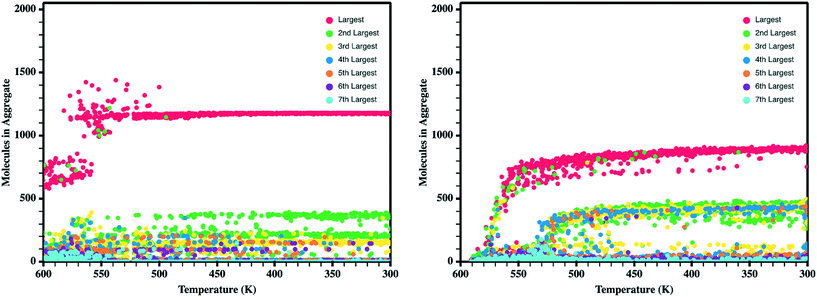

Fig. 5 Number of molecules in each crystalline aggregate in antiADT (left) and synADT (right) as the simulation boxes are cooled. Note a total of 1600 antiADT molecules and 2000 synADT molecules.

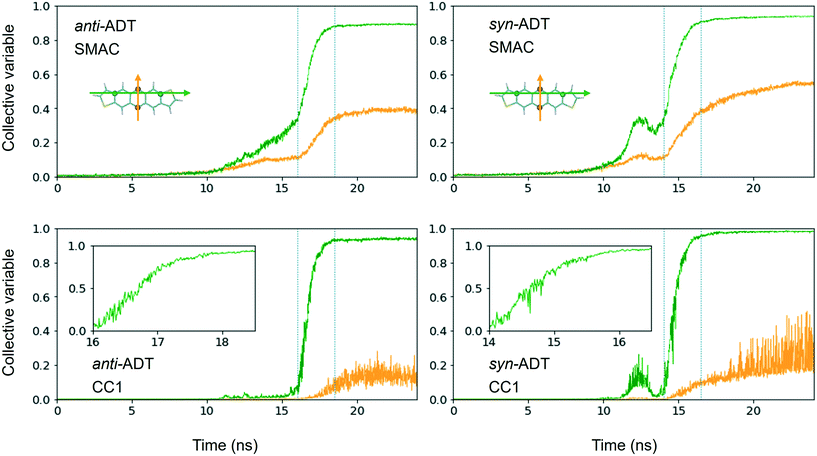
Comparing synADT and antiADT solidification in terms of SMAC and CC1 reveals clear distinctions in terms of the impact of the different molecular structures (Fig. 6). Note that the CV behavior with time shows a distinction from the solid phase from any gas or liquid phase, where crystalline order is marked by the large constant, with crystallization highlighted in the region between the dotted lines. Smooth assembly during condensation is revealed by a linear CV that eventually turns into an exponential curve. On the other hand, the presence of intermediate features highlights rough/uneven assembly process followed by distinct molecular rearrangements. Notably, the long-axis order of antiADT shows a linear process during condensation for SMAC that ultimately turns into exponential growth, whereas that of synADT displays a bump before achieving exponential growth. CC1 further highlights this feature in synADT, indicating rapid but temporary droplet formation during condensation with relatively high order, which is then lost, due to the instabilities of the arrangements to continue growth. Comparing the crystalline regions of the two systems, the short-axis order, especially CC1, for synADT shows more disorder versus antiADT, consistent with Fig. 7, a result indicative of the differences of the molecular symmetries on regulating order. Notably, there are distinct, uneven/rough features that appear in the crystallization region of synADT (the region between the dotted vertical lines), when compared to the smoother transition observed for antiADT, suggesting a more difficult or constrained ordering of the long axis for synADT.

Fig. 6 Normalized crystallinity descriptor collective variables (CV) SMAC (top row) and CC1 (bottom row) derived for the cooling of antiADT and synADT as a function of simulation time in terms of the long-axis (green) and short-axis (yellow) vectors. The inserts in the figures in the bottom row highlight the CV changes during crystallization, which fall between the dotted lines in the full images.

Fig. 7 Relative molecular long-axis alignment for antiADT (A, B) and synADT (C, D) upon initial system condensation (A, C) and the final crystallized system (B, D). Theta is the angle between the long axes of two molecules while phi is their relative rotation with respect to each other.

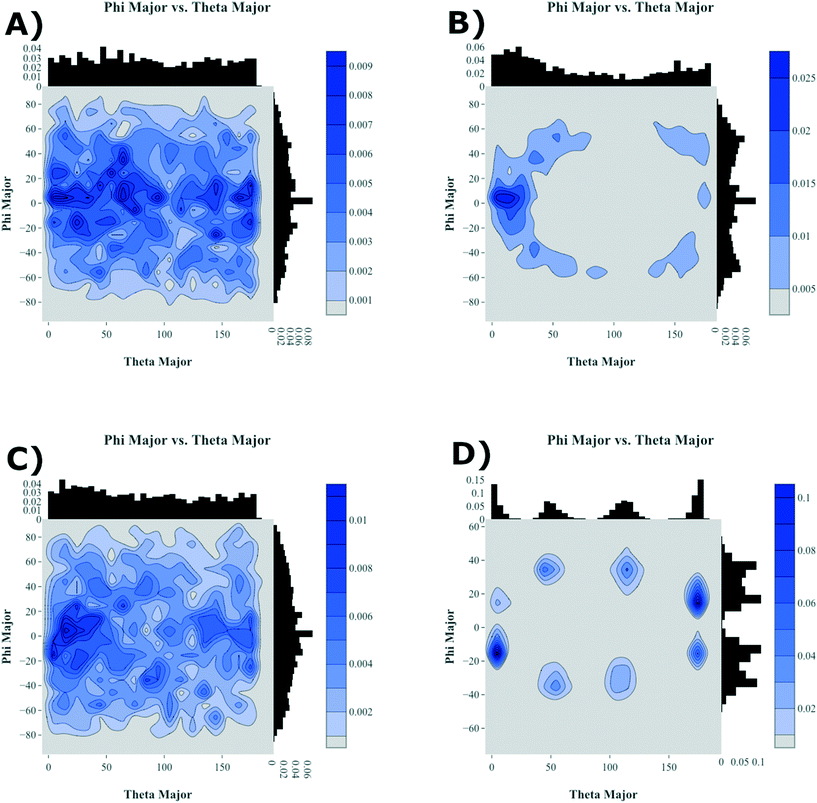
To further highlight how the ordered, crystalline morphology evolves as a function of time and temperature, we used the graph features, as described in Computational methods section, to monitor the relative long- and short-axis distributions of the individual antiADT and synADT molecules. This method was applied to several snapshots during the MD simulations starting at the formation of the initial condensed phase through equilibration at room temperature. The results are summarized in Fig. 7 for rotations about the long axis (θ) and the short axis (φ). We note that while the initial disorder present in antiADT and synADT is qualitatively similar, the final crystal morphology is quite different between the two systems.

From Fig. 5 and 6, we note that antiADT forms a single bulk phase with surrounding regions of disorder. This presents itself in Fig. 7 as θ being heavily concentrated between 0° and 60°, while most of the molecules generally have aligned long axes (φ centered at 0°). The variability of θ corresponds to various co-facial and herringbone packing motifs. Note that the distribution about 0° is inflated due the disorder surrounding the primary crystalline aggregate; the number of disordered molecules accounts for approximately one-quarter of the total number of molecules within the simulation box.

In stark contrast, synADT forms several crystalline domains of similar size, with less than 10% of the total molecules constituting disordered material between crystalline domains. The presence of several crystallites that are each rotated with respect to each other results in the relative long-axis distribution having peaks at about 15° and 45°, a situation not observed for antiADT. The distribution of the rotations about the short axes is also not as broad as antiADT due the reduced amount of disorder among crystallites and the increased order within the crystallites.

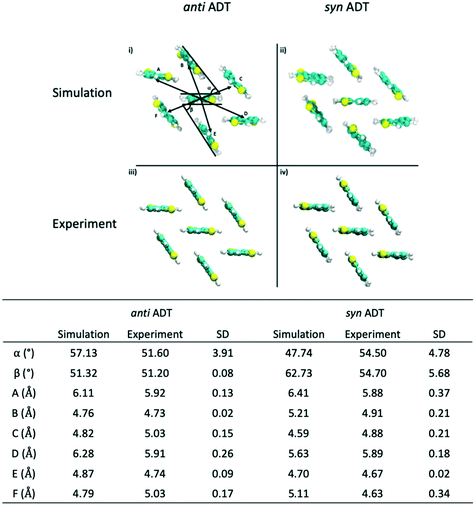
Since the crystallites that are formed during the simulations encompass hundreds of molecules, we are able to sample morphologies within the crystallites that are relatively unperturbed due to crystallite/grain boundaries. Comparing these simulated crystalline packings to the idealized experimental crystalline packing gives an additional measure of the quality of the force field and an additional validation metric for the annealing process that we have used. Data presented in Fig. 8 reveals that the mean absolute error (MAE) between the experimental crystal structure and the average packing extracted from the MD simulations for angles α and β for antiADT is 2.88° while the MAE for the center-of-mass (COM) to COM distance is 0.20 Å. These differences represent errors of 5.6% and 3.7%, respectively. For synADT the MAE for angles α and β is 7.40° (13.5%) while the COM-to-COM distance MAE is 0.32 Å (6%). These small average differences point to the ability of the force field to accurately model both antiADT and synADT and lend credence to the results presented here.

Fig. 8 Comparison of crystalline packing of antiADT and synADT as extracted from a series of snapshots after simulation box crystallization to the experimentally reported crystal structure. Molecular distances and angles are reported in table with standard deviations for each angle and distance.

Reheating of the crystalline aggregates

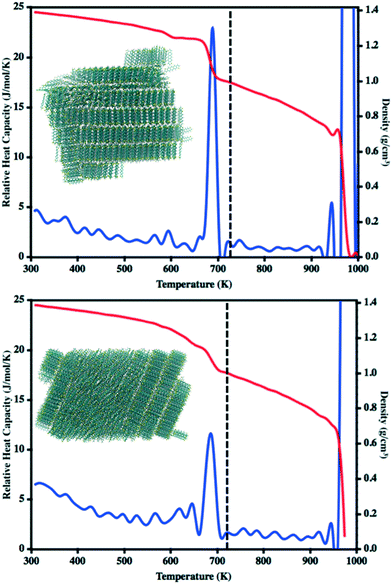
During our previous work we investigated the melt process in ADT as a function of introducing a vacuum gap along different crystalline faces.⁵⁸ This proved necessary to mitigate the superheating that often occurs in MD simulations due to the very short time scales of the simulations relative to experimental processes. During these simulations we noted differing melting points along the individual crystalline faces due to changes in the cohesive energies associated with the various faces. Another method by which to reduce the effects of superheating is to introduce disorder within the crystalline lattice that allows for initiation of the melt process at these disordered sites rather than within the uniform lattice. Since the condensation and crystallization process described in the previous sections also introduces small regions of disorder within the simulation box, these equilibrated systems are ideal for again revisiting the phase transitions that occur during the heating process and compliment the vacuum interface and void simulations previously described.

To model the heating process, the final snapshot from the crystallization simulations was used as the starting point and the antiADT and synADT simulation boxes were heated as discussed in the Computational methods section. Recall that the experimental melting points of antiADT and synADT as determined via differential scanning calorimetry (DSC) are 725 K and 720 K, respectively. Fig. 9 shows the initial simulation cells and heat capacity/density vs. temperature plots of the heating process. For both synADT and antiADT, there is a small transition that occurs at about 600 K corresponding to an internal rearrangement that may be due to those molecules that have a cohesive energy similar to the low melting-point (100) surfaces of the experimental crystals; however, due to the confined environment this is not sufficient to initiate the melting process. Both antiADT and synADT show a large spike in heat capacity and drop in density at about 680 K indicating the primary melting event; this agrees well with our previous estimates of the (010) surface melting point.

Fig. 9 Relative heat capacity (blue) and simulation box density (red) of antiADT (top) and synADT (bottom) as the recrystallized system is heated from 300 K to 1000 K The experimental melting points of the antiADT (725 K) and synADT (720 K) are highlighted with dashed, black lines. The insets show the respective initial system morphologies prior to reheating.

IV. Synopsis

In this work, we demonstrate a combined MD and graph characterization approach to follow the crystallization of molecular-based OSC starting from a highly dispersed gas through a condensed liquid to the solid state. The approach is shown to be sensitive to small differences in chemical structure, as the isomeric ADT systems studied here differ slightly in their molecular symmetry, yet show distinctive features in how the molecular systems nucleate and grow into crystallites. Moreover, we show how the resulting solid-state structures can be used to probe the thermal properties of the materials, as the disorder that is present allows for commonly encountered superheating effects to be overcome. We note, however, that this paper represents a first step in the development of this combined approach to explore crystalline OSC nucleation and growth, as more work is needed to explore specific features related to nucleation and to overcome limitations due to stochastic processes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work at the University in Kentucky was supported in part by Office of Naval Research (Award Numbers N00014-16-1-2985 and N00014-18-1-2448), for the MD simulations, and the National Science Foundation (Award Number CMMI 1563412) for the crystallinity descriptions and connections made with the graph-based methods. Computing resources were provided by the Department of Defense (DoD) Centennial, Hokule'a, Lightning, Onyx, Thunder, and Topaz supercomputing resources through the DoD High Performance Computing Modernization Program (HPCMP; Project Number ONRDC40433481), the Lipscomb High Performance Computing Cluster were provided by the University of Kentucky Information Technology Department and Center for Computational Sciences (CCS), and on the Holly computing cluster by the University of Kentucky College of Arts & Sciences. The work at Iowa State University was supported in part by the National Science Foundation (Award Number CMMI 1563359) and the Office of Naval Research (Award N00014-19-1-2453).

References

1. L. Friedman, Phys. Rev., 1964, 133, A1668–A1679.
2. V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952.
3. H. Sirringhaus, Adv. Mater., 2014, 26, 1319–1335.
4. P. Kordt, Charge Dynamics in Organic Semiconductors: From Chemical Structures to Devices, De Gruyter, 2016.
5. S. R. Marder and J. Bredas, Wspc Reference On Organic Electronics, The: Organic Semiconductors (In 2 Volumes), World Scientific Publishing Company, 2016.
6. C. Wang, H. Dong, L. Jiang and W. Hu, Chem. Soc. Rev., 2018, 47, 422–500.
7. A. Naibi Lakshminarayana, A. Ong and C. Chi, J. Mater. Chem. C, 2018, 6, 3551–3563.
8. H. F. Haneef, A. M. Zeidell and O. D. Jurchescu, J. Mater. Chem. C, 2020, 8, 759–787.
9. W. Tang, Y. Huang, L. Han, R. Liu, Y. Su, X. Guo and F. Yan, J. Mater. Chem. C, 2019, 7, 790–808.
10. H. Bronstein, C. B. Nielsen, B. C. Schroeder and I. McCulloch, Nat. Rev. Chem., 2020, 4, 66–77.
11. S.-J. Zou, Y. Shen, F.-M. Xie, J.-D. Chen, Y.-Q. Li and J.-X. Tang, Mater. Chem. Phys., 2020, 4, 788–820.
12. M. A. Baklar, F. Koch, A. Kumar, E. B. Domingo, M. Campoy-Quiles, K. Feldman, L. Yu, P. Wobkenberg, J. Ball, R. M. Wilson, I. McCulloch, T. Kreouzis, M. Heeney, T. Anthopoulos, P. Smith and N. Stingelin, Adv. Mater., 2010, 22, 3942–3947.
13. M. R. Niazi, R. Li, E. Qiang Li, A. R. Kirmani, M. Abdelsamie, Q. Wang, W. Pan, M. M. Payne, J. E. Anthony, D.-M. Smilgies, S. T. Thoroddsen, E. P. Giannelis and A. Amassian, Nat. Commun., 2015, 6, 8598.
14. Y.-J. Kwon, Y. D. Park and W. H. Lee, Materials, 2016, 9, 650.
15. G. Qu, J. J. Kwok and Y. Diao, Acc. Chem. Res., 2016, 49, 2756–2764.
16. J. Sun, H. Park, Y. Jung, G. Rajbhandari, B. B. Maskey, A. Sapkota, Y. Azuma, Y. Majima and G. Cho, ACS Omega, 2017, 2, 5766–5774.
17. P. J. Diemer, A. F. Harper, M. R. Niazi, A. J. Petty II, J. E. Anthony, A. Amassian and O. D. Jurchescu, Adv. Mater. Technol., 2017, 2, 1700167.
18. C. R. Snyder and D. M. DeLongchamp, Curr. Opin. Solid State Mater. Sci., 2018, 22, 41–48.
19. S. Chung, K. Cho and T. Lee, Adv. Sci., 2019, 6, 1801445.
20. U. Zschieschang and H. Klauk, J. Mater. Chem. C, 2019, 7, 5522–5533.
21. H. Matsui, Y. Takeda and S. Tokito, Org. Electron., 2019, 75, 105432.
22. M. J. Griffith, S. Cottam, J. Stamenkovic, J. A. Posar and M. Petasecca, Front. Phys., 2020, 8, 22.
23. J. Wiklund, A. Karakoç, T. Palko, H. Yiğitler, K. Ruttik, R. Jäntti and J. Paltakari, J. Manuf. Mater. Process., 2021, 5, 89.
24. J. Mei, Y. Diao, A. L. Appleton, L. Fang and Z. Bao, J. Am. Chem. Soc., 2013, 135, 6724–6746.
25. D. M. Walters, R. Richert and M. D. Ediger, J. Chem. Phys., 2015, 142, 134504.
26. J. B. Sherman, C.-Y. Chiu, R. Fagenson, G. Wu, C. J. Hawker and M. L. Chabinyc, MRS Commun., 2015, 5, 447–452.
27. A. Pick and G. Witte, Langmuir, 2016, 32, 8019–8028.
28. L. Yu, M. R. Niazi, G. O. N. Ndjawa, R. Li, A. R. Kirmani, R. Munir, A. H. Balawi, F. Laquai and A. Amassian, Sci. Adv., 2017, 3, e1602462.
29. K. Zong, Y. Ma, K. Shayan, J. Ly, E. Renjilian, C. Hu, S. Strauf, A. Briseño and S. S. Lee, Cryst. Growth Des., 2019, 19, 3461–3468.
30. H. Chen, M. Li, Z. Lu, X. Wang, J. Yang, Z. Wang, F. Zhang, C. Gu, W. Zhang, Y. Sun, J. Sun, W. Zhu and X. Guo, Nat. Commun., 2019, 10, 3872.
31. P. Yu, Y. Zhen, H. Dong and W. Hu, Chem, 2019, 5, 2814–2853.
32. K. Bagchi and M. D. Ediger, J. Phys. Chem. Lett., 2020, 11, 6935–6945.
33. Z. He, Z. Zhang, K. Asare-Yeboah, S. Bi, J. Chen and D. Li, Curr. Appl. Phys., 2021, 21, 107–115.
34. L. Yu, A. M. Zeidell, J. E. Anthony, O. D. Jurchescu and C. Müller, J. Mater. Chem. C, 2021, 9, 11745–11752.
35. Y. Diao, L. Shaw, Z. Bao and S. C. B. Mannsfeld, Energy Environ. Sci., 2014, 7, 2145–2159.
36. J. T. Dull, Y. Wang, H. Johnson, K. Shayegan, E. Shapiro, R. D. Priestley, Y. H. Geerts and B. P. Rand, J. Phys. Chem. C, 2020, 124, 27213–27221.
37. R. Janneck, N. Pilet, S. P. Bommanaboyena, B. Watts, P. Heremans, J. Genoe and C. Rolin, Adv. Mater., 2017, 29, 1703864.
38. S. Verlaak, S. Steudel, P. Heremans, D. Janssen and M. S. Deleuze, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195409.
39. K. Palczynski, G. Heimel, J. Heyda and J. Dzubiella, Cryst. Growth Des., 2014, 14, 3791–3799.
40. N. Kleppmann and S. H. L. Klapp, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045436.
41. N. Kleppmann and S. H. L. Klapp, J. Chem. Phys., 2015, 142, 064701.
42. S. S. Dalal, D. M. Walters, I. Lyubimov, J. J. de Pablo and M. D. Ediger, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4227.
43. G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Chem. Rev., 2016, 116, 7078–7116.
44. M. Casalegno, M. Moret, R. Resel and G. Raos, Cryst. Growth Des., 2016, 16, 412–422.
45. D. M. Walters, L. Antony, J. J. de Pablo and M. D. Ediger, J. Phys. Chem. Lett., 2017, 8, 3380–3386.
46. T. Martynec and S. H. L. Klapp, Phys. Rev. E, 2018, 98, 042801.
47. D. L. Patrick, C. Schaaf, R. Morehouse and B. L. Johnson, Phys. Chem. Chem. Phys., 2019, 21, 9538–9546.
48. N. E. Jackson, J. Phys. Chem. B, 2021, 125, 485–496.
49. O. Wodo, S. Tirthapura, S. Chaudhary and B. Ganapathysubramanian, J. Appl. Phys., 2012, 112, 064316.
50. O. Wodo, J. D. Roehling, A. J. Moulé and B. Ganapathysubramanian, Energy Environ. Sci., 2013, 6, 3060–3070.
51. T. H. Cormen, C. E. Leiserson, R. L. Rivest and C. Stein, Introduction to Algorithms, The MIT Press, 2nd edn, 2001.
52. R. J. Trudeau, Introduction to Graph Theory, Courier Corporation, 2013.
53. boost C++ Libraries, https://www.boost.org/, (accessed October 30, 2021).
54. NetworkX, https://networkx.org/, (accessed October 30, 2021).
55. E. Van, M. Jones, E. Jankowski and O. Wodo, Mol. Syst. Des. Eng., 2018, 3, 853–867.
56. C.-K. Lee, O. Wodo, B. Ganapathysubramanian and C.-W. Pao, ACS Appl. Mater. Interfaces, 2014, 6, 20612–20624.
57. N. E. Jackson, L. X. Chen and M. A. Ratner, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8595–8600.
58. S. Li, S. M. Ryno and C. Risko, J. Mater. Chem. C, 2018, 6, 10924–10934.
59. J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048.
60. D. Lehnherr, R. Hallani, R. McDonald, J. E. Anthony and R. R. Tykwinski, Org. Lett., 2012, 14, 62–65.
61. M. Mamada, T. Minamiki, H. Katagiri and S. Tokito, Org. Lett., 2012, 14, 4062–4065.
62. D. Lehnherr, A. R. Waterloo, K. P. Goetz, M. M. Payne, F. Hampel, J. E. Anthony, O. D. Jurchescu and R. R. Tykwinski, Org. Lett., 2012, 14, 3660–3663.
63. M. Mamada, H. Katagiri, M. Mizukami, K. Honda, T. Minamiki, R. Teraoka, T. Uemura and S. Tokito, ACS Appl. Mater. Interfaces, 2013, 5, 9670–9677.
64. K. J. Thorley and C. Risko, J. Mater. Chem. C, 2016, 4, 4040–4048.
65. R. K. Hallani, K. J. Thorley, Y. Mei, S. R. Parkin, O. D. Jurchescu and J. E. Anthony, Adv. Funct. Mater., 2016, 26, 2341–2348.
66. H. J. C. Berendsen, D. Vanderspoel and R. Vandrunen, Comput. Phys. Commun., 1995, 91, 43–56.
67. B. Hess, C. Kutzner, D. V. D. Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
68. C. E. Bernardes and A. Joseph, J. Phys. Chem. A, 2015, 119, 3023–3034.
69. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
70. K. N. Schwarz, T. W. Kee and D. M. Huang, Nanoscale, 2013, 5, 2017–2027.
71. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
72. M. Mamada, H. Katagiri, M. Mizukami, K. Honda, T. Minamiki, R. Teraoka, T. Uemura and S. Tokito, ACS Appl. Mater. Interfaces, 2013, 5, 9670–9677.
73. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
74. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
75. M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello, P. Banáš, A. Barducci, M. Bernetti, P. G. Bolhuis, S. Bottaro, D. Branduardi, R. Capelli, P. Carloni, M. Ceriotti, A. Cesari, H. Chen, W. Chen, F. Colizzi, S. De, M. De La Pierre, D. Donadio, V. Drobot, B. Ensing, A. L. Ferguson, M. Filizola, J. S. Fraser, H. Fu, P. Gasparotto, F. L. Gervasio, F. Giberti, A. Gil-Ley, T. Giorgino, G. T. Heller, G. M. Hocky, M. Iannuzzi, M. Invernizzi, K. E. Jelfs, A. Jussupow, E. Kirilin, A. Laio, V. Limongelli, K. Lindorff-Larsen, T. Löhr, F. Marinelli, L. Martin-Samos, M. Masetti, R. Meyer, A. Michaelides, C. Molteni, T. Morishita, M. Nava, C. Paissoni, E. Papaleo, M. Parrinello, J. Pfaendtner, P. Piaggi, G. Piccini, A. Pietropaolo, F. Pietrucci, S. Pipolo, D. Provasi, D. Quigley, P. Raiteri, S. Raniolo, J. Rydzewski, M. Salvalaglio, G. C. Sosso, V. Spiwok, J. Šponer, D. W. H. Swenson, P. Tiwary, O. Valsson, M. Vendruscolo, G. A. Voth, A. White and P. C. The, Nat. Methods, 2019, 16, 670–673.
76. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
77. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972.
78. F. Giberti, M. Salvalaglio, M. Mazzotti and M. Parrinello, Chem. Eng. Sci., 2015, 121, 51–59.
79. G. A. Tribello, F. Giberti, G. C. Sosso, M. Salvalaglio and M. Parrinello, J. Chem. Theory Comput., 2017, 13, 1317–1327.
80. S. T. Gentry, S. F. Kendra and M. W. Bezpalko, J. Phys. Chem. C, 2011, 115, 12736–12741.
81. I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50.
82. J. A. Marqusee and J. Ross, J. Chem. Phys., 1983, 79, 373–378.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1me00157d

---