Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure sensitive enantioselectivity on surfaces: tartaric acid on all surfaces vicinal to Cu(111)†
Carlos
Fernández-Cabán
a,
Burcu
Karagoz
a,
Petro
Kondratyuk
a and
Andrew J.
Gellman
 *ab
*ab
aDepartment of Chemical Engineering, Carnegie Mellon University, 5000 Forbes Ave., Pittsburgh, PA 15213, USA. E-mail: gellman@cmu.edu; Fax: +1 412-268-3848
bW. E. Scott Institute for Energy Innovation, Carnegie Mellon University, 5000 Forbes Ave., Pittsburgh, PA 15213, USA
First published on 18th January 2022
Abstract
Comprehensive mapping of enantiospecific surface reactivity versus the crystallographic orientation of Cu(hkl) surfaces vicinal to Cu(111) has been conducted using a spherically shaped single crystal on which the surface normal vectors, [hkl], span all possible orientations lying with 14° of the [111] direction. This has allowed direct measurement on 169 different Cu(hkl) surfaces of the two rate constants, k(hkl)i and k(hkl)e, that determine the kinetics of the vacancy-mediated, explosive decomposition of tartaric acid (TA). The initiation rate constant, k(hkl)i, quantifies the kinetics of an initiation step that creates vacancies in the adsorbed TA monolayer. The explosion rate constant, k(hkl)e, quantifies the kinetics of a vacancy-mediated explosion step that results in TA decomposition and product desorption. Enantiospecificity is revealed by the dependence of TA decomposition kinetics on the chirality of the local surface orientation. Diastereomerism is demonstrated by the fact that D-TA is more reactive than L-TA on S surfaces while L-TA is more reactive on R surfaces. The time to reach half coverage, t(hkl)1/2, during isothermal TA decomposition at 433 K allowed determination of the most enantiospecific surface orientation; Cu(754). The ideal Cu(754) surface structure consists of (111) terraces separated by monoatomic steps formed by the (100) and (110) microfacets.
1. Introduction
The kinetics of surface processes such as catalysis are often dictated by the atomistic structures of the surfaces on which they occur. In principle, this means that atomistic surface structure should be one of the design parameters considered in the development of catalysts. However, rigorous surface design would require the existence and use of quantitative models for prediction of reaction kinetics on surfaces of arbitrary atomic structure. Examples of structure sensitivity in catalytic processes include ammonia synthesis on Fe and Ru,1–5 hydrocarbon catalysis,6–9 and many other reactions.10–12 The basic approach to understanding the origin of the structure sensitivity of these processes requires determination of the reaction mechanism at the level of individual elementary steps and identification of the reaction step (or steps) that are rate controlling. Then one must understand the influence of surface structure on the rate constants for those reaction steps. In this work, a high throughput approach was used to measure the surface structure dependence of the two rate constants, k(hkl)i and k(hkl)e, that determine the overall kinetics of tartaric acid (TA, HO2CCH(OH)CH(OH)CO2H) decomposition on Cu(hkl) surfaces. The initiation rate constant, k(hkl)i, quantifies the kinetics of an initiation step that creates vacancies in the adsorbed TA monolayer. The explosion rate constant, k(hkl)e, quantifies the kinetics of the vacancy-mediated explosion step that results in auto-catalytic TA decomposition and product desorption.13An understanding of the relationship between surface reaction kinetics and surface structure is important to the design and optimization of catalytic processes. This work studies enantiospecificity of the reactions of chiral molecules on chiral surfaces. This is perhaps the subtlest form of surface structure sensitivity or chemical selectivity. Enantioselectivity is solely dictated by the diastereomeric structural relationship between the chiral adsorbate and the chiral surface.14,15 Chiral surfaces are good candidates for the development and understanding of enantioselective processes because they play an important role in enantioselective chemical processes such as adsorption, catalysis and crystallization. One of the challenges to optimizing enantioselective processes on chiral surfaces is that it requires a fundamental understanding of the enantiospecific interactions between chiral molecules and chiral surfaces.14,16,17 The optimization of enantioselective processes on chiral surfaces requires an understanding of the influence of surface structure on surface reaction kinetics. This is complicated by the fact that there are an infinite number of surface orientations that can be exposed by any bulk crystal structure. A high throughput approach is needed to study comprehensively the kinetics of enantioselective reactions on chiral surfaces of different crystallographic orientations.
Chiral surfaces can be prepared by a variety of means. Many examples of chiral surfaces are made by the adsorption of chiral molecules onto achiral surfaces. The presence of a chiral adsorbate renders the surface chiral by breaking the structural symmetry of the initially achiral surface.6 Some inorganic materials such as quartz and intermetallic compounds such as GaPd have chiral bulk structures that expose chiral surfaces.14,18 Intrinsically chiral surfaces can also be obtained from materials with achiral bulk structures, e.g. pure metals. These can be obtained by cleaving the bulk metal lattice along a low-symmetry plane. A face-centered-cubic (FCC) crystal surface is achiral, if any two of its Miller indices (hkl) are equal to one another or, if any of them are zero. This means that, a FCC(hkl) surface is chiral, if h ≠ k ≠ l ≠ h and h × k × l ≠ 0.19–22 The ideal structures of chiral metal surfaces have low-Miller-index terraces separated by monoatomic kinked step edges as shown for the Cu(3,1,17) surface in the ESI,† Fig. SI 1.22 These chiral surfaces vary in terms of which low-Miller-index facets form the terraces, the straight portions of the step edges and the kinks. These surfaces also vary in terms of the spacing between the steps separating the terraces and the spacing between the kinks along the step edges. Intrinsically chiral metal surfaces have been shown to exhibit enantiospecific interactions with chiral adsorbates.13,14,23–26
The emergence of the use of single crystal samples in surface science made it possible to measure rates of individual elementary reaction steps and overall catalytic reaction rates on isolated surface orientations.1–5,27 The ability to perform studies on isolated facets of metal single crystals has revealed surface structure sensitivity. However, that work also reveals the limitations of the flat single crystal approach in being able to provide a comprehensive understanding of structure sensitivity that would allow prediction of surface reaction kinetics across all possible surface orientations. Because of the infinite number of surface orientations, this requires an unrealistic amount of work. For this reason, a high throughput approach is needed to study comprehensively the kinetics of enantioselective reactions on chiral surface orientations spanning crystallographic orientation space.28,29
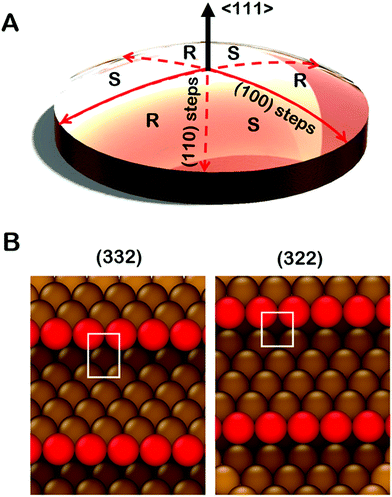
Significant development and application of high throughput experimental methods has occurred over the last decade. This allows rapid collection and analysis of datasets spanning broad continuous parameter spaces.30–33 Curved single crystal surfaces, which we refer to as surface structure spread single crystals (S4Cs), shown in Fig. 1A, expose a continuous distribution of crystallographic surface orientations and, thereby, serve as high throughput libraries for study of structure dependent surface properties.34 The first use of a curved sample surface was reported by Linder in 1927 in a study of the photoelectric current emitted from the surface of a single crystal cylinder of Zn.35 The measured photocurrent under UV irradiation varied periodically around the perimeter of the cylinder. In the 1940's Gwathmey used Cu single crystal spheres to reveal surface structure dependent trends in processes such as corrosion and surface oxidation that could be detected visually.36–39 In the 1970's Woodruff et al. used Auger spectroscopy to detect structure sensitive oxygen uptake on clean Cu(hkl) surfaces around the perimeter of a single crystal Cu cylinder.40,41 They observed that the order of oxygen uptake on the low-Miller-index surface orientations was Cu(111) < Cu(100) < Cu(110) with a smooth variation between each. More recently, Ortega et al. have used cylindrical curved surfaces of Pd, Ag, and Ni to study surface structure and CO oxidation catalysis on high-Miller-index surfaces with a continuous distribution of step densities.42–44 Juurlink et al. have used cylindrical crystals of Pt and Ag to study the influence of steps on the adsorption and desorption kinetics of H2, CO and H2O.45–47 These cylindrical single crystal samples expose surfaces that span the length of a 1D trajectory through crystallographic orientation space.
Spherical S4Cs span a continuous portion (2D area) of the stereographic triangle (ESI,† Fig. SI 2) thereby enabling study of a continuous 2D distribution of surface orientations, all treated using the same experimental conditions. This is critical to our study of chiral surfaces. A graphic illustration of a Cu(111)±14°-S4C is shown in Fig. 1A. The Cu(111)±14°-S4C was used to map the enantiospecific decomposition kinetics of TA decomposition across 169 surface orientations lying within 14° of the [111] direction. The curved dome of the Cu sample is spherical with a 21 mm radius of curvature. The (111) plane is located at the top center point of the dome. As one moves away from the [111] facet, the step density increases with (110) steps being exposed along three symmetry-equivalent directions, and (100) steps along the three opposite directions. The six high symmetry directions divide the S4C into six regions containing surfaces alternating between R- and S-chirality.19,21,48,49 The points along the solid red lines in Fig. 1A expose achiral surfaces with (111) terraces separated by (100) steps. The points along the dashed red lines expose achiral surfaces with (111) terraces separated by (110) steps. The terrace widths between steps on the S4C decrease continuously from the (111) center point to the edges where the terrace widths are ∼1 nm. Surface structures at the edges of the Cu(111)±14°-S4C and in the high symmetry directions (red lines) are shown in Fig. 1B. They have (111) terraces that are ∼5 close-packed rows in width separated by monoatomic step edges. The steps are formed by either (100) or (110) microfacets. The use of a S4C that exposes both chiral and achiral crystal surfaces, coupled with spatially resolved experimental techniques allows study of enantiospecific surface reaction kinetics across a continuous distribution of surface orientations. This enables the detection of enantiospecificity during surface reactions of chiral adsorbates.
It is important to point out that the real structures of these chiral high-Miller-index surfaces need not be the same as one would predict on the basis of simply cleaving and ideal single crystal bulk lattice. The ideal structures of surfaces are subject to phenomena such as relaxation, reconstruction, step bunching and thermal roughening. The structures of the surfaces of a Cu(111)±14°-S4C have been studied using scanning tunneling microscopy.34 These have shown that the center point is truly a large terrace of Cu(111) orientation. As one moves radially from the (111) center point, monoatomic steps are observed with average spacings that are consistent with expectations based on the lattice spacing of bulk Cu. Furthermore, these steps have roughly the expected orientation as one moves azimuthally around the center point. Although the steps meander with respect to the ideal orientation, there is no sign of gross surface reconstruction or step bunching. High resolution images have also been obtained from the Cu(643) surface.50 These reveal the expected structure of dense steps with kinks, however, the step edges are thermally roughened such that the kinks are no longer just single atom kinks spaced periodically along the step edge. Although this reduces the areal density of kinks relative to that of the ideal Cu(643) structure, the surface retains its net chirality in the sense that the kinks all have the same orientation of their surrounding low Miller index microfacets. This represents our current understanding of the real structure across the clean Cu(111)±14°-S4C surface. That said, it is important to realize also, that adsorbates can complicate this understanding by influencing the underlying structure of the surfaces to which they are adsorbed.51
TA is an ideal chiral probe for study of enantiospecific surface chemistry because its decomposition mechanism and kinetics are well understood on Cu single crystal surfaces.52–57 After adsorption at 400 K on Cu(110), the saturation coverage has 5/16 TA/Cu atom and with TA singly deprotonated (HO2CCH(OH)CH(OH)CO2–Cu). At a lower absolute coverage of ¼ TA/Cu atom, the TA is doubly deprotonated copper tartrate (Cu–O2CCH(OH)CH(OH)CO2–Cu). During heating, the adsorbed TA decomposes into CO2, CO, H2O, H2 and leaves some C and O atoms adsorbed to the surface. The decomposition process occurs by a vacancy-mediated explosion reaction in which the reaction rate depends on both the TA coverage, θTA, and the coverage of vacancies or empty sites in the adsorbed monolayer, θvac = (1 − θTA).54,55,58 The rate law is given by
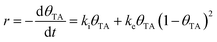 | (1) |
In order to extract the rate constants k(hkl)i and k(hkl)e we must measure the time-dependent coverage of TA, θ(hkl)TA(t;Tiso), at many different surface orientations during isothermal decomposition of adsorbed TA. Herein, we demonstrate the use of a high throughput approach to measure TA coverage, θ(hkl)TA(t;Tiso), at Tiso = 433 K and at 169 discrete points evenly distributed across the surface of the Cu(111)±14°-S4C. From these we have been able to extract values for the surface structure dependence of the rate constants, k(hkl)i and k(hkl)e, and thereby gain insight into the origins of the observed surface structure dependence of TA decomposition and enantiospecificity on chiral Cu(hkl) surfaces that are vicinal to Cu(111).
2. Experimental
2.1 Apparatus
TA adsorption and decomposition on the Cu(111)±14°-S4C was studied in a ThetaProbe™. This apparatus consists of a preparation chamber and an analysis chamber. The preparation chamber is equipped with a homemade sublimation source for TA deposition onto the surface. The analysis chamber is equipped with a focused and monochromated X-ray source, a sputter ion gun to clean the surface, and a hemispherical energy analyzer to perform Spatially Resolved X-ray Photoelectron Spectroscopy (SR-XPS). A Tescan Vega3 SEM equipped with a detector for Electron Back Scatter Diffraction (EBSD) was used to determine the rotational orientation of the crystal lattice vectors. A pole figure assembled from the EBSD pattern is shown in the ESI† Fig. SI 3.2.2 S4C preparation
The Cu(111)±14°-S4C was prepared from a flat Cu(111) single crystal (Monocrystals Inc.) with dimensions of 10 mm in diameter and 2 mm in thickness. One side was shaped by a commercial vendor of nanomachining services using single point diamond turning. The final shape was a section of a 21 mm radius spherical dome. The S4C was then mounted by vacuum brazing with a Cu–Ag braze to a 14 × 14 × 3 mm3 Cu block. It was then mounted onto the manipulator of a UHV chamber and subjected to cycles of Ar+ ion sputtering and annealing at 900 K until the surface yielded a low energy electron diffraction (LEED) pattern.To determine the rotational orientation of the crystal lattice vectors, the sample was inserted into a Tescan Vega3 SEM equipped with an EBSD detector. A pole figure from the sample assembled from the EBSD pattern is shown in Fig. SI 3 of the ESI.† The S4C on the Cu block was then mounted to a sample holder that allows heating, cooling, and temperature measurement in the ThetaProbe™. This apparatus is used for SR-XPS. Within the ThetaProbe™, the S4C surface was sputtered and annealed further until the surface was clean of contaminants.
2.3 TA/S4C surface preparation
To prepare the Cu(111)±14°-S4C surface for measurements of the TA decomposition kinetics, the surface was held at 400 K while being exposed to TA vapor in the preparation chamber of the ThetaProbe™. TA was adsorbed on the surface from the sublimation source held at ∼390 K. A saturated monolayer of L- or D-TA was adsorbed by exposure of the surface to an L- or D-TA flux for 25 minutes. Once the S4C surface was coated with a uniform, saturated monolayer of TA, it was transferred on its holder into the analysis chamber of the ThetaProbe™ and mounted onto an automated xyz positioning stage. On the positioning stage, the sample can be heated and the temperature measured.2.4 SR-XPS analysis
After first adsorbing the TA monolayer, the spatio-temporal evolution of TA coverage, θ(hkl)TA(t), across the Cu(111)±14°-S4C was measured using SR-XPS during isothermal heating at 433 K. The O 1s XPS signal was measured on the circular grid of 169 points shown in the ESI,† Fig. SI 4. Measuring the isothermal decomposition kinetics of TA on the Cu(111)±14°-S4C surface consisted of cycles in which the sample was heated to 433 K at 1 K s−1, held at 433 K for a prescribed period of time, cooled back to room temperature, and then analyzed using spatially resolved XPS, once the temperature had decreased to below 400 K. This process was repeated 29 times for a total time of 4000 s at 433 K. TA decomposition does leave some residual O adsorbed on the surface, but at that point there was no further decrease in the O 1s signal with additional annealing at 433 K. The heating and cooling schedule is shown by the hash marks at the top of Fig. 2 indicating the quench times.Mapping of the TA coverage across the S4C surface was accomplished by measuring the intensity (area) of the O 1s XPS signal at 169 points on the surface. The concentric circular grid of points radiated from the center of the S4C to a radial distance of 4.5 mm with a spacing of 0.75 mm between circles. The points around each circle were also spaced by ∼0.75 mm.
Adsorption of TA on the Cu S4C surface at 400 K results in its adsorption in a deprotonated state that then decomposes during heating to yield CO2, CO, H2 and other species in the gas phase. This results in the deposition of ∼10% of the O atoms onto the Cu surface.54–56,58 This atomically adsorbed O remains on the surface indefinitely during further heating at 433 K. The TA coverage can be estimated from the XPS spectra using eqn (2).
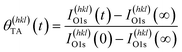 | (2) |
3. Results
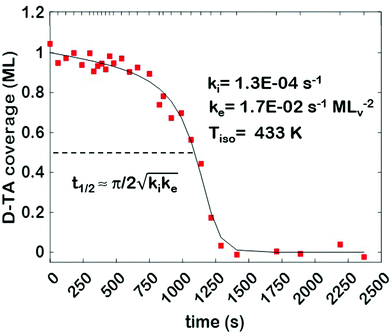
The core dataset collected during the course of this study consists of the O 1s spectra obtained from D- and L-TA adsorbed at 169 points on the Cu(111)±14°-S4C surface and measured as functions of time during heating at Tiso = 433 K. These data have been translated into isothermal coverage decay curves for D- and L-TA versus time, θ(hkl)TA(t), all starting at a value of θ(hkl)TA(0) = 1 monolayer (ML). The D-TA coverage versus time at the Cu(111) point of the Cu(111)±14°-S4C, θ(111)D-TA(t), is shown in Fig. 2. The 29 hash marks at the top of the figure indicate the points in time at which the sample temperature was quenched during heating at 433 K. SR-XPS was used after each quench to map the local TA coverage across the Cu(111)±14°-S4C. The slow initiation process is observed from t = 0 to 750 s. The explosive autocatalytic acceleration step of the decomposition rate follows from t = 750 to 1250 s, as indicated by the rapid decay in D-TA coverage. After the explosion step and depletion of the adsorbed D-TA, θ(111)D-TA goes to zero. The initiation and explosion features are also observed in the isothermal coverage decay curves obtained from the other 168 surface orientations sampled on the Cu(111)±14°-S4C.The simplest metric of reactivity to be extracted from these decay curves is the half-time, t(hkl)1/2, to reach a coverage of θ(hkl)TA = 0.5 ML having started at a saturation coverage of 1 ML. It is important to note that the value of t(hkl)1/2 can be measured with higher accuracy than either the initiation or explosion rate constants.62 The optimal fit of the D-TA decomposition rate law (eqn (1)) to the measured data for θ(111)D-TA(t) is shown by the black curve in Fig. 2. The optimal fit yields estimates of k(111)i = 1.3 ± 0.2 × 10−4 s−1 and k(111)e = 1.7 ± 0.3 × 10−2 s−1 MLv−2, where MLv is the unit of vacancy coverage. All surface orientations on the Cu(111)±14°-S4C exhibit k(hkl)e ≫ k(hkl)i. This has also been observed in the case of TA and Asp decomposition on a Cu(110)±14°-S4C and Cu(111)±14°-S4C, respectively.28,63 The analytical solution of eqn (1) allows expression of t(hkl)1/2 in terms of k(hkl)e and k(hkl)i.62 Given the condition that k(hkl)e ≫ k(hkl)i, it can be shown that 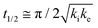 . The relationship between t1/2 and kike serves as a metric for the enantiospecificity of the decomposition kinetics. The high accuracy of estimates of t1/2 from the fits to the θ(hkl)D-TA(t) data can be obtained because of the nature of the solution to eqn (1).62
. The relationship between t1/2 and kike serves as a metric for the enantiospecificity of the decomposition kinetics. The high accuracy of estimates of t1/2 from the fits to the θ(hkl)D-TA(t) data can be obtained because of the nature of the solution to eqn (1).62
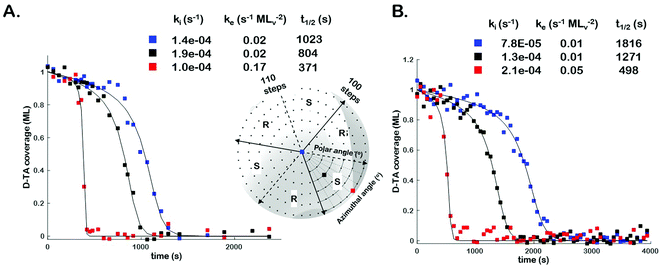
In order to assess the impact of intermittent temperature quenching on the values of k(hkl)i, k(hkl)e, and t(hkl)1/2 obtained from θ(hkl)TA(t), we conducted measurements of θ(hkl)D-TA(t) at three points on the Cu(111)±14°-S4C using continuous isothermal conditions, Tiso = 433 K, without quenching of the temperature. Fig. 3 (inset) shows a map of the points (blue, black and red squares) studied on the Cu(111)±14°-S4C. This experiment first saturated the surface with D-TA and then heated the sample to Tiso = 433 K and held it there continuously while obtaining O 1s XP spectra from each of the three points sequentially until the TA coverage dropped to zero at all three. Fig. 3 shows the D-TA coverage decay curves, θ(hkl)D-TA(t), during decomposition at 433 K on the three different Cu(hkl) surfaces for non-quenching (Fig. 3B) and quenching experiments (Fig. 3A). Also shown are the values of k(hkl)i, k(hkl)e, and t(hkl)1/2 estimated from the XPS data obtained using the two different heating profiles. These data demonstrate that quenching introduces a systematic error leading to over estimation of the rate constants by ∼2 ×.
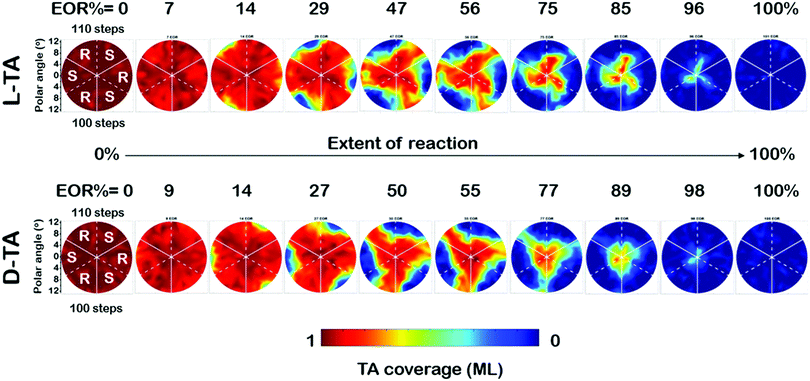
The full dataset of rate constants at all 169 points on the Cu(111)±14°-S4C was obtained from θ(hkl)D-TA(t) decay curves obtained from O 1s XPS spectra obtained during 29 periods of intermittent quenching. The coverage maps, θ(hkl)TA(t), for D- and L-TA are shown in Fig. 4 at 10 of the 29 time intervals used in the experiment. These are plotted versus increasing extent of reaction (EOR), determined using the average value of the local TA coverages remaining on the Cu(111)±14°-S4C after each annealing period, EOR = 1 − 〈θ(hkl)TA〉. The high symmetry directions are marked on the maps with solid and dashed white lines. The coverage maps reveal a 3-fold rotational symmetry for both TA enantiomers about the Cu(111) center point. The Cu(111) center point is the least reactive for both TA enantiomers. The maps at EOR = 14 and 29% reveal the onset of decomposition for both D- and L-TA at the edges of the crystal where the step density is highest. However, the decomposition kinetics are not isotropic around the edge of the Cu(111)±14°-S4C. The decomposition of L-TA starts in the regions of the surface with R-chirality, whereas, the decomposition of D-TA is initiated in the regions of S-chirality. The maps for EOR = 14 to 75% reveal clear diastereomerism in the TA decomposition kinetics on chiral Cu(hkl)R&S surfaces.
4. Discussion
The objective of this work is to map enantiospecific surface reaction rate constants, k(hkl)i and k(hkl)e, versus surface crystallographic orientation. The resulting data can serve as the basis for future development of predictive models for the origins of structure sensitive surface reaction kinetics. The focus of this work is enantioselectivity which is a purely structural form of selectivity. Enantioselectivity is perhaps one of the most subtle forms of reaction selectivity, in the sense that the enantiospecificities of surface reaction energetics are typically only on the order of a few kJ per mole; i.e. ΔΔER−S ∼ kBT.23,24,64,65 This work provides insight into the origins of enantioselectivity in the decomposition of L- and D-TA. A comprehensive study of enantiospecific surface structure sensitivity requires the use of curved samples such as our S4C. These span both dimensions of surface orientation. The spherical S4C sample spans surface orientations that lack mirror symmetry and, therefore, expose chiral surface structures. The origins of structure sensitivity and enantioselectivity in surface chemistry lie in the surface structure dependence of the rate constants. Estimates of the surface structure dependence of the rate constants k(hkl)i and k(hkl)ewere obtained from the coverage decay curves of D- and L-TA on Cu(hkl) surfaces vicinal to Cu(111). Bear in mind that, as indicated by the data in Fig. 3, the rate constants are overestimated systematically by ∼2×. This does not, however, influence the relative values of the rate constants obtained from different points on the S4C.4.1 The TA explosion initiation rate constant, k(hkl)i
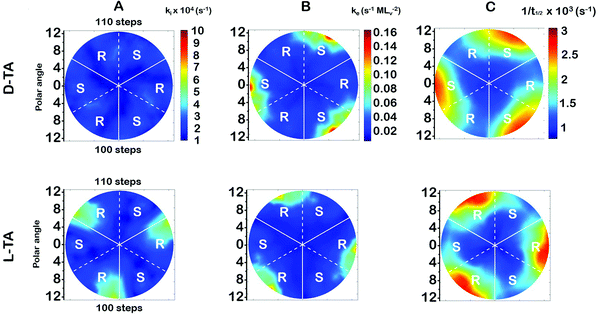
The surface explosion rate constants k(hkl)i and k(hkl)e for the decomposition of D- and L-TA on the Cu(111)±14°-S4C were estimated by fitting eqn (1) to the coverage decay curves at each of the 169 points. Fig. 5A shows the rotationally averaged initiation rate constant, k(hkl)i, maps for D- and L-TA, across the Cu(111)±14°-S4C. By ‘rotationally averaged’ we mean that the values at each point on the surface have been averaged with those on the other two symmetry equivalent points exposed by the Cu(111)±14°-S4C. The values of k(hkl)i are lowest at the Cu(111) center point and on surfaces vicinal to Cu(111) having low step density. The values for L-TA are largest on R-chirality surfaces with polar angles of ≳ 9°. This is consistent with the initial onset of decomposition at EOR ≅ 29% for L-TA as observed in Fig. 4. The values of k(hkl)iare structure insensitive for both D- and L-TA across the central region of the S4C; i.e. within ∼9° of Cu(111) point. While Fig. 5A reveals clear enantiospecificity of the initiation rate constants for L-TA, the same cannot be said of D-TA. Our best assessment is that this difference arises from small differences in the purity of the D- and L-TA.4.2 The TA explosion rate constant, k(hkl)e
The values of the explosion rate constants, k(hkl)e, obtained from the fit of eqn (1) to the θ(hkl)TA(t) data are shown in Fig. 5B for D- and L-TA. These maps of k(hkl)e clearly show structure sensitivity and enaniospecificity for both D- and L-TA. The values of k(hkl)e span a range of ∼8× for each enantiomer. The values for D- and L-TA are largest on surfaces exposed at the edge of the sample; i.e. polar angles greater than ≳9°. The values of k(hkl)e are lowest for both enantiomers on surfaces close to the center Cu(111) point. The largest values for k(hkl)e are on R-regions for L-TA and on the S-regions for D-TA, showing both enantiospecificity and diastereomerism.4.3 Values of the halftime for TA decomposition
The analytical solution for θ(hkl)TA(t) allows one to relate features of the decay curves directly to the reaction rate constants. The time to reach a coverage of θTA = 0.5 is given by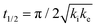 .62 The values of t(hkl)1/2 measured across the Cu(111)±14°-S4C span the range t(hkl)1/2 = 350 to 1300 s. The dependence of t1/2 on surface orientation, (hkl), is a clear indicator of surface structure sensitivity and enantiospecificity. Rather than using t1/2, the values of t1/2−1 are used as a metric of enantiospecificity on chiral surfaces because it has the units of a pseudo first-order rate constant and it can be estimated more accurately from the data than either ki or ke. The rotationally averaged values of t1/2−1 across the Cu(111)±14°-S4C are shown in Fig. 5C for D- and L-TA. The maps of t1/2−1 show both structure sensitivity and enaniospecificity. The values of t1/2−1 range from 1.0 × 10−3 to 3.0 × 10−3 s−1. The regions vicinal to the Cu(111) center of the S4C reveal minima in t1/2−1 for both enantiomers; i.e. surfaces with no or low step density are relatively unreactive for TA decomposition. Reactivity increases with step density, but enantiospecifically. The values of t1/2−1 become significantly enantiospecific for surfaces with polar angles ≳9° relative to the (111) plane. Enantiospecificity is revealed by the fact that the values of t1/2−1 are greater for L-TA in the R-regions than in the S-regions. Consistent with the expected diastereomerism, the values of t1/2−1 are greater for D-TA in the S-regions than in the R-regions.
.62 The values of t(hkl)1/2 measured across the Cu(111)±14°-S4C span the range t(hkl)1/2 = 350 to 1300 s. The dependence of t1/2 on surface orientation, (hkl), is a clear indicator of surface structure sensitivity and enantiospecificity. Rather than using t1/2, the values of t1/2−1 are used as a metric of enantiospecificity on chiral surfaces because it has the units of a pseudo first-order rate constant and it can be estimated more accurately from the data than either ki or ke. The rotationally averaged values of t1/2−1 across the Cu(111)±14°-S4C are shown in Fig. 5C for D- and L-TA. The maps of t1/2−1 show both structure sensitivity and enaniospecificity. The values of t1/2−1 range from 1.0 × 10−3 to 3.0 × 10−3 s−1. The regions vicinal to the Cu(111) center of the S4C reveal minima in t1/2−1 for both enantiomers; i.e. surfaces with no or low step density are relatively unreactive for TA decomposition. Reactivity increases with step density, but enantiospecifically. The values of t1/2−1 become significantly enantiospecific for surfaces with polar angles ≳9° relative to the (111) plane. Enantiospecificity is revealed by the fact that the values of t1/2−1 are greater for L-TA in the R-regions than in the S-regions. Consistent with the expected diastereomerism, the values of t1/2−1 are greater for D-TA in the S-regions than in the R-regions.
4.4 Most enantiospecific surface orientation
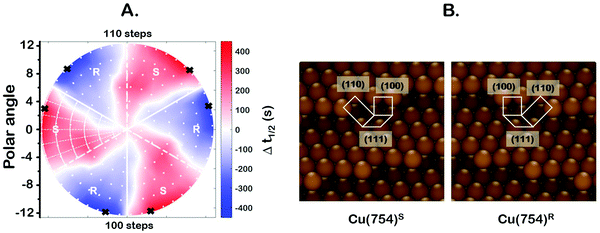
One of the most interesting and potentially valuable characteristics of enantiospecific surface chemistry that can be garnered from data obtained using an S4C is the orientation of the surface that is most enantiospecific for the reaction of interest. This requires identification of some reaction metric that can be shown to exhibit a maximum in its difference on the R- and S-enantiomorphs of a given surface orientation.In this work, the most enantiospecific surface orientation vicinal to Cu(111) was determined using the half time, t(hkl)1/2, needed to reach a coverage of θ(hkl)TA(t1/2) = 0.5. All surface orientations showed that k(hkl)e ≫ k(hkl)i. The relationship 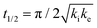 is useful because it serves as a metric for the enantiospecificity of the TA decomposition kinetics.62 The nature of the solution to eqn (1) allows high accuracy estimates of t(hkl)1/2 from the fits to the θ(hkl)TA(t) data. The polar maps of Δt(hkl)1/2 = tL-TA1/2 − tD-TA1/2 values and the ideal structure of the most enantiospecific surface are shown in Fig. 6A and B, respectively. The values of Δt(hkl)1/2 in Fig. 6A span the range −400 to 400 s with positive (red) values in the S-chirality zones and negative (blue) values in the R-chirality zones. Note that the white curves in Fig. 6A denote points along which Δt(hkl)1/2 = 0 and the surfaces exhibit no enantioselectivity. In an ideal world, these white curves would be aligned with the solid and dashed white lines along which the surfaces are achiral.
is useful because it serves as a metric for the enantiospecificity of the TA decomposition kinetics.62 The nature of the solution to eqn (1) allows high accuracy estimates of t(hkl)1/2 from the fits to the θ(hkl)TA(t) data. The polar maps of Δt(hkl)1/2 = tL-TA1/2 − tD-TA1/2 values and the ideal structure of the most enantiospecific surface are shown in Fig. 6A and B, respectively. The values of Δt(hkl)1/2 in Fig. 6A span the range −400 to 400 s with positive (red) values in the S-chirality zones and negative (blue) values in the R-chirality zones. Note that the white curves in Fig. 6A denote points along which Δt(hkl)1/2 = 0 and the surfaces exhibit no enantioselectivity. In an ideal world, these white curves would be aligned with the solid and dashed white lines along which the surfaces are achiral.
By determining the locations exhibiting highest magnitude of Δt(hkl)1/2 = tL-TA1/2 − tD-TA1/2, the most enantiospecific surface orientation was determined. The largest difference is Δt(hkl)1/2 = 430 s and most enantiospecific surface orientation is Cu(754)R&S. The various equivalent points denoting the positions of the family of Cu{754}R&S surfaces are marked on Fig. 6A with black crosses. At these points, the magnitude of Δt(754)1/2 reaches ∼430 seconds which is a reasonably large fraction of a process that takes ∼2500 s to reach completion. One obvious point to make is that the Cu(754) orientation lies at the edge of the area sampled on the Cu(111)±14°-S4C and the data clearly suggest that at polar angles >12° one will find surfaces with Δt(hkl)1/2 > 430 s.
The ideal chiral surface structures of Cu(754)R&S are depicted in Fig. 6B. These are formed of (111) terraces separated by (310) monoatomic step edges formed by two (100) unit cells separated by kinks formed by one (110) unit cell. The terraces are ∼4 Cu spacings across or, in other words, ∼1 nm in width. In microfacet notation, the ideal surface structure can be described as 4(111) × (310).66 The chirality is dictated by the rotational ordering of the (111), (100) and (110) microfacets about the surface normal. It is interesting to note that this structure is similar to that of the Cu(643)R&S surfaces that can be described as having 3(111) × (310) structure. In other words, (643) is formed by (111) terraces that are ∼3 atoms wide and separated by (310) step edges. It lies at the same azimuthal angle as (754) but at a longer radial distance from the (111) point; i.e. just off the edge of our Cu(111)±14°-S4C. Cu(643) shows very high enantiospecificity for D- and L-TA decomposition.13 More importantly, that study on a flat Cu(643)R&S single crystal yielded the same enantiospecificity as the current study on the curved Cu(111)±14°-S4C; i.e.D-TA exhibits higher reactivity, t1/2−1, on the S-surfaces than on the R-surfaces.
The highest enantiospecificity for TA decomposition on our Cu(111)±14°-S4C is observed on chiral regions having high step density at large polar angles. We can only speculate on the origin of the observed enantiospecificity. One microscopic explanation could be that the packing density of D- or L-TA on the narrow terraces at the edge of the sample is influenced enantiospecifically by the chirality of the nearby kinks in the (310) step edges. The difference in the packing densities of the two TA enantiomers may influence the rates of formation of the vacancies needed for the explosion reaction.
5. Conclusions
Both rate constants, k(hkl)i and k(hkl)e, for D- and L-TA decomposition on surfaces vicinal to Cu(111) reveal clear signs of structure sensitivity and enantiospecificity. The TA decomposition kinetics are well-described by the two rate constants across the entire range of surface orientations probed on the Cu(111)±14°-S4C. Enantiospecificity is most pronounced in the chiral zones of the S4C having high step density; i.e. at polar angles ≳ 9° from the Cu(111) surface. The values of k(hkl)e show enantiospecificity and structure sensitivity for both TA enantiomers. The clearest manifestation of enantiospecificity and diastereoemerism are observed in the values of t(hkl)1/2, with D-TA exhibiting greatest reactivity (lowest t(hkl)1/2) on the surface orientations with S-chirality and the least reactivity on the surface orientation with R-chirality. As dictated by diastereomerism, L-TA exhibits the opposite trend in reactivity. Using Δt(hkl)1/2 as a metric, we have identified surfaces having (754) orientation as the ‘most’ enantioselective for TA decomposition on the Cu(111)±14°-S4C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the NSF under grant number CHE2102082.References
- G. Ertl, Angew. Chem., Int. Ed. Engl., 1990, 29, 1219–1227 CrossRef.
- G. Ertl, Angew. Chem., Int. Ed., 2008, 47, 3524–3535 CrossRef CAS PubMed.
- N. D. Spencer, R. C. Schoonmaker and G. A. Somorjai, Nature, 1981, 294, 643–644 CrossRef CAS.
- N. D. Spencer, R. C. Schoonmaker and G. A. Somorjai, J. Catal., 1982, 74, 129–135 CrossRef CAS.
- N. D. Spencer and G. A. Somorjai, J. Catal., 1982, 78, 142–146 CrossRef CAS.
- D. W. Goodman, Surf. Sci., 1982, 123, L679–L685 CrossRef CAS.
- R. M. Rioux, H. Song, M. Grass, S. Habas, K. Niesz, J. D. Hoefelmeyer, P. Yang and G. A. Somorjai, Top. Catal., 2006, 39, 167–174 CrossRef CAS.
- Q. X. Cai, J. G. Wang, Y. G. Wang and D. H. Mei, AIChE J., 2015, 61, 3812–3824 CrossRef CAS.
- A. J. Gellman, J. Phys. Chem. B, 2002, 106, 10509–10517 CrossRef CAS.
- W. X. Huang, K. Qian, Z. F. Wu and S. L. Chen, Acta Phys. -Chim. Sin., 2016, 32, 48–60 CAS.
- N. Musselwhite and G. A. Somorjai, Top. Catal., 2013, 56, 1277–1283 CrossRef CAS.
- M. T. M. Koper, Nanoscale, 2011, 3, 2054–2073 RSC.
- A. J. Gellman, Y. Huang, X. Feng, V. V. Pushkarev, B. Holsclaw and B. S. Mhatre, J. Am. Chem. Soc., 2013, 135, 19208–19214 CrossRef CAS PubMed.
- A. J. Gellman, ACS Nano, 2010, 4, 5–10 CrossRef CAS PubMed.
- D. S. Sholl and A. J. Gellman, AIChE J., 2009, 55, 2484–2490 CrossRef CAS.
- A. J. Gellman, W. T. Tysoe and F. Zaera, Catal. Lett., 2015, 145, 220–232 CrossRef CAS.
- A. J. Gellman and K. H. Ernst, Catal. Lett., 2018, 148, 1610–1621 CrossRef CAS.
- J. Prinz, O. Gröning, H. Brune and R. Widmer, Angew. Chem., Int. Ed., 2015, 54, 3902–3906 CrossRef CAS PubMed.
- S. R. Jenkins, Chirality at Solid Surfaces, John Wiley & Sons, Hoboken, NJ, 2018 Search PubMed.
- R. M. Hazen and D. S. Sholl, Nat. Mater., 2003, 2, 367–374 CrossRef CAS PubMed.
- C. F. McFadden, P. S. Cremer and A. J. Gellman, Langmuir, 1996, 12, 2483–2487 CrossRef CAS.
- S. J. Jenkins and S. J. Pratt, Surf. Sci. Rep., 2007, 62, 373–429 CrossRef CAS.
- J. D. Horvath and A. J. Gellman, J. Am. Chem. Soc., 2002, 124, 2384–2392 CrossRef CAS PubMed.
- Y. Yun and A. J. Gellman, Angew. Chem., Int. Ed., 2013, 52, 3394–3397 CrossRef CAS PubMed.
- D. M. Rampulla and A. J. Gellman, Surf. Sci., 2006, 600, 2823–2829 CrossRef CAS.
- D. M. Rampulla, A. J. Francis, K. S. Knight and A. J. Gellman, J. Phys. Chem. B, 2006, 110, 10411–10420 CrossRef CAS PubMed.
- F. Zaera, A. J. Gellman and G. A. Somorjai, Acc. Chem. Res., 1986, 19, 24–31 CrossRef CAS.
- B. Karagoz, M. Payne, A. Reinicker, P. Kondratyuk and A. J. Gellman, Langmuir, 2019, 35, 16438–16443 CrossRef CAS PubMed.
- T. J. Lawton, V. Pushkarev, E. Broitman, A. Reinicker, E. C. H. Sykes and A. J. Gellman, J. Phys. Chem. C, 2012, 116, 16054–16062 CrossRef CAS.
- J. R. Kitchin and A. J. Gellman, AIChE J., 2016, 62, 3826–3835 CrossRef CAS.
- M. A. Payne, J. B. Miller and A. J. Gellman, Corros. Sci., 2016, 106, 61–81 CrossRef CAS.
- D. Farrusseng, Surf. Sci. Rep., 2008, 63, 487–513 CrossRef CAS.
- I. Takeuchi, R. Bruce Van Dover and H. Koinuma, MRS Bull., 2002, 27, 301–308 CrossRef CAS.
- A. De Alwis, B. Holsclaw, V. V. Pushkarev, A. Reinicker, T. J. Lawton, M. E. Blecher, E. C. H. Sykes and A. J. Gellman, Surf. Sci., 2013, 608, 80–87 CrossRef CAS.
- E. G. Linder, Phys. Rev., 1927, 30, 649–655 CrossRef CAS.
- A. T. Gwathmey and A. F. Benton, Trans. Electrochem. Soc., 1940, 77, 211 CrossRef.
- A. T. Gwathmey and A. F. Benton, J. Chem. Phys., 1940, 8, 431–432 CrossRef CAS.
- A. T. Gwathmey and A. F. Benton, J. Chem. Phys., 1940, 8, 569–570 CrossRef CAS.
- A. T. Gwathmey and A. F. Benton, J. Phys. Chem., 1942, 46, 969–980 CrossRef CAS.
- A. Armitage, H. Liu and D. Woodruff, Vacuum, 1981, 31, 519–522 CrossRef CAS.
- A. F. Armitage and D. P. Woodruff, Surf. Sci., 1982, 114, 414–430 CrossRef CAS.
- M. Ilyn, A. Magaña, A. L. Walter, J. Lobo-Checa, D. G. De Oteyza, F. Schiller and J. E. Ortega, J. Phys. Chem. C, 2017, 121, 3880–3886 CrossRef CAS.
- J. E. Ortega, G. Vasseur, I. Piquero-Zulaica, S. Matencio, M. A. Valbuena, J. E. Rault, F. Schiller, M. Corso, A. Mugarza and J. Lobo-Checa, New J. Phys., 2018, 20 Search PubMed.
- F. Schiller, M. Ilyn, V. Pérez-Dieste, C. Escudero, C. Huck-Iriart, N. Ruiz Del Arbol, B. Hagman, L. R. Merte, F. Bertram, M. Shipilin, S. Blomberg, J. Gustafson, E. Lundgren and J. E. Ortega, J. Am. Chem. Soc., 2018, 140, 16245–16252 CrossRef CAS PubMed.
- J. Janlamool, D. Bashlakov, O. Berg, P. Praserthdam, B. Jongsomjit and L. B. F. Juurlink, Molecules, 2014, 19, 10845–10862 CrossRef PubMed.
- R. van Lent, S. V. Auras, K. Cao, A. J. Walsh, M. A. Gleeson and L. B. F. Juurlink, Science, 2019, 157, 155–157 CrossRef PubMed.
- A. J. Walsh, R. van Lent, S. V. Auras, M. A. Gleeson, O. T. Berg and L. B. F. Juurlink, J. Vac. Sci. Technol., A, 2017, 35, 03E102 CrossRef.
- A. Ahmadi, G. Attard, J. Feliu and A. Rodes, Langmuir, 1999, 15, 2420–2424 CrossRef CAS.
- G. A. Attard, A. Ahmadi, J. Feliu, A. Rodes, E. Herrero, S. Blais and G. Jerkiewicz, J. Phys. Chem. B, 1999, 103, 1381–1385 CrossRef CAS.
- A. E. Baber, A. J. Gellman, D. S. Sholl and E. C. H. Sykes, J. Phys. Chem. C, 2008, 112, 11086–11089 CrossRef CAS.
- X. Zhao, S. S. Perry, J. D. Horvath and A. J. Gellman, Surf. Sci., 2004, 563, 217–224 CrossRef CAS.
- M. O. Lorenzo, S. Haq, T. Bertrams, P. Murray, R. Raval and C. J. Baddeley, J. Phys. Chem. B, 1999, 103, 10661–10669 CrossRef CAS.
- M. O. Lorenzo, C. J. Baddeley, C. Muryn and R. Raval, Nature, 2000, 404, 376–379 CrossRef CAS PubMed.
- M. O. Lorenzo, V. Humblot, P. Murray, C. J. Baddeley, S. Haq and R. Raval, J. Catal., 2002, 205, 123–134 CrossRef CAS.
- B. Behzadi, S. Romer, R. Fasel and K. H. Ernst, J. Am. Chem. Soc., 2004, 126, 9176–9177 CrossRef CAS PubMed.
- S. Romer, B. Behzadi, R. Fasel and K. H. Ernst, Chem. – Eur. J., 2005, 11, 4149–4154 CrossRef CAS PubMed.
- A. J. Gellman and K. H. Ernst, Catal. Lett., 2018, 148, 1610–1621 CrossRef CAS.
- B. S. Mhatre, V. Pushkarev, B. Holsclaw, T. J. Lawton, E. C. H. Sykes and A. J. Gellman, J. Phys. Chem. C, 2013, 117, 7577–7588 CrossRef CAS.
- B. S. Mhatre, S. Dutta, A. Reinicker, B. Karagoz and A. J. Gellman, Chem. Commun., 2016, 52, 14125–14128 RSC.
- A. J. Therrien, T. J. Lawton, B. Mernoff, F. R. Lucci, V. V. Pushkarev, A. J. Gellman and E. C. H. Sykes, Chem. Commun., 2016, 52, 14282–14285 RSC.
- A. J. Gellman, Acc. Mater. Res., 2021, 2, 1024–1032 CrossRef CAS.
- P. Kondratyuk, B. Karagoz, Y. Yun and A. J. Gellman, J. Phys. Chem. C, 2019, 123, 18978–18985 CrossRef CAS.
- C. Fernández-Cabán and A. J. Gellman, J. Phys. Chem. C, 2021, 125, 9766–9773 CrossRef.
- D. S. Wei, B. S. Mhatre, A. J. Gellman and D. S. Sholl, Surf. Sci., 2014, 629, 35–40 CrossRef CAS.
- A. J. Gellman, Y. Huang, A. J. Koritnik and J. D. Horvath, J. Phys.: Condens. Matter, 2017, 29, 034001 CrossRef PubMed.
- M. A. Van Hove and G. A. Somorjai, Surf. Sci., 1980, 92, 489–518 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Graphical illustration of the chiral Cu(3,1,17)R&S surfaces; stereographic triangle of all possible surface orientations for an FCC lattice; electron backscatter diffraction of the Cu(111)±14°-S4C; grid of points used for mapping the coverage of TA; maps of ki(hkl), ke(hkl) and t1/2−1 not rotationally averaged. See DOI: 10.1039/d1ma00876e |
| This journal is © The Royal Society of Chemistry 2022 |