Solvent selection for polymers enabled by generalized chemical fingerprinting and machine learning†
Joseph
Kern
 ,
Shruti
Venkatram
,
Manali
Banerjee
,
Blair
Brettmann
,
Shruti
Venkatram
,
Manali
Banerjee
,
Blair
Brettmann
 and
Rampi
Ramprasad
*
and
Rampi
Ramprasad
*
School of Materials Science and Engineering, College of Engineering, Georgia Institute of Technology, 771 Ferst Drive, J. Erskine Love Building, Atlanta, GA 30332-0245, USA. E-mail: rampi.ramprasad@mse.gatech.edu
First published on 31st October 2022
Abstract
We present machine learning models trained on experimental data to predict room-temperature solubility for any polymer–solvent pair. The new models are a significant advancement over past data-driven work, in terms of protocol, validity, and versatility. A generalizable fingerprinting method is used for the polymers and solvents, making it possible, in principle, to handle any polymer–solvent combination. Our data-driven approach achieves high accuracy when either both the polymer and solvent or just the polymer has been seen during the training phase. Model performance is modest though when a solvent (in a newly queried polymer–solvent pair) is not part of the training set. This is likely because the number of unique solvents in our data set is small (much smaller than the number of polymers). Nevertheless, as the data set increases in size, especially as the solvent set becomes more diverse, the overall predictive performance is expected to improve.
1 Introduction
Solvent selection is an important component of polymer synthesis and processing as well as a multitude of polymer applications like microlithography, membrane formation, drug delivery systems, recycling, and waste processing.1 In microlithography, polymers are exposed to electromagnetic radiation to cause changes to their chemical structure, then immersed in a solvent to dissolve either the exposed or unexposed region.2 When forming membranes using non-solvent induced phase separation, a polymer is dissolved in a solvent to create a homogeneous dope solution. This solution is cast as a liquid film on a substrate which is then placed in a coagulation non-solvent bath to remove the solvent and form the membrane.3 In drug delivery systems, water soluble polymers are used to increase the solubility of poorly soluble drugs by dispersing the drug in the polymer structure.4,5 Water soluble polymers are also used as stabilisers and mechanical supports for sustained release of drugs.6 In efforts to chemically recycle industrially relevant polymers like polystyrene and high-density polyethylene in a single process stream, solvent selection was identified as the most critical parameter.7 In water treatment, water-soluble polymeric materials are used to remove heavy metal ions and arsenic.8 Water soluble polymers used in cosmetics and laundry detergents can also leach into the environment and need to be removed via sorption.9 When using solvents during the creation of polymers, toxic solvents can remain in the polymers post-processing and come into contact with humans, so ideally safe alternatives to commonly used solvents could also be determined for every polymer.10 Given how important polymer solubility is in these numerous processes, it is critical to have a method of estimating what solvents will dissolve polymers.To enable informed solvent identification, several empirical methods have been proposed with varying degrees of success, including the Hildebrand and Hansen methods. In the Hildebrand method, polymers and solvents with similar Hildebrand parametric values (which are related to the cohesive energy density) are predicted as good solvents and those with values differing by more than a threshold are predicted as bad solvents.1,11 In the Hansen method, the difference between three parameters quantifying dispersion, dipolar, and hydrogen bonding interactions for the polymer and solvent are used to provide an estimate of the solubility of the polymer in the solvent.12 Previous work by Venkatram et al. showed the Hansen method performed only marginally better than the Hildebrand method despite its greater complexity.13
Several computational approaches have been used to estimate these solubility parameters, including group contribution methods14 and a variety of machine learning techniques. Sanchez-Lengeling et al. used Gaussian process regression with Morgan and MACCS fingerprints to estimate Hansen solubility parameters for 31 polymers and 193 solvents, achieving reasonable R2 performance (0.56–0.83).15 Kurotani et al. used only four pieces of analytical data to predict Hansen solubility parameters for polymers as well, and while their R2 performance was lower than Sanchez-Lengeling et al., they posited that it may be useful for new polymers with unknown SMILES strings.16 Others have used descriptors derived from atomic structure and quantum chemical calculation for small molecules representing polymer repeat units to predict the Hildebrand solubility parameters using kernel ridge regression and multi-linear regression models.17 Most recently, Liu et al. collected data on 81 polymers and 1221 solvents and created more easily interpretable regression models to predict Chi, Hildebrand, and Hansen parameters.18 They featurized their polymers and solvents using RDKit generated chemical fingerprints such as the count, density and weighted sum for atoms, and 2nd order features generated from the 3d structures of trimers and solvents such as LUMO, HOMO and heat of formation.
Meanwhile, previous work by Chandrasekaran et al.,19 inspired by the promise of machine learning in the materials domain,20,21 showed that a deep neural network trained on a data set of 4595 polymers and 24 solvents could dramatically outperform the Hildebrand approach to estimating solubility.1,11 This method utilized chemical features to represent polymers and a one-hot (label-based) encoding to represent the solvents which were used to train a multilayer perceptron neural network that could classify whether a particular polymer–solvent combination was soluble or insoluble. They also found that a Hildebrand Gaussian process model's classification accuracy was much worse than the neural network, correctly classifying good-solvents only 50% of the time and bad solvents 70% as opposed to the over 90% accuracy for the neural network. The downside to their neural network approach, however, was that solubility estimations could be performed for only the 24 solvents within the training data due to the one-hot encoding; i.e., predictions could not be generalized to cases outside the list of 24 solvents.
In the present work, we demonstrate a method to generalize machine learning models to any solvent so predictions can be made on previously unseen solvents. Moreover, we perform a critical analysis of the strengths and weaknesses of any such data-driven approach and identify situations where caution is mandated. First, a data set of 3373 polymers and 51 solvents was collected. Next, we structurally fingerprinted the polymers and solvents using a hierarchical methodology that is generalizable to any polymer–solvent pair, unlike the one-hot encoding method. Finally, these fingerprints and solubility data were used to train a random forest classifier and a deep neural network binary classifier that predicts if a polymer–solvent pair is soluble or insoluble. A production version of the random forest model has been deployed to our online polymer informatics platform, polymer genome (https://www.polymergenome.org).22,23
In the Methods section we provide details on the dataset, featurization of the polymers and solvents, and the model infrastructures. In the Results and discussion section, we analyze the performance of the two machine learning models with respect to the quality and diversity of the data they have been exposed to, the differences between the two models, areas of caution, and potential next steps.
2 Methods
2.1 Dataset
The dataset used is manually curated from a plethora of published works including published journals, printed handbooks, and online repositories.24–29 The chemical space the polymers span included the following elements: C, O, Se, N, F, P, S, Br, Si, Cl, I, B, and H. Copolymers, polymer blends, polymers with additives, and cross-linked polymers are not considered in this study. We also limit this study to the investigation of room-temperature solubility and do not consider partial solubility or high-temperature solubility.The training data set consisted of 3373 polymers and 51 solvents (see Table S1, ESI†) making up 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913 soluble pairs and 8843 insoluble pairs. An additional 2909 polymers and 7 solvents (see Table S2, ESI†) making up 7736 soluble data points and 1129 insoluble data points were tested with the final model. These 2909 polymers and 7 solvents did not have instances of being both soluble and insoluble, thus, they were excluded from the training data to prevent the model from incorrectly learning that the specific polymer or solvent is always one class (either soluble or insoluble). A full analysis is available in the section (Fig. S1 and S2, ESI†) describing why this was done.
913 soluble pairs and 8843 insoluble pairs. An additional 2909 polymers and 7 solvents (see Table S2, ESI†) making up 7736 soluble data points and 1129 insoluble data points were tested with the final model. These 2909 polymers and 7 solvents did not have instances of being both soluble and insoluble, thus, they were excluded from the training data to prevent the model from incorrectly learning that the specific polymer or solvent is always one class (either soluble or insoluble). A full analysis is available in the section (Fig. S1 and S2, ESI†) describing why this was done.
2.2 Fingerprinting
For polymers, three hierarchical levels of descriptors, comprising 690 features, that correspond to three different length scales were used.22,30 The first (lowest) level counts the number of atomic triplets (e.g., H1–C4–H1, representing two one-fold coordinated hydrogen, and a four-fold coordinated carbon). The second (middle) level of fingerprint components captures a population of predefined chemical building blocks (e.g., –C6H4–, –CH2–, –C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–). The third (highest) level comprises quantitative structure–property relationship (QSPR) descriptors that are characteristic features of the polymers, such as molecular features including molecular quantum numbers and molecular connectivity chi indices, as well as additional descriptors such as the number of non-hydrogen atoms, molecular weight, the fraction of atoms that are part of side chains and the length of the largest side chain. Note that the total number of features can vary due to factors such as the number of atomic triplets and the blocks in the data set.
O)–). The third (highest) level comprises quantitative structure–property relationship (QSPR) descriptors that are characteristic features of the polymers, such as molecular features including molecular quantum numbers and molecular connectivity chi indices, as well as additional descriptors such as the number of non-hydrogen atoms, molecular weight, the fraction of atoms that are part of side chains and the length of the largest side chain. Note that the total number of features can vary due to factors such as the number of atomic triplets and the blocks in the data set.
For solvents, either one-hot encoding or structural fingerprinting was used. One-hot encoding creates 51 columns (corresponding to the number of training solvents). Each row represents a polymer/solvent combination with the column corresponding to the solvent being 1 and all other solvent columns being 0. The structural fingerprint uses the same three hierarchical levels of descriptors, comprising 155 features, inspired by previous work on polymer fingerprinting.22,30 There are differences between the solvent and polymer fingerprints, however. For instance, the solvent fingerprints sample separate blocks and some QSPR descriptors are not used, such as the fraction of atoms that are part of side chains and length of the largest side chain.
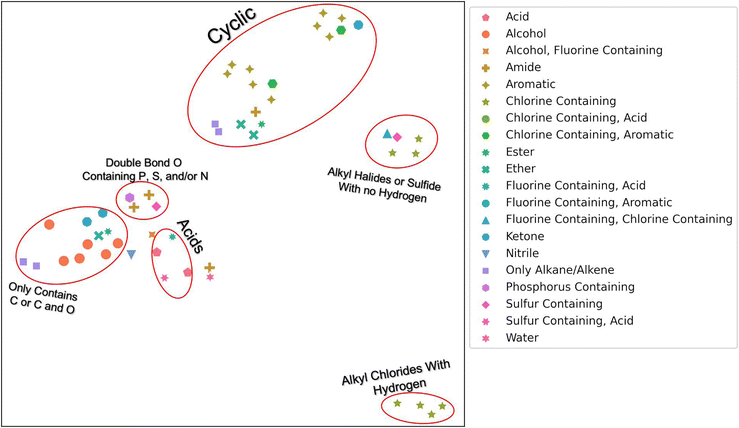
To determine if our hierarchical solvent fingerprint adequately represents the solvents and to visualize the high dimensional fingerprint in two dimensions, we used a Uniform Manifold Approximation and Projection (UMAP) plot shown in Fig. 1. From this plot, we find that similar solvents cluster together in the fingerprint space. Acids, like nitric acid or formic acid, are clustered together, as are cyclic compounds like benzene and phenol. There were two grouping of halides: ones with carbons that contain hydrogen atoms, like chloroform, and ones without hydrogen atoms, like trichloro(fluoro)methane. The second grouping also contains carbon disulfide. There is a small grouping of dimethyl solvents that contain either P, S, and or N that also contain a double bond O. These include solvents like dimethylformamide (DMF) and dimethylsulfoxide (DMSO). Finally, there are the alkanes, alcohols, and other solvents that contain only carbon or carbon and oxygen. Note that UMAP plots are stochastic and affected by hyper-parameters such as n_neighbors (a constraint in the size of the local neighborhood UMAP looks at), min_dist (the minimum distance apart points are allowed to be in the low dimensional representation) and metric (how distance is computed in the ambient space of the input data). We used default values except for n_neighbors = 3, min_dist = 0.99, with a cosine metric for this image.31 The n_neighbors value of 3 allowed us to observe the local manifold structure as opposed to global. The min_dist of 0.99 was to prevent points from being too close together for visualization purposes. The cosine metric was chosen because it has been found to be a better metric for chemical similarity calculations than Euclidean or Manhattan metrics.32
2.3 Model details
We have employed two ML algorithms, one based on deep neural networks and another based on random forests. Each model was assessed using the F1 score, which is defined as a harmonic sum of precision and recall, with precision being the proportion of predicted positives that are truly positive, and recall being the proportion of actual positives correctly classified.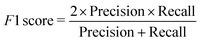 | (1) |
 | (2) |
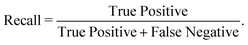 | (3) |
When assessing performance, the training dataset of 3373 polymers and 51 solvents was split using five-fold cross validation. Three types of splits were done: a random split stratified by solubility, a split by the polymer, and a split by the solvent. The random split stratified by solubility was meant to measure how the model performed on previously seen polymers and solvents. The split by the polymer was meant to measure how the model performed on unseen polymers but previously seen solvents. The split by solvent was meant to measure how the model performed on unseen solvents but previously seen polymers. Each split type created five-folds of equal size. The model was trained on four of the folds and tested on the fifth five times, so each fold was a test fold once.
For the neural network, We used the same multilayer perceptron neural network infrastructure and hyperparameters as described by Chandrasekaran et al. The neural network consists of two input branches, one for the solvent fingerprints and the other for the polymer fingerprints. Two hidden layers are used for the solvent branch and three are used for the polymer branch. Each hidden layer has 100 neurons. A final layer of 20 neurons is added to the end of each branch which are concatenated and fed into a final set of layers. The final set of layers consists of four hidden layers with 100 neurons each. The final output of the NN is a single neuron with a sigmoid activation function. An activation value of 1 means the polymer is soluble in the solvent and an activation of 0 means it is insoluble. The threshold to differentiate between the two is 0.5. Each hidden layer in the NN uses a parametrized rectified linear unit (PReLU) activation function.19 The input layer for the solvent is altered when the structural fingerprint is used instead of the one-hot encoding. This neural network will be referred to as SolNet2 to distinguish it from an earlier model (SolNet) that used one-hot fingerprinting for solvents.
For the random forest classifier, SciKit-Learn was used.33,34 BayesSearchCV, a method using Bayesian optimization over hyper parameters implemented with the scikit optimize package,35 with five-fold cross validation for 25 iterations optimizing max_depth = [None, 50, 100], max_features = [0.5, 0.75, ‘log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2’, ‘sqrt’], min_samples_leaf = [2, 6], and n_estimators = [100, 500] was used for hyperparameter optimization. We performed hyperparameter optimization for each split type, but found that model test F1 score did not significantly improve after hyperparameter optimization, whereas the model training time was dramatically slowed. As such, we used the default parameters with n_estimators = 100, max_depth = None, max_features = ‘sqrt’, and min_samples_leaf = 1 for the reported trees.
2’, ‘sqrt’], min_samples_leaf = [2, 6], and n_estimators = [100, 500] was used for hyperparameter optimization. We performed hyperparameter optimization for each split type, but found that model test F1 score did not significantly improve after hyperparameter optimization, whereas the model training time was dramatically slowed. As such, we used the default parameters with n_estimators = 100, max_depth = None, max_features = ‘sqrt’, and min_samples_leaf = 1 for the reported trees.
3 Results and discussion
First, we analyzed how the SolNet2 model performed when a solvent structural fingerprint was used as opposed to a one-hot encoding (SolNet). Next, we compared the SolNet2 model to a random forest classifier. Then, learning curves were generated for the random forest model to assess how the models performs on polymer–solvent pairings where both the polymer and solvent have not been seen before. Finally, we analyzed how the random forest classifier did when estimating solubility for the held out 2909 polymers and 7 solvents (refer back to Table S2 for details on this data set, ESI†). The SolNet2 model was not considered as the random forest model outperformed it in all metrics.3.1 SolNet2 model performance
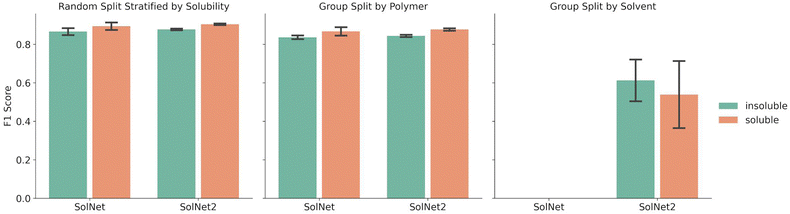
Fig. 2 shows a comparison between the F1 scores of the SolNet model trained using a one-hot encoding for solvents vs. the SolNet2 model trained using the structural fingerprint. The error bars indicate the standard deviation of F1 score between test folds of 5-fold cross validation splits. The split was done via a random split stratified by solubility, group split by polymer, or group split by solvent. For both solvent encodings, the same data was used for each split with only the solvent fingerprint changing.The splitting method used for five-fold cross validation dictated model F1 score. For instance, when a random split stratified by solubility was chosen to split the training and test sets of the model, the F1 score for insoluble pairing predictions was 0.866 ± 0.020 for SolNet. When the training and test data was split so no polymer in the training data was in the test data, the F1 score for insoluble pairing predictions dropped to 0.840 ± 0.010 for SolNet. This was likely because, in the former case, i.e., when a random split was used, the model had seen most of the polymers and solvents before in the training data. Even though the test polymer–solvent combination was unique, the model could more readily extrapolate to this new case based on similar experiences with the same polymer and solvent in the past. In a polymer split, the model hadn't seen the test polymers before, so it had to solely extrapolate from train polymers that had similar chemistry to the test polymers. The differences in the polymer chemistry would then have an impact on the predictive accuracy. This trend held for the models trained using a structural fingerprint too.
The model performed slightly better with the solvent structural encoding (SolNet2) and had tighter error bars. For example, the F1 score for insoluble predictions for a random split was 0.877 ± 0.004 as opposed to 0.866 ± 0.020 for SolNet. However, this difference is small and the structural fingerprint required a dramatically larger fingerprint. The main strength of the structural encoding was that it was able to generalize to solvents outside of the data set. In fact, SolNet is incapable of handling the solvent split case (which is why Fig. 2 does not have this case represented). SolNet2, on the other hand, can handle solvent splits. Nevertheless, even in this case, a solvent split resulted in poorer performance than the random-split and polymer split (having a smaller F1 score of 0.612 ± 0.121 for insoluble pairings). This was likely due to three reasons: solvent scarcity, polymer scarcity within splits, and a greater imbalance in classes.
Regarding solvent scarcity, only 51 solvents were in the data set in contrast to the 3373 polymers. During a polymer split, the test polymers are more likely to have chemically similar neighbors that have been paired with the specific solvent before, whereas this was unlikely in the solvent split due to solvent scarcity. This may provide an explanation for why the polymer split F1 score was between 0.83–0.89 for each of the five test fold versus 0.34–0.74 for the solvent split test folds.
The second potential reason for the low F1 score of the solvent split could be the polymer scarcity within a train-test split. For instance, a polymer in the test set may have nine instances in the train set, but each instance in the train set may be soluble while the test case pairing was insoluble. Thus the model will incorrectly classify the test polymer–solvent combination as soluble when it is actually insoluble because it has never seen an instance of this polymer being soluble. For each split there are between 122 to 194 polymers that have soluble pairings in the test set but only insoluble pairings in the train set and between 48 to 994 polymers that have insoluble pairings in the test set but only soluble pairings in the train set. This does not fully explain the variation in F1 score between splits though. For instance, while one split had 994 polymers that had an insoluble pairing in the test set but only soluble pairings in the train set, the model correctly predicted the class in 83.6% of these test pairings and the total insoluble F1 score for that split was 0.734. Conversely, splits with relatively low numbers of these cases (where <5% of data has a class for a polymer in the test split that has not been seen in the train split) have low F1 scores of 0.32 to 0.48. Thus, while the polymer scarcity within a train-test may contribute to the variation in the F1 score, it does not seem to be the dominant reason for the discrepancy.
The final possibility could be due to class imbalance within the test splits. The F1 metric is a harmonic mean of precision and recall, and precision is highly affected by class imbalances.36 Some generated examples of the effect of data imbalance on F1 scores are shown in Fig. S3 in the ESI.† During stratified random splits, 57% of the test data is soluble and 43% is insoluble. Polymer splits are very close to this as well (55% to 59% of test data is soluble). For both these split types, the variability in class imbalance was lower and the classes were not heavily imbalanced, so variability in precision due to class imbalance was expected to be low. For solvent splits, the soluble test data makes up 41%, 50%, 50%, 71%, and 75% of the data with insoluble data being the remainder. When the soluble percentage is close to 50%, precision for soluble and insoluble predictions are almost equivalent (0.02 difference between precision values). When the soluble percentage is larger (71 or 75%), precision values for soluble predictions are 0.81 and 0.90 respectively, whereas precision for insoluble predictions are 0.4 and 0.34 respectively. This large difference is likely due to the class imbalance. However, after assessing the cross-fold variability in recall (shown in Fig. S4, ESI†), this effect does not seem to be the main cause of the variability in F1 score for folds. As such, we believe the dominant issue was the solvent scarcity, as discussed further below.
3.2 Random forest performance
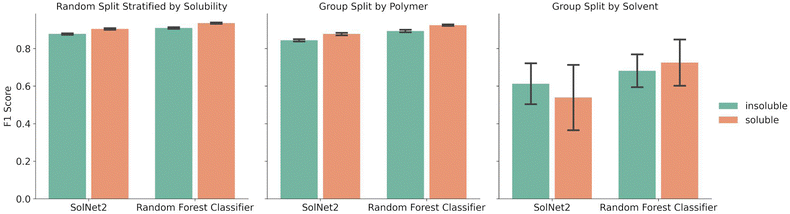
A random forest classifier was also trained on the solvent structural fingerprint, but not the one-hot encoding. The random forest approach was chosen because it requires less training time than the SolNet2 model, it is good at binary predictions on tabular data, and ensemble models typically perform well while avoiding over fitting. A comparison between the performance of the random forest model and SolNet2 model is shown in Fig. 3. As before, the splits were done via a random split stratified by solubility, group split by polymer, or group split by solvent. Both models were trained and tested on the same train-test splits of data, with the error bars resulting from the different test result from five-fold cross validation.The random forest classifier outperforms the SolNet2 model across all methods of splitting data. For instance, in the random split stratified by solubility the average F1 score was 0.935 ± 0.003 for soluble pairings vs. the SolNet2 performance of 0.904 ± 0.005. The largest improvement was in the group split by solvents, with a jump for insoluble predictions from 0.612 ± 0.121 in the SolNet2 model to 0.682 ± 0.097 in the random forest model and a jump for soluble predictions from 0.539 ± 0.195 in the SolNet2 model to 0.725 ± 0.137 in the random forest model. The superior performance of the random forest classifier could be because the random forest's ensemble method reduces the chance of over-fitting or because the dataset is too small for a neural network to outperform the random forest.
3.3 Performance on completely unseen data
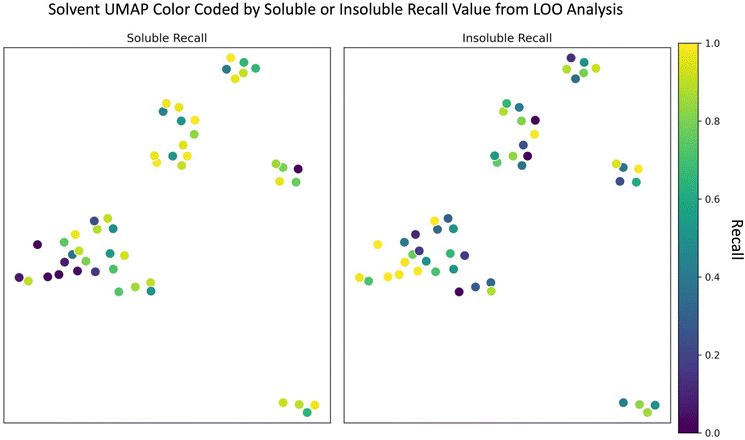
Since the random forest model outperformed the SolNet2 model and trains faster, we used it for the remaining analysis. To test how the random forest model performed on completely unseen data, especially unseen solvents, we performed a leave one out (LOO) analysis of the solvents. Each of the 51 solvents and all of their associated polymers were held out as a test case and 51 models were trained with the remaining polymers and solvents. The models' recall metric on their test solvent/polymer combinations was used in this analysis instead of F1 score due to the large test set imbalance in classes for some solvents. The UMAP from Fig. 1 was modified into two plots shown in Fig. 4: one color coded according to soluble recall, and the other to insoluble recall.As seen in Fig. 4, there are, in general, two cases that occur depending on the solvent: one where the recall for one class is high and the other low (e.g., for many alcohols) and another where both soluble and insoluble recalls are roughly the same (e.g., for several aromatic compounds). In either case, the model performs best when (1) the left-out solvent is similar to some training solvents, (2) the polymers accompanying the left-out solvent are similar to the polymers accompanying the similar training solvents, and (3) the polymer–solvent combination of the test cases fall in the same class as the similar pairs in the train set. The model performs worst if there is a similar test solvent with similar training polymers, but the classification of the similar training combinations are opposite (i.e., counter to requirement (3) above). For instance, despite the alcohols having many similar solvents in the training data (according to Fig. 1 and 4), the model often struggled to correctly classify soluble pairings. For the alcohol methanol, this is due to the addition of water. Based on Fig. 1 and a Tanimoto similarity score of 0.53 (eqn (S1), 0 is completely different, 1 is chemically equivalent, ESI†), water is somewhat chemically similar to methanol. The water data also contains a significant number of training polymers that are chemically similar to the test polymers paired with methanol. For insoluble methanol–polymer combinations these chemically similar water–polymer combinations were the same class, but for soluble methanol–polymer pairings the chemically similar water–polymer combinations were the opposite class (i.e., insoluble). Thus, the model often performs poorly for these soluble methanol–polymer pairings because it's been trained on oppositely classified but chemically similar water–polymer pairs, hence the low soluble recall. A more in-depth learning curve analysis of the LOO analysis is shown in the “Learning Curve” section in the ESI.†
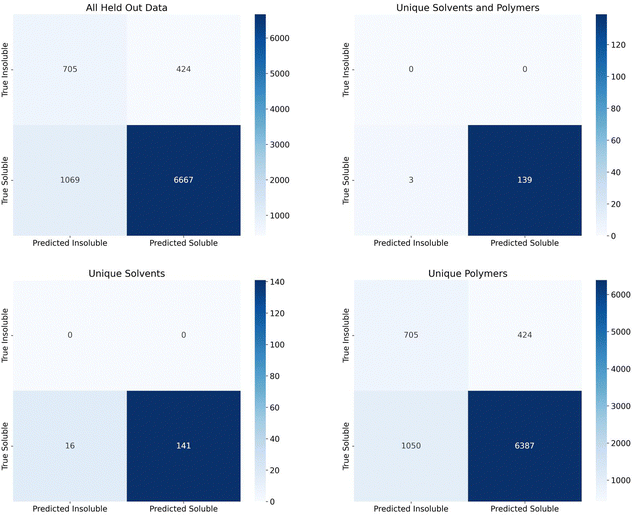
Finally, we assessed the random forest model's performance on the additional 2909 polymers and 7 solvents making up 7736 soluble data points and 1129 insoluble data points that were held out since the polymers and solvents only had one class associated with them. Confusion matrices for the predictions on this set are shown in Fig. 5. The top left matrix represents all data, the top right represents the pairings where both the polymer and solvent were unseen by the model, the bottom right represent the pairings where the solvents had been seen by the model but the polymers had not been, and the bottom left represents the pairings where the polymers had been seen by the model, but the solvents had not been.
The recall for these predictions was 0.624 for insoluble points and 0.862 for soluble points. Due to the extremely large imbalance in soluble to insoluble data points (87% of data is soluble), assessing precision and F1 score would not be useful. All insoluble pairs were instances where the polymer was not seen by the model before, but the solvent was seen previously. This suggests we should have seen an insoluble recall closer to the group split by polymer levels (0.83–0.89). This lower recall could be due to a number of factors such as an extremely new polymer space or inaccuracies in the experimental data set. With regards to the new polymer space, these new polymers had 42 new, unique chemical fragments that were not seen in the training data, 32 unique atomic triplets, and the element iodine only appeared once in the training data vs. six times in the test data. On the other hand, there were only 31 test polymers with no similar training polymers (defined as a Tanimoto similarity score, eqn (S1) (ESI†), greater than 0.75). As such, it's also possible that, while the polymers had been seen before, they had not been tested in solvents similar to the test solvents or, if they had been tested in similar solvents, it's possible that the true solubility was opposite in those similar solvents. With respect to inaccuracies in the experimental data set, this is hard to measure without manual experiments. We collaborated with experimentalists to test some combinations at room temperature and found that a small percentage did conflict. However, polymer solubility can be significantly impacted by molecular weight and concentration, so two experiments could have different results depending on these values. Future work could explore how this uncertainty can impact model performance, as has been done with Tg predictions on polymers, and it is important future work consider these critical engineering parameters.37
4 Conclusions & outlook
The two-fold goal of this work was to (1) create a generalizable fingerprint for solvents that allows machine learning models to predict polymer solubility in solvents not seen during the training phase, and (2) evaluate the strengths and limitations of these machine-learning-based methods for solubility prediction while considering the data the models are exposed to during training. We experimented with random forest machine learning models and compared these models and the generalizable fingerprint, respectively, to previously designed neural network-based models and a one-hot (or labeling-based) encoding for solvents.19 The generalizable solvent fingerprint used covered three hierarchical levels of descriptors (atomic, block, and QSPR based) and was inspired by previous work on polymer fingerprinting.22,30 To test where solubility predictions succeeded and failed for the different ML models, five-fold cross validation was used with three different data splitting methods: a random split stratified by solubility, a split by polymer, and a split by solvent. The random split represented a scenario where the polymer and solvent had been seen by the model during training, but the combination was unique. The split by polymer (solvent) represented a scenario where the solvent (polymer) had been seen by the model during training, but the polymer hadn't. A leave one out analysis of solvents and their respective polymers was also performed with the random forest models to assess the scenario where both the polymer and solvent had not been seen before. Finally, a random forest model trained on all of the data was used to predict on an additional data set of polymers and solvents that was not used for testing. A production level random forest model to predict polymer solubility in solvents has been deployed at polymer genome (https://www.polymergenome.org).23This work has a few key takeaways:
1. Our generalizable solvent fingerprint was as effective as a previously used one-hot encoding method and could predict on solvents unseen by the model during training, unlike the one-hot encoding method.
2. The models were more accurate for predictions on unseen polymers vs. unseen solvents, likely due the larger polymer data set size (3373) compared to solvent data set size (51).
3. The model performance was modest on unseen solvents, likely because the model either had not seen similar solvents during training, or because the polymer–solvent combinations seen during training were too dissimilar (either chemically or by classification) to the test polymer–solvent combinations.
4. The random forest model outperformed the neural network based models in all splitting methods.
5. The random forest models can make accurate predictions for polymer–solvent pairings where both the polymer and solvent had never been seen if they were trained on similar polymer–solvent pairings (chemically and by classification).
The purely data-driven framework described in this work can be systematically improved as it is exposed to an even larger quantity and diversity of data. It is critical that future data incorporates more solvents, and that the quantity and chemical diversity of polymers tested in each of these solvents is increased. Future works should also focus on including other features that affect solubility, such as concentration, molecular weight, and temperature, and it could expand to include partial solubility and solvent mixtures. Additionally, lower-fidelity solubility predictions (e.g., Hildebrand predictions) may be useful for creating multi-fidelity models with increased data set size and diversity. Finally, an active learning approach might be beneficial, where the chemical space of both polymers and solvents are evaluated in order to choose representative samples to experiment on.
Author contributions
Joseph Kern: investigation, formal analysis, conceptualization, methodology, software, visualization, writing original draft – review & editing. Shruti Venkatram: investigation, formal analysis, conceptualization, methodology, software, data curation, visualization writing original draft – review & editing. Manali Banerjee: methodology, data curation, investigation. Blair Brettmann: methodology, investigation, conceptualization, project administration, resources. Rampi Ramprasad: methodology, conceptualization, review & editing, project administration, funding acquisition, resources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Office of Naval Research through a Multidisciplinary University Research Initiative (MURI) Grant (N00014-20-1-2586). J. K. gratefully acknowledges support through the National Defense Science and Engineering (NDSEG) Fellowship Program from the Department of Defense (DoD). J. K. also thanks Camilla Johnson for her assistance in manuscript review.Notes and references
- B. A. Miller-Chou and J. L. Koenig, Prog. Polym. Sci., 2003, 28, 1223–1270 CrossRef.
- C. Acikgoz, M. A. Hempenius, J. Huskens and G. J. Vancso, Eur. Polym. J., 2011, 47, 2033–2052 CrossRef CAS.
- X. Dong, D. Lu, T. A. L. Harris and I. C. Escobar, Membranes, 2021, 11, 309 CrossRef CAS.
- M.-J. Choi, M. R. Woo, H.-G. Choi and S. G. Jin, Int. J. Mol. Sci., 2022, 23, 9491 CrossRef CAS PubMed.
- D. Medarević, J. Djuriš, P. Barmpalexis, K. Kachrimanis and S. Ibrić, Pharmaceutics, 2019, 11, 372 CrossRef PubMed.
- V. G. Kadajji and G. V. Betageri, Polymers, 2011, 3, 1972–2009 CrossRef CAS.
- I. Tsampanakis and A. Orbaek White, Polymers, 2021, 14, 112 CrossRef PubMed.
- B. L. Rivas, B. F. Urbano and J. Sánchez, Front. Chem., 2018, 6, 320 CrossRef PubMed.
- K. Duis, T. Junker and A. Coors, Environ. Sci. Europe, 2021, 33, 21 CrossRef CAS.
- D. Lithner, A. Larsson and G. Dave, Sci. Total Environ., 2011, 409, 3309–3324 CrossRef CAS PubMed.
- A. F. M. Barton, Chem. Rev., 1975, 75, 731–753 CrossRef CAS.
- C. M. Hansen, Hansen solubility parameters: a user's handbook, CRC Press, Boca Raton, Fla, 2000 Search PubMed.
- S. Venkatram, C. Kim, A. Chandrasekaran and R. Ramprasad, J. Chem. Inf. Model., 2019, 59, 4188–4194 CrossRef CAS PubMed.
- S. Thakral and N. K. Thakral, J. Pharm. Sci., 2013, 102, 2254–2263 CrossRef CAS.
- B. Sanchez-Lengeling, L. M. Roch, J. D. Perea, S. Langner, C. J. Brabec and A. Aspuru-Guzik, Adv. Theory Simul., 2019, 2, 1800069 CrossRef.
- A. Kurotani, T. Kakiuchi and J. Kikuchi, ACS Omega, 2021, 6, 14278–14287 CrossRef CAS.
- M. Chi, R. Gargouri, T. Schrader, K. Damak, R. Maâlej and M. Sierka, Polymers, 2021, 14, 26 CrossRef PubMed.
- T.-L. Liu, L.-Y. Liu, F. Ding and Y.-Q. Li, Chin. J. Polym. Sci., 2022, 40, 834–842 CrossRef.
- A. Chandrasekaran, C. Kim, S. Venkatram and R. Ramprasad, Macromolecules, 2020, 53, 4764–4769 CrossRef.
- L. Chen, G. Pilania, R. Batra, T. D. Huan, C. Kim, C. Kuenneth and R. Ramprasad, Mater. Sci. Eng., R, 2021, 144, 100595 CrossRef.
- R. Batra, L. Song and R. Ramprasad, Nat. Rev. Mater., 2021, 6, 655–678 CrossRef.
- H. Doan Tran, C. Kim, L. Chen, A. Chandrasekaran, R. Batra, S. Venkatram, D. Kamal, J. P. Lightstone, R. Gurnani, P. Shetty, M. Ramprasad, J. Laws, M. Shelton and R. Ramprasad, J. Appl. Phys., 2020, 128, 171104 CrossRef CAS.
- Polymer Genome, https://polymergenome.org/.
- D. W. Van Krevelen and K. Te Nijenhuis, Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions, Elsevier, 2009 Search PubMed.
- J. E. Mark, Physical properties of polymers handbook, Springer, 2007, vol. 1076 Search PubMed.
- Polymer Database, https://polymerdatabase.com/.
- S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu and M. Yamazaki, International Conference on Emerging Intelligent Data and Web Technologies, 2011, pp. 22–29.
- J. Brandrup, E. H. Immergut, E. A. Grulke, A. Abe and D. R. Bloch, Polymer handbook, Wiley, New York, 1999, vol. 89 Search PubMed.
- G. Wypych, Handbook of polymers, Elsevier, 2016 Search PubMed.
- C. Kim, A. Chandrasekaran, T. D. Huan, D. Das and R. Ramprasad, J. Phys. Chem. C, 2018, 122, 17575–17585 CrossRef CAS.
- L. McInnes, J. Healy, N. Saul and L. Großberger, J. Open Source Software, 2018, 3, 861 CrossRef.
- D. Bajusz, A. Rácz and K. Héberger, J. Cheminf., 2015, 7, 20 Search PubMed.
- sklearn.ensemble.RandomForestClassifier, https://scikit-learn/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, A. Muller, J. Nothman, G. Louppe, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- skopt.BayesSearchCV—scikit-optimize 0.8.1 documentation, https://scikit-optimize.github.io/stable/modules/generated/skopt.BayesSearchCV.html.
- A. Luque, A. Carrasco, A. Martín and A. de las Heras, Pattern Recogn., 2019, 91, 216–231 CrossRef.
- A. Jha, A. Chandrasekaran, C. Kim and R. Ramprasad, Modell. Simul. Mater. Sci. Eng., 2019, 27, 024002 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03735a |
| This journal is © the Owner Societies 2022 |