The states that hide in the shadows: the potential role of conical intersections in the ground state unimolecular decay of a Criegee intermediate

Abstract

Criegee intermediates are of great significance to Earth's troposphere – implicated in altering the tropospheric oxidation cycle and in forming low volatility products that typically condense to form secondary organic aerosols (SOAs). As such, their chemistry has attracted vast attention in recent years. In particular, the unimolecular decay of thermal and vibrationally-excited Criegee intermediates has been the focus of several experimental and computational studies, and it is now recognized that Criegee intermediates undergo unimolecular decay to form OH radicals. In this contribution we reveal insight into the chemistry of Criegee intermediates by highlighting the hitherto neglected multi-state contribution to the ground state unimolecular decay dynamics of the Criegee intermediate products. The two key intermediates of present focus are dioxirane and vinylhydroperoxide – known to be active intermediates that mediate the unimolecular decay of CH₂OO and CH₃CHOO, respectively. In both cases the unimolecular decay path encounters conical intersections, which may play a pivotal role in the ensuing dynamics. This hitherto unrecognized phenomenon may be vital in the way in which the reactivity of Criegee intermediates are modelled and is likely to affect the ensuing dynamics associated with the unimolecular decay of a given Criegee intermediate.

---

Introduction

Criegee intermediates are a class of highly reactive organic compounds, known most prominently as reactive atmospheric oxidants. They are distinguishable by their carbonyl oxide functional group that contains Zwitterionic (or biradical) character. Criegee intermediates are an important source of non-photolytic OH radicals,^1–5 and are well-known for their role in promoting the oxidizing capacity of the troposphere and for forming low volatility products that typically condense to form secondary organic aerosols (SOAs). In the atmosphere, Criegee intermediates are formed via the oxidation of volatile alkenes with ozone.^6–9 The nascent Criegee intermediates are formed highly internally excited and may undergo prompt unimolecular decay or vibrational energy relaxation via collisions with bath molecules in the troposphere (e.g., N₂).^10–13 If the latter prevails, the resulting state is known as a stabilized Criegee intermediate, which may then undergo unimolecular decay or bimolecular reaction with trace tropospheric gas molecules (notably H₂O, SO₂ and organic acids).^14–17 Both processes are implicated in enhancing the oxidizing capacity of the troposphere and in forming SOAs.

The chemistry of Criegee intermediates of varying molecular complexities have been at the centre of several experimental and computational studies.^11,18–23 It is now recognized that the unimolecular decay of Criegee intermediates is an important source of OH radicals – which is the main oxidizer in the troposphere. The simplest Criegee intermediates, formaldehyde oxide (henceforth CH₂OO) undergoes unimolecular decay to form OH radicals – as well as CO, CO₂ and formic acid.^24,25 This unimolecular decay is summarized in Scheme 1 and is driven by isomerization of CH₂OO to form a dioxirane intermediate, which then undergoes ring-opening to form formic acid via a bisoxy biradical intermediate.²⁴ Recent work has detected formic acid, CO, CO₂ and OH products from CH₂OO. The Criegee intermediates in this case is formed by initial photolysis of CH₂I₂ and subsequent reaction of the nascent CH₂I radical with seed O₂ gas molecules – forming CH₂OO + I products.²⁵

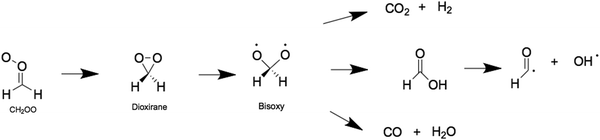Scheme 1 Reaction mechanism associated with the unimolecular decay of CH₂OO to form the bisoxy biradical.

The simplest alkyl substituted Criegee intermediates, acetaldehyde oxide, CH₃CHOO, may also undergo unimolecular rearrangement to form acetic acid, via rearrangement of an methyldioxirane intermediate. This however constitutes a minor channel in CH₃CHOO and the dominant unimolecular decay pathway is intramolecular H-atom transfer to form vinylhydroperoxide (VHP), followed by unimolecular decay to form CH₂CHO + OH radicals.^4,26–31 This latter process is highlighted in Scheme 2 and is now understood to be a key contributor to the OH radical yield in the troposphere. Criegee intermediates with >C₂ are also known to undergo unimolecular decay to form OH radicals.^29,32 In such Criegee intermediates the mechanism is the same as that outlined in Scheme 2 for CH₃CHOO.

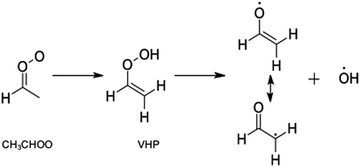Scheme 2 Reaction mechanism associated with the unimolecular decay of CH₃CHOO to form the CH₂CHO + OH radicals via a VHP intermediate.

In the present study, we use state-of-the-art multi-reference quantum chemical methods to access the extent to which coupling between multiple electronic states contributes to the ground state (thermal or vibrationally excited) unimolecular decay dynamics of Criegee intermediates. In so doing, we assess the ground and excited state energy profiles of two key intermediates, dioxirane and VHP, which are known to mediate unimolecular decay in Criegee intermediates. The recognition that the ensuing dynamics occurs on multiple energy profiles may potentially influence the dynamics – including altering the product branching ratios and yields.

Computational methodology

All optimizations (ground state minima and conical intersections) were performed in the Gaussian 16 computational package.³³ The (X)MS-CASPT2 computations were undertaken in the Molpro computational package.^34,35

The ground state minimum energy geometry of dioxirane was optimized with Density Functional Theory (DFT), using Grimme's B2PLYP-D3³⁶ functional coupled to the 6-311+G(d,p) basis set.^37,38 This functional has been shown to perform well in optimizing geometries and obtaining normal modes in Criegee intermediates.^29,31

Relaxed potential energy profiles along the O–O stretch coordinate (R_OO) were constructed by fixing R_OO at various values and optimizing the remainder of the nuclear with the Møller–Plesset second-order perturbation theory^39,40 or the complete active space second-order perturbation theory (CASPT2), method coupled to the aug-cc-pVTZ basis set.⁴¹ At each relaxed geometry, multi-state complete active space second-order perturbation theory (MS-CASPT2),⁴² coupled to the aug-cc-pVTZ basis set, was used to obtain the ground and lowest three electronically excited state energies. The lowest four states of singlet spin-multiplicity were mixed in the MS-CASPT2 calculations and were based on a state-average complete active space self-consistent field (SA4-CASSCF) reference wavefunction. An active space consisting of twelve electrons in ten orbitals was used in the CASSCF and MS-CASPT2 calculations. The active orbitals are displayed in Fig. S1 of the ESI.†

A conical intersection between the ground and first electronically excited state of dioxirane was located at the CASSCF/6-31G(d) level of theory. In this case a smaller active space of six electrons in five orbitals was used. This smaller active space (cf. PE profiles) is adequate for describing the two-state interaction between the S₀ and S₁ states at a localized region, while in the PE profiles, the larger active space is required to describe the long-range PE profiles of the four coupled electronic states (vide infra).

The ground state minimum energy geometry of VHP was optimized using Grimme's B2PLYP-D3 functional coupled to the 6-311+G(d,p) basis set. Unrelaxed (rigid body) potential energy profiles along the R_OO coordinate were constructed by elongating the R_OO bond length and performing single-point calculations of the four lowest singlet electronic states at each geometry. All other coordinates were fixed at their equilibrium geometry. The single-point calculations were performed using Extended Multi-State complete active space second-order perturbation theory (XMS-CASPT2)⁴³ in conjunction with the aug-cc-pVTZ basis set. All 4 states were mixed in the XMS-CASPT2 wavefunction and were based on a 4 state-averaged CASSCF (SA4-CASSCF) reference wavefunction using the same basis set. An active space of twelve electrons in nine orbitals was used, the latter of which are visualized in Fig. S2 of the ESI.† CASPT2 relaxed scans were also conducted along R_OO, by fixing R_OO at various values and allowing the remainder of the nuclear framework to relax to their ground state minimum energy configurations.

The active spaces for both dioxirane and VHP were selected in order describe all significant electronic effects while maintaining an appropriate computational expense. The reactant and product vertical excitation energies were benchmarked with various active spaces. These results are displayed in Table S1 and S2 of the ESI† and show that variations in the active space show only modest changes to the excitation energies.

Results and discussion

Ground state structures and vertical excitation energies

Fig. 1 presents the ground state minimum energy geometry of dioxirane and VHP – calculated at the B2PLYP-D3/6-311+G(d,p) level of theory. As previously noted,^26,44 the ground state minimum energy geometry of both dioxirane and VHP are with all carbon and oxygen atoms in a common plane. In dioxirane, the carbon atom is at the centre of a pseudo-tetrahedral geometry, in which the carbon-hydrogen and carbon–oxygen bonds form a symmetric arrangement around the central carbon-atom. In VHP the hydrogen atom on the terminal OH moiety is out of the molecular plane – forming a staggered conformation. This is consistent with the molecular geometry of hydrogen peroxide which also shows a staggered conformation.^45,46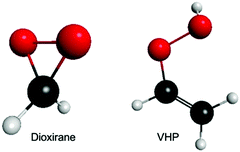

Fig. 1 Ground state minimum energy geometry of dioxirane and VHP – calculated at the B2PLYP-D3/6-311+G(d,p) level of theory.

Fig. 2 presents the dominant electronic configurations associated with the ground and excitation to the lowest three electronically excited singlet states of dioxirane and VHP.

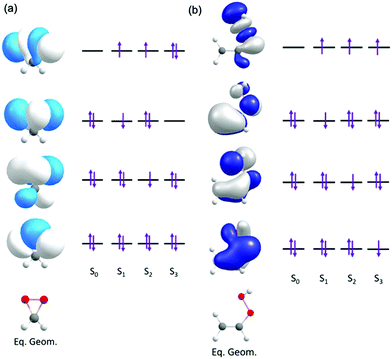Fig. 2 Orbitals and orbital promotions associated with the vertically excited electronic states of (a) dioxirane and (b) VHP.

In dioxirane the ground state involves an expected electronic configuration in which all bonding and non-bonding valence orbitals are doubly occupied. The first and second vertically excited states involve single-excited electronic configurations, involving promotion from an out-of-plane valence orbitals to a common in-plane σ* virtual orbital. This σ* orbital is localized along the O–O bond of the dioxirane. The third excited state also arises by electron transition to the same σ* orbital but in this case the configuration is doubly-excited – with the σ* orbital doubly occupied.

In VHP the ground state also involves an expected electronic configuration in which all orbitals are doubly occupied. The excited electronic states all involve promotion of an electron to a common σ* orbital localized along the O-O bond. The first, second and third electronically excited state configurations are distinguishable by the different π orbital from which the electron is promoted.

Unimolecular decay paths

Dioxirane

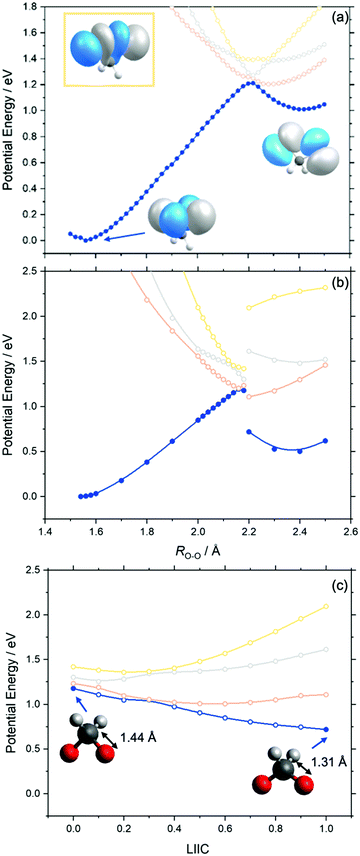
Fig. 3 presents the adiabatic MS-CASPT2 potential energy (PE) profiles along the O–O stretch coordinate (henceforth R_OO) of dioxirane. Panels (a) and (b) are distinguishable by the relaxation of the nuclear framework with MP2 or CASPT2, respectively. These will henceforth be referred to as MS-CASPT2/AVTZ//MP2/AVTZ and MS-CASPT2/AVTZ//CASPT2/AVTZ, respectively. Additional details are given in the methodology section. The geometry at R_OO = 1.56 Å corresponds to the dioxirane reactant whilst that at R_OO ∼ 2.4 Å corresponds to the bisoxy biradical – which is the intermediate precursor for forming formic acid. As shown, the PE profiles of the adiabatic ground state (blue curve in Fig. 3) follows that of a typical ground state reaction, wherein the reactant dioxirane and the product bisoxy biradical are separated by a PE barrier at ca. R_OO ∼ 2.2 Å. The molecular structures of the reactant, product and saddle point (of dioxirane and the bisoxy diradical) accord well with previous single point computations by Guo and co-workers.⁴⁴Fig. 3 also displays the adiabatic S₁, S₂ and S₃ states along the R_OO coordinate. In both the MS-CASPT2/AVTZ//MP2/AVTZ and MS-CASPT2/AVTZ//CASPT2/AVTZ PE profiles, all three excited states show a net decrease in PE upon increasing R_OO from that of the ground state equilibrium value. This can be understood by recognizing that all vertically excited electronic states correspond to excitations to a common σ* orbital, localized on the O–O bond (as outlined in the previously section). This will inevitably lead to a long-range repulsive interaction upon decreasing R_OO when viewed from the bisoxy biradical geometry. The relative gradients along R_OO, of the excited electronic states at the Franck–Condon region, qualitatively increases from S₁ to S₃. This steepest gradient of the S₃ state (cf. S₁ and S₂ states) can be understood by recognizing that the electronic state arises via promotion of an electron-pair to the σ* orbital (see Fig. 3) – leading to a doubly excited state configuration. This manifests in a lower bond order for S₃ (cf. S₁ and S₂ states). Instead, the S₁ and S₂ states arise via a single excitation to the σ* orbital – leading to a singly occupied configuration and thus a greater O–O bond order when compared to S₃.

Fig. 3 Relaxed PE profiles along the O–O stretch coordinate of dioxirane of the lowest four singlet states, calculated at the (a) MS-CASPT2/AVTZ//MP2/AVTZ and (b) MS-CASPT2/AVTZ//CASPT2/AVTZ levels of theory. The orbitals represent the highest doubly occupied molecular orbital and various points, two of which are indicated by arrow. The orbital displayed in the yellow box is the highest doubly occupied molecular orbital of the S₃ state (yellow profile) at R_OO = 1.56 Å. The step change between R_OO = 2.18 Å and R_OO = 2.2 Å represents a change in the C–O bond distance from 1.44 Å to 1.31 Å. Panel (c) shows a LIIC between this step change in energy between the relaxed R_OO = 2.18 Å and R_OO = 2.2 Å geometries displayed in (b).

The S₁ state becomes degenerate with the S₀ state at ca. R_OO = 2.2 Å, at which point the S₂ and S₃ states are also close in energy to the S₀ state. This is particularly noteworthy as R_OO ∼ 2.2 Å also corresponds to the transition state geometry associated with the ground state unimolecular decay of dioxirane to the bisoxy biradical. From the dioxirane parent molecule, progressive elongation of R_OO leads to an adiabatic change in the ground state electronic configuration from the dioxirane to the bisoxy biradical. This change in the electronic wavefunction is illustrated by the change in the highest occupied molecular orbital upon forming the bisoxy biradical from dioxirane. The highest occupied molecular orbital of the bisoxy biradical is of anti-bonding (σ*) character and is therefore unoccupied in the ground state dioxirane. The ground state electronic configuration of the bisoxy biradical product therefore correlates with an excited electronic state configuration of the reactant dioxirane structure that is distinct from that of ground state dioxirane.

Although the PE profiles calculated at the MS-CASPT2/AVTZ//MP2/AVTZ and MS-CASPT2/AVTZ//CASPT2/AVTZ level are similar in the region between R_OO = 1.56 Å and R_OO = 2.18 Å, we note an important distinction at long R_OO. As shown in Fig. 3(b), the MS-CASPT2/AVTZ//CASPT2/AVTZ PE profiles show a step discontinuity in the energy profiles between R_OO = 2.18 Å and R_OO = 2.2 Å, which arises via the reduction of the C–O bond distance from ca. R_CO = 1.44 Å (at R_OO ≤ 2.18 Å) to R_CO = 1.31 Å (at R_OO ≥ 2.2 Å). This behaviour is not captured in the MP2 relaxation due to its inherent single-reference nature. To investigate this step change in energy further, additional MS-CASPT2 PE profiles connecting the CASPT2 relaxed geometries at R_OO = 2.18 Å to R_OO = 2.2 Å were constructed using a Linear interpolation in internal coordinates (LIIC). Fig. 3(c) presents the resulting LIIC between the CASPT2 relaxed geometries at R_OO = 2.18 Å and R_OO = 2.2 Å, which shows the smooth barrierless variation of the ground state from R_OO = 2.18 Å to R_OO = 2.2 Å. When comparing the bisoxy biradical relative energy (cf. to the dioxirane parent molecule), calculated at the MS-CASPT2/AVTZ//MP2/AVTZ and MS-CASPT2/AVTZ//CASPT2/AVTZ levels, the latter is in excellent agreement with previous high-level CCSD(T)-F12 calculations of the energy difference between dioxirane and bisoxy.⁴⁴ The variation is noteworthy since it shows that MP2 relaxation does not sufficiently describe the multi-reference nature of the bisoxy biradical (beyond R_OO = 2.18 Å).

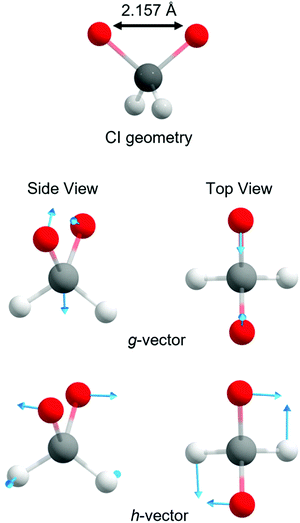
With these topographic details in mind, the ground state reaction from dioxirane to the bisoxy biradical may involve substantial non-adiabaticity as the change in the electronic wavefunction is associated with a transition state that is close in energy to the several excited states. This is reinforced by recognizing that the transition state and degeneracy at ca. R_OO = 2.2 Å is associated with a conical intersection. Fig. 4 displays the optimized S₀/S₁ conical intersection geometry, which although performed with a different level of theory (i.e., smaller active space, basis set and CASSCF method) than the PE profiles in Fig. 3 (see Methodology section), is consistent with the same point at R_OO = 2.2 Å. Any changes in the geometry are minor – as revealed by R_OO = 2.157 Å in the optimized structure vs. R_OO = 2.2 Å (MP2 relaxed) and R_OO = 2.16 Å (CASPT2 relaxed) in Fig. 3(a) and (b), respectively. Fig. 4 also displays the g and h vectors associated with the optimized conical intersection. It is reassuring that the g-vector – i.e., the gradient-difference vector (or tuning coordinate) – is associated with the reactive coordinate. The h-vector – i.e., the derivative-coupling vector (or coupling coordinate) requires anti-symmetric wagging of the oxygen and hydrogen atoms in order to lift the degeneracy associated with the conical intersection.

Fig. 4 g and h vectors associated with the optimized S₀/S₁ conical intersection of dioxirane.

The transition state at R_OO = 2.2 Å in Fig. 3 is the lower part of a conical intersection and is therefore expected to undergo non-adiabatic coupling with the excited electronic states. Motion around the lower cone of the conical intersection may give rise to the geometric phase (GP) effect as the electronic wavefunction bifurcates around the point of degeneracy. The GP effect is a characteristic signature of conical intersections and arises when the adiabatic electronic wavefunction changes sign when transported around the conical intersection. The inherent GP effect may then control the exit channel energy dissipation and thus the ensuing chemistry for formic acid formation. Such effects are common in molecular reactions that are analogous to the current system of interest and it is known that such effects persist even in cases in which the conical intersection is much higher in energy than the initially excited vibrational resonance of the ground state.⁴⁷ Ample studies have demonstrated that the GP needs to be considered in treating the adiabatic dynamics around a conical intersection.^47–53

We make one caveat that since dioxirane is likely prepared highly vibrationally excited, the subsequent O–O bond fission to form the bisoxy biradical may not necessarily follow the minimum energy path as given by the relaxed PE profiles. Although these side routes are possible at high internal energies, the most energetically probable route is the minimum energy path.

Vinyl hydroperoxide (VHP)

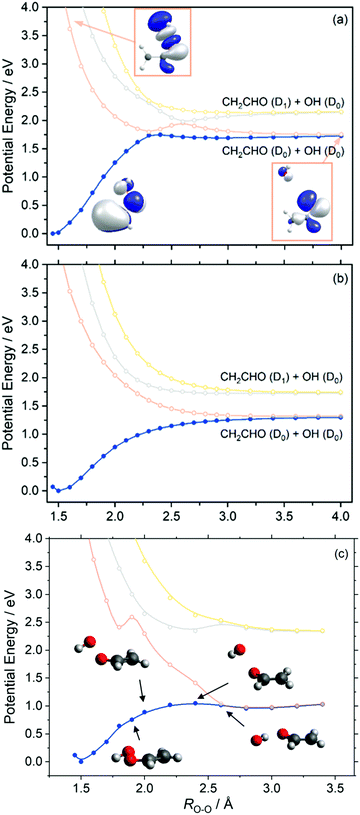
Similar behaviour is observed in our next case study vinyl hydroperoxide (VHP). VHP is formed when thermalized or vibrationally excited CH₃CHOO undergoes intramolecular 1,4-H-atom transfer. The nascent VHP is formed with high internal excitation – which is excess of the energetic limit for forming CH₂CHO + OH products. This process is the dominant unimolecular decay path for alkyl-substituted Criegee intermediates.

Fig. 5 presents the adiabatic PE profiles along the O–O stretch coordinate (R_OO – identified in the molecule inset in Fig. 5(a)) of VHP. Panels (a) and (b) indicate the PE profiles along R_OO at geometries at which the CCOO torsional angle (τ_CCOO – identified in the yellow highlight on the VHP in Fig. 5(a)) is at τ_CCOO = 0° and 90°, respectively. τ_CCOO = 0° is a planar configuration and corresponds to the minimum energy geometry displayed in Fig. 1 while τ_CCOO = 90° corresponds to an out-of-plane configuration.

Fig. 5 Unrelaxed adiabatic PE profile of VHP along the O–O stretch coordinate at (a) τ_CCOO = 0° and (b) τ_CCOO = 90°, calculated at the XMS-CASPT2/aug-cc-pVTZ level of theory. (c) XMS-CASPT2/AVTZ//CASPT2/AVTZ relaxed PE profiles along the R_OO coordinate.

Focussing on Fig. 5(a), the energy at R_OO = 1.45 Å corresponds to the VHP parent molecule, while the asymptotic region beyond R_OO > 2.5 Å corresponds to the OH + CH₂CHO radical products. The ground state PE profile shows a characteristic topology associated with a bond dissociation process – wherein the energy rises upon increasing R_OO and then plateaus as the PE profile becomes asymptotic. In the asymptotic region and under gas phase conditions, the OH and CH₂CHO fragment partners are at a terminal separation. As with dioxirane, the ground state PE profile along R_OO shows an avoided crossing with the S₁ state at ca. R_OO = 2.3 Å. As Fig. 3 implies, the degeneracy observed at R_OO = 2.3 Å and τ_CCOO = 0° is lifted by motion along τ_CCOO which is consistent with coupling mode behaviour at a conical intersection. The lowest three excited states of VHP are dissociative with respect to R_OO, which can be understood by considering that all three electronic states correspond to excitation into a common σ* orbital localized along the O–O bond.

To investigate the minimum energy path associated with VHP further, fully relaxed PE profiles along the R_OO coordinate were undertaken. These are presented in Fig. 5(c). The CASPT2 relaxed PE profile shows that the parent VHP molecule is planar at short range R_OO and undergoes progressive motion out of plane at 1.9 Å ≥ R_OO ≥ 2.4 Å. This aligns with the unrelaxed PE profiles which show that the most stable configuration of VHP is planar, while motion around the crossing R_OO = 2.3 Å along τ_CCOO shows a lower energy route to OH elimination. Although motion along τ_CCOO manifests in the ground state minimum energy path at 1.9 Å ≥ R_OO ≥ 2.4 Å, the S₁ state is unstable with respect to increasing τ_CCOO in this R_OO range. This is highlighted by the step increase in energy from R_OO = 1.8 Å to R_OO = 1.9 Å in Fig. 5(c) and supported by the unrelaxed PE profiles in Fig. 5(a) and (b). At R_OO = 2.6 Å, the ground state minimum energy path shows a planar geometry and a rotation of the OH moiety so as to undergo hydrogen bonding of the H-atom with the nascent vinoxy centred O-atom. Such a geometry along R_OO is consistent with earlier study by Kidwell et al.⁵⁴ and is attributed to a frustrated submerged transition state.

As with dioxirane, we note however that since VHP is prepared highly vibrationally excited and undergoes intramolecular vibrationally energy redistribution, the subsequent OH elimination may not necessarily follow the minimum energy path as given by the relaxed PE profiles.

As shown in the PE profiles in Fig. 5 the lowest energy asymptote corresponds to OH (D₀) + CH₂CHO (D₀) products and correlates with an excited state electronic configuration – as indicated by the change in the highest occupied molecular orbital of the ground state VHP at R_OO = 4.0 Å relative to the ground state. Again, unimolecular decay of ground state VHP clearly involves coupling of energy surfaces en route to forming OH + CH₂CHO. Although motion along τ_CCOO lifts the degeneracy at R_OO = 2.3 Å and provides a lower energy route around this crossing point, the ensuing dynamics is likely perturbed by the intersection at R_OO = 2.3 Å as the evolving wavepacket bifurcates as it traverses the region around the crossing point. Unimolecular decay is therefore likely to involve substantial non-adiabaticity upon dissociation, wherein the GP effect may play a role in the ensuing dynamics as described above for dioxirane. This feature is analogous to the ground state unimolecular decay of vibrationally excited hydroxymethyl radical which is known to occur non-adiabatically.⁴⁷

Conclusions

In this study, we have demonstrated the multi-state character associated with two well-known unimolecular decay paths available to Criegee intermediates. This hitherto unrecognized multi-state character, in the context of the products of Criegee intermediates, is an important recognition as it may control the nascent product yields formed upon unimolecular decay of Criegee intermediates. In 2018, Guo and co-workers discovered the role of conical intersections in the unimolecular decay of the hydroxymethyl radical and demonstrated that the geometric phase effect plays a role in controlling the rovibrational energy dissipation of the nascent formaldehyde product.⁴⁷ In the context of the systems explored here, similar behaviour may effect on the product state branching in the nascent intermediates and fragments formed during the unimolecular decay of dioxirane or VHP. Providing that the nascent products react on timescales that are shorter than collisional energy relaxation, the preselected rovibrational energy distribution may have an implication on the resulting reactions of these atmospherically relevant products, but we note that these most likely undergo vibrational energy relaxation and thermalization prior to bimolecular chemistry. Notwithstanding, we demonstrate that such multi-state behaviour should be considered in future computational studies of molecular reactions that are relevant in the atmosphere or in combustion – especially in the context of Criegee intermediates.

Given the details of the PE profiles above, our future plan is to generate full-dimensional energy profiles and to undertake time-dependent quantum wavepacket dynamics simulations on the subsequent energy surfaces. Such simulations will reveal the extent to which the unimolecular dynamics involves coupling to the excited state energy surfaces and thus if the reaction occurs non-adiabatically. One of the key questions that such simulations will answer is if the GP effect plays a role in the product state energy distributions of the nascent products.

The most exciting prospect is to explore how such electronic state couplings associated with the unimolecular decay of a dioxirane or a hydroperoxide change upon increasing molecular complexity of the starting Criegee intermediate. Future studies on the geometric and electronic effects of increasing molecules complexity are therefore also anticipated.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was supported by the National Science Foundation, under grant no. 2003422 (TNVK) and the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1845298 (VJE). The authors would also like to thank the reviewers for their invaluable suggestions during the review stage.

References

1. L. Lu, J. M. Beames and M. I. Lester, Early time detection of OH radical products from energized Criegee intermediates CH₂OO and CH₃CHOO, Chem. Phys. Lett., 2014, 598, 23–27.
2. A. M. Green, V. P. Barber, Y. Fang, S. J. Klippenstein and M. I. Lester, Selective deuteration illuminates the importance of tunneling in the unimolecular decay of Criegee intermediates to hydroxyl radical products, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12372 LP–12377 LP.
3. Y. Fang, V. P. Barber, S. J. Klippenstein, A. B. McCoy and M. I. Lester, Tunneling effects in the unimolecular decay of (CH₃)₂COO Criegee intermediates to OH radical products, J. Chem. Phys., 2017, 146, 134307.
4. M. I. Lester and S. J. Klippenstein, Unimolecular Decay of Criegee Intermediates to OH Radical Products: Prompt and Thermal Decay Processes, Acc. Chem. Res., 2018, 51, 978–985.
5. R. L. Caravan, M. F. Vansco and M. I. Lester, Open questions on the reactivity of Criegee intermediates, Commun. Chem., 2021, 4, 2012–2015.
6. J. G. Calvert, R. Atkinson, J. A. Kerr, S. Madronich, G. K. Moortgat, T. J. Wallington and G. Yarwood, The Mechanisms of Atmospheric Oxidation of the Alkenes, Oxford University Press, 2000.
7. B. J. Finlayson and J. N. Pitts, Chemistry of the Upper and Lower Atmosphere, Academic Press, San Diego, 2000.
8. R. P. Wayne, Chemistry of atmospheres: An introduction to the chemistry of the atmospheres of earth, the planets, and their satellites, Oxford University Press, Oxford, 3rd edn, 2000.
9. S. E. Paulson and J. J. Orlando, The reactions of ozone with alkenes: An important source of HOx in the boundary layer, Geophys. Res. Lett., 1996, 23, 3727–3730.
10. D. Johnson and G. Marston, The gas-phase ozonolysis of unsaturated volatile organic compounds in the troposphere, Chem. Soc. Rev., 2008, 37, 699–716.
11. M. S. Alam, M. Camredon, A. R. Rickard, T. Carr, K. P. Wyche, K. E. Hornsby, P. S. Monks and W. J. Bloss, Total radical yields from tropospheric ethene ozonolysis, Phys. Chem. Chem. Phys., 2011, 13, 11002–11015.
12. K. M. Emmerson and N. Carslaw, Night-time radical chemistry during the TORCH campaign, Atmos. Environ., 2009, 43, 3220–3226.
13. K. M. Emmerson, N. Carslaw, D. C. Carslaw, J. D. Lee, G. McFiggans, W. J. Bloss, T. Gravestock, D. E. Heard, J. Hopkins, T. Ingham, M. J. Pilling, S. C. Smith, M. Jacob and P. S. Monks, Free radical modelling studies during the UK TORCH Campaign in Summer 2003, Atmos. Chem. Phys., 2007, 7, 167–181.
14. Criegee mechanism of ozonolysis BT - Name Reactions: A Collection of Detailed Reaction Mechanisms, ed. J. J. Li, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014.
15. R. Criegee, Mechanism of Ozonolysis, Angew. Chem., Int. Ed. Engl., 1975, 14, 745–752.
16. C. Geletneky and S. Berger, The Mechanism of Ozonolysis Revisited by 17O-NMR Spectroscopy, Eur. J. Org. Chem., 1998, 1625–1627.
17. O. Horie and G. K. Moortgat, Gas-Phase Ozonolysis of Alkenes. Recent Advances in Mechanistic Investigations, Acc. Chem. Res., 1998, 31, 387–396.
18. N. M. Donahue, G. T. Drozd, S. A. Epstein, A. A. Presto and J. H. Kroll, Adventures in ozoneland: down the rabbit-hole, Phys. Chem. Chem. Phys., 2011, 13, 10848–10857.
19. A. Novelli, L. Vereecken, J. Lelieveld and H. Harder, Direct observation of OH formation from stabilised Criegee intermediates, Phys. Chem. Chem. Phys., 2014, 16, 19941–19951.
20. J. H. Kroll, J. S. Clarke, N. M. Donahue and J. G. Anderson, Mechanism of HOx Formation in the Gas-Phase Ozone−Alkene Reaction. 1. Direct, Pressure-Dependent Measurements of Prompt OH Yields, J. Phys. Chem. A, 2001, 105, 1554–1560.
21. H. L. Huang, W. Chao and J. J. M. Lin, Kinetics of a Criegee intermediate that would survive high humidity and may oxidize atmospheric SO₂, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10857–10862.
22. D. L. Osborn and C. A. Taatjes, The physical chemistry of Criegee intermediates in the gas phase, Int. Rev. Phys. Chem., 2015, 34, 309–360.
23. R. Chhantyal-Pun, M. A. H. Khan, R. Martin, N. Zachhuber, Z. J. Buras, C. J. Percival, D. E. Shallcross and A. J. Orr-Ewing, Direct Kinetic and Atmospheric Modeling Studies of Criegee Intermediate Reactions with Acetone, ACS Earth Space Chem., 2019, 3(10), 2363–2371.
24. C. C. Womack, M. A. Martin-Drumel, G. G. Brown, R. W. Field and M. C. McCarthy, Observation of the simplest Criegee intermediate CH₂OO in the gas-phase ozonolysis of ethylene, Sci. Adv., 2015, 1, 1–7.
25. T. Y. Chen and Y. P. Lee, Dynamics of the reaction CH₂I + O₂ probed: via infrared emission of CO, CO₂, OH and H₂CO, Phys. Chem. Chem. Phys., 2020, 22, 17540–17553.
26. Y. Fang, F. Liu, V. P. Barber, S. J. Klippenstein, A. B. McCoy and M. I. Lester, Deep tunneling in the unimolecular decay of CH₃CHOO Criegee intermediates to OH radical products, J. Chem. Phys., 2016, 145, 234308.
27. Y. Fang, F. Liu, S. J. Klippenstein and M. I. Lester, Direct observation of unimolecular decay of CH₃CH₂CHOO Criegee intermediates to OH radical products, J. Chem. Phys., 2016, 145, 44312.
28. Y. Fang, F. Liu, V. P. Barber, S. J. Klippenstein, A. B. McCoy and M. I. Lester, Communication: Real time observation of unimolecular decay of Criegee intermediates to OH radical products, J. Chem. Phys., 2016, 144, 61102.
29. V. P. Barber, S. Pandit, A. M. Green, N. Trongsiriwat, P. J. Walsh, S. J. Klippenstein and M. I. Lester, Four-Carbon Criegee Intermediate from Isoprene Ozonolysis: Methyl Vinyl Ketone Oxide Synthesis, Infrared Spectrum, and OH Production, J. Am. Chem. Soc., 2018, 140, 10866–10880.
30. F. Liu, J. M. Beames, A. S. Petit, A. B. McCoy and M. I. Lester, Infrared-driven unimolecular reaction of CH₃CHOO Criegee intermediates to OH radical products, Science, 2014, 345, 1596–1598.
31. V. P. Barber, S. Pandit, V. J. Esposito, A. B. McCoy and M. I. Lester, CH Stretch Activation of CH₃CHOO: Deep Tunneling to Hydroxyl Radical Products, J. Phys. Chem. A, 2019, 123, 2559–2569.
32. F. Liu, J. M. Beames, A. M. Green and M. I. Lester, UV Spectroscopic Characterization of Dimethyl- and Ethyl-Substituted Carbonyl Oxides, J. Phys. Chem. A, 2014, 118, 2298–2306.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., 2016.
34. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, WIREs Comput. Mol. Sci., 2012, 2, 242–253.
35. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller, III, M. E. Mura, A. Nicklass, D. P. O’Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 1, a package of ab initio programs, 2018.
36. S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124, 34108.
37. W. J. Hehre, R. F. Stewart and J. A. Pople, Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals, J. Chem. Phys., 1969, 51, 2657–2664.
38. W. J. Hehre, R. Ditchfield, R. F. Stewart and J. A. Pople, Self-Consistent Molecular Orbital Methods. IV. Use of Gaussian Expansions of Slater-Type Orbitals. Extension to Second-Row Molecules, J. Chem. Phys., 1970, 52, 2769–2773.
39. M. J. Frisch, M. Head-Gordon and J. A. Pople, Semi-direct algorithms for the MP2 energy and gradient, Chem. Phys. Lett., 1990, 166, 281–289.
40. M. J. Frisch, M. Head-Gordon and J. A. Pople, A direct MP2 gradient method, Chem. Phys. Lett., 1990, 166, 275–280.
41. T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
42. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299–306.
43. A. A. Granovsky, Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory, J. Chem. Phys., 2011, 134, 214113.
44. J. Li and H. Guo, Full-Dimensional Potential Energy Surface and Ro-vibrational Levels of Dioxirane, J. Phys. Chem. A, 2016, 120, 2991–2998.
45. P. A. Giguère, The Infra-Red Spectrum of Hydrogen Peroxide, J. Chem. Phys., 1950, 18, 88–92.
46. P. A. Giguère, Molecular association and structure of hydrogen peroxide, J. Chem. Educ., 1983, 60, 399.
47. C. Xie, C. L. Malbon, D. R. Yarkony, D. Xie and H. Guo, Signatures of a Conical Intersection in Adiabatic Dissociation on the Ground Electronic State, J. Am. Chem. Soc., 2018, 140, 1986–1989.
48. C. Xie, J. Ma, X. Zhu, D. R. Yarkony, D. Xie and H. Guo, Nonadiabatic Tunneling in Photodissociation of Phenol, J. Am. Chem. Soc., 2016, 138, 7828–7831.
49. B. K. Kendrick, J. Hazra and N. Balakrishnan, Geometric Phase Appears in the Ultracold Hydrogen Exchange Reaction, Phys. Rev. Lett., 2015, 115, 153201.
50. B. K. Kendrick, J. Hazra and N. Balakrishnan, The geometric phase controls ultracold chemistry, Nat. Commun., 2015, 6, 7918.
51. J. Jankunas, M. Sneha, R. N. Zare, F. Bouakline and S. C. Althorpe, Hunt for geometric phase effects in H + HD → HD(v′, j′) + H, J. Chem. Phys., 2013, 139, 144316.
52. J. F. E. Croft, J. Hazra, N. Balakrishnan and B. K. Kendrick, Symmetry and the geometric phase in ultracold hydrogen-exchange reactions, J. Chem. Phys., 2017, 147, 74302.
53. J. C. Juanes-Marcos, S. C. Althorpe and E. Wrede, Theoretical Study of Geometric Phase Effects in the Hydrogen-Exchange Reaction, Science, 2005, 309, 1227–1230.
54. N. M. Kidwell, H. Li, X. Wang, J. M. Bowman and M. I. Lester, Unimolecular dissociation dynamics of vibrationally activated CH₃CHOO Criegee intermediates to OH radical products, Nat. Chem., 2016, 8, 509.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02601a

---