Sensitization-initiated electron transfer via upconversion: mechanism and photocatalytic applications

Abstract

Sensitization-initiated electron transfer (SenI-ET) describes a recently discovered photoredox strategy that relies on two consecutive light absorption events, triggering a sequence of energy and electron transfer steps. The cumulative energy input from two visible photons gives access to thermodynamically demanding reactions, which would be unattainable by single excitation with visible light. For this reason, SenI-ET has become a very useful strategy in synthetic photochemistry, but the mechanism has been difficult to clarify due to its complexity. We demonstrate that SenI-ET can operate via sensitized triplet–triplet annihilation upconversion, and we provide the first direct spectroscopic evidence for the catalytically active species. In our system comprised of fac-[Ir(ppy)₃] as a light absorber, 2,7-di-tert-butylpyrene as an annihilator, and N,N-dimethylaniline as a sacrificial reductant, all photochemical reaction steps proceed with remarkable rates and efficiencies, and this system is furthermore suitable for photocatalytic aryl dehalogenations, pinacol couplings and detosylation reactions. The insights presented here are relevant for the further rational development of photoredox processes based on multi-photon excitation, and they could have important implications in the greater contexts of synthetic photochemistry and solar energy conversion.

---

1. Introduction

The consecutive excitation of a catalytic system with two (or more) photons can lead to highly reactive intermediates that are able to trigger chemical transformations, which would not be feasible with the energy input from a single excitation.^1–3 Over the past seven years,⁴ such multi-photon excitation strategies have become remarkably popular in photoredox catalysis, and this enabled much progress in synthetic organic photochemistry. Mechanistic understanding has been elusive in many cases due to the chemical complexity of the considered systems and the multitude of possible reaction pathways associated with consecutive multi-photon excitation. The involvement of short-lived radical intermediates and the simultaneous presence of different excited species can make the disentanglement of competing mechanistic paths very challenging. However, to make further rational progress in this thriving research domain, a more thorough mechanistic understanding seems highly desirable.

In a similar spirit as spectroscopic studies of the photo-ionization of [Ru(bpy)₃]²⁺via consecutive excitation with two green photons,^5,6 a synthetically oriented landmark paper introduced the so-called “ConPET” mechanism to photoredox catalysis.⁴ A perylene diimide (PDI) chromophore was excited and converted to its one-electron reduced form via photoinduced electron transfer (PET) from a sacrificial donor. The resulting PDI˙⁻ species can absorb another photon to yield an electronically excited radical anion (^2*PDI˙⁻), which is sufficiently reactive for a broad range of reductive (aryl) dehalogenations.⁷ One key advantage of this mechanism is the need for only one single catalyst, but the excited radical anion is usually a very short-lived species, limiting its kinetic reactivity.^8–10 Alternative mechanisms to ConPET are therefore of interest.

Among multi-component systems for two-photon mechanisms, sensitized triplet–triplet annihilation upconversion (sTTA-UC) is currently one of the most intensively pursued approaches,¹ enabling photoreactions to proceed with NIR or red light instead of UV or blue excitation.^2,11–18 In sTTA-UC the sensitizer is photo-excited, and then transfers its excitation energy to a co-catalyst with an energetically lower lying triplet excited state, the so-called annihilator.^19–21 Subsequent triplet–triplet annihilation leads to upconversion, populating the fluorescent singlet excited state of the annihilator. In photocatalysis, that highly energetic excited state is commonly used for substrate activation through oxidative quenching with a suitable electron acceptor, typically one of the substrates.^22–26

Another prominent strategy for photoredox catalysis via multi-photon excitation relies on a combination of energy and electron transfer steps to generate the catalytic key species. Following closely related work with a spectroscopic focus,⁶ the concept of “sensitization-initiated electron transfer” (SenI-ET) was introduced to preparative-scale photoredox catalysis, in particular to activate aryl halides.²⁷ The authors proposed the mechanism in Fig. 1A, which begins with triplet–triplet energy transfer (TTET) from photo-excited [Ru(bpy)₃]²⁺ to the pyrene co-catalyst, followed by reductive quenching of triplet-excited pyrene (^3*Py) by diisopropylethylamine (DIPEA) to result in the (presumed) catalytic key species, the pyrenyl radical anion (Py˙⁻). With a reducing power of −2.1 V vs. SCE,²⁷ Py˙⁻ is thermodynamically competent for reductive dehalogenation of aryl bromides and chlorides, and this was exploited in a broad range of photoredox reactions.^7,27 The groups of Ceroni and Balzani commented that the mechanism in Fig. 1A has several shortcomings,²⁸ and they proposed the mechanism in Fig. 1B, in which Py˙⁻ is formed after sensitized triplet–triplet annihilation upconversion (sTTA-UC) and subsequent reductive quenching of singlet-excited pyrene (^1*Py) by DIPEA. The authors of the initial study argued in reply that a multitude of mechanisms are conceivable and furthermore they noted that mechanistic studies often occur under idealized conditions that are not strictly identical to the conditions under which preparative photoredox catalysis takes place.²⁹ In 2020, Moore and coworkers disclosed a mechanistic study based on laser spectroscopy and reached the conclusion that the mechanism in Fig. 1C is dominant under the specific reaction conditions used in the initial study.³⁰ Specifically, they found based on a kinetic analysis that reductive quenching of photo-excited [Ru(bpy)₃]²⁺ by DIPEA competes with energy-transfer quenching by pyrene, leading to the parallel formation of both [Ru(bpy)₃]⁺ and ^3*Py, which can react with one another to form Py˙⁻.

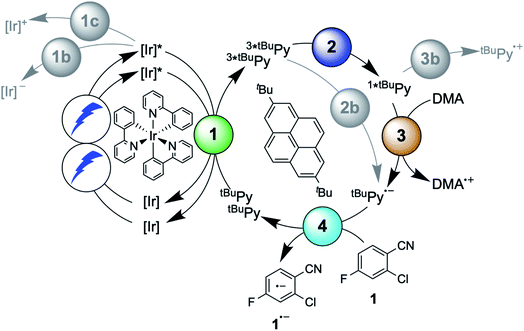
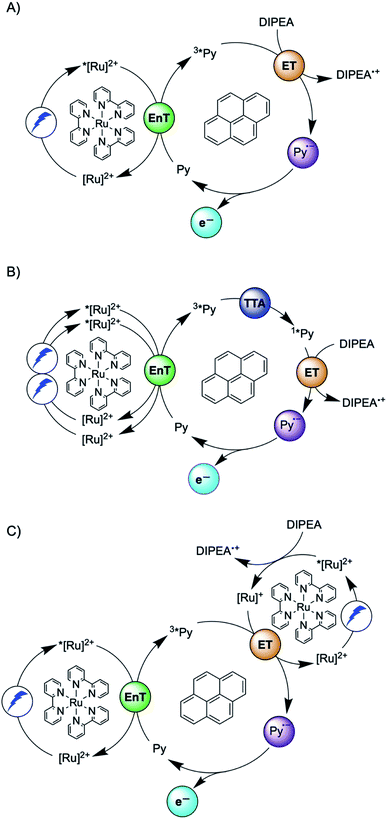Fig. 1 Sensitization-initiated mechanism postulated by König and coworkers (A);²⁷ alternative mechanism proposed by a team around Ceroni and Balzani (B);²⁸ alternative mechanism found by Moore and coworkers (C).³⁰ [Ru]²⁺ = [Ru(bpy)₃]²⁺, Py = pyrene, EnT = energy transfer, ET = electron transfer, TTA = triplet–triplet annihilation.

Three facts are particularly remarkable concerning the studies illustrated in Fig. 1: (i) the concept of sensitization-initiated electron transfer, and in particular the initial key preparative study,²⁷ has received considerable attention in synthetic organic photochemistry; (ii) there is important mechanistic controversy;^28,29 and (iii) the presumed key catalytic species, the pyrenyl radical anion (Py˙⁻), has escaped detection until now.³⁰

Here, we report a new photosensitizer-catalyst combination, which operates via a clear-cut mechanism for which we are able to detect all relevant reaction intermediates directly by transient absorption and emission spectroscopy, leading to an unambiguous picture of how sensitization-initiated electron transfer works for this system. Specifically, we employed the well-known fac-[Ir(ppy)₃] complex (ppy = 2-phenylpyridine) and 2,7-di-tert-butylpyrene (^tBuPy), along with N,N-dimethylaniline (DMA) as sacrificial reductant. With this particular sensitizer/co-catalyst/reductant combination, the mechanism in Fig. 1B, postulated initially by Ceroni and Balzani in their commentary but never verified experimentally until now,²⁸ is clearly dominant. Favorable lifetimes of singlet-excited pyrenes and the high cage-escape yields reported for their reductive quenching by DMA make this system ideal for the mechanism presented in Fig. 1B.^31,32 We report rate constants for all elementary processes up to the initial substrate activation step and we demonstrate that the fac-[Ir(ppy)₃]/^tBuPy couple can be employed for preparative-scale photoredox catalysis, analogously to the previously reported [Ru(bpy)₃]²⁺/pyrene couple. Our work demonstrates that mechanistic insight into complex reaction mixtures and multi-photon excitation processes of SenI-ET is indeed accessible, at least for careful sensitizer/co-catalyst choices. Our work complements recent mechanistic studies of biphotonic excitation in photoredox catalysis,^{2,6,8,18,28–30,33–42} and this seems important for the further rational development of this thriving research area.

2. Results and discussion

The debate over how sensitization-initiated electron transfer really works involved the proposal of a mechanism based on sTTA-UC (Fig. 1B),^28,29 but experimentally this very plausible option has not been confirmed until now, as noted above. Since the previously used [Ru(bpy)₃]²⁺/pyrene/DIPEA combination leads to two concurrent initial photoreactions (energy transfer and electron transfer, Fig. 1C), the mechanistic analysis is particularly convoluted in this case.³⁰ We anticipated that with the fac-[Ir(ppy)₃]/2,7-di-tert-butylpyrene/N,N-dimethylaniline combination, the initial electron transfer step could be suppressed, and that this could greatly simplify the mechanistic investigation. Specifically, DMA is unable to quench photoexcited fac-[Ir(ppy)₃] reductively (see below), and the tert-butyl substitution on pyrene improves its sTTA-UC properties.^43–46 We therefore speculated that the elusive mechanism in Fig. 2 could become dominant, and we furthermore anticipated that this could allow us to observe the pyrenyl radical anion (^tBuPy˙⁻), which seems quite important, because this has been considered the key catalytic species though it had not been observed until now.^27–30

Fig. 2 Mechanism for sensitization-initiated electron transfer (SenI-ET) with the fac-[Ir(ppy)₃]/2,7-di-tert-butylpyrene (^tBuPy)/N,N-dimethylaniline (DMA) combination. Colored circles mark the four key elementary reaction steps of (1) triplet–triplet energy transfer (TTET, Section 2.1), (2) triplet–triplet annihilation upconversion (TTA-UC, Section 2.2), (3) pyrenyl radical anion formation (Section 2.3), and (4) substrate activation (Section 2.4). Grey circles mark possible side reactions.

In the following we use Fig. 2 as a roadmap for our mechanistic discussion. All spectroscopic experiments were performed in de-aerated DMF, because this is the preferred solvent for the photoredox catalysis applications demonstrated at the end.

2.1 Triplet–triplet energy transfer from fac-[Ir(ppy)₃] to ^tBuPy

The photophysical properties of fac-[Ir(ppy)₃] are in principle well known, but here it seemed meaningful to re-explore them in de-aerated DMF, because this solvent is best suited for the photoredox reactions in Section 2.6.²⁷ The fac-[Ir(ppy)₃] complex can be excited selectively with blue light and exhibits a luminescence quantum yield of 0.88, and an excited-state lifetime (τ₀) of 1590 ns in de-aerated DMF at 20 °C (Section 2.1.1 in the ESI†).

Addition of excess ^tBuPy to a 10 μM solution of fac-[Ir(ppy)₃] leads to rapid emission quenching (Fig. S3†). The transient absorption spectrum recorded on a mixture of 10 μM fac-[Ir(ppy)₃] and 5 mM ^tBuPy shows the diagnostic spectral signature of triplet-excited ^tBuPy (Fig. 3A), abbreviated henceforth as ^3*tBuPy, with its most characteristic absorption bands featuring maxima at 416 and 525 nm.^46–48 Excited-state quenching of fac-[Ir(ppy)₃] by ^tBuPy occurs with a rate constant of 2.1 × 10⁹ M⁻¹ s⁻¹ (Table 1), according to a Stern–Volmer analysis (ESI† Section 2.2). Given the unambiguous spectral identification of ^3*tBuPy in Fig. 3A and the fact that the transient absorption kinetics at 416 nm (see Fig. S4†) match those of the fac-[Ir(ppy)₃] excited-state decays, this quenching constant can be unambiguously assigned to the rate constant for triplet–triplet energy transfer (k_TTET) of step 1 in Fig. 2. This value is relatively close to the diffusion limit for DMF at 20 °C (7.6 × 10⁹ M⁻¹ s⁻¹).⁴⁹ The ^3*tBuPy photoproduct exhibits a natural (unquenched) lifetime of 335 μs in de-aerated DMF at 20 °C (Fig. S7†).

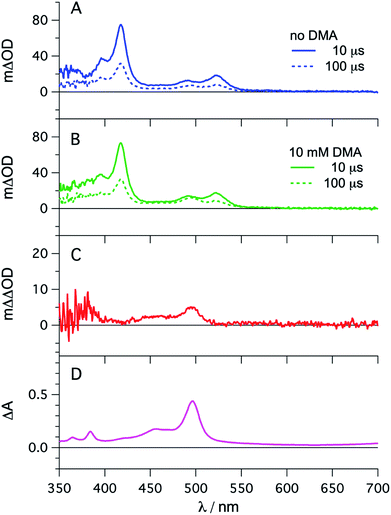Fig. 3 fac-[Ir(ppy)₃] (10 μM) in de-aerated DMF at 20 °C was excited at 450 nm in the presence of ^tBuPy (5 mM) and the transient signals were monitored in the absence (A) and in the presence of 10 mM DMA (B) using delay times of 10 μs (solid lines) and 100 μs (dotted lines). The red trace (C) is the difference obtained by direct subtraction of the dotted blue trace from the dotted green trace. For comparison, the difference absorption spectrum corresponding to the ^tBuPy radical anion (^tBuPy˙⁻) in DMF formed upon electrochemical reduction at −2.25 V vs. SCE in the presence of 0.1 M tetra-n-butylammonium hexafluorophosphate (TBAPF₆) is shown in (D). Further details are in the ESI.†

Table 1 Rate constants (k) and efficiencies (η) for the individual elementary processes illustrated in Fig. 2; abbreviations as defined in the text. All values for de-aerated DMF at 20 °C

Step no.	Description of step	k/M^−1 s^−1	η
a Efficiencies estimated based on the initial concentrations of fac-[Ir(ppy)3], ^tBuPy, DMA and substrate 1 in the photocatalytic reactions of Section 2.6. b A concentration of 0.027 mM is assumed for ^3*tBuPy on the basis of 10% photoexcited fac-[Ir(ppy)3] and TTET with 90% efficiency. Further details are given in Section 2.11 of the ESI.
1	TTET from fac-[Ir(ppy)3] to ^tBuPy	2.1 × 10^9	0.91
1b	Reductive quenching of fac-[Ir(ppy)3] by DMA	1.1 × 10^4	0.003
1c	Oxidative quenching of fac-[Ir(ppy)3] by substrate 1	9.8 × 10^5	0.05
2	TTA-UC of ^tBuPy	1.1 × 10^10	0.99^b
2b	Reductive quenching of ^3*tBuPy by DMA	<1.0 × 10^3	<0.05
3	Reductive quenching of ^1*tBuPy by DMA	4.8 × 10^9	0.99
3b	Oxidative quenching of ^1*tBuPy by substrate 1	6.4 × 10^7	0.31
4	Electron transfer from ^tBuPy˙^− to substrate 1	1.1 × 10^9	0.99

---

When performing the same transient absorption experiment containing 10 μM fac-[Ir(ppy)₃] and 5 mM ^tBuPy (exactly as above), but now in the presence of 10 mM DMA (Fig. 3B), the dominant spectral features are still those of ^3*tBuPy (absorption bands at 416 nm and 525 nm). This indicates that TTET from photo-excited fac-[Ir(ppy)₃] to ^tBuPy remains the dominant reaction pathway even in presence of excess sacrificial electron donor (DMA). Indeed, a separate experiment demonstrates that DMA is unable to quench ³MLCT-excited fac-[Ir(ppy)₃] (Fig. S5†); the rate constant for that reductive quenching (step 1b in Fig. 2) is 1.1 × 10⁴ M⁻¹ s⁻¹. This is a key difference to the previously investigated [Ru(bpy)₃]²⁺/pyrene combination, in which substantial concentrations of [Ru(bpy)₃]⁺ are formed, complicating mechanistic analysis and ultimately leading to another dominant mechanism for SenI-ET.³⁰

Going back to the transient absorption spectra in Fig. 3A and B, we note that an additional transient absorption band at 495 nm appears in the presence of DMA (Fig. 3B), which is not observable in the absence of DMA (Fig. 3A). This additional band becomes particularly prominent at long delay times (100 μs rather than 10 μs, dotted traces in Fig. 3A and B). In Fig. 3C we show a subtraction of the 100 μs delay spectra from Fig. 3A and B; this difference of difference spectrum matches the UV-vis spectrum of pyrene radical anion (^tBuPy˙⁻) generated electrochemically (Fig. 3D) and will be discussed further in Section 2.3. The concentration of ^tBuPy˙⁻ formed in the experiments leading to Fig. 3C is discussed briefly in Section 2.9 of the ESI.† Excimers are not detectable in Fig. 3, due to their comparatively short lifetimes (∼50 ns), their much slower formation and the long detection delay times used to record these spectra.

2.2 Triplet–triplet annihilation upconversion of ^tBuPy and formation of singlet-excited ^tBuPy

The initial mechanistic proposal for SenI-ET with the [Ru(bpy)₃]²⁺/pyrene couple implied reductive quenching of triplet-excited pyrene by the sacrificial electron donor diisopropylethylamine.²⁷ This is clearly not occurring in the fac-[Ir(ppy)₃]/^tBuPy/DMA system, as demonstrated by a transient absorption experiment in which the ^3*tBuPy decay is unaffected by addition of large excess (up to 125 mM) of DMA to a solution containing 10 μM fac-[Ir(ppy)₃] and 5 mM ^tBuPy (Fig. S6†). Consequently, step 2b in Fig. 2 (gray circle) is unimportant in our case, in analogy to what was proposed by others for the [Ru(bpy)₃]²⁺/pyrene couple.²⁸

Triplet–triplet annihilation upconversion (TTA-UC) is instead the dominant next step on the way to productive sensitization-initiated electron transfer (step 2 in Fig. 2, blue circle). Using a solution containing 10 μM fac-[Ir(ppy)₃] and 5 mM ^tBuPy, we excited fac-[Ir(ppy)₃] selectively at 450 nm with pulses of different powers between 4.0 and 16.0 mJ. Thereby we generated different initial concentrations of ^3*tBuPy, which we quantified by using the known extinction coefficient of 37 700 M⁻¹ cm⁻¹ at 415 nm for triplet-excited pyrene.⁵⁰ Fits of the different experimental ^3*tBuPy decay curves (see ESI page S10† for details) provided a rate constant for triplet–triplet annihilation (k_TTA) of (1.1 ± 0.2) × 10¹⁰ M⁻¹ s⁻¹ in DMF at 20 °C (Fig. S7†).

To determine the quantum yield of sTTA-UC, the delayed fluorescence emitted by ^1*tBuPy (Fig. 4A) following excitation of fac-[Ir(ppy)₃] at 447 nm and the prompt ³MLCT luminescence of fac-[Ir(ppy)₃] (Fig. 4B) were measured under strictly identical conditions as a function of excitation power density. Using a solution containing 30 μM fac-[Ir(ppy)₃] and 5 mM ^tBuPy (Fig. 4A) and a solution of 30 μM fac-[Ir(ppy)₃] without ^tBuPy (Fig. 4B), the integrated emission intensities I_sTTA-UC and I_ref were determined. Taking into account that both solutions had identical absorbance at the excitation wavelength (A_sTTA-UC = A_ref = 0.106) and given a ³MLCT luminescence quantum yield (ϕ_ref) of 0.88 in de-aerated DMF at 20 °C (see above), eqn (1) yields the data set in Fig. 4C.^19,20 The upconversion efficiency increases strongly up to an excitation power density of ca. 0.7 W cm⁻², then increases less steeply and finally seems to approach a plateau at ca. 2.5 W cm⁻². At this point, the quantum yield for sTTA-UC reaches a value of 0.048, whereby ϕ_sTTA-UC is defined such that a maximum value of 0.5 is theoretically attainable.^20,51 This compares favorably to many previously investigated cases of sTTA-UC,¹⁹ and furthermore is in line with prior studies of sTTA-UC with cyclometalated iridium/^tBuPy systems performed in other contexts.^44,45

ϕ_sTTA-UC = ϕ_ref × (A_ref/A_sTTA-UC) × (I_sTTA-UC/I_ref) (1)

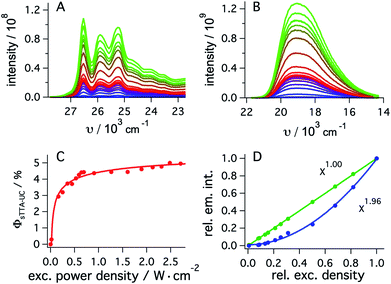Fig. 4 (A) Upconverted ^tBuPy fluorescence sensitized by fac-[Ir(ppy)₃] (30 μM) in de-aerated DMF at 20 °C. Excitation occurred with a 447 nm cw-laser at various excitation densities in the presence of ^tBuPy (5 mM). Excitation powers ranged from 2 mW to 338 mW. (B) Emission spectra of fac-[Ir(ppy)₃] recorded under identical conditions as for (A) but in the absence of ^tBuPy. (C) Upconversion quantum yield (ϕ_sTTA-IC) as a function of excitation power density as determined from eqn (1) and the data in (A) and (B), using a luminescence quantum yield (ϕ_ref) of 0.88 for fac-[Ir(ppy)₃]. (D) Relative integrated intensities of upconverted ^tBuPy (1 mM) fluorescence (blue circles) sensitized by fac-[Ir(ppy)₃] (10 μM) upon excitation at 450 nm as a function of the relative excitation density. The solid blue line represents the best fit with a power function (f(x) = a × x^b + y) to the experimental data, yielding b = 1.96 as indicated by the inset. The green circles result from an analogous experiment in which fac-[Ir(ppy)₃] was excited in the absence of ^tBuPy under otherwise identical conditions, and the prompt luminescence emitted by fac-[Ir(ppy)₃] was monitored (Section 2.5.2 of the ESI†). In this case, a fit to the same power function (green solid line) yields an exponent of 1.00. Measurements in C occurred with the abovementioned cw-laser source, whilst measurements in D were performed using the excitation beam of the luminescence spectrometer.

As expected, the delayed ^1*tBuPy fluorescence exhibits quadratic excitation power dependence (blue trace in Fig. 4D), whilst the prompt ³MLCT luminescence of fac-[Ir(ppy)₃] (green trace in Fig. 4D) is linearly dependent on excitation power density. For the measurements in Fig. 4D, the excitation beam of a luminescence spectrometer was employed in order to access considerably lower excitation power densities than those associated with cw-laser irradiation (Fig. 4A–C). This is important because the strong annihilation limit seems easily reachable with our system, leading to significant deviation from quadratic excitation power dependence when using the cw-laser.⁵²

2.3 Reductive quenching of singlet-excited ^tBuPy to form the pyrenyl radical anion

Spectro-electrochemistry of a solution containing 1 mM ^tBuPy and 100 mM TBAPF₆ under an applied potential of −2.25 V vs. SCE yields the absorption spectrum of the pyrenyl radical anion (^tBuPy˙⁻) in Fig. 3D, featuring a maximum at 496 nm and a side band at 456 nm, which matches the published reference spectrum of the (unsubstituted) pyrenyl radical anion.⁵³ This spectrum is furthermore in excellent agreement with the double difference spectrum in Fig. 3C, which was obtained by subtracting the dotted green trace in Fig. 3B from the dotted blue trace in Fig. 3A. As noted in Section 2.1, the respective transient absorption spectra in Fig. 3A and B were recorded after excitation of 10 μM fac-[Ir(ppy)₃] in de-aerated DMF solutions containing 5 mM ^tBuPy and 10 mM DMA (Fig. 3B) or no DMA at all (Fig. 3A). This subtraction serves to eliminate spectral contributions from triplet-excited pyrene (^3*tBuPy) and leaves behind a spectral contribution (Fig. 3C) that is readily attributable to the pyrenyl radical anion (^tBuPy˙⁻) on the basis of the comparison with Fig. 3D. Thus, it seems very plausible that following sTTA-UC, ^tBuPy˙⁻ is formed via reductive quenching of ^1*tBuPy by DMA. The redox properties of our selected sensitizer (fac-[Ir(ppy)₃]) – photoredox catalyst (^tBuPy) couple lay the grounds for the accumulation of significant ^tBuPy˙⁻ concentrations. The latter is lower in energy than reduced fac-[Ir(ppy)₃] (see ESI† Section 2.13 for the reduction potentials) and, therefore, does not react rapidly with the sensitizer in its ground state. By contrast, in the previously investigated [Ru(bpy)₃]²⁺-containing systems,^6,27,30 the metal complex reduction by the pyrene radical anion is diffusion-controlled. Owing to this undesired side reaction, detectable concentrations of Py˙⁻ could not be obtained, as the production of this key species was always (even under optimized conditions) faster than its decay.^27,30 Our system is designed such that this side reaction cannot occur, and this should be beneficial for its performance in photoredox applications.

The hypothesis of reductive quenching of ^1*tBuPy by DMA is verified by an experiment in which 50 μM ^tBuPy in de-aerated DMF at 20 °C was excited directly at 355 nm (Fig. S10†). The prompt fluorescence of ^1*tBuPy is quenched by DMA with a rate constant of 4.8 × 10⁹ M⁻¹ s⁻¹ (Table 1), attributable to electron transfer from DMA to ^1*tBuPy (step 3 in Fig. 2). Thus, it is clear that in the fac-[Ir(ppy)₃]/2,7-di-tert-butylpyrene/DMA system, the ^tBuPy˙⁻ species forms via the sequence of reactions proposed for the [Ru(bpy)₃]²⁺/pyrene/DIPEA system by Ceroni, Balzani, and coworkers (Fig. 1B).^28,29 Furthermore, there is no reductive quenching of fac-[Ir(ppy)₃] by DMA (step 1b in Fig. 2 and Table 1), and consequently the mechanism postulated by Moore and colleagues for the [Ru(bpy)₃]²⁺/pyrene/DIPEA combination (Fig. 1C)³⁰ is unimportant in our system.

We furthermore explored the possibility of oxidative quenching of ^1*tBuPy by a typical aryl halide compound, substrate 1 (2-chloro-4-fluorobenzonitrile), and found that this process occurs with a rate constant of 6.4 × 10⁷ M⁻¹ s⁻¹ (Table 1) in de-aerated DMF at 20 °C (Fig. S11,† step 3b in Fig. 2). Consequently, when both DMA and substrate 1 are simultaneously present at similar concentrations, reductive quenching of ^1*tBuPy by DMA (step 3) clearly outcompetes oxidative quenching of ^1*tBuPy by substrate 1 (step 3b). In the photoredox experiments presented below, typically more DMA than substrate is present. The predicted efficiency calculations of Table 1 (see Section 2.5 for details) give a clear picture for one of those reactions in isolation (99 vs. 31% quenching efficiency), but a more sophisticated analysis has to be carried out for competing reactions with known kinetics. Comparing the respective products of the second order rate constants and the respective quencher concentration for both step 3 and step 3b (see Table S5† for details) reveals that (desired) reductive quenching is faster by a factor of ∼400 than oxidative quenching starting from ^1*tBuPy in our complete system.

2.4 Substrate activation by pyrenyl radical anion

Except for the control experiment at the end of the preceding section, spectroscopic results presented until here did not involve any substrates, but only the fac-[Ir(ppy)₃]/2,7-di-tert-butylpyrene/DMA components. In the now following elementary step, the onward reaction of ^tBuPy˙⁻ with substrates becomes of central interest. Aryl chlorides are suitable and common substrates for sensitization-initiated electron transfer; photochemical dechlorination is typically observed.^27,36,54 We chose the activated aryl chloride 1 (2-chloro-4-fluorobenzonitrile) as model substrate for mechanistic investigations of the substrate activation step.

First, we note that substrate 1 quenches the ³MLCT-excited state of fac-[Ir(ppy)₃] inefficiently (step 1c in Fig. 2), as a Stern–Volmer analysis (Fig. S16†) yields a rate constant of only 9.8 × 10⁵ M⁻¹ s⁻¹ for photoinduced electron transfer from fac-[Ir(ppy)₃] to substrate 1 (Table 1). The same holds true for all other substrates reported below (ESI,† Section 2.8). The comparatively low rate constant for step 1c in Fig. 2 is unsurprising, because ³MLCT-excited fac-[Ir(ppy)₃] is oxidized at a potential of −1.7 V vs. SCE,⁵⁵ whereas substrate 1 requires a potential of −2.0 V vs. SCE for one-electron reduction (Table S6†) hence step 1c is thermodynamically disfavored by ca. 0.3 eV. Consequently, efficient reduction of substrate 1 (and of all other substrates considered below) is only possible with ^tBuPy˙⁻ as reductant, as discussed in the following.

To obtain direct spectroscopic insight into electron transfer from ^tBuPy˙⁻ to substrate 1, we excited 50 μM ^tBuPy directly at 355 nm in the presence of excess (10 mM) DMA to form ^tBuPy˙⁻ (via reductive quenching of ^1*tBuPy). Then we performed comparative transient absorption measurements in the absence (Fig. 5A) and in the presence of 200 μM substrate 1 (Fig. 5B). Under these conditions, ^tBuPy˙⁻ (with its diagnostic absorption band at 495 nm as discussed above in Fig. 3C and D) is formed in both cases. Unsurprisingly, the kinetics of the ^tBuPy˙⁻ signal at 495 nm do not follow single-exponential decay kinetics regardless of whether substrate 1 is present (inset of Fig. 5B) or not (inset of Fig. 5A), yet it is clear that the presence of 200 μM substrate 1 accelerates the disappearance of ^tBuPy˙⁻ markedly. In the presence of such low concentrations of substrate 1, the consumption of substrate over time (as a function of spectral data acquisition over a series of laser excitation pulses) and ensuing changes of concentrations can start to play a non-negligible role. Therefore, careful data acquisition with only a few laser pulses for each measurement is needed to obtain reliable transient spectra, and to make estimation of the rate for electron transfer from ^tBuPy˙⁻ to substrate 1 (step 4 in Fig. 2) in a Stern–Volmer type analysis possible (for more details see ESI,† Section 2.10). A biexponential fit to the data in the absence of substrate 1 yields time constants of 1.07 ms (44%) and 54.7 μs (56%). In the corresponding series of spectra of Fig. 5A, the characteristic band at 495 nm persists even after a delay time of 1 ms, and thus it seems that both of these two time constants are associated with ^tBuPy˙⁻, but reflect its disappearance by two different decay paths. Analogous analysis of the decay in Fig. 5B leads to time constants of 3.1 μs (79%) and 28.9 μs (21%), but the corresponding spectra in Fig. 5B indicate that in this case only the shorter of the two decay constants is associated with ^tBuPy˙⁻, because the prominent band at 495 nm has essentially disappeared after 40 μs. Thus, the decay time of ^tBuPy˙⁻ shortens from 1.07 ms/54.7 μs to 3.1 μs upon addition of 200 μM substrate 1. Performing the same analysis with different concentrations of substrate 1, a rate constant of roughly 1.1 × 10⁹ M⁻¹ s⁻¹ is estimated in a Stern–Volmer type analysis based on the faster decay components of the kinetic fits in the presence of substrate 1 (Fig. 5C, see also Section 2.10 in the ESI†).

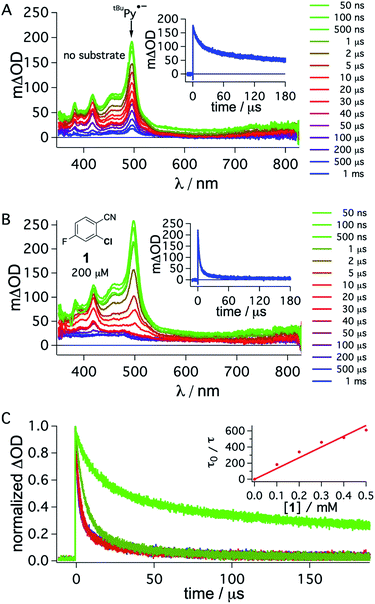Fig. 5 Transient absorption spectra obtained after direct 355 nm excitation of ^tBuPy (50 μM) in de-aerated DMF in the presence of DMA (10 mM) (A), recorded at different delay times as indicated in the inset. Same experiment series performed on a solution containing substrate 1 (200 μM) in addition to 50 μM ^tBuPy and 10 mM DMA (B). Corresponding kinetic traces monitoring the decay of the ^tBuPy˙⁻ signal at 495 nm over 180 μs in the respective solutions without and with substrate 1 are given in the insets of (A) and (B). ^tBuPy˙⁻ disappears considerably more rapidly in the presence of substrate 1 (B) than in its absence (A). For clarity the most prominent spectroscopic feature of ^tBuPy˙⁻ is marked by an arrow in (A). Kinetic traces at 495 nm (C) were monitored in the absence (bright green) and in the presence of different concentrations of 1 (0.1, 0.2, 0.3, 0.4, 0.5 mM). The Stern–Volmer plot for the shorter lifetime components obtained from biexponential fits to this data set is given in the inset of (C). A quenching constant of ca. 1.1 × 10⁹ M⁻¹ s⁻¹ is estimated for the electron transfer from ^tBuPy˙⁻ to substrate 1, based on an unquenched decay constant of 1.07 ms for ^tBuPy˙⁻. A 385 nm long-pass cut-off filter was installed between the sample and the flashlamp to prevent direct UV flashlamp excitation. Further details are in the main text and the ESI.†

Though this crude analysis of the substrate activation kinetics seems reasonable, it is evident from the spectra in Fig. 5A and B that other species than ^tBuPy˙⁻ contribute to the transient spectra, particularly after longer delay times (>10 μs).⁴⁷ In addition to the DMA radical cation, which has a comparably low extinction coefficient in the spectral range below 550 nm and is presumably challenging to clearly identify with respect to the high absorbance of ^tBuPy˙⁻,^56–58 one possible complication is that exciplex interaction (formation of electron donor–acceptor (EDA) complexes) between ^tBuPy and DMA can lead to the formation of ^3*tBuPy over time (see ESI† Section 2.10 for further details),^59–61 and this can affect the transients recorded at 495 nm. Further complications may arise for example through protonation of ^tBuPy˙⁻.^47,53,62

2.5 Holistic picture and efficiencies of individual elementary steps

The main reaction pathway of the mechanism in Fig. 2 can be summarized in the Jablonski-type diagram presented in Fig. 6. For each elementary step of the mechanism in Fig. 2 and 6, one can estimate an efficiency (η) based on the expression η = 1 − τ/τ₀. τ₀ is the natural excited-state lifetime of the reactant for a given step (or its pseudo-first order decay time in case of ^tBuPy˙⁻), and τ is the observable lifetime (or pseudo-first order decay time) in presence of a given concentration of reaction partner. For instance, for TTET between ³MLCT-excited fac-[Ir(ppy)₃] to ^tBuPy (step 1 in Fig. 2 and 6) we found k_TTET = 2.1 × 10⁹ M⁻¹ s⁻¹ (Table 1), and consequently, for a ^tBuPy concentration of 3 mM (corresponding to 10 mol% present under catalytic conditions, see below), one obtains τ = 144 ns (see Section 2.11 of the ESI† for further details). Given τ₀ = 1590 ns for fac-[Ir(ppy)₃] in de-aerated DMF at 20 °C (Fig. S3†), one obtains η = 0.91 for this particular elementary step (last column in Table 1).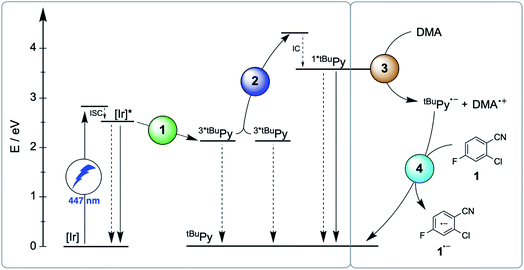

Fig. 6 Jablonski-type diagram summarizing triplet–triplet annihilation upconversion (left) and photoredox catalysis (right) as the two main mechanistic parts. In analogy to Fig. 2, the colored circles mark the four key elementary reaction steps of (1) triplet–triplet energy transfer (TTET, Section 2.1), (2) triplet–triplet annihilation upconversion (TTA-UC, Section 2.2), (3) pyrenyl radical anion formation (Section 2.3), and (4) substrate activation (Section 2.4). Rate constants and efficiencies for these steps are summarized in Table 1. Unproductive pathways are omitted for clarity. ISC = intersystem crossing, IC = internal conversion.

For the calculation of all other η values in Table 1 we proceeded in analogous manner, meaning that we employed the rate constants (k) resulting from the laser spectroscopic measurements in the prior sections and then determined the respective τ values using the synthetically relevant concentrations. This somewhat crude approach implies that one can simply extrapolate from spectroscopic measurements performed with photosensitizers at 10–50 μM to considerably more concentrated reaction solutions. The synthetically relevant conditions (as discussed further below) typically involved 1 mol% fac-[Ir(ppy)₃], 10 mol% ^tBuPy, 5 equivalents of DMA, and substrate concentrations of 30 mM.

For the productive elementary steps 1–4 of Fig. 2 and 6, the efficiencies η range from 0.91 to 0.99 (Table 1, see ESI Table S5† for details). It should be noted that η for sTTA-UC adopts a value of 0.99 in Table 1, whereas the quantum yield for upconversion (ϕ_sTTA-UC in eqn (1)) only reaches a value of 0.048 under optimized conditions (Fig. 4C). The η values in Table 1 describe the efficiency of an onward reaction step for a given intermediate once it has been formed, whereas ϕ_sTTA-UC is an absolute (overall) quantum yield taking into account several reaction steps (including unproductive or counterproductive events).

Among all considered side reactions (1b, c, 2b, 3b in Fig. 2), oxidative quenching of ^1*tBuPy by substrate 1 is the most efficient (η = 0.31), whilst all others have considerably lower η values (≤0.05) and therefore seem negligible. Thus, depending on what substrate is considered, ^1*tBuPy should be kept in mind as a possible photoreductant, yet the dominant mechanism is clearly the one highlighted in Fig. 2 and 6, particularly for substrates with more negative reduction potentials than −1.9 V vs. SCE (corresponding to the excited state oxidation potential of ^1*tBuPy). ^tBuPy˙⁻ (−2.1 V vs. SCE, see above) is not only more reducing than ^1*tBuPy, but it is also considerably longer-lived, making the radical anion both a thermodynamically and kinetically preferred reactant.

Deactivation pathways such as the recombination between substrate radical anion (1˙⁻) and DMA oxidation products cannot be tracked spectroscopically, and the η value for step 4 does not take into account the possibility of in-cage charge recombination. Our choice of DMA was partly motivated by the fact that (alkylated) anilines as sacrificial electron donors seem to provide higher cage-escape yields than other (tertiary) amines.^31,63 Onward reactions of substrates were not possible to follow in our system.

The choice of fac-[Ir(ppy)₃] (instead of [Ru(bpy)₃]²⁺) has been essential for achieving the remarkably high rate constants and efficiencies of all productive elementary steps in Fig. 2 and Table 1. The key point here is that reductive excited-state quenching of fac-[Ir(ppy)₃] 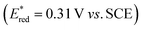is considerably more difficult than for [Ru(bpy)₃]²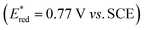⁺.⁵⁵ This opens the possibility to select a sacrificial electron donor, which is able to reductively quench only ^1*tBuPy (but not the photosensitizer), and consequently leads to a reaction mechanism with one clearly defined sequence of thermodynamically and kinetically preferred elementary steps. In our case, DMA was a good choice (E_ox = 0.81 V vs. SCE in MeCN).⁶⁴

2.6 Application of the fac-[Ir(ppy)₃]/^tBuPy/DMA system to photoredox catalysis

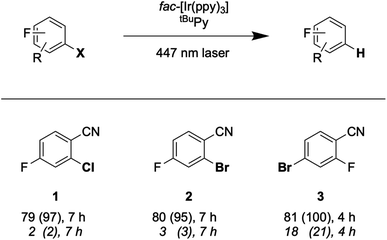
The prior seminal studies of sensitization-initiated electron transfer already established the broad synthetic scope of this photochemical reaction type for the [Ru(bpy)₃]²⁺/pyrene/DIPEA combination.²⁷ Whilst a similarly detailed exploration of reaction scope for the fac-[Ir(ppy)₃]/^tBuPy/DMA system seems superfluous, it nevertheless is desirable to demonstrate its applicability to photoredox catalysis on a few carefully selected examples.

Hydrodehalogenation reactions of substrates 1, 2, and 3 were first explored under 447 nm cw-laser excitation conditions, because this excitation source is particularly powerful and resembles most closely that used in the spectroscopic studies presented above. All three substrates contain fluoro-substituents as ¹⁹F-NMR markers, and the reactions were performed in the presence of 4-fluorotoluene as internal standard. This permits convenient determination of yields and conversions by ¹⁹F-NMR spectroscopy.^65,66

The reaction conditions were optimized with substrate 1 present at 30 mM concentration in de-aerated DMF at room temperature (Table 2). When using 1 mol% fac-[Ir(ppy)₃], 5 mol% of ^tBuPy, and 5 equivalents of DMA, a hydrodechlorination product (1-P) yield of 79% was determined after 16 hours of irradiation (with a conversion of 96%, entry 1 in Table 2). Increasing the ^tBuPy annihilator concentration from 5 to 10 mol% leads to very similar yield and conversion (entry 2), but already after an irradiation time of 7 instead of 16 hours. When replacing DMA by DIPEA whilst keeping all other parameters unchanged, both the yield and the conversion drop substantially (entry 3), demonstrating that DMA is important as sacrificial reductant. Control experiments without ^tBuPy (entry 4), fac-[Ir(ppy)₃] (entry 5) or light (entry 6) do not yield any significant conversion, demonstrating that all three components are vital.

Table 2 Optimization of reaction conditions^a

Entry	fac-[Ir(ppy)3]/mol%	^tBuPyrene/mol%	Time/h	Yield (conv.)^b/%
a Reaction conditions: 30 mM substrate 1 in 3 mL de-aerated DMF. Sample irradiated in a quartz cuvette under an Argon atmosphere at room temperature. b Yields and conversions (in parentheses) were determined by quantitative ^19F-NMR analysis using 4-fluorotoluene as internal standard. c DIPEA (5 eq.) instead of DMA used as sacrificial electron donor. d Sample not irradiated.
1	1	5	16	79 (96)
2	1	10	7	79 (97)
3^c	1	10	7	53 (67)
4	1	—	7	2 (2)
5	—	10	7	0 (0)
6^d	1	10	7	0 (0)

---

With the optimized reaction conditions identified, complete conversions and hydrodehalogenation yields of ca. 80% were obtainable for substrates 1 to 3 (Fig. 7) over reaction times of 4 to 7 hours. Fig. 8 illustrates the typical reaction progress as a function of irradiation time for substrate 1. The initial ¹⁹F-NMR spectrum (top trace in Fig. 8A) contains resonances at −101.50 ppm due to the substrate and at −119.15 ppm attributable to the internal standard, 4-fluorotoluene. The final spectrum recorded after 7 hours (bottom trace in Fig. 8A) exhibits essentially only the hydrodechlorination product (1-P) resonance at −104.05 ppm in addition to that of the internal standard, whilst the spectra recorded at intermediate times are essentially linear combinations of the top and bottom traces. This data set results in the expectable kinetics (Fig. 8B), with the rate of product formation decreasing with increasing reaction progress, due to consumption of the starting material (minor resonances appearing in Fig. 8 at −104.85 ppm and −104.93 ppm are unidentified side products, most likely based on side reactions with DMA-related degradation intermediates).

Fig. 7 Hydrodehalogenation of selected aryl halide substrates through SenI-ET with a 447 nm cw-laser. Reaction conditions: 30 mM substrate, fac-[Ir(ppy)₃] (1 mol%), ^tBuPy (10 mol%) and DMA (5 eq.) in 3 mL DMF under Argon at 20 °C. Yields and conversions (in parentheses) are reported for the complete reaction system (upper lines below substrate numbers) and for the reaction system without ^tBuPy annihilator (lower lines in italic font). Conversions and yields were determined by quantitative ¹⁹F-NMR analysis using 4-fluorotoluene as internal standard.

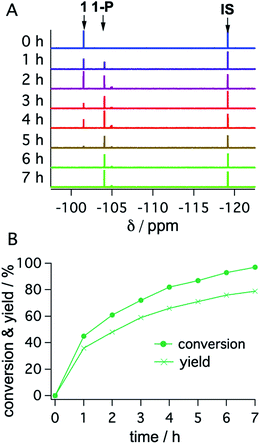Fig. 8 ¹⁹F-NMR signals (1 at −101.50 ppm; 1-P at −104.05 ppm; 4-fluorotoluene (IS) at −119.15 ppm) (A) and corresponding conversion (dots) and yield (crosses) of substrate 1 as a function of irradiation time with a 447 nm cw-laser (B). Conditions were identical to those given in Table 2. Further details are in Section 4.3 of the ESI.†

As noted in Fig. 7, the conversion of substrate 3 requires only 4 hours, whereas the full conversion of substrates 1 and 2 necessitates 7 hours. This suggests that substrate activation (step 4 in (Fig. 2 and 6)) is decisive for the rate of product formation, because bromo-substrate 3 is easier to reduce (E_red ≈ −1.8 V vs. SCE) than chloro-substrate 1 and bromo-substrate 2 (E_red ≈ −2.0 V vs. SCE) (Fig. S25 and Table S6†). Reductive debromination is typically thermodynamically less demanding than reductive dechlorination.^36,67–74

Lastly, we explored the possibility of using a high-power LED (440 nm, 40 W) as irradiation source, because this is more widely available than cw-lasers, and we investigated detosylation and pinacol coupling reactions in addition to hydrodehalogenations (Fig. 9). Gratifyingly, the dechlorination of substrate 1 does also proceed well under LED-irradiation, although the reaction is slightly slower than when using the cw-laser. The pinacol coupling reaction of 4′-fluoroacetophenone 4 demonstrates that carbon–carbon bond formation is possible. Although the one-electron reduction potential of compound 4 is ca. 0.2 V more negative than that of substrate 1, the pinacol coupling reaction of 4 proceeded much faster (0.5 h) than the dechlorination reactions (7 h), even with less catalyst. The pinacol coupling reaction was furthermore performed on a 0.5 mmol scale and 54 mg of product 4 were isolated, corresponding to a yield of 68% (see ESI† Section 4.2.2). Considering that the established mechanism in Fig. 2 is bi-photonic (i.e., requires two photo-excitations of the iridium sensitizer per substrate molecule), a turnover number (TON) of ca. 600 for fac-[Ir(ppy)₃] is achieved in this case. This compares favourably to a recent study in which a water-soluble variant of the same photosensitizer was employed in a bi-photonic photoredox dechlorination, and where a TON of 203 was found.⁷⁵ The multi-photonic nature of this photoredox reaction furthermore manifests in its dependence on LED excitation power (Fig. S27†). Specifically, when increasing the LED power from 50% to 100%, the rate of substrate conversion increases by a factor of 3.3, in line with a process requiring more than one photon per turnover. For reference, an ordinary mono-photonic process would lead to a doubling of the product formation rate when the irradiation power is doubled, at least under idealized conditions. The deviation from the theoretically expected factor of 4.0 observed here for the bi-photonic reaction might have its origin in the fact that under the catalytic conditions with rather elevated photosensitizer and annihilator concentrations, the overall system operates near the so-called strong annihilation limit, in which the power-dependence is no longer strictly quadratic.⁵² Furthermore, catalyst inhibition and lowered substrate concentrations might start to play a non-negligible role with increasing irradiation time and substrate turnover (see ESI† Sections 2.1.2 and 4.4).

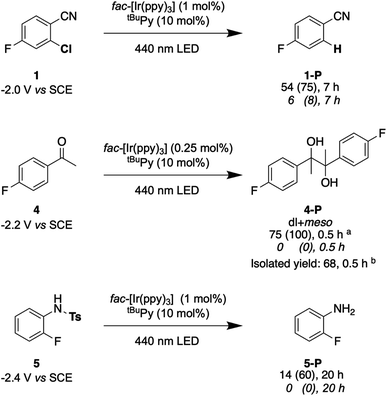Fig. 9 Selected examples for light-driven reduction reactions performed with an LED (440 nm, 40 W). Reactions were performed with 30 mM substrate in presence of 5 eq. DMA, fac-[Ir(ppy)₃] (0.25–1 mol%), and ^tBuPy (10 mol%) in 3 mL de-aerated DMF in a Schlenk tube under Argon at room temperature. Yields and conversions (in parentheses) are reported for the complete reaction system (upper lines below substrate numbers) and for the reaction system without ^tBuPy annihilator (lower lines in italic font). Conversions and yields were determined by ¹⁹F-NMR analysis using 4-fluorotoluene as internal standard and averaged over two independent measurements. (a) dl : meso ratio of 1.05 : 1. (b) dl : meso ratio of 1.06 : 1. Electrochemical potentials for one-electron reduction are indicated below each substrate (see ESI† Section 2.13).

Lastly, the photochemical detosylation of the protected fluoroaniline 5 was explored (Fig. 9, bottom). Thermodynamically, this is a rather challenging reaction because it requires a reduction potential of −2.4 V vs. SCE for the initial substrate activation step, compared to “only” −2.0 V vs. SCE for compound 1. Thus, it is not surprising that this detosylation reaction is considerably slower than the previous examples, requiring 20 h instead of 7 h. Nevertheless, a conversion of 60% of substrate 5 was achievable, but several unidentified side-products were detectable. This example therefore illustrates the performance limit of our system with ^tBuPy˙⁻ as reactive species.

3. Summary and conclusions

Photoredox catalysis frequently relies on multi-component systems comprised of a sensitizer and a (co-)catalyst in addition to a sacrificial redox reagent.^76–78 Over the past few years the level of complexity has been further increased by the exploration of bi-photonic reactions, which function on the basis of two consecutive photo-excitations per substrate turnover.^{1,2,4,7,18,23,27,39,79–83} This is an attractive strategy because it gives access to reactions requiring more energy input than that of a single visible photon. Such multi-component, multi-photon excitation systems allowed remarkable advances in synthetic organic photochemistry, but mechanistic insight was very tricky to obtain due to the high level of complexity.^28,30,34 To the best of our knowledge, our work represents the first complete mechanistic investigation of sensitization-initiated electron transfer (SenI-ET) with clear-cut spectroscopic characterization of all relevant reaction intermediates up to the substrate activation step, which includes the elusive key catalytic species, the pyrenyl radical anion. Our study demonstrates that SenI-ET can indeed operate through a mechanism based on sensitized triplet–triplet annihilation upconversion (sTTA-UC), as suspected earlier (but never confirmed experimentally).²⁸

Furthermore, we demonstrate here that a change of one component in a multi-photon excitation system can lead to a complete change of the mechanism. The design of our fac-[Ir(ppy)₃]/^tBuPy/DMA combination is geared at favoring the sTTA-UC mechanism, particularly because reductive quenching of fac-[Ir(ppy)₃] is thermodynamically uphill, thereby favoring energy transfer to the pyrene annihilator.

Triplet–triplet annihilation upconversion recently gained increasing attention in the context of photoredox catalysis,^{2,11,18,22,23} yet in most cases investigated to date, the upconverted singlet excited state of the annihilator acted as electron donor to substrates or co-catalysts.¹ Our study provides a rare example in which the upconverted annihilator is quenched reductively by a sacrificial electron donor, and where the one-electron reduced form of the annihilator becomes the key species leading to substrate activation. This is associated with significant kinetic advantages, because the annihilator radical anion is considerably longer-lived (typically tens of microseconds) than the annihilator singlet excited state (typically a few nanoseconds).

Due to their quadratic power-dependence, bi-photonic reactions need higher photon fluxes than more traditional photoreactions functioning on the basis of single excitations.⁵² This in turn increases the likelihood for photodegradation of the catalytic system. In this respect, fac-[Ir(ppy)₃] and related homoleptic tris(cyclometalated) iridium(III) complexes are particularly advantageous,⁷⁵ as they seem more photorobust in presence of large excess of sacrificial reductant than [Ru(bpy)₃]²⁺ (and its congeners)⁸⁴ and heteroleptic iridium(III) complexes comprised of cyclometalating and α-diimine ligands.³⁹

Multi-component photoredox systems and bi-photonic excitation schemes will likely continue to attract considerable attention in the future, and our study contributes to understanding them at the most fundamental mechanistic level. This seems essential for future rational progress development in this thriving research area and could have important implications for organic synthetic photochemistry and solar energy conversion.^85–87

Data availability

All experimental data, procedures for data analysis and pertinent data sets are provided in the ESI.

Author contributions

F. G. designed photochemical studies, carried out spectroscopic, synthetic and electrochemical work, analysed data and performed photocatalytic measurements; C. K. conceived the project and provided guidance in data analysis; O. S. W. conceived the project and provided guidance. All authors contributed to the writing and editing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Swiss National Science Foundation through grant number 200021_178760 and by the Research Fund of the University of Basel (Novartis University of Basel Excellence Scholarship for Life Sciences (3CH1038) to C. K.).

References

1. F. Glaser, C. Kerzig and O. S. Wenger, Angew. Chem., Int. Ed., 2020, 59, 10266–10284.
2. B. D. Ravetz, A. B. Pun, E. M. Churchill, D. N. Congreve, T. Rovis and L. M. Campos, Nature, 2019, 565, 343–346.
3. I. A. MacKenzie, L. Wang, N. P. R. Onuska, O. F. Williams, K. Begam, A. M. Moran, B. D. Dunietz and D. A. Nicewicz, Nature, 2020, 580, 76–80.
4. I. Ghosh, T. Ghosh, J. I. Bardagi and B. König, Science, 2014, 346, 725–728.
5. M. Goez, C. Kerzig and R. Naumann, Angew. Chem., Int. Ed., 2014, 53, 9914–9916.
6. C. Kerzig and M. Goez, Chem. Sci., 2016, 7, 3862–3868.
7. I. Ghosh, L. Marzo, A. Das, R. Shaikh and B. König, Acc. Chem. Res., 2016, 49, 1566–1577.
8. C. J. Zeman, S. Kim, F. Zhang and K. S. Schanze, J. Am. Chem. Soc., 2020, 142, 2204–2207.
9. N. T. La Porte, J. F. Martinez, S. Chaudhuri, S. Hedström, V. S. Batista and M. R. Wasielewski, Coord. Chem. Rev., 2018, 361, 98–119.
10. N. T. La Porte, J. F. Martinez, S. Hedström, B. Rudshteyn, B. T. Phelan, C. M. Mauck, R. M. Young, V. S. Batista and M. R. Wasielewski, Chem. Sci., 2017, 8, 3821–3831.
11. L. Huang, W. Wu, Y. Li, K. Huang, L. Zeng, W. Lin and G. Han, J. Am. Chem. Soc., 2020, 142, 18460–18470.
12. M. Neumeier, D. Sampedro, M. Májek, V. A. de la Peña O'Shea, A. Jacobi von Wangelin and R. Pérez-Ruiz, Chem.–Eur. J., 2018, 24, 105–108.
13. M. Freitag, N. Möller, A. Rühling, C. A. Strassert, B. J. Ravoo and F. Glorius, ChemPhotoChem, 2019, 3, 24–27.
14. C. Y. Fan, L. L. Wei, T. Niu, M. Rao, G. Cheng, J. J. Chruma, W. H. Wu and C. Yang, J. Am. Chem. Soc., 2019, 141, 15070–15077.
15. N. Nishimura, V. Gray, J. R. Allardice, Z. Zhang, A. Pershin, D. Beljonne and A. Rao, ACS Mater. Lett., 2019, 1, 660–664.
16. R. S. Khnayzer, J. Blumhoff, J. A. Harrington, A. Haefele, F. Deng and F. N. Castellano, Chem. Commun., 2012, 48, 209–211.
17. C. E. Elgar, H. Y. Otaif, X. Zhang, J. Zhao, P. N. Horton, S. J. Coles, J. M. Beames and S. J. A. Pope, Chem.–Eur. J., 2021, 27, 3427–3439.
18. B. D. Ravetz, N. E. S. Tay, C. L. Joe, M. Sezen-Edmonds, M. A. Schmidt, Y. Tan, J. M. Janey, M. D. Eastgate and T. Rovis, ACS Cent. Sci., 2020, 6, 2053–2059.
19. P. Bharmoria, H. Bildirir and K. Moth-Poulsen, Chem. Soc. Rev., 2020, 49, 6529–6554.
20. T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573.
21. V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71.
22. C. G. López-Calixto, M. Liras, V. A. D. O'Shea and R. Pérez-Ruiz, Appl. Catal., B, 2018, 237, 18–23.
23. M. Majek, U. Faltermeier, B. Dick, R. Pérez-Ruiz and A. Jacobi von Wangelin, Chem.–Eur. J., 2015, 21, 15496–15501.
24. C. Kerzig and O. S. Wenger, Chem. Sci., 2018, 9, 6670–6678.
25. M. Majek and A. Jacobi von Wangelin, Acc. Chem. Res., 2016, 49, 2316–2327.
26. B. Pfund, D. M. Steffen, M. R. Schreier, M. S. Bertrams, C. Ye, K. Börjesson, O. S. Wenger and C. Kerzig, J. Am. Chem. Soc., 2020, 142, 10468–10476.
27. I. Ghosh, R. S. Shaikh and B. König, Angew. Chem., Int. Ed., 2017, 56, 8544–8549.
28. M. Marchini, G. Bergamini, P. G. Cozzi, P. Ceroni and V. Balzani, Angew. Chem., Int. Ed., 2017, 56, 12820–12821.
29. I. Ghosh, J. I. Bardagi and B. König, Angew. Chem., Int. Ed., 2017, 56, 12822–12824.
30. M. S. Coles, G. Quach, J. E. Beves and E. G. Moore, Angew. Chem., Int. Ed., 2020, 59, 9522–9526.
31. T. Yoshio, N. Yasuzo and M. Noboru, Bull. Chem. Soc. Jpn., 1972, 45, 764–769.
32. Y. Waka, K. Hamamoto and N. Mataga, Chem. Phys. Lett., 1978, 53, 242–246.
33. J. Haimerl, I. Ghosh, B. König, J. Vogelsang and J. M. Lupton, Chem. Sci., 2019, 10, 681–687.
34. M. Marchini, A. Gualandi, L. Mengozzi, P. Franchi, M. Lucarini, P. G. Cozzi, V. Balzani and P. Ceroni, Phys. Chem. Chem. Phys., 2018, 20, 8071–8076.
35. R. Naumann, C. Kerzig and M. Goez, Chem. Sci., 2017, 8, 7510–7520.
36. M. Giedyk, R. Narobe, S. Weiß, D. Touraud, W. Kunz and B. König, Nat. Catal., 2019, 3, 40–47.
37. M. Schmalzbauer, M. Marcon and B. König, Angew. Chem., Int. Ed., 2021, 60, 6270–6292.
38. Y. S. Qiao and E. J. Schelter, Acc. Chem. Res., 2018, 51, 2926–2936.
39. T. U. Connell, C. L. Fraser, M. L. Czyz, Z. M. Smith, D. J. Hayne, E. H. Doeven, J. Agugiaro, D. J. D. Wilson, J. L. Adcock, A. D. Scully, D. E. Gomez, N. W. Barnett, A. Polyzos and P. S. Francis, J. Am. Chem. Soc., 2019, 141, 17646–17658.
40. A. Aguirre-Soto, K. Kaastrup, S. Kim, K. Ugo-Beke and H. D. Sikes, ACS Catal., 2018, 8, 6394–6400.
41. J. Castellanos-Soriano, J. C. Herrera-Luna, D. Díaz Díaz, M. C. Jiménez and R. Pérez-Ruiz, Org. Chem. Front., 2020, 7, 1709–1716.
42. D. Dzebo, K. Moth-Poulsen and B. Albinsson, Photochem. Photobiol., 2017, 16, 1327–1334.
43. C. Ye, V. Gray, K. Kushwaha, S. Kumar Singh, P. Erhart and K. Börjesson, Phys. Chem. Chem. Phys., 2020, 22, 1715–1720.
44. W. Zhao and F. N. Castellano, J. Phys. Chem. A, 2006, 110, 11440–11445.
45. P. Duan, N. Yanai and N. Kimizuka, Chem. Commun., 2014, 50, 13111–13113.
46. Q. Chen, Y. Liu, X. Guo, J. Peng, S. Garakyaraghi, C. M. Papa, F. N. Castellano, D. Zhao and Y. Ma, J. Phys. Chem. A, 2018, 122, 6673–6682.
47. T. G. Pavlopoulos, J. Chem. Phys., 1970, 52, 3307–3308.
48. M. Ottolenghi, C. R. Goldschmidt and R. Potashnik, J. Phys. Chem., 1971, 75, 1025–1031.
49. M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, CRC Taylor & Francis, Boca Raton, Florida, 2006.
50. I. Carmichael, W. P. Helman and G. L. Hug, J. Phys. Chem. Ref. Data, 1987, 16, 239–260.
51. Y. Zhou, F. N. Castellano, T. W. Schmidt and K. Hanson, ACS Energy Lett., 2020, 5, 2322–2326.
52. A. Haefele, J. Blumhoff, R. S. Khnayzer and F. N. Castellano, J. Phys. Chem. Lett., 2012, 3, 299–303.
53. A. M. Funston, S. V. Lymar, B. Saunders-Price, G. Czapski and J. R. Miller, J. Phys. Chem. B, 2007, 111, 6895–6902.
54. I. Ghosh, Phys. Sci. Rev., 2019, 4, 20170185.
55. D. M. Arias-Rotondo and J. K. McCusker, Chem. Soc. Rev., 2016, 45, 5803–5820.
56. R. G. Brown, A. Harriman and L. Harris, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1193–1199.
57. C. D. Borsarelli, J. J. Cosa and C. M. Previtali, Photochem. Photobiol., 1998, 68, 438–446.
58. F. Cao, J. Kim and A. J. Bard, J. Am. Chem. Soc., 2014, 136, 18163–18169.
59. J. F. Delouis, J. A. Delaire and N. Ivanoff, Chem. Phys. Lett., 1979, 61, 343–346.
60. M. Ottolenghi, Acc. Chem. Res., 1973, 6, 153–160.
61. G. Zhang, J. K. Thomas, A. Eremenko, T. Kikteva and F. Wilkinson, J. Phys. Chem. B, 1997, 101, 8569–8577.
62. T. N. Das and K. I. Priyadarsini, J. Chem. Soc., Perkin Trans. 2, 1993, 733–739.
63. H. Masuhara and N. Mataga, Acc. Chem. Res., 1981, 14, 312–318.
64. Y. Pellegrin and F. Odobel, C. R. Chim., 2017, 20, 283–295.
65. F. Glaser, C. B. Larsen, C. Kerzig and O. S. Wenger, Photochem. Photobiol. Sci., 2020, 19, 1035–1041.
66. C. P. Rosenau, B. J. Jelier, A. D. Gossert and A. Togni, Angew. Chem., Int. Ed., 2018, 57, 9528–9533.
67. L. Pause, M. Robert and J. M. Savéant, J. Am. Chem. Soc., 1999, 121, 7158–7159.
68. J.-H. Shon, S. Sittel and T. S. Teets, ACS Catal., 2019, 9, 8646–8658.
69. T. Constantin, M. Zanini, A. Regni, N. S. Sheikh, F. Juliá and D. Leonori, Science, 2020, 367, 1021–1026.
70. R. Matsubara, T. Yabuta, U. Md Idros, M. Hayashi, F. Ema, Y. Kobori and K. Sakata, J. Org. Chem., 2018, 83, 9381–9390.
71. Q. Wang, M. Poznik, M. Li, P. J. Walsh and J. J. Chruma, Adv. Synth. Catal., 2018, 360, 2854–2868.
72. J.-H. Shon, D. Kim, M. D. Rathnayake, S. Sittel, J. Weaver and T. S. Teets, Chem. Sci., 2021, 12, 4069–4078.
73. M. Cybularczyk-Cecotka, J. Szczepanik and M. Giedyk, Nat. Catal., 2020, 3, 872–886.
74. F. Strieth-Kalthoff, C. Henkel, M. Teders, A. Kahnt, W. Knolle, A. Gomez-Suarez, K. Dirian, W. Alex, K. Bergander, C. G. Daniliuc, B. Abel, D. M. Guldi and F. Glorius, Chem, 2019, 5, 2183–2194.
75. C. Kerzig, X. Guo and O. S. Wenger, J. Am. Chem. Soc., 2019, 141, 2122–2127.
76. J. Twilton, C. Le, P. Zhang, M. H. Shaw, R. W. Evans and D. W. C. MacMillan, Nat. Rev. Chem., 2017, 1, 0052.
77. K. L. Skubi, T. R. Blum and T. P. Yoon, Chem. Rev., 2016, 116, 10035–10074.
78. K. Zeitler and M. Neumann, in 11. Synergistic visible light photoredox catalysis, ed. K. Burkhard, De Gruyter, 2020, pp. 245–284,  DOI:10.1515/9783110576764-011.
79. M. Haring, R. Pérez-Ruiz, A. Jacobi von Wangelin and D. D. Diaz, Chem. Commun., 2015, 51, 16848–16851.
80. A. K. Pal, C. F. Li, G. S. Hanan and E. Zysman-Colman, Angew. Chem., Int. Ed., 2018, 57, 8027–8031.
81. P. W. Antoni and M. M. Hansmann, J. Am. Chem. Soc., 2018, 140, 14823–14835.
82. A. H. Hu, Y. L. Chen, J. J. Guo, N. Yu, Q. An and Z. W. Zuo, J. Am. Chem. Soc., 2018, 140, 13580–13585.
83. L. Næsborg, C. Jandl, A. Zech and T. Bach, Angew. Chem., Int. Ed., 2020, 59, 5656–5659.
84. C. Bachmann, B. Probst, M. Oberholzer, T. Fox and R. Alberto, Chem. Sci., 2016, 7, 436–445.
85. N. T. Vo, Y. Mekmouche, T. Tron, R. Guillot, F. Banse, Z. Halime, M. Sircoglou, W. Leibl and A. Aukauloo, Angew. Chem., Int. Ed., 2019, 58, 16023–16027.
86. A. Magnuson, M. Anderlund, O. Johansson, P. Lindblad, R. Lomoth, T. Polivka, S. Ott, K. Stensjö, S. Styring, V. Sundström and L. Hammarström, Acc. Chem. Res., 2009, 42, 1899–1909.
87. C. Mongin, C. K. Liang, B. Bibal and D. M. Bassani, Pure Appl. Chem., 2017, 89, 269–277.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02085d

‡ Present address: Department of Chemistry, Johannes Gutenberg University Mainz, Duesbergweg 10-14, 55128 Mainz, Germany

---