DOI:
10.1039/D0SM00492H
(Paper)
Soft Matter, 2020,
16, 6328-6343
Mechanical interplay between cell shape and actin cytoskeleton organization†
Received
20th March 2020
, Accepted 19th May 2020
First published on 21st May 2020
Abstract
We investigate the mechanical interplay between the spatial organization of the actin cytoskeleton and the shape of animal cells adhering on micropillar arrays. Using a combination of analytical work, computer simulations and in vitro experiments, we demonstrate that the orientation of the stress fibers strongly influences the geometry of the cell edge. In the presence of a uniformly aligned cytoskeleton, the cell edge can be well approximated by elliptical arcs, whose eccentricity reflects the degree of anisotropy of the cell's internal stresses. Upon modeling the actin cytoskeleton as a nematic liquid crystal, we further show that the geometry of the cell edge feeds back on the organization of the stress fibers by altering the length scale at which these are confined. This feedback mechanism is controlled by a dimensionless number, the anchoring number, representing the relative weight of surface-anchoring and bulk-aligning torques. Our model allows to predict both cellular shape and the internal structure of the actin cytoskeleton and is in good quantitative agreement with experiments on fibroblastoid (GDβ1, GDβ3) and epithelioid (GEβ1, GEβ3) cells.
I. Introduction
Mechanical cues play a vital role in many cellular processes, such as durotaxis,1,2 cell–cell communication,3 stress-regulated protein expression4 or rigidity-dependent stem cell differentiation.5,6 Whereas mechanical forces can directly activate biochemical signaling pathways, via the mechanotransduction machinery,7 their effect is often mediated by the cortical cytoskeleton, which, in turn, affects and can be affected by the geometry of the cell envelope.
By adjusting their shape, cells can sense the mechanical properties of their microenvironment and regulate traction forces,8–10 with prominent consequences on bio-mechanical processes such as cell division, differentiation, growth, death, nuclear deformation and gene expression.11–16 On the other hand, the cellular shape itself depends on the mechanical properties of the environment. Experiments on adherent cells have shown that the stiffness of the substrate strongly affects cell morphology17,18 and triggers the formation of stress fibers.19,20 The cell spreading area increases with the substrate stiffness for several cell types, including cardiac myocytes,17 myoblasts,18 endothelial cells and fibroblasts,19 and mesenchymal stem cells.21
In our previous work22 we have investigated the shape and traction forces of concave cells, adhering to a limited number of discrete adhesion sites and characterized by highly anisotropic actin cytoskeletons. Using a contour model of cellular adhesion,8,23–26 we demonstrated that the edge of these cells can be accurately approximated by a collection of elliptical arcs obtained from a unique ellipse, whose eccentricity depends on the degree of anisotropy of the contractile stresses arising from the actin cytoskeleton. Furthermore, our model quantitatively predicts how the anisotropy of the actin cytoskeleton determines the magnitudes and directions of traction forces. Both predictions were tested in experiments on highly anisotropic fibroblastoid and epithelioid cells27 supported by microfabricated elastomeric pillar arrays,28–30 finding good quantitative agreement.
Whereas these findings shed light on how cytoskeletal anisotropy controls the geometry and forces of adherent cells, they raise questions on how anisotropy emerges from the three-fold interplay between isotropic and directed stresses arising within the cytoskeleton, the shape of the cell envelope and the geometrical constraints introduced by focal adhesions. It is well known that the orientation of the stress fibers in elongated cells strongly correlates with the polarization direction of the cell.31–34 Consistently, our results indicate that, in highly anisotropic cells, stress fibers align with each other and with the cell's longitudinal direction (see, e.g., Fig. 1A).22 However, the physical origin of these alignment mechanisms is less clear and inevitably leads to a chicken-and-egg causality dilemma: do the stress fibers align along the cell's axis or does the cell elongate in the direction of the stress fibers?
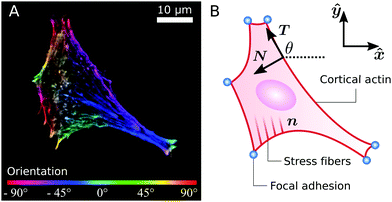 |
| | Fig. 1 (A) A fibroblastoid cell with an anisotropic actin cytoskeleton cultured on a microfabricated elastomeric pillar array.22 The color scale indicates the measured orientation of the actin stress fibers. (B) Schematic representation of a contour model for the cell in (A). The cell contour consists of a collection of concave cellular arcs (red lines) that connect pairs of adhesion sites (blue dots). These arcs are parameterized as curves spanned counterclockwise around the cell by the arclength s, and are entirely described via the tangent unit vector T = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,sin θ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and the normal vector N = (−sin θ) and the normal vector N = (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with θ the turning angle. The unit vector n = (cos θ), with θ the turning angle. The unit vector n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) describes the local orientation θSF of the stress fibers. θSF) describes the local orientation θSF of the stress fibers. | |
The biophysical literature is not scarce of cellular processes that might possibly contribute to alignment of stress fibers with each other and with the cell edge. Mechanical feedback between the cell and the extracellular matrix or substrate, for instance, has been shown to play an important role in the orientation and alignment of stress fibers.21,35–38 Molecular motors have also been demonstrated to produce an aligning effect on cytoskeletal filaments, both in mesenchymal stem cells39 and in purified cytoskeletal extracts,40 where the observation is further corroborated by agent-based simulations.41 A similar mechanism has been theoretically proposed for microtubules–kinesin mixtures.42 Studies in microchambers demonstrated that steric interactions can also drive alignment of actin filaments with each other and with the microchamber walls.43–45 Theoretical studies have highlighted the importance of the stress fibers' assembly and dissociation dynamics,35,46 the dynamics of focal adhesion complexes,47,48 or both.49,50 Also the geometry of actin nucleation sites has been shown to affect the growth direction of actin filaments, thus promoting alignment.51,52 Finally, mechanical coupling between the actin cytoskeleton and the plasma membrane has been theoretically shown to lead to fiber alignment, as bending moments arising in the membrane result into torques that reduce the amount of splay within the filaments.53 Despite such a wealth of possible mechanisms, it is presently unclear which one or which combination is ultimately responsible for the observed alignment of stress fibers between each other and with the cell's longitudinal direction. Analogously, it is unclear to what extent these mechanisms are sensitive to the specific mechanical and topographic properties of the environment, although some mechanisms rely on specific environmental conditions that are evidently absent in certain circumstances (e.g., the mechanical feedback between the cell and the substrate discussed in ref. 35, 37, 48 and 54 relies on deformations of the substrate and is unlikely to play an important role in experiments performed on micro-pillar arrays).
In this paper we investigate the interplay between the anisotropy of the actin cytoskeleton and the shape of cells adhering to microfabricated elastomeric pillar arrays.28–30 Rather than pinpointing a specific alignment mechanism, among those reviewed above, we focus on the interplay between cell shape and the spatial organization of the actin cytoskeleton. This is achieved by means of a phenomenological treatment of the stress fiber orientation based on the continuum description of nematic liquid crystals, coupled with a contour model of the cell edge.22 The paper is organized as follows: in Section II we introduce our contour model for cells with anisotropic cytoskeleton. We first review the key theoretical results, already reported in ref. 22, followed by an in-depth and previously unreported analysis of the model. In Section III we further generalize this approach by studying the mechanical interplay between the shape of the cell, described by our contour model, and the orientation of the actin cytoskeleton, modeled as a nematic liquid crystal confined by the cell edge, and we compare our results to experimental data on highly anisotropic cells. In both sections we assume that the coordinates of the adhesion sites along the cell contour are constant in time and known. A theoretical description of the dynamics of these adhesion sites, as a result of focal adhesion dynamics, is beyond the scope of this study and can be found, for example, in ref. 47 and 48.
II. Equilibrium configuration of the cell contour
Many animal cells spread out after coming into contact with a stiff adhesive surface. They develop transmembrane adhesion receptors at a limited number of adhesion sites that lie mainly along the cell contour (i.e., focal adhesions55). These cells are then essentially flat and assume a typical concave shape characterized by arcs which span between the sites of adhesion, while forces are mainly contractile.25 This makes it possible to describe adherent cells as two-dimensional contractile films, whose shape is unambiguously identified by the position r = (x,y) of the cell contour.8,22–24,26,56,57Fig. 1B illustrates a schematic representation of the cell (fibroblastoid) in Fig. 1A, where the cell contour consists of a collection of curves, referred to as “cellular arcs”, that connect two consecutive adhesion sites. These arcs are parameterized by the arclength s as curves spanned counterclockwise around the cell, oriented along the tangent unit vector T = ∂sr = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,sin
θ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with θ = θ(s) the turning angle of the arc with respect to the horizontal axis of the frame of reference. The normal vector N = ∂sr⊥ = (−sin
θ), with θ = θ(s) the turning angle of the arc with respect to the horizontal axis of the frame of reference. The normal vector N = ∂sr⊥ = (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with r⊥ = (−y,x), is directed toward the interior of the cell. The equation describing the shape of a cellular arc is obtained upon balancing all the conservative and dissipative forces experienced by the cell contour. These are:
θ), with r⊥ = (−y,x), is directed toward the interior of the cell. The equation describing the shape of a cellular arc is obtained upon balancing all the conservative and dissipative forces experienced by the cell contour. These are:| | ξt∂tr = ∂sFcortex + (![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) out − out − ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) in)·N, in)·N, | (1) |
where t is time and ξt is a (translational) drag coefficient measuring the resistance, arising from cell–substrate interactions, against motion of the cell contour. ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) out and
out and ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) in are the stress tensors on the two sides of the cell boundary and Fcortex is the stress resultant along the cell contour.8,22,24–26,56 We assume the substrate to be rigid and the adhesion sites, lying along the cell contour, to be stationary. For theoretical models of cell adhesion on compliant substrates, see, e.g., ref. 8, 26 and 56. The temporal evolution of the cell contour is then dictated by a competition between internal and external bulk stresses acting on the cell boundary and the tension arising within the cell cortex. The former give rise to a contractile (i.e., inward-directed) force on the cell contour, thereby tend to decrease the cell area. By contrast, cortical tension decreases the cell perimeter, thus resulting in an extensile (i.e., outward-directed) force, as a consequence of the cell concavity. As the planar contour represents the two-dimensional projection of the full three-dimensional body of the cell, changes in the area affect neither the density of the cytoplasm nor the internal pressure. Finally, we assume the dynamics of the cell contour to be overdamped.
in are the stress tensors on the two sides of the cell boundary and Fcortex is the stress resultant along the cell contour.8,22,24–26,56 We assume the substrate to be rigid and the adhesion sites, lying along the cell contour, to be stationary. For theoretical models of cell adhesion on compliant substrates, see, e.g., ref. 8, 26 and 56. The temporal evolution of the cell contour is then dictated by a competition between internal and external bulk stresses acting on the cell boundary and the tension arising within the cell cortex. The former give rise to a contractile (i.e., inward-directed) force on the cell contour, thereby tend to decrease the cell area. By contrast, cortical tension decreases the cell perimeter, thus resulting in an extensile (i.e., outward-directed) force, as a consequence of the cell concavity. As the planar contour represents the two-dimensional projection of the full three-dimensional body of the cell, changes in the area affect neither the density of the cytoplasm nor the internal pressure. Finally, we assume the dynamics of the cell contour to be overdamped.
The stress tensor can be modeled upon taking into account isotropic and directed stresses. The latter are constructed by treating the stress fibers as contractile force dipoles, whose average orientation θSF is parallel to the unit vector n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) (see Fig. 1B). This gives rise to an overall contractile bulk stress of the form:58,59
θSF) (see Fig. 1B). This gives rise to an overall contractile bulk stress of the form:58,59
| | ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) out − out − ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) in = σÎ + αnn, in = σÎ + αnn, | (2) |
where
Î is the identity matrix,
σ > 0 embodies the magnitude of all isotropic stresses (passive and active) experienced by the cell edge and
α > 0 is the magnitude of the directed contractile stresses and is proportional to the local degree of alignment between the stress fibers, in such a way that
α is maximal for perfectly aligned fibers, and vanishes if these are randomly oriented. In Section III we will explicitly account for the local orientational order of the stress fibers using the language of nematic liquid crystals. Furthermore, since
Î =
nn +
n⊥n⊥, the nematic director
n and its normal
n⊥ = (−sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF
θSF,cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF
θSF) correspond to the principal stress directions, whereas
σmax =
σ +
α and
σmin =
σ are, respectively, the maximal and minimal principal stresses. The degree of anisotropy of the bulk stress is thus determined by the ratio between the isotropic contractility
σ and the directed contractility
α. Finally, the tension within the cell cortex is modeled as
Fcortex =
λT, where the line tension
λ embodies the contractile forces arising from myosin activity in the cell cortex. This quantity varies, in general, along an arc and can be expressed as a function of the arclength
s. In the presence of anisotropic bulk stresses, in particular,
λ(
s) cannot be constant, as we will see in Section II.A. The force balance condition,
eqn (1), becomes then
| | | ξt∂tr = ∂s(λT) + σN + α(n·N)n. | (3) |
In this section we describe the position of the cell boundary under the assumption that the timescale required for the equilibration of the forces in
eqn (3) is much shorter than the typical timescale of cell migration on the substrate (
i.e., minutes). Under this assumption, ∂
tr =
0 and
eqn (3) can be cast in the form:
| | | 0 = (∂sλ)T + (λκ + σ)N + α(n·N)n, | (4) |
where we have used ∂
sT =
κN, with
κ = ∂
sθ the curvature of the cell edge. In the following, we review (Section II.A) and extend (Sections II.B–II.D) the results previously reported in
ref. 22 about the geometry and mechanics of anisotropic cells adhering to micropillar arrays.
Finally, all the material parameters appearing in eqn (4) depend, in principle, on the density of actin. Here we focus on the orientational structure of the cytoskeleton and, for sake of simplicity, we assume the density of actin to be uniform throughout the cell. Therefore our model does not account for local density variations that have been found experimentally on several cell types, where stress fibers occur most prominently along concave cell edges.60–63 A complementary approach, where the density rather than the orientation of the actin fibers is explicitly modeled, can be found in ref. 64.
A. Equilibrium cell shape and line tension
In this section we review the results previously reported in ref. 22. A derivation of the main equations can be found in ref. 26 and, for the sake of completeness, in the ESI.†
For α = 0, eqn (4) describes the special case of a cell endowed with a purely isotropic cytoskeleton.8,23,24 Force balance requires λ to be constant along a single cellular arc (i.e. ∂sλ = 0), whereas the bulk and cortical tension compromise along an arc of constant curvature, i.e. κ = −σ/λ, with the negative sign of κ indicating that the arcs are curved inwards. The cell edge is then described by a sequence of circular arcs, whose radius R = 1/|κ| = λ/σ depends on the local cortical tension λ of the arc. This model successfully describes the shape of adherent cells in the presence of strictly isotropic forces. However, as we showed in ref. 22, isotropic models are not suited for describing cells whose anisotropic cytoskeleton develops strong directed forces originating from actin stress fibers.65,66
In the presence of an anisotropic cytoskeleton, α > 0 and the cell contour is no longer subject to purely normal forces. As a consequence, the cortical tension λ varies along a given cellular arc to balance the tangential component of the contractile forces arising from the actin cytoskeleton. In order to highlight the physical mechanisms described, in this case, by eqn (4), we introduce a number of simplifications that make the problem analytically tractable. These will be lifted in Section III, where we will consider the most general scenario. First, because the orientation of the stress fibers typically varies only slightly along a single arc, we assume the orientation of the stress fibers, θSF, to be constant along a single cellular arc, but different from arc to arc. Furthermore, without loss of generality, we orient the reference frame such that the stress fibers are parallel to the y-axis. Thus, θSF = π/2 and n = ŷ. Then, solving eqn (4) with respect to λ yields:
| | 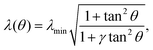 | (5) |
where the constant
γ =
σ/(
σ +
α) quantifies the anisotropy of the bulk contractile stress. The quantity
λmin represent the minimal cortical tension attained along each cellular arc, where the stress fibers are perpendicular to the cell contour (
i.e.,
θ = 0). By contrast, the actin cortex exerts maximal tension when the stress fibers are parallel to the cell contour,
i.e.,
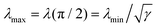
. We note that these variations in line tension along a single arc do not necessarily have to be regulated by the cell. Instead, they could simply be a result of passive mechanical forces in a way very similar to the space-dependent tension in a simple cable hanging under gravity. Although the minimal line tension
λmin could, in principle, be arc-dependent, for example if the cell cortex displays substantial variations in the myosin densities,
24 here we approximate
λmin as a constant. This approximation is motivated by the fact that our previous
in vitro observations of anisotropic epithelioid and fibroblastoid cells did not identify a correlation between the arc length and curvature,
22 which, on the other hand, is expected if
λmin was to vary significantly from arc to arc.
24 Hence,
α,
σ and
λmin represent the independent material parameters of our model.
The shape of a cellular arc is given by a segment of an ellipse, which is given by:22
| | 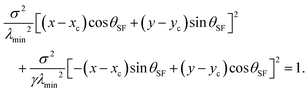 | (6) |
The longitudinal direction of the ellipse is always parallel to the stress fibers, hence tilted by an angle
θSF with respect to the
x-axis, as illustrated in
Fig. 2 for
n =
ŷ. The direct relation between the contractile forces arising from the cytoskeleton and the shape of the cell is highlighted by the dimensionless parameter
γ =
σ/(
σ +
α): on the one hand,
γ defines the anisotropy of the contractile bulk stress, on the other hand it dictates the anisotropy of the cell shape. This, in turn, does not depend on the positions of the adhesion sites, which instead affect the traction forces experienced by the substrate (see Section II.C). Both these properties arise from the fact that, in our model, cellular arcs have no preferred length, and are consistent with experimental observations on fibroblastoids and epithelioids.
22 The coordinates of the center of the ellipse (
xc,
yc) and the angular coordinates of the adhesion sites along the ellipse,
ψ0 and
ψ1 in
Fig. 2, can be calculated using standard algebraic manipulation and are given in the ESI.
†
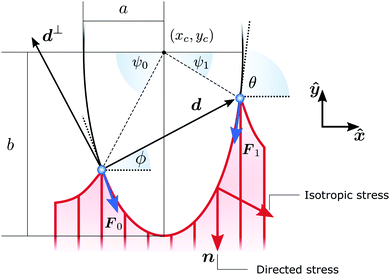 |
| | Fig. 2 Schematic representation of a cellular arc, described by eqn (6), for n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) = ŷ, hence θSF = π/2. A force balance between isotropic stress, directed stress and line tension results in the description of each cell edge segment (red curve) as part of an ellipse of aspect ratio θSF) = ŷ, hence θSF = π/2. A force balance between isotropic stress, directed stress and line tension results in the description of each cell edge segment (red curve) as part of an ellipse of aspect ratio 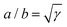 . The cell exerts forces F0 and F1 on the adhesion sites (blue). The vector d = d(cos . The cell exerts forces F0 and F1 on the adhesion sites (blue). The vector d = d(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) describes the relative position of the two adhesion sites, d⊥ = d(−sin ϕ) describes the relative position of the two adhesion sites, d⊥ = d(−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,cos ϕ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) is a vector perpendicular to d, and θ is the turning angle of the cellular arc. The coordinates of the ellipse center (xc,yc) and the angular coordinates of the adhesion sites along the ellipse ψ0 and ψ1 are given in the ESI.† ϕ) is a vector perpendicular to d, and θ is the turning angle of the cellular arc. The coordinates of the ellipse center (xc,yc) and the angular coordinates of the adhesion sites along the ellipse ψ0 and ψ1 are given in the ESI.† | |
Fig. 3A shows an example of a fibroblastoid cell with ellipses fitted to its arcs. Because ellipse fitting is very sensitive to noise on the cell shape, only the longer arcs are considered here (see Materials and methods). We stress that, as long as the contractile stresses arising from the actin cytoskeleton are roughly uniform across the cell (i.e., α, σ and λmin are constant), all cellular arcs of sufficient length are approximated by a unique ellipse (see Fig. 3A). The parameters that describe this ellipse are, in general, different for each individual cell. A survey of these parameters over a sample of 285 fibroblastoid and epithelioid cells yields the distributions displayed in Fig. 3B–D for the parameters λmin, α and σ. The corresponding population averages are: λmin = 7.6 ± 5.6 nN, α = 1.7 ± 1.7 nN μm−1, σ = 0.87 ± 0.70 nN μm−1 and γ = 0.33 ± 0.20. Evidently, the variance in the parameter values is in part due to the natural variations across the cell population, and in part to possible statistical fluctuations in the experiments. Further insight about the distribution of material parameters can be addressed in the future by combining our model with experiments of cells adhering to micropatterned substrates, which impose reproducible cell shapes.67 Finally, we note that some of the smaller cellular arcs, such as those in the bottom left corner of Fig. 3, cannot be approximated by the same ellipse as the longer arcs. This may be due to local fluctuations in the density and orientation of stress fibers at the small scale or to other effects that are not captured by our model. For a description of the selection of the fitted arcs and of the endpoints of the arcs, see Materials and methods. For more experimental data on the elliptical fits, see ref. 22.
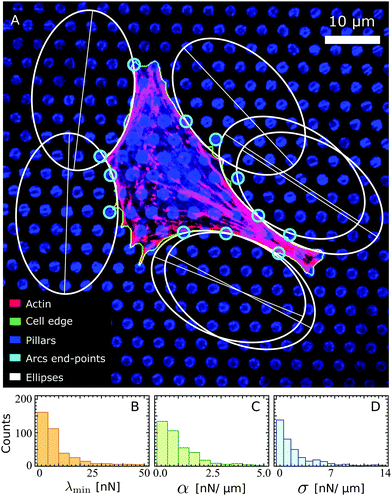 |
| | Fig. 3 (A) A fibroblastoid cell with an anisotropic actin cytoskeleton on a microfabricated elastomeric pillar array22 (same cell as in Fig. 1A), with a unique ellipse (white) fitted to its arcs of sufficient length (see Materials and methods). The actin, cell edge, and micropillar tops are in the red, green, and blue channels respectively. The endpoints of the arcs (cyan) are identified based on the forces that the cell exerts on the pillars (Materials and methods). Scale bar is 10 μm. (B–D) Histograms of the parameters λmin, α and σ estimated from a survey of these parameters over a sample of 285 fibroblastoid and epithelioid cells. | |
B. Curvature
One of the most striking consequences of the elliptical shape of the cellular arcs is that the local curvature is no longer constant, consistent with experimental observations on epithelioid and fibroblastoid cells in ref. 22. This can be calculated from eqn (6) in the form:| | 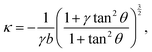 | (7) |
with the negative sign indicating that the arcs are curved inwards. A cellular arc thus attains its maximal (minimal) absolute curvature, where θ = 0 (θ = π/2) and the stress fibers are parallel (perpendicular) to the arc tangent vector, namely| | 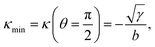 | (8a) |
| | 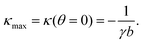 | (8b) |
Consistent with experimental evidence, the radius of curvature of arcs perpendicular to stress fibers is smaller than the radius of curvature of arcs parallel to the stress fiber direction. Thus, regions of the cell edge having higher and lower local curvature correspond to different portions of the same ellipse, depending on the relative orientation of the local tangent vector and the stress fibers. For a more detailed comparison between theory and experiment, see ref. 22.
C. Traction forces
With the expressions for shape of the cellular arcs [eqn (6)] and cortical tension [eqn (5)] in hand, we now calculate the traction forces exerted by the cell via the focal adhesions positioned at the end-points of a given cellular arc (Fig. 2). Calling these F0 and F1 and recalling the cell edge is oriented counter-clockwise, we have F0 = −λ(θ0)T(θ0) and F1 = λ(θ1)T(θ1), where θ0 and θ1 are the turning angles at the end-points of the arc. For practical applications, it is often convenient to express the position of the adhesion sites in terms of their relative distance d = d(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) (Fig. 2). This yields
ϕ) (Fig. 2). This yields| | 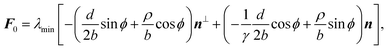 | (9a) |
| | 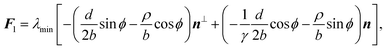 | (9b) |
where the length scale ρ is defined as| | 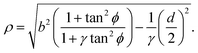 | (10) |
The total traction force exerted by the cell can be calculated by summing the two forces associated with the arcs joining at a given adhesion site, while taking into account that the orientation n of the stress fibers is generally different from arc to arc.
Another interesting quantity is obtained by adding the forces F0 and F1 from the same arc. Although these two forces act on two different adhesion sites, their sum represents the total net force that a single cellular arc exerts on the substrate. This is given by
| | 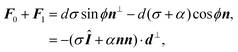 | (11) |
where
d⊥ =
d(−sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ,cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ) (
Fig. 2).
eqn (11) presents the force resulting from the integrated contractile bulk stress [see
eqn (1)], which is independent of the line tension
λmin but scales linearly with the distance between adhesions. This implies that the total traction increases with the cell size, consistent with earlier contour models
8,56 and various experimental observations.
63,68,69 Because the cell size is expected to be larger on stiffer substrates, as these stretch only slightly in response to the cell contraction, the total amount of traction also increases with substrate stiffness.
D. Mechanical invariants
We conclude this section by highlighting two mechanical invariants, local quantities that are constant along a cellular arc, thus showing the intimate relation between the geometry of the cell and the mechanical forces it exerts on the environment. From eqn (9) we findwhere F‖ and F⊥ are the components of the force, parallel and perpendicular to n, at any point along a same cellular arc. Furthermore, by inspection of eqn (7) and (5) we observe that| | | λ3κ = −λmin2(α + σ) = const. | (13) |
From this, we find that the normal component of the cortical force, λκ [see eqn (4)], is then given by| | 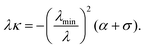 | (14) |
This relation is an analog of the Young–Laplace law for our anisotropic system. In the isotropic limit, α = 0 and λmin = λ, thus we recover the standard force-balance expression λκ = −σ. Eqn (14) shows that the normal force λκ decreases with increasing line tension λ, because an increase in line tension is accompanied by an even stronger decrease in the curvature κ.
III. Interplay between orientation of the cytoskeleton and cellular shape
In this section we generalize our approach by allowing the orientation of the stress fibers to vary along individual cellular arcs. This is achieved by combining the contour model for the cell shape, reviewed in Section II, with a continuous phenomenological model of the actin cytoskeleton, rooted into the hydrodynamics of nematic liquid crystals.70 This setting can account for the mechanical feedback between the orientation of the stress fibers and the concave cellular shape and allows us to predict both these features starting from the positions of the adhesions sites along the cell edge alone. Although experimental studies have shown the biophysical importance of substrate adhesions in the cell interior,28,71,72 here we only describe a limited number of discrete adhesion sites at the cell periphery, where the largest traction stresses are found.73–75 A treatment of the dynamics of focal adhesions is beyond the scope of this paper and can be found elsewhere, e.g., in ref. 47 and 48.
As mentioned in the Introduction, experimental observations, by us22 and others,31–34 have indicated that stress fibers tend to align with each other and with the cell's longitudinal direction. As we discussed, several cellular processes might contribute to these alignment mechanisms, such as mechanical cell–matrix feedback,21,35–38 motor-mediated alignment,39–42 steric interactions,43–45 stress fiber formation and dissociation,35,46,49,50 focal adhesion dynamics,47–50 the geometry of actin nucleation sites,51,52 or membrane-mediated alignment,53 but it is presently unclear which combination of mechanisms is ultimately responsible for the orientational correlation observed in experiments. Our phenomenological description of the actin cytoskeleton allows us to focus on the interplay between cellular shape and the orientation of the stress fibers, without the loss of generality that would inevitably result from selecting a specific alignment mechanism among those listed above.
This phenomenological description necessitates a number of simplifying assumptions that can be addressed in future work. First, we again assume the typical timescale associated with the equilibration of the forces (hence the reorientation of the actin filaments) to be much shorter than that associated with cell motility (see also Section II.A). Consequently, experiments on migrating cells76 or cells subject to cyclic mechanical loading77,78 are outside of the scope of the present paper. Moreover, our model does not take into account dynamical effects, such as actin filament turnover and the viscoelasticity of stress fibers.79,80 Second, as we did with in Section II, we restrict our model to effectively two-dimensional cells. This is not unreasonable, as cells adhering to a stiff surface have a largely flat shape,25 but it does imply that our model cannot capture three-dimensional stress fiber structures around the nucleus, such as the actin cap,81 or distinguish between the orientations of apical and basal stress fibers.82 Third, we do not model signalling pathways, thus our approach cannot account for variations of myosin activity (thus contractile stress) in response to the substrate stiffness and other mechanical cues, but, as already discussed in Section II, it can describe the modulation in spread-area and traction force originating from the mechanical coupling between the cell and the substrate63,68,69,71 (see Section II.C). Fourth, our model describes the overall cell-scale structure of the actin cytoskeleton and does not include local effects such as the interactions of individual stress fibers with focal adhesions in the cell interior.28,71,72
A. Model of the actin cytoskeleton
The actin cytoskeleton is modeled as a nematic liquid crystal confined within the cellular contour. This is conveniently represented in terms of the two-dimensional nematic tensor (see, e.g., ref. 70):| | 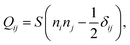 | (15) |
where δij is the Kronecker delta and 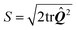 is the so called nematic order parameter, measuring the amount of local nematic order. Here, 0 ≤ S ≤ 1, where S = 1 represents perfect nematic order and S = 0 represents randomly oriented stress fibers. In the standard {
is the so called nematic order parameter, measuring the amount of local nematic order. Here, 0 ≤ S ≤ 1, where S = 1 represents perfect nematic order and S = 0 represents randomly oriented stress fibers. In the standard {![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ,ŷ} Cartesian basis, eqn (15) yields
,ŷ} Cartesian basis, eqn (15) yields| | 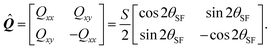 | (16) |
The preferred orientation of stress fibers within the cell is captured by the Landau–de Gennes free-energy Fcyto:70| | 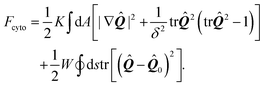 | (17) |
The first integral in eqn (17) corresponds to a standard mean-field free-energy, favoring perfect nematic order (i.e., S = 1), while penalizing gradients in the orientation of the stress fibers and their local alignment. For simplicity, we neglect the dependence on the nematic order parameter on the density of actin (here assumed to be uniform) and we assume the system to be away from the isotropic/nematic phase transition.70 The quantity K is known as Frank's elastic constant and, in this context, expresses the stiffness of the actin cytoskeleton with respect to both splay and bending deformations, on a scale larger than that of the individual actin filaments. The length scale δ sets the size of the boundary layer in regions where the order parameter drops to zero to compensate a strong distortion of the nematic director n, such as in proximity of topological defects. Hence, δ measures the typical size of regions where stress fibers are randomly oriented.
The second integral, which is extended over the cell contour, is the Nobili–Durand anchoring energy83 and determines the orientation of the stress fibers along the edge of the cell, with the tensor ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) 0 representing their preferential orientation. Experimental evidence form our (Fig. 3 and ref. 22) and other's work (e.g., ref. 31–34), suggests that, in highly anisotropic cells, peripheral stress fibers are preferentially parallel to the cell edge. The same trend is recovered in experiments with purified actin bundles confined in microchambers.43,44 In the language of Landau–de Gennes theory, this effect can be straightforwardly reproduced by setting
0 representing their preferential orientation. Experimental evidence form our (Fig. 3 and ref. 22) and other's work (e.g., ref. 31–34), suggests that, in highly anisotropic cells, peripheral stress fibers are preferentially parallel to the cell edge. The same trend is recovered in experiments with purified actin bundles confined in microchambers.43,44 In the language of Landau–de Gennes theory, this effect can be straightforwardly reproduced by setting
| | 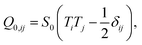 | (18) |
with
T the tangent unit vector of the cell edge. Along concave edges the local orientation of stress fibers tends to be well defined,
60,61 so we further assume a large nematic order along the contour:
S0 = 1. The phenomenological constant
W > 0 measures the strength of this parallel anchoring, hence it is a measure for the preference of stress fibers to align parallel to the cell boundary. Finally, although stress fiber formation, hence the material properties of the actin cytoskeleton, is known to be affected by the pre-existing cytoskeletal tension,
19,20 here we treat our bulk parameters
K,
W, and
δ independently from the active stresses,
α0 and
σ, for sake of simplicity.
In order to generate stationary configurations of the actin cytoskeleton, we numerically integrate the following overdamped equation:
| | 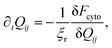 | (19) |
where
ξr is a rotational drag coefficient, controlling the relaxation rate of the system, but without affecting the steady-state configurations.
Eqn (19) is numerically integrated with Neumann boundary conditions:
| | | KN·∇Qij − 2W(Qij − Q0,ij) = 0. | (20) |
This guarantees the steady-state configurations to be energy-minimizing, but without imposing a specific non-physical orientation of the stress fibers along the contour of the cell.
B. The dynamics of the cell contour
The relaxational dynamics of the cell contour are governed, in our model, by eqn (3), which is now lifted from the assumption that the orientation n of the stress fibers is uniform along individual cellular arcs. Furthermore, the contractile stress given by eqn (2) can now be generalized as:| | 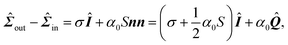 | (21) |
with α0 a constant independent on the local order parameter. Comparing eqn (2) and (21) yields α = α0S, thus the formalism introduced in this section allows us to explicitly account for the effect of the local orientational order of the stress fibers on the amount of contractile stress that they exert.
Next, we decompose eqn (3) along the normal and tangent directions of the cell contour. Since the cells considered here are pinned at the adhesion sites, which we again assume to be rigid, and the density of actin along the cell contour is assumed to be constant, tangential motion is suppressed, i.e., T·∂tr = 0. Together with eqn (21) this yields:
| | 0 = ∂sλ + α0T·![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) ·N, ·N, | (22a) |
| | 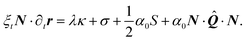 | (22b) |
Eqn (22a) describes then the relaxation of tension
λ within the cell edge, given its shape, whereas
eqn (22b) describes the relaxation of the cellular shape itself. The variations in the cortical tension might result from a regulation of the myosin activity or simply form a passive response of the cortical actin to the tangential stresses.
Integrating eqn (22a) then yields the cortical tension along an arc:
| | 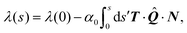 | (23) |
where
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif)
=
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif)
(
s) varies, in general, along an individual cellular arc. The integration constant
λ(0), which represents the cortical tension at one of the adhesion sites, is related to the minimal tension
λmin withstood by the cortical actin which we used, in Section II, as material parameter of the problem. In practice, we first calculate
λ over an entire arc using a arbitrary guess for
λ(0). Then, we apply a uniform shift in such a way that the minimal
λ value coincides with
λmin.
Combining the dynamics of the cell contour and that of the cell bulk, we obtain the following coupled differential equations:
| | 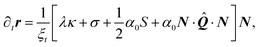 | (24a) |
| | 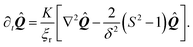 | (24b) |
These are complemented by the condition that
r is fixed in a number of specific adhesion sites, the boundary condition given by
eqn (20) for the nematic tensor
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif)
and the requirement that min
sλ(
s) =
λmin on each arc.
IV. Numerical results
Eqn (24) are numerically solved using a finite difference integration scheme with moving boundary.84 As we detail in the ESI,† the time-integration is performed iteratively using the forward Euler algorithm by alternating updates of the cell contour and of the bulk nematic tensor. This process is iterated until both the cell shape and the orientation reach a steady state.
To highlight the physical meaning of our numerical results, we introduce two dimensionless numbers, namely the contractility number, Co, and the anchoring number, An. Co is defined as the ratio between the typical distance between two adhesion sites d and the major semi-axis of the ellipse approximating the corresponding cellular arc (b = λmin/σ, see Section II.A):
| | 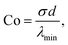 | (25) |
and provides a dimensionless measure of the cell contraction (thus of the cell average curvature). The anchoring number, on the other hand, is defined as the ratio between a typical length scale
R in which the internal cell structure is confined (not necessarily equal to the distance
d) and the length scale
K/
W, which sets the size of the boundary layer where
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif)
crosses over from its bulk configuration to
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) 0
0:
| | 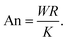 | (26) |
This number expresses the ratio between the anchoring energy, which scales as
WR [
i.e., last term in
eqn (17)], and the bulk energy, which scales as
K, thus independently on cell size [
i.e., first term in
eqn (17)]. Hence, An represents the competition between boundary alignment (with strength
W) and bulk alignment (strength
K) within the length scale of the cell
R. For An ≪ 1, bulk elasticity dominates over boundary anchoring and the orientation of the stress fibers in the bulk propagates into the boundary, resulting into a uniform orientation throughout the cell and large deviations from parallel anchoring in proximity of the edge. Conversely, for An ≫ 1, boundary anchoring dominates bulk elasticity and the orientation of the stress fibers along the cell edge propagates into the bulk, leading to non-uniform alignment in the interior of the cell.
To get insight on the effect of the combinations of these dimensionless parameters on the spatial organization of the cell, we first consider the simple case in which the adhesion sites are located at the corners of squares and rectangles (Section IV.A). In Section IV.B we consider more realistic adhesion geometries and compare our numerical results with experimental observations on highly anisotropic cells adhering to a small number of discrete adhesions.
A. Rectangular cells
Fig. 4 shows the possible configurations of a model cell whose adhesion sites are located at the vertices of a square, obtained upon varying An and Co, while keeping γ = σ/(σ + α0) constant. Fig. S2 in the ESI† shows the effect of varying the ratio between σ and α0 for this model cell. The thick black line represents the cell boundary, the black lines in the interior of the cells represent the orientation field n of the stress fibers and the background color indicates the local nematic order parameter S, or equivalently, the magnitude of the maximal principal stress σmax = σ + α0S.
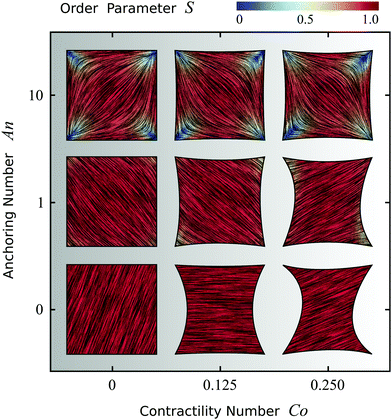 |
| | Fig. 4 Configurations of cells whose adhesion sites are located at the vertices of a square. The thick black line represents the cell boundary, the black lines in the interior of the cells represent the orientation field n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.80; 0.80; 0.77 (top row), 0.94; 0.92; 0.92 (middle row), and 1.0; 1.0; 1.0 (bottom row). The vertical axis corresponds to the anchoring number An = WR/K and the horizontal axis to the contractility number Co = σd/λmin. The cells shown correspond to values of An = 0, 1, 10 and Co = 0, 0.125, 0.25, where we take both d and R equal to the length of the square side. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R, Narc = 20, and Δx = R/19 are the same for all cells. The number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.† θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.80; 0.80; 0.77 (top row), 0.94; 0.92; 0.92 (middle row), and 1.0; 1.0; 1.0 (bottom row). The vertical axis corresponds to the anchoring number An = WR/K and the horizontal axis to the contractility number Co = σd/λmin. The cells shown correspond to values of An = 0, 1, 10 and Co = 0, 0.125, 0.25, where we take both d and R equal to the length of the square side. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R, Narc = 20, and Δx = R/19 are the same for all cells. The number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.† | |
As expected, for low Co values (left column), cells with large An exhibit better parallel anchoring than cells with small An values, but lower nematic order parameter S in the cell interior (spatial average of S decreases from 1.0 at the bottom left to 0.80 at the top left, see Fig. 4). Interestingly, the alignment of stress fibers with the walls in the configuration with large An value (top left) resembles the configurations found by Deshpande et al.,35,46 who specifically accounted for the assembly and dissociation dynamics of the stress fibers. More strikingly, the structure reported in the top left of Fig. 4 appears very similar to those found in experiments of dense suspensions of pure actin in cell-sized square microchambers,43,44 simulations of hard rods in quasi-2D confinement,43 and results based on Frank elasticity,85 even though these systems are very different from living cells. As is the case in our simulations, in these studies the tendency of the filaments to align along the square edges competes with that of aligning along the diagonal.
For large Co values (right column of Fig. 4), the cell deviates from the square shape. Interestingly, although the contractile stresses (σ and α0) do not directly affect the configuration of the cytoskeleton, they do it indirectly by influencing the shape of the cell. This results into an intricate interplay between shape and orientation, controlled by the numbers An and Co. In particular, for constant Co, i.e., for fixed stress fiber contractility, increasing An leads to higher tangential alignment of the stress fibers with the cell edge, thus increasing An decreases the contractile force experienced by the cell edge, which is proportional to (n·N)2 [eqn (24a)]. Conversely, for constant An, increasing Co leads to a more concave cell shape which forces the stress fibers to bend more. Consequently, the average order parameter in the cell decreases with increasing Co (see Fig. 4).
Finally, we note that all configurations in Fig. 4 display a broken rotational and/or chiral symmetry. For An = 0 the stress fibers are uniformly oriented, but any direction is equally likely. For non-zero An, the stress fibers tend to align along either of the diagonals (with the same probability) to reduce the amount of distortion. Upon increasing Co, chirality emerges in the cytoskeleton and in the cell contour (see, e.g., the cell in the middle of the right column in Fig. 4). In light of the recent interest in chiral symmetry breaking in single cells86 and in multicellular environments,87 we find it particularly interesting that chiral symmetry breaking can originate from the natural interplay between the orientation of the stress fibers and the shape of the cell.
To conclude this section, we focus on four-sided cells whose adhesion sites are located at the vertices of a rectangle and explore the effect of the cell aspect ratio (i.e., height/width). Fig. 5 displays three configurations having fixed maximal width and aspect ratio varying from 1 to 2. Fig. S3 in the ESI† shows the effect of increasing the aspect ratio while keeping instead the area of the rectangle fixed. Upon increasing the cell aspect ratio, the mean orientation of the stress fibers switches from the diagonal (aspect ratio 1) to longitudinal (aspect ratio 2), along with an increase in the order parameter in the cell bulk, as can be seen in Fig. 5 by the slightly more red-shifted cell interior (spatial average of S increases from 0.92 to 0.96). This behavior originates from the competition between bulk and boundary effects. Whereas the bulk energy favors longitudinal alignment, as this reduces the amount of bending of the nematic director, the anchoring energy favors alignment along all four edges alike, thus favoring highly bent configurations at the expense of the bulk elastic energy. When the aspect ratio increases, the bending energy of the bulk in the diagonal configuration increases, whereas the longitudinal state only pays the anchoring energy at the short edges, hence independently on the aspect ratio. Therefore, elongating the cell causes the stress fibers to transition from tangential to longitudinal alignment, with a consequent increase of the nematic order parameter. Interestingly, similar observations were made in experiments on pure actin filaments in cell-sized microchambers.43,44 More importantly, the longitudinal orientation of the stress fibers in cells of aspect ratio 2 is consistent with several experimental studies of cells adhering on adhesive stripes and elongated adhesive micropatterns.33,34,62,63,88 Fig. S4 and S5 in the ESI† show the effect of the anchoring number An, the contractility number Co, and the ratio between σ and α0 on a cell with aspect ratio 2.
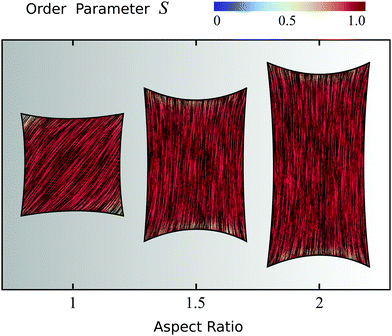 |
| | Fig. 5 Effect of the aspect ratio of the cell, ranging from 1 to 2, on cytoskeletal organization for cells whose four adhesion sites are located at the vertices of a rectangle. The thick black line represents the cell boundary, the black lines in the interior of the cells represent the orientation field n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.92; 0.95; 0.96. The simulations shown are performed with An = WR/K = 1 where R is equal to the short side of the rectangle, and Co = σd/λmin equal to 0.125, 0.1875, and 0.25 respectively, where d is equal to the long side of the rectangle. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R and Δx = R/19 are the same for all cells. Narc = 20, 30, 40 from left to right and the number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.† θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.92; 0.95; 0.96. The simulations shown are performed with An = WR/K = 1 where R is equal to the short side of the rectangle, and Co = σd/λmin equal to 0.125, 0.1875, and 0.25 respectively, where d is equal to the long side of the rectangle. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R and Δx = R/19 are the same for all cells. Narc = 20, 30, 40 from left to right and the number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.† | |
B. Cells on micropillar arrays
In order to validate our model experimentally, we compare our numerical results with experiments on fibroblastoid and epithelioid cells27 plated on micropillar arrays.28–30 The cells are imaged using spinning disk confocal microscopy (see, e.g., Fig. 6A) and the images are then processed in order to detect the orientation of the stress fibers. Upon coarse-graining the local gradients of the image intensity, we reconstruct both the nematic director n (black lines, representing the orientation of the stress fibers) and order parameter S (background color, representing the degree of alignment), as visualized in Fig. 6B. Because of this coarse-graining, which takes place on a length scale comparable to the radius of the micropillars (∼1 μm) (see Materials and methods), local variations in orientations and densities of stress fibers are smoothened out and the influence of individual micropillars under the cell interior, as visible in Fig. 6A, is no longer visible in Fig. 6B. Regions in the cell with low actin expression, that do not show a clear structural orientation, have a low order parameter S. Hence, in the experimental data, a low S value might result from either a low local density of stress fibers, or from a high density of randomly oriented stress fibers. See Materials and methods for more detail on the experimental methods and image processing.
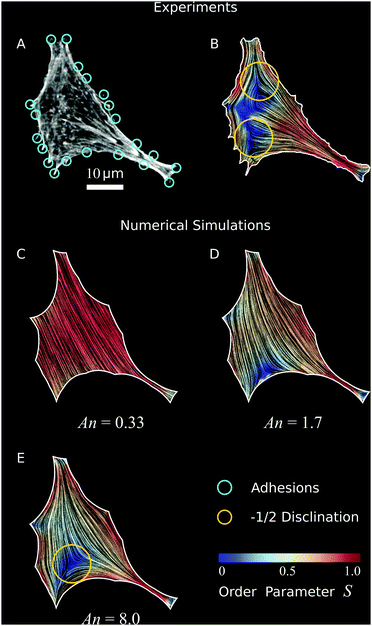 |
| | Fig. 6 Validation of our model to experimental data. (A) Optical micrograph (TRITC–Phalloidin) of a fibroblastoid cell (same cell as in Fig. 1 and 3).22 The adhesions (cyan circles) are determined by selecting micropillars that are close to the cell edge and experience a significant force (Materials and methods). (B) Experimental data of cell shape and coarse-grained cytoskeletal structure of this cell. The white line represents the cell boundary, black lines in the interior of the cells represent the orientation field n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial average of the order parameter is S = 0.54. (C–E) Configurations obtained from a numerical solution of eqn (24) using the adhesion sites of the experimental data (cyan circles) as input, and with various anchoring number (An) values. This is calculated from eqn (26), with R = 23.6 μm the square root of the cell area. The corresponding values of the length scale K/W are 71 μm (C), 14 μm (D), and 2.9 μm (E) respectively. The spatial averages of the order parameter S are given by: 0.85 (C), 0.60 (D), and 0.56 (E) respectively. The values for λmin/σ = 14.7 μm and σ/(σ + α0) = 0.40 are found by an analysis of the elliptical shape of this cell.22 The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for figures (C–E). The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.† θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial average of the order parameter is S = 0.54. (C–E) Configurations obtained from a numerical solution of eqn (24) using the adhesion sites of the experimental data (cyan circles) as input, and with various anchoring number (An) values. This is calculated from eqn (26), with R = 23.6 μm the square root of the cell area. The corresponding values of the length scale K/W are 71 μm (C), 14 μm (D), and 2.9 μm (E) respectively. The spatial averages of the order parameter S are given by: 0.85 (C), 0.60 (D), and 0.56 (E) respectively. The values for λmin/σ = 14.7 μm and σ/(σ + α0) = 0.40 are found by an analysis of the elliptical shape of this cell.22 The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for figures (C–E). The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.† | |
Consistent with our results on rectangular cells (Fig. 5), the stress fibers align parallel to the cell's longitudinal direction and perpendicularly to the cell's shorter edges. Furthermore, the nematic order parameter is close to unity in proximity of the cell contour, indicating strong orientational order near the cell edge, but drops in the interior. This behavior is in part originating from the lower density of stress fibers around the center of mass of the cell, and in part from the presence of ±1/2 nematic disclinations away from the cell edge. These topological defects naturally arise from the tangential orientation along the boundary. Albeit not uniform throughout the whole cell contour, thus not sufficient to impose hard topological constraints on the configuration of the director in the bulk (i.e., Poincaré–Hopf theorem), this forces a non-zero winding of the stress fibers, which in turn is accommodated via the formation of one or more disclinations. As a consequence of the concave shape of the cell boundary, these defects have most commonly strength −1/2. The average order parameter in the cell is S = 0.54.
To compare our theoretical and experimental results, we extract the locations of the adhesion sites from the experimental data by selecting micropillars that are close to the cell edge and experience a significant force (for details, see Materials and methods), and use them as input parameters for the simulations. In Fig. 6C–E we show results of simulations of the cell in Fig. 6A and B for increasing An values, thus decreasing magnitude of the length scale K/W. Here, we take the length scale R = 23.6 μm to be the square root of the cell area and we use constant values for the ratios λmin/σ = 14.7 μm and σ/(σ + α0) = 0.40 as found by an analysis of the elliptical shape of this cell.22Fig. 6C shows the results of a simulation where bulk alignment dominates over boundary alignment (An = 0.33, K/W = 71 μm), resulting in an approximately uniform cytoskeleton oriented along the cell's longitudinal direction. The nematic order parameter is also approximatively uniform and close to unity (spatial average of the order parameter is S = 0.85). For larger An values (Fig. 6D, An = 1.7 and K/W = 14 μm), anchoring effects become more prominent, resulting in distortions of the bulk nematic director, a lower nematic order parameter (spatial average S = 0.60), and the emergence of a −1/2 disclination in the bottom left side of the cell. Upon further increasing An (Fig. 6E, An = 8.0 and K/W = 2.9 μm), the −1/2 topological defect moves towards the interior, as a consequence of the increased nematic order along the boundary. This results in a decrease in nematic order parameter in the bulk of the cell, consistent with our experimental data. The spatial average is S = 0.56, close to the experimental average of S = 0.54.
A qualitative comparison between our in vitro (Fig. 6B) and in silico cells (Fig. 6E) highlights a number of striking similarities, such as the overall structure of the nematic director, the large value of the order parameter along the cell edge and in the thin neck at the bottom-right of the cell and the occurrence of a −1/2 disclination on the bottom-left side. The main difference is the order parameter away from the cell edges, which is lower in the experimental data than in the numerical prediction. The lower order parameter also results in an additional −1/2 disclination at the top-left of the cell in Fig. 6B which is absent in Fig. 6E. We hypothesize that this discrepancy is caused by a lower actin density in the cell interior, as observed before in many other experimental studies.60–63 As a consequence of the actin depletion, the nematic order parameter can decrease, and potentially vanish, in a way that cannot be described by our model, where the density of the actin fibers is, by contrast, assumed to be uniform across the cell.
In order to make this comparison quantitative and infer the value of the phenomenological parameters introduced in this section, we have further analyzed the residual function
| | 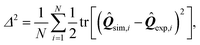 | (27) |
expressing the departure of the predicted configurations of the nematic tensor,
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) sim
sim, from the experimental ones,
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) exp
exp. The index
i identifies a pixel in the cell and
N is the total number of pixels common to both numerical and experimental configurations. By construction,
Δ2 captures both differences in the nematic director
n and in the order parameter
S [see
eqn (15)], and 0 ≤
Δ2 ≤ 1, with 0 representing perfect agreement.
Fig. 7 shows a plot of
Δ2versus the anchoring number An for the cell shown in
Fig. 6. Consistent with the previous qualitative comparison, the agreement is best at large An values, indicating a substantial preference of the stress fibers for parallel anchoring along the cell edge. For the cell in
Fig. 6,
Δ2 is minimized for An = 8.0 (
Δ2 = 0.027), corresponding to a boundary layer
K/
W = 2.9 μm. The corresponding numerically calculated configuration is shown in
Fig. 6E. However, the flattening of
Δ2 for large An values implies that the actual value of An becomes unimportant once the anchoring torques (with magnitude
W), which determine the tangential alignment of the stress fibers in the cell's periphery, outcompete the bulk elastic torques (with magnitude
K). Therefore, we conclude that the cell illustrated in
Fig. 6 is best described by An ≳ 5, corresponding to a boundary layer
K/
W ≲ 5 μm. The corresponding value of
Δ2 = 0.027 indicates good quantitative agreement between the experimental (
Fig. 6B) and simulated (
Fig. 6E) data, despite the difference in order parameter away from the cell edges. This quantitative agreement indicates that, although oversimplified in comparison with the complexity of living cells, our model satisfactorily describes the stationary configuration of both the nematic order parameter and the stress fibers orientation.
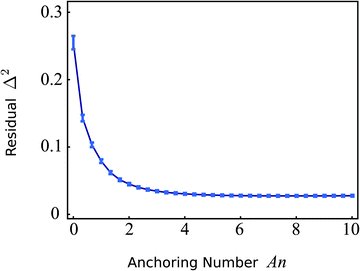 |
| | Fig. 7 Residual function Δ2, defined in eqn (27), as a function of the anchoring number An (eqn (26) with R = 23.6 μm) for the cell displayed in Fig. 6. The error bars display the standard deviation obtained using jackknife resampling. For large An values the residual flattens, indicating that the actual value of An becomes unimportant once the anchoring torques (with magnitude W), which determine the tangential alignment of the stress fibers in the cell's periphery, outcompete the bulk elastic torques (with magnitude K). The minimum (Δ2 = 0.027) is found for An = 8.0. | |
The same analysis presented above has been repeated for five other cells (Fig. 8). The first column shows the raw experimental data, the second column shows the coarse-grained experimental data, and the third column shows the simulations. For these we used the values of λmin/σ and σ/(σ + α0) obtained from a previous analysis of the cell morphology22 and the An values found by a numerical minimization of Δ2 (see Fig. S6 in the ESI†). Also for these cells Δ2 flattens for large An values, and we estimate An ≳ 3 and K/W ≲ 7 μm. The minima of Δ2 are given, from top to bottom, by 0.016, 0.058, 0.057, 0.034, and 0.037. This indicates reasonable quantitative agreement between experiment and simulation for all cells, even though the agreement is significantly better for the cell in Fig. 8F than for those in Fig. 8G and H. Similar to the cell in Fig. 6, we observe that the main discrepancies are the order parameter in the cell interior, which is smaller in the experimental data than in the numerical results, and a number of topological defects in this low nematic order region of the experimental data that are absent in the numerical data. The cell in Fig. 8F shows good agreement between the average order parameter in the experimental (S = 0.54) and numerical (S = 0.52) data, but for the other cells the average order parameter is overestimated by the simulations. We again attribute this discrepancy to actin density variations in the experiments that are not captured by the theory. On the other hand, we note that the overall structure of the stress fiber orientation, including the emergence of a number of −1/2 topological defects (see, e.g., Fig. 8F and K), is captured well by our approach. By contrast, because of the overall convexity of the cells and the lack of strong anchoring at the boundary, + 1/2 disclinations are less prominent in both our in vitro and in silico cells and are mainly localized at the actin-depleted regions.
 |
| | Fig. 8 Comparison of experimental data on five anisotropic cells with the results of computer simulations. (A–E) Optical micrographs (TRITC–Phalloidin) of epithelioid (A, B and E) and fibroblastoid (C and D) cells on a microfabricated elastomeric pillar array.22 The adhesions (cyan circles) are determined by selecting micropillars that are close to the cell edge and experience a significant force (Materials and methods). (F–J) Experimental data of cell shape and coarse-grained cytoskeletal structure on a square lattice of these cells. The white line represents the cell boundary, the black lines in the interior of the cells represent the orientation field n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from top to bottom, by: 0.54; 0.44; 0.45; 0.46; 0.37. (K–O) Simulations with the adhesion sites of the experimental data as input. The spatial averages of the order parameter S are given, from top to bottom, by: 0.52; 0.68; 0.61; 0.59; 0.53. The values for λmin/σ = 12.6; 15.7; 18.0; 10.8; 13.4 μm and σ/(σ + α0) = 0.75; 0.25; 0.46; 0.95; 0.52 are found by an analysis of the elliptical shape of these cells.22 The values of An = 4.4; 4.1; 19; 4.6; 4.7, where R = 17.3; 24.4; 39.9; 24.9; 25.3 μm is defined as the square root of the cell area, are determined by minimizing Δ2, with the minima given by Δ2 = 0.016; 0.058; 0.057; 0.034; 0.037. These An values correspond to K/W = 3.9; 5.9; 2.1; 5.4; 5.4 μm. The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for all cells. The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.† θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from top to bottom, by: 0.54; 0.44; 0.45; 0.46; 0.37. (K–O) Simulations with the adhesion sites of the experimental data as input. The spatial averages of the order parameter S are given, from top to bottom, by: 0.52; 0.68; 0.61; 0.59; 0.53. The values for λmin/σ = 12.6; 15.7; 18.0; 10.8; 13.4 μm and σ/(σ + α0) = 0.75; 0.25; 0.46; 0.95; 0.52 are found by an analysis of the elliptical shape of these cells.22 The values of An = 4.4; 4.1; 19; 4.6; 4.7, where R = 17.3; 24.4; 39.9; 24.9; 25.3 μm is defined as the square root of the cell area, are determined by minimizing Δ2, with the minima given by Δ2 = 0.016; 0.058; 0.057; 0.034; 0.037. These An values correspond to K/W = 3.9; 5.9; 2.1; 5.4; 5.4 μm. The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for all cells. The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.† | |
Finally, in nematic liquid crystals, anchoring, namely the orientation of the nematogens by a surface, originates at the molecular scale as consequence of steric, van der Waals and dipolar interactions, and, similarly to epitaxy in solids, can be controlled via the surface chemistry (see e.g.ref. 89). Whereas the biological role of anchoring in the actin cytoskeleton is yet to be explored and understood, the prevalence of parallel anchoring (i.e. the stress fibers are tangent to the cell contour) highlighted by our comparative analysis, suggests that steric interactions may be instrumental in the organization of the actin cytoskeleton, consistently with studies of actin assemblies in microchambers.43–45
V. Conclusions
In this article we investigated the spatial organization of cells adhering on a rigid substrate at a discrete number of points. Our approach is based on a contour model for the cell shape8,23–26 coupled with a continuous phenomenological model for the actin cytoskeleton, inspired by the physics of nematic liquid crystals.70 This approach can be carried out at various levels of complexity, offering progressively insightful results. Assuming that the orientation of the stress fibers is uniform along individual cellular arcs (but varies from arc to arc), it is possible to achieve a complete analytical description of the geometry of the cell, in which all arcs are approximated by different portions of a unique ellipse. The eccentricity of this ellipse depends on the ratio between the isotropic and directed stresses arising in the actin cytoskeleton, and the orientation of the major axis of this ellipse is parallel to the stress fibers. This parallel alignment highlights the ability of cells to employ their actin cytoskeleton to regulate their shape. The method further allows to analytically calculate the traction forces exerted by the cell on the adhesion sites and compare them with traction force microscopy data.
Lifting the assumption that the stress fibers are uniformly oriented along individual cellular arcs allows one to describe the mechanical interplay between cellular shape and the configuration of the actin cytoskeleton. Using numerical simulations and inputs from experiments on fibroblastoid and epithelioid cells plated on micropillar arrays, we identified a feedback mechanism rooted in the competition between the tendency of stress fibers to align uniformly in the bulk of the cell, but tangentially with respect to the cell edge. Our approach enables us to predict both the shape of the cell and the orientation of the stress fibers and can account for the emergence of topological defects and other distinctive morphological features. The predicted stress fiber orientations are in good agreement with the experimental data and further offer an indirect way to estimate quantities that are generally precluded to direct measurement, such as the cell's internal stresses and the orientational stiffness of the actin cytoskeleton. The main discrepancy between our predictions and the experimental data is the overestimation of the nematic order parameter in the cell interior, which should be addressed in future work by explicitely accounting for actin density variations.
The success of this relatively simple approach is remarkable given the enormous complexity of the cytoskeleton and the many physical, chemical, and biological mechanisms associated with stress fiber dynamics and alignment.21,35–53 Yet, the agreement between our theoretical and experimental results suggests that, on the scale of the whole cell, the myriad of complex mechanisms that govern the dynamics of the stress fibers in adherent cells can be effectively described in terms of simple entropic mechanisms, as those at the heart of the physics of liquid crystals. Moreover, this quantitative agreement further establishes the fact that the dynamics and alignment of stress fibers in cells cannot be understood from dynamics at the sub-cellular scale alone, and highlights the crucial role of the boundary conditions inferred by cellular shape.60,61
In addition, our analysis demonstrates that chiral symmetry breaking can originate from the natural interplay between the orientation of the stress fibers and the shape of the cell. A more detailed investigation of this mechanism is beyond the scope of this study, but will represent a challenge in the near future with the goal of shedding light on the fascinating examples of chiral symmetry breaking observed both in single cells86 and tissues.87
In the future, we plan to use our model to investigate the mechanics of cells adhering to micropatterned substrates that impose reproducible cell shapes,67 with special emphasis to the interplay between cytoskeletal anisotropy and the geometry of the adhesive patches. These systems are not new to theoretical research, but previous studies have focused on either the cytoskeleton49 or on cell shape,90 rather then on their interaction. This will enable us to more rigorously compare our model predictions with existing experimental data on stress fiber orientation in various adhesive geometries,16,60–62,91 including convex shapes such as circles or spherocylinders.63,86,92 Additionally, our model could be further extended to account for the mechanical feedback on myosin activity (see e.g.ref. 63, 68, 69 and 71) as well as the interactions of the stress fibers with the micropillars in the bulk of the cell body.28,71,72 Furthermore, our framework could be extended to study the role of cytoskeletal anisotropy in cell motility, for instance by taking into account the dynamics of focal adhesions,47,48 biochemical pathways in the actin cytoskeleton,93 actin filament turnover and the viscoelasticity of stress fibers,79,80 or cellular protrusions and retractions.94 Finally, our approach could be extended to computational frameworks such as vertex models, Cellular Potts Models, or phase field models,95 and could provide a starting point for exploring the role of anisotropy in multicellular environments such as tissues.96–103
Author contributions
L. G. designed this study with the help of T. S., R. M. H. M. and E. H. J. D. K. S. and L. G. developed the theoretical framework. K. S. and J. E. developed the code, and J. E. performed the simulations. J. E. and W. P. carried out the analysis of the experimental data. K. S. and L. G. wrote the article. All authors commented on the manuscript.
Conflicts of interest
There are no conflicts to declare.
Appendix A: materials and methods
1 Cell culture and fluorescent labeling
Epithelioid GE11 and fibroblastoid GD25 cells27 expressing either α5β1 or αvβ3 (GDβ1, GDβ3, GEβ1 and GEβ3) have been cultured as described before.104 Cells have cultured in medium (DMEM; Dulbecco's Modified Eagle's Medium, Invitrogen/Fisher Scientific) supplemented with 10% fetal bovine serum (HyClone, Etten-Leur, The Netherlands), 25 U ml−1 penicillin and 25 μg ml−1 streptomycin (Invitrogen/Fisher Scientific cat. # 15070-063). Cells were fixed in 4% formaldehyde and then permeabilised with 0.1% Triton-X and 0.5% BSA in PBS. Tetramethylrhodamine (TRITC)–Phalloidin (Fisher Emergo B.V. cat. # A12380, Thermo Fisher) was subsequently used to stain F-actin.
2. Micropillar arrays
Micropillar arrays were fabricated using polydimethylsiloxane (PDMS) as described in ref. 29 and 30. The 2 μm diameter micropillars are arranged in a hexagonal lattice with a 4 μm center-to-center distance. The micropillar height is 6.9 μm, resulting in a stiffness of 16.2 nN μm−1. The pillar tops were fluorescently labeled using an Alexa 405-fibronectin conjugate (Alexa Fluor®, Invitrogen/Fisher Scientific, Breda, The Netherlands; Fibronectin cat. #1141, Sigma Aldrich, Zwijndrecht, The Netherlands). Pillar deflections were determined with ∼30 nm precision using a specifically designed Matlab script resulting in a ∼0.5 nN precision in force.30
3. Imaging
High-resolution imaging was performed on an in-house constructed spinning disk confocal microscope based on an Axiovert200 microscope body with a Zeiss Plan-Apochromat 100× 1.4NA objective (Zeiss, Sliedrecht, The Netherlands) and a CSU-X1 spinning disk unit (CSU-X1, Yokogawa, Amersfoort, The Netherlands). Imaging was done using an emCCD camera (iXon 897, Andor, Belfast, UK). Alexa405 and TRITC were exited using 405 nm (Crystalaser, Reno, NV) and 561 nm (Cobolt, Stockholm, Sweden) lasers, respectively. This results in a resolution of approximately 150 nm and 200 nm respectively.
4. Image analysis
The locations of the cell interior and the cell edge were found by applying a low-pass filter on the images using Matlab. The interior of the cell was then sampled by overlaying a square lattice of 512 × 512 pixels (1 pixel = 0.138 × 0.138 μm2) on the microscope field-of-view (Fig. 6A and 8A–E).
For all pixels that are inside the cell, the configuration of the stress fibers was analyzed by calculating the nematic tensor using ImageJ with the OrientationJ plugin,105 see the ESI.† The data were further coarse-grained in blocks of 8 × 8 pixels corresponding to regions of size 1.104 × 1.104 μm2 in real space. This results in a new 64 × 64 lattice. The value of the nematic tensor in the new coarse-grained pixels was obtained from an average over those of the original 8 × 8 pixels located inside the cell. In turn, the coarse-grained pixels were considered inside the cell if more than half of the original pixels were inside the cell.
5. Force analysis
The forces that the cells exert on the micropillar array were measured. We selected the pillars in Fig. 6 and 8 as adhesion sites according to the following two criteria: (1) they are within 10 pixels (1.38 μm) from the edge of the cell. (2) They are subject to a force that is at least 3 times larger than the average force on all the pillars or the tangent vector along the cell contour rotates by an angle of at least 30° at the location of that pillar.
6. Ellipse fitting
Ellipses in Fig. 3 are fitted, using Matlab, to the part of the cell edge delimited by two consecutive pillars, provided the pillars satisfy the two criteria listed in Section A.5 and the distance between them is larger than 50 pixels (6.90 μm). Each ellipse is described by five parameters: the two coordinates of the center, the two semi-axes and the orientation of the ellipse's longitudinal direction. In fitting ellipses to cellular arcs, the orientation of the longitudinal direction of a given ellipse is constrained to be equal to the local orientation of stress fibers along the same arc, consistent with our predictions [eqn (6)]. This local stress fiber orientation is found by averaging the nematic director (Section A.4) over all pixels which are between 2.07 μm and 6.90 μm (15 and 50 non-coarse-grained pixels) away from the corresponding cell edge and whose nematic order parameter S is larger than 0.15. Then, each cellular arc is fitted separately to obtain the coordinates of the center and the lengths of the two semi-axes of the ellipse, and the resulting lengths are averaged over the N ellipses in the cell that meet the criteria listed above. The resulting numbers serve as initial parameters for a global fit, which simultaneously fits N cellular arcs to a unique ellipse. This global fit then finds optimal values for the coordinates of the center of each ellipse, and for the length of the two semi-axes of the unique ellipse, by minimizing the distance between fitted ellipses and the cellular arcs using χ2. All reported ellipse parameters are obtained using this global fit. Ellipses whose χ2 is greater than 10 were discarded, which occurs in case of membrane ruffling and other out-of-equilibrium events.
Acknowledgements
This work was supported by funds from the Netherlands Organisation for Scientific Research (NWO/OCW), as part of the Frontiers of Nanoscience program (L. G.), the Netherlands Organization for Scientific Research (NWO-FOM) within the program on Barriers in the Brain (W. P. and T. S.; No. FOM L1714M), the Netherlands Organization for Scientific Research (NWO-ALW and NWO-ENW) within the Innovational Research Incentives Scheme (R. M. H. M.; Vidi 2010, No. 864.10.009 and Vici 2017, No. 865.17.004), and the Leiden/Huygens fellowship (K. S.).
References
- C. M. Lo, H. B. Wang, M. Dembo and Y. L. Wang, Biophys. J., 2000, 79, 144–152 CrossRef CAS PubMed.
- R. D. Sochol, A. T. Higa, R. R. R. Janairo, S. Li and L. Lin, Soft Matter, 2011, 7, 4606 RSC.
- C. A. Reinhart-King, M. Dembo and D. A. Hammer, Biophys. J., 2008, 95, 6044–6051 CrossRef CAS PubMed.
- Y. Sawada, M. Tamada, B. J. Dubin-Thaler, O. Cherniavskaya, R. Sakai, S. Tanaka and M. P. Sheetz, Cell, 2006, 127, 1015–1026 CrossRef CAS PubMed.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689 CrossRef CAS PubMed.
- B. Trappmann, J. E. Gautrot, J. T. Connelly, D. G. T. Strange, Y. Li, M. L. Oyen, M. A. Cohen Stuart, H. Boehm, B. Li, V. Vogel, J. P. Spatz, F. M. Watt and W. T. S. Huck, Nat. Mater., 2012, 11, 642–649 CrossRef CAS PubMed.
- T. Panciera, L. Azzolin, M. Cordenonsi and S. Piccolo, Nat. Rev. Mol. Cell Biol., 2017, 18, 758 CrossRef CAS PubMed.
- I. Bischofs, S. Schmidt and U. Schwarz, Phys. Rev. Lett., 2009, 103, 1–4 CrossRef PubMed.
- M. Ghibaudo, L. Trichet, J. Le Digabel, A. Richert, P. Hersen and B. Ladoux, Biophys. J., 2009, 97, 357–368 CrossRef CAS PubMed.
- D. A. Fletcher and R. D. Mullins, Nature, 2010, 463, 485–492 CrossRef CAS PubMed.
- N. Minc, D. Burgess and F. Chang, Cell, 2011, 144, 414–426 CrossRef CAS PubMed.
- M. Versaevel, T. Grevesse and S. Gabriele, Nat. Commun., 2012, 3, 671 CrossRef PubMed.
- C. S. Chen, M. Mrksich, S. Huang, G. M. Whitesides and D. E. Ingber, Science, 1997, 276, 1425–1428 CrossRef CAS PubMed.
- N. Jain, K. V. Iyer, A. Kumar and G. V. Shivashankar, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11349–11354 CrossRef CAS PubMed.
- R. McBeath, D. M. Pirone, C. M. Nelson, K. Bhadriraju and C. S. Chen, Dev. Cell, 2004, 6, 483–495 CrossRef CAS PubMed.
- K. A. Kilian, B. Bugarija, B. T. Lahn and M. Mrksich, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4872–4877 CrossRef CAS PubMed.
- A. Chopra, E. Tabdanov, H. Patel, P. A. Janmey and J. Y. Kresh, Am. J. Physiol.: Heart Circ. Physiol., 2011, 300, H1252–H1266 CrossRef CAS PubMed.
- A. J. Engler, M. A. Griffin, S. Sen, C. G. Bönnemann, H. L. Sweeney and D. E. Discher, J. Cell Biol., 2004, 166, 877–887 CrossRef CAS PubMed.
- T. Yeung, P. C. Georges, L. A. Flanagan, B. Marg, M. Ortiz, M. Funaki, N. Zahir, W. Ming, V. Weaver and P. A. Janmey, Cell Motil., 2005, 60, 24–34 CrossRef PubMed.
- F. Grinnell, Trends Cell Biol., 2000, 10, 362–365 CrossRef CAS.
- A. Zemel, F. Rehfeldt, A. E. X. Brown, D. E. Discher and S. A. Safran, J. Phys.: Condens. Matter, 2010, 22, 194110 CrossRef CAS.
- W. Pomp, K. Schakenraad, H. E. Balcıoğlu, H. van Hoorn, E. H. J. Danen, R. M. H. Merks, T. Schmidt and L. Giomi, Phys. Rev. Lett., 2018, 121, 178101 CrossRef CAS PubMed.
- R. Bar-Ziv, T. Tlusty, E. Moses, S. A. Safran and A. Bershadsky, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 10140–10145 CrossRef CAS PubMed.
- I. B. Bischofs, F. Klein, D. Lehnert, M. Bastmeyer and U. S. Schwarz, Biophys. J., 2008, 95, 3488–3496 CrossRef CAS PubMed.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
-
L. Giomi, Advances in Experimental Medicine and Biology, in Cell migrations: causes and function, ed. S. Zapperi and C. A. M. La Porta, Springer International Publishing, 2019, vol. 1146, DOI:10.1007/978-3-030-17593-1.
- E. H. J. Danen, P. Sonneveld, C. Brakebusch, R. Fässler and A. Sonnenberg, J. Cell Biol., 2002, 159, 1071–1086 CrossRef CAS PubMed.
- J. L. Tan, J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 1484–1489 CrossRef CAS.
- L. Trichet, J. Le Digabel, R. J. Hawkins, S. R. K. Vedula, M. Gupta, C. Ribrault, P. Hersen, R. Voituriez and B. Ladoux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6933–6938 CrossRef CAS PubMed.
- H. Van Hoorn, R. Harkes, E. M. Spiesz, C. Storm, D. Van Noort, B. Ladoux and T. Schmidt, Nano Lett., 2014, 14, 4257–4262 CrossRef CAS PubMed.
- T. Vignaud, L. Blanchoin and M. Théry, Trends Cell Biol., 2012, 22, 671–682 CrossRef CAS PubMed.
- B. Ladoux, R.-M. Mège and X. Trepat, Trends Cell Biol., 2016, 26, 420–433 CrossRef PubMed.
- N. T. Lam, T. J. Muldoon, K. P. Quinn, N. Rajaram and K. Balachandran, Integr. Biol., 2016, 8, 1079–1089 CrossRef CAS PubMed.
- S. K. Gupta, Y. Li and M. Guo, Soft Matter, 2019, 15, 190–199 RSC.
- V. S. Deshpande, R. M. McMeeking and A. G. Evans, Proc. R. Soc. London, Ser. A, 2007, 463, 787–815 CrossRef CAS.
- S. Walcott and S. X. Sun, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7757–7762 CrossRef CAS PubMed.
- A. Zemel, F. Rehfeldt, A. E. X. Brown, D. E. Discher and S. A. Safran, Nat. Phys., 2010, 6, 468 Search PubMed.
- N. Nisenholz, M. Botton and A. Zemel, Soft Matter, 2014, 10, 2453–2462 RSC.
- M. Raab, J. Swift, P. D. P. Dingal, P. Shah, J.-W. Shin and D. E. Discher, J. Cell Biol., 2012, 199, 669–683 CrossRef CAS.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73 CrossRef CAS.
- P. Kraikivski, R. Lipowsky and J. Kierfeld, Phys. Rev. Lett., 2006, 96, 258103 CrossRef PubMed.
- S. Swaminathan, F. Ziebert, D. Karpeev and I. S. Aranson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 036207 CrossRef PubMed.
- M. Soares e Silva, J. Alvarado, J. Nguyen, N. Georgoulia, B. M. Mulder and G. H. Koenderink, Soft Matter, 2011, 7, 10631–10641 RSC.
- J. Alvarado, B. M. Mulder and G. H. Koenderink, Soft Matter, 2014, 10, 2354–2364 RSC.
- S. Deshpande and T. Pfohl, Biomicrofluidics, 2012, 6, 034120 CrossRef PubMed.
- V. S. Deshpande, R. M. McMeeking and A. G. Evans, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14015–14020 CrossRef CAS PubMed.
- V. S. Deshpande, M. Mrksich, R. M. McMeeking and A. G. Evans, J. Mech. Phys. Solids, 2008, 56, 1484–1510 CrossRef CAS.
-
E. G. Rens and R. M. H. Merks, 2019, arXiv e-prints, arXiv:1906.08962.
- A. Pathak, V. S. Deshpande, R. M. McMeeking and A. G. Evans, J. R. Soc., Interface, 2008, 5, 507–524 CrossRef.
- W. Ronan, V. S. Deshpande, R. M. McMeeking and J. P. McGarry, Biomech. Model. Mechanobiol., 2014, 13, 417–435 CrossRef.
- A.-C. Reymann, J.-L. Martiel, T. Cambier, L. Blanchoin, R. Boujemaa-Paterski and M. Théry, Nat. Mater., 2010, 9, 827 CrossRef CAS PubMed.
- G. Letort, A. Z. Politi, H. Ennomani, M. Théry, F. Nedelec and L. Blanchoin, PLoS Comput. Biol., 2015, 11, 1–21 CrossRef PubMed.
- A. P. Liu, D. L. Richmond, L. Maibaum, S. Pronk, P. L. Geissler and D. A. Fletcher, Nat. Phys., 2008, 4, 789 Search PubMed.
- S. Thomopoulos, G. M. Fomovsky and J. W. Holmes, J. Biomech. Eng., 2005, 127, 742–750 CrossRef PubMed.
- K. Burridge and M. Chrzanowska-Wodnicka, Annu. Rev. Cell Dev. Biol., 1996, 12, 463–519 CrossRef CAS PubMed.
- S. Banerjee and L. Giomi, Soft Matter, 2013, 9, 5251–5260 RSC.
- L. Giomi, Soft Matter, 2013, 9, 8121 RSC.
- T. J. Pedley and J. O. Kessler, Annu. Rev. Fluid Mech., 1992, 24, 313–358 CrossRef.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef PubMed.
- M. Théry, A. Pépin, E. Dressaire, Y. Chen and M. Bornens, Cell Motil., 2006, 63, 341–355 CrossRef PubMed.
- M. Théry, V. Racine, M. Piel, A. Pépin, A. Dimitrov, Y. Chen, J.-B. Sibarita and M. Bornens, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19771–19776 CrossRef PubMed.
- J. James, E. D. Goluch, H. Hu, C. Liu and M. Mrksich, Cell Motil., 2008, 65, 841–852 CrossRef PubMed.
- P. W. Oakes, S. Banerjee, M. C. Marchetti and M. L. Gardel, Biophys. J., 2014, 107, 825–833 CrossRef CAS PubMed.
- J. P. McGarry, J. Fu, M. T. Yang, C. S. Chen, R. M. McMeeking, A. G. Evans and V. S. Deshpande, Philos. Trans. R. Soc., A, 2009, 367, 3477–3497 CrossRef CAS PubMed.
- S. Pellegrin and H. Mellor, J. Cell Sci., 2007, 120, 3491–3499 CrossRef CAS PubMed.
- K. Burridge and E. S. Wittchen, J. Cell Biol., 2013, 200, 9–19 CrossRef CAS PubMed.
- M. Théry, J. Cell Sci., 2010, 123, 4201–4213 CrossRef PubMed.
- A. D. Rape, W.-H. Guo and Y.-L. Wang, Biomaterials, 2011, 32, 2043–2051 CrossRef CAS.
- J. Hanke, D. Probst, A. Zemel, U. S. Schwarz and S. Köster, Soft Matter, 2018, 14, 6571–6581 RSC.
-
P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, 1995 Search PubMed.
- J. Fu, Y.-K. Wang, M. T. Yang, R. A. Desai, X. Yu, Z. Liu and C. S. Chen, Nat. Methods, 2010, 7, 733–736 CrossRef CAS.
- G. L. Lin, D. M. Cohen, R. A. Desai, M. T. Breckenridge, L. Gao, M. J. Humphries and C. S. Chen, FEBS Lett., 2013, 587, 763–769 CrossRef CAS.
- C. Roux, A. Duperray, V. M. Laurent, R. Michel, V. Peschetola, C. Verdier and J. Étienne, Interface Focus, 2016, 6, 20160042 CrossRef.
- D. Riveline, E. Zamir, N. Q. Balaban, U. S. Schwarz, T. Ishizaki, S. Narumiya, Z. Kam, B. Geiger and A. D. Bershadsky, J. Cell Biol., 2001, 153, 1175–1186 CrossRef CAS PubMed.
- N. Q. Balaban, U. S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi and B. Geiger, Nat. Cell Biol., 2001, 3, 466–472 CrossRef CAS.
- B. Wehrle-Haller and B. A. Imhof, Int. J. Biochem. Cell Biol., 2003, 35, 39–50 CrossRef CAS.
- R. De, A. Zemel and S. A. Safran, Nat. Phys., 2007, 3, 655 Search PubMed.
- A. Livne, E. Bouchbinder and B. Geiger, Nat. Commun., 2014, 5, 3938 Search PubMed.
- J. Étienne, J. Fouchard, D. Mitrossilis, N. Bufi, P. Durand-Smet and A. Asnacios, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2740–2745 CrossRef PubMed.
- P. W. Oakes, E. Wagner, C. A. Brand, D. Probst, M. Linke, U. S. Schwarz, M. Glotzer and M. L. Gardel, Nat. Commun., 2017, 8, 15817 CrossRef CAS PubMed.
- S. B. Khatau, C. M. Hale, P. J. Stewart-Hutchinson, M. S. Patel, C. L. Stewart, P. C. Searson, D. Hodzic and D. Wirtz, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19017–19022 CrossRef CAS PubMed.
- K. Nagayama, Y. Yahiro and T. Matsumoto, Cell. Mol. Bioeng., 2013, 6, 473–481 CrossRef CAS.
- M. Nobili and G. Durand, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, R6174–R6177 CrossRef CAS.
- Our code is available for download on GitHub: https://github.com/rmerks/CellQTensor.
- J. Galanis, D. Harries, D. L. Sackett, W. Losert and R. Nossal, Phys. Rev. Lett., 2006, 96, 028002 CrossRef.
- Y. H. Tee, T. Shemesh, V. Thiagarajan, R. F. Hariadi, K. L. Anderson, C. Page, N. Volkmann, D. Hanein, S. Sivaramakrishnan, M. M. Kozlov and A. D. Bershadsky, Nat. Cell Biol., 2015, 17, 445 CrossRef CAS.
- G. Duclos, C. Blanch-Mercader, V. Yashunsky, G. Salbreux, J.-F. Joanny, J. Prost and P. Silberzan, Nat. Phys., 2018, 14, 728–732 Search PubMed.
- P. Roca-Cusachs, J. Alcaraz, R. Sunyer, J. Samitier, R. Farré and D. Navajas, Biophys. J., 2008, 94, 4984–4995 CrossRef CAS PubMed.
- B. Jerome, Rep. Prog. Phys., 1991, 54, 391–451 CrossRef CAS.
- P. J. Albert and U. S. Schwarz, Biophys. J., 2014, 106, 2340–2352 CrossRef CAS PubMed.
- Q. Tseng, I. Wang, E. Duchemin-Pelletier, A. Azioune, N. Carpi, J. Gao, O. Filhol, M. Piel, M. Théry and M. Balland, Lab Chip, 2011, 11, 2231–2240 RSC.
- S. Jalal, S. Shi, V. Acharya, R. Y.-J. Huang, V. Viasnoff, A. D. Bershadsky and Y. H. Tee, J. Cell Sci., 2019, 132, jcs220780 CrossRef CAS PubMed.
- A. F. M. Marée, V. A. Grieneisen and L. Edelstein-Keshet, PLoS Comput. Biol., 2012, 8, 1–20 CrossRef PubMed.
- F. J. Segerer, F. Thüroff, A. Piera Alberola, E. Frey and J. O. Rädler, Phys. Rev. Lett., 2015, 114, 228102 CrossRef PubMed.
- P. J. Albert and U. S. Schwarz, Cell Adhes. Migr., 2016, 10, 516–528 CrossRef CAS PubMed.
- M. Eastwood, V. C. Mudera, D. A. McGrouther and R. A. Brown, Cell Motil. Cytoskeleton, 1998, 40, 13–21 CrossRef CAS PubMed.
- D. W. J. Van der Schaft, A. C. C. Van Spreeuwel, H. C. Van Assen and F. P. T. Baaijens, Tissue Eng., Part A, 2011, 17, 2857–2865 CrossRef CAS PubMed.
- O. Wartlick, P. Mumcu, F. Jülicher and M. Gonzalez-Gaitan, Nat. Rev. Mol. Cell Biol., 2011, 12, 594–604 CrossRef CAS PubMed.
- R. F. M. Van Oers, E. G. Rens, D. J. LaValley, C. A. Reinhart-King and R. M. H. Merks, PLoS Comput. Biol., 2014, 10, e1003774 CrossRef PubMed.
- P. Santos-Oliveira, A. Correia, T. Rodrigues, T. M. Ribeiro-Rodrigues, P. Matafome, J. C. Rodríguez-Manzaneque, R. Seiça, H. Girão and R. D. M. Travasso, PLoS Comput. Biol., 2015, 11, 1–20 CrossRef PubMed.
- D. S. Vijayraghavan and L. A. Davidson, Birth Defects Res., 2017, 109, 153–168 CrossRef CAS PubMed.
- T. B. Saw, A. Doostmohammadi, V. Nier, L. Kocgozlu, S. Thampi, Y. Toyama, P. Marcq, C. T. Lim, J. M. Yeomans and B. Ladoux, Nature, 2017, 544, 212 CrossRef CAS PubMed.
- D. L. Barton, S. Henkes, C. J. Weijer and R. Sknepnek, PLoS Comput. Biol., 2017, 13, 1–34 CrossRef PubMed.
- H. E. Balcioglu, H. van Hoorn, D. M. Donato, T. Schmidt and E. H. J. Danen, J. Cell Sci., 2015, 128, 1316–1326 CrossRef CAS PubMed.
- OrientationJ, http://bigwww.epfl.ch/demo/orientation.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00492h |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article cd,
Erik H. J.
Danen
e,
Roeland M. H.
Merks
bf,
Thomas
Schmidt
c and
Luca
Giomi
cd,
Erik H. J.
Danen
e,
Roeland M. H.
Merks
bf,
Thomas
Schmidt
c and
Luca
Giomi
 *a
*a

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,sin
θ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and the normal vector N = (−sin
θ) and the normal vector N = (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with θ the turning angle. The unit vector n = (cos
θ), with θ the turning angle. The unit vector n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) describes the local orientation θSF of the stress fibers.
θSF) describes the local orientation θSF of the stress fibers.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,sin
θ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with θ = θ(s) the turning angle of the arc with respect to the horizontal axis of the frame of reference. The normal vector N = ∂sr⊥ = (−sin
θ), with θ = θ(s) the turning angle of the arc with respect to the horizontal axis of the frame of reference. The normal vector N = ∂sr⊥ = (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with r⊥ = (−y,x), is directed toward the interior of the cell. The equation describing the shape of a cellular arc is obtained upon balancing all the conservative and dissipative forces experienced by the cell contour. These are:
θ), with r⊥ = (−y,x), is directed toward the interior of the cell. The equation describing the shape of a cellular arc is obtained upon balancing all the conservative and dissipative forces experienced by the cell contour. These are:![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) out −
out − ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) in)·N,
in)·N,![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) out and
out and ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e139.gif) in are the stress tensors on the two sides of the cell boundary and Fcortex is the stress resultant along the cell contour.8,22,24–26,56 We assume the substrate to be rigid and the adhesion sites, lying along the cell contour, to be stationary. For theoretical models of cell adhesion on compliant substrates, see, e.g., ref. 8, 26 and 56. The temporal evolution of the cell contour is then dictated by a competition between internal and external bulk stresses acting on the cell boundary and the tension arising within the cell cortex. The former give rise to a contractile (i.e., inward-directed) force on the cell contour, thereby tend to decrease the cell area. By contrast, cortical tension decreases the cell perimeter, thus resulting in an extensile (i.e., outward-directed) force, as a consequence of the cell concavity. As the planar contour represents the two-dimensional projection of the full three-dimensional body of the cell, changes in the area affect neither the density of the cytoplasm nor the internal pressure. Finally, we assume the dynamics of the cell contour to be overdamped.
in are the stress tensors on the two sides of the cell boundary and Fcortex is the stress resultant along the cell contour.8,22,24–26,56 We assume the substrate to be rigid and the adhesion sites, lying along the cell contour, to be stationary. For theoretical models of cell adhesion on compliant substrates, see, e.g., ref. 8, 26 and 56. The temporal evolution of the cell contour is then dictated by a competition between internal and external bulk stresses acting on the cell boundary and the tension arising within the cell cortex. The former give rise to a contractile (i.e., inward-directed) force on the cell contour, thereby tend to decrease the cell area. By contrast, cortical tension decreases the cell perimeter, thus resulting in an extensile (i.e., outward-directed) force, as a consequence of the cell concavity. As the planar contour represents the two-dimensional projection of the full three-dimensional body of the cell, changes in the area affect neither the density of the cytoplasm nor the internal pressure. Finally, we assume the dynamics of the cell contour to be overdamped.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) (see Fig. 1B). This gives rise to an overall contractile bulk stress of the form:58,59
θSF) (see Fig. 1B). This gives rise to an overall contractile bulk stress of the form:58,59![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) out −
out − ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) in = σÎ + αnn,
in = σÎ + αnn,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,cos
θSF,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) correspond to the principal stress directions, whereas σmax = σ + α and σmin = σ are, respectively, the maximal and minimal principal stresses. The degree of anisotropy of the bulk stress is thus determined by the ratio between the isotropic contractility σ and the directed contractility α. Finally, the tension within the cell cortex is modeled as Fcortex = λT, where the line tension λ embodies the contractile forces arising from myosin activity in the cell cortex. This quantity varies, in general, along an arc and can be expressed as a function of the arclength s. In the presence of anisotropic bulk stresses, in particular, λ(s) cannot be constant, as we will see in Section II.A. The force balance condition, eqn (1), becomes then
θSF) correspond to the principal stress directions, whereas σmax = σ + α and σmin = σ are, respectively, the maximal and minimal principal stresses. The degree of anisotropy of the bulk stress is thus determined by the ratio between the isotropic contractility σ and the directed contractility α. Finally, the tension within the cell cortex is modeled as Fcortex = λT, where the line tension λ embodies the contractile forces arising from myosin activity in the cell cortex. This quantity varies, in general, along an arc and can be expressed as a function of the arclength s. In the presence of anisotropic bulk stresses, in particular, λ(s) cannot be constant, as we will see in Section II.A. The force balance condition, eqn (1), becomes then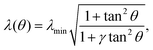
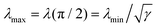 . We note that these variations in line tension along a single arc do not necessarily have to be regulated by the cell. Instead, they could simply be a result of passive mechanical forces in a way very similar to the space-dependent tension in a simple cable hanging under gravity. Although the minimal line tension λmin could, in principle, be arc-dependent, for example if the cell cortex displays substantial variations in the myosin densities,24 here we approximate λmin as a constant. This approximation is motivated by the fact that our previous in vitro observations of anisotropic epithelioid and fibroblastoid cells did not identify a correlation between the arc length and curvature,22 which, on the other hand, is expected if λmin was to vary significantly from arc to arc.24 Hence, α, σ and λmin represent the independent material parameters of our model.
. We note that these variations in line tension along a single arc do not necessarily have to be regulated by the cell. Instead, they could simply be a result of passive mechanical forces in a way very similar to the space-dependent tension in a simple cable hanging under gravity. Although the minimal line tension λmin could, in principle, be arc-dependent, for example if the cell cortex displays substantial variations in the myosin densities,24 here we approximate λmin as a constant. This approximation is motivated by the fact that our previous in vitro observations of anisotropic epithelioid and fibroblastoid cells did not identify a correlation between the arc length and curvature,22 which, on the other hand, is expected if λmin was to vary significantly from arc to arc.24 Hence, α, σ and λmin represent the independent material parameters of our model.
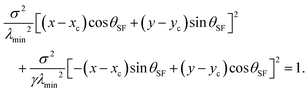

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) = ŷ, hence θSF = π/2. A force balance between isotropic stress, directed stress and line tension results in the description of each cell edge segment (red curve) as part of an ellipse of aspect ratio
θSF) = ŷ, hence θSF = π/2. A force balance between isotropic stress, directed stress and line tension results in the description of each cell edge segment (red curve) as part of an ellipse of aspect ratio 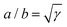 . The cell exerts forces F0 and F1 on the adhesion sites (blue). The vector d = d(cos
. The cell exerts forces F0 and F1 on the adhesion sites (blue). The vector d = d(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) describes the relative position of the two adhesion sites, d⊥ = d(−sin
ϕ) describes the relative position of the two adhesion sites, d⊥ = d(−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,cos
ϕ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) is a vector perpendicular to d, and θ is the turning angle of the cellular arc. The coordinates of the ellipse center (xc,yc) and the angular coordinates of the adhesion sites along the ellipse ψ0 and ψ1 are given in the ESI.†
ϕ) is a vector perpendicular to d, and θ is the turning angle of the cellular arc. The coordinates of the ellipse center (xc,yc) and the angular coordinates of the adhesion sites along the ellipse ψ0 and ψ1 are given in the ESI.†
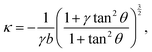
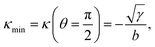
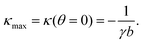
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) (Fig. 2). This yields
ϕ) (Fig. 2). This yields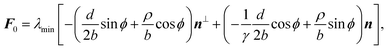
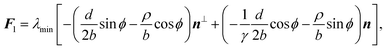
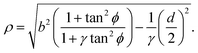
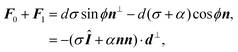
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,cos
ϕ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) (Fig. 2). eqn (11) presents the force resulting from the integrated contractile bulk stress [see eqn (1)], which is independent of the line tension λmin but scales linearly with the distance between adhesions. This implies that the total traction increases with the cell size, consistent with earlier contour models8,56 and various experimental observations.63,68,69 Because the cell size is expected to be larger on stiffer substrates, as these stretch only slightly in response to the cell contraction, the total amount of traction also increases with substrate stiffness.
ϕ) (Fig. 2). eqn (11) presents the force resulting from the integrated contractile bulk stress [see eqn (1)], which is independent of the line tension λmin but scales linearly with the distance between adhesions. This implies that the total traction increases with the cell size, consistent with earlier contour models8,56 and various experimental observations.63,68,69 Because the cell size is expected to be larger on stiffer substrates, as these stretch only slightly in response to the cell contraction, the total amount of traction also increases with substrate stiffness.
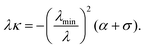
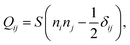
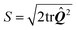 is the so called nematic order parameter, measuring the amount of local nematic order. Here, 0 ≤ S ≤ 1, where S = 1 represents perfect nematic order and S = 0 represents randomly oriented stress fibers. In the standard {
is the so called nematic order parameter, measuring the amount of local nematic order. Here, 0 ≤ S ≤ 1, where S = 1 represents perfect nematic order and S = 0 represents randomly oriented stress fibers. In the standard {![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ,ŷ} Cartesian basis, eqn (15) yields
,ŷ} Cartesian basis, eqn (15) yields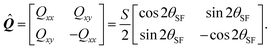
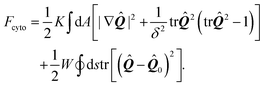
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) 0 representing their preferential orientation. Experimental evidence form our (Fig. 3 and ref. 22) and other's work (e.g., ref. 31–34), suggests that, in highly anisotropic cells, peripheral stress fibers are preferentially parallel to the cell edge. The same trend is recovered in experiments with purified actin bundles confined in microchambers.43,44 In the language of Landau–de Gennes theory, this effect can be straightforwardly reproduced by setting
0 representing their preferential orientation. Experimental evidence form our (Fig. 3 and ref. 22) and other's work (e.g., ref. 31–34), suggests that, in highly anisotropic cells, peripheral stress fibers are preferentially parallel to the cell edge. The same trend is recovered in experiments with purified actin bundles confined in microchambers.43,44 In the language of Landau–de Gennes theory, this effect can be straightforwardly reproduced by setting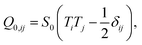
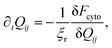
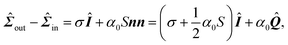
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) ·N,
·N,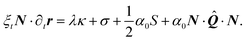
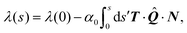
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) =
= ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) (s) varies, in general, along an individual cellular arc. The integration constant λ(0), which represents the cortical tension at one of the adhesion sites, is related to the minimal tension λmin withstood by the cortical actin which we used, in Section II, as material parameter of the problem. In practice, we first calculate λ over an entire arc using a arbitrary guess for λ(0). Then, we apply a uniform shift in such a way that the minimal λ value coincides with λmin.
(s) varies, in general, along an individual cellular arc. The integration constant λ(0), which represents the cortical tension at one of the adhesion sites, is related to the minimal tension λmin withstood by the cortical actin which we used, in Section II, as material parameter of the problem. In practice, we first calculate λ over an entire arc using a arbitrary guess for λ(0). Then, we apply a uniform shift in such a way that the minimal λ value coincides with λmin.
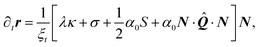
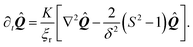
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) and the requirement that minsλ(s) = λmin on each arc.
and the requirement that minsλ(s) = λmin on each arc.
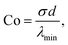
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) crosses over from its bulk configuration to
crosses over from its bulk configuration to ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) 0:
0: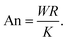

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.80; 0.80; 0.77 (top row), 0.94; 0.92; 0.92 (middle row), and 1.0; 1.0; 1.0 (bottom row). The vertical axis corresponds to the anchoring number An = WR/K and the horizontal axis to the contractility number Co = σd/λmin. The cells shown correspond to values of An = 0, 1, 10 and Co = 0, 0.125, 0.25, where we take both d and R equal to the length of the square side. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R, Narc = 20, and Δx = R/19 are the same for all cells. The number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.†
θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.80; 0.80; 0.77 (top row), 0.94; 0.92; 0.92 (middle row), and 1.0; 1.0; 1.0 (bottom row). The vertical axis corresponds to the anchoring number An = WR/K and the horizontal axis to the contractility number Co = σd/λmin. The cells shown correspond to values of An = 0, 1, 10 and Co = 0, 0.125, 0.25, where we take both d and R equal to the length of the square side. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R, Narc = 20, and Δx = R/19 are the same for all cells. The number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.92; 0.95; 0.96. The simulations shown are performed with An = WR/K = 1 where R is equal to the short side of the rectangle, and Co = σd/λmin equal to 0.125, 0.1875, and 0.25 respectively, where d is equal to the long side of the rectangle. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R and Δx = R/19 are the same for all cells. Narc = 20, 30, 40 from left to right and the number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.†
θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from left to right, by: 0.92; 0.95; 0.96. The simulations shown are performed with An = WR/K = 1 where R is equal to the short side of the rectangle, and Co = σd/λmin equal to 0.125, 0.1875, and 0.25 respectively, where d is equal to the long side of the rectangle. The ratios σ/(σ + α0) = 1/9, λminΔt/(ξtR2) = 2.8 × 10−6, and KΔt/(ξrR2) = 2.8 × 10−6, and the parameters δ = 0.15R and Δx = R/19 are the same for all cells. Narc = 20, 30, 40 from left to right and the number of iterations is 5.5 × 105. For definitions of Δt, Δx, and Narc, see the ESI.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial average of the order parameter is S = 0.54. (C–E) Configurations obtained from a numerical solution of eqn (24) using the adhesion sites of the experimental data (cyan circles) as input, and with various anchoring number (An) values. This is calculated from eqn (26), with R = 23.6 μm the square root of the cell area. The corresponding values of the length scale K/W are 71 μm (C), 14 μm (D), and 2.9 μm (E) respectively. The spatial averages of the order parameter S are given by: 0.85 (C), 0.60 (D), and 0.56 (E) respectively. The values for λmin/σ = 14.7 μm and σ/(σ + α0) = 0.40 are found by an analysis of the elliptical shape of this cell.22 The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for figures (C–E). The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.†
θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial average of the order parameter is S = 0.54. (C–E) Configurations obtained from a numerical solution of eqn (24) using the adhesion sites of the experimental data (cyan circles) as input, and with various anchoring number (An) values. This is calculated from eqn (26), with R = 23.6 μm the square root of the cell area. The corresponding values of the length scale K/W are 71 μm (C), 14 μm (D), and 2.9 μm (E) respectively. The spatial averages of the order parameter S are given by: 0.85 (C), 0.60 (D), and 0.56 (E) respectively. The values for λmin/σ = 14.7 μm and σ/(σ + α0) = 0.40 are found by an analysis of the elliptical shape of this cell.22 The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for figures (C–E). The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.†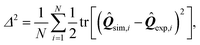
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) sim, from the experimental ones,
sim, from the experimental ones, ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) exp. The index i identifies a pixel in the cell and N is the total number of pixels common to both numerical and experimental configurations. By construction, Δ2 captures both differences in the nematic director n and in the order parameter S [see eqn (15)], and 0 ≤ Δ2 ≤ 1, with 0 representing perfect agreement. Fig. 7 shows a plot of Δ2versus the anchoring number An for the cell shown in Fig. 6. Consistent with the previous qualitative comparison, the agreement is best at large An values, indicating a substantial preference of the stress fibers for parallel anchoring along the cell edge. For the cell in Fig. 6, Δ2 is minimized for An = 8.0 (Δ2 = 0.027), corresponding to a boundary layer K/W = 2.9 μm. The corresponding numerically calculated configuration is shown in Fig. 6E. However, the flattening of Δ2 for large An values implies that the actual value of An becomes unimportant once the anchoring torques (with magnitude W), which determine the tangential alignment of the stress fibers in the cell's periphery, outcompete the bulk elastic torques (with magnitude K). Therefore, we conclude that the cell illustrated in Fig. 6 is best described by An ≳ 5, corresponding to a boundary layer K/W ≲ 5 μm. The corresponding value of Δ2 = 0.027 indicates good quantitative agreement between the experimental (Fig. 6B) and simulated (Fig. 6E) data, despite the difference in order parameter away from the cell edges. This quantitative agreement indicates that, although oversimplified in comparison with the complexity of living cells, our model satisfactorily describes the stationary configuration of both the nematic order parameter and the stress fibers orientation.
exp. The index i identifies a pixel in the cell and N is the total number of pixels common to both numerical and experimental configurations. By construction, Δ2 captures both differences in the nematic director n and in the order parameter S [see eqn (15)], and 0 ≤ Δ2 ≤ 1, with 0 representing perfect agreement. Fig. 7 shows a plot of Δ2versus the anchoring number An for the cell shown in Fig. 6. Consistent with the previous qualitative comparison, the agreement is best at large An values, indicating a substantial preference of the stress fibers for parallel anchoring along the cell edge. For the cell in Fig. 6, Δ2 is minimized for An = 8.0 (Δ2 = 0.027), corresponding to a boundary layer K/W = 2.9 μm. The corresponding numerically calculated configuration is shown in Fig. 6E. However, the flattening of Δ2 for large An values implies that the actual value of An becomes unimportant once the anchoring torques (with magnitude W), which determine the tangential alignment of the stress fibers in the cell's periphery, outcompete the bulk elastic torques (with magnitude K). Therefore, we conclude that the cell illustrated in Fig. 6 is best described by An ≳ 5, corresponding to a boundary layer K/W ≲ 5 μm. The corresponding value of Δ2 = 0.027 indicates good quantitative agreement between the experimental (Fig. 6B) and simulated (Fig. 6E) data, despite the difference in order parameter away from the cell edges. This quantitative agreement indicates that, although oversimplified in comparison with the complexity of living cells, our model satisfactorily describes the stationary configuration of both the nematic order parameter and the stress fibers orientation.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF,sin
θSF,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from top to bottom, by: 0.54; 0.44; 0.45; 0.46; 0.37. (K–O) Simulations with the adhesion sites of the experimental data as input. The spatial averages of the order parameter S are given, from top to bottom, by: 0.52; 0.68; 0.61; 0.59; 0.53. The values for λmin/σ = 12.6; 15.7; 18.0; 10.8; 13.4 μm and σ/(σ + α0) = 0.75; 0.25; 0.46; 0.95; 0.52 are found by an analysis of the elliptical shape of these cells.22 The values of An = 4.4; 4.1; 19; 4.6; 4.7, where R = 17.3; 24.4; 39.9; 24.9; 25.3 μm is defined as the square root of the cell area, are determined by minimizing Δ2, with the minima given by Δ2 = 0.016; 0.058; 0.057; 0.034; 0.037. These An values correspond to K/W = 3.9; 5.9; 2.1; 5.4; 5.4 μm. The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for all cells. The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.†
θSF) of the stress fibers and the background color indicates the local nematic order parameter S. The spatial averages of the order parameter S are given, from top to bottom, by: 0.54; 0.44; 0.45; 0.46; 0.37. (K–O) Simulations with the adhesion sites of the experimental data as input. The spatial averages of the order parameter S are given, from top to bottom, by: 0.52; 0.68; 0.61; 0.59; 0.53. The values for λmin/σ = 12.6; 15.7; 18.0; 10.8; 13.4 μm and σ/(σ + α0) = 0.75; 0.25; 0.46; 0.95; 0.52 are found by an analysis of the elliptical shape of these cells.22 The values of An = 4.4; 4.1; 19; 4.6; 4.7, where R = 17.3; 24.4; 39.9; 24.9; 25.3 μm is defined as the square root of the cell area, are determined by minimizing Δ2, with the minima given by Δ2 = 0.016; 0.058; 0.057; 0.034; 0.037. These An values correspond to K/W = 3.9; 5.9; 2.1; 5.4; 5.4 μm. The ratios λminΔt/ξt = 1.2 × 10−3 μm2 and KΔt/ξr = 1.2 × 10−3 μm2, and the parameters δ = 11 μm, Narc = 20, and Δx = 1.1 μm are the same for all cells. The number of iterations is 2.1 × 106. For definitions of Δt, Δx, and Narc, see the ESI.†