The slow magnetic relaxation regulated by ligand conformation of a lanthanide single-ion magnet [Hex4N][Dy(DBM)4]†
Wen-Bin
Sun
ab,
Bing
Yan
a,
Yi-Quan
Zhang
a,
Bing-Wu
Wang
*a,
Zhe-Ming
Wang
a,
Jun-Hua
Jia
a and
Song
Gao
*a
aBeijing National Laboratory of Molecular Science State Key Laboratory of Rare Earth Materials Chemistry and Applications, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China. E-mail: wangbw@pku.edu.cn; gaosong@pku.edu.cn
bKey Laboratory of Functional Inorganic Material Chemistry, Ministry of Education, Heilongjiang University, Harbin 150080, China
First published on 6th June 2014
Abstract
A mononuclear Dysprosium(III) complex [Hex4N][Dy(DBM)4] (1) was synthesized using dibenzoylmethane (DBM) anion ligand with a tetrahexylammonium (Hex4N+) cation balancing the charge. Complex 1 was structurally and magnetically characterized. The local geometry of Dy(III) ions is close to the ideal D4d symmetry. The temperature and frequency-dependent out-of-phase ac susceptibility peaks were observed in the absence of a static dc field. The relaxation energy barrier Ueff = 27.7 K and τ0 = 1.3 × 10−7 s were obtained by Arrhenius fitting. It is interesting that the quantum tunneling of the magnetization was suppressed when two optimum dc fields (300 and 1500 Oe) were applied. Two distinct thermal relaxation processes were observed with Ueff = 56.6 K, τ0 = 6.6 × 10−10 s for 300 Oe and Ueff = 68.1 K, τ0 = 3.4 × 10−11 s and Ueff = 88.0 K, τ0 = 5.0 × 10−10 s for 1500 Oe. The two thermal relaxation processes were also recognized clearly under zero dc field for the analogue with 20 times magnetic site dilution by Y(III). Nevertheless there is only one crystallographically independent Dy(III) ion in this system. Further inspection of the crystallographic structure reveals that the benzene disorder within the conjugated system of the β-diketonate ligand could change the delocalized electron distribution on the carbonyl coordination oxygen atoms and result in small different ligand fields, which account for the multiple relaxation processes. Ab initio calculations confirm the two energy barriers derived from two disordered structures.
Introduction
Single-molecule magnets (SMMs) are attracting increasing interest due to their potential applications in high density information storage, quantum computing, spintronics devices1–6 and magnetic refrigeration.7 Transition metal clusters once dominated this investigation field since the archetype Mn12-acetate SMMs, in which possessing a large spin ground state (S) in combination with a large uniaxial (or Ising-type) magnetic anisotropy (D) leads to an anisotropic energy barrier (Ueff) to block the magnetization reversal.8–11 In recent years, however, there has been a growing trend that enhancing magnetic anisotropy rather than ever-larger spins may be a more effective strategy to increase Ueff and block the temperature (TB).12,13 Lanthanide-containing SMMs are widely studied due to their strong spin–orbit coupling and significant magnetic anisotropy. To date, a number of lanthanide SMMs, involving d–f and pure f-based polynuclear SMMs,14–18 have been developed and exhibit significant SMM behavior with higher Ueff and TB compared to transition metal SMMs.19–21 Meanwhile, pure mononuclear 4f and 5f-based SMMs as well as mononuclear transition (3d) metals, also named single-ion magnets (SIM), appeared as a kind of promising SMMs in recent years.22–28 The relatively simple geometry structure of SIMs facilitates studying and understanding the relationship between the structure and the magnetic properties. From the point of view of ligand field theory, to date, the local symmetry of lanthanide ions in many of the known examples of SIMs reported so far could be regarded approximately as square antiprismatic (SAP). This has steered our efforts to achieve high magnetic axiality via designing the local environment of lanthanide ions and tuning the anisotropy of SMM systems. However, the relationship between the geometry structure and relaxation barrier is not clear for most of lanthanide based SIMs. Small changes in the coordination environment and ligand field strength may induce big changes in the relaxation properties. Unfortunately, it is very difficult to control tiny changes in ligand field around the metal ion by ligand modification because of geometry distortion and complicated inter-molecular interactions. The conformation change of the ligand may provide a subtle way to deepen our understanding of the magneto-structural correlations of SIMs. In this report, we use a classic organic compound, β-diketonate dibenzoylmethane (DBM), as ligand to construct an approximate square antiprismatic coordination geometry. This kind of complexes with four β-diketonate ligands have been previously investigated for their prominent luminescent properties, but their single-molecule magnetic properties are unexplored.29 Herein, we demonstrate that the tetrakis(β-diketonate) complex [Hex4N][Dy(DBM)4] (1) which behaves as a SIM and represents one of the few examples with well-defined multiple relaxation modes in SIM systems.Results and discussion
The reaction of 4 equiv. of dibenzoylmethane anions deprotonated by NaOH with 1 equiv. of DyCl3 and 1 equiv. of tetrahexylammonium (Hex4N+) cation balancing the system in anhydrous ethanol (EtOH) for 4 h gives rise to the mononuclear complex 1 with formula [Hex4N][Dy(DBM)4]. The collected filtrate was recrystallized from 2-butanone to provide fine needles of 1, which crystallizes in the monoclinic space group P21/n and contains a complete mononuclear complex in the asymmetric unit. The molecular structure of 1 is depicted in Fig. 1, and pertinent data are summarized in Tables 1 and 2, in which there are eight O atoms from four DBM ligands coordinating to the central Dy(III) ion. On the top of [Dy(DBM)4]− unit, there is a tetrahexylammonium [Hex4N]+ cation to balance the system charge resulting in a helicopter-like structure. The center Dy(III) ion coordinated by eight oxygens forms an approximate square antiprismatic (SAP) geometry. The shortest inter-molecular Dy⋯Dy distance is 10.7370 Å. There exists a partial disorder of the carbon atoms from the cation alkyl chain and benzene rings although the crystal data were collected under 123 K (Fig. S1†).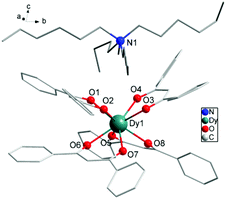 | ||
| Fig. 1 Partially labelled molecular structure of [Hex4N][Dy(DBM)4], 1. Colour code: Dy (teal), O (red), N (blue), C (grey). H atoms and disordered atoms were omitted for clarity. | ||
| 1 | Y-analogue | |
|---|---|---|
| Empirical formula | C84H96DyNO8 | C84H92YNO8 |
| FW (g mol−1) | 1410.12 | 1332.50 |
| Crystal system | Monoclinic | Monoclinic |
| Space group | P21/n | P21/n |
| Temperature (K) | 123.01(10) | 293(2) |
| a (Å) | 16.5109(4) | 16.5033(4) |
| b (Å) | 24.3839(9) | 24.3631(8) |
| c (Å) | 18.6385(5) | 18.6445(4) |
| α (°) | 90 | 90 |
| β (°) | 105.084(3) | 105.028 |
| γ (°) | 90 | 90 |
| V (Å3) | 7245.3(4) | 7240.1(3) |
| ρ cacd (Mg m−3) | 1.286 | 1.222 |
| μ (mm−1) | 1.088 | 1.576 |
| F(000) | 2920 | 2824 |
| Collected reflections | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 668 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 791 791 |
| Independent reflections | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
| R int | 0.0518 | 0.0429 |
| R 1 [I > 2σ(I)] | 0.0701 | 0.1042 |
| wR2 (all data) | 0.1338 | 0.2743 |
| Goodness of fit on F2 | 1.139 | 1.043 |
| Dy1–O4 | 2.350(3) | Dy1–O3 | 2.342(4) |
| Dy1–O6 | 2.368(4) | Dy1–O2 | 2.337(3) |
| Dy1–O8 | 2.315(4) | Dy1–O1 | 2.335(4) |
| Dy1–O5 | 2.328(3) | Dy1–O7 | 2.329(3) |
| O5–Dy1–O4 | 77.30(12) | O3–Dy1–O4 | 71.63(13) |
| O5–Dy1–O3 | 140.72(13) | O3–Dy1–O6 | 143.55(12) |
| O5–Dy1–O1 | 80.11(14) | O1–Dy1–O4 | 79.20(13) |
| O5–Dy1–O2 | 146.06(15) | O1–Dy1–O3 | 115.95(13) |
| O5–Dy1–O6 | 73.27(12) | O1–Dy1–O2 | 71.43(13) |
| O5–Dy1–O7 | 115.54(12) | O1–Dy1–O6 | 75.01(14) |
| O8–Dy1–O5 | 71.78(14) | O2–Dy1–O4 | 113.90(11) |
| O8–Dy1–O4 | 77.35(12) | O2–Dy1–O3 | 70.78(13) |
| O8–Dy1–O3 | 78.38(13) | O2–Dy1–O6 | 81.65(12) |
| O8–Dy1–O1 | 146.60(12) | O7–Dy1–O4 | 143.51(15) |
| O8–Dy1–O2 | 140.55(14) | O7–Dy1–O3 | 79.55(13) |
| O8–Dy1–O6 | 112.33(12) | O7–Dy1–O1 | 134.88(12) |
| O8–Dy1–O7 | 75.27(12) | O7–Dy1–O2 | 75.45(12) |
| O4–Dy1–O6 | 143.54(14) | O7–Dy1–O6 | 70.57(14) |
As shown in Fig. 1 and Fig. S1,† four O atoms from two DBM ligands compose an upper and a lower square of SAP defined by the mean planes through the coordinating oxygen atoms (O1, O2, O3, O4 and O5, O6, O7, O8) and each moiety is twisted with respect to the other with the smallest angle of 44.42°. This angle is very close to that expected for an ideal D4d symmetry (ϕ = 45°). The average distance between the four neighboring oxygen atoms din is 2.7805 Å and the interplanar distance (dpp) is 2.5830 Å between the upper and lower planes. The two planes are in a nearly parallel arrangement with a slight tilt angle of 1.09°. The ratio din/dpp is indicative of an axial distortion (elongation or compression) of the square antiprism around the Dy(III) ions (Fig. S1†). As for the first two 4f-based SIMs,22,23 both of which possess a pseudo-D4d symmetry, the different distortion of the antiprismatic site is axially compressing for [Er(W5O18)2]9− and axially elongating for the [TbPc2]−, which leads to a different splitting of the ±MJ levels of 4f electrons. For the SIM species, the ligand field may play a crucial role in determining the anisotropy of the paramagnetic ion center. The analysis using the method of Continuous Shape Measures (CShMs)30,31 gives a deviation parameter P of 0.287 for D4d symmetry and the [TbPc2]− (ref. 23b) system gives a P of 1.307. In this case, the small P value is consistent with a din/dpp value of 1.076 close to 1 which represents an ideal square antiprismatic geometry. It indicates that the coordination geometry surrounding the Dy(III) center is close to the ideal D4d symmetry. This geometrical deviation from an ideal D4d symmetry in the crystal field, although small, seems to be sufficient to induce a complete change in the magnetic relaxation properties of these 4f-based SIMs.
Magnetic measurements were performed on polycrystalline samples of 1 using Quantum-Design MPMS and PPMS magnetometers. The temperature dependence of the magnetic susceptibility χMT for 1 is shown in Fig. 2. The value of χMT is 14.18 cm3 K mol−1 at 300 K, which is in good agreement with the theoretical value for one isolated Dy(III) ion (S = 5/2, L = 5, 6H15/2, g = 4/3). On lowering the temperature, the χMT product decreases gradually and more rapidly below 50 K, which is likely due to crystal-field effects (i.e. thermal depopulation of the Ln(III) Stark sublevels) and/or the possible antiferromagnetic dipole–dipole interaction between the molecules. On the other hand, a plateau of the χMT value around 10.8 cm3 K mol−1 at low temperature is observed, suggesting negligible magnetic interactions.
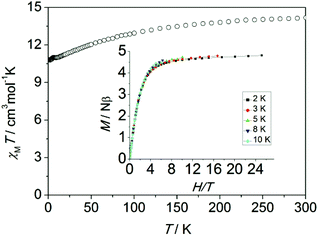 | ||
| Fig. 2 Temperature dependence of χMT measured at 1 kOe for 1 (inset: experimental M vs. H/T plots at different temperatures 2, 3, 5, 8 and 10 K). | ||
The magnetization of 1 under zero to 50 kOe dc field at 2, 3 5, 8 and 10 K is shown in Fig. S2.† The corresponding maximum value of 4.8Nβ and the lack of saturation of magnetization at 50 kOe can be attributed to crystal-field effects and the low lying excited states. The non-superposition of the M vs. H/T plots at higher field (inset, Fig. 2) indicates the presence of significant magnetic anisotropy. In addition, it is worth mentioning that the M vs. H data do not exhibit a hysteresis at 1.8 K with the sweep rate used in a traditional SQUID magnetometer (100–300 Oe min−1), while it could be observed when a 50 Oe s−1 sweep rate was used in a Quantum Design PPMS magnetometer on polycrystalline sample, vide infra (Fig. S3†).
To probe the magnetic dynamic behavior of 1, the alternating-current (ac) susceptibilities at various frequencies and temperatures under the absence of dc field were measured and depicted in Fig. 3 and Fig. S4†. Both in-phase (χ′) and out-of-phase (χ′′) susceptibilities show a frequency dependence behavior, which clearly indicates the slow relaxation of magnetization of 1. The peaks can only be observed at frequencies higher than 3160 Hz, and a broad slope between 5.5 and 10 K can also be found, as well as a tail of the peak below 4 K. The former slope is likely indicative of the existence of another relaxation process whereas the latter tails could be attributed to the quantum tunneling of magnetization (QTM) at a zero dc field. The QTM process was also found in some other lanthanide-containing SMMs.
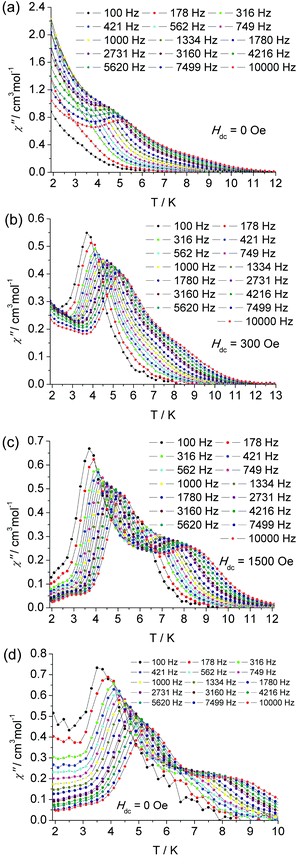 | ||
| Fig. 3 The temperature dependence of ac susceptibility at indicated frequencies for complex 1 under zero (a), 300 Oe (b), 1500 Oe (c) dc field and for diluted sample under zero dc field (d). | ||
In the frequency dependent susceptibility measurements, temperature independent peaks in the low temperature range were observed (Fig. S6†), which further proved the occurrence of a resonant QTM process. Usually, an optimum dc field could be used to suppress the QTM process, since it could lift the degeneracy of the ±MJ energy levels and reduce the probability of the zero-field QTM between the two states. The optimum field was selected by determining which field was able to slow the frequency dependent χ′′ maxima to the slowest relaxation rate. For the low temperature relaxation process centered at 5 K, the optimum field was found to be 300 Oe (Fig. S11 and 13†). Therefore, the ac susceptibility was measured under this optimum field, as shown in Fig. 3 and Fig. S8.† Significant χ′′ peaks were detected even at low frequency as 100 Hz. The thermally activated relaxation process was characterized by the frequency dependent χ′′ peaks at the temperature range 3.5 (100 Hz) to 5.5 K (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz). The QTM process overlaps this relaxation in the absence of an external dc field. As mentioned above, there is a broad slope in the temperature range 5.5 to 9.5 K, which is most likely indicative of another relaxation process. To confirm another process possibly being prominent in high temperature regimes, a similar selection of the optimum external dc field was performed at 6.5 K. An optimum 1500 Oe external dc field was extracted (Fig. S12 and 13†). Thus the ac susceptibility was measured under 1500 Oe dc field, as shown in Fig. 3. As expected, the second relaxation process is unequivocally detected from 5.5 K (100 Hz) to 8 K (10
000 Hz). The QTM process overlaps this relaxation in the absence of an external dc field. As mentioned above, there is a broad slope in the temperature range 5.5 to 9.5 K, which is most likely indicative of another relaxation process. To confirm another process possibly being prominent in high temperature regimes, a similar selection of the optimum external dc field was performed at 6.5 K. An optimum 1500 Oe external dc field was extracted (Fig. S12 and 13†). Thus the ac susceptibility was measured under 1500 Oe dc field, as shown in Fig. 3. As expected, the second relaxation process is unequivocally detected from 5.5 K (100 Hz) to 8 K (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz). The two thermally activated regimes are also confirmed by the measurement of frequency dependent χ′′ (Fig. S9†), in which two distinct frequency dependent regions with ac susceptibility peaks are detected relating to the low temperature relaxation (LR) process in 4 K–5.25 K and high temperature relaxation (HR) 6.5 K–9 K.
000 Hz). The two thermally activated regimes are also confirmed by the measurement of frequency dependent χ′′ (Fig. S9†), in which two distinct frequency dependent regions with ac susceptibility peaks are detected relating to the low temperature relaxation (LR) process in 4 K–5.25 K and high temperature relaxation (HR) 6.5 K–9 K.
Multiple relaxation processes have been observed in several reported f-based SMMs due to the existence of different anisotropic centers or isomers and conformers in the crystal. Nevertheless, the observation of a multiple relaxation process in a Dy-based SIM with only one crystallographically independent center has been rarely reported.32–37 The synthesis of SIMs with well-defined multiple relaxation and control of the multiple relaxation pathways is also challenging. However, this type of studies will improve our understanding of such unusual relaxation mechanisms and further provide new clues to enhance the properties of SMMs. Recently, we have reported an organometallic SIM (Cp*ErCOT), displaying two relaxation processes due to the different conformers caused by the disorder of COT group in molecule.25,38 There are four other SIM examples showing multiple relaxations with one single metal center, while few of them have been clearly shown to exhibit well-resolved pathways for slow magnetic relaxation. The source of these multiple pathways is not very clear either. In order to investigate the role of the intermolecular interaction for this unusual SMM behavior, we repeated the magnetic investigation on a magnetically diluted sample with an isostructural Y(III) analogue with a molecular ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 (Fig. S14–S19†). The structure of Y(III) analogue has been also confirmed crystallographically (Table S1†).
20 (Fig. S14–S19†). The structure of Y(III) analogue has been also confirmed crystallographically (Table S1†).
The static magnetic properties are nearly unaffected by magnetic dilution (Fig. S14†). But the characteristic χ′′ peaks undergo a significant low-frequency shift. The first peak is observed at 32 Hz (Fig. S15 and 16†), and there is a shoulder plateau at temperatures higher than 5 K and frequencies larger than 100 Hz. In the higher frequency range from 100 Hz to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz, another relaxation process can be recognized clearly in the absence of an external field (Fig. 3 bottom and Fig. S17†). Therefore, these two relaxation processes are confirmed to be attributed to the intrinsic properties of the centered Dy(III) ions, which is not induced by an intermolecular interaction. By diluting the samples, the QTM is efficiently suppressed as was the case under an applied external dc field.
000 Hz, another relaxation process can be recognized clearly in the absence of an external field (Fig. 3 bottom and Fig. S17†). Therefore, these two relaxation processes are confirmed to be attributed to the intrinsic properties of the centered Dy(III) ions, which is not induced by an intermolecular interaction. By diluting the samples, the QTM is efficiently suppressed as was the case under an applied external dc field.
The hysteresis loop, as an important characteristic of magnetic bistability of magnets, was observed on the undiluted polycrystalline sample with a sweep rate 50 Oe s−1. The waist-constricted hysteresis loop is closed at zero field for the undiluted sample, which is associated with the QTM process in the absence of external field. In contrast, the diluted sample displays a small opening loop at zero field as the dipole–dipole interaction is reduced and the QTM process compressed (Fig. S3†).
For a thermal assisted Orbach relaxation, magnetic data fitting using Arrhenius’ law (τ = τ0 exp(Ueff/kT), Fig. 4) could provide an effective relaxation energy barrier Ueff and a pre-exponential factor τ0. The fitting results are collected in Table S1.† As for the low temperature relaxation process, the increase of the anisotropic barrier from 27.7 K (τ0 = 1.3 × 10−7 s) at zero dc field to 56.6 (τ0 = 6.6 × 10−10 s) and 68.1 K (τ0 = 3.4 × 10−11 s) after applying a 300 and 1500 Oe dc field was observed as usually seen in 4f-based SMMs. The relatively lower energy barrier and longer τ0 are indicative of the QTM process dominating and the pre-exponential factors are consistent with the expected values around 10−6–10−11 s for a SMM system. The estimated energy barrier for a high temperature relaxation process is 88.0 K with τ0 = 5.0 × 10−10 s, which was not obviously affected even when a 5000 Oe dc field was applied (Fig. S5†). The diluted system displays two relaxation processes with barriers of 63.8 K (τ0 = 1.6 × 10−10) for LR and 79.8 K (τ0 = 1.5 × 10−9) for HR. The LR and HR energy barriers and pre-exponential factors are consistent with values under 1500 Oe for the external dc field. The presence of two relaxation processes was further examined using a graphical representation, χ′′ versus χ′ (Cole–Cole plot), which showed the evolution from a low temperature relaxation to a high temperature process under a 1500 Oe dc field, as well as in the diluted system (Fig. S10†).
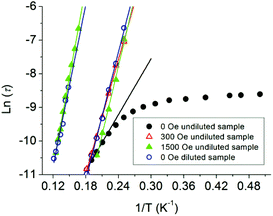 | ||
| Fig. 4 Plots of ln(τ) vs. T−1 at Hdc = 0, 300 and 1500 Oe for the undiluted and diluted sample (DS). The solid lines represent Arrhenius fits of the frequency-dependent data. | ||
These facts led us to the conclusion that an enlarged intermolecular distance or an applied external dc field can suppress the QTM processes and make the relaxation process (mainly a thermally activated one) distinguished. The various diluted concentrations or ac frequencies could make the multiple relaxation pathways apparent when lacking an external dc field. The different magnitude external dc field can also separate the multiple relaxation processes. These phenomena have been sparsely observed except for few actinide (U)39 and lanthanide-based SIM systems with a single geometrical metal center. Nevertheless few of them were successful in separating the multiple processes. The source of these multiple relaxation processes is yet to be understood.34–36
In our case, the alkyl chain of the counter Hex4N+ cation and the benzene ring are partially disordered (see Fig. S1†). Particularly the disordered benzene rings in the conjugated system of the β-diketonate ligand DBM, although the benzene ring is remote from the Dy(III) center, could disturb the delocalized electron distribution on the carbonyl oxygen atoms, which are in the first coordination sphere of the Dy(III) ion and construct the main negative charge density of the ligand field. In order to examine if the disorder could change the magnetic relaxation, ab initio calculations of the relaxation barrier were performed on two possible geometry configurations of the molecule. The two disordered structures for 1 are labeled as 1a and 1b (Fig. S1†), for which the magnetic easy axial and corresponding g tensors and energy difference ΔE between ground state and first excited state, which is related to the thermal relaxation energy barriers in lanthanide-based SMMs, are listed in Tables S2–S4.† The calculation results reveal that both disordered structures possess significant uniaxial magnetic anisotropy with a relatively large gz value of 19.5, while the calculated energy difference ΔE is distinct with ΔE1a = 80 K and ΔE1b = 102 K, however the relaxation process with a relatively lower energy barrier can be cautiously assigned to the 1a conformer because of the larger transverse gX,Y values. Although the calculated energy barriers are slightly higher than the ones from experiment, the difference of 22 K between them is well consistent with the difference in Ueff of 20 K and 16 K for the 1500 Oe and dilution conditions in the magnetic measurements. Therefore we proposed that the two relaxations processes were attributed to the different disordered coordination environments in 1. The very recent report about a Dy-based SIM with disordered ligands supports our inference.37 The role of the second coordination sphere on the magnetic anisotropy was predicted for Co(II) ions. It was also found in a DOTA-Dy SIM system.40 In the latter case, the apical coordination water molecule could influence the direction of the magnetic axes. The rotation of the water molecule could then affect the relative population of the Dy 5d orbitals through a p interaction with the oxygen atom. These interesting phenomena of two relaxation processes in one crystallographically independent Dy(III) site are recently also considered to be related to the condensed phase, i.e. they may not be related to the chemical nature of the relaxing centers.41 Whereas our investigation demonstrates how sensitive the magnetic relaxation of the Dy(III) center is to subtle changes in the local coordination environment involving minor distortions possibly caused by the ligand disorder albeit beyond the first coordination sphere.
Experimental section
All chemicals and solvents were obtained from commercial sources and were used as received, without further purification.Synthesis of [Hex4N][Dy(DBM)4] (1)
This was prepared according to the literature42 procedure with slight modifications. To a solution of dibenzoylmethane (4 mmol, 0.900 g), DyCl3·6H2O (1 mmol, 0.389 g) and Hex4NCl (1 mmol, 0.390 g) in 35 mL of hot ethanol were added 2.0 ml of 2.0 M sodium hydroxide solution under stirring. A dense off-white microcrystalline precipitate separated immediately. After cooling the mixture, the solid was collected and recrystallized from 2-butanone to give 1.098 g of 1 with 77.9% yield. Elemental analysis calcd for C84H96DyNO8: C, 71.54; H, 6.86; N, 0.99%. Found: C, 71.45; H, 6.84; N, 1.08. IR (KBr/cm−1): 3415, 1616, 1573, 1522, 1458, 1387, 1309, 1259, 1192, 1136, 671.The diluted sample was synthesized by the same procedure as that employed for complex 1, except that DyCl3·6H2O (0.05 mmol, 0.0193 g) and YCl3·6H2O (1 mmol, 0.3041 g) were employed as rare-earth salts and the final filtrate was collected and recrystallized from 2-butanone to give 1.1651 g of 1 with 82.27% yield. The ICP and EA analyses reveal the ratio of Dy(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y(III) is 17.2
Y(III) is 17.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Elemental analysis calcd for C84H96Y0.95Dy0.05NO8: C, 75.28; H, 7.22; N, 1.05%. Found: C, 75.45; H, 7.31; N, 1.10.
1. Elemental analysis calcd for C84H96Y0.95Dy0.05NO8: C, 75.28; H, 7.22; N, 1.05%. Found: C, 75.45; H, 7.31; N, 1.10.
Physical measurements
Elemental (C, H and N) analyses (EA) were performed on a Perkin-Elmer 2400 analyzer. Fourier transform IR spectra were measured on a Perkin-Elmer Spectrum One spectrometer with samples prepared as KBr pellets. For the magnetic properties measurement, samples were fixed by eicosane to avoid moving during measurement. The elements Dy and Y were quantitatively analysed by Inductively Coupled Plasma-Atomic Emission Spectrometer (ICP-AES) using a Leeman PROFILE SPEC spectrometer. Direct current susceptibility and alternative current susceptibility measurements were carried out under an oscillating ac field of 3 Oe with frequencies in the range from 1 to 997 Hz and 10 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz and were performed on a Quantum Design MPMS XL-5 SQUID and Quantum Design PPMS magnetometer on polycrystalline samples, respectively. Data were corrected for the diamagnetism of the samples using Pascal constants and the sample holder by measurement. The amount of diluted sample used for magnetic measurements had to be doubled with respect to the other measurements in order to obtain a reliable signal from the SQUID magnetometer.
000 Hz and were performed on a Quantum Design MPMS XL-5 SQUID and Quantum Design PPMS magnetometer on polycrystalline samples, respectively. Data were corrected for the diamagnetism of the samples using Pascal constants and the sample holder by measurement. The amount of diluted sample used for magnetic measurements had to be doubled with respect to the other measurements in order to obtain a reliable signal from the SQUID magnetometer.
X-ray crystallography
Data were collected on a Nonius Kappa CCD diffractometer with Mo Kα radiation (λ = 0.71073 Å). Empirical absorption corrections were applied using the Sortav program. All structures were solved by direct methods and refined by full-matrix least squares on F2 using the SHELX program.43 H atoms can be located from the difference Fourier synthesis but added details of the crystal parameters, data collection and refinements for 1 are summarized in Tables 1 and 2. CCDC 902442 and 927860 contain the supplementary crystallographic data for complex 1 and the Y(III) analogue.Computational details
The g tensor and fine electronic structure were calculated using CASPT2 method based on preceding CASSCF calculation on the model structure 1a and 1b with MOLCAS 7.8 program package.44 The spin–orbit coupling was included by state interactions under the mean-field spin–orbit Hamiltonian with RASSI program. In all calculations, the basis sets are atomic natural orbitals from the MOLCAS ANO-RCC library. The following contractions were used: [8s7p5d4f2g1h] for Dy, [4s3p2d] for O and C, and [2s] for H.Conclusions
We have presented the structural and magnetic properties for a mononuclear Dy(III) compound, [Hex4N][Dy(DBM)4] (1), which behaves as a new type of SIM. It displays an unusual two relaxation processes deriving from a visually unique crystallographically independent center. These two processes are well separated by dilution or applying a gradient enhanced field. In this case, the behaviour of multiple relaxations from a single paramagnetic center is an interesting phenomenon, which was tentatively attributed to the different ligand field configuration caused by disorder in the conjugated system of the β-diketonate ligand which generates different magnetic anisotropy. This system provides a synthetic strategy for isolation of lanthanide-based SIMs exclusively encapsuled by simple β-diketonate analogues. This also presents an opportunity to shed light on the fine-tuning of the magnetic properties of these SIMs by modifying the encapsulating and balancing ligands, and further to explore the influence of local symmetry and ligand field strength on this relatively simple SIM system.Acknowledgements
This work was supported by the NSFC (21290171, 21321001 and 21102039), BJSFC (2122023) and the National Basic Research Program of China (2010CB934601, 2013CB933401) and Educational Commission of Heilongjiang Province (1254G045, 12541639).Notes and references
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed.
- J. van Slageren, Top. Curr. Chem., 2012, 321, 199 CrossRef CAS.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357 CrossRef CAS PubMed.
- F. Torres, J. M. Herńandez, X. Bohigas and J. Tejada, J. Appl. Phys. Lett., 2000, 77, 3248 CrossRef CAS PubMed.
- A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873 CrossRef CAS.
- G. E. Kostakis, A. M. Ako and A. K. Powell, Chem. Soc. Rev., 2010, 39, 2238 RSC.
- M. Murugesu, M. Habrych, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2004, 126, 4766 CrossRef CAS PubMed.
- A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clérac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 4926 CrossRef CAS PubMed.
- E. Ruiz, J. Cirera, K. Cano, S. Alvarez, C. Loosec and K. Kortus, Chem. Commun., 2008, 52 RSC.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C. Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125 RSC.
- S. Osa, T. Kido, N. Matsumoto, N. Re, A. Pochaba and J. Mrozinski, J. Am. Chem. Soc., 2004, 126, 420 CrossRef CAS PubMed.
- J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729 CrossRef CAS PubMed.
- D. P. Mills, F. Moro, J. McMaster, J. van Slageren, W. Lewis, A. J. Blake and S. T. Liddle, Nat. Chem., 2011, 3, 454 CAS.
- P.-H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, Angew. Chem., Int. Ed., 2009, 48, 9489 CrossRef CAS PubMed.
- B. W. Wang, S. D. Jiang, X. T. Wang and S. Gao, Sci. China, Ser. B: Chem., 2009, 52, 1739–1758 CrossRef CAS.
- R. J. Blagg, C. A. Muryn, E. J. L. McInnes, F. Tuna and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2011, 50, 6530 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS PubMed.
- (a) N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed; (b) F. Branzoli, P. Carretta, M. Filibian, G. Zoppellaro, M. J. Graf, J. R. Galan-Mascaros, O. Fuhr, S. Brink and M. Ruben, J. Am. Chem. Soc., 2009, 131, 4387 CrossRef CAS PubMed.
- (a) M. A. AlDamen, J. Clemente Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874 CrossRef CAS PubMed; (b) M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Arinño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467 CrossRef CAS PubMed.
- S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448 CrossRef CAS PubMed.
- S. D. Jiang, B. W. Wang, H. L. Sun, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730 CrossRef CAS PubMed.
- S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, A. Camón, M. Evangelisti, F. Luis, M. J. Martínez-Pérez and J. Sesé, J. Am. Chem. Soc., 2012, 134, 14982 CrossRef CAS PubMed.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, J. Am. Chem. Soc., 2009, 131, 12558 CrossRef CAS PubMed.
- L. R. Melby, N. J. Rose, E. Abramson and J. C. Caris, J. Am. Chem. Soc., 1964, 86, 5117 CrossRef CAS.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693 CrossRef CAS PubMed.
- J. Cirera, E. Ruiz and S. Alvarez, Organometallics, 2005, 24, 1556 CrossRef CAS.
- P. E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Chem. Commun., 2011, 47, 3751 RSC.
- A. Watanabe, A. Yamashita, M. Nakano, T. Yamamura and T. Kajiwara, Chem. – Eur. J., 2011, 17, 7428 CrossRef CAS PubMed.
- M. Jeletic, P. H. Lin, J. J. Le Roy, I. Korobkov, S. I. Gorelsky and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 19286 CrossRef CAS PubMed.
- J. Ruiz, A. J. Mota, A. Rodríguez-Diéguez, S. Titos, J. M. Herrera, E. Ruiz, E. Cremades, J. P. Costes and E. Colacio, Chem. Commun., 2012, 48, 7916 RSC.
- F. R. Fortea-Pérez, J. Vallejo, M. Julve, F. Lloret, G. De Munno, D. Armentano and E. Pardo, Inorg. Chem., 2013, 52, 4777 CrossRef PubMed.
- P. Martín-Ramos, M. R. Silva, J. T. Coutinho, L. C. J. Pereira, P. Chamorro-Posada and J. Martín-Gil, Eur. J. Inorg. Chem., 2014, 511 CrossRef.
- S. D. Jiang, S. S. Liu, L. N. Zhou, B. W. Wang, Z. M. Wang and S. Gao, Inorg. Chem., 2012, 51, 3079 CrossRef CAS PubMed.
- J. D. Rinehart, K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7572 CrossRef CAS PubMed.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606 CrossRef CAS PubMed.
- G. Cosquer, F. Pointillart, S. Golhen, O. Cador and L. Ouahab, Chem. – Eur. J., 2013, 19, 7895 CrossRef CAS PubMed.
- H. Bauer, J. Blanc and D. L. Ross, J. Am. Chem. Soc., 1964, 86, 5125 CrossRef CAS.
- (a) G. M. Sheldrick, SHELXS-97, Program for X-ray Crystal Structure Solution, University of Göttingen, Germany, 1997 Search PubMed; (b) G. M. Sheldrick, SHELXL-97, Program for X-ray Crystal Structure Refinement, University of Göttingen, Germany, 1997 Search PubMed.
- G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, MOLCAS: a Program Package for Computational Chemistry, Comput. Mater. Sci., 2003, 28, 222 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures and magnetic data and ab initio calculations results. CCDC 902442 and 927860. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4qi00057a |
| This journal is © the Partner Organisations 2014 |
