Micromechanics of colloidal aggregates at the oil–water interface

Abstract

The micromechanics of two-dimensional (2D) colloidal aggregates at the oil–water interface are measured using optical tweezers. Aggregates form from stable 2D suspensions after introducing either 0.25 M NaCl/0.1 mM SDS in the aqueous sub-phase or 25 μM sorbitan monooleate (SPAN 80) in the oil super-phase. Aggregates formed with NaCl/SDS have strong bond bending rigidities due to tangential forces between particles, leading to an average aggregate rigidity κ_a = 4.9 ± 3.1 mN m⁻¹. Rigid aggregates are consistent with previously reported open microstructures and irreversible, diffusion-limited cluster aggregation kinetics. In contrast, aggregates formed by SPAN 80 exhibit weak bond rigidities (κ_a = 0.28 ± 0.31 mN m⁻¹), enabling particle rearrangements that lead to a denser microstructure. The micromechanical properties of aggregates that constitute the macrocolloidal structure of 2D suspensions provide a critical link between their colloidal interactions and interfacial rheology.

---

1 Introduction

Recently, studies of the quiescent and flow-induced structures of particulate gels have been extended to two-dimensional (2D) suspensions, in which the particles are confined to an air–water or oil–water interface.^1,2 2D suspensions are not only important models for studying the relationship between suspension microstructure and rheology,³ but are significant in their own right in numerous technological applications.⁴

The far-field electrostatic repulsion between particles at the oil–water interface is significant for maintaining colloidal stability at an interface.^5,6 Like bulk suspensions, the repulsive interactions are sensitive to the addition of salts or surfactants.^2,7,8 By reducing the repulsion, particles are driven by strong capillary attraction⁸ to form aggregates and percolated networks, or 2D gels.² The relative magnitudes of the repulsive and attractive interactions can be tailored sufficiently to affect the aggregation kinetics, such that the gels formed are described by either diffusion- or reaction-limited fractal dimensions.² However, little is known about how these particle interactions affect the micromechanics underlying the deformation of quiescent or flow-induced 2D gel microstructures. In contrast, the yield stress and elastic modulus of bulk particulate gels can be effectively modeled and controlled once the contact or near-contact interactions are known.^9–12 It is the latter application that motivates the studies described in this paper.

Here, we use optical tweezers to measure the rigidities and rearrangements under compressive and tensile forces of colloidal aggregates formed at an oil–water interface. We find that the micromechanics, specifically, the bond rigidity in aggregates, depends strongly on the type of additive used to induce aggregation. Overall, this work provides an important link between the molecular-scale interactions governed by the surface chemistry of the particles to the rheology of 2D suspensions. Before presenting and discussing our results, we first provide the details of the experiments.

2 Materials and methods

2.1 Materials and sample preparation

Suspensions are studied at an oil–water interface formed by water and n-decane.^2,7,8,13 Ultra-purified water (electrical resistivity >18.2 MΩ·cm) is used as the sub-phase. The super-phase is n-decane (Acros Organics, 99+%), which is rinsed through a column of aluminum oxide (Acros Chemical, acidic activated, particle size 100–500 μm) prior to use in order to remove polar contaminants. The experiments are performed using surfactant-free, charge stabilized polystyrene particles with an average diameter of 2a = 3.1 ± 0.2 μm and a charge density of σ = −7.4 μC cm⁻² (Interfacial Dynamics). The charge is the result of the presence of sulfate groups at the particle surface. The particles are prepared by repeated centrifugation and redispersion steps to eliminate impurities from the original particle solution.¹³Isopropyl alcohol (Sigma Aldrich) is used as a spreading solvent to introduce particles into the interface. To control the particle interactions, we add a monovalent salt (NaCl) and an anionic surfactant (sodium dodecyl sulfate, SDS, Sigma Aldrich) to the aqueous sub-phase.^2,7,8 Additionally, we tested the effects of adding a nonionic surfactant (sorbitan monooleate, SPAN 80, Spectrum Chemicals) to the oil super-phase.⁸

Due to the short working distance of the microscope objective (W.D. = 200 μm), a fluid cell capable of maintaining a thin water layer is required. A detailed schematic of the cell geometry is provided in ref. 13. Briefly, we construct the cell using a glass outer cylinder and an inner cylinder made of Teflon and aluminum. The inner ring provides a pinning junction for the oil–water interface to minimize curvature. The outer ring is attached a 40 mm circular glass coverslip (No. 1.5 Fisher Scientific) using a UV curing epoxy (Norland Products, NOA 81). A gap between the inner ring and the coverslip enables us to manipulate the water layer thickness after the particles have been added to the interface by adjusting the hydrostatic pressure between the inner and outer rings. In order to prevent the evaporation of water and convection, the entire cell is sealed using a glass top and vacuum grease. All glassware is cleaned using a plasma cleaner (Harrick Plasma, PDC 32-G), immediately before constructing the cell to achieve good wetting conditions for the water. The sample cell is illuminated by a halogen lamp, allowing us to capture the images using a charge-coupled device (ccd) camera (KPM1-AN, Hitachi) at a rate of approximately 30 frames per second. Experiments are recorded onto digital video tape (PDV-184ME, Sony DVCAM) and individual digitized frames are later transferred to an image processing workstation and analyzed using established particle tracking methods.¹⁴

2.2 Aggregate micromechanics

Measurements of colloid aggregate micromechanics are performed with time-shared optical traps.¹⁵ Aggregates are formed by the introduction of NaCl/SDS in the aqueous sub-phase or SPAN 80 in the oil super-phase. Using the laser tweezers, we hold two particles in the aggregate. One particle is held with a stationary trap, while the other particle is held by a translating trap. The latter trap moves continuously at 10–100 nm s⁻¹ either towards or away from the stationary trap; the speed is slow enough to prevent hydrodynamic disturbances in the suspension. The force is measured by the displacement of the particle in the stationary trap from its equilibrium position after calibrating the trap stiffness, κ_t.

The laser tweezer apparatus used in this work is constructed around an inverted microscope (Zeiss Axiovert 200), to enable simultaneous trapping and imaging using video microscopy. A 4 W Nd:YAG laser (vacuum wavelength λ = 1064 nm, Coherent Compass 1064-400M) operating in a continuous wave (cw) mode is used to generate the traps. A detailed description of the experimental is provided by Pantina et al.¹⁵

Drag calibration at the interface is used to obtain the optical trap stiffness and maximum trapping force.¹⁶ Stokes drag force, F_S = 6πaη_effU is measured at several velocities U is related to the displacement of a particle from the equilibrium position Δx, where η_eff = [η_oil(1 − cos θ) + η_water(1 + cos θ)]/2 is the effective viscosity at the interface, which depends on the viscosities of the sub- and super-phases and the three-phase contact angle.^7,16 The trap rigidity κ_t is then given by the slope of F_SversusΔx, and subsequent forces are quantified by measuring the displacement of a trapped particle from its equilibrium position. We also verify the trapping forces using a geometrical optics approximation (GOA) calculation.¹⁶

3 Results

3.1 Micromechanics of particle aggregates

3.1.1 NaCl and SDS in the aqueous sub-phase. We first investigate the micromechanics of aggregates at the oil–water interface when the aqueous sub-phase contains 0.25 M NaCl and 0.1 mM SDS. Fig. 1 shows a typical aggregate response while applying a tensile force. The initial structure (Fig. 1a) of the aggregate stretches out in response to the tension. At the same time, the force increases steeply, as shown by the steps from a→b in Fig. 1I. During this stretching, the tensile force is stored as elastic energy. If the external stress is removed prior to a permanent structural deformation, a reversible recovery in microstructure occurs. Yielding is characterized by overcoming the resistance to a tangential stress (i.e., sliding or rolling motion)^12,17–19 as well as the tensile stress (i.e., bond breakage).¹⁵

Fig. 1 Micromechanics of aggregate (SS1) at an oil–water interface containing 0.25 M NaCl and 0.1 mM SDS in the aqueous sub-phase. (I) The force profile during the application of a tensile force with two optical traps and (II) the corresponding bond angle change. In the bottom are image frames corresponding to discontinuities in the force profile. The movement vectors for the steps b→c and d→e are shown to the right.

After a certain point (b→c in Fig. 1I) the tension is great enough to overcome a critical value, and the particles rearrange, releasing the stored energy. This is clearly shown by the discontinuity of the force profile (Fig. 1I) as well as the sudden angle changes (Fig. 1II) between particles 1-2-3 and 2-3-4. The displacement vectors (b→c, right-bottom) indicate that sliding or rolling occurs between particles 1–2 and 3–4. At this time, the restitutive force of the optical spring pushes the stationary particle back. The stored elastic force in the aggregate, however, is not completely released due to the following stick motion at the new contact between particles. This behavior (i.e., slip-stick, roll-stick) is determined by the applied tangential force,^{11,12,19–21} and the resistance to the sliding or rolling events.^17,18,22,23

After building up the elastic energy again (c→d in Fig. 1I), a sudden bond stretching between particles 1–2 induces another discontinuous jump in the force (d→e). The particles appear to move into a secondary energy minimum at a separation beyond contact. The separation between particles 1–2, r₁₂/2a changes from ∼1.0 to ∼1.2 (see image e in Fig. 1II). Following this, the bond between particles 2–3 (e→f) ruptures.

A possible explanation for the last two steps is that the depth of the secondary minimum between bonds 1–2 is larger than both the contact energy and the secondary energy minimum between 2–3, regardless of the different contribution of tangential stress between bonds 1–2 and 2–3. This suggests that the interparticle interaction is heterogeneous as well as anisotropic on short length scales.^7,8,13,24 Interaction heterogeneity has been observed for the pairwise potentials previously, and can be attributed to variations in the both the electrostatic repulsion and the quadrupole capillary attraction.⁸ This clearly demonstrates an important difference between 2D and bulk suspensions; due to the range of the repulsive and attractive interactions in 2D suspensions, strong secondary minima can occur over large distances.

3.1.2 SPAN 80 in the oil super-phase. The addition of SPAN 80 to the decane super-phase also induces aggregation, but results in significantly different micromechanical properties, including weaker bonds and the ability of particles to slide and rotate around each other with relative ease. In Fig. 2, we show an aggregate composed of 8 particles as a tensile force is applied. The tensile force builds (Fig. 2I) increasing to a rupture force, at which the bond between particles 3 and 4 breaks. The corresponding rupture force is approximately ∼1.5 pN, which is an order of magnitude smaller than the rupture force measured for aggregate SS1 in SDS/NaCl (see Fig. 1). Bond rearrangements, such as breakage or formation, are not observed until the rupture occurs, but it is obvious that there is rolling or sliding during the elongation, since the angle between particles 2-3-4 and 3-4-5 decreases and increases, respectively, as shown in Fig. 2II.

Fig. 2 (I) Force profile and (II) bond angle change during the applications of tension to a small aggregate formed with 25 μM SPAN 80 in the decane super-phase (SP1). The bottom images (a–c) show snapshots corresponding to the moment of discontinuity in the force profile. The colors on the particles correspond to their bond number.

The detached fragments from aggregate SP1 in Fig. 2 are brought back together using the optical traps to reform the aggregate. This is followed by two sequential compressions (SP1-1 and SP1-2), which end with the particle in the translating trap escaping after approaching closely to the stationary trapped particle. As shown in Fig. 3, bond angle changes (IV) are nearly identical in each case and the bond breakage between particles 3–4 (ruptured bond in SP1) is also observed in both compressions.

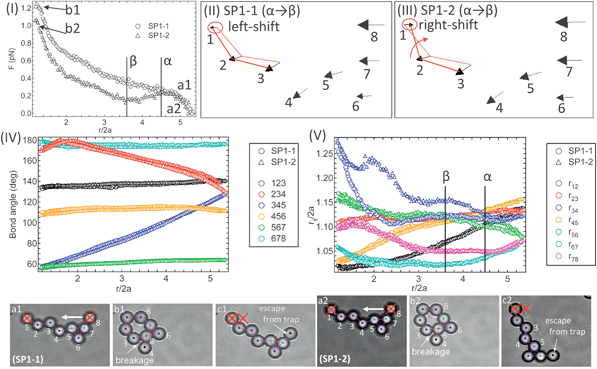Fig. 3 Micromechanics of aggregate during the first (SP1-1) and second (SP1-2) compressions. This aggregate is reformed from the ruptured aggregate (SP1) in Fig. 2. Force profiles (I), movement vectors (II, III), bond angle changes (IV), and particle separations between two neighboring particles (V). The bottom images are the corresponding aggregate images. The colors on the particles correspond to their bond number.

It is interesting to note that during the second compression, unlike the first compression, the force profile decreases in the separation range 3.8 < r/2a < 4.5 (denoted by the points α→β). The shift of the stationary particle 1 also indicates a decrease in the resistance to compression (see the movement vectors III for SP1-2). As shown in Fig. 3V, the separation between particles 3–4, r₃₄/2a for SP1-2 increases more than SP1-1. This may be due to a change of the contact point between particles 3–4 after reforming the aggregate, and thus evidence of multiple local minima in the interaction potential. In addition, the bond length difference, r₃₄/2a between SP1-1 and SP1-2 also suggests that the complex multibody interactions among the three particles 3, 4, and 5 likely occurs when they form a triangular structure.^25,26 After further compression prior to the contact of two trapped particles, the force monotonically increases in both cases.

4 Discussion

The micromechanics of colloidal aggregates in a single fluid medium are well understood, and can be modeled by the effect of colloidal and surface forces (van der Waals attraction, specific ion interactions, electrostatic repulsion and steric forces) on the work of adhesion between particles.^11,19–21 The deformation, rearrangement, and rupture of bonds in aggregates underlie the elasticity and yield behavior of the colloidal microstructures, and ultimately determine the bulk rheological properties, such as the viscosity, yield stress and elastic modulus of colloidal gels.^27–29

In previous work, we showed that the micromechanics of colloidal aggregates of single-bonded linear chains exhibited elastic rigidity, critical bending moments, and yield (rupture) forces.^11,19–21 In particular, the aggregate elasticity is determined by the single-bond bending rigidity between two particles κ₀,

where a is the radius of particle and E is the particle Young's modulus. In the absence of an applied load, JKR theory³⁰ gives a contact radius a_c between elastic spheres,where W_A is the energy of adhesion and the bulk modulus is K = 2E/3(1 − ν²) where ν is the Poisson ratio.

The power of eqn (1) and (2) is the ability to directly associate the surface forces (in terms of the energy of adhesion) to the bending mechanics of the colloidal aggregates, and subsequently, the bulk rheology of a colloidal gel. For instance, the elastic modulus of fractal colloidal gel is³¹

G = κ(ξ)/ξ, (3)

where ξ is the average radius of the clusters comprising the gel microstructure and κ(ξ) is the rigidity of the largest clusters over a length ξ. The latter is related to the single-bond rigidity κ₀ and bond dimension d_b by^31–33

κ(ξ) = κ₀(a/ξ)^2+d_b. (4)

Similarly, the yield stress σ_y can arise from either rupturing bonds that are pulled beyond their maximum tension F_r, leading to σ_y ∼ F_r/ξ², or when the bending moment imposed by the macroscopic deformation overcomes the microscopic maximum bending moment M_c, in which case σ_y ∼ M_c/ξ³.¹¹

The aggregate rigidity is averaged for each step in the deformation as κ_a = ∑F̄_iΔL_i/2aL, where L is the distance between the stationary and moving trap, ΔL_i and F̄_i are the step size of the translating particle and the corresponding force averaged over the initial and final positions for each step, respectively. The aggregates are similar to segments of length s within a gel microstructure. The rigidity over a segment is given by κ(s) = κ₀(a/s)^d_b, which is the basis for eqn (4).³¹ Since d_b ≈ 1.1,³² to a reasonable approximation, κ_a ≈ κ₀. The rigidities for several 2D aggregates are tabulated in Table 1. Notably, the averaged rigidities differ by an order of magnitude depending on the surfactant additive used: [small kappa, Greek, macron]_a = 4.9 ± 3.1 mN m⁻¹ for NaCl/SDS and [small kappa, Greek, macron]_a = 0.28 ± 0.31 mN m⁻¹ for SPAN 80.

Table 1 Comparison of the rigidities κ_a (mN m⁻¹) of aggregates at the oil–water interfaces containing 0.25 M NaCl/0.1 mM SDS in the sub-phase and 25 μM SPAN 80 in the super-phase. SS^# and SP^* indicate the fluid conditions of NaCl/SDS (or salt/SDS) and SPAN 80, respectively. [small kappa, Greek, macron]_a is the mean value of the rigidities for the examined aggregates. The movies for micromechanics of all aggregates are available in the ESI

Aggregate	Additive	κ a (mN m^−1)
SS1^#	NaCl/SDS	1.2
SS2	NaCl/SDS	3.2
SS3	NaCl/SDS	7.2
SS4	NaCl/SDS	3.4
SS5	NaCl/SDS	9.7
		[small kappa, Greek, macron] a = 4.9 ± 3.1
SP1^*	SPAN 80	0.15
SP1-1	SPAN 80	0.11
SP1-2	SPAN 80	0.10
SP2	SPAN 80	0.95
SP3	SPAN 80	0.04
SP4	SPAN 80	0.30
		[small kappa, Greek, macron] a = 0.28 ± 0.31

---

Such dissimiliar rigidities are likely a result of the different partitioning nature of the surfactants. Both SDS and SPAN 80 increase the three-phase contact angle (i.e., ∼20% increase in the contact angle relatively from the neutral wetting in the both fluid conditions using the cast-film/goniometer method).^2,8,34 The increase in contact angle causes the equilibrium position of the particles to reside further into the oil phase, as illustrated in Fig. 4. However, the SDS and SPAN 80 have different hydrophilic-lipophilic balance (HLB) values. The HLB for SDS is ≈40 and the HLB for SPAN 80 is ≈4.3. Thus, SPAN 80 reaches significant concentrations in the oil phase, leading to adsorption on the particle-oil interface, in contrast to SDS. Adsorption changes the adhesive energy between particles, leading to a lower bond rigidity and critical bending moment, similar to aggregates studied previously for particle aggregates in bulk electrolyte solutions.²¹

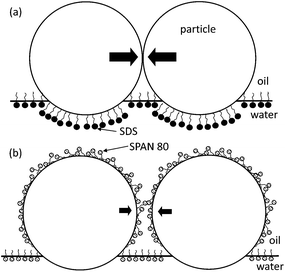Fig. 4 Proposed origin of the difference of aggregate rigidities under the conditions of SDS in the sub-phase (a) and SPAN 80 in the super-phase (b). The particle at the interface in both conditions dominantly belongs to the oil-side, compared to the one at the neat oil–water interface (i.e., neutral wetting).³⁴ SPAN 80 molecules adsorbed in the super-phase on the particle surface, considering the relatively polar alcohol head groups. The scale is exaggerated for illustration.

Finally, the micromechanical rigidity of aggregates in each fluid condition is consistent with the microstructure observed previously.⁸ The weaker rigidity of aggregates in SPAN 80 results in frequent particle rearrangements and lower sticking probability, which leads to the formation of denser aggregate structures, while the relatively strong rigidity in NaCl/SDS and large resistance to tangential motion suppresses rearrangements, and causes the more open percolated network.

5 Conclusions

In conclusion, we studied colloidal aggregate micromechanics in order to understand the structure and rheology of suspensions at the oil–water interface. Micromechanical experiments lead to two important observations: First, the aggregate micromechanics provide evidence of long-range secondary energy minima between neighboring particles. Since the attraction between particles arises due to capillary interactions, we expect that 2D colloidal gels probably have complex interactions that may be difficult to model by pairwise interactions alone in simulations. Nonetheless, we demonstrated that different surfactants can be used to tailor the micromechanical properties of colloidal aggregates at the interface. This second observation means that the linear and non-linear rheology of 2D gels can be controlled by changing the surface chemistry of particles, and provides a direct link between the molecular-scale interfacial phenomena of particle–particle interactions and macroscopic interfacial rheology. In all, the aggregate micromechanics provide an important connection between the previously reported experiments at the micro-scale (i.e., pair interactions^7,8,13) and macro-scale, such as the aggregate structure and rheology.^1–3,35

Acknowledgements

We gratefully acknowledge the financial support from the National Science Foundation (NSF CBET-0553656) and NASA (Grant no. NNX10AE44G).

References

1. H. Hoekstra, J. Vermant, J. Mewis and G. G. Fuller, Langmuir, 2003, 19, 9134–9141.
2. S. Reynaert, P. Moldenaers and J. Vermant, Langmuir, 2006, 22, 4936–4945.
3. E. J. Stancik, M. J. O. Widenbrant, A. T. Laschitsch, J. Vermant and G. G. Fuller, Langmuir, 2002, 18, 4372–4375.
4. B. P. Binks and T. S. Horozov, Colloidal particles at liquid interfaces, Cambridge University Press, 2006.
5. P. Pieranski, Phys. Rev. Lett., 1980, 45, 569–572.
6. A. J. Hurd, J. Phys. A: Math. Gen., 1985, 45, L1055–L1060.
7. A. J. Park, J. P. Pantina, E. M. Furst, M. Oettel, S. Reynaert and J. Vermant, Langmuir, 2008, 24, 1686–1694.
8. A. J. Park and E. M. Furst, Soft Matter, 2011 10.1039/c1sm00005e.
9. S. B. Johnson, G. V. Franks, P. J. Scales and T. W. Healy, Int. J. Miner. Process., 1999, 58, 267–304.
10. P. B. Laxton and J. C. Berg, Colloids Surf., A, 2007, 301, 137–140.
11. E. M. Furst and J. P. Pantina, Phys. Rev. E, 2007, 75, 050402 (R).
12. V. Becker and H. Briesen, Phys. Rev. E, 2008, 78, 061404.
13. B. J. Park, J. Vermant and E. M. Furst, Soft Matter, 2010, 6, 5327–5333.
14. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298.
15. J. P. Pantina and E. M. Furst, Langmuir, 2004, 20, 3940–3946.
16. B. J. Park and E. M. Furst, Langmuir, 2008, 24, 13383–13392.
17. C. S. Chang and C. L. Liao, Int. J. Solids Struct., 1990, 26, 437–453.
18. A. Tordesillas and S. D. C. Walsh, Powder Technol., 2002, 124, 106–111.
19. J. P. Pantina and E. M. Furst, Phys. Rev. Lett., 2005, 94, 138301–4.
20. J. P. Pantina and E. M. Furst, Langmuir, 2006, 22, 5282–5288.
21. J. P. Pantina and E. M. Furst, Langmuir, 2008, 24, 1141–1146.
22. K. Iwashita and M. Oda, Powder Technol., 2000, 109, 192–205.
23. N. Estrada, A. Taboada and F. Radjai, Phys. Rev. E, 2008, 78, 021301.
24. A. Dominguez, D. Frydel and M. Oettel, Phys. Rev. E, 2008, 77, 020401 (R).
25. J. Dobnikar, M. Brunner and H.-H. von Grünberg, Phys. Rev. E, 2004, 69, 031402.
26. D. Stamou, C. Duschl and D. Johannsmann, Phys. Rev. E, 2000, 62, 5263–5272.
27. R. De Rooij, A. A. Potanin, D. Van den Ende and J. Mellema, J. Chem. Phys., 1993, 99, 9213–9223.
28. A. A. Potanin, R. De Rooij, D. Van den Ende and J. Mellema, J. Chem. Phys., 1995, 102, 5845–5853.
29. H. L. West, J. R. Melrose and R. C. Ball, Phys. Rev. E, 1994, 49, 4237–4249.
30. K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313.
31. A. H. Krall and D. A. Weitz, Phys. Rev. Lett., 1998, 80, 778–781.
32. P. Meakin, I. Majid, S. Havlin and H. Eugene Stanley, J. Phys. A: Math. Gen., 1984, 17, L975–L981.
33. S. Manley, B. Davidovitch, N. R. Davies, L. Cipelletti, A. E. Bailey, R. J. Christianson, U. Gasser, V. Prasad, P. N. Segre, M. P. Doherty, S. Sankaran, A. L. Jankovsky, B. Shiley, J. Bowen, J. Eggers, C. Kurta, T. Lorik and D. A. Weitz, Phys. Rev. Lett., 2005, 95, 048302.
34. K. Masschaele, B. J. Park, J. Fransaer, E. M. Furst and J. Vermant, Phys. Rev. Lett., 2010, 105, 048303.
35. E. J. Stancik, M. Kouhkan and G. G. Fuller, Langmuir, 2004, 20, 90–94.

---

Footnotes

† Electronic supplementary information (ESI) available: Supporting movies of the aggregate micromechanics are available. See DOI: 10.1039/c1sm05254c

‡ Current address: Department of Chemical and Biomolecular Engineering, University of Pennsylvania, 220 South 33rd Street, Philadelphia, PA 19104, USA.

---