Attractive interactions between colloids at the oil–water interface†
Bum Jun
Park‡
and
Eric M.
Furst
*
Department of Chemical Engineering and Center for Molecular and Engineering Thermodynamics, University of Delaware, 150 Academy Street, Newark, Delaware 19716, USA. E-mail: furst@udel.edu; Tel: +1 302 8310102
First published on 26th April 2011
Abstract
The effects of salts and surfactants on the interaction force between colloidal polystyrene latex particles confined to a decane–water interface are measured directly using optical tweezers. After adding 0.25 M NaCl, 0.25 M NaCl and 0.1 mM sodium dodecyl sulfate (SDS) to the aqueous sub-phase, or 25 μM sorbitan monooleate (SPAN 80) to the decane super-phase, the strong repulsive force between particles is reduced and an attractive force becomes significant. The magnitude and dependence of the attraction on particle separation is consistent with a capillary quadrupole interaction. Similar interaction forces between polystyrene latex doublet particles at a pristine interface are measured, however, the anisotropic particles exhibit only a long-range attraction that is approximately two orders of magnitude stronger than spherical colloids. These results confirm the presence of long-range capillary attractions and provide a guide for manipulating colloidal interactions with additives or particle shape at fluid interfaces to control suspension structure and surface rheology.
1 Introduction
Understanding and manipulating the interaction forces between dispersed particles is a crucial aspect of colloid science and engineering, whether the aim is to achieve a stable suspension, control its consolidation in a gravitational field, or modify its rheology and resulting flow behavior.1 This work has given rise to theories such as the Derjaugin–Landau–Verwey–Overbeek (DLVO) potential that captures the principal interactions between colloids and enables the prediction and control of suspension stability.2,3 The DLVO potential accounts for the attraction via van der Waals forces and repulsion due to interactions between charged double layers that dominate most aqueous dispersions. Recent technologies such as electronic inks employ colloids suspended in non-polar solvents, further extending models of double layer interactions and particle stability.4,5Particles irreversibly adsorbed to the interface between immiscible fluids present a novel challenge for understanding and controlling colloidal interactions. Applications of such confined suspensions include Pickering–Ramsden emulsions, in which particles are used to stabilize a dispersed phase,6,7 as well as more recent applications in novel materials, such as “colloidosomes”8,9 and “bijels”.10–14 Similar to bulk suspensions, the interaction between particles confined to an oil–water interface can be altered in order to induce changes in the microstructure, by aggregation for instance, and thus modifying the interfacial rheology15–18 and interface mechanics.19
While suspensions at fluid interfaces share many of the characteristics of bulk suspensions, interactions at fluid interfaces are not captured by common theories of colloidal stability like DLVO. The repulsive interactions arise from the asymmetric charge dissociation across the interface, which creates a dipole–dipole interaction that is significantly stronger and longer-ranged than screened Coulomb interactions in an aqueous medium.20–22 Under pristine conditions, these interactions lead to a long-range repulsion and remarkable two-dimensional crystals that are highly stable.20 Similar to bulk suspensions, 2D suspensions are destabilized by the addition of salts to the aqueous sub-phase, giving rise to fractal aggregates.17 Such destabilization implies that the repulsion between particles is sufficient to impart a strong kinetic barrier,1 but once reduced, that the particles are subject to a stronger attractive interaction.
The nature of the underlying attractive interactions between spherical colloids at fluid interfaces that lead to aggregated structures is not well understood. In contrast, for nonspherical particles, the undulating contact line is known to give rise to long-range capillary attractions23,24 in order to minimize the local interface deformation. Such deformations were recently visualized using interferometry.25 Indeed, these capillary attractions have been controlled using lithographically patterned particles to direct their assembly at an air–water interface.26 Recently, Stamou and co-workers proposed that similar capillary forces may arise for spherical particles due to a slightly irregular shape of the contact line caused by chemical or topographic heterogeneity.27
The aim of the current work is to study the interactions between colloidal particles at an oil–water interface under conditions in which aggregation has been observed.17 To do this, we use optical tweezers to directly measure the force between pairs of colloidal particles. This paper consists of two parts: In the first part, we examine the effect of additives, including salt, anionic, or nonionic surfactants, on the colloidal interactions between spherical particles at the oil–water interface. In the second part, we investigate the effect of particle shape using doublet particles. Before discussing our results, we first detail the materials and methods used for this study.
2 Materials and methods
2.1 Materials
We measure the interactions of colloidal particles for two types of particles: the first are monodisperse spherical polystyrene latex particles (diameter 2a = 3.1 ± 0.2 μm, Invitrogen Corporation) that are charge-stabilized with surface sulfate groups (titratable surface charge σ = 7.4 μC cm−2 and zeta-potential ζ ≈ −80 mV). The second is a doublet polystyrene particle (ζ ≈ −10 mV) synthesized by a seeded emulsion polymerization.28 These particles consist of two fused spheres with diameters 3.9 μm and a center-to-center separation of approximately 2.2 μm. A scanning electron microscopy image of a doublet particle is provided in the Supplementary Information.† Particles are treated by multiple centrifugation and redispersion steps prior to use to remove unwanted contaminants that may affect the particle interaction measurements. In previous work, we showed that such “washing” leads to more strongly repulsive interaction potentials between spheres on average.29 We introduce the spherical particles at the oil–water interface using isopropyl alcohol (Sigma Aldrich) as a spreading solvent,17,30 while a method of directly transferring particles to the interface from the aqueous sub-phase is used for the doublet particles. We explain the transfer method in detail below.Our experimental geometry consists of an interface formed by water and decane. Ultra-purified water (resistivity >18.2 MΩ cm) is used as the sub-phase. The super-phase is n-decane (Acros Organics, 99+%), which is passed through an aluminium oxide column (Acros Chemical, acidic activated, particle size 100–500 μm) to remove polar contaminants. A specially designed flow cell (Fig. 1), constructed from a glass outer cylinder and an inner cylinder made of aluminium, is placed on the stage of an inverted microscope. The outer cylinder is attached to a 40 mm circular cover glass (No. 1.5 Fisher Scientific) using an ultra-violet curing optical adhesive (NOA 81, Norland Products). A teflon ring is inserted into the bottom of the inner cylinder in order to pin the contact line of the oil–water interface and keep it flat. Glass beads act as spacers to provide contact between the aqueous sub-phase and the water reservoir outside of the inner cylinder assembly. Salts and surfactants added to the aqueous phase are introduced into the outer reservoir and rapidly equilibrate into the inner cylinder sub-phase. We use sodium chloride (NaCl, Sigma Aldrich), sodium dodecyl sulfate (SDS, Sigma Aldrich) and sorbitan monooleate (SPAN 80, Spectrum Chemicals) as received by the manufacturer. SPAN 80 is added directly to the inner cylinder decane phase. To prevent evaporation and convection, we seal the vessel using a second circular glass cover slide and vacuum grease. All glassware is cleaned using a plasma cleaner (Harrick Plasma, PDC 32-G), immediately before constructing the sample chamber in order to achieve good wetting conditions for the water. All experiments are performed at room temperature.
 | ||
| Fig. 1 Schematic of the flow cell. | ||
2.2 Direct interaction measurements
Particles at the interface are held individually by time-shared optical traps.31 The pair interaction forces are directly measured as one particle is brought towards another stationary particle.30 The particle displacement Δx in the stationary trap provides a quantitative measurement of the forces (F = κtΔx) exerted between the two particles. Fig. 2 shows a pair interaction measurement in which the pair experiences a repulsive energy barrier in a far field and an attractive energy well at a close separation. The two particles are initially trapped with a large separation such that the interaction between them is negligible. As the right-most particle approaches the stationary particle, the latter is displaced from its equilibrium position, depending on the magnitude of repulsion (displaced left) or attraction (displaced right). In some cases, at a certain critical separation, the particles jump into contact. This represents a condition in which the gradient of the interparticle force is stronger than the stiffness of the optical trap. | ||
| Fig. 2 Snapshots for the direct measurement of the interaction force between two spherical particles using time-shared optical traps. The left particle is held by a stationary trap while the right particle approaches stepwise by translating its trap. The vertical line indicates the equilibrium position of the particle in the stationary trap. The scale bar is 5 μm. | ||
Prior to these force measurements, the optical trap is calibrated to obtain the optical trap stiffness κt and maximum trapping force Fmaxt. Particles trapped at the oil–water interface are subjected to solvent drag forces by translating the microscope stage at a constant velocity, U.29,30 The particle displacement from the optical trap Δx is measured as a function of the imposed Stokes drag force, FS = 6πaηeffU, where ηeff = [ηoil(1 − cosθ) + ηwater(1 + cosθ)]/2 is the effective viscosity. We verify, both experimentally and by calculation, that the optical traps do not induce artifacts in the pair interaction measurements.32
2.3 Doublet particle interaction measurements
Doublet particles immediately form aggregates when spread on the oil–water interface using the standard spreading procedure described above.17,30 These aggregated particles are firmly attached to each other and cannot be detached by optical tweezers. To measure the pair interactions, we transfer individual particles to the interface directly from the aqueous sub-phase using optical tweezers. As shown in Fig. 3, we trap two doublets and bring them upward until they transfer to the interface (note in Fig. 3 that the right-most doublet particle is already located at the interface). The lower zeta potential of these particles ensures that the repulsive electrostatic disjoining pressure between the particles and the oil–water interface is low.33,34 | ||
| Fig. 3 Transition method for the doublet particles using optical tweezers (see the text). A movie is available in the Supplementary Information†. The scale bar is 5 μm. | ||
The interaction force between doublets is measured by both active and passive methods. The active measurement is identical to the method used for spherical colloids. We use the drag calibration method to obtain the optical trap stiffness κt, correcting the Stokes drag force by Fs = 6πRhηeffUλ, where Rh is the hydrodynamic radius of the doublet. Considering the geometry of the doublet particle, Zabarankin found the correction factor λ, depending on the angle θ between the long-axis of the particle and the direction of the translation. For the particles used here, the λ varies from minimum λ ≈ 1.13 for θ = 0° to maximum λ ≈ 1.22 for θ = 90°. In passive measurements, the doublet particles are positioned at an initial separation and the optical traps are removed. The force between the particles is calculated from the relative drift velocity of the particles, u as the function of separation r. Then, the Stokes drag force F = 6πRhηeffuλθ is related to r, where λθ depends on the measured value of the particle orientation angle θ.
3 Results and discussion
3.1 Pair interactions between spherical particles: The effect of additives
Force measurements for many particle pairs in the presence of 0.25 M NaCl in the aqueous sub-phase, 0.25 M NaCl/0.1 mM SDS in the sub-phase, or 25 μM SPAN 80 in the decane super-phase are shown in Fig. 4. Consistent with our previous experiments, the pair interactions vary considerably, and depend strongly on the particle pair used in each force measurement.29 The most repulsive of these interactions exhibit forces in agreement with a dipole–dipole repulsion,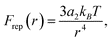 | (1) |
 | ||
| Fig. 4 Comparison of the interaction forces between spherical particles at the oil–water interfaces in the presence of additives (a) 0.25 M NaCl in the aqueous sub-phase, (b) 0.25 M NaCl/0.1 mM SDS in the sub-phase and (c) 25 μM SPAN 80 the decane super-phase. In each condition, the interaction forces for approximately one hundred particle pairs are measured. Black curves show force profiles that exhibit repulsive interactions that scale as F ∼ r−4 (illustrated by the dashed lines) and red curves are force profiles that exhibit a “jump-in” to contact. Blue curves exhibit softer repulsion, but no jump into contact. Fig. (a) includes the force profiles at an oil–water interface without salt or surfactant added (green curves). | ||
The addition of salt and surfactants for particles at the oil–water interface is reminiscent of the screening that occurs when salt is added to a suspension of electrostatically stabilized particles in a bulk aqueous phase.1 In the current case, however, the attraction is much longer ranged than expected for van der Waals forces. Particle pairs jump into contact at surface separations on the order of 2–4 μm, while retarded van der Waals forces typically extend over a range of tens of nanometers for micrometer sized colloids.36
Such a strong and long-ranged attraction between particles at the oil–water interface can be explained by capillary forces.27,37–40 It is known that the capillary interactions are caused by the deformation of the interface in the vicinity of particles; these arise from various factors, including the gravitational force exerted on the particles39 and thermal fluctuations.41,42 However, an interface deformation induced by gravity is not of sufficient magnitude to cause the attraction between micrometer sized colloids (the Bond number, Bo = Δρga2/γ, where Δρ is the difference in density with the surrounding medium, g is the gravitational acceleration and γ is the surface tension, satisfies Bo ≪ 1). Likewise, colloids are strongly trapped and pinned at the interface and are thus stable against significant thermal fluctuations.
A better explanation for the long-range capillary forces between spherical particles when Bo ≪ 1 is given by Stamou and co-workers, who show that such forces may arise from a slightly irregular shape of the contact line, caused by chemical or topographic heterogeneity.27 In the far field, distortions of the interface caused by the irregularly shaped meniscus give rise to a quadrupolar interaction force with magnitude,37
 | (2) |
All of the force profiles can be described by a combination of the repulsive and attractive force laws given by eqn (1) and (2). In Fig. 5, we plot four representative force measurements taken from the 0.25 M NaCl experiments (Fig. 4a). One force profile exhibits a repulsive interaction (having the property that F ∼ r−4, consistent with the dipole–dipole repulsion), one curve exhibits a softer repulsion, and two exhibit a small to moderate maximum, then a jump into attractive contact. Each of these curves is fit using a total force expression
| Ftot = Frep + Fcap, | (3) |
 | ||
| Fig. 5 Four representative force curves from Fig. 4a fitted with eqn (3), (1) and (2). The fitting parameters a2 and a3 for each curve are given in the legend. The arrows indicate the jump-into contact due to the mechanical instability when the gradient of the attractive force exceeds the optical trap stiffness, κt. | ||
Next, all of the force profiles shown in Fig. 4a–c are fit using eqn (3). Fig. 6 shows the values of a2 and a3 for each of the three conditions studied. In the case of 0.25 M NaCl added to the aqueous sub-phase, the values of a2 vary between 5 × 10−14 m3 and 5 × 10−13 m3. As shown in the corresponding histogram, a2 is distributed evenly around an average value 〈a2〉 = 2.3 ± 0.6 × 10−13 m3. This is approximately half the average value measured for the same particles in the absence of salt,29〈a2〉 = 5.1 ± 2.4 × 10−13 m3.
 | ||
| Fig. 6 Values of a2 and a3 for all force curves reported in Fig. 4 for (a) 0.25 M NaCl in the aqueous sub-phase, (b) 0.25 M NaCl/0.1 mM SDS in the sub-phase and (c) 25 μM SPAN 80 the decane super-phase. The histograms on the corresponding axes show the number of particle pair interaction measurements with the values of a2 and a3. | ||
The attractive interaction parameter a3 exhibits a skewed distribution of values, with many particle pairs exhibiting weak or negligible attraction. The average value for 0.25 M NaCl is 〈a3〉 = 4.7 ± 4.5 × 10−19 m4. Using eqn (2), this corresponds to a contact line height H2 ≈ 45 nm, which is reasonable, and only about 3% of the particle radius.
The repulsive and attractive interactions become weaker in the presence of surfactants. The values are shown in Fig. 6b and 6c for 0.25 M NaCl/0.1 mM SDS to the aqueous sub-phase and 25 μM SPAN 80 added to the decane super-phase, respectively. The average value of the repulsion coefficient for 0.25 M NaCl/0.1 mM SDS is 〈a2〉 = 1.5 ± 0.9 × 10−13 m3. The average value for 25 μM SPAN 80 is still lower, 〈a2〉 = 1.1 ± 0.7 × 10−13 m3. The attractive interaction coefficient has an exponential-like distribution, similar to the NaCl samples, but the figures and histograms clearly show a trend towards lower values. The average values are 〈a3〉 = 2.7 ± 2.4 × 10−19 m4 for 0.25 M NaCl/0.1 mM SDS and 〈a3〉 = 2.2 ± 1.4 × 10−19 m4 for 25 μM SPAN 80.
The repulsive interaction is expected to decrease in the presence of salt in the aqueous sub-phase due to a decrease in the number of dissociated charges that produce the long-range dipolar repulsion.22,30 We can make sense of further effects with the addition of surfactants by considering how these additives affect the surface tension and the three-phase contact angles of the particles. First, the attractive force should decrease in proportion to the decrease in surface tension, since a3 ∼ γ. The measured decane–water interfacial tension in the presence of 0.25 M NaCl/0.1 mM SDS and 25 μM SPAN 80 are γNaCl/SDS = 20 mN m−1 and γSPAN80 = 40 mN m−1, respectively (see the Supplementary Information†), consistent with the lower average values of a3.
Second, with the addition of surfactants, particles push further into the low permittivity oil phase, due to the higher three-phase contact angle (θ is defined relative to the water phase; i.e. for θ < 90°, the particle favors a position further in the water phase and θ > 90° means the particles will sit preferentially in the oil phase). This reduces the amount of charge dissociated in the aqueous phase.21,22 The repulsion is proportional to the particle contact angle as Frep ∝ sin4θ. Three phase bulk contact angle measurements (see Supplementary Information†) provide an estimate of the change in the particle contact angle with the addition of surfactants, which is an increase of approximately 30° in both cases. From the increase in contact angle, we expect a decrease to approximately 56% of the value of a2 in the absence of surfactant. Indeed, the value of 〈a2〉 = 1.5 ± 0.9 × 10−13 m3 for 0.25 M NaCl/0.1 mM SDS is in good agreement with the expected decrease when compared to the value of a2 for 0.25 M NaCl (〈a2〉 = 2.3 ± 0.6 × 10−13 m3). The decrease in 〈a2〉 for SPAN 80 is significantly larger, from 5.1 × 10−13 m3 for the neat system to 1.1 × 10−13 m3 after the surfactant is added. This may reflect a higher particle contact angle than estimated from the bulk three-phase contact angle; a particle contact angle larger only by 10° would account for this discrepancy.
It is important to recognize that these measurements preclude other mechanisms that have been suggested to account for the attraction between colloids at an oil–water interface, including the hypothesis that in-plane dipoles, due to an uneven distribution of charge on the particles, lead to attractive interactions.43 In-plane dipoles exhibit a separation dependence identical to the repulsion, which is inconsistent with the far-field repulsion followed by jumps into an attractive contact as particles approach each other that is observed in many force profiles. Likewise, if the repulsion mainly originates from small surface charges in the decane super-phase,35,44 one is left with contradictory observations: first, that the repulsion in the neat system is stronger than when SDS/NaCl or SPAN 80 are added, despite the larger surface area exposed to the super-phase in the latter cases, and second, that the repulsive force in the high salt concentration is significantly lower than the virgin system with the same contact angle.
3.2 Interactions between doublet particles: Effect of particle shape
Fig. 7 shows examples of both the active and passive interaction measurements for doublet particles. The active method, shown in frames a–c, is similar to measurements between spherical particles. As two trapped doublet particles are brought together, the left-most particle is displaced toward the right-most particle. After further approach, the right-particle escapes from the optical trap, overcoming the maximum trapping force. Interestingly, the angle θ between the long-axis of the particle and the translational direction varies with the separation, suggesting the anisotropy of the attractive interactions. In the case of the passive measurement method (Fig. 7d–f), two particles are released from the optical traps at a sufficient separation after transferring them to the interface. Due to the long-rang attraction, they migrate together. | ||
| Fig. 7 Snapshots of the force measurements using active (a–c) and passive methods (d–f). The movies of both methods can be viewed in the Supplementary Information.† The scale bar is 5 μm. | ||
The resulting interaction forces for four doublet pairs are shown in Fig. 8. Both active and passive interaction force measurement methods give identical results. The power law exponent for the separation dependence is fitted from the force curves and found to be −5.4 ± 0.7 for the active method (closed circles) and −4.8 ± 0.4 for the passive method (open circles). The dashed curves in Fig. 8 show guide lines representing F ∼ r−5. These values agree with both the model of the capillary quadrupolar interactions (i.e. Fcap ∼ r−5) which Kralchevsky et al. calculate for the far field capillary interaction37 and the experimental value which Loudet et al. obtained for the tip-to-tip interactions between two ellipsoidal particles.23
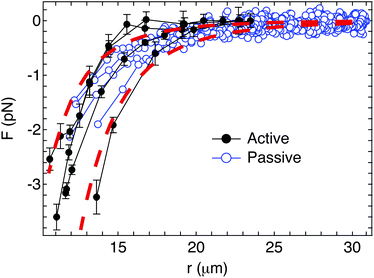 | ||
| Fig. 8 Comparison of the interaction forces between two doublet particles using active (closed circles) and passive (open circles) methods. The dashed curves show the guide lines for the capillary quadrupole interactions (Fcap ∼ r−5). | ||
It is striking that the measured interactions between doublet particles are purely attractive, with no evidence of the long-range repulsion that are observed for colloidal spheres. In part, this is due to the smaller zeta potential of the doublet particles, which significantly reduces the amount of charge dissociated in the aqueous phase. However, the force curves in Fig. 8 also correspond to values of the capillary interaction parameter a3 between 2 × 10−17 and 7 × 10−17m4, which is two orders of magnitude greater than those measured for spherical particles in the absence of surfactants. This highlights a significant challenge for stabilizing non-spherical particles at immiscible fluid interfaces, since it appears that their aggregation due to strong, long-range capillary attraction cannot easily be mitigated. Nonetheless, it also demonstrates that the aggregation of particles at fluid interfaces may be induced independent of the addition of destabilizing agents, such as salts and surfactants. This latter fact may have important implications for controlling the rheology of fluid interfaces.15
4 Conclusions
We measured the interaction forces between particle pairs at the oil–water interface directly using optical tweezers. By manipulating the aqueous sub-phase or decane super-phase conditions through the addition of salt, anionic, or nonionic surfactants, we identified two factors that lead to reductions in the long-range repulsive electrostatic force and enable attractive interactions to be measured. One is by enhancing screening in the aqueous sub-phase by the addition of salt. The second is by reducing the area exposed to the aqueous sub-phase through changes in the three-phase particle contact angle. This verifies that the dissociated charges of the particles in the aqueous sub-phase are the dominant contribution to the repulsive interaction.The attractive interaction measured between colloidal spheres is consistent, in both magnitude and separation dependence, with the quadrupolar capillary interactions arising from the slowest decaying term in the interface distortion. In the absence of gravity, such interface distortions are likely a result of chemical or topographic heterogeneity of the particles, as suggested by Stamou and co-workers.27 The measured interaction forces between doublet particles, which distort the interface due to particle shape, are also consistent with capillary quadrupole interactions, but are significantly stronger than the capillary interactions between spherical particles.
Overall, the results reported in this paper support the hypothesis that electrostatic interactions and capillary attractions are the dominant contributions to the interactions between micrometer diameter colloids dispersed at an oil–water interface. The interaction force laws and statistical distribution of interaction parameters should be of particular use for modeling the aggregation kinetics, structure and rheology of suspensions at fluid interfaces.
Acknowledgements
We thank J.-G. Park and E. Dufresne for providing doublet particles and J. Vermant and K. Masschaele for helpful discussions. We gratefully acknowledge the financial support from the National Science Foundation (NSF CBET-0553656) and NASA (NNX10AE44G).References
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, New York, 1989 Search PubMed.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- B. Derjaugin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633–662 Search PubMed.
- S. K. Sainis, J. W. Merrill and E. R. Dufresne, Langmuir, 2008, 24, 13334–13347 CrossRef CAS.
- S. K. Sainis, V. Germain, C. O. Mejean and E. R. Dufresne, Langmuir, 2008, 24, 1160–1164 CrossRef CAS.
- S. U. Pickering, J. Chem. Soc., 1907, 91, 2001–2021 RSC.
- W. Ramsden, Proc. R. Soc. London, 1903, 72, 156–164 CAS.
- O. Velev, K. Furusawa and K. Nagayama, Langmuir, 1996, 12, 2374–2384 CrossRef CAS.
- A. Dinsmore, M. Hsu, M. Nikolaides, M. Marquez, A. Bausch and D. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS.
- K. Stratford, R. Adhikari, I. Pagonabarraga, J. Desplat and M. E. Cates, Science, 2005, 309, 2198–2201 CrossRef CAS.
- E. Sanz, K. A. White, P. S. Clegg and M. E. Cates, Phys. Rev. Lett., 2009, 103, 255502 CrossRef.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966–971 CrossRef CAS.
- M. E. Cates and P. S. Clegg, Soft Matter, 2008, 4, 2132–2138 RSC.
- M. N. Lee and A. Mohraz, Adv. Mater., 2010, 22, 4836–4841 Search PubMed.
- H. Hoekstra, J. Vermant, J. Mewis and G. G. Fuller, Langmuir, 2003, 19, 9134–9141 CrossRef CAS.
- E. Stancik, G. Gavranovic, M. Widenbrant, A. Laschitsch, J. Vermant and G. Fuller, Faraday Discuss., 2003, 123, 145–156 RSC.
- S. Reynaert, P. Moldenaers and J. Vermant, Langmuir, 2006, 22, 4936–4945 CrossRef CAS.
- S. Reynaert, P. Moldenaers and J. Vermant, Phys. Chem. Chem. Phys., 2007, 9, 6463–6475 RSC.
- C. Monteux, J. Kirkwood, H. Xu, E. Jung and G. G. Fuller, Phys. Chem. Chem. Phys., 2007, 9, 6344–6350 RSC.
- P. Pieranski, Phys. Rev. Lett., 1980, 45, 569–572 CrossRef CAS.
- A. J. Hurd, J. Phys. A: Math. Gen., 1985, 18, 1055–1060 Search PubMed.
- K. Masschaele, B. J. Park, J. Fansaer, E. M. Furst and J. Vermant, Phys. Rev. Lett., 2010, 105, 048303 CrossRef.
- J. Loudet, A. Alsayed, J. Zhang and A. Yodh, Phys. Rev. Lett., 2005, 94, 018301 CrossRef CAS.
- E. P. Lewandowski, M. Cavallaro, L. Botto, J. C. Bernate, V. Garbin and K. J. Stebe, Langmuir, 2010, 26, 15142–15154 Search PubMed.
- J. C. Loudet, A. G. Yodh and B. Pouligny, Phys. Rev. Lett., 2006, 97, 018304 CrossRef CAS.
- E. P. Lewandowski, J. A. Bernate, A. Tseng, P. C. Searson and K. J. Stebe, Soft Matter, 2009, 5, 886–890 RSC.
- D. Stamou, C. Duschl and D. Johannsmann, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5263–5272 CrossRef CAS.
- H. R. Sheu, M. S. El-Aasser and J. W. Vanderhoff, J. Polym. Sci., Part A: Polym. Chem., 1990, 28, 629–651 CrossRef CAS.
- B. J. Park, J. Vermant and E. M. Furst, Soft Matter, 2010, 6, 5327–5333 RSC.
- B. J. Park, J. P. Pantina, E. M. Furst, M. Oettel, S. Reynaert and J. Vermant, Langmuir, 2008, 24, 1686–1694 CrossRef CAS.
- J. P. Pantina and E. M. Furst, Langmuir, 2004, 20, 3940–3946 CrossRef CAS.
- B. Park and E. Furst, Langmuir, 2008, 24, 13383–13392 CrossRef CAS.
- D. Bachmann and S. Miklavcic, Langmuir, 1996, 12, 4197–4204 CrossRef CAS.
- B. J. Park and E. M. Furst, Soft Matter, 2010, 6, 485–488 RSC.
- R. Aveyard, B. P. Binks, J. H. Clint, P. D. I. Fletcher, T. S. Horozov, B. Neumann, V. N. Paunov, J. Annesley, S. W. Botchway, D. Nees, A. W. Parker, A. D. Ward and A. N. Bergess, Phys. Rev. Lett., 2002, 88, 246102 CrossRef CAS.
- J. M. Israelachvili, Intermolecular and Surface Forces, Academic Press, New York, 1992 Search PubMed.
- P. A. Kralchevsky, V. N. Paunov, I. B. Ivanov and K. Nagayama, J. Colloid Interface Sci., 1992, 151, 79–94 CrossRef.
- V. N. Paunov, P. A. Kralchevsky, N. D. Denkov and K. Nagayama, J. Colloid Interface Sci., 1993, 157, 100–112 CrossRef CAS.
- N. Vassileva, D. V. den Ende, F. Mugele and J. Mellema, Langmuir, 2005, 21, 11190–11200 CrossRef CAS.
- M. Oettel, A. Dominguez and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051401 CrossRef CAS.
- R. Golestanian, M. Goulian and M. Kardar, Europhys. Lett., 1996, 33, 241–245 Search PubMed.
- R. Golestanian, M. Goulian and M. Kardar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6725–6734 Search PubMed.
- W. Chen, S. Tan, T.-K. Ng, W. T. Ford and P. Tong, Phys. Rev. Lett., 2005, 95, 218301 CrossRef.
- R. Aveyard, J. Clint, D. Nees and V. N. Paunov, Langmuir, 2000, 16, 1969–1979 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Doublet particle characterization, interfacial tension and three-phase contact angles, and movies showing active and passive dumbells. See DOI: 10.1039/c1sm00005e |
| ‡ Current address: Department of Chemical and Biomolecular Engineering, University of Pennsylvania, 220 South 33rd Street, Philadelphia, PA 19104. |
| This journal is © The Royal Society of Chemistry 2011 |
