Odd–even width effect on persistent current in zigzag hexagonal graphene rings
M. M.
Ma
,
J. W.
Ding
* and
N.
Xu
Department of Physics & Institute for Nanophysics and Rare-earth Luminescence, Xiangtan University, Xiangtan, 411105 Hunan, China. E-mail: jwding@xtu.edu.cn
First published on 29th September 2009
Abstract
The electronic structure and thus the persistent current of zigzag hexagonal graphene rings are investigated within the tight-binding formalism. The flux-dependent energy spectrum is grouped into bands with six levels per band due to inter-valley scattering at the corners of the ring. It is found that the degeneracy at the Fermi level is determined by the even or odd quality of the ring width N. The sample ring becomes metallic at odd N but semiconducting at even N, showing up a strange odd–even width effect. In metallic rings, the persistent current within a flux period is linearly changed with magnetic flux ϕ, while it is a sinusoidal periodical function of ϕ in semiconducting rings. In addition, with increasing N, the persistent current exponentially decreases (increases) at odd (even) N, but finally falls into the consistence with each other at enough large N, showing that the odd–even effect may be experimentally observable only in narrow rings.
Graphene, a single atomic layer of graphite adhered from natural graphite,1,2 has been attracting much intensive research in both theory and experiment due to its peculiar electronic and magnetic transport properties.3–7 Indeed, a mass of graphene-based structures have been fabricated due to experimental and theoretical breakthroughs over the past decade, which may be used as building blocks for nanometre-scale devices. More recently, it was reported that graphene can be cut or patterned into well-defined geometric structures by different techniques,8–14 further opening the door to the fabrication of graphene-based nanodevices. For instance, various graphene-based functional elements and components have been obtained experimentally such as quantum dots,9–11 field-effect transistors,12,13 integrated graphene circuits14etc. Especially, a new style of ring-shaped graphene was fabricated with inner and outer radii of about 350 nm and 500 nm,15 which may be one of the most novel building blocks for future electromagnetic nanodevices. Due to their similarity to mesoscopic rings, the unusual electronic properties of graphene rings have attracted great interest in theory,16,17 indicating they are a useful candidate for probing both quantum coherence and dephasing rates of systems. Of special interest is the persistent current18–20 in such a two-dimensional (2D) ring-shaped device, induced by magnetic flux, ϕ, threaded through the centre of the ring.
For graphene-based structures, the electronic properties of graphenenanoribbons (GNRs), carbon nanotubes (CNTs), and toroidal carbon nanotubes (TCNs) have been well studied, and are dependent upon their geometries. It is well known that all zigzag GNRs are metallic regardless of width,21,22 while armchair GNRs can be either metallic or insulating depending on their widths.22–25 As for armchair CNTs and TCNs, they have the same armchair-type cross-section as in zigzag GNRs. Not considering the curvature, all armchair CNTs and TCNs are expected to be metallic,26–29 similar to zigzag GNRs. For zigzag hexagonal graphene rings (HGRs), it is interesting to explore whether similar characteristics come into existence and how the metallicity depends on its geometry. The study of zigzag HGRs would be very helpful to obtain universal laws of quantum-size effects on electronic transport in graphene-based structures.
For various-shaped HGRs, recently, the inner- and outer-edge states have been obtained, which depend on the edge symmetries and the corner structures.30 For zigzag HGRs, especially, the charge density is spread out on the two opposite edges, indicating the coupling of states localized at two opposite edges. Therefore, one may expect that the effects of ring size and edge-state coupling are very important for determining the electronic structures and thus the persistent currents in zigzag HGRs, which should be further explored.
By developing the supercell method,31 we present a detailed investigation on the electronic structures, and thus the persistent currents of zigzag HGRs. The results show that the flux-dependent energy spectrum is grouped into bands with six levels per band, due to the inter-valley scattering at the corners of the ring. More interestingly, it is found that the parity of the ring width N determines the degeneracy at the Fermi level (EF = 0) and thus the metallicity of the samples, which are metallic at odd N but semiconducting at even N, showing up a strange odd–even width effect. For a metallic ring, the persistent current is a linearly periodical function of magnetic flux, ϕ, while it is a sinusoidal periodical function of ϕ for semiconducting rings. In addition, with increasing N, the persistent current decreases (increases) at odd (even) N, but finally falls into consistence with each other at enough large N. This indicates that the odd–even width effect may be experimentally observable only in narrow rings.
A HGR of zigzag edge is shown in Fig. 1(a) consisting of six arms with l the lattice spacing, the inner ring radius r is given in units of r0, and r = 4r0 with 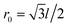 . The geometry of one arm is schematized for width W = Nr0 in Fig. 1(b), with N = 5 the number of zigzag carbon chains. We use the single-orbital nearest-neighbor tight-binding model for the finite-size HGR, which has been successfully applied to the study of GNRs,22–25CNTs26,27 and other carbon-related materials.28,29 In the present model, the magnetic field is limited to the central region of the ring. The Hamiltonian , neglecting electron–electron interactions, is given by
. The geometry of one arm is schematized for width W = Nr0 in Fig. 1(b), with N = 5 the number of zigzag carbon chains. We use the single-orbital nearest-neighbor tight-binding model for the finite-size HGR, which has been successfully applied to the study of GNRs,22–25CNTs26,27 and other carbon-related materials.28,29 In the present model, the magnetic field is limited to the central region of the ring. The Hamiltonian , neglecting electron–electron interactions, is given by
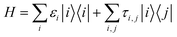 | (1) |
![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) exp[(i2e/h)∫jidr·A] with τ = 2.9 eV the hopping integral constant, and A is the vector potential. The electronic spectrum can be obtained by the supercell method recently developed by Liu and Ding.31 In terms of the rotational symmetry of six-fold, the effective Hamiltonian of a supercell is given by
exp[(i2e/h)∫jidr·A] with τ = 2.9 eV the hopping integral constant, and A is the vector potential. The electronic spectrum can be obtained by the supercell method recently developed by Liu and Ding.31 In terms of the rotational symmetry of six-fold, the effective Hamiltonian of a supercell is given by| Heff = H0 + eiβH1 + e−iβH+1 | (2) |
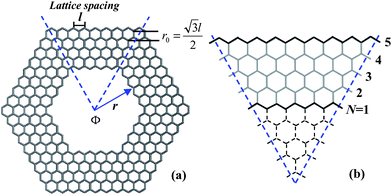 | ||
Fig. 1 (a) A zigzag HGR of ring width N = 5 and inner ring radius r = 4r0 with l the lattice spacing and 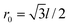 . Magnetic flux , ϕ, passes through the hole. (b) Schematic illustration of one arm in the ring, of which the dashed hexagons in the centre are cut out. . Magnetic flux , ϕ, passes through the hole. (b) Schematic illustration of one arm in the ring, of which the dashed hexagons in the centre are cut out. | ||
At zero temperature, the total persistent current of system is given by
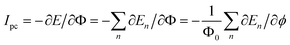 | (3) |
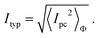 | (4) |
In our calculations, the site energies εi and energy E are given in units of τ, and thus the persistent currents in units of τ/Φ0. As typical examples, Fig. 2 shows the energy spectrum near the Fermi level of the zigzag HGRs of N = 7 (a) and N = 8 (b). Both rings have the same inner ring radius of r = 13r0. From Fig. 2, it is seen that the flux-dependent energy spectrum is grouped into bands, with six levels per band in both cases, which may be due to the high-symmetry structure of HGRs. For each site in such a ring, there exist other five equivalent sites, due to the six-fold rotational symmetry. Because of the long distance between them, the six sites are weakly coupled to each other by other sites. This may lead to a six-level group of bands. For the sites located in a supercell, however, there exists not only strong interactions with the neighboring sites but also the inter-valley scattering at the corners,16 which would result in the presence of inter-band gaps. From Fig. 2, especially, it is found that the energy spectrum strongly depends on the odd or even quality of the ring width N. In the case of N = 7 in Fig. 2(a), the highest occupied state (HOS) and the lowest unoccupied state (LUS) are degenerate at Φ = ± 0.5Φ0, showing the sample ring to be metallic. In Fig. 2(b) with N = 8, a narrow energy gap appears at Φ = ± 0.5Φ0, indicating the sample ring to be a narrow-gap semiconductor. Further calculations have been done for other zigzag HGRs of both odd and even N. It follows that zigzag HGRs are metallic at odd N and semiconducting at even N. The result can be understood by the following consideration.
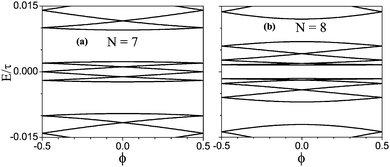 | ||
| Fig. 2 Energy spectra of zigzag HGRs as a function of magnetic flux for the sizes r = 13r0, (a) N = 7 and (b) N = 8. | ||
From Fig. 1(b), it is clearly seen that for a zigzag HGR, the number of atoms within each zigzag chain in one arm must be odd, irrespective of inner radius r. Thus, the number of atoms N1 in one arm must be odd (even) only if N is odd (even). Due to spin degeneration and the rotational symmetry of six-fold, further, the highest occupied band is obtained to be N1/2. This means that for an odd N (or N1), the Fermi level is located at the centre of the (N1 + 1)/2 band, while it falls into the gap between N1/2 and N1/2 + 1 at even N (or N1). Therefore, the even or odd quality of the ring width N determines completely the degeneracy at the Fermi level and thus the metallicity of a zigzag HGR. The result is different from the observation of odd–even effect in the conductance of zigzag GNRs under gate potentials,32–34 which is attributed to the symmetry and asymmetry of the zigzag chains of GNRs.
From the energy spectrum of the studied samples, in Fig. 3, we calculate the persistent currents (Ipc) of the zigzag HGRs as a function of magnetic flux , ϕ, for metallic rings with odd N (a) and semiconducting rings with even N (b). For the metallic ring in Fig. 3(a), it is shown that the flux-dependent Ipc within a period flux changes linearly with ϕ. A jump of Ipc is observed at Φ = ± 0.5Φ0, corresponding to the level degeneracy at Φ = ± 0.5Φ0 as shown in Fig. 2(a), similar to that of TCNs of metallic-type I.28,29 For semiconducting rings, it is seen from Fig. 3(b) that at a given inner radius r, the persistent current may decline by 2–3 orders of magnitude at small N, compared with the metallic ring. This may be due to the energy gap and an almost zero slope of energy curves near the Fermi level in the semiconducting ring, as shown in Fig. 2(b). Also, its behavior of flux-dependent Ipc is a smooth sinusoidal periodical function of ϕ, different from the metallic HGR. From Figs. 3 (a) and (b), in addition, it is seen that with increasing N, Ipc decreases at odd N but increases at even N, further showing up a strange odd–even width effect.
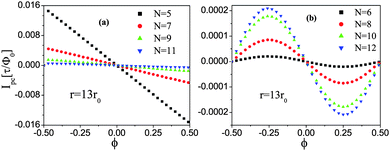 | ||
| Fig. 3 Persistent currents of zigzag HGRs as a function of magnetic flux for (a) odd N, and (b) even N. | ||
To explore the quantum-size effect on persistent current, in Fig. 4(a), we plot the logarithm of the typical currents (Ityp) in zigzag HGRs as a function of the inner ring radius r. From Fig. 4(a), it is seen that for both metallic and semiconducting rings, the overall Ityp decreases with increasing r, as expected in the previous theory of mesoscopic metallic rings.20 From a more careful analysis, it is found that the data of Itypvs.r are well fitted to Ityp ∼ exp(−κr/r0). The decay exponent κ is obtained to be κ = 0.4937, 0.5616, and 0.6450 at N = 5, 7, and 9 respectively, while κ = 1.3168, 0.9956, and 0.8223 at N = 4, 6, and 8 respectively. This means that the typical currents also depend strongly on ring width N, κ decreasing (increasing) with N in metallic (semiconducting ) rings, different from the previous results.19,20
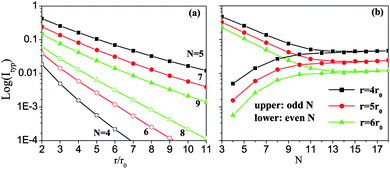 | ||
| Fig. 4 Typical currents, Ityp, of zigzag HGRs as a function of (a) the inner ring radius r and (b) ring width N. | ||
In Fig. 4(b), we further show the logarithm of Ityp as a function of the ring width N. In the case of metallic rings (odd N), it is seen from Fig. 4(b) that with increasing N, Ityp firstly decreases exponentially at small N but becomes invariable at larger N. For semiconducting rings (even N), however, Ityp firstly increases exponentially with N, in spite of a constant Ityp at larger N. At a given inner ring radius r, especially, Ityp at two neighboring odd and even N falls finally into consistency at enough large N. Such changes in Ityp can be understood from the calculated energy spectra, of which the slopes of energy curves and the energy gaps change with N. For a large N, in fact, the wide ring can be regarded as a graphene sheet with vacancies in the presence of a perpendicular magnetic field,35 in which the odd–even effect would disappear. Therefore, the odd–even width effect should be experimentally observable in narrow zigzag HGRs.
In conclusion, a detailed investigation is presented for the electronic structure and the persistent currents in zigzag HGRs by developing a supercell method within the single-orbital nearest-neighbor tight-binding model. The results show that the energy spectrum is grouped into bands with six levels per band, due to the inter-valley scattering at the corners of the ring. Interestingly, it is found that the parity of the ring width N determines the degeneracy at the Fermi level and thus the metallicity of the samples. It is shown that a sample ring of width N is metallic at odd N but semiconducting at even N, showing up a strange odd–even width effect. For metallic rings, the persistent current is a linearly periodical function of magnetic flux , ϕ, while it is a sinusoidal periodical function of ϕ for semiconducting rings. With increasing N, in addition, the persistent current exponentially decreases (increases) at odd (even) N and falls finally into consistency at large enough N, showing the strange odd–even width effect existing only in narrow rings. The results may be very helpful for the design and application of HGR-based nanodevices.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 10674113), the Program for New Century Excellent Talents in University (NCET-06-0707), and the Foundation for the Author of National Excellent Doctoral Dissertation of China (Grant No. 200726).References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef.
- E. McCann, K. Kechedzhi, V. I. Falko, H. Suzuura, T. Ando and B. L. Altshuler, Phys. Rev. Lett., 2006, 97, 146805–146808 CrossRef CAS.
- S. V. Morozov, K. S. Novoselov, M. I. Katsnelson, F. Schedin, L. A. Ponomarenko, D. Jiang and A. K. Geim, Phys. Rev. Lett., 2006, 97, 016801–016804 CrossRef CAS.
- N. Xu and J. W. Ding, J. Phys.: Condens. Matter, 2008, 20, 485213–485217 CrossRef.
- Y. B. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS.
- T. Ohta, A. Bostwick, T. Seyller, K. Horn and E. Rotenberg, Science, 2006, 313, 951–954 CrossRef CAS.
- C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. Heer, Science, 2006, 312, 1191–1196 CrossRef CAS.
- K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozo, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379–1379 CrossRef CAS.
- L. A. Ponomarenko, F. Schedin, M. I. Katsnelson, R. Yang, E. W. Hill, K. S. Novolevov and A. K. Geim, Science, 2008, 320, 356–358 CrossRef CAS.
- S. Schnez, F. Molitor, C. Stampfer, J. Güttinger, I. Shorubalko, T. Ihn and K. Ensslin, Appl. Phys. Lett., 2009, 94, 012107–012109 CrossRef.
- B. Obradovic, R. Kotlyar, F. Heinz, P. Matagne, T. Rakshit, M. D. Giles, M. A. Stettler and D. E. Nikonov, Appl. Phys. Lett., 2006, 88, 142102–142104 CrossRef.
- T. J. Echtermeyer, M. C. Lemme, J. Bolten, M. Baus, M. Ramsteiner and H. Kurz, Eur. Phys. J. Spec. Top., 2007, 148, 19–26 Search PubMed.
- D. A. Areshkin and C. T. White, Nano Lett., 2007, 7, 3253–3259 CrossRef CAS.
- S. Russo, J. B. Oostinga, D. Wehenkel, H. B. Heersche, S. S. Sobhani, L. M. K. Vandersypen and A. F. Morpurgo, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085413–085417 CrossRef.
- P. Recher, B. Trauzettel, A. Rycerz, Y. M. Blanter, C. W. J. Beenakker and A. F. Morpurgo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235404–235408 CrossRef.
- A. Rycerz, Acta Physica Polonica A, 2009, 115, 322–325 Search PubMed.
- M. Büttiker, Y. Imry and R. Landauer, Phys. Lett. A, 1983, 96, 365–367 CrossRef.
- H. F. Cheung, Y. Gefen, E. K. Riedel and W. H. Shih, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6050–6062 CrossRef.
- E. Louis, J. A. Verges and G. Chiappe, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6912–6919 CrossRef CAS.
- M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045432–045439 CrossRef.
- K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresslhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954–17961 CrossRef CAS.
- K. Wakabayashi, M. Fujita, H. Ajiki and M. Sigrist, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8271–8282 CrossRef CAS.
- Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS.
- H. X. Zheng, Z. F. Wang, T. Luo, Q. W. Shi and J. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165414–165419 CrossRef.
- J. W. Mintmire, B. I. Dunlap and C. T. White, Phys. Rev. Lett., 1992, 68, 631–634 CrossRef CAS.
- R. Saito, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 1804–1811 CrossRef CAS.
- M. F. Lin and D. S. Chuu, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 6731–6737 CrossRef CAS.
- S. Latil, S. Roche and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 165420–165428 CrossRef.
- D. A. Bahamon, A. L. C. Pereira and P. A. Schulz, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125414–125420 CrossRef.
- C. P. Liu and J. W. Ding, J. Phys.: Condens. Matter, 2006, 18, 4077–4084 CrossRef CAS.
- A. R. Akhmerov, J. H. Bardarson, A. Rycerz and C. W. J. Beenakker, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 205416–205420 CrossRef.
- A. Cresti, G. Grosso and G. P. Parravicini, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 233402–233405 CrossRef.
- Z. Li, H. Qian, J. Wu, B. L. Gu and W. Duan, Phys. Rev. Lett., 2008, 100, 206802–206805 CrossRef.
- A. L. C. Pereira and P. A. Schulz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125402–125406 CrossRef.
| This journal is © The Royal Society of Chemistry 2009 |
