 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New pyroelectric figures of merit for harvesting dynamic temperature fluctuations†
Bastola
Narayan
a,
Qingping
Wang
 *ab,
James
Roscow
a,
Chaoying
Wan
*ab,
James
Roscow
a,
Chaoying
Wan
 c and
Chris
Bowen
a
c and
Chris
Bowen
a
aCentre of Integrated Materials, Processes and Structures (IMPS), Department of Mechanical Engineering, University of Bath, Bath, BA2 2ET, UK. E-mail: qw608@bath.ac.uk
bDepartment of Physics & Mechanical and Electronic Engineering, Hubei University of Education, Wuhan 430205, P. R. China
cInternational Institute for Nanocomposites Manufacturing (IINM), WMG, University of Warwick, CV4 7AL, UK
First published on 1st April 2025
Abstract
Pyroelectric materials are attracting increasing attention for a variety of applications including thermal imaging, thermal sensing, and energy harvesting. To select and design pyroelectric materials with optimal performance, figures of merit (FoMs) are utilized in terms of energy, voltage, and current sensitivity. However, existing FoMs do not take into account heat transfer parameters, such as thermal conductivity and thermal diffusivity. To address this challenge, this paper formulates new performance figures of merit for the selection and design of pyroelectric materials for harvesting dynamic temperature fluctuations. The new figures of merit are of interest for the selection of pyroelectric materials, the design of new materials, or the creation of novel composites for pyroelectric applications, in particular when there is a need for rapid thermal cycles to increase the frequency of operation and maximize the power output for thermal harvesting. High performance materials based on the new figures of merit are highlighted and evaluated, and comparisons between the material classes are discussed, including polycrystalline ceramics, single crystal materials, polymers, thin films, composites and 2D materials. Potential future high-performance pyroelectric materials for thermal harvesting are outlined.
1. Introduction
To address the energy demand in our modern society, two primary strategies have often been considered: reducing energy consumption through enhanced energy efficiency, or expanding our energy production. There is also growing interest in the development self-powered sensors and systems, to mitigate against the challenges associated with the management of the power delivery to a large number of discrete sensors. Energy harvesting has therefore emerged as a critical area of research focus, since it aims to address key challenges related to sustainability, technological innovation, our escalating global energy needs, and the need for continuous sensing and monitoring.Among the range of available energy harvesting technologies, thermal energy harvesting using pyroelectric materials has attracted interest in an attempt to capture and reuse waste heat.1 These materials have been produced as macroscopic devices that consist of pyroelectric sensors, energy harvesters and detectors.2,3 The power levels of these devices are often relatively low, where a common aspect is the low frequency of the thermal cycles; there is therefore a clear need to increase the maximum thermal excitation frequency, or maximise the volume of material that can exhibit a specific thermal cycle.
Pyroelectric materials, as a specialized subset of dielectric materials, exhibit a spontaneous polarization that changes with temperature to generate electrical charge. This unique property enables a pyroelectric material to convert thermal fluctuations into electrical energy, making them a promising solution for waste heat harvesting,4–7 in particular when there are large and/or rapid changes in temperature.8 The pyroelectric effect is also employed in thermal sensing, where the charge, current, or voltage, generated as a result of a temperature change in used for thermal imaging and infrared detection, including person/body heat sensors, and fire detectors.9,10 These fascinating materials also offer possibilities in X-ray generation,11 neutron generation,12 pyro-electrocatalytic disinfection,13 hydrogen production,14 and electrocaloric cooling.15
The origin of the pyroelectric effect stems from a change in the electric dipole moment, namely the polarisation, of a polar material with temperature. As an example, an increase in temperature excites the ions that constitute the dipole moment to a higher energy level in the potential well, thereby changing the mean equilibrium position in the lattice and the resulting dipole moment.16 There are generally two approaches to changing the temperature of a pyroelectric material to stimulate the dipole and generate an electrical charge, current or a voltage. The first approach relates to subjecting the pyroelectric material to a temperature shift from one steady state temperature (T1) to another temperature (T2), leading to a change in temperature (ΔT = T2 − T1) and a change in polarisation (ΔP) to produce electric charge at the surface of the material, thereby converting thermal to electrical energy. An example of such an approach is repeatedly placing a pyroelectric element in a high temperature (T1) and low temperature (T2) source, such as a hot and cold liquid6,17,18 and waiting for the pyroelectric to reach thermal equilibrium. An alternative approach involves the continuous variation of the temperature of a pyroelectric material over time using an oscillating heat source that induces a temperature–time function to generate a change in temperature (dT/dt). This is of interest when heat is generated cyclically at a relatively high frequency; examples include a fluctuating radiation thermal source, such as the intensity of sunlight which fluctuates due to natural processes such as the presence of moving clouds,19 or heat produced by high-speed electronic switches for computing and data transmission.20
While a number of performance figures of merit exist1,9 for thermal sensing, imaging and harvesting, there are currently no performance figures of merit that take into account the limits imposed due to thermal phenomena and the time–temperature thermal response of a pyroelectric element, such as the thermal conductivity (λ) or thermal diffusivity (K). These parameters are of interest since, intuitively, they can improve the rate of change in temperature and provide a limit to the maximum achievable operating frequency in terms of thermal cycling. Methods to enhance the heat transfer have included patterning the surface of the pyroelectric to improve the absorption of incident radiation21,22 or combining a pyroelectric with plasmonic nanomaterials.19,23 However, less attention has been given to the design and selection of the pyroelectric material in terms of their heat transfer parameters.
Before outlining new figures of merit that take into account the ability of a materials to achieve rapid thermal cycles, it is necessary to first outline the range of existing pyroelectric-related figures of merit.
2. Pyroelectric effect and existing figures of merit (FoMs)
Fig. 1 is a schematic of the pyroelectric effect, where we will consider a pyroelectric thermal harvester polarised through its thickness, with electrically conductive electrode located on its upper and lower surfaces. Initially the pyroelectric material is at a temperature (T1) and is at electrostatic equilibrium since the polarisation of the material is balanced by surface screening charges on the upper and lower electrode surfaces located normal to the polarisation direction, see Fig. 1a. An increase in the temperature of a pyroelectric material (dT/dt > 0) to T2, as shown in Fig. 1b, leads to a reduction in spontaneous polarisation due to an enhanced dipole oscillation. This, in turn, triggers electron migration and current flow (I) in an external circuit to establish a new electrostatic equilibrium, as seen in Fig. 1c. In contrast, when the pyroelectric element is cooled (dT/dt < 0), the spontaneous polarisation of the pyroelectric increases, therefore disturbing the electrical equilibrium and inducing reverse electron migration, so that current flows in the opposite direction,1Fig. 1d, to establish to new state of equilibrium. Since pyroelectric charge is generated by a change in temperature, the power output is naturally also varying time, where the current will change direction during each heating and cooling cycle. As with a piezoelectric energy harvester the output is therefore AC in nature, and some form of rectification is typically required to provide a DC output, or store the electrical energy.1 The pyroelectric coefficient (p, units of C m−2 K−1) quantifies the pyroelectric effect by measuring the capacity of a material to modify its polarisation intensity (Ps), and produce electrical charge (Q), in response to a change in temperature. The pyroelectric coefficient of an unclamped material, under a constant stress and electric field is defined by eqn (1),1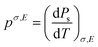 | (1) |
Under short-circuit conditions, the resulting pyroelectric electric current (Isc) generated by a pyroelectric material with an electrode area (A) can be determined from,1
 | (2) |
2.1 Pyroelectric figures of merit (FoMs) for thermal sensing
A variety of FoMs have been developed for thermal sensing using pyroelectric materials, with the most popular being the pyroelectric current sensitivity (Fi), voltage sensitivity (FV), and detectivity (FD), which are now defined.A pyroelectric current can be used for sensing changes in temperature, and the relevant figure of merit regarding the current responsivity (Fi) for a given thermal input can be expressed as:24
 | (3) |
The voltage generated can also be used for thermal sensing, where the pyroelectric voltage sensitivity (FV) can be written as:25
 | (4) |
An additional figure of merit for pyroelectric-based thermal detection also considers the impact of Johnson noise,16 by including the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the pyroelectric material in the specific detectivity figure of merit:
δ) of the pyroelectric material in the specific detectivity figure of merit:
 | (5) |
A final voltage-based pyroelectric sensing figure of merit has been developed that aims to minimise lateral thermal diffusion of heat for high special frequencies in the image, by including the thermal diffusivity of the pyroelectric:1
 | (6) |
 ,26 In this case, a low thermal diffusivity reduces the lateral diffusion of heat in pyroelectric detector.
,26 In this case, a low thermal diffusivity reduces the lateral diffusion of heat in pyroelectric detector.
For a thermal detector, the figures of merit shown in eqn (3)–(6) are employed to enable effective materials or materials design to maximise device performance. The ideal pyroelectric material in this regard should have (i) a low specific heat to produce a large change in temperature for a given thermal input, (ii) a high pyroelectric coefficient to maximise the charge generated for a given dT/dt, (iii) a low dielectric loss, and (iv) a low dielectric permittivity to maximise the voltage output for a given level of charge. A low thermal diffusivity (K) also reduces lateral diffusion of heat for detectors.
The pyroelectric sensing figures of merit, eqn (3)–(6) are related to the generated voltage or current. However, a current or voltage in isolation does not provide an indication of the electrical energy (or potential power), and is therefore unsuitable for energy harvesting applications, where the generation of energy, power or assessing the overall efficiency of converting thermal energy to electrical energy are important criteria.
2.2 Pyroelectric figures of merit for thermal energy harvesting
For pyroelectric energy harvesting applications, the pyroelectric element usually operates in one of two different modes. For example, it can (i) cycle between two specific temperatures, T1 and T2 (e.g. of hot and cold source), as in Fig. 2a, or (ii) is exposed to an incident heat source that modulates its output and provides a specific power density, W, as in Fig. 2b; in this case the final temperature change of the pyroelectric is dependent on specific heat capacity of the material for a given thermal input.Two examples of the figures of merit for thermal harvesting using pyroelectrics have been proposed.27,28 Firstly, an electro-thermal coupling factor (k) has been defined to estimate the efficiency of thermal harvesting when cycling between two temperatures, as shown in eqn (7): 27
 | (7) |
A pyroelectric energy-harvesting figure of merit, FE, has also been proposed as:28
 | (8) |
It is of interest to note that compared to the voltage (Fv) and current (Fi) responsivities, the energy harvesting figure of merit, FE, does not include the volume heat capacity since it is based on cycling between two specific temperatures (e.g. T1 and T2), rather than a given thermal input (which is the case for thermal imaging applications). To assess the energy generated for a given thermal input, a modified figure of merit 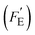 was recently derived which is the product of Fi (eqn (3)) and FV (eqn (4)), expressed as:32
was recently derived which is the product of Fi (eqn (3)) and FV (eqn (4)), expressed as:32
 | (9) |
3. New pyroelectric FoMs for harvesting dynamic temperature fluctuations
The figures of merit derived above for energy harvesting (eqn (8) and (9)) can be used to assess the electrical energy generated for a single thermal cycle. For example, FE is related to the electrical energy (E) generated for a specific temperature change (ΔT), as shown in Fig. 2a, while relates to the electrical energy for a given thermal input, see Fig. 2b. Since power (P) is related to the energy generated per cycle (E) and frequency (f), where P = Ef, the maximum frequency of operation (fmax) is of interest; namely how fast the material can realistically be heated and cooled.
relates to the electrical energy for a given thermal input, see Fig. 2b. Since power (P) is related to the energy generated per cycle (E) and frequency (f), where P = Ef, the maximum frequency of operation (fmax) is of interest; namely how fast the material can realistically be heated and cooled.
As an example, Pandya et al.33 examined the pyroelectric power density when operating a thermal cycling frequencies in the range of 10–2000 Hz. The maximum operating frequency to achieve thermal cycling is likely to be related to the heat transfer properties of the material, which are rarely included in the FE and 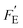 figures of merit outlined above. We now derive new figures of merit to take this into account based on the two modes of operation in Fig. 2.
figures of merit outlined above. We now derive new figures of merit to take this into account based on the two modes of operation in Fig. 2.
Let us consider a pyroelectric material exposed to a heat source or radiation at a power density W (J s−1 m−2), that is modulated at a frequency (f). The heat is absorbed by the surface of the material, leading to an increase in temperature. For the energy harvesting figures of merit outlined above (eqn (8) and (9)), it is often assumed that the thermal energy is absorbed rapidly and is homogenously distributed throughout the volume of the pyroelectric, resulting in a uniform temperature change (ΔT). For example, for FE, the material is cycled between two temperatures T1 and T2, and assumed to have attained thermal equilibrium. Likewise,  relates to the electrical energy for a given thermal input, leading to a uniform temperature change (ΔT) throughout the whole volume of the pyroelectric.32
relates to the electrical energy for a given thermal input, leading to a uniform temperature change (ΔT) throughout the whole volume of the pyroelectric.32
However, to achieve a uniform change in temperature throughout the pyroelectric, it is important to establish a thermal equilibrium between the pyroelectric and the heat source. The need for a state of thermal equilibrium has an impact on the frequency of temperature cycles, the rate of heating, and the time intervals between temperature changes. As a result, it is important to recognise that it takes a finite time for the material to reach thermal equilibrium, which determines how quickly the material can respond to a fluctuating heat source. This in turn impacts the maximum frequency of thermal changes, and the maximum power output since Pmax = Efmax.
In this regard, we can take inspiration from heating concepts that are used to undertake pyroelectric measurements, where homogeneous heating of the sample under test is also a requirement for precise measurement of the pyroelectric coefficient (p). The time required to establish a thermal equilibrium between the pyroelectric sample and a heat source determines the excitation frequency, heating rate, or duration between the temperature cycles. Jachalke et al.26 have provided a detailed overview of methods to undertake pyroelectric measurements, where the maximum thermal excitation frequency to achieve homogeneous heating of a pyroelectric element of thickness, t, is achieved at the condition  , where ω is the angular frequency,
, where ω is the angular frequency,  is the thermal diffusivity, λ is the thermal conductivity, ρ is the mass density and cp is the specific heat capacity. Thus, the maximum thermal excitation frequency can be written as26,34
is the thermal diffusivity, λ is the thermal conductivity, ρ is the mass density and cp is the specific heat capacity. Thus, the maximum thermal excitation frequency can be written as26,34
 | (10) |
This maximum frequency is derived based on the assumption that the sample is heated on both sides to achieve thermal equilibrium. Jachalke et al.26 has also provided a detailed evaluation of single-sided heating, leading to a fmax that is four times smaller. Eqn (10) implies that for thermal energy harvesting via thermal cycling, (i) bulk pyroelectric materials, which have a large t, face limitations in terms of operating at high frequencies since it takes longer to change the temperature and reach thermal equilibrium throughout the material; (ii) pyroelectric thin film materials, which have a low t, have potential to be cycled at high frequencies, since they will take short time to reach thermal equilibrium;34 for example, thin films with a large surface diameter and small thickness (t) can achieve maximum cycling frequencies in the kHz range;26 and (iii) pyroelectric materials with a low thermal diffusivity (K) also have a limit on their ability to be rapidly thermally cycled. While a low thermal diffusivity is desirable for thermal sensing since it reduces unwanted lateral diffusion (see eqn (6)), a high thermal diffusivity is therefore preferable for rapid thermal cycling for energy harvesting since it facilitates a higher operating frequency, or allows a larger thickness (and therefore volume) of pyroelectric material to be employed when operating at specific frequency.35
In terms of heat transfer properties, semiconductors, where electron transport dominates thermal conduction (as opposed to phonons in insulators36) can exhibit high thermal conductivity and diffusivity, although dielectric losses may increase. Single crystals, which are characterized by long-range atomic order,37 also facilitate efficient heat transfer. The inherent structure of 2D materials is also attractive since it enables efficient heat transfer as a result of surface scattering that alters the contribution of phonons with long mean free paths.38 In contrast, bulk polycrystalline ceramics can lead to strong phonon localization, thereby reducing the thermal conductivity.39 Similarly, materials incorporating nanoscale electrically insulating dopants exhibit a low thermal conductivity and diffusivity as a result of defect scattering, which can hinder heat transfer and impede achieving thermal equilibrium.36,39 Polymers and polymer-derived composites can also contain air-filled gaps, voids, or interfaces, resulting in a significant interfacial thermal resistance across any contacting surfaces, thereby limiting heat transfer.40
While eqn (10) indicates that the search for materials with low volumetric heat capacity (cE = ρcp) is beneficial, this property tends to be relatively consistent across different materials as a result of the Dulong-Petit law,41 which states that the molar heat capacity of a solid is equal to approximately 3R, where R is the gas constant.42 As a result, low thickness and high thermal conductivity are the most important criteria for maximizing the thermal excitation frequency.
Based on this knowledge, we can now introduce two new figures of merit to generate a large amount of energy per cycle (E) while also enabling high-frequency heating and cooling (a high fmax) to produce a high-power output, since Pmax = Efmax. First, we consider a pyroelectric energy harvesting element undergoes a temperature change from T1 to T2 by placing a pyroelectric material in thermal contact with a cold and a hot source, as in Fig. 2a.17,19
The temperature change is given by:
| ΔT = T2 − T1 | (11) |
When a pyroelectric is subjected to a temperature change (ΔT), the charge (ΔQ) released by the area (A) of pyroelectric material due to a change in polarisation is given by,
| ΔQ = pAΔT | (12) |
It is evident from eqn (12) that the amount of pyroelectric charge can be optimized by increasing the area (and the corresponding screening charge, Fig. 1b), increasing the pyroelectric coefficient (the change in polarisation), or having a large change in temperature.
The pyroelectric element can be considered as a parallel plate capacitor with conducting electrodes of area A on either side of a dielectric pyroelectric material with a thickness, t, as shown in Fig. 1. The capacitance, C, of the pyroelectric element is given by:
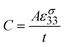 | (13) |
Since the charge (Q) is correlated with the capacitance (C) and voltage (V) by Q = CV, the open circuit voltage, VOC, generated due to the temperature change can be written as:
 | (14) |
Eqn (14) indicates that the open circuit voltage, VOC, can be increased by increasing the thickness of the pyroelectric element, the pyroelectric coefficient, and the temperature change, or by reducing the permittivity of the material.
For energy harvesting applications, we are interested in the electrical energy (E) produced and stored in the parallel plate capacitor of capacitance of C, which can be written as  , so that,
, so that,
 | (15) |
It can be seen that the pyroelectric charge (eqn (12)), open circuit voltage (eqn (14)), and energy per thermal cycle (eqn (15)) are independent of frequency and are simply a function of the temperature change (ΔT), while the short circuit current (eqn (2)) is a function of the rate of change of temperature (dT/dt) and is dependent on the frequency of the thermal cycle. Whatmore16 has provided an excellent overview and discussion of the analysis of pyroelectric detectors, and their frequency dependence, on considering both the thermal and electrical circuits.
Based on eqn (15), the corresponding energy density (energy per unit volume) for a single thermal cycle, can therefore be written as:
 | (16) |
This leads to the pyroelectric energy harvesting figure of merit, FE, that maximises the energy produced for a given temperature change ΔT and volume of material (At):26,32–35
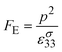 | (17) |
However, based on a maximum operating frequency (fmax) where the materials can be cycled between T1 and T2, the maximum power (Pmax) is:
| Pmax = Efmax | (18) |
Therefore, while the energy (E) per thermal cycle (eqn (15)) is independent of the temperature change, since power (eqn (18)) is related to the number of cycles per unit time, it is advantageous to achieve high-frequency thermal oscillations, where fmax is given by eqn (10).
Using eqn (10), (15) and (18) the maximum achievable power density when attempting to cycle the pyroelectric element between a given hot and cold temperature source is,
 | (19) |
If we consider the case for a pyroelectric energy harvester with a specific surface area A and thickness t, that is subjected to a specific temperature change ΔT, the maximum power output can be expressed by a new figure of merit, which is termed the first pyroelectric power figure of merit, FP1, as defined as:
 | (20) |
This figure of merit can also be written in terms of the thermal diffusivity (K) as:
 | (21) |
Therefore, in the mode of thermal harvesting in Fig. 2a there is benefit in using materials with a combination of a high pyroelectric coefficient (to enhance the charge generated), a low permittivity (to increase the output voltage) and a high thermal diffusivity (to increase the maximum operational frequency).
In addition to harvesting between two distinct temperature sources (T1 and T2), there may also be energy harvesters that are subject to an oscillating/modulating thermal energy source. An example of this approach involves varying the temperature by using a heating lamp, or sunlight, as a radiation source that is combined with a rotating disc chopper to periodically heat a pyroelectric element.43–45
In this configuration, the system directly harnesses a fluctuating/modulated thermal source, as illustrated in Fig. 2b, and the temperature increase of the pyroelectric is dependent on the volumetric specific heat. For example, if a pyroelectric material is exposed to radiation of power density W (J s−1 m−2) for a time, Δt, radiation is absorbed onto the surface of the material and results in an increase in the temperature, ΔT. If we assume that the radiation absorbed is evenly distributed throughout the pyroelectric element, there is a uniform temperature increase. Neglecting heat losses from the pyroelectric, the increase in temperature is related to incident power density by,
 | (22) |
Based on this assumption, the 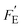 figure of merit (eqn (9)) determines the energy density for a single cycle when harvesting in such a configuration. This concept can also be combined with the maximum frequency of operation (fmax) based on a homogeneous temperature, defined by eqn (10), to provide a new figure of merit based on ability to generate power for a modulated thermal input:
figure of merit (eqn (9)) determines the energy density for a single cycle when harvesting in such a configuration. This concept can also be combined with the maximum frequency of operation (fmax) based on a homogeneous temperature, defined by eqn (10), to provide a new figure of merit based on ability to generate power for a modulated thermal input:
 | (23) |
This leads to a second pyroelectric power figure of merit, FP2
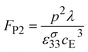 | (24) |
In terms of thermal diffusivity (K), the dynamic pyroelectric power figure of merit is given by:
 | (25) |
Both FP1 (eqn (21)) and FP2 (eqn (25)) represent two new pyroelectric power figures of merit for the selection and design of materials for pyroelectric energy harvesters. The new figures of merit are of interest for the selection of materials, and the design of pyroelectric materials for thermal harvesting devices. They provide guidance for the development of novel materials and composites for pyroelectric energy harvesting applications, in particular when there is a need for rapid thermal cycling to increase the frequency of operation and power output, depending on the mode of operation, as outlined in Fig. 2.
3.1 Materials selection based on new power figures of merit (FP1 and FP2)
Table 1 outlines the range of relevant properties for a variety of pyroelectric materials, which includes the relevant pyroelectric material properties (p, εσ33, ρ, cE, cp, λ and K) and a range of pyroelectric figures of merit for sensing (Fv and Fi), energy harvesting (FE and ) and the two new power-related figures of merit (FP1 and FP2). Table 1 provides the materials parameters and corresponding figures of merit of ceramics, semiconductors, single crystals, thin film, polymers, composites and 2D pyroelectric materials.
) and the two new power-related figures of merit (FP1 and FP2). Table 1 provides the materials parameters and corresponding figures of merit of ceramics, semiconductors, single crystals, thin film, polymers, composites and 2D pyroelectric materials.
| Material and class | |p| (×10−6 C m−2 K−1) | ε r | ρ (kg m−3) | c p (J kg−1 K−1) | c E (×106 J m−3 K−1) | λ (W m−1 K−1) | K (×10−7 m2 s−1) | F i (×10−12 m V−1) | F v (m2 C−1) | F E (J m−3 K−2) | (×10−12 m3 J−1) | F P1 (×10−6 W m−1 K−2) | F P2 (×10−18 m5 J−1 s−1) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PZT-5H ceramic | 533 (ref. 27) | 1116 (ref. 27) | 7600 | 340 | 2.58 | 1.4 (ref. 50) | 5.4 | 206.6 | 0.02 | 28.76 | 4.13 | 15.53 | 2.33 | 50 |
| BaTiO3 ceramic | 800 (ref. 54) | 2350 | 5710 | 360 | 2.06 (ref. 54) | 6.0 (ref. 55) | 29.1 | 388.3 | 0.019 | 30.77 | 7.37 | 89.54 | 21.1 | 54 and 55 |
| PLZT ceramic | 1200 (ref. 55) | 4285 | 6307 | 418.6 | 2.64 (ref. 55) | 0.77 | 2.9 (ref. 56) | 454.5 | 0.012 | 37.97 | 5.45 | 11.01 | 1.58 | 55 and 56 |
| AlN semiconductor | 5.0 | 9.1 | 5250 | 600 | 3.15 | 285 (ref. 57) | 904.8 | 1.59 | 0.02 | 0.31 | 0.03 | 28.05 | 2.83 | 55 and 57 |
| GaN semiconductor | 5.3 | 10.4 | 6428 | 490 | 3.15 | 130 (ref. 57) | 412.7 | 1.68 | 0.018 | 0.305 | 0.03 | 12.59 | 1.27 | 55 and 57 |
| 0.75PMN-0.25 PT single crystal | 1790 | 961 | — | — | 2.5 | 1.43 (ref. 58) | 5.7 | 716 | 0.0844 | 376.95 | 60.14 | 214.86 | 34.38 | 25 |
| LiNbO3 single crystal | 72 | 31.4 | 4652 | 627.6 | 2.92 | 5.6 | 19.2 | 24.66 | 0.089 | 18.65 | 2.19 | 35.81 | 4.19 | 55 |
| LiTaO3 single crystal | 180 | 47 | — | — | 3.2 | 4.6 | 14.37 | 56.25 | 0.135 | 77.89 | 7.59 | 111.93 | 10.93 | 59 |
| PVDF polymer | 25 | 9 | 1740 (ref. 58) | 1322 | 2.3 | 0.22 | 0.956 | 10.87 | 0.136 | 7.85 | 1.48 | 0.75 | 0.14 | 55 and 60 |
| PVDF–TrFE polymer | 35 | 8 | 1900 (ref. 60) | 1211 | 2.3 | 0.22 | 0.956 | 15.22 | 0.215 | 17.30 | 3.27 | 1.65 | 0.31 | 55 and 60 |
| HfO2 thin film | 46.2 | 31.5 | — | — | 2.63 | 14.1 (ref. 61) | 53.6 | 17.55 | 0.063 | 7.64 | 1.11 | 40.96 | 5.92 | 61 and 62 |
| PMN-PMS-PZT:0.2AlN | 4146 | 5357 | 6300 | 284 | 1.79 | 0.70 | 3.9 | 2316.2 | 0.049 | 362.6 | 113.49 | 142.5 | 44.47 | 24 |
| PMN-PMS-PZT:0.1BN | 3423 | 5730 | 6810 | 285 | 1.94 | 0.895 | 4.6 | 1764.4 | 0.035 | 231.06 | 61.75 | 106.52 | 28.3 | 47 |
| 2D-BP | 5287 (ref. 63) | 8.3 (ref. 64) | 2690 (ref. 65) | 800 (ref. 66) | 2.15 | 40 (ref. 67) | 186 | 2459.1 | 33.48 | 0.38 × 106 | 0.08 × 106 | 7.08 × 106 | 1.53 × 106 | 63–67 |
| In2Se3 | 5500 (ref. 68) | 17 (ref. 69) | — | — | 1.4 (ref. 70) | 60 (ref. 71) | 428.6 | 3928.6 | 26.1 | 0.2 × 106 | 0.1 × 106 | 8.57 × 106 | 4.372 × 106 | 68–71 |
Ashby materials selection charts have been produced to provide a visual representation of the data in Table 1. This is achieved by taking logarithms and selecting specific properties for the x- and y-axes and has been recently used for Fv (eqn (3)) and FD (eqn (5)).46
From eqn (21), for the selection of materials with high FP1 when thermally cycling between two temperature sources T1 and T2, this leads to:
 | (26) |
Therefore, on a log–log graph where FE is the y-axis and thermal diffusivity (K) is the x-axis, it is possible to produce lines of constant FP1, by placing a line of gradient n = −1 on the chart, as shown in Fig. 3a.
 | ||
Fig. 3 Ashby charts. (a) Selection of materials with high FP1 = FEK, lines of constant FP1 can be drawn via a gradient of n = −1, based on eqn (26). (b) Selection of materials with high  , lines of constant FP2 can be drawn via a gradient of n = −1, based on eqn (27). , lines of constant FP2 can be drawn via a gradient of n = −1, based on eqn (27). | ||
From eqn (25), for the selection of materials with high FP2, when harvesting a modulated thermal input, this leads to:
 | (27) |
Likewise, on a log–log graph with  on the y-axis and thermal diffusivity (K) on the x-axis, it is possible to draw lines of constant FP2 by placing a line of gradient n = −1 on the chart, as in Fig. 3b.
on the y-axis and thermal diffusivity (K) on the x-axis, it is possible to draw lines of constant FP2 by placing a line of gradient n = −1 on the chart, as in Fig. 3b.
There are no significant changes in order or relative location of materials in the Ashby charts in Fig. 3a and b, which is a result of the relatively small variation in volumetric specific heat between the range of materials in the literature; see Table 1. The polymeric ferroelectric materials have relatively low FP1 and FP2, due to the low thermal diffusivity and low pyroelectric coefficients (Fig. 3 and Table 1). The pyroelectric semiconductor materials (GaN and AlN) have a high thermal diffusivity but relatively low FP1 and FP2 due to their low pyroelectric coefficients. Polycrystalline ferroelectric materials (PZT, PLZT and BaTiO3) exhibit relatively high FP1 and FP2 due to their high pyroelectric coefficients and intermediate values of thermal diffusivity. The single-crystal and thin-film materials (LiTaO3, LiNbO3, HfO2, and PMN-PT) are of interest since they exhibit high pyroelectric coefficients and relatively high thermal diffusivity. The composite materials perform relatively well, see both Fig. 3 and Table 1; composites are of interest since they provide a route to tailor the pyroelectric, dielectric and heat transfer properties. Composites could be developed to combine a material with high pyroelectric coefficient and a high thermal conductivity; for example, Wang et al. explored the potential of ferroelectric ceramics that contain a thermally conductive network with AlN or BN nanoparticles for thermal harvesting applications.24,47
Recently, two-dimensional pyroelectric materials have attracted interest in waste thermal energy harvesting.48 There is evidence that such materials can exhibit large thermal conductivities, up to 500 W m−1 K−1,49 although less work has aimed at producing both thermal properties and pyroelectric coefficient, and is a potential topic of future interest. The 2D few-layer black phosphorus material in Fig. 3 and Table 1 indicates potential to achieve a very high FP1 and FP2 values due to a combination of a high pyroelectric coefficient and high thermal diffusivity.
Interestingly, external factors can also have an impact on the heat transfer properties. Shekhan et al.50 indicated a difference in the thermal conductivity of a pyroelectric in the poling direction depending on whether the materials was under a short-circuit (λE33), open-circuit (λD33) and unpoled (λu) condition, whereby λE33 > λD33 > λu. This indicates the mode of operation of a pyroelectric can have on influence on thermal response. Changes in the thermal conductivity of ferroelectrics have also been linked to variations in the piezoelectric coefficient,51 applied electric field52 and light.53
In addition to the figures of merit, the equations above can also indicate simple geometric considerations for thermal energy harvesting. Clearly, there is a need to maximise the active area (A) of the pyroelectric to maximise the amount of surface charge, see eqn (12) and Fig. 1. While a large volume (At) is desirable to maximise the amount of electrical energy produced in a single cycle, see eqn (15), the pyroelectric should be as thin as possible to maximise the frequency of operation by reducing the time required to establish thermal equilibrium between the pyroelectric sample and the heat source, see eqn (10). While the two new figures of merit (eqn (21) and (25)), have been derived based on attempting to maximise the thermal excitation frequency (fmax) for a pyroelectric element with a specific thickness, it is also of interest to consider thermal harvesting of a heat source that is fluctuating at a specific frequency, f. In this case, a high thermal diffusivity material enables homogeneous heating of pyroelectric element of larger thickness (eqn (10)), and therefore volume, to increase the energy per cycle; for example, when thermal cycles are provided by a rotating disc chopper rotating at a constant speed.45 From eqn (10) it can be seen that the maximum thickness (tmax) is given by tmax = (K/πf)0.5, and this leads to a modified figure of merit,  ; a full derivation of this figure of merit, and FP1, are included in the supplemental material. There is potential to produce Ashby diagrams that include both materials properties and shape-factors for optimising the material-and-shape combination.72
; a full derivation of this figure of merit, and FP1, are included in the supplemental material. There is potential to produce Ashby diagrams that include both materials properties and shape-factors for optimising the material-and-shape combination.72
4. Conclusions
This paper has outlined new performance figures of merit for the selection and design of pyroelectric materials for harvesting dynamic temperature fluctuations. These new figures of merit are able to assist in selection of the most suitable pyroelectric materials for optimal power output while harvesting thermal cycles for a range of thermal cycles. According to these new criteria, materials for thermal harvesting should exhibit (i) a high pyroelectric coefficient to maximise the generated charge for a given change in temperature (ΔT), (ii) a low permittivity to maximise the voltage and electrical energy for a given charge (eqn (14) and (15)), (iii) a high thermal diffusivity or thermal conductivity to maximise the operational frequency by reducing the time required to establish a thermal equilibrium (eqn (10)), and (iv) a low heat capacity to maximise the temperature change, when the pyroelectric is subjected to a varying thermal input; however, for many materials this parameter is similar as a result of the Dulong–Petit law.42 A clear route to increase the power output significantly is therefore to design, or discover, new materials with this attractive combination of properties. The analysis here also provides guidelines for geometric considerations where the pyroelectric should be as thin as possible, to maximise the frequency of operation, but of high active area to maximise the amount of charge generated. A high thermal diffusivity also enables a pyroelectric element with a larger thickness, and therefore volume, to be employed when a thermal cycle is at a specific frequency. The new figures of merit therefore provide a quantitative approach for the selection and design of materials where composites, single crystal-like and emerging two-dimensional pyroelectrics appear particularly attractive as a route to produce materials with a unique combination of high pyroelectric activity and high heat transfer properties.Data availability
The data supporting this article have been included as references.Author contributions
Bastola Narayan: writing of the original draft, conceptualization, analysis, methodology and investigation, editing, review. Qingping Wang: writing of the original draft, conceptualization, methodology, data collection and investigation, editing, review. James Roscow: editing, review. Chaoying Wan: editing, review. Chris Bowen: conceptualization, methodology, supervision, analysis, writing of the original draft, editing, review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
BN and CB acknowledge support of UKRI Frontier Research Guarantee on “Processing of Smart Porous Electro-Ceramic Transducers – ProSPECT”, Project No. EP/X023265/1. QW acknowledges support of UKRI Postdoctoral Fellowship Guarantee (Project No. EP/Y017412/1), and the National Natural Science Foundation of China (Project No. 51902094).References
- C. R. Bowen, J. Taylor, E. LeBoulbar, D. Zabek, A. Chauhan and R. Vaish, Energy Environ. Sci., 2014, 7, 3836–3856 Search PubMed.
- P. Lheritier, A. Torello, T. Usui, Y. Nouchokgwe, A. Aravindhan, J. Li, U. Prah, V. Kovacova, O. Bouton, S. Hirose and E. Defay, Nature, 2022, 609, 718–721 CAS.
- Q. Q. Wu, Y. Zhao and X. C. Li, Sens. Actuators, A, 2024, 367, 115050 CrossRef CAS.
- L. Kouchachvili and M. Ikura, Int. J. Energy Res., 2008, 32, 328–335 CrossRef CAS.
- I. M. McKinley, S. Goljahi, C. S. Lynch and L. Pilon, J. Appl. Phys., 2013, 114, 224111 CrossRef.
- A. Navid and L. Pilon, Smart Mater. Struct., 2011, 20, 025012 Search PubMed.
- Q. Wang, Q. Sun, Z. Xu, H. Luo, S. Li and T. Wu, Surf. Interfaces, 2024, 51, 104657 CAS.
- S. Jachalke, E. Mehner, H. Stöcker, J. Hanzig, M. Sonntag, T. Weigel, T. Leisegang and D. C. Meyer, Appl. Phys. Rev., 2017, 4, 021303 Search PubMed.
- R. Whatmore, in Characterisation of Ferroelectric Bulk Materials and Thin Films, ed. M. G. Cain, Springer Netherlands, Dordrecht, 2014, pp. 65–86 Search PubMed.
- S. B. Lang, Phys. Today, 2005, 58, 31–36 CAS.
- J. D. Brownridge, Nature, 1992, 358, 287–288 Search PubMed.
- S. Mohtashami, H. Afarideh and K. Moshkbar-Bakhshayesh, J. Appl. Phys., 2024, 135, 200701 CAS.
- E. Gutmann, A. Benke, K. Gerth, H. Böttcher, E. Mehner, C. Klein, U. Krause-Buchholz, U. Bergmann, W. Pompe and D. C. Meyer, J. Phys. Chem. C, 2012, 116, 5383–5393 CrossRef CAS.
- A. Kakekhani and S. Ismail-Beigi, J. Mater. Chem. A, 2016, 4, 5235–5246 CAS.
- Z. Kutnjak, B. Rožič and R. Pirc, in Wiley Encyclopedia of Electrical and Electronics Engineering, John Wiley & Sons, Ltd, 2015, pp. 1–19 Search PubMed.
- R. W. Whatmore, Rep. Prog. Phys., 1986, 49, 1335 CAS.
- F. Y. Lee, A. Navid and L. Pilon, Appl. Therm. Eng., 2012, 37, 30–37 CAS.
- Q. Leng, L. Chen, H. Guo, J. Liu, G. Liu, C. Hu and Y. Xi, J. Mater. Chem. A, 2014, 2, 11940–11947 CAS.
- M. Shiran Chaharsoughi, D. Tordera, A. Grimoldi, I. Engquist, M. Berggren, S. Fabiano and M. P. Jonsson, Adv. Opt. Mater., 2018, 6, 1701051 Search PubMed.
- J. P. Feser and J. Ravichandran, Nat. Mater., 2018, 17, 385–386 CAS.
- C. S. Wei, Y. Y. Lin, Y. C. Hu, C. W. Wu, C. K. Shih, C. T. Huang and S. H. Chang, Sens. Actuators, A, 2006, 128, 18–24 CAS.
- D. Zabek, J. Taylor, E. L. Boulbar and C. R. Bowen, Adv. Energy Mater., 2015, 5, 1401891 Search PubMed.
- Q. Wang, C. R. Bowen and V. K. Valev, Adv. Funct. Mater., 2024, 34, 2312245 CAS.
- Q. Wang, C. R. Bowen, W. Lei, H. Zhang, B. Xie, S. Qiu, M.-Y. Li and S. Jiang, J. Mater. Chem. A, 2018, 6, 5040–5051 CAS.
- Q. Wang, X. Zhang, C. R. Bowen, M.-Y. Li, J. Ma, S. Qiu, H. Liu and S. Jiang, J. Alloys Compd., 2017, 710, 869–874 CrossRef CAS.
- S. Jachalke, E. Mehner, E. Mehner, H. Stöcker, J. Hanzig, M. Sonntag, T. Weigel, T. Leisegang and D. C. Meyer, Appl. Phys. Rev., 2017, 4, 021303 Search PubMed.
- G. Sebald, E. Lefeuvre and D. Guyomar, IEEE Trans. Ultrason. Ferroelectrics Freq. Control, 2008, 55, 538–551 Search PubMed.
- G. Sebald, L. Seveyrat, D. Guyomar, L. Lebrun, B. Guiffard and S. Pruvost, J. Appl. Phys., 2006, 100, 124112 Search PubMed.
- R. V. K. Mangalam, J. C. Agar, A. R. Damodaran, J. Karthik and L. W. Martin, ACS Appl. Mater. Interfaces, 2013, 5, 13235–13241 CrossRef CAS PubMed.
- S. K. T. Ravindran, T. Huesgen, M. Kroener and P. Woias, Appl. Phys. Lett., 2011, 99, 104102 Search PubMed.
- A. Navid, C. S. Lynch and L. Pilon, Smart Mater. Struct., 2010, 19, 055006 Search PubMed.
- C. R. Bowen, J. Taylor, E. Le Boulbar, D. Zabek and V. Yu. Topolov, Mater. Lett., 2015, 138, 243–246 CAS.
- S. Pandya, J. Wilbur, J. Kim, R. Gao, A. Dasgupta, C. Dames and L. W. Martin, Nat. Mater., 2018, 17, 432–438 CAS.
- C. Dias, M. Simon, R. Quad and D. K. Das-Gupta, J. Phys. D: Appl. Phys., 1993, 26, 106 CAS.
- D. Zhang, H. Wu, C. R. Bowen and Y. Yang, Small, 2021, 17, 2103960 CAS.
- G. Burns. Solid State Physics; Academic Press, Inc., 1985, pp: 433–441 Search PubMed.
- https://www.sciencedirect.com/topics/engineering/thermal-equilibrium .
- Z. Luo, J. Maassen, Y. Deng, Y. Du, R. P. Garrelts, M. S. Lundstrom, P. D. Ye and X. Xu, Nat. Commun., 2015, 6, 8572 CAS.
- R. J. Balsano, Thermal Conductivity Measurement of (TiO2)1-x(HfO2)x, Master thesis, Binghamton University, 2007.
- X. Xu, J. Chen, J. Zhou and B. Li, Adv. Mater., 2018, 30, 1705544 CrossRef.
- Y. Qizhen, Z. Zhang, G. Haibo and W. Yang, Physical properties and effect of helium-vacancy pair on tungsten/graphene composite as plasma-facing materials from first principles, Fusion Sci. Technol., 2023, 80, 178–195 CrossRef.
- L. D. Landau and E. M. Lifshitz, Statistical Physics Pt. 1. Course in Theoretical Physics: Pergamon Press, Oxford, 3rd edn, 1980, vol. 5, pp. 193–196 Search PubMed.
- P. Mane, J. Xie, K. K. Leang and K. Mossi, IEEE Trans. Ultrason. Ferroelectrics Freq. Control, 2011, 58, 10–17 Search PubMed.
- M. Xie, D. Zabek, C. Bowen, M. Abdelmageed and M. Arafa, Smart Mater. Struct., 2016, 25, 125023 CrossRef.
- S. H. Krishnan, D. Ezhilarasi, G. Uma and M. Umapathy, IEEE Trans. Sustain. Energy, 2014, 5, 73–81 Search PubMed.
- M. Ashby, T. Davies and S. Gorsse, The CES EduPack DB for Bulk Functional Materials, 2015, pp. 1–45, https://www.teachingresources.grantadesign.com Search PubMed.
- Q. Wang, C. R. Bowen, R. Lewis, J. Chen, W. Lei, H. Zhang, M.-Y. Li and S. Jiang, Nano Energy, 2019, 60, 144–152 CrossRef CAS.
- A. Kumar and D. Mandal, Adv. Energy Mater., 2024, 14, 2403319 CrossRef CAS.
- B. Mortazavi, B. Javvaji, F. Shojaei, T. Rabczuk, A. V. Shapeev and X. Zhuang, Nano Energy, 2021, 82, 105716 CrossRef CAS.
- H. N. Shekhan, E. A. Gurdal, L. Ganapatibhotla, J. K. Maranas, R. Staut and K. Uchino, Insight - Mater. Sci., 2020, 3, 10 CrossRef.
- D. Rashadfar, B. L. Wooten and J. P. Heremans, arXiv, 2025, preprint, arXiv:2402.08516, DOI:10.48550/arXiv.2402.08516.
- C. Liu, Z. Chen, C. Wu, J. Qi, M. Hao, P. Lu and Y. Chen, ACS Appl. Mater. Interfaces, 2022, 14, 46716–46725 CrossRef CAS.
- C. Cazorla, S. Bichelmaier, C. Escorihuela-Sayalero, J. Íñiguez, J. Carrete and R. Rurali, Nanoscale, 2024, 16, 8335–8344 RSC.
- K. K. Deb, M. D. Hill and J. F. Kelly, J. Mater. Res., 1992, 7, 3296–3305 CrossRef CAS.
- S. Jachalke, Characterization of Novel Pyroelectrics: From Bulk to Thin Film HfO2, PhD thesis, Technische Universität Bergakademie Freiberg, 2019.
- T. H. Lin, D. Edwards, R. E. Reedy, K. Das, W. McGinnis and S. H. Lee, Ferroelectrics, 1988, 77, 153–160 CrossRef CAS.
- NSM Archive - Aluminium Nitride (AlN) - Thermal properties, https://www.matprop.ru/AlN_thermal, accessed January 20, 2025 Search PubMed.
- A. Negi, H. P. Kim, Z. Hua, A. Timofeeva, X. Zhang, Y. Zhu, K. Peters, D. Kumah, X. Jiang and J. Liu, Adv. Mater., 2023, 35, 2211286 CrossRef CAS PubMed.
- B. Ploss and S. Bauer, Sens. Actuators, A, 1991, 26, 407–411 CrossRef CAS.
- R. d. Simoes, M. a. Rodriguez-Perez, J. a. De Saja and C. j. l. Constantino, Polym. Eng. Sci., 2009, 49, 2150–2157 CAS.
- S. Zhang, S. Yi, J.-Y. Yang, J. Liu and L. Liu, Int. J. Heat Mass Transfer, 2023, 207, 123971 CAS.
- S. Jachalke, T. Schenk, M. H. Park, U. Schroeder, T. Mikolajick, H. Stöcker, E. Mehner and D. C. Meyer, Appl. Phys. Lett., 2018, 112, 142901 Search PubMed.
- H. You, Y. Jia, Z. Wu, F. Wang, H. Huang and Y. Wang, Nat. Commun., 2018, 9, 2889 Search PubMed.
- P. Kumar, B. S. Bhadoria, S. Kumar, S. Bhowmick, Y. S. Chauhan and A. Agarwal, Phys. Rev. B, 2016, 93, 195428 Search PubMed.
- P. Chen, N. Li, X. Chen, W.-J. Ong and X. Zhao, 2D Mater., 2017, 5, 014002 Search PubMed.
- Y. Aierken, D. Çakır, C. Sevik and F. M. Peeters, Phys. Rev. B, 2015, 92, 081408 Search PubMed.
- Z. Luo, J. Maassen, Y. Deng, Y. Du, R. P. Garrelts, M. S. Lundstrom, P. D. Ye and X. Xu, Nat. Commun., 2015, 6, 8572 CAS.
- J. Jiang, L. Zhang, C. Ming, H. Zhou, P. Bose, Y. Guo, Y. Hu, B. Wang, Z. Chen, R. Jia, S. Pendse, Y. Xiang, Y. Xia, Z. Lu, X. Wen, Y. Cai, C. Sun, G.-C. Wang, T.-M. Lu, D. Gall, Y.-Y. Sun, N. Koratkar, E. Fohtung, Y. Shi and J. Shi, Nature, 2022, 607, 480 CAS.
- D. Wu, A. J. Pak, Y. Liu, Y. Zhou, X. Wu, Y. Zhu, M. Lin, Y. Han, Y. Ren, H. Peng, Y.-H. Tsai, G. S. Hwang and K. La, Nano Lett., 2015, 15, 8136–8140 CrossRef CAS.
- H. Qi, C. Wu, P. Lu and C. Liu, Nanotechnology, 2024, 35, 085701 CrossRef CAS.
- S. Zhou, X. Tao and Y. Gu, J. Phys. Chem. C, 2016, 120, 4753–4758 CAS.
- M. F. Ashby, Acta Mater., 1991, 39, 1025 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta00704f |
| This journal is © The Royal Society of Chemistry 2025 |



