Graphendofullerene: a novel molecular two-dimensional ferromagnet

Abstract

Carbon chemistry has attracted a lot of attention from chemists, physicists and material scientists in the last few decades. The recent discovery of graphullerene provides a promising platform for many applications due to its exceptional electronic properties and the possibility to host molecules or clusters inside the fullerene units. Herein, we introduce graphendofullerene, a novel molecular-based two-dimensional (2D) magnetic material formed by trimetallic nitride clusters encapsulated on graphullerene. Through first-principles calculations, we demonstrate the successful incorporation of the molecules into the 2D network formed by C₈₀ fullerenes, which leads to robust long-range ferromagnetic order with a Curie temperature (T_C) of 38 K. Additionally, we achieve a 45% and 18% increase in T_C by strain engineering and electrostatic doping, respectively. These findings open the way for a new family of molecular 2D magnets based on graphendofullerene for advanced technologies.

---

Introduction

Since the mid 80s carbon chemistry has emerged as a prominent research field due to the discovery of synthetic carbon allotropes such as fullerenes^1,2 and carbon nanotubes,³ and the isolation of graphene in 2004,^4,5 thus offering countless possibilities for exploiting different physical phenomena.⁶ This is due to the different orbital hybridizations and arrangements that provide them with unique optical and electronic properties. In particular, graphene pioneered the field of 2D materials that nowadays covers a wide range of functionalities,^7,8 from insulators⁹ to superconductors¹⁰ and magnetic systems,¹¹ leading to applications in catalysis,¹² gas sensing,¹³ valleytronics¹⁴ and spintronics.¹⁵ Moreover, they can be assembled into van der Waals (vdW) heterostructures,¹⁶ and their layers can be twisted with respect to each other, to create novel multifunctional materials and devices.¹⁷

Fullerenes stand out due to their advanced applications in photovoltaics,¹⁸ biomedicine^19,20 or catalysis.²¹ These arise from their structural morphology, which allows them to harbor small molecules or clusters inside the carbon backbone,^22–24 forming the so-called endohedral fullerenes or metallofullerenes.^25,26 Due to their heterogeneous nature, these systems have enormous potential in cutting-edge technologies such as information storage^27–29 or spintronics.^30–34 Very recently, a 2D fullerene-based material equivalent to graphene, the so-called graphullerene, has been synthesized.^35,36 Graphullerene's structure consists of a 2D network of fullerenes covalently interconnected, which provides the system with robust structural stability,^37,38 and remarkable electronic,^39–42 mechanical^43–46 and optical^47–49 properties. This makes graphullerene well suited as an exciting platform for many different technological applications.^50–52 However, the capability of the fullerene building blocks as host structures within the 2D network still remains unexplored, even from a theoretical point of view, which would provide infinite possibilities emerging from the versatility of chemistry, in the 2D limit.

In this work, we report a first-principles study on a novel 2D material that we named ‘graphendofullerene’ by analogy to graphullerene and endohedral fullerene. The graphullerene-based material that we propose as a proof of concept is formed by using magnetic endohedral metallofullerene cages (V₃N@C₈₀) as building blocks. First, we demonstrate the thermodynamic stability of graphendofullerene and calculate its electronic structure, magnetic properties and spin dynamics. Interestingly, our microscopic analysis reveals that intermolecular magnetic interactions in the network lead to long-range ferromagnetic (FM) order. Finally, we apply strain engineering and electrostatic doping to enhance the magnetic behavior of the system. Our results pave the way for the preparation of magnetic graphullerene-based materials and their future optimization for emerging applications, since a wide range of possibilities arise from the host capabilities of fullerene building blocks.

Computational details

Structural relaxations and AIMD simulations were performed using the Vienna ab initio Simulation Package (VASP).^53,54 The generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) parametrization was used to account for exchange-correlation energy.⁵⁵ van der Waals interactions were considered using the Grimme D3 method approximation.⁵⁶ The projector-augmented wave (PAW) method was used with an energy cutoff of 530 eV. A 4 × 5 × 1 k-point grid was used to sample reciprocal space (Fig. S9†). The lattice constant and atomic coordinates were relaxed until forces were less than 0.03 eV Å⁻¹. AIMD simulations were performed using the NVT canonical ensemble for 9 ps with a time step of 2 fs, using the optimized lattice parameters and structure. Charge transfer analysis was performed using Bader charge partition as proposed by the Henkelman group.⁵⁷ Total energies for the FM and three different AFM configurations (single-stripe, double-stripe and zig-zag, see Fig. 2), and magnetic properties were calculated using the SIESTA code,^58,59 in order to take advantage of the localized pseudoatomic orbital approach. We used norm-conserving scalar relativistic pseudo-potentials taken from the Pseudo-Dojo database⁶⁰ in the psml format.⁶¹ The same k-point grid was used in combination with a real-space mesh cutoff of 700 Ry, with a double-ζ polarized basis set for all atoms. We fed the TB2J package⁶² with SIESTA wavefunctions to calculate magnetic exchange couplings. We used as a spin Hamiltonian, where S_i and S_j are distinct magnetic moments present in the lattice and J_ij is the magnetic exchange interaction between them. Atomistic spin dynamics simulations were carried out using Vampire software,⁶³ where a 30 nm × 30 nm sample was considered in combination with 500 000 equilibration and loop time steps.

Results and discussion

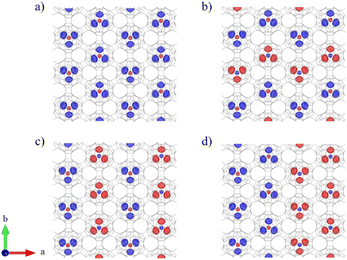
C₆₀ is the smallest fullerene which obeys the isolated pentagonal ring (IPR) rule,⁶⁴ but its reduced inner space limits the incorporation of a wide variety of guest molecules. This limitation is overcome by C₈₀, the next member that follows the IPR rule in the fullerene family with the same point group symmetry (I_h), due to its larger volume.⁶⁵ Graphullerene has been reported to exist in several polymorph forms.³⁶ Among them, the quasi-hexagonal phase (qHP) (Fig. S1a†) has shown higher stability and robustness since it maximizes the number of sp³ C atoms bridging the fullerene cages, which creates a more dense arrangement of cages and releases surface tension, thus stabilizing the entire system.^38,66 Therefore, we selected a 2D qHP I_h-C₈₀ graphullerene network in which each fullerene cage is surrounded by six neighboring cages (Fig. S1a†). This phase corresponds to a hexagonal lattice with a Pmna (No. 53) space group, where the fully optimized lattice parameters are a = 17.84 Å and b = 10.29 Å. The chemical bonds between adjacent cages are based on [2 + 2] cycloaddition along a and b lattice vectors and diagonal lines of the rectangular unit cell. Covalent intramolecular C–C σ bonds have a length of 1.42 Å, whereas intermolecular bonds are 1.59 Å, owing to the novel sp³ character of the C attaching C₈₀ cages. Our calculations show that the fullerene units are slightly distorted after polymerization, where the cages adopt an ellipsoidal shape, as we can observe in Fig. S1b.† The calculated out-of-plane diameter of the cages is 8 Å, whereas in the plane parallel to the lattice we can observe that the presence of covalent bonds between C cages generates a larger diameter of 8.9 Å.

Encapsulation of trimetallic nitrides has been demonstrated to be a powerful methodology to stabilize highly symmetric icosahedral fullerenes,⁶⁷ since the isolation of monometallofullerene is still challenging because of their minimal charge transfer to the C atoms that limits the stability of the host–guest system.²² Previous studies have reported the successful synthesis of V_xSc_3–xN@C₈₀ (x = 1, 2);⁶⁸ nevertheless the incorporation of V₃N remains challenging from an experimental point of view but it has been theoretically predicted to be feasible.⁶⁹ This guest molecule would represent the best candidate to induce magnetism in the 2D network of graphullerene since it has a higher presence of V magnetic atoms. Given this, we explore the feasibility of incorporating V₃N into fullerene units that form a 2D graphullerene network. We selected a V₃N@C₈₀ conformation where the guest clusters adopt a configuration with V³⁺ atoms pointing towards half of the sp³ bridges in a C₃-symmetry fashion (Fig. 1a), as the linking C atoms have shown a pronounced electronic localization (Fig. S2†). We can see that the clusters present a slight distortion from planarity, due to unpaired electrons in N, but they mostly lay in the network plane. Also, the incorporation of the clusters barely distorts the fullerene cages, where the average host–guest distance is ∼2.5 Å. Then, we calculate the formation energy (E_F), that is defined as E_F = E_V3N@C80 − (E_V3N + E_C80. We found an E_F of −10.73 eV/molecule that is compatible with similar theoretical studies for the endohedral metallofullerene cages.⁷⁰ This indicates a favorable formation of the V₃N@C₈₀ network, because the system is stabilized with respect to its separate V₃N and C₈₀ units. A charge transfer of 2.4 electrons per V₃N cluster to the graphullerene network is revealed by Bader charge analysis, where the V atoms are responsible to donate charge density to the C skeleton (Fig. 1c). We do not observe any further redistribution of the charge density after encapsulation, which prevents the exhibition of radical character in the system, as has been observed in endohedral metallofullerenes.⁷¹ Furthermore, in order to corroborate the stability of the herein proposed graphendofullerene, we performed ab initio molecular dynamics (AIMD) simulations and phonon calculations to monitor the dynamic stability of the system at a given temperature. Our calculations unveil that the structure is thermodynamically stable at room temperature and up to 600 K since the structure is retained under the inclusion of thermal fluctuations (ESI† Sections 2.1 and 2.2).

Fig. 1 (a) V₃N@C₈₀ graphendofullerene top view. Color code: carbon (grey), vanadium (red) and nitrogen (blue). (b) Electronic band structure (left) and projected density of states (PDOS) (right) for the V₃N@C₈₀ monolayer. Blue (red) color in (a) represents spin up (down) electrons. (c) Charge density difference after V₃N encapsulation. Yellow (blue) regions represent charge accumulation (depletion). (d) Energy level polarization of C₈₀.

The electronic band structure and density of states of the V₃N@C₈₀ network are shown in Fig. 1b. One can observe a clear influence of the host–guest interaction due to strong spin-dependent hybridization between energy levels around the Fermi energy level due to the charge transfer interaction, leading to half-metallicity of the system as it shows metallic and semiconductor behavior for spin up and down components, respectively. The half-metal ground state can provide the system with 100% polarized spin currents, which can lead to an enormous interest in spintronics for spin-dependent tunnel junctions and magnetoresistance devices.^72,73 Consequently, the energy levels of C atoms on the network are polarized due to the interaction with magnetic clusters, as illustrated in Fig. 1d. This interaction is responsible for redistributing the charge density of the system after encapsulation and harnessing the stabilization of the network.

The electronic polarization around the Fermi level arising from the half-metallic band structure of V₃N@C₈₀ makes this system a promising candidate for spintronics. Therefore, we systematically study the magnetic properties of graphendofullerene as a novel molecule-based 2D magnet. The calculated magnetic moments are 2.7 μ_B for V atoms, whereas the long-range magnetic order present in the monolayer is predicted to be ferromagnetic. We computed the energy difference between the possible antiferromagnetic (AFM) and the FM configurations, namely E_AFM and E_FM, respectively (Fig. 2). We observe that the FM order is the most stable magnetic configuration in V₃N@C₈₀ (Table S1†). As depicted in Fig. 1b, around the Fermi level the energy levels are completely polarized, which stabilizes the FM order in the network. Regarding magnetic exchange interactions (J), the arrangement of C₈₀ cages and the morphology of the guest clusters allow several Js in the network (Fig. 3a). We categorize them into two different groups, namely (i) intramolecular interactions, i.e. those interactions between V atoms from the same molecule (J₁) and, (ii) intermolecular interactions, which are those magnetic interactions between adjacent molecules in the network (J₂). Due to the close distance between V atoms forming guest clusters (∼3.2 Å), J₁ interactions have a high intensity of ∼50 meV and short-range intrinsic character, mainly due to a robust hybridization of d orbitals around the Fermi level that enhances magnetic intramolecular interactions (Fig. 3c) but prevents the participation of J₁ in the magnetic reciprocity of the network. These intramolecular interactions stabilize a ferromagnetic coupling between the V atoms inside the guest molecules. On the other hand, the main factor in the stabilization of a long-range magnetic order in graphendofullerene is intermolecular ferromagnetic exchange interactions between adjacent V₃N molecules. The orientation of guest clusters inside C₈₀ cages provides two different first neighbor intermolecular interactions, namely, J₂₁, that arises from the V atoms directly oriented along the x axis of the network, and J₂₂, which is aligned with the y axis. In the case of J₂₁, the V atoms point directly towards them, and the resulting interaction at 6.7 Å is 2.28 meV, whereas J₂₂ is equal to 0.33 meV due to a longer distance of interaction (7.8 Å). J₂₁ (J₂₂) are one (two) order of magnitude lower than J₁ but connect magnetic molecules and provides the V₃N@C₈₀ network with a robust long-range magnetic order, that opens the way to observe critical properties of a ferromagnet such as Curie temperature (T_C) or coercivity on this molecule-based 2D network. We applied the same methodology to V₂ScN@C₈₀ (Fig. S10 and S11†), where we observe that the magnetic intermolecular interactions are preserved despite the lower presence of magnetic V atoms.

Fig. 2 Spin density of considered magnetic configurations for V₃N@C₈₀. (a) Ferromagnetic (FM), (b) zig-zag, (c) single-stripe and (d) double-stripe antiferromagnetic (AFM) configurations. Color code: spin up (blue) and down (red) electrons.

Fig. 3 (a) Schematic representation of intra/intermolecular magnetic interactions in the V₃N@C₈₀ network. (b) Orbital contribution to J₂₁ from interacting first neighbor V atoms. (c) PDOS of d orbitals of V atoms in J₂₁ and C atoms in linking moieties of V₃N@C₈₀.

In order to check the role of C₈₀ graphullerene in the mediation of intermolecular magnetic exchange coupling, we recomputed the magnetic exchange interactions in a free-standing molecular array (i.e. removing all C atoms from the calculation). We found that intermolecular interactions are suppressed, whereas J₁ remains present (see Fig. S5†). This result is a useful hint that points to the carbon skeleton as a mediator of the magnetic interactions that stabilize ferromagnetism in the network. Magnetic interactions between two atoms are governed by all the possible interactions of their orbitals. In our case we considered the interactions between d orbitals of V atoms in the network, so we can decompose the magnetic exchange interactions into all the pairing possibilities between these orbitals. Our calculations reveal that intermolecular interactions are mainly governed by a ferromagnetic d_yz–d_yz contribution, with moderate d_xz–d_yz and d_xz–d_xz ferromagnetic and d_z²–d_z² antiferromagnetic pathways between adjacent V atoms (Fig. 3b). This can be rationalized since a positive contribution to the magnetic exchange coupling tends to favor FM interactions and a negative contribution has an AFM character as depicted in Fig. 3b in red and blue colors for FM and AFM characters, respectively. The influence of these d orbitals is mainly governed by their hybridization with the p orbitals of C atoms in the linking moieties. Around the Fermi level, the contributions of d_yz, d_xz and d_z² are dominant and their hybridization with the energy levels of C atoms that link the C₈₀ cages is deduced (Fig. 3c). One can note that this is the main factor in the mediation of intermolecular magnetic interactions. This analysis highlights the critical role of d orbital occupancy of magnetic transition metal atoms in intermolecular exchange, as reported for similar magnetic molecular systems.⁷⁴

Subsequently, we performed well-converged spin–orbit calculations in V₃N@C₈₀ graphendofullerene to elucidate the preferential spin orientation. We computed the magnetic anisotropy energy (MAE) as the difference in energy in the different possible spin orientations along the Cartesian axis. We found that the in-plane spin configurations are more stable –only differing by 0.03 meV per atom along the x and y directions–, with 0.18 meV per atom MAE with respect to the off-plane direction z. These results indicate a favorable in-plane spin orientation, similar to those observed in the MPX₃ (M = Mn, Ni, Fe; X = S, Se) family.⁷⁵

To further understand the magnetic behavior of graphendofullerene we performed atomistic spin dynamics simulations. This approach offers a deeper investigation of the more complex magnetic interactions at play, revealing dynamic behaviors that extend beyond the static properties previously described. We predict a T_C of 38 K for V₃N@C₈₀ graphendofullerene (Fig. 4a), which is similar to that of the first 2D magnetic materials studied (CrI₃ or Cr₂Ge₂Te₆)^76,77 but still far from that of the recently synthesized above-room-temperature Fe₃GaTe₂ or VSe₂.^78,79 Although this value is still far from room temperature, the interplay between molecular design and intricate magnetic phenomena presents a fertile ground for future enhancements. Analogous to other 2D materials, the magnetic response has been proven to be particularly tunable using tensile strain,⁸⁰ electrostatic doping⁸¹ and proximity effects.⁸² We also simulated T_C by only considering J₁ interactions, which result in a suppression of ferromagnetism above 0 K (Fig. S6†). This unveils the critical role of intermolecular interactions in the stabilization of long-range magnetic order in the network, as graphullerene enables a pathway to connect nearest neighbor magnetic molecules via polarized charge transfer between host and guest species in the network.

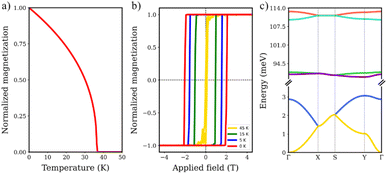Fig. 4 Simulated (a) Curie temperature, (b) hysteresis loop at different temperatures and (c) magnon dispersion for the V₃N@C₈₀ graphendofullerene network.

We next focus on two key aspects that further highlight the magnetic performance for future applications of V₃N@C₈₀ graphendofullerene: the hysteresis loop and magnon dispersion. First, we focus on the magnetic hysteresis behavior of the network, which indicates the relationship between an applied magnetic field (B) and the magnetization of the system. We compute it at different temperatures to simulate the effect of thermal fluctuations until T_C is exceeded (Fig. 4b). These findings support the results observed in critical temperature simulations, as the evolution of temperature is closing the loop revealing the transition from the ferromagnetic to paramagnetic order at temperatures above T_C. Besides, we found a coercive field (H_c) of 2 T at 0 K, which is consistent with the expected value of 2.34 T following the classical H_c limit as H_c ≈ 2K/μ₀M_s, where K is the magnetic anisotropy, μ₀ is the vacuum permeability and M_s is the saturation magnetization.

From the calculated magnetic exchange couplings, we simulate the spin-wave spectrum of V₃N@C₈₀ graphendofullerene using the Holstein–Primakoff transformation as introduced by linear spin-wave theory (LSWT) (Fig. 4c). At high frequencies, we can observe four magnon bands (between ∼90 and ∼115 meV) dominated by J₁, which are the strongest magnetic interactions in the material and localized inside the guest molecules. On the other hand, the two magnon bands that have more contribution of J₂ interactions are lying at lower energies (between 0 and ∼3 meV) due to the less intense character of these intermolecular interactions. Arising from the anisotropy of the magnetic exchange interactions, we observe a higher dispersion of spin excitations in the Г–X and S–Y k-paths (corresponding to the x axis in real space). This observation matches the magnetic configuration described above, as we predict that J₂₁ interactions stabilize the ferromagnetic order in the network and this magnetic interaction takes place along the x axis.

Additionally, we explore the effect of mechanical deformation and electrostatic doping on the magnetic properties of the V₃N@C₈₀ monolayer. Fig. 5a shows the variation of first neighbor inter/intramolecular interactions in a reasonable range of ± 4% of biaxial strain, since graphullerene has been predicted to have a fracture strain in the range of 6.5–8%.⁴⁴ As any mechanical deformation of the lattice will affect the distance between the C₈₀ cages, J₂₁ is critically affected by strain, since this interaction mainly depends on the communication between fullerene units. On the other hand, one may observe that intramolecular interactions are affected to a much lesser extent. According to our calculations, a biaxial compression of the lattice parameters up to 4% would enhance the strength of magnetic exchange interactions by 8% and 37% for J₁ and J₂₁, respectively. With respect to the calculated trend of J₂₁ upon strain, we can observe a deviation from linearity at elongations close to 4%, owing to a competition between FM and AFM orders that appears due to the larger distance between magnetic molecules. We can conclude that the enhancement of J₂₁ is mainly due to a higher overlap between d_xz and d_yz with the C sp³ linkers between cages, as any other competing pathway of interaction is playing a role. We corroborate this fact by looking at the orbital contributions to magnetic exchange couplings, where the same picture is observed compared to the former case (Fig. S7†). In the case of J₁, the increased intensity is driven by stronger intramolecular interactions, as the reduced volume of fullerene brings the atoms inside the cage closer. By contrast, when positive strain is applied, we observe a distinct shift in the magnetic behavior of the system. As the lattice expands, the intermolecular distances between C₈₀ cages increase, weakening the magnetic interactions. This reduction in coupling strength leads to a noticeable decrease in both J₁ and J₂₁, highlighting the sensitivity of these interactions to tensile strain. Obviously, this change in magnetic interactions has a direct impact on the T_C of the system. Fig. 5b shows the evolution of T_C of V₃N@C₈₀ graphendofullerene as a function of strain. As magnetic interactions weaken under elongation, T_C is critically diminished, indicating a loss of magnetic ordering at lower temperatures. However, the opposite result comes from the application of negative strain. Our results show that compressive strain leads to a significant increase in T_C, which increases up to 55 K within a 4% compression of the 2D molecular ferromagnetic network. This enhancement in T_C is compatible with those observed for a similar range of strain in inorganic 2D ferromagnets, such as Cr₂Ge₂Te₆ (ref. 83) and CrI₃.⁸⁴

Fig. 5 Evolution with strain of (a) intra/intermolecular magnetic exchange couplings and (b) Curie temperature and evolution with electrostatic doping of (c) intra/intermolecular magnetic exchange couplings and (d) Curie temperature of V₃N@C₈₀ graphendofullerene. A positive (negative) sign of the carrier density is equivalent to an excess of holes (electrons).

Analogously, the manipulation of the magnetic properties of V₃N@C₈₀ graphendofullerene could be achieved by external manipulation using electrostatic doping, which has been shown to represent a powerful tool to tune the properties of 2D materials due to their reduced dimensionality.⁸⁵ Fig. 5c shows how intra/intermolecular magnetic interactions change with the introduction of carrier density in the network. One can see that the introduction of holes enhances the magnetic exchange couplings present in the system, which increases the Curie temperature of the system up to 45 K (Fig. 5d). On the other hand, the introduction of electrons in the systems drastically suppresses the intermolecular interactions, resulting in a diminution of the Curie temperature of V₃N@C₈₀. The drastic diminution of J₂₁ upon the introduction of electron carriers could be explained with a remarkable suppression of the FM d_xz–d_yz and d_xz–d_xz pathways (Fig. S8†), which has an enormous impact on the strength of the intermolecular magnetic interactions.

The present work represents the first investigation of magnetism in a single layer of graphullerene. By using endohedral metallofullerenes, we induce and tailor magnetic properties in this carbon-based 2D covalent network. The intrinsic properties of the fullerene units can provide a plethora of graphendofullerene networks with a wide range of emerging possibilities, since fullerenes (i) are able to host different molecules inside them, and (ii) have different shapes and geometries. Recent advances in chemistry have allowed the incorporation of a wide range of molecules on endohedral fullerenes, from mono-, di- and tri-metallofullerenes to molecules with a higher degree of complexity such as nitride-, carbide- and methanoclusterfullerenes, mainly containing transition metals and rare-earth ions.²⁴ These unique structures combine the electronic and geometric properties of fullerenes with the specific characteristics of guest species, which permits the application of these structures for a wide range of applications in optoelectronics, nanomagnetism, or energy harvesting and conversion.²² Indeed, graphendofullerene is not constrained to the network investigated in this work, but it will also transfer the infinite possibilities of endohedral fullerenes to the 2D limit, thus generating a new family of functional materials which represents a fertile playground to explore many interesting phenomena for applications in optoelectronics, spintronics, magnonics and quantum technologies, among others. Furthermore, the highly organized covalent network presents superior stability to conventional 2D magnets, facilitating its transferability to other substrates or matrices. This significantly enhances the practical integration of 2D magnetic materials into scalable spintronic devices for applications in next-generation technologies, and their tunability by using different metallic endofullerenes, whose properties are preserved, as building blocks.

Conclusions

In summary, we introduce graphendofullerene, a two-dimensional magnetic network based on a V₃N cluster encapsulated on C₈₀ graphullerene, using first principles calculations. Our systematic study provides a detailed understanding of the magnetic properties of V₃N@C₈₀ graphendofullerene, which shows a robust ferromagnetic behavior sustained by long-range magnetic interactions enabled by the carbon network. Our atomistic spin simulations reveal that magnetic order can persist up to 38 K and we also determine the hysteresis loop and magnon dispersion of graphendofullerene. Finally, we apply strain engineering and electrostatic doping that allows us to achieve a 45% increase in T_C under the application of 4% compressive strain, evidencing the successful improvement of the magnetic properties of V₃N@C₈₀ graphendofullerene with external manipulation. This work not only bridges molecular chemistry and carbon chemistry but also provides a versatile platform for the future development of tunable, high-performance next generation molecular-based 2D magnets.

Data availability

Data is available upon request to the corresponding author.

Author contributions

This work is part of the PhD thesis of D. L. A. D. L. A. performed the DFT calculations. Z. H. provided experimental insights and contributed to the interpretation of results. J. J. B. conceived and supervised the work. The manuscript was written by D. L. A. and J. J. B. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the European Union (ERC-2021-StG 101042680 2D-SMARTiES), the Generalitat Valenciana (grant CIDEXG/2023/1), the National Natural Science Foundation of China (52302052) and the Anhui Provincial Natural Science Foundation (2308085MB33).

Notes and references

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. F. Diederich, R. Ettl, Y. Rubin, R. L. Whetten, R. Beck, M. Alvare, S. Anz, D. Sensharma, F. Wudl, K. C. Khemani and A. Koch, Science, 1991, 252, 548–551.
3. S. Iijima, Nature, 1991, 354, 56–58.
4. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
5. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
6. A. Hirsch, Nat. Mater., 2010, 9, 868–871.
7. G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, ACS Nano, 2015, 9, 11509–11539.
8. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Terrones, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 2898–2926.
9. Y. Yu. Illarionov, T. Knobloch, M. Jech, M. Lanza, D. Akinwande, M. I. Vexler, T. Mueller, M. C. Lemme, G. Fiori, F. Schwierz and T. Grasser, Nat. Commun., 2020, 11, 3385.
10. Y. Saito, T. Nojima and Y. Iwasa, Nat. Rev. Mater., 2016, 2, 16094.
11. M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419.
12. D. Deng, K. S. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Nat. Nanotechnol., 2016, 11, 218–230.
13. S. Yang, C. Jiang and S. Wei, Appl. Phys. Rev., 2017, 4, 021304.
14. J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 16055.
15. E. C. Ahn, npj 2D Mater. Appl., 2020, 4, 17.
16. K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439.
17. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50.
18. C.-Z. Li, H.-L. Yip and A. K.-Y. Jen, J. Mater. Chem., 2012, 22, 4161.
19. S. H. Friedman, D. L. DeCamp, R. P. Sijbesma, G. Srdanov, F. Wudl and G. L. Kenyon, J. Am. Chem. Soc., 1993, 115, 6506–6509.
20. A. Montellano, T. Da Ros, A. Bianco and M. Prato, Nanoscale, 2011, 3, 4035.
21. Y. Pan, X. Liu, W. Zhang, Z. Liu, G. Zeng, B. Shao, Q. Liang, Q. He, X. Yuan, D. Huang and M. Chen, Appl. Catal., B, 2020, 265, 118579.
22. A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113.
23. S. Yang, T. Wei and F. Jin, Chem. Soc. Rev., 2017, 46, 5005–5058.
24. Z. Hu and S. Yang, Chem. Soc. Rev., 2024, 53, 2863–2897.
25. H. Kato, A. Taninaka, T. Sugai and H. Shinohara, J. Am. Chem. Soc., 2003, 125, 7782–7783.
26. C.-R. Wang, T. Kai, T. Tomiyama, T. Yoshida, Y. Kobayashi, E. Nishibori, M. Takata, M. Sakata and H. Shinohara, Nature, 2000, 408, 426–427.
27. R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, H. Brune, S. Rusponi, F. Nolting, A. Popov, S. Yang, L. Dunsch and T. Greber, J. Am. Chem. Soc., 2012, 134, 9840–9843.
28. F. Liu, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, S. Wang, Y.-Z. Tan, J. Tao, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, J. Am. Chem. Soc., 2016, 138, 14764–14771.
29. F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098.
30. T. Wang, J. Wu, W. Xu, J. Xiang, X. Lu, B. Li, L. Jiang, C. Shu and C. Wang, Angew. Chem., Int. Ed., 2010, 49, 1786–1789.
31. Y. Feng, T. Wang, Y. Li, J. Li, J. Wu, B. Wu, L. Jiang and C. Wang, J. Am. Chem. Soc., 2015, 137, 15055–15060.
32. Y. Ma, T. Wang, J. Wu, Y. Feng, L. Jiang, C. Shu and C. Wang, Chem. Commun., 2012, 48, 11570.
33. B. Wu, T. Wang, Y. Feng, Z. Zhang, L. Jiang and C. Wang, Nat. Commun., 2015, 6, 6468.
34. H. Kurihara, Y. Iiduka, Y. Rubin, M. Waelchli, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, J. Am. Chem. Soc., 2012, 134, 4092–4095.
35. E. Meirzadeh, A. M. Evans, M. Rezaee, M. Milich, C. J. Dionne, T. P. Darlington, S. T. Bao, A. K. Bartholomew, T. Handa, D. J. Rizzo, R. A. Wiscons, M. Reza, A. Zangiabadi, N. Fardian-Melamed, A. C. Crowther, P. J. Schuck, D. N. Basov, X. Zhu, A. Giri, P. E. Hopkins, P. Kim, M. L. Steigerwald, J. Yang, C. Nuckolls and X. Roy, Nature, 2023, 613, 71–76.
36. L. Hou, X. Cui, B. Guan, S. Wang, R. Li, Y. Liu, D. Zhu and J. Zheng, Nature, 2022, 606, 507–510.
37. G. Shen, L. Li, S. Tang, J. Jin, X.-J. Chen and Q. Peng, Crystals, 2023, 13, 224.
38. B. Peng, Nano Lett., 2023, 23, 652–658.
39. R. M. Tromer, L. A. Ribeiro and D. S. Galvão, Chem. Phys. Lett., 2022, 804, 139925.
40. U. Argaman and G. Makov, npj Comput. Mater., 2023, 9, 211.
41. A. Capobianco, J. Wiktor, A. Landi, F. Ambrosio and A. Peluso, Nano Lett., 2024, 24, 8335–8342.
42. T. S. A. Cassiano, M. L. Pereira, G. M. e Silva, P. H. de Oliveira Neto and L. A. Ribeiro, Nanoscale, 2024, 16, 2337–2346.
43. S. Zhao, X. Zhang, Y. Ni, Q. Peng and Y. Wei, Carbon, 2023, 202, 118–124.
44. P. Ying, H. Dong, T. Liang, Z. Fan, Z. Zhong and J. Zhang, Extreme Mech. Lett., 2023, 58, 101929.
45. L. Yu, J. Xu, B. Peng, G. Qin and G. Su, J. Phys. Chem. Lett., 2022, 13, 11622–11629.
46. P. Ying, O. Hod and M. Urbakh, Nano Lett., 2024, 24, 10599–10604.
47. A. Champagne, M. Camarasa-Gómez, F. Ricci, L. Kronik and J. B. Neaton, Nano Lett., 2024, 24, 7033–7039.
48. D. Yuan, H. Pi, Y. Jiang, Y. Hu, L. Zhou, Y. Jia, G. Su, Z. Fang, H. Weng, X. Ren and W. Zhang, Sci. China Phys. Mech. Astron., 2023, 66, 247211.
49. G.-Y. Li, S.-C. Mo, X.-Y. Qiu, J. Nie, J.-X. Li, P.-Y. Liang, F. Ning and S.-Z. Chen, ACS Appl. Nano Mater., 2025, 8, 649–658.
50. B. Peng, J. Am. Chem. Soc., 2022, 144, 19921–19931.
51. Y. Tong, H. Liu, S. Dai and D. Jiang, Nano Lett., 2023, 23, 7470–7476.
52. X. Chang, X. Liu, W. Zheng, L. Zhou and J. Zhang, Appl. Surf. Sci., 2023, 637, 157909.
53. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
54. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
55. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
56. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
57. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
58. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
59. A. García, N. Papior, A. Akhtar, E. Artacho, V. Blum, E. Bosoni, P. Brandimarte, M. Brandbyge, J. I. Cerdá, F. Corsetti, R. Cuadrado, V. Dikan, J. Ferrer, J. Gale, P. García-Fernández, V. M. García-Suárez, S. García, G. Huhs, S. Illera, R. Korytár, P. Koval, I. Lebedeva, L. Lin, P. López-Tarifa, S. G. Mayo, S. Mohr, P. Ordejón, A. Postnikov, Y. Pouillon, M. Pruneda, R. Robles, D. Sánchez-Portal, J. M. Soler, R. Ullah, V. W. Yu and J. Junquera, J. Chem. Phys., 2020, 152, 204108.
60. M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G.-M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
61. A. García, M. J. Verstraete, Y. Pouillon and J. Junquera, Comput. Phys. Commun., 2018, 227, 51–71.
62. X. He, N. Helbig, M. J. Verstraete and E. Bousquet, Comput. Phys. Commun., 2021, 264, 107938.
63. R. F. L. Evans, W. J. Fan, P. Chureemart, T. A. Ostler, M. O. A. Ellis and R. W. Chantrell, J. Phys.: Condens. Matter, 2014, 26, 103202.
64. H. W. Kroto, Nature, 1987, 329, 529–531.
65. A. R. Khamatgalimov and V. I. Kovalenko, Fullerenes, Nanotubes Carbon Nanostruct., 2011, 19, 599–604.
66. A. R. Khamatgalimov, A. V. Luzhetskii and V. I. Kovalenko, Int. J. Quantum Chem., 2008, 108, 1334–1339.
67. S. Stevenson, G. Rice, T. Glass, K. Harich, F. Cromer, M. R. Jordan, J. Craft, E. Hadju, R. Bible, M. M. Olmstead, K. Maitra, A. J. Fisher, A. L. Balch and H. C. Dorn, Nature, 1999, 401, 55–57.
68. T. Wei, S. Wang, X. Lu, Y. Tan, J. Huang, F. Liu, Q. Li, S. Xie and S. Yang, J. Am. Chem. Soc., 2016, 138, 207–214.
69. M. Li, Y. Zhao, K. Yuan, R. Zhao, P. Zhao and X. Zhao, Carbon, 2018, 132, 312–322.
70. S. Bhusal, T. Baruah, Y. Yamamoto and R. R. Zope, Int. J. Quantum Chem., 2018, 118, e25785.
71. M. K. Singh, P. Shukla, M. Khatua and G. Rajaraman, Chem.–Eur. J., 2020, 26, 464–477.
72. X. Li and J. Yang, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2017, 7, e1314.
73. M. Ashton, D. Gluhovic, S. B. Sinnott, J. Guo, D. A. Stewart and R. G. Hennig, Nano Lett., 2017, 17, 5251–5257.
74. S. Ghosh, S. K. Singh, S. Tewary and G. Rajaraman, Dalton Trans., 2013, 42, 16490.
75. M. Rybak, P. E. Faria Junior, T. Woźniak, P. Scharoch, J. Fabian and M. Birowska, Phys. Rev. B:Condens. Matter Mater. Phys., 2024, 109, 054426.
76. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273.
77. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269.
78. Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94–99.
79. W. Yu, J. Li, T. S. Herng, Z. Wang, X. Zhao, X. Chi, W. Fu, I. Abdelwahab, J. Zhou, J. Dan, Z. Chen, Z. Chen, Z. Li, J. Lu, S. J. Pennycook, Y. P. Feng, J. Ding and K. P. Loh, Adv. Mater., 2019, 31, 1903779.
80. F. Miao, S.-J. Liang and B. Cheng, npj Quantum Mater., 2021, 6, 59.
81. S. Jiang, L. Li, Z. Wang, K. F. Mak and J. Shan, Nat. Nanotechnol., 2018, 13, 549–553.
82. Z. Wang, C. Tang, R. Sachs, Y. Barlas and J. Shi, Phys. Rev. Lett., 2015, 114, 016603.
83. X.-J. Dong, J.-Y. You, B. Gu and G. Su, Phys. Rev. Appl., 2019, 12, 014020.
84. A. M. León, J. W. González, J. Mejía-López, F. Crasto de Lima and E. Suárez Morell, 2D Mater., 2020, 7, 035008.
85. Y. Wang, J. Xiao, H. Zhu, Y. Li, Y. Alsaid, K. Y. Fong, Y. Zhou, S. Wang, W. Shi, Y. Wang, A. Zettl, E. J. Reed and X. Zhang, Nature, 2017, 550, 487–491.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc01278c

---