 Open Access Article
Open Access ArticleThe role of the droplet interface in controlling the multiphase oxidation of thiosulfate by ozone†
Alexandra M. Deal a,
Franky Bernal
a,
Franky Bernal ab,
Andreas Siebert
ab,
Andreas Siebert ac,
Alexander M. Prophetab,
Mauricio Lopez Lunaa,
Monika Blum
ac,
Alexander M. Prophetab,
Mauricio Lopez Lunaa,
Monika Blum ac,
Richard J. Saykally
ac,
Richard J. Saykally ab and
Kevin R. Wilson
ab and
Kevin R. Wilson *a
*a
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: krwilson@lbl.gov
bDepartment of Chemistry, University of California, Berkeley, Berkeley, CA 94720, USA
cAdvanced Light Source, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 17th March 2025
Abstract
Predicting reaction kinetics in aqueous microdroplets, including aerosols and cloud droplets, is challenging due to the probability that the underlying reaction mechanism can occur both at the surface and in the interior of the droplet. Additionally, few studies directly measure the surface activities of doubly charged anions, despite their prevalence in the atmosphere. Here, deep-UV second harmonic generation spectroscopy is used to probe surface affinities of the doubly charged anions thiosulfate, sulfate, and sulfite, key species in the thiosulfate ozonation reaction mechanism. Thiosulfate has an appreciable surface affinity with a measured Gibbs free energy of adsorption of −7.3 ± 2.5 kJ mol−1 in neutral solution, while sulfate and sulfite exhibit negligible surface propensity. The Gibbs free energy is combined with data from liquid flat jet ambient pressure X-ray photoelectron spectroscopy to constrain the concentration of thiosulfate at the surface in our model. Stochastic kinetic simulations leveraging these novel measurements show that the primary reaction between thiosulfate and ozone occurs at the interface and in the bulk, with the contribution of the interface decreasing from ∼65% at pH 5 to ∼45% at pH 13. Additionally, sulfate, the major product of thiosulfate ozonation and an important species in atmospheric processes, can be produced by two different pathways at pH 5, one with a contribution from the interface of >70% and the other occurring predominantly in the bulk (>98%). The observations in this work have implications for mining wastewater remediation, atmospheric chemistry, and understanding other complex reaction mechanisms in multiphase environments. Future interfacial or microdroplet/aerosol chemistry studies should carefully consider the role of both surface and bulk chemistry.
1. Introduction
Chemistry in microdroplets has garnered interest in recent years for its (sometimes extreme) differences from either purely gas-phase or condensed phase chemistry.1 Some studies have shown that microdroplet reaction rates increase with decreasing droplet size and reactant concentration, attributing this rate enhancement to high surface-to-volume ratios and increased reaction contributions from droplet interfaces. However, there is debate regarding the source of reaction rate enhancement,2–4 and determining the exact drivers in microdroplet chemistry, including the individual contributions from surface and bulk phases, is notoriously challenging due to experimental constraints and a lack of available surface activity data. Chemistry in microdroplets, including aerosols and cloud droplets, has a crucial role in atmospheric chemistry,5 hence a thorough understanding of microdroplet reaction mechanisms will be vital for accurate atmospheric chemistry modeling.The oxidation of sulfur and its impact on global climate has long been studied, but new sulfur intermediates are still being identified6 and sulfur oxyanions like thiosulfate may be underappreciated atmospheric intermediates. Thiosulfate might be released into the environment from incompletely treated mining tailings or formed from H2S and SO2 in volcanic stratospheric aerosols.7 Once released or formed, the ozonation of thiosulfate can acidify the reaction environment and form a mixture of fully oxidized sulfur (sulfate, SO42−) and partially oxidized sulfur (sulfur dioxide, SO2, trithionate, S3O62−, and tetrathionate, S4O62−). While sulfate directly contributes to the global radiation budget through new particle formation, thiosulfate, SO2, trithionate, and tetrathionate can act as long-lived metastable intermediates in the atmospheric sulfur cycle with down-stream environmental effects. Despite these potential impacts, the chemistry of thiosulfate in microdroplets has largely been unaccounted for in modeling the atmospheric sulfur cycle, and few studies have directly addressed the aqueous surface activity of sulfur oxyanions.
Efforts towards understanding the ozone oxidation of thiosulfate can also provide an excellent model system for understanding complex multistep reaction kinetics in microdroplets. Thiosulfate is often used as an O3 scavenger in laboratory uptake studies due to its fast reaction with ozone,8 and trapped droplet studies suggest that thiosulfate is relatively surface active.9 In fact, previous work from Wilson and co-workers has shown that ozone reactions with organic and inorganic species in aqueous microdroplets are mediated by the non-reactive partitioning and diffusion of reactants, but many of these studies had undetectable products.10,11 A detailed investigation of the multiphase chemistry of thiosulfate in microdroplets can therefore add to this body of work by exploring the role of the droplet surface for a reaction where the quantitative kinetics of intermediates and products are measured.
Our previous study7 presented the ozone oxidation of thiosulfate in aqueous droplets as a function of solution pH and gas-phase ozone concentration. This work prompted the formulation of a new reaction mechanism, shown in Scheme 1, which incorporates a previously unobserved intermediate, dithionite (S2O42−), as well as explains the pH-dependence of the reaction by a series of elementary reaction steps, as described in Deal, et al.7 Briefly, the primary reaction between thiosulfate and ozone forms an ozonide intermediate ([S2O3OOO]2−), which can decompose via three different reaction steps to form sulfate (SO42−), sulfur dioxide (SO2), dithionite (S2O42−), and dithionite's conjugate acid (HS2O4−). S2O42− can then react with dissolved oxygen to form SO42− and SO2 or react with SO2 to form trithionate (S3O62−). HS2O4− can react with another thiosulfate molecule to form tetrathionate (S4O62−). Any SO2 produced can either desorb to the gas phase or hydrolyze to form bisulfite (HSO3−) and sulfite (SO32−), which acidifies the solution. Lastly, SO32− can be oxidized by ozone to form SO42−. In this mechanism, the pH of the solution has an explicit role in the branching ratio of the three [S2O3OOO]2− decomposition pathways and controls the acid–base equilibria for S2O42−/HS2O4− and SO2/HSO3−/SO32−. A kinetic model using this proposed mechanism was validated against prior literature experiments.9,12
 | ||
| Scheme 1 Reaction mechanism for the oxidation of aqueous thiosulfate (S2O32−) by ozone (O3). Reprinted with permission from Deal, et al.7 Copyright 2024 American Chemical Society. | ||
The kinetic model of the mechanism in Scheme 1 showed that accurate modeling of an experiment requires a thorough understanding of partitioning, but few studies have directly assessed the surface activity of thiosulfate or other intermediate sulfur oxyanions.7,13,14 Here, Deep UV-Second Harmonic Generation (DUV-SHG) is used to determine the Gibbs free energy of adsorption of thiosulfate, sulfate, and sulfite, and ambient pressure X-ray photoelectron spectroscopy (APXPS) of a liquid flat jet is used to determine the maximum surface concentration of thiosulfate. There is a longstanding history of using nonlinear SHG measurements to extract thermodynamic information about surface-active species.15–17 These experiments help establish the molecular driving force for ions at the air–water interface when combined with corroborating information, typically from molecular dynamics simulations. In this work, we instead couple SHG studies with APXPS and kinetic experiments to assess the macroscopic impact of ions partitioning to interfaces during multiphase reactions. We use our kinetic models to test the Gibbs free energy of adsorption from SHG experiments and the maximum surface concentration from APXPS experiments. Thus, we bridge surface-specific (SHG and APXPS) and bulk (levitated microdroplet reactions) techniques to refine our understanding of the surface activity of thiosulfate and the mechanism for ozone oxidation of thiosulfate.
Finally, we use the kinetic model to explore the interaction between microscale reactors and reaction kinetics using calculated surface reaction fractions and demonstrate the potential impacts on product distributions for a range of environmentally relevant droplet sizes and reactant concentrations.
2. Methods
2.1. Deep UV second harmonic generation (DUV-SHG)
In DUV-SHG, two photons are simultaneously annihilated to generate a third photon at twice the input frequency (Fig. 1B). The input wavelength is chosen such that the second harmonic is resonant with the charge-transfer-to-solvent (CTTS) transition of the anions for signal enhancement. Much work has been done to characterize the energy and magnitude of CTTS transitions of common ions, including the sulfur oxyanions studied here.19 Despite the broad absorption features typical of these transitions, the center absorption wavelengths are well separated for each of the three species studied here (Fig. 1C) and therefore require different input wavelengths. Note that the sulfate measurements were made with the second harmonic ca. 20 nm away from the expected CTTS transition maximum due to optics limitations and to avoid water molecule transitions. However, we are still weakly resonant with the low energy tail of the CTTS as seen in Fig. 1C, SHG is sensitive enough to capture signal changes even under non-resonant conditions, and our results agree with previous studies.20
| [water(ads)] + [ion(b)] ↔ [water(b)] + [ion(ads)] | (1) |
 | (2) |
From eqn (2), we solve for the surface ion concentration to generate eqn (3), which is in the form of a typical Langmuir expression relating ion concentration to the equilibrium constant for ion adsorption.
 | (3) |
The measured intensity of the SHG signal (I2ω) is proportional to the susceptibility of the interface comprising contributions from water molecules and ions (χwater(2), χion(2)), and the input intensity squared (Iω2):
| I2ω ∝ |χwater(2) + χion(2)|2 × Iω2 | (4) |
Under resonant conditions, χion(2) is a complex quantity with both real and imaginary components. The water molecules are far from resonance and therefore χwater(2) has only a real contribution. Additionally, susceptibilities can be expressed as the product of the number interfacial species (N) and an average hyperpolarizability (〈β〉eff):
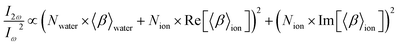 | (5) |
Numbers of interfacial species, N, are converted to interfacial concentrations by dividing with Nwater:
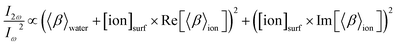 | (6) |
We substitute eqn (3) into eqn (6) and group the hyperpolarizability and maximum surface site terms into A, B, and C parameters in eqn (7).
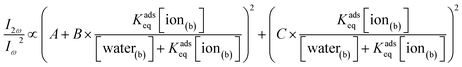 | (7) |
We can simplify eqn (7) and express all concentration terms as ion mole fractions (Xion). Additionally, we multiply the fraction terms by (Kadseq)−1/(Kadseq)−1 and use the relation  to reach the final fitting equation used to relate normalized SHG intensities to Gibbs free energies of adsorption.
to reach the final fitting equation used to relate normalized SHG intensities to Gibbs free energies of adsorption.
 | (8) |
2.2. Ambient pressure photoelectron spectroscopy (APXPS)
We directly probe the surface concentration, [S2O32−(ads)], of thiosulfate given its known bulk concentration, [S2O32−(b)], using APXPS on a liquid flat jet. APXPS measurements were conducted at the Advanced Light Source (ALS) at beamline 11.0.2.1 in the LARaXS endstation using a colliding liquid flat jet system, as described in Section S2.1 in the ESI.† O 1s core level spectra were recorded with varying excitation energies (Section S2.2 in ESI†) to probe the first ∼1.5–5 nm of the liquid surface. Thiosulfate and water peak areas were determined from the O 1s spectrum, which probes the first ∼1.5 nm of the surface (i.e., the O 1s spectrum taken with an excitation energy producing electrons with 100 eV excess kinetic energy). These areas were used to calculate the concentration of adsorbed thiosulfate at a bulk concentration of 0.5 M, [S2O32−(ads)]b=0.5 M = 0.4 ± 0.2 M (Section S2.3 in ESI†). The average value for [S2O32−(ads)]b=0.5 M (0.4 M), the average plus one standard deviation (0.6 M), and the average minus one standard deviation (0.2 M) were then used with the average value for the Gibbs free energy of absorption from the DUV-SHG experiments (−7.3 kJ mol−1, discussed later in Section 3.1.1) to calculate a range for the maximum concentration of adsorbed thiosulfate, which is equal to [sites]max in eqn (3) (see ESI Section S3 for more details†). This resulted in [S2O32−(ads)]max = 2.7 ± 1.3 M. Note that although[S2O32−(ads)]max should only have 1 significant figure, two are used here to avoid confusion due to rounding.2.3. Kinetic modeling of thiosulfate ozonation
A stochastic reaction–diffusion model is implemented in Kinetiscope©,21 which has been used to model kinetics in a variety of systems, including organic aerosols, aqueous microdroplets, and emulsions.10,11,22,23 The model used in this work was developed previously in Deal, et al.7 and validated against experimental data, which is replicated here in Section 3.1.2. These data7 were collected using levitated microdroplets that were trapped using a quadrupole electrodynamic trap (QET), exposed to ozone, and ejected into an open-port sampling interface (OPSI) for analysis by mass spectrometry (see Fig. S14 in ESI for an experimental schematic†). The droplets comprised a 0.25 M solution of sodium thiosulfate at pH 5, 9, or 13. Solutions at pH 5 and 9 were buffered using malonic acid and NaOH or glycine and HCl, respectively. The pH 13 solution was adjusted using NaOH and was unbuffered due to a lack of viable buffers in this pH range. Single droplets were ejected sequentially and their contents at each time point were analyzed using OPSI-MS as described in Deal, et al.,7 providing concentrations of reactants, intermediates, and products over time. A kinetic model was constructed based on the mechanism shown in Scheme 1, with reaction rate constants and diffusion coefficients from the literature or benchmarked against the experimental data (see Table S1 in ESI†). This kinetic model is the basis for many of the observations in this paper and we thus describe the model in more detail here.Kinetiscope© is a kinetic modeling software package that uses a Monte Carlo approach to simulate chemical kinetics wherein probabilities for each reaction step are used to propagate concentrations in time. To account for the multiphase nature of the droplet, the system is modeled as two rectangular compartments: a surface compartment and a bulk compartment. The surface compartment has a depth of 1 nm, representing the depth of favorable solvation of ozone as determined by molecular dynamics simulations,10 and the bulk compartment has a length of r/3, which preserves the correct surface-to-volume ratio of spherical droplets.24 Both surface and bulk compartments have cross sections of 1 nm2. We note that the probing depth of DUV-SHG is a few molecular layers and APXPS is the first ∼1.5 nm of the surface, but we model the depth of the interface as 1 nm to represent the region where ozone is expected to have enhanced concentration relative to the gas and bulk phases (see ESI Fig. S15†). Using a larger depth for the surface compartment would over predict the amount of adsorbed ozone and erroneously enhance thiosulfate decay.
When modeling ‘bulk-only’ chemistry and calculating surface reaction fractions, we add a third ‘reaction–diffusion’ compartment between the surface and bulk compartments, as described in Section S1.2 in ESI.† While this 3-compartment model provides more detailed simulations, it is also computationally expensive and takes up to 24 hours to simulate ∼500 seconds of reaction time, while the 2-compartment model takes 15 minutes to simulate ∼1,500 seconds of reaction time. Given that the 2-compartment model adequately replicates the kinetics simulated in three compartments (see Section S1.3 in ESI†), the 2-compartment model is used for all simulations unless noted otherwise.
 | (9) |
 is the maximum 2D surface concentration and δ is the thickness of the interface being simulated. To calculate
is the maximum 2D surface concentration and δ is the thickness of the interface being simulated. To calculate  , we use the inverse of the molecular area of ozone calculated by Vieceli, et al.26 (18.5 Å2). Note that although sites are not molecules, we use the units molec per cm3 for consistency with kinetic rates.
, we use the inverse of the molecular area of ozone calculated by Vieceli, et al.26 (18.5 Å2). Note that although sites are not molecules, we use the units molec per cm3 for consistency with kinetic rates.To determine the relevant kinetic rates, we first decompose the dimensionless Henry's law constant, Hgbcc, into the gas-to-surface (gs) and surface-to-bulk (sb) components, Hgbcc = Hgscc·Hsbcc, as originally shown in Willis and Wilson.11 Molecular Dynamics (MD) simulations published by Prophet, et al.10 provided solvation free energies, which were used to calculate the Henry's Law components, giving Hgscc = 4.97, Hsbcc = 0.023, and Hgbcc = 0.145. Note that here we use Hgscc = 4.97, which is obtained by averaging the solvation free energy across the interfacial region, while Prophet, et al.10 used Hgscc = 9.30, which is computed from the maximum solvation free energy in the interfacial region. The simulation is not sensitive to this difference, but we believe that Hgscc = 4.97 is a more realistic representation of O3 in the interfacial regime. Both Prophet, et al.10 and this work use Hgbcc = 0.145, which is consistent with previous studies on ozone solvation in 1 M sodium chloride solutions.27,28
The Henry's Law equilibrium constants are related to kinetic parameters to describe partitioning between the phases (adsorption/desorption between the gas-phase and interface and solvation/desolvation between the interface and bulk liquid):11
 | (10) |
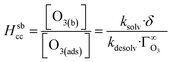 | (11) |
 | (12) |
 | (13) |
This results in rates of adsorption to the interface from the gas-phase of kads = 1.77 × 10−11 cm3 per molec per s and from the bulk liquid to the interface of kdesolv = 1.20 × 10−12 cm3 per molec per s. These fast rates, in a stochastic simulation, often result in a rapid ‘shuttling’ of ozone back and forth between the gas-phase and interface, significantly lengthening simulation times. Thus, most simulations were run with 100X slower rates; i.e., kads = 1.77 × 10−13 cm3 per molec per s and kdes = 1.93 × 108 s−1. In both cases, ozone transfer happens much faster than the reaction and the slower adsorption and desorption rate constants do not affect the overall reaction kinetics while dramatically decreasing computational time.
 | (14) |
and
| Kadseq = kdesolv/ksolv. | (15) |
Note that the number of sites available is different for volatile solutes (O3 and SO2) and non-volatile solutes (S2O32− and all other reaction intermediates and products). To our knowledge, the equilibrium constant for adsorption, Kadseq, and maximum surface concentration, [S2O32−(ads)]max, for thiosulfate has not been measured. We obtain Kadseq from DUV-SHG experiments via the relationship,  , where R is the universal gas constant, T is 298 K, and the concentration of water, CW, is 55.5 M. We also combine data obtained from DUV-SHG (Section 2.1 above) and APXPS (Section 2.2 above and Section S2 in ESI†) to constrain the maximum concentration of adsorbed thiosulfate in the kinetic experiments, [S2O32−(ads)]max (see Section S3 in ESI†).
, where R is the universal gas constant, T is 298 K, and the concentration of water, CW, is 55.5 M. We also combine data obtained from DUV-SHG (Section 2.1 above) and APXPS (Section 2.2 above and Section S2 in ESI†) to constrain the maximum concentration of adsorbed thiosulfate in the kinetic experiments, [S2O32−(ads)]max (see Section S3 in ESI†).
The surface affinities for other non-volatile intermediates and products are also not well quantified. Therefore, we adopt a relative surface activity framework wherein the Langmuir equilibrium coefficient for each species is set relative to that of thiosulfate. At least one molecular dynamics study showed that sulfate is repelled from the interface.13 Similarly, a combined X-ray photoelectron spectroscopy and MD study showed that sulfite and its conjugate acid, bisulfite, are also repelled from the interface.14 The DUV-SHG results discussed later in Section 3.1.1 demonstrate a flat response, which is consistent with sulfite and sulfate being repelled from the interface. Thus, the Langmuir equilibrium coefficients for sulfate and sulfite are set as one order of magnitude smaller than that for thiosulfate. On the other hand, other species are likely to be at least as surface active as thiosulfate, thus we set the Langmuir equilibrium coefficients for HS2O4−, S3O62−, and S4O62− equal to that of thiosulfate. The remaining species, S2O42−, is assigned a Langmuir equilibrium coefficient one order of magnitude larger than that of thiosulfate, which provided the best match between simulations and experiments.7 The reverse rate constants, ksolv, are set to 1.00 × 103 s−1 for all adsorbing species, as in Prophet, et al.10 This value is large enough such that the simulated kinetics are not sensitive to changes in the magnitude of ksolv, but small enough to prevent excessive computation time. The forward rate constants, kdesolv, are calculated using eqn (15).
3. Results & discussion
3.1. Sulfur oxyanion surface activities
Fig. 2A plots the normalized SHG response of sulfite and sulfate as a function of bulk concentration. As part of the Hoffmeister series, sulfate is a known kosmotrope and several studies have found it is well-solvated in water with no significant interfacial presence.29–32 Here, sulfate solutions exhibit a flat SHG response across the measured concentration range, which is consistent with sulfate being repelled from the interface. Sodium sulfite measurements collected at 200 nm display a weak signal increase above 1 M (Fig. 2A). Previous SHG work has attributed this weak linear response to an interfacial thickening of the water layer due to an increased solute concentration, which alters the hyperpolarizability of interfacial water molecules.18,20,33 Given the linewidth of the sulfite CTTS transition shown in Fig. 1C, we also measured sodium sulfite at 390 nm (195 nm SHG), and observed a clear uniform response similar to sulfate measurements. If sulfite ions were indeed surface-active, a 5 nm shift away from the resonant transition center would not completely diminish the SHG response.
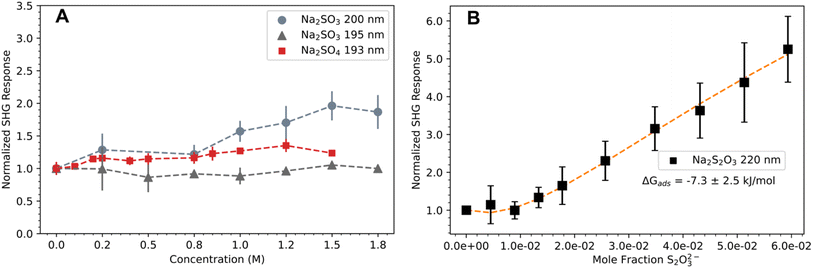 | ||
| Fig. 2 Normalized DUV-SHG response of sulfur oxyanions at the air–water interface. (A) Response of sodium sulfite and sodium sulfate solutions exhibiting a weak concentration-dependent SHG response. Dashed lines act as a visual guide. (B) Response of sodium thiosulfate exhibiting a clear concentration dependent DUV-SHG signal. Orange dashed line represents the fit to a Langmuir model. Error bars represent one standard deviation. Note that y-axis scales are different for clarity, panel A is shown with concentration on the x-axis for ease of interpretation, and panel B is shown with mole fraction on the x-axis for consistency with the Langmuir fit (eqn (8)). | ||
Unlike sodium sulfate and sodium sulfite solutions, Fig. 2B shows a strong concentration dependent SHG signal for solutions of sodium thiosulfate. Fitting the normalized SHG response to eqn (8), we extract ΔGads = −7.3 ± 2.5 kJ mol−1 for thiosulfate anions at the air–water interface. These results indicate that thiosulfate, a doubly charged anion, exhibits a strong propensity for the interface not seen in the similarly charged sulfite and sulfate anions. This behavior is striking since early theories of ions at interfaces by Onsager and Samaras predict a strong repulsion of doubly charged ions based on electrostatic arguments.34 Even as early experimental and theoretical studies began to uncover support for interfacial ions, it was thought that only large, highly polarizable anions could be surface enhanced and excluded multicharged anions and cations. However, much progress has been made in our understanding of interfacial ions and studies have found favorable ion pairing effects contributing to the surface affinity of these previously overlooked ions.18,33,35 While we do not yet have a mechanism to explain the surface adsorption of thiosulfate, we propose that favorable ion-pairing effects are likely involved. Without MD simulations, we lack a theoretical route to validate and interpret the measured ΔGads of thiosulfate and instead use the kinetic model to compare simulated reaction kinetics using the measured ΔGads to experimental reaction kinetics.
Deal, et al.7 performed a sensitivity analysis comparing experimental data at each pH to simulations assuming ΔGads = −4.8 kJ mol−1, −7.3 kJ mol−1, and −9.8 kJ mol−1 (see Fig. S6 in ESI†) and proposed that thiosulfate is less surface-active at pH 13. Here, we perform additional DUV-SHG measurements of thiosulfate solutions adjusted to pH 13 (see Section S4 in ESI†). The average ΔGads value at pH 13 is more positive (−4.1 ± 2.9 kJ mol−1, Fig. S9 in ESI†) than that for the neutral solution (−7.3 ± 2.5 kJ mol−1, Fig. 2B), which may be consistent with a decreased surface activity at pH 13. However, the uncertainty in these measurements remains large and the intensity of the SHG response is not significantly different than the pH 6 measurements, which is inconsistent with decreased surface activity. Thus, while our data suggest that the ΔGads of thiosulfate at the air–water interface could be less favorable with increased pH, DUV-SHG results are inconclusive on their own (see Section S4 in ESI for more details†).
 | ||
| Fig. 3 Representative reaction kinetics for the ozone oxidation of thiosulfate (S2O32−) in pH 5 (A, D, and G), pH 9 (B, E, and H), and pH 13 (C, F, and I) solutions compared with simulation results using ΔGads = −4.8 kJ mol−1 and three values for the maximum concentration of adsorbed thiosulfate (values shown in legend). Experimental data (points) are recreated from Deal, et al.7 with error bars representing one standard deviation in a set of 5 repeats. The term ‘S loss’, or the total amount of reacted sulfur that is not detected in products, encompasses all potential unaccountable sulfur sinks, including evaporation as gasses, precipitation as elemental sulfur, and experimental error.7 | ||
Interestingly, we find that the ΔGads = −4.8 kJ mol−1 simulations with varying [S2O3(ads)2−]max recreate the experimental data at all three pH values (Fig. 3), while the ΔGads = −7.3 kJ mol−1 simulations only recreate experimental data at pH 5 and pH 9 (Fig. S7 in ESI†). In Fig. 3, we see that [S2O32−(ads)]max = 4.0 M (dotted lines) most closely recreates the pH 5 experimental data, [S2O32−(ads)]max = 2.7 M (solid lines) most closely recreates the pH 9 experimental data, and [S2O32−(ads)]max = 1.3 M (dashed lines) most closely recreates the pH 13 experimental data. See Section S3 in ESI† for more detailed discussion. This suggests that less thiosulfate adsorbs to the interface with increasing pH, which may indicate competitive adsorption between thiosulfate and OH−, especially at pH 13 when [OH−] = 0.10 M compared with [S2O32−] = 0.25 M. We note that APXPS measurements have only been collected at neutral pH, and the exact mechanism for decreased thiosulfate surface concentration with increasing pH remains to be determined, but the general trend is consistent with previous literature.10 Regardless, both experimental and simulated kinetics results show a fast reaction between thiosulfate and ozone which suggests a significant amount of adsorbed thiosulfate at all three pH values studied here.
3.2. Interface vs. bulk contributions to reaction kinetics
To examine the relative contribution of surface and bulk reactions, we run the kinetic model allowing only surface or bulk chemistry, respectively. Given the findings above, the kinetic models use ΔGads = −4.8 kJ mol−1 for all pH values, and [S2O32−(ads)]max = 4.0 M for pH 5, [S2O32−(ads)]max = 2.7 M for pH 9, and [S2O32−(ads)]max = 1.3 M for pH 13. ‘Bulk only’ simulations require an additional reaction–diffusion compartment between the surface and bulk compartments to account for near-surface reactions (see ESI Section S1.2†). In both ‘surface only’ and ‘bulk only’ simulations, acid–base equilibria are still enforced throughout the simulation volume and all species are allowed to adsorb to the interface, desorb from the interface, and diffuse throughout the surface and bulk compartments. Simulations run with only surface chemistry show significant thiosulfate decay (black dashed lines in Fig. 3A–C), while modeling only bulk chemistry (dotted lines) predicts a slower thiosulfate decay at pH 5 and pH 9.At all pH values studied here, thiosulfate decay kinetics appear decoupled from subsequent reaction steps, and neither surface chemistry nor bulk chemistry alone recreate the observed kinetics for reaction intermediates and final products (see Section S5 in ESI†). This is especially clear for pH 5 and pH 9 solutions, wherein the thiosulfate decay kinetics (Fig. S10A and B in ESI†) can be described using only surface reactions, but the kinetics of reaction intermediates (Fig. S10D and E†) and products (Fig. S10G and H†) must be described using both surface and bulk reactions. To better understand this, we examine the percent surface reaction for each reaction step using a 3-compartment model (see Section S1.2 and S1.3 in ESI†). Use of a 3-compartment model, as outlined previously for the ozone oxidation of aqueous iodide,36 simulates bulk reactivity in the droplet accounting for diffusional constraints governed by the short reaction–diffusion length for O3 in this system. Although computationally expensive, a 3-compartment model also prevents an artificial enhancement of the surface reaction fraction, and the reaction–diffusion compartment (noted as ‘rxn’) is considered part of the bulk. The selection frequency, n, or number of times a specific reaction step occurs, is extracted from the Kinetiscope© model for each reaction step in the bulk, reaction–diffusion, and surface compartments. The percent surface reaction, fxsurf, for each reaction step, x, is then calculated as  . The results are shown in Fig. 4.
. The results are shown in Fig. 4.
Fig. 4A, D and F shows that the primary reaction between thiosulfate and ozone occurs both at the surface and in the bulk at all pH values, with fxsurf decreasing from over 65% at pH 5 to ∼45% at pH 13, which is consistent with the decreasing value of [S2O32−(ads)]max used here. The subsequent decomposition of the ozonide intermediate [S2O3OOO]− to form SO2 and sulfate, S2O42−, or HS2O4− (reactions 1a, 1b, 1c in Fig. 4A, D and F) primarily occurs at the droplet surface at pH 9 (Fig. 4D; fxsurf >80%), but has a larger contribution from the bulk at pH 5 (Fig. 4A; fxsurf ∼70%) and pH 13 (Fig. 4F; fxsurf ∼65%). On the other hand, the oxygen-mediated decomposition of S2O42− to form SO2 and SO42− (reaction 2a in Fig. 4C and E) and the reaction of HS2O4− with thiosulfate to form S4O62− (reaction 2c in Fig. 4C) occur primarily in the droplet bulk with fxsurf <2%. Interestingly, the location of the S2O42− + SO2 reaction to form S3O62− (reaction 2b in Fig. 4B and E) is both pH and reaction time dependent. Using this information, we can overlay the reaction mechanism shown in Scheme 1 with the interface or bulk reaction locations suggested in Fig. 4 and create a detailed reaction–diffusion mechanism as demonstrated in Fig. 5.
 | ||
| Fig. 5 Schematic of the interface-mediated reaction–diffusion mechanism for the ozonation of thiosulfate in aqueous droplets at pH 5. Bolded species are detected in experiments7 and colors are set to match those used in Scheme 1 and other figures in this work. | ||
The combined role of pH and the interface in the production of sulfate, the main product, is particularly interesting. Sulfate can either be formed by direct decomposition of the ozonide intermediate, which primarily occurs at the interface (r1a in Fig. 4A), or by the reaction of S2O42− with O2, which primarily occurs in the bulk (r2a in Fig. 4C, E and G). However, reaction 1a is pH dependent, meaning that reaction 2a is the main sulfate formation pathway at pH 9 and pH 13. Ultimately, sulfate forms mostly in the bulk at higher pH, but some will form at the surface at lower pH. Accurate accounting of sulfate is important for climate modeling due to its hygroscopic nature and ability to form cloud condensation nuclei, meaning that such a detailed analysis of sulfate formation in droplets may be useful to atmospheric scientists.
3.3. Reactant concentration & droplet size effects
Microdroplets in the atmosphere may be exposed to a range of gas-phase reactant concentrations or have a variety of size distributions and solute concentrations. With this in mind, we seek to address how aerosol/droplet size, thiosulfate concentration, and ozone concentration affect the relative importance of the surface and bulk chemistry illustrated in Fig. 5.First, we compare our kinetic model with data published by Hsu, et al.9 which utilized smaller droplets (∼3 μm) and larger ranges of thiosulfate (2.86 to 10.1 M) and ozone concentrations (0.4 to 15 ppm). Hsu, et al.9 used optical tweezers to capture single droplets and Raman spectroscopy to determine reactant and product concentrations. Droplets were unbuffered, and the pH likely decreased from 7 at the start of the reaction to 1 or 2 at the end of the reaction. The kinetic model used here assumes a fixed pH to reduce computation time and pH = 7, which has been accurate when modeling other unbuffered thiosulfate ozonation experiments.7 Despite this assumption, our model adequately predicts the thiosulfate decay detected in some of the Hsu, et al.9 experiments, as shown in Fig. 6. We note, however, that our model does not explain all of the Hsu, et al.9 data as shown in Section S6 in ESI,† especially at low ozone concentrations where the thiosulfate decay rate decreases and experimental error increases (Experiments 6–9 in Fig. S10 and S12 in ESI†).
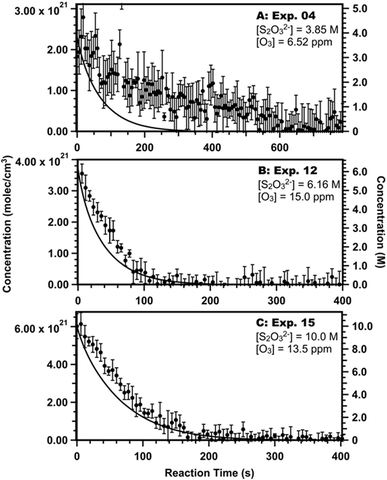 | ||
| Fig. 6 Select comparisons between data from experiments 4 (A), 12, (B), and 15 (C) in Hsu, et al.9 and the kinetic model (lines). Data with error bars are recreated from ref. 9. See Section S6 in ESI† for all comparisons between model and experiments. | ||
Next, we investigate a range of atmospherically relevant initial bulk thiosulfate concentrations, gas-phase ozone concentrations, and droplet radii using the kinetic model described here. Note that although most aerosols are very acidic (pH 1–3), our current kinetic model has not been benchmarked against experiments at such low acidity. Additionally, there are some instances where aerosols may reach pH 4–6, including over Hawaii, São Paulo, and mainland China.37 As such, the simulations presented here use the pH 5 kinetic model to offer novel insights into the ozonation of thiosulfate in acidic environments.
The droplet experiments presented in Deal, et al.7 were performed with an initial bulk thiosulfate concentration of 250 mM, but thiosulfate concentrations in the natural environment are likely very low (<10 mM). Similarly, the experiments presented in Deal, et al.7 were performed with gas-phase ozone concentrations between 1 and 6 ppm, but gas-phase ozone concentrations in the natural environment are much lower (<1 ppm). Here, we connect experiment and natural environment concentration ranges by simulating droplet chemistry with [S2O32−]0 = 1, 10, 100, and 250 mM and [O3]gas = 0.1, 0.5, and 1 ppm. Atmospheric chemistry is most impacted by aerosols/droplets with radii between 0.001 and 5 μm, but at sufficiently small droplet sizes (<∼0.01 μm), curvature can affect droplet chemistry due to the similarity between molecular and droplet sizes. Given that our kinetic model does not account for droplet curvature, we simulate droplets with r = 0.2 μm (which represents a maximum in the volume distribution for a typical urban model aerosol38), 3 μm (representative of Hsu, et al.9), and 25 μm (representative of Deal, et al.7). Sets of simulations were run with fixed thiosulfate concentration ([S2O32−]0 = 100 mM) or fixed ozone concentration ([O3]gas = 1 ppm), and the concentrations of each product and the percent surface reactions were calculated using the values after all thiosulfate was reacted. Note that of the four products examined here, SO42−, S3O62−, and S4O62− were detectable in experiments and SO2 was undetectable.7,9 However, SO2 is likely a major source of the S loss noted in the Deal, et al.7 experiments and Fig. 3, thus we model its production here. The % yield for each product represents the total amount of reacted sulfur that is incorporated into the given product, and the % surface reaction is calculated as described previously.
Fig. 7 shows the impact of [S2O32−]0, [O3]gas, and aerosol size on the product distribution, or % yield of each product, and relative importance of surface chemistry to bulk chemistry for a given reaction, or the % surface reaction. Note that the results in Fig. 7 were calculated with the 2-compartment model described in Methods Section 2.3 to reduce computation time, and results were checked against a 3-compartment model (see Section S9 in ESI†). Although the 3-compartment model showed decreased % surface reaction values, the overall trends with changes in [S2O32−]0, [O3]gas, and r remained constant, and there were negligible differences in the calculated % yield.
Several observations can be drawn from Fig. 7. First, changes in [O3]gas have minimal impacts on the product distribution (Fig. 7A) and relative importance of surface vs. bulk chemistry (Fig. 7C). In contrast, [S2O32−]0 has a significant effect on both product distributions (Fig. 7B) and surface vs. bulk chemistry (Fig. 7D). The difference in product distributions shown in Fig. 7B largely stems from the competition between SO2 evaporation (desorb in Scheme 1) and the downstream reactions that form SO42−, S3O62−, and S4O62− (2a, 2b, and 2c in Scheme 1 and Fig. 5). Specifically, we see that as [S2O32−]0 increases, the % yield of S4O62− also increases, because its production requires two thiosulfate molecules, while the % yield of SO42− and SO2 decreases. As [S2O32−]0 increases, more thiosulfate decay, SO42− production, and S3O62− production occur at the surface (Fig. 7D) due to the Langmuir adsorption of thiosulfate to the interface. At higher bulk concentrations, more thiosulfate will adsorb to the interface, depleting a significant portion of the adsorbed ozone before it can enter the droplet bulk. At lower thiosulfate concentrations, which will have less adsorbed thiosulfate, less surface adsorbed ozone will be reacted, allowing more ozone to enter the droplet bulk, thereby increasing the number of bulk reactions and decreasing the relative importance of surface reactions.
Finally, we examine the role of droplet size in relationship to the reacto–diffusive length, l. The reacto-diffusive length is calculated as:
 | (16) |
For a given [O3]gas and [S2O32−]0, increasing droplet size increases the % surface reaction for S2O32− decay and decreases the % surface reaction for S3O62− production (gray and blue in Fig. 7C and D). In larger droplets, where the radius is much larger than the reacto-diffusive length, bulk chemistry is limited by diffusion, resulting in ozonation reactions occurring mostly at the surface. In smaller droplets, the radius of the droplet nears the reacto-diffusive length, approaching phase mixing where ozone diffusion no longer limits bulk phase reactions. This also leads to differences in product distributions due to the phase dependent competition of downstream reaction steps, as shown in Fig. 5. Generally, for a given [O3]gas and [S2O32−]0, the % yields of SO42− and SO2 increase with increasing droplet size, while the relationships between droplet size and the % yields of S3O62− or S4O62− are more complicated (Fig. 7A and B).
Droplet size and [S2O32−]0 effects on product distributions are particularly interesting when considering the impacts on the overall oxidation state of sulfur, as shown in Fig. S17 in ESI.† S2O32− has an average oxidation state of 2.0, while the major products have a variety of oxidation states. SO42− has an oxidation state of 6.0, SO2 has an oxidation state of 4.0, S3O62− has an average oxidation state of 3.3, and S4O62− has an average oxidation state of 2.5. This means that reaction environments that favor S3O62− and/or S4O62− will, on average, produce less oxidized sulfur than reaction environments that favor SO2 and/or SO42−. Among the test environments simulated here, the smallest droplets (r = 0.2 μm) with the lowest [S2O32−]0 (1 mM) produce the most sulfate and SO2, resulting in the highest average oxidation state at reaction completion (4.7). This is in contrast with midsize droplets (r = 3 μm) with the highest [S2O32−]0 (250 mM), which produce the most S4O62−, resulting in the lowest average oxidation state at reaction completion (4.0).
In summary, the average sulfur oxidation state is a function of the product distribution, which will be determined by a combination of droplet size and thiosulfate concentration, primarily due to an interface-mediated competition between SO42− and S4O62− production. As depicted in Fig. 5, S4O62− production requires the reaction of thiosulfate with ozone, which primarily occurs at the surface, followed by the secondary reaction of HS2O4− with another thiosulfate molecule, which primarily occurs in the bulk. In contrast, SO42− production occurs by two independent pathways, occurring at the interface or in bulk. Given this complex role of the droplet interface in controlling individual reaction steps, it is unsurprising that the product distribution, and thus the overall oxidation state, is a complex function of thiosulfate concentration and droplet size. This example demonstrates the multiphase control of the thiosulfate ozonation reaction mechanism, which may have implications for complex reaction mechanisms involving microdroplets.
4. Conclusions
Chemistry in droplets has rapidly gained interest due to evidence of accelerated reactivity, the enhanced role of the interface, and the unique interactions that can occur between the gas-phase, interface, and droplet bulk. However, one of the key challenges when investigating multiphase chemistry involving droplets is connecting molecular-level detail to macroscale reactivity, especially at the interface. Here, we use advanced experimental and theoretical methodologies to assess the surface activity of the doubly charged thiosulfate anion, address the root cause of accelerated thiosulfate ozonation in droplets, and understand the role of the interface in thiosulfate ozonation.We use two state-of-the-art techniques, DUV-SHG and APXPS, to directly quantify the surface activity of thiosulfate. We show unequivocally that thiosulfate is surface-active, in contrast to dated notions that all doubly charged anions would be repelled from the interface, but consistent with recent emerging evidence for favorable ion-pairing. The molecular-level detail provided by DUV-SHG and APXPS is also exploited by a sophisticated stochastic kinetic model to explain macroscale reactivity measured by mass spectrometry of trapped droplets. Previous studies suggested that the rate constant for the reaction of thiosulfate with ozone is faster at the surface than in the bulk. Here, we clarify that the reaction rate is enhanced due to significant concentrations of adsorbed ozone and thiosulfate, which may have implications for other studies showing enhanced reaction rates in droplets.
The resultant kinetic model is also used to provide unprecedented detail regarding a complex reaction mechanism, the ozonation of thiosulfate, and the multiphase nature of the droplet reactor. Specifically, we track the propagation of each reaction step throughout the gas, interface, and bulk phases. We find that individual steps tend to occur throughout smaller droplets, where the reacto-diffusive length nears the droplet radius, while individual reaction steps become separated in larger droplets, where the reacto-diffusive length is much smaller than the droplet radius. Additionally, primary reaction steps typically occur more often at the interface than in the bulk, while some downstream reaction steps occur predominantly in the bulk. The thiosulfate ozonation example shown in this work demonstrates that deeming a reaction as “surface-limited” or “diffusion-limited” may be a significant oversimplification when considering other microdroplet chemistries.
The interaction of thiosulfate (in large bodies of water or aqueous aerosols) with the environment will be heavily dependent on its oxidative processing. In the case of ozone oxidation, we find that the product distribution, and thus the average sulfur oxidation state, is dependent on a non-trivial combination of droplet size and reactant concentration. S2O32− has two sulfurs with an average oxidation state of +2.0, while its ozonation products have a range of oxidation states. Fully oxidized sulfur (S6+) in the form of sulfate attracts water, increasing the size of the aerosol/droplet or forming cloud condensation nuclei (CCN), directly affecting radiative forcing. While we show that most sulfate will be formed in the bulk of the droplet, in more acidic conditions some sulfate will be formed at the surface of the droplet, potentially increasing the likelihood that it can impact the surrounding environment. On the other hand, SO2, S3O62−, and S4O62− are incompletely oxidized with average sulfur oxidation states of +4.0, +3.3, and +2.5, respectively. The incompletely oxidized sulfur in these stable intermediates remains susceptible to further oxidation in large bodies of water or atmospheric aerosols/droplets, which typically also results in downstream acidification.
This study addresses the relevant parameters for thorough modeling of potential thiosulfate ozonation. For example, recent efforts have suggested using ozone-microbubbles for mining wastewater remediation including thiosalt removal. This study shows that these processes should consider solution pH and bubble size to ensure maximum sulfur oxidation and prevent downstream acidification of the natural environment. Additionally, the sulfur cycle, and specifically the oxidation state of sulfur, can have a large impact on the global radiation budget. Atmospheric chemistry models thus require a thorough understanding of sulfur chemistry to predict CCN formation and aerosol/droplet acidification. Similar experimental and theoretical frameworks will be useful to those seeking to better understand or leverage chemistry at interfaces or in droplets.
Data availability
Data are available from the corresponding author upon request.Author contributions
Conceptualization: A. M. D. and K. R. W. Kinetic modeling methodology: A. M. D., A. M. P., and K. R. W. Model implementation and simulations: A. M. D. DUV-SHG experimental methodology: F. B. and R. J. S. DUV-SHG collection: F. B. APXPS experimental methodology: M. B. APXPS data collection: M. L. L., A. S., M. B. APXPS data analysis: A. S. Writing – original draft: A. M. D. Writing – review and editing: all.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Condensed Phase and Interfacial Molecular Science Program (CPIMS), in the Chemical Sciences Geosciences and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. The APXPS measurements used the Advanced Light Source, which is a U.S. Department of Energy Scientific User Facility under contract no. DE-AC02-05CH11231. We thank Professor Yuan-Pin Chang (National Sun Yat-sen University) for providing the data in Fig. 6 and Section S6 in ESI.†References
- Z. Wei, Y. Li, R. G. Cooks and X. Yan, Accelerated reaction kinetics in microdroplets: Overview and recent developments, Annu. Rev. Phys. Chem., 2020, 71, 31–51 CrossRef CAS PubMed.
- G. Rovelli, M. I. Jacobs, M. D. Willis, R. J. Rapf, A. M. Prophet and K. R. Wilson, A critical analysis of electrospray techniques for the determination of accelerated rates and mechanisms of chemical reactions in droplets, Chem. Sci., 2020, 11, 13026–13043 CAS.
- C. J. Chen and E. Williams, Are hydroxyl radicals spontaneously generated in unactivated water droplets?, Angew. Chem., 2024, e202407433 CAS.
- A. Gallo, A. S. Farinha, M. Dinis, A.-H. Emwas, A. Santana, R. J. Nielsen, W. A. Goddard and H. Mishra, The chemical reactions in electrosprays of water do not always correspond to those at the pristine air–water interface, Chem. Sci., 2019, 10, 2566–2577 RSC.
- V. Masson-Delmotte, P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb and M. Gomis, IPC 2021. Summary for policymakers. Climate change 2021, The physical science Basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change, 2023 Search PubMed.
- P. R. Veres, J. A. Neuman, T. H. Bertram, E. Assaf, G. M. Wolfe, C. J. Williamson, B. Weinzierl, S. Tilmes, C. R. Thompson, A. B. Thames, J. C. Schroder, A. Saiz-Lopez, A. W. Rollins, J. M. Roberts, D. Price, J. Peischl, B. A. Nault, K. H. Møller, D. O. Miller, S. Meinardi, Q. Li, J.-F. Lamarque, A. Kupc, H. G. Kjaergaard, D. Kinnison, J. Jimenez, C. M. Jernigan, R. S. Hornbrook, A. Hills, M. Dollner, D. A. Day, C. A. Cuevs, P. Campuzano-Jost, J. Burkholder, T. P. Bui, W. H. Brune, S. S. Brown, C. A. Brock, I. Bourgeois, D. R. Blake, E. C. Apel and T. B. Ryerson, Global airborne sampling reveals a previously unobserved dimethyl sulfide oxidation mechanism in the marine atmosphere, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 4505–4510 CrossRef CAS PubMed.
- A. M. Deal, A. M. Prophet, F. Bernal, R. J. Saykally and K. R. Wilson, A detailed reaction mechanism for thiosulfate oxidation by ozone in aqueous environments, Environ. Sci. Technol., 2024, 58, 18959–18968 CrossRef CAS PubMed.
- A. J. Atkinson, H. Ray and E. C. Wert, Efficiency of ozone quenching agents at different temperature, pH, and hydrodynamic conditions, Ozone: Sci. Eng., 2024, 1–20 Search PubMed.
- S.-H. Hsu, F.-Y. Lin, G. G. Huang and Y.-P. Chang, Accelerated sulfur oxidation by ozone on surfaces of single optically trapped aerosol particles, J. Phys. Chem. C, 2023, 127, 6248–6261 CrossRef CAS.
- A. M. Prophet, K. Polley, G. J. Van Berkel, D. T. Limmer and K. R. Wilson, Iodide oxidation by ozone at the surface of aqueous microdroplets, Chem. Sci., 2024, 15, 736–756 RSC.
- M. D. Willis and K. R. Wilson, Coupled interfacial and bulk kinetics govern the timescales of multiphase ozonolysis reactions, J. Phys. Chem. A, 2022, 126, 4991–5010 CrossRef CAS PubMed.
- M. Takizawa, A. Okuwaki and T. Okabe, The chemical behavior of low valence sulfur compounds. VIII. the oxidation of sodium thiosulfate with ozone, Bull. Chem. Soc. Jpn., 1973, 46, 3785–3789 CrossRef CAS.
- S. Gopalakrishnan, P. Jungwirth, D. J. Tobias and H. C. Allen, Air–liquid interfaces of aqueous solutions containing ammonium and sulfate: Spectroscopic and molecular dynamics studies, J. Phys. Chem. B, 2005, 109, 8861–8872 CAS.
- T. Buttersack, I. Gladich, S. Gholami, C. Richter, R. Dupuy, C. Nicolas, F. Trinter, A. Trunschke, D. Delgado, P. Corral Arroyo, E. Parmentier, B. Winter, L. Iezzi, A. Roose, A. Boucly, L. Artiglia, M. Ammann, R. Signorell and H. Bluhm, Direct observation of the complex S (IV) equilibria at the liquid-vapor interface, Nat. Commun., 2024, 15, 8987 CAS.
- H. M. Eckenrode, S.-H. Jen, J. Han, A.-G. Yeh and H.-L. Dai, Adsorption of a cationic dye molecule on polystyrene microspheres in colloids: Effect of surface charge and composition probed by second harmonic generation, J. Phys. Chem. B, 2005, 109, 4646–4653 CAS.
- P. B. Petersen and R. J. Saykally, Probing the interfacial structure of aqueous electrolytes with femtosecond second harmonic generation spectroscopy, J. Phys. Chem. B, 2006, 110, 14060–14073 CrossRef CAS PubMed.
- D. E. Otten, P. R. Shaffer, P. L. Geissler and R. J. Saykally, Elucidating the mechanism of selective ion adsorption to the liquid water surface, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 701–705 CrossRef CAS.
- F. Bernal, A. Dodin, C. Kyprianou, D. T. Limmer and R. J. Saykally, Strong adsorption of guanidinium cations to the air–water interface, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2418443122 CAS.
- M. J. Blandamer and M. F. Fox, Theory and applications of charge-transfer-to-solvent spectra, Chem. Rev., 1970, 70, 59–93 CAS.
- H.-t. Bian, R.-r. Feng, Y.-y. Xu, Y. Guo and H.-f. Wang, Increased interfacial thickness of the NaF, NaCl and NaBr salt aqueous solutions probed with non-resonant surface second harmonic generation (SHG), Phys. Chem. Chem. Phys., 2008, 10, 4920–4931 CAS.
- W. Hinsberg and F. Houle, Kinetiscope – a stochastic kinetics simulator, https://hinsberg.net/kinetiscope/index.html, accessed 1/24/2025.
- M. I. Jacobs, J. F. Davies, L. Lee, R. D. Davis, F. Houle and K. R. Wilson, Exploring chemistry in microcompartments using guided droplet collisions in a branched quadrupole trap coupled to a single droplet, paper spray mass spectrometer, Anal. Chem., 2017, 89, 12511–12519 CAS.
- M. D. Willis, G. Rovelli and K. R. Wilson, Combining mass spectrometry of picoliter samples with a multicompartment electrodynamic trap for probing the chemistry of droplet arrays, Anal. Chem., 2020, 92, 11943–11952 CAS.
- A. Wiegel, K. Wilson, W. Hinsberg and F. Houle, Stochastic methods for aerosol chemistry: a compact molecular description of functionalization and fragmentation in the heterogeneous oxidation of squalane aerosol by OH radicals, Phys. Chem. Chem. Phys., 2015, 17, 4398–4411 RSC.
- I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- J. Vieceli, M. Roeselova, N. Potter, L. X. Dang, B. C. Garrett and D. J. Tobias, Molecular dynamics simulations of atmospheric oxidants at the air–water interface: solvation and accommodation of OH and O3, J. Phys. Chem. B, 2005, 109, 15876–15892 CrossRef CAS PubMed.
- R. Sander, Compilation of Henry's law constants (version 5.0. 0) for water as solvent, Atmos. Chem. Phys., 2023, 23, 10901–12440 CrossRef CAS.
- N. Panich, B. Ershov, A. Seliverstov and A. Basiev, Ozone solubility in concentrated aqueous solutions of salts, Russ. J. Appl. Chem., 2007, 80, 1812–1815 CrossRef CAS.
- W. S. Drisdell, R. J. Saykally and R. C. Cohen, On the evaporation of ammonium sulfate solution, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18897–18901 CrossRef CAS PubMed.
- Y. Litman, K.-Y. Chiang, T. Seki, Y. Nagata and M. Bonn, Surface stratification determines the interfacial water structure of simple electrolyte solutions, Nat. Chem., 2024, 16, 644–650 CrossRef CAS PubMed.
- L. M. Pegram and M. T. Record, Hofmeister salt effects on surface tension arise from partitioning of anions and cations between bulk water and the air–water interface, J. Phys. Chem. B, 2007, 111, 5411–5417 CrossRef CAS PubMed.
- T. Seki, C.-C. Yu, K.-Y. Chiang, A. Greco, X. Yu, F. Matsumura, M. Bonn and Y. Nagata, Ions speciation at the water–air interface, J. Am. Chem. Soc., 2023, 145, 10622–10630 CrossRef CAS PubMed.
- S. W. Devlin, S. Jamnuch, Q. Xu, A. A. Chen, J. Qian, T. A. Pascal and R. J. Saykally, Agglomeration drives the reversed fractionation of aqueous carbonate and bicarbonate at the air–water interface, J. Am. Chem. Soc., 2023, 145, 22384–22393 CrossRef CAS PubMed.
- L. Onsager and N. N. Samaras, The surface tension of Debye-Hückel electrolytes, J. Chem. Phys., 1934, 2, 528–536 CrossRef CAS.
- R. K. Lam, J. W. Smith, A. M. Rizzuto, O. Karslıoğlu, H. Bluhm and R. J. Saykally, Reversed interfacial fractionation of carbonate and bicarbonate evidenced by X-ray photoemission spectroscopy, J. Chem. Phys., 2017, 146 Search PubMed.
- A. M. Prophet, K. Polley, E. K. Brown, D. T. Limmer and K. R. Wilson, Distinguishing surface and bulk reactivity: concentration-dependent kinetics of Iodide oxidation by ozone in microdroplets, J. Phys. Chem. A, 2024, 128, 8970–8982 CrossRef CAS PubMed.
- H. O. Pye, A. Nenes, B. Alexander, A. P. Ault, M. C. Barth, S. L. Clegg, J. L. Collett Jr, K. M. Fahey, C. J. Hennigan and H. Herrmann, The acidity of atmospheric particles and clouds, Atmos. Chem. Phys., 2020, 20, 4809–4888 CrossRef CAS PubMed.
- B. J. Finlayson-Pitts and J. N. Pitts Jr, Particles in the troposphere, in Chemistry of the upper and lower atmosphere: theory, experiments, and applications, Elsevier, 1999 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00379b |
| This journal is © The Royal Society of Chemistry 2025 |



