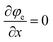Advancing next-generation proton exchange membrane fuel cell design through multi-physics and AI modeling

Abstract

Next-generation proton exchange membrane (PEM) fuel cells of high power density and durability are a cornerstone technology for future sustainable energy systems. While traditional three-dimensional (3D) full-size computational fluid dynamics (CFD) modeling has been pivotal in fuel cell design by numerically resolving electrochemically coupled multi-physics transfers, it faces persistent challenges, including a major theoretical gap in channel two-phase flow physics, oversimplified representations of catalyst layer (CL) microstructures, outdated membrane correlations, inadequate validation, and lack of consideration on material degradation. This perspective paper identifies key challenges and opportunities for fuel cell design through multi-physics and artificial intelligence (AI) modeling. Data-driven sub-models describing specific physics (e.g., multi-physics transfers within CLs) can be integrated with traditional modeling frameworks to balance the trade-off between computational efficiency and accuracy. Moreover, by utilizing physics-informed operator learning (e.g., PI-DeepONet) for evolution of multi-physics distributions and generating datasets via transient 3D models incorporating balance of plant (BOP) components, it is foreseeable to ultimately pave the way for predictive digital twins enabling health monitoring and degradation analysis throughout the life cycle, crucial for developing next-generation high-power-density and durable PEM fuel cells.

---

Broader context

Proton exchange membrane (PEM) fuel cells, which can directly convert green hydrogen energy into electricity, represent a pivotal technology for future sustainable energy systems to achieve the carbon neutrality target, due to their promising merits such as zero emission, high energy density, and fast dynamic response. Overcoming the power density and durability bottlenecks for large-scale commercial application urgently requires further fundamental understanding of the electrochemically coupled multi-physics transfer mechanisms within fuel cells. Traditional multi-physics modeling struggles with critical theoretical gaps (e.g. channel two-phase flow dynamics), oversimplified catalyst layer (CL) microstructures, outdated correlations for membranes, and low computational efficiency. In this Perspective, we identify key challenges and opportunities in advancing next-generation PEM fuel cell design through multi-physics and artificial intelligence (AI) modeling, including degradation-oriented design, transient system-level integration, and AI-augmented approaches, for evolution of multi-physics distributions under real conditions and enabling of health monitoring and degradation analysis. Ultimately, this work provides a critical roadmap to transition PEM fuel cell digital design from theory and laboratory level to industrial application.

1. Introduction

Green hydrogen, produced via water electrolysis using solar, wind, and other renewables, is emerging as a cornerstone of future sustainable energy systems.^1,2 Proton exchange membrane (PEM) fuel cells, which can efficiently convert hydrogen into electricity with zero emissions, high energy density, and rapid response capabilities, have found promising applications in transportation,³ aerospace,^4,5 distributed power generation,⁶ among others. Notably, the automotive sector has witnessed significant advancements since Toyota pioneered the commercial fuel cell vehicle (FCV) market with the first Mirai FCV launched in 2015,⁷ followed by models like Honda Clarity,⁸ Hyundai NEXO,⁹ and Chinese counterparts such as Shanghai Automotive Industry Corporation (SAIC) Maxus EUNIQ 7,¹⁰ First Automotive Works (FAW) Hongqi H5, Changan Deep Blue SL03,¹¹ etc. These FCVs offer distinct advantages over battery-electric vehicles (BEVs),¹² including faster refueling, extended driving ranges,¹³ and exceptional subfreezing-temperature operability (down to −40 °C).¹⁴ However, the commercialization trajectory of FCVs lags behind BEVs due to persistent challenges,¹⁵ including lack of supporting hydrogen infrastructure,¹⁶ relatively high cost,¹⁷ low performance^18,19 and insufficient durability under low loading of precious catalysts.²⁰

Fig. 1 illustrates the schematic architecture of a PEM fuel cell across three hierarchical levels: unit cell, stack, and system levels for automobiles. The fundamental unit cell comprises a central PEM coated with catalyst layers (CLs) on its two sides, i.e., catalyst coated membrane (CCM), which is sandwiched by two gas diffusion media, including micro-porous layers (MPLs) and gas diffusion layers (GDLs), to form the membrane electrode assembly (MEA).²¹ Bipolar plates (BPs) are integrally arranged on both anode and cathode terminals, in which flow fields are embedded for reactant supply and water removal.²² Stack-level integration involves multiple unit cells connected in series to achieve higher voltage and power capabilities.²³ This modular assembly approach enables scalable power delivery while maintaining compactness. And the balance of plant (BOP) subsystems are integrated to facilitate optimal stack operation such as temperature and humidity by regulating hydrogen and air supply, humification, and thermal management units.²⁴

Fig. 1 Schematic of a PEM fuel cell at unit cell, stack and system levels for automobile applications,²⁵ key materials, and the targets of next-generation PEM fuel cells, adapted/reproduced from ref. 25 with permission from Elsevier,²⁵ copyright 2024, and from ref. 26 with permission from John Wiley & Sons,²⁶ copyright 2023.

From the perspective of polarization curves characterizing overall fuel cell performance, it is axiomatically recognized that the output voltage at specific current densities is mainly determined by three distinct polarization mechanisms: the activation polarization, ohmic polarization, and concentration polarization (as diagrammatically illustrated in Fig. 2).²⁷ These voltage loss mechanisms exhibit strong dependence on interdependent factors including catalyst activity, electrochemical surface area (ECSA), operational temperature, proton and electron conductivity, and multi-phase transport (e.g. gas/liquid flow dynamics),²⁸ etc. Ideally, concurrent optimization of all these mechanisms for highest output voltage through enhanced gas–liquid–heat–electron–proton transfers could maximize fuel cell performance. However, significant challenges exist due to the inherent coupling and competing relationships among these factors.²⁶

Fig. 2 Schematic of ‘gas–liquid–heat–electron–proton’ transport in conjunction with electrochemical reaction and their mechanism of influence on the electrochemical performance of PEM fuel cells.

Furthermore, fuel cell component degradation inevitably induces deterioration in multi-physics transfer efficiencies, primarily attributed to progressive structural modifications (e.g., CL microstructure collapse, carbon corrosion, platinum dissolution, ionomer redistribution),²⁹ ultimately accelerating performance decay and reducing lifespan.³⁰ Simultaneously, the pursuit of cost-effective PEM fuel cell commercialization necessitates substantial reduction of precious catalyst (platinum, Pt) loadings, but this often induces increased oxygen transfer resistance at the ionomer–catalyst interface and diminished ECSA in CLs,³¹ which compromises both fuel cell performance and long-term durability.³² This multifaceted technical challenge underscores the critical need for systematic investigation of multi-scale and multi-physics transport phenomena, their coupling with electrochemical reactions, and their interactions among cell components in unit cell, individual cells in a stack, and subsystems in a fuel cell system, as such fundamental understanding is crucial for developing next-generation PEM fuel cells that simultaneously achieve high efficiency, extended operational durability, and cost reduction targets.³³

To date, scientific understanding of multi-scale and multi-physics transport phenomena in PEM fuel cells remains insufficient, necessitating integrated research methodologies that synergize experimental characterization, computational modeling/simulation, and emerging techniques like machine learning. Among these approaches, first-principles-based models couple multi-physics transport processes with electrochemical reactions, exhibiting high fidelity, flexibility, and capability of disclosing detailed spatial and temporal processes. Table 1 summaries typical first-principles-based models across different scales. Clearly, first-principles-based models can be classified according to their targeted level, including component, cell, stack, and system levels; the first one mainly focuses on the multiple transfers in a single component (e.g., membrane,³⁴ CL,^35,36 MPL,³⁷ GDL,³⁸ or channel/flow field³⁹), the second on a unit cell consisting of all basic components,⁴⁰ the third on a stack of multiple cells connected in series,⁴¹ and the forth on a fuel cell system (also called fuel cell engine) including stacks and auxiliary BOP components.⁴²

Table 1 Characteristics of PEM fuel cell modeling methods across different scales

Models	Advantages	Limitations	Computational cost	Application scenarios
MD model	Takes into account detailed molecular structures in simulations	Limited to very-short-period nano-scale phenomena with accuracy highly dependent on the potential energy functions	High	Proton, heat, oxygen, or water transfers at nano-scale within CL and membrane
LB model	Captures pore-scale multi-physics, multi-component and multiphase reactive transport processes in electrodes	Hard to couple all the multi-physics transport processes simultaneously due to the different time-scales of the transport scalars	High	Two-phase flow in GDLs, MPLs, and gas flow channels
	Easy to handle complex porous structures			Multi-physics transfers and electrochemical reactions in CLs for CL microstructure design and optimization
VOF model	Track the gas/liquid phase interface with surface tension effect	Low calculation efficiency due to small time step	High	Two-phase flow dynamics in gas flow channels, GDLs, MPLs
		Not applicable when the continuum assumption is invalid		Channel and electrode design for liquid water drains or retention
Reduced-dimensional cell/stack model	High calculation efficiency	Poor prediction accuracy	Low	Parameter sensitivity analysis
	Suitable for large-scale cell- and stack-level calculation			Transient analysis of multi-physics transfers and performance evolution
3D full-size model at cell/stack level	Captures almost all the multi-physics transfers and electrochemical activities in detail	Low computational efficiency	High (increase with cell/stack size)	3D cell/stack structure (e.g., BP and flow field) design and optimization
	High prediction accuracy	Difficult to use for long-time transient simulations
System-level model	Capture influence of BOP's dynamic features on fuel cell/stack performance	No/low dimension detail in fuel cell/stack	Ultrahigh (if 3D models are considered)	System-level analysis of multi-physics transfers for system control strategy optimization
		Large calculating burden if 3D sub-system models are considered		Impact of humidifier responses on fuel cell/stack performance
Degradation model	Predict degradation rate or its influence on multi-physics transfer and fuel cell/stack performance	Low prediction accuracy if only considering degradation mechanisms	Ultrahigh (if 3D models are considered)	Predict ECSA decay with time
		Difficult to achieve real two-way coupling between multi-physics transfer and degradation		Design anti-degradation structure
		Large calculating burden if 3D models and long-term operation are considered		Investigate interaction between degradation and fuel cell structure
AI assisted model	High calculation efficiency	Prediction accuracy relies on training data quality	Low	Prediction of fuel cell/stack performance considering complex phenomena
	High accuracy if properly trained	Require a large amount of experimental/simulation data for training		Prediction of impacts of different scale phenomena
	Suitable for handling complex non-linear relationships	Need to select appropriate AI algorithms		Optimization of fuel cell/stack multiscale structure
	Suitable for cross-scale problems			Rapid control of fuel cell/stack dynamics in real-world conditions

---

In power generation, a single cell serves as an elemental unit; and its inherent complexity necessitates systematic investigation of multi-physics interactions among its constituent components and their impacts on electrochemical performance. Three-dimensional (3D) full-size models integrating complete fuel cell morphologies and multi-physics transfers as well as electrochemical reactions demonstrate high fidelity in prediction for fuel cell performance in diverse cell structures (e.g. different flow field structures,^43,44 GDL/MPL materials, and dimensions) and operation conditions.²⁶ Notably, commercial software platforms including ANSYS FLUENT,^28,45 COMSOL,⁴⁶ and AVL Fire⁴⁷ have developed specialized modules for PEM fuel cell simulation over the past decade, significantly accelerating fuel cell R&D and have become increasingly popular in FCV development. Currently, PEM fuel cell deployment remains largely constrained by commercialization barriers, which requires substantial advancements in cell structure and materials to achieve the targets of power density, durability, and cost.^13,48 The existing PEM fuel cell module in commercial software cannot fully support these targets due to multiple limitations, such as restricted capability, poor extensibility, outdated correlations for properties, etc. Self-developing 3D PEM fuel cell models are still essential and under active development to account for new physics and model capabilities.⁴⁹

Despite the past three decades of research efforts, the 3D full-size modeling of PEM fuel cells needs further major advancement due to persistent technical challenges.⁵⁰ The inherent complexity arises from multi-physics couplings among the ‘gas–liquid–electron–proton–heat’ transfers in conjunction with electrochemical reactions across multiple scales, ranging from microscale to macroscale (Fig. 2). This necessitates solving over ten highly-coupled second-order partial differential equations (PDEs) with the reaction kinetics (e.g. the Butler–Volmer equation) embedded in their source terms, which will be more challenging when integrating the channel two-phase flow physics into fuel cell model frameworks.⁵¹ State-of-the-art modeling frameworks also exhibit size limitations: though most show a good capacity of handling single-channel or lab-scale fuel cells with performance validation, their extension to commercial-size cells (>300 cm² active area) and stacks frequently faces major challenges of computational scalability and numerical stability against divergence.⁵² This perspective systematically identifies key challenges and future advancements in 3D full-size modeling for PEM fuel cells, along with integration of artificial intelligence (AI) modeling for achieving a digital twin in next-generation fuel cell design.

2. Multi-physics model framework

2.1 Fuel cell components in design

As mentioned above, traditional 3D PEM fuel cell models are typically constrained by computational efficiency and numerical stability, often limited to single-channel⁵³ and lab-scale analyses.⁵⁴ It is crucial to emphasize that the multi-physics transport mechanisms revealed at these simplified scales may not be directly extrapolated to full-size commercial fuel cells.⁵⁵ For instance, it has been demonstrated that single-channel models significantly underestimate challenges in liquid water removal.⁵⁶ Notably, commercial fuel cell architectures exhibit substantially greater complexity,⁵⁷ rendering single-channel and lab-scale models inadequate to directly support industrial design.⁵⁸ This limitation arises primarily because accurate prediction of multiple variable distribution characteristics and electrochemical behavior fundamentally depends on analysis of flow field across the entire cell.⁵⁹

Table S1 lists typical flow field structures in 3D full-size fuel cell modeling. Fig. 3A presents a schematic representation of commercial PEM fuel cells for automobiles in 3D full-size modeling. The geometry encompasses not only essential components such as the MEA and two BPs, but also incorporates coolant channels and flow-guiding zones that distribute hydrogen, air, and coolant from the stack manifolds to the cell's active region.⁶⁰ Recent numerical studies by Wang et al.,⁵⁵ Zhang et al.,⁶¹ Wu et al.⁶² and Deng et al.⁶³ systematically investigated how the geometric configurations of these flow-guiding zones may greatly influence gas flow uniformity among individual channels. Compared with single-channel approaches, full-size fuel cell models can reproduce the cross-flow enhancement effect caused by gas pressure differences between adjacent channels, as pointed out by Wang et al.,⁵⁵ which can lead to reductions of 16.0% in the concentration loss and 8.2% in the ohmic one.

Fig. 3 (A) Schematic of commercial PEM fuel cell and flow plates for automobile applications;⁶⁰ (B) computational domain in 3D full-size fuel cell stack modeling, images in A adapted/reproduced from ref. 60 with permission from Elsevier,⁶⁰ copyright 2024.

Current 3D full-size modeling approaches can theoretically be extended to stack-level simulations, as most physicochemical processes within fuel cell stacks occur in the constituent fuel cells. Practical implementation remains scarce due to substantial computational demands, with existing studies predominantly focusing on short stacks with no more than 10 cells.^64–66 The computational complexity primarily arises from the massive grid resolution required to capture detailed BP structures and flow field geometries.⁶⁷ Consequently, homogenization of the BP component has emerged as a viable strategy for developing large-scale stack models. Recent advancements by Zhang et al.⁶⁸ demonstrate this approach through a 30-cell air-cooled stack model integrated with fan-assisted air supply using a multiple reference frame (MRF) framework.⁶⁹ These findings revealed that non-uniform airflow induced by mechanical fans significantly impairs output voltage uniformity among the stack's cells.

Fig. 3B illustrates the computational domain configuration for a 3D stack model comprising hundreds of interconnected cells. The geometry includes not only serially connected unit cells but also headers and manifolds guiding the hydrogen, air, and coolant flow from the stack inlet into each cell, which are essential for accurately assessing the uniformity characteristics of key parameters such as gas concentration, liquid saturation, voltage, etc. among stack cells. Notably, flow regimes in stack-level headers predominantly exhibit turbulent characteristics under operational conditions, contrasting to the laminar flow behaviors observed within individual cells. To balance computational efficiency and predictive accuracy, Reynolds-averaged Navier–Stokes (RANS) turbulence modeling approaches (e.g., k–ε model⁷⁰) are universally adopted for these high-velocity, high-Reynolds-number flow regions in industrial-size stack simulations.⁷¹

2.2 Governing equations of electrochemically coupled multi-physics processes

The detailed governing equations describing the electrochemically coupled multi-physics processes are listed in the SI. Table S2 lists the source terms of the above governing equations and a typical CL agglomerate model and Table S3 lists physical properties and correlations in 3D full-size fuel cell modeling. The mass flow rates together with gas species mass fraction and boundary pressures are separately specified at the inlets and outlets of the anode and cathode gas flow fields, and the mass flow rates are calculated according to the stoichiometric ratio (ξ), working current density (I, A cm⁻²), MEA area (A_MEA, m²), inlet area (A_inlet, m²), relative humidity (RH), saturation vapor pressure at the inlet temperature (p^sat, Pa), as shown below:where M (kg mol⁻¹) and C (mol m⁻³) are gas molar mass and concentration, respectively, and the subscripts/superscripts a, c, H₂ and O₂ denote anode side, cathode side, hydrogen, and oxygen, respectively. The constant flow velocities and pressures are specified at the inlets and outlets in the coolant distribution zones, respectively.

As for the electron conduction equation, the reference voltage (0 V) and working current density are specified at the outer surfaces of cathode and anode BPs, respectively.

As listed in Table 2, the through-plane directional boundary conditions for proton conduction and membrane water transport equations both specify Neumann-type flux constraints. Mathematically, these boundary configurations yield non-unique solutions without supplementary constraints, as Neumann boundary conditions inherently lack mathematically stable steady-state solutions. Fundamental coupling between proton and electron conduction mechanisms in fuel cell models requires careful consideration: the source terms exhibit exact mutual negation (0 = S_e + S_ion), thereby satisfying global charge conservation principles. Crucially, these source terms correspond to the corresponding electrochemical reaction rates, which inherently depend on both electronic and protonic potentials. This dual dependency between electronic and protonic potentials enables the determination of unique steady-state protonic potential distribution through two Neumann boundary conditions.²⁷

Table 2 Boundary conditions in multi-physics modeling

Equations	Solution zones	Boundary conditions
Electron conduction (eqn (S11))	BPs, GDLs, MPLs, CLs	1: φe = ηtotal = Er − Vout or ;
		2-1, 5, 6, 9-1: ;
		10: φe = 0;
		2-2, 3, 4, 7, 8, 9-2: continuous boundary
Proton conduction (eqn (S12))	PEM, CLs	4: ; 7:
		5, 6: continuous boundary
Membrane water content (eqn (S10))	PEM, CLs	4: ; 7:
		5, 6: continuous boundary
Liquid pressure (eqn (S9))	GDLs, MPLs, CLs	2-1, 9-1: pl = pg − pc;
		2-2, 5, 6, 9-2: ;
		3, 4, 7, 8: continuous boundary

---

Regarding the membrane water equation, within the CLs the membrane water content correlates with liquid water saturation or water vapor concentration. Most PEM fuel cell models introduce the concept of equivalent membrane water content (λ_eq), expressed as a function of water activity (a), as below:

The phase change between membrane water and liquid water or water vapor is systematically incorporated into the source term:In these circumstances, the membrane water content in CLs is resolved through both the water vapor concentration and liquid saturation.

2.3 Numerical implementation

To date, 3D PEM fuel cell models have been systematically validated across multiple computational platforms, including ANSYS FLUENT, COMSOL,⁷² AVL Fire,⁷³ and OpenFoam,⁴⁹ with the first two demonstrating predominant adoption in published studies. Notably, large-scale PEM fuel cell simulations⁷⁴ involving complex BP/flow field architectures⁷⁵ predominantly employ ANSYS FLUENT, due to its capability of handling massive computational grids and numerical stability in solving the continuity and momentum conservation equations.

Computational grid generation constitutes a critical bottleneck in PEM fuel cell modeling. While orthogonal grids are popularly adopted for conventional single-channel simulations, large-scale fuel cell/stack architectures present unique challenges due to complex BP & flow field structure. This challenge is systematically addressed through a hybrid meshing strategy: decomposing complex geometries into modular subdomains for localized unstructured grid generation followed by merging into full cell configurations. Such partitioning methodology achieves optimal trade-offs between grid quality metrics (orthogonality, skewness) and discretization density requirements, which has been successfully implemented to simulate PEM fuel cells with complicated BP & flow field structures (e.g., metal foam^75,76 and 3D fine mesh flow fields⁷⁷) and large-scale fuel cells.⁶²

2.4 Model validation and parametric calibration

Though 3D full-size PEM fuel cell models show great promise for predicting detailed electrochemical performance and spatial distributions of over ten critical variables (e.g., gas concentration, liquid saturation, current density, temperature, velocity, etc.), reported experimental validations remain insufficient to fully verify these predictions. Current diagnostic capabilities (e.g., segmented fuel cells⁷⁸) are largely constrained by multiple technical limitations and state-of-the-art techniques are only capable of simultaneously resolving spatial distributions of current density, temperature, and relative humidity to some degree.⁷⁹ This limited experimental dataset creates a major bottleneck for comprehensive model validation, particularly given the complex multi-physics coupling inherent in PEM fuel cells.

Notably, existing validation efforts prioritize overall performances such as the polarization curves under diverse operating conditions and geometric configurations,⁸⁰ alongside individual electrochemical losses. However, this approach is largely insufficient, as the polarization curves represent aggregated metrics influenced by multiple intertwined variables. Only a few of studies successfully validated the spatial distributions of critical parameters, including current density, temperature, and water content.^81–83 Recently, Huo et al.⁸⁴ conducted a systematic comparative study on the polarization characteristics of commercial-scale PEM fuel cells (SinoHytec, MEA area: 332 cm²), evaluating the impact of five important parameters—namely anode/cathode stoichiometric ratios, cathode pressure, relative humidity, and operating temperature—on performance metrics across seven discrete current densities ranging from 0.265 to 2.2 A cm⁻². Their work not only validated the polarization curves under varying load conditions but also pioneered the use of a high-resolution segmented print circuit board (PCB, 408 measurement points, 0.8 cm² per segment) to map current density distributions.

Despite significant advancements, the insufficient validation status of 3D full-size PEM fuel cell models continues to undermine their predictive reliability across diverse operational conditions and geometric configurations. Future validation of the 3D full-size model requires more rationally designed experimental datasets. Beyond conventional polarization curve and electrochemical losses, it is crucial to obtain comprehensive spatiotemporal distribution data for key variables,^85,86 including current density, gas species concentration, relative humidity, liquid water saturation, membrane hydration, and temperature, etc. Critically, even with abundant experimental data, achieving complete validation of electrochemical performance and multi-variable distributions (e.g., temperature, current density, water content) at the same time remains elusive. Empirical evidence indicates that validation complexity escalates exponentially with the diversity of the experimental dataset, including variations in operating conditions, cell architectures, and the number of distributed variables. This issue is primarily attributed to the inherent trade-off in current modeling, where use of empirical formulas to enhance computational efficiency and stability inevitably compromises prediction fidelity. Consequently, the universal applicability of existing models remains questionable, particularly for edge-case scenarios that fall outside the validation dataset.

To address this gap, parametric calibration has emerged as an indispensable prerequisite for the practical deployment of 3D full-size fuel cell models in structural optimization. At its core, parametric calibration ensures that models maintain high fidelity within the localized operating regimes prioritized during product design, thereby enhancing their application as design tools. Given computational resource constraints, a hierarchical calibration strategy is recommended: initial refinements should focus on single-channel architectures to establish baseline correlations, followed by scalability to full-size commercial cells. Wen et al.⁵⁷ established a general calibration procedure for a commercial 310 cm² fuel cell. First, a single-channel computational domain was selected as the representative unit. Next, experimentally determined parameters were incorporated into this model, and all the other unknown parameters were calibrated within physically plausible ranges. Finally, the complete set of calibrated parameters was applied to the 3D full-size model for validation. A similar procedure was also adopted by Huo et al.⁵⁹ and Xie et al.⁵⁶ This approach can significantly reduce computational costs and expedite the parametric calibration process, thereby enhancing the practical implementation of 3D full-size models in fuel cell design, control, and optimization.

3. Advancements in multi-physics model

3.1 Channel two-phase flow physics

Current 3D fuel cell models typically simplify or even neglect liquid water in channels, with most assuming it exists in a mist state while disregarding the gas/liquid interface for computational efficiency. This simplification leads to discrepancies between simulated water states in fuel cells and the reality.⁸⁷ Several two-phase flow physics in fuel cell channels were revealed experimentally, including various two-phase flow patterns,^88,89 droplet dynamics,^90,91 and flow instability at outlet/manifold interfaces,^92,93 which can greatly influence gaseous reactant supply and water removal. In our previous studies, it was found that neglecting liquid water in the channels caused approximately 5% overestimation in the ohmic loss,⁸² and an 8% underestimation in the concentration one.⁵¹ These errors, which grew with current density, were mainly due to underestimation of the liquid water removal difficulty within the electrodes. And it was also found that neglecting the liquid water in channels underestimates the nonuniformity of current density distribution by about 40%.⁸²

Currently, the volume of fluid (VOF) and lattice Boltzmann (LB)⁹⁴ models are widely adopted for simulating channel two-phase flow because of the capacity of tracking the gas/liquid interface, their computational inefficiency—mainly constrained by small time steps (10⁻⁸–10⁻⁵ s) and huge grid size—poses significant challenges when directly integrated with 3D fuel cell models. In application, although the VOF and LB models yield similar predictions regarding the liquid water dynamics in channel (∼0.3–1 mm in size) and GDL (pore diameter of 50–150 µm), the VOF method is severely constrained by narrow spatial scales (where the Knudsen number is larger than 0.01), and the LB model is suitable for simulating two-phase flow phenomena within the MPL (pore size of 0.1–1 µm) and CL (pore size of ∼1–10 nm) due to the inherent advantages of the Boltzmann equation-based approach and its capability to handle complex porous structures.

To address this, some VOF models incorporate simplified 1D models describing the multi-physics transfer in conjunction with the electrochemical reactions in MEAs.^95,96 Besides, Zhang et al.⁹⁷ developed a 2D PEM fuel cell model at the single-channel level, directly integrating a VOF model that tracks the gas/liquid interface in the cathode channel. Through this model, they revealed the influence mechanism of two-phase flow pattern in the cathode channel on cell performance. However, their model framework neglected the liquid transport between GDL and channel.

Recent advancements by Wu et al.^98,99 and Xu et al.¹⁰⁰ in PEM water electrolysis (PEMWE), which has a similar structure to PEM fuel cells, achieved integration of VOF models with 3D full-size models through bidirectional data exchange at the liquid/gas diffusion layer (L/GDL)/channel interface. Specifically, the 3D full-size model is first executed to obtain the oxygen flux from the L/GDL into the channel, which is then input into the VOF model to simulate channel two-phase flow. The VOF simulation is terminated once the average channel oxygen volume fraction and distribution reach a quasi-steady state, characterized by minimal variation in the average gas volume fraction within the channel. Conversely, the gas volume fraction distribution at the L/GDL surface from the VOF model is extracted and applied as the boundary condition for solving the gas pressure equation in the L/GDL and CL zones, initiating a new computational loop. Approximately 2–4 loops are required to achieve convergence, where the simulated oxygen distribution in the channel and electrochemical performance of PEMWE remain stable across further loops. This method's reliability was validated against experimental measurements of gas bubble distributions in parallel and serpentine flow fields, alongside corresponding PEMWE operational voltages.⁹⁹

However, directly applying this integration framework to PEM fuel cells introduces additional complexities. The formation of liquid water at the GDL surface occurs much slower than gas bubble formation, with a typical timescale of several minutes for the former. This discrepancy limits the direct implementation of liquid water flow velocity from the GDL into the VOF model due to this computational burden.¹⁰¹ In most VOF simulations, this velocity is often amplified by 10–1000 times to cut the simulation time.^102,103 Nevertheless, the inherently low computational efficiency of such integration remains a substantial barrier for large-scale full-size fuel cell simulations.¹⁰⁴

Developing a reliable model describing the gas/liquid two-phase flow while maintaining computational efficiency is likely to be the optimal solution for tackling this challenge. Zhang et al.⁵¹ proposed a modified two-fluid model to address this issue, deriving the relationship between gas and liquid velocities through a two-phase Darcy's law framework. The capillary action is assumed to be negligible because the capillary pressure gradient along the channel is very small,⁶⁶ which yields:

p_c = 0 ⇒ p_g = p₁ (9)

where K (m²) is the intrinsic permeability (or hydraulic conductance) of the channel and k_g and k_l the relative permeabilities of gas and liquid phases, respectively.

The dynamic viscosity of the gas mixture can be adaptively adjusted to account for two-phase pressure drop predictions along the channel, as shown in eqn (11), which exceeds the single-phase pressure drop due to the hindrance caused by liquid water on gas flow. The validity of this viscosity adjustment requires experimental validation in future studies. In the coming years, a central focus can be on developing computationally efficient models for gas and liquid two-phase flow in channels to integrate with a 3D full-size PEM fuel cell model, enabling accurate prediction of the water distribution throughout the fuel cell and its impact on electrochemical performance.

3.2 Pore-scale physics in CL

Current 3D PEM fuel cell modeling frameworks mostly treat the electrode materials (e.g. GDL, MPL, or CL) as homogenous porous media characterized by porosity and permeability parameters. While this assumption offers high calculation efficiency, it largely oversimplifies the porous electrode structures. For popular GDL materials, carbon papers exhibit distinct anisotropic transport properties between in-plane and through-plane directions,¹⁰⁵ which can be addressed by implementing anisotropic transport equations (e.g. electron conduction, heat transfer, intrinsic permeability, gas diffusion) in 3D PEM fuel cell models.^106,107 In addition, CLs present greater complexity due to their heterogeneous composition (e.g. micro/mesopore structure and ionomer coverage over Pt particles on carbon support) and intricate multi-physics processes encompassing co-transport of gas, liquid, heat, proton and electron, and water in multiple phases, and the electrochemical reactions.^108,109 Nevertheless, the CL's thin thickness (5–10 µm) and micro/nanoscale phenomena make the influence mechanisms of its structure on cell performance particularly challenging to elucidate.^110,111

In current 3D full-size PEM fuel cell modeling frameworks, the multi-physics transport phenomena and electrochemical reactions in CLs are predominantly characterized through agglomerate sub-models.¹¹² This approach conceptualizes the CL's representative unit structure as agglomerates comprising platinum nanoparticles of about 1–5 nm size on carbon support of about 50–100 nm in size, enveloped by thin ionomer films of about 1–10 nm thickness.¹¹³ While this methodology demonstrates improved predictive accuracy relative to primitive interface models (assuming CL is an interface without a thickness) and homogeneous CL (assuming constant Pt/C and ionomer volume fractions and porosity¹¹⁴) approximations, particularly in capturing proton and oxygen transport resistances critical for high-current-density performance simulations,⁷⁷ it remains significantly oversimplified, compared to realistic CL microstructures. The model's dependence on multiple empirical fitting parameters fundamentally limits its capacity to establish quantitative correlations between microstructural characteristics (e.g., multi-layered structure,¹¹⁵ pore morphology, agglomerate size) and macroscopic fuel cell performance metrics.^116,117 Consequently, current 3D fuel cell simulations remain largely incapable of comprehensively evaluating and optimizing CL microstructure from a holistic system performance perspective, particularly to address the complex interfacial phenomena and multiphase transport dynamics inherent to fuel cell operation.

Currently, the LBM has been widely employed to investigate multi-physical transport and electrochemical reactions based on reconstructed CL microstructures.¹¹⁸ Two main limitations persist: first, discrepancies exist between reconstructed CL microstructures and actual configurations, particularly regarding ionomer distribution patterns which are difficult to characterize through experiment. Secondly, few LB models fully incorporate all the coupled multi-physics processes with electrochemical reactions. This mainly stems from fundamental challenges in three aspects: the transient nature of LBM creates inherent difficulties in handling transport coefficients which can differ by multiple orders of magnitude (e.g., ionomer proton conductivity and oxygen diffusivity), which drives relaxation times toward 0.5 with a risk of numerical instability or excessive computational costs – a potential solution is to implement different time resolutions for coupled physical fields. Beyond this temporal challenge, modeling electrochemical reactions at heterogeneous active sites introduces complexity, which requires a modification of unknown distribution functions to account for source terms (e.g., species and energy equations), particularly when using complex discrete velocity models. Furthermore, precisely capturing water phase-change processes within CLs presents persistent difficulties for LBM.

Moreover, direct integration of LB-based pore-scale CL models into full-size 3D fuel cell models faces a challenge in computational efficiency. A promising solution is to develop a multi-scale modeling framework through two-way data exchange between CL models and 3D full-size models.^119,120 This approach first reconstructs CL microstructures either through stochastic algorithms based on key parameters (Pt loading, I/C ratio, etc.), or advanced characterization techniques (e.g., FIB-SEM,¹²¹ nano-CT, electron tomography at cryogenic temperatures (cryo-ET),¹²² etc.). Subsequently, electrochemical surface area (ECSA) is calculated by evaluating proton/oxygen/electron accessibility at the Pt particle surface. LB simulations then compute effective CL transport parameters (gas diffusivity, electron/proton conductivity, permeability, and interfacial oxygen transport resistance) for integration into a 3D full-size model. Concurrently, full-model outputs of non-uniform multi-physics distributions (e.g. temperature, relative humidity, and liquid saturation) feed back into LB simulations to refine the transport properties’ calculation. This iterative coupling could bridge microstructural effects with macroscopic performance predictions while ensuring computational feasibility to facilitate optimal CL microstructure design for both conventional and novel order-structured configurations.^123,124

In the coming years, research efforts should prioritize the development of science-based multiscale modeling frameworks that incorporate reconstructed CL microstructural details and facilitate two-way data exchange with fuel cell performance predictions. Simultaneously, it is also crucial to enhance the physical fidelity of pore-scale CL models by incorporating coupled multi-physics processes, in particular phase change and electrochemical reactions along with experimentally validated CL microstructural parameters, thereby enabling effective optimization of CL microstructures.

3.3 Update of water phase change mechanisms and membrane property correlations

The model fidelity under diverse operating conditions and geometric configurations is significantly constrained by its assumptions regarding the multiphase water states in fuel cells (i.e., gas vapor, liquid water, and membrane water) and their phase transition mechanisms.¹²⁵ Fig. 4 illustrates the schematic of water phase transitions and their correlated impacts on fuel cell performance. Specifically, the membrane water content determines proton conductivity and consequently the ohmic loss; liquid water obstructs gaseous reactant transport and can cover active catalyst sites, contributing to the concentration and activation losses, respectively; while water vapor influences gaseous reactant partial pressures and associated concentration loss. Given that cell output voltage depends on the cumulative effects of the activation, ohmic, and concentration losses, which are all sensitive to water distribution, accurate prediction of the phase-specific water content, which is greatly influenced by operation conditions (pressure, temperature, etc.), becomes paramount.

Fig. 4 Schematic of water phase transition and its mechanism of influence on fuel cell performance.

Currently, experimental characterization is largely limited due to the inability to directly quantify in situ water states at high resolution: membrane hydration can be indirectly assessed through the ohmic loss or resistance measurement using EIS or HFR techniques; liquid water can be visualized by employing transparent fuel cells,¹²⁶ X-CT,¹²⁷ neutron radiography,^128,129 nuclear magnetic resonance (NMR) and so on, which however can hardly distinguish detailed water contents in CLs, MPLs and GDLs; while the water vapor distribution relies on relative humidity mapping.⁷⁹ But it remains challenging to directly probe and robustly characterize the state of electrochemically generated water within the complex nano-porous structure of CLs using in situ techniques.

Existing phase transition models make certain assumptions to achieve simplified formulations for computational efficiency. For water evaporation and condensation, the phase change rate is given by:

where γ_1–v(γ_v–1, s⁻¹) is the evaporation (condensation) rate typically ranging from 1.0 to 10 000 s⁻¹.

For membrane water absorption and release, the equation is:

where γ_{d–v or 1} (s⁻¹) is the membrane water absorption or release rate set as 1.0 or 1.3.²⁷ It should be noted that the membrane water may transition into or from liquid water and water vapor. This water transition scheme may not support an accurate prediction at various conditions. Xie et al.⁵⁶ proposed a self-adaptive water transition mechanism in relation to local vapor saturation state by fitting the experimentally measured polarization curve and ohmic loss, which improves the model adaptivity to various operation conditions. However, this approach lacks a sufficient theoretical base to support it.

On the other hand, current key membrane transport equations remain based on the experimental results by Springer et al.¹³⁰ and Zawodzinski et al.¹³¹ published in 1991 for Nafion 117 with EW of 1100 g mol⁻¹, as shown below,

Proton conductivity:

Electro-osmotic drag (EOD) coefficient:¹³⁰

Membrane water diffusion coefficient, measured by Motupally et al. (Nafion 115 with EW of 1100 g mol⁻¹):¹³²

While foundational transport equations derive from experimental data for Nafion 117/115 membranes,¹³³ commercial fuel cells usually adopt Nafion 211 and reinforced membranes such as Gore membranes. Moreover, the industry-wide push to elevate PEM fuel cell operating temperatures from conventional 60–95 °C to over 100 °C demands novel thermally stable membranes,^134,135 a transition possibly to alternative molecular architectures and consequently different proton/water transport mechanisms.^136,137 This high-temperature operation leads to multiple benefits, including enhanced heat dissipation, accelerated electrochemical kinetics, improved CO tolerance, and simplified water management. However, current PEM fuel cell models predominantly adopt traditional transport equations and properties developed for obsolete membranes.

Recent progress includes Wang et al.'s¹³⁸ and Han et al.'s¹³⁹ comprehensive characterization of anion exchange membrane and proton exchange membrane transport properties. Beyond experimental approaches,¹⁴⁰ molecular dynamics (MD) simulations offer a viable pathway to decode proton/water/heat transport phenomena across varying molecular architectures.¹⁴¹ Such computational models enable quantitative derivation of the critical transport equations governing modern membranes, particularly addressing the structure–property relationships that show more physical insights than empirical correlations.

The fundamental water mass balance indicates that the water flow rates exiting out of both anode and cathode outlets must equal the sum of inlet water flow rates plus electrochemically produced water rate. Under fixed inlet flow conditions and specified current density, cross-membrane water transport (i.e. water flux across the membrane) directly influences the water flow rates at the anode and cathode outlets. These water flow rates at outlets can be validated against corresponding experimental measurements¹⁴² to verify the membrane water transport model. The quantitative agreement between simulated and experimentally measured outlet water flow rates can validate two transport correlations: the EOD coefficient in eqn (15) and the back-diffusion characteristics in eqn (16).

Future work ought to focus on developing adaptive water phase transition mechanisms based on local thermodynamic conditions, such as saturation and temperature, moving beyond fixed-rate assumptions. It is equally important to develop accurate transport equations for modern or emerging membranes using structure–property relationships derived from integrated experimental–computational approaches (such as MD simulations), rather than relying on legacy Nafion-based correlations.

3.4 System-level transient characteristics

Most 3D full-size models of PEM fuel cells are focused on steady-state analyses partly due to computational burden, which elucidate the structural influences on overall cell performance and spatial distributions of important variables. However, real-world operation of PEM fuel cells inherently involves transient fluctuations.¹⁴³ As illustrated in Fig. 5A, the speed variation of fuel cell vehicles (FCVs) under the Worldwide Harmonized Light Vehicle Test Procedure (WLTP) will induce significant water and thermal dynamics in the fuel cell stack. Such dynamics may raise operational risks, including water flooding,¹⁴⁴ membrane drying,¹⁴⁵ and accelerated degradation, making it more challenging to predict transient spatial distributions within stacks.¹⁴⁶ Moreover, the interaction between stacks and balance of plants (BOP) (e.g., hydrogen/air supply,¹⁴⁷ cooling,¹⁴⁸ and humidification subsystem) further amplifies the challenge of predicting transient responses under practical operating conditions.

Fig. 5 (A) FCV driving speed at different times (from WLPT);¹⁴⁹ (B) schematic of integrating a 3D stack model with hydrogen, air, and coolant BOP subsystems.¹⁵⁰ The images in (B) were adapted/reproduced from ref. 150 with permission from Elsevier,¹⁵⁰ copyright 2018.

Recent advancements in system-level modeling integrated PEM fuel cell stacks with auxiliary subsystems.^151–153 Leveraging such integrated frameworks, Hu et al.¹⁴⁹ simulated voltage and membrane water content variations during dynamic operation under New European Driving Cycle (NEDC) and WLTP driving cycles. Similarly, Kim et al.¹⁵⁴ developed a system-level model by incorporating membrane humidifiers, cathode backpressure valves, air compressors, and anode hydrogen recirculation systems (e.g., ejectors) to investigate the impacts of air compressor and backpressure control. However, these models are based on 0D or 1D simplification for multiphysics transport to enable computational feasibility.

To address spatial resolution limitations, Liu et al.¹⁵⁵ coupled a 3D fuel cell model (implemented in FLUENT) with a 1D dynamic system model (in Simulink) to analyze 3D transient of vehicular PEM fuel cells under system-level load variations. Despite this progress, their work only considered the hydrogen and air supply subsystems, notably excluding crucial thermal management, and assumed an isothermal condition. Luo et al.¹⁵⁶ conducted a comprehensive investigation of temperature distribution characteristics in PEM fuel cells through integration of a 2D stack thermal model in MATLAB/Simulink with a 3D single-cell model in FLUENT. This method enabled simultaneous evaluation of three thermal management strategies for stack temperature regulation and detailed analysis of internal temperature field evolution under dynamic operating conditions. Zhang et al.⁶⁹ advanced 3D modeling by incorporating realistic fan geometries via the multiple reference frame (MRF) method, revealing the influence of fan-induced airflow on stack performance and spatial distributions of cell voltage, temperature, and so on in an air-cooled stack. However, extending such detailed 3D models to transient conditions remains challenging due to computational burden.

A promising approach involves directly embedding 0D/1D BOP models into 3D PEM fuel cell simulations. As depicted in Fig. 5B, this method dynamically integrates the boundary conditions (e.g., hydrogen/air/coolant inlets and outlets) of the 3D stack model with corresponding BOP subsystems. By considering single-channel or single-cell scales, this hybrid methodology balances computational efficiency with spatial-temporal resolution,¹⁵⁷ enabling prediction of the current density, temperature, and water content distributions and evolution during realistic FCV operation. Such high-fidelity simulations hold significant potential for diagnosing health status,¹⁵⁸ identifying degradation mechanisms and optimizing system durability for fuel cells.

However, the development of system-level 3D models that integrate a fuel cell stack with the BOP faces several critical challenges. First, a significant time constant discrepancy exists between the 0D/1D BOP model and the 3D stack model, making it challenging to couple their dynamics. Secondly, integrated models may exhibit substantial robustness issues, making it unable to reach numerical stability under dynamic operating conditions. Furthermore, high-fidelity 3D stack models require a large number of computational grids, which severely limits computational efficiency and consequently impedes the application of real-time control strategies.

Looking forward, emphasis should be placed on multi-scale hybrid modeling frameworks that combine high-fidelity 3D stack models with BOP subsystems. Meanwhile, developing experimentally validated digital twins capable of predicting transient spatial distributions of key variables such as current density, temperature, and water content, under realistic operating conditions is also crucial for proactive health monitoring and durability optimization of fuel cell systems.

3.5 Degradation sub-model

3D full-size PEM fuel cell models have become instrumental in optimizing component structure, particularly BP/flow field architectures. While these models reveal the deterministic influence of cell structure on spatial distribution characteristics, its impact on overall electrochemical performance always becomes significant at high current densities near the limiting current regime, where the concentration loss dominates.²⁶ However, practical fuel cell operation predominantly targets medium current densities, where structural optimization exerts limited influence on global performance even though it may induce substantial variations in local variable distributions.¹⁵⁹

Critically, such substantial variations may profoundly affect fuel cell degradation.¹⁶⁰ Recent experimental work by Han et al.¹⁶¹ demonstrated that non-uniform current density distributions drive in-plane platinum (Pt) particle degradation, with elevated operating current density accelerating Pt dissolution and voltage decay. Chu et al.¹⁶² experimentally demonstrated that BP & flow field geometry optimization effectively homogenizes thermal gradients and reactant gas distribution patterns, thereby significantly alleviating localized degradation phenomena such as Pt agglomeration and carbon support corrosion. These findings underscore the necessity of incorporating detailed degradation mechanisms into 3D fuel cell models to evaluate fuel cell structural designs in terms of degradation and cell voltage decay rates.¹⁶³ However, a challenge arises from the vast disparity in timescale: multiphysics transport processes typically operate on a sub-100-second timescale, whereas degradation usually occurs over 100–5000 hours. Bridging this orders-of-magnitude timescale difference remains a pivotal obstacle in full-size model integration to tackle degradation prediction.

Recent efforts have explored hybrid modeling frameworks to address this challenge. Hao et al.¹⁶⁴ coupled a Pt degradation sub-model with a 3D fuel cell model, through exchanging spatially resolved overpotential and humidity data with the electrochemical surface area (ECSA) loss iteratively. This approach enabled analysis of heterogeneous catalyst degradation and optimization of Pt distribution for enhanced durability, though it was limited to steady-state snapshots at discrete cycle intervals. Haslinger and Lauer⁷³ incorporated a 1D CL degradation model into a single-channel 3D model, simulating localized degradation under 600-second dynamic load profiles derived from the EPA US06 drive cycle. While insightful, this method faces scalability limitation for stack or long-duration simulation. Yang et al.¹⁶⁵ incorporated PtCo catalyst degradation and dissolved Co²⁺ effects into a 3D fuel cell model to electrochemical surface area (ECSA) reduction and oxygen transport resistance increase. Their framework employs empirical time-dependent formulas to describe CL degradation, where the ECSA and Co²⁺ concentration are parametrized as explicit functions of operating duration. By iteratively coupling these degradation metrics with 3D multiphysics simulations, they successfully predicted spatial distributions of electrochemical performance and internal operating state at discrete degradation intervals. This methodology enabled systematic investigations into flow field design's impact on PtCo degradation uniformity¹⁶⁶ and cooling configuration's effect on stack lifetime.¹⁶⁷ While this approach significantly alleviates computational burden compared to full-size transient degradation models, it neglected the transient interactions between dynamic load variation and fluctuation of internal operating state during real-world operation.

Future advancements demand innovative integration methodologies that can bridge timescale disparities while preserving spatial-temporal resolution. A promising framework based on interval data storage and staggered coupling proves effective in mitigating timescale mismatch. It can be assumed that over a specific number of cycles (e.g., 500 dynamic voltage cycles) or a typical varying load cycle corresponding to realistic working conditions, the water-thermal state variation process remains consistent across each individual cycle. Under this assumption, water-thermal state distribution data from a single cycle can be stored at predefined time intervals and subsequently coupled with the degradation model. Specifically, during the computation of the transient degradation mechanism model, the corresponding time-step water-thermal state distribution data are invoked as input. The resulting degraded parameters (e.g., ECSA) are then fed into the 3D fuel cell model to predict performance and water-thermal state distribution after the specified number of cycles. Using this approach, it is estimated that simulating cell-scale (5 cm²) degradation over 10 000 voltage cycles (each lasting 16 s) can be completed within approximately 120 hours. Consequently, the extension of this integration method to commercial stack levels necessitates a substantial reduction in computational burden and time. A promising strategy involves the development of a 3D + 1D model, which simplifies the multi-physics transport and electrochemical reaction processes within the MEA region into a 1D framework through dimensionality reduction. This approach achieves significant computational efficiency gains, often by orders of magnitude, when compared to 3D full-size models. Such frameworks would empower predictive analysis of lifetime performance under realistic operating profiles, facilitating the design of degradation-resistant flow fields, thermal management strategies, and adaptive control systems.

Furthermore, coupling these models with machine learning-based surrogate models or reduced-order approximations could dramatically enhance computational efficiency, enabling system-scale durability simulations. By bridging the gap between multiphysics transport and degradation kinetics, next-generation full-size models can provide critical insights for structural optimization and operational strategy development—ultimately accelerating the commercialization of durable, high-performance PEM fuel cells. This paradigm shift toward degradation-aware design will not only extend fuel cell lifetimes but also enable predictive real-time health monitoring systems, revolutionizing the sustainability and economic viability of fuel cell technologies.

4. Integration of AI with multi-physics modeling

The development and implementation of 3D PEM fuel cell models in practical applications face significant challenges stemming from computational burden and instability. Recent advances in AI, particularly deep learning methodologies, introduced transformative approaches to fuel cell modeling,¹⁶⁸ and Table 3 lists the main characteristics and application assessment of several typical AI algorithms. Data-driven models trained by high-fidelity simulation and experimental datasets demonstrate remarkable capability in autonomously identifying complex nonlinear correlations between operational parameters and multiphysics responses, bypassing the need for coupled differential governing equations.

Table 3 Characteristics and application assessment of AI algorithms in fuel cell modeling

AI algorithms	Characteristics	Existing/potential fuel cell application scenarios	Application maturity
Support vector regression (SVR)	Good accuracy with medium/small datasets; dependent on kernel function	Predict fuel cell/stack performance at different operation conditions, geometry parameters, etc.	Relatively widespread use
Random forest (RF)	High interpretability	Identify and rank critical operation parameters for optimizing fuel cells under dynamic operation conditions^182	Nascent stage
	Insensitive to missing data
	Adaptive to high dimensionality
Boosting	Good accuracy	Develop surrogate models to predict liquid water and oxygen transport resistance in electrodes^174	Nascent stage
	High data demands
Gaussian process regression (GPR)	Uncertainty quantification ability	Predict fuel cell performance under different operation conditions^183	Nascent stage
	Easy to use for Bayesian optimization	Predict spatio-temporal distribution of multiple variables^184
	Unsuitable for large datasets	Control strategy optimization^185
Artificial neural network (ANN)	High accuracy and efficiency	Predict fuel cell performance under different operation conditions, geometry parameters, etc.	Widespread use
	Low interpretability
Convolutional neural network (CNN)	Highly efficient for image-like data	Rapid water quantification^186	Relatively widespread use
	End-to-end learning without handcrafted features	Generate high-resolution porous structure of electrodes^187
	Low interpretability	Predict variable field and effective transport coefficients of porous electrodes^188
Recurrent neural network (RNN)	Highly accurate and efficient for sequence data	Short- and long-term degradation prediction^189,190	Relatively widespread use
	End-to-end learning without handcrafted features	Predict remaining useful lifetime
	Low interpretability
Physics-informed neural network (PINN)	Lower data demand and higher accuracy than ANN	Predict remaining useful lifetime^191	Nascent stage
	Higher computational cost and slower convergence than ANN	Identify unknown parameters in governing equations^192
		Predict spatial distributions of variables
Fourier neural operator (FNO)	High accuracy and efficiency for functional mapping on grid-like data	Predict temporal variation^193	Not implemented
Deep Operator Network (DeepONet)	Flexible for data with irregular grids	Accelerate multi-physics modeling	Not implemented
Physics-informed neural operator (PI-NO)	Lower data demands and higher accuracy than FNO	Accelerate multi-physics modeling	Not implemented
Physics-informed deep operator network (PI-DeepONet)	Lower data demand and higher accuracy than DeepONet	Accelerate multi-physics modeling	Not implemented

---

4.1 Data-driven surrogate models

Table S4 presents a short summary of AI works focusing on integration with a 3D full-size PEM fuel cell model. Overall, current approaches mainly focus on building data-driven surrogate models for rapid prediction using a dataset generated from 3D full-size fuel cell models, which establish relationships between operating/structural parameters and performance to optimize input conditions. However, such end-to-end mapping approaches lack resolution of localized physical field distributions. Wang et al.¹⁶⁹ developed a digital twin (DT) model for multi-physics field analysis in fuel cells using artificial neural networks (ANNs) and support vector machines (SVMs) based on 3D full-size simulation data. Besides, Bai et al.^170–172 progressively advanced machine learning (ML)-enabled DT for predicting 3D multi-physics distributions of variables such as voltage, temperature, water content, and saturation within PEM fuel cells, which was subsequently extended to commercial stacks. This work efficiently maps complex operational conditions to high-fidelity internal field distributions, enabling computationally viable design and control while capturing critical field interactions.

Moreover, some scholars also developed data-driven surrogate models for specific physical processes that can be coupled with 3D full-size models. For instance, Pan et al.¹⁷³ introduces a hybrid 3D + 1D modeling framework augmented by machine learning, where a neural network surrogate replaces the computationally intensive 1D electrochemical module while preserving nonlinear transport phenomena. After being trained by synthetic datasets generated from a full 1D physical model, the neural network achieves sub-0.2% root-mean-square-error in flux predictions by using merely 0.5% of the computational cost of its physics-based counterpart. Coupled with a 3D gas channel model, the hybrid approach maintains broad applicability across operating conditions, as validated against experimental polarization curves and impedance spectra under varying humidity. Ghasabehi and Shams¹⁷⁴ developed a surrogate model predicting the water saturation and oxygen transport resistance trained by the dataset generated by a 3D full-size fuel cell model, which is used to construct a hybrid “3D + 1D” model that captures the two-phase flow in flow field (3D domain) and electrochemical characteristics in MEA (1D domain). Through this method, some significant simplifications of complex physical processes-such as gas and liquid two-phase flow dynamics and complicated mass transport mechanisms in CLs in traditional 3D full-size fuel cell models can be replaced by surrogate models trained by the dataset from high-fidelity component-level models, e.g., two-phase model (VOF or LBM) and mesoscopic CL models, respectively, which is promising to balance the trade-off between calculation burden and accuracy in 3D full-size models.

Going forward, a promising direction lies in integrating high-fidelity multidimensional data, such as from channel two-phase VOF models or pore-scale CL simulations, into surrogate training sets, improving both spatial predictive accuracy and computational efficiency. Future efforts should prioritize multi-fidelity learning frameworks that dynamically incorporate data from diverse sources and scales, enhancing the surrogate's ability to resolve critical local transients and physical interactions under realistic operating conditions.

4.2 AI-assisted multi-physics modelling

As proposed in Section 3.4, coupling auxiliary BOP components with 3D full-size models through boundary conditions can enable accurate prediction of multiphysics distribution characteristics under real-world dynamic loading conditions. While this information is valuable for health monitoring and degradation mechanism analysis, computational burden severely restricts its practical implementation. Zuo et al.¹⁷⁵ integrated DT technology with dynamic mode decomposition (DMD) to efficiently reconstruct multiphysics fields in PEM fuel cells. By processing transient data (20 s at 0.1 s interval, 200 snapshots) of current density, water content, and oxygen concentration, DMD extracted low-dimensional spatiotemporal modes capturing the dominant dynamics. The reconstructed fields achieved high fidelity to full-size simulations while significantly reducing computational time from hours to seconds. Though effective for gradual transients under known conditions, the approach faces limitation in predicting strongly nonlinear behaviors or abrupt changes in uncharacterized scenarios. To enhance robustness across complex transient regimes, the methodology would benefit from complementary techniques that address nonlinear dynamics and adaptive learning mechanisms.

Deep learning-based methods have demonstrated breakthrough potential in solving partial differential equations (PDEs), leveraging neural networks’ universal approximation capability to learn from data and physics-informed constraints—achieving superior adaptability and flexibility compared to conventional numerical methods. While utilizing a neural network (NN) to build surrogates was discussed in the preceding section, the quantity and quality of data significantly impact the accuracy of these surrogates, yet obtaining reliable training data is costly. To reduce the demand for training data, researchers proposed Physics-Informed Neural Networks (PINN), which employ automatic differentiation to incorporate physical equations as regularity in the loss function, drastically reducing the need for labeled training data. Moreover, the introduction of physical equations as a global constraint overcomes the limitation of observational data, which only provides local constraints, thereby enhancing the model's generalization capability in unseen scenarios. PINN is essentially a highly flexible information fusion framework that can simultaneously integrate information from both observations and physical equations.¹⁷⁶ When only observational data on initial/boundary conditions and collocation points formed by the equations are provided, PINN can achieve an approximate solution to the PDE. It also avoids the significant computational burden associated with mesh generation, a capability that has been applied and validated in disciplines like fluid dynamics and heat transfer problems. Raissi et al.¹⁷⁷ introduced hidden fluid mechanics (HFM), a physics-informed deep learning framework that reconstructs hidden velocity/pressure fields from sparse flow visualizations through direct encoding of the Navier–Stokes equations into neural networks via automatic differentiation. This physics-constrained AI learns from passive scalar transport data (e.g., dye concentrations) without requiring velocity measurement or predefined boundary conditions, enabling accurate flow prediction in complex geometries with robustness to noise and low-resolution inputs.

Recent studies also demonstrated PINN's effectiveness in accelerating two-phase flow predictions using the data from VOF models. Jalili et al.¹⁷⁸ developed a PINN framework to model vapor bubble growth in superheated liquids, utilizing 50% of VOF simulations as training data to predict interfacial dynamics and heat transfer with errors below 3.42%. Their approach combined phase-field equations and Navier–Stokes constraints to maintain sharp two-phase interfaces and enable rapid parametric studies. In complementary work, Jalili et al.¹⁷⁹ extended PINNs to multiphase heat transfer, successfully reconstructing bubble-wall thermal interactions and wake vortices using VOF-derived interface tracking data. These studies highlight PINNs’ ability to fuse VOF-computed interfacial data and governing equations, achieving order-of-magnitude reduction on computational cost compared to traditional CFD while preserving interfacial sharpness through physics-constrained learning. Lee¹⁸⁰ presented an extended multiphysics-informed neural network (EM-PINN) framework to advance conjugate heat transfer modeling through specialized sub-networks for distinct physical domains and novel interface constraints. It effectively resolved abrupt temperature transitions while ensuring energy conservation.

Beyond efficiently solving PDEs, PINN can also be used for solving inverse problems such as parameter estimation and optimization. This is because, when encoding the physical equations, the unknown parameters within the equations can be treated as learnable variables, optimized along with the NN parameters during training,¹⁸¹ which can accelerate the parametric calibration work mentioned in Section 2.4.

Researchers are encouraged to advance PINN for modeling strongly nonlinear and uncharacterized transient processes. A key aim is to build computationally efficient digital twins that integrate source training data with embedded physical constraints, thereby enabling robust multi-physics reconstruction and predictive degradation analysis under varying operational conditions.

4.3 AI-driven digital twins for multi-physics prediction in fuel cells

Although PINN flexibly fuses multi-source information and unifies the solution of forward and inverse problems within one framework, it essentially performs function approximation. This still faces multiple limitations in practical applications. For example, though PINN might solve a PDE efficiently and predict the solution at arbitrary spacetime points, upon altered initial/boundary conditions a new PINN model typically needs to be trained from scratch, which can increase modeling costs. To further enhance the generality of NN in solving equations, approximating the PDE solution operator using NN-based operator learning has been proposed. This method can handle varying initial/boundary conditions without the requirement of retraining a new model. The most common operator learning approaches are DeepONet¹⁹⁴ and Fourier Neural Operator (FNO).¹⁹⁵ DeepONet has just started to be used in applications to assist in solving fuel cell equations, while FNO, although lacking fuel cell applications to date, has been used in numerous case studies in fluid dynamics.¹⁹⁶ Building upon DeepONet and FNO, researchers further integrated the concept of PINN to propose Physics-Informed DeepONet (PI-DeepONet)¹⁹⁷ and Physics-Informed Neural Operator (PINO).¹⁹⁸ They aimed to reduce the data requirements of operator learning and enable data-driven equation solving through operator models at lower cost.

To date, limited studies have been devoted to addressing the multi-physics problem. In this regard, Cai et al.¹⁹⁹ introduced a novel data assimilation framework named DeepM&Mnet for rapid prediction of coupled multi-physics systems. It solves the multi-physics distribution within the electroconvection problem by firstly pre-training specialized DeepONets that independently learn mappings between physics fields from numerical simulation results, which are subsequently integrated into a unified network that infers full coupled variables from sparse measurements. Crucially, DeepONets serve as physics-constrained “building blocks”, enforcing solution consistency without solving governing PDEs numerically. This architecture enables accurate, real-time predictions for unseen boundary conditions while dramatically reducing computational costs.

Fig. 6 shows a promising flowchart for predicting the evolution of multiphysics distributions in PEM fuel cells through PI-DeepONet with multiple inputs and outputs,^200,201 taking continuity, momentum, and energy equations as an example. In this framework, the initial conditions, boundary conditions, and model parameters are the model inputs for the branch nets, while the space coordinates and time are for trunk net in PI-DeepONet, which can predict the spatial and temporal distribution of multiple variables. The continuity and momentum conservation equations share initial and boundary conditions, which are input into Branch 1 and Branch 2 respectively. The output of these two branch networks each has 2q neurons. The first q neurons from the output of Branch 1 and the first q neurons from the output of Branch 2, along with the output of the trunk net (which has q neurons), undergo element-wise multiplication followed by summation to yield the pressure. Similarly, the remaining latter q neurons from the output of Branch 1 and 3q neurons from Branch 2 (for u, v, w, respectively) are combined with the output of the trunk net to generate the velocity. The energy conservation equation has its own separate initial and boundary conditions, which are handled by Branch 3 and Branch 4. Their outputs each have q neurons. This equation also shares the same space-time coordinates with the other two equations, meaning it can share the same trunk net. Therefore, the outputs of Branch 3, Branch 4, and the trunk net are combined to generate the temperature.

Fig. 6 Physics-informed operator learning for evolution of multi-physics distributions in PEM fuel cells (taking continuity, momentum, and energy equations as an example), images of 3D PEM fuel cell model adapted/reproduced from ref. 60 with permission from Elsevier,⁶⁰ copyright 2024.

Next, the dataset generated by conventional 3D full-size models is used to train the PI-DeepONet, via constituting the data loss. To further enhance prediction robustness and reduce reliance on numerical simulation data, a physical loss is introduced, which is constructed using model predictions and automatic differentiation techniques to compute spatiotemporal derivatives required by the governing equations. Residuals from the equations and initial/boundary conditions collectively form this physical loss. The resulting PI-DeepONet, which integrates data-driven and physical information, achieves high accuracy and efficiency while exhibiting strong potential for rapid, precise predictions across diverse scenarios. Overall, the core idea of the multi-input multi-output PI-DeepONet is to use different branch networks to receive different input variables. The outputs of different branches can be freely combined with the trunk network's output to obtain the dependent variables of interest.

Despite these advances, current AI algorithms remain insufficient for achieving rapid and accurate predictions of coupled multiphysics transport and electrochemical reactions in fuel cells. Future work should aim to advance PI-DeepONet frameworks capable of simultaneously solving a set of governing equations describing electrochemically coupled multiphysics phenomena. Such computationally efficient digital twins are critical for achieving real-time, high-fidelity reconstruction of internal states under dynamic operating conditions, paving the way for robust control and predictive health management in next-generation fuel cells.

5. Summary and outlook

Multi-physics modeling of PEM fuel cells has demonstrated a capability to substantially enhance the understanding of electrochemical and transport phenomena for advanced design/optimization, yet major challenges still exist, hindering predictive accuracy and commercial-scale applications in next-generation fuel cell development. Limitations mainly arise from oversimplified representations of gas–liquid two-phase flow physics in channels, insufficient accounting for CL microstructures, and reliance on outdated membrane properties derived from limited material datasets.

In the short-term priorities (Table 4, by 2028), future work should prioritize the development of physics-based channel two-phase flow models that are compatible with existing modeling frameworks. Equally critical is to establish effective bidirectional coupling between full-size fuel cell models and pore-scale LB simulations to address microstructural simplification in CLs. Simultaneously, modernizing membrane transport descriptions through integrated experimental characterization and micro/nanoscale simulations remains urgent for new class or high-temperature membrane materials. Current validation is still constrained by limited experimental data, primarily restricted to polarization curves, and localized measurements of current density, temperature, or water content in a few segments under narrow steady-state conditions. Furthermore, systematic parametric calibration is indispensable when deploying 3D full-size models for product development. Another critical step is incorporating detailed degradation mechanisms—such as carbon corrosion and platinum dissolution—via effective bidirectional data exchange between 3D full-size models and degradation sub-models could enable durable component/fuel cell design.

Table 4 Roadmap for multi-physics and AI modeling development in PEM fuel cells

Time	Tasks & goals
Short-term priorities (by 2028)	Integrate channel two-phase flow with 3D fuel cell model via two-way data exchange method
	Integrate pore-scale CL model with 3D fuel cell model via two-way data exchange method
	Integrate degradation model with 3D fuel cell model via two-way data exchange method
	Update water phase change mechanisms and advance membrane property correlations
	Develop commercial 3D stack model consisting of hundreds of cells
	Comprehensive model validation, including polarization curve & electrochemical losses at multiple operation conditions, temporal spatial variable distributions (e.g., current density, temperature, water content)
Medium-term priorities (by 2030)	Train data-driven surrogate model of channel two-phase flow
	Train data-driven surrogate model of multi-physics transfers and electrochemical reactions in realistic CL microstructure
	Develop system-level transient model by integrating BOP sub-models with stack model
	Achieve the integration of degradation model with 3D commercial stack-level model
Long-term priorities (by 2035)	Train PI-DeepONet model for evolution of multi-physics distribution in fuel cells
	Achieve digital twin of PEM fuel cells for long-term operation

---

For the medium-term priorities (by 2030), integrating BOP units with full-size models for transient simulations will help clarify dynamic water/thermal distribution during real-world operation, linking load cycle characteristics to degradation patterns for control optimization strategies. Additionally, data-driven surrogate models can target specific physical processes to couple with 3D full-size models, such as channel two-phase flow dynamics and multi-physics transfers within CLs to balance the trade-off between calculation burden and accuracy. It is also vital to extend the integration of degradation models to commercial stack-level configurations.

In the long-term priorities (by 2035), AI-augmented frameworks utilizing PI-DeepONet to replace conventional solvers are expected to overcome computational bottlenecks while preserving physical fidelity. Hybrid approaches combining machine learning with physics-based first-principles laws will enable rapid real-time prediction of spatial gradients, paving the way for digital twins in predictive maintenance and control optimization. Together, these advancements aim to bridge the major gap between high-fidelity mathematical full-size modeling and industrial requirements for the development of next-generation high-power-density durable PEM fuel cells.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ee04599a.

Acknowledgements

Zhiguo Qu thanks the National Science Foundation for Distinguished Young Scholars (No. 52025065), Guobin Zhang thanks the National Natural Science Foundation of China (No. 52206112) and Yun Wang is thankful for the UCI's CORLOR award.

References

1. D. Guan, B. Wang, J. Zhang, R. Shi, K. Jiao, L. Li, Y. Wang, B. Xie, Q. Zhang, J. Yu, Y. Zhu, Z. Shao and M. Ni, Hydrogen society: from present to future, Energy Environ. Sci., 2023, 16(11), 4926–4943.
2. J. Tang, C. Su and Z. Shao, Advanced membrane-based electrode engineering toward efficient and durable water electrolysis and cost-effective seawater electrolysis in membrane electrolyzers, Exploration, 2024, 4(1), 20220112.
3. D. A. Cullen, K. C. Neyerlin, R. K. Ahluwalia, R. Mukundan, K. L. More, R. L. Borup, A. Z. Weber, D. J. Myers and A. Kusoglu, New roads and challenges for fuel cells in heavy-duty transportation, Nat. Energy, 2021, 6(5), 462–474.
4. Y. Zhang, Z. Hu, L. Xu, H. Liu, K. Ye, J. Li and M. Ouyang, Fuel cell system for aviation applications: Modeling, parameter sensitivity, and control, Energy Convers. Manage., 2024, 312, 118555.
5. M. Seddiq, M. Alnajideen and R. Navaratne, Thermal Transient Performance of PEM Fuel Cells in Aerospace Applications: A Numerical Study, Energy Fuels, 2025, 39(16), 7876–7889.
6. Y. Wang, Y. Pang, H. Xu, A. Martinez and K. S. Chen, PEM Fuel Cell and Electrolysis Cell Technologies and Hydrogen Infrastructure Development – A Review, Energy Environ. Sci., 2022, 15(6), 2288–2328.
7. Y. Toshihiko and K. Koichi, Toyota MIRAI fuel cell vehicle and progress toward a future hydrogen society, Electrochem. Soc. Interface, 2015, 24(2), 45–49.
8. S. Tanaka, K. Nagumo, M. Yamamoto, H. Chiba, K. Yoshida and R. Okano, Fuel cell system for Honda CLARITY fuel cell, eTransportation, 2020, 3, 100046.
9. B. K. Hong and S. H. Kim, Recent Advances in Fuel Cell Electric Vehicle Technologies of Hyundai, ECS Trans., 2018, 86(13), 3–11.
10. P. Liu and S. Xu, A review of low-temperature proton exchange membrane fuel cell degradation caused by repeated freezing start, Int. J. Hydrogen Energy, 2023, 48(22), 8216–8246.
11. Y. Liu, Z. Li, X. Huang, F. Liu, F. Zhou and M. K. Lim, Uncovering determinants and barriers to hydrogen fuel cell vehicle adoption: Evidence from Chongqing, China, Int. J. Hydrogen Energy, 2025, 106, 875–887.
12. H. Sahin, Hydrogen refueling of a fuel cell electric vehicle, Int. J. Hydrogen Energy, 2024, 75, 604–612.
13. K. Jiao, J. Xuan, Q. Du, Z. Bao, B. Xie, B. Wang, Y. Zhao, L. Fan, H. Wang, Z. Hou, S. Huo, N. P. Brandon, Y. Yin and M. D. Guiver, Designing the Next Generation of Proton Exchange Membrane Fuel Cells, Nature, 2021, 595(7867), 361–369.
14. T. Yoshizumi, H. Kubo and M. Okumura, Development of High-Performance FC Stack for the New MIRAI, SAE Technical Paper Series, 2021, p. 2021-01-0740.
15. Z. P. Cano, D. Banham, S. Ye, A. Hintennach, J. Lu, M. Fowler and Z. Chen, Batteries and fuel cells for emerging electric vehicle markets, Nat. Energy, 2018, 3(4), 279–289.
16. D. L. Greene, J. M. Ogden and Z. Lin, Challenges in the designing, planning and deployment of hydrogen refueling infrastructure for fuel cell electric vehicles, eTransportation, 2020, 6, 100086.
17. L. Fan, H. Deng, Y. Zhang, Q. Du, D. Y. C. Leung, Y. Wang and K. Jiao, Towards ultralow platinum loading proton exchange membrane fuel cells, Energy Environ. Sci., 2023, 16(4), 1466–1479.
18. C. Tongsh, S. Wu, K. Jiao, W. Huo, Q. Du, J. W. Park, J. Xuan, H. Wang, N. P. Brandon and M. D. Guiver, Fuel cell stack redesign and component integration radically increase power density, Joule, 2024, 8(1), 175–192.
19. X. Wang, Y. Wu, Y. Cheng, G. Lu and C. Tan, Collective improvements in flow maldistribution and interface contact resistance of flow field in proton exchange membrane fuel cells via coupling manipulation of gradient porosity and unit cell topology, J. Power Sources, 2025, 653, 237711.
20. F. Zhang, B. Zu, B. Wang, Z. Qin, J. Yao, Z. Wang, L. Fan and K. Jiao, Developing long-durability proton-exchange membrane fuel cells, Joule, 2025, 9(3), 101853.
21. Y. Wang, D. F. Ruiz Diaz, K. S. Chen, Z. Wang and X. C. Adroher, Materials, technological status, and fundamentals of PEM fuel cells – A review, Mater. Today, 2020, 32, 178–203.
22. G. Zhang, Z. Qu, W.-Q. Tao, X. Wang, L. Wu, S. Wu, X. Xie, C. Tongsh, W. Huo, Z. Bao, K. Jiao and Y. Wang, Porous Flow Field for Next-Generation Proton Exchange Membrane Fuel Cells: Materials, Characterization, Design, and Challenges, Chem. Rev., 2022, 123(3), 989–1039.
23. X. Tu, B. Yan, Z. Tu and S. H. Chan, A novel development of an unmanned surface vehicle directly powered by an air-cooled proton exchange membrane fuel cell stack, Appl. Energy, 2024, 374, 124002.
24. Y. Wang, X. Yang, Z. Sun and Z. Chen, A systematic review of system modeling and control strategy of proton exchange membrane fuel cell, Energy Rev., 2024, 3(1), 100054.
25. J. Pu, Q. Xie, J. Li, Z. Zhao, J. Lai, K. Li and F. Zhou, Research on the technical scheme of multi-stack common rail fuel cell engine based on the demand of commercial vehicle, Energy AI, 2024, 16, 100353.
26. G. Zhang, L. Wu, C. Tongsh, Z. Qu, S. Wu, B. Xie, W. Huo, Q. Du, H. Wang, L. An, N. Wang, J. Xuan, W. Chen, F. Xi, Z. Wang and K. Jiao, Structure Design for Ultrahigh Power Density Proton Exchange Membrane Fuel Cell, Small Methods, 2023, 7(3), 2201537.
27. K. Jiao and X. Li, Water transport in polymer electrolyte membrane fuel cells, Prog. Energy Combust. Sci., 2011, 37(3), 221–291.
28. Z. Yong, H. Shirong, J. Xiaohui, X. Mu, Y. Yuntao and Y. Xi, Three-dimensional simulation of large-scale proton exchange membrane fuel cell considering the liquid water removal characteristics on the cathode side, Int. J. Hydrogen Energy, 2023, 48(27), 10160–10179.
29. A. Kneer, J. Jankovic, D. Susac, A. Putz, N. Wagner, M. Sabharwal and M. Secanell, Correlation of Changes in Electrochemical and Structural Parameters due to Voltage Cycling Induced Degradation in PEM Fuel Cells, J. Electrochem. Soc., 2018, 165(6), F3241–F3250.
30. H. Li, X. Cheng, X. Yan, S. Shen and J. Zhang, A perspective on influences of cathode material degradation on oxygen transport resistance in low Pt PEMFC, Nano Res., 2022, 16(1), 377–390.
31. S. Ott, A. Orfanidi, H. Schmies, B. Anke, H. N. Nong, J. Hubner, U. Gernert, M. Gliech, M. Lerch and P. Strasser, Ionomer distribution control in porous carbon-supported catalyst layers for high-power and low Pt-loaded proton exchange membrane fuel cells, Nat. Mater., 2020, 19(1), 77–85.
32. R. Zhang, T. Min, L. Chen, Q. Kang, Y.-L. He and W.-Q. Tao, Pore-scale and multiscale study of effects of Pt degradation on reactive transport processes in proton exchange membrane fuel cells, Appl. Energy, 2019, 253, 113590.
33. G. Zhang, Z. Qu, W.-Q. Tao, Y. Mu, K. Jiao, H. Xu and Y. Wang, Advancing next-generation proton-exchange membrane fuel cell development in multi-physics transfer, Joule, 2024, 8(1), 45–63.
34. L. Fan, F. Xi, X. Wang, J. Xuan and K. Jiao, Effects of Side Chain Length on the Structure, Oxygen Transport and Thermal Conductivity for Perfluorosulfonic Acid Membrane: Molecular Dynamics Simulation, J. Electrochem. Soc., 2019, 166(8), F511–F518.
35. Y.-T. Mu, S.-R. Yang, P. He and W.-Q. Tao, Mesoscopic modeling impacts of liquid water saturation, and platinum distribution on gas transport resistances in a PEMFC catalyst layer, Electrochim. Acta, 2021, 388, 138659.
36. L. Fan, J. Wang, D. F. Ruiz Diaz, L. Li, Y. Wang and K. Jiao, Molecular dynamics modeling in catalyst layer development for PEM fuel cell, Prog. Energy Combust. Sci., 2025, 108, 101220.
37. Y. Hou, X. Li, Q. Du, K. Jiao and N. Zamel, Pore-Scale Investigation of the Effect of Micro-Porous Layer on Water Transport in Proton Exchange Membrane Fuel Cell, J. Electrochem. Soc., 2020, 167(14), 144504.
38. Z. Bao, Y. Li, X. Zhou, F. Gao, Q. Du and K. Jiao, Transport properties of gas diffusion layer of proton exchange membrane fuel cells: Effects of compression, Int. J. Heat Mass Transfer, 2021, 178, 121608.
39. J. Chen, Z. Bao, Y. Xu, L. Fan, Q. Du, G. Qu, F. Li and K. Jiao, Investigation of liquid retention behavior in the flow field plate of large-size proton exchange membrane fuel cells: Effects of sub-distribution zone, Appl. Energy, 2024, 358, 122651.
40. S. Zhang, Q. Yang, H. Xu and Y. Mao, Numerical investigation on the performance of PEMFC with rib-like flow channels, Int. J. Hydrogen Energy, 2022, 47(85), 36254–36263.
41. Z. Yong, H. Shirong, J. Xiaohui, X. Mu, Y. Yuntao and Y. Xi, 3D multi-phase simulation of metal bipolar plate proton exchange membrane fuel cell stack with cooling flow field, Energy Convers. Manage., 2022, 273.
42. R. K. Ahluwalia, X. Wang and A. J. Steinbach, Performance of advanced automotive fuel cell systems with heat rejection constraint, J. Power Sources, 2016, 309, 178–191.
43. G. Zhang, F. Duan, Z. Qu, H. Bai and J. Zhang, Airfoil flow field for proton exchange membrane fuel cells enhancing mass transfer with low pressure drop, Int. J. Heat Mass Transfer, 2024, 225, 125420.
44. T. Cheng, Q. Liu, G. Jiang, B. Yang, X. Wang and P. Wang, Numerical study of proton exchange membrane fuel cells with airfoil cross flow field, J. Power Sources, 2025, 631, 236232.
45. S. Zhang, S. Liu, H. Xu, G. Liu and K. Wang, Performance of proton exchange membrane fuel cells with honeycomb-like flow channel design, Energy, 2022, 239, 122102.
46. X. Mao, S. Liu, Y. Huang, Z. Kang and D. Xuan, Multi-flow channel proton exchange membrane fuel cell mass transfer and performance analysis, Int. J. Heat Mass Transfer, 2023, 215, 124497.
47. D. Benkovic, C. Fink and A. Iranzo, Qualitative and quantitative determination of liquid water distribution in a PEM fuel cell, Int. J. Hydrogen Energy, 2024, 52, 1360–1370.
48. C. Tongsh, S. Wu, K. Jiao, W. Huo, Q. Du, J. W. Park, J. Xuan, H. Wang, N. P. Brandon and M. D. Guiver, Fuel cell stack redesign and component integration radically increase power density, Joule, 2024, 8, 1–18.
49. Z. Bao, B. Xie, W. Li, S. Zhong, L. Fan, C. Tongsh, F. Gao, Q. Du, M. Benbouzid and K. Jiao, High-consistency proton exchange membrane fuel cells enabled by oxygen-electron mixed-pathway electrodes via digitalization design, Sci. Bull., 2023, 68, 266–275.
50. G. Zhang and K. Jiao, Multi-phase models for water and thermal management of proton exchange membrane fuel cell: A review, J. Power Sources, 2018, 391, 120–133.
51. G. Zhang, L. Wu, Z. Qin, J. Wu, F. Xi, G. Mou, Y. Wang and K. Jiao, A comprehensive three-dimensional model coupling channel multi-phase flow and electrochemical reactions in proton exchange membrane fuel cell, Adv. Appl. Energy, 2021, 2, 100033.
52. L. Wu, G. Zhang, B. Xie, W. Huo, K. Jiao and L. An, Elucidating the automobile proton exchange membrane fuel cell of innovative double-cell structure by full-morphology simulation, Int. J. Heat Mass Transfer, 2023, 217, 124666.
53. S.-F. Sun and Z. Y. Sun, Water distribution and transmission within perforated gas diffusion layer and layered gas diffusion layer of a proton exchange membrane fuel cell, J. Power Sources, 2025, 643, 237024.
54. Y. Zhang, S. He, X. Jiang, Z. Wang, Y. Wang, M. Gu, X. Yang, S. Zhang, J. Cao, H. Fang and Q. Li, Performance and configuration optimization of proton exchange membrane fuel cell considering dual symmetric Tesla valve flow field, Energy, 2024, 288.
55. N. Wang, Z. Qu, G. Zhang, Z. Tang and Y. Wang, Cross flow and distribution characteristics in automobile polymer electrolyte membrane fuel cells: A three-dimensional full-scale modeling study, J. Power Sources, 2023, 580, 233348.
56. B. Xie, H. Zhang, W. Huo, R. Wang, Y. Zhu, L. Wu, G. Zhang, M. Ni and K. Jiao, Large-scale three-dimensional simulation of proton exchange membrane fuel cell considering detailed water transition mechanism, Appl. Energy, 2023, 331, 120469.
57. X. Wen, N. Wang, X. Huang, Q. Wang, Z. Tang, Z. Qu and G. Xie, Dynamic transport characteristics and performance response of commercial-size polymer electrolyte membrane fuel cell stack: An experimental study, Chem. Eng. J., 2024, 486, 150270.
58. Z. Zhang, H.-B. Quan, S.-J. Cai, Z.-D. Li and W.-Q. Tao, Design strategies for mainstream flow channels in large-area PEMFC: From typical units to large areas, Appl. Energy, 2025, 388, 125628.
59. W. Huo, B. Xie, S. Wu, L. Wu, G. Zhang, H. Zhang, Z. Qin, Y. Zhu, R. Wang and K. Jiao, Full-scale multiphase simulation of automobile PEM fuel cells with different flow field configurations, Int. J. Green Energy, 2023, 21(1), 154–169.
60. G. Zhang, Z. Qu, N. Wang and Y. Wang, Spatial distribution characteristics in segmented PEM fuel cells: Three-dimensional full-morphology simulation, Electrochim. Acta, 2024, 484, 144061.
61. Y. Zhang, S. He, X. Jiang, H. Fang, Z. Wang, J. Cao, X. Yang and Q. Li, Performance evaluation on full-scale proton exchange membrane fuel cell: Mutual validation of one-dimensional, three-dimensional and experimental investigations, Energy Convers. Manage., 2024, 299, 117905.
62. L. Wu, G. Zhang, X. Shi, Z. Pan, B. Xie, W. Huo, K. Jiao and L. An, All-scale investigation of a commercial proton exchange membrane fuel cell with partially narrow channels, J. Power Sources, 2024, 589, 233779.
63. Q. Deng, K. Meng, W. Chen, N. Zhang and B. Chen, Comprehensive evaluation on heat and mass transfer mechanisms in full-scale high-power PEMFC, Chem. Eng. J., 2025, 162998.
64. Y. Zhang, S. He, X. Jiang, X. Yang, Z. Wang, S. Zhang, J. Cao, H. Fang and Q. Li, Full-scale three-dimensional simulation of air cooling metal bipolar plate proton exchange membrane fuel cell stack considering a non-isothermal multiphase model, Appl. Energy, 2024, 357, 122507.
65. G. Zhang, H. Yuan, Y. Wang and K. Jiao, Three-dimensional simulation of a new cooling strategy for proton exchange membrane fuel cell stack using a non-isothermal multiphase model, Appl. Energy, 2019, 255, 113865.
66. T. Tsukamoto, T. Aoki, H. Kanesaka, T. Taniguchi, T. Takayama, H. Motegi, R. Takayama, S. Tanaka, K. Komiyama and M. Yoneda, Three-dimensional numerical simulation of full-scale proton exchange membrane fuel cells at high current densities, J. Power Sources, 2021, 488, 229412.
67. J. Macedo-Valencia, J. M. Sierra, S. J. Figueroa-Ramírez, S. E. Díaz and M. Meza, 3D CFD modeling of a PEM fuel cell stack, Int. J. Hydrogen Energy, 2016, 41(48), 23425–23433.
68. G. Zhang, Z. Qu and Y. Wang, Full-scale three-dimensional simulation of air-cooled proton exchange membrane fuel cell stack: Temperature spatial variation and comprehensive validation, Energy Convers. Manage., 2022, 270, 116211.
69. G. Zhang, Z. Qu, H. Yang, Y. Mu and Y. Wang, Integrating full fan morphology and configuration in three-dimensional simulation of air-cooled proton exchange membrane fuel cell stack, Fuel, 2024, 368, 131628.
70. Y. Xia, Y. Hu, G. Hu, H. Lei, J. Lu, Z. Wang and Q. Wang, Numerical analysis on the effects of manifold design on flow uniformity in a large proton exchange membrane fuel cell stack, Int. J. Hydrogen Energy, 2023, 48(14), 5643–5655.
71. F. Huang, D. Qiu, L. Peng and X. Lai, Optimization of entrance geometry and analysis of fluid distribution in manifold for high-power proton exchange membrane fuel cell stacks, Int. J. Hydrogen Energy, 2022, 47(52), 22180–22191.
72. X. Chen, X. Luo, Y. Liang, J. Chen, J. He, Z. Yang, Y. Chen, C. Wang and Y. Du, Modeling and performance investigation on the deformed gas diffusion layer of PEM fuel cell, Int. J. Hydrogen Energy, 2024, 50, 169–180.
73. M. Haslinger and T. Lauer, Analyzing local degradation in an industrial PEMFC under EPA US06 drive cycle via 3D-CFD, J. Power Sources, 2024, 606, 234523.
74. Y. Zhang, D. Zhang, Y. Zhang, X. Jiang, X. Yang, J. Cao, H. Fang, Q. Deng, B. Chen, Q. Liu and Y. Chen, Spatial distribution characteristics of various physical quantities in PEM fuel cells: Entire morphology investigation based on bifurcated gas distribution zones, Appl. Energy, 2025, 381, 125180.
75. G. Zhang, Z. Bao, B. Xie, Y. Wang and K. Jiao, Three-dimensional multi-phase simulation of PEM fuel cell considering the full morphology of metal foam flow field, Int. J. Hydrogen Energy, 2021, 46(3), 2978–2989.
76. L. Fu, Y. Tang, J. Liu, L. Chen and N. Qiu, Mass transfer capability and performance of proton exchange membrane fuel cell with three-dimensional flow field based on triply periodic minimal surfaces structure, J. Power Sources, 2025, 643, 236997.
77. G. Zhang, B. Xie, Z. Bao, Z. Niu and K. Jiao, Multi-phase simulation of proton exchange membrane fuel cell with 3D fine mesh flow field, Int. J. Energy Res., 2018, 42(15), 4697–4709.
78. A. Ma, C. Yin, H. Yang, J. Yu, K. Huang, Z. Qiao and H. Tang, Dynamic internal performance of PEMFC under fuel starvation with high-resolution current mapping: An experimental study, Int. J. Hydrogen Energy, 2024, 54, 990–1000.
79. Y. Wang, X. Xie, C. Zhou, Q. Feng, Y. Zhou, X.-Z. Yuan, J. Xu, J. Fan, L. Zeng, H. Li and H. Wang, Study of relative humidity on durability of the reversal tolerant proton exchange membrane fuel cell anode using a segmented cell, J. Power Sources, 2020, 449, 227542.
80. Q. Liu, T. Cheng, G. Jiang, P. Wang and X. Wang, Airfoil cross flow field to enhance mass transfer capacity and performance for PEMFC, Int. J. Heat Mass Transfer, 2024, 235, 126205.
81. L. Hao, K. Moriyama, W. Gu and C.-Y. Wang, Three Dimensional Computations and Experimental Comparisons for a Large-Scale Proton Exchange Membrane Fuel Cell, J. Electrochem. Soc., 2016, 163(7), F744–F751.
82. B. Xie, M. Ni, G. Zhang, X. Sheng, H. Tang, Y. Xu, G. Zhai and K. Jiao, Validation methodology for PEM fuel cell three-dimensional simulation, Int. J. Heat Mass Transfer, 2022, 189, 122705.
83. G. Zhang, J. Wu, Y. Wang, Y. Yin and K. Jiao, Investigation of current density spatial distribution in PEM fuel cells using a comprehensively validated multi-phase non-isothermal model, Int. J. Heat Mass Transfer, 2020, 150, 119294.
84. W. Huo, L. Fan, Y. Xu, M. Benbouzid, W. Xu, F. Gao, W. Li, N. Shan, B. Xie, H. Huang, B. Liu, Y. Amirat, C. Fang, X. Li, Q. Gan, F. Li and K. Jiao, Digitally-assisted structure design of a large-size proton exchange membrane fuel cell, Energy Environ. Sci., 2025, 18(2), 631–644.
85. C. Yin, H. Yang, X. Gong, J. Cao and H. Tang, Experimental and numerical investigation of the reverse current evolution during the start-up of a fuel cell, Appl. Energy, 2025, 377, 124470.
86. C. Yin, J. Cao, Q. Tang, Y. Su, R. Wang, K. Li and H. Tang, Study of internal performance of commercial-size fuel cell stack with 3D multi-physical model and high resolution current mapping, Appl. Energy, 2022, 323, 119567.
87. L. F. Carneiro, E. F. da Costa Junior and T. Matencio, Comparative study of single-phase and two-phase physics-based models for proton-exchange membrane fuel cells, J. Power Sources, 2025, 653, 237782.
88. S. C. Cho and Y. Wang, Two-phase flow dynamics in a micro channel with heterogeneous surfaces, Int. J. Heat Mass Transfer, 2014, 71, 349–360.
89. J. M. Lewis, Two-phase Flow in High Aspect-ratio Microchannels, University of California, Irvine, 2018.
90. S. C. Cho, Y. Wang and K. S. Chen, Droplet dynamics in a polymer electrolyte fuel cell gas flow channel: Forces, Deformation and detachment. II: Comparisons of analytical solution with numerical and experimental results, J. Power Sources, 2012, 210, 191–197.
91. P. Liao, D. Yang, S. Xu, B. Li, P. Ming, Z. Li and X. Zhou, Effect of three-dimensional geometric structure and surface wettability on two-phase flow behavior in a proton exchange membrane fuel cell gas flow channel: modeling and simulation, Int. J. Hydrogen Energy, 2024, 50, 1183–1199.
92. X. C. Adroher and Y. Wang, Ex situ and modeling study of two-phase flow in a single channel of polymer electrolyte membrane fuel cells, J. Power Sources, 2011, 196(22), 9544–9551.
93. J. Wu, Two-phase Flow Dynamics in Two Parallel Thin Micro-channels, PhD thesis, UC Irvine, 2020.
94. Y. Hou, H. Deng, N. Zamel, Q. Du and K. Jiao, 3D lattice Boltzmann modeling of droplet motion in PEM fuel cell channel with realistic GDL microstructure and fluid properties, Int. J. Hydrogen Energy, 2020, 45(22), 12476–12488.
95. P. Feng, L. Tan, Y. Cao and D. Chen, Numerical investigations of two-phase flow coupled with species transport in proton exchange membrane fuel cells, Energy, 2023, 278, 127918.
96. R. B. Ferreira, D. S. Falcão, V. B. Oliveira and A. M. F. R. Pinto, 1D + 3D two-phase flow numerical model of a proton exchange membrane fuel cell, Appl. Energy, 2017, 203, 474–495.
97. X. Zhang, X. Ma, J. Yang, X. Zhu, S. Tai and S. Shuai, Effect of liquid water in flow channel on proton exchange membrane fuel cell: Focusing on flow pattern, Energy Convers. Manage., 2022, 258, 115528.
98. L. Wu, G. Zhang, B. Xie, C. Tongsh and K. Jiao, Integration of the detailed channel two-phase flow into three-dimensional multi-phase simulation of proton exchange membrane electrolyzer cell, Int. J. Green Energy, 2021, 18(6), 541–555.
99. L. Wu, L. An, D. Jiao, Y. Xu, G. Zhang and K. Jiao, Enhanced oxygen discharge with structured mesh channel in proton exchange membrane electrolysis cell, Appl. Energy, 2022, 323, 119651.
100. Y. Xu, G. Zhang, L. Wu, Z. Bao, B. Zu and K. Jiao, A 3-D multiphase model of proton exchange membrane electrolyzer based on open-source CFD, Digital Chem. Eng., 2021, 1, 100004.
101. L. Zhang, S. Liu, Z. Wang, R. Li and Q. Zhang, Numerical simulation of two-phase flow in a multi-gas channel of a proton exchange membrane fuel cell, Int. J. Hydrogen Energy, 2022, 47(40), 17713–17736.
102. Y. Ding, X. T. Bi and D. P. Wilkinson, Numerical investigation of the impact of two-phase flow maldistribution on PEM fuel cell performance, Int. J. Hydrogen Energy, 2014, 39(1), 469–480.
103. D. Yang, H. Garg and M. Andersson, Numerical simulation of two-phase flow in gas diffusion layer and gas channel of proton exchange membrane fuel cells, Int. J. Hydrogen Energy, 2023, 48(41), 15677–15694.
104. Y. Liu, Z. Bao, J. Chen, F. Lv and K. Jiao, Design of a partially narrowed flow channel with a sub-distribution zone for the water management of large-size proton exchange membrane fuel cells, Energy, 2024, 310, 133292.
105. Y. Pan, H. Wang and N. P. Brandon, Gas diffusion layer degradation in proton exchange membrane fuel cells: Mechanisms, characterization techniques and modelling approaches, J. Power Sources, 2021, 513, 230560.
106. G. Zhang, L. Fan, J. Sun and K. Jiao, A 3D model of PEMFC considering detailed multiphase flow and anisotropic transport properties, Int. J. Heat Mass Transfer, 2017, 115, 714–724.
107. H. Zhang, M. A. Rahman, F. Mojica, P. C. Sui and P. Y. A. Chuang, A comprehensive two-phase proton exchange membrane fuel cell model coupled with anisotropic properties and mechanical deformation of the gas diffusion layer, Electrochim. Acta, 2021, 382, 138273.
108. J. Zhao, H. Liu and X. Li, Structure, Property, and Performance of Catalyst Layers in Proton Exchange Membrane Fuel Cells, Electrochem. Energy Rev., 2023, 6(1), 13.
109. M. Eppler, M. Hanauer, U. Berner, V. Leduc, T. Kadyk and M. Eikerling, Modeling of Mass Transport Resistance in PEM Fuel Cells and Validation through Novel Transient Limiting Current Techniques, J. Electrochem. Soc., 2025, 172(5), 054509.
110. X. Li, Y. Hou, C. Wu, Q. Du and K. Jiao, Interlink among catalyst loading, transport and performance of proton exchange membrane fuel cells: a pore-scale study, Nanoscale Horiz., 2022, 7(3), 255–266.
111. Y. Du, Y. Li, P. Ren, L. Zhang, D. Wang and X. Xu, Oxygen transfer at mesoscale catalyst layer in proton exchange membrane fuel cell: Mechanism, model and resistance characterization, Chem. Eng. J., 2024, 494, 153021.
112. N. Wang, Z. G. Qu, Z. Y. Jiang and G. B. Zhang, A unified catalyst layer design classification criterion on proton exchange membrane fuel cell performance based on a modified agglomerate model, Chem. Eng. J., 2022, 447.
113. B. Xie, G. Zhang, J. Xuan and K. Jiao, Three-dimensional multi-phase model of PEM fuel cell coupled with improved agglomerate sub-model of catalyst layer, Energy Convers. Manage., 2019, 199, 112051.
114. G. Zhang and K. Jiao, Three-dimensional multi-phase simulation of PEMFC at high current density utilizing Eulerian-Eulerian model and two-fluid model, Energy Convers. Manage., 2018, 176, 409–421.
115. Y. Wang and X. Feng, . Analysis of the reaction rates in the cathode electrode of polymer electrolyte fuel Cells II. Dual-Layer electrodes, J. Electrochem. Soc., 2009, 156(3), B403–B409.
116. P. He, Y.-T. Mu, J. W. Park and W.-Q. Tao, Modeling of the effects of cathode catalyst layer design parameters on performance of polymer electrolyte membrane fuel cell, Appl. Energy, 2020, 277, 115555.
117. F. C. Cetinbas, S. G. Advani and A. K. Prasad, A Modified Agglomerate Model with Discrete Catalyst Particles for the PEM Fuel Cell Catalyst Layer, J. Electrochem. Soc., 2013, 160(8), F750–F756.
118. L. Chen, A. He, J. Zhao, Q. Kang, Z.-Y. Li, J. Carmeliet, N. Shikazono and W.-Q. Tao, Pore-scale modeling of complex transport phenomena in porous media, Prog. Energy Combust. Sci., 2022, 88.
119. N. Wang, T. Lai, W. Wang, Z. Qu, X. Wen, G. Xie and W. Tao, Challenges and perspectives towards multi-physics modeling for porous electrode of ultrahigh performance durable polymer electrolyte membrane fuel cells, eTransportation, 2025, 25, 100449.
120. R. Zhang, L. Chen, T. Min, Y.-T. Mu, L. Hao and W.-Q. Tao, Multiscale study of reactive transport and multiphase heat transfer processes in catalyst layers of proton exchange membrane fuel cells, Carbon Neutrality, 2024, 3(1), 14.
121. N. Goswami, A. N. Mistry, J. B. Grunewald, T. F. Fuller and P. P. Mukherjee, Corrosion-Induced Microstructural Variability Affects Transport-Kinetics Interaction in PEM Fuel Cell Catalyst Layers, J. Electrochem. Soc., 2020, 167(8), 084519.
122. R. Girod, T. Lazaridis, H. A. Gasteiger and V. Tileli, Three-dimensional nanoimaging of fuel cell catalyst layers, Nat. Catal., 2023, 6(5), 383–391.
123. C. Lee, W. J. M. Kort-Kamp, H. Yu, D. A. Cullen, B. M. Patterson, T. A. Arman, S. Komini Babu, R. Mukundan, R. L. Borup and J. S. Spendelow, Grooved electrodes for high-power-density fuel cells, Nat. Energy, 2023, 8(7), 685–694.
124. C. Li, K. Yu, A. Bird, F. Guo, J. Ilavsky, Y. Liu, D. A. Cullen, A. Kusoglu, A. Z. Weber, P. J. Ferreira and J. Xie, Unraveling the core of fuel cell performance: engineering the ionomer/catalyst interface, Energy Environ. Sci., 2023, 16(7), 2977–2990.
125. S. Huo, K. Jiao and J. W. Park, On the water transport behavior and phase transition mechanisms in cold start operation of PEM fuel cell, Appl. Energy, 2019, 233–234, 776–788.
126. J. Na, G. Park, J. Park, S. Yang, H.-M. Oh, J. Baek, D. Kim, J. Youn, J. Lim and T. Park, Visualization of initial evolution of flooding in proton exchange membrane fuel cells with parallel flow channels, Int. J. Hydrogen Energy, 2025, 114, 239–249.
127. A. Kato, S. Yamaguchi, W. Yoshimune, K. Isegawa, M. Maeda, D. Hayashi, T. Suzuki and S. Kato, Operando X-ray radiography of liquid water distribution in 100 mm polymer electrolyte fuel cell channels, Electrochem. Commun., 2024, 165, 107772.
128. Y. Higuchi, W. Yoshimune, S. Kato, S. Hibi, D. Setoyama, K. Isegawa, Y. Matsumoto, H. Hayashida, H. Nozaki, M. Harada, N. Fukaya, T. Suzuki, T. Shinohara and Y. Nagai, Experimental visualization of water/ice phase distribution at cold start for practical-sized polymer electrolyte fuel cells, Commun. Eng., 2024, 3(1), 33.
129. W. Yoshimune, Y. Higuchi, F. Song, S. Hibi, Y. Matsumoto, H. Hayashida, H. Nozaki, T. Shinohara and S. Kato, Neutron imaging for automotive polymer electrolyte fuel cells during rapid cold starts, Phys. Chem. Chem. Phys., 2024, 26(47), 29466–29474.
130. T. E. Springer, T. A. Zawodzinski and S. Gottesfeld, Polymer Electrolyte Fuel Cell Model, J. Electrochem. Soc., 1991, 138(8), 2334–2342.
131. T. A. Zawodzinski Jr, M. Neeman, L. O. Sillerud and S. Gottesfeld, Determination of water diffusion coefficients in perfluorosulfonate ionomeric membranes, J. Phys. Chem., 1991, 95(15), 6040–6044.
132. S. Motupally, A. J. Becker and J. W. Weidner, Diffusion of water in Nafion 115 membranes, J. Electrochem. Soc., 2000, 147(9), 3171–3177.
133. S. Ge, B. Yi and P. Ming, Experimental Determination of Electro-Osmotic Drag Coefficient in Nafion Membrane for Fuel Cells, J. Electrochem. Soc., 2006, 153(8), A1443–A1450.
134. J. Yang, H. Xu, J. Li, K. Gong, F. Yue, X. Han, K. Wu, P. Shao, Q. Fu, Y. Zhu, W. Xu, X. Huang, J. Xie, F. Wang, W. Yang, T. Zhang, Z. Xu, X. Feng and B. Wang, Oxygen- and proton-transporting open framework ionomer for medium-temperature fuel cells, Science, 2024, 385(6713), 1115–1120.
135. K. H. Lim, A. S. Lee, V. Atanasov, J. Kerres, E. J. Park, S. Adhikari, S. Maurya, L. D. Manriquez, J. Jung, C. Fujimoto, I. Matanovic, J. Jankovic, Z. Hu, H. Jia and Y. S. Kim, Protonated phosphonic acid electrodes for high power heavy-duty vehicle fuel cells, Nat. Energy, 2022, 7(3), 248–259.
136. F. Liu, I. S. Kim and K. Miyatake, Proton-conductive aromatic membranes reinforced with poly(vinylidene fluoride) nanofibers for high-performance durable fuel cells, Sci. Adv., 2023, 9(30), eadg9057.
137. P. Guan, Y. Zou, M. Zhang, W. Zhong, J. Xu, J. Lei, H. Ding, W. Feng, F. Liu and Y. Zhang, High-temperature low-humidity proton exchange membrane with “stream-reservoir” ionic channels for high-power-density fuel cells, Sci. Adv., 2023, 9(17), eadh1386.
138. Z. Wang, K. Chen, J. Han, X. Zhang, B. Wang, Q. Du and K. Jiao, Anion Exchange Membranes for Fuel Cells: Equilibrium Water Content and Conductivity Characterization, Adv. Funct. Mater., 2023, 33(40), 202303857.
139. J. Han, Z. Wang, L. Fan, C. Tongsh, Y. Xu, Q. Du and K. Jiao, Correlating the In-Plane and Through-Plane Proton Conductivity and Equilibrium Water Content of State-of-the-Art Proton Exchange Membranes, Adv. Funct. Mater., 2025, e13442.
140. J. Kim, S. Kim, S.-Y. Woo, H. Chun, J. Sim, S. Kang and K. Min, In situ analysis of water transport properties through a reinforced composite membrane in polymer electrolyte membrane fuel cells, Chem. Eng. J., 2024, 502, 158078.
141. W. Wang and Z. Qu, Molecular dynamics simulation of the mechanical properties and thermal conductivity of aromatic electrolytes in proton exchange membrane fuel cells, J. Power Sources, 2023, 585, 233622.
142. Y. Lu, H. Wu, D. Yang, W. Zhuge, P. Ming, Y. Zhang, J. Chen and X. Pan, Theoretical and Experimental Study of a Fuel Cell Stack Based on Perfluoro-sulfonic Acid Membranes Facing High Temperature Application Environments, Energy Fuels, 2024, 38(8), 7331–7343.
143. Y. Li, Z. Zheng, Y. Guo, X. Cheng, X. Yan, G. Wei, S. Shen and J. Zhang, Control-oriented thermal management strategies for large-load fluctuation PEM fuel cell systems, Appl. Energy, 2025, 392, 125915.
144. H. L. Nguyen, Y. Kim, D. H. Trinh and S. Yu, Dynamic flooding management strategy for automotive proton exchange membrane fuel cell system using cathode membrane water content, Appl. Therm. Eng., 2025, 273, 126485.
145. W. Tang, G. Chang, Z. Liu, J. Xie, X. Pan, H. Yuan, X. Wei and H. Dai, Investigating the effects of multi-dimensional parameters on the internal hydrothermal characteristics of proton exchange membrane fuel cells via an enhanced impedance dimensional model, Energy Convers. Manage., 2024, 318, 118887.
146. P. Ren, P. Pei, Y. Li, Z. Wu, D. Chen and S. Huang, Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions, Prog. Energy Combust. Sci., 2020, 80, 100859.
147. Y. Chen, H. Lv, R. Li, X. Liu, L. Wang, J. Feng, X. Peng and F. Cao, Effects of operating parameters and fluids on the performance of a hydrogen regenerative flow compressor in a proton exchange membrane fuel cell system, Appl. Therm. Eng., 2025, 271, 126326.
148. R. Zeng, H. Kang, M. Umar, X. Liang and Y.-N. Zhao, Design and thermal management study of fuel cell spray cooling system, Appl. Therm. Eng., 2025, 270, 126271.
149. B. B. Hu, Z. G. Qu and W. Q. Tao, A comprehensive system-level model for performance evaluation of proton exchange membrane fuel cell system with dead-ended anode mode, Appl. Energy, 2023, 347, 121327.
150. G. Zhang, X. Xie, B. Xie, Q. Du and K. Jiao, Large-scale multi-phase simulation of proton exchange membrane fuel cell, Int. J. Heat Mass Transfer, 2019, 130, 555–563.
151. Y. Shao, L. Xu, X. Zhao, J. Li, Z. Hu, C. Fang, J. Hu, D. Guo and M. Ouyang, Comparison of self-humidification effect on polymer electrolyte membrane fuel cell with anodic and cathodic exhaust gas recirculation, Int. J. Hydrogen Energy, 2020, 45(4), 3108–3122.
152. Z. Yang, Q. Du, Z. Jia, C. Yang and K. Jiao, Effects of operating conditions on water and heat management by a transient multi-dimensional PEMFC system model, Energy, 2019, 183, 462–476.
153. X. Chen, S. Long, L. He, C. Wang, F. Chai, X. Kong, Z. Wan, X. Song and Z. Tu, Performance evaluation on thermodynamics-economy-environment of PEMFC vehicle power system under dynamic condition, Energy Convers. Manage., 2022, 269, 116082.
154. D. K. Kim, H. E. Min, I. M. Kong, M. K. Lee, C. H. Lee, M. S. Kim and H. H. Song, Parametric study on interaction of blower and back pressure control valve for a 80-kW class PEM fuel cell vehicle, Int. J. Hydrogen Energy, 2016, 41(39), 17595–17615.
155. B. Liu, H. Chen, T. Zhang and P. Pei, A vehicular proton exchange membrane fuel cell system co-simulation modeling method based on the stack internal distribution parameters monitoring, Energy Convers. Manage., 2019, 197, 111898.
156. Y. Luo, M. A. H. Ali, N. N. Nik Ghazali, R. Apsari, W. T. Chong, Z. Yang and H. Liu, Modeling and simulation of a novel thermal management strategy and temperature distribution in PEMFC, Appl. Therm. Eng., 2025, 274, 126772.
157. B. Xu, Y. Yang, J. Li, Y. Wang, D. Ye, L. Zhang, X. Zhu and Q. Liao, Computational assessment of response to fluctuating load of renewable energy in proton exchange membrane water electrolyzer, Renewable Energy, 2024, 232, 121084.
158. L. Huang, X. Zhang, Y. Jiang, S. Dong, R. Huang, H. Liao and S. Tang, Degradation analysis of dynamic voltage response characteristics of proton exchange membrane fuel cells for health evaluation under dynamic load, Appl. Energy, 2025, 389, 125741.
159. G. Zhang, Z. Qu, N. Wang, X. Wang, Y. Wu and Y. Wang, Structured mesh material with gradient surface wettability for high-power-density proton exchange membrane fuel cells, Int. J. Green Energy, 2024, 21(13), 3001–3009.
160. Y. Yang, M. Bai, Z. Zhou, W.-T. Wu, L. Wei, Y. Li, X. Lv, Y. Li and Y. Song, 3D carbon corrosion kinetic mechanism modeling study for proton exchange membrane fuel cells under localized flooding, Int. J. Heat Mass Transfer, 2024, 235, 126206.
161. K. Han, X. Li, R. Zhang, Y. Wang, C. Li, M. Fan, C. Huang, H. Liu, Z. Zhao and Z. Ni, New factors driving in-plane uneven degradation of Pt in proton exchange membrane fuel cells at high current density, Chem. Eng. J., 2025, 510, 161876.
162. T. Chu, Z. Zhang, X. Hou, M. Xie, D. Yang, B. Li, P. Ming and C. Zhang, Inhomogeneous degradation mechanism of proton exchange membrane fuel cell stack based on inter-cell and intra-cell cases, J. Power Sources, 2025, 646, 237195.
163. Y. Yu, Q. Yu, R. Luo, S. Chen, J. Yang and F. Yan, Study on the relationship between lifetime and flow channel in proton exchange membrane fuel cells, Renewable Energy, 2026, 256, 124057.
164. M. Hao, Y. Hu, S. Chen and Y. Li, A scale-bridging model for proton exchange membrane fuel cells: Understanding interactions among multi-physics transports, electrochemical reactions and heterogeneous aging, Nano Energy, 2024, 128, 109957.
165. Y. Yang, M. Bai, Z. Zhou, W.-T. Wu, C. Hu, L. Gao, Y. Li, Y. Li and Y. Song, Numerical simulation for non-uniform PtCo catalyst degradation under constant voltage condition and its impact on PEMFC performance, Int. J. Heat Mass Transfer, 2024, 218, 124793.
166. Y. Yang, M. Bai, Z. Zhou, W.-T. Wu, L. Wei, C. Hu, Y. Li, Y. Li and Y. Song, Numerical simulation for non-uniform PtCo catalyst degradation under different coolant conditions and its effect on PEMFC performance, Int. J. Hydrogen Energy, 2024, 64, 965–980.
167. Y. Yang, M. Bai, Z. Zhou, W.-T. Wu, L. Wei, J. Lyu, C. Hu, Y. Li, Y. Li and Y. Song, Comparison of lifetime performance of PEMFC stacks with two cooling strategies under different humidity, Int. J. Heat Mass Transfer, 2024, 231, 125870.
168. R. Ding, S. Zhang, Y. Chen, Z. Rui, K. Hua, Y. Wu, X. Li, X. Duan, X. Wang, J. Li and J. Liu, Application of Machine Learning in Optimizing Proton Exchange Membrane Fuel Cells: A Review, Energy AI, 2022, 9, 100170.
169. B. Wang, G. Zhang, H. Wang, J. Xuan and K. Jiao, Multi-physics-resolved digital twin of proton exchange membrane fuel cells with a data-driven surrogate model, Energy AI, 2020, 1, 100004.
170. F. Bai, H.-B. Quan, R.-J. Yin, Z. Zhang, S.-Q. Jin, P. He, Y.-T. Mu, X.-M. Gong and W.-Q. Tao, Three-dimensional multi-field digital twin technology for proton exchange membrane fuel cells, Appl. Energy, 2022, 324, 119763.
171. F. Bai, Z. Tang, R.-J. Yin, H.-B. Quan, L. Chen, D. Dai and W.-Q. Tao, A novel ‘3D + digital twin + 3D’ upscaling strategy for predicting the detailed multi-physics distributions in a commercial-size proton exchange membrane fuel cell stack, Appl. Energy, 2024, 374, 124012.
172. F. Bai, Z. Tang, R.-J. Yin, S.-Q. Jin, L. Chen, W.-Z. Fang, Y.-T. Mu and W.-Q. Tao, Optimization of the operational conditions of PEMFC by a novel CFD-DT-GA approach, Appl. Energy, 2025, 387, 125620.
173. Y. Pan, H. Ruan, B. Wu, Y. N. Regmi, H. Wang and N. P. Brandon, A machine learning driven 3D + 1D model for efficient characterization of proton exchange membrane fuel cells, Energy AI, 2024, 17, 100397.
174. M. Ghasabehi and M. Shams, Predicting water saturation and oxygen transport resistance in proton exchange membrane fuel cell by artificial intelligence, Fuel, 2024, 368, 131557.
175. Q. Zuo, G. Wang, Z. Shen, X. Zhu, Y. Xie, Y. Li, Y. Ma and H. Zhang, Digital twinning of multi-physics field performance of faceted novel snake coil flow field proton exchange membrane fuel cells, J. Power Sources, 2025, 649, 237442.
176. G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang and L. Yang, Physics-informed machine learning, Nat. Rev. Phys., 2021, 3(6), 422–440.
177. M. Raissi, A. Yazdani and G. E. Karniadakis, Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations, Science, 2020, 367(6481), 1026–1030.
178. D. Jalili, M. Jadidi, A. Keshmiri, B. Chakraborty, A. Georgoulas and Y. Mahmoudi, Transfer learning through physics-informed neural networks for bubble growth in superheated liquid domains, Int. J. Heat Mass Transfer, 2024, 232, 125940.
179. D. Jalili, S. Jang, M. Jadidi, G. Giustini, A. Keshmiri and Y. Mahmoudi, Physics-informed neural networks for heat transfer prediction in two-phase flows, Int. J. Heat Mass Transfer, 2024, 221, 125089.
180. J. Lee, S. Shin, H. Choi, A. Lee, B. Park and S. Lee, Extended multiphysics-informed neural network for conjugate heat transfer problems, Int. J. Heat Mass Transfer, 2025, 246, 127098.
181. J. Wang, Q. Peng, J. Meng, T. Liu, J. Peng and R. Teodorescu, A physics-informed neural network approach to parameter estimation of lithium-ion battery electrochemical model, J. Power Sources, 2024, 621, 235271.
182. A. S. Abed Al Sailawi, H. A. Hameed Al-Hamzawi and M. M. Mijwil, Sensitivity analysis and optimization of PEMFCs for realistic dynamic operating conditions, J. Power Sources, 2025, 659, 238335.
183. M. Alibeigi, R. Jazmi, R. Maddahian and H. Khaleghi, Integrated study of prediction and optimization performance of PBI-HTPEM fuel cell using deep learning, machine learning and statistical correlation, Renewable Energy, 2024, 235, 121295.
184. W. W. Xing, F. Yu, P. K. Leung, X. Li, P. Wang and A. A. Shah, A new multi-task learning framework for fuel cell model outputs in high-dimensional spaces, J. Power Sources, 2021, 482, 228930.
185. B. Jiang, M. D. Berliner, K. Lai, P. A. Asinger, H. Zhao, P. K. Herring, M. Z. Bazant and R. D. Braatz, Fast charging design for Lithium-ion batteries via Bayesian optimization, Appl. Energy, 2022, 307, 118244.
186. Y. Pang, L. Hao and Y. Wang, Convolutional neural network analysis of radiography images for rapid water quantification in PEM fuel cell, Appl. Energy, 2022, 321, 119352.
187. Y. D. Wang, Q. Meyer, K. Tang, J. E. McClure, R. T. White, S. T. Kelly, M. M. Crawford, F. Iacoviello, D. J. L. Brett, P. R. Shearing, P. Mostaghimi, C. Zhao and R. T. Armstrong, Large-scale physically accurate modelling of real proton exchange membrane fuel cell with deep learning, Nat. Commun., 2023, 14(1), 745.
188. M. Wang, H. Wang, Y. Yin, S. Rahardja and Z. Qu, Temperature field prediction for various porous media considering variable boundary conditions using deep learning method, Int. Commun. Heat Mass Transfer, 2022, 132, 105916.
189. R. Xie, R. Ma, S. Pu, L. Xu, D. Zhao and Y. Huangfu, Prognostic for fuel cell based on particle filter and recurrent neural network fusion structure, Energy AI, 2020, 2, 100017.
190. L. Zheng, Y. Hou, T. Zhang and X. Pan, Performance prediction of fuel cells using long short-term memory recurrent neural network, Int. J. Energy Res., 2021, 45(6), 9141–9161.
191. T. Ko, D. Kim, J. Park and S. H. Lee, Physics-informed neural network for long-term prognostics of proton exchange membrane fuel cells, Appl. Energy, 2025, 382, 125318.
192. I. Zerrougui, Z. Li and D. Hissel, Physics-Informed Neural Network for modeling and predicting temperature fluctuations in proton exchange membrane electrolysis, Energy AI, 2025, 20, 100474.
193. M. Kwak, H. S. Jin, B. Lkhagvasuren and D. Oyunmunkh, A Robust State of Charge Estimator Based on the Fourier Neural Operator for xEV Batteries, J. Electrochem. Soc., 2023, 170(10), 100504.
194. L. Lu, P. Jin, G. Pang, Z. Zhang and G. E. Karniadakis, Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators, Nat. Mach. Intell., 2021, 3(3), 218–229.
195. Z. Li, N. Kovachki, K. Azizzadenesheli, B. Liu, K. Bhattacharya, A. Stuart and A. Anandkumar, Fourier neural operator for parametric partial differential equations, arXiv, 2020, preprint, arXiv:201008895 DOI:10.48550/arXiv.2010.08895.
196. G. Wen, Z. Li, K. Azizzadenesheli, A. Anandkumar and S. M. Benson, U-FNO—An enhanced Fourier neural operator-based deep-learning model for multiphase flow, Adv. Water Resour., 2022, 163, 104180.
197. S. Wang, H. Wang and P. Perdikaris, Learning the solution operator of parametric partial differential equations with physics-informed DeepONets, Sci. Adv., 2021, 7(40), eabi8605.
198. Z. Li, H. Zheng, N. Kovachki, D. Jin, H. Chen, B. Liu, K. Azizzadenesheli and A. Anandkumar, Physics-Informed Neural Operator for Learning Partial Differential Equations, ACM/IMS J. Data Sci., 2024, 1(3), 1–27.
199. S. Cai, Z. Wang, L. Lu, T. A. Zaki and G. E. Karniadakis, DeepM&Mnet: Inferring the electroconvection multiphysics fields based on operator approximation by neural networks, J. Comput. Phys., 2021, 436, 110296.
200. V. Kumar, S. Goswami, K. Kontolati, M. D. Shields and G. E. Karniadakis, Synergistic learning with multi-task DeepONet for efficient PDE problem solving, Neural Networks, 2025, 184, 107113.
201. P. Jin, S. Meng and L. Lu, MIONet: Learning Multiple-Input Operators via Tensor Product, SIAM J. Sci. Comput., 2022, 44(6), A3490–A3514.

---