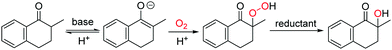Aerobic α-hydroxylation of 2-Me-1-tetralone in 1-alkyl-3-methylimidazolium ionic liquids†
Yongtao
Wang‡
 ab,
Zeyu
Wen‡
ab,
Zeyu
Wen‡
 ab,
Yue
Zhang
a,
Xinyu
Wang
a,
Jia
Yao
ab,
Yue
Zhang
a,
Xinyu
Wang
a,
Jia
Yao
 *a and
Haoran
Li
*a and
Haoran
Li
 *ac
*ac
aDepartment of Chemistry, ZJU-NHU United R&D Center, Zhejiang University, 38 Zheda Road, Hangzhou, 310027, China. E-mail: lihr@zju.edu.cn; yaojia@zju.edu.cn
bCenter of Chemistry for Frontier Technologies, Zhejiang University, Hangzhou, 310027, China
cState Key Laboratory of Chemical Engineering, College of Chemical and Biological Engineering, Zhejiang University, Hangzhou, 310027, China
First published on 20th February 2021
Abstract
The aerobic α-hydroxylation of 2-Me-1-tetralone was investigated in imidazol-based ionic liquids (ILs), where reactions in 1-alkyl-3-methylimidazolium tetrafluoroborates were found to generate considerable products. By correlating the conversion at 2 h with viscosity, relative permittivity and the ET(30) value of ILs, we found that the local polarity in ILs represented by the ET(30) value or the chemical shift of α-proton at the substrate was the critical factor influencing the reaction rate. Furthermore, two-dimensional nuclear Overhauser effect spectroscopy (2D NOESY) was used to characterize the distribution of 2-Me-1-tetralone in ILs. As a result, the mesoscopic structures in ILs were recommended to have crucial influences on the distribution of the substrate in ILs, and the caused local polarity could affect the activation of 2-Me-1-tetralone. These findings revealed the solvent effects of ILs with different structures on the α-hydroxylation of 2-Me-1-tetralone, and may encourage the explorations of more types of aerobic oxidations in ILs.
Introduction
Aerobic oxidation is an important field in industry and chemical science, where the greenest and most abundant dioxygen is used as the oxidant, producing diverse compounds with functional groups.1,2 In this kind of reactions, solvent effects generally influence the outcome of oxidized products significantly.3 In place of conventional molecular solvents, the application of ionic liquids (ILs) in aerobic oxidations has many advantages, such as their low vapor pressure, low explosion risk, and high stability under oxidative and heated conditions.4–6 However, because the aerobic oxidations are gas–liquid phase reactions, the high viscosity of ILs could limit the mass transport velocity,5 and the solubility of dioxygen was found quite low in ILs.7 Therefore, only a few studies reported more efficient aerobic oxidations in ILs than in molecular solvents.5,6,8 For example, the oxidation of benzylic alcohols has been efficiently carried out in imidazole-based ILs,9,10 selectively producing aldehydes or ketones. Moreover, the highly selective aerobic oxidation of sulfides to sulfoxides has also been developed in [C12mim]NO3.11For reactions in molecular solvents, solvent polarity has been found to significantly affect the reactivity, even giving rise to totally different products in different solvents.3 The polarity of molecular solvents can be similarly represented by relative permittivity as well as various empirical parameters,3,12 including reaction rate constant, the ET(30) value, and the hyperfine coupling constant of nitrogen (AN). Unlike molecular solvents, the polarity of ionic liquids (ILs) is much more complicated, because the different empirical parameters of ILs usually lead to quite different polarity order.5,13–15 The previous work in our laboratory has modified the classical Onsager reaction field to relate the spectral parameters, the ET(30) value and AN, with the relative permittivity of polar molecular solvents and ILs.16,17 The volume of the reaction field was redefined toward different types of solvents, where the radius of the reaction field for ILs was much smaller than that for molecular solvents, indicating that the local polarity truly affects the electronic structure and reactivity of solutes in ILs. Moreover, the heterogeneous mesoscopic structures have been revealed in ILs with small- and wide-angle X-ray scattering, Raman spectroscopy, mass spectrometry, and molecular dynamics, where there are polar and nonpolar domains.18–23 The local polarity of ILs may be caused by their stable mesoscopic structures,24 and the distribution of reactants in ILs should be also heterogeneous.22 We previously addressed the restricting effect of solvent aggregations on the selectivity of aerobic oxidation of 2,3,6-trimethylphenol in 3-hexanol,25 so the mesoscopic structures in ILs may also affect the aerobic oxidations.
In this work, the aerobic α-hydroxylation of ketones was selected to explore the efficiency of ILs as a solvent, and to investigate the influencing factors of ILs on the aerobic oxidations. As an important reaction in organic chemistry, the aerobic α-hydroxylation of carbonyl compounds has been efficiently realized in polar solvents like DMSO, catalyzed by strong bases, such as Cs2O3, NaOH and KOtBu.26–30 Recently, we reported a guanidine catalyzed α-hydroxylation of ketones,31 and uncovered the crucial role of double hydrogen bonds. Talking about the mechanism (Fig. 1), the α-proton at ketone was abstracted by the base, then dioxygen reacts with the carbanion to form a peroxide intermediate, which is reduced by the phosphine reductant, and generate the hydroxylated product.30 Due to the ionic reaction route of this reaction, we anticipate that the aerobic α-hydroxylation could be achieved in ILs.
Herein, we investigated the aerobic α-hydroxylation of 2-Me-1-tetralone in various 1-alkyl-3-methylimidazolium ILs, catalyzed by Cs2CO3. To make out the solvent effects, we correlated the conversion at 2 h with different properties of ILs, and found the essential role of local polarity for reaction rate. Moreover, by means of one- and two-dimensional proton nuclear magnetic resonance (1D and 2D 1H NMR), as well as theoretical calculations, we suggested the essential role of ILs’ mesoscopic structure and local polarity during the activation of 2-Me-1-tetralone.
Results and discussion
Reaction developments
The hydroxylation of ketones has been realized in molecular solvents, where the highly polar solvent, DMSO, was commonly used to gain high yields. In this work, we developed the method for the hydroxylation of ketones in 1-alkyl-3-methylimidazolium ILs, and the cyclic ketone, 2-methyl-1-tetralone (1), was chosen as the model substrate. Liang et al. have reported that Cs2CO3 was an efficient catalyst for the hydroxylation of ketones with 2.0 equiv. P(OEt)3 as the reductant.26 Therefore, we explored the Cs2CO3 catalyzed hydroxylation of 1 in 1-ethyl-3-methylimidazolium tetrafluoroborate ([Emim]BF4), with P(OEt)3 as the reductant (Table 1).| Entry | Cs2CO3 | P(OEt)3 | Solvent | Conv. [%] | Sel. [%] |
|---|---|---|---|---|---|
| a Reaction conditions: 1 (0.5 mmol), Cs2CO3 (0.1–0.5 mmol), P(OEt)3 (0.25–1.0 mmol), solvent (2 mL); the reaction was performed at room temperature under 1 atm dioxygen, and was determined with GC after extraction. The selectivity was calculated by dividing the yield with conversion. b In this reaction, 0.2 mL water was added, and the reaction was performed for 30 h. | |||||
| 1 | 20 mol% | 1.1 equiv. | [Emim]BF4 | 90.7 | 83.3 |
| 2 | 50 mol% | 1.1 equiv. | [Emim]BF4 | 97.3 | 88.7 |
| 3 | 1 equiv. | 1.1 equiv. | [Emim]BF4 | 99.6 | 84.0 |
| 4 | 50 mol% | 0.5 equiv. | [Emim]BF4 | 81.5 | 73.6 |
| 5 | 50 mol% | 2.0 equiv. | [Emim]BF4 | 99.4 | 84.6 |
| 6 | 50 mol% | 1.1 equiv. | [Emim]BF4 | 98.4 | 86.1 |
| 7b | 50 mol% | 1.1 equiv. | [Emim]BF4 | 27.6 | 30.3 |
| 8 | 50 mol% | 1.1 equiv. | [Bmim]BF4 | 99.4 | 93.6 |
| 9 | 50 mol% | 1.1 equiv. | [Bmim]PF6 | 98.0 | 82.5 |
The reaction in [Emim]BF4 was fast enough to be terminated within 3 h. The conversion and selectivity were determined using gas chromatography (GC). Increasing the usage of Cs2CO3 from 20 to 100 mol%, we found that the selectivity was not sensitive to the catalyst loading. However, the selectivity decreased with the decrease of the reductant, P(OEt)3. In order to exclude the influence of possibly contained water in [Emim]BF4,5 we added 0.2 mL water into the reaction, then the reaction rate and the selectivity were both reduced significantly (Table 1, entry 7). The results in [Emim]BF4 encouraged us to investigate this reaction in other ILs. In place of [Emim]BF4, the reactions in 1-butyl-3-methylimidazolium tetrafluoroborate ([Bmim]BF4) and 1-butyl-3-methylimidazolium hexafluorophosphate ([Bmim]PF6) also generate 2 in a considerable yield (Table 1, entries 8 and 9). Following this, in order to have a deep insight on reactions in ILs, we studied the solvent effect.
Solvent effects in aerobic hydroxylation
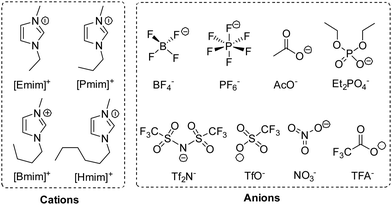
To investigate the effect of a solvent, we performed this reaction in various 1-alkyl-3-methylimidazolium ILs, whose structures and abbreviations are given in Fig. 2. To exclude the influence of solubility, a 20 mol% catalyst was used, and the reaction was performed at 35 °C. The solvent effect was studied via comparing reaction rate, which was represented by the conversion of 1 at 2 h. Moreover, to make sure the intrinsic reaction rate was determined rather than the rate of diffusion, the stirring rate and the rotor size were both increased to obtain an unincremented reaction rate. After extraction, the conversion and selectivity were obtained in use of GC.As shown in Table 2, the reactions in different 1-alkyl-3-methylimidazolium ILs showed quite different rates, with apparent differences in conversion at 2 h, and the higher conversion was also along with a higher selectivity for 2. Having the same cation, for example, the oxidations in [Emim]TFA, [Emim]AcO and [Emim]Et2PO4 were much slower than that in [Emim]BF4 (entries 5–7 vs. entry 1). Moreover, with the same BF4− anion, the increasing length of the carbon chain at imidazolium cations leads to decreasing reaction rate (entries 1–4). Being aware of the different reaction rate, we investigated the solvent effects causing different reactivities in different ILs.
| Entry | Ionic liquid | Label | δα–H (ppm) | Conv. [%] | Sel. [%] |
|---|---|---|---|---|---|
| a Reaction conditions: 1 (0.5 mmol), Cs2CO3 (0.1 mmol), P(OEt)3 (0.55 mmol), solvent (2 mL); the reaction was performed at 35 °C under 1 atm dioxygen. The selectivity was calculated by dividing the yield with conversion. | |||||
| 1 | [Emim]BF4 | EB | 2.347 | 87.4 | 75.2 |
| 2 | [Pmim]BF4 | PB | 2.387 | 71.4 | 70.3 |
| 3 | [Bmim]BF4 | BB | 2.428 | 80.4 | 70.2 |
| 4 | [Hmim]BF4 | HB | 2.474 | 40.2 | 56.2 |
| 5 | [Emim]TFA | EAF | 2.486 | 10.3 | Trace |
| 6 | [Emim]AcO | EA | 2.592 | 14.2 | 13.8 |
| 7 | [Emim]Et2PO4 | EPO | 2.601 | 8.3 | Trace |
| 8 | [Pmim]Tf2N | PN | 2.533 | 17.6 | 1.0 |
| 9 | [Bmim]Tf2N | BN | 2.540 | 14.7 | 3.2 |
| 10 | [Bmim]TfO | BSO | 2.521 | 12.7 | 8.9 |
| 11 | [Bmim]PF6 | BP | 2.423 | 52.1 | 77.9 |
| 12 | [Bmim]NO3 | BNO | 2.617 | 11.2 | 1.1 |
Factors causing solvent effects
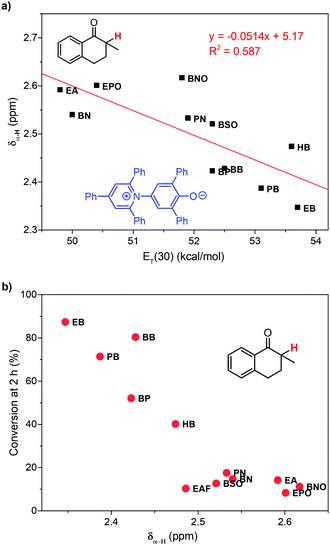
To learn the reason for different reactivities in different ILs, we tried to relate the conversion of 1 at 2 h with the properties of ILs. Because this reaction is a gas–liquid phase reaction, the viscosity of the solvent may influence the diffusion process of dioxygen in liquid phase. Though we have increased stirring rate and rotor size to exclude the influence of diffusion, in this case, we correlated the conversion of 1 at 2 h with the viscosity of ILs obtained from references (Fig. 3a).32,33 As expected, very poor relationship was observed, indicating that viscosity is not an important factor to affect this reaction.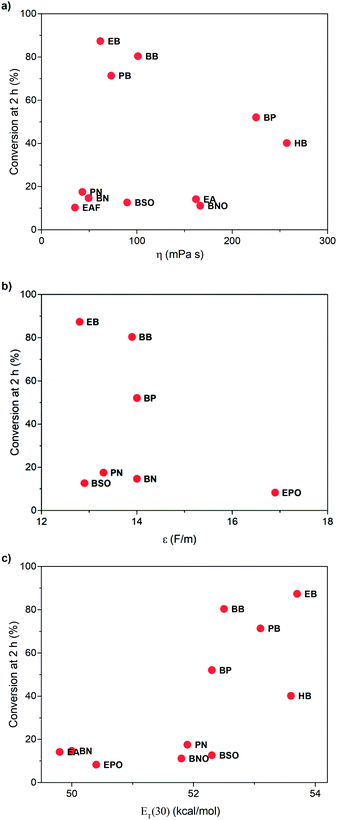 | ||
| Fig. 3 Relationship between the conversion of 1 at 2 h and the viscosity (a), relative permittivity (b), and the ET(30) value (c) of ILs. | ||
Afterwards, we evaluated the relative permittivity, which is generally used to represent the polarity of molecular solvents. It has been revealed that the aerobic hydroxylation of ketone went through an ionic mechanism, involving anion intermediates.30 Thus, the high polar solvent should benefit the hydroxylation. We used the relative permittivity data from the work by Huang et al.,34 detected by the frequency-dependent dielectric dispersion curve. As illustrated in Fig. 3b, the conversion of 1 at 2 h in ILs was poorly correlated with the relative permittivity data.
Our previous work has revealed that relative permittivity is not a good indicator of the polarity of ILs.17 Instead, the ET(30) value is widely used to represent the polarity of ILs, which is the molar electronic transition energy of the longest-wavelength intramolecular CT absorption band of betaine dye no. 30.35 Reichardt et al. have obtained ET(30) values of abundant ILs.36 Using these data, we found the ET(30) value a better parameter to correlate with the reaction rate (Fig. 3c), and higher ET(30) values were associated with faster conversion of 1. The ET(30) values in 1-alkyl-3-methylimidazolium ILs were higher than those in molecular solvents, and this may give rise to their excellent performance as the solvent for aerobic hydroxylation. Next, we focused on how the ET(30) value presented polarity affects the selectivity as well as the reaction rate.
Mesoscopic structure of ILs and its effect on the reaction
The reactivity of hydroxylation in ILs may be mainly influenced by the mesoscopic structure of solvents. The relative permittivities of 1-alkyl-3-methylimidazolium ILs are much lower than that of DMSO (46.7), but their ET(30) values are larger. The existence of the mesoscopic structure in ILs should be a possible interpretation. Nanostructural organization has been observed in 1-alkyl-3-methylimidazolium ILs by Lopes and Pádua using molecular simulation,18,20 in which the ILs are constructed with charged domains and nonpolar domains. Consequently, different types of solutes should distribute in different domains in ILs, and the polarity perceived by the solutes should be a local property other than a global property. As an indicator of local polarity of ILs, the ET(30) value was calculated according to the visible absorption of negatively solvatochromic pyridinium N-phenolate betaine dyes.35 Because of the ionic mechanism, it was reasonable that the reaction rate was more relevant with ET(30) values, rather than the relative permittivities, which represented the global polarity.Considering the effect of local polarity on the reaction, we correlated the chemical shift of α-proton at 1 (δα-H) with the ET(30) value in 1-alkyl-3-methylimidazolium ILs (Fig. 4a), and a negative correlation was revealed. Therefore, the carbonyl group of ketones and the hydroxyl anion of betaine dye no. 30 should reflect the same local polarity in ILs, which possibly is of the charged domain. As to the negative relationship, the more polar local surroundings should result in more electron density, transferring from the benzyl part of 1 to the carbonyl part, leading to the upfield peak shift of the α-proton. As a result, the conversion of 1 at 2 h was in good correlation with the δα-H (Fig. 4b), which should be a better indicator of the local polarity perceived by the reactive site of 1 in ILs. Thus, the higher local polarity around the substrate leads to the faster conversion of 1 to the ionic intermediate.
We suggested above that the carbonyl group distributed close to the imidazole cation in ILs. As an evidence, the chemical shift of the α-proton at 1 was found well related with that of the methyl group proton at imidazole cations (Fig. 5a). Distributing in the same region, the methyl group in the imidazole cation has the similar response to the local polarity as the α-proton at 1. Further 1H NMR characterization was also conducted to confirm the neighboring carbonyl group and the imidazole cation. As two protons are spatially close, the two-dimensional nuclear Overhauser effect spectroscopy (2D NOESY) could detect the dipolar cross-relaxation. Therefore, we investigated the NOESY spectrum of the solution of 1 in [Emim]BF4 (Fig. 5b), and the clear correlation between the methyl protons in 1 (Hb) and the N-methyl protons in [Emim] (Ha) was observed. Consequently, the spatially neighbouring unit between the carbonyl group at 1 and the imidazole cation was confirmed.
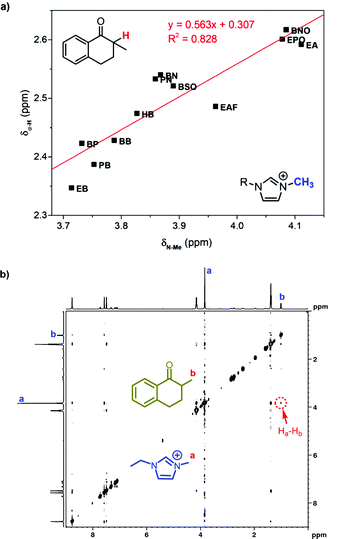 | ||
| Fig. 5 (a) Correlated chemical shift of the α-proton in 1 with that of the methyl group in 1-alkyl-3-methylimidazolium ILs. (b) The H,H-NOESY spectrum of 1 mol L−11 in [Emim]BF4. | ||
Effect of local polarity on the activation of 1
According to the discussions above, the oxidation of 1 in ILs with higher local polarity was fastened. The local polarity was caused by the special mesoscopic structures in ILs, and the dissolved 1 should distribute at the polar regions, where the local polarity could be much larger than the global polarity represented by relative permittivity. The activation of 1 by proton abstraction mainly determined the reaction rate. Therefore, we proposed that higher local polarity should benefit the proton abstraction from 1 to generate the carbanion intermediate, leading to faster conversion of 1.As a support of our proposal, the Gibbs free energy change for proton abstraction of 1 was calculated using the Onsager model37–39 to simplistically evaluate the effect of local polarity. The dielectric constant was set from 10 to 60, and the solute radius was obtained by a volume calculation. The calculated differences of Gibbs free energy change are shown in Fig. 6. The proton abstraction was obviously preferred at a larger dielectric constant, due to the smaller Gibbs free energy change.
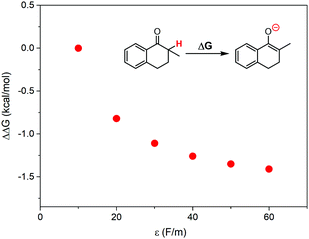 | ||
| Fig. 6 Calculated differences of Gibbs free energy change for proton abstraction of 1 at various dielectric constants, where the Onsager model was used as the solvent reaction field. | ||
Conclusions
In summary, we uncovered a gas–liquid phase reaction, the aerobic hydroxylation of 2-methyl-1-tetralone (1) in 1-alkyl-3-methylimidazolium ILs, where the considerable yield of a hydroxylated product was obtained. While correlating the conversion of 1 at 2 h with the properties of ILs, we revealed that the local polarity represented by the ET(30) value or δα-H of 1 was a critical factor to affect the reactivity, rather than the viscosity or the relative permittivity. To explain the effect of local polarity, the mesoscopic structure of ILs was introduced to restrict the distribution of 1, whose carbonyl group was suggested to neighbor the imidazole cations by 1H NMR and NOESY spectra.This work revealed that imidazole-based ILs were efficient solvents for aerobic reactions, while gas–liquid phase reactions were generally considered hardly executable in ILs with high viscosity. With these findings, more applications of ILs for aerobic oxidations are predictable. Moreover, the mesoscopic structure of ILs was found crucial for the reaction rate, shedding light on the quite different performance of ILs with different structures.
Methodology
General methods
Unless otherwise stated, all reagents were purchased from commercial sources without further treatment. GC-MS spectra were recorded on a Shimadzu GC/MS-QP2010 system (Shimadzu, Germany). Gas chromatography with a flame ionization detector (GC-FID) was carried out on GC-2014 (Shimadzu, Japan). 1H NMR, 13C NMR and NOESY spectra were recorded on Bruker AVANCE III 500.Procedures for aerobic α-hydroxylation
To a 25 mL Schlenk tube equipped the magnetic bar, Cs2CO3 (33 mg, 0.1 mmol), 1 (80 mg, 0.5 mmol) and P(OEt)3 (93 mg, 0.55mmol) were added in succession, and solvents (2.0 mL) at last. After mixing and vacuation, the suspension was charged with 1 atm O2 and linked to a 20 mL injector filled with O2. And then the suspension was stirred at 35 °C. After the reaction, the solution was quenched with 10 mL water and diluted with ethyl acetate (4 mL). Then 1.0 mL ethyl acetate solution of phenylbenzene was added as an inner standard. Washed by saturated brine (20 mL), the solution was extracted with ethyl acetate (10 mL × 3). Then the organic phase was characterized with GC-FID or GC-MS.NMR characterizations
The solution of 0.5 mmol 1 with 2.0 mL solvent was stirred in room temperature for 1 hour, then 0.3 mL solution was put into a 5 mm NMR tube. Following this, a sealed 3 mm NMR tube charged with CDCl3 was put in the 5 mm NMR tube, and the 1H NMR spectrum was obtained at room temperature. For NOESY detection, 1 mmol 1 was mixed with 2.0 mL [Emim]BF4.Theoretical methods
DFT calculations were carried out using Gaussian 09 D.01.40 The geometries were fully optimized using the B3LYP41,42/6-31+G(d,p)43–46 method. At the same level, the volumes were calculated, and frequency analyses were performed to confirm the minimum structure. The Onsager model37–39 was applied to calculate the solvent effct, and the dielectric constant was set from 10 to 60.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Fundamental Research Funds for the Central Universities, and the National Natural Science Foundation of China (No. 22073081).Notes and references
- H. Sterckx, B. Morel and B. U. W. Maes, Angew. Chem., Int. Ed., 2019, 58, 7946–7970 CrossRef CAS PubMed.
- A. Gavriilidis, A. Constantinou, K. Hellgardt, K. K. M. Hii, G. J. Hutchings, G. L. Brett, S. Kuhn and S. P. Marsden, React. Chem. Eng., 2016, 1, 595–612 RSC.
- C. Reichardt and T. Welton, Solvents and solvent effects in organic chemistry, John Wiley & Sons, 2011 Search PubMed.
- J. Muzart, Adv. Synth. Catal., 2006, 348, 275–295 CrossRef CAS.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- C. Dai, J. Zhang, C. Huang and Z. Lei, Chem. Rev., 2017, 117, 6929–6983 CrossRef CAS PubMed.
- J. L. Anthony, E. J. Maginn and J. F. Brennecke, J. Phys. Chem. B, 2002, 106, 7315–7320 CrossRef CAS.
- W. Guan, C. Wang, X. Yun, X. Hu, Y. Wang and H. Li, Catal. Commun., 2008, 9, 1979–1981 CrossRef CAS.
- N. Jiang and A. J. Ragauskas, J. Org. Chem., 2007, 72, 7030–7033 CrossRef CAS PubMed.
- Y. Oda, K. Hirano, T. Satoh, S. Kuwabata and M. Miura, Tetrahedron Lett., 2011, 52, 5392–5394 CrossRef CAS.
- Y.-L. Hu, D. Fang and R. Xing, RSC Adv., 2014, 4, 51140–51145 RSC.
- A. R. Katritzky, D. C. Fara, H. Yang, K. Tämm, T. Tamm and M. Karelson, Chem. Rev., 2004, 104, 175–198 CrossRef CAS PubMed.
- X. Wang, K. Chen, J. Yao and H. Li, Sci. China: Chem., 2016, 59, 517–525 CrossRef CAS.
- O. Zech, J. Hunger, J. R. Sangoro, C. Iacob, F. Kremer, W. Kunz and R. Buchner, Phys. Chem. Chem. Phys., 2010, 12, 14341–14350 RSC.
- A. Pandey, R. Rai, M. Pal and S. Pandey, Phys. Chem. Chem. Phys., 2014, 16, 1559–1568 RSC.
- X. Wang, R. Dao, J. Yao, D. Peng and H. Li, ChemPhysChem, 2017, 18, 763–771 CrossRef CAS PubMed.
- X. Wang, S. Zhang, J. Yao and H. Li, Ind. Eng. Chem. Res., 2019, 58, 7352–7361 CrossRef CAS.
- J. N. A. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef CAS PubMed.
- K. Iwata, H. Okajima, S. Saha and H.-O. Hamaguchi, Acc. Chem. Res., 2007, 40, 1174–1181 CrossRef CAS PubMed.
- A. S. Pensado, M. F. Costa Gomes, J. N. Canongia Lopes, P. Malfreyt and A. A. Padua, Phys. Chem. Chem. Phys., 2011, 13, 13518–13526 RSC.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- Y. L. Wang, B. Li, S. Sarman, F. Mocci, Z. Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877 CrossRef CAS PubMed.
- F. Endres and Phys Chem, Chem. Phys., 2010, 12, 1648 CAS.
- K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903–21929 RSC.
- Y. Wang, G. Wang, J. Yao and H. Li, ACS Catal., 2019, 9, 6588–6595 CrossRef CAS.
- Y. F. Liang and N. Jiao, Angew. Chem., Int. Ed., 2014, 53, 548–552 CrossRef CAS PubMed.
- S.-B. D. Sim, M. Wang and Y. Zhao, ACS Catal., 2015, 5, 3609–3612 CrossRef CAS.
- A. S. Tsang, A. Kapat and F. Schoenebeck, J. Am. Chem. Soc., 2016, 138, 518–526 CrossRef CAS PubMed.
- M. B. Chaudhari, Y. Sutar, S. Malpathak, A. Hazra and B. Gnanaprakasam, Org. Lett., 2017, 19, 3628–3631 CrossRef CAS PubMed.
- Y. F. Liang and N. Jiao, Acc. Chem. Res., 2017, 50, 1640–1653 CrossRef CAS PubMed.
- Y. Wang, R. Lu, J. Yao and H. Li, Angew. Chem., Int. Ed., 2021 DOI:10.1002/anie.202014478.
- K. Tochigi and H. Yamamoto, J. Phys. Chem. C, 2007, 111, 15989–15994 CrossRef CAS.
- H. Shirota, T. Mandai, H. Fukazawa and T. Kato, J. Chem. Eng. Data, 2011, 56, 2453–2459 CrossRef CAS.
- M.-M. Huang, Y. Jiang, P. Sasisanker, G. W. Driver and H. Weingärtner, J. Chem. Eng. Data, 2011, 56, 1494–1499 CrossRef CAS.
- V. G. Machado, R. I. Stock and C. Reichardt, Chem. Rev., 2014, 114, 10429–10475 CrossRef CAS PubMed.
- C. Reichardt, Green Chem., 2005, 7, 339–351 RSC.
- L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493 CrossRef CAS.
- M. W. Wong, M. J. Frisch and K. B. Wiberg, J. Am. Chem. Soc., 1991, 113, 4776–4782 CrossRef CAS.
- M. W. Wong, K. B. Wiberg and M. Frisch, J. Chem. Phys., 1991, 95, 8991–8998 CrossRef CAS.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Characterization spectra, property data, and Cartesian coordinates. See DOI: 10.1039/d0cp06047j |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2021 |