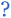Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A perspective on the building blocks of a solid-state battery: from solid electrolytes to quantum power harvesting and storage
Beatriz Moura
Gomes
abcd,
J. Francisco
Ribeiro Moutinho
ab and
Maria Helena
Braga
 *acd
*acd
aEngineering Physics Department, Engineering Faculty, University of Porto, 4200-465 Porto, Portugal. E-mail: mbraga@fe.up.pt
bPhysics and Astronomy Department, Science Faculty, University of Porto, 4200-465 Porto, Portugal
cMatER – Materials for Energy Research Laboratory, Engineering Faculty, University of Porto, Portugal
dLAETA – INEGI, Institute of Science and Innovation in Mechanical and Industrial Engineering, 4200-465 Porto, Portugal
First published on 3rd November 2023
Abstract
We present a comprehensive perspective on the fundamental components of a solid-state battery, starting from all-solid-state electrolytes and extending to quantum power harvesting and storage. First, we delve into the key characteristics that define an effective electrolyte. It is confirmed that the most promising electrolytes are semiconductors with a low work function, displaying behavior akin to anodes. Moreover, electrolyte classes composed of multiple dominant elements S, O, and Cl, such as argyrodites and oxyhalide electrolytes, show more significant potential than those with only one dominant element, such as sulfide, oxide, and halide electrolytes. We also explore ferroelectric-electrolyte-based devices capable of both energy harvesting and storage. Ferroelectric materials possess exceptional properties that hold the promise to revolutionize the next generation of electronic devices. Likewise, we explore the realm of ferroelectric topological insulators (FETIs), which open up a new world of possibilities. Pioneering studies in this area are reported herein. Continuing our assessment, we investigate the domain of the small and provide an overview of the principles behind quantum batteries. We explain the general quantum model and present three different types of quantum batteries: the Dicke model, the spin-chain model, and the quantum thermal machines, whose function mechanism is based on Maxwell's demons (isothermal baths) and quantum refrigerators. By presenting these insights, we hope to contribute to advancing solid-state batteries and quantum power harvesting and storage technologies that maintain coherence even at macrosizes, paving the way for more efficient and sustainable electronic devices.
1. Introduction
As we enter a new era, fossil fuels are no longer considered the forthcoming primary means of powering society. It has become imperative to seek sustainable technologies capable of producing and storing green energy.1 Over time, batteries have undergone tremendous advancements and have now become the leading technology for energy storage. The most significant breakthrough in this field came with the development of lithium-ion batteries (LIBs), which have revolutionized energy storage, from portable charging devices to electric vehicles.2Liquid or gel electrolytes form the fundamental building blocks of LIBs, enabling Li+-ions to be transported from one electrode toward the other while cycling a battery. However, in some cases, when the charging process is too rapid, for example, due to low temperatures, cations cannot be inserted into the negative electrode. As a result, lithium accumulates at the surface, leading to the formation of dendrites. These dendrites are fractals and may eventually penetrate the separator, connecting both electrodes and creating a short circuit. The formation of dendrites poses significant safety risks due to the flammable character of liquid and gel electrolytes, the likelihood of thermal runways, and cathodes' oxygen release.3 To overcome the challenges associated with traditional liquid and gel electrolytes, researchers have developed non-flammable solid-state electrolytes that exhibit cationic conduction, such as Li+, Na+, and K+.4,5 Solid-state electrolytes are generally not flammable, offer increased stability to dendrite formation, and are compatible with high-potential electrodes, allowing for higher energy-density batteries as they permit using electrodes with higher theoretical capacity, such as lithium (3860 mA g−1).
This perspective will start by looking into the driving forces of a solid-state battery, which are unified with other energy harvesting, storage and switching devices such as photovoltaics, thermoelectrics, capacitors, diodes, and transistors, among others, some of them punctually chosen for comparison here. A solid-state electrolyte is not just a variety of its liquid sibling; in solid electrolytes, usually, there is a main mobile species that leaves behind opposite sign-charging regions. The latter has implications for the velocity of these charge carriers and their position about the mobile ion, which affects how an electrical impedance spectroscopy (EIS) plot is analyzed, resulting in very different determinations of the ionic conductivity for similar data.
On the other hand, the polarization that has traditionally been tried to be avoided is not worth the effort, as polarization arises spontaneously from the difference in Fermi levels of the electrode/electrolyte that may not be overcome by the tunneling of electrons from the electrode to the electrolyte, as the electrolyte is an insulator with a specific relative position of its lower energy of the conduction band in regard to the Fermi level or electrochemical potential of the conductor-electrode. Therefore, it is paramount to remember these principles, which are shared across solid-state devices. Lately, it has been shown6 that electrolytes may demonstrate themselves as p-type semiconductors.
The analysis of the electrolytes will be based on the type of elements they contain and the impact on their properties. Their crystalline structures or other properties, such as ferroelectricity, will also distinguish them for the same reasons pointed out before, similar to what happens in the photovoltaics world.
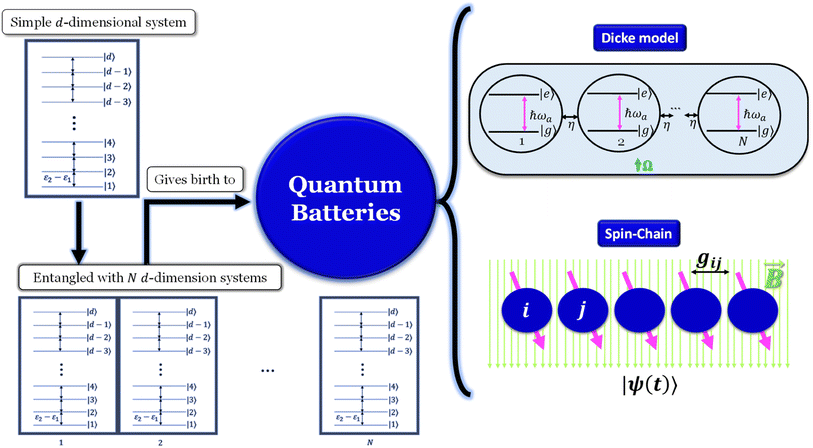
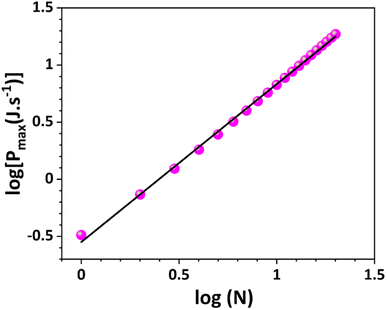
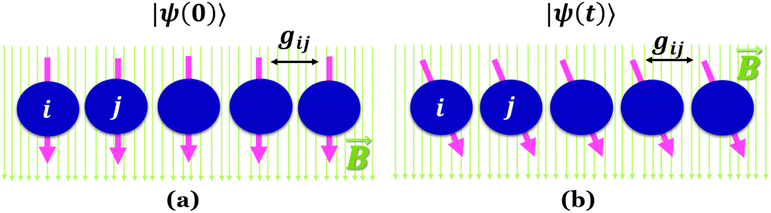
Quantum batteries will be discussed in all their known variations. Their macro-size versions are already working prototypes and may harvest thermal energy besides electrical energy storage through coherent properties.
1.1. Features enabling energy storage
Ionic conductivity in solid electrolytes depends on parameters such as the mobile ions' concentration, size and mobility, lattice structure and defects, and conduction mechanisms. Solid electrolytes, like liquid electrolytes, display mass and charge transport. The solid electrolytes herein typically exhibit cation conductivity as opposed to liquid electrolytes, which rely on both ion mobilities, thus creating the need for intensive research on ionic transport in solid electrolytes to obtain fast ionic conductivity at room temperature (RT).In solid electrolytes, ions move through disordered sublattices within an enclosed, cage-like framework. The equation expresses the ion conduction in solid-state electrolytes as σi = niqθi where ni, q, and θi are the mobile ion concentration, the elementary charge, and the ionic mobility. These parameters are dependent on the temperature following an Arrhenius-type behavior. The ionic conductivity is related to the diffusivity of mobile ions – which is given by the Nernst–Einstein equation, 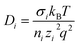 , where kB and T are the Boltzmann's constant and the absolute temperature, zi is the number of transferred charges per ion, and e is the unitary charge of the electron.
, where kB and T are the Boltzmann's constant and the absolute temperature, zi is the number of transferred charges per ion, and e is the unitary charge of the electron.
Ionic diffusion in inorganic materials consists of ions hopping between adjacent available sites, overcoming a higher energy barrier, the activation energy, due to geometry constraints and electrostatic interactions. Generally, two different hopping mechanisms can be distinguished: direct and knock-off. In the direct hopping mechanism, an individual ion hops from one lattice site to its adjacent vacant site. In contrast, knock-off-hopping is due to an indirect interstitial mechanism where an interstitial atom pushes the matrix atom toward another interstitial site and realizes ionic transport.
In solid electrolytes, creating highly disordered defects for ions to move, designated Schottky and Frenkel point defects, is necessary to enhance the ionic conductivity. According to the Arrhenius model, ionic conductivity in crystalline solids is given by the equation 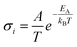 , where A is a pre-exponential factor and EA is the activation energy of diffusion. The predominant carriers for ion conduction are point defects in solids; this characteristic excludes most inorganic materials due to the lack of functional defects for ion migration or high activation energy. Thanks to advances in crystal structure engineering, it was discovered that only a limited number of materials sharing particular types of structures could diffuse Li+ and Na+ ions efficiently. However, minor concentration substitutions of the monovalent mobile cation by multivalent cations with a high ionic radius may tailor new solid electrolyte solutions.
, where A is a pre-exponential factor and EA is the activation energy of diffusion. The predominant carriers for ion conduction are point defects in solids; this characteristic excludes most inorganic materials due to the lack of functional defects for ion migration or high activation energy. Thanks to advances in crystal structure engineering, it was discovered that only a limited number of materials sharing particular types of structures could diffuse Li+ and Na+ ions efficiently. However, minor concentration substitutions of the monovalent mobile cation by multivalent cations with a high ionic radius may tailor new solid electrolyte solutions.
However, the fundamentals of solid-state batteries surpass the properties associated with the internal impedance associated with ionic transport, which is a consequence, not the driving force for the ionic and electric mechanisms within the cell.
The driving force in a battery is associated with the necessity of aligning the electrochemical potentials, according to the equation
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) j − j − ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i = i = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) j − j − ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i + zie(ϕj − ϕi) i + zie(ϕj − ϕi) | (1) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) j, μj, and ϕj are the electrochemical potential or Fermi level for the solid species, chemical potential, and surface potential of species j; zieϕj is an electrical work performed by i on the surface of j; zi is the valence of the mobile charge (e.g., zLi = +1). When the electrochemical potentials are equalized,
j, μj, and ϕj are the electrochemical potential or Fermi level for the solid species, chemical potential, and surface potential of species j; zieϕj is an electrical work performed by i on the surface of j; zi is the valence of the mobile charge (e.g., zLi = +1). When the electrochemical potentials are equalized, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) j −
j − ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i = 0 = μj − μi + zie(ϕj − ϕi) ⇒ μj − μi = zie(ϕi − ϕj) = zieΔVij. If both i and j are conductors, such as the electrodes, they may equalize their chemical potentials by exchanging electrons upon electrical contact. Nonetheless, if one of the species is an insulator or semiconductor, when possible, electrical double-layer capacitors (EDLCs) of potential difference ΔVij will form at the interfaces to equalize the difference in chemical potentials. In a solid-state device such as a battery, EDLCs store the energy. Therefore, for energy storage to happen, an interface involving at least one semiconductor or insulator must be present. A battery cell's asymmetry relies on one or two double-layer capacitors formed at the interface of the negative electrode/electrolyte or electrolyte/positive electrode.
i = 0 = μj − μi + zie(ϕj − ϕi) ⇒ μj − μi = zie(ϕi − ϕj) = zieΔVij. If both i and j are conductors, such as the electrodes, they may equalize their chemical potentials by exchanging electrons upon electrical contact. Nonetheless, if one of the species is an insulator or semiconductor, when possible, electrical double-layer capacitors (EDLCs) of potential difference ΔVij will form at the interfaces to equalize the difference in chemical potentials. In a solid-state device such as a battery, EDLCs store the energy. Therefore, for energy storage to happen, an interface involving at least one semiconductor or insulator must be present. A battery cell's asymmetry relies on one or two double-layer capacitors formed at the interface of the negative electrode/electrolyte or electrolyte/positive electrode.
If the negative electrode is lithiated graphite, the battery cell may discharge without any change in the electrochemical potential of the negative electrode. As to the equilibrium LiC6 ⇔ (1 − 2x)LiC6 + xLiC12 + x(Li+ + ē), 0 ≤ x ≤ 0.5 corresponds to a capacity of 177 mA h g−1, which is usually enough to discharge a traditional cathode with an experimental capacity inferior to 170 mA h g−1. At equilibrium, xLiC12 and x(Li+ + ē) form from LiC6, while the chemical potentials of the species are kept constant. Therefore, if the anode is lithiated graphite (LiC6), while discharging, the voltage versus time/capacity curve reflects the equilibria at the cathode side. The cathode's chemical potential increases while the electrons are transported to the cathode through an external circuit from the anode. Then, a new phase rich in mobile ions Li+ will start to form, and while the initial/charged cathode phase does not run out, the discharge curve is at a plateau because the chemical potential of both phases is equal (Fig. 1b), as pointed out earlier.
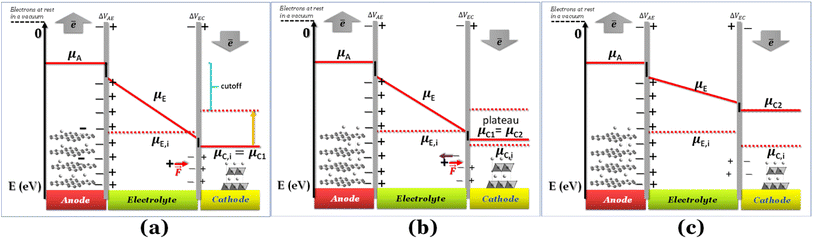 | ||
Fig. 1 Schematic discharge of a battery as a function of the chemical potentials of the electrodes and electrolyte; (a) cell was charged and started to discharge; ΔVbattery cell = ΔVAE + ΔVEC; (b) a new phase is formed at the cathode, and the two phases become at equilibrium (μC1 = μC2), corresponding to the plateau voltage; A+ + ē (e.g. A+ = Li+) forms more μC2; ΔVbattery cell = ΔVAE + ΔVEC; (c) as the chemical potential overcomes the intrinsic chemical potential of the electrolyte, both surfaces of the electrolyte are charged positively; ΔVbattery cell = ΔVAE − ΔVEC. The black lines at the interfaces are the walls of the potential quantum well/barrier related to interfacial impedances/resistances. Note: for simplification, no band gap is represented here for the electrolyte; however μE,i = −(Ec + Ev)/2 = −Eg/2, where Ec, Ev, and Eg are the minimum energy of the conduction band, the maximum energy of the valence band, and the band gap, respectively; μE,i is the chemical potential of the electrically insulated electrolyte, and μA, μE, and μC1 are the chemical potentials of the anode, electrolyte, and cathode (phase 1).  is coulombic force. Schematics with the band gap of the electrolyte are shown in Fig. 4. is coulombic force. Schematics with the band gap of the electrolyte are shown in Fig. 4. | ||
Here, we have considered μC ≤ μE ≤ μA for E0 = 0 for electrons at rest in a vacuum at the surface of the correspondent material (Fig. 1a); in fact, the chemical potential of the electrolyte may also assume different relative values, μE ≤ μC ≤ μA and μC ≤ μA ≤ μE, depending on the electrolyte,6 while the cathode and anode must have chemical potentials μC ≤ μA per definition of the cathode and anode. If the electrolyte's potential μC ≤ μA ≤ μE, the quantum well in Fig. 1 becomes a quantum barrier.6
When the Li+-poor phase runs out, the Li+-rich phase is the only one present in the cathode, and its chemical potential will increase with more electrons and Li+ transported to the cathode. The cations Li+ move by the action of coulombic forces as the electric field points to the cathode within the electrolyte (Fig. 1a).
While Gauss's law determines that the electric field outside an EDLC is null, as the cathode's chemical potential increases, the equilibrium between the electrolyte's electrochemical potentials and the cathode is dynamic. Fewer negative charges must accumulate at the electrolyte's surface on the cathode side. Therefore, the Li+-ion diffuses towards the cathode. In most electrolytes, the negative charges are negatively charged vacancies, 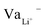 . Therefore, neutrality is restored when a Li+-ion occupies a
. Therefore, neutrality is restored when a Li+-ion occupies a 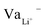 .
.
The potential difference between the two EDLCs in series sum is equal to the battery's voltage, ΔVbattery cell = ΔVAE + ΔVEC. As the chemical potential of the cathode increases due to electron transport from the anode, the voltage of the battery decreases, ΔVbattery cell. When the cathode's chemical potential surpasses the electrolyte's intrinsic chemical potential, then the cell's potential difference is ΔVbattery cell = ΔVAE − ΔVEC. The voltage will be zero when ΔVAE = ΔVEC. No EDLC forms when μE = μC. At this point, the Li+ is free to diffuse under Fick's law. From the EDLCs, electrons may tunnel to the electrolyte's surface, reducing the Li+ to Li0, which then diffuses to the cathode under Fick's law of diffusion. The latter mechanism is more likely if the electrolytes' surface states are dense enough, ≥1012 states per cm2, to hold a specific concentration of electrons. The EDLC is a triangular quantum well or barrier, depending on the electrolyte/cathode relative chemical potentials. However, the anode/electrolyte/cathode will represent a quantum well or barrier themselves depending on the relative positions of the chemical potentials, as described previously.
When the electrolyte is ferroelectric, the difference in chemical potentials at the interfaces is minimized6 and the internal resistance is reduced to the activation energy associated with the mobility of the ions.
1.2. Solid electrolytes: Li/Na-SICON, argyrodite, garnet, perovskites, double perovskites, antiperovskites, halides, and oxyhalides
One key component of a battery is the electrolyte, making it one of the essential factors for battery performance. An ideal solid-state electrolyte is said to possess the following properties: (1) high ionic conductivity (Fig. 2); (2) low electrical conductivity; (3) a wide electrochemical window of stability to match with high-voltage cathodes (Fig. 3); (4) a high A+-ion transference number for inhibiting the formation of negative space charge near the anode and promoting uniform ion deposition; (5) sufficient mechanical strength to inhibit ion growth; (6) good electrode wettability and low interfacial resistance with electrodes; (7) good flexibility to accommodate the change of the electrodes' volume during battery charge and discharge; (8) good thermal stability to ensure safe and stable operation of batteries at lower and higher temperatures; (9) easy fabrication and low cost.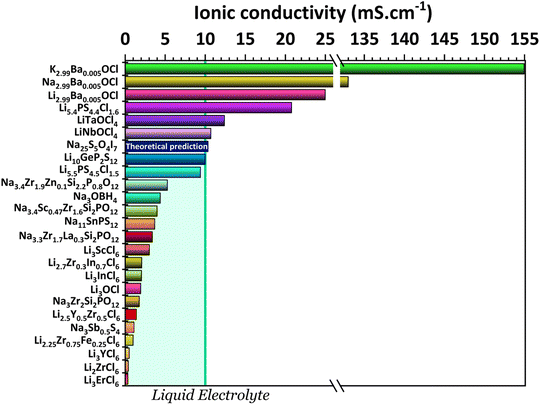 | ||
| Fig. 2 Ionic conductivities for the electrolytes: K2.99Ba0.005OCl and Na2.99Ba0.005OCl;28 Li2.99Ba0.005OCl;29 Li5.4PS4.4Cl1.6;30 LiTaOCl4 and LiNbOCl4;31 Na25S5O4I7 (theoretical study);32 Li10GeP2S12;11 Li5.5PS4.5Cl1.533 and Na3.4Zr1.9Zn0.1Si2.2P0.8O12;34 Na3OBH4;35 Na3.4Sc0.47Zr1.6Si2PO12;36 Na11Sn2PS12;37 Na3.3Zr1.7La0.3Si2PO12;38 Li3ScCl6;39 Li2.7Zr0.3In0.7Cl6;40 Li3InCl6;41 Li3OCl;29 Na3Zr2Si2PO12;42 Li2.5Y0.5Zr0.5Cl6;43 Na3Sb0.5S4;44 Li2.25Zr0.75Fe0.25Cl6;45 Li3YCl6;46 Li2ZrCl6;45 and Li3ErCl6.47 | ||
It is possible to distinguish three types of solid electrolytes: inorganic electrolytes (ISEs),7 polymer electrolytes (SPEs),8 and organic and inorganic composite electrolytes (O-ICSEs). O-ICSE is the most recent class of electrolyte, as its composition combines ISE and SPE characteristics. However, studying these composites is a relatively recent subject, and much research still needs to be carried out. SPEs consist of a polymer matrix and Li salts without any liquid solvents. These electrolytes are light weight and easy to shape, therefore capable of adapting to different battery structures. They also have good electrode wettability and flexibility that reduces the impact of electrode volume change during the charge–discharge process. However, they cannot always suppress the formation of Li dendritic structures, and the ionic conductivity of SPEs is very low, 10−4 − 0.01 mS cm−1, representing a significant drawback for application in all-solid-state batteries. On the other hand, inorganic solid electrolytes possess high ionic conductivities capable of competing even with liquid electrolytes >10 mS cm−1 (Fig. 2). ISE is also associated with higher mechanical modules; they inhibit the growth of Li dendrites, are non-flammable, and are therefore associated with a higher safety level. Inorganic solid-state electrolytes can be divided into different types of structures or element-containing compounds that summarize the characteristics of the most studied families of electrolytes, such as Li/Na-SICON, argyrodite, garnet, and perovskite structures.
The general structure of LISICON (lithium superionic conductor) materials is based on the NASICON (sodium superionic conductor) crystal structure. LISICON belongs to a broader family of solid-state materials with the general chemical formula A11B2Ch12, where A represents alkali metal cations (e.g., Li, Na, and K), B represents metal cations (e.g., Ge, Ti, and Zr), and Ch denotes chalcogen anions (e.g., O, S, and Se). The crystal structure of LISICON can be described as a three-dimensional framework of corner-sharing polyhedral units. The B cations are surrounded by oxygen anions or other chalcogens, forming a B-centered polyhedron. These polyhedra are connected by shared oxygen (or chalcogen) ions to create a 3D network. Within this framework, the A cations (e.g., Li) occupy the interstitial spaces between the B-centered polyhedra. Lithium ions in these interstitial sites allow for efficient lithium-ion transport, making LISICON materials candidates for solid-state electrolytes.
LISICON and argyrodite structures are usually found in sulfide-and-oxide-based electrolytes. The first LISICON electrolyte report can be traced back to 1980 when Li3.6Ge0.6V0.4O4 was successfully synthesized, resulting in an ionic conductivity of approximately 0.04 mS cm−1 at room temperature (RT).9 The crystalline structure of oxide-based LISICON electrolytes commonly resembles Li4SiO4 (monoclinic, P21/m space group) or γ-Li3PO4 (orthorhombic, Pnma space group) structures. These structures consist of tetrahedral units based on XO4 (where X can be P, Al, Si, Ge, S, or Ti) and Li–O polyhedral units. For LISICON-oxide-based electrolytes, the highest reported value of ionic conductivity is approximately 0.9 mS cm−1 at 27 °C, for the Li4Al1/3Si1/6Ge1/6P1/3O4 electrolyte.10 LISICON-oxide-based electrolytes are associated with relatively low ionic conductivity at RT, a significant limitation for employing these electrolytes in all-solid-state batteries.
Thio-LISICON solid-state electrolytes are derived from LISICON-oxide electrolytes by substituting the O2− anion with the S2−. This substitution improved the ionic conductivity of LISICON electrolytes up to 12 mS cm−1 at RT for Li10GeP2S12 LGPS,11 which meets the demands of commercial all-solid-state-batteries (ASSBs). Although thio-LISICON presents higher ionic conductivities due to the presence of sulfur in the backbone, this same element leads to a decrease in the overall stability of the electrolyte towards moisture.
Argyrodites are a group of compounds with the general chemical formula A7−xBCh6−xHalx, where A represents alkali metal cations (e.g., Li, Na, and K), B is P or As, Ch is a chalcogen (e.g., S and Se) and Hal is Cl, Br, or I. In the argyrodite structure, Ch chalcogens share the corners of the cube with Hal halides; the P or As form a B-centered polyhedron with Ch at the corners. A cations are positioned at the cube's center, and the tetrahedral voids are within the B-centered polyhedron. This crystal structure creates a three-dimensional network of corner-sharing polyhedra, providing pathways for efficient ion transport, particularly for lithium ions. Argyrodites are known for their high lithium-ion conductivity, making them promising candidates for solid-state electrolytes in advanced lithium-ion batteries and other electrochemical devices.
Among argyrodite-type sulfur electrolytes, Li6PS5Hal (Hal = Cl, Br, I) stands out as the most extensively studied and promising.12 Substituting the halogen element between Cl, Br, and I leads to an evident variation in lattice site disorder, increasing the unit cell volume and the intra-cage and inter-cage jump distance.13
In this perspective, our primary focus is on chloride anion-based electrolytes. This choice is based on the following reasons: (1) fluorine is the most electronegative element, resulting in a strong bond with Li ions and further impeding fast Li-ion conduction; at the same time, as they have a small radius, the lattice volume is smaller, further hindering the Li+ conductivity; (2) bromine is toxic, and as the world seeks safer and more environmentally friendly options, it has been disregarded; (3) iodine, while expected to yield better results, has limitations due to its photosensitivity, which poses challenges for mass-scale production applicability. Considering these factors, chloride anion-based electrolytes are a more favorable option, as they offer better Li-ion conduction while addressing the concerns associated with fluorine, bromine, and iodine.
Regarding Li6PS5Cl, the highest value of ionic conductivity reported for this electrolyte is 4.96 mS cm−1 at 26 °C when prepared via the solid-state reaction.14 The most common preparation method for this electrolyte is ball-milling;15 however, several groups adopted a multiple-step synthesis that included both annealing and ball-milling to improve the crystallinity and ionic conductivity. Argyrodite-sulfur electrolytes display high ionic conductivity. However, the presence of sulfur in the backbone leads to decreased stability toward moisture.16 In 2010, the first synthesis of oxide-based argyrodite Li6PO5Hal was reported.17 The ionic conductivity of the oxygen-based Li6PO5Cl electrolyte reported at RT was 10−6 mS cm−1, a value quite inferior to its sulfide-argyrodite counterpart.
The garnet structure is observed in oxide-based electrolytes, exhibiting exceptional stability when in contact with lithium metal and demonstrating satisfactory ionic conductivity. Garnet structures are commonly found in orthosilicates, characterized by the general formula, AII3BIII2(SiO4)3 (A = Ca, Mg; B = Al, Cr, Fe) where A, B, and Si cations occupy the eight, six, and four coordination sites, respectively. These structures typically crystallize in a cubic arrangement with an Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d space group. Among garnet-type electrolytes, there are four main subtypes: Li3, Li5, Li6, and Li7. Notably, the ionic conductivity of garnets containing lithium demonstrates substantial exponential growth as the Li content expands throughout a wide range. Among all the famous garnet-type electrolytes, the one that has emerged as the most promising is LLZO, Li7La3Zr2O12.18 This electrolyte has an ionic conductivity of 0.3–0.5 mS cm−1 at 25 °C,19 good thermal and chemical stability against reactions with prospective electrode materials, low cost of production, and environmental availability. On the downside, the total ionic conductivity in this electrolyte is highly sensitive to grain boundaries. These structures tend to reduce the ionic conductivity of the electrolyte, introducing the need for careful control over a high-temperature sintering process to reduce grain boundaries and, therefore, achieve higher ionic densities and conductivities.
d space group. Among garnet-type electrolytes, there are four main subtypes: Li3, Li5, Li6, and Li7. Notably, the ionic conductivity of garnets containing lithium demonstrates substantial exponential growth as the Li content expands throughout a wide range. Among all the famous garnet-type electrolytes, the one that has emerged as the most promising is LLZO, Li7La3Zr2O12.18 This electrolyte has an ionic conductivity of 0.3–0.5 mS cm−1 at 25 °C,19 good thermal and chemical stability against reactions with prospective electrode materials, low cost of production, and environmental availability. On the downside, the total ionic conductivity in this electrolyte is highly sensitive to grain boundaries. These structures tend to reduce the ionic conductivity of the electrolyte, introducing the need for careful control over a high-temperature sintering process to reduce grain boundaries and, therefore, achieve higher ionic densities and conductivities.
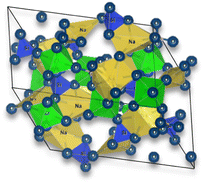
The general structure of NASICON is based on a three-dimensional framework of corner-sharing polyhedral units. NASICON is a family of solid-state materials with the general chemical formula AM2(PO4)3, where A represents monovalent cations (e.g., Li and Na) and M represents a combination of divalent and trivalent cations (e.g., Sn, Ti, and Zr).
In the NASICON crystal structure, the M cations are located at the corners of a distorted octahedron, forming an M-centered polyhedron. The PO4 tetrahedral units (phosphate anions) are connected to these M-centered polyhedra, creating a three-dimensional network. The A cations are positioned in the interstitial sites between these polyhedral units.
The general structure of perovskites is based on a three-dimensional framework of corner-sharing polyhedral units. Perovskites are a family of materials with the general chemical formula ABX3, where A (e.g., Ba) and B (e.g., Ti) are cations and X is an anion, for example, oxygen; the structure is cubic and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. In the perovskite crystal structure, the X atoms (e.g., O) are located at the corners of an octahedron, forming a BO6 polyhedral unit. The B cations are located at the center of the octahedron. The A cations are positioned in the center of the cube. The arrangement of these polyhedral units creates a three-dimensional network with a cubic symmetry. The general formula ABX3 signifies that six X anions surround each B cation and each A cation is coordinated to six X anions in an octahedral arrangement.
m. In the perovskite crystal structure, the X atoms (e.g., O) are located at the corners of an octahedron, forming a BO6 polyhedral unit. The B cations are located at the center of the octahedron. The A cations are positioned in the center of the cube. The arrangement of these polyhedral units creates a three-dimensional network with a cubic symmetry. The general formula ABX3 signifies that six X anions surround each B cation and each A cation is coordinated to six X anions in an octahedral arrangement.
Perovskites exhibit many properties and have applications in various fields, including solid-state materials, electronics, energy conversion and storage (e.g., photovoltaics and fuel cells), and catalysis. The versatility of perovskite materials stems from the ability to modify the A, B, and X elements, resulting in diverse electronic, magnetic, and optical properties.
The NASICON and the perovskite structures have lower ionic conductivity than previously mentioned electrolyte types and are still highly subjective to grain boundary issues. NASICON electrolytes, discovered in 1976 by Goodenough et al.,20 have a general formula of AM2(PO4)3, where A = Li, Na and M = Ge, Zr, Ti, and may be doped with Al. Generally, the ionic conductivity is higher when the A element is sodium Na rather than lithium (Li). For instance, LiGe2(PO4)3 – LGP exhibits an ionic conductivity of approximately 10−4 mS cm−1. Adding aluminum as a dopant in Li1.5Al0.5Ge1.5(PO4)3 – LAGP significantly improves the ionic conductivity of this electrolyte, with a maximum achieved value of 0.58 mS cm−1 at RT.21 Comparatively, the LAGP electrolyte showed a remarkable enhancement in ionic conductivity, surpassing LGP by approximately four orders of magnitude. Considering the sodium ion version, Na1+xZr2SixP3−xO12, the highest ionic conductivity obtained is for x = 2, Na3Zr2PSi2O12 with an ionic conductivity of approximately 1.13 mS cm−1 at RT.22 However, several doping strategies have been employed to achieve higher ionic conductivities: (1) doping with potassium ions, which demonstrated for Na2.303K0.099Zr2Si1.880P1.106O12 an ionic conductivity of 0.8 mS cm−1 at RT;23 (2) doping with Ge, Na3.125Zr1.75Sc0.125Ge0.125Si2PO12, resulted in total ionic conductivity 4.6 mS cm−1;24 (3) doping with Sc, Na3.4Zr1.6Sc0.4Si2PO12 provides an RT ionic conductivity of 4.0 mS cm−1.22
As for perovskite electrolytes, one notable example is Li3xLa(2/3)−xTiO3 LLTO. In 1987, Belous et al.25 synthesized the LLTO perovskite for 0.04 ≤ x ≤ 0.17 for the first time. In the LLTO solid electrolytes' structure, the Li-ion occupies the A-site, resulting in a lower activation energy. This electrolyte shows several advantages: (1) large ionic transference numbers, (2) superior chemical and (3) thermal stabilities in air, and (4) environmentally friendly character without any release of toxic gases during decomposition reactions. However, the significant grain boundary resistance reduces the total ionic conductivity of this electrolyte to <0.01 mS cm−1 at RT. LLTO is also very unstable in the presence of Li metal. For potentials below −1.7 V vs. Li0 (−1.39 eV per e for E = 0 eV, electrons at rest in a vacuum), LLTO is reduced, and Li can be intercalated in it, which causes the reduction of Ti4+ and enhances the electrical conductivity of Li0.29La0.57TiO3 LLTO.26 The latter observation indicates that the lowest energy of the conduction band is approximately −3.1 eV (E = 0 eV, electrons at rest in a vacuum). The original calculations hereafter demonstrate that the lowest energy of the conduction band for LLTO is −3.6 eV, which is in good agreement with the experimental result, considering that this value is the result of two different simulations: (1) the average potentials from a simulated surface; (2) the band structure from the bulk electrolyte.27 Note that herein, the simulated LLTO was Li2La2Ti3O10.
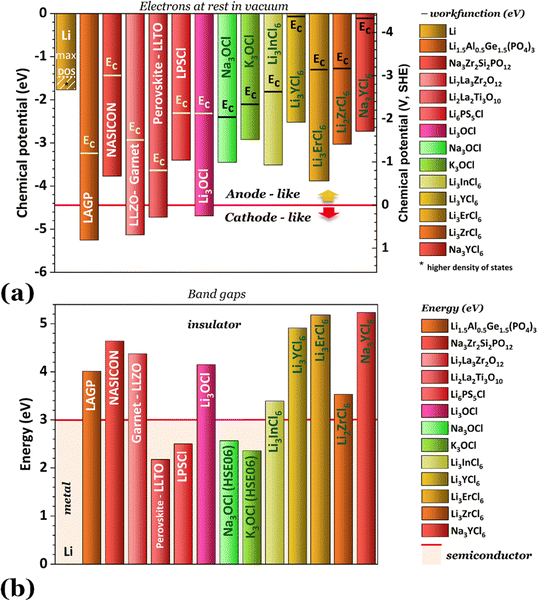
Fig. 2 shows the highest ionic conductivities in the literature, and Fig. 3 shows our data on the simulated chemical potentials and band gaps for a selection of solid electrolytes.
1.3. What makes a good solid electrolyte?
Our perspective showed that every electrolyte class has advantages and disadvantages. This realization highlights the necessity of identifying a set of parameters to answer the question, what truly defines a GOOD electrolyte?To address this question, we have conducted ab initio simulations using density functional theory (DFT) and exchange–correlation GGA-PBE or, when doubts arise concerning the electronic properties of the semiconductors, a hybrid functional HS06 was employed. These simulations allowed us to determine band structures and electronic properties (Fig. 3b and 4)48,49 and the chemical potentials (Fig. 3a)50,51 and to compare them with their respective ionic conductivity and the performance of the electrolytes in general. The crystal structures used are described in Table 1. The surfaces were simulated with a minimum of a 10 Å vacuum layer to break the periodicity. The planewave cutoff was 500 eV, and the projection was in the reciprocal space. The spacing of k-points was 0.2–0.3 Å−1. The cell contained the minimum number of atoms, allowing for a better approach to stoichiometry and experimental occupancy. The chemical potentials were obtained from the average potentials integrated over 10 Å.
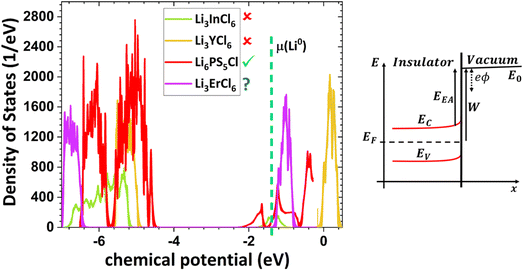
Solely relying on ionic conductivity (Fig. 2) to enumerate the characteristics of a suitable electrolyte proves to be complex since it merely represents a property and is likely not a driving force of good performance. To progress with this discussion, the energy width of the band gaps has been calculated for various electrolytes representing the previously mentioned categories in Fig. 3b. It is anticipated that, in general, solid electrolytes exhibit insulator behavior, characterized by a band gap greater than 3 eV, indicating poor electrical conductivity. The band gap values may be distinguished into three different categories: (1) conductors or metals, Eg = 0 eV; (2) semiconductors, Eg ≤ 3 eV, and (3) insulators, Eg > 3 eV. In Fig. 3b, the semiconductor/insulator barrier is represented by a red horizontal line marking 3 eV.
Based on this perspective, it can be inferred that LAGP, NASICON, garnet, Li3OCl, Li3YCl6, Li3ErCl6, and Na3YCl6 exhibit insulating behavior. However, Li3YCl6 and Na3YCl6 are not stable against Li0 and Na0. The latter is understandable as, in contrast to most insulator materials, there is a considerable density of states (DOS) at the lower energy of the conduction band corresponding to the orbitals d of Y3+ (Fig. 4). As this energy corresponds to an almost null electron affinity, however entirely above the chemical potential of the lithium μ(Li0) = −1.39 eV, the reduction of Y3+ may occur from the surface exposure directly. The Li+ required to form Y is 3Li+ + 3ē + Li3YCl6 → 6LiCl + Y, which may also be obtained within the electrolyte while charging the cell, as Li+ will move toward the negative electrode to accommodate the crescent bias between electrodes' voltages.
An equivalent process should drive the reactive character of Na3YCl6 and likely Li3ErCl6, although the latter has a higher electron affinity but similar DOS at Ec (Fig. 4).
The cathode-like solid electrolytes (Fig. 3) have low DOS on the conduction band, which prevents the drift of electrons from the alkali metal to the conduction band of the electrolytes.
The ferroelectric character of the perovskites, antiperovskites, and glass electrolytes promotes stability against alkali metals. In the electrolytes of the family A3−2xMxOHal, with A = Li, Na, K, M = Mg, Ca, Sr, Ba, Hal = Cl, Br, I, and x ≤ 0.5, a ferroelectric topologic insulator character was found to protect alkali metals as self-charge happens with electrons tunneling from the electrolytes' surface to the negative electrode. Like the latter, other perovskites were found to manifest the phenomenon discussed hereafter. This phenomenon may also protect the perovskite Li2La2Ti3O10 LLTO, also used as a cathode. Zhang et al.52 reported Li2La2Ti3O10 electrolytes as displaying ferroelectric behavior.
The stability of Li6PS5Cl LPSCl toward Li0 is not expected because of its semiconductor character and the position of its lower conduction band energy level, allowing the drift of electrons from the alkali metal. We have detected a reversible reaction with Cu, μ(Cu0) ≈ −4.6 eV, which may indicate electronic surface conduction in the electrolyte and tunneling from its surface to the negative electrode. However, this result requires further confirmation.
From the analysis with different electrolytes, it is possible to establish a pattern for the best-performing electrolytes (Fig. 2, 3, and 4): (1) display semiconductor behavior instead of insulator behavior (e.g., LPSCl, LLTO, Na3OCl, K3OCl, and A2.99Ba0.005OCl – glass with A = Li, Na, K); (2) possess a low energy work function W, i.e., anode-like behavior; but not as small as to have a null, or almost null, electron affinity energy (Fig. 4); (3) show a ferroelectric behavior where the ionic movement establishes the polarization; (4) display topologic electronic emergent phenomena. These latter phenomena require further demonstrations in different electrolytes.
Details on the properties and behavior of all-solid-state electrolytes and all-solid devices, including synthesis methods, electrolytes showing ferroelectric and topologic insulator features, and quantum thermal batteries, will be given hereafter.
1.4. Synthesis methods
When different methods prepare an electrolyte, the final characteristics of the electrolyte differ; this occurs because the preparation methods influence the crystal structure of the solid, the structural disorder, and mobile ion distributions, resulting in significantly different values of ionic conductivities as shown in Table 2.| Electrolyte | Fabrication method | Parameters | Ionic conductivity (mS cm−1) | Crystal structure | Ref. |
|---|---|---|---|---|---|
| Li6PS5Cl – LPSCl | Ball milling | 10 h – 600 rpm | 1.3 (25 °C) |
|
67 |
| Solid state reaction | (1) LiCl + Li2S + P2S5 100 rpm for 1 h | 5.0 (26 °C) | 14 | ||
| (2) 10 h of annealing | |||||
| Wet phase | Mixture with ethanol solution | 1.4 × 10−2 (RT) | 68 | ||
| Wet phase (LiCl + Li2S + P2S5 + pyridine) | (1) P2S5 + pyridine 400 rpm, RT | 4.3 (RT) | 69 | ||
| (2) Add LiCl + Li2S to 400 rpm at 70 °C | |||||
| (3) Removing pyridine in a vacuum at 120 °C | |||||
| Li7La3Zr2O12 – LLZO | Solid state reaction | (1) 200 rpm 12 h in 2-propanol | 0.2 (25 °C) |
|
19 |
| (2) 900 °C 4 h | |||||
| (3) 200 rpm 12 h | |||||
| Radio frequency magnetron sputtering | RF power of 40, 60, and 80 W at a working pressure of 7 MPa under an Ar atmosphere | 4 × 10−4 (25 °C) | 70 | ||
| Pulsed laser deposition – laser annealed | f laser pulse = 10 Hz; 7.5 J cm−2; 7700 shots; thickness ∼1 μm; laser annealing | 7.4 × 10−4 (RT) | 71 | ||
| Pulsed laser deposition – annealed at 800 °C | f laser pulse = 10 Hz; 7.5 J cm−2; 7700 shots; thickness ∼1 μm; annealing 800 °C | 1.8 × 10−4 (RT) | 71 | ||
| Na3Zr2Si2PO12 – NASICON | Solid-state reaction | (1) Calcined at 1100 °C for 12 h | 0.2 (50 °C) |
|
72 |
| (2) Ball milling at 150 rpm for 18 h | |||||
| Solid-state reaction (nanoprecursors) | 1230 °C for 40 h | 1.2 (RT) | 73 | ||
| Co-precipitation | • Solution 1: NaOH + NH4H2PO4 stirred with deionized water for 1 h at 70 °C | 1.7 (25 °C) | 74 | ||
| • Solution 2: Zr(OC3H7)4 diluted with 1-propanol; solution 1 dipped in solution 2, forming a precipitate | |||||
| Spark plasma sintering | Powders were placed into a 10 mm graphite die; 1000 A; 62 MPa; 100 °C min−1; 900–1200 °C – 30 min | 1.8 (RT) | 75 |
Mechanochemical methods, specifically ball-milling (Fig. 5a), are commonly linked to forming distinct phases, such as amorphous and/or nanocrystalline structures. On the other hand, when solid-state electrolytes (SSEs) are annealed at elevated temperatures, they tend to exhibit thermodynamically stable phases.
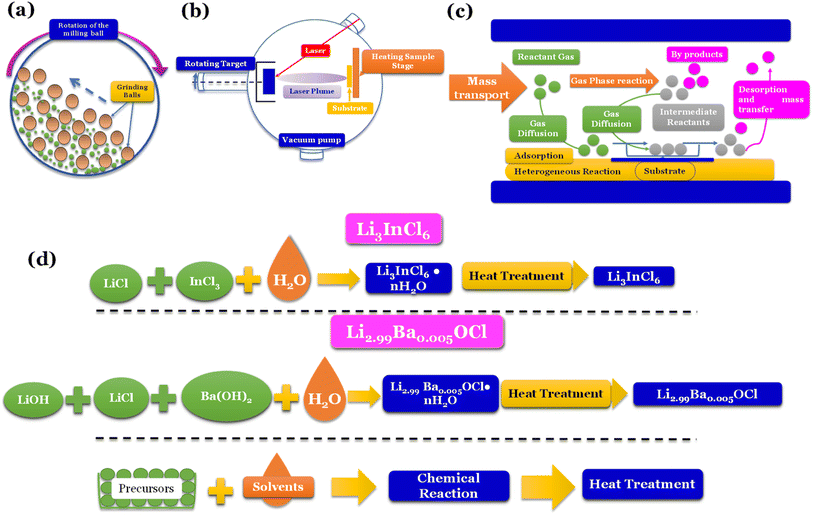 | ||
| Fig. 5 Synthesis methods: (a) high energy density ball milling;76 (b) pulsed laser deposition (PLD);77 (c) chemical vapor deposition (CVD);78 (d) water mediated synthesis of Li3InCl6,41 Li2.99Ba0.005OCl,29 K2.99Ba0.005OCl and Na2.99Ba0.005OCl.28 | ||
Vapor-phase deposition is widely used to prepare inorganic SSE membranes for thin-film batteries. These methods involve the formation of the vapor phases of the reactants, subsequent nucleation, and product growth on substrates, allowing the achievement of a homogeneous mix of reactants on a molecular or atomic level. Gas-phase techniques involve deposition methods such as pulse laser deposition (PLD) (Fig. 5b), atomic layer deposition (ALD), and chemical vapor deposition (CVD) (Fig. 5c).
To secure a dominant role in industry, SSEs must be easily reproducible, and the cost of fabrication must be low. Techniques such as ball milling don't allow reproducibility, and vapor-phase deposition techniques are usually expensive. Recently, a new technique only compatible with some types of electrolytes has been developed; the latter is a water-mediated synthesis (Fig. 5d) with great potential for mass production due to the relatively low cost of implementation.
Additionally, ball-milling can induce defects in inorganic solid electrolytes, enhancing their ionic transport. However, the results obtained by this technique don't show satisfactory reproducibility. Even when using the same equipment, the ball milling process is influenced by chamber atmosphere, ball milling time, rotation speed, and ball size; this represents a significant setback for using this technique for mass-scale production.
The CVD technique is relatively new for fabricating thin film batteries.80 The main advantage of CVD is its dependence on relatively low kinetic energy particles and the multitude of chemistries available to perform the deposition.
Nevertheless, despite the incompatibility of sulfide-electrolytes with water-mediated synthesis, various oxyhalides and halide electrolytes have demonstrated compatibility with this method, as shown in Fig. 5d. Moreover, these electrolytes exhibit exceptional ionic conductivities, further emphasizing their potential for practical applications. For example, Li3InCl6, when synthesized via solid-state synthesis, shows an ionic conductivity of 1.49 mS cm−1.82 When prepared via water-mediated synthesis, the ionic conductivity is 2.04 mS cm−1.41 However, the most significant advantage of this method is the increased humidity resistance when prepared by water-mediated synthesis.
1.5. Argyrodite electrolytes
Argyrodite electrolytes are derived from the Ag8GeS6 mineral and are reported in sulfide and oxide-based electrolytes. Considering the great interest in the mobility of Li+ ions in solids, it was surprising that the argyrodite structure had not been reported more in association with electrolytes until the beginning of the 21st century. In the Li-argyrodite family, compounds are described by the general formula, Li7+x−yMIVxMV1−xCh6−yHaly (MIV = Si, Ge, Sn; MV = P, Sb; Ch = O, S, Se; Hal = Cl, Br, I, BH4; 0 ≤ x ≤ 1; 0 ≤ y ≤ 2).87 In 2008, Deiseroth et al.88 reported the first Li6PS5Hal, Hal = Cl, Br, I, argyrodite electrolyte, showcasing its ionic conductivity in the 1 to 10 mS cm−1 range at RT. Since then, numerous reports have emerged regarding this stoichiometry, with the highest ionic conductivity obtained for Li6PS5Cl (LPSCl) being 4.96 mS cm−1 at 26.2 °C when prepared via the solid-state reaction.14 However, this is not the only stoichiometry configuration possible for a lithium argyrodite (Fig. 6).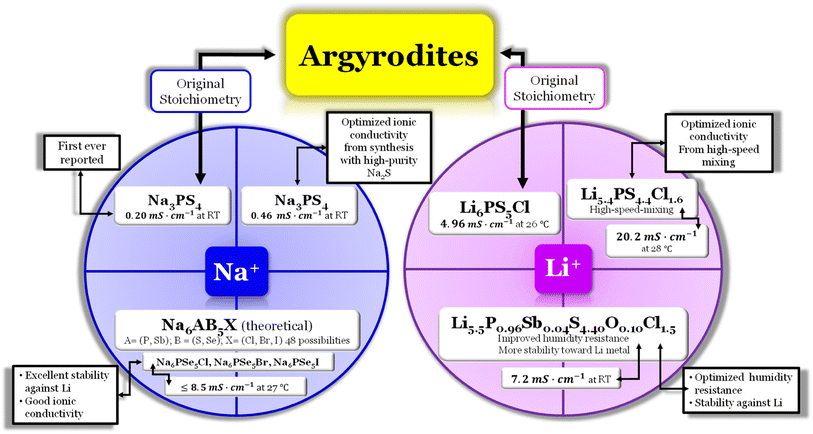 | ||
Fig. 6 Argyrodite summary scheme, Li6PS5Cl;14 Li5.4PS4.4Cl1.6;30 Li5.5P0.96Sb0.04S4.40O0.10Cl1.5;83 Na3PS4,84,85 and Na6AB5X, A = (P, Sb), B = ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (S, Se), and X = (Cl, Br, I).86 (S, Se), and X = (Cl, Br, I).86 | ||
In a recent study30 the Li-argyrodite electrolyte Li5.4PS4.4Cl1.6 was synthesized using high-speed mixing. This electrolyte demonstrated an astonishingly high ionic conductivity of 20.2 mS cm−1 at 28 °C, Fig. 2 and 6, the highest reported value for a lithium argyrodite. The highest reported ionic conductivity for the standard high-energy ball milling, Fig. 6, is 9.4 mS cm−1.33 The study by Chen et al.30 introduced a cost-effective and efficient method known as high-speed mixing, which utilizes an affordable consumer-grade commercial mixer. The high-speed mixing process enables rapid material mixing, producing more than 500 g per batch of LSPCl solid electrolyte. In contrast, the traditional high-energy ball-milling method is limited to 50 g per batch. Notably, the high-speed mixing technique is both energy-efficient and highly effective.
But how does this high-speed mixing technique affect the observed high ionic conductivity?
Using the ultra-high speed mixing preparation process, no obvious grain boundary was observed in the cross-sectional microstructure, which is one of the main factors for the reported high ionic conduction. This presents an effective mixing method for the mass production of Li5.4PS4.4Cl1.6 solid electrolyte. The authors also noted that an all-solid-state electrolyte cell containing graphite/LPSC-mixing/NMC622 delivered an outstanding discharge capacity of 165 mA h g−1 at C/10 and a coulombic efficiency of 82.4%.
Despite the numerous advantages offered by the conventional argyrodite electrolyte, concerns have been raised due to its vulnerability to atmospheric air and its limited structural and electrochemical stabilities. Nevertheless, completely replacing sulfur with oxygen in the argyrodite structure has significantly reduced ionic conductivity,17 indicating that this approach may not be the ideal solution. However, an alternative worth exploring involves doping the argyrodite structure with oxygen (Fig. 6). This approach combines the best attributes of sulfur and oxygen, leading to meaningful results.89
Hwang et al.89 investigated the substitution of oxygen (O) by sulfur (S) in Li6POxS5−xBr0.5Cl0.5 SEs to comprehend the underlying mechanisms and improve the stability of these materials. In his study, the author combined first-principles calculations and electrochemical experiments, spanning from bulk to surface models. Moreover, the author developed systematic experimental investigations to explore the impact of oxygen substitution on suppressing/reducing structural decomposition. The materials were synthesized and thoroughly characterized. The goal of doping the sulfide electrolyte with oxygen is to increase the resistance to moisture absorption, delaying phase decomposition. However, what is the mechanism underlying this effect? To answer this question, these electrolytes' atomic and electronic structures were calculated from bulk to surface. The theoretical analysis determined that the introduction of oxygen causes a more noticeable contraction of the lattice constants compared to the substitution of halogen elements. This suggests that replacing sulfur (S) with oxygen (O) significantly impacts the chemical bonding between isovalent chalcogens, leading to stronger electrostatic bonding between O and Li ions. This strong bonding is closely associated with structural stability. Following this hypothesis, the authors studied the effect of the introduction of oxygen in the electrochemical environment of the electrolyte. The latter realization was made by considering that oxygen has a superior electronegativity to sulfur.
A new study by Wei et al.83 described the synthesis of a chlorine-rich lithium argyrodite, Li5.5P0.96Sb0.04S4.40O0.10Cl1.5, which demonstrated enhanced stability in the presence of air and lithium-ion stability (Fig. 2 and 6). The reported ionic conductivity of this compound is 7.2 mS cm−1 at RT, slightly lower than that of the Li5.5PS4.5Cl1.5 electrolyte that exhibits 9.4 mS cm−1 at RT. However, it was observed that when both electrolytes were exposed to moisture, the ionic conductivity of Li5.5PS4.5Cl1.5 decreased significantly to 1.1 mS cm−1, while the Li5.5P0.96Sb0.04S4.40O0.10Cl1.5 electrolyte showed a comparatively higher ionic conductivity of 3.6 mS cm−1. Furthermore, a comparison of the X-ray diffraction (XRD) spectra revealed that the Li5.5PS4.5Cl1.5 electrolyte exhibited weakened diffraction peaks and the presence of various impurity phases when exposed to open air for 20 minutes. In contrast, the Li5.5P0.96Sb0.04S4.40O0.10Cl1.5 electrolyte displayed improved stability with fewer impurity phases, indicating its superior moisture resistance compared to the bare Li5.5PS4.5Cl1.5 electrolyte. The introduction of the Sb element helped enhance the stability of the electrolyte towards lithium metal.
The compound known as sulfur argyrodite is commonly found in Li+-ion conducting electrolytes. However, there have been reports of Na+-ion argyrodite electrolytes as well (Fig. 6). In 2012, Hayashi et al.84 reported the synthesis of Na3PS4 as a superionic glass-ceramic electrolyte for the first time, displaying an ionic conductivity of 0.2 mS cm−1 at RT. In 2014, the same author reported the synthesis of the same electrolyte with an improvement in the ionic conductivity of 0.46 mS cm−1 at RT.85 The improvement was a result of an optimization during the synthesis mode. The author synthesized Na3PS4 in the cubic phase directly via mechanical milling using a highly pure Na2S reagent; with this, the authors could reduce the reaction time necessary to produce the glass ceramic effectively. This glass–ceramic electrolyte was synthesized by milling 75 mol% Na2S and 25 mol% P2S5 for 1.5 hours and subsequent heat treatment at 270 °C for 1 hour, as reported in ref. 84. This method reduces the reaction time and facilitates the production of glass ceramics. Moreover, in this study, the author also synthesized an all-solid-state cell containing Na15Sn4/Na3PS4/NaCrO2. The cell was tested electrochemically at RT and displayed an average capacity of 60 mA h g−1 of NaCrO2 for 15 cycles.
Following the previous reports, in 2016 De Klerk and Wagemaker90 conducted a study to comprehend the diffusion mechanism in Na3PS4 and explore potential ways to enhance Na+-ion conductivity. Na3PS4 is known to exist in two distinct phases, cubic and tetragonal. However, the differences between these phases are small; the tetragonal phase is tetragonally distorted from the cubic phase.90 The main difference between these two structures lies in the positioning of sodium within the crystal. Regardless of whether both phases are synthesized similarly, they display similar ionic conductivity. A significant boost in ionic conductivity is observed when transitioning from the crystalline to the glass–ceramic form of the cubic phase, increasing 30 times the ionic conductivity. The introduction of halogen dopants plays a crucial role in enhancing ion conductivity. This effect is attributed to a significant increase in the concentration of Na+ vacancies, which is vital to microscopic diffusion. The role of temperature is also an essential factor in Na+-ion diffusion. In this study, the authors90 conducted molecular dynamics simulations to investigate the effects of the lattice parameter increase on the conductivity of cubic Na2.50PS4 and Na2.94PS4 at 252 °C. Considering a 1% expansion in lattice parameters, corresponding to a 3% volume expansion, the conductivity increased by 10% for Na2.94PS4 and 17% for Na2.50PS4, highlighting the significant impact of lattice expansion on conductivity when the temperature increases.
In 2020, Ouyang et al.,86 conducted research utilizing computational simulations to explore the discovery of halogen-substituted Na+-argyrodites. In this study, the author gained insights into the necessary conditions to achieve high ionic conductivity in Na+ argyrodites, Fig. 6. This investigation focused on the phase stability, electrochemical stability, and ionic conductivity of 48 potential Na-based argyrodites. In the Na+-based argyrodite Na6ACh5Hal, A represents a pnictogen atom P or Sb, Ch is typically a chalcogenide atom such as S or Se, and Hal is a halogen element, similar to its Li+ counterpart (Fig. 6). Regarding the phase stability, the authors concluded that the formation of the SbS4 polyanion in Na+ argyrodites occurs more favorably compared to the PS4 polyanion. The halogen element Hal had minimal impact on the electrochemical stability or the decomposition phases, considering the established limits imposed by the polyanion and chalcogen elements. Na+ argyrodites are generally electrochemically stable within the potential range of 1–2 V vs. Na/Na+, which means that the lower energy of the conduction band of Na+ argyrodites varies from −1.73 ≤ Ec (eV) ≤ −2.73 where E0 = 0 eV is the energy of the electrons at rest in a vacuum. The latter value for the lowest energy of the conduction band is shown to agree with the equivalent value for the Li+ argyrodite, LPSCl, calculated herein and shown in Fig. 3a. The previous limits, as already mentioned, are imposed by the pnictogen element, which reduces from +5 to +3 for potentials above the stability window for E > EC and by the chalcogen element since it oxidizes for values of potentials lower than the argyrodite stability window E < EV86 (Fig. 4). Furthermore, a comparison of stability windows revealed that Na–Sb–S(Se)–Hal systems have a narrow electrochemical window, whereas Na–P–S(Se)–Hal systems generally possess a wider electrochemical window.86 When considering the ionic conductivity, the halogen element has a dominant role since the occupancy of the halogen, especially in a sulfide-based system, deeply affects the ionic conductivity. In contrast, the ionic conductivity in selenide-based systems remains similar, regardless of the halogen occupancy. The compression effect generated by halogen substitution is less significant in selenide systems, which generally leads to good ionic conductivity.86 Ouyang et al.86 concluded that among the predicted Na+ argyrodites, the compositions within the Na–P–Se–Hal (Hal = Cl, Br, or I) system demonstrated excellent stability and ionic conductivity.
1.6. Antiperovskites
Recently, a new type of structure called antiperovskites has been receiving increased attention in inorganic material research. Antiperovskites have the same structure as perovskites. However, they adopt a reversed ionic arrangement, which means unique anion-centered cubic units in antiperovskites compared to the conventional cation-centered ones in perovskites. The cation position in the antiperovskite causes significant differences in these structures, providing a distinct local environment for mobile ions and altering their mobility. The first time ionic conductive antiperovskites with X3BA structures were reported dates to 1960 when Reuter et al.92 reported the Ag3SI compound with Ag+ as a mobile cation. In 2012, Zhao et al. synthesized and designed the first Li+ conducting X3BA shape antiperovskites.93 In the antiperovskite formula X3BA, X is a cation and A and B are different-sized anions. The high-temperature superionic conductivity of NaMgF3 perovskites inspired the discovery of the ionic conductivity of Li-rich antiperovskites (LIRAP). The electronically inverted antiperovskite Li3OHal (Hal = Cl, Br, I) allowed Li+ ionic conductivity like the F− superionic conductivity in NaMgF3. However, perfect X3BA antiperovskite structures are considered a disadvantage for ionic conduction due to the lack of intrinsic defects that would work as charge carriers in ionic conduction.94 A variety of methods for defect engineering, such as mixing, doping, and depletion by doping, for example, with divalent ions such as Ba2+, were proposed theoretically in ref. 94. Following this study, Braga et al.29 also reported a series of divalent cation-doped Li3OCl glass electrolytes, Li3−2xMxOCl with M = Mg, Ca, Sr, Ba, synthesized by water-mediated synthesis followed by a heat treatment to remove the solvent. These latter electrolytes are not antiperovskites anymore as they are glassy-amorphous, disordered materials.In solids, as explained before, ion conduction occurs by ion hopping from one lattice site to another by vacancy mechanisms. The rate of ion transport in a lattice is dictated by diffusivity and concentration of vacancies mediating transport. Glassy materials are usually associated with high ionic conductivity because their open structures facilitate the hoping process.
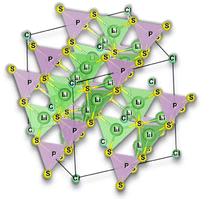
In the Li3OCl crystalline allotrope, the antiperovskite structure, the pattern followed is the following: (1) the Cl−occupies the center atom of the cube−; (2) the O2− occupies the center of the octahedron; (3) the Li+ occupies the vertices of the octahedron, making it a Li+-rich structure, Fig. 7. Doping this structure with higher valence cations such as Ba2+ and Ca2+ creates vacancies in the cation sublattice, one per each Ba2+ that replaces two Li+. This substitution lowers the activation energy for Li+-ion diffusion as the formation of vacancies is unnecessary or assured at synthesis.
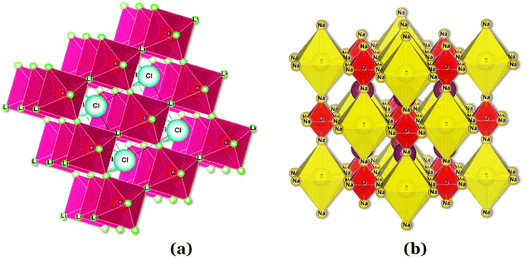 | ||
| Fig. 7 Antiperovskite electrolytes structures: (a) Li3OCl;29 (b) Li6SO(BH4)2;91 CIF files: ref. 53–66. | ||
Of all the reported electrolytes,29 the one that displayed better results was the one doped with the Ba2+ cation; the barium ion has a larger doping ion radius, resulting in a higher anisotropy of the lattice, which favors a higher ionic conductivity. The glassy electrolyte Li2.99Ba0.005OCl obtained a ground-breaking ionic conductivity of 25 mS cm−1 at 25 °C. After this study, Braga et al. synthesized analogous Na+ and K+ electrolytes.28 The Na2.99Ba0.005OCl and K2.99Ba0.005OCl electrolytes, synthesized as glass materials, displayed an astonishing ionic conductivity of 133 mS cm−1 and 155 mS cm−1 at RT. The high ionic conductivity reported in these electrolytes is attributed to their ferroelectricity driven by the mobility of the ions and the electrolytes' semiconductor nature with surface-protected states as in higher-order topological insulators that contribute to the fast polarization of the electrolytes. These concepts will be further discussed in detail in Section 3.1.
Recently, a structural modification of Li+/Na+ antiperovskite electrolytes has been proposed with the introduction of large polyatomic units to replace single ions on crystallographic sites. In 2017, Fang et al.95 developed a simulation that allowed them to propose a new Li+ antiperovskite structure composed of BH4− polyatomic ions in A-sites (i.e., Li3O(BH4)). BH4− is commonly known as a super-halogen, which has been suggested to replace halogen ions due to their similar chemistry but stronger electron affinity when compared to halogens. In 2019, Sun et al.35 synthesized a sodium electrolyte containing BH4− polyatomic ions into an X3BA-type antiperovskite structure for the first time, Na3O(BH4), from a solid reaction between Na2O and NaBH4 mixtures. This material was identified as having an antiperovskite structure and exhibiting an ionic conductivity of 4.4 mS cm−1 at RT and additionally displayed a low activation energy of 0.25 eV. Since the first synthesis reported for this electrolyte, other attempts to synthesize this double antiperovskite have been performed. In 2020, Ahiavi et al.96 reported the mechanochemical synthesis of the Na3O(BH4) electrolyte; however, the reported ionic conductivity was seven orders of magnitude inferior to that of the one proposed by Sun et al.35 The author explained that the hot-pressing pellet method used in ref. 35 could alleviate the effects of blocking grain boundaries, improving the ionic conductivity. Further research is still necessary to determine which synthesis method enhances the characteristics and nature of this electrolyte.
Recently Tsai et al. reported the synthesis of double paddle-wheel sodium amide borohydride Na3−xO1−x(NH2)x(BH4).97 The electrolyte contains two clusters of anions, the super halogen BH−4 and the amide cluster anion NH−2. They can incorporate various ionic substitutions, including multiple cluster anions. This characteristic makes them highly versatile for investigating and understanding the paddle-wheel phenomenon. The paddle-wheel effect refers to the correlated rotations of cluster anions, enabling more accessible cation translation with reduced energy barriers and thereby enhancing cation mobility. Antiperovskites are appealing for studying paddle-wheel effects due to their ability to accommodate a wide range of ionic substitutions, including multiple cluster anions. The Na3O(BH4) electrolyte already discussed corresponds to a single paddle wheel system, whereas Na3−xO1−x(NH2)x(BH4) corresponds to a double paddle wheel system. The authors verified97 that for x = 1 Na2(NH2)BH4 has a low activation energy of 0.268 eV, and when x = 0.5, the ionic conductivity is a hundred times greater than the extrapolated conductivity at x = 1.
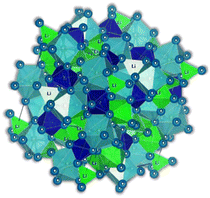
Another common structural modification performed on X3BA antiperovskite is the formation of double antiperovskites. Islam et al.91 reported the first synthesis of a super-halogen Li-rich double antiperovskite Li6OS(BH4)2 as a solid electrolyte. The synthesis consisted of a 3-step process starting with ball milling and liquid phase processes, followed by heat treatment at 380–400 °C and water removal under high vacuum to promote the creation of the Li6OS(BH4)2 product, Li2O + Li2S + 2Li(BH4) → Li6OS(BH4)2.91,98 In the study,91 the band gap of the electrolyte was determined to be 4.03 eV. Furthermore, a symmetric cell was fabricated as Li/Li6OS(BH4)2/Li; this cell is reported to have a long cycling stability of about 3000 h at 60 μA cm−2 current density, even though the increment of the current density seems to reduce the cycling stability. The crystal structure of Li6SO(BH4) has been found to stabilize in the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase91 which is consistent with the antiperovskite structures of Li3O(BH4) and Li3S(BH4) but different from that of Li3OCl whose cubic crystalline structure belongs to the perovskite conventional Pm
m phase91 which is consistent with the antiperovskite structures of Li3O(BH4) and Li3S(BH4) but different from that of Li3OCl whose cubic crystalline structure belongs to the perovskite conventional Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (Table 1). Moreover, this electrolyte exhibits exceptional mechanical stability, with a bulk modulus of 128.5 GPa. The combination of these properties renders this double perovskite suitable for ensuring a safe operation in all-solid-state ASS technologies.
m space group (Table 1). Moreover, this electrolyte exhibits exceptional mechanical stability, with a bulk modulus of 128.5 GPa. The combination of these properties renders this double perovskite suitable for ensuring a safe operation in all-solid-state ASS technologies.
1.7. Halide electrolytes
Classifying inorganic electrolytes considering the dominant element is also possible. Sulfide and oxide electrolytes are the most studied; however, several challenges must be considered before their employment in ASSBs. The stability of oxide electrolytes in the presence of air and their excellent electrochemical and oxidation stability are noteworthy. However, they suffer from poor ionic contact with electrode materials and cannot prevent the infiltration of liquids or polymer electrolytes.104 On the other hand, sulfide electrolytes offer a significant advantage related to their high Li+-ion conductivity, surpassing even that of liquid electrolytes (Fig. 2). Nevertheless, these electrolytes are highly susceptible to moisture, leading to detrimental hydrolysis and the release of toxic H2S. This drawback poses a significant obstacle to the widespread use of sulfide electrolytes in large-scale applications. In addition to these problems, sulfide electrolytes are usually expensive.To address these challenges, a new class of solid electrolytes containing halogen elements has emerged as a promising alternative. Halide electrolytes capitalize on the unique properties of halogen elements compared to elements such as S and O. The monovalent halogen anion exhibits a weaker interaction with Li ions than the divalent S and O, resulting in faster Li-ion conduction. Moreover, the larger radius of halogen anions leads to longer ionic bonds and increased polarizability in the electrolytes, facilitating the migration and plasticity of Li+-ions.91,105
Most halide electrolytes show a general formula, LiaMHalb, where M = Y, Er, Yb, In,…, Hal = F, Cl, Br, and I. In this subsection, the analysis is mainly focused on electrolytes based on chloride ions as the halogen element. This path was chosen considering several factors already explained in this section's introduction.
Selecting the proper central element M is fundamental to designing halide SSEs successfully. Halide electrolytes can be divided into three classes, considering the central element: (1) group 3, Li3YCl6,46 Li3ErCl6,47 and Li3YbCl6;100 (2) group 13, LiAlCl4,106 LiGaCl4,99 and Li3InCl6;41 (3) divalent metals: (1) Li2ZnCl4 standard spinel structure at RT;103 (2) Li2ZnCl4 olivine structures;103 (3) Li2FeCl4 inverse spinel structure102 and (4) Li6FeCl8 Suzuki structure,101Fig. 8. Considering the group 3 and 13 of halogen electrolytes, it is possible to highlight three structures: (1) orthorhombic (Pna21), (2) monoclinic (P121/c1), and (3) trigonal (P321). The trigonal and orthorhombic structures are based on the hexagonal closed-packed (hcp) anion arrangement, and the monoclinic structure is based on the cubic closed-packed (ccp) anion arrangement, respectively. The ccp structures are usually found in relatively large anionic compounds, such as Cl− and Br−, or relatively smaller metal cations. Regarding divalent metal electrolytes, the reported structures are (1) olivine, (2) spinel, (3) spinel inverse, and (4) Suzuki; however, these structures are usually associated with lower ionic conductivity electrolytes.
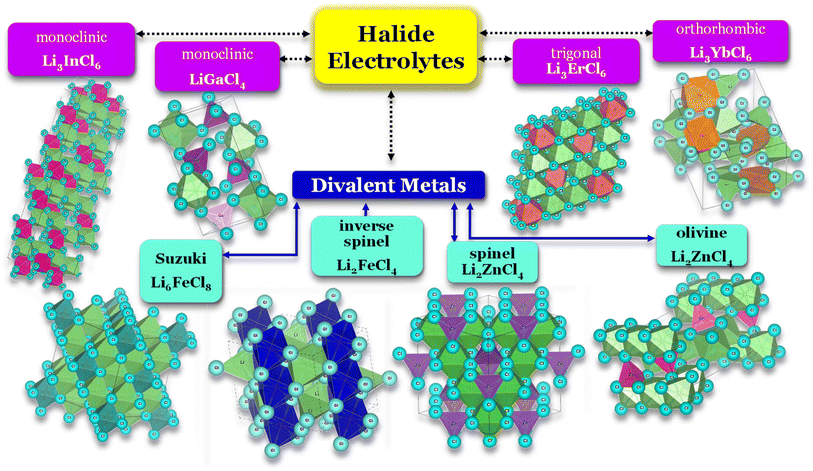 | ||
| Fig. 8 Halide electrolytes LixMHaly, where M = Ga, In, Er, Yb or divalent metals Fe and Zn and Hal is a halogen atom. Hal = F, Cl, Br, I. Li3InCl6,41 LiGaCl4,99 LiErCl6,47 Li3YbCl6,100 Li6FeCl8,101 Li2FeCl4,102 and Li2ZnCl4.103 CIF files: ref. 53–66. | ||
The first ionic conduction was detected on lithium halide electrolytes in 1930 with the synthesis of LiHal (Hal = F, Cl, Br, I).107 However, the electrolytes had low ionic conductivities, with the maximum being 0.001 mS cm−1 at RT.107 Only in 2018, this class of electrolytes gained the interest of the scientific community when, for the first time, Tetsuya Asano et al.46 mechanochemically synthesized Li3YCl6 LYC using a stoichiometric mixture of LiCl and YCl3. LYC electrolyte consists of a hexagonal close-packed (hcp)-like anion arrangement structure, where yttrium resides at the octahedral sites, and yttrium halides display high stability octahedra YX63−. The ionic conductivity of the LYC electrolyte is 0.51 mS cm−1 at RT. The previous conductivity was found to be a revelation since it was observed in a close-packed anion sublattice material; the latter varies from the source of high Li+-ion conductivity found for sulfide or oxide lithium-ion conductors. The electronic conductivity of LYC is 2.8 × 10−6 mS cm−1 which corresponds to the upper characteristic values of electronic conductivities of an insulator46 and agrees with our data for the band gap and DOS in Fig. 3 and 4. The activation energy was determined to be 0.40 eV.46 In 2021, Roman Schlem et al.108 developed a study to assess the lithium sub-structure in lithium conducting halides via temperature-dependent neutron diffraction of the LYC electrolyte. In this study, the author considered two different synthesis methods: ball milling and ampule synthesis. It was verified that for the LYC, the mechanochemical synthesis led to a local distortion of the structure, therefore improving the ionic conductivity. Large disorders motivated by a frustrated energy landscape enhance ionic transport. The disorder in the LYC electrolyte affects the polyhedral volumes of Li+ and their directional thermal amplitude. Sendek et al.109 performed a DFT simulation guided by a machine learning-based approach to find new fast ionic conductors. From this study, it was concluded that Li3ErCl6 was an acceptable candidate to achieve good ionic conductivity and was expected to demonstrate an ionic conductivity of 3 mS cm−1 at 25 °C. However, when synthesized via ball milling and annealing, this electrolyte only displayed an RT ionic conductivity of 0.3 and 0.02 mS cm−1, respectively.47 This electrolyte shows a trigonal structure P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1,109Table 1, Fig. 2–4. Similarly to what was reported for the LYC electrolyte, the ionic conductivity is reduced with increasing crystallinity during subsequent annealing processes.109
m1,109Table 1, Fig. 2–4. Similarly to what was reported for the LYC electrolyte, the ionic conductivity is reduced with increasing crystallinity during subsequent annealing processes.109
Of all the halide electrolytes, the one that showed a higher conductivity at RT was Li3InCl6. This electrolyte was first synthesized by a mechanochemical method in 2019 by Li et al.,82 which obtained an ionic conductivity of 1.49 mS cm−1, surpassing all its predecessors. Additionally, this electrolyte exhibited good stability toward conventional oxide cathode materials and good stability in air. The breakthrough of this electrolyte study arose when Li et al.82 proposed a water-mediated synthesis technique to prepare Li3InCl6 (ref. 41) (Fig. 5d). The obtained RT ionic conductivity was 2.04 mS cm−1 (Fig. 2).
All the previously reported halide electrolytes have a setback to mass production; the middle element is usually a rare earth metal, leading to high production costs and compromising the commercialization of halide-based solid-state batteries.
In 2021, Kwak et al. reported the first cost-effective halide SSE, Li2ZrCl6.45 This electrolyte was prepared via ball milling and heat treatment (Fig. 5a). The use of different synthesis methods introduced considerable variations in the crystal structure and ionic conductivity. When prepared by heat treatment, the electrolyte presented a monoclinic structure with poor Li+ conduction 0.006 mS cm−1 at 30 °C. When it was synthesized by ball milling, it showed a hcp structure with a Li-ion conduction of 0.4 mS cm−1 at 30 °C. These results are atypical in the halide electrolyte world; the monoclinic structure is usually associated with fast ionic conduction, for example, in the Li3InCl6 electrolyte. Zirconium is an abundant metal on Earth, approximately an order of magnitude greater than yttrium or scandium and more than three orders of magnitude greater than indium.110 The cost to produce most no-Li-containing chlorides needed to synthesize Li3MCl6 is usually above $1000 per kg, completely offsetting the cost-effectiveness of the LiCl precursor is approximately ($5.88 per kg).110 Kai Wang et al.110 reported the synthesis of Li2ZrCl6 electrolyte, using LiCl and ZrCl4 as precursors. The cost of the raw material for Li2ZrCl6 at a thickness of 50 μm is approximately $1.38 per m2, which is significantly lower than the cost of Li3YCl6 ($23.05 per m2).110 Li2ZrCl6 is considered the most economical chloride system based on the existing literature. Moreover, its cost is well below the $10 per m2 threshold required for cost-competitive all-solid-state batteries. Additionally, the electrolyte was reported to be moisture-resistant at 5% relative humidity and displayed an ionic conductivity at room temperature of 0.81 mS cm−1.
Until now, solely lithium halide electrolytes have been introduced. Nevertheless, some sodium halide analogues have already been synthesized. The primary challenge encountered in synthesizing sodium-based halides lies in achieving a significant ionic conductivity while preserving the thermal stability of the electrolyte.
In 2020, Schelm et al.111 reported successfully synthesizing Na2.4Er0.4Zr0.6Cl6 with an ionic conductivity of ∼0.035 mS cm−1 at RT. The research centered around synthesizing the Na3−xEr1−xZrxCl6 compound series, exploring different values of 0 ≤ x ≤ 1 to identify the optimal stoichiometry that maximizes the electrolyte properties. The study investigated the case where x = 0 corresponds to Na3ErCl6. The analysis revealed that Na3ErCl6 crystallizes with a monoclinic structure containing ErCl63−octahedral frameworks at the corners of the unit cell. Each NaCl65−prism is connected by an edge or corner sharing arrangement with another NaCl65− octahedron. The obtained ionic conductivity for the Na3ErCl6 electrolyte at approximately 25 °C was 10−6 mS cm−1. In the case where x = 1 corresponds to the electrolyte Na2ZrCl6 displaying a trigonal crystal structure, the maximum reported ionic conductivity is 3.5 × 10−7 mS cm−1. When the incorporation of Zr4+ occurs, the structure adopted by Na3−xEr1−xZrxCl6 is monoclinic, as already discussed. Introducing smaller Zr4+ ions reduces lattice parameters. Additionally, the substitution of Er3+ by Zr4+ introduces sodium vacancies, leading to a tuneable ionic conductivity in the series of solid solutions Na3−xEr1−xZrxCl6, which in turn provides a promising step toward halide-based sodium-ion conductors.
In the realm of yttrium metal sodium halide electrolytes, a recent contribution by Xu et al.112 presented a new electrolyte, Na3Y2Cl9, designed using a building block method. A 3-step structure was proposed to create new structures incorporating Na+ ions and (Y2Cl9)3− units. Theoretical analysis conducted in the study demonstrates that this electrolyte exhibits a low energy barrier for ionic diffusion, leading to an ionic conductivity of 0.1 mS cm−1 at RT. Although the ionic conductivity may not be considered exceptional, the electrolyte demonstrates excellent chemical and electrochemical stability. Additionally, the calculated band gap for this electrolyte was determined to be 7.34 eV. Both agree with the wide herein simulated band gap of 5.2 eV and lower energy value for the conduction band EC = −0.11 eV (for E = 0, the electrons at rest in a vacuum) for Na3YCl6 (Fig. 3a and b). The lowest energy for the EC of Na3YCl6 is 1.62 eV higher than Na0; therefore, Na3YCl6 is supposedly very stable against Na-metal, although with such a reduced electron affinity energy that it may decompose by being reduced from the surface in contact with a reductant.
Using DFT simulations, Liu et al.113 proposed a new spinel chloride sodium electrolyte, Na2Y2/3Cl4. This electrolyte is expected to exhibit a high ionic conductivity of 0.94 mS cm−1 at RT with a low activation energy barrier for Na+ ion diffusion of 0.29 eV while possessing a semiconductor energy gap113 from −3.85 to −0.68 eV, E0 = 0 electrons at rest in a vacuum, Eg = 3.17 eV; Fig. 4 shows the energy concepts.
Changing to indium, in April 2023, Zhao et al.114 reported the controlled synthesis of Na2+xZr1−xInxCl6 electrolyte. The study was motivated by the limited number of reports on sodium halides, none of which discussed sodium halides containing indium. The authors investigated a series of solid solutions of Na2+xZr1−xInxCl6 (0 ≤ x ≤ 1). The most promising candidate from this study was the electrolyte for which x = 0.5, N2.5Zr0.5In0.5Cl6, with an ionic conductivity of 0.066 mS cm−1 at RT.
Even though some promising improvements have been made in the production of halide electrolytes, the ionic conductivities remain considerably low when compared to other electrolytes, such as sulfide electrolytes. The advantages of doping existing electrolytes with halide elements such as chlorine are clear. A new class of electrolytes called oxyhalides seems to be the most promising. The previously discussed electrolytes and two recently reported ones, LiTaOCl4 and LiNbOCl4,31 are plotted considering their optimized stoichiometry and reported ionic conductivities (Fig. 2).
Both oxide and halide electrolytes show considerably lower ionic conductivities than sulfide-based electrolytes. Overall, oxyhalides display groundbreaking ionic conductivities, highlighting the Na+ and K+-glass electrolytes that have been reported to display self-charging behavior due to their ferroelectric nature28,115,116 (Fig. 9).
2. Towards the future: quantum power harvesting and storage
Although perhaps the future will bring diversity into energy harvesting and storage-tailored devices, expensive solutions, such as the current rule in the switching (transistor) world, must be much superior to others to compensate for the extra cost. In the battery field, this means being safe, having high energy and power densities, and having cycle and shelf lives. Solid electrolytes potentially better cover the first two, but being sustainable, permitting high cycle and shelf life, and being affordable are attributes just for a few chosen electrolytes.Ferroelectrics are complex systems based on quantum mechanics principles; they may be protagonists of a disruption in the energy storage realm. Notably, halide-perovskites are being successfully used as photoelectric semiconductors in solar cells and may achieve ∼35% cell efficiency today,117 some with ferroelectric heterojunctions with BaTiO3.118 Ferroelectrics, for example, HfO2, may also recently be found in field effect transistors (FETs) for a more efficient switch at RT.119
Until now, to the best of our knowledge, the only electrolytes displaying a ferroelectric character, having Li+, Na+, or K+ mobile ions, are LLTO, Na3OCl, K3OCl, and A2.99Ba0.005OCl – glass with A = Li, Na, K with LLTO sub-performing when compared to the others. These ferroelectric electrolytes are glassy-oxyhalides, uniting the best properties previously discussed. They are also inexpensive, especially the sodium-based versions, and are eco-friendly. However, they are hygroscopic, but from our experience, promising sulfides such as LPSCl, compared with A2.99Ba0.005OCl – electrolytes, are slightly more hygroscopic but, worse, release hazardous vapors (e.g., H2S).
As reported hereafter, not only are A2.99Ba0.005OCl – glass with A = Li, Na, K ferroelectric, but they also show other properties such as self-charging and self-cycling based on coherent complex dynamics28,115,116 sustained by internal feedback, picturing Otto cycles in quantum thermal machines such as described hereafter. Therefore, quantum battery solutions are a reality, and they are based on spontaneous polarization of the material driven by the difference in Fermi levels of the electrodes; polarization that, in traditional batteries, was seen as an obstacle.
The caveat of these neophytes is the difficulty in taming their properties driven by what they have best, their complex behavior, and their vast possibility of increasing their energy information even while set to discharge with a load.
Hereafter, the working principles of quantum batteries in their panoply of possibilities will be discussed.
2.1. Ferroelectric devices for harvesting and storing energy
The development of self-charging systems is fundamental to elevating the next generation of electronic devices. These systems will simultaneously display the ability to store energy as well as the ability to harvest energy. Piezoelectric materials are an option to transition the concept of self-charging to reality, specifically when these piezoelectric materials are also ferroelectric materials. The piezoelectric phenomenon occurs in dielectric materials that, when subjected to mechanical stress, can generate charge carriers and polarize (Fig. 9). Under an electrical field, the piezoelectric material undergoes a mechanical deformation or strain.Ferroelectric materials have awakened the scientific community's interest due to their ability to display negative capacitance and, therefore, are expected to overcome fundamental limits of power dissipation in integrated circuits.120 Ferroelectric materials can polarize spontaneously below the Curie temperature, forming permanent dipoles, even when no electric field is applied. However, above the Curie temperature, ferroelectric materials transition into a paraelectric phase with no spontaneous polarization. The negative capacitance (NC) was predicted using the Landau model for ferroelectricity.120 From this model, it is possible to define capacitance as the reciprocal of the second derivative of the potential energy U with respect to the electric polarization charge, 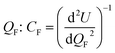 .121 These phenomena have been studied and observed in different harvesting and storage devices. In 2014, Salvatore et al.122 verified experimentally that the negative capacitance phase stability in a field transistor (FET) varies with temperature. The NC region narrows down at high temperatures when approaching the Curie temperature of the ferroelectric material, validating experimentally Landau's theory. In 2015, Khan et al.123 first synthesized a thin epitaxial ferroelectric film displaying negative capacitance. When the applied potential difference is inferior to the coercive voltage (Fig. 9), the capacity is positive, and therefore, the ferroelectric transistor behaves as a simple transistor. However, the authors verified that the ferroelectric switched to negative capacitance when the applied potential difference was superior to the coercive voltage (Fig. 9).
.121 These phenomena have been studied and observed in different harvesting and storage devices. In 2014, Salvatore et al.122 verified experimentally that the negative capacitance phase stability in a field transistor (FET) varies with temperature. The NC region narrows down at high temperatures when approaching the Curie temperature of the ferroelectric material, validating experimentally Landau's theory. In 2015, Khan et al.123 first synthesized a thin epitaxial ferroelectric film displaying negative capacitance. When the applied potential difference is inferior to the coercive voltage (Fig. 9), the capacity is positive, and therefore, the ferroelectric transistor behaves as a simple transistor. However, the authors verified that the ferroelectric switched to negative capacitance when the applied potential difference was superior to the coercive voltage (Fig. 9).
The negative capacitance phenomenon is not limited to transistor technology alone; it has also been observed in the field of batteries. In 2020, Braga et al.116 reported the discovery of negative capacitance in an electrochemical cell that demonstrated the ability to self-charge. The researchers conducted the study using a cell containing two electrodes separated by a ferroelectric oxyhalide glass-electrolyte, previously investigated by the author in ref. 28 and 29. The study established a clear linear relationship between negative capacitance double-layer capacitors and the system's remarkable capacity for self-charging, even when initially configured to discharge with a material load; the cells were set to discharge while maintaining a fixed external resistance. Although the current was set to be negative (discharge direction), the recorded voltage increased and the current consistently remained above zero, indicating the presence of negative resistance alongside a negative capacitance regime. During this period of negative resistance, the battery exhibited self-oscillations, entering a self-cycling regime.
2.2. Topologic insulators for harvesting and storing energy
The theoretical underpinnings of solid-state physics rest on two fundamental pillars: electromagnetism and quantum mechanics. One fascinating concept built on these two pillars is quantum topological materials, highlighting topological insulators (TIs). Studying topological insulators without referring to the quantum anomalous Hall effect is impossible.What are, in fact, topological insulators? A topological insulator is a material whose bulk behaves as an electrical insulator. In contrast, its surface or edges behave as an electrical conductor due to protected surface states, Fig. 10. The scientific community’s interest and potential applications of TIs in electronics, spintronics, and quantum information have driven tremendous efforts to find robust material realizations of TIs. The TI state has already been reported and observed in some materials. Some examples of topological insulator behavior have already been reported: halide perovskites displaying a non-trivial topological insulator phase,127 oxide topological insulators based on the superconductor BaBiO3,128 and the existence of a topological phase in the non-centrosymmetric NaSnBi material.129
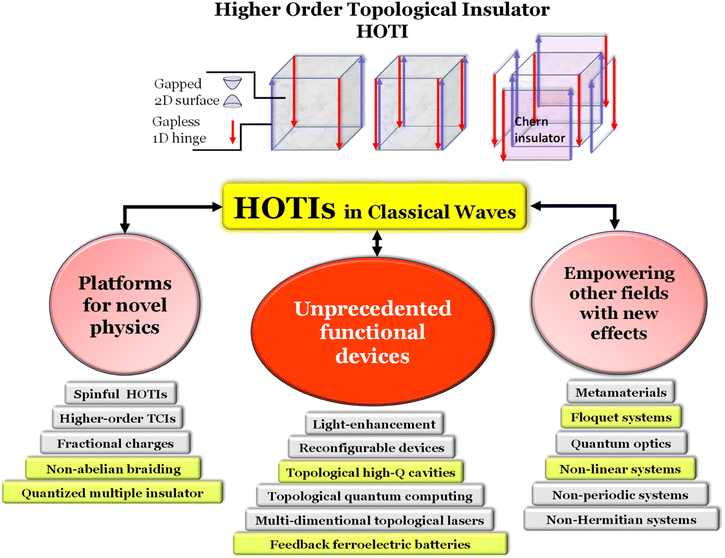 | ||
| Fig. 10 Higher order topologic insulators, HOTIs. From left to right, the arrows in HOTIs indicate chiral hinge currents, pairs of hinge modes running along the corners, and a Chern insulator with Hall conductivity. Below are possible future applications of HOTIs124–126 highlighting possible harvesting and storage coherent systems. | ||
A prominent area of research involves the search for materials displaying ferroelectricity and a topological insulator phase. A ferroelectric topological insulator (FETI) is expected to combine switchable polarization and robust topological surface states. In 2016, Liu et al.130 performed a theoretical study on the cubic halide perovskite CsPbI3 to understand the consequences of the coexistence of ferroelectricity and the nontrivial topology. The cubic halide perovskite under study experiences a paraelectric–ferroelectric structural phase transition under strain. Pressure can also induce a topological phase transition from a standard insulator to a topological insulator in CsPbI3. One of the clear advantages of FETIs over ferroelectric normal insulators (FENIs) is the guaranteed presence of metallic surface states, which can serve as metallic electrodes to create intrinsic short circuit conditions, allowing automatic surface charge dissipation and internal device self-charging feedback. An FETI may, therefore, work as a dual tandem dielectric-electrode with the advantage of reducing the interfacial resistance to the minimum and configuring a one-electrode battery or capacitor where the electrode performs to maximize the potential bias in the cell.
Another interesting study was in 2017 by Monserrat et al. in 2017.131 They reported antiferroelectric topological insulators (AFTIs) in an orthorhombic AMgBi compound where A = Li, Na, K. From this study, the authors started to distinguish three types of AFTIs, depending on which states are topological insulators: (1) type-I AFTIs with an antipolar normal state and polar topological state, (2) type-II AFTIs with an antipolar topological state and polar normal states, and (3) type-III AFTIs with antipolar and polar topological states. From the first principles calculations, the authors determined the conditions under which each material behaves as the most promising candidate. LiMgBi performs better under epitaxial strain, whereas KMgBi performs better under hydrostatic pressure. In the LiMgBi and KMgBi AFTI phases of type I, an electric field could induce a topological phase transition by switching between the antipolar and polar states. The author concluded the crucial necessity of undertaking experimental investigations to explore these systems, particularly studying KMgBi under standard or moderate pressure and examining LiMgBi under epitaxial strain. Such experimental exploration may contribute valuable insights to our understanding of these materials.
High-order topological insulators (HOTIs) (Fig. 10) are a type of topological insulator that exhibits topologically protected states on their surfaces and on their boundaries in higher dimensions. This means that in addition to surface states, HOTIs possess robust and protected states along their hinges, corners, or other high-dimensional boundaries.
The unique properties of HOTIs make them attractive for potential applications in energy harvesting and storage devices. Here are a few ways HOTIs can be related to such devices:121 (1) HOTIs can be utilized for efficient energy harvesting due to their topologically protected edge or boundary states. For example, hinge states in 3D HOTIs can carry current and be engineered to exhibit specific energy-momentum dispersion relations. By properly designing the device geometry and connecting appropriate electrodes, energy can be extracted from external sources, such as heat or mechanical vibrations, by converting these topologically protected states; (2) energy storage: HOTIs can also be relevant for energy storage applications. Their topologically protected states can facilitate the efficient transport and storage of charge carriers, enhancing the performance of energy storage devices such as batteries or supercapacitors. By leveraging the unique electronic properties of HOTIs, it may be possible to design more efficient and stable energy storage systems.
2.3. Quantum or condensed matter batteries
The primary function of a battery is to be a reservoir of energy. Currently, technologies are evolving towards smaller devices, and batteries power these devices and, therefore, are needed to follow this tendency. However, as the unit cell of a battery approaches the size of a molecule or atom, quantum effects must be considered. The study of quantum batteries was first introduced in ref. 129 in 2013 as a small quantum mechanism that temporarily stores energy. These batteries are described as d-dimensional quantum systems without degenerated energy levels, as demonstrated in Fig. 11. Work can be reversely extracted and deposited at energy levels. As a result, the time evolution of the battery will be described by unitary operations. , of the wave function of the battery can be chosen to be d-dimensional,132 with a Hamiltonian,
, of the wave function of the battery can be chosen to be d-dimensional,132 with a Hamiltonian,  , written in its base |j〉 as
, written in its base |j〉 as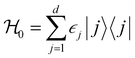 | (2) |
 are the eigenvalues of |j〉 and |j + 1〉, respectively. This condition assumes no degeneracy.
are the eigenvalues of |j〉 and |j + 1〉, respectively. This condition assumes no degeneracy.
Considering a Hermitian operator field 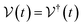 , which is used to extract energy and is only different from zero for time t, so that 0 < t < τc, where τc is the charging time. This field allows for a temporal evolution of the system, which is described by the Schrödinger equation, where the Hamiltonian,
, which is used to extract energy and is only different from zero for time t, so that 0 < t < τc, where τc is the charging time. This field allows for a temporal evolution of the system, which is described by the Schrödinger equation, where the Hamiltonian,  , will be
, will be  . The general solution for this equation can be given by the unitary operator
. The general solution for this equation can be given by the unitary operator 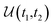 , where a given state |ψ(t1)〉 evolves to the state |ψ(t2)〉, mathematically represented as
, where a given state |ψ(t1)〉 evolves to the state |ψ(t2)〉, mathematically represented as 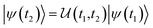 . This operator is the solution for the Schrödinger equation when defined as the time-ordered exponential, with ℏ being the reduced Planck constant,
. This operator is the solution for the Schrödinger equation when defined as the time-ordered exponential, with ℏ being the reduced Planck constant,
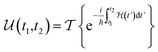 | (3) |
The state |ψ(τc) is then written as,
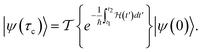 | (4) |
It is possible to describe a state as its density matrix ρ(t) = |ψ(t)〉〈ψ(t)|, making it clear that the value of ρ(τc) is given by
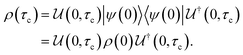 | (5) |
The work extracted from the state is W,
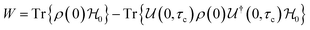 | (6) |
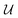 depends on
depends on 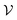 , a controllable variable, it is possible to control
, a controllable variable, it is possible to control 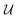 by choosing
by choosing 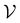 , allowing for the work extracted to be maximized (ergotropy) and defined as
, allowing for the work extracted to be maximized (ergotropy) and defined as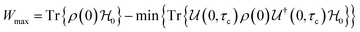 | (7) |
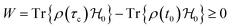 . Conversely, discharging will take the state ρ(t0) to a lower energy state ρ(τd), where τd is the discharging time,
. Conversely, discharging will take the state ρ(t0) to a lower energy state ρ(τd), where τd is the discharging time, 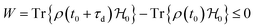 . As shown in the previous section, this can be achieved by applying a
. As shown in the previous section, this can be achieved by applying a 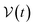 field.
field.
In practice, it is generally preferable to charge a battery quickly, which mathematically means maximizing the power P ∝ 1/t. However, the average work must be considered, as it also needs to be maximized. The way to ensure both P and W are maximized without one being a detriment to the other is by maximizing the function 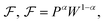 where α is a free parameter 0 ≤ α ≤ 1. Note that for α = 0,
where α is a free parameter 0 ≤ α ≤ 1. Note that for α = 0, 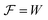 and for α = 1,
and for α = 1, 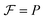 .
.
In ref. 133 some remarks are made: (1) the cyclicity of the process is an important requirement since we are interested in the power; (2) if t → 0, the quantum speed limits, which bond the time evolution by the inverse of the mean energy, would be violated; (3) there are natural constraints to the Hamiltonian that must be incorporated into the analysis. In particular, ref. 133 restricts the trace norm of the Hamiltonian 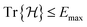 with the gauge convention that states that the lowest eigenvalue of the Hamiltonian is zero.
with the gauge convention that states that the lowest eigenvalue of the Hamiltonian is zero.
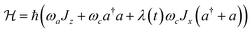 , where parameter ℏωa is the energy between the ground state |g〉 and the excited state |e〉, a and a† annihilates and creates a cavity photon with frequency ωc,
, where parameter ℏωa is the energy between the ground state |g〉 and the excited state |e〉, a and a† annihilates and creates a cavity photon with frequency ωc, 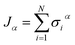 , for α = {x, y, z}, and
, for α = {x, y, z}, and 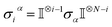 is the Pauli matrix of the i-th term, and
is the Pauli matrix of the i-th term, and  is the identity matrix;
is the identity matrix;  is the step function,
is the step function,  where τc is the charging time.
where τc is the charging time.
However, this model does not take into account the interatomic interactions and the driving field. To include these aspects, ref. 135 proposes a model with new terms in the Hamiltonian that considers those interactions. The two-level systems will be regarded as having infinite-range interactions and are coupled to the single cavity mode via single-photon coupling. The Hamiltonian can be divided into two parts: (1)  the Hamiltonian of the battery and (2)
the Hamiltonian of the battery and (2) 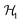 the charging Hamiltonian
the charging Hamiltonian 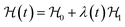 . The two Hamiltonian parts are given by
. The two Hamiltonian parts are given by
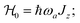 | (8) |
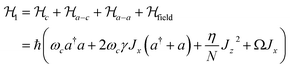 | (9) |
In eqn (9)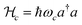 is the Hamiltonian of the cavity,
is the Hamiltonian of the cavity, 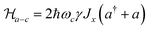 describes the interaction between the atom and the cavity,
describes the interaction between the atom and the cavity, 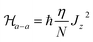 is the interaction between atoms and
is the interaction between atoms and 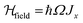 is the Hamiltonian due to the applied magnetic field along the x axis. The parameter ℏωa is the energy difference between the ground state |g〉 and the excited state |e〉, γ is the two-level system cavity coupling strength, η is the atomic interaction strength, and Ω is the driving field strength.
is the Hamiltonian due to the applied magnetic field along the x axis. The parameter ℏωa is the energy difference between the ground state |g〉 and the excited state |e〉, γ is the two-level system cavity coupling strength, η is the atomic interaction strength, and Ω is the driving field strength.
Considering a close quantum system where the N two-level systems are in the ground state and coupled to the single-mode cavity in the N photon Fock state. The initial state of the total system is |ψ(0)〉 = |N〉 ⊗ |g, g, …, g〉.
The battery will start to charge when λ(t) ≠ 0. By defining the density matrix ρ(t) = |ψ(t)〉〈ψ(t)|, the total energy storage at a time t is obtained using 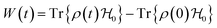 . In these operators' basis, the initial state |ψ(0)〉, can be written as
. In these operators' basis, the initial state |ψ(0)〉, can be written as 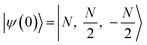 , giving all the two-level systems in the ground state (state of minimal energy).
, giving all the two-level systems in the ground state (state of minimal energy).
The matrix element of eqn (9) can be obtained by proceeding step by step and fixing  , so
, so  . Summing all components, it is possible to obtain the Hamiltonian matrix. It is important to note that the number of photons is neither conserved nor bounded by the Dicke Hamiltonian; thus, it can take an arbitrarily large integer value. In practice, it is necessary to design a cut-off so that Nph > N on the maximum number of photons Nph. In studies136,134 the authors show that excellent numerical convergence can be achieved by selecting the maximum number of photons as Nph = 4N.
. Summing all components, it is possible to obtain the Hamiltonian matrix. It is important to note that the number of photons is neither conserved nor bounded by the Dicke Hamiltonian; thus, it can take an arbitrarily large integer value. In practice, it is necessary to design a cut-off so that Nph > N on the maximum number of photons Nph. In studies136,134 the authors show that excellent numerical convergence can be achieved by selecting the maximum number of photons as Nph = 4N.
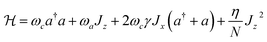 . If η < 0, attractive interactions are being considered, whereas if η > 0, these interactions are repulsive. Additionally, in ref. 135η = 0 means no interactions.
. If η < 0, attractive interactions are being considered, whereas if η > 0, these interactions are repulsive. Additionally, in ref. 135η = 0 means no interactions.
When the battery system is in a weak ultra-strong coupling regime, the light-matter interaction energy is a comparable fraction of the bare frequencies of the uncoupled systems, and the atomic interaction, whether repulsive or attractive, always has a negative impact on the energy stored by the quantum battery. However, the repulsive interaction increases the charging power while attractive interaction decreases it. It is also possible to notice that the atomic interaction grows weaker as the coupling strength increases. When the coupling strength increases to the deep-strong coupling regime, characterized by interaction strengths surpassing the bare frequencies, the energy and charging power of the battery remain largely unaffected.135 The latter shows an interesting feature from the atom–atom and atom–cavity field interactions. It is also shown that the maximum energy stored always has a critical behavior. The critical atomic interaction ηcrit was calculated in ref. 135 as 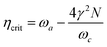 and at the critical point
and at the critical point 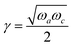 , where the system is in its normal-super radiant phase.
, where the system is in its normal-super radiant phase.
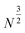 for large N. Therefore, ref. 135 assumes that it is reasonable to consider
for large N. Therefore, ref. 135 assumes that it is reasonable to consider 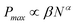 , for this extensive Dicke model. Then, log(Pmax) ∝ α
, for this extensive Dicke model. Then, log(Pmax) ∝ α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N) + log(β), which by linear fitting allows us to obtain α.
log(N) + log(β), which by linear fitting allows us to obtain α.
In the ultra-strong coupling regime, the scaling exponent can be approximately α = 1.8 > 3/2. On the other hand, in the deep-strong coupling regime, the scaling exponent is approximately α = 1.5 = 3/2.135 Regardless of the coupling regime, the external driving field strength increases the maximum charging power of the quantum battery. However, as the driving field strength increases, the advantage of the system's maximum charging power capabilities weakens.
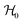 , so that,
, so that, 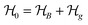 .
. 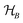 is the Hamiltonian due to the magnetic field
is the Hamiltonian due to the magnetic field 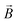 and is defined as
and is defined as 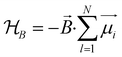 , where
, where  is the magnetic momentum. Assuming
is the magnetic momentum. Assuming  in the −z direction (Fig. 13) and assuming that the magnetic moment of the i-th member of the chain is given by
in the −z direction (Fig. 13) and assuming that the magnetic moment of the i-th member of the chain is given by 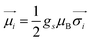 , where gs ≈ 2, μB is the Bohr magneton and
, where gs ≈ 2, μB is the Bohr magneton and 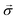 is the vector of Pauli matrices,
is the vector of Pauli matrices,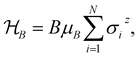 | (10) |
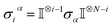 .
.
The second term of the Hamiltonian, 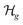 , defines the interaction between different spins,
, defines the interaction between different spins,
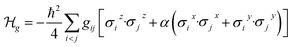 | (11) |
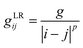 , respectively, where g is the interaction strength and assuming that the spin-chain is ferromagnetic g ≥ 0, p is the decaying power of the long-range interaction.
, respectively, where g is the interaction strength and assuming that the spin-chain is ferromagnetic g ≥ 0, p is the decaying power of the long-range interaction.
Considering a ferromagnetic spin-chain, the ground state |GS〉 can be written as |GS〉 = |↓〉 ⊗ |↓〉 ⊗ … ⊗|↓〉 the tensorial product is obtained N times. All spins are, then, aligned with the  field. In this way, the density matrix of the ground state ρ↓ is ρ↓ = |GS〉〈GS|.
field. In this way, the density matrix of the ground state ρ↓ is ρ↓ = |GS〉〈GS|.
Therefore, the initial energy will be given by 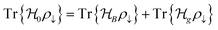 and using σa|↓〉 = −δza|↓〉 having into account that σa is the Pauli matrix for the a coordinate, and δza is only one when a = z and zero in all the other cases.
and using σa|↓〉 = −δza|↓〉 having into account that σa is the Pauli matrix for the a coordinate, and δza is only one when a = z and zero in all the other cases.
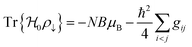 | (12) |
To import energy into the system142 a charging Hamiltonian  was considered, eqn (13). This Hamiltonian is obtained by varying
was considered, eqn (13). This Hamiltonian is obtained by varying  the energy splitting Hamiltonian, eqn (10),
the energy splitting Hamiltonian, eqn (10),
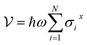 | (13) |
Charging can be time-dependent; despite that, it is possible to consider the simpler case where 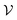 is constant, 0 < t<τc. From eqn (3) yet considering that
is constant, 0 < t<τc. From eqn (3) yet considering that  is constant with time, it is only necessary to use the exponential definition.
is constant with time, it is only necessary to use the exponential definition.
 | (14) |
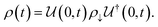 . The work is then obtained using
. The work is then obtained using 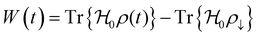 and the charging power using
and the charging power using 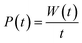 .
.
2.4. Quantum thermal machines
Quantum thermal machines (QTMs) are advanced devices that operate on nanoscale systems, utilizing small two-level system quasi-particles known as qubits. These machines perform thermodynamic cycles and have various applications (Fig. 15). For example, they can function as nano-heat engines,144 leveraging the AC Josephson effect, or serve as quantum thermal thermometers as shown by Hofer et al.145 and transistors by Joulain et al.146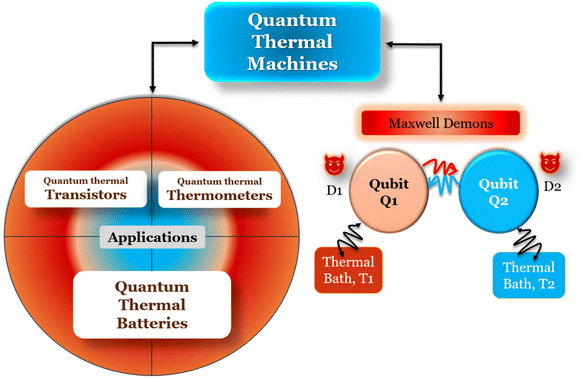 | ||
| Fig. 15 Quantum feedback thermal machines and their applications. Qubits Q1 and Q2 are monitored by D1 and D2, connected to thermal baths T1 and T2. In the case of Maxwell's demons, T1 = T2 = T. The two baths can also have different temperatures148 and work as refrigerators. | ||
One of the most significant challenges in quantum thermal machines is achieving optimal control of open quantum systems; therefore, improving this aspect has a crucial role in developing quantum information technologies. Erdman et al.147 proposed an innovative approach that utilizes reinforcement learning (RL) to optimize the performance of QTMs. RL is a framework in which a computer agent learns and masters tasks through repeated interactions with an environment. The developed study focused on finite-time thermodynamics of QTMs within the Markovian regime, employing a commonly used master equation. The case studies considered were (1) a heat engine based on a two-level system, (2) a refrigerator based on a superconductor, and (3) a heat engine based on a quantum harmonic oscillator.
In the first case, the authors observed that initially, when the agent had no prior experience, it performed random actions, dissipating work into heat baths instead of harvesting. However, the agent learned to control the heat engine over time, resulting in the average power saturating at a maximum positive value. Moving forward, the author considered a second system, which involved a refrigerator based on a superconducting qubit coupled to two resonant circuits acting as heat baths. In this case, unlike the previous scenario, the existence of coherence between instantaneous eigenstates needed to be considered. Similarly to the first case, in the beginning, the agent performs random actions; however, as time moves forward, the agent gains experience saturating the value of the average cooling power to a positive value. The study of the qubit-based refrigerator ended by evaluating the coefficient of performance (COP) at maximum power. From this, it was possible to conclude that the COP at maximum power is 6%; even though this value seems low, on-chip cooling applications typically aim to maximize the cooling power regardless of the efficiency of such a process. To end the study, the authors147 considered a heat engine based on a collection of non-interacting particles confined in a harmonic potential. As in the first case, the agent makes the decision of which bath to couple with the oscillator. As it was observed in the first case, the power is negative for small steps, while it converges to a positive value as the agent gains experience. In this study, the cycle discovered by the agent is similar to the Otto cycle (Fig. 16); however, it possesses some additional features. The crucial difference regarding the Otto cycle is the ramping up of (t) while in contact with the baths, benefiting simultaneously from exchanging heat and modulating instead of achieving this in two separate systems.
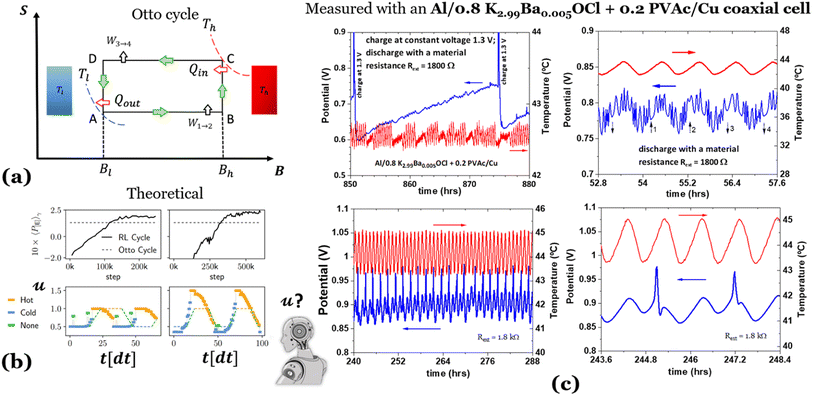 | ||
Fig. 16 Otto cycle. (a) Entropy S vs. applied magnetic field B. Tl – low reservoir temperature; Th –high reservoir temperature; W – work; Q – heat. The system contacts the baths in the isomagnetic portions of the cycle (i.e., A → D and A → C). At A, T = Tl, and at C, the system's temperature reaches T = Th. For the quantum version, the entropy SB and SD are calculated using the same thermal probabilities in A and C to ensure the quantum adiabatic portions A → B and C → D of the two-level quantum system. Reproduced from ref. 149 CC BY 4.0; (b) results of training the agent on the quantum harmonic oscillator heat engine model; the dashed lines represent the Otto cycle; actions chosen by the agent, represented by the value of 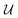 , as a function of time. Reproduced from ref. 147 CC BY 4.0; (c) the quantum thermal battery is a reality and shows spontaneous coherence obtained with a FETI in a double layer or, in this case, in a Al/0.8K2.99Ba0.005OCl + 0.2 PVAc/Cu coaxial cell when connected to a material resistor of 1.8 kΩ; the Otto field is an internal spontaneous electric field established to equilibrate the Fermi levels between the materials in electrical contact; the self-cycling drives the oscillation of the temperature of the cell.28 , as a function of time. Reproduced from ref. 147 CC BY 4.0; (c) the quantum thermal battery is a reality and shows spontaneous coherence obtained with a FETI in a double layer or, in this case, in a Al/0.8K2.99Ba0.005OCl + 0.2 PVAc/Cu coaxial cell when connected to a material resistor of 1.8 kΩ; the Otto field is an internal spontaneous electric field established to equilibrate the Fermi levels between the materials in electrical contact; the self-cycling drives the oscillation of the temperature of the cell.28 | ||
Manzano150 conducted a study to comprehend the influence of quantum effects on the operation and characteristics of thermal machines. Specifically, they focused on analyzing the entropy production and fluctuations in Maxwell's refrigerator with squeezing (Fig. 15). This study holds significant importance as it addresses a key challenge in quantum thermodynamics, which is to determine the impact of genuine quantum effects on the thermodynamic behavior and properties of small systems subjected to fluctuations. The study involved a thermal device between two resonant bosonic reservoirs at different inverse temperatures and an external memory system capable of erasing or storing information when in contact with the device. In this study, the authors verified that in scenarios of squeezed thermal reservoirs, the changes in entropy within the environment result from the exchange of energy and coherence between nonequilibrium reservoirs. This exchange mechanism also led to the induction of squeezing in the memory system at the steady state. While the fluctuation theorem for total entropy production remained valid in this case, the fundamental processes associated with its increase were no longer straightforward jumps linked to the exchange of energy quanta between reservoirs.
How are quantum thermal machines related to quantum batteries? A recent study conducted by Tacchino et al.151 aimed to prove that a battery can be charged when traversed by an incoherent heat flow. This heat flow arises from the weak interaction between a quantum system and two thermal baths at different temperatures. The process of charging the battery is initiated by applying a thermal gradient, which drives the transfer of energy and results in the battery being charged. The authors studied this subject by analyzing a model of two coupled qubits as the working fluid. The most important concepts to be taken into account were (1) the Hamiltonian of the two coupled qubits, eqn (15), and (2) the heat absorbed from the hot bath.
| H = ℏω0(σ(1)+σ(1)− + σ(2)+σ(2)−) − λ(σ(1)+σ(2)− + h.c.) | (15) |
A study from October 2022 by Santos et al.152 aimed to investigate the thermodynamic costs and limitations in the simplest case of optically pumping energy into an effective two-level quantum battery, as analyzed herein with the Dicke model (Fig. 11 and 12). The author started the study by analyzing a single quantum battery, highlighting the relationship between the pump system and efficiency and the dependence of the charging efficiency and the frequency of the pumping field. From this, it was possible to conclude that there is no optimal set of parameters to charge the battery. The process is more efficient for shorter times. For this time scale, the power storage in the battery is maximized; however, the efficiency decreases due to heat loss. The charging process is not affected by temperature if adiabatic elimination is verified. This condition is not verified unless the dissipative thermal reservoir temperature is high enough compared to the energy gap at the eliminated level. Charging is most efficient at resonance, making this the optimal charging scenario.
Following, the author studied a second situation considering a quantum engine. It was verified that the best performance is achieved at low temperatures and short cycles. The maximum efficiency obtained is equivalent to a machine operating on an Otto cycle between two different reservoirs (Fig. 16). However, the efficiency of the Otto cycle is reduced due to energy dissipation in creating an effective high-temperature reservoir through optical pumping. This, however, can be minimized if the energy difference between the adiabatically eliminated level and the optically pumped level is not significant (Fig. 16). The highest efficiency in a short cycle situation is achieved when the pumping frequency matches the Bohr frequency of the optically pumped transition. The two-stroke machine cannot work at every pump frequency and temperature combination; if the temperature of the cold reservoir is higher, then the machine needs to be closer to resonance. However, when the machine operates at resonance, its efficiency is not affected by the temperature of the cold reservoir in a significant way.
Bhandari et al.148 conducted a study in May 2023 to explore using quantum measurements and feedback in coupled-qubit-based thermal machines. The researchers examined two configurations of these devices: (1) Maxwell's demon and (2) measurement-assisted refrigerator (Fig. 15). Before reviewing the results reported by the authors, it's fundamental to understand the model underlying both experiments. In their investigation, the authors employed a setup consisting of two coupled qubits, denoted as Q1 and Q2. These qubits were connected to two thermal baths at temperatures T1 and T2, respectively. Additionally, two measurement apparatuses, D1 and D2, enabled local quantum measurements on the respective qubits. The total Hamiltonian for the system was the sum of three components: (1)  describing the coupled-qubit system, (2)
describing the coupled-qubit system, (2) 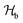 representing the Hamiltonian of the heat baths, and (3)
representing the Hamiltonian of the heat baths, and (3)  , characterizing the tunnel-like coupling between the baths and the system. Hence, the total Hamiltonian can be expressed as
, characterizing the tunnel-like coupling between the baths and the system. Hence, the total Hamiltonian can be expressed as  .
.
In the case of Maxwell's demons, the environment has a uniform temperature, denoted as T1 = T2 = T. This configuration aimed to extract heat from a single-temperature bath by leveraging invasive quantum measurements and feedback. On the other hand, the measurement-assisted refrigerator involved two distinct temperatures, T1 and T2, to maximize the heat extracted from the cold bath. The authors studied continuous and discrete measurements for Maxwell's demon scenario. In the case of one qubit measurement and considering a feedback-favorable situation, it was observed that the heat extraction from the thermal bath increases monotonously as a function of the coupling strength between the two qubits σZ − σZ. By comparing the heat extracted from a single setup when both qubits were measured together to the heat extracted from two parallel setups where only individual qubits were measured, the authors concluded that the former outperforms the latter due to a collective effect. The distribution of heat extraction for both one and two-qubit measurements was considered for continuous measurement. The combined measurement of two qubits has a superior average heat extraction compared to individually measuring each qubit in two parallel setups. However, it is essential to note that higher fluctuations consistently accompanied this enhanced average heat extraction. In the study's second phase, the researchers examined the application of measurement-assisted refrigeration in a system consisting of coupled qubits connected to two thermal baths with different temperatures. It was demonstrated that while refrigeration can be achieved by using either measurement or swap operations independently, combining them leads to even more effective refrigeration.
3. Conclusion
All-solid-state batteries are expected to be widely adopted once they become cost-effective or significantly more efficient than their liquid counterparts. Sustainability is a driving force for their adoption, as it requires promoting renewable energy sources, implementing energy-efficient practices, reducing greenhouse gas emissions, and promoting waste reduction and recycling. Consequently, the materials used must be non-hazardous. An exemplary achievement would be converting a portion of the wasted heat and thermal energy into electrical energy.The best-performing solid electrolytes currently being adopted by industry include argyrodites, oxyhalides, and combinations of argyrodites with oxides and halides and oxyhalides with sulfur. These solid electrolytes can be enhanced by doping them with higher valence cations to create vacancies that decrease the activation energy.
The synthesis method is also crucial as it relates to crystallinity and defects. Wet chemistry synthesis has proven to be the best method for obtaining higher ionic conductivity and even lower hygroscopicity. Being nanocrystalline or glass-amorphous has also been shown to improve cationic mobility within the solid electrolyte.
In addition to being an electrolyte, being a ferroelectric (e.g., perovskite LLTO and A3−2xMxOCl where A = Li, Na, K and M = Mg, Ca, Sr, Ba) enhances ionic performance due to the spontaneous polarization of the ferroelectric driving ionic mobility, and vice versa.
Another intriguing characteristic, second only to the ferroelectricity dynamics described above, is the semiconductor anode-like behavior of the best-performing electrolytes, including Li6PS5Cl, Na3OCl, K3OCl, and Li3InCl6. These electrolytes are semiconductors or have a band gap energy slightly above 3 eV, but their conduction band is placed at a similar energy level to the well-performing electrolytes. This characteristic suggests that electrons likely play a role in the excellent performance of an electrolyte, even though an SEI layer forms as Li+-ions, Li-batteries, and Na+-ion traditional anodes have chemical potentials well above the conduction band of these electrolytes, facilitating the tunneling and drift of the electrons to the electrolyte's surface.
The ferroelectric electrolytes of the A3−2xMxOCl family, where A = Li, Na, K, and M = Mg, Ca, Sr, Ba, are FETIs (ferroelectric topological insulators) and, as previously mentioned, they have the guaranteed presence of metallically protected surface states that can serve as metallic electrodes. FETIs can, therefore, function as a tandem dielectric-electrode, reducing interfacial resistance and configuring a one-electrode-battery or capacitor, where the electrode raises the bias between the chemical potential of the ferroelectrics' surfaces. Other ferroelectrics that have been proven to be topological insulators, although not electrolytes, are BaBiO3, NaSnBi, and the cubic halide perovskite CsPbI3, which has applications in photovoltaics and optoelectronics.
FETI electrolytes used in energy storage devices exhibit features of quantum thermal batteries, such as the possibility of establishing positive feedback from the positive to the negative electrode through their surface, leading to stability and self-charge even when the battery is set to discharge with a resistive material load.
Whether an FETI is used in batteries or not, the future lies in carefully tailoring electrolytes and devices, utilizing quantum mechanics to our advantage. The future may be centered on quantum batteries with harvesting capabilities, which may exhibit coherent states even at macroscopic dimensions and room temperature. Combining energy harvesting and storage in one cell is environmentally advisable, especially if no additional efforts are required for their fabrication and use; the materials used are non-hazardous and are recyclable, safe, and readily available. These efforts and tendencies are not limited to batteries and energy storage devices but extend to photovoltaics, memories, optoelectronics, and transistors (Fig. 17).
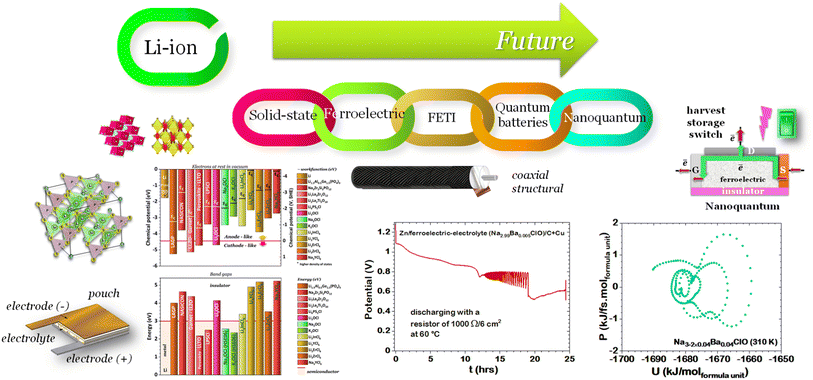 | ||
| Fig. 17 A perspective journey into the present and future of all-solid-state batteries. Note: for more information on the graphs on the right115 reproduced under CC BY 4.0. | ||
Author contributions
Original draft, visualization, and quantum battery simulation analysis: BMG; original draft on quantum batteries and simulations' code: JFM; original draft on main perspectives, conceptualization, visualization, ab initio simulations, and supervision: MHB; review and editing: all. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by PULSELiON – PUlsed Laser depoSition tEchnology for soLid State battery manufacturIng supported by digitalization funded by Horizon Europe, EU; the CAVALI project, reference POCI-01-0247-FEDER-047728, co-funded by the ERDF, through the COMPETE 2020, under the PORTUGAL 2020 Partnership Agreement; the Portuguese Foundation for Science and Technology FCT UIDP/50022/2020 Emerging Technologies–LAETA, and PTDC/QUI-ELT/2593/2021 “Redox-active Metal–Organic Frameworks as Electrode Materials for Lithium-Ion Batteries” projects. This work is also the result of Agenda CVB – Cadeia de Valor das Baterias em Portugal, nr. C644864613-00000003, financed by the Recovery and Resilience Plan (PRR) and by European Union – NextGeneration EU and of Agenda NGS – New Generation Storage, nr. C644936001-00000045, investment project No. 58, financed by the Recovery and Resilience Plan (PRR) and by European Union – NextGeneration EU.References
- T. B. Clarke, M. W. Glasscott and J. E. Dick, The Role of Oxygen in the Voltaic Pile, J. Chem. Educ., 2021, 98(9), 2927–2936, DOI:10.1021/acs.jchemed.1c00016.
- M. Li, J. Lu, Z. Chen and K. Amine, 30 Years of Lithium-Ion Batteries, Adv. Mater., 2018, 30, 33, DOI:10.1002/adma.201800561.
- J. Wen, Y. Yu and C. Chen, A review on lithium-ion batteries safety issues: Existing problems and possible solutions, Mater. Express, 2012, 2(3), 197–212, DOI:10.1166/mex.2012.1075.
- R. Sliz, P. Molaiyan, T. Fabritius and U. Lassi, Printed electronics to accelerate solid-state battery development, Nano Express, 2022, 3(2), 021002, DOI:10.1088/2632-959X/ac5d8e.
- J. Wu, S. Liu, F. Han, X. Yao and C. Wang, Lithium/Sulfide All-Solid-State Batteries using Sulfide Electrolytes, Adv. Mater., 2021, 33(6), 2000751, DOI:10.1002/adma.202000751.
- A. N. Guerreiro, B. A. Maia, H. Khalifa, M. C. Baptista and M. H. Braga, What Differentiates Dielectric Oxides and Solid Electrolytes on the Pathway toward More Efficient Energy Storage?, Batteries, 2022, 8(11), 232, DOI:10.3390/BATTERIES8110232.
- J. C. Bachman, et al., Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction, Chem. Rev., 2016, 116(1), 140–162, DOI:10.1021/acs.chemrev.5b00563.
- V. Bocharova and A. P. Sokolov, Perspectives for Polymer Electrolytes: A View from Fundamentals of Ionic Conductivity, Macromolecules, 2020, 53(11), 4141–4157, DOI:10.1021/acs.macromol.9b02742.
- L. Hoffart and D. M. Schleich, Morphological Investigations on the Solid Electrolyte Li3.6Geo.6Vo.404 and Use in a Solid State Lithium Battery, 1995 Search PubMed.
- Y. Deng, et al., Enhancing the Lithium Ion Conductivity in Lithium Superionic Conductor (LISICON) Solid Electrolytes through a Mixed Polyanion Effect, ACS Appl. Mater. Interfaces, 2017, 9(8), 7050, DOI:10.1021/acsami.6b14402 –7058.
- N. Kamaya, et al., A lithium superionic conductor, Nat. Mater., 2011, 10(9), 682–686, DOI:10.1038/nmat3066.
- S. Boulineau, M. Courty, J.-M. Tarascon and V. Viallet, Mechanochemical synthesis of Li-argyrodite Li6PS5X (X=Cl, Br, I) as sulfur-based solid electrolytes for all solid state batteries application, Solid State Ionics, 2012, 221, 1–5, DOI:10.1016/j.ssi.2012.06.008.
- I. Hanghofer, et al., Substitutional disorder: Structure and ion dynamics of the argyrodites Li6PS5Cl, Li6PS5Br and Li6PS5I, Phys. Chem. Chem. Phys., 2019, 21(16), 8489–8507, 10.1039/c9cp00664h.
- C. Yu, et al., Facile Synthesis toward the Optimal Structure-Conductivity Characteristics of the Argyrodite Li6PS5Cl Solid-State Electrolyte, ACS Appl. Mater. Interfaces, 2018, 10(39), 33296–33306, DOI:10.1021/acsami.8b07476.
- S. Boulineau, J.-M. Tarascon, J.-B. Leriche and V. Viallet, Electrochemical properties of all-solid-state lithium secondary batteries using Li-argyrodite Li6PS5Cl as solid electrolyte, Solid State Ionics, 2013, 242, 45–48, DOI:10.1016/j.ssi.2013.04.012.
- W. Xia, et al., Antiperovskite Electrolytes for Solid-State Batteries, Chem. Rev., 2022, 122(3), 3763–3819, DOI:10.1021/acs.chemrev.1c00594.
- S. T. Kong, H. J. Deiseroth, J. Maier, V. Nickel, K. Weichert and C. Reiner, Li6PO5Br and Li6PO5Cl: The first lithium-oxide-argyrodites, Z. Anorg. Allg. Chem., 2010, 636(11), 1920–1924, DOI:10.1002/zaac.201000121.
- R. Murugan, V. Thangadurai and W. Weppner, Fast Lithium Ion Conduction in Garnet-Type Li7La3Zr2O12, Angew. Chem., Int. Ed., 2007, 46(41), 7778–7781, DOI:10.1002/anie.200701144.
- X. Tong, V. Thangadurai and E. D. Wachsman, Highly conductive Li garnets by a multielement doping strategy, Inorg. Chem., 2015, 54(7), 3600–3607, DOI:10.1021/acs.inorgchem.5b00184.
- J. B. Goodenough, H. Y.-P. Hong and J. A. Kafalas, Fast Na+-ion transport in skeleton structures, Mater. Res. Bull., 1976, 11(2), 203–220, DOI:10.1016/0025-5408(76)90077-5.
- Y. Zhang, H. Liu, Z. Xie, W. Qu, D. J. Freschi and J. Liu, Progress and Perspectives of Lithium Aluminum Germanium Phosphate-Based Solid Electrolytes for Lithium Batteries, Adv. Funct. Mater., 2023, 33(32), 2300973, DOI:10.1002/adfm.202300973.
- Y. B. Rao, K. K. Bharathi and L. N. Patro, Review on the synthesis and doping strategies in enhancing the Na ion conductivity of Na3Zr2Si2PO12 (NASICON) based solid electrolytes, Solid State Ionics, 2021, 366–367, 115671, DOI:10.1016/j.ssi.2021.115671.
- E. Heo, J. E. Wang, J. H. Yun, J. H. Kim, D. J. Kim and D. K. Kim, Improving Room Temperature Ionic Conductivity of Na3- xKxZr2Si2PO12Solid-Electrolytes: Effects of Potassium Substitution, Inorg. Chem., 2021, 60(15), 11147–11153, DOI:10.1021/acs.inorgchem.1c01118.
- L. Ran, et al., Sc, Ge co-doping NASICON boosts solid-state sodium ion batteries' performance, Energy Storage Mater., 2021, 40, 282–291, DOI:10.1016/j.ensm.2021.05.017.
- A. G. Belous, G. N. Novitskaya, S. V Polyanetskaya and Y. I. Gornikov, Investigation into complex oxides of La 2/3-x Li 3x TiO 3 composition, Izv. Akad. Nauk SSSR, Neorg. Mater., 1987, 23(3), 470–472 CAS.
- P. Birke, S. Scharner, R. A. Huggins and W. Weppner, Electrolytic Stability Limit and Rapid Lithium Insertion in the Fast-Ion-Conducting Li0.29La0.57TiO3 Perovskite-Type Compound, J. Electrochem. Soc., 1997, 144(6), L167–L169, DOI:10.1149/1.1837713.
- A. N. Guerreiro, B. A. Maia, H. Khalifa, M. C. Baptista and M. H. Braga, What Differentiates Dielectric Oxides and Solid Electrolytes on the Pathway toward More Efficient Energy Storage?, Batteries, 2022, 8(11), 232, DOI:10.3390/batteries8110232.
- F. Danzi, M. Valente, S. Terlicka and M. H. Braga, Sodium and potassium ion rich ferroelectric solid electrolytes for traditional and electrode-less structural batteries, APL Mater., 2022, 10(3), 31111, DOI:10.1063/5.0080054.
- M. H. Braga, J. A. Ferreira, V. Stockhausen, J. E. Oliveira and A. El-Azab, Novel Li _3 ClO based glasses with superionic properties for lithium batteries, J. Mater. Chem. A, 2014, 2(15), 5470–5480, 10.1039/C3TA15087A.
- H. Chen, et al., 20 mS cm−1 Li-argyrodite solid electrolyte produced via facile high-speed-mixing, Chem. Commun., 2023, 59, 7220–7223, 10.1039/d3cc01387a.
- Y. Tanaka, K. Ueno, K. Mizuno, K. Takeuchi, T. Asano and A. Sakai, New Oxyhalide Solid Electrolytes with High Lithium Ionic Conductivity >10 mS cm−1 for All-Solid-State Batteries, Angew. Chem., Int. Ed., 2023, 62(13), e202217581, DOI:10.1002/anie.202217581.
- Y. Yu, Z. Wang and G. Shao, Theoretical design of double anti-perovskite Na6SOI2 as a super-fast ion conductor for solid Na+ ion batteries, J. Mater. Chem. A, 2018, 6(40), 19843–19852, 10.1039/c8ta08412b.
- P. Adeli, et al., Boosting Solid-State Diffusivity and Conductivity in Lithium Superionic Argyrodites by Halide Substitution, Angew. Chem., Int. Ed., 2019, 58(26), 8681–8686, DOI:10.1002/anie.201814222.
- J. Yang, et al., Ultrastable all-solid-state sodium rechargeable batteries, ACS Energy Lett., 2020, 5(9), 2835–2841, DOI:10.1021/acsenergylett.0c01432.
- Y. Sun, et al., Rotational Cluster Anion Enabling Superionic Conductivity in Sodium-Rich Antiperovskite Na _3 OBH _4, J. Am. Chem. Soc., 2019, 141(14), 5640–5644, DOI:10.1021/jacs.9b01746.
- Q. Ma, M. Guin, S. Naqash, C. L. Tsai, F. Tietz and O. Guillon, Scandium-substituted Na3Zr2(SiO4)2(PO4) prepared by a solution-assisted solid-state reaction method as sodium-ion conductors, Chem. Mater., 2016, 28(13), 4821–4828, DOI:10.1021/acs.chemmater.6b02059.
- M. Duchardt, U. Ruschewitz, S. Adams, S. Dehnen and B. Roling, Vacancy-Controlled Na+ Superion Conduction in Na11Sn2PS12, Angew. Chem., Int. Ed., 2018, 57(5), 1351–1355, DOI:10.1002/anie.201712769.
- Z. Zhang, et al., A Self-Forming Composite Electrolyte for Solid-State Sodium Battery with Ultralong Cycle Life, Adv. Energy Mater., 2017, 7(4), 1601196, DOI:10.1002/aenm.201601196.
- J. Liang, et al., Site-Occupation-Tuned Superionic LixScCl3+ xHalide Solid Electrolytes for All-Solid-State Batteries, J. Am. Chem. Soc., 2020, 142(15), 7012–7022, DOI:10.1021/jacs.0c00134.
- H. Kwak, et al., Li+ conduction in aliovalent-substituted monoclinic Li2ZrCl6 for all-solid-state batteries: Li2+xZr1-xMxCl6 (M = In, Sc), Chem. Eng. J., 2022, 437, 135413, DOI:10.1016/j.cej.2022.135413.
- X. Li, et al., Water-Mediated Synthesis of a Superionic Halide Solid Electrolyte, Angew. Chem., 2019, 131(46), 16579–16584, DOI:10.1002/ange.201909805.
- Y. Shao, et al., A novel NASICON-based glass-ceramic composite electrolyte with enhanced Na-ion conductivity, Energy Storage Mater., 2019, 23, 514–521, DOI:10.1016/j.ensm.2019.04.009.
- K. H. Park, K. Kaup, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, High-Voltage Superionic Halide Solid Electrolytes for All-Solid-State Li-Ion Batteries, ACS Energy Lett., 2020, 533–539, DOI:10.1021/acsenergylett.9b02599.
- A. Banerjee, et al., Na 3 SbS 4 : A Solution Processable Sodium Superionic Conductor for All-Solid-State Sodium-Ion Batteries, Angew. Chem., 2016, 128(33), 9786–9790, DOI:10.1002/ange.201604158.
- H. Kwak, et al., New Cost-Effective Halide Solid Electrolytes for All-Solid-State Batteries: Mechanochemically Prepared Fe3+-Substituted Li2ZrCl6, Adv. Energy Mater., 2021, 11(12), 2003190, DOI:10.1002/aenm.202003190.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Solid Halide Electrolytes with High Lithium-Ion Conductivity for Application in 4 V Class Bulk-Type All-Solid-State Batteries, Adv. Mater., 2018, 30(44), 1803075, DOI:10.1002/adma.201803075.
- R. Schlem, et al., Mechanochemical Synthesis: A Tool to Tune Cation Site Disorder and Ionic Transport Properties of Li3MCl6 (M = Y, Er) Superionic Conductors, Adv. Energy Mater., 2020, 10(6), 1903719, DOI:10.1002/aenm.201903719.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B, 1992, 45(23), 13244–13249, DOI:10.1103/PhysRevB.45.13244.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71, DOI:10.1016/j.cpc.2006.03.007.
- MedeA version 3.0; MedeA is a registered trademark of Materials Design, Inc., San Diego, USA.
- B. H. Zhang, D. Xu, B. H. Chen, X. Q. Liu, J. R. Hester and X. M. Chen, Hybrid improper ferroelectricity in A -site cation ordered Li2La2Ti3O10ceramic with triple-layer Ruddlesden-Popper structure, Appl. Phys. Lett., 2021, 118(5), 052903, DOI:10.1063/5.0038142.
- A. M. Patel, J. K. Nørskov, K. A. Persson and J. H. Montoya, Efficient Pourbaix diagrams of many-element compounds, Phys. Chem. Chem. Phys., 2019, 21(45), 25323–25327, 10.1039/C9CP04799A.
- A. Jain, et al., Formation enthalpies by mixing GGA and GGA $+$ $U$ calculations, Phys. Rev. B, 2011, 84(4), 45115, DOI:10.1103/PhysRevB.84.045115.
- K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Prediction of solid-aqueous equilibria: Scheme to combine first-principles calculations of solids with experimental aqueous states, Phys. Rev. B, 2012, 85(23), 235438, DOI:10.1103/PhysRevB.85.235438.
- M. Aykol, S. S. Dwaraknath, W. Sun and K. A. Persson, Thermodynamic limit for synthesis of metastable inorganic materials, Sci. Adv., 2023, 4(4), eaaq0148, DOI:10.1126/sciadv.aaq0148.
- I. Petousis, et al., Data Descriptor: High-throughput screening of inorganic compounds for the discovery of novel dielectric and optical materials, Sci. Data, 2017, 4, 160134, DOI:10.1038/sdata.2016.134.
- M. De Jong, W. Chen, H. Geerlings, M. Asta and K. A. Persson, A database to enable discovery and design of piezoelectric materials, Sci. Data, 2015, 2, 150053, DOI:10.1038/sdata.2015.53.
- M. K. Horton, J. H. Montoya, M. Liu and K. A. Persson, High-throughput prediction of the ground-state collinear magnetic order of inorganic materials using Density Functional Theory, npj Comput. Mater., 2019, 5(1), 64, DOI:10.1038/s41524-019-0199-7.
- R. Tran, et al., Data Descriptor: Surface energies of elemental crystals, Sci. Data, 2016, 3, 160080, DOI:10.1038/sdata.2016.80.
- M. De Jong, et al., Charting the complete elastic properties of inorganic crystalline compounds, Sci. Data, 2015, 2, 150009, DOI:10.1038/sdata.2015.9.
- J. M. Munro, K. Latimer, M. K. Horton, S. Dwaraknath and K. A. Persson, An improved symmetry-based approach to reciprocal space path selection in band structure calculations, npj Comput. Mater., 2020, 6(1), 112, DOI:10.1038/s41524-020-00383-7.
- K. Latimer, S. Dwaraknath, K. Mathew, D. Winston and K. A. Persson, Evaluation of thermodynamic equations of state across chemistry and structure in the materials project, npj Comput. Mater., 2018, 4(1), 40, DOI:10.1038/s41524-018-0091-x.
- A. K. Singh, et al., Electrochemical Stability of Metastable Materials, Chem. Mater., 2017, 29(23), 10159–10167, DOI:10.1021/acs.chemmater.7b03980.
- H. Zheng, et al., Grain boundary properties of elemental metals, Acta Mater., 2020, 186, 40–49, DOI:10.1016/j.actamat.2019.12.030.
- A. Wang et al., A framework for quantifying uncertainty in DFT energy corrections, [online], available: https://materialsproject.org/.
- S. Boulineau, M. Courty, J. M. Tarascon and V. Viallet, Mechanochemical synthesis of Li-argyrodite Li 6PS 5X (X = Cl, Br, I) as sulfur-based solid electrolytes for all solid state batteries application, Solid State Ionics, 2012, 221, 1–5, DOI:10.1016/j.ssi.2012.06.008.
- S. Yubuchi, S. Teragawa, K. Aso, K. Tadanaga, A. Hayashi and M. Tatsumisago, Preparation of high lithium-ion conducting Li6PS5Cl solid electrolyte from ethanol solution for all-solid-state lithium batteries, J. Power Sources, 2015, 293, 941–945, DOI:10.1016/j.jpowsour.2015.05.093.
- R. Rajagopal, Y. Subramanian, Y. J. Jung, S. Kang and K. S. Ryu, Rapid Synthesis of Highly Conductive Li6PS5Cl Argyrodite-Type Solid Electrolytes Using Pyridine Solvent, ACS Appl. Energy Mater., 2022, 5(8), 9266–9272, DOI:10.1021/acsaem.2c01157.
- D. J. Kalita, S. H. Lee, K. S. Lee, D. H. Ko and Y. S. Yoon, Ionic conductivity properties of amorphous Li-La-Zr-O solid electrolyte for thin film batteries, Solid State Ionics, 2012, 229, 14–19, DOI:10.1016/j.ssi.2012.09.011.
- J. Tan and A. Tiwari, Fabrication and characterization of Li7La3Zr 2O12 thin films for lithium ion battery, ECS Solid State Lett., 2012, 1(6), Q57, DOI:10.1149/2.013206ssl.
- K. Hayashi, K. Shima and F. Sugiyama, A Mixed Aqueous/Aprotic Sodium/Air Cell Using a NASICON Ceramic Separator, J. Electrochem. Soc., 2013, 160(9), A1467–A1472, DOI:10.1149/2.067309jes.
- A. Jalalian-Khakshour, C. O. Phillips, L. Jackson, T. O. Dunlop, S. Margadonna and D. Deganello, Solid-state synthesis of NASICON (Na3Zr2Si2PO12) using nanoparticle precursors for optimisation of ionic conductivity, J. Mater. Sci., 2020, 55(6), 2291–2302, DOI:10.1007/s10853-019-04162-8.
- M. Niazmand, Z. Khakpour and A. Mortazavi, Electrochemical properties of nanostructure NASICON synthesized by chemical routes: A comparison between coprecipitation and sol-gel, J. Alloys Compd., 2019, 798, 311–319, DOI:10.1016/j.jallcom.2019.05.170.
- J.-S. Lee, C.-M. Chang, Y. Il Lee, J.-H. Lee and S.-H. Hong, Spark Plasma Sintering (SPS) of NASICON Ceramics, J. Am. Ceram. Soc., 2004, 87(2), 305–307, DOI:10.1111/j.1551-2916.2004.00305.x.
- V. Baheti, R. Abbasi and J. Militky, Ball milling of jute fibre wastes to prepare nanocellulose, World J. Eng., 2012, 9(1), 45–50, DOI:10.1260/1708-5284.9.1.45.
- J. Mittra et al., Role of substrate temperature in the pulsed laser deposition of zirconium oxide thin film, in Materials Science Forum, Trans Tech Publications Ltd, 2012, pp. 757–761, DOI:10.4028/www.scientific.net/MSF.710.757.
- M. Saeed, Y. Alshammari, S. A. Majeed and E. Al-Nasrallah, Chemical Vapour Deposition of Graphene—Synthesis, Characterisation, and Applications: A Review, Molecules, 2020, 25(17), 3856, DOI:10.3390/molecules25173856.
- A. Hayashi, S. Hama, H. Morimoto, M. Tatsumisago and T. Minami, Preparation of Li2S–P2S5 Amorphous Solid Electrolytes by Mechanical Milling, J. Am. Ceram. Soc., 2001, 84(2), 477–479, DOI:10.1111/j.1151-2916.2001.tb00685.x.
- J. F. M. Oudenhoven, L. Baggetto and P. H. L. Notten, All-solid-state lithium-ion microbatteries: A review of various three-dimensional concepts, Adv. Energy Mater., 2011, 1(1), 10–33, DOI:10.1002/aenm.201000002.
- S. Zhao, W. Jiang, X. Zhu, M. Ling and C. Liang, Understanding the synthesis of inorganic solid-state electrolytes for Li ion batteries: Features and progress, Sustainable Mater. Technol., 2022, 33, e00491, DOI:10.1016/j.susmat.2022.e00491.
- X. Li, et al., Air-stable Li _3 InCl _6 electrolyte with high voltage compatibility for all-solid-state batteries, Energy Environ. Sci., 2019, 12(9), 2665–2671, 10.1039/C9EE02311A.
- C. Wei, et al., Sb and O dual doping of Chlorine-rich lithium argyrodite to improve air stability and lithium compatibility for all-solid-state batteries, J. Power Sources, 2023, 559, 232659, DOI:10.1016/j.jpowsour.2023.232659.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Superionic glass-ceramic electrolytes for room-temperature rechargeable sodium batteries, Nat. Commun., 2012, 3, 856, DOI:10.1038/ncomms1843.
- A. Hayashi, K. Noi, N. Tanibata, M. Nagao and M. Tatsumisago, High sodium ion conductivity of glass-ceramic electrolytes with cubic Na3PS4, J. Power Sources, 2014, 258, 420–423, DOI:10.1016/j.jpowsour.2014.02.054.
- B. Ouyang, Y. Wang, Y. Sun and G. Ceder, Computational Investigation of Halogen-Substituted Na Argyrodites as Solid-State Superionic Conductors, Chem. Mater., 2020, 32(5), 1896–1903, DOI:10.1021/acs.chemmater.9b04541.
- L. Zhou, N. Minafra, W. G. Zeier and L. F. Nazar, Innovative Approaches to Li-Argyrodite Solid Electrolytes for All-Solid-State Lithium Batteries, Acc. Chem. Res., 2021, 54(12), 2717–2728, DOI:10.1021/acs.accounts.0c00874.
- H. J. Deiseroth, et al., Li6PS5X: A class of crystalline Li-rich solids with an unusually high Li+ mobility, Angew. Chem., Int. Ed., 2008, 47(4), 755–758, DOI:10.1002/anie.200703900.
- T. Hwang, et al., The crucial role of oxygen substitution in argyrodite solid electrolytes from the bulk to the surface under atmospheric conditions, J. Mater. Chem. A, 2022, 10(32), 16908–16919, 10.1039/d2ta03649e.
- N. J. J. De Klerk and M. Wagemaker, Diffusion Mechanism of the Sodium-Ion Solid Electrolyte Na3PS4 and Potential Improvements of Halogen Doping, Chem. Mater., 2016, 28(9), 3122–3130, DOI:10.1021/acs.chemmater.6b00698.
- M. M. Islam, A. Al Maruf, J. Pokharel and Y. Zhou, Superhalogen-based Li-rich double antiperovskite Li6OS(BH4)2 as solid electrolyte, MRS Commun., 2022, 12(6), 1140–1146, DOI:10.1557/s43579-022-00290-6.
- B. Reuter, J. Pickardt and K. Hardel, Silbersulfidbromid Ag3SBr und Silbersulfidjodid Ag3SJ, Z. Phys. Chem., 1967, 56(5_6), 309–313 CrossRef CAS.
- Y. Zhao, L. Daemen, and M. Helena Braga, Anti-Perovskite Solid Electrolyte Compositions, 2011, accessed: Jul. 13, 2023, [online], available: https://hdl.handle.net/10216/67190.
- Y. Zhao and L. L. Daemen, Superionic conductivity in lithium-rich anti-perovskites, J. Am. Chem. Soc., 2012, 134(36), 15042–15047, DOI:10.1021/ja305709z.
- H. Fang and P. Jena, Molecular Origin of Properties of Organic-Inorganic Hybrid Perovskites: The Big Picture from Small Clusters, J. Phys. Chem. Lett., 2016, 7(8), 1596–1603, DOI:10.1021/acs.jpclett.6b00435.
- E. Ahiavi, et al., Mechanochemical synthesis and ion transport properties of Na3OX (X = Cl, Br, I and BH4) antiperovskite solid electrolytes, J. Power Sources, 2020, 471, 228489, DOI:10.1016/j.jpowsour.2020.228489.
- P. C. Tsai, et al., Double Paddle-Wheel Enhanced Sodium Ion Conduction in an Antiperovskite Solid Electrolyte, Adv. Energy Mater., 2023, 13(7), 2203284, DOI:10.1002/aenm.202203284.
- Q. Zhao, et al., Design Principles for Rotational Cluster Anion [BH _4 ] ^− Promote Superionic Conductivity in Sodium-Rich Antiperovskite Na _3 OBH _4, J. Phys. Chem. C, 2022, 126(38), 16546–16555, DOI:10.1021/acs.jpcc.2c05262.
- W. Hönle, B. Hettich and A. Simon, Darstellung und Kristallstrukturen von LiGaCl4 und LiGaI4/Preparation and Crystal Structure of LiGaCL4 and LiGaI4, Z. Naturforsch. B, 1987, 42(2), 248–250, DOI:10.1515/znb-1987-0222.
- J. Park, et al., Heat treatment protocol for modulating ionic conductivity via structural evolution of Li3-xYb1-xMxCl6 (M = Hf4+, Zr4+) new halide superionic conductors for all-solid-state batteries, Chem. Eng. J., 2021, 425, 130630, DOI:10.1016/j.cej.2021.130630.
- R. Kanno, Y. Takeda, M. Mori and O. Yamamoto, Ionic Conductivity and Structure of New Double Chloride Li6FeCl8 in the LiCl-FeCl2 System, Chem. Lett., 1987, 16(7), 1465–1468, DOI:10.1246/cl.1987.1465.
- H. D. Lutz, A. Pfitzner and J. K. Cockcroft, Structural Phase Transition and Nonstoichiometry of Li2FeCl4—Neutron Diffraction Studies, J. Solid State Chem., 1993, 107(1), 245–249 CrossRef CAS.
- R. Kanno, Y. Takeda, M. Mori and O. Yamamoto, Ionic Conductivity and Structure of Double Chloride Li2ZnCl4 in the LiCl–ZnCl2 System, Chem. Lett., 1989, 18, 223–226 CrossRef.
- H. Kwak, et al., Emerging Halide Superionic Conductors for All-Solid-State Batteries: Design, Synthesis, and Practical Applications, ACS Energy Lett., 2022, 7(5), 1776–1805, DOI:10.1021/acsenergylett.2c00438.
- Y. He, et al., Recent developments and progress of halogen elements in enhancing the performance of all-solid-state lithium metal batteries, Energy Storage Mater., 2022, 49, 19–57, DOI:10.1016/j.ensm.2022.03.043.
- W. Weppner and R. A. Huggins, Ionic conductivity of solid and liquid LiAlCl4, J. Electrochem. Soc., 1977, 124(1), 35 CrossRef CAS.
- D. C. Ginnings and T. E. Phipps, TEMPERATURE-CONDUCTANCE CURVES OF SOLID SALTS. III. HALIDES OF LITHIUM, J. Am. Chem. Soc., 1930, 52(4), 1340–1345, DOI:10.1021/ja01367a006.
- R. Schlem, A. Banik, S. Ohno, E. Suard and W. G. Zeier, Insights into the Lithium Sub-structure of Superionic Conductors Li3YCl6and Li3YBr6, Chem. Mater., 2021, 33(1), 327–337, DOI:10.1021/acs.chemmater.0c04352.
- A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Machine Learning-Assisted Discovery of Solid Li-Ion Conducting Materials, Chem. Mater., 2019, 31(2), 342–352, DOI:10.1021/acs.chemmater.8b03272.
- K. Wang, et al., A cost-effective and humidity-tolerant chloride solid electrolyte for lithium batteries, Nat. Commun., 2021, 12(1), 4410, DOI:10.1038/s41467-021-24697-2.
- W. G. Zeier, R. Schlem, A. Banik, M. Eckardt and M. Zobel, Na3−xEr1−xZrxCl6-A halide-based fast sodium-ion conductor with vacancy-driven ionic transport, ACS Appl. Energy Mater., 2020, 3(10), 10164–10173, DOI:10.1021/acsaem.0c01870.
- J. Xu, et al., New Halide-Based Sodium-Ion Conductors Na3Y2Cl9 Inversely Designed by Building Block Construction, ACS Appl. Mater. Interfaces, 2023, 15(17), 21086–21096, DOI:10.1021/acsami.3c01570.
- J. Liu, S. Wang, Y. Kawazoe and Q. Sun, A New Spinel Chloride Solid Electrolyte with High Ionic Conductivity and Stability for Na-Ion Batteries, ACS Mater. Lett., 2023, 1009–1017, DOI:10.1021/acsmaterialslett.3c00119.
- T. Zhao, A. N. Sobolev, R. Schlem, B. Helm, M. A. Kraft and W. G. Zeier, Synthesis-Controlled Cation Solubility in Solid Sodium Ion Conductors Na2+xZr1-xInxCl6, ACS Appl. Energy Mater., 2023, 6(8), 4334–4341, DOI:10.1021/acsaem.3c00277.
- M. H. Braga, Coherence in the Ferroelectric A3ClO (A = Li, Na) Family of Electrolytes, Materials, 2021, 14(9), 2398, DOI:10.3390/ma14092398.
- M. H. Braga, J. E. Oliveira, A. J. Murchison and J. B. Goodenough, Performance of a ferroelectric glass electrolyte in a self-charging electrochemical cell with negative capacitance and resistance, Appl. Phys. Rev., 2020, 7(1), 011406, DOI:10.1063/1.5132841.
- Best Research-Cell Efficiency Chart, accessed: Oct 20, 2023, online, available: https://www.nrel.gov/pv/cell-efficiency.html.
- S. M. Young and A. M. Rappe, First Principles Calculation of the Shift Current Photovoltaic Effect in Ferroelectrics, Phys. Rev. Lett., 2012, 109(11), 116601, DOI:10.1103/PhysRevLett.109.116601.
- F. Mo, et al., Low-Voltage Operating Ferroelectric FET with Ultrathin IGZO Channel for High-Density Memory Application, IEEE J. Electron Devices Soc., 2020, 8, 717–723, DOI:10.1109/JEDS.2020.3008789.
- M. Hoffmann, P. V. Ravindran and A. I. Khan, Why do ferroelectrics exhibit negative capacitance?, Materials, 2019, 12(22), 3743, DOI:10.3390/ma12223743.
- L. Tu, X. Wang, J. Wang, X. Meng and J. Chu, Ferroelectric Negative Capacitance Field Effect Transistor, Adv. Electron. Mater., 2018, 4(11), 1800231, DOI:10.1002/aelm.201800231.
- G. A. Salvatore, A. Rusu and A. M. Ionescu, Experimental confirmation of temperature dependent negative capacitance in ferroelectric field effect transistor, Appl. Phys. Lett., 2012, 100(16), 163504, DOI:10.1063/1.4704179.
- A. I. Khan, et al., Negative capacitance in a ferroelectric capacitor, Nat. Mater., 2015, 14(2), 182–186, DOI:10.1038/nmat4148.
- B. Xie, et al., Higher-order band topology, Nat. Rev. Phys., 2021, 3(7), 520–532, DOI:10.1038/s42254-021-00323-4.
- P.-L. Zhao, X.-B. Qiang, H.-Z. Lu and X. C. Xie, Coulomb Instabilities of a Three-Dimensional Higher-Order Topological Insulator, Phys. Rev. Lett., 2021, 127(17), 176601, DOI:10.1103/PhysRevLett.127.176601.
- A. Dutt, M. Minkov, I. A. D. Williamson and S. Fan, Higher-order topological insulators in synthetic dimensions, Light: Sci. Appl., 2020, 9(1), 131, DOI:10.1038/s41377-020-0334-8.
- H. Jin, J. Im and A. J. Freeman, Topological insulator phase in halide perovskite structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(12), 121102, DOI:10.1103/PhysRevB.86.121102.
- B. Yan, M. Jansen and C. Felser, A large-energy-gap oxide topological insulator based on the superconductor BaBiO 3, Nat. Phys., 2013, 9, 709–711, DOI:10.1038/NPHYS2762.
- X. Dai, C. C. Le, X. X. Wu, S. S. Qin, Z. P. Lin and J. P. Hu, Topological Phase in Non-centrosymmetric Material NaSnBi, Chin. Phys. Lett., 2016, 33(12), 127301, DOI:10.1088/0256-307X/33/12/127301.
- S. Liu, Y. Kim, L. Z. Tan and A. M. Rappe, Strain-Induced Ferroelectric Topological Insulator, Nano Lett., 2016, 16(3), 1663–1668, DOI:10.1021/acs.nanolett.5b04545.
- B. Monserrat, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Antiferroelectric topological insulators in orthorhombic AMgBi compounds (A = Li, Na, K), Phys. Rev. Lett., 2017, 119(3), 036802, DOI:10.1103/PhysRevLett.119.036802.
- R. Alicki and M. Fannes, Entanglement boost for extractable work from ensembles of quantum batteries, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87(4), 042123, DOI:10.1103/PhysRevE.87.042123.
- F. C. Binder, S. Vinjanampathy, K. Modi and J. Goold, Quantacell: Powerful charging of quantum batteries, New J. Phys., 2015, 17, 075015, DOI:10.1088/1367-2630/17/7/075015.
- D. Ferraro, M. Campisi, G. M. Andolina, V. Pellegrini and M. Polini, High-Power Collective Charging of a Solid-State Quantum Battery, Phys. Rev. Lett., 2018, 120(11), 117702, DOI:10.1103/PhysRevLett.120.117702.
- F.-Q. Dou, Y.-Q. Lu, Y.-J. Wang and J.-A. Sun, Extended Dicke quantum battery with interatomic interactions and driving field, Phys. Rev. B, 2021, 105, 115405, DOI:10.1103/PhysRevB.105.115405.
- A. Crescente, M. Carrega, M. Sassetti and D. Ferraro, Ultrafast charging in a two-photon Dicke quantum battery, Phys. Rev. B, 2020, 102, 245407, DOI:10.1103/PhysRevB.102.245407.
- Python.org, accessed: Apr. 28, 2023, [online], available: https://www.python.org/downloads/.
- Jupyter notebook – Download without anaconda, accessed: Apr. 28, 2023, [online], available: https://jupyter.org/install.
- Anaconda” accessed: Apr. 28, 2023, [online], available: https://www.anaconda.com/download/.
- G. Chen, X. Wang, J.-Q. Liang and Z. D. Wang, Exotic quantum phase transitions in a Bose-Einstein condensate coupled to an optical cavity, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 023634, DOI:10.1103/PhysRevA.78.023634.
- F. Brennecke, T. Donner, S. Ritter, T. Bourdel, M. Köhl and T. Esslinger, Cavity QED with a Bose-Einstein condensate, Nature, 2007, 450(7167), 268–271, DOI:10.1038/nature06120.
- T. P. Le, J. Levinsen, K. Modi, M. Parish and F. A. Pollock, Spin-chain model of a many-body quantum battery, Phys. Rev. A, 2017, 97, 022106, DOI:10.1103/PhysRevA.97.022106.
- D. Pompa, Encoding a 1-D Heisenberg Spin 1/2 Chain in a Simulated Encoding a 1-D Heisenberg Spin 1/2 Chain in a Simulated Annealing Algorithm for Machine Learning Annealing Algorithm for Machine Learning, 2019, [online], available: https://egrove.olemiss.edu/hon_thesis/1012.
- G. Marchegiani, P. Virtanen, F. Giazotto and M. Campisi, Self-oscillating Josephson quantum heat engine, Phys. Rev. Appl., 2016, 6, 054014, DOI:10.1103/PhysRevApplied.6.054014.
- P. P. Hofer, J. B. Brask, M. Perarnau-Llobet and N. Brunner, Quantum Thermal Machine as a Thermometer, Phys. Rev. Lett., 2017, 119, 090603, DOI:10.1103/PhysRevLett.119.090603.
- K. Joulain, J. Drevillon, Y. Ezzahri and J. Ordonez-Miranda, Quantum thermal transistor, Phys. Rev. Lett., 2016, 116, 200601, DOI:10.1103/PhysRevLett.116.200601.
- P. A. Erdman and F. Noé, Identifying optimal cycles in quantum thermal machines with reinforcement-learning, npj Quantum Inf., 2022, 8(1) DOI:10.1038/s41534-021-00512-0.
- B. Bhandari, R. Czupryniak, P. A. Erdman and A. N. Jordan, Measurement-based quantum thermal machines with feedback control, Entropy, 2023, 25(2), 204, DOI:10.3390/e25020204.
- F. J. Peña, O. Negrete, N. Cortés and P. Vargas, Otto engine: Classical and quantum approach, Entropy, 2020, 22(7), 755, DOI:10.3390/e22070755.
- G. Manzano, Entropy production and fluctuations in a Maxwell's refrigerator with squeezing, Eur. Phys. J.: Spec. Top., 2018, 227, 285–300, DOI:10.1140/epjst/e2018-00093-9.
- F. Tacchino, T. F. F. Santos, D. Gerace, M. Campisi and M. F. Santos, Charging a quantum battery via non equilibrium heat current, Phys. Rev. E, 2020, 102, 062133, DOI:10.1103/PhysRevE.102.062133.
- T. F. F. Santos and M. F. Santos, Efficiency of optically pumping a quantum battery and a two-stroke heat engine, Phys. Rev. A, 2022, 106, 052203, DOI:10.1103/PhysRevA.106.052203.
| This journal is © The Royal Society of Chemistry 2024 |