HFM-Tracker: a cell tracking algorithm based on hybrid feature matching†
Yan
Zhao‡
a,
Ke-Le
Chen‡
b,
Xin-Yu
Shen‡
c,
Ming-Kang
Li
b,
Yong-Jing
Wan
*a,
Cheng
Yang
c,
Ru-Jia
Yu
 *b,
Yi-Tao
Long
*b,
Yi-Tao
Long
 b,
Feng
Yan
c and
Yi-Lun
Ying
b,
Feng
Yan
c and
Yi-Lun
Ying
 ad
ad
aSchool of Information Science and Engineering, East China University of Science and Technology, 130 Meilong Road, 200237 Shanghai, P. R. China. E-mail: wanyongjing@ecust.edu.cn
bSchool of Chemistry and Chemical Engineering, Molecular Sensing and Imaging Center (MSIC), Nanjing University, Nanjing 210023, P. R. China. E-mail: yurujia@nju.edu.cn
cSchool of Electronic Sciences and Engineering, Nanjing University, Nanjing, 210023, China
dChemistry and Biomedicine Innovation Center, Nanjing University, Nanjing 210023, P. R. China
First published on 19th March 2024
Abstract
Cell migration is known to be a fundamental biological process, playing an essential role in development, homeostasis, and diseases. This paper introduces a cell tracking algorithm named HFM-Tracker (Hybrid Feature Matching Tracker) that automatically identifies cell migration behaviours in consecutive images. It combines Contour Attention (CA) and Adaptive Confusion Matrix (ACM) modules to accurately capture cell contours in each image and track the dynamic behaviors of migrating cells in the field of view. Cells are firstly located and identified via the CA module-based cell detection network, and then associated and tracked via a cell tracking algorithm employing a hybrid feature-matching strategy. This proposed HFM-Tracker exhibits superiorities in cell detection and tracking, achieving 75% in MOTA (Multiple Object Tracking Accuracy) and 65% in IDF1 (ID F1 score). It provides quantitative analysis of the cell morphology and migration features, which could further help in understanding the complicated and diverse cell migration processes.
1. Introduction
Cell behaviour, including both morphological and migratory changes, serves as an instantaneous reflection of intracellular tension dynamics. Understanding cell behaviour is crucial for comprehending fundamental biological processes such as tissue formation, immune response, and wound healing.1 Abnormal cell migration can result in unexpected disruptions to biological functions, further associated with diseases such as malformations,2 autoimmune diseases,3 and cancer metastasis.4 For example, the directional migration of tumour cells during metastasis is one of the leading causes of cancer-related deaths.5,6 During metastasis, tumour cells detach from the primary tumour, migrate and transport through vessels and survive anoikis, and ultimately form the secondary sites, resulting in severe organ failure. Both cell movements and alterations in cell shapes are greatly involved in these complex cellular processes.7,8 Thus it is crucial to track and observe the migratory movement as well as the diverse cell morphology changes of cancer cells, which can help identify and study abnormal cell behaviours and provide insights into cancer development. As cell migration is key to the metastatic process, continuous tracking of the collective cell migrations over time is of great significance,9–12 but remains a challenge due to the diverse and dynamic shapes of individual cells. Considering the frequent deformations of single cells, such as elongation, contraction, and division, accurate identification of cell contours is particularly required. The accompanying rapid migration of cells across large fields of view further complicates the cell tracking, which involves the processing of large volumes of time-series image data.In recent years, with the rapid development of computer science and bioimage informatics, cell tracking methods have received extensive attention and have made great progress. Historically, traditional cell segmentation methods were often designed for specific applications, such as the TWANG algorithm,13 which was tailored for segmenting circular objects. These conventional approaches14 typically relied on preprocessing filters, e.g., Gaussian or median filters as well as complex segmentation operations, such as region-adaptive thresholding followed by watershed transformations. Achieving reasonable segmentation results required fine-tuning these methods for different cell types and imaging conditions. Several automated cell tracking methods have been developed,15–18 but some require fluorescent labeling.19–21 This may affect the intrinsic behaviour of living cells,20 posing challenges for long-term living cell tracking. With the advancement of deep learning, its application in the field of cell tracking has become increasingly prevalent.22–25 For instance, He et al.22 combined motion models with a classification neural network for cell tracking, effectively leveraging the advantages of motion information and cell feature classification. Hayashida et al.23,24 achieved joint detection and tracking of cells by predicting cell positions and motion mapping through a neural network without providing cell segmentation contours. Furthermore, Payer et al.25 employed a single recurrent hourglass network to simultaneously perform cell segmentation and tracking, simplifying the processing pipeline. Overall, cell tracking methods based on deep learning technology are mainly categorized into two types: detection-based tracking26–29 and model evolution-based tracking.14,30 The former is generally performed through cell segmentation and association, focusing respectively on the spatial and temporal information of cell tracking. The latter method tracks cells by searching for similarities31 in adjacent images and is suitable for objects whose positions and features change over time. Both methods require the target objects to have high-contrast edges and minimal deformation. In comparison, detection-based tracking exhibits significant advantages in processing speed and simplification of computational workflow, particularly in the rapid and effective handling of cell segmentation and association. This method initially identifies cells from the background using features such as texture or gradient. Subsequently, by optimizing a probabilistic objective function, these detected cells are matched and connected in a continuous image sequence to form the trajectory of cell movement. The essence of this detection-based tracking lies in accurately segmenting individual cells and maintaining correct identification and association of the same cells in subsequent frames, enabling the acquisition of time-series trajectories for a large number of cells.
Herein, we develop a cell tracking algorithm named HFM-Tracker to accurately capture the dynamic cell behaviour from image sequences. The algorithm applies a cell detection network with a Contour Attention (CA) module to localized moving cells. Subsequently, a tracking algorithm based on an Adaptive Confusion Matrix (ACM) module is utilized to associate and track the detected cells. This proposed HFM-Tracker shows superiority in capturing diverse cell morphological and migratory behaviours, providing essential characteristics such as cellular morphological parameters and migration trajectories. Furthermore, we apply this algorithm for real-time tracking of label-free cancer cells in bright-field microscopic images, where cell viability can be easily distinguished. This method proves valuable for better understanding the intrinsic migratory properties of living cells and provides insights into biological processes associated with cell migration.
2. Experimental section
2.1 Cells and cell culture
Briefly, the MCF-7 cells (human breast cancer cell line, a kind gift from Yuncong Chen's laboratory, Nanjing University) were cultured in a 24-well plate using RPMI 1640 medium supplemented with 10% fetal bovine serum and 1% antibiotics (penicillin and streptomycin). Cells were maintained at 37 °C under a 5% CO2 atmosphere within an incubator. Time-lapse cell images were captured using incubator-enclosed microscopy (zenCELL owl, Germany) at 10 minute intervals. For the cell tracking experiments, MCF-7 cells were cultured with or without 0.5 mM hydrogen peroxide in the culture medium.2.2 Cell image acquisition
The dataset employed in this study consists of a series of cell images obtained through real-time cell culture under different conditions. Each set of images contains 144 time-lapse images (2588 × 1942 pixels), captured at 10-minute intervals, with a total recording duration of 24 hours. 70 images were selected from this dataset for manual cell detection and tracking using LabelMe software (version 5.0.1), with annotation made for all the cells present in these images. All experiments were conducted on an Intel Core i5-13500HX with 32GB RAM.2.3 HFM-Tracker procedures
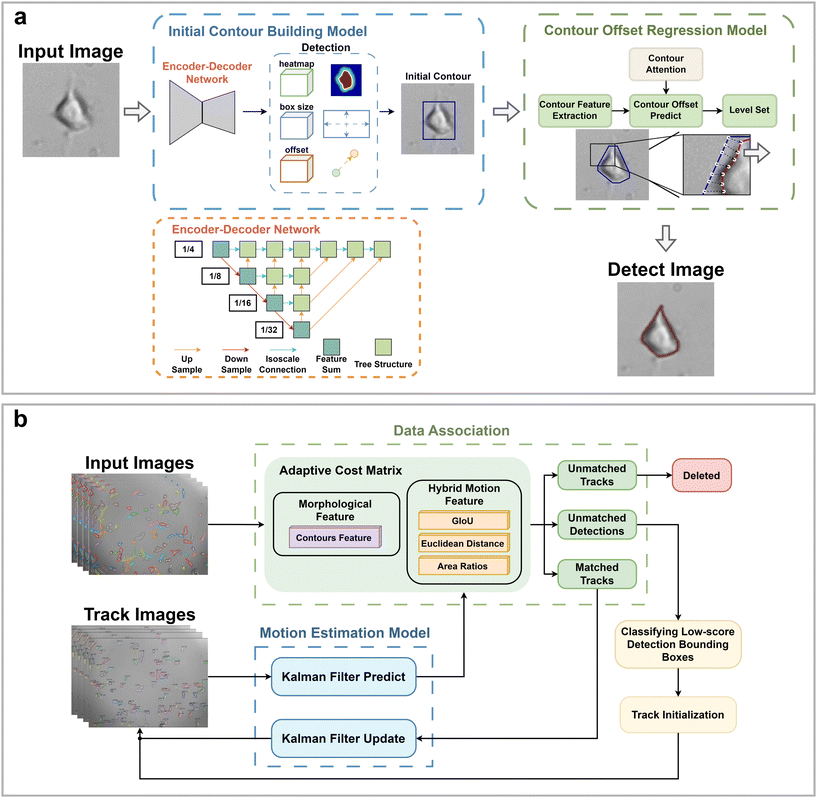
HFM-Tracker integrates a CA module-based cell detection algorithm and an ACM module-based cell tracking algorithm. It enables precise recognition and localization of individual cells, tracking the accurate cell morphology and their movement trajectories. Briefly, the main procedure of this algorithm consists of two steps: (1) cell recognition and detection and (2) cell association and tracking.| costmotion = aLGIoUij + bLdistij + cLareaij | (1) |
| costGIoU,mor = ωcostGIoU + (1 − ω)costmor | (2) |
| costada = min(costmotion, costGIoU,mor) | (3) |
The ACM employs a two-stage matching strategy. In the first phase, Hungarian matching is performed separately using a hybrid motion cost matrix costmotion and a morphological cost matrix constrained by GIoU, costGIoU,mor, resulting in two sets of matches, MA and MB. Within costGIoU,mor, GIoU serves as a constraint to eliminate cells that appear similar but are too distant from each other. Subsequently, matching pairs common to both MA and MB are extracted and consolidated into a match set M1. In the second phase, for unmatched detection boxes and tracking trajectories not included in the M1 set, the cost matrix costada is recalculated in an adaptively selected manner. Then, the Hungarian algorithm is applied based on costada to obtain the match set M2. Finally, the match sets M1 and M2 are combined to produce the final matching result, denoted as M, for output. This adaptive strategy allows the tracking algorithm to achieve highly accurate cell trajectories even in complex situations such as cell overlap or crossing.
2.4 Model validation
In this study, a total of 70 images are selected from the dataset and divided into training, validation and test sets in a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to facilitate accurate evaluation of the model. Specifically, the training set includes 56 images containing 5574 cells, the validation set includes 7 images with 694 cells, while the test set includes 7 images with a total of 680 cells. MCF-7 cells were cultured under normal conditions with time-lapse images collected, exhibiting natural cell elongation or division (Fig. S2†). To validate the performance of cell detection, AP (Average Precision)32 is employed to evaluate the detection accuracy, which is derived by plotting the precision–recall curve across various confidence threshold values and calculating the area under this curve. The calculation for AP is as follows:
1 to facilitate accurate evaluation of the model. Specifically, the training set includes 56 images containing 5574 cells, the validation set includes 7 images with 694 cells, while the test set includes 7 images with a total of 680 cells. MCF-7 cells were cultured under normal conditions with time-lapse images collected, exhibiting natural cell elongation or division (Fig. S2†). To validate the performance of cell detection, AP (Average Precision)32 is employed to evaluate the detection accuracy, which is derived by plotting the precision–recall curve across various confidence threshold values and calculating the area under this curve. The calculation for AP is as follows: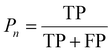 | (4) |
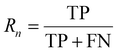 | (5) |
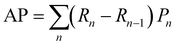 | (6) |
MOTA (Multiple Object Tracking Accuracy) and IDF1 (ID F1 score)33 are utilized to evaluate the accuracy of cell tracking. MOTA calculates tracking accuracy by comprehensively considering the number of errors, cells missed during tracking, and cell ID switches. The calculation is as follows:
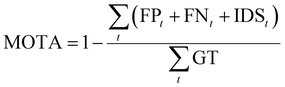 | (7) |
IDF1 is the F1 score based on matching cell tracking IDs. It is calculated as the ratio of correctly matched cell IDs to the sum of all actual detected cells. The calculations for ID Precision (IDP), ID Recall (IDR), and IDF1 are as follows:
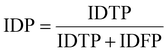 | (8) |
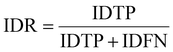 | (9) |
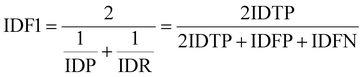 | (10) |
3. Results and discussion
To thoroughly evaluate the performance of HFM-Tracker, we assessed its detection and tracking capabilities on an independent test dataset that was not previously used for either model training or validation. Cells were categorized into three classes according to the number of pixels they occupied in the image: small cells, medium cells and large cells referred to the cells occupying fewer than 322, 322 to 962, and more than 962 pixels, respectively. As shown in Table 1, HFM-Tracker performed well in detecting and tracking cells of different sizes. The highest AP value of 48.2% was obtained for large cells, indicating that the algorithm is particularly adept at recognizing features of larger cells, thereby ensuring tracking accuracy. Large cells also exhibited the highest IDF1 and IDP values, at 65.2% and 73.3%, respectively. The highest MOTA value of 75.7% was achieved for medium cells. These data indicate that large cells perform better regarding average accuracy and consistency in cell ID maintenance. In contrast, medium cells show higher precision in multi-object tracking, whereas small cells exhibit slightly lower performance across the proposed metrics. The dynamic cellular processes including growth and division mainly involve cells that are large and medium in size, only showing small sizes for short periods. Therefore, this HFM-Tracker can still be used for time-resolved cell tracking, providing clear morphological characteristics and migration trajectories.| Cell category | AP | MOTA | IDP | IDR | IDF1 |
|---|---|---|---|---|---|
| Small | 45.2% | 74.9% | 71.7% | 57.7% | 64.0% |
| Medium | 47.3% | 75.7% | 72.3% | 60.2% | 65.7% |
| Large | 48.2% | 74.5% | 73.3% | 59.1% | 65.2% |
Further ablation experiments were performed to validate the effectiveness of each module in the HFM-Tracker algorithm. Table 2 presents the performance metrics under different model configurations, showing that the introduction of the CA module and ACM module improved various performance indicators. The indicators of AP, MOTA, and IDF1 were respectively improved by 0.7%, 0.7%, and 0.8% compared to the Backbone model. This indicates that the introduction of the ACM model to the cell tracking algorithm contributed less to the cell detection part. Nevertheless, the CA module applied in the cell detection network not only improves the recognition and detection of polymorphic cells, but also enhances the cell tracking performance.
| Model | AP | MOTA | IDP | IDR | IDF1 |
|---|---|---|---|---|---|
| Backbone | 46.5% | 74.7% | 71.9% | 58.5% | 64.9% |
| Backbone + CA | 47.7% | 75.1% | 72.5% | 58.8% | 65.3% |
| Backbone + ACM | 47.7% | 75.2% | 72.6% | 59.1% | 65.4% |
| This work | 47.7% | 75.4% | 72.9% | 59.2% | 65.7% |
The time-series migration trajectories were plotted to visualize the moving tumour cells and better show the migration characteristics. Trajectories of a set of MCF-7 cells over 6 hours are depicted in Fig. 2a, showing the various migration behaviours in plate culture. One image was selected every hour to capture these dynamics. Most of the cells in the field of view were successfully detected and tracked with this HFM-Tracker. We marked the contour shape of each cell and its corresponding motion trajectory with the same colour and assigned unique cell IDs such as “cell-1”, “cell-2”, etc. (Fig. 2b). Besides, the trajectory and morphological changes of a representative “cell-42” over a period of 6 hours were highlighted for better visualization (Fig. 2c). This method enables the identification and tracking of each cell from the ensemble, providing detailed cellular characterization with individual heterogeneity.
HFM-Tracker further provides morphological characteristics of the motile cells via the CA module-based detection algorithm, such as perimeter, area, roundness and aspect ratio. Roundness is specifically used to describe how closely the shape of a cell resembles a perfect circle. It can be calculated as follows:
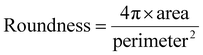 | (11) |
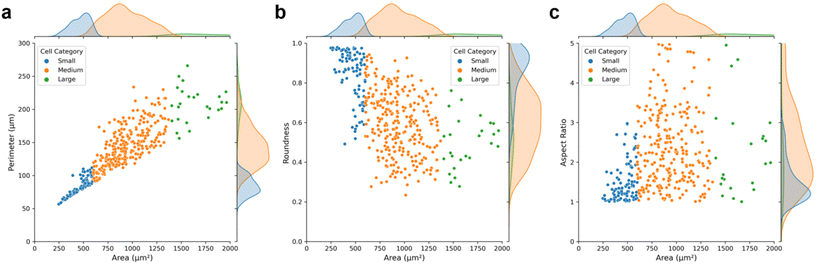
As depicted in Fig. 3, medium cells constitute a large portion of the cultured MCF-7, and these could be assigned as the interphase cells. Large and small cells are mainly in the mitotic phases, as their sizes grow quickly and then divide into two small-sized daughter cells. As expected, the perimeter of the cells is positively correlated with the cell area (Fig. 3a). And the characteristic of roundness generally shows an inverse relationship with the cell area, while the aspect ratio exhibits the opposite trend (Fig. 3b and c). Furthermore, it indicates that the average cell perimeter, roundness, and aspect ratio are approximately 150 μm, 0.6 and 2.2 respectively, suggesting the majority of cells exhibit low sphericity and angular morphologies. The roundness of small cells is closer to 1, which further confirms that small cells are mainly newly divided cells with spherical shape.
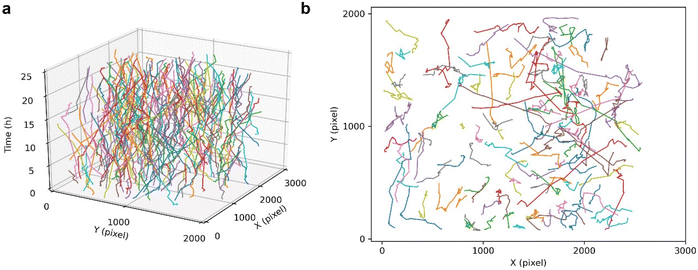
The cell tracking performance of this HFM-Tracker algorithm was further validated by depicting the trajectories of cancer cells over a long period of time. As shown in Fig. 4, the cultured MCF-7 cells actively migrate through the field of view during a 24-hour recording, with several cells even migrating 1000 pixels. The colours in the time-resolved motion trajectories represent individual cells, and it can be easily seen that most cells in the field of view were continuously tracked during the 24-hour recording. Although there are overlapping and crossing motion trajectories of some cells, this proposed HFM-Tracker algorithm could still achieve effective cell recognition and cell tracking.
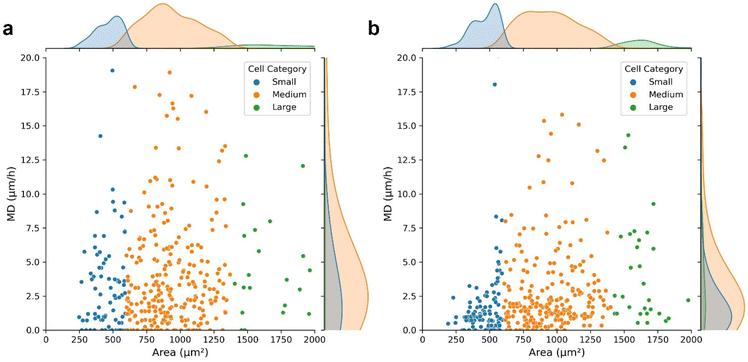
Moreover, the HFM-Tracker algorithm was further applied for the evaluation of the effect of hydrogen peroxide on cellular morphologies and migrations. The cell motion trajectories in Fig. S3† demonstrated that the presence of hydrogen peroxide reduced the cellular mobility effectively. MCF-7 cells in normal conditions (Fig. 5a) and in the presence of 0.5 mM hydrogen peroxide (Fig. 5b) were recognized via the HFM-Tracker algorithm by collecting six images within one hour. The capabilities of cell migration could be revealed by employing the mean displacement (MD), which represents the mean distance (μm) migrated per hour by the cell centroid. Fig. 5 shows the scatter plots of the MD versus the cell area comparing the cells in the absence and presence of hydrogen peroxide. It is observable that the MD of MCF-7 cells was greatly reduced by the incubation with hydrogen peroxide, with more concentrated area distributions of all the cells.
Further time-resolved characteristics, including cell perimeter, area, roundness, aspect ratio and MD are shown in Fig. S4.† It is shown that the MD shows a more obvious distinction to reveal the effect of hydrogen peroxide on the cellular activity. Therefore, HFM-Tracker could be used to comprehensively characterize cells with minimal requirement of bright field images, and serve as a well-adapted algorithm for rapid cell tracking.
4. Conclusion
In summary, a cell tracking algorithm named HFM-Tracker was developed for accurate cell identification and migratory trajectory tracking. The algorithm first obtained the initial octagonal contour frame of target cells by constructing the initial contours of cell images. A CA-module-based regression model was subsequently involved to predict the changes in the cell contours, determining the shape and position of each cell accurately. Finally, an ACM module-based cell tracking algorithm achieved the efficient association and tracking of the motile cells. It is demonstrated that HFM-Tracker exhibits superior performance in various evaluation metrics for detection and tracking, achieving 75% in MOTA and 65% in IDF1. Furthermore, this algorithm provides important insights for broad applications as it allows for a detailed examination of cell morphology changes and migration rates. This is crucial for elucidating the complex interplay between aberrant cellular behaviours in migration-related biological processes, playing an important role in biochemical and clinical fields.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (No. 2022YFA1205004), the National Natural Science Foundation of China (22276089), and Programs for High-Level Entrepreneurial and Innovative Talents Introduction of Jiangsu Province.References
- A. Ortega-Carrion, L. Feo-Lucas and M. Vicente-Manzanares, in Encyclopedia of Cell Biology, ed. R. Bradshaw and P. Stahl, Academic Press, Waltham, 2016, pp. 720–730, DOI:10.1016/b978-0-12-394447-4.20070-9.
- B. Laviña, M. Castro, C. Niaudet, B. Cruys, A. Álvarez-Aznar, P. Carmeliet, K. Bentley, C. Brakebusch, C. Betsholtz and K. Gaengel, Development, 2018, 145, dev161182 CrossRef PubMed.
- A. A. Mosabbir, A. Qudrat and K. Truong, Biotechnol. Bioeng., 2018, 115, 1028–1036 CrossRef PubMed.
- F. Entschladen, T. L. t. Drell, K. Lang, J. Joseph and K. S. Zaenker, Lancet Oncol., 2004, 5, 254–258 CrossRef CAS PubMed.
- W. Fang, X. Lv, Z. Ma, J. Liu, W. Pei and Z. Geng, Micromachines, 2022, 13, 631 CrossRef PubMed.
- C. M. Fife, J. A. McCarroll and M. Kavallaris, Br. J. Pharmacol., 2014, 171, 5507–5523 CrossRef CAS PubMed.
- X. Jin, Z. Demere, K. Nair, A. Ali, G. B. Ferraro, T. Natoli, A. Deik, L. Petronio, A. A. Tang, C. Zhu, L. Wang, D. Rosenberg, V. Mangena, J. Roth, K. Chung, R. K. Jain, C. B. Clish, M. G. Vander Heiden and T. R. Golub, Nature, 2020, 588, 331–336 CrossRef CAS PubMed.
- N. M. Novikov, S. Y. Zolotaryova, A. M. Gautreau and E. V. Denisov, Br. J. Cancer, 2021, 124, 102–114 CrossRef PubMed.
- C. Zimmer, E. Labruyere, V. Meas-Yedid, N. Guillen and J. C. Olivo-Marin, IEEE Trans. Med. Imaging, 2002, 21, 1212–1221 CrossRef PubMed.
- F. Bunyak, K. Palaniappan, S. K. Nath, T. Baskin and G. Dong, presented in part at the 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro, 2006, 2006.
- E. Mendoz and C. T. Lim, Cell. Mol. Bioeng., 2011, 4, 411–426 CrossRef.
- N. Scherf, K. Franke, I. Glauche, I. Kurth, M. Bornhauser, C. Werner, T. Pompe and I. Roeder, Exp. Hematol., 2012, 40, 119–130 CrossRef PubMed.
- J. Stegmaier, J. C. Otte, A. Kobitski, A. Bartschat, A. Garcia, G. U. Nienhaus, U. Strähle and R. Mikut, PLoS One, 2014, 9, e90036 CrossRef PubMed.
- M. Maška, V. Ulman, D. Svoboda, P. Matula, P. Matula, C. Ederra, A. Urbiola, T. España, S. Venkatesan and D. M. Balak, Bioinformatics, 2014, 30, 1609–1617 CrossRef PubMed.
- A. Y. L. Yew and G. Sulong, J. Teknol., 2015, 75, 19–26 Search PubMed.
- V. Ulman, M. Maska, K. E. G. Magnusson, O. Ronneberger, C. Haubold, N. Harder, P. Matula, P. Matula, D. Svoboda, M. Radojevic, I. Smal, K. Rohr, J. Jalden, H. M. Blau, O. Dzyubachyk, B. Lelieveldt, P. Xiao, Y. Li, S. Y. Cho, A. C. Dufour, J. C. Olivo-Marin, C. C. Reyes-Aldasoro, J. A. Solis-Lemus, R. Bensch, T. Brox, J. Stegmaier, R. Mikut, S. Wolf, F. A. Hamprecht, T. Esteves, P. Quelhas, O. Demirel, L. Malmstrom, F. Jug, P. Tomancak, E. Meijering, A. Munoz-Barrutia, M. Kozubek and C. Ortiz-de-Solorzano, Nat. Methods, 2017, 14, 1141–1152 CrossRef CAS PubMed.
- B. Schott, M. Traub, C. Schlagenhauf, M. Takamiya, T. Antritter, A. Bartschat, K. Loffler, D. Blessing, J. C. Otte, A. Y. Kobitski, G. U. Nienhaus, U. Strahle, R. Mikut and J. Stegmaier, PLoS Comput. Biol., 2018, 14, e1006128 CrossRef PubMed.
- N. Emami, Z. Sedaei and R. Ferdousi, Vis. Inform., 2021, 5, 1–13 CrossRef.
- E. Meijering, O. Dzyubachyk and I. Smal, Methods Enzymol., 2012, 504, 183–200 Search PubMed.
- N. Al-Zaben, A. Medyukhina, S. Dietrich, A. Marolda, K. Hunniger, O. Kurzai and M. T. Figge, Sci. Rep., 2019, 9, 3317 CrossRef PubMed.
- H.-F. Tsai, J. Gajda, T. F. Sloan, A. Rares and A. Q. Shen, SoftwareX, 2019, 9, 230–237 CrossRef.
- T. He, H. Mao, J. Guo and Z. Yi, Image Vis. Comput., 2017, 60, 142–153 CrossRef.
- J. Hayashida and R. Bise, presented in part at the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, October 13–17, 2019, Proceedings, Part I 22, 2019.
- J. Hayashida, K. Nishimura and R. Bise, presented in part at the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020.
- C. Payer, D. Štern, T. Neff, H. Bischof and M. Urschler, presented in part at the International Conference on Medical Image Computing and Computer-Assisted Intervention, 2018.
- C. Payer, D. Stern, M. Feiner, H. Bischof and M. Urschler, Med. Image Anal., 2019, 57, 106–119 CrossRef PubMed.
- T. Scherr, K. Loffler, M. Bohland and R. Mikut, PLoS One, 2020, 15, e0243219 CrossRef CAS PubMed.
- N. Aharon, R. Orfaig and B.-Z. Bobrovsky, arXiv, preprint, arXiv:2206.14651, DOI:10.48550/arXiv.2206.14651.
- Y. Zhang, P. Sun, Y. Jiang, D. Yu, F. Weng, Z. Yuan, P. Luo, W. Liu and X. Wang, presented in part at the European Conference on Computer Vision, 2022.
- Y. Chen, Y. Song, C. Zhang, F. Zhang, L. O'Donnell, W. Chrzanowski and W. Cai, presented in part at the 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), 2021.
- S. C. Noctor, V. Martínez-Cerdeño, L. Ivic and A. R. Kriegstein, Nat. Neurosci., 2004, 7, 136–144 CrossRef CAS PubMed.
- T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollár and C. L. Zitnick, presented in part at the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part V 13, Zurich, Switzerland, 2014.
- K. Bernardin and R. Stiefelhagen, EURASIP J. Image Video Process., 2008, 2008, 1–10 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4an00199k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |