Open Access Article
Open Access ArticleEffects of mixed-valence states of Eu-doped FAPbI3 perovskite crystals studied by first-principles calculation
Atsushi
Suzuki
 * and
Takeo
Oku
* and
Takeo
Oku

Department of Materials Science, The University of Shiga Prefecture, 2500 Hassaka, Hikone, Shiga 522-8533, Japan. E-mail: suzuki@mat.usp.ac.jp
First published on 15th March 2021
Abstract
Effects of mixed-valence states of europium (Eu)-incorporated CH(NH2)2PbI3 (FAPbI3) and CH3NH3PbI3 (MAPbI3) perovskite crystals on electronic structures were investigated by first-principles calculation. Partial replacements of europium ions into the perovskite crystal influenced the electronic structures and the effective mass related to carrier mobility. In the case of the FAPb(Eu+3)I3 crystal, there was wide distribution of the 5p orbital of iodine near the valence band, and the 3d orbital of the Eu3+ ion near the conductive band. The incorporation of Eu3+ ion into the crystal slightly caused to increase the effective mass ratio (me*/me, mh*/me) as compared with those of the FAPbI3 crystal, provided the wide distribution of 3d, 4f-5p hybrid orbitals near the valence band, and influenced the band dispersion with a decrease of me*/me and mh*/me, which is expected for improving the carrier mobility. The chemical shifts of 127I-NMR of the MAPb(Eu2+)I3 crystal indicated isotropic behavior. The chemical shifts of 157Eu-NMR and g-tensor depended on the quadrupole interaction based on the electron field gradient and asymmetry parameter in the coordination structure. The electronic correlation based on hybrization of the 3d, 4f-5p orbital in the Eu2+-iodine band promoted the carrier itinerary, which was expected to improve the carrier mobility related to the short circuit current density and the conversion efficiency as the photovoltaic performance.
1 Introduction
Perovskite solar cells have a great advantage for the development of photovoltaic applications using various perovskite crystals with different chemical elements, crystal structures and multilayer cells.1–3 Perovskite solar cells demonstrate high performance of the photovoltaic properties, such as open short circuit voltage, conversion efficiency and single-film by the spin-coating method. The wide-band gap perovskite tandem solar cell with multi-terminal configuration using silicon and gallium arsenide has been developed for the practical use of photovoltaic devices.4,5 The photovoltaic properties were influenced by chemical elements and the crystalline structure in the active layer.6–8 The photovoltaic performance was based on optimization with tuning of the electronic structure, band gap, and the effective mass related to the carrier mobility. For example, the incorporation of an alkali metal,9–12 organic cation,13,14 transition metal,15–23 tin,24,25 and halogen ion,26,27 improved the photovoltaic performance based on the surface modification, and promotion of the crystal nucleation and growth in the perovskite layer. The perovskite solar cells had many problems to solve regarding the long-term stability of the photovoltaic performance for practical use of the photovoltaic devices. To improve the long-term stability of the photovoltaic performance, the decomposition of the perovskite crystal was suppressed by the partial substitution of formamidinium (FA), guanidinium (GA), ethylammonium (EA) and alkali metal ions (sodium, potassium, rubidium and cesium) instead of methyl ammonium (MA) at the A-sites; and transition metals (copper,21 cobalt,28 and nickel29) instead of lead (Pb) ions at the B-sites into the CH3NH3PbX3 (MAPbX3) perovskite crystal, where X indicated the halogen ions (iodine, bromine and chlorine). The surface modifications of the uniform morphology and crystal growth, while suppressing the deterioration, and the formation of the pinhole and cluck had a crucial role in promoting the carrier generation and diffusion without carrier recombination. The photovoltaic performance was associated with the uniform crystal growth, electronic structure and thermodynamic stability.30,31 The tolerance factor varied with the effective ionic radii used for predicting the thermodynamic stability of the crystal as a cubic crystal system.32The transition metal-incorporated perovskite crystal had a high potential to improve the photovoltaic properties based on the electronic structure with the promotion of the photo-induced carrier generation and diffusion in the crystalline layer without defect and pinhole.33,34 For example, a slight addition of copper, cobalt or nickel into the perovskite crystal promoted the crystal nucleation and growth with increasing surface coverage, which improved the photovoltaic performance, while optimizing with the tuning of the electronic structure, band gap and energy levels at the valence band and conduction bands. The photovoltaic performance based on the carrier mobility related with the effective mass was expected by the band dispersion of the perovskite crystals along the direction of the wave vector.
Recently, the slight addition of a lanthanide compound into the perovskite crystal improved the long-term stability of the photovoltaic performance with the reduction of the internal defect and suppression of the degradation.35,36 The photovoltaic properties and the electronic structures of the lanthanide and actinide perovskite compounds were characterized by experimental results using first-principles calculation.37–39
Rare-earth-based compounds have unique types of physical phenomena owing to their heavy-electron behaviours, such as their magnetic properties, fluorescence characteristics, superconductivity and photovoltaic application.40–43 For example, the 4f orbitals of europium are blocked by the closed shell structure of 5s–5p6, making them less susceptible to crystal fields in the coordination structure. The europium compound Eu(III) emits a sharp red fluorescence based on the 4f–4f transition, applying a wavelength converter for the solar cells. The europium compound Eu(II) had a wide area of fluorescence derived from the 4f6–5d1 transition, and the electron correlation of the d, f–p hybrid orbital on the europium ion and ligand, which depended on the degree of metal–ligand charge transfer in the coordination structure. The heavy-electron behaviour based on the Ruderman–Kittel–Kasuya–Yosida exchange interaction of the localized inner 3d and 4f spin through the conduction carrier has the advantage of controlling the electronic structure and effective mass related to the carrier mobility in the perovskite crystal. To better understand the photovoltaic mechanism, the photovoltaic performance, electronic structure, band gap, effective mass of the electron and hole, and the total and partial densities of state have been studied on the basis of experimental results and the first-principles calculation using density functional theory (DFT).44–46 The partial replacement of the europium ion with the B site in the perovskite crystal prevented the decomposition, improving the long-term stability of the performance with the reduction of the internal defect, while suppressing the degradation by the Eu2+–Eu3+ redox shuttle reaction.
The purpose of the present study is to focus on the improvement of the photovoltaic properties by investigating the effects of the mixed valence of europium in the FAPbI3 perovskite crystal. The electronic structure of the Eu-incorporated FAPbI3 perovskite crystal at mixed valence was predicted by first-principles calculation. In particular, the effects of the mixed valence (Eu2+–Eu3+) state, itinerant and localization of the p-3d, 4f hybrid orbital through the europium ion and iodine ligand in the coordination structure were investigated. The electronic structures, electron density distribution, band structure, effective mass related with the carrier mobility, partial density of state (pDOS), g-tensor, chemical shifts of 127I-NMR, 207Pb-NMR and 153Eu-NMR, electronic field gradient (EFG) and asymmetric parameter (η) were considered in the Eu-incorporated FAPbI3 or MAPbI3 perovskite crystal at the Eu2+–Eu3+ valence states. The photovoltaic mechanism was discussed on the basis of the band structure with the effective masses of the electron and hole, band gap, pDOS, and electronic correlation between the 3d, 4f orbital of the europium ion and 5p orbital of iodine as the nearest neighbour ligand in the coordination structure.
2 Calculation
The electronic structures of the perovskite crystals were single-point-calculated with crystallographic structural data obtained from X-ray diffraction patterns. The ab initio quantum calculations were performed using the Vanderbilt ultrasoft pseudo-potentials, scalar relativistic generalized gradient approximations and Perdew–Burke–Ernzerhof (GGA-PBE) exchange–correlation functional and density functional theory (DFT+U, U = 6.0 eV) without considering the spin-orbital coupling effect. (Quantum Espresso software). The basis-functions were used properly according to the cases of the itinerant and localized electron system. Plane-wave basis set cut offs for the wave functions and charge density were set at 25 and 225 Rydberg (Ry). The perovskite crystals were constructed with experimental lattice constants (a = 6.362 Å) and crystal system (cubic Pm![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m).47 The uniform k-point grid (4 × 4 × 4) in the Brillouin zone was used to calculate the electronic structure and partial density of state. The FAPbI3 perovskite crystals (cubic Pm
m).47 The uniform k-point grid (4 × 4 × 4) in the Brillouin zone was used to calculate the electronic structure and partial density of state. The FAPbI3 perovskite crystals (cubic Pm![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m) were formed as the cubic system with an initial unit cell (1 × 1 × 1) using the experimental lattice constant measured by X-ray diffraction data. As for the Eu-incorporated perovskite crystal modeling with supercells (2 × 2 × 2), parts of the Pb atom at the B-sites were substituted with the europium ion for the one-atom substitution at the center of the cubic structure. The Eu-incorporated FAPbI3 perovskite cubic crystals as models were constructed with the supercells (2 × 2 × 2) as an initial unit cell, and were used for the band calculation. The charge of the Eu-incorporated FAPbI3 perovskite crystal was fixed to be +1 positive charge and in the neutral state in the unit cell, which corresponded to the +3 and +2 charges of the Eu ion substituted in the Pb2+ ion in the perovskite crystal. The band structures, effective mass and band gap were analysed for the Brillouin zone of the lattice of the perovskite crystal along the direction of the wave vector. The path for the FAPbI3 perovskite crystal was set as follows: Γ (0, 0, 0) → X (0, 1/2, 0) → M (1/2, 1/2, 0) → Γ → R (1/2, 1/2, 1/2) → X, M → R. The Pb cation was set at the position of Γ (0, 0, 0). The FA cation was set in the center position of the unit cell (1 × 1 × 1). The path for the FAPb(Eu)I3 perovskite crystals was set as follows: Γ (0, 0, 0) → X (1/2, 0, 1/2) → W (1/2, 1/4, 3/4) → K (3/8, 3/8, 3/4) → Γ → L (1/2, 1/2, 1/2) → U (5/8, 1/4, 5/8) → W (1/2, 1/4, 3/4) → L → K|U → X. For the minor partial replacement, the Eu cation was replaced with a Pb cation in the center position of the supercell (2 × 2 × 2). The Fermi energy was set at zero. The density of states (DOS) and partial density of states (pDOS) were calculated to better understand the energy level for each orbital near the valence band (VB) and conduction band (CB). The chemical shifts of the 127I-NMR, 207Pb-NMR, and 157Eu-NMR spectra, and the electronic field gradient (EFG) and asymmetry parameter (η) of the Eu-doped MAPbI3 crystal were calculated by hybrid DFT using the unrestricted B3LYP (UB3LYP) and GIAO with SSDall as the basis set (Gaussian 09). The Eu-doped MAPbI3 perovskite crystal and the MAPbI3 perovskite crystals as the cluster model were formed using the experimental lattice constants (a = 6.391 Å) measured by X-ray diffraction data.48,49 The perovskite crystals (cubic Pm
m) were formed as the cubic system with an initial unit cell (1 × 1 × 1) using the experimental lattice constant measured by X-ray diffraction data. As for the Eu-incorporated perovskite crystal modeling with supercells (2 × 2 × 2), parts of the Pb atom at the B-sites were substituted with the europium ion for the one-atom substitution at the center of the cubic structure. The Eu-incorporated FAPbI3 perovskite cubic crystals as models were constructed with the supercells (2 × 2 × 2) as an initial unit cell, and were used for the band calculation. The charge of the Eu-incorporated FAPbI3 perovskite crystal was fixed to be +1 positive charge and in the neutral state in the unit cell, which corresponded to the +3 and +2 charges of the Eu ion substituted in the Pb2+ ion in the perovskite crystal. The band structures, effective mass and band gap were analysed for the Brillouin zone of the lattice of the perovskite crystal along the direction of the wave vector. The path for the FAPbI3 perovskite crystal was set as follows: Γ (0, 0, 0) → X (0, 1/2, 0) → M (1/2, 1/2, 0) → Γ → R (1/2, 1/2, 1/2) → X, M → R. The Pb cation was set at the position of Γ (0, 0, 0). The FA cation was set in the center position of the unit cell (1 × 1 × 1). The path for the FAPb(Eu)I3 perovskite crystals was set as follows: Γ (0, 0, 0) → X (1/2, 0, 1/2) → W (1/2, 1/4, 3/4) → K (3/8, 3/8, 3/4) → Γ → L (1/2, 1/2, 1/2) → U (5/8, 1/4, 5/8) → W (1/2, 1/4, 3/4) → L → K|U → X. For the minor partial replacement, the Eu cation was replaced with a Pb cation in the center position of the supercell (2 × 2 × 2). The Fermi energy was set at zero. The density of states (DOS) and partial density of states (pDOS) were calculated to better understand the energy level for each orbital near the valence band (VB) and conduction band (CB). The chemical shifts of the 127I-NMR, 207Pb-NMR, and 157Eu-NMR spectra, and the electronic field gradient (EFG) and asymmetry parameter (η) of the Eu-doped MAPbI3 crystal were calculated by hybrid DFT using the unrestricted B3LYP (UB3LYP) and GIAO with SSDall as the basis set (Gaussian 09). The Eu-doped MAPbI3 perovskite crystal and the MAPbI3 perovskite crystals as the cluster model were formed using the experimental lattice constants (a = 6.391 Å) measured by X-ray diffraction data.48,49 The perovskite crystals (cubic Pm![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m) were constructed with supercells (2 × 2 × 2) as cluster models, which were fixed to be 8 as the positive charge of MA. The numbers of the charge and spin were adjusted to be +9 and 0 (singlet) for the Eu3+-doped MAPbI3 perovskite crystal, and +8 and 7/2 (octet) for the Eu2+-doped MAPbI3 perovskite crystal.
m) were constructed with supercells (2 × 2 × 2) as cluster models, which were fixed to be 8 as the positive charge of MA. The numbers of the charge and spin were adjusted to be +9 and 0 (singlet) for the Eu3+-doped MAPbI3 perovskite crystal, and +8 and 7/2 (octet) for the Eu2+-doped MAPbI3 perovskite crystal.
3 Results and discussion
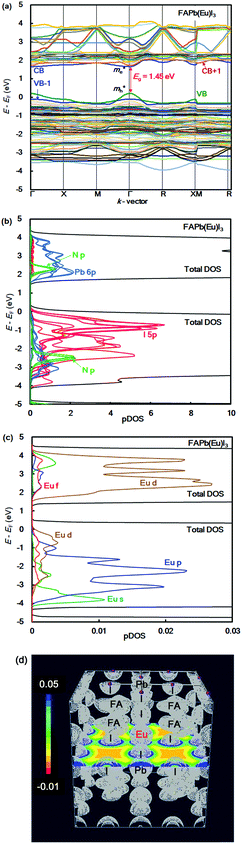
The band structure, partial density of state, and electronic density distribution in the FAPb(Eu+3)I3 perovskite crystal were calculated by first-principles calculation. The band structure and partial density of state (pDOS), and the electronic density distribution in the FAPb(Eu3+)I3 perovskite crystal are shown in Fig. 1(a)–(d). The calculated energy levels at the valence band and conduction band, band gap, and effective mass ratio of the electron and hole in the electron structure are listed in Table 1. The obtained direct band gap was found to be 1.45 eV, as shown in Fig. 1(a) and Table 1. From the band dispersion curvature at the wave vector near Γ(0, 0, 0), the effective mass ratio of the electron and hole were estimated to be 0.04 and 0.07, respectively. This result indicates the light electronic system that makes it easy for the carriers to diffuse into the crystal, which is expected to improve the carrier mobility, short circuit current density and conversion efficiency. The partial density of state and enlarged view of 3p, 3d and 4f of Eu3+ in the FAPb(Eu3+)I3 perovskite crystal were considered, as shown in Fig. 1(b) and (c). The 5p orbital of iodine, and the 3d and p orbitals of Eu3+ were widely distributed near the valence band state. Near the conduction band, the 6p orbital of Pb, and the 3d and 4f orbitals of Eu3+ were widely distributed. The electron density distribution of the FAPb(Eu)I3 perovskite crystal are shown in Fig. 1(d). The electronic density distributions were delocalized near the nearest neighbour Eu–I band in the coordination structure. The itinerant behaviour indicates a different tendency from the localized system of the FAEuI3 perovskite crystal.45| Perovskite crystals | VB (eV) | CB (eV) | Eg (eV) | Total E (eV per cell) | m e*/m0 | m h*/m0 |
|---|---|---|---|---|---|---|
| FAPb0.875(Eu3+)0.125I3 | 2.90 | 4.35 | 1.45 | −273 | 0.04 | 0.07 |
| FAPb0.875(Eu2+)0.125I3 | 2.72 | 4.25 | 1.53 | −337 | 0.03 | 0.01 |
| FAPbI3 | 3.94 | 5.30 | 1.36 | −275 | 0.02 | 0.03 |
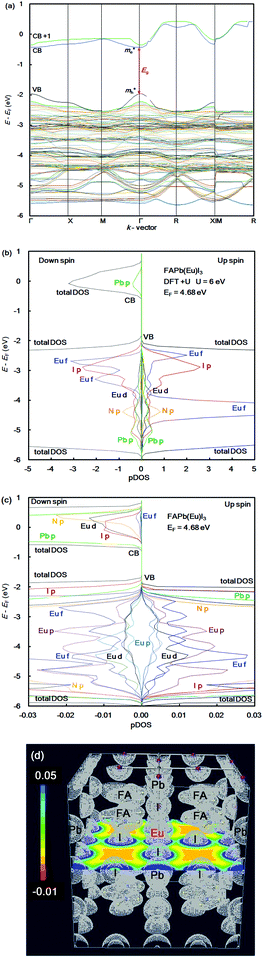
In the case of the FAPb(Eu2+)I3 perovskite crystal, the band structure, pDOS and the electronic density distribution were considered, as shown in Fig. 2(a)–(c). The band structure had the direct band gap of Eg of 1.53 eV near the wave vector at Γ (0, 0, 0). By the band dispersion curvature near Γ (0, 0, 0), the effective mass of the electron and hole was calculated to be 0.03 and 0.01, respectively. The itinerary characteristics based on the small values of the effective mass ratio indicates the light electronic system, where the carriers can easily diffuse with an increase of mobility in the FAPb(Eu2+)I3 perovskite crystal, as compared with those of the FAPb(Eu3+)I3 perovskite crystal. The partial density of state and enlarged view of the 3p, 3d and 4f orbitals of Eu2+ in the crystal were considered, as shown in Fig. 2(b) and (c). The 5p orbital of iodine, and the 3d, 4f orbitals of Eu2+ were widely distributed. Intensities of the 4f orbitals were increased near the valence band. Near the conduction band, the 6p orbitals of Pb were distributed and increased. Incorporation of the Eu2+ ion into the crystal did not influence the pDOS of the 5p orbital of Pb and the 5p orbital of iodine in the crystal. This behaviour is expected to have a slight influence on the carrier mobility. The electron density distribution in the perovskite crystal was considered, as shown in Fig. 2(d). The electronic density distribution of the 3d, 4f-p hybrid orbital between the Eu–I band was delocalized. The electronic behaviour should have the itinerant characteristics with the promotion of the carrier diffusion on the 5p orbital of I in the crystal structure. In the case of the standard system using the FAPbI3 perovskite crystal, the band structure, pDOS and the electronic density distribution were considered as shown in Fig. 3(a)–(c). As the direct transition near the wave vector near R (1/2, 1/2, 1/2), the band gap of Eg was obtained to be 1.36 eV. Based on the band dispersion curvature, the effective mass ratio of the electron and hole to the free electron were estimated to be 0.02 and 0.03, respectively. The calculated effective mass indicates the itinerant characteristics as the light electronic system with the increase of the carrier mobility, improving the photovoltaic performance. In the partial density of state, as shown in Fig. 3(b), the 5p orbital of iodine was widely distributed, and the intensity of DOS was increased near the valence band. Near the conduction band, the 6p orbitals of Pb were distributed. The electronic density distribution was localized near the 2p orbital of nitrogen in FA, as shown in Fig. 3(c). The calculated results were consistent with what was previously reported. The energy levels at the VB and CB, band gap and effective mass ratio were compared in the three systems, as listed in Table 1. Incorporation of the Eu2+ ion into the perovskite crystal provided low energy levels at VB with an increase of the band gap, and decrease of mh*/m0. The behaviour should improve the open circuit voltage and carrier-mobility related to the short circuit current and the conversion efficiency. In particular, the incorporation of the Eu2+ ion into the crystal improved the photovoltaic performance and the thermal stability based on the total energy per cell, as compared with the incorporation of the Eu3+ ion into the perovskite crystal.
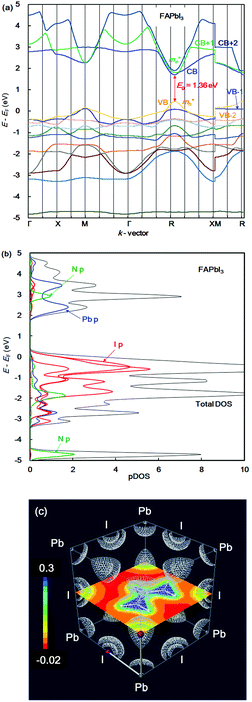 | ||
| Fig. 3 (a) Band structure, (b) partial density of state, and (c) contour map of the electron density distribution of the FAPbI3 perovskite crystal. | ||
The electronic correlation was considered by the magnetic parameters, such as chemical shift of 127I-NMR, 157Eu-NMR, g-tensor, EFG and η near the coordination structure. The magnetic interaction based on the electron correlation will be explained by the spin Hamiltonian. The spin Hamiltonian (Htotal) can be formulated with four terms, as noted by eqn (1). These terms represent the following interactions: electron and nuclear Zeeman interaction, hyperfine structure of spin-nuclear interaction, fine structure of dipole–dipole interaction, and nuclear quadrupole interaction. The magnetic parameter of the principal values and axes of g-tensor are the sum of the isotropic and anisotropic parts, as noted by eqn (2) and (3). The anisotropic g-tensor is mainly related to the second perturbation with regards to the extent of the spin-local interaction based on the electron density distribution and hybridization of the s, p and d-hybrid orbitals on the central metal in the coordination structure.
| Htotal = gsβsSH − gNβNIH + SAI + IQI | (1) |
| gij = geδij − 2λΛij ge = 2.002319 | (2) |
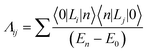 | (3) |
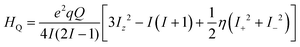 | (4) |
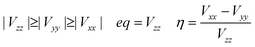 | (5) |
In the case of the nuclear spin quantum number of 5/2 for the 153Eu and 127I ions, the influence of the nuclear quadrupole interaction on the chemical shift and g-tensor needs to be considered in accordance with the first and second perturbations. The nuclear quadrupole interaction is based on the multiplication of the electron density distribution and nuclear quadrupole moment based on the Q-tensor, EFG and η generated by the charge distribution around the nucleus. The chemical shifts are remarkably shifted by the nuclear quadrupole interaction in proportion to the extent of the value in Q, atomic charge, EFG tensor and η. In particular, the chemical shifts of 127I-NMR in the MAPb(Eu)I3 perovskite crystal depend on the extent of the nuclear quadrupole interaction based on the Q-tensor related with EFG and η of the iodine ligand with a slight extent of the atomic charge and electron density distribution on the Eu–I band.
The effects of the mixed-valence state of the europium ion on the chemical shifts of 127I-NMR, 207Pb-NMR and 153Eu-NMR of the MAPb(Eu)I3 perovskite crystal were investigated, as shown in Fig. 4. As shown in Fig. 4(a), the chemical shifts of 127I-NMR of the MAPb(Eu3+)I3 perovskite crystal were widely split in the high magnetic field. The behaviour indicates the anisotropy behaviour. The chemical shifts were based on the magnetic interaction between the nearest neighbour ligand and europium ion in the coordination structure. The magnetic parameters, chemical shift of 153Eu-NMR, g-tensor, EFG and η are listed in Table 2. The magnetic parameters of EFG and η were estimated to be −0.0028, −0.0063, 0.0091 and 0.38, respectively. The chemical shifts of 153Eu-NMR of the MAPb(Eu3+)I3 perovskite crystal worked on the basis of the nuclear quadruple interaction based on EFG and η in the coordination structure.
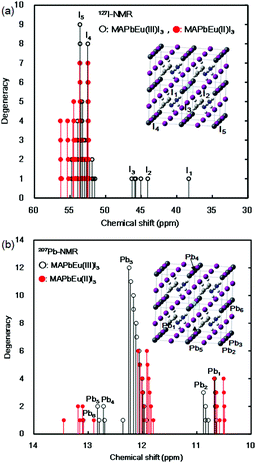 | ||
| Fig. 4 Chemical shifts of: (a) 127I-NMR and (b) 207Pb-NMR spectra of the MAPb(Eu)I3 perovskite crystals. | ||
| Spin charge | Chemical shift | g-Tensor | EFG (×10−4) | Eu (ppm) | η (e) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| g xx | g yy | g zz | V xx | V yy | V zz | |||||
| Eu(III) | 0 | 0.62 | — | — | — | −28 | −63 | 91 | −424![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 857 |
0.38 |
| Eu(II) | 7.08 | 0.68 | 2.27070 | 2.27615 | 2.30975 | −3 | −5 | 9 | −424![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868 868 |
0.20 |
In the case of the MAPb(Eu2+)I3 perovskite crystal, the chemical shifts of 127I-NMR indicate the isotropic behaviour with shifting to a low magnetic field, as shown in Fig. 4(a). The isotropic magnetic interaction slightly worked on the slight effect of EFG and η near the coordination structure. The chemical shifts of 207Pb-NMR in the perovskite crystals are shown in Fig. 4(b). By comparing both cases, the chemical shifts of 207Pb-NMR of the MAPb(Eu2+)I3 crystal slightly shifted to the high magnetic field. This behaviour would be derived from the nuclear-nuclear spin interaction between the lead ion and iodine ligand in the coordination structure with a slight perturbation due to the incorporation of the Eu2+ ion. As listed in Table 2, the principal values of g-tensor of the Eu2+ ion in the MAPb(Eu2+)I3 crystal were calculated to be 2.27070, 2.27615 and 2.30975, respectively. The anisotropic g-tensor was mainly related with the second perturbation with the extent of the spin-local interaction based on the electron density distribution and hybridization of the 3d, 4f, 5p hybrid orbitals in the coordination structure with a slight distortion. The chemical shifts of the 153Eu-NMR of the MAPb(Eu2+)I3 crystal were associated with the weak magnetic interaction of the nuclear quadrupole interaction based on EFG (Vxx, Vyy, Vzz = −0.0003, −0.0005, 0.0009) and η = 0.20. The electronic correlation based on the charge transfer from the 3d, 4f hybrid orbitals of the europium ion to the 5p orbital of the iodine ion as the ligand determined the itinerary system with an increase of the carrier mobility was related to the reciprocal of the effective mass of the hole. Incorporation of the Eu ion at the mixed-valence state influenced the electronic correlation based on the nuclear quadrupole interaction of the 3d, 4f, 5p hybrid orbitals in the coordination structure.
The crystal field perturbation with incorporation of the Eu ion at the mixed-valence state was associated with the hybrid state of the 3d, 4f, 5p orbitals on the Eu and iodine ions in the coordination structure. The fluctuations of the electron density distribution with the electron level splitting of the 3d, 4f, 5p hybrid orbitals influenced the band dispersion behaviour with an effective mass related to the carrier mobility. The narrow band dispersions in a certain path indicate the anisotropic and maximum carrier mobility related with a decrease of the efficiency mass in the path Γ (0, 0, 0) → R (1/2, 1/2, 1/2) for the FAPbI3 crystal, and path M (1/2, 1/2, 0) → Γ (0, 0, 0) for the Eu-incorporated FAPbI3 crystals. The anisotropic behaviour of the effective mass related to the carrier mobility, and the magnetic parameters of the chemical shift and g-tensor of the Eu and iodine ions were associated with the crystal field perturbation of the energy level splitting and the nuclear quadruple interaction based on EFG and η in the coordination structure. The itinerary behaviour would be promoted to increase the carrier mobility, predicting an improvement of the short circuit current density and conversion efficiency as the photovoltaic performance. Actually, the perovskite crystals have some grain boundaries, which cause decomposition, while desorbing the methyl ammonium cation and iodine anion.13 When europium ions at the mixed-valence state exist near the grain boundaries, the perovskite decomposition is suppressed, while maintaining the crystal structure and the lattice constant.36 In this case, the valence fluctuation of the europium ion would not influence the electronic structure related to the electron density distribution of the 3d, 4f, 5p hybrid orbitals in the coordination structure. A partial replacement for the Eu ion instead of the Pb ion in the crystal structure slightly caused fluctuations in the coordination structure due to a slight difference in the radius of the lead ion and europium ion at the mixed-valence state.
The valence fluctuation of the Eu2+ and Eu3+ ions as the mixed-valence state influences the redox shuttle reaction, and charge transfer between the metal and ligand in the perovskite crystal. The mechanisms have an itinerant variation of the conduction characteristics based on the exchange interaction between the 3d–4f hybrid orbitals of the Eu ion and 5p orbital of the iodine ion in the coordination structure. The crystal field distortion depends on the amount of Eu ion. The distortion of the coordination structure is reflected in the band structure, chemical shift of the 127I-NMR and g-tensor of the Eu ion. The crystal field perturbations of the energy level splitting of the 3d, 4f, 5p hybrid orbitals are associated with the band dispersion related to the effective mass, and magnetic interaction of the nuclear quadrupole interaction based on EFG and η. The electronic structures of the lattice doping of the lanthanide ions into the MAPbI3 perovskite crystals were considered.37–39 The complete replacement of the lanthanide ions strongly influenced the electronic and optical properties in association with the carrier localization. The addition of a small amount of Eu ions in the range of 0.15–4.8% will not influence the state of the crystal structure with defects and magnetic interaction based on the exchange interaction between the 4f–4f spins in the europium ion.36 The valence change of the europium ion will not cause new defects, promoting the redox shuttle reaction, the crystal nucleation and the long-term stability of the performance with a reduction of the internal decomposition. When the Eu ion is partially replaced, the band structures based on the electronic correlation are affected by the crystal field perturbation with incorporation of the europium ion at the mixed-valence state. Adjusting the doping concentration of europium was investigated by experimental results.50 As an optimum value, the mole ratio of Eu to Pb atom of 4% will improve the long-term photovoltaic performance. In the case of the over-addition of the Eu ion to more than 5%, the degenerate energy level splitting will be caused by the crystal structure distortion. Excessive addition of Eu will cause precipitation of the unreacted materials in the perovskite crystal. Depending on the addition concentration, the competitive action of the Kondo effect and Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction between the conductive electron and the localized 4f-spin in the perovskite crystal effectively work on the photovoltaic performance. The electronic correlation between the electronic structures and magnetic interactions based on the nuclear quadrupole interactions will be associated with the photovoltaic characteristics in the case of other rare metal ions. The electronic correlation based on the crystal field perturbation is expected to improve the photovoltaic mechanism and the long-term conversion efficiency.
4 Conclusions
The partial replacement of Eu at the Pb site in the perovskite crystal influenced the electronic structure, the effective mass related to the carrier mobility and Eg with the energy level at the valence band. In the case of the FAPb(Eu3+)I3 crystal, the 3d and 4f orbitals of the Eu ion appeared near the VB, and the 3d orbital was widely distributed near CB. From the slope of the band dispersion near the VB and CB, the effective mass ratios (me*/me and mh*/me) were slightly increased by the incorporation of the Eu3+ ion. In the case of the FAPb(Eu2+)I3 crystal, the 4f orbitals of the Eu2+ ion and 5p orbital of the iodine ion strongly appeared near VB, and the 3d orbital of the Eu2+ ion and 5p orbital on the Pb ion were distributed near CB. Incorporation of the Eu2+ ion into the crystal decreased the effective mass ratio (me*/me and mh*/me). These results indicate the promotion of the carrier itinerary related to the mobility, which is expected for improvement of the short circuit current density and conversion efficiency. The chemical shifts of 127I-NMR of the MAPb(Eu3+)I3 crystal showed the splitting behaviour in the high magnetic field side. The chemical shifts of the 127I-NMR of the MAPb(Eu2+)I3 crystal demonstrated a narrow splitting in the low magnetic field, suggesting the isotropic behaviour. The magnetic behaviours were dependent on the extent of the nuclear quadrupole interaction based on EFG and η in the coordination structure. The electronic correlation of the 3d, 4f, and 5p hybrid orbitals through the nearest neighbour Eu2+-iodine band promoted the carrier itinerary, predicting improvement of the carrier mobility related to the short circuit current density and conversion efficiency as the photovoltaic performance.Conflicts of interest
There are no conflicts to declare.Notes and references
- S. P. Dunfield, L. Bliss, F. Zhang, J. M. Luther, K. Zhu, M. F. A. M. Hest, M. O. Reese and J. J. Berry, Adv. Energy Mater., 2020, 10, 1904054, DOI:10.1002/aenm.201904054.
- M. Jeong, I. W. Choi, E. M. Go, Y. Cho, M. Kim, B. Lee, S. Jeong, Y. Jo, H. W. Choi, J. Lee, J.-H. Bae, S. K. Kwak, D. S. Kim and C. Yang, Science, 2020, 369, 1615–1620, DOI:10.1126/science.abb7167.
- Z. Yang, Z. Yu, H. Wei, X. Xiao, Z. Ni, B. Chen, Y. Deng, S. N. Habisreutinger, X. Chen, K. Wang, J. Zhao, P. N. Rudd, J. J. Berry, M. C. Beard and J. Huang, Nat. Commun., 2019, 10, 4498, DOI:10.1038/s41467-019-12513-x.
- Z. Li, T. H. Kim, S. Y. Han, Y. J. Yun, S. Jeong, B. Jo, S. A. Ok, W. Yim, S. H. Lee, K. Kim, S. Moon, J. Y. Park, T. K. Ahn, H. S. J. Lee and H. J. Park, Adv. Energy Mater., 2020, 10, 1903085, DOI:10.1002/aenm.201903085.
- D. Kim, H. J. Jung, I. J. Park, B. W. Larson, S. P. Dunfield, C. Xiao, J. Kim, J. Tong, P. Boonmongkolras, S. G. Ji, F. Zhang, S. R. Pae, M. Kim, S. B. Kang, V. Dravid, J. J. Berry, J. Y. Kim, K. Zhu, D. H. Kim and B. Shin, Science, 2020, 368, 155–160, DOI:10.1126/science.aba3433.
- D. P. McMeekin, G. Sadoughi, W. Rehman, G. E. Eperon, M. Saliba, M. T. Hörantner, A. Haghighirad, N. Sakai, L. Korte, B. Rech, M. B. Johnston, L. M. Herz and H. J. Snaith, Science, 2016, 351, 151–155, DOI:10.1126/science.aad5845.
- A. Suzuki, H. Okada and T. Oku, Energies, 2016, 9, 376, DOI:10.3390/en9050376.
- T. Kishimoto, A. Suzuki, N. Ueoka and T. Oku, J. Ceram. Soc. Jpn., 2019, 127, 491–497, DOI:10.2109/jcersj2.18214.
- Y. Wang, M. I. Dar, L. K. Ono, T. Zhang, M. Kan, Y. Li, L. Zhang, X. Wang, Y. Yang, X. Gao, Y. Qi, M. Grätzel and Y. Zhao, Science, 2019, 365, 591–595, DOI:10.1126/science.aav8680.
- Z. Tanga, S. Uchida, T. Bessho, T. Kinoshita, H. Wang, F. Awai, R. Jono, M. M. Maitani, J. Nakazaki, T. Kubo and H. Segawa, Nano Energy, 2018, 45, 184–192, DOI:10.1016/j.nanoen.2017.12.047.
- Y. Chen, N. Li, L. Wang, L. Li, Z. Xu, H. Jiao, P. Liu, C. Zhu, H. Zai, M. Sun, W. Zou, S. Zhang, G. Xing, X. Liu, J. Wang, D. Li, B. Huang, Q. Chen and H. Zhou, Nat. Commun., 2019, 10, 1112, DOI:10.1038/s41467-019-09093-1.
- T. Oku, S. Kandori, M. Taguchi, A. Suzuki, M. Okita, S. Minami, S. Fukunishi and T. Tachikawa, Energies, 2020, 13, 4776, DOI:10.3390/en13184776.
- A. D. Jodlowski, C. R. Carmona, G. Grancini, M. Salado, M. Ralaiarisoa, S. Ahmad, N. Koch, L. Camacho, G. Miguel and M. K. Nazeeruddin, Nat. Energy, 2017, 2, 972–979, DOI:10.1038/s41560-017-0054-3.
- M. I. Saidaminov, J. Kim, A. Jain, R. Q. Bermudez, H. Tan, G. Long, F. Tan, A. Johnston, Y. Zhao, O. Voznyy and E. H. Sargent, Nat. Energy, 2018, 3, 648–654, DOI:10.1038/s41560-018-0192-2.
- W. Xu, L. Zheng, X. Zhang, Y. Cao, T. Meng, D. Wu, L. Liu, W. Hu and X. Gong, Adv. Energy Mater., 2018, 8, 1703178, DOI:10.1002/aenm.201703178.
- X. Gong, L. Guan, H. Pan, Q. Sun, X. Zhao, H. Li, H. Pan, Y. Shen, Y. Shao, L. Sun, Z. Cui, L. Ding and M. Wang, Adv. Funct. Mater., 2018, 28, 1804286, DOI:10.1002/adfm.201804286.
- H. Zheng, G. Liu, X. Xu, A. Alsaedi, T. Hayat, X. Pan and S. Dai, ChemSusChem, 2018, 11, 3269–3275, DOI:10.1002/cssc.201801171.
- A. Suzuki and T. Oku, Heliyon, 2018, 4, e00755, DOI:10.1016/j.heliyon.2018.e00755.
- A. Kooijman, L. A. Muscarella and R. M. Williams, Appl. Sci., 2019, 9, 1678, DOI:10.3390/app9081678.
- H. X. Zhu, X. H. Wang and G. C. Zhuang, Appl. Phys. A, 2019, 125, 45, DOI:10.1007/s00339-018-2347-1.
- N. Ueoka, T. Oku and A. Suzuki, RSC Adv., 2019, 9, 24231, 10.1039/c9ra03068a.
- K. L. Wang, R. Wang, Z. K. Wang, M. Li, Y. Zhang, H. Ma, L. S. Liao and Y. Yang, Nano Lett., 2019, 19, 5176, DOI:10.1021/acs.nanolett.9b01553.
- N. Ueoka and T. Oku, ACS Appl. Energy Mater., 2020, 3, 7272–7283, DOI:10.1021/acsaem.0c00182.
- J. Tong, Z. Song, D. H. Kim, X. Chen, C. Chen, A. F. Palmstrom, P. F. Ndione, M. O. Reese1, S. P. Dunfield, O. G. Reid, J. Liu, F. Zhang, S. P. Harvey, Z. Li, S. T. Christensen, G. Teeter, D. Zhao, M. M. A. Jassim, M. F. A. M. Hest, M. C. Beard, S. E. Shaheen, J. J. Berry, Y. Yan and K. Zhu, Science, 2019, 364, 475–479, DOI:10.1126/science.aav7911.
- L. Peng and W. Xie, RSC Adv., 2020, 10, 14679–14688, 10.1039/D0RA02584D.
- A. Suzuki, M. Kato, N. Ueoka and T. Oku, J. Electron. Mater., 2019, 48, 3900–3907, DOI:10.1007/s11664-019-07153-2.
- N. Li, S. Tao, Y. Chen, X. Niu, C. K. Onwudinanti, C. Hu, Z. Qiu, Z. Xu, G. Zheng, L. Wang, Y. Zhang, L. Li, H. Liu, Y. Lun, J. Hong, X. Wang, Y. Liu, H. Xie, Y. Gao, Y. Bai, S. Yang, G. Brocks, Q. Chen and H. Zhou, Nat. Energy, 2019, 4, 408–415, DOI:10.1038/s41560-019-0382-6.
- W. Xu, L. Zheng, X. Zhang, Y. Cao, T. Meng, D. Wu, L. Liu, W. Hu and X. Gong, Adv. Energy Mater., 2018, 8, 1703178, DOI:10.1002/aenm.201703178.
- X. Gong, L. Guan, H. Pan, Q. Sun, X. Zhao, H. Li, H. Pan, Y. Shen, Y. Shao, L. Sun, Z. Cui, L. Ding and M. Wang, Adv. Funct. Mater., 2018, 28, 1804286, DOI:10.1002/adfm.201804286.
- A. Suzuki and T. Oku, Appl. Surf. Sci., 2019, 483, 912–921, DOI:10.1016/j.apsusc.2019.04.049.
- A. Suzuki, Y. Miyamoto and T. Oku, J. Mater. Sci., 2020, 55, 9728–9738, DOI:10.1007/s10853-020-04511-y.
- T. Oku, Rev. Adv. Mater. Sci., 2020, 59, 264–305, DOI:10.1515/rams-2020-0015.
- A. Suzuki and T. Oku, Phys. Solid State, 2019, 61, 1074–1085, DOI:10.1134/S1063783419060258.
- A. Suzuki, M. Oe and T. Oku, J. Electron. Mater, 2021, 50 DOI:10.1007/s11664-021-08759-1.
- M. Pazoki and T. Edvinsson, Sustainable Energy Fuels, 2018, 2, 1430–1445, 10.1039/C8SE00143J.
- L. Wang, H. Zhou, J. Hu, B. Huang, M. Sun, B. Dong, G. Zheng, Y. Huang, Y. Chen, L. Li, Z. Xu, N. Li, Z. Liu, Q. Chen, L. D. Sun and C. H. Yan, Science, 2019, 363, 265–270, DOI:10.1126/science.aau5701.
- A. Bala and V. Kumar, J. Phys. Chem. C, 2019, 123, 6965–6969, DOI:10.1021/acs.jpcc.8b10261.
- J. Duan, Y. Zhao, X. Yang, Y. Wang, B. He and Q. Tang, Adv. Energy Mater., 2018, 8, 1802346, DOI:10.1002/aenm.201802346.
- J. Tian, Q. Xue, Q. Yao, N. Li, C. J. Brabec and H.-L. Yip, Adv. Energy Mater., 2020, 10, 2000183, DOI:10.1002/aenm.202000183.
- J. A. F. Livas, R. S. Pérez, S. Botti, S. Goedecker and M. A. L. Marques, J. Phys. Mater., 2019, 2, 025003, DOI:10.1088/2515-7639/ab083e.
- S. Gabani, K. Flachbart, K. Siemensmeyer and T. Mori, J. Alloys Compd., 2020, 821, 153201, DOI:10.1016/j.jallcom.2019.153201.
- Y. Chen, S. Liu, N. Zhou, N. Li, H. Zhou, L.-D. Sun and C.-H. Yan, Prog. Mater. Sci., 2020, 18, 100737, DOI:10.1016/j.pmatsci.2020.100737.
- S. Yang, H. Zhao, Y. Han, C. Duan, Z. Liu and S. F. Liu, Small, 2019, 15, 1904387, DOI:10.1002/smll.201904387.
- Z. Song, W. Xu, Y. Wu, S. Liu, W. Bi, X. Chen and H. Song, Small, 2020, 16, 2001770, DOI:10.1002/smll.202001770.
- M. Pazoki, A. Röckert, M. J. Wolf, R. Imani, T. Edvinsson and J. Kullgren, J. Mater. Chem. A, 2017, 5, 23131–23138, 10.1039/C7TA07716E.
- Y. Yang, D.-W. Han, Y. Yang, S.-W. Yi, Q. Yuan, D.-Y. Zhou and L. Feng, APL Mater., 2020, 8, 071102, DOI:10.1063/5.0011918.
- M. T. Weller, O. J. Weber, J. M. Frost and A. Walsh, J. Phys. Chem. Lett., 2015, 6, 3209–3212, DOI:10.1021/acs.jpclett.5b01432.
- H. Mashiyama, Y. Kurihara and T. Azetsu, J. Korean Phys. Soc., 1998, 32, S156–S158 CAS.
- T. Oku, Solar cells and energy materials, De Gruyter, Berlin, 2017. DOI:10.1515/9783110298505.
- X. Wu, H. Li, K. Wang, X. Sun and L. Wang, RSC Adv., 2018, 8, 11095–11101, 10.1039/C7RA12754E.
| This journal is © The Royal Society of Chemistry 2021 |