Mutually-dependent kinetics and energetics of photocatalyst/co-catalyst/two-redox liquid junctions†
Zhenhua
Pan‡
 ab,
Rito
Yanagi‡
ab,
Qian
Wang
c,
Xin
Shen
ab,
Qianhong
Zhu
ab,
Yudong
Xue
abd,
Jason A.
Röhr
ab,
Takashi
Hisatomi
ab,
Rito
Yanagi‡
ab,
Qian
Wang
c,
Xin
Shen
ab,
Qianhong
Zhu
ab,
Yudong
Xue
abd,
Jason A.
Röhr
ab,
Takashi
Hisatomi
 e,
Kazunari
Domen
e,
Kazunari
Domen
 ef and
Shu
Hu
ef and
Shu
Hu
 *ab
*ab
aDepartment of Chemical and Environmental Engineering, Yale University, New Haven, CT 06520, USA. E-mail: shu.hu@yale.edu; Fax: +1-203-432-4387; Tel: +1-203-737-6521
bEnergy Sciences Institute, Yale University, 810 West Campus Drive, West Haven, CT 06516, USA
cDepartment of Chemical System Engineering, School of Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan
dNational Engineering Laboratory for Hydrometallurgical Cleaner Production Technology, CAS Key Laboratory of Green Process and Engineering, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China
eResearch Initiative for Supra-Materials, Shinshu University, 4-17-1 Wakasato, Nagano-shi, Nagano 380-8553, Japan
fOffice of University Professor, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan
First published on 21st October 2019
Abstract
Water-splitting by photocatalyst particles has attracted much attention recently for its potential to produce renewable H2 at scale. However, the correlation between the energetics at photocatalyst/co-catalyst/water interfaces and their interfacial charge-transfer kinetics is still elusive, especially when the energetics are expected to vary spatially along the liquid-junction interface. First, we derived a kinetic model for photocatalyst particles in contact with two-redox potentials, H+/H2 and O2/H2O, i.e., a semiconductor/two-redox liquid junction. We adopted the principle of detailed balance proven for one-redox liquid junctions and extended this principle to a locally out-of-equilibrium electrolyte containing multiple redox potentials, the condition typical for photocatalysts. To validate the model, we established a characterization framework to simulate photocatalyst operation by using photoelectrodes. The open-circuit conditions mimicked operating photocatalyst surfaces; and the (quasi-) Fermi levels, probed by ohmic back contacts, indicated charge-separation efficiency. Quantitative data fitting further validated the two-redox kinetic model. These characterizations correlated local energetics with multi-electron charge-transfer kinetics, which exhibit tuneable branching ratios controlled by H2-and-O2 gas-mixture compositions and co-catalyst selectivity. Unlike the conventional photoelectrode/electrolyte interfaces, SrTiO3 model particles decorated with Pt co-catalysts were found to bear liquid-junction interfaces of spatially varying energetics with designated reductive and oxidative sites. It is shown that, uniquely for photocatalysts, the local kinetic-controlled energetics vary spatially across photocatalyst/co-catalyst/water interfaces of individual particles, and affect charge-separation efficiency sensitively. The mutually dependent behaviour between local kinetics and spatially varying energetics were confirmed for two practical photocatalytic systems, Al-doped SrTiO3 and Ta3N5. This study exemplified and elucidated the design principles for developing efficient photocatalysts.
Broader contextPhotocatalytic water-splitting for hydrogen generation is a promising approach for converting solar energy to chemical energy. However, the application of photocatalytic water-splitting is still limited by its low efficiency with 0.4% being its current state-of-the-art. Photocatalytic water-splitting involves coupled photophysical and electrocatalytic processes: light absorption, generation of electron–hole pairs, charge separation and bulk transport, charge transfer across interfaces for catalytic reactions, and mass transfer of reactants and products. To develop efficient photocatalyst particles for commercial applications, it is necessary to fully understand individual steps and their coupled processes. Among these processes, charge separation in bulk and charge transfer across the photocatalyst/water interface have not been well investigated. The driving force and process of charge separation in photocatalysts have been investigated in one of our latest studies. Herein, we are deciphering the charge-transfer process across the photocatalyst/(co-catalyst)/water interface and further integrating it into a dynamic photocatalyst model. Our work revealed that the energetics of photocatalysts during operation was correlated with the kinetics of the charge-transfer process and the kinetic-controlled energetics affect charge separation efficiency sensitively. |
1. Introduction
Solar-driven water-splitting by using photocatalyst particles has the potential to produce cost-effective hydrogen (H2) fuels at scale.1,2 So far, several visible-light active photocatalysts such as Ta3N5 semiconductors have been demonstrated for water splitting.3–7 For example, the predicted solar-to-hydrogen conversion efficiency limit for Ta3N5 is ∼17%,8 but the record remains <1% under sunlight indicating a big gap between experiments and theory. One of the biggest hurdles to improve the efficiency of each type of photocatalysts is the insufficient understanding of their charge-separation processes, which are coupled with the charge-transfer processes across the photocatalyst/water interfaces.9 Individual photocatalysts of 20–500 nm in diameter, decorated with co-catalysts of <5 nm in diameter and surrounded by water under sunlight, undergo the following processes: light absorption, generation of electron–hole pairs, charge separation and transport to photocatalyst/water interfaces, charge transfer across the interfaces to drive multi-electron catalysis, and mass transfer of reactants (e.g., H2O, H+) and products (e.g., H2 and O2).10 Uniquely, each photocatalyst particle co-evolves H2 and O2 at their respective and nearby sites on the same surface of the particles. Subsequent H2 and O2 separation ensures a safe solar-fuel production. To reveal photocatalyst design principles, ab initio simulation of mesoscale photocatalysts at an excited state should fully reveal the interdependence of these processes. This simulation is applicable to molecular sensitized and quantum-dot photochemical systems so far, but remains too complex for >10 nm-diameter particles.11–13Conventionally, a photocatalyst/co-catalyst/water junction is described by thermodynamic equilibration of the electrochemical potentials between the semiconductor and the liquid, assuming the photocatalyst is in contact with only one redox couple. The photocatalyst/co-catalyst/water junction may be an adaptive junction of variable barrier heights,14 or a buried junction.15 However, this description is not sufficiently relevant to photocatalyst particles considering that the two redox couples of H+/H2 and O2/H2O co-exist, which drives the local solution environment out of equilibrium. For these reasons, the photocatalysis community need a photocatalyst particle model to explicitly describe the complex photocatalyst/co-catalyst/water junction under non-equilibrium conditions.
Since the model based on thermodynamic equilibration is limited, the Gerischer–Lewis kinetic model for semiconductor/liquid junctions was applied to the model systems. It embodies the forward and backward charge-transfer process, i.e., microscopic reversibility, which underpins the thermodynamic equilibration behaviour at the semiconductor/liquid junctions. This kinetics model is useful because it can be extended to multiple redox charge-transfer pathways simply by invoking the principle of detailed balance. Lewis and co-workers chose a single-crystal SrTiO3 photoanode system to elucidate the kinetic model: current–potential behaviour is a statistical outcome of all the concurring interfacial charge-transfer events, in both forward and backward directions.16,17 However, their model used a bare SrTiO3 photoanode without a well-defined H+/H2 redox and thus not applicable to practical photocatalysts suspended in an out-of-equilibrium solution. Besides, water-oxidation catalysis then was not well characterized, and so were the kinetics for the multi-electron water-oxidation process as well as the reductive processes of H2 evolution and O2 reduction. For metal–liquid interfaces, Bard and Faulkner discussed that the poised potential of a metallic electrode in non-equilibrium solutions reflects the potential of zero currents.18 But this notion has not yet been applied to semiconductor/two-redox liquid junctions with out-of-equilibrium solutions. Furthermore, because efficient photocatalyst particles, by design, always employ co-catalyst nanoparticles, kinetics and energetics at reaction sites are expected to vary spatially. For these reasons, the photocatalysis community need a photocatalyst particle model to explicitly describe the complex photocatalyst/co-catalyst/water junction under non-equilibrium conditions. The liquid-junction energetics at local catalytic sites should be applied with the Gerischer–Lewis semiconductor/two-redox kinetic model.
To develop a semiconductor/two-redox kinetic model for photocatalyst particles, we extended the principle of detailed balance (see the Glossary in ESI†) by explicitly involving the H+/H2 and O2/H2O redox couples and acquiring their reported multi-electron catalytic kinetics (to be elaborated in Section 2). “Detailed balance” herein refers to a host of charge-transfer rate processes at local catalytic sites. For each catalytic site distributed spatially across the liquid-junction interface, its microscopic pathways involve both forward and backward charge-transfer directions for all operative acceptor/donor couples. Here, the notations of H+/H2 and H2O/H2 will be used interchangeably, the choice of which should depend on local pH. Potentials and energetics are referenced to the reversible hydrogen electrodes (RHE) for a range of operational pH values.
First, single-crystalline SrTiO3, SrTiO3/Pt and SrTiO3/(Cr2O3/Pt) photoelectrode systems will be used to step-wise validate the semiconductor/two-redox kinetic model for photocatalysts. The front liquid interface of these model photoelectrodes simulates the photocatalyst/(co-catalyst)/water junctions. We will establish an initial set of experimental methods to simulate and diagnose photocatalysts by systematically controlling their interfacial charge-transfer kinetics. In parallel with measuring the energetics, we vary kinetic branching ratios of charge-transfer rates to both H+/H2 and O2/H2O redox couples, and correlated the experimentally controlled kinetics with the measured energetics. We then realized that although the Gerischer–Lewis model accounts for charge-transfer kinetics of multiple redox couples in describing the current–potential behaviour, it so far rather concerns spatially uniform liquid junctions, where co-catalysts only make perturbations to band-bending energetics according to the pinch-off effect; the performance of most photoelectrodes does not concern lateral charge separation along the liquid-junction interface.17,19 We had shown that photocatalyst particles can be fully depleted with charges when suspended in water. The charge separation is likely dominated by lateral, diffusion-dominated transport of charge carriers.9 We therefore suggest a renewed picture: at photocatalysts, separation of electrons and holes is driven by small gradients of electron and hole quasi-Fermi levels. These gradients distribute laterally along the same liquid-junction interface, and the local energetics may change under varying local gas compositions dynamically. Specifically, the charge separation along the lateral dimension of liquid interfaces induces charge accumulation at the respective sites for H2 and O2 evolution. The lateral charge separation competes with the bulk or interfacial charge recombination. As the charges accumulate locally, the asymmetry of band bending will be reduced and so is the lateral potential gradient. As a result, the internal electric field makes less contribution to the local charge separation efficiency.
After quantitatively validating the semiconductor/two-redox kinetic model, we then applied it to practical photocatalysts of Al-doped SrTiO3 and Ta3N5, to elucidate their kinetics and energetics during operation. Ta3N5 represents an emerging class of visible-light-responsive photocatalysts, which still require guidance for substantial activity improvement.5,20,21 Al-doped SrTiO3 (Al:SrTiO3) was chosen because this photocatalyst exhibits efficient charge separation, despite only active with ultraviolet irradiation.22–24 What makes photocatalysts interesting is the mutually dependent kinetics and energetics. In these photocatalysts, the kinetic branching ratios of local catalytic pathways should determine the local liquid-junction energetics, which affects the lateral potential gradient and thus the charge-separation efficiency; and in return, the charge-separation efficiency affects local catalytic rates, which determine local kinetics. We used these examples to elucidate how co-catalysts affect water-splitting activity, charge-separation efficiency, and back reactions due to H2/O2 recombination.
2. Theory of semiconductor/two-redox junctions
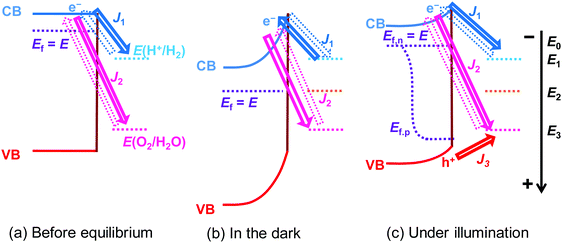
2.1 Semiconductor/two-redox kinetic model in the dark
A kinetic model was used to describe the charge-transfer processes at semiconductor/liquid junctions. The model accounts for the detailed balance of kinetic rates for all the microscopic forward and reverse charge-transfer pathways at a semiconductor/liquid junction. At the original semiconductor/one-redox liquid junction, the rates of forward electron transfer from the conduction band (CB) states to the acceptor species of a redox couple were hypothesized to be proportional to both concentrations of local acceptor species and surface electrons, multiplied with the charge-transfer rate constant as a pre-factor.17 The forward hole-transfer kinetics can be described similarly: valence band (VB) states accept electrons from the donor species. The net charge carrier fluxes are determined by the offset of electrochemical potentials. Electron or hole forward transfer establishes microscopic reversibility with the respective backward transfer. Under steady-state zero currents, the total forward rates are equal to the total reverse rates. The derivation is outlined in Section S1 and illustrated in Fig. S1 of the ESI.† In this case, thermodynamic equilibration is defined as in the dark and in the absence of a net current flow. The electrochemical potentials of semiconductor and co-catalyst always equilibrate, despite co-catalysts reaching a steady-state potential with a non-equilibrium solution purged with a (H2 + O2) gas mixture (see the Glossary in ESI†).Regarding the semiconductor/two-redox liquid junction, a SrTiO3/Pt/water model junction was employed. SrTiO3 was chosen as the model photocatalyst due to its stability and its suitable band edge positions for overall water-splitting. Pt was chosen as a co-catalyst since Pt serves as electron accumulation sites on photocatalysts and is kinetically active for charge transfer to both H+/H2 and O2/H2O redox couples.25,26 In our experiments, n-type SrTiO3 is chosen because intrinsic single-crystal SrTiO3 is too resistive. The SrTiO3/Pt/water junction has the barrier height dominated by the SrTiO3/water junction with negligible contributions from the local SrTiO3/Pt barrier, i.e., pinch-off effects, because the size of Pt particles deposited on SrTiO3 is small (see Section S2 and Fig. S2–S5, ESI†). We also assume that the SrTiO3/Pt interface exhibits variable barrier heights, i.e., the adaptive junction behaviour but not a buried junction with a fixed barrier height: the potential of Pt particles varies with the surface chemistry of Pt (e.g., by forming a surface hydride/hydroxide/oxyhydroxide surrounding Pt) in a way that can affect local band bending as Pt potentials vary. The assumption of being an adaptive junction will be verified in Section 3.4 by quantitative analysis and in Section 5 by the SrTiO3:Al-particle study.
In the derivation for the charge-transfer processes at a SrTiO3/Pt/water junction, the rate constants for both forward and backward electron-transfer pathways had only been deduced for outer-sphere one-electron redox couples. For each pathway in water-splitting photocatalysis, we took the respective multi-step micro-kinetics as reported in the literature,27–29 and expressed the rate law based on concentrations of surface charges and surface-bound intermediates involved in the rate-determining step. We expressed the rate law regarding the reaction intermediates on Pt surfaces following two assumptions: (i) SrTiO3/Pt in water forms an adaptive junction as discussed above; (ii) the exchange current densities at SrTiO3/Pt junctions are much larger than those at Pt/water junctions under operation (see Section S2, ESI†). When SrTiO3/Pt is brought into contact with water, electrons at the CB edge of SrTiO3 will transfer to both H+/H2 and O2/H2O through the Pt co-catalysts. Each pathway results in a branching ratio which depends on the respective kinetic rate, as illustrated in Fig. 1a and b.16 Here, “H+/H2” and “O2/H2O” represent the respective half-reactions but are not the actual intermediates involved. Intermediates such as O2/O2˙−, O2/H2O2 or H2O2/OH* couples are catalytic site specific and are not expressed in the generic model.
The kinetic pathways for electron transfer from the CB to the H+/H2 redox in alkaline electrolytes can be expressed as
 | (1) |
| H2O + Pt* + e− → Had + OH− (Volmer step) | (2) |
| Had + H2O + e− → H2+ OH− (heterolytic Heyrovsky step) | (3) |
| 2Had → H2 (homolytic Tafel step) | (4) |
J1,forward = −qk1[Pt*]ns = −qk1[Pt*]ns0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[q(E0 − E)/n1kBT] exp[q(E0 − E)/n1kBT] | (5) |
J1,backward = qk1−1[Had] = qk1[Pt*]ns1 = qk1[Pt*]ns0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[q(E0 − E1)/n1kBT] exp[q(E0 − E1)/n1kBT] | (6) |
| J1 = −qk1[Pt*](ns − ns1) = −qk1[Pt*]ns0{exp[q(E0 − E)/n1kBT] − exp[q(E0 − E1)/n1kBT]} | (7) |
The forward interfacial electron transfer to the O2/H2O redox can be expressed by
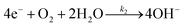 | (8) |
| O2(ad) + H2O + e− → HOOad + OH− | (9) |
J2,forward = −qk2[O2(ad)]ns = −qk2[O2(ad)]ns0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[q(E0 − E)/n2kBT] exp[q(E0 − E)/n2kBT] | (10) |
The backward electron transfer (i.e. reverse direction of eqn (8)) to the CB of SrTiO3 involves both the backward reaction of water oxidation and Pt oxidation.29 This backward electron transfer pathway is two steps in series, from liquids to Pt and then from Pt to the CB of SrTiO3. The second step of Pt to the CB of SrTiO3 is not considered the rate limiting step (see Section S2, ESI†). The first step of the backward transfer can be via water or hydroxyl oxidation catalyzed by PtO surfaces (according to experimental pH, the half-reactions in base are listed):
 | (11) |
 | (12) |
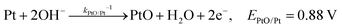 | (13) |
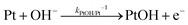 | (14) |
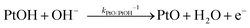 | (15) |
| J2,backward = q(kPtOH/Pt−1[Pt] + kPtO/PtOH−1[PtOH] + kPtOOH/PtO−1[PtO] + kPt/PtOOH−1[PtOOH]) | (16) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and Pt–OOH sites, respectively. kPtOH/Pt−1, kPtO/PtOH−1, kPtOOH/PtO−1, and kPt/PtOOH−1 are the respective rate constants for eqn (11)–(15). Applying detailed balance, the net interfacial electron current density to O2/H2O via Pt co-catalysts (assuming that SrTiO3 surfaces are not active for O2 reduction) can be expressed as
O and Pt–OOH sites, respectively. kPtOH/Pt−1, kPtO/PtOH−1, kPtOOH/PtO−1, and kPt/PtOOH−1 are the respective rate constants for eqn (11)–(15). Applying detailed balance, the net interfacial electron current density to O2/H2O via Pt co-catalysts (assuming that SrTiO3 surfaces are not active for O2 reduction) can be expressed asJ2 = −qk2[O2(ad)]ns0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[q(E0 − E)/n2kBT] + q(kPtOH/Pt−1[Pt] + kPtO/PtOH−1[PtOH] + kPtOOH/PtO−1[PtO] + kPt/PtOOH−1[PtOOH]) exp[q(E0 − E)/n2kBT] + q(kPtOH/Pt−1[Pt] + kPtO/PtOH−1[PtOH] + kPtOOH/PtO−1[PtO] + kPt/PtOOH−1[PtOOH]) | (17) |
At steady state in the dark, the net current density across the SrTiO3/Pt/water junction should be zero:
| J1 + J2 = 0 | (18) |
These equations imply that J1 and J2 can be modulated independently by controlling the partial pressure of H2 and O2 in the gas mixture that purges the solution; and if the partial pressure of H2 and O2 is fixed, all the rate constants should be held invariable, which determines the potential of SrTiO3 under steady-state in the dark (E2). These considerations will be used in Section 3.4 to quantitatively validate the semiconductor/two-redox model.
2.2 Semiconductor/two-redox kinetic model under illumination
Hole transfer occurs via bare SrTiO3 sites but not via Pt sites. As shown in Fig. S6 (ESI†), the J–E behaviour of SrTiO3/Pt photoanodes under illumination were indistinguishable during flow of O2 or H2. Otherwise, Pt would serve for H2 oxidation and the J–E behaviour would be different. The oxidation of H2 on bare SrTiO3 has never been reported, which is most likely due to poor H2 adsorption on SrTiO3. Based on these observations, we can deduce that the hole transfer from SrTiO3 to H+/H2 is negligible and that hole transfer is mainly through bare SrTiO3 to O2/OH−, as described by | (19) |
| OH− + h+ → OHad | (20) |
where OH− and OHad are the hydroxide ions in the double layer and the surface-bound hydroxyl groups on SrTiO3, respectively. The photocurrent J3, which is the net interfacial hole current density to O2/H2O, can be expressed as
| J3 = J3,forward + J3,backward = qk3[OH−]ps − qk3−1[OHad] ≈ qk3[OH−]ps | (21) |
Under steady-state illumination as shown in Fig. 1c, J3 balances with J1 and J2:
| J1 + J2 + J3 = 0 | (22) |
2.3 Expected behaviour of a SrTiO3/Pt/water junction under open-circuit conditions
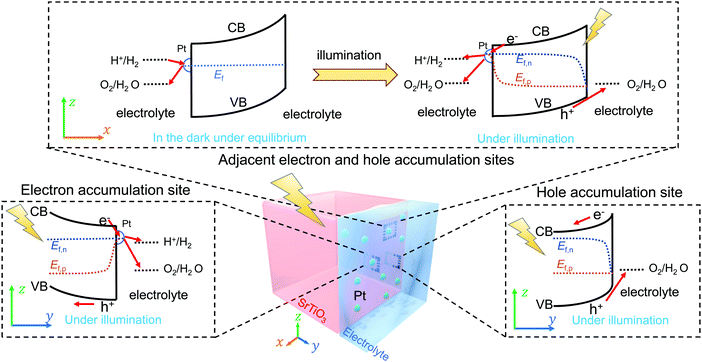
To verify the proposed kinetic model, the SrTiO3/Pt/water junction was evaluated using a single-crystal SrTiO3 photoelectrode. The front liquid contact of the SrTiO3/Pt model photoelectrode consists of hole accumulation and electron accumulation sites, respectively, for light-driven water oxidation and H2 evolution. The back contact is an indium layer. This ohmic back contact enables probing of the open-circuit potential (OCP) with negligible perturbation to the charge separation processes at the front SrTiO3/Pt/water interfaces. At steady-state open circuits where the net current density is zero, the front liquid interface of the SrTiO3/Pt model photoelectrode can be considered a two-dimensional planar photocatalyst (Fig. 2). In this configuration, the OCP represents an area-averaged Fermi level in the dark and an area-averaged electron quasi-Fermi level under steady-steady illumination for all the Pt sites. Note that the local Fermi level may vary spatially, but the measurement only produces one value due to its statistical nature. Measuring these variations is out of the scope of this study, but it is possible by developing liquid-phase electrochemical scanning probe microscopy in a future study.34Based on the theoretical analysis in Sections 2.1 and 2.2, we expect the following experimental behaviour for a SrTiO3/Pt photoelectrode:
3. Experiments to validate the two-redox kinetic model
3.1 Charge-transfer behaviour at SrTiO3/water junctions
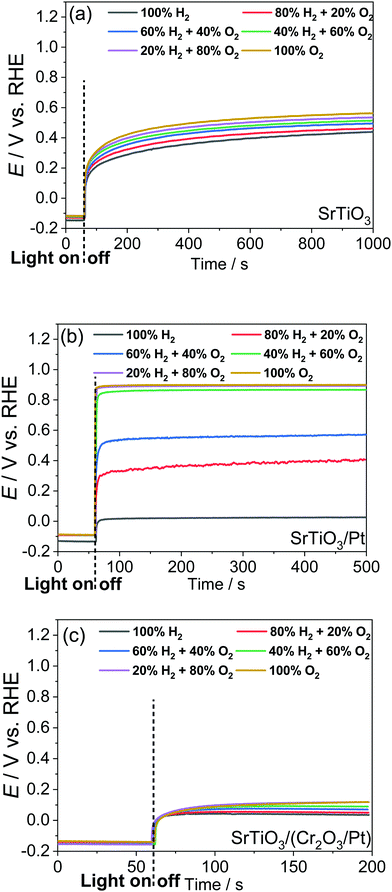
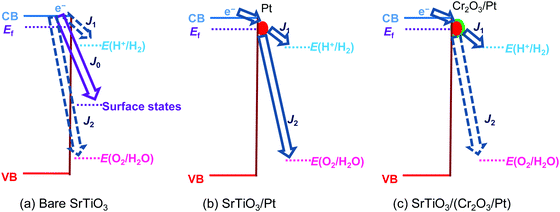
Single-crystalline n-type SrTiO3 in a photoelectrode configuration was used to verify the kinetic model. The band edge positions of SrTiO3 in water were −0.4 V vs. RHE for the CB and 2.9 V vs. RHE for the VB.3 The flat band potential was −0.15 V vs. RHE as explained in Section S5 with Fig. S9 and S10 (ESI†). The potential vs. RHE will be used, because E(H+/H2) and E(O2/H2O) will be involved in the discussion. The OCPs of bare SrTiO3 were measured in a “light-on and light-off” sequence in an aqueous electrolyte (0.5 M Na2SO4, pH = 12.5) purged with a (H2 + O2) gas mixture of several well-controlled compositions. After every “light-on” or “light-off,” we waited long enough to let the OCP reach steady state, so that the measurement error was reduced to less than 50 mV. The OCPs in the dark were recorded after cutting off the illumination because illumination served to establish a steady state of product/reagent concentrations at the liquid junction. The kinetic branching ratios for the several co-existing electron-transfer pathways were monitored via the OCPs of SrTiO3 in water. Under steady state, the net current density across SrTiO3/water junction became zero, as described in eqn (18) (in the dark) or eqn (22) (under illumination).The OCPs of a SrTiO3 photoelectrode contacting an electrolyte purged with a (H2 + O2) gas mixture is shown in Fig. 3a. This weak dependence on H2 and O2 compositions, as discussed in Section S6 (ESI†), indicates a charge-transfer process dominated by surface states. The SrTiO3/water junction can be approximated as a SrTiO3/surface-state junction as illustrated in Fig. 4a, which reveals the operation of an inactive photocatalyst.
3.2 Charge-transfer behaviour at SrTiO3/Pt/water junctions
To develop a semiconductor/water two-redox liquid junction and to reveal the operation of an active photocatalyst as illustrated in Fig. 4b, Pt was electro-deposited on SrTiO3 (see the Experimental section). Fig. 3b shows the measured OCPs of a SrTiO3/Pt photoelectrode contacting an electrolyte purged with a (H2 + O2) gas. When light was blocked, its OCP reached steady state in less than 100 s, shown in Fig. 3b, a much shorter time than 1000 s for a SrTiO3 electrode, shown in Fig. 3a. The OCPs in the dark shifted from 0.02 V (at 100% H2) to 0.90 V vs. RHE (at 100% O2) with a wider span than those of bare SrTiO3. The 0.88 V OCP range for SrTiO3/Pt was comparable to the 1.02 V of FTO/Pt electrodes, as shown in Fig. S11 (ESI†). These results indicate that Pt effectively facilitated the electron exchange with both H+/H2 and O2/H2O couples, and overwhelmed the electron transfer to surface states. The OCP in pure O2 (0.90 V vs. RHE) was still 0.33 V more negative than 1.23 V vs. RHE, e.g. E(O2/H2O), because this OCP was showing the mixed potential of Pt oxidation reactions and oxygen reduction reactions (see Section S3, ESI†). The OCP in pure H2 (0.02 V vs. RHE) was also slightly more positive than the 0 V vs. RHE, e.g. E(H+/H2), possibly due to the concurrent but non-negligible involvement of electron transfer to surface states. To further confirm the effects of H2 and O2 compositions on the surface kinetics of SrTiO3/Pt, the OCPs of SrTiO3/Pt in electrolytes purged under a flow of (H2 + N2) mixture and (O2 + N2) mixture were shown in Fig. S12 with the result further discussed in Section S7 (ESI†). In summary, the gas-composition dependence of OCPs of SrTiO3/Pt in the dark qualitatively verified the proposed kinetic model for semiconductor/two-redox liquid junctions.3.3 Charge-transfer behaviour at a SrTiO3/(Cr2O3/Pt)/water junction with co-catalyst selectivity
We further verified the kinetic model for semiconductor/two-redox liquid junctions by tuning the electron-transfer branching rates to H+/H2vs. O2/H2O couples in water. We experimented with a Cr2O3 layer coated on Pt particles to adjust the magnitude of H2 evolution and O2 reduction rates, k1 in eqn (7) and k2 in eqn (17), respectively. Coating a Cr2O3 layer over Pt co-catalyst particles was reported to suppress O2 reduction to a negligible rate (greatly decreasing k2 in eqn (17)),35 but only marginally suppress electron transfer to H+/H2 (moderately decreasing k1 in eqn (7)). The kinetic model with Cr2O3 was illustrated in Fig. 4c. The OCPs of SrTiO3/(Cr2O3/Pt) in water were expected to be around E(H+/H2) irrespective of the O2 concentration in the gas mixture, because the J2 pathway via Pt was effectively suppressed.The OCPs of SrTiO3/(Cr2O3/Pt) in water with a (H2 + O2) and with a (H2 + N2) gas mixture were shown in Fig. 3c and Fig. S13, respectively (ESI†). The OCPs of SrTiO3/(Cr2O3/Pt) in the (H2 + O2) gas mixture was near E(H+/H2) for the whole range of 0–100% O2 compositions. The OCPs measured in the (H2 + O2) and the (H2 + N2) gas mixture at the same concentration of H2 were very close. In the (H2 + O2) gas mixture, the OCP shifted from 0.03 to 0.12 V vs. RHE with decreasing H2 concentrations from 100% to 0%. This change only corresponds to the Nernstian potential change under dilution. The results obtained matched well with the expected outcome by imposing the two-redox kinetic model.
3.4 Quantitative validation of the semiconductor/two-redox kinetic model
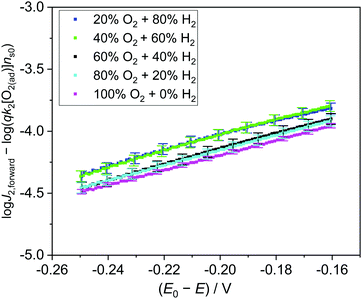
To quantitatively validate the proposed kinetic model, we fit the kinetic rate law of the forward interfacial electron transfer from SrTiO3/Pt to O2/H2O, as expressed in eqn (10), with experimental data. Taking the logarithm of both sides of eqn (10), the equation can be expressed as: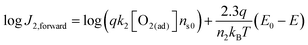 | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J2,forwardvs. (E0 − E) curve should be linear and the slope is independent of the gas composition. Furthermore, the intercept of the linear curve with the log
J2,forwardvs. (E0 − E) curve should be linear and the slope is independent of the gas composition. Furthermore, the intercept of the linear curve with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J2,forward axis is equal to log(qk2[O2(ad)]ns0), the pre-factor of eqn (10) in a logarithm scale. The pre-factors extrapolated from log fitting are supposed to be consistent with those extrapolated from the detailed balance by using the dark OCPs measured in a series of (O2 + N2) mixtures. Here, we assumed that the pre-factors should be identical for the same composition of O2 in the gas mixture, e.g., irrespective of the balancing gas of H2 or N2 in the (H2 + O2) or (O2 + N2) mixtures.
J2,forward axis is equal to log(qk2[O2(ad)]ns0), the pre-factor of eqn (10) in a logarithm scale. The pre-factors extrapolated from log fitting are supposed to be consistent with those extrapolated from the detailed balance by using the dark OCPs measured in a series of (O2 + N2) mixtures. Here, we assumed that the pre-factors should be identical for the same composition of O2 in the gas mixture, e.g., irrespective of the balancing gas of H2 or N2 in the (H2 + O2) or (O2 + N2) mixtures.
Experimentally, we measured the total electron current density across the SrTiO3/Pt/water junction (J) vs. E in the dark (Fig. S14, ESI†), then extracted the J2,forward component from the total J, and plotted the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J2,forwardvs. (E0 − E) curve (Fig. S15, ESI†). The linear region of the log
J2,forwardvs. (E0 − E) curve (Fig. S15, ESI†). The linear region of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J2,forwardvs. (E0 − E) curves were fitted for various gas compositions. The slopes and the intercepts of these log-linear lines were extracted (Fig. S16 and Table S3, ESI†). The process for extracting the J2,forward component and the pre-factors is elaborated in Section S8 (ESI†).
J2,forwardvs. (E0 − E) curves were fitted for various gas compositions. The slopes and the intercepts of these log-linear lines were extracted (Fig. S16 and Table S3, ESI†). The process for extracting the J2,forward component and the pre-factors is elaborated in Section S8 (ESI†).
The slopes of these log-linear lines were found to be independent of gas compositions. However, the slope of ∼160 mV dec−1 is more than twice of the ideal semiconductor/liquid junction exponential behaviour of 59 mV dec−1, that is, the ideality factor n2 > 2. This departure from the ideal behavior was consistent with our adaptive junction assumption because the catalytic current is limiting J2,forward. In this case, n2 is correlated with the Tafel slope of Pt's catalytic behaviour. Furthermore, the pre-factors of qk2[O2(ad)]ns0 extracted from the intercepts of the log-linear plots (Table S3, ESI†) matched well with those independently obtained from dark OCP measurements (Table S5, ESI†), as compared in Fig. S17 (ESI†). To summarize our fitting results, (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J2,forward − log(qk2[O2(ad)]ns0)) vs. (E0 − E) was plotted in Fig. 5, where qk2[O2(ad)]ns0 was independently obtained by dark OCP measurements. These log-linear lines overlapped with each other under various gas compositions, which directly validates eqn (23). The agreement above quantitatively validates the kinetic rate law of eqn (10) and further validates the detailed balance principle of our two-redox kinetic model. The kinetic rate law of the forward interfacial electron transfer from SrTiO3/Pt to H+/H2, i.e., J1,forward expressed by eqn (5), can be validated using a similar procedure.
J2,forward − log(qk2[O2(ad)]ns0)) vs. (E0 − E) was plotted in Fig. 5, where qk2[O2(ad)]ns0 was independently obtained by dark OCP measurements. These log-linear lines overlapped with each other under various gas compositions, which directly validates eqn (23). The agreement above quantitatively validates the kinetic rate law of eqn (10) and further validates the detailed balance principle of our two-redox kinetic model. The kinetic rate law of the forward interfacial electron transfer from SrTiO3/Pt to H+/H2, i.e., J1,forward expressed by eqn (5), can be validated using a similar procedure.
4. A dynamic model for photocatalyst particles
We recently reported that asymmetric band bending between low barrier-height electron accumulation sites and high barrier-height hole accumulation sites on a photocatalyst drove charge separation.9 For a SrTiO3/Pt/water junction, we consider that an electric field is dropped across the Pt-decorated SrTiO3 surfaces and native SrTiO3 surfaces locally, which drives local charge separation. As discussed in Section 2.1, the barrier-height energetics along the Pt-decorated SrTiO3 surfaces in the dark were expected to vary with the potential of Pt depending on the surface kinetics. This feature was confirmed in Section 3. As discussed in Section 2.2, the barrier-height energetics on the native SrTiO3 surfaces in the dark did not vary with the local gas compositions. Hence, we introduce a photocatalyst particle model by combining the adaptive liquid junction assumption, kinetic-controlled local energetics (extended Gerischer–Lewis model), and spatially varying barrier heights (asymmetric band bending) for charge separation. This comprehensive photocatalyst particle model was illustrated by a two-dimensional diagram, Fig. 2: Pt-decorated SrTiO3 surfaces feature kinetics dependent barrier heights; to drive efficient charge separation, Pt-decorated SrTiO3 surfaces (electron accumulation sites) exhibit a low barrier height and native SrTiO3 surfaces (hole accumulation sites) exhibit a high barrier height; at the respective local electron- or hole-accumulation site, the current–potential behaviour follows the two-redox kinetic model.Under illumination, Ef splits into individual Ef,n and Ef,p at the respective photocatalytic sites. The direction of local charge separation is distributed along the particle/liquid interface. Ef,n can be monitored by OCPs, while Ef,p cannot be directly measured by the current electrochemical method. Section S9 (ESI†) discussed the position of Ef,p and the estimation of photovoltages under illumination. It is deduced that the hole quasi-Fermi level was located at (1.23 V vs. RHE + an overpotential). Moreover, the more negative the OCP under identical illumination conditions, the higher the photovoltage and the better the charge separation. In Section 5, the measured OCP under illumination, i.e., the potential of Ef,n, will be used to indicate charge-separation efficiency.
Through OCP measurements of photocatalyst-assembled photoelectrodes, the asymmetry of local barrier heights in the dark and the efficiency of charge separation under illumination at photocatalysts can be readily quantified. If the local kinetics varies (indicated by the OCP in the dark), the kinetics-controlled energetics is expected to adjust the band bending asymmetry and dynamically modulate charge separation efficiency (indicated by OCPs under illumination). This narrative of mutually-dependent kinetics and energetics at a SrTiO3/Pt/water junction will be applied to diagnose the operation of SrTiO3:Al and Ta3N5 photocatalysts in Section 5.
5. Application of the particle model to particulate SrTiO3:Al and Ta3N5 photocatalysts
We elucidated the mutually-dependent charge-separation and charge-transfer behaviour at the operative photocatalyst/co-catalyst/water interfaces. These findings will be applied to optimizing practical photocatalyst/co-catalyst combinations. SrTiO3:Al (ultraviolet-light responsive) and Ta3N5 (visible-light responsive) absorbers were taken as examples to diagnose photocatalyst activity and to elucidate co-catalyst functionality. The control experiments (see Section S10 with Fig. S18 and S19, ESI†) showed that the Ti back contacts that are ohmic to SrTiO3:Al particles displayed no redox activity despite their contact with electrolytes; the Ti back contacts were not affecting the OCP measurement of photocatalysts.The OCPs of Ti/SrTiO3:Al particle-assembled photoelectrodes in water purged with a (H2 + O2) gas mixture were summarized in Fig. 6a, and those with a (H2 + O2), a (H2 + N2) or a (O2 + N2) gas mixture were shown in Fig. S20 (ESI†). The OCP trend in the dark was comparable to that shown in Section 3.1 for single-crystalline SrTiO3. The OCPs of <0 V vs. RHE under illumination showed that water-splitting on SrTiO3:Al was possible but realistically limited by the slow electron-transfer kinetics between SrTiO3:Al and H+/H2 in water. This observation was consistent with the small but non-zero water-splitting activity of particulate SrTiO3:Al suspensions as quantified by gas chromatography (Fig. S21, ESI†).
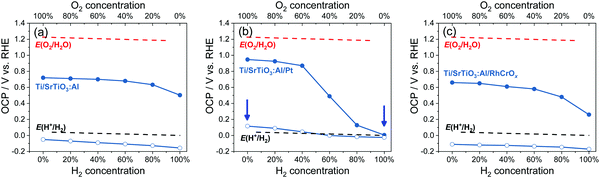 | ||
| Fig. 6 Summary of OCPs in the dark (filled circles) and OCPs under illumination (hollow circles) for (a) Ti/SrTiO3:Al, (b) Ti/SrTiO3:Al/Pt and (c) Ti/SrTiO3:Al/RhCrOx particle-assembled photoelectrodes in an electrolyte purged with a (H2 + O2) gas mixture. E(H+/H2) and E(O2/H2O) were calculated based on the Nernst equation. The arrows point to two conditions for the energy diagrams of SrTiO3:Al/Pt shown in Fig. S23 (ESI†). The electrolyte is 0.5 M Na2SO4(aq) solution with pH adjusted to 12.5. | ||
The OCPs of Ti/SrTiO3:Al/Pt particle-assembled photoelectrodes in water purged with a (H2 + O2) gas mixture were summarized in Fig. 6b, and those with a (H2 + O2), a (H2 + N2) or a (O2 + N2) gas mixture were shown in Fig. S22 (ESI†). The trend of this OCP data set measured in the dark was similar with that for single-crystalline SrTiO3/Pt, indicating the improved electron-transfer kinetics. The OCPs of Ti/SrTiO3:Al/Pt photoelectrodes under illumination were dependent on the O2 concentration, as shown in Fig. 6b. The OCPs shifted positively as the O2 concentration increased. The OCP in 100% O2 is 150 mV more positive than that in 100% H2. Moreover, only when the O2 concentration was lower than 20%, the electron quasi-Fermi level was <0 V vs. RHE, i.e., E(H+/H2).
As illustrated in Fig. S23 (ESI†), the presence of O2 reduced the band bending in SrTiO3:Al/Pt, which reduced the electric field between SrTiO3:Al/Pt and bare SrTiO3:Al sites, made charge separation less effective, and thus reduced the charge-separation efficiency. The gas-composition dependent OCPs under illumination revealed that the water-splitting activities of particulate SrTiO3:Al/Pt was determined by the redox selectivity of Pt. Deduction from OCP measurements was consistent with the measured water-splitting activities of particulate SrTiO3:Al/Pt, where the H2 evolution rates in H2 and O2 environments, respectively, were shown to be 13 μmol h−1 and ∼0 μmol h−1, respectively (see Fig. S24, ESI†). SrTiO3:Al/Pt photocatalysts switched from inactive to active, when O2 compositions reduce to <40%.
The trend of OCPs of Ti/SrTiO3:Al/Pt photoelectrodes in water purged with a (H2 + O2) gas mixture also confirms that the SrTiO3:Al/Pt junction is adaptive. If SrTiO3:Al/Pt were to form a buried junction, its barrier height at Pt sites would be a constant and high value. As a result, the charge separation efficiency should remain the same. In this case, OCPs under illumination would not vary with H2 and O2 gas compositions. This buried-junction assumption contradicts the gas-composition dependent OCPs shown in Fig. 6b.
SrTiO3:Al/Pt was capable of splitting water but its activity was about two orders of magnitude lower than that of SrTiO3:Al/RhCrOx by comparing Fig. S24 and S25 (ESI†). The OCPs of Ti/SrTiO3:Al/RhCrOx in water purged with a (H2 + O2) gas mixture were summarized in Fig. 6c, and those with a (H2 + O2), a (H2 + N2) or a (O2 + N2) gas mixture were shown in Fig. S26 (ESI†). By comparing the charge-separation and charge-transfer processes of SrTiO3:Al/RhCrOx with SrTiO3:Al/Pt (see Section S11 and Fig. S24–S28, ESI†), it was concluded that the advantages of loading RhCrOx on SrTiO3:Al were (1) less charge-carrier recombination at the SrTiO3:Al/RhCrOx interfaces, and (2) enough band bending asymmetry for efficient charge separation, across local electron and hole accumulation sites under the full span of gas compositions. For these reasons, the combination of SrTiO3:Al/RhCrOx was the most active for photocatalytic water splitting, with the operational band energetics illustrated in Fig. S28 (ESI†).
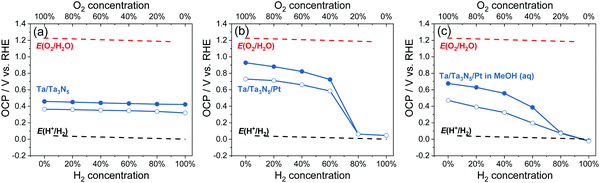
The OCPs of Ta/Ta3N5, and Ta/Ta3N5/Pt in water, and Ta/Ta3N5/Pt thin-film photoelectrodes in 20 vol% MeOH aqueous solution purged with a (H2 + O2) gas mixture were summarized in Fig. 7; the full data set appears in Fig. S29 (ESI†). The trend of OCPs of Ta/Ta3N5/Pt in the dark was similar with that of SrTiO3/Pt in Section 3.2, but the trend of OCPs under illumination was different. It reveals that Ta3N5/Pt and SrTiO3/Pt showed similar charge-transfer kinetics, but Ta3N5 were much less efficient for charge separation under illumination. As shown in Fig. 7b, the OCPs of Ta/Ta3N5/Pt under illumination and at any gas composition were more positive than E(H+/H2). Moreover, when the O2 concentration in a (H2 + O2) gas mixture was less than 20%, there was almost no difference between OCPs in the dark and under illumination. This meant that most of the photo-generated carriers recombined even though a maximum amount of band-bending asymmetry was achieved for Ta3N5 in pure H2 (see Fig. S23, ESI†). The severe recombination of photo-generated carriers implies that Ta3N5 bulk was too defective to split water. To improve the charge separation on Ta3N5, we used methanol as a sacrificial electron donor to immediately consume the photo-generated holes from Ta3N5, and to reduce recombination. As shown in Fig. 7c, the OCPs of Ta/Ta3N5/Pt in the dark and under illumination split regardless of the composition of the gas flow. This result confirmed that the fast and irreversible kinetics of methanol oxidation alleviated severe charge recombination. This point was further supported by the observed non-activity of particulate Ta3N5/Pt suspension in pure H2, and the observed activity in 20 vol% MeOH aqueous solution, as shown in Fig. S30 (ESI†). Our OCP study indicated that improving optoelectronic properties of Ta3N5, such as the lifetimes of charge carriers, should be the priority at the current stage.
6. Conclusion
Our study offers quantitative design principles for optimizing the solar-to-fuel conversion efficiency of photocatalyst particles. The correlation between charge-transfer rates and band energetics at the photocatalyst/(co-catalyst)/water junction were described using a semiconductor/two-redox kinetic model. This model considered all the forward and backward charge-transfer pathways with the acceptor and donor species or intermediates at the liquid-junction interface. These interfacial charge-transfer events were accounted for under the principles of detailed balance and microscopic reversibility. The kinetic model was validated experimentally by using single-crystalline SrTiO3, SrTiO3/Pt and SrTiO3/(Cr2O3/Pt) model photoelectrodes. The kinetic model further provided in-depth understanding of the dynamic interplay between kinetic-controlled energetics and local charge-separation processes at a photocatalyst/(co-catalyst)/water liquid junction.Applying the established experimental framework for the SrTiO3 model photocatalysts, we further elucidated the mutually dependent kinetics and energetics of photocatalyst particles, such as SrTiO3:Al and Ta3N5. The experimental OCP study on SrTiO3:Al/Pt particle-assembled photoelectrodes revealed the importance of manipulating the surface kinetics for photocatalytic water splitting, especially in the comparison between the SrTiO3:Al/Pt and SrTiO3:Al/RhCrOx combinations: it is necessary to tailor the energetics between photocatalysts and co-catalysts to reduce the interfacial charge recombination. In contrast, Ta3N5 was so defective in bulk that at the current stage, studies on this photocatalyst should focus on improving its optoelectronic properties, such as the lifetimes of charge carriers. Our model provides insights into optimizing a photocatalyst/co-catalyst junction by quantitatively identifying the effects of asymmetric band bending on charge separation, which competes with the loss of efficiency due to bulk recombination controlled by semiconductor optoelectronic properties and due to interfacial recombination controlled by photocatalyst/co-catalyst interfacial properties. We recognize the merit of using high turnover-frequency co-catalysts such as Pt, but rather emphasize their other functionalities shown in the photocatalyst/co-catalyst combination, such as passivating surface electronic defects and creating asymmetric barrier heights.
Author contributions
All the authors contributed to the manuscript, and all authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors would like to thank Dr Min Li at Yale's Materials Characterization Core for his invaluable help with XRD and SEM measurements, Mr Hao Lyu for preparing Al-doped SrTiO3 particles and Mr Yutaka Sasaki for preparing Ta3N5 thin films. The authors also recognize the start-up support from the Tomkat Foundation, and thank Dr Tianshuo Zhao for the helpful discussion. RY acknowledges a fellowship support from the Japan Student Services Organization.References
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC
.
- T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535 RSC
.
- Q. Wang, T. Hisatomi, Q. Jia, H. Tokudome, M. Zhong, C. Wang, Z. Pan, T. Takata, M. Nakabayashi, N. Shibata, Y. Li, I. D. Sharp, A. Kudo, T. Yamada and K. Domen, Nat. Mater., 2016, 15, 611–615 CrossRef CAS
.
- C. Pan, T. Takata, M. Nakabayashi, T. Matsumoto, N. Shibata, Y. Ikuhara and K. Domen, Angew. Chem., Int. Ed., 2015, 54, 2955–2959 CrossRef CAS
.
- Z. Wang, Y. Inoue, T. Hisatomi, R. Ishikawa, Q. Wang, T. Takata, S. Chen, N. Shibata, Y. Ikuhara and K. Domen, Nat. Catal., 2018, 1, 756–763 CrossRef CAS
.
- K. Maeda, K. Teramura, D. Lu, T. Takata, N. Saito, Y. Inoue and K. Domen, Nature, 2006, 440, 295 CrossRef CAS
.
- R. Asai, H. Nemoto, Q. Jia, K. Saito, A. Iwase and A. Kudo, Chem. Commun., 2014, 50, 2543–2546 RSC
.
- E. Nurlaela, A. Ziani and K. Takanabe, Mater. Renewable Sustainable Energy, 2016, 5, 18 CrossRef
.
- Z. Pan, J. Rohr, Z. Ye, Z. Fishman, Q. Zhu, X. Shen and S. Hu, Sustainable Energy Fuels, 2019, 3, 850–864 RSC
.
- K. Takanabe, ACS Catal., 2017, 7, 8006–8022 CrossRef CAS
.
- T. A. Pham, Y. Ping and G. Galli, Nat. Mater., 2017, 16, 401 CrossRef CAS
.
- L. G. C. Rego and V. S. Batista, J. Am. Chem. Soc., 2003, 125, 7989–7997 CrossRef CAS
.
- R. Long and O. V. Prezhdo, J. Am. Chem. Soc., 2011, 133, 19240–19249 CrossRef CAS
.
- F. Lin and S. W. Boettcher, Nat. Mater., 2014, 13, 81–86 CrossRef CAS
.
- M. R. Shaner, K. T. Fountaine and H.-J. Lewerenz, Appl. Phys. Lett., 2013, 103, 143905 CrossRef
.
- A. Kumar, P. G. Santangelo and N. S. Lewis, J. Phys. Chem., 1992, 96, 834–842 CrossRef CAS
.
- G. A. Shreve and N. S. Lewis, J. Electrochem. Soc., 1995, 142, 112–119 CrossRef CAS
.
- A. J. Bard and L. R. Faulkner, Electrochem. Methods, 2001, 2, 482 Search PubMed
.
- H. Gerischer, J. Electroanal. Chem. Interfacial Electrochem., 1975, 58, 263–274 CrossRef CAS
.
- W.-J. Chun, A. Ishikawa, H. Fujisawa, T. Takata, J. N. Kondo, M. Hara, M. Kawai, Y. Matsumoto and K. Domen, J. Phys. Chem. B, 2003, 107, 1798–1803 CrossRef CAS
.
- T. Takata, G. Hitoki, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, Res. Chem. Intermed., 2007, 33, 13–25 CrossRef CAS
.
- Y. Ham, T. Hisatomi, Y. Goto, Y. Moriya, Y. Sakata, A. Yamakata, J. Kubota and K. Domen, J. Mater. Chem. A, 2016, 4, 3027–3033 RSC
.
- Z. Zhao, E. J. Willard, H. Li, Z. Wu, R. H. R. Castro and F. E. Osterloh, J. Mater. Chem. A, 2018, 6, 16170–16176 RSC
.
- Z. Zhao, R. V. Goncalves, S. K. Barman, E. J. Willard, E. Byle, R. Perry, Z. Wu, M. N. Huda, A. J. Moulé and F. E. Osterloh, Energy Environ. Sci., 2019, 12, 1385–1395 RSC
.
- J. Ran, J. Zhang, J. Yu, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2014, 43, 7787–7812 RSC
.
-
C. Song and J. Zhang, in PEM Fuel Cell Electrocatalysts and Catalyst Layers: Fundamentals and Applications, ed. J. Zhang, Springer London, London, 2008, pp. 89–134 DOI:10.1007/978-1-84800-936-3_2
.
- S. Intikhab, J. D. Snyder and M. H. Tang, ACS Catal., 2017, 7, 8314–8319 CrossRef CAS
.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 3722–3730 RSC
.
-
J. Zhang and H. Liu, Electrocatalysis of direct methanol fuel cells: from fundamentals to applications, John Wiley & Sons, 2009 Search PubMed
.
- N. Mahmood, Y. Yao, J.-W. Zhang, L. Pan, X. Zhang and J.-J. Zou, Adv. Sci., 2018, 5, 1700464 CrossRef
.
- R. Subbaraman, D. Tripkovic, D. Strmcnik, K.-C. Chang, M. Uchimura, A. P. Paulikas, V. Stamenkovic and N. M. Markovic, Science, 2011, 334, 1256 CrossRef CAS
.
- J. Chen, Y.-F. Li, P. Sit and A. Selloni, J. Am. Chem. Soc., 2013, 135, 18774–18777 CrossRef CAS
.
- M. M. Waegele, X. Chen, D. M. Herlihy and T. Cuk, J. Am. Chem. Soc., 2014, 136, 10632–10639 CrossRef CAS
.
- M. R. Nellist, F. A. L. Laskowski, J. Qiu, H. Hajibabaei, K. Sivula, T. W. Hamann and S. W. Boettcher, Nat. Energy, 2018, 3, 46–52 CrossRef CAS
; F. A. L. Laskowski, S. Z. Oener, M. R. Nellist, A. M. Gordon, D. C. Bain, J. L. Fehrs and S. W. Boettcher, Nat. Mater., 2019 DOI:10.1038/s41563-019-0488-z
.
- K. Maeda, K. Teramura, D. Lu, N. Saito, Y. Inoue and K. Domen, Angew. Chem., Int. Ed., 2006, 45, 7806–7809 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional results are provided. See DOI: 10.1039/c9ee02910a |
| ‡ Both authors contributed equally to this manuscript. |
| This journal is © The Royal Society of Chemistry 2020 |