High-density equilibrium phases of colloidal ellipsoids by application of optically enhanced, direct current electric fields
Mahesh
Ganesan
 and
Michael J.
Solomon
and
Michael J.
Solomon
 *
*
Department of Chemical Engineering, University of Michigan, Ann Arbor, MI 48105, USA. E-mail: mjsolo@umich.edu
First published on 28th April 2017
Abstract
We use direct current (DC) electric fields in conjunction with ultraviolet light to self-assemble highly dense structures of colloidal ellipsoids with three-dimensional order and volume fraction as large as 67%. Ellipsoidal phases of colloids are of fundamental interest because novel packing structures are predicted to occur at high volume fractions; the symmetries of these crystal unit cells can also contribute to a variety of applications, including structural color materials. Previously, the very high volume fraction range of ellipsoidal phases has been inaccessible because of limitations such as vitrification and kinetic trapping. Here we report that the coupling of light to DC electric fields causes electrophoretic deposition that yields ellipsoid phases that are significantly denser than previous reports. The applied voltage across the capacitor-like device used for self-assembly was varied from 1.75–2.3 V and the power density of incident UV light was varied between 75–400 W m−2. As the coupled field strengths were increased, the assembled colloids underwent a phase transition from an isotropic fluid to a nematic liquid crystal phase consistent with previous reports. When the voltage and light intensity were between 1.9–2.1 V and 100–200 W m−2 respectively, the assembly had a high degree of orientational ordering and a degree of positional order along axes both parallel and perpendicular to the plane of the electrode surface. For the densest assembly achieved, the interlaying spacing is 0.9D, where D is the ellipsoid minor axis.
1. Introduction
Colloids, because of their Brownian motion and inter-particle potential interactions, can self-assemble into a variety of equilibrium phases.1 A colloid's excluded volume is a fundamental determinant of its phase diagram; study of the self-assembly of hard particles therefore identifies the variety of phases and unit cell symmetries possible in colloidal systems. Close-packed and nematic phases of hard spheres and rods, respectively, were discovered in early work.2–4 Recent simulation studies have identified the role of convex shape in determining the symmetry of self-assembled phases, especially as the particle density approaches maximum packing.5 Theoretical work identifying maximum packing of particles of different shapes also suggests directions for self-assembly.6,7 Dense colloidal packings have technological applications, particularly in the field of structural color,8 in which phases of dielectric particles of complex symmetry can produce optical responses that depend on the wavelength, angle, and polarization of the incident light.The ellipsoid is a hard particle shape whose colloidal phase diagram is of fundamental interest.9 Experimentally, ellipsoids can be produced by the quenched elongational deformation of temperature softened polymeric spheres.10,11 The maximum packing fraction of ellipsoids is greater than that of spheres.7 Dense packings of non-spherical colloids have been prepared in a number of cases.12–14 The present experimental effort to identify high-density phases of ellipsoids is motivated by the fundamental interest in the relationship between packing and self-assembly of anisotropic particles, as well as the potential applications of ellipsoids of revolution for optical materials.15 For example, the dielectric anisotropy of dense ellipsoidal phases could generate an angular dependence of structural color that differs from that observed in more symmetric phases, such as face centered cubic packing of spheres. Ordered ellipsoids also exhibit interesting phononic characteristics such as anisotropic phonon transport in films of ordered ellipsoids.16,17 Ellipsoidal colloids can be synthesized in significant quantities.18 Moreover, sedimentation,19 centrifugation,20 and electrophoretic deposition12 have been used to produce dense phases with orientation and spatial order. These studies have all identified nematic phases of varying domain size. To date, the densest self-assembled phase (volume fraction = 49% for aspect ratio 4.3) was described as body-centered tetragonal.12 Probing the phase diagram of colloidal ellipsoids at higher volume fraction is complicated by their slow dynamics;21 efforts to increase the osmotic pressure into regions for which crystallization is predicted have instead resulted in either vitrification20 or self-organization of particles into small tactoids, with random orientation of the tactoid directors.12
Here we use phoretic deposition to produce dense equilibrium phases of ellipsoids. An initially electrophoretic deposition process22 (as described in Section 3.1) is augmented by the addition of UV light23 as addressed in Section 3.2. In Section 3.3 we show that the combined fields generate a stronger driving force for assembly than previous work, extending the volume fraction range of self-assembly from 49% to 67%. This stronger driving force produces increased ellipsoid packing in a region extending six or more layers above the deposition substrate. As discussed in Section 3.4, the phases generated show clear indications of orientational order and developing positional order parallel to the plane of the electrode surface. The phoretic deposition methods and the phases identified are compared to previous experiment, simulation, and packing theory.
2. Materials and methods
2.1 Synthesis of ellipsoidal particles
Polystyrene (PS) ellipsoids were synthesized by uniaxial stretching of microspheres following Shah and co-workers.12,24 Briefly, 300 μL of PS microsphere solution in water (2 vol%) was mixed with 7.5 mL of a polyvinyl alcohol stock solution (10 wt% PVA, 30–70 kDa, Sigma Aldrich). The PS spheres used in this study are fluorescent carboxylate modified spheres with a diameter of 1.10 ± 0.02 μm (Fluospheres, Invitrogen). The PVA solution containing the particles was transferred into flat trays (Nunc OmniTray, ThermoFisher Scientific) and let to dry over night on leveled platforms. The dried films were cut into strips and loaded onto a stretching device contained in an oven.12 The films were stretched uniaxially (elongation strain of 2.5) at an oven temperature of 120 °C (which is above the glass transition temperature – 100 °C – of polystyrene12). The stretched portions of the film were taken and the PVA matrix dissolved in DI water for 24 h with gentle rolling (10 rpm). The released ellipsoids were dispersed in dimethyl sulfoxide (DMSO, Fisher Scientific) by solvent transfer. Tetrabutyl ammonium chloride (TBAC, Sigma-Aldrich) at 0.1 mM was added to control the Debye screening length and supplement the solvent conductivity.12 The ellipsoids obtained in this process had an aspect ratio of 5.5 ± 0.2 (major axis L = 2.96 ± 0.10 μm and minor axis D = 0.54 ± 0.01 μm) and their initial volume fraction for self-assembly experiments was 2.0 vol%.2.2 Ellipsoid self-assembly device
The device used to assemble the ellipsoids was built following Shah et al.12 and Ferrar and Solomon.22 Two ITO coated glass coverslips (coverslip thickness 0.17 mm, ITO coating thickness ∼10 nm, ITO coating resistance ∼600 Ω) were bonded, using UV curable glue (Light weld, Dymax Corporation), on either surface of a 1.15 mm thick glass spacer with the ITO coated side of the coverslips in contact with the spacer. The spacer had a hole of diameter 5 mm drilled in the center. T2 thermocouple wires (0.5 mm diameter, Goodfellow Inc.) were attached to the ITO coated side of the coverslips using an electrical conductive tape (3 M 9713 XYZ-Axis Electrically Conductive Tape, Ted Pella Inc.). In this capacitor like device, the ITO coated slides, together with the T2 wires served as the electrodes for supplying DC voltage, the hole in the spacer served as the sample chamber capable of containing ∼25 μL colloidal solution and 19.6 mm2 of the ITO coated side of each electrode is in direct contact with the suspensions. The gap between the electrodes in all experiments was 1.15 mm.2.3 Visualization and field conditions for ellipsoidal assembly
The assembly process was visualized using a Nikon A1Rsi confocal laser scanning microscope (CLSM, Nikon) by directly placing the assembly device on the stage of the CLSM (Nikon AI Piezo z-drive) above the microscope objective (100× oil immersion type, NA 1.4). The ellipsoids were assembled by applying a DC electric field (as per Shah et al.12) coupled with an incident UV light source (as per Kim et al.23). The direction of the electric field is normal to the objective plane of the microscope. The DC current was generated by connecting the electrode wires of the assembly device to a power supply that applied a constant voltage across the colloidal suspension. The electrode that was closer to the objective was given positive polarity while the top coverslip was connected to the negative terminal of the power supply.An incident UV light source (OBIS 405 LX, Coherent Inc., 405 nm) was focused on the bottom cover slip of the device, illuminating an assembly area of 31.8 μm × 31.8 μm. The laser light was supplied, and its power controlled using the CLSM that was itself used to visualize the assembly process. The light was focused using the 100× oil immersion objective lens (NA = 1.40).
The DC field voltage was varied between 1.7–2.3 V and the light power density was varied between 75–400 W m−2 (Optical Power Meter 1916-C, detector 818-ST, Newport). The wavelength of the light was kept constant at 405 nm for all experiments reported here. Using higher wavelengths (up to 532 nm was tested) also resulted in self-assembly but required higher power densities. In all assembly experiments, the solvent is DMSO containing 0.1 mM TBAC and the initial volume fraction of the colloidal suspension is 2.0 vol%.
2.4 Image analysis of assembled structures
Image analysis was used to characterize the kinetics of self-assembly and the structures formed. The fluorescent particles were visualized by excitation using a laser of wavelength 561 nm. The excitation laser had a power density ∼102 less than the UV light source. Therefore, the imaging laser had negligible effect on the self-assembly process itself. Self-assembly kinetics were studied by acquiring two-dimensional images (31 μm × 31 μm) immediately above the coverslip as a function of time. The rate of assembly was measured by computing a two-dimensional packing density as a function of time at different field conditions. The 2D packing density was calculated as an area density – here defined as the fraction of the total surface area occupied by particles. The surface area of the image occupied by particles was calculated by binarizing the image using an Otsu's threshold and counting pixels with non-zero intensity.For characterizing the volume fraction, 3D image volumes of size 31 × 31 × 3 μm3 of voxel size 62 × 62 × 62 nm3 were acquired after 1 hour of assembly time. Particle centroids and the number of particles as a function of height were identified using a watershed-cut based image analysis algorithm described in Hsiao et al.25 (cf.Fig. 5f for a 3D rendering of ellipsoids identified by image analysis). Particle volume fractions were then calculated for five layers closest to the coverslip.
3. Results
3.1 Influence of UV light on DC field assembly of microspheres
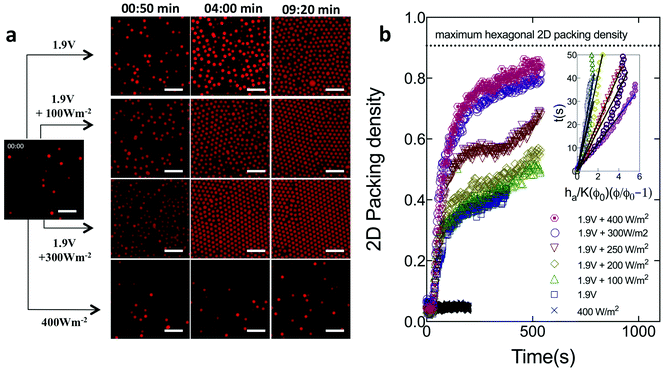
We first describe how combining DC electric fields and light affects the self-assembly of microspheres, before progressing to the case of ellipsoids. Fig. 1 shows image sequences as a function time for the assembly the 1.0 μm fluorescent PS microspheres at an applied voltage of 1.9 V and light power densities varying from 0–400 W m−2. As a control, we also study if assembly is induced under UV light illumination only. The images were taken in a plane parallel to and directly above the coverslip.After t = 30 s, for experiments conducted at 1.9 V, the negatively charged spheres migrated towards the bottom (positive) cover slip and began to assemble. At t ∼ 4 min, the increase in volume fraction (number density) is greater for the case of a DC field coupled to UV light than for spheres assembled with DC field alone (e.g. compare panels for 1.9 V and 1.9 V + 300 W m−2 at 04:00 min). After an assembly time of t ∼ 10 min, the fraction of the image area occupied by spheres continues to be higher in the combined case. By comparison, light illumination alone – in the absence of a DC field – yields no densification, even after 10 min.
Fig. 1b characterizes the deposition kinetics by plotting the 2D packing density as a function of time. The 2D packing density is measured at the layer closest to the cover slip, as per the Methods section. Ferrar and Solomon22 have shown that, for electric field assisted deposition of colloidal particles, the assembly volume fraction is highest at the coverslip. For the experiments at 1.9 V (DC electric field only), the packing density rapidly increases at early times (t ≤ 150 s). The increase is then more gradual (Fig. 1b). At t = 150 s, the 2D packing density rapidly increases from 0.35 to 0.70 as the light is switched on from 0 W m−2 to 400 W m−2. The change quantifies the degree to which light illumination enhances the DC field-induced assembly process. After t = 600 s, the structure assembled at 1.9 V and 400 W m−2, has a 2D packing density of 0.84. This density is only 7% less than the maximum 2D packing density (0.9069) for perfect hexagonal closed packing in 2D. For experiments done in the absence of DC field (with light only), the particle density remained constant, consistent with the absence of deposition.
For spheres, we infer the strength of the applied DC + UV field by a direct measurement of the deposition translational Peclet number, Pet – the ratio of the particle's characteristic rate of motion under the applied field to that of its translational Brownian motion. Here, Pet = (U0R)/D0, where, U0 is the sedimentation velocity of the particle, R is the particle radius and D0 is its translational diffusivity. We compute U0 at each field condition from Fig. 1b using an adaptation of the colloidal sedimentation theory as implemented by Ferrar and Solomon22 and Kim et al.23 Briefly, under dilute conditions, U0 is the reciprocal slope of t versus ha/K(Φ0)(Φ/Φ0 − 1), where, Φ0 = 0.02 is the initial volume fraction, Φ is the volume fraction at time t (from Fig. 1b), ha = 0.95 μm is the height of a single assembly layer and K(Φ0) = (1 − Φ0)6.55 to account for the effect of volume fraction on deposition. D0 is calculated from the Stokes–Einstein relation. The inset in Fig. 1b shows this characterization. The Peclet number, for the assembly process shown in Fig. 1, increased from Pet = 0.1 to Pet = 0.55 as the UV light intensity was increased from 0 W m−2 to 400 W m−2 at a constant DC field of 1.9 V. The Peclet number characterization shows that UV light enhanced DC fields result in field strengths that are sufficiently strong to cause rapid deposition, but still allow for significant translational Brownian motion for the particles to assemble into ordered structures. This Peclet number range has previously been found to yield high quality colloidal crystallization.22
The method reported in Fig. 1 differs from other light-induced phoretic assembly techniques reported in the literature. One such technique, as reported by Saville and coworkers,26 combines AC electric fields and light to generate 2D self-assembly of colloids. In these reports, the AC electric fields generate electrohydrodynamic flows that are enhanced by the incident light. However, in the present case, electrodeposition (flux of particles normal to the electrode) dominates electrohydrodynamic flow (flux of particles parallel to the electrode). The colloidal electrodeposition generated by the applied DC electric field is consistent with prior reports by Shah et al. and Ferrar and Solomon for this system of particles, solvent and applied field.12,22 Indeed, when the light is combined with the DC field, we measure current densities ∼0.1 A m−2 (for 1.9 V, 300 W m−2 in a particle-free test cell), consistent with enhancement of electrophoretic deposition by the incident light.
Although the incident light acts in conjunction with the DC field, it generates no assembly on its own (Fig. 1). Hence, the method used here differs from the photo-induced assembly produced by Kim et al.,23 where, the light was the sole generator of the field driving colloidal assembly. Kim et al.23 applied light power densities 103 fold greater than that used in Fig. 1 and reported current densities ∼3 × 10−3 A m−2. In the present case, the current density measured for 400 W m−2 with no applied DC field was only 2 × 10−5 A m−2. Therefore, the effect identified by Kim et al., is only weakly present in this system. Furthermore, the Kim et al. deposition mechanism generated Pet ∼ 0.5 only at ∼104 W m−2 UV light, whereas, the present method of UV enhanced DC fields requires a much more modest level of UV excitation to generate a similar deposition Pe number.
In addition, using finite difference simulations and thermal measurements, Kim et al.23 showed that light power densities 103 fold greater than that used in Fig. 1 generated very low temperature gradients within a similar colloid – solvent system. Therefore, the wavelength and power density of the light used in this study do not generate thermal gradients.23 Consequently, the assembly method is different from light-induced thermophoresis27 and AC electro-thermal hydrodynamics28 where, localized heating by an incident laser generates convective currents that drive colloidal motion.
We therefore describe the self-assembly method as light induced enhancement of electrophoretic deposition. Electrophoretic deposition in steady, direct current electric fields occurs when Faradaic reactions at the electrodes generate a current density across the gap of the cell.12 This current density creates an electric field, which couples to the charge on the colloid surface, generating electrophoretic motion leading to deposition.12,22 Because ITO is a semiconductor, there is good evidence26,29 that light incident on it can affect the Faradaic reactions that drive the deposition, thereby enhancing the current density, electric field magnitude, and deposition process.
3.2 Kinetics of optically enhanced DC field assembly of ellipsoids
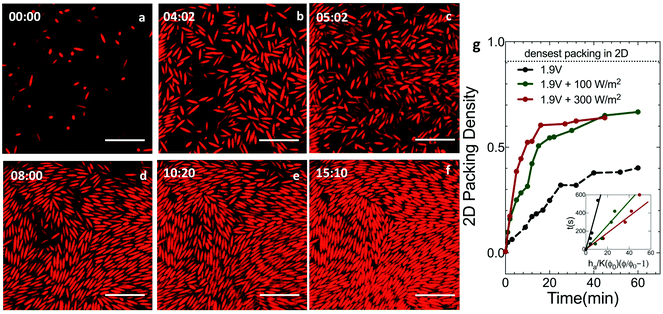
Ellipsoids of aspect 5.5, dispersed in DMSO + 0.1 mM TBAC at an initial volume fraction of 2.0% were introduced into the electric field device for self-assembly. Deposition and assembly of the ellipsoids was monitored with CLSM as a function of time under a constant DC voltage and varying UV light intensities.Fig. 2 reports CLSM images, taken in a plane parallel and close to the coverslip at 1.9 V and 300 W m−2 illumination. At the start of assembly (Fig. 2a), the particles are dilute and unaligned. Under the applied field, the particles exhibit downward phoretic motion that leads to densification at the electrode (Fig. 2b). After an assembly time of t ∼ 5 min (Fig. 2c), increased particle densities are observed at the cover slip; however, the ellipsoids are largely orientationally disordered. At t ∼ 8 min (Fig. 2d), the particle concentration continues to grow. This growth is accompanied by the onset of positional order and orientational alignment on the scale of small clusters. After t ∼ 10 min (Fig. 2e and f), the assembly showed increased alignment and ordering spanning over larger domains, increasing to cross sectional areas spanning up to ∼102 particles. This order persists until the conclusion of the experiment (t ∼ 90 min). Alignment and positional ordering is facilitated by the fact the ellipsoids remain mobile – with significant Brownian rotation and translation – at these field conditions and volume fractions.
We evaluate the impact of combined UV light and DC fields on the assembly kinetics of ellipsoids by tracking their 2D packing density with time (Fig. 2g). For the case of ellipsoids, the strength of the applied field is quantified using the rotational Peclet number; Per = (U0/l)/Dr where l is the half-length of the ellipsoid major axis and Dr = 0.12 ± 0.01 s−1 is the ellipsoid rotational diffusivity calculated using Brenner's theory.12 The deposition velocity, U0, is computed as discussed earlier in the context of Fig. 1b; this characterization is shown in the inset of Fig. 2g. In Fig. 2g, the UV light intensity is set at zero, 100 W m−2 and 300 W m−2 for DC fields of 1.9 V. In the presence of light, packing density increases rapidly at short times; the packing density is also greater by the end of the experiment. After 1 hour, the 2D packing density of ellipsoids at the electrode surface is 0.40 for 1.9 V DC field alone (Per = 0.14); the packing density is 0.67 when the DC field is coupled with 300 W m−2 UV light (Per = 0.74). In 2D, the theoretical maximum for the packing density of ellipses is 0.9069.30 Therefore, the assembly produced by DC electric fields alone yields a packing density less than half the theoretical maximum; optically enhanced DC fields produce a 2D packing density that is 26% less than the theoretical maximum. Increased packing density in the presence of UV light can be correlated to the increase in the Peclet number (Per = 0.14 at 1.9 V, Per = 0.50 at 1.9 V + 100 W m−2 and Per = 0.74 at 1.9 V + 300 W m−2) that enhances the deposition of the ellipsoids leading to denser assembly.
Fig. 3 reports images of ellipsoid assemblies produced by varying the DC voltage from 1.7–2.3 V and the power density from 0–400 W m−2. The assembly time was 1 hour in all cases, within the steady-state regime (cf.Fig. 2b). The CLSM images are taken at the cover slip, which in the present case is the positive electrode.
We organize the observations into three regimes, as shown in Fig. 3a. The regimes are disordered fluid (region I), liquid crystal (region II) and tactoid (region III). We also report the 2D nematic order parameter, S, for the self-assembled structures observed at different field conditions. The parameter, calculated from image analysis as per Mohraz and Solomon,19 represents the quality of orientational ordering where, S = 1 for perfectly oriented ellipsoids and S = 0 for a random distribution of orientation angles. Region I – disordered fluid phase – is observed at applied voltages of 1.7 V and all light power densities. In this region, the assembled structure at the electrode surface is denser than the initial suspension (Fig. 3b), but is both orientationally and positionally disordered (Fig. 3c) with S = 0.11. At applied voltages between 1.75 V to 2.1 V, and light intensities ≤250 W m−2 – region II – a liquid crystal phase characterized by highly dense structures, with a high degree of positional and orientational ordering (S = 0.89) observed over large domains (Fig. 3d). Finally, for DC voltages greater than 2.1 V and light intensities greater than 250 W m−2, the ellipsoids in the final structures appear to have no apparent long-range order but possess local positional and orientational order (region III, Fig. 3e), characteristic of tactoid microdomains, as often observed in transitions between isotropic and liquid crystal phases. In region III (S = 0.13), the particles appeared dynamically jammed in this intermediate structural state, with limited fluctuations, perhaps due to the rapid process of densification that occurs at high field strengths.
Fig. 3d and f–i are CLSM images of structures from region II that displayed the highest degree of alignment and orientational ordering with S = 0.74–0.93. The assembly conditions were DC voltages and light intensities in the range 1.9 V–2.1 V and 100–200 W m−2, respectively. These field conditions are just sufficient to support densification and annealing of the assembled ellipsoids at the electrode surface. In these structures, the ellipsoids in the image plane appear to be collectively orientated in a preferred direction. The domain size of the regions with orientational order was as large as ∼20 × 20 μm2 in the plane parallel to the electrode surface. In addition to the orientational order, the ellipsoids are also regularly stacked side to side, at least on the scale of 5–10 particles.
3.3 Volume fraction of dense ellipsoid assemblies
We compute the equilibrium volume fraction of the ellipsoidal packings formed by applying the field conditions as in Fig. 3a. For each specimen, image analysis was used to identify centroids of the particles contained in image volumes of size 31 × 31 × 3 μm3. The axial dimension is sufficient to capture about 5–6 layers of rods. (Imaging beyond above this height was not possible for this particle–solvent system due to the refractive index contrast between the PS particles and the DMSO solvent. Given the initial volume fraction of the suspension and the device gap, mass conservation indicates that there are particles above these six layers; however, the density, orientation, and positional order of this region of the self-assembled structure is unknown.) The near-wall volume fraction was quantified after an assembly time of 1 hour.Fig. 4 plots the ellipsoidal volume fraction as a function of applied field. Stem lines represent the conditions at which experiments were performed; volume fraction was calculated at these conditions from image analysis results (cf. Methods); the intermediate surfaces were obtained by a triangulation linear interpolation. At 1.7 V DC, the volume fraction of the structure was nearly constant at 6%, even up to 300 W m−2 incident light (Fig. 4). For applied voltages in the range 1.8–1.9 V, the equilibrium volume fraction increased from 41% to 67% as the incident light intensity was increased from 0 W m−2 to 200 W m−2.
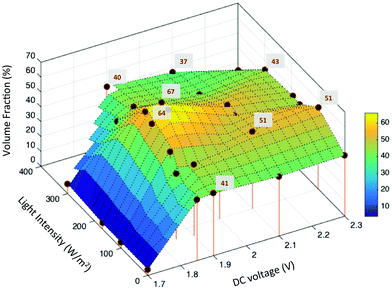 | ||
| Fig. 4 Volume fraction of ellipsoid assembly structure as a function of applied field strength. The volume fractions of local maxima are indicated. | ||
The maximum ellipsoidal volume fraction of 67% was obtained for self-assemblies produced at 1.85 V + 200 W m−2, 1.9 V + 170 W m−2 and 1.9 V + 200 W m−2. At the same voltage conditions, when the light power density was increased beyond 200 W m−2, the volume fraction decreased toward an average value of 45%. At 2.0 V, the maximum volume fraction was 52% at 200 W m−2 light intensity. Finally, for voltages greater than 2.0 V, the value was, on average, between 40–45% at all light intensities studied.
The volume fraction measurements support the following conclusions. First, for self-assembled structures obtained under DC fields alone, the volume fraction initially increases with voltage and then stays nearly constant at 42% for voltages greater than 1.9 V (Fig. 4). This behavior is consistent with the results reported by Shah et al.,12 for electrophoretic deposition of ellipsoids under similar conditions. Second, at 1.7 V, the steady-state volume fraction attained – 6% – is well below the reported nematic volume fraction of 42% for ellipsoids with aspect ratio five.31 Therefore, the observation that these assemblies do not display orientational order is consistent with theory. Third, ellipsoids assembled at 1.8–2 V DC and 100–200 W m−2 incident light achieve volume fractions that exceed the order–disorder phase transition boundary. Deposition with orientational alignment and positional order in three dimensions is the result in this operating window (Fig. 3a region II, Fig. 3d and f–i).
The maximum volume fraction of 67% reported in Fig. 4 is significantly higher than the previously reported maximum of 45% for ellipsoids assembled using DC fields alone.12 Finally, increasing both the applied voltage and light intensity beyond 2 V and 200 W m−2 decreases assembly volume fraction and ordering (Fig. 3a region III, Fig. 3e). This decrease is inconsistent with thermodynamic equilibrium; the increased applied field should generate a larger countervailing osmotic pressure gradient with a concomitant increase in volume fraction in the near wall region. We believe this discrepancy arises because the high field strength drives rapid deposition of the ellipsoids. In this limit, convective deposition into a dense configuration occurs more rapidly than the ellipsoids can adopt anything more than local equilibrium by means of Brownian translation and rotation motion.12,22 Therefore, ellipsoidal assemblies formed at these field conditions do not have long-range order but show only local ordering (Fig. 3e), consistent with the tactoid assignment reported in Fig. 3.
3.4 Ordering in dense self-assembled ellipsoids
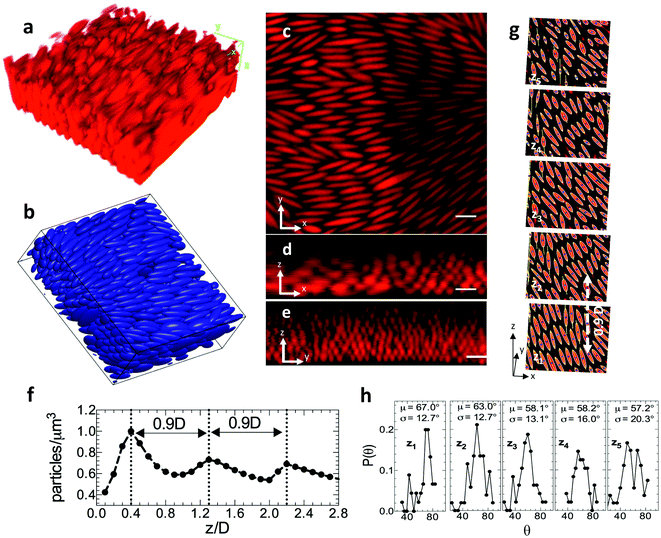
Within the operating range of 1.9–2.0 V plus 100–200 W m−2, we obtain ellipsoidal assemblies with the highest volume fraction. In Fig. 5, we characterize the positional and orientational order of these structures. Fig. 5a is a representative three-dimensional image volume of a dense assembly – formed at 1.9 V + 200 W m−2 – as acquired by confocal microscopy. The 3D rendering of this assembly structure, using centroids identified by image analysis of the CLSM acquired images, is shown in Fig. 5b. Fig. 5c–e shows representative orthogonal slices of the image volume showing an xy slice (Fig. 5b) in the plane closest and parallel to the electrode as well as xz (Fig. 5c) and yz (Fig. 5d) slices of the image volume, each perpendicular to the electrode surface. In Fig. 5c and d, the electrode surface is apparent at image bottom, where the ellipsoid fluorescence abruptly terminates.Fig. 5c–e indicate that the assembly shows a high degree of orientational order, as well as the existence of layered positional order. Fig. 5d and e indicates at least six ellipsoid layers. These layers persist contiguously over lateral dimensions of at least 20 microns. By image analysis of the volume represented in Fig. 5c–e, we find the ellipsoid centroids from which we calculate the particle number density distribution as a function of height. The periodic variation in rod density (Fig. 5f) – with interlayer spacing 0.9D – is good evidence of a layered structure, consistent with the positional order expected of a colloidal crystal.
We compare the observed 0.9D interlayer spacing to potential unit cell assignments derived from previous been reports for ellipsoids. The interlayer spacing for the face-centered orthorhombic crystal structure studied by Frenkel and Mulder32 was 0.866D with volume fraction 74%. For the experimental volume fraction of 67% measured in this study, this structure would have an interlayer spacing of 0.89D. The dense monoclinic crystal (SM2) predicted by Pfleiderer and Schilling33 had an interlayer spacing of 0.5D at volume fraction of 77%. This structure, at 67%, would have an interlayer spacing of 0.55D. Finally, the body-centered tetragonal crystal experimentally observed by Shah et al.,12 at 49% had interlayer spacing of 0.5D, corresponding to 0.45D at 67%. Therefore, the interlayer spacing of the ellipsoidal assembly observed in Fig. 5 appears more consistent with a close packed structure such as face-centered orthorhombic rather than with the tight layer interdigitation that is characteristic of the SM2 structure. Fig. 5g exhibits further signatures of developing crystallinity. These features include uniform orientational order, row ordering of ellipsoids within each oriented layer in the 3D assembly, and the appearance of some correlation between the position of the rows in each of the layers. This positional order appears only in the densest ellipsoidal packings produced.
To further study the orientational ordering, we identify major axis of ellipsoids in each layer by constructing ellipses around the set of all connected points in an image. Fig. 5g shows xy slices of five assembly layers for the structure shown in Fig. 5a–e. Here, z1 is the layer closest to the cover slip and z5 is the layer furthest from the cover slip. The bounding ellipse, major axis and centroid are shown. The probability distribution of ellipsoid orientation angle, θ, in every layer is plotted in Fig. 5h. Layers closest to the coverslip (z1 − z3) have better orientational ordering with low standard deviations in θ (∼±12°). As we go higher up in the assembly (z4, z5), the mean orientation angle remains constant, but the quality of the ordering broadens out with larger standard deviations in orientation angle (∼±20°). From the orientation angles we obtain the order parameter for the assembly shown in Fig. 5g as S = 0.85, consistent with substantial ellipsoid alignment.
4. Conclusions
The present study identifies a dual-field assembly technique that yields highly dense assemblies of colloidal ellipsoids, which exhibit a high degree of orientational ordering and emerging 3D positional ordering. The structures obtained using this method are denser than any previously obtained liquid crystal assemblies of colloidal ellipsoids. The study suggests the following future work. First, for ellipsoids, the unit cell that results in the densest known packing7 has been identified by simulation33–35 to be monoclinic, with a two-particle basis (SM2). The two particles in the unit cell are oriented relative to each other by an angle that depends on the ellipsoid aspect ratio. The SM2 structure is more stable than face centered orthorhombic for the aspect ratio here studied.33 However, the developing structures seen in Fig. 5 and their inter-layer spacing of 0.9D appears to be more consistent with the face-centered orthorhombic than the SM2 structure. Additional image analysis of confocal microscopy volumes and small angle light scattering of larger specimens is warranted to identify the crystalline unit cell produced by the dual field approach; crystals with larger domain size will facilitate such characterization. This effort might identify crystal defect states such as disclination line defects36 and its correlation to the observed order parameter for ellipsoidal assemblies. Second, characterizing the strength of the applied fields by means of the rotational Peclet number or by analyzing the dynamics of the particles will inform design rules for the application of this field-assisted assembly method to generate dense structures. Third, the dual application of fields – such as DC current and incident light used in this study – appear advantageous to develop large-scale colloidal crystals because of the method's reversibility and the potential for annealing of assembled structures by toggling the applied fields.37 Finally, the dual-field assembly method could potentially be used to further explore the high density features of anisotropic colloids such as discoids, faceted polyhedra, colloidal molecules, and patterned particles.38Acknowledgements
This work was supported by the Department of Energy, Basic Energy Sciences under grant DE-SC0013562.References
- V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811–815 CrossRef CAS PubMed.
- P. N. Pusey and W. Van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- Z. Dogic and S. Fraden, Curr. Opin. Colloid Interface Sci., 2006, 11, 47–55 CrossRef CAS.
- G. J. Vroege and H. N. W. Lekkerkerker, Rep. Prog. Phys., 1992, 55, 1241–1309 CrossRef CAS.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS PubMed.
- A. Donev, I. Cisse, D. Sachs, E. A. Variano, F. H. Stillinger, R. Connelly, S. Torquato and P. M. Chaikin, Science, 2004, 303, 990–993 CrossRef CAS PubMed.
- A. Donev, F. H. Stillinger, P. M. Chaikin and S. Torquato, Phys. Rev. Lett., 2004, 92, 255506 CrossRef PubMed.
- S. Kinoshita, S. Yoshioka and J. Miyazaki, Rep. Prog. Phys., 2008, 71, 076401 CrossRef.
- M. J. Solomon, Curr. Opin. Colloid Interface Sci., 2011, 16, 158–167 CrossRef CAS.
- C. C. Ho, A. Keller, J. A. Odell and R. H. Ottewill, Colloid Polym. Sci., 1993, 271, 469–479 CAS.
- K. M. Keville, E. I. Franses and J. M. Caruthers, J. Colloid Interface Sci., 1991, 144, 103–126 CrossRef CAS.
- A. A. Shah, H. Kang, K. L. Kohlstedt, K. H. Ahn, S. C. Glotzer, C. W. Monroe and M. J. Solomon, Small, 2012, 8, 1551–1562 CrossRef CAS PubMed.
- S. Sacanna, L. Rossi, A. Wouterse and A. P. Philipse, J. Phys.: Condens. Matter, 2007, 19, 376108 CrossRef.
- J. Henzie, M. Grünwald, A. Widmer-Cooper, P. L. Geissler and P. Yang, Nat. Mater., 2011, 11, 131–137 CrossRef PubMed.
- M. Mittal and E. M. Furst, Adv. Funct. Mater., 2009, 19, 3271–3278 CrossRef CAS.
- P. J. Beltramo, D. Schneider, G. Fytas and E. M. Furst, Phys. Rev. Lett., 2014, 113, 205503 CrossRef PubMed.
- D. Schneider, P. J. Beltramo, M. Mattarelli, P. Pfleiderer, J. Vermant, D. Crespy, M. Montagna, E. M. Furst and G. Fytas, Soft Matter, 2013, 9, 9129–9136 RSC.
- L. Palangetic, K. Feldman, R. Schaller, R. Kalt, W. R. Caseri and J. Vermant, Faraday Discuss., 2016, 191, 325–349 RSC.
- A. Mohraz and M. J. Solomon, Langmuir, 2005, 21, 5298–5306 CrossRef CAS PubMed.
- D. Mukhija and M. J. Solomon, Soft Matter, 2011, 7, 540–545 RSC.
- D. Mukhija and M. J. Solomon, J. Colloid Interface Sci., 2007, 314, 98–106 CrossRef CAS PubMed.
- J. A. Ferrar and M. J. Solomon, Soft Matter, 2015, 11, 3599–3611 RSC.
- Y. Kim, A. A. Shah and M. J. Solomon, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- A. A. Shah, B. Schultz, W. Zhang, S. C. Glotzer and M. J. Solomon, Nat. Mater., 2014, 14, 117–124 CrossRef PubMed.
- L. C. Hsiao, B. A. Schultz, J. Glaser, M. Engel, M. E. Szakasits, S. C. Glotzer and M. J. Solomon, Nat. Commun., 2015, 6, 8507 CrossRef CAS PubMed.
- R. C. Hayward, D. A. Saville and I. A. Aksay, Nature, 2000, 404, 56–59 CrossRef CAS PubMed.
- S. Duhr and D. Braun, Appl. Phys. Lett., 2005, 86, 1–3 CrossRef.
- A. H. Work and S. J. Williams, Soft Matter, 2015, 11, 4266–4272 RSC.
- J. E. van den Meerakker, E. Meulenkap and M. Scholten, J. Appl. Phys., 1993, 74, 3282–3288 CrossRef CAS.
- A. Donev, F. H. Stillinger, P. M. Chaikin and S. Torquato, Phys. Rev. Lett., 2004, 92, 255506 CrossRef PubMed.
- B. Tjipto-Margo and G. T. Evans, J. Chem. Phys., 1990, 93, 4254–4265 CrossRef CAS.
- D. Frenkel and B. M. Mulder, Mol. Phys., 1985, 55, 1171–1192 CrossRef CAS.
- P. Pfleiderer and T. Schilling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 20402 CrossRef CAS PubMed.
- M. Radu, P. Pfleiderer and T. Schilling, J. Chem. Phys., 2009, 131, 164513 CrossRef CAS PubMed.
- G. Odriozola, J. Chem. Phys., 2012, 136, 134505 CrossRef PubMed.
- M. Mittal, R. K. Niles and E. M. Furst, Nanoscale, 2010, 2, 2237–2243 RSC.
- J. W. Swan, J. L. Bauer, Y. Liu and E. M. Furst, Soft Matter, 2014, 10, 1102–1109 RSC.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |