Compression of hard core–soft shell nanoparticles at liquid–liquid interfaces: influence of the shell thickness†
A.
Rauh‡
a,
M.
Rey‡
b,
L.
Barbera
b,
M.
Zanini
b,
M.
Karg
*ac and
L.
Isa
*b
aPhysical Chemistry, University of Bayreuth, Universitätsstr. 30, 95440 Bayreuth, Germany
bLaboratory for Interfaces, Soft matter and Assembly, Departments of Materials, ETH Zurich, Vladimir-Prelog Weg 5, 8093 Zurich, Switzerland. E-mail: lucio.isa@mat.ethz.ch
cPhysical Chemistry, Heinrich-Heine-University, 40204 Düsseldorf, Germany. E-mail: karg@hhu.de
First published on 3rd August 2016
Abstract
Soft hydrogel particles show a rich structural and mechanical behaviour compared to hard particles, both in bulk and when confined in two dimensions at a fluid interface. Moreover, encapsulation into hydrogel shells makes it possible to transfer the tunability of soft steric interactions to hard nanoparticle cores, which bear interest for applications, e.g. in terms of optical, magnetic and reinforcement properties. In this work, we investigate the microstructures formed by hard core–soft shell particles at liquid–liquid interfaces upon compression. We produced model particles with the same silica core and systematically varied the shell-to-core ratio by synthesising shells with three different thicknesses. These particles were spread at an oil–water interface in a Langmuir–Blodgett trough and continuously transferred onto a solid support during compression. The transferred microstructures were analysed by atomic force and scanning electron microscopy. Quantitative image analysis provided information on the particle packing density, the inter-particle distance, and the degree of order of the monolayers. We discovered several essential differences compared to purely soft hydrogel particles, which shed light on the role played by the hard cores in the assembly and compression of these composite monolayers.
1 Introduction
Understanding and controlling the microstructure of nanoparticle monolayers at liquid–liquid interfaces is of significant interest for applications including surface patterning,1 biological membranes2 and the stabilisation of emulsions.3–5 Hard colloids, such as rigid polymer particles, e.g. of poly(methylmethacrylate) (PMMA) or polystyrene (PS), or inorganic colloids, e.g. of silica, are often used as stabilisers for Pickering emulsions. The colloidal stability of the particles, their size and contact angle at the interface are all crucial aspects for the successful stabilisation of liquid–liquid interfaces. In contrast to small amphiphilic molecules, such as surfactants, the adsorption of hard particles at the interface is typically irreversible leading to extremely stable emulsions.6–9 Using hard colloids presents though only a limited working space to tune the aforementioned properties. A possible route to overcome these limitations and impart additional functions to the materials consists of using soft deformable polymer particles.10 In recent years, soft microgel particles have for instance gained significant interest as novel emulsion stabilisers due to their responsive behaviour allowing for “smart” emulsions that can be actuated by external stimuli.4,5,11–13 In contrast to hard spheres, electrostatic repulsion and van der Waals interactions are usually less important than particle deformability and soft steric interactions at the interface, which ultimately govern the interface microstructure.6,14 Microgels are physically assigned between classical hard-sphere colloids and ultra-soft colloids, such as polymer coils and star polymers in solution.6,15Poly-N-isopropylacrylamide (PNIPAM) particles are the most prominent microgel model system to date. Their structure is often described as “core–shell”, since they typically have a gradient in cross-linking density from their centre towards their periphery.16,17 It is also known, mostly from freeze-fracture cryogenic scanning electron microscopy investigations, that the microgel morphology at liquid–liquid interfaces differs strongly form the one of hard spheres.18,19 The surface activity of the polymer chains drives a spreading of the particles until the deformation is balanced by internal elasticity,20 leading to dimensions at the interface usually larger than the bulk size. The extent of the deformation at the interface moreover depends on the cross-linking density of the microgel particles.19,21,22 The microgel shell appears flattened, giving a morphology that is often described as “core-corona” or “fried-egg”. The particle mainly stays in the water phase and only a small part of it protrudes into the oil phase.
The behaviour of microgel interfacial monolayers under compression and the link between their mechanical and structural properties has been studied with experiments in a Langmuir–Blodgett trough and in a pendant-drop apparatus. With compression, highly ordered microgel arrays and controllable inter-particle distances were obtained.23–25 The soft character of microgels extends the range of interfacial microstructures usually accessible for hard particles. This is due to the fact that the polymer chains of neighbouring nanoparticles can squeeze and interpenetrate to give area fractions above the maximum two-dimensional close packing value of 0.91. The large tunability of the microstructure of monolayers enables using microgels in applications, e.g. in microlens arrays,26 for structural colours27 or as novel lithography masks for nanopatterning.1 However, for many other applications it is desirable to be able to produce nanostructured interfacial monolayers using hard nanoparticles such as metal, metal oxide or semiconductor particles, owing to their unique optical, magnetic and/or electronic properties or to act as reinforcement elements. As suitable route to achieve this aim, it has been shown that a combination of hard, functional cores with soft, deformable hydrogel shells, i.e. in hybrid core–shell colloids, allows the tunable assembly of hard nanoparticles, while benefitting from unique interactions of soft hydrogels at interfaces.28 For instance, Vogel et al. performed experiments compressing a monolayer of Au–PNIPAM particles in a Langmuir–Blodgett trough.29 Their results showed that the inter-particle distance could be adjusted over several hundreds of nanometers. Similarly, Honold et al. used hydrogel encapsulation and interfacial assembly to produce highly ordered and macroscopically homogeneous plasmonic surface coatings with gold and silver nanoparticles of various sizes.30 Independent of the core size, the authors obtained similar inter-particle distances, and hence particle densities, because all of their core–shell particles had almost identical overall dimensions. Geisel et al. investigated the interfacial behaviour of silica particles encapsulated in a cross-linked hydrogel network and of their hollow counterparts at oil–water interfaces upon compression.31 They found that the core restricted the spreading of polymer chains at the interface when comparing the core–shell nanoparticles with the respective hollow spheres, indicating the existence of a complex balance between particle compliance and interface microstructure. Nazli et al. observed that a thicker hydrogel shell and a decreased cross-linking density in the shell of silica–PNIPAM core–shell particles led to a better stabilisation of oil–water interfaces due to a denser and more regular packing of particles at the interface.32 This points again to the strong influence of particle compliance on the assembly behaviour at interfaces. Finally, very recently, Volk et al. have shown the time-dependent expansion of a freely-floating monolayer of hard core–soft shell particles assembled at the air–water interface due to the strong deformation of the hydrogel shells.33 Interestingly, these monolayers showed very high degrees of hexagonal order independent of the inter-particle distance, which points to the existence of attractive interactions between the particles at the interface, as also proposed in the aforementioned work by Vogel et al.29 These examples highlight the unique potential of soft hydrogel systems assembled at interfaces, but also call for further fundamental understanding of the role played by the presence of the hard core in comparison to the more studied case of purely soft microgel particles without rigid cores. However, so far a detailed and systematic study addressing the influence of the shell size in comparison to the size of the non-deformable core is still missing. Additionally, the origin of the attractive interactions mentioned before is unknown, but highly important. Knowing, avoiding or harnessing these interactions gives in fact additional possibilities to tune the microstructure and properties of those composite monolayers.
In this work, we focus on a microstructural investigation of monolayers made of hard core–soft shell nanoparticles adsorbed at an oil–water interface upon compression and as a function of their shell-to-core ratio. Hard silica cores of the same size were encapsulated in soft, cross-linked PNIPAM hydrogel shells. The thickness of the polymer shell was systematically varied while the cross-linking density was kept constant. As evidenced by bulk measurements using dynamic light scattering, the relative swelling capacity of the different hydrogel shells was very similar. To reveal the particle morphology at the interface, freeze-fracture shadow-casting cryogenic scanning electron microscopy (FreSCa cryo-SEM) was applied. Langmuir–Blodgett depositions were also performed to study the interfacial microstructures upon compression while measuring the surface pressure. Both FreSCa and compression experiments allowed drawing conclusions on the correlation between the shell-to-core size ratio and the interfacial microstructure as a function of the surface pressure. We find significant differences in the assembly behaviour as compared to purely organic hydrogel particles without hard cores.
2 Results and discussion
Core–shell (CS) colloids with solid cores, such as silica nanoparticles, and soft hydrogel shells can be synthesised by seeded precipitation polymerisation using cores of different sizes.34 In this work, we focus on the role of shell thickness on the assembly and compression behaviour of core–shell particles at liquid–liquid interfaces, highlighting the differences to purely organic microgels without a rigid core along the way. The core–shell particles consist of spherical silica nanoparticle cores (diameter σ = 125 ± 10 nm) homogeneously encapsulated in cross-linked PNIPAM shells with varying thickness (see Fig. 1 and Section 3.2 for synthesis details). The same batch of silica particles was used for all syntheses and the overall bulk particle diameters, including the soft shells, are listed in Table 1. We use the shell-to-core ratio λ, where λσ provides the overall core–shell particle size, in order to classify the particles. Higher values of λ indicate thicker shells. As it will be shown later, shells deform upon adsorption at an oil–water interface, in analogy to microgels.18λ therefore varies depending on whether the particles are in bulk or at the interface, and the two cases lead to different values λb and λi, respectively. Throughout the manuscript the core–shell nanoparticles are labelled as CSλb, using the bulk size as a reference.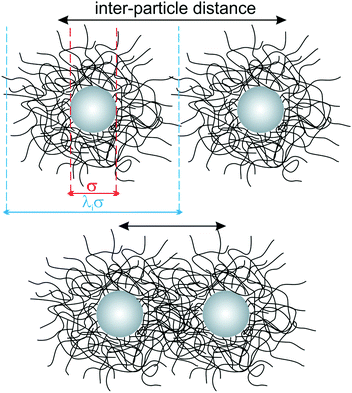 | ||
| Fig. 1 Schematic top-view of the particle morphology for a low (top) and high (bottom) packing fraction. | ||
All hydrogel shells for the CS particle batches were prepared using the same nominal cross-linker content and thus we expect them to have a similar cross-linking density. As previously reported, the hydrogel exhibits a radial cross-linking density profile, with higher densities in the inner region and a decreasing density towards the outer region, including the presence of loosely- or un-cross-linked chains.35Fig. 1 illustrates the particle morphology for two different packing fractions, i.e. different inter-particle distances, corresponding to different levels of compression. At large centre-to-centre distances, the shells are isotropically swollen, while upon compression, they interpenetrate and deform in the contact region because of their soft character.
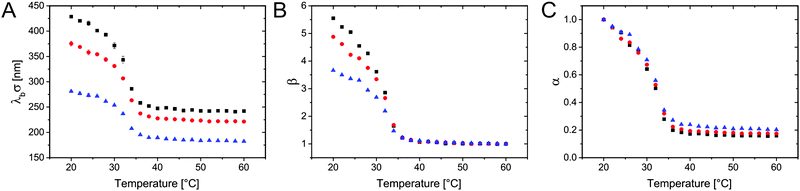
Due to the lower critical solution temperature (LCST) of PNIPAM in water, the PNIPAM hydrogel shells of our core–shell particles show a volume-phase-transition (VPT) behaviour. This means that the shell volume depends strongly on temperature for temperatures close to the volume-phase-transition temperature (VPTT). Their bulk hydrodynamic dimensions are a good measure for the softness of our CS particles. Therefore, we used temperature-dependent dynamic light scattering (DLS) to analyse the CS particle hydrodynamic diameter in bulk at different temperatures. Below the VPTT, the hydrogel shell is highly swollen with water. Above the VPTT, polymer–polymer interactions are favoured and the hydrogel shell collapses while releasing water, which leads to reduced particle dimensions.36,37Fig. 2A shows the hydrodynamic diameter λbσ of the CS particles. All CS particles show the typical VPT behaviour of cross-linked PNIPAM in water with transition temperatures around 32 °C.
Fig. 2B shows the temperature-dependent evolution of the swelling ratio β. This parameter is defined as β = Vcs(T)/Vcs(60 °C), i.e. as the total core-plus-shell particle volume at temperature T, Vcs(T), divided by the total volume of the particle when the shell is in its fully collapsed state at 60 °C, Vcs(60 °C). β is hence a measure for the swelling capacity of the particles. Comparing the CS particles with varying λb, the ones with a thicker shell achieve larger values of β at temperatures below the VPTT. This means that the total degree of swelling, i.e. the relative water uptake, increases for CS particles with increasing hydrogel thicknesses. In other words the volume of the swellable hydrogel shells relative to the volume of the non-swellable silica core increases for larger values of λb, as expected. Since we used the same nominal cross-linker content of 5 mol% for all syntheses, we also expect that the maximum swelling capacity of the hydrogel shells should be similar for all CS particles. Therefore, we calculated the de-swelling ratio α = Vs(T)/Vs(20 °C), only taking into account the volume of the swellable hydrogel shell Vs(T) = Vcs(T) − Vc, defined as the total particle volume minus the core volume. The core volume Vc was determined using the radius measured by SEM (see Table 1 and ESI,† Fig. S1), while the reference volume Vs(20 °C) was obtained using the radius from DLS measured at 20 °C. The data reported in Fig. 2C nicely overlap, reaching very similar maximum de-swelling ratios of approximately 0.2 at temperatures well above the VPTT. The good agreement of α as a function of temperature is a clear indication of the similar cross-linking in the different hydrogel networks. Therefore, we can conclude that the bulk hydrogel morphology in all CS samples is nearly independent on the shell thickness. This is an important prerequisite for the comparison of the compression behaviour at the liquid–liquid interface.
As known from literature, the deformability of the hydrogel shells can lead to different effective particle dimensions after adsorption at the oil–water interface. We therefore employed FreSCa cryo-SEM38 to investigate the particle morphology at the interface. In these experiments, particles spontaneously adsorbed at a macroscopically flat interface are immobilised by shock-freezing the samples. The particles are then imaged from the top after removing the frozen oil phase following fracture (see Section 3.2 for details). The FreSCa cryo-SEM images are shown in Fig. 3 (left) in comparison to the corresponding SEM images of dried particles deposited on a silicon wafer (right). The solid light blue circles illustrate the average dimensions of the silica cores, while the values of λbσ from DLS are highlighted by the solid white circles. The core–shell structure of the particles at the interface is nicely visible in the FreSCa cryo-SEM images. In particular, the top left image of CS3.4 was taken under harsher freeze-etching conditions that allowed the removal of larger amounts of water and thus the direct visualisation of the polymer shells. We observe a characteristic “fried-egg” morphology with a fuzzy boundary and demonstrate that the shells enter into contact at average distances much larger than the white solid circle representing the bulk particle diameter. From the absence of a shadow following the standard oblique metal coating in FreSCa, we deduce furthermore that the portion of the particle protruding into the oil forms an effective contact angle at the interface below 30°.39
This suggests that the hydrogel shell adsorbs at the interface but stays hydrated, and the particles find the position relative to the interface where polymer adsorption and hydration are maximised. Grafting the hydrogel onto a solid nanoparticle negates the possibility to release part of the shell strain at the interface by deforming the core, differently to the case of fully organic microgels without rigid cores. As a consequence, this causes an upward deformation of the interface around the particles, which is clearly seen in Fig. 3B and C. These interfacial deformations consequently cause attractive capillary interactions, driven by a minimisation of the deformations themselves.40 In the literature, these deformations are called capillary monopoles and are typically observed due to gravity for much larger and heavier particles or due to electrodipping for small colloids.41 Here, we highlight a new mechanism behind their origin caused by the wetting of a deformable, surface-active shell anchored onto a rigid core. As it will be shown in more detail later, the presence of such attractive forces drives the particles into contact even below complete coverage of the interface. As a consequence of this, the size occupied by the particles at the interface λiσ can be extracted from the average inter-particle distance at the interface in the absence of compression. The values of λiσ measured from the FreSCa images are represented as the inner dotted yellow circles. As we can see in Fig. 3A, these closely match the shell diameter. The solid outer yellow line represents the same quantity measured from the compression experiments, as it will be described later. Both techniques, FreSCa and the compression–deposition experiments, yield consistent results. The particle sizes at the interface and the differences to bulk values are reported in Table 2. Differences between the data obtained with the two methods may stem from the existence of a small “precompression” upon spontaneous adsorption in the FreSCa experiments, leading to an underestimation of λi. Previous work has in fact shown that spontaneous adsorption may lead to internal compression of the monolayer.23 In agreement with the data shown in Fig. 2C, the degree of shell deformation upon adsorption is the same for all particle types, meaning that all the systems exhibit a comparable proportional size increase at the interface, quantified by λi/λb.
| Core–shell system | λ i σ i [nm] (FreSCa) | λ i σ i [nm] (C–D) | λ i/λb (FreSCa) | λ i/λb (C–D) |
|---|---|---|---|---|
| CS3.4 | 650 ± 50 | 734 ± 30 | 1.51 | 1.71 |
| CS3.0 | 600 ± 50 | 674 ± 50 | 1.59 | 1.79 |
| CS2.2 | 425 ± 50 | 498 ± 37 | 1.51 | 1.77 |
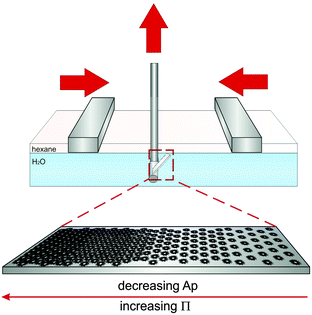
To study how compression affects the microstructure of monolayers of the different CS particles at an oil(n-hexane)–water interface, we used a modified Langmuir–Blodgett deposition protocol, as schematically depicted in Fig. 4. During compression, the monolayers were continuously transferred from the interface onto a silicon wafer. The monolayer structure was then studied mostly by atomic force microscopy (AFM), as described in Section 3.25 In some cases SEM was employed for imaging instead. Briefly, a given volume of the CS particle dispersion was spread at an n-hexane–water interface in a Langmuir–Blodgett trough. A Si wafer was positioned at an angle of 30° with respect to the interface. During continuous compression of the interface by the two barriers of the trough, the substrate was simultaneously withdrawn through the interface, transferring the monolayer onto the wafer. In this way, the wafer collected a particle monolayer deposited at different states of compression depending on the position along the main axis of the wafer. Due to the limited dimensions of the trough, we could not measure a complete compression curve in one single experiment. Therefore, a set of experiments using different initial volumes of the particle dispersions was performed for each CS particle system. After deposition, AFM or SEM images were taken systematically in intervals of 1 millimetre along the main axis of the wafer for each sample. By counting the number of particles per unit area in the images, the area per particle Ap was determined. Plotting the surface pressure Π versus Ap for the core–shell nanoparticles with varying λ, allows obtaining the compression curves illustrated in Fig. 5. Each data point of a compression curve indicates a different position along the wafer. Fig. 5A shows a representative compression curve for CS2.2, accompanied by the compression curves for all particle types shown in Fig. 5B. At first glance, the shape of the curve appears analogous to what has been measured for microgels without solid cores.25 At large specific areas Ap, very low surface pressures are measured due to the absence of inter-particle contacts, followed by a steep increase upon contact. For microgels, these regions are followed by a quasi-plateau in the surface pressures corresponding to a phase transition between shell–shell and core–core contacts, in turns followed by a small compression of a close-packed phase that precedes monolayer buckling and failure. It is important to note that “core” here corresponds to the inner, more highly cross-linked region for purely organic microgels, different from the hard inorganic core of our CS particles. This initial apparent similarity hides instead significant differences, which emerge when we investigate the microstructure of the monolayers by AFM or SEM after deposition.
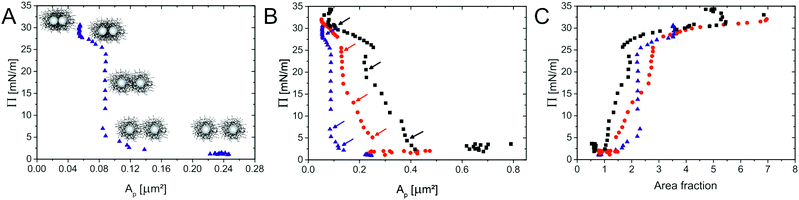 | ||
| Fig. 5 Compression curves of the various CS particles: CS3.4 (black), CS3.0 (red) and CS2.2 (blue). (A) Representation (using CS2.2) of the different inter-particle interactions during compression. (B) Different compression curves of the CS particles with varying λ. The arrows indicate the data points corresponding to the AFM images in Fig. 7. (C) Normalised compression curves: surface pressure as a function of area fraction. | ||
The first difference occurs in the large specific-area region. If we examine the microstructure of the deposited layers in these conditions, as shown in Fig. 6, we see that the particles are not uniformly distributed, but that they form regions where particles are arranged in local regular lattices, separated by voids. Here, as it will be shown later in Fig. 9, the inter-particle distance does not change upon decreasing the specific area, i.e. the distance between particles in the local lattices remains the same, but the area occupied by the voids decreases as the monolayer is compressed. This fact is a direct consequence of the presence of the attractive capillary forces introduced before, which stem from the local interface distortion caused by the wetting of the CS particles. Even at large specific areas, where the average inter-particle distance exceeds the particle size at the interface, particles cluster together driven by capillarity and come together to a fixed distance representative of their effective size at the interface. In other words, no “gas phase” is found at low pressure, as opposed to the case of microgels.23 We can use the inter-particle distance within the clustered phase to estimate particle size, as reported in Table 2.
 | ||
| Fig. 6 SEM images of monolayers deposited at large specific area/low surface pressure. (A) CS3.4. (B) CS3.0. (C) CS2.2. | ||
Further observations can be made by combining the results of Fig. 5B and the microscopic structure of the monolayers at various compressions reported in Fig. 7. From Fig. 5B we note, as expected, that the particles with thicker shells show a rise of surface pressure upon compression at larger values of specific area, i.e. at larger distances. This is a simple consequence of the fact that the overall particle dimensions change with changing λi. More interestingly, we note that with decreasing λi, the rise of the compression curves changes significantly, becoming steeper. Although the cross-linking density of the samples is similar, the thickness of the shell changes. Therefore, the range of distances over which the latter can be compressed before hard repulsion between cores takes place also changes. In other words, the absolute degree of compressibility of the various hydrogel shells differs substantially. At low values of λ the particles are less swollen (Fig. 2B) and, more importantly, are less spread out at the interface (Fig. 3 and Table 2). When we examine the interface microstructure in correspondence to the surface pressure rise (left column of Fig. 7), we observe that here, in analogy to microgels, a regular, space-filling hexagonal particle lattice is found. The presence of a well-ordered lattice is confirmed by the corresponding radial distribution functions (g(r)) plotted in black in Fig. 8, showing well-defined nearest-neighbour peaks and several oscillations.
 | ||
| Fig. 7 AFM height images of the transferred monolayers of the core–shell particles CS3.4 (black); CS3.0 (red); CS2.2 (blue). Increasing surface pressure from left to right. The images correspond to the data points marked by the arrows in Fig. 5B. | ||
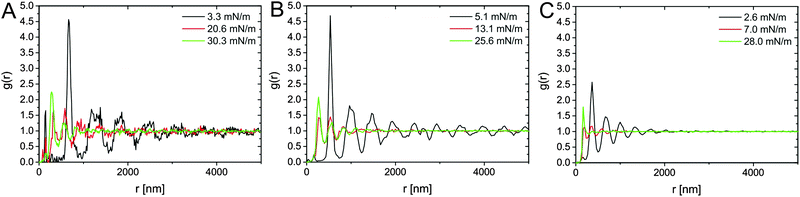 | ||
| Fig. 8 Representative radial distribution functions g(r) obtained for the monolayers of the core–shell nanoparticles CS3.4 in (A), CS3.0 in (B), CS2.2 in (C) at different stages of compression. | ||
Very rapidly though, upon further compression, some of the inter-particle contacts fail and particles aggregate into more closely packed clusters. The AFM images in the central column of Fig. 7 correspond in fact to the point where equal numbers of particles are found in the lattices and in the clusters. This is identified from the radial distribution functions at the intermediate value of surface pressure for which the peak corresponding to nearest neighbours in the lattice has the same height as the peak corresponding to the nearest neighbours in the clusters (red curves in Fig. 8). From those graphs, especially for CS3.0 and CS3.4, we notice that the position of the nearest-neighbours peak in the lattice has hardly changed upon compression, and that instead particles tend to aggregate rather than deform the whole lattice in a continuous way. Remarkably, this occurs at surface pressures significantly below the quasi-plateau, in stark contrast to microgels. Moreover, the range of specific areas and surface pressures over which this transition occurs depends on λ, as highlighted by the position of the arrows in Fig. 5B. In particular, the transition occurs at increasing surface pressure for increasing λ, indicating a larger compliance of the thicker shells against the nucleation of defects in the clusters. The images in the right column of Fig. 7 correspond to the point where the clustering transition has proceeded to completion. All particles are within closely packed clusters separated by voids of a thickness comparable to the nearest-neighbouring spacing of the non-closed-packed phase. The green curves in Fig. 8 indicate that the position of the nearest neighbours in the clusters does not change, but that their probability increases. This region also presents some significant differences to completely soft particles.25 The first one is that it is not possible for the cores to touch within the clusters. This is at odds with fully deformable microgels which can freely restructure their shape to minimize the energy associated to particle deformation. In the case of our CS particles, the permanent grafting of the hydrogel onto the silica cores makes it impossible to squeeze the shell out of the contact region, leading to a minimum inter-particle distance corresponding to a fully compressed shell. The latter is an increasing function of λ, as qualitatively seen in the AFM images. The second main feature to be noted is that, even if compressed beyond the point of full clustering, the monolayers can never be brought into a state where the voids in between the clusters disappear and a homogeneous lattice of particles in close contact is formed. In practice, the monolayer buckles and fails before this state is reached. This corresponds to the last parts of the compression curves, where the surface pressure increases very steeply with decreasing Ap.
In order to compare the compression curves directly, normalising for the effect of shell thickness, we calculated the particle area fraction at the interface as the ratio between the particle area, calculated from the interfacial dimensions (obtained by compression and deposition; see Table 2), and the measured Ap. Fig. 5C shows the compression curves as a function of area fraction. An area fraction above the two-dimensional close packing value of 0.91 implies that the particles are in a compressed state. As expected, the surface pressure starts to rise significantly for all particles at a value of the area fraction around 1.
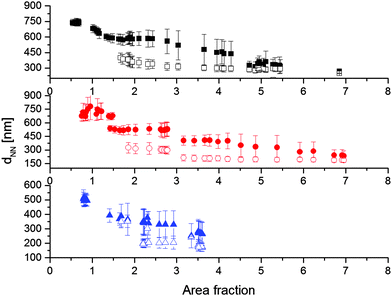
Further conclusions can be drawn by analysing the nearest-neighbour distances dNN as a function of area fraction (Fig. 9). The values of dNN are directly measured from the AFM or SEM images by fitting the distributions of the nearest-neighbour distance with Gaussian curves and identifying the position of the mean. The standard deviation is used to estimate the errors in the data points shown in the figure (see the ESI† for more details). For each CS system, only one value of dNN is present at low area fractions. Moreover, we observe that for all particles there is a range of area fractions for which the inter-particle distance is constant. This is the region where attractive capillary forces bring the particles together into a defined separation. The values of dNN in this region have been used to define the particle size λiσ reported in Table 2 and for the calculation of the area fraction. In particular, λiσ is defined as the average distance between particles corresponding to area fractions below 0.91. Upon further compression, there is a small range of area fractions, up to 1.5, where the non-close packed lattice is compressed and therefore dNN decreases smoothly, before the clustering transition starts and a second, smaller value of dNN appears, which is practically constant as a function of area fraction. As previously mentioned, this corresponds to the thickness of the fully collapsed hydrogel shell in the region of contact between particles. During the clustering transition, the non-close packed dNN stays constant, but, at an area fraction around 2.5, it starts decreasing until it approaches the close-packed distance at the highest area fractions. This can be attributed to the compression of the separation distance between the different clusters, which again tends to approach the thickness of the fully compressed shells. In practice, the accessible range of center-to-center distances can thus be easily tuned by varying λ and all particles show the same qualitative behaviour.
Finally, we address the degree of order of the monolayers by looking at the hexagonal order parameter Ψ6 (see Section 3.2 for details). Fig. 10 shows a non-monotonic trend of Ψ6 as a function of area fraction, which can be correlated with the structural transitions discussed above. We observe an initial plateau of Ψ6 corresponding to the regime where locally ordered regions are formed due to capillary interactions at low surface coverage. Hexagonal order reaches a maximum when complete surface coverage is achieved and the monolayers are compressed up to the point where the clusters nucleate. We notice that the maximum value of Ψ6 depends on λ, with thicker and more compliant shells that allow for annealing of defects in the crystals and therefore enable the formation of more highly ordered monolayers.
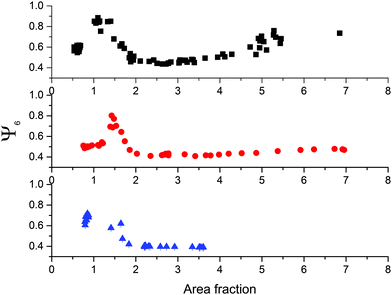 | ||
| Fig. 10 Hexagonal bond-order parameter Ψ6 as a function of area fraction for CS3.4, CS3.0 and CS2.2 from top to bottom. | ||
The presence of the clusters causes a sharp drop in Ψ6 due to particles at the edges of the clusters that are no longer in an isotropic hexagonal lattice. As the transition proceeds, there is a second increase in the order parameter, corresponding to the local hexagonal packing of particles within the clusters. Here the three CS particles behave differently. The thicker the shell, the higher the values of Ψ6 that are recovered at high area fractions. The reason for this is again related to the different compliance of the shells as a function of their thickness, which has a direct consequence on how the close-packed phase is formed. From the images in Fig. 7, we in fact see that for CS3.4 when the close-packed clusters are formed, they do not strongly distort the underlying non-close-packed crystal. This can be more clearly understood if we measure the orientation of the hexagonal clusters, as shown in Fig. 11.
 | ||
| Fig. 11 Local orientation of the hexagonal domains in the clusters. The images correspond to the AFM images in the right column of Fig. 7. (A) CS3.4, (B) CS3.0, (C) CS2.2. The colours indicate the orientation extracted from the phase angle of Ψ6 for each particle and vary between −π and π. | ||
The uniform colour coding for the CS3.4 particles indicates that all the clusters in the field of view have the same orientation, which corresponds to the orientation of the non-close packed crystal before cluster formation, as noticeable in the middle image of the top row in Fig. 7. The opposite is found for the CS2.2 particles, where the colour map in Fig. 11 indicates that the clusters show every possible orientation, implying that local hexagonal order is not recovered and that the transition destroys the non-close-packed phase completely. An intermediate situation is seen for the CS3.0 particles, where several orientations are visible in the field of view. The pathway for the transition and the final structure is once more radically different compared to the case of fully deformable microgels.25
3 Experimental
3.1 Materials
Tetraethylorthosilicate (TEOS; Sigma-Aldrich; 98%), ammonium hydroxide solution (NH3 (aq.); Sigma-Aldrich; 30–33%), ethanol (EtOH; Sigma-Aldrich; ≥99.8%), rhodamine b isothiocyanate (RITC; Sigma-Aldrich; mixed isomers), (3-aminopropyl) trimethoxysilane (APS; Sigma-Aldrich; 97%), 3-(trimethoxysilyl)propyl methacrylate (MPS; Sigma-Aldrich; 98%), sodium dodecyl sulfate (SDS; Merck; Ph. Eur.), N-isopropylacrylamide (NIPAM; Sigma-Aldrich; 97%), N,N′-methylenebisacrylamide (BIS; Fluka; ≥98%), potassium peroxodisulfate (PPS; Fluka; ≥99%), isopropyl alcohol (Fischer Chemical; 99.97%), toluene (Fluka Analytical; 99.7%), n-decane (Sigma-Aldrich; ≥99%) and n-hexane (Sigma-Aldrich; 99%) were used as received. Water was purified using a Milli-Q system which led to a final resistivity of 18 MΩ cm.3.2 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
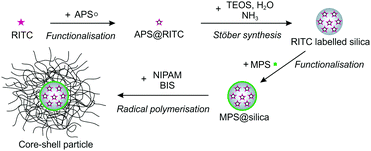
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) prior to addition. The silica particles were synthesized according to the established protocol by Stöber et al.42 Briefly, a mixture of 125 mL of EtOH and 10 mL of ammonium hydroxide solution (30–33%) was heated to 50 °C and equilibrated for 20 min in a 250 mL three-neck round-bottom flask equipped with a reflux condenser. After rapid addition of a mixture of 20 mL of EtOH and 5 mL of TEOS that was heated to 50 °C, the clear solution became slightly turbid indicating the nucleation of silica particles. Once the seed nucleation started, 2 mL of a dilute ethanolic RITC solution functionalised with APS were added dropwise. The reaction proceeded overnight. Afterwards, the mixture was allowed to cool to room temperature. To remove residues from the reaction, the particles were cleaned twice by centrifugation at a rotation speed of 2599 rcf for 90 min and redispersed in ethanol. For the functionalisation of the silica particles MPS was used. Prior to the addition of MPS under continuous stirring, the pH of the silica dispersion was adjusted to 9–10 by drop-wise addition of an ammonium hydroxide solution (30–33%). The amount of MPS was adapted to obtain a surface density of 1 molecule per 40 Å2. The mixture was stirred for 24 h and subsequently refluxed for 1 h to guarantee covalent binding of the MPS molecules. During cooling to room temperature, SDS that was dissolved in a small volume of ethanol was added dropwise giving a final SDS concentration of 0.2 mM to stabilise the functionalised silica particles. The silica particles were concentrated and purified by 3 centrifugation steps (2599 rcf, 90 min). The final particle number concentration of the purified silica particle dispersion was 0.197 μM.
5) prior to addition. The silica particles were synthesized according to the established protocol by Stöber et al.42 Briefly, a mixture of 125 mL of EtOH and 10 mL of ammonium hydroxide solution (30–33%) was heated to 50 °C and equilibrated for 20 min in a 250 mL three-neck round-bottom flask equipped with a reflux condenser. After rapid addition of a mixture of 20 mL of EtOH and 5 mL of TEOS that was heated to 50 °C, the clear solution became slightly turbid indicating the nucleation of silica particles. Once the seed nucleation started, 2 mL of a dilute ethanolic RITC solution functionalised with APS were added dropwise. The reaction proceeded overnight. Afterwards, the mixture was allowed to cool to room temperature. To remove residues from the reaction, the particles were cleaned twice by centrifugation at a rotation speed of 2599 rcf for 90 min and redispersed in ethanol. For the functionalisation of the silica particles MPS was used. Prior to the addition of MPS under continuous stirring, the pH of the silica dispersion was adjusted to 9–10 by drop-wise addition of an ammonium hydroxide solution (30–33%). The amount of MPS was adapted to obtain a surface density of 1 molecule per 40 Å2. The mixture was stirred for 24 h and subsequently refluxed for 1 h to guarantee covalent binding of the MPS molecules. During cooling to room temperature, SDS that was dissolved in a small volume of ethanol was added dropwise giving a final SDS concentration of 0.2 mM to stabilise the functionalised silica particles. The silica particles were concentrated and purified by 3 centrifugation steps (2599 rcf, 90 min). The final particle number concentration of the purified silica particle dispersion was 0.197 μM.
| SiO2–PNIPAM particles | m (NIPAM) [mg] | m (BIS) [mg] | V (H2O) [mL] | V (SiO2) [μL] | m (PPS) [mg] |
|---|---|---|---|---|---|
| CS2.2 | 136 | 10 | 40 | 1125 | 4 |
| CS3.0 | 113 | 8 | 20 | 438 | 2 |
| CS3.4 | 113 | 8 | 20 | 250 | 2 |
The holder allowed a continuous adjustment of the position of the substrate at the interface during the experiment. The wafer was mounted at an angle of 30° relative to the horizontal interface. To remove impurities on the wafer, it was cleaned by three ultrasonication treatments of 15 min. First in toluene, then in isopropanol and finally in water. A UV-ozone cleaner (Bioforce Nanosciences) treatment was applied for 30 min to remove remaining organic impurities and to hydrophilise the surface for the deposition experiment. After opening the barriers of the trough, water was filled until the edge at which the oil–water interface is formed. Subsequently, a Wilhelmy plate (20 × 10 mm2) was mounted so that it was immersed by one third in the water phase. The surface pressure was set to zero and a test run was conducted in which the surface pressure should stay below 0.2 mN m−1 upon compression of the trough area by the barriers. A higher surface pressure was assigned to the presence of contaminants in the experiment, which may influence the experiment. In this case the water was removed using a pipette tip (Tip One) attached to a vacuum pump (Vacuum Brand PC3000). The procedure was repeated until the described conditions were achieved. Subsequently, the substrate was mounted on the dipper arm, which was fixed in the trough. 100 mL of n-hexane were added on top of the water phase and the surface pressure was set to zero. The diluted particle dispersion consisting of the 1 wt% particle dispersion, water and isopropanol in a ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 were injected at the oil–water interface using a 100 μL Hamilton glass syringe. For the gradient depositions, the barrier speed was kept constant at 2.3 mm min−1 and the dipper was raised with a speed of 0.3 mm min−1. While the substrate is lifted during the experiment, the surface pressure is measured and the trough area is compressed. The mentioned velocities were chosen to ensure that the entire wafer substrate passed through the interface at the same time as the compression was finished. After each experiment, the parts of the instrumental setup were thoroughly rinsed with water and ethanol and dried with a nitrogen jet.
2 were injected at the oil–water interface using a 100 μL Hamilton glass syringe. For the gradient depositions, the barrier speed was kept constant at 2.3 mm min−1 and the dipper was raised with a speed of 0.3 mm min−1. While the substrate is lifted during the experiment, the surface pressure is measured and the trough area is compressed. The mentioned velocities were chosen to ensure that the entire wafer substrate passed through the interface at the same time as the compression was finished. After each experiment, the parts of the instrumental setup were thoroughly rinsed with water and ethanol and dried with a nitrogen jet.
The 2D hexagonal order parameter Ψ6 is calculated as:44
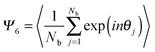 | (1) |
4 Conclusions
The assembly of hard core–soft shell particles at liquid–liquid interfaces is the result of a complex interplay of interactions. In this paper we focussed on the correlation between shell thickness and interfacial microstructure of these particles, keeping all other factors constant. In spite of the fact that other parameters, such as the core size and the overall core + shell particle size may have an influence on the interface microstructure, our choice was dictated by the idea to study the systematic influence of one single parameter without the need to decouple combined effects. Changing the core size, for instance, may lead to differences in the grafting density of the shells, rendering the comparison between different systems more complicated. For this purpose we employed FreSCa cryo-SEM investigations and compression experiments in a Langmuir–Blodgett trough. We synthesized core–shell particles containing silica cores of the same size encapsulated in cross-linked hydrogel shells of PNIPAM of varying thickness, leading to different shell-to-core ratios λ for each particle system. The nominal cross-linking density in the polymer network was found to be similar because the particles showed comparable swelling properties, as revealed by dynamic light scattering. The FreSCa cryo-SEM investigations furthermore exposed that systems with increasing λ stretch out more in absolute value at the interface, but that a relative size increase of 1.6–1.8 compared to the bulk is observed for all particles. FreSCa also showed that the majority of the hydrogel shell resides in the water phase, with an effective contact angle with the interface below 30° for all particle systems. Crucially, single-particle investigations enabled us to detect an upward deformation of the interface around the particles. As previously described, this fact stems from the drive for the particles to maximize the amount of polymer adsorbed at the interface, while maintaining shell hydration. The presence of a rigid core limits the possibility for the shell to rearrange and the final balance between interfacial forces, shell hydration, adsorption and internal elasticity determines the shape and position of the particles at the interface and leads to local deformations of the interface. These deformations consequently lead to attractive capillary interactions, which cause shell–shell contacts between the particles and the formation of islands already at low surface coverage. This finding is in contrast to microgels without hard cores that form a uniformly distributed “gas phase” at low surface coverage. Consequently, we have identified a new mechanism causing capillary forces between core–shell objects whose shell has a thickness comparable to the core size. Compression experiments showed that, after the formation of a uniform monolayer, the surface pressure increased steeply displaying the compression of the hydrogel shell. In this region the degree of compressibility plays an important role; decreasing λ corresponds to a steeper slope in the compression curves. As a result, the range of specific areas over which the deformation takes place also strongly depends on the shell thickness. In the course of the ongoing compression experiments, closely packed clusters separated by voids were formed instead of a continuous deformation of the crystal lattice. In contrast to microgels without hard cores, this transition to clusters appeared at much lower surface pressures. Within these clusters the silica cores cannot touch, which displays another difference to pure microgels that are not restricted in restructuring their interfacial morphology. Before the voids can close, monolayer buckling occurs upon further compression. We also analysed the structural order in the system monitoring the hexagonal order parameter Ψ6 upon compression. Ψ6 increases first until a complete surface coverage is obtained. As soon as clustering occurs, local order drops, but stabilises again upon further compression due to the local hexagonal packing within the clusters. The compliance of the shell is more pronounced for larger values of λ, which leads to a better defect compensation in the system and therefore to higher values of Ψ6. For systems with a large λ, we also found that the orientation of the underlying crystalline phase at low compression is maintained upon clustering.Concluding, our findings indicate that the tailoring of a specific interfacial microstructure can be achieved by tuning the inter-particle interactions using hard core–soft shell particles with different shell thicknesses. This enables future, more applied work, aimed at fabrication of defined nanostructures through the clever design of core–shell particles with hard functional cores, such as gold or silver nanoparticles, and soft hydrogel shells, which can be assembled and deposited from fluid–fluid interfaces. Additionally, the presence of attractive capillary interactions generated solely by the presence of a rigid core may also have positive implications in using such systems as effective emulsions stabilizers. Previous work has in fact shown that attractive capillary forces between anisotropic particles lead to mechanically stronger interfaces and thus more stable emulsions.45 The possibility of obtaining similar results with shape-isotropic nanoscale objects opens up new routes for the design of advanced emulsifiers.
Acknowledgements
MK acknowledges financial support from the German Research Foundation (DFG) through the Emmy Noether-Programme (KA 3880/1). AR was supported by the Elite Network Bavaria in the framework of the Elite Study Program “Macromolecular Science”. LI and MZ acknowledge financial support from the SNSF grant PP00P2_144646/1. The authors acknowledge Hendrik Spanke for the code on the angular orientation of crystalline domains and Dr Martin Dulle for the code concerning the calculation of the radial distribution functions.Notes and references
- B. M. Rey, R. Elnathan, R. Ditcovski, K. Geisel, M. Zanini, M. A. Fernandez-Rodriguez, V. V. Naik, A. Frutiger, W. Richtering, T. Ellenbogen, N. H. Voelcker and L. Isa, Nano Lett., 2016, 16, 157 CrossRef CAS PubMed.
- A. Verma, O. Uzun, Y. Hu, Y. Hu, H. S. Han, N. Watson, S. Chen, D. J. Irvine and F. Stellacci, Nat. Mater., 2008, 7, 588 CrossRef CAS PubMed.
- S. U. Pickering, J. Chem. Soc. Trans., 1907, 91, 2001 RSC.
- V. Schmitt and V. Ravaine, Curr. Opin. Colloid Interface Sci., 2013, 18, 532 CrossRef CAS.
- W. Richtering, Langmuir, 2012, 28, 17218 CrossRef CAS PubMed.
- O. S. Deshmukh, D. van den Ende, M. C. Stuart, F. Mugele and M. H. Duits, Adv. Colloid Interface Sci., 2015, 222, 215 CrossRef CAS PubMed.
- B. P. Binks, Curr. Opin. Colloid Interface Sci., 2002, 7, 21 CrossRef CAS.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503 CrossRef CAS.
- S. Arditty, V. Schmitt, J. Giermanska-Kahn and F. Leal-Calderon, J. Colloid Interface Sci., 2004, 275, 659 CrossRef CAS PubMed.
- V. Garbin, J. C. Crocker and K. J. Stebe, J. Colloid Interface Sci., 2012, 387, 1 CrossRef CAS PubMed.
- B. Brugger, B. A. Rosen and W. Richtering, Langmuir, 2008, 24, 12202 CrossRef CAS PubMed.
- Z. Li, W. Richtering and T. Ngai, Soft Matter, 2014, 10, 6182 RSC.
- C. Monteux, C. Marlière, P. Paris, N. Pantoustier, N. Sanson and P. Perrin, Langmuir, 2010, 26, 13839 CrossRef CAS PubMed.
- K. Geisel, L. Isa and W. Richtering, Angew. Chem., Int. Ed., 2014, 53, 4905 CrossRef CAS PubMed.
- D. M. Heyes and A. C. Brańka, Soft Matter, 2009, 5, 2681 RSC.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197 CrossRef CAS PubMed.
- A. Fernández-Barbero, A. Fernández-Nieves, I. Grillo and E. López-Cabarcos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051803 CrossRef PubMed.
- K. Geisel, L. Isa and W. Richtering, Langmuir, 2012, 28, 15770 CrossRef CAS PubMed.
- M. Destribats, V. Lapeyre, M. Wolfs, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Soft Matter, 2011, 7, 7689 RSC.
- R. W. Style, L. Isa and E. R. Dufresne, Soft Matter, 2015, 11, 7412 RSC.
- M. Destribats, V. Lapeyre, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Langmuir, 2012, 28, 3744 CrossRef CAS PubMed.
- Z. Li, K. Geisel, W. Richtering and T. Ngai, Soft Matter, 2013, 9, 9939 RSC.
- K. Geisel, W. Richtering and L. Isa, Soft Matter, 2014, 10, 7968 RSC.
- F. Pinaud, K. Geisel, P. Massé, B. Catargi, L. Isa, W. Richtering, V. Ravaine and V. Schmitt, Soft Matter, 2014, 10, 6963 RSC.
- M. Rey, M. Á. Fernández-Rodríguez, M. Steinacher, L. Scheidegger, K. Geisel, W. Richtering, T. M. Squires and L. Isa, Soft Matter, 2016, 12, 3545 RSC.
- J. Kim, M. J. Serpe and L. A. Lyon, J. Am. Chem. Soc., 2004, 126, 9512 CrossRef CAS PubMed.
- S. Tsuji and H. Kawaguchi, Langmuir, 2005, 21, 8439 CrossRef CAS PubMed.
- M. Karg, Macromol. Chem. Phys., 2016, 217, 242 CrossRef CAS.
- N. Vogel, C. Fernández-López, J. Pérez-Juste, L. M. Liz-Marzán, K. Landfester and C. K. Weiss, Langmuir, 2012, 28, 8985 CrossRef CAS PubMed.
- T. Honold, K. Volk, A. Rauh, J. P. S. Fitzgerald and M. Karg, J. Mater. Chem. C, 2015, 3, 11449 RSC.
- K. Geisel, A. A. Rudov, I. I. Potemkin and W. Richtering, Langmuir, 2015, 31, 13145 CrossRef CAS PubMed.
- K. O. Nazli, C. W. Pester, A. Konradi, A. Böker and P. van Rijn, Chemistry, 2013, 19, 5586 CrossRef PubMed.
- K. Volk, J. P. Fitzgerald, M. Retsch and M. Karg, Adv. Mater., 2015, 27, 7332 CrossRef CAS PubMed.
- M. Karg, S. Wellert, S. Prevost, R. Schweins, C. Dewhurst, L. M. Liz-Marzán and T. Hellweg, Colloid Polym. Sci., 2011, 289, 699 CAS.
- J. Dubbert, T. Honold, J. S. Pedersen, A. Radulescu, M. Drechsler, M. Karg and W. Richtering, Macromolecules, 2014, 47, 8700 CrossRef CAS.
- K. Kratz, T. Hellweg and W. Eimer, Polymer, 2001, 42, 6631 CrossRef CAS.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1 CrossRef CAS PubMed.
- L. Isa, F. Lucas, R. Wepf and E. Reimhult, Nat. Commun., 2011, 2, 438 CrossRef PubMed.
- L. Isa, Chimia, 2013, 67, 231 CrossRef CAS PubMed.
- K. D. Danov and P. A. Kralchevsky, Adv. Colloid Interface Sci., 2010, 154, 91 CrossRef CAS PubMed.
- F. Bresme and M. Oettel, J. Phys.: Condens. Matter, 2007, 19, 413101 CrossRef.
- W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62 CrossRef.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298 CrossRef CAS.
- M. Schmidt and H. Löwen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 7228 CrossRef CAS.
- B. Madivala, S. Vandebril, J. Fransaer and J. Vermant, Soft Matter, 2009, 5, 1717 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm01020b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |