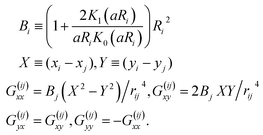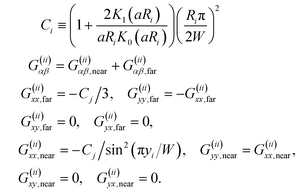Self-organizing microfluidic crystals†
William E.
Uspal
a and
Patrick S.
Doyle
*b
aDepartment of Physics, Massachusetts Institute of Technology, USA
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: pdoyle@mit.edu
First published on 8th May 2014
Abstract
We consider how to design a microfluidic system in which suspended particles spontaneously order into flowing crystals when driven by external pressure. Via theory and numerics, we find that particle–particle hydrodynamic interactions drive self-organization under suitable conditions of particle morphology and geometric confinement. Small clusters of asymmetric “tadpole” particles, strongly confined in one direction and weakly confined in another, spontaneously order in a direction perpendicular to the external flow, forming one dimensional lattices. Large suspensions of tadpoles exhibit strong density heterogeneities and form aggregates. By rationally tailoring particle shape, we tame this aggregation and achieve formation of large two-dimensional crystals.
1 Introduction
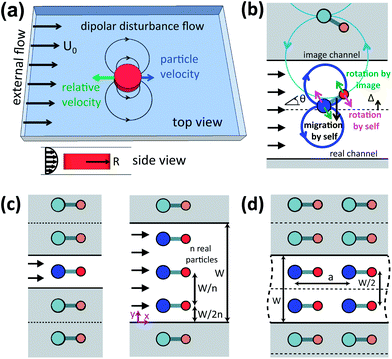
The shape of interacting particles can control their spontaneous organization into larger ordered structures. Recently, innovations in colloidal synthesis providing precise control over particle morphology have driven fresh efforts to relate shape to self-assembled equilibrium structure.1,2 Particle “designers” have exploited depletion interactions,3 steric effects,4 and Janus patterning5 for self-assembly of novel complex materials. On the other hand, comparatively few studies have sought to relate shape to self-organization out of equilibrium, despite the rich set of static and dynamic structures that can be sustained through continuous dissipation of energy.6 In particular, suspensions that self-organize under flow into flowing crystals are of great interest from both theoretical and practical perspectives. They provide a natural arena for extension and revision of theoretical ideas developed in the context of equilibrium crystallization. Moreover, they can be harnessed for microfluidic and lab-on-a-chip applications. Orderly flow eases recognition and interrogation of suspended objects in cytometry7 and bioassays.8 Flowing crystals could be used as dynamically programmable metamaterials, assembled with high throughput in continuously operating microdevices, or as tunable diffraction gratings.9 Researchers have achieved self-organizing flowing crystals with acoustically excited bubbles10 and weakly inertial spheres.11 However, the possibility that self-organization of flowing crystals can be encoded via design of particle shape has remained largely unexplored.When particles are driven by flow, they are coupled via the disturbances they create in the suspending fluid. These hydrodynamic interactions (HI) are central to most examples of flow-driven self-organization at the microscale.11,12 The tensorial form and spatial decay of hydrodynamic interactions can change dramatically in the presence of confining boundaries. In particular, we consider hydrodynamic interactions when the typical size of a particle is comparable to the height of a confining slit, such that the particles are constrained to “quasi-two-dimensional” (q2D) motion [Fig. 1(a)]. The tightly confined particles experience strong friction from the confining plates, and will therefore lag a pressure-driven external flow. Due to this lag, the particles create flow disturbances with a characteristic dipolar structure: moving upstream relative to the fluid, particles push fluid mass away from their upstream edges and draw fluid mass into their downstream edges.13,14 The strength of this leading order flow disturbance is proportional to the particle area, and decays as the inverse square distance from the particle center. That mass conservation determines the leading order disturbance is ultimately due to the presence of the two confining plates. The plates exert friction on the fluid, removing momentum from the system and screening long-range momentum transport. In contrast, in three dimensions, conservation of momentum determines the leading order far-field flow disturbance, the “Stokeslet.”
Quasi-two-dimensional microchannels have proven to be a rich setting for collective phenomena involving flowing droplets or solid particles, including flowing crystals.15 One-dimensional flowing crystals of “pancake shaped” droplets, ordered in the streamwise direction, can sustain transverse and longitudinal acoustic waves, or “microfluidic phonons”.16,17 Small clusters of discs, ordered perpendicular to the flow direction, can maintain relative positions as they are carried by the flow.18 Various two-dimensional crystal lattices are possible in unbounded q2D.19 However, in each example of a flowing crystal, the crystal is only marginally stable: the amplitude of a collective mode neither grows nor decays in time. Consequently, crystals have no “restoring force” against perturbation by channel defects, and do not self-organize from disorder. However, disordered droplet suspensions exhibit large, freely propagating fluctuations in density,20 as well as directionally dependent, long-range orientational order in droplet velocity,21 hinting that underlying collective effects could be molded to promote crystallization.
Recently, we have shown via theory and experiments that a single asymmetric dumbbell comprising two rigidly connected discs, or “tadpole,” will align with the external flow and focus to the channel centerline.22 We isolated three viscous hydrodynamic mechanisms that together produce this “self-steering,” and which are shown schematically in Fig. 1(b). The “head” and “tail” discs of a particle interact hydrodynamically. Since the discs are unequal in size, they have unequal hydrodynamic strength, and the larger head disc pushes the tail downstream. Therefore, self-interaction drives alignment with the flow. Secondly, when the particle is not aligned, self-interaction drives cross-streamline or lateral migration, since the scattered flow produced by a disc has a component perpendicular to the direction of the external flow. Finally, when the particle is displaced from the centerline, interaction with its own hydrodynamic images across the channel side walls drives rotation away from alignment. Through the combination of these three effects, the aligned and focused configuration is an attractor for particle dynamics.
This single particle picture provides a starting point for consideration of how flowing crystals might self-organize in multiple particle systems. In Fig. 1(c), we consider a single aligned and focused particle. The particle translates in the flow direction without any rotation or lateral motion, and is part of an infinite lattice of real and image particles. If one or more of the image particles is exchanged for a real particle, and the associated image channels are exchanged for fluid, the resulting configuration should also steadily translate with no relative particle motion. Each real particle in the “triplet” at the right of Fig. 1(c) experiences the same flow fields as the “singlet” at left, and therefore must have the same motion as the singlet. The triplet configuration is a “fixed point” in phase space for the dynamics of the system, and, in view of the infinite lattice, can be regarded as a one-dimensional flowing crystal. In general, for a group of n real particles, the n-let configuration is a fixed point. For an n-let, the real particles are located at y = W/2n + (i − 1)W/n, where i ∈ {1…n}, ŷ is the transverse direction, and y = W/2 is the channel centerline. For instance, particle i = 1 in a triplet is located at y = W/6 and has two neighbors: a real particle at y = W/2, and its reflected image particle at y = −W/6. The transverse positions are determined by translational symmetry: each particle, real or image, is separated from its nearest neighbors by a distance W/n.
Furthermore, symmetry considerations extend to two-dimensional crystals. Fig. 1(d) shows two “columns” of a “doublet crystal” that has translational symmetry in the streamwise direction. This configuration is also a fixed point. For instance, for the column shown at left, the influence of all other columns vanishes by symmetry. In general, two-dimensional n-let crystals are dynamical fixed points for suspension dynamics.
While we have argued that one and two-dimensional flowing crystals are dynamical fixed points – i.e. have no relative particle motion – we have not examined their stability. For instance, a lattice might be linearly unstable, subject to a clumping instability resembling that found for a row of sedimenting spheres.23,24 Even if a lattice is linearly stable, its basin of attraction might not be significant if the dynamics of the system are multistable.25 Addressing these questions requires a quantitative approach.
In this work, we develop a numerical technique to study suspensions and small clusters of flow-driven q2D particles. This technique can accommodate any particle shape that can be modelled as a collection of discs connected by springs. Applying this technique to initially disordered dumbbells, we find that while small clusters can assemble with significant yield into one-dimensional lattices, large suspensions fail to crystallize. We trace this failure to the formation of tightly bound pairs, or “defects,” which tend to pack into aggregates. To eliminate these defects, we design a “trumbbell” shape for which chaining of particles in the streamwise direction is favored by the influence of particle shape on the flow field. Through a multistage self-organization process, the trumbbells can form perfect doublet crystals.
2 Theory and numerical method
A common and widely successful approach in polymer dynamics is to represent a molecule as a coarse-grained chain of beads connected by springs. These bead-spring models can incorporate many different physical effects, including hydrodynamic interactions in confined geometries.26 In this section, we develop model equations suited to disc-spring representations of q2D particles. The equations include dipolar hydrodynamic interactions through a q2D mobility tensor, derived below, and can accommodate conservative interaction potentials. We discuss our method for numerical integration of the deterministic model equations. Finally, we present the model particle architectures and conservative interaction potentials which will be used in this work.2.1 The q2D Brinkman equation
As our starting point, we seek an effective equation describing the dynamics of the suspending fluid in a q2D channel. Assuming the familiar creeping flow limit, the fluid obeys the Stokes equation| −∇P + μ∇2v = 0, | (1) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) direction by external pressure. The direction of the channel with thinnest geometric length is ẑ, which is bounded by two plates separated by a height H. The channel is bounded in ŷ by two side walls separated by width W. Far from channel side walls or suspended particles, the velocity profile is parabolic:
direction by external pressure. The direction of the channel with thinnest geometric length is ẑ, which is bounded by two plates separated by a height H. The channel is bounded in ŷ by two side walls separated by width W. Far from channel side walls or suspended particles, the velocity profile is parabolic: | (2) |
 | (3) |
 . We define u(x, y) as the depth averaged velocity, where u = 2umax/3. We average eqn (3) over the channel depth H to remove the z dependence and obtain
. We define u(x, y) as the depth averaged velocity, where u = 2umax/3. We average eqn (3) over the channel depth H to remove the z dependence and obtain| −∇P + μ∇2D2u − (12μ/H2)u = 0. | (4) |
We define the two-dimensional pressure field P2D(x, y) ≡ P(x, y)H, so that P2D has the same units as surface tension, and the two-dimensional dynamic viscosity μ2D ≡ μH. Multiplying the previous equation by H, we obtain the two-dimensional Brinkman equation
| −∇P2D + μH∇2u − (12μ/H)u = 0. | (5) |
Near suspended particles and side walls, this effectively two-dimensional governing equation necessarily omits possible ẑ components to the flow, and the separation of variables assumed by eqn (2) may not be exact. These edge effects are negligible for distances greater than ∼H from side walls and suspended particles.18,27 It is interesting to note that eqn (5) is the two-dimensional Stokes equation with an additional third term. This term, which breaks Galilean invariance, represents the friction exerted by the plates on the fluid.
2.2 Motion of a single disc
Now we consider a simple problem in two dimensions. A single disc with radius R and velocity Up is subject to a uniform external flow U. The fluid obeys eqn (5), and is subject to no-slip and no-penetration conditions on the solid boundary. Solution of eqn (5) determines two items of interest: (i) the velocity field u, including the disturbance created by the disc, and (ii) the force fq2D on the disc from the fluid, obtained from (i) by integrating the fluid stress tensor over the particle surface.This is a simplified model for the drag forces on, and the disturbance velocity created by, a discoidal particle between two parallel plates. The force fq2D is exerted by the fluid flowing around the disc. The disc also has thin gaps separating it from the plates [Fig. 1(a)], but forces from these lubricating gaps are not included in fq2D, since the gaps are not modeled by the Brinkman equation.
The force fq2D can be calculated as
| fq2D = ζ(U − Up) + πR2(12μ/H)U, | (6) |
| ζ ≡ 4πμH(ε2/4 + εK1(ε)/K0(ε)), | (7) |
 . Since Galilean invariance is broken, fq2D does not only depend on the difference between fluid and disc velocities, but also directly on the fluid velocity. The second term of eqn (6) is due to the external pressure needed to drive the fluid between the plates.
. Since Galilean invariance is broken, fq2D does not only depend on the difference between fluid and disc velocities, but also directly on the fluid velocity. The second term of eqn (6) is due to the external pressure needed to drive the fluid between the plates.
Now we consider the complete set of forces on a disc, including from the lubricating gaps. Since we assumed the zero Reynolds number limit, all forces must balance:
| ζ(U − Up) + πR2(12μ/H)U − πR2(2μ/h)Up + fn.h. = 0. | (8) |
We have assumed shear flow in the two thin lubricating gaps, each of height h, that separate a disc from the confining plates, resulting in the frictional third term. fn.h. represents any non-hydrodynamic forces on the disc. We define friction coefficients γc ≡ πR2(12μ/H) and γp ≡ πR2(2μ/h), and rearrange eqn (8) as
| ζ′(U − Up) − (γp − γc)Up + fn.h. = 0 | (9) |
We rearrange again to obtain
| Up = U − (γp − γc)Up/ζ′ + fn.h./ζ′, | (10) |
| Up = U + f/ζ′. | (11) |
The disc moves at the fluid velocity plus a linear superposition of perturbations from friction and other forces. A force on the disc is related to a velocity perturbation by the single particle mobility 1/ζ′. In the following subsections, we will seek to generalize this single particle quantity to a mobility tensor for systems of multiple interacting discs.
Before turning to the many-disc problem, we consider item (i), the flow field u. Leaving the details of the solution to an Appendix, we note a few salient features. Far away from the disc, the velocity field is a potential flow:
| u = U + ∇ϕd.p.. | (12) |
The dipole potential is
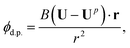 | (13) |
 | (14) |
The coefficient B, given in Appendix B, is proportional to the disc area: B ∼ R2.
In Section 2.1, we mentioned possible edge effects that the Brinkman equation necessarily omits. Edge effects would affect the forces on a disc, but not the far-field disturbance flow. Nevertheless, in a previous work we found good quantitative agreement between our simplified model and the detailed lubrication analysis of Halpern and Secomb for the velocity of a flow-driven disc.22,27
2.3 Systems of multiple discs
We seek a generalization of eqn (11) for a system of N discs:| V = V0 + M·F. | (15) |
We separate the friction on the particles from the non-hydrodynamic forces:
| V = V0 − M·Γ·V + M·Fn.h., | (16) |
Eqn (16) can be rearranged to isolate V:
| V = (1 + M·Γ)−1(V0 + M·Fn.h.). | (17) |
Although M is constructed from pairwise interactions, the inversion of (1 + M·Γ) recovers many-body contributions to particle dynamics. Furthermore, particles interact hydrodynamically even when Fn.h. = 0, i.e. when they are driven only by external flow.
2.4 Mobility tensor
We write M as| Mijαβ = δijδαβ/ζ′i + Gijαβ/ζ′j. | (18) |
The mobility tensor relates a force on disc j in the β direction to a contribution to the velocity of disc i in the α direction. The first term is simply the single particle mobility obtained previously. The second term contains disc–disc hydrodynamic interactions and the effects of confining side walls. The friction tensor is diagonal:
| Γijαβ ≡ δijδαβ(γp,i − γc,i). | (19) |
As a simple demonstration, we consider how to obtain Gijαβ in unbounded q2D, i.e. neglecting the effect of side walls. Clearly, Giiαβ = 0, since a disc is not subject to its own flow disturbance. To obtain Gijαβ for i ≠ j, consider the quantity Gij·(fj,/ζ′j). This quantity expresses the fluid velocity disturbance at disc i created by the force fj on disc j, as can be seen upon substituting eqn (18) into (15). Since the velocity disturbance is dipolar, we can use eqn (14) to obtain
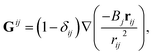 | (20) |
Throughout this work, we use Gijαβ for a channel geometry, obtained by the method of images.28 A disc generates an infinite series of image discs across the two channel side walls. The disturbance field created by this set of discs satisfies the no-penetration boundary condition at the two side walls. We sum over the series of discs, obtaining a “dressed” or effective disc–disc interaction. This interaction is screened in the streamwise direction, with a screening length proportional to the channel width W. Furthermore, Giiαβ ≠ 0, as a disc will experience a flow disturbance created by its own images. We give Gijαβ for a channel geometry in detail in Appendix B.
2.5 Particle architecture and conservative forces
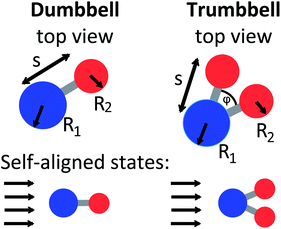
We consider two particle architectures in this work (Fig. 2). A dumbbell comprises two hydrodynamically interacting discs with centers connected by a stiff spring. A trumbbell has two tail discs, each connected to the head by a stiff spring. The tail discs have the same radius, and the two tails have identical length. The angle between the two tails is ψ. We connect the two tail discs by a third stiff spring in order to maintain this angle. (Alternatively, a three-body angle potential could be accommodated in our mobility framework.) For both architectures, the radius of a head disc is R1 and the radius of a tail disc is R2. The tail length is determined by the equilibrium spring distance s.The spring force is Hookean. If discs i and j are connected, the force on i due to j is
 | (21) |
All discs, whether within the same or different particles, interact via repulsive excluded volume forces:29
 | (22) |
Discs are also repelled from the channel side walls. Via the length scale κ−1, the excluded volume interaction can be tuned to resemble a hard disc interaction (κ−1 → 0) or a screened electrostatic interaction in q2D (κ−1 ∼ H).30
Both dumbbells and trumbbells align under flow via hydrodynamic self-interaction so that the head disc is upstream. It should be noted that we have neglected the rotation of individual discs. For instance, if a rigid dumbbell comprising two linked discs rotates, the two discs should rotate with the same angular velocity. (To see this, consider the motion during rotation of a dumbbell of a point marked on a disc edge.) Disc rotations do not contribute to far-field hydrodynamics, since they require no displacement of fluid mass. However, the rotational resistance of a disc does contribute to the overall torque balance on a particle. Previously, we have shown that inclusion of disc rotations has a moderate quantitative effect on particle dynamics, but does not change the qualitative behavior sustained by hydrodynamics.22
2.6 Numerical integration scheme
In order to integrate the equations of motion, we modify an adaptive time-stepping scheme from Ball and Melrose.31 At each timestep, we calculate M and the spring and excluded volume forces from the disc positions, and obtain V from eqn (16). We calculate Δtmax as the largest timestep that can be taken in an Euler step without disc/disc or disc/wall overlap. We choose Δt as gΔtmax, where g = 0.2. We then advance the simulation over a timestep Δt via the midpoint method.3 Results
We consider two model problems. In the first model problem, we consider the dynamics of small clusters of particles in a channel. The particles are initially seeded with random initial angle and position in an finite area with length lx and width equal to the channel width W. Angles and positions are chosen with uniform probability. The simulation domain is unbounded in the flow direction.In the second model problem, we consider large particle suspensions. Periodic boundary conditions are imposed in the flow direction. When particles cross a periodic boundary, they are mapped to the other side of the simulation domain. Moreover, particles experience disturbance flows created by periodic images. Since the hydrodynamic interaction decays exponentially in the flow direction, we consider only two image cells on each side of the real domain. The simulation domain has length Lx in the flow direction, and particles are seeded with random initial angle and position in the domain.
We take the external flow to be U0 = U0![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . Particles move in the xy plane, with channel side walls bounding the y direction. Owing to the linearity of Stokes flow, the only effect of U0 is to set a timescale R2/U0 for particle dynamics. The particles' trajectories in space do not depend on the magnitude of U0. Therefore, when showing results, we parameterize trajectories by average particle position in the streamwise direction,
. Particles move in the xy plane, with channel side walls bounding the y direction. Owing to the linearity of Stokes flow, the only effect of U0 is to set a timescale R2/U0 for particle dynamics. The particles' trajectories in space do not depend on the magnitude of U0. Therefore, when showing results, we parameterize trajectories by average particle position in the streamwise direction,  , instead of by time.
, instead of by time.
If the particles are effectively rigid, the dimensionless parameters governing the model problems are purely geometric. Particle architecture is characterized by head/tail asymmetry ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ≡ R1/R2, bond length
≡ R1/R2, bond length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ≡ s/R2, dimensionless lubricating gap height
≡ s/R2, dimensionless lubricating gap height ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ≡ h/H, and trumbbell angle ψ. The channel has dimensionless width
≡ h/H, and trumbbell angle ψ. The channel has dimensionless width ![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) ≡ W/R2 and height
≡ W/R2 and height ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ≡ H/R2. We fix
≡ H/R2. We fix ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = 1.5,
= 1.5, ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 3.5, ψ = 50°,
= 3.5, ψ = 50°, ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = 0.08, and
= 0.08, and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = 1.6.
= 1.6. ![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) varies as indicated in the text. Additionally, suspensions are characterized by the two-dimensional particle number density ϕ0 ≡ N/(LxW), where N is the number of particles in the simulation domain.
varies as indicated in the text. Additionally, suspensions are characterized by the two-dimensional particle number density ϕ0 ≡ N/(LxW), where N is the number of particles in the simulation domain.
To approximate a rigid constraint, we use a stiff spring constant 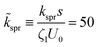 , where ζ1 is evaluated for the head disc. The dimensionless constant
, where ζ1 is evaluated for the head disc. The dimensionless constant ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) spr characterizes the ability of a spring to resist stretch or compression by viscous hydrodynamic forces. We found negligible quantitative difference when we compared the dynamics of a single dumbbell with this spring constant and previous results for a single dumbbell with an explicit rigid constraint.22 For the excluded volume potential, we use
spr characterizes the ability of a spring to resist stretch or compression by viscous hydrodynamic forces. We found negligible quantitative difference when we compared the dynamics of a single dumbbell with this spring constant and previous results for a single dumbbell with an explicit rigid constraint.22 For the excluded volume potential, we use ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) ≡ κR2 = 10 and
≡ κR2 = 10 and  .
.
3.1 Small cluster of dumbbells
The dynamics of a dumbbell pair provide an obvious starting point for our investigation. A doublet is the simplest self-organized structure predicted by the geometric framework of Fig. 1. Moreover, pairwise interactions are likely to play a significant role in determination of the behavior of large suspensions. In Fig. 3, we show results from a pair seeded in a section with length lx = 2W of a channel with width![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) = 30. One hundred random initial configurations were simulated for
= 30. One hundred random initial configurations were simulated for ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = 5.0 × 104.
= 5.0 × 104.
Pair behaviors can be divided into four classes, with simulation snapshots of each shown in Fig. 3(c). As predicted by the geometric construction of Fig. 1(c), pairs can self-organize into doublets. The two particles of a doublet are positioned at y/W = 1/4 and y/W = 3/4, which are determined by the geometric construction of the Introduction. In Fig. 3(b), we show the final positions of dumbbell head discs in the transverse direction. Approximately one fifth of the trajectories form doublets. Given that particles were seeded over a large area and with any possible angle, it is clear that the doublet basin of attraction in the system's five-dimensional phase space is substantial. We also obtain singlets, in which both particles align and focus to the channel centerline. We previously obtained this behavior for a single dumbbell,22 and it is most likely to occur in the two particle system when the particles are initially widely separated. There is no steady x separation for two singlets; they weakly repel.
However, we also obtain two behaviors that were not predicted by symmetry considerations. These “defects” are undesirable from the standpoint of crystal self-organization. In the stable defect, two particles adopt a staggered formation near a side wall, remaining in a steady transverse position. In the unstable defect, particles adopt a head-to-tail configuration. The particles translate back and forth across a section of the channel width before eventually breaking up to form a doublet. The time-dependent behavior of the unstable defect stands out in Fig. 3(a), which shows the y position of head discs as a function of downstream position xc. A majority of trajectories are clearly included in the exponential envelope that focuses to the centerline; these are singlets. The doublets and stable defects can also be seen quite easily.
3.2 Dumbbell suspension
For the large volume of parameter space tested, dumbbell suspensions fail to form the two-dimensional crystals predicted in Fig. 1(c). Instead, the dominant behavior is the formation of large, dynamic aggregates of dumbbells. Nevertheless, dumbbell suspensions qualitatively and quantitatively show tantalizing signs of intermittent self-organization. Hindrance of this self-organization can be traced qualitatively and quantitatively to two-body defect formation.Snapshots from a representative simulation are shown in Fig. 4. In (a), three particles have clearly formed a triplet, with the particle in the y = 5W/6 position indicated by a black arrow. (This and other triplet positions are determined by the geometric construction discussed in the Introduction.) Additionally, two particles have organized into a doublet. However, other particles have paired head-to-tail, like the unstable defect, and in staggered formation, like the stable defect, and five particles have packed into an aggregate. The particle indicated by the green arrow moves more slowly than the triplet. It therefore encounters the triplet in (b), forming a staggered pair with the black arrow particle, and disrupting the crystalline order. In (c), the triplet has completely broken up. It is also apparent from (a) through (c) that the aggregates are dynamic, continuously gaining and losing particles.
These observations are typical of a dumbbell suspension, as we show in Fig. 4(d) by plotting the pair distribution function g(Δx, Δy). This function is calculated from thirty-three dumbbell suspension simulations. Each simulation is carried out for a time ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = 5.0 × 104 and with the same parameters as in (a)–(c). The pair distribution function expresses the probability of finding two head discs separated by Δx in the external flow direction and Δy in the transverse direction. The normalization of g(Δx, Δy) accounts for the variation of the particle density across the channel width, which is shown in Fig. 4(e).32 The value of g(Δx, Δy) expresses, as a multiplicative factor, the two-body deviation from what would be expected from the density. In Fig. 4(d), the central dark area is sterically forbidden. There is clearly a ring of strongly enhanced probability around the excluded volume region: particles pair as closely as excluded volume allows. Peaks that correspond to formation of doublets and triplets, indicated by arrows are clearly visible. Doublets occur for Δx = 0 and Δy = ±W/2, while triplets occur for Δx = 0 and Δy = ±W/3 or Δy = ±2W/3. While we have presented our findings for one particular set of parameters, we obtain similar results upon varying
= 5.0 × 104 and with the same parameters as in (a)–(c). The pair distribution function expresses the probability of finding two head discs separated by Δx in the external flow direction and Δy in the transverse direction. The normalization of g(Δx, Δy) accounts for the variation of the particle density across the channel width, which is shown in Fig. 4(e).32 The value of g(Δx, Δy) expresses, as a multiplicative factor, the two-body deviation from what would be expected from the density. In Fig. 4(d), the central dark area is sterically forbidden. There is clearly a ring of strongly enhanced probability around the excluded volume region: particles pair as closely as excluded volume allows. Peaks that correspond to formation of doublets and triplets, indicated by arrows are clearly visible. Doublets occur for Δx = 0 and Δy = ±W/2, while triplets occur for Δx = 0 and Δy = ±W/3 or Δy = ±2W/3. While we have presented our findings for one particular set of parameters, we obtain similar results upon varying ![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) and ϕ0.
and ϕ0.
3.3 Engineering hydrodynamic interactions via particle shape
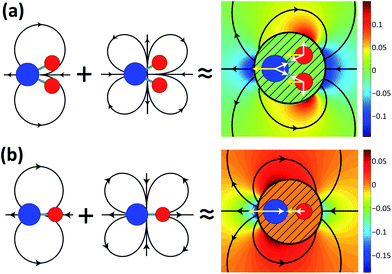
In dumbbell suspensions, crystal self-organization is frustrated by formation of defects. In a defect, particles pair side-by-side in either a staggered or head-to-tail configuration. We wish to design a particle architecture that disfavors defect formation while preserving the essential features promoting crystal self-organization. For instance, defect formation would be disfavored for rod-like particles with a particular anisotropic interaction: repulsion in the direction of the short axis and attraction along the long axis. Such particles would tend to chain in the flow direction. If the particles are fore-aft asymmetric, they would still order laterally as doublets and triplets.The far-field disturbance created by a disc is dipolar. There are no other long-range terms; all other contributions to the flow disturbance are exponentially screened by the confining plates. The complete disturbance field created by a particle composed of linked discs is a superposition of dipolar fields. Since the various dipoles are located at different points on the particle, the complete particle field is not strictly dipolar. However, the complete field can be expressed as a multipole expansion which is always dipolar at leading order. The universality of the dipolar term owes to the fact that all particles, regardless of shape, obstruct and redirect the external flow.
The quadrupole is the first subleading term, decaying as 1/r.3 Unlike the dipole, it captures the effects of shape anisotropy. While the dipolar term expresses the total fluid mass displaced by the particle, the quadrupolar term captures how much of the mass displacement owes to the front of the particle and how much to the back. Consider Fig. 5(a). At right, we have plotted the disturbance flow field created by a “trumbbell” particle comprising three discs linked by springs. The complete disturbance flow field is a superposition of nine dipolar fields: three from friction on the discs (yellow arrows), and six from the spring forces (white arrows). The disturbance flow field is approximately dipolar, but streamlines are bent towards the back of the particle. The two rear discs are responsible for more mass displacement than the front disc. The superposition of a dipolar term and a quadrupolar term can produce bent streamlines, as we show at left. The dipole streamlines are fore-aft symmetric. When we add a quadrupole field of appropriate sign, we enhance mass transport towards the rear of the particle and decrease mass transport from the front, bending the streamlines towards the rear.
Quadrupolar interactions bear a crucial difference from dipolar interactions: quadrupolar interactions can drive relative motion of two identical particles, as shown by Janssen et al.33 Consider two identical particles separated in the external flow direction (Δx ≠ 0, Δy = 0) in unbounded q2D, with particle A upstream of particle B. Considering only dipolar interactions, particle A drives particle B upstream, and particle B drives A upstream with equal strength. Via dipolar interactions, the two particles are slower than they would be individually, but do not move relative to each other. However, if we add a quadrupolar interaction with the same sign as in Fig. 5(a), particle A drives B upstream, and particle B drives A downstream. The particles are hydrodynamically attracted. A quadrupolar interaction with opposite sign would drive the particles apart.
We are now in a position to understand why two dumbbell singlets repel each other, as observed during study of dumbbell pair dynamics. The disturbance flow field of a single dumbbell is shown in Fig. 5(b). The streamlines are bent forward, since the head disc displaces more mass than the tail disc. Accordingly, the quadrupolar field created by a dumbbell is repulsive.
Although two trumbbells are attracted through quadrupolar interactions, repulsion by higher order, shorter range multipole terms stabilizes the particles against collision. As a result, there is an equilibrium pairing distance for trumbbells, as previously found for deformable droplets.33 This equilibrium is most clearly illustrated with an effective potential. We define Ueff by dΔx/dt = −dUeff/dx. For the trumbbell architecture studied, a pair has a potential well with minimum at Δxeq/R2 = 7.4, as shown in Fig. 6. Dumbbells clearly repel with no equilibrium pairing distance.
Significantly, quadrupolar interactions disfavor the side-by-side configurations characteristic of defects. As can be seen in Fig. 5(b), quadrupole streamlines issue from the side of a trumbbell and terminate at the front and rear. Two side-by-side trumbbells will rotate around each other until Δy = 0. If the sign of the quadrupole is negated, as with the dumbbells, quadrupolar interactions favor side-by-side pairing.
Although the focus of this work is on the qualitative effect of hydrodynamic interactions, in Appendix D we briefly outline an approach for calculation of the strengths of the dipolar, quadrupolar, and higher order terms in the multipole expansion of a particle's disturbance flow. Our approach confirms that the dumbbell and trumbbell have quadrupolar terms of opposite sign. Moreover, it reveals that the dipolar and quadrupolar coefficients are of the same order of magnitude.
3.4 Trumbbell suspensions
The simulation snapshots in Fig. 7 illustrate the various stages of self-organization. In (a), particles are initially placed with random positions and angles. In (b), nearly all particles have individually aligned with the flow. Sections of the suspension have locally self-organized: some particle pairs have formed doublets spanning the channel width, while other particles have formed strings in the flow direction via quadrupolar HI. In (c), the particles have completely partitioned into two separate lanes located near the doublet crystal positions. However, the lanes are not spread evenly across the channel, and many particles are not unambiguously matched with a partner in a neighboring lane. This mismatch produces two characteristic lattice defect structures that can be seen in a still image, such as (c). In a triangle formation, two particles seem to share a partner; for instance, particles 4 and 10 share particle 1. For other particles, such as 14 and 9, the partner position is vacant. In (d), the lanes have spread across the channel, but vacancies and triangle formations persist. In (e), the suspension resembles a strained crystal. Vacancies have annihilated by pairing across the two lanes. The crystal is on the threshold of relaxation to an unstrained lattice: particle 2 is about to capture particle 16, allowing 6 and 19 to pair. Finally, in (f), the suspension has relaxed to an apparently perfect lattice.
Quantitatively, in Fig. 7(g) we show six different order parameters as a function of average downstream position xc. The values of xc for frames (b) through (f) are indicated on the plot. We briefly describe the parameters here, leaving their details to an Appendix. Φ describes the average orientation of particles with the external flow. Ψ4, Ψ4,r, and Ψ6 are bond orientational order parameters, expressing whether neighboring particles generally have a square, rectangular, or hexagonal structure. These parameters capture the geometric arrangement of particles, but not whether they are in the correct spatial positions. The parameter ΨT quantifies translational order: how evenly the particles are spread in the streamwise direction, and how close the row separation is to W/2. Finally, ΨT,y isolates the partitioning of particles into lanes separated by W/2 in the y direction.
At the beginning of the simulation, particles individually align with the flow through hydrodynamic self-interaction, and Φ rapidly evolves to unity. ΨT,y rapidly increases between frames (b) and (c) as the particles partition into two lanes. All five Ψ parameters exhibit a crossover at frame (e), confirming that it marks the beginning of rapid relaxation to an unstrained crystalline structure. As the appearance of frame (f) suggests, the lattice is rectangular, and Ψ4,r evolves to unity. On the other hand, ΨT approaches unity only very slowly. In fact, although (f) appears to be a perfect lattice, there are very small imperfections in the particle positions in the flow direction. In (h), we show particle positions in the flow direction as function of xc. A small amplitude, low frequency density wave propagates in x, but particles are otherwise evenly spaced. The value of xc for frame (f) is indicated on the plot.
 | ||
| Fig. 8 Vacancy defects propagate by a simple mechanism. (a) A cluster of three isolated particles. Particles 1 and 2 are initially placed in a doublet crystal configuration, and particle 3 is placed next to particle 2. Due to dipolar HI, a doublet crystal has a greater downstream velocity than an isolated particle, since each particle in the crystal increases the local fluid velocity of its partner in what has been called “transverse anti-drag”.34 The crystal collides with the slower particle 3. Particle 3 slows down particle 2 and speeds up particle 1, forming a triangular configuration. Particle 1 swaps partners, leaving particle 2 upstream. (b) The same mechanism occurs in a two-dimensional crystal. As a result of defect motion, the two rows of the crystal slide past each other: particle 24 has exchanges particle 15 for particle 10, and particle 22 is about to exchange particle 2 for particle 15. | ||
 | ||
| Fig. 9 Two vacancy defects in parallel lanes can annihilate each other on close approach. If an equal number of particles partition to two lanes, defect annihilation precedes relaxation to a defect-free crystal. (a) The doublet lattice shown here has two vacancy defects in different lanes. (b) The vacancies flow upstream. Since they move at different speeds, they come close enough to each other to initiate annihilation. (c) The particles indicated by magenta and green arrows begin to displace the particles immediately upstream, forming the characteristic triangle structures of Fig. 8(a). (d) The particle with the green arrow successfully acquires a doublet partner, pushing the particle indicated by the cyan arrow upstream. The magenta arrow particle, on the other hand, has not yet finished acquiring a doublet particle. It will be captured by the cyan arrow particle. (e) The particle with the cyan arrow captures the green arrow particle. The lattice is locally strained, initiating a shear wave. (f) The shear wave propagates upstream. (g) The shear wave has dissipated, and the crystal has relaxed to equilibrium. | ||
 | ||
| Fig. 10 Suspensions can crystallize with two types of permanent defect. If an unequal number of particles is partitioned between the crystal lanes, then vacancies have no means to heal. Secondly, a stray particle on the centerline can propagate freely through a doublet crystal. Frames (a) through (e) show both types of defect. A vacancy switches from particle 4 to particle 9 through the mechanism discussed in Fig. 8, moving upstream. Particle 7 strains the lattice as it moves down the centerline. Particles flow around it, returning to their previous y positions upstream of the defect. The inclusion has a higher velocity than doublet pairs, due to the “transverse anti-drag” effect discussed above. | ||
![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) , self-organizing crystals with more than two lanes (e.g. triplet or quadruplet crystals) are possible in principle. We have not observed the formation of perfect triplet crystals. However, for
, self-organizing crystals with more than two lanes (e.g. triplet or quadruplet crystals) are possible in principle. We have not observed the formation of perfect triplet crystals. However, for ![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) = 30, particles generally organize into three lanes that are approximately located at the triplet transverse positions. Lanes have always been observed to have unequal numbers of particles. In Fig. 11, an initially random configuration of N = 45 particles in a wide channel (
= 30, particles generally organize into three lanes that are approximately located at the triplet transverse positions. Lanes have always been observed to have unequal numbers of particles. In Fig. 11, an initially random configuration of N = 45 particles in a wide channel (![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) = 30, Lx/W = 6) evolves into a configuration of three lanes through stages of self-alignment and local self-organization. Notably, local self-organization includes such events as transient formation of quadruplets, as shown in frame (b), and the organization of long strings of particles held together by quadrupolar HI, appearing in frames (b), (c), and (d). When finally organized, as in frame (e), the lanes have density heterogenities in the flow direction that propagate through the lanes.
= 30, Lx/W = 6) evolves into a configuration of three lanes through stages of self-alignment and local self-organization. Notably, local self-organization includes such events as transient formation of quadruplets, as shown in frame (b), and the organization of long strings of particles held together by quadrupolar HI, appearing in frames (b), (c), and (d). When finally organized, as in frame (e), the lanes have density heterogenities in the flow direction that propagate through the lanes.
As with dumbbell suspensions, we can quantitatively examine self-organization in wide channels with correlation functions. The head disc pair correlation functions g(Δx, Δy) of Fig. 12(a) was calculated for the entire trajectory of Fig. 11. Notably, the central dark spot extends beyond the sterically excluded region. Hydrodynamic interactions are repulsive at short range, preventing particles from aggregating. There are clear peaks in the triplet positions (Δx = 0, Δy = ±W/3) and (Δx = 0, Δy = ±2W/3), as well as (Δx = ±W/2, Δy = ±W/3). These peaks are indicative of local crystalline order. In Fig. 11(e), particles adopt local crystalline configurations where the densities of neighboring lanes match. Finally, the streaks in Fig. 12(a) extending over all Δx/W are due to both the relative motion of neighboring lanes and the variation of density within a lane. In Fig. 12(b), we have limited calculation of g(Δx, Δy) to the beginning of the simulation through frame (c) of Fig. 11. The streaks and crystal peaks have not yet appeared, but quadrupolar HI drives pairing in the flow direction, with a peak at (Δx = ±6.5R2, Δy = 0).
 | ||
| Fig. 12 (a) Head disc pair correlation function g(Δx, Δy) calculated over the entire trajectory of Fig. 11. The dashed white line indicates the sterically excluded area. Particles are depleted from close contact not only by steric interactions, but also by hydrodynamic interactions. The five streaks are due to particle laning. Each lane has localized peaks, indicating local crystalline order. In Fig. 11(e), particles and their neighbors in other lanes adopt crystalline order where the local lane densities match. (b) Correlation function calculated from the beginning of the simulation through frame (c) of Fig. 11. Particles have not yet partitioned into lanes, but particle pairing by quadrupolar HI leads to peaks at (Δx = ±6.5, Δy = 0). | ||
4 Conclusions
We have shown that a flow-driven suspension of microparticles can self-organize into flowing crystals under suitable conditions of particle shape and geometric confinement. Shape and confinement modify hydrodynamic interactions between particles. They can be tailored so that hydrodynamic interactions drive organization in multiple spatial directions and over multiple time and length scales.In our system, organization into a two-dimensional crystal occurs through several stages in which one, two, and multiple-body mechanisms are successively important. Particles first align with the flow via hydrodynamic self-interaction. This self-alignment generically occurs for asymmetric particles in quasi-two-dimensional confinement.22 In the next stage, particles spatially order in both the streamwise and transverse directions via two distinct two-body mechanisms. While the transverse mechanism is generic for asymmetric q2D particles, we engineered the streamwise mechanism by breaking the coaxial geometry of the model particle. Particles form lanes with lattice defects that propagate and eventually annihilate via coordinated motions of multiple particles. Finally, the lattice collectively relaxes to an unstrained and nearly perfect crystal.
To our knowledge, our study is to first to demonstrate that flowing lattices can be stabilized purely by viscous hydrodynamic interactions. It provides a particularly simple system for the development and examination of theoretical ideas in non-equilibrium self-organization. For instance, one might ask if crystallization is described by the minimization of a functional, such as rate of energy dissipation.15 Our study also provides a starting point for further exploration of the collective dynamics of complex particles in q2D confinement. Our theoretical and numerical framework can accommodate suspension polydispersity, particle deformability, other interaction potentials, and more complex particle morphologies. For instance, a trumbbell with unequal size tail discs is a model chiral particle. The dynamics of DNA driven by flow in slit-like confinement35 or flow-driven confined fibers36 or microsprings37 could be studied with a bead-spring chain representation. The statistics and kinetics of dumbbell aggregation could be studied in further detail, especially in comparison with the dynamic clustering that occurs in q2D droplet suspensions.20,38 Finally, we have exploited the effects of only the first two terms in the multipole expansion of a particle's disturbance field, and our consideration of these terms was largely qualitative. Shape and multipole expansions could be quantitatively related via the approach outlined in Appendix D, as well as conformal mapping.39 A systematic and parametric study of shape could obtain the scaling dependence of the multipole coefficients on the governing dimensionless groups. It could also obtain the dependence on these groups of the location and depth of the effective potential well for interacting pairs, as in Fig. 6.
Experimentally, our findings could be tested with Continuous Flow Lithography (CFL).40 In this technique, hydrogel particles with two-dimensional extruded shape are “optically stamped” with UV light in a flowing stream of photopolymerizable prepolymer solution. Particle shape is dictated by the choice of photomask. Since particles are fabricated in situ, this technique allows precise control over the initial positions and orientations of one or more quasi-two-dimensional particles. In a recent work, we used CFL to study the dynamics of a single asymmetric dumbbell, obtaining qualitative and semi-quantitative agreement between theory and experiment.22 We note that the model problems appropriate for our numerical study are not ideal for experimental work. For instance, the suspension in Fig. 7 settled into a flowing lattice only after flowing approximately one thousand channel widths downstream. For a typical channel width of 300 μm, the required channel length would be 30 cm, which is impractical. Fortunately, the control over initial configuration afforded by CFL, guided by insight provided by numerics, should allow study of initial configurations that self-organize over realistic microchannel lengths. Furthermore, the completely disordered initial condition of Fig. 7 does not represent typical device operation conditions. Ordinarily, particles in solution are continuously injected into a channel through an inlet port. A possible experiment would be to synthesize particles with CFL, collect them at the channel outlet, and then inject them into a flow-through device. We previously performed such an experiment with dilute solutions in order to study single particle dynamics.22 Our numerical scheme could be modified so that particles continuously enter and exit the flow domain, modeling typical device operation conditions.
Appendix
A Single disc flow field
Since the problem of Section 2.2 is two-dimensional, it can be solved with a stream function approach. In cylindrical coordinates, the stream function Ψ is defined by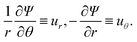 | (23) |
Eqn (5) becomes
| ∇4Ψ − λ2∇2Ψ = 0, | (24) |
We take Up = Up![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . The solution for ub, where the subscript designates the subproblem, is subject to the following boundary conditions. Far away from the disc, the flow field must vanish, so that ub,r|r→∞ = 0 and ub,θ|r→∞. On the edge of the disc, the no-slip and no-penetration conditions hold, and we have ur|b,r =R = Up cos(θ) and ub,θ|r=R = −Up
. The solution for ub, where the subscript designates the subproblem, is subject to the following boundary conditions. Far away from the disc, the flow field must vanish, so that ub,r|r→∞ = 0 and ub,θ|r→∞. On the edge of the disc, the no-slip and no-penetration conditions hold, and we have ur|b,r =R = Up cos(θ) and ub,θ|r=R = −Up![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ). These boundary conditions suggest a solution of the form Ψ(r, θ) = f(r)sin(θ). The boundary conditions reduce to conditions on f(r): f(R) = RUp and
sin(θ). These boundary conditions suggest a solution of the form Ψ(r, θ) = f(r)sin(θ). The boundary conditions reduce to conditions on f(r): f(R) = RUp and  . substituting f(r)sin(θ) into eqn (24) and solving the equation, we obtain
. substituting f(r)sin(θ) into eqn (24) and solving the equation, we obtain
 | (25) |
Imposing the boundary conditions, we find the integration constants to be c1 = 0,
 | (26) |
 | (27) |
Eqn (25) has a revealing interpretation. The second, long-range term is the dipolar flow disturbance. The third term decays exponentially with screening length ∼H. This term represents the viscous boundary layer in the vicinity of the disc. The boundary layer is associated with the Laplacian term in eqn (5), which constitutes a singular perturbation to the equation.
B Hydrodynamic interaction tensor
The hydrodynamic interaction tensor for unbounded q2D directly follows from the results of the previous section. It is non-zero only for i ≠ j. Transforming to cartesian coordinates,To obtain the HI tensor in a channel geometry, we must include the effect of confining side walls. The no-penetration condition on the side walls can be imposed by the method of images. A disc and its images split into two sets. The “far” set includes the real disc, as well as periodic images displaced from the real disc in the y direction with periodicity 2W. Each disc in the “far” set has the same velocity as the real disc. The “near” set is seeded from the original disc's mirror image across the closest side wall and includes periodic copies of this image. The “near” set includes the image nearest to the real disc. The y component of velocities in this set are negated relative to the original disc, while the x component remains unchanged. Summing over images, the self-interaction (i = j) is determined as:
For i ≠ j,
| X− ≡ π(xi− xj)/2W, Y± ≡ π(yi ± yj)/2W |
For fixed Y+ and Y−, the two body interaction decays exponentially with screening length W/π or W/2π as |X−| → ∞.
C Definition of order parameters
The order parameters are defined as follows. Φ measures the average alignment of particles with the flow: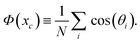 | (28) |
The angle θi is defined by the flow direction and the vector between particle i's head disc and the midpoint between its two tail discs.
The bond order parameters Ψ4, Ψ4,r, Ψ6 capture whether the particles are in a square, rectangular, or hexagonal lattice, respectively. For each frame of a simulation, we find each particle's neighbors via a Voronoi tesselation, taking periodic boundaries into account. We obtain Ψ4 and Ψ6 as
 | (29) |
 | (30) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and the vector between the head discs of i and j.
and the vector between the head discs of i and j.
The bond order parameter Ψ4 will be less than one for a rectangular lattice, since the set of next nearest lattice neighbors will not generally have angles θij that are an integer multiple of π/4. The inner sum in the rectangular bond order parameter is limited to the closest three particles:
 | (31) |
We consider three particles instead of four because the doublet lattice has only two lanes of real particles.
We define ΨT as
 | (32) |
Finally, we define
 | (33) |
D Calculation of multipole coefficients
We briefly outline a method to calculate the coefficients in the multipole expansion of the disturbance velocity created by a particle. As a concrete example, we consider a trumbbell particle. First, we numerically calculate the spring and friction forces on an isolated trumbbell in unbounded q2D using the framework developed in Section 2. These forces are shown in Fig. 5(a) as yellow and white vectors. So that we can use complex variable techniques, here we consider the forces to be distributed on the complex plane at positions zhead (of the head disc) and ztail,1 and ztail,2 (of the two tail discs.) The complex potential F(z) is given by a superposition of dipolar singularities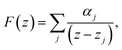 | (34) |
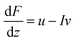 . The dipole strengths αj are given by αj = Bjfj/ζ′j. The sum is taken over the forces fj, which here are taken to be complex numbers. A force fj occurs at zj ∈ {zhead, ztail,1, ztail,2}, and has direction and magnitude given by the phase and modulus of fi. Additionally, ζ′j ∈ {ζ′head, ζ′tail} and Bj ∈ {Bhead, Btail}, as appropriate. We wish to find the coefficients βk in a multipole expansion for F(z),
. The dipole strengths αj are given by αj = Bjfj/ζ′j. The sum is taken over the forces fj, which here are taken to be complex numbers. A force fj occurs at zj ∈ {zhead, ztail,1, ztail,2}, and has direction and magnitude given by the phase and modulus of fi. Additionally, ζ′j ∈ {ζ′head, ζ′tail} and Bj ∈ {Bhead, Btail}, as appropriate. We wish to find the coefficients βk in a multipole expansion for F(z),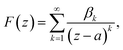 | (35) |
The expansion is centered at a, the hydrodynamic center of resistance. Here, we approximate a as a ≈ (zheadζ′head + ztail,1ζ′tail + ztail,2ζ′tail)/(ζ′head + 2ζ′tail).41,42 Using the residue theorem, we find that the coefficients βk are given by moments of the dipolar strengths
 | (36) |
Notably, the dipolar coefficient β1 does not depend on the expansion center a. Therefore, the (equal and opposite) spring forces cancel out, and β1 is simply the sum of the dipolar coefficients associated with the friction forces. For the trumbbell, we obtain β1/U0R22 ≈ 1.78 and β2/U0R23 ≈ 0.78. According to these calculations, the quadrupolar interaction is weak but not negligible: for instance, for a position a distance 5R2 from the trumbbell center, the quadrupolar contribution to the flow field is ∼1.3% of the external flow strength, whereas the dipolar contribution is ∼7.1%. For the dumbbell in Fig. 5(b), we obtain β1/U0R22 ≈ 1.29 and β2/U0R23 ≈ −0.19. Therefore, the dumbbell and trumbbell have quadrupole terms of opposite sign, as expected. Moreover, the dipole and quadrupole coefficients are of the same order of magnitude for both architectures. However, we note that the exact value of the quadrupole strength β2 is sensitive to the value of a, especially for the dumbbell. Our approximation for a neglected the effect of hydrodynamic interactions on the center of resistance. In future studies that focus on the quantitative details of the multipole expansion, the exact value of the hydrodynamic center of resistance should be rigorously calculated.42
Acknowledgements
This work was supported by the Institute for Collaborative Biotechnologies through contract no. W911NF-09-D-0001 from the U.S. Army Research Office. The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred.References
- M. E. Helgeson, S. C. Chapin and P. S. Doyle, Curr. Opin. Colloid Interface Sci., 2011, 16, 106–117 CrossRef CAS PubMed.
- S. Sacanna, D. J. Pine and G.-R. Yi, Soft Matter, 2013, 9, 8096–8106 RSC.
- S. Sacanna, W. T. M. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575–578 CrossRef CAS PubMed.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS PubMed.
- A. Walther and A. H. E. Müller, Chem. Rev., 2013, 113, 5194–5261 CrossRef CAS PubMed.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418 CrossRef CAS PubMed.
- S. C. Hur, H. T. K. Tseb and D. Di Carlo, Lab Chip, 2010, 10, 274–280 RSC.
- S. C. Chapin, D. C. Pregibon and P. S. Doyle, Lab Chip, 2009, 9, 3100–3109 RSC.
- M. Hashimoto, B. Mayers, P. Garstecki and G. M. Whitesides, Small, 2006, 2, 1292 CrossRef CAS PubMed.
- D. Raubaud, P. Thibault, M. Mathieu and P. Marmottant, Phys. Rev. Lett., 2011, 106, 134501 CrossRef.
- W. Lee, H. Amini, H. A. Stone and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22413 CrossRef CAS PubMed.
- J. L. McWhirter, H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6039 CrossRef CAS PubMed.
- H. Diamant, J. Phys. Soc. Jpn., 2009, 78, 041002 CrossRef.
- N. Liron and S. Mochon, J. Eng. Math., 1976, 10, 287 CrossRef.
- T. Beatus, R. Bar-Ziv and T. Tlusty, Phys. Rep., 2012, 516, 103–145 CrossRef PubMed.
- T. Beatus, T. Tlusty and R. Bar-Ziv, Nat. Phys., 2006, 2, 743 CrossRef CAS.
- T. Beatus, R. Bar-Ziv and T. Tlusty, Phys. Rev. Lett., 2007, 99, 124502 CrossRef.
- W. E. Uspal and P. S. Doyle, Soft Matter, 2012, 8, 10676–10686 RSC.
- N. Desreumaux, N. Florent, E. Lauga and D. Bartolo, Eur. Phys. J. E, 2012, 35, 68 CrossRef CAS PubMed.
- N. Desreumaux, J.-B. Caussin, R. Jeanneret, E. Lauga and D. Bartolo, Phys. Rev. Lett., 2013, 111, 118301 CrossRef.
- I. Shani, T. Beatus, R. H. Bar-Ziv and T. Tlusty, Nat. Phys., 2014, 10, 140–144 CrossRef CAS.
- W. E. Uspal, H. B. Eral and P. S. Doyle, Nat. Commun., 2013, 4, 2666 CrossRef PubMed.
- J. M. Crowley, J. Fluid Mech., 1971, 45, 151 CrossRef.
- S. Ramaswamy, Adv. Phys., 2001, 50, 297–341 CrossRef CAS.
- P. J. Menck, J. Heitzig, N. Marwan and J. Kurths, Nat. Phys., 2013, 9, 89–92 CrossRef CAS.
- M. D. Graham, Annu. Rev. Fluid Mech., 2011, 43, 273–298 CrossRef.
- D. Halpern and T. W. Secomb, J. Fluid Mech., 1991, 231, 545–560 CrossRef.
- W. E. Uspal and P. S. Doyle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016325 CrossRef.
- P. R. Nott and J. F. Brady, J. Fluid Mech., 1994, 275, 157–199 CrossRef CAS.
- R. Pesché and G. Nägele, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5432–5443 CrossRef.
- R. C. Ball and J. R. Melrose, Phys. A, 1997, 247, 444–472 CrossRef CAS.
- Specifically, we define
 , where p(r + Δr|r) is the conditional probability of finding a particle at position r + Δr given that a particle is at position r.
, where p(r + Δr|r) is the conditional probability of finding a particle at position r + Δr given that a particle is at position r. - P. J. A. Janssen, M. D. Baron, P. Anderson, J. Blawzdziewicz, M. Loewenberg and E. Wajnryb, Soft Matter, 2012, 8, 7495–7506 RSC.
- H. Diamant, B. Cui, B. Lin and S. A. Rice, J. Phys.: Condens. Matter, 2005, 17, S2787 CrossRef CAS.
- D. Stein, F. H. J. van der Heyden, W. J. A. Koopmans and C. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15853 CrossRef CAS PubMed.
- J. S. Wexler, P. H. Trinh, H. Berthet, N. Quennoz, O. du Roure, H. E. Huppert, A. Lindner and H. A. Stone, J. Fluid Mech., 2013, 720, 517–544 CrossRef.
- R. Attia, D. C. Pregibon, P. S. Doyle, J.-L. Viovy and D. Bartolo, Lab Chip, 2009, 9, 1213–1218 RSC.
- T. Beatus, T. Tlusty and R. Bar-Ziv, Phys. Rev. Lett., 2009, 103, 114502 CrossRef.
- R. Bouffanais, G. D. Weymouth and D. K. P. Yue, Proc. R. Soc. A, 2011, 467, 19–38 CrossRef.
- D. Dendukuri, D. Pregibon, J. Collins, T. A. Hatton and P. Doyle, Nat. Mater., 2006, 5, 365–369 CrossRef CAS PubMed.
- A. Baskaran and M. C. Marchetti, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15567 CrossRef CAS PubMed.
- S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Dover, 2005 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm00664j |
| This journal is © The Royal Society of Chemistry 2014 |