Open Access Article
Open Access ArticleMechanism of RGD-conjugated nanodevice binding to its target protein integrin αVβ3 by atomistic molecular dynamics and machine learning†
Giulia
Frigerio
 a,
Edoardo
Donadoni
a,
Edoardo
Donadoni
 a,
Paulo
Siani
a,
Jacopo
Vertemara
b,
Stefano
Motta
c,
Laura
Bonati
a,
Paulo
Siani
a,
Jacopo
Vertemara
b,
Stefano
Motta
c,
Laura
Bonati
 c,
Luca De
Gioia
b and
Cristiana Di
Valentin
c,
Luca De
Gioia
b and
Cristiana Di
Valentin
 *ad
*ad
aDipartimento di Scienza dei Materiali, Università di Milano-Bicocca, via R. Cozzi 55, 20125 Milano, Italy. E-mail: cristiana.divalentin@unimib.it
bDipartimento di Biotecnologie e Bioscienze, Università di Milano-Bicocca, Piazza della Scienza 1, 20126 Milan, Italy
cDipartimento di Scienze dell'Ambiente e del Territorio, Università di Milano-Bicocca, Piazza della Scienza 1, 20126 Milan, Italy
dBioNanoMedicine Center NANOMIB, Università di Milano-Bicocca, Italy
First published on 5th February 2024
Abstract
Active targeting strategies have been proposed to enhance the selective uptake of nanoparticles (NPs) by diseased cells, and recent experimental findings have proven the effectiveness of this approach. However, no mechanistic studies have yet revealed the atomistic details of the interactions between ligand-activated NPs and integrins. As a case study, here we investigate, by means of advanced molecular dynamics simulations (MD) and machine learning methods (namely equilibrium MD, binding free energy calculations and training of self-organized maps), the interaction of a cyclic-RGD-conjugated PEGylated TiO2 NP (the nanodevice) with the extracellular segment of integrin αVβ3 (the target), the latter experimentally well-known to be over-expressed in several solid tumors. Firstly, we proved that the cyclic-RGD ligand binding to the integrin pocket is established and kept stable even in the presence of the cumbersome realistic model of the nanodevice. In this respect, the unsupervised machine learning analysis allowed a detailed comparison of the ligand/integrin binding in the presence and in the absence of the nanodevice, which unveiled differences in the chemical features. Then, we discovered that unbound cyclic RGDs conjugated to the NP largely contribute to the interactions between the nanodevice and the integrin. Finally, by increasing the density of cyclic RGDs on the PEGylated TiO2 NP, we observed a proportional enhancement of the nanodevice/target binding. All these findings can be exploited to achieve an improved targeting selectivity and cellular uptake, and thus a more successful clinical outcome.
1. Introduction
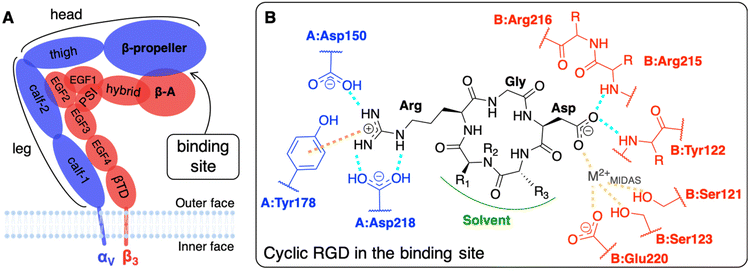
The main limit in using nanoparticles (NPs) for cancer therapy is their poor selectivity towards diseased tissues and cells.1 Two types of targeting strategies have been proposed to enhance the NP accumulation in the tumor site (passive targeting) and their internalization in cancer cells (active targeting).2 At the basis of the passive targeting3 is the enhanced permeability and retention (EPR) effect,4 whose limitations and failures could be overcome by the use of multifunctional NPs3–6 conjugated with targeting ligands. The active targeting strategy, which is the focus of this work, relies on specific biological interactions between ligands exposed by NPs and target proteins that are over-expressed or expressed only by cancer cells.Integrins αVβ3, which are known to have very low expression levels in normal tissues and to be over-expressed on both cancer and endothelial cells in several types of solid tumors, are among the most common cellular targets.2,7,8 They belong to a family of heterodimeric transmembrane proteins (integrins) of at least 24 different members. Integrins modulate cell–cell adhesions and the cell adhesion to the extracellular matrix (ECM) in healthy cells, but also cell survival, migration, and proliferation in tumors, by interacting with their natural ligands, such as collagen, laminin, and fibronectin. Each integrin is formed by one α (18 types) and one β (8 types) subunit, which are non-covalently associated into a dimer that resembles a head with two legs (Fig. 1A), whose different conformations correspond to various states in integrin activation, signaling, and functioning.9,10
The most common strategy to use integrins αVβ3 as targets for active targeting of cancer cells11,12 is to exploit the ligand binding pocket that is in the headpiece of the integrin at the interface between the β-propeller (α subunit) and the β-A (β subunit) domains. For that purpose, NPs must be covered with integrin-affine ligands, which should contain or mimic adhesive aminoacidic sequences of ECM proteins, such as, in the case of integrins αVβ3, the Arg-Gly-Asp (RGD) sequence that is naturally present in fibronectin, vitronectin, fibrinogen, among others.9 Several RGD-based ligands have been proposed to target integrins αVβ3, selectively.8,11 Small cyclic RGD-based ligands are the preferred ones because their synthesis is simple and controllable, they are less immunogenic with respect to larger peptides (such as antibodies)3 and, thanks to their cyclic nature, they are resistant to enzymatic hydrolysis and rigid enough to favor integrin binding.8,13,14 Additionally, NPs exposing multiple ligands may be able to bind more integrins simultaneously, as multivalent ligands do, resulting in a stronger nanodevice/protein interaction.15–18 Atomic force microscopy (AFM) experiments have recently shown that the multivalent interaction of pancreatic cells integrins αVβ3 with two or three cyclic RGD-based ligands agrees with a noncooperative, parallel bond model.19 Furthermore, integrins are physiologically involved in cyclic endocytosis and exocytosis processes, which can be exploited to internalize NPs once bound to the integrin's extracellular segment.8 Besides, integrins αVβ3-mediated phagocyte hitchhiking proved to be a plausible mechanism for NPs to escape blood vessels and enter tumor tissues.20 Noteworthy, it has been experimentally demonstrated, with 100 nm polystyrene NPs covered with RGD ligands, that due to their mechanosensors role21 integrins favor the cellular uptake as a consequence of the enhanced cytoskeleton structuring.22
The affinity of cyclic RGD-based pentapeptide ligands for integrins αVβ3 has been proven experimentally both by low (nM) IC50 values14 and by the co-crystallization of the extracellular segment of integrin αVβ3 with the cyclic pentapeptide c(RGDf(NMe)V), also known as cilengitide, hereafter shortened as CGT. The latter X-ray crystal structure was experimentally obtained in 2002 with a resolution of 3.2 Å (PBD ID: 1L5G).23 Recently, Alhalhooly et al.19 probed the strength of the interaction of a cyclic RGD ligand with integrin αVβ3 on live pancreatic cancer cells with single-molecule binding force spectroscopic methods.
The interaction of integrin αVβ3 with either natural ligands24 or RGD-based synthetic ligands13,25,26 has also been modeled using computational chemistry methods. The existing computational studies, in line with experimental findings, agree that the two fundamental interactions involve Arg and Asp side chains of RGD, bearing +1 and −1 charge at physiological pH, respectively.13,14,23,25,27,28 In particular, in the CGT/integrin αVβ3 co-crystal, the following is observed: the Arg guanidinium group establishes a double side-on H-bond with Asp218 and a simple one with Asp150, both in the α subunit; one O atom of the Asp carboxylate group coordinates a divalent cation that belongs to the binding site, whereas the other O atom establishes two H-bonds with the backbone N atoms in Asn215 and Tyr122 of the β subunit; Gly participates in several hydrophobic interactions with Arg216 of the β subunit (Fig. 1B).23,28,29 Interestingly, three divalent cations, whose role and dependence upon ligand binding is still unclear and debated, were experimentally found close to the binding site in the crystal structure.27 They are commonly named according to the site where they are located: (i) Metal Ion-Dependent Adhesion Site (MIDAS) is the site of the cation coordinated by RGD Asp (Fig. 1B), (ii) Adjacent to MIDAS (ADMIDAS) is the site more exposed to the solvent, and (iii) Ligand-Induced Metal Binding Site (LIMBS) is buried into the protein. Additionally, Molecular Dynamics (MD) simulations of RGD linear and cyclic peptides revealed that more than one RGD linear molecule could simultaneously bind the same integrin αVβ3.25 Through Steered MD (SMD) simulations, the association and dissociation pathways of both linear and cyclic RGD molecules based on the same RGD sequence were reproduced, proving that the interaction of cyclic RGD with integrins is more stable and more difficult to be disrupted due to the cyclic RGD's lower flexibility and enhanced protection from attacks by water molecules.13
Several in vitro and in vivo experiments proved the efficacy of active targeting of integrins αVβ3 by RGD-conjugated NPs.11,30–32 For example, the encapsulation of a prodrug of cisplatin into poly(D,L-lactic-co-glycolic acid)-block-polyethylene glycol (PLGA-PEG) NPs conjugated with cyclic RGD ligands enhanced the drug cytotoxicity in comparison to conventional cisplatin treatment in in vitro experiments and increased its efficiency reducing the side effects on breast cancer cells in vivo.33 Similarly, the cytotoxic efficacy of paclitaxel was found to improve when loaded in PEG-PLGA micelles that are conjugated to cyclic RGD molecules for glioblastoma treatment34 or in RGD-modified PLGA-chitosan NPs for the delivery to lung cancer cells.35 RGD-conjugated chitosan NPs were also demonstrated to improve the therapeutic efficacy of other chemotherapeutic drugs, such as raloxifene, by enhancing the cellular uptake by breast cancer cells and reducing cells migration and angiogenesis in vitro and by reducing the tumor tissue growth without affecting normal tissues in vivo.36 As a further example, PEG-coated long-circulating liposomes (LCL) conjugated to RGD ligands made the liposomes target angiogenic endothelial cells in vitro and in vivo.37 Interestingly, other types of cancer treatments can exploit the targeting of integrins: for instance, Dayan et al.38 conjugated a modified protein, namely RGD-modified dihydrolipoamide dehydrogenase, with TiO2 NPs for tumor-targeted photodynamic therapy (PDT).
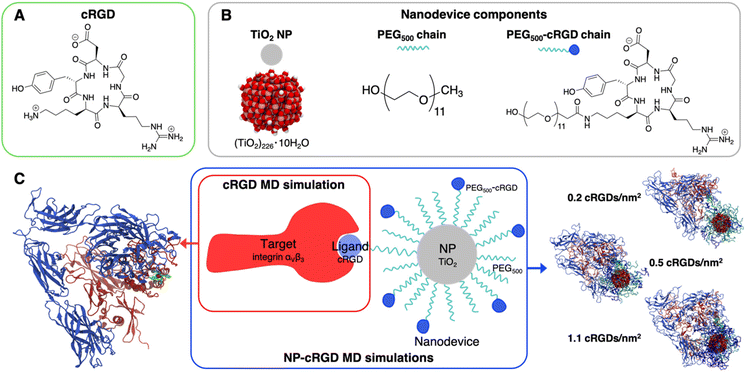
To our best knowledge, no computational study has yet provided atomistic insights into the mechanism of interaction between integrin αVβ3 and targeting NPs. As discussed above, so far computational chemistry methods have only been applied to investigate either the interaction of the integrin αVβ3 with its ligands13,24,25,27–29 or integrins activation mechanisms.24,39–43 Here, we use atomistic MD simulations to investigate the interaction between the extracellular segment of integrin αVβ3 and a cyclic-RGD-conjugated PEGylated TiO2 NP, where the cyclic RGD is c(RGDyK), hereafter cRGD. The novel aspects of this study are related to the complexity of the systems and to the level of resolution adopted in the MD simulations herein, since previous computational works investigating the interaction between proteins and functionalized NPs has been generally performed at lower levels of resolution (e.g., coarse-grained and mesoscale models),44–54 as reviewed by Brancolini et al.55 Moreover, the vast majorities of MD simulations56–62 studies reported in the literature focused on protein corona formation56–62 rather than investigating the molecular mechanisms underlying active targeting.63 The cRGD-conjugated PEGylated TiO2 NP models were obtained in a previous work by some of us.64 The conjugation densities that we considered are in accordance with experimental reports.65–69 The main goals of the present work are to assess (i) the binding stability of integrin αVβ3 and cRGD, when the latter is conjugated to PEGylated TiO2 NPs, (ii) the influence of the nanodevice/integrin interaction on the protein conformation and (iii) the impact of using different cRGD densities. Results are presented comparatively with respect to the corresponding simpler system, where only the cRGD ligand is bound into the integrin's pocket. This approach highlights the effect of the presence of the connecting PEG chain and of the heavy NP.
The system under investigation (cRGD-conjugated PEGylated TiO2 NP/integrin αVβ3) is a multifunctional nanodevice that, on one side, can target overexpressed integrins αVβ3 through cRGD ligand, but, on the other, can also perform PDT under light irradiation, as a consequence of TiO2 excellent photoabsorption and photocatalytic properties towards reactive oxygen species (ROS) formation.70 It can be considered a pertinent case study to unveil the crucial molecular features which selectively target integrins αVβ3 and, consequently, cancer cells. Both the experimental and the computational communities will benefit from the atomistic knowledge derived from this study on a nanodevice/target interaction.3
2. Computational details
We report in Fig. 2 the structural formula of the ligand, the nanodevice components and the summary of the unbiased MD simulations performed in this study. Hereinafter, the simulation of the complex between the integrin αVβ3 extracellular segment and a single cRGD molecule is named “cRGD MD simulation”, whereas the simulations involving the integrin αVβ3 extracellular segment in complex with a cRGD-conjugated PEGylated TiO2 NP, characterized by an increasing cRGD density in each simulation, are named “NP-cRGD MD simulations”.2.1. Simulation details
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, with a diameter of about 10 Å). The eight Mn2+ ions found in the crystal structure were substituted with Ca2+ ions, following a common practice in integrin modeling25,39,71 and since Ca2+-containing and Mn2+-containing experimental crystal structures of integrin αVβ3 extracellular segment did not differ much in their structure.23
000 atoms, with a diameter of about 10 Å). The eight Mn2+ ions found in the crystal structure were substituted with Ca2+ ions, following a common practice in integrin modeling25,39,71 and since Ca2+-containing and Mn2+-containing experimental crystal structures of integrin αVβ3 extracellular segment did not differ much in their structure.23
After the steepest descent energy minimization, the system was heated to 300 K in 2 ns and equilibrated for another 2 ns, applying restraints on the protein structure: backbone heavy atoms coordinates were restrained to their initial values with a force constant of 400.0 kJ mol−1 nm−2, side chains heavy atoms coordinates with a force constant of 40.0 kJ mol−1 nm−2 and backbone dihedral angles with a force constant of 4.0 kJ mol−1 nm−2. The restraints were removed, and an NPT MD simulation was run up to 500 ns. The V-rescale thermostat84 with a coupling constant of 1.0 ps and Parrinello-Rahman barostat85 with a coupling constant of 2.0 ps were used to control temperature (300 K) and pressure (1 bar). We employed LINCS algorithm86 to constrain the bonds involving H atoms and Newton's equations of motion were integrated in time using the Velocity-Verlet leap-frog algorithm87 with a timestep of 2.0 fs. Long-range electrostatic interactions were handled with Particle Mesh Ewald method88 with a cutoff distance of 12 Å, while short-range repulsive and attractive interactions were treated by Lennard–Jones potential and Lorentz–Berthelot combining rules with an energy switching function that ramps the energy smoothly between an inner cutoff of 10 Å and an outer cutoff of 12 Å. Periodic Boundary Conditions were imposed. All minimization, equilibration, and production steps were performed with open source GPU-accelerated GROMACS code (version 2020.3).89
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90,91 and functionalized with 50 PEG500 chains (MW ∼ 500 Da),92,93 which are partly conjugated to cRGD ligands (see Fig. 2B). In brief, the TiO2 NP model, previously designed by some of us,90,91 was carved from a large bulk anatase supercell with the desired diameter. The 3-fold and some 4-fold coordinated Ti atoms or mono-coordinated O atoms were either removed or saturated with –OH groups or H atoms, respectively. This model then underwent simulated annealing at 700 K at the DFTB (Density Functional Tight-Binding) level of theory and full atomic relaxation at the hybrid DFT (Density Functional Theory) level. In a following work,92,93 the NP was grafted with 50 methyl-terminated PEG500 chains, whose –OH terminal groups bind to the most reactive 4-fold coordinated Ti atoms and to 5-fold coordinated Ti atoms on the surface, resulting in a grafting density equal to 0.02252 chains per Å2. Lastly, some of the PEG chains were conjugated with cRGD targeting ligands through an amide bond with GaussView program.94 Further details on the methods employed to build these models can be found elsewhere.64,90–93 In particular, the three models differ for the cRGD density: the lowest density model (5 out of 50 PEG chains conjugated with cRGD, degree of conjugation of 10%, 0.2 cRGDs per nm2) is referred to as NP-PEG-cRGD10, the intermediate density model (10 out of 50 PEG chains conjugated with cRGD, degree of conjugation of 20%, 0.5 cRGDs per nm2) as NP-PEG-cRGD20 and the highest density model (25 out of 50 PEG chains conjugated with cRGD, degree of conjugation of 50%, 1.1 cRGDs per nm2) as NP-PEG-cRGD50.
90,91 and functionalized with 50 PEG500 chains (MW ∼ 500 Da),92,93 which are partly conjugated to cRGD ligands (see Fig. 2B). In brief, the TiO2 NP model, previously designed by some of us,90,91 was carved from a large bulk anatase supercell with the desired diameter. The 3-fold and some 4-fold coordinated Ti atoms or mono-coordinated O atoms were either removed or saturated with –OH groups or H atoms, respectively. This model then underwent simulated annealing at 700 K at the DFTB (Density Functional Tight-Binding) level of theory and full atomic relaxation at the hybrid DFT (Density Functional Theory) level. In a following work,92,93 the NP was grafted with 50 methyl-terminated PEG500 chains, whose –OH terminal groups bind to the most reactive 4-fold coordinated Ti atoms and to 5-fold coordinated Ti atoms on the surface, resulting in a grafting density equal to 0.02252 chains per Å2. Lastly, some of the PEG chains were conjugated with cRGD targeting ligands through an amide bond with GaussView program.94 Further details on the methods employed to build these models can be found elsewhere.64,90–93 In particular, the three models differ for the cRGD density: the lowest density model (5 out of 50 PEG chains conjugated with cRGD, degree of conjugation of 10%, 0.2 cRGDs per nm2) is referred to as NP-PEG-cRGD10, the intermediate density model (10 out of 50 PEG chains conjugated with cRGD, degree of conjugation of 20%, 0.5 cRGDs per nm2) as NP-PEG-cRGD20 and the highest density model (25 out of 50 PEG chains conjugated with cRGD, degree of conjugation of 50%, 1.1 cRGDs per nm2) as NP-PEG-cRGD50.
For the integrin, we used the same set of FF parameters cited in the previous section. For the PEG500 and PEG500-cRGD chains, we used CGenFF,77–79 and for the TiO2 NP we assigned the partial atomic charges and Lennard–Jones (12,6) parameters according to the coordination number of titanium and oxygen atoms from the version optimized by Brandt et al.95 of the original Matsui–Akaogi FF for TiO2.96 The FF chosen for the functionalized NP has been tested and validated for a TiO2 NP tethered with small organic molecules by some of us97 and used in previous works by some of us.64,98Moltemplate99 facilitated us in merging the FF parameters of the different components of the system.
The starting-point geometry of the complex between a cRGD-conjugated PEGylated TiO2 NP and integrin was built keeping the original configuration found in the crystal structure for the RGD sequence in the integrin binding site. PACKMOL100 was used to solvate the integrin/NP complexes in cubic boxes of 200 × 200 × 200 Å3 filled up with mTIP3P water molecules at the experimental density of ca. 0.99 g cm−3 and with proper number of Na+ and Cl− ions to counterbalance the solute charge and mimic the physiological concentration of 0.15 M. A minimization step was run with conjugate gradient algorithm to minimize the initial energy of the system. Following the standard CHARMM protocol, the system was heated up to 303.15 K in 1 ns with positional restraints on the heavy atoms of the protein, which were eliminated during the following NVT MD simulation of 150 ns. The Nosé–Hoover thermostat with a dumping coefficient of 0.1 ps−1 kept the temperature constant at 303.15 K. We employed SHAKE algorithm101 to constrain the bonds involving H atoms and Newton's equations of motion were integrated in time using the Velocity-Verlet integrator102 with a timestep of 2.0 fs. Non-bonded interactions were treated with CHARMM potential energy functions:76,103,104 long-range electrostatic interactions were handled with Particle–Particle Particle-Mesh solver105 with a real-space cutoff distance of 12 Å and a threshold for error tolerance in forces of 10−5, while short-range repulsive and attractive interactions were treated by Lennard–Jones potential with Lorentz–Berthelot combining rules and using an energy switching function between an inner cutoff of 10 Å and an outer cutoff of 12 Å. Periodic Boundary Conditions were imposed. In all MD simulations with NP models, the TiO2 NP and the PEG anchoring groups were treated as a rigid body only able to translate and rotate, as done in previous works by some of us.56,64,98 This approach keeps the DFTB relative atomic positions within the TiO2 NP and avoids any misshaping core during the MD simulation, as observed in previous calculations.106 All NP-cRGD MD simulations were performed with the open source GPU-accelerated LAMMPS code (version 29 Sep 2021, https://www.lammps.org).107
2.2. Simulations analysis
For the cRGD MD simulation (i.e., integrin with a single cRGD bound to it), we carried out an equilibration phase until satisfactory convergence of selected intermolecular distances (Fig. 4), occurring at about 50 ns of MD simulation. Further, we extended the MD simulation up to 500 ns (production phase), averaging out relevant MD descriptors over specific regions of the MD trajectory in which the Asp residue of cRGD switches between the two binding modes found in this work.For NP-cRGD MD simulations (i.e., integrin with NP-PEG-cRGD systems), we used the intermolecular distance between the COMs of the NP and the Ca2+MIDAS (Fig. S19†) as the index to assess the MD simulation convergence. All three NP-containing systems showed fair convergence of this latter descriptor within the first 120 ns of MD simulation, therefore considered herein the equilibration phase. Further, we extended the MD simulations up to 150 ns, and the analyses were done over the last 30 ns of the MD production phase.
To unveil the features of cRGD binding to integrin αVβ3 and the driving forces behind the interaction of cRGD-conjugated PEGylated TiO2 NP with integrin αVβ3, we quantified the following structural, conformational and thermodynamic MD properties.
The SOMs reported in Section S3† and in Section 3.3.3 were trained with the only cRGD MD simulation and with all the four unbiased MD simulations, respectively.
2.3. Umbrella sampling method
To estimate the binding free energy profiles with the umbrella sampling (US) method, we first used steered molecular dynamics (SMD) to collect a series of configurations along the selected reaction coordinate, that represents the unbinding of the complex. During SMD simulations, the subunits were pushed away one from the other by applying a biasing potential to one collective variable ξ, which is the distance between the center of mass (COM) of cRGD and the COM of the heavy atoms of the residues within 10 Å from the ligand (Fig. 5A). The two COMs are oriented along x-direction of the reference cartesian space. During the pulling simulations, a harmonic potential of 1000 kJ mol−1 nm−2 was applied only along x-direction with a pull rate of 0.005 nm ps−1 in order to obtain a COM displacement of 50 Å in 1 ns. Each simulation box was enlarged to guarantee that the pull distance was always less than one-half the length of the box vector along which the pulling was being conducted. Frames representing a COM spacing of 0.5 Å, referred to as configurations, were extracted from the pulling trajectories and were used as starting-point structures for the US simulations. US simulations 10 ns-long were performed at 300 K and 1 atm for each configuration restraining it within a window corresponding to the chosen COM distance by applying harmonic potential of 2000 kJ mol−1 nm−2. A proper number of additional configurations were added to reach a good sampling over all the collective variable range.The PMF (Potential of Mean Force) profiles were calculated from umbrella histograms using the weighted histogram analysis method (WHAM)119 implemented in GROMACS and were shifted to zero when the distance between the COMs was long enough to have a plateau. To estimate the average PMF profiles and their error bars, we used the bootstrap method with 100 bootstraps and 400 bins per 20 Å. Individual umbrella histograms were weighted with estimated integrated autocorrelation times (IACTs) smoothed along the reaction coordinate (x-direction) using gaussians with standard deviation σ = 0.15 nm.120
The same protocol was applied for the two different binding modes that were found in the unbiased MD simulation of cRGD in complex with integrin αVβ3. For all the SMD and US simulations we used GROMACS code.89
3. Results and discussion
We investigated the interaction of integrin αVβ3 with cRGD-conjugated PEGylated TiO2 NPs through four MD simulations: one involves the integrin αVβ3 extracellular segment and a single cRGD molecule (cRGD MD simulation), whereas the other three (NP-cRGD MD simulations) involve the integrin αVβ3 extracellular segment in complex with a cRGD-conjugated PEGylated TiO2 NP characterized by an increasing cRGD density in each simulation (Fig. 2C).The cRGD-conjugated PEGylated TiO2 NP model, sketched in Fig. 2, is composed of a TiO2 NP with a diameter of 2.2 nm covered with 50 PEG500 chains, which are, in part, conjugated with cRGD molecules. This is a proper and complete biomedical nanodevice since it can be used for photodynamic therapy by exploitation of its semiconducting oxide core, it is protected from protein corona formation by the surrounding PEG layer, and it is designed to target integrins αVβ3 on cancer cells.
Among integrin ligands, the cRGD (short for c(RGDyK)) ligand, considered in this work, is widely used to target integrins αVβ3, since it has a high binding affinity towards this protein (IC50 value of 3.8 ± 0.42 nM (ref. 14) and it can be easily conjugated to nanomaterials through its lysine amine group. We modeled three cRGD densities in line with our previous study in ref. 64 contemplating the range of cRGD density values commonly adopted experimentally,65–69i.e. 0.2 cRGDs per nm2 (NP-PEG-cRGD10, 10% conjugated PEG chains), 0.5 cRGDs per nm2 (NP-PEG-cRGD20, 20% conjugated PEG chains) and 1.1 cRGDs per nm2 (NP-PEG-cRGD50, 50% conjugated PEG chains). In the following we will refer to the cRGD bound to the integrin αVβ3 binding site as “ligand” to distinguish it from all the other cRGD molecules on the NP, as it is shown in Fig. 2.
The cRGD backbone conformational study based on REMD simulations, which we used to identify a reliable starting-point geometry for MD simulations, is reported in Section 3.1. The MD simulation of a single cRGD bound to the integrin αVβ3 binding pocket (Section 3.2) is taken herein as the reference to unveil how the ligand conjugation to a PEGylated TiO2 NP affects the stability of ligand/integrin interactions (Section 3.3). The interaction of the complete nanodevice with the integrin αVβ3 extracellular segment and its influence on the conformation and behavior of each of them is analyzed in Section 3.4. Finally, the impact of different cRGD densities is evaluated in Section 3.5.
One important and general result we wish to stress here is that during all our simulations the cRGD ligand remains bound to the integrin binding site.
3.1. cRGD backbone conformational analysis
Since integrin/ligand selectivity is not only based on the recognition sequence composition but also on its conformation,18 we performed a preliminary conformational analysis of cRGD backbone to identify a reliable starting-point for cRGD and NP-cRGD MD simulations. Since the rigid-receptor docking did not reproduce the experimentally observed interaction pattern of the carboxylate group of aspartate with the MIDAS ion and protein residues (see Section S1.2 in the ESI†), we decided to proceed through an enhanced sampling technique.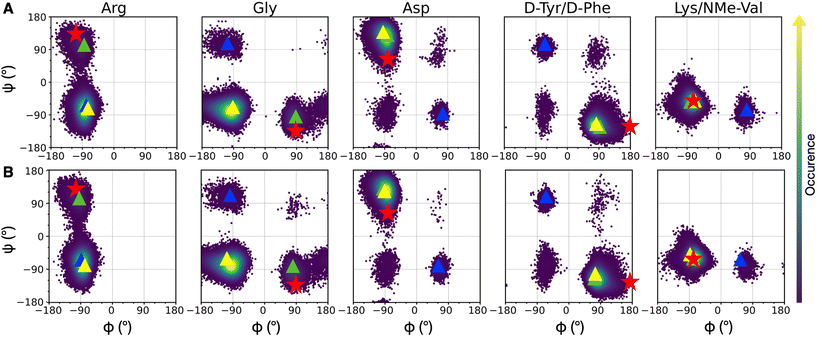 | ||
| Fig. 3 Density plots of Ramachandran dihedral angles for cRGD (A) and PEG150-cRGD (B) for the lowest T replica simulation. Red stars indicate the co-crystallized cilengitide dihedral values (PDB ID: 1L5G). The color scale represents the occurrence of values, ranging from purple (low occurrence) to yellow (high occurrence). The color code for clusters, based on population percentage, is as follows: yellow (87% populated), green (10% populated), blue (1% populated). | ||
To evaluate the population of the different conformational basins, we performed a cluster analysis based on the coordinates of backbone heavy atoms with the GROMOS algorithm, as detailed in Section S1.3 in the ESI.† We found 27 clusters for cRGD and 26 for PEG150-cRGD. In both cases, the first three clusters, which collect the majority of the conformations, account for approximately 87%, 10% and 1% of the population, respectively. From Fig. 3, we can see that the dihedral values of the centroid of the most populated cluster (yellow) lie in the basins of the most recurrent conformation and that the dihedral values in the second most populated cluster (green) are similar to those of the co-crystallized cilengitide structure.
Therefore, we assume that the crystal structure of integrin αVβ3/cilengitide complex, in which the cilengitide structure is mutated into cRGD, is a reliable starting point for MD simulations. Indeed, both cilengitide and cRGD have a strong affinity for integrin αVβ3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and, thus, they likely share a similar conformation when bound to integrin αVβ3. On top of this, the REMD analysis proves that the co-crystallized cilengitide conformation is not only accessible to cRGD in solution, but it corresponds to the second most populated cluster.
14 and, thus, they likely share a similar conformation when bound to integrin αVβ3. On top of this, the REMD analysis proves that the co-crystallized cilengitide conformation is not only accessible to cRGD in solution, but it corresponds to the second most populated cluster.
First, we observe that cRGD is able to interconvert between the two most populated conformations in solution not only when bound to the integrin pocket in cRGD MD simulation, but also when bound to the integrin pocket and simultaneously conjugated to a PEGylated NP, in NP-cRGD MD simulations (Fig. S9 in the ESI†). This switching behavior is particularly frequent in the case of the longer cRGD MD simulation (Fig. S10 in the ESI†). Moreover, on the basis of structural and conformational analyses that will be presented in Sections 3.2.1, 3.3.1 and 3.3.3, we do not observe any correlation between changes in the interaction features and shifts in the cRGD backbone conformation.
Secondly, we evaluated the backbone dihedrals for the other cRGDs attached to the NPs (Fig. S11 in the ESI†). We observe that the same regions of the conformational space as those for cRGD and PEG150-cRGD in REMD simulations are sampled here, too.
3.2. The binding of cRGD to integrin αVβ3
In this section, we identify the features of cRGD binding to the integrin αVβ3 and calculate its binding free energy through the US method. As discussed in the previous section, in all our simulations we used the geometry found for CGT in complex with integrin αVβ3 in the crystal structure PBD ID: 1L5G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 as the starting-point geometry for the RGD portion of cRGD ligand.
23 as the starting-point geometry for the RGD portion of cRGD ligand.
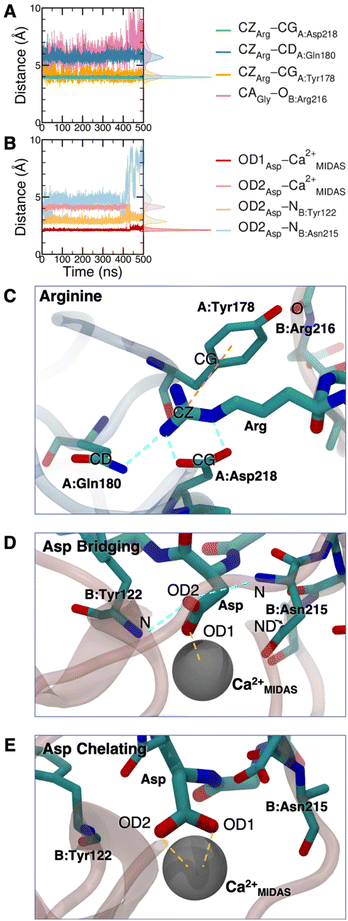
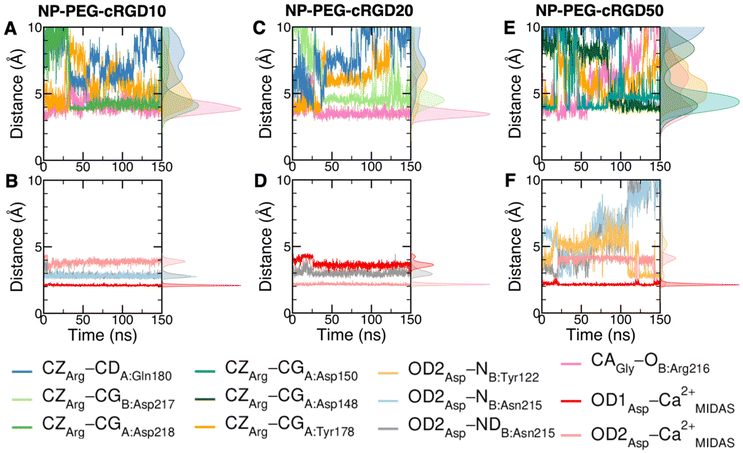
The cRGD Arg side chain is found to form one side-on double H-bond with A:Asp218, in fair agreement with previous experimental findings,23 and one single H-bond with A:Gln180, in place of the one with A:Asp150 found in the crystal for CGT,23 and to interact with the phenyl ring of A:Tyr178 through an ion–π interaction (Fig. 4A and C). These interactions are stable all over the 500 ns-long MD run.
The contact between Cα(CA) in cRGD glycine and the O atom of B:Arg216 (Fig. 4A), found to contribute to the specificity of the CGT/integrin αVβ3 interaction by Bella et al.,29 is quite stable in our simulation apart from the last few nanoseconds when the binding mode of aspartate changes.
For what concerns the cRGD aspartate (Fig. 4B), one of the two O atoms (OD1) of its carboxylate group is stably coordinating Ca2+MIDAS, while the second O atom (OD2) is making two H-bonds with backbone N atoms of B:Tyr122 and B:Asn215, up to 400 ns and coordinates the Ca2+MIDAS ion for the rest of the MD simulation. The first binding mode of cRGD aspartate (Fig. 4D) matches exactly the one found in the CGT crystal reference structure and we will refer to it as “bridging” binding mode, since the carboxylate is bridging the integrin backbone with the Ca2+MIDAS ion. The second binding mode (after 400 ns), where the carboxylate is chelating the Ca2+MIDAS ion, is defined “chelating” binding mode (Fig. 4E). From a chemical point of view, the chelating binding mode, which was not observed neither experimentally23 nor in previous MD simulations of similar systems,13,25 is chemically sound for an Asp group in the proximity of a divalent cation. However, this may be an artifact of the simulation due to inaccuracies in the FF and/or ion parameters in describing the situation involving a carboxylate group coordinating a divalent ion and establishing H-bonds at the same time. From now on, the average values of the bridging and the chelating binding modes refer to the ranges of 50–350 ns and 450–500 ns, respectively.
To corroborate our finding of two principal binding modes, selected cRGD–integrin αVβ3 intermolecular distances (Fig. S12 in the ESI†) were used to train a SOM composed of 100 neurons (Fig. S13 in the ESI†), each of them representing a microstate of the system, namely an ensemble of configurations for cRGD binding to integrin αVβ3 (see Section S3 in the ESI†). Similar neurons were collected in clusters, each representing a different ligand binding mode. According to the average distance between neurons in Fig. S13,† all clusters are quite similar apart from Cluster C, which is the only one where the aspartate is in the chelating binding mode (see structures in Fig. S13D in the ESI†). Then, we can infer that the change in the binding mode of the Asp side chain is the one that causes the major conformational rearrangement of cRGD.
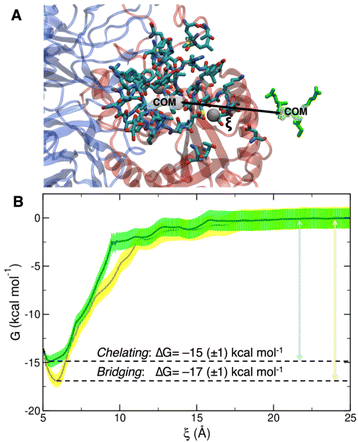
To collect the different configurations necessary to start US simulations, we first ran one steered MD unbinding simulation for each binding mode, in which the ligand was pulled away from the binding site along the collective variable represented in Fig. 5A.
For the bridging mode, the rupture of cRGD-protein binding (Fig. S14A and B in the ESI†) in SMD simulation happens between 200 and 300 ps and requires a force of ∼800 kJ mol−1 nm−1, which corresponds to ∼500 pN, much higher than the one used in experiments (100–200 pN).19 First, the Arg interactions break (Fig. S14C†), while the Asp interactions shift to the chelating binding mode for few picoseconds and, then, Asp interactions definitely break (Fig. S14D†).
When starting the SMD from the chelating binding mode, the rupture happens slightly later in the SMD simulation (300–350 ps) and requires a higher force (1100 kJ mol−1 nm−1) with respect to the bridging binding mode (Fig. S15A and B†). The interactions are lost in the same order as above (Fig. S15C and D†): the first ones to break are those involving the Arg side chain, proving them to be the weakest interactions, in agreement with previous SMD simulations.27 For a more detailed analysis of SMD simulations we refer to Section S4.1 in the ESI.†
The PMF profiles for the bridging and chelating binding modes are overlaid in Fig. 5B. The bridging binding mode, which is the one found for cilengitide co-crystallized in complex with integrin αVβ3,23 appears to be the most stable. However, if we consider the intrinsic error bar associated with the ΔG estimation, the difference between the values of ΔG of binding for the bridging (−17 ± 1 kcal mol−1) and chelating (−15 ± 1 kcal mol−1) binding modes is tiny. In the literature, affinity constants of the order of 105–107 M−1 have been reported for a generic integrin-ligand binding,16 corresponding to values of ΔG of binding in the range from −7 to −10 kcal mol−1. Also, Silva et al. used US method to predict a ΔG value for the binding of the antiviral pentapeptide ATN-161 with α5β1 integrin which is of the same order of magnitude as the one calculated by us.124
To the best of our knowledge no estimation of the binding free energy to integrin αVβ3 has been reported in the literature neither for the specific targeting ligand used in this work, cRGD, nor for cilengitide. In this case, we can only refer to the experimentally measured IC50 value of 3.8 ± 0.42 nM for the cRGD–integrin αVβ3 specific interaction.14 Being IC50 the ligand concentration value at which half of the receptors are bound, the comparison with the calculated ΔG value is not straightforward because the latter one is, instead, related to the dissociation constant, Kd. According to recent literature,125 IC50 can only be considered as the upper limit for the Kd of a ligand. Therefore, if we take the IC50 = 3.8 nM = Kd-MAX and calculate the corresponding minimum ΔG absolute value, we obtain ΔG ≤ –11.5 kcal mol−1. In fact, the one calculated by us ranging from −15 to −17 kcal mol−1 is less than −11.5 kcal mol−1.
Overall, based on the analysis in Section 3.2, we conclude that the cRGD/integrin αVβ3 complex is stable along all the 500 ns-long MD simulation. For the RGD portion of the molecule, which is undoubtedly the most relevant for the binding process, we observe almost all the interactions found in the crystal reference structure, whereas neither D-Tyr nor Lys make significant interactions with the protein. This observation supports the possibility to use Lys sidechain as the anchoring point for cRGD targeting ligand, which is a crucial aspect for the next step when we attach the ligand to the NP through a PEG chain. We wish to conclude this section saying that we validated the bridging binding mode found in the crystal structure, by means of free energy calculations, and found another stable binding mode where the Ca2+MIDAS ion is chelated by the ligand carboxylate group, which however may be an artifact of the MD simulation.
3.3. The effect of conjugation to PEGylated TiO2 NPs on the ligand binding to integrin αVβ3
Taking as a reference the cRGD MD simulation discussed in the previous section (Section 3.2), here we investigate the effect that the conjugation of the cRGD ligand to a PEGylated TiO2 NP has on the binding into the integrin αVβ3 pocket on a structural, conformational, and energetic basis. Increasing cRGD density on the NP will be taken into account, but we refer to Section 3.5 to discuss its effect on the cRGD binding.To evaluate how close to the CGT crystal structure the molecular conformation of the RGD portion of the ligand is, we measured three geometrical criteria (Table 1), which were defined by Kostidis et al.126 and by Othman et al.127 to predict the biological activity of RGD containing peptides and which we recently evaluated for a free cRGD and for free cRGD-conjugated PEGylated TiO2 NPs in water.64 The three criteria are (i) d1, the distance between Arg CZ and Asp CG, i.e. between the two charged groups; (ii) d2, the distance between Arg CB and Asp CB; (iii) θ, the angle formed by Arg CB, Gly CA and Asp CB (Fig. 8D). Indeed, the optimal values of these criteria are not universal, but depend on the integrin subtype. For example, integrin αVβ3 specific ligands share a lower value for d1 than the RGD hexapeptide ligands with higher affinity for αIIbβ3 integrins (∼16 Å).18 In the cRGD MD simulation, the CGT crystal structure is better reproduced by the ligand in its bridging binding mode. In contrast, upon shifting to the chelating binding mode, which, however, might be an artifact of the simulation as pointed out in Section 3.2.1, the RGD portion assumes a more bent conformation, characterized by lower values for all the three criteria (Table 1). For the simulations including the NP, the averaged values slightly differ from the CGT values. The largest deviation is registered for the angle θ, suggesting a more bent conformation for the ligand in the integrin pocket in all three cases. It has to be noted that the values measured for the ligand in NP-cRGD MD simulations are closer to the CGT crystal structure with respect to the lower ones that we found for cRGD ligands of free cRGD-conjugated PEGylated TiO2 NPs in water in our previous MD simulations study.64 Noteworthy, in all our simulations d1 is close to or lower than the CGT one, which is in line with the “kinked” RGD conformation that has been observed to be crucial for integrin αVβ3 selective ligands.18
| Criterium | CGT | cRGD: bridging | cRGD: chelating | NP-PEG-cRGD10 | NP-PEG-cRGD20 | NP-PEG-cRGD50 |
|---|---|---|---|---|---|---|
| d 1 (Å) | 13.7 | 14.3 (±0.4) | 13.2 (±0.4) | 12.4 (±0.5) | 11.4 (±0.5) | 12.5 (±1.1) |
| d 2 (Å) | 8.9 | 8.8 (±0.3) | 8.2 (±0.5) | 8.3 (±0.3) | 7.4 (±0.4) | 7.7 (±0.6) |
| θ (°) | 136 | 136 (±24) | 111 (±31) | 117 (±7) | 107 (±8) | 115 (±13) |
We also computed the H-bonds established by the ligand with the integrin or with water (Table S3 and Fig. S16 in the ESI†). We observe that in general the average number of H-bonds between the ligand and the protein and between the ligand and water in NP-cRGD MD simulations is similar to the one found in cRGD MD simulation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or higher), which is rationalized by the cRGD ligand bearing two oppositely charged groups, i.e., Arg and Asp side chains. The ratio between ligand–integrin and ligand–solution non-bonded energies varies in the range of 1.0, 1.3, 0.6 and 1.8 for cRGD, NP-PEG-cRDG10, NP-PEG-cRDG20 and NP-PEG-cRDG50, respectively. This variability can be attributed to the small differences in the binding environment of the ligand, which are highlighted in more detail in the structural (Section 3.3.1) and in the conformational analysis (Section 3.3.3). However, overall, the sum of ligand–integrin and ligand–solution non-bonded energies in the NP-cRGD MD simulations is comparable to that in the cRGD MD simulation for the same simulation length (Fig. S17A up to 150 ns vs. Fig. S17B in the ESI†), but slightly lower, as expected, because the cRGD Lys side chain, when conjugated to PEG and, thus, indirectly to the NP, is not available for these interactions anymore.
1 or higher), which is rationalized by the cRGD ligand bearing two oppositely charged groups, i.e., Arg and Asp side chains. The ratio between ligand–integrin and ligand–solution non-bonded energies varies in the range of 1.0, 1.3, 0.6 and 1.8 for cRGD, NP-PEG-cRDG10, NP-PEG-cRDG20 and NP-PEG-cRDG50, respectively. This variability can be attributed to the small differences in the binding environment of the ligand, which are highlighted in more detail in the structural (Section 3.3.1) and in the conformational analysis (Section 3.3.3). However, overall, the sum of ligand–integrin and ligand–solution non-bonded energies in the NP-cRGD MD simulations is comparable to that in the cRGD MD simulation for the same simulation length (Fig. S17A up to 150 ns vs. Fig. S17B in the ESI†), but slightly lower, as expected, because the cRGD Lys side chain, when conjugated to PEG and, thus, indirectly to the NP, is not available for these interactions anymore.
| Energy (kcal mol−1) | Ligand–integrin | Ligand–solution | Total | ||||
|---|---|---|---|---|---|---|---|
| Electrostatic | vdW | Total | Electrostatic | vdW | Total | ||
| cRGD | −160 (±14) | −18 (±5) | −178 (±13) | −153 (±18) | −18 (±5) | −170 (±16) | −348 (±21) |
| NP-PEG-cRGD10 | −152 (±13) | −27 (±4) | −178 (±14) | −119 (±15) | −18 (±5) | −138 (±16) | −316 (±24) |
| NP-PEG-cRGD20 | −101 (±14) | −22 (±4) | −123 (±14) | −172 (±18) | −17 (±6) | −190 (±19) | −313 (±24) |
| NP-PEG-cRGD50 | −194 (±21) | −5 (±5) | −199 (±22) | −87 (±23) | −20 (±6) | −107 (±24) | −306 (±33) |
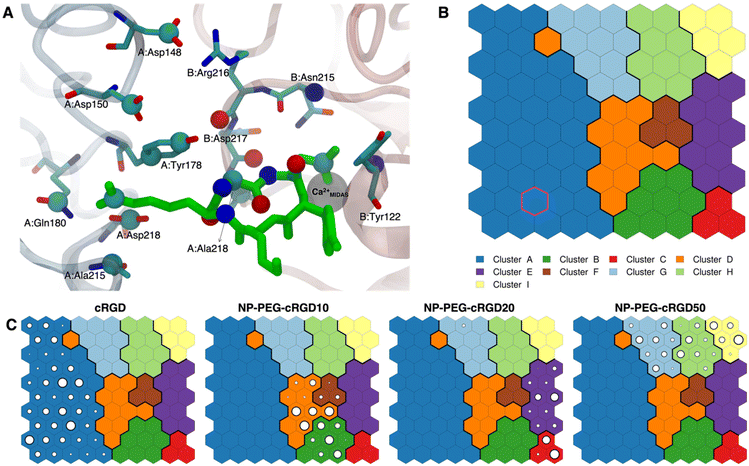 | ||
| Fig. 7 (A) The integrin αVβ3 binding site where the atoms selected for intermolecular distances calculation for SOM training are represented with spheres and labeled with the residue they belong to. cRGD ligand is shown in green, while C atoms are in cyan, N atoms in blue, O atoms in red, and H atoms and water molecules are not shown for the sake of clarity. (B) The SOM trained with the selected intermolecular distances evaluated all along the four MD simulations. Each hexagon represents a neuron, namely a set of trajectory frames, and each color represents a cluster of neurons, that is the set of binding modes with similar features. The binding mode found in the crystal PDBID: 1L5G for the RGD portion of CGT belongs to the neuron contoured in magenta. (C) Population maps for the four different MD simulations. The size of each circle is directly proportional to the population of the neuron. | ||
The trained SOM is represented in Fig. 7B, where each neuron (hexagon) corresponds to a ligand/protein configurational microstate, i.e. a ligand binding mode defined by specific values of the ligand–protein intermolecular distances used as input features, and neurons close to each other represent similar configurations, forming 9 different clusters. The number of clusters was chosen to be the one corresponding to the second maximum in the Silhouette profile (Fig. S18B in the ESI†). We refer the reader to Section 2.2.2 for the methodological details of SOM training and clustering, which may help in the results interpretation. From the population maps in Fig. 7C, we note that configurations belonging to different simulations are populating quite different areas on the map (Fig. 8E). In particular, the cRGD MD simulation populates only cluster A, NP-PEG-cRGD10 is in clusters B, D, and F, NP-PEG-cRGD20 is populating mainly clusters C and E, and NP-PEG-cRGD50 is spread among clusters G, H, and I. The binding mode of the crystal PDBID: 1L5G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 for the RGD portion of CGT belongs to the neuron contoured in magenta, which is sampled only during the cRGD MD simulation (Fig. 7C and S18C†).
23 for the RGD portion of CGT belongs to the neuron contoured in magenta, which is sampled only during the cRGD MD simulation (Fig. 7C and S18C†).
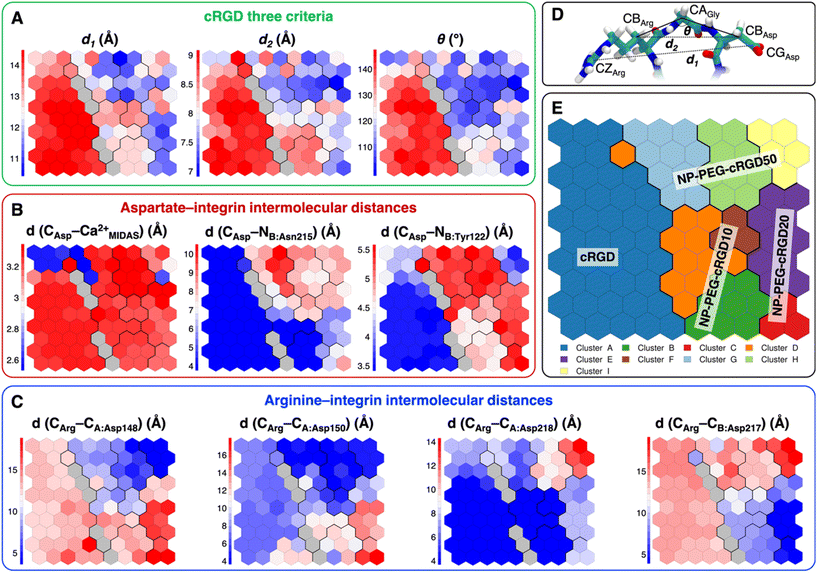 | ||
| Fig. 8 Values of selected distances and descriptors for each neuron of the map: (A) the values of the three criteria discussed in Section 3.3.1, (B) the Arg–integrin interaction distance values, (C) the Asp–integrin interaction distance values. (D) Definition of three geometrical criteria proposed by Kostidis et al.126 and by Othman et al.127 to assess the biological activity of RGD-containing ligands. (E) The SOM with the indication of the area with the higher population from each MD simulation. Blue and red neurons are the ones in which the descriptor has a low or a high value, respectively. Gray neurons are empty ones. | ||
We mapped the geometrical parameters discussed in Section 3.3.1 on the SOM (Fig. 8A) and we found that, when the cRGD is conjugated to the PEG chains on the NP, the conformation of the RGD portion is more bent (θ angle). Moreover, by mapping some selected intermolecular distances (Fig. 8B and C), we spotted some differences in the interactions of cRGD Arg and Asp groups when the ligand is conjugated to the NP. However, these differences appear to be only marginal to the stability of the ligand/integrin binding, because even if the protein interacting residue changes, the nature of the interaction is preserved (for example, cRGD arginine is always interacting with at least one aspartate and the carboxylate group is found bridging the Ca2+MIDAS in the majority of the neurons). For a more detailed analysis of Fig. 8 we refer to Section S4.2 in the ESI.†
To conclude this Section 3.3, one can state that the conjugation to PEGylated TiO2 NPs does not hamper the ligand binding to integrin αVβ3 at any of the cRGD densities tested in this work but causes the cRGD into the pocket to assume a bent conformation. Moreover, the Asp bridging binding mode, which was found to be slightly more stable than the chelating one in the previous section, is the most populated in all the NP-cRGD MD simulations.
3.4. Besides the ligand binding to the pocket: all the other nanodevice/integrin interactions
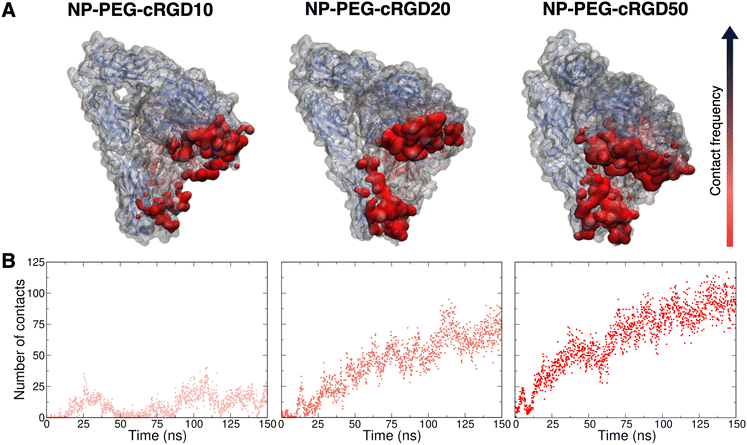
Simultaneously to the ligand binding to the protein pocket, we assist to the interaction of other elements of the nanodevices with the integrin αVβ3 surface. Therefore, in this section, we discuss and detail the structural, conformational and energetic aspects of the interaction between the whole cRGD-conjugated PEGylated TiO2 NP and the extracellular segment of integrin αVβ3. As in Section 3.3, increasing cRGD density on the NP will be taken into account, but we refer to Section 3.5 for the discussion of its effect on the cRGD binding.The descriptors that we consider to assess the extent of the nanodevice/integrin interaction are (i) the distance between the center of the NP and the Ca2+MIDAS (Fig. S19 in the ESI†), which is a measure of the distance between the nanodevice and the integrin binding site, (ii) the number of H-bonds (Fig. S20 in the ESI†), which can be established between the nanodevice and the protein surface that is typically polar, and (iii) the surface contact area (Fig. S21 in the ESI†), which takes into account all the possible types of interactions. From the descriptors’ average over the production phase in Table 3, we can state that, even at the lowest ligand density tested in this work, a non-negligible number of H-bonds and other types of intermolecular interactions form between cRGD-conjugated PEGylated TiO2 NPs and integrin αVβ3. Moreover, the decreasing trend of NPcenter–Ca2+MIDAS distance, as opposed to the other two descriptors, reveals that the formation of additional nanodevice/integrin interactions, besides the ones in the binding site discussed in Section 3.3, is directly proportional to the closeness of the NP to the binding site.
| Descriptor | NP-PEG-cRGD10 | NP-PEG-cRGD20 | NP-PEG-cRGD50 |
|---|---|---|---|
| a In this case, the nanodevice corresponds to NP-PEG-cRGD systems excluding the ligand in the pocket. | |||
| Distance: NPcenter–Ca2+MIDAS | 51 (±2) | 44 (±1) | 36 (±1) |
| H-bonds number: nanodevicea–integrin | 1.5 (±1.1) | 6.5 (±2.0) | 11.7 (±3.0) |
| Surface contact area: nanodevicea–integrin | 322 (±90) | 1493 (±150) | 1912 (±166) |
Noteworthy, in the case of the highest ligand density, while the NPcenter–Ca2+MIDAS distance reaches a constant value after only 20 ns (Fig. S19 in the ESI†), requiring a shorter equilibration time compared to the other systems, both the H-bonds number and the surface contact area constantly increase up to 120 ns (Fig. S20 and S21 in the ESI†). This is probably because the additional interactions do not form immediately after NP approaching but take time to be established.
In principle, both the PEG chains and the other cRGDs, besides the ligand, are available to interact with the protein surface. To understand the degree of the interaction of each of the two portions of the nanodevice, we report in Table 4 an additional energetic analysis that is complementary to the one in Section 3.3.2, because here we consider the total non-bonded interactions between the nanosystem (excluding the ligand) and the protein, whereas before we limited the analysis to the ligand/protein interactions. If we split the total nanodevice–integrin interaction energy (Fig. S22 in the ESI†) into its energetic contributions, we note that, in general, the cRGD–integrin interaction is greater than the one of the PEG chains. Based on data in Table 4, we can also observe that the nanodevice–integrin electrostatic contribution, mostly related to the cRGDs, is twice the van der Waals one, related to the PEG chains, at any cRGD density. Clearly, a further trend emerges from the energy values in Table 4: the nanodevice–integrin interaction becomes stronger as the cRGD density increases, but the two quantities are not linearly proportional. Indeed, as the cRGD density doubles from NP-PEG-cRGD10 to NP-PEG-cRGD20, the interaction energy quadruples, whereas when the ligand density increases fivefold (from NP-PEG-cRGD10 to NP-PEG-cRGD50), the interaction energy grows only six times. This observation can be rationalized as due to a sort of saturation effect caused by the spatial disposition of the cRGDs and PEG chains around the NP and by their steric hindrance, preventing further interactions with the protein surface.
| Energy (kcal mol−1) | Electrostatic | vdW | Total | |
|---|---|---|---|---|
| NP-PEG-cRGD10 | PEG–integrin | −13 (±16) | −24 (±8) | −37 (±19) |
| Other cRGDs–integrin | −47 (±19) | −15 (±7) | −62 (±22) | |
| Nanodevice–integrin | −60 (±23) | −39 (±12) | −99 (±26) | |
| NP-PEG-cRGD20 | PEG–integrin | −92 (±26) | −109 (±16) | −201 (±37) |
| Other cRGDs–integrin | −195 (±21) | −59 (±7) | −254 (±22) | |
| Nanodevice–integrin | −287 (±26) | −169 (±19) | −456 (±33) | |
| NP-PEG-cRGD50 | PEG–integrin | −24 (±12) | −86 (±15) | −112 (±21) |
| Other cRGDs–integrin | −404 (±37) | −139 (±13) | −543 (±39) | |
| Nanodevice–integrin | −428 (±37) | −228 (±20) | −657 (±42) |
Moreover, we report on the location and the orientation of the different cRGD molecules around the NP. Based on the number density profiles of PEG chains and cRGD molecules with respect to the center of the NP, we can infer that the PEG chains distribution around the TiO2 NP is not affected by their interaction with the integrin surface (Fig. S23 in the ESI†), whereas the distribution of other cRGDs shifts towards higher distances when they interact more with the protein surface (Fig. 9). Reasonably, the region explored by the bound ligand, which is constrained in the pocket, is much narrower than those explored by the other cRGDs (Fig. S24 in the ESI†), which behave similarly to what previously reported for free cRGD-conjugated PEGylated TiO2 NPs in water.64
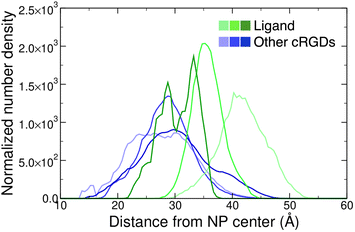 | ||
| Fig. 9 Normalized number density profiles of the ligand (green lines), and the other cRGD molecules (blue lines) from the geometric center of the NP. The color intensity increases according to the cRGD density. The PEG profiles for different cRGD densities are shown in Fig. S23 in the ESI.† | ||
To gain atomic-level insights into the additional interactions, we performed a contact analysis between the nanodevice (excluding the ligand) and the protein. As shown in Fig. 10B, the trends of the number of contacts profiles over time at the different ligand densities resemble the ones of the surface contact area (Fig. 10). Moreover, the representations in Fig. 10A provide further details on the nanodevice/integrin interaction. In these representations, we color the protein surface in correspondence to the atoms that establish contacts with the nanodevice: the color transitions from red to blue as the frequency of contacts established by the atom increases. Because of the multivalent nature of the nanodevice, being multiple copies of the same cRGD exposed on its surface, the contact analysis might also be useful in identifying recurrent binding regions, which may serve as secondary binding sites that can contribute to increase the binding affinity of multivalent entities.18 However, within the simulation time scale, we do not identify any additional binding site. Nevertheless, we notice that a wide region of the protein surface interacts with the nanodevice without a proper specificity.
Given that several other residues of the integrin are involved in the interaction with cRGD-conjugated PEGylated TiO2 NPs, we investigated the presence/absence of any immediate effect of these contacts on the integrin structure, conformation and dynamics, by evaluating the RMSF and the secondary structure of the integrin domains forming the binding pocket, i.e. β-propeller and β-A domains in αV and β3 subunits, respectively (Fig. 1). From the secondary structure analysis in Fig. S25 in the ESI,† we observe that the overall integrin structure is not deeply perturbed within the simulation time scale, even though it is affected by the interaction with the nanodevices. The most relevant change in the secondary structure is that some α-helixes are lost or turned into 3–10 and π-helixes and 3–10 helixes have a higher degree of instability.
In Fig. S26 in the ESI,† we report the RMSF for two selected domains. In particular, the residues directly involved in the binding of the cRGD ligand are residue 150 and the ones around residue 215 in the β-propeller domain and residues between 120 and 125 and around residue 216 in β-A domain. In the cRGD MD simulation, the RMSF of the residues involved in the ligand binding is always low, while the more flexible segments are around residue 80 in β-propeller domain and residue 200 in β-A domain (Fig. S26A†). In NP-cRGD MD simulations, the shape of the RMSF partially resembles the one in the case of the cRGD MD simulation, but the intensity is different, especially for the β-A domain. The different degree of protein residues’ fluctuation with respect to the cRGD MD simulation may also induce the ligand to assume the bent conformation that was found in Section 3.3, especially at the highest cRGD density.
To conclude this Section 3.4, we can state that the presence of the PEGylated NP in conjunction with all the unbound cRGDs causes the establishment of several new interactions with the protein surface. However, these intermolecular interactions have only minor impact on the protein's secondary structure and internal dynamical fluctuations at the limited simulation time scale considered.
3.5. The effect of cRGD density
Since three models of the nanodevice at increasing cRGD density have been considered in this study, here we aim at highlighting the impact of the conjugation density on the ligand/pocket binding and on the other nanodevice/integrin interactions.From the analyses presented in Section 3.3, we can say that the density of cRGDs exposed on the NP plays a marginal role in the ligand binding as compared to the cRGDs conjugation itself that causes the ligand to assume a more bent conformation in all the cases (three criteria in Table 1). In fact, the overall non-bonded interaction energy of the ligand has comparable values in all our simulations (energetic analysis in Table 2), the nature of ligand/integrin interactions is preserved at all the cRGD densities (SOM analysis in Fig. 7 and 8) and only their stability in time is slightly influenced by the cRGD density increase since we observe that the oscillation of Arg–integrin distances and the water accessibility to the binding site are enhanced in the case of NP-PEG-cRGD50 (distance analysis in Fig. 6).
The most evident effect of the cRGD density emerges from the results discussed in Section 3.4. The higher the number of cRGDs, the greater the extent of interaction between the nanodevice and the protein and the closer the NP gets to the integrin binding site, as proven by trends found in the structural and energetic analyses in Tables 3 and 4. Interestingly, from the number density profiles in Fig. 9 we note that going from low to high cRGD densities the nanodevice gradually shifts from a conformation in which the ligand is the farthest cRGD from the surface, i.e. the most exposed one, to the situation in which the ligand is as exposed as the other cRGDs. Also, the closeness of the whole nanodevice to the protein at high cRGD densities not only favors the interaction of other cRGDs but also of a higher number of PEG chains to the protein surface (energetic analysis in Table 4 and Fig. S22†). As a consequence of these additional interactions, such as H-bonds or hydrophobic contacts, the protein structure and dynamics of β-propeller and β-A domains are affected by the increased adsorption of PEG and cRGD at high cRGD densities (RMSF and secondary structure analysis in Fig. S25 and S26†).
In conclusion, the increasing degree of interaction registered at all the cRGD coverages here considered (note that for NP-PEG-cRGD50 half of the PEG chains are conjugated with cRGDs) means that not all available binding spots on the protein surface are saturated but there is still opportunity to establish additional nanodevice/integrin interactions. Moreover, considering that when the cRGD density increases the ligand binding is not substantially perturbed and a growing number of PEG and cRGD interactions with the protein surface is established, the overall nanodevice/integrin interaction is getting stronger and can favor the nanodevice selectivity and, eventually, its cell uptake. Finally, it should also be said that, being integrins transmembrane proteins, the membrane may be able to slightly modulate the nanodevice interaction with the target protein, which may be investigated in future studies.
4. Conclusions
In this study, we performed atomistic MD simulations of four complex systems composed by the extracellular segment of integrin αVβ3 and a single isolated cRGD molecule or cRGD-conjugated PEGylated TiO2 NPs at three cRGD densities: 0.2 cRGDs per nm2, 0.5 cRGDs per nm2 and 1.1 cRGDs per nm2.With REMD simulations, we proved that the co-crystallized cilengitide backbone conformation lies within a region of the cRGD conformational space that is accessible to the molecule in solution, independently of it being free or conjugated to a short PEG chain. We used this structure as the starting point of the reference cRGD MD simulation (with a single isolated cRGD in complex with integrin αVβ3). Based on these results, we validated the stability of the cRGD ligand interactions with the protein and, through US, we calculated the free energy of binding for cRGD to the integrin αVβ3, which is on average −16 kcal mol−1.
From the analysis of distances, H-bonds, and non-bonded interaction energy, we found that the binding of a cRGD conjugated to PEGylated TiO2 NPs in the NP-cRGD MD simulations is stable and shares similar features with the one of a single free cRGD in the reference cRGD MD simulation, especially at low cRGD densities on the NP. From the SOM training, we found that the higher the cRGD density is, the more the RGD portion of the molecule is bent, and the binding is disturbed, especially for the weaker Arg non-covalent bonds to the integrin binding pocket.
Moreover, apart from the ligand, the other cRGDs and PEG chains attached to the NP can also interact with the superficial residues of the protein. At increasing cRGD density, the extent and, therefore, the effect of the interaction on the protein structure and dynamics enhances, as discussed from the structural/conformational and energetic points of view.
To conclude, this study has proved that the fundamental interaction for the active targeting of integrin αVβ3, i.e., the binding between the cRGD ligand and the integrin pocket, is effective and stable also when cRGD is covalently conjugated to a fully PEGylated TiO2 NP of realistic size. The presence of a high density of cRGDs on the NP is found to strengthen the nanodevice/integrin interplay, perhaps favoring the selectivity and the cellular uptake. These outcomes strongly support the use of cRGD-conjugated nanosystems for an efficacious targeting of cancer cells11,30,31,33–38 in view of their clinical application. In a more general sense, here we have also developed and presented a rigorous computational protocol to determine the nature and extent of interaction between NPs covalently linked to targeting molecules and their target proteins.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Lorenzo Ferraro for his technical support. The research leading to these results has received funding from the European Union – NextGenerationEU through the Italian Ministry of University and Research under PNRR – M4C2-I1.3 Project PE_00000019 “HEAL ITALIA” to Prof. Cristiana Di Valentin and Prof. Luca De Gioia CUP H43C22000830006 of University of Milano Bicocca.References
- S. Wilhelm, A. J. Tavares, Q. Dai, S. Ohta, J. Audet, H. F. Dvorak and W. C. W. Chan, Nat. Rev. Mater., 2016, 1, 16014 CrossRef CAS.
- F. Danhier, O. Feron and V. Préat, J. Controlled Release, 2010, 148, 135–146 CrossRef CAS PubMed.
- A. K. Pearce and R. K. O'Reilly, Bioconjugate Chem., 2019, 30, 2300–2311 CrossRef CAS PubMed.
- F. Danhier, J. Controlled Release, 2016, 244, 108–121 CrossRef CAS PubMed.
- B. Dutta, K. C. Barick and P. A. Hassan, Adv. Colloid Interface Sci., 2021, 296, 102509 CrossRef CAS PubMed.
- D. Rosenblum, N. Joshi, W. Tao, J. M. Karp and D. Peer, Nat. Commun., 2021, 12(1), 1–13 CrossRef PubMed.
- J. S. Desgrosellier and D. A. Cheresh, Nat. Rev. Cancer, 2010, 10, 9–22 CrossRef CAS PubMed.
- B. S. Ludwig, H. Kessler, S. Kossatz and U. Reuning, Cancers, 2021, 13(7), 1711 CrossRef CAS PubMed.
- M. Barczyk, S. Carracedo and D. Gullberg, Cell Tissue Res., 2010, 339, 269–280 CrossRef CAS PubMed.
- R. O. Hynes, Cell, 2002, 110, 673–687 CrossRef CAS PubMed.
- F. Danhier, A. Le Breton and V. Préat, Mol. Pharm., 2012, 9, 2961–2973 CrossRef CAS PubMed.
- U. K. Marelli, F. Rechenmacher, T. R. Ali Sobahi, C. Mas-Moruno and H. Kessler, Front. Oncol., 2013, 3, 222 Search PubMed.
- N. Li, S. Qiu, Y. Fang, J. Wu and Q. Li, Biology, 2021, 10, 688 CrossRef CAS PubMed.
- T. G. Kapp, F. Rechenmacher, S. Neubauer, O. V. Maltsev, E. A. Cavalcanti-Adam, R. Zarka, U. Reuning, J. Notni, H. J. Wester, C. Mas-Moruno, J. Spatz, B. Geiger and H. Kessler, Sci. Rep., 2017, 7, 1–13 CrossRef PubMed.
- F. Karimi, A. J. O'Connor, G. G. Qiao and D. E. Heath, Adv. Healthc. Mater., 2018, 7, 1–28 CrossRef.
- X. Montet, M. Funovics, K. Montet-Abou, R. Weissleder and L. Josephson, J. Med. Chem., 2006, 49, 6087–6093 CrossRef CAS PubMed.
- X. Dong, Y. Yu, Q. Wang, Y. Xi and Y. Liu, Mol. Inf., 2017, 36(5–6), 1600069 CrossRef PubMed.
- D. Heckmann and H. Kessler, in Methods in Enzymology, 2007, vol. 426, pp. 463–503 Search PubMed.
- L. Alhalhooly, M. I. Confeld, S. O. Woo, B. Mamnoon, R. Jacobson, S. Ghosh, J. Kim, S. Mallik and Y. Choi, ACS Appl. Mater. Interfaces, 2022, 14, 7671–7679 CrossRef CAS PubMed.
- A. M. Sofias, Y. C. Toner, A. E. Meerwaldt, M. M. T. van Leent, G. Soultanidis, M. Elschot, H. Gonai, K. Grendstad, Å. Flobak, U. Neckmann, C. Wolowczyk, E. L. Fisher, T. Reiner, C. de L. Davies, G. Bjørkøy, A. J. P. Teunissen, J. Ochando, C. Pérez-Medina, W. J. M. Mulder and S. Hak, ACS Nano, 2020, 14, 7832–7846 CrossRef CAS PubMed.
- J. Z. Kechagia, J. Ivaska and P. Roca-Cusachs, Nat. Rev. Mol. Cell Biol., 2019, 20, 457–473 CrossRef CAS PubMed.
- V. Panzetta, D. Guarnieri, A. Paciello, F. Della Sala, O. Muscetti, L. Raiola, P. Netti and S. Fusco, ACS Biomater. Sci. Eng., 2017, 3, 1586–1594 CrossRef CAS PubMed.
- J.-P. Xiong, S. Thilo, R. Zhang, A. Joachimiak, M. Frech, S. L. Goodman and M. A. Arnaout, Science, 2002, 296, 151–155 CrossRef CAS PubMed.
- L. Wang, D. Pan, Q. Yan and Y. Song, Protein Sci., 2017, 26, 1124–1137 CrossRef CAS PubMed.
- Y.-P. Yu, Q. Wang, Y.-C. Liu and Y. Xie, Biomaterials, 2014, 35, 1667–1675 CrossRef CAS PubMed.
- A. Wang, K. Yue, Y. Wei, W. Zhong and G. Zhang, Pept. Sci., 2022, 115, e24302 CrossRef.
- D. Craig, M. Gao, K. Schulten and V. Vogel, Structure, 2004, 12, 2049–2058 CrossRef CAS PubMed.
- A. K. Malde, T. A. Hill, A. Iyer and D. P. Fairlie, Chem. Rev., 2019, 119, 9861–9914 CrossRef CAS PubMed.
- J. Bella and M. J. Humphries, BMC Struct. Biol., 2005, 5, 1–13 CrossRef PubMed.
- C. Pazzagli and S. Donnini, For. Immunopathol. Dis. Therap., 2014, 5, 233–241 Search PubMed.
- Y. Cheng and Y. Ji, Eur. J. Pharm. Sci., 2019, 128, 8–17 CrossRef CAS PubMed.
- H. Zhao, M. Wang, P. Zhou, Q. Wang, Z. Zhou, D. Wang, H. Yang and S. Yang, J. Mater. Sci., 2017, 52, 13356–13364 CrossRef CAS.
- N. Graf, D. R. Bielenberg, N. Kolishetti, C. Muus, J. Banyard, O. C. Farokhzad and S. J. Lippard, ACS Nano, 2012, 6, 4530–4539 CrossRef CAS PubMed.
- C. Zhan, B. Gu, C. Xie, J. Li, Y. Liu and W. Lu, J. Controlled Release, 2010, 143, 136–142 CrossRef CAS PubMed.
- A. Babu, N. Amreddy, R. Muralidharan, G. Pathuri, H. Gali, A. Chen, Y. D. Zhao, A. Munshi and R. Ramesh, Sci. Rep., 2017, 7, 14674 CrossRef PubMed.
- A. S. Yadav, N. N. V. Radharani, M. Gorain, A. Bulbule, D. Shetti, G. Roy, T. Baby and G. C. Kundu, Nanoscale, 2020, 12, 10664–10684 RSC.
- R. M. Schiffelers, G. A. Koning, T. L. M. Ten Hagen, M. H. A. M. Fens, A. J. Schraa, A. P. C. A. Janssen, R. J. Kok, G. Molema and G. Storm, J. Controlled Release, 2003, 91, 115–122 CrossRef CAS PubMed.
- A. Dayan, G. Fleminger and O. Ashur-Fabian, RSC Adv., 2018, 8, 9112–9119 RSC.
- M. Kulke and W. Langel, Proteins: Struct., Funct., Bioinf., 2020, 88, 679–688 CrossRef CAS PubMed.
- A. C. Kalli, T. Rog, I. Vattulainen, I. D. Campbell and M. S. P. Sansom, J. Membr. Biol., 2017, 250, 337–351 CrossRef CAS PubMed.
- X. Rui, M. Mehrbod, J. F. Van Agthoven, S. Anand, J. P. Xiong, M. R. K. Mofrad and M. A. Arnaout, J. Biol. Chem., 2014, 289, 23256–23263 CrossRef CAS PubMed.
- T. Gaillard, A. Dejaegere and R. H. Stote, Proteins: Struct., Funct., Bioinf., 2009, 76, 977–994 CrossRef CAS PubMed.
- T. C. Bidone, A. Polley, J. Jin, T. Driscoll, D. V. Iwamoto, D. A. Calderwood, M. A. Schwartz and G. A. Voth, Biophys. J., 2019, 116, 1000–1010 CrossRef CAS PubMed.
- F. Tavanti, A. Pedone and M. C. Menziani, Int. J. Mol. Sci., 2019, 20, 3539 CrossRef CAS PubMed.
- F. Ding, S. Radic, R. Chen, P. Chen, N. K. Geitner, J. M. Brown and P. C. Ke, Nanoscale, 2013, 5, 9162 RSC.
- H. Lopez and V. Lobaskin, J. Chem. Phys., 2015, 143, 243138 CrossRef PubMed.
- H. Ding and Y. Ma, Biomaterials, 2014, 35, 8703–8710 CrossRef CAS PubMed.
- Q. Shao and C. K. Hall, J. Phys.: Condens. Matter, 2016, 28, 414019 CrossRef PubMed.
- F. Tavanti, A. Pedone and M. C. Menziani, J. Phys. Chem. C, 2015, 119, 22172–22180 CrossRef CAS.
- G. Brancolini, A. Corazza, M. Vuano, F. Fogolari, M. C. Mimmi, V. Bellotti, M. Stoppini, S. Corni and G. Esposito, ACS Nano, 2015, 9, 2600–2613 CrossRef CAS PubMed.
- A. Hung, S. Mwenifumbo, M. Mager, J. J. Kuna, F. Stellacci, I. Yarovsky and M. M. Stevens, J. Am. Chem. Soc., 2011, 133, 1438–1450 CrossRef CAS PubMed.
- W. Lin, T. Insley, M. D. Tuttle, L. Zhu, D. A. Berthold, P. Král, C. M. Rienstra and C. J. Murphy, J. Phys. Chem. C, 2015, 119, 21035–21043 CrossRef CAS PubMed.
- F. Tavanti, A. Pedone and M. C. Menziani, New J. Chem., 2015, 39, 2474–2482 RSC.
- L. Li, Y. Yang, L. Wang, F. Xu, Y. Li and X. He, J. Mol. Biol., 2023, 435, 167771 CrossRef CAS PubMed.
- G. Brancolini and V. Tozzini, Curr. Opin. Colloid Interface Sci., 2019, 41, 66–73 CrossRef CAS.
- P. Siani and C. Di Valentin, Nanoscale, 2022, 14, 5121–5137 RSC.
- G. Brancolini, L. Bellucci, M. C. Maschio, R. Di Felice and S. Corni, Curr. Opin. Colloid Interface Sci., 2019, 41, 86–94 CrossRef CAS.
- H. Lee, Small, 2020, 16, 1906598 CrossRef CAS PubMed.
- G. Brancolini, D. Toroz and S. Corni, Nanoscale, 2014, 6, 7903–7911 RSC.
- G. Hosseinzadeh, A. Maghari, S. M. F. Farnia and A. A. Moosavi-Movahedi, J. Biomol. Struct. Dyn., 2018, 36, 3623–3635 CrossRef CAS PubMed.
- M.-E. Aubin-Tam, W. Hwang and K. Hamad-Schifferli, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 4095–4100 CrossRef CAS PubMed.
- O. Stueker, V. A. Ortega, G. G. Goss and M. Stepanova, Small, 2014, 10, 2006–2021 CrossRef CAS PubMed.
- E. Donadoni, G. Frigerio, P. Siani, S. Motta, J. Vertemara, L. De Gioia, L. Bonati and C. Di Valentin, ACS Biomater. Sci. Eng., 2023, 9, 6123–6137 CrossRef CAS PubMed.
- P. Siani, G. Frigerio, E. Donadoni and C. Di Valentin, J. Colloid Interface Sci., 2022, 627, 126–141 CrossRef CAS PubMed.
- P. M. Valencia, M. H. Hanewich-Hollatz, W. Gao, F. Karim, R. Langer, R. Karnik and O. C. Farokhzad, Biomaterials, 2011, 32, 6226–6233 CrossRef CAS PubMed.
- K. Abstiens, M. Gregoritza and A. M. Goepferich, ACS Appl. Mater. Interfaces, 2019, 11, 1311–1320 CrossRef CAS PubMed.
- W. Kawamura, Y. Miura, D. Kokuryo, K. Toh, N. Yamada, T. Nomoto, Y. Matsumoto, D. Sueyoshi, X. Liu, I. Aoki, M. R. Kano, N. Nishiyama, T. Saga, A. Kishimura and K. Kataoka, Sci. Technol. Adv. Mater., 2015, 16, 035004 CrossRef PubMed.
- J. Li, Y. Chen, N. Kawazoe and G. Chen, Nano Res., 2018, 11, 1247–1261 CrossRef CAS.
- G. Su, H. Jiang, B. Xu, Y. Yu and X. Chen, Mol. Pharm., 2018, 15, 5019–5030 CrossRef CAS PubMed.
- T. Rajh, N. M. Dimitrijevic, M. Bissonnette, T. Koritarov and V. Konda, Chem. Rev., 2014, 114, 10177–10216 CrossRef CAS PubMed.
- W. Chen, J. Lou, J. Hsin, K. Schulten, S. C. Harvey and C. Zhu, PLoS Comput. Biol., 2011, 7, e1001086 CrossRef CAS PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- S. Kim, J. Lee, S. Jo, C. L. Brooks, H. S. Lee and W. Im, J. Comput. Chem., 2017, 38, 1879–1886 CrossRef CAS PubMed.
- R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. MacKerell, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS PubMed.
- K. Vanommeslaeghe and A. D. MacKerell, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- I. Soteras Gutiérrez, F. Y. Lin, K. Vanommeslaeghe, J. A. Lemkul, K. A. Armacost, C. L. Brooks and A. D. MacKerell, Bioorg. Med. Chem., 2016, 24, 4812–4825 CrossRef PubMed.
- J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda and W. Im, J. Chem. Theory Comput., 2016, 12, 405–413 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- E. Neria, S. Fischer and M. Karplus, J. Chem. Phys., 1996, 105, 1902–1921 CrossRef CAS.
- S. R. Durell, B. R. Brooks and A. Ben-Naim, J. Phys. Chem., 1994, 98, 2198–2202 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- R. W. Hockney, S. P. Goel and J. W. Eastwood, J. Comput. Phys., 1974, 14, 148–158 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- G. Fazio, L. Ferrighi and C. Di Valentin, J. Phys. Chem. C, 2015, 119, 20735–20746 CrossRef CAS.
- D. Selli, G. Fazio and C. Di Valentin, J. Chem. Phys., 2017, 147, 164701 CrossRef PubMed.
- D. Selli, S. Motta and C. Di Valentin, J. Colloid Interface Sci., 2019, 555, 519–531 CrossRef CAS PubMed.
- D. Selli, M. Tawfilas, M. Mauri, R. Simonutti and C. Di Valentin, Chem. Mater., 2019, 31, 7531–7546 CrossRef CAS PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- E. G. Brandt and A. P. Lyubartsev, J. Phys. Chem. C, 2015, 119, 18110–18125 CrossRef CAS.
- M. Matsui and M. Akaogi, Mol. Simul., 1991, 6, 239–244 CrossRef.
- P. Siani, S. Motta, L. Ferraro, A. Dohn and C. Di Valentin, J. Chem. Theory Comput., 2020, 16, 6560–6574 CrossRef CAS PubMed.
- E. Donadoni, P. Siani, G. Frigerio and C. Di Valentin, Nanoscale, 2022, 14, 12099–12116 RSC.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J. E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1998, 76, 637 CrossRef.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- P. J. Steinbach and B. R. Brooks, J. Comput. Chem., 1994, 15, 667–683 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, Boca Raton, 2021 Search PubMed.
- A. Levy, Molecular dynamics study of the interaction between the anticancer drug doxorubicin and a functionalized TiO2 nanocarrier, University of Milano-Bicocca, 2020 Search PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ‘t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J Mol Graph, 1996, 14, 33–38 CrossRef CAS PubMed.
- C. H. Rycroft, VORO++: A three-dimensional Voronoi cell library in C++, Lawrence Berkeley National Lab, Berkeley CA, 2009, vol. 19 Search PubMed.
- T. Kohonen, Neural Networks, 2013, 37, 52–65 CrossRef PubMed.
- S. Motta, C. Minici, D. Corrada, L. Bonati and A. Pandini, PLoS Comput. Biol., 2018, 14, e1006021 CrossRef PubMed.
- S. Motta, A. Pandini, A. Fornili and L. Bonati, J. Chem. Theory Comput., 2021, 17, 2080–2089 CrossRef CAS PubMed.
- T. Li, S. Motta, A. O. Stevens, S. Song, E. Hendrix, A. Pandini and Y. He, JACS Au, 2022, 2, 1935–1945 CrossRef CAS PubMed.
- E. Hendrix, S. Motta, R. F. Gahl and Y. He, J. Phys. Chem. B, 2022, 126, 7934–7942 CrossRef CAS PubMed.
- S. Motta, L. Callea, L. Bonati and A. Pandini, J. Chem. Theory Comput., 2022, 18, 1957–1968 CrossRef CAS PubMed.
- R. Wehrens and L. M. C. Buydens, J Stat Softw, 2007, 21, 1–19 Search PubMed.
- R. Wehrens and J. Kruisselbrink, J Stat Softw, 2018, 87, 1–18 Search PubMed.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS.
- D. Jakubec and J. Vondrášek, J. Chem. Theory Comput., 2019, 15, 2635–2648 CrossRef CAS PubMed.
- J. Damjanovic, J. Miao, H. Huang and Y.-S. Lin, Chem. Rev., 2021, 121, 2292–2324 CrossRef CAS PubMed.
- A. Spitaleri, S. Mari, F. Curnis, C. Traversari, R. Longhi, C. Bordignon, A. Corti, G.-P. Rizzardi and G. Musco, J. Biol. Chem., 2008, 283, 19757–19768 CrossRef CAS PubMed.
- A. E. Wakefield, W. M. Wuest and V. A. Voelz, J. Chem. Inf. Model., 2015, 55, 806–813 CrossRef CAS PubMed.
- R. S. Silva, L. M. P. Souza, R. K. M. Costa, F. R. Souza and A. S. Pimentel, J. Biomol. Struct. Dyn., 2023, 41, 10546–10557 CrossRef CAS PubMed.
- Z. Cournia, B. Allen and W. Sherman, J. Chem. Inf. Model., 2017, 57, 2911–2937 CrossRef CAS PubMed.
- S. Kostidis, A. Stavrakoudis, N. Biris, D. Tsoukatos, C. Sakarellos and V. Tsikaris, J. Pept. Sci., 2004, 10, 494–509 CrossRef CAS PubMed.
- H. Othman, H. Ben Messaoud, O. Khamessi, H. Ben-Mabrouk, K. Ghedira, A. Bharuthram, F. Treurnicht, I. Achilonu, Y. Sayed and N. Srairi-Abid, Front Mol Biosci, 2022, 9, 834857 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05123d |
| This journal is © The Royal Society of Chemistry 2024 |