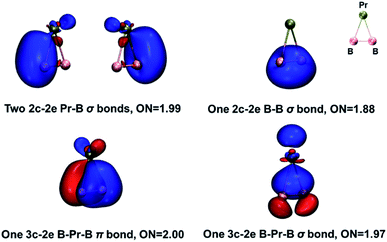Open Access Article
Open Access ArticleThe smallest 4f-metalla-aromatic molecule of cyclo-PrB2− with Pr–B multiple bonds†‡
Zhen-Ling
Wang§
a,
Teng-Teng
Chen§
b,
Wei-Jia
Chen
b,
Wan-Lu
Li
a,
Jing
Zhao
 a,
Xue-Lian
Jiang
c,
Jun
Li
a,
Xue-Lian
Jiang
c,
Jun
Li
 c,
Lai-Sheng
Wang
c,
Lai-Sheng
Wang
 *b and
Han-Shi
Hu
*b and
Han-Shi
Hu
 *a
*a
aDepartment of Chemistry & Key Laboratory of Organic Optoelectronics and Molecular Engineering of the Ministry of Education, Tsinghua University, Beijing, 100084, China. E-mail: hshu@mail.tsinghua.edu.cn
bDepartment of Chemistry, Brown University, Providence 02912, Rhode Island, USA. E-mail: Lai-Sheng_Wang@brown.edu
cDepartment of Chemistry, Southern University of Science and Technology, Shenzhen 518055, China
First published on 8th August 2022
Abstract
The concept of metalla-aromaticity proposed by Thorn–Hoffmann (Nouv. J. Chim. 1979, 3, 39) has been expanded to organometallic molecules of transition metals that have more than one independent electron-delocalized system. Lanthanides, with highly contracted 4f atomic orbitals, are rarely found in multiply aromatic systems. Here we report the discovery of a doubly aromatic triatomic lanthanide-boron molecule PrB2− based on a joint photoelectron spectroscopy and quantum chemical investigation. Global minimum structural searches reveal that PrB2− has a C2v triangular structure with a paramagnetic triplet 3B2 electronic ground state, which can be viewed as featuring a trivalent Pr(III,f2) and B24−. Chemical bonding analyses show that this cyclo-PrB2− species is the smallest 4f-metalla-aromatic system exhibiting σ and π double aromaticity and multiple Pr–B bonding characters. It also sheds light on the formation of the rare B24− tetraanion by the high-lying 5d orbitals of the 4f-elements, completing the isoelectronic B24−, C22−, N2, and O22+ series.
1 Introduction
The concept of aromaticity and its role in stabilizing molecules, clusters and materials have been well developed in chemistry. Classical aromaticity usually refers to delocalized (p–p)π systems in unsaturated cyclic hydrocarbons such as benzene. In recent years, the concept of multiple aromaticity has been developed, which involves multiple independent delocalized electron systems (σ, π, δ, or even φ) coexisting in the same molecular systems. The first molecule with σ + π double aromaticity was observed in C6H3+ in 1979.1 In the same year, a seminal paper by Thorn and Hoffmann2 introduced transition metals into the field of aromaticity, which broadened the scope of this subject into “metalla-aromatic chemistry”. In this scenario, a carbon atom of an aromatic hydrocarbon is substituted by a transition metal atom, such that the bonding situation changes into a (d-p)π system. Since then, numerous transition metal compounds with metalla-aromaticity have been synthesized.3,4 Additionally, many metal clusters have been found to be multiply aromatic, e.g., Mo3S44+, Al42−, Li3+, Hg46−, Ta3O3−, Hf3, and U4(NH)4.5–16 However, organolanthanide systems with metalla-aromaticity are rare because the 5d orbitals of lanthanides are energetically too high, while the 4f orbitals are radially too contracted to participate in effective bonding with carbon-based ligands.Compared with its carbon neighbour, the electron-deficient boron element possesses higher 2p-orbital energy and larger 2s-2p orbital radii than carbon,17,18 which favours efficient bonding with energetically high-lying 5d orbitals of lanthanides, as exemplified by a number of lanthanide boride materials.19 Joint photoelectron spectroscopy (PES) and quantum chemical studies have shown that size-selected anionic boron clusters (Bn−) are planar or quasi-planar up to B38−.20 All the planar boron clusters feature multi-centre delocalized σ and π bonds over the boron plane, which is a direct consequence of boron's electron efficiency.21–25 These delocalized σ and π bonds give rise to multiple aromaticity, which stabilizes the planar structures and leads to the concept of all-boron analogues (e.g. borophene) of polycyclic aromatic hydrocarbons.23 Metal-doped boron clusters have recently become a new direction in the study of boron chemistry. It has been discovered that transition metals can be doped into the plane of boron clusters due to the strong metal–boron bonding.26–28 The d AOs of transition metals are found to participate in electron delocalization in doped planar boron clusters, resulting in the discovery of aromatic metal-centred borometallic wheels, M©Bn− (n = 8–10).29–34 Very recently, it has been shown that the Re atom can be positioned on the edge of small planar boron clusters, resulting in the realization of the first cyclic Mobius aromatic metalla-borocycle in ReB4− (ref. 35) and the metalla-benzene of ReB6−.36
Lanthanides (Ln = La–Lu) are a distinct group of elements in the Periodic Table in terms of chemical bonding. On the one hand, they have rather contracted and low-energy 4f AOs that can hardly participate in covalent bonding due to the quantum primogenic effect.37 On the other hand, promoting electrons from 4f to high-lying 5d AOs requires significant energies even though their 5d AOs can contribute to chemical bonding because of apt radial extension.38 Thus, the covalent bonding capability of lanthanides is rather limited in comparison with transition metals, especially in their participation in electron delocalization and multiple bonding. It is rare to find f-block atoms in aromatic systems,8,39–41 let alone multiple aromaticity. A representative case is the triangular La3− molecule, which is shown to display σ + π double aromaticity formed by 5d orbitals.42,43 While compounds with multiple bonds between lanthanides and main group elements, such as Ln![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, Ln
C, Ln![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, and Ln
N, and Ln![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,44,45 have been synthesized,46,47 Ln–B multiple bonds have been rarely studied so far.40 Yet recent studies on lanthanide boride clusters have discovered some new structures like half-sandwiches,48 inverse sandwiches,49–51 inverse triple-deckers,52 and spherical trihedral cages,53 very different from transition metal borides. In most of these systems, the lanthanide atoms interact with a large boron moiety to form delocalized multi-centred chemical bonds, resulting in Ln–B bonds with average bond orders smaller than one.
O,44,45 have been synthesized,46,47 Ln–B multiple bonds have been rarely studied so far.40 Yet recent studies on lanthanide boride clusters have discovered some new structures like half-sandwiches,48 inverse sandwiches,49–51 inverse triple-deckers,52 and spherical trihedral cages,53 very different from transition metal borides. In most of these systems, the lanthanide atoms interact with a large boron moiety to form delocalized multi-centred chemical bonds, resulting in Ln–B bonds with average bond orders smaller than one.
Here we report a PES and quantum chemical investigation of the triatomic PrB2− molecule, which is found to have a cyclo-triangular C2v structure with double σ and π aromaticity. This molecule can be viewed as a trivalent Pr(III,f2) coordinated by a so-far unidentified B24− ligand. Chemical bonding analyses show that this triatomic system is the smallest metalla-aromatic ring containing a magnetic lanthanide atom and two Pr–B multiple bonds.
2 Experimental and computational methods
2.1. Experimental methods
The experiment was carried out using a magnetic-bottle PES apparatus coupled with a laser vaporization supersonic cluster source and a time-of-flight mass spectrometer.54,55 Briefly, the PrB2− anion was generated by laser ablation of a Pr–B disc target prepared by cold-pressing a mixed powder of Pr and 11B (97% enriched). Clusters formed in the nozzle were entrained by a He carrier gas seeded with 10% argon, undergoing a supersonic expansion. A series of PrBn− clusters were produced and the PrB2− of current interest was mass-selected, decelerated, and then photodetached by the 193 nm (6.424 eV) radiation from an ArF excimer laser and the third harmonics (355 nm, 3.496 eV) from an Nd:YAG laser. The photoelectron spectra were calibrated using the known transitions of Bi−. The energy resolution of the apparatus was about 2.5%, that is, ∼25 meV for 1 eV electrons.2.2. Computational methods
Quantum chemical calculations were performed by using ADF 2019.1,56,57 Molpro 2018,58 and Gaussian 16 programs.59 Unless otherwise specified, ADF calculations were done at PBE0/TZP level60,61 with scalar relativistic ZORA correction62 and 1s–4d electrons frozen for Pr; Gaussian calculations were performed with PBE0 functional and quasi-relativistic effective core potential (ECP) of MWB28 used for Pr,63,64 together with MWB28 basis set for Pr and the cc-pVTZ basis set65 for light elements; Molpro calculations utilized MWB28 ECP and MWB28_ANO basis set for Pr, and the cc-pVTZ basis set for B.Global geometry minimum searches for PrB2− were carried out by ADF 2019.1, with three chemically reasonable starting states (linear Pr–B–B, Cs triangle, and C2v triangle) and different spin multiplicities. A C2v triangle with 3B2 electronic state is the global minimum. We also performed two confirmative geometry optimizations for PrB2− using the optimized triplet C2v triangle as an initial guess: using ADF with non-collinear ZORA spin–orbit coupling correction,66 and using Gaussian with DKH2 relativistic Hamiltonian,67,68 PBE0 functional, SARC-DKH2 basis set for Pr,69 and cc-pVTZ basis set for B. The neutral PrB2 was optimized by ADF at doublet and quartet spin states. PBE0 geometries were used for all following calculations. CASSCF-(14o, 12e) calculations were performed by Molpro to verify the reliability of those DFT methods. To compared with the PES, the adiabatic detachment energy (ADE) and the first vertical detachment energy (VDE1) were calculated at SAOP/TZP level70 without a frozen core by ADF and at CCSD(T) level by Molpro. TDDFT excitation energies of PrB2 were added to VDE1 to obtain higher VDEs, and those calculations were carried out by ADF at SAOP/TZP level, with no frozen core used. Atomic valence-orbital radial-densities of Pr and B were calculated by ADF 2019.1 with PBE functional.71 The broken spin state was also computed by ADF with care.
Most calculations related to magnetic properties of PrB2−, including electron localization function (ELF), diamagnetic anisotropy,72 nucleus independent chemical shift (NICS),73 and the input for AICD and GIMIC program,74,75 were obtained through Gaussian. Those calculations were done properly at the triplet state and as the molecule is not fully symmetric, we picked the centre of the induced-current at 1.5 a0 above the molecule plane (Fig. 6(b), coordinates in Table S5‡) as the centre of NICS and integrated ring-current76 calculations. Ring-current integrating planes reach that centre and are orthogonal to the intersected chemical bonds. For readers' reference, NICS values and the GIMIC current strengths were also computed by BHandHLYP and B3LYP functionals.77,78 The ADF code was used to calculate NICS values with noncollinear spin–orbit effect and a TZP all-electron basis set. These magnetic properties were also computed for two reference molecules, B3− and C3H3+, at the same level.
For further discussions on chemical bonding, we performed an energy decomposition analysis from the natural orbitals for chemical valence79 (EDA-NOCV) by ADF, a principal interaction orbital analysis80 (PIO) by Gaussian 16 and the PIO package, and an adaptive natural density partitioning analysis81 (AdNDP) by Gaussian 16 and Multiwfn 3.6,82 all on PrB2−. Bond orders of PrB2− were computed by ADF, including Mayer, Gopinathan–Jug, and Nalewajski–Mrozek indices.83–86
3 Results and discussions
3.1. Photoelectron spectrum
The 355 nm spectrum of PrB2− (Fig. 1(a)) exhibits a sharp and intense ground-state detachment transition (X), yielding an adiabatic detachment energy (ADE) of 1.72 eV, which is also the electron affinity (EA) of neutral PrB2. A closely-spaced band A at 1.90 eV is observed at 355 nm, but less resolved at 193 nm (Fig. 1(b)). Following a small energy gap, a band B at 2.29 eV is observed with a relatively weak intensity at 355 nm, but it becomes the most intense band in the 193 nm spectrum. A weak and broad band C at 3.13 eV is not clearly resolved at 355 nm, but better defined at 193 nm. Beyond band C, the PES signal is almost continuous, and a band D at around 3.9 eV is tentatively labelled for the sake of discussion. The vertical detachment energies (VDEs) of the observed spectral bands for PrB2− are given in Table 1, where they are compared with the theoretical results.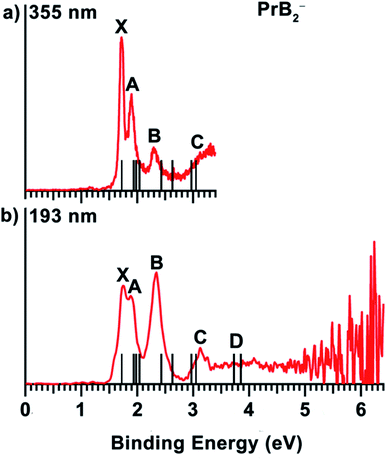 | ||
| Fig. 1 The photoelectron spectra of PrB2− at (a) 355 nm (3.496 eV) and (b) 193 nm (6.424 eV). The vertical bars represent the calculated VDEs (see Table 1). | ||
| VDE (eV) (expt.) | VDE (eV) (comput.)a | State | Configurationb,c | |
|---|---|---|---|---|
| a The calculated VDEs at the level of SAOP/TZP (at the PBE0 geometry) using ADF code are systematically shifted up by 0.20 eV to align calculated VDE1 value with band X. b “↑” and “↓” in the electron configurations stand for α and β electrons, respectively. c The α-MOs 5a1 and 4b2 mainly arise from quasi-atomic Pr(III, f2) configuration. | ||||
| PrB2− | 3B2 | {…4a123b222b12 [5a1↑4b2↑] 5a1↓6a1↑7a1↑6a1↓} | ||
| X | 1.72 | 1.72 | 4B2 | {…4a123b222b12 [5a1↑4b2↑] 5a1↓6a1↑7a1↑6a10} |
| A | 1.90 | 1.95 | 4B2 | {…4a123b222b12 [5a1↑4b2↑] 5a106a1↑7a1↑6a1↓} |
| 1.98 | 2B2 | {…4a123b222b12 [5a1↑4b2↑] 5a1↓6a1↑7a106a1↓} | ||
| 2.05 | 2B2 | {…4a123b222b12 [5a1↑4b2↑] 5a1↓6a107a1↑6a1↓} | ||
| B | 2.29 | 2.42 | 4A2 | {…4a123b222b1↑ [5a1↑4b2↑] 5a1↓6a1↑7a1↑6a1↓} |
| 2.64 | 2A2 | {…4a123b222b1↓ [5a1↑4b2↑] 5a1↓6a1↑7a1↑6a1↓} | ||
| C | 3.13 | 2.98 | 2B2 | {…4a123b222b12 [5a10 4b2↑] 5a1↓6a1↑7a1↑6a1↓} |
| 3.07 | 2A1 | {…4a123b222b12 [5a1↑4b20] 5a1↓6a1↑7a1↑6a1↓} | ||
| D | ∼3.9 | 3.72 | 4A1 | {…4a123b2↑2b12 [5a1↑4b2↑] 5a1↓6a1↑7a1↑6a1↓} |
| 3.88 | 2A1 | {…4a123b2↓2b12 [5a1↑4b2↑] 5a1↓6a1↑7a1↑6a1↓} | ||
3.2. Global-minimum structure searches
The triatomic PrB2− can take four types of structures: linear Pr–B–B and B–Pr–B, and bent Cs and C2v triangles. The linear B–Pr–B is ruled out because the B–B bond is significantly stronger than the Pr–B bond. Therefore, only the linear Pr–B–B (C∞v), Cs scalene triangle, and C2v unilateral triangle isomers are likely. We conducted systematic geometry optimizations for these initial structures with various electronic states and different spin multiplicities (singlet, triplet, and quintet). It is found that the most stable structure of PrB2− within 20 kcal mol−1 is the unilateral triangle with C2v symmetry and a triplet 3B2 ground state (Fig. 2). The C2v PrB2− consists of a Pr(III) f2 valence electron configuration and strongly spin-polarized (π⊥)2(π‖)2(σBB)2 bonding orbitals (Fig. 4 and Table S1‡), where π⊥ and π‖ are the out-of-plane (perpendicular) and in-plane components of the B–B π orbitals, respectively. The most stable structure of the neutral PrB2 molecule with a quartet 4B2 state is found to be similar in structure to that of the PrB2− anion with very little structural change (Fig. 2), which is 15 kcal mol−1 below any doublet state of the neutral. There is a small decrease of the B–B bond length and a small increase of the Pr–B bond length in neutral PrB2. The calculated bond lengths and bond angles are given in Fig. 2.3.3. Comparison between the experimental and computational results
The electronic structures of PrB2− and PrB2 are calculated using several methods of density functional theory (DFT) and wavefunction theory (WFT). More computational details are given in the ESI‡. We have computed the ADE and VDEs of PrB2− to compare with the experimental photoelectron spectra (Fig. 1). The VDEs were calculated using the ΔSCF-TDDFT approach.87,88 Based on the optimized geometry of the PrB2− anion and time-dependent DFT, vertical excitation energies of PrB2 are added to the first VDE (VDE1) to obtain higher VDEs.Single-configurational DFT at the PBE0/TZP level using ADF code and CCSD(T) calculations using MOLPRO code with the Stuttgart ECP28MWB effective core potential (ECP) for Pr, the cc-pVTZ basis set for B, and SDD basis set for Pr yielded VDE1/ADE of 1.52/1.37 eV and 1.50/1.41 eV, respectively. For better comparison with experiment, we systematically shifted the predicted VDEs in Table 1 to align the calculated VDE1 value with band X. Multi-configurational CASSCF calculations (Fig. S1, S2, and Tables S2, S3 in ESI‡) indicate that the multi-electron wavefunctions of PrB2− and PrB2 are both dominated by a single configuration with the configuration-interaction (CI) weights of 79.6% and 82.1%, respectively, while all other configurations each contributes less than 2%. Thus, these systems can be approximately described by single-configurational methods such as DFT and CCSD(T).
As shown in Table 1, the VDE1 of X band is derived from removing the β electron from the 6a1 molecular orbital (MO), while the next band A corresponds to three detachment channels: 5a1β, 7a1α, and 6a1α. Band B comes from the electron removal from the 2b1 α- and β-MOs. All X, A and B bands correspond to removing the electrons from the B2 moiety: the B–B 2pσ MO and the vertical (π⊥) and horizontal (π‖) B–B 2pπ MOs, which all interact with 6s or 5d orbitals of Pr in an in-plane or out-of-plane fashion (Fig. 4). These bands have relatively high intensities due to the large detachment cross sections of the B 2p orbitals. The fact that the 6a1β and 5a1β electrons are detached before 7a1α and 6a1α is due to the favoured exchange interaction with the paramagnetic, quasi-atomic Pr f2 configuration. Detachments of the 4f electrons in the singly occupied molecular orbitals (SOMOs), 5a1 and 4b2, give rise to band C, which has relatively low intensity. Electron detachment from 3b2 α- and β-MOs derived from the B–B  antibonding orbital (Fig. 4) account tentatively for the signals near 3.9 eV of band D. When an electron is detached from a doubly occupied MOs (α- and β-MOs with little spin polarization), it can result in either a doublet or quartet final state. Since the quartet state has a higher exchange energy, its VDE is usually lower than its doublet counterpart, as one can see in bands B and D. It should also be noted that, as is common in strongly correlated f-systems,89,90 generalized Koopmans' theorem (GKT) is violated even qualitatively, making it difficult to assign PES transitions based on GKT with simple Kohn–Sham (K–S) MO energies without calculating the actual initial and final state energies of the electron detachment process. Overall, considering the complicated electron correlation and limited basis sets, the calculated VDEs from ΔSCF-TDDFT approach agree well with the experimental data, confirming the C2v global minimum structure and the ground state of PrB2−.
antibonding orbital (Fig. 4) account tentatively for the signals near 3.9 eV of band D. When an electron is detached from a doubly occupied MOs (α- and β-MOs with little spin polarization), it can result in either a doublet or quartet final state. Since the quartet state has a higher exchange energy, its VDE is usually lower than its doublet counterpart, as one can see in bands B and D. It should also be noted that, as is common in strongly correlated f-systems,89,90 generalized Koopmans' theorem (GKT) is violated even qualitatively, making it difficult to assign PES transitions based on GKT with simple Kohn–Sham (K–S) MO energies without calculating the actual initial and final state energies of the electron detachment process. Overall, considering the complicated electron correlation and limited basis sets, the calculated VDEs from ΔSCF-TDDFT approach agree well with the experimental data, confirming the C2v global minimum structure and the ground state of PrB2−.
3.4. The electronic structure and chemical bonding of PrB2−
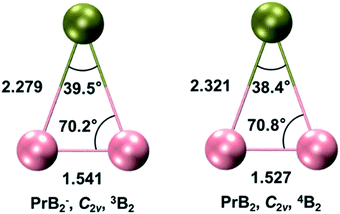
Systematic theoretical analyses have been performed to gain insights into the electronic structure and chemical bonding of PrB2−. Fig. 3 depicts the radial distribution probability D(r) = r2R(r)2 of the Pr3+ 5d and 4f orbitals as well as the B 2s and 2p orbitals lying at 2.3 Å (the average Pr–B distance in PrB2− and PrB2). The Pr 4f is much more contracted (rmax ∼0.34 Å) than the 5d orbitals (rmax ∼1.03 Å) in the radial distribution, leading to nearly negligible orbital overlap between Pr 4f and B 2s/2p. In contrast, the Pr 5d orbitals have significant orbital overlap with B 2s/2p, which accounts for the covalent bonding interaction between Pr 5d and B 2s-2p hybrid orbitals. It is worth noting that B 2p orbitals are radially quite contracted because of the quantum primogenic effect.91 As a result, both the 2p and 2s orbitals of B atom can overlap with Pr 5d orbitals.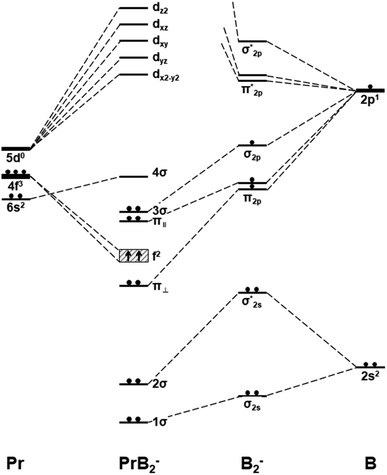 | ||
| Fig. 4 Schematic orbital energy levels of triangle Pr(η2-B2)−, B2−, and Pr. The symbol π‖ and π⊥ denotes the in-plane and out-of-plane π MOs, and their respective orbital interaction with Pr 5dx2−y2 and 5dxz orbitals are shown in Scheme 1. | ||
Fig. 4 presents the schematic energy-level correlation diagram between the presumed fragments Pr and B2−. From group theory, with molecular plane σyz of C2v symmetry, the Pr AOs transform as 6s (a1) as well as 5dz2 (a1), 5dxz (b1), 5dyz (b2), 5dxy (a2) and 5dx2-y2 (a1), respectively. As shown in Fig. 3, the Pr 4f orbitals are too contracted to overlap with B2 ligand orbitals, so they span a narrow band consisting of 4fz3 (a1), 4fxz2 (b1), 4fyz2 (b2), 4fxyz (a2), 4fz(x2-y2) (a1), 4fx(x2-y2) (b1), 4fy(x2−y2) (b2), with the 5a1 and 4b2 α-MOs occupied in the f2 electron configuration. As the B(2s22p1) atom has three valence electrons, from the well-known Mulliken qualitative MO levels of diatomic molecule (Fig. 4), one can obtain the familiar 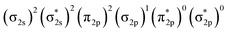 electron configuration for B2− ion, where 2s/2p indicating the composing atomic orbitals (AOs) and asterisk (*) denotes antibonding MOs.
electron configuration for B2− ion, where 2s/2p indicating the composing atomic orbitals (AOs) and asterisk (*) denotes antibonding MOs.
In Fig. 4, σ2s of B2− is rather low in energy compared with the valence AOs of Pr; therefore, it participates weakly in bonding with 6s as well as 5dz2/5dx2−y2 when Pr is coordinated by B2−. However, as the size of B 2s is as large as the 2p orbitals based on the radial distribution function (Fig. 3), B 2s can interact with Pr 5d orbitals when they are not too far apart energetically. Indeed, the antibonding 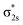 MO in B2− forms the bonding 3b2 MO upon interaction with Pr 5dyz AOs. The two degenerate π2p MOs of B2− also interact with the Pr 5d AOs, in two different ways: the π2p MO perpendicular to the molecular plane (π⊥) forms a 3c–2e π bonding 2b1 MO with Pr 5dxz while the π2p MO in the plane of the molecule (π‖) forms a 3c–2e σ bonding 6a1 MO with Pr 5dz2/5dx2−y2 AOs, as is illustrated in Scheme 1. The σ2p MO of B2− is slightly stabilized by interacting with Pr 6s as well as 5dz2/5dx2−y2 AOs. As a result, the Pr 6s AO has been pushed up significantly by interacting with the σ2s and σ2p MOs of B2− with the same symmetry, forming the lowest unoccupied MO (4σ). Overall, the orbital interaction between σ2p and π2p MOs of B2− and Pr 5d/6s AOs leads to significant bonding stabilization of π⊥, π‖, and 3σ MOs of PrB2−, which causes Pr to lose three electrons to fill the B-2p based MOs to form the electron configuration of (π⊥)2(π‖)2(σBB)2 PrIII(4f26s0). Therefore, the PrB2− molecule can be described as composed of a +3-oxidation-state Pr3+ (i.e., PrIII) with f2-configuration and formally a coordinated B24− tetraanion, namely PrIII[B24−]. Interestingly, the B24− tetraanion is isoelectronic with the C22−, N2, and O22+ diatomic moiety that has the well-known
MO in B2− forms the bonding 3b2 MO upon interaction with Pr 5dyz AOs. The two degenerate π2p MOs of B2− also interact with the Pr 5d AOs, in two different ways: the π2p MO perpendicular to the molecular plane (π⊥) forms a 3c–2e π bonding 2b1 MO with Pr 5dxz while the π2p MO in the plane of the molecule (π‖) forms a 3c–2e σ bonding 6a1 MO with Pr 5dz2/5dx2−y2 AOs, as is illustrated in Scheme 1. The σ2p MO of B2− is slightly stabilized by interacting with Pr 6s as well as 5dz2/5dx2−y2 AOs. As a result, the Pr 6s AO has been pushed up significantly by interacting with the σ2s and σ2p MOs of B2− with the same symmetry, forming the lowest unoccupied MO (4σ). Overall, the orbital interaction between σ2p and π2p MOs of B2− and Pr 5d/6s AOs leads to significant bonding stabilization of π⊥, π‖, and 3σ MOs of PrB2−, which causes Pr to lose three electrons to fill the B-2p based MOs to form the electron configuration of (π⊥)2(π‖)2(σBB)2 PrIII(4f26s0). Therefore, the PrB2− molecule can be described as composed of a +3-oxidation-state Pr3+ (i.e., PrIII) with f2-configuration and formally a coordinated B24− tetraanion, namely PrIII[B24−]. Interestingly, the B24− tetraanion is isoelectronic with the C22−, N2, and O22+ diatomic moiety that has the well-known 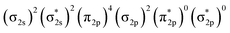 electron configuration, despite the much higher σ2p and π2p orbital energies of B24− due to smaller electronegativity of B than C, N and O. The spin-polarized α and β sets of MOs and the contour surfaces of the PrB2− valence MOs are shown in Table 2. Therefore, there are five sets of interactions among the three atoms of PrB2−, including the α + β sets of 4a1, 3b2, 2b1, as well as the more spin polarized 6a1α + 6a1β and 7a1α + 5a1β.
electron configuration, despite the much higher σ2p and π2p orbital energies of B24− due to smaller electronegativity of B than C, N and O. The spin-polarized α and β sets of MOs and the contour surfaces of the PrB2− valence MOs are shown in Table 2. Therefore, there are five sets of interactions among the three atoms of PrB2−, including the α + β sets of 4a1, 3b2, 2b1, as well as the more spin polarized 6a1α + 6a1β and 7a1α + 5a1β.
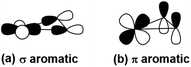 | ||
| Scheme 1 The σ-type and π-type orbital interaction between Pr-5d and B-2p orbitals, leading to (a) σ- and (b) π- metalla-aromaticity, respectively. | ||
It should be noted that the nearly degenerate 4f MO levels are stabilized in Pr(III) and slightly split due to the presence of B2−, similar to the crystal field splitting. As a result, the lowest energy state corresponds to the two 4f electrons staying in two specific 4f MOs, i.e., the 5a1α and 4b2α sets, forming a paramagnetic ground state. The calculated magnetic exchange coupling constant 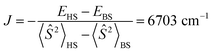 , where EHS and EBS are the energies of the triplet high-spin (HS) and broken-symmetry (BS) singlet states. However, in DFT calculations, due to the self-interaction error (SIE)92 and hybrid mixing of Hartree–Fock exchange, virtual 4f orbitals are much higher in energy, resulting in only two occupied 4f α-MOs having relatively low energies.
, where EHS and EBS are the energies of the triplet high-spin (HS) and broken-symmetry (BS) singlet states. However, in DFT calculations, due to the self-interaction error (SIE)92 and hybrid mixing of Hartree–Fock exchange, virtual 4f orbitals are much higher in energy, resulting in only two occupied 4f α-MOs having relatively low energies.
Interestingly, the linear Pr–B–B isomer shares a similar bonding pattern with the C2v global minimum (Fig. S4–S5 and Table S7‡). The σ2s MO is still too low in energy to be bonded with Pr, and the bonding 6σ MO is formed by 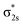 . The two π2p MOs in B2− form a pair of degenerate π bonding MOs with Pr 5d AOs. Also, the 6s AO in Pr is now non-bonded and occupied in the 7σα MO, while σ2p interacts with a 5d AO forming a 7σβ bonding MO. The Pr oxidation state of this linear isomer is thus +2. As the 6s electron is unpaired, the total bonding interaction in the linear structure is weaker than that in the triangle structure, implying that a linear PrB2− would tend to bend into a triangle arrangement by the second-order Jahn–Teller effect.93
. The two π2p MOs in B2− form a pair of degenerate π bonding MOs with Pr 5d AOs. Also, the 6s AO in Pr is now non-bonded and occupied in the 7σα MO, while σ2p interacts with a 5d AO forming a 7σβ bonding MO. The Pr oxidation state of this linear isomer is thus +2. As the 6s electron is unpaired, the total bonding interaction in the linear structure is weaker than that in the triangle structure, implying that a linear PrB2− would tend to bend into a triangle arrangement by the second-order Jahn–Teller effect.93
The global minimum of PrB2− is found to be doubly aromatic, as verified by various analyses including the canonical K–S MOs, adaptive natural density partitioning81 (AdNDP) analysis, induced ring-current strength,76 the anisotropy of the induced current density75 (AICD), the diamagnetic anisotropy,72 the nucleus-independent chemical shift (NICS)73 and the bifurcation analysis of electron localization function (ELF) of the σ and π electrons.94 In the K–S MOs, there are two delocalized 3c–2e MOs consisting of Pr and B2 moity: a σ bonding MO of 6a1 and a π bonding MO of 2b1. These two delocalized 3c–2e bonding MOs of 6a1 and 2b1 in Table 2 can also be verified by the AdNDP results (Fig. 5), where the first row describes three localized σ bonds and the second row represents delocalized σ and π bonds within the PrB2 framework. Therefore, PrB2− has two independent delocalized systems each containing two electrons, satisfying the 4n + 2 Hückel rule (n = 0) and giving rise to double σ + π aromaticity. The delocalized π bonding is similar to that in [Sc]C2RR′, a metalla-cyclopropene reported by Zhang et al.95 and that in LaB2− and LaB3 molecules.40
Aromaticity is a useful concept despite its many facets. NICS values are often used to assess aromaticity because the negative value of the diamagnetic anisotropy suggests delocalization, also consistent with its aromaticity. Albeit being widely used, the NICS values may be artificially lowered by the local paramagnetic current around the Pr nucleus in PrB2−, thus may give negative values even if a global ring-current is non-existent and fail to assess aromaticity in some metallic systems.96–100 However, the NICS values can still help to provide helpful information about aromaticity when combining with other criteria. NICSzz(ζ) (the out-of-plane component of the chemical shift tensor calculated at ζ distance above the molecular plane) of PrB2− and two reference molecules (the singly π aromatic C3H3+ and the doubly σ + π aromatic B3−) are compared in Table S8.‡ Although in the literature,101,102 the ring critical point is the common point for calculating NICS values, PrB2− does not have one and as the molecule is less symmetric compared with B3− and C3H3+, the centre of the ring current (Fig. 6(b), coordinates in Table S5‡) is used instead of the geometry centre. The NICS values calculated both at the scalar relativistic and spin–orbit coupling relativistic levels of theory are listed in Tables S8(a) and (b),‡ as long as it would be ideal to include the spin–orbit coupling effect, which has been proved to influence NICS and ring-current values.103–106 One can see that the NICSzz(ζ) originating from the π-aromatic ring in C3H3+ remains almost the same as ζ increases from 0 to 1 because the π bonding MOs are perpendicular to the molecular plane. Comparatively, the NICSzz(ζ) values of the doubly σ + π aromatic B3− and PrB2− molecules decreases more significantly as ζ increases, which is because of the delocalized in-plane σ bond. The large negative NICSzz values of PrB2− in comparison with those of C3H3+ and B3− further help to confirm its double aromaticity.
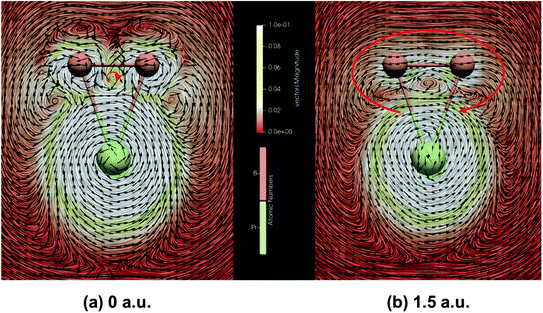
In addition, due to the cyclic electron delocalization, when applying a magnetic field to a molecule, a global diamagnetic induced ring-current also suggests aromaticity. Therefore, we have calculated the integrated amount of the induced current, using the same centre as the NICS calculations, passing along the B–B bond. As listed in Table 3, the results indicate that PrB2− is magnetically aromatic. Fig. 6 represents the line integral convolution (LIC) visualization of the induced current PrB2−. The small clockwise current in (a) can be attributed to the delocalized σ bond, and the global clockwise current in (b) results from the delocalized π bond. The clockwise global diamagnetic currents are diatropic and clear, providing support for the double aromaticity of PrB2−. Fig. S6‡ also presents the isosurfaces of AICD of B3− and PrB2− calculated from all valence electrons for the delocalized σ MO and the delocalized π MO. The isosurfaces decorated by green arrows show the strength and the direction of the induced current, which shows that apart from the counter-clockwise paramagnetic current on Pr, there also exists a global diamagnetic ring-current for PrB2− in all three cases, supporting double aromaticity. The connected isosurface of AICD and the bifurcation analysis of ELF (Fig. S7‡) both indicate that the relevant σ and π electrons in PrB2− are well delocalized, providing another proof that PrB2− is doubly aromatic.
| B3− | PrB2− | |
|---|---|---|
| Integrated ring-current | 16.5 | 7.0 |
| Diamagnetic anisotropy | −5.9 | −22.0 |
We have also carried out an energy decomposition analysis from the natural orbitals for chemical valence79 (EDA-NOCV, Table S10‡) and the principal interaction orbital analysis80 (PIO, Fig. S8‡) to illustrate the bonding pattern between Pr and B2−. Both the EDA-NOCV and PIO results suggest four significant sets of orbital interactions between Pr and B2−. The AdNDP analysis (Fig. 5) shows three peripheral 2c-2e σ bond in PrB2−, in addition to the 3c–2e σ bond and 3c–2e π bond. Therefore, the bond order of the Pr–B bond can be viewed roughly as 1 + (1/3) × 2 = 5/3, indicating multiple Pr–B bond character. The bonding in PrB2− is identical to that in the smallest doubly aromatic boron cluster, B3−, which has also been suggested to have a 5/3 bond order by Kuznetsov and Boldyrev.107 Finally, the five types of bond order indices83–86 listed in Table 4 reveal that both Pr–B interactions in PrB2− have a bond order greater than one, consistent with the Pr–B multiple bond character. Interestingly, both the Gopinathan–Jug bond order and the Nalewajski–Mrozek bond orders support the assignment of triple B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B bond in the B24− tetraanion, similar to the isoelectronic N
B bond in the B24− tetraanion, similar to the isoelectronic N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N.
N.
4 Conclusion
In summary, we report a photoelectron spectroscopy and quantum chemistry study of PrB2−, which is found to have a C2v unilateral triangle structure with a paramagnetic triplet ground state 3B2. The Pr atom is shown to lose three electrons to form the trivalent Pr(III) with f2 configuration and an unprecedented B24− tetraanion, which is in contrast to the PrBx− (x = 3, 4) clusters with Pr(II) and B33− as well as Pr(I) and B42−, respectively.108 The π orbitals of the B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B triple bonds in B24− participate in bonding with PrIII, forming an in-plane σ-type and out-of-plane π-type three-centred delocalized systems (Scheme 1) and giving rise to double aromaticity involving a 4f metal atom. The localized peripheral Pr–B σ-bond plus the two 3c–2e delocalized bonds results in multiple bond characters for the Pr–B bonds. The current study demonstrates that metalla-aromaticity and multiple chemical bonds between 4f metals and boron are viable and broadens the chemistry between lanthanide and boron. The present work also reveals that the high-lying 5d orbitals of the 4f-elements can facilitate the formation of the B24− tetraanion, which complete the isoelectronic B24−, C22− and N2 and O22+ series.109,110 The insight of the characteristic high-lying 5d orbitals of the 4f-elements can provide guidance in preparing organometallic complexes with highly negatively charged organic ligands of rare-earth elements.111,112
B triple bonds in B24− participate in bonding with PrIII, forming an in-plane σ-type and out-of-plane π-type three-centred delocalized systems (Scheme 1) and giving rise to double aromaticity involving a 4f metal atom. The localized peripheral Pr–B σ-bond plus the two 3c–2e delocalized bonds results in multiple bond characters for the Pr–B bonds. The current study demonstrates that metalla-aromaticity and multiple chemical bonds between 4f metals and boron are viable and broadens the chemistry between lanthanide and boron. The present work also reveals that the high-lying 5d orbitals of the 4f-elements can facilitate the formation of the B24− tetraanion, which complete the isoelectronic B24−, C22− and N2 and O22+ series.109,110 The insight of the characteristic high-lying 5d orbitals of the 4f-elements can provide guidance in preparing organometallic complexes with highly negatively charged organic ligands of rare-earth elements.111,112
Data availability
The data that supports the findings of this study is available from the corresponding author upon reasonable request.Author contributions
H. S. H. and L. S. W. designed the project. T. T. C. and W. J. C. performed the experiments. Z. L. W., W. L. L., J. Z., and X. L. J. performed the computational calculations. Z. L. W., T. T. C., J. L., L. S. W. and H. S. H. wrote and edited the manuscript. All authors helped to analyse the experimental and theoretical results.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The experiment done at Brown University was supported by the National Science Foundation (CHE-2053541). The theoretical work was supported by the National Natural Science Foundation of China (Grant No. 21906094, 22076095, 22033005) and the support of Guangdong Provincial Key Laboratory of Catalysis (No. 2020B121201002). The calculations were done using supercomputers at Tsinghua National Laboratory for Information Science and Technology, and the Computational Chemistry Laboratory of the Department of Chemistry under the Tsinghua Xuetang Talents Program.References
- J. Chandrasekhar, E. D. Jemmis and P. von Ragué Schleyer, Double Aromaticity: Aromaticity in Orthogonal Planes. The 3,5-Dehydrophenyl Cation, Tetrahedron Lett., 1979, 20(39), 3707–3710, DOI:10.1016/S0040-4039(01)95503-0.
- D. L. Thorn and R. Hoffman, Delocalization in Metallacycles, Nouv. J. Chim., 1979, 3, 39–45 CAS.
- D. Chen, Y. Hua and H. Xia, Metallaaromatic Chemistry: History and Development, Chem. Rev., 2020, 120(23), 12994–13086, DOI:10.1021/acs.chemrev.0c00392.
- I. Fernández, G. Frenking and G. Merino, Aromaticity of Metallabenzenes and Related Compounds, Chem. Soc. Rev., 2015, 44(18), 6452–6463, 10.1039/c5cs00004a.
- A. I. Boldyrev and L. S. Wang, All-Metal Aromaticity and Antiaromaticity, Chem. Rev., 2005, 105(10), 3716–3757, DOI:10.1021/cr030091t.
- D. Y. Zubarev, B. B. Averkiev, H. J. Zhai, L. S. Wang and A. I. Boldyrev, Aromaticity and Antiaromaticity in Transition-Metal Systems, Phys. Chem. Chem. Phys., 2008, 10(2), 257–267, 10.1039/b713646c.
- B. B. Averkiev and A. I. Boldyrev, Hf3 Cluster Is Triply (σ-, π-, and δ-) Aromatic in the Lowest D3h, 1A1′ State, J. Phys. Chem. A, 2007, 111(50), 12864–12866, DOI:10.1021/jp077528b.
- A. C. Tsipis, C. E. Kefalidis and C. A. Tsipis, The Role of the 5f Orbitals in Bonding, Aromaticity, and Reactivity of Planar Isocyclic and Heterocyclic Uranium Clusters, J. Am. Chem. Soc., 2008, 130(28), 9144–9155, DOI:10.1021/ja802344z.
- D. Y. Zubarev and A. I. Boldyrev, Multiple Aromaticity, Multiple Antiaromaticity, and Conflicting Aromaticity in Inorganic Systems, Encycl. Inorg. Chem., 2009 DOI:10.1002/0470862106.ia633.
- C. A. Tsipis, Aromaticity/Antiaromaticity in “Bare” and “Ligand-Stabilized” Rings of Metal Atoms, Structure and Bonding, ed. Parkin G., Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 136, pp. 217–274. DOI:10.1007/978-3-642-05243-9_7.
- A. P. Sergeeva, B. B. Averkiev, and A. I. Boldyrev, All-Transition Metal Aromaticity and Antiaromaticity, ed. Parkin G., Structure and Bonding, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 136, pp. 275–305. DOI:10.1007/978-3-642-05243-9_8.
- J. Li, C.-W. Liu and J.-X. Lu, Ab Initio Studies of Electronic Structures and Quasi-Aromaticity in M3S4 –nO4+n(M = Mo, W; n = 0–4) Clusters, J. Chem. Soc., Faraday Trans., 1994, 90(1), 39–45, 10.1039/FT9949000039.
- X. Li, A. E. Kuznetsov, H.-F. Zhang, A. I. Boldyrev and L.-S. Wang, Observation of All-Metal Aromatic Molecules, Science, 2001, 291(5505), 859–861, DOI:10.1126/science.291.5505.859.
- A. N. Alexandrova and A. I. Boldyrev, σ-Aromaticity and σ-Antiaromaticity in Alkali Metal and Alkaline Earth Metal Small Clusters, J. Phys. Chem. A, 2003, 107(4), 554–560, DOI:10.1021/jp027008a.
- A. E. Kuznetsov, J. D. Corbett, L.-S. Wang and A. I. Boldyrev, Aromatic Mercury Clusters in Ancient Amalgams, Angew. Chem., Int. Ed., 2001, 40(18), 3369–3372, DOI:10.1002/1521-3773(20010917)40:18<3369::AID-ANIE3369>3.0.CO;2-Z.
- H.-J. Zhai, B. B. Averkiev, D. Y. Zubarev, L. Wang and A. I. Boldyrev, δ Aromaticity in [Ta3O3]−, Angew. Chem., Int. Ed., 2007, 46(23), 4277–4280, DOI:10.1002/anie.200700442.
- M. Zhou, N. Tsumori, Z. Li, K. Fan, L. Andrews and Q. Xu, OCBBCO: A Neutral Molecule with Some Boron-Boron Triple Bond Character, J. Am. Chem. Soc., 2002, 124(44), 12936–12937, DOI:10.1021/ja026257+.
- W.-L. Li, H.-S. Hu, Y.-F. Zhao, X. Chen, T.-T. Chen, T. Jian, L.-S. Wang and J. Li, Recent Progress on the Investigations of Boron Clusters and Boron-Based Materials (I): Borophene, Sci. Sin.: Chim., 2018, 48(2), 98–107, DOI:10.1360/N032017-00185.
- T. Mori, Lanthanides: Boride, Carbide, and Nitride Compounds, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Ltd, Chichester, UK, 2012. DOI:10.1002/9781119951438.eibc2028.
- T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Probing the Structures and Bonding of Size-Selected Boron and Doped-Boron Clusters, Chem. Soc. Rev., 2019, 48(13), 3550–3591, 10.1039/c9cs00233b.
- A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W.-L. Li, C. Romanescu, L.-S. Wang and A. I. Boldyrev, Understanding Boron through Size-Selected Clusters: Structure, Chemical Bonding, and Fluxionality, Acc. Chem. Res., 2014, 47(4), 1349–1358, DOI:10.1021/ar400310g.
- H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Hepta- and Octacoordinate Boron in Molecular Wheels of Eight- and Nine-Atom Boron Clusters: Observation and Confirmation, Angew. Chem., Int. Ed., 2003, 42(48), 6004–6008, DOI:10.1002/anie.200351874.
- H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Hydrocarbon Analogues of Boron Clusters Planarity, Aromaticity and Antiaromaticity, Nat. Mater., 2003, 2(12), 827–833, DOI:10.1038/nmat1012.
- D. Y. Zubarev and A. I. Boldyrev, Comprehensive Analysis of Chemical Bonding in Boron Clusters, J. Comput. Chem., 2007, 28(1), 251–268, DOI:10.1002/jcc.20518.
- A. I. Boldyrev and L.-S. Wang, Beyond Organic Chemistry: Aromaticity in Atomic Clusters, Phys. Chem. Chem. Phys., 2016, 18(17), 11589–11605, 10.1039/C5CP07465G.
- W. Li, T. Jian, X. Chen, T. Chen, G. V. Lopez, J. Li and L. Wang, The Planar CoB18− Cluster as a Motif for Metallo-Borophenes, Angew. Chem., Int. Ed., 2016, 55(26), 7358–7363, DOI:10.1002/anie.201601548.
- T. Jian, W.-L. Li, X. Chen, T.-T. Chen, G. V. Lopez, J. Li and L.-S. Wang, Competition between Drum and Quasi-Planar Structures in RhB18− : Motifs for Metallo-Boronanotubes and Metallo-Borophenes, Chem. Sci., 2016, 7(12), 7020–7027, 10.1039/C6SC02623K.
- W.-L. Li, X. Chen, T. Jian, T.-T. Chen, J. Li and L.-S. Wang, From Planar Boron Clusters to Borophenes and Metalloborophenes, Nat. Rev. Chem., 2017, 1(10), 0071, DOI:10.1038/s41570-017-0071.
- C. Romanescu, T. R. Galeev, W.-L. Li, A. I. Boldyrev and L.-S. Wang, Aromatic Metal-Centered Monocyclic Boron Rings: Co©B8− and Ru©B9−, Angew. Chem., Int. Ed., 2011, 50(40), 9334–9337, DOI:10.1002/anie.201104166.
- T. R. Galeev, C. Romanescu, W.-L. Li, L.-S. Wang and A. I. Boldyrev, Observation of the Highest Coordination Number in Planar Species: Decacoordinated Ta©B10− and Nb©B10− Anions, Angew. Chem., Int. Ed., 2012, 51(9), 2101–2105, DOI:10.1002/anie.201107880.
- W.-L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L.-S. Wang, Transition-Metal-Centered Nine-Membered Boron Rings: M©B9 and M©B9– (M = Rh, Ir), J. Am. Chem. Soc., 2012, 134(1), 165–168, DOI:10.1021/ja209808k.
- C. Romanescu, T. R. Galeev, A. P. Sergeeva, W.-L. Li, L.-S. Wang and A. I. Boldyrev, Experimental and Computational Evidence of Octa- and Nona-Coordinated Planar Iron-Doped Boron Clusters: Fe©B8− and Fe©B9−, J. Organomet. Chem., 2012, 721–722, 148–154, DOI:10.1016/j.jorganchem.2012.07.050.
- C. Romanescu, T. R. Galeev, W.-L. Li, A. I. Boldyrev and L.-S. Wang, Transition-Metal-Centered Monocyclic Boron Wheel Clusters (M©Bn): A New Class of Aromatic Borometallic Compounds, Acc. Chem. Res., 2013, 46(2), 350–358, DOI:10.1021/ar300149a.
- T.-T. Chen, W.-L. Li, H. Bai, W.-J. Chen, X.-R. Dong, J. Li and L.-S. Wang, Re©B8– and Re©B9– : New Members of the Transition-Metal-Centered Borometallic Molecular Wheel Family, J. Phys. Chem. A, 2019, 123(25), 5317–5324, DOI:10.1021/acs.jpca.9b03942.
- L. F. Cheung, G. S. Kocheril, J. Czekner and L.-S. Wang, Observation of Möbius Aromatic Planar Metallaborocycles, J. Am. Chem. Soc., 2020, 142(7), 3356–3360, DOI:10.1021/jacs.9b13417.
- L. F. Cheung, J. Czekner, G. S. Kocheril and L. S. Wang, ReB6-: A Metallaboron Analog of Metallabenzenes, J. Am. Chem. Soc., 2019, 141(44), 17854–17860, DOI:10.1021/jacs.9b09110.
- Y. Tang, S. Zhao, B. Long, J.-C. Liu and J. Li, On the Nature of Support Effects of Metal Dioxides MO2 (M = Ti, Zr, Hf, Ce, Th) in Single-Atom Gold Catalysts: Importance of Quantum Primogenic Effect, J. Phys. Chem. C, 2016, 120(31), 17514–17526, DOI:10.1021/acs.jpcc.6b05338.
- J.-B. Lu, D. C. Cantu, M.-T. Nguyen, J. Li, V.-A. Glezakou and R. Rousseau, Norm-Conserving Pseudopotentials and Basis Sets To Explore Lanthanide Chemistry in Complex Environments, J. Chem. Theory Comput., 2019, 15(11), 5987–5997, DOI:10.1021/acs.jctc.9b00553.
- Y. Luo and Z. Hou, Prediction of Binary Lanthanide(III) Hydride Clusters LnnH3n (Ln = La, Gd, and Lu; n = 3 and 4), J. Phys. Chem. C, 2008, 112(2), 635–638, DOI:10.1021/jp077318z.
- S.-B. Cheng, C. Berkdemir and A. W. Castleman, Observation of d–p Hybridized Aromaticity in Lanthanum-Doped Boron Clusters, Phys. Chem. Chem. Phys., 2014, 16(2), 533–539, 10.1039/C3CP53245C.
- J. T. Boronski, J. A. Seed, D. Hunger, A. W. Woodward, J. van Slageren, A. J. Wooles, L. S. Natrajan, N. Kaltsoyannis and S. T. Liddle, A Crystalline Tri-Thorium Cluster with σ-Aromatic Metal–Metal Bonding, Nature, 2021, 598(7879), 72–75, DOI:10.1038/s41586-021-03888-3.
- X. X. Chi and Y. Liu, Theoretical Evidence of d-Orbital Aromaticity in Anionic Metal X3- (X = Sc, Y, La) Clusters, Int. J. Quantum Chem., 2007, 107(9), 1886–1896, DOI:10.1002/qua.21326.
- A. S. Ivanov, X. Zhang, H. Wang, A. I. Boldyrev, G. Gantefoer, K. H. Bowen and I. Černušák, Anion Photoelectron Spectroscopy and CASSCF/CASPT2/RASSI Study of Lan– (n = 1, 3–7), J. Phys. Chem. A, 2015, 119(46), 11293–11303, DOI:10.1021/acs.jpca.5b08076.
- O. T. Summerscales and J. C. Gordon, Complexes Containing Multiple Bonding Interactions between Lanthanoid Elements and Main-Group Fragments, RSC Adv., 2013, 3(19), 6682–6692, 10.1039/c3ra23151h.
- Q. Zhu, J. Zhu and C. Zhu, Recent Progress in the Chemistry of Lanthanide-Ligand Multiple Bonds, Tetrahedron Lett., 2018, 59(6), 514–520, DOI:10.1016/j.tetlet.2017.12.079.
- D. Schädle and R. Anwander, Rare-Earth Metal and Actinide Organoimide Chemistry, Chem. Soc. Rev., 2019, 48(24), 5752–5805, 10.1039/c8cs00932e.
- T. Cheisson, K. D. Kersey, N. Mahieu, A. McSkimming, M. R. Gau, P. J. Carroll and E. J. Schelter, Multiple Bonding in Lanthanides and Actinides: Direct Comparison of Covalency in Thorium(IV)- and Cerium(IV)-Imido Complexes, J. Am. Chem. Soc., 2019, 141(23), 9185–9190, DOI:10.1021/jacs.9b04061.
- T. T. Chen, W. L. Li, T. Jian, X. Chen, J. Li and L. S. Wang, PrB7−: A Praseodymium-Doped Boron Cluster with a PrII Center Coordinated by a Doubly Aromatic Planar η7-B73− Ligand, Angew. Chem., Int. Ed., 2017, 56(24), 6916–6920, DOI:10.1002/anie.201703111.
- W. L. Li, T. T. Chen, D. H. Xing, X. Chen, J. Li and L. S. Wang, Observation of Highly Stable and Symmetric Lanthanide Octa-Boron Inverse Sandwich Complexes, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(30), E6972–E6977, DOI:10.1073/pnas.1806476115.
- T. T. Chen, W. L. Li, J. Li and L. S. Wang, [La(Hx-Bx)La]− (x = 7-9): A New Class of Inverse Sandwich Complexes, Chem. Sci., 2019, 10(8), 2534–2542, 10.1039/c8sc05443f.
- Z.-Y. Jiang, T.-T. Chen, W.-J. Chen, W.-L. Li, J. Li and L.-S. Wang, Expanded Inverse-Sandwich Complexes of Lanthanum Borides: La2B10– and La2B11–, J. Phys. Chem. A, 2021, 125(12), 2622–2630, DOI:10.1021/acs.jpca.1c01149.
- T. T. Chen, W. L. Li, W. J. Chen, J. Li and L. S. Wang, La3B14−: An Inverse Triple-Decker Lanthanide Boron Cluster, Chem. Commun., 2019, 55(54), 7864–7867, 10.1039/c9cc03807h.
- T.-T. Chen, W.-L. Li, W.-J. Chen, X.-H. Yu, X.-R. Dong, J. Li and L.-S. Wang, Spherical Trihedral Metallo-Borospherenes, Nat. Commun., 2020, 11(1), 2766, DOI:10.1038/s41467-020-16532-x.
- L. S. Wang, H. S. Cheng and J. Fan, Photoelectron Spectroscopy of Size-Selected Transition Metal Clusters: Fen−, n = 3-24, J. Chem. Phys., 1995, 102(24), 9480–9493, DOI:10.1063/1.468817.
- L. S. Wang, Photoelectron Spectroscopy of Size-Selected Boron Clusters: From Planar Structures to Borophenes and Borospherenes, Int. Rev. Phys. Chem., 2016, 35(1), 69–142, DOI:10.1080/0144235X.2016.1147816.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22(9), 931–967, DOI:10.1002/jcc.1056.
- SCM Theoretical Chemistry, ADF 2019.1, Vrije Universiteit, Amsterdam, the Netherlands, 2019 Search PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: A General-Purpose Quantum Chemistry Program Package, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2(2), 242–253, DOI:10.1002/wcms.82.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158–6170, DOI:10.1063/1.478522.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-Type Basis Sets for the Elements 1-118, J. Comput. Chem., 2003, 24(9), 1142–1156, DOI:10.1002/jcc.10255.
- E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Relativistic Regular Two-Component Hamiltonians, Int. J. Quantum Chem., 1996, 57(3), 281–293, DOI:10.1002/(SICI)1097-461X(1996)57:3<281::AID-QUA2>3.0.CO;2-U.
- X. Cao and M. Dolg, Valence Basis Sets for Relativistic Energy-Consistent Small-Core Lanthanide Pseudopotentials, J. Chem. Phys., 2001, 115(16), 7348–7355, DOI:10.1063/1.1406535.
- X. Cao and M. Dolg, Basis Set Limit Extrapolation of ACPF and CCSD(T) Results for the Third and Fourth Lanthanide Ionization Potentials, Chem. Phys. Lett., 2001, 349(5–6), 489–495, DOI:10.1016/S0009-2614(01)01211-8.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023, DOI:10.1063/1.456153.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, The Zero-order Regular Approximation for Relativistic Effects: The Effect of Spin-Orbit Coupling in Closed Shell Molecules, J. Chem. Phys., 1996, 105(15), 6505–6516, DOI:10.1063/1.472460.
- M. Douglas and N. M. Kroll, Quantum Electrodynamical Corrections to the Fine Structure of Helium, Ann. Phys., 1974, 82(1), 89–155, DOI:10.1016/0003-4916(74)90333-9.
- B. A. Hess, Applicability of the No-Pair Equation with Free-Particle Projection Operators to Atomic and Molecular Structure Calculations, Phys. Rev. A, 1985, 32(2), 756–763, DOI:10.1103/PhysRevA.32.756.
- J. D. Rolfes, F. Neese and D. A. Pantazis, All-electron Scalar Relativistic Basis Sets for the Elements Rb–Xe, J. Comput. Chem., 2020, 41(20), 1842–1849, DOI:10.1002/jcc.26355.
- P. R. T. Schipper, O. V. Gritsenko, S. J. A. Van Gisbergen and E. J. Baerends, Molecular Calculations of Excitation Energies and (Hyper)Polarizabilities with a Statistical Average of Orbital Model Exchange-Correlation Potentials, J. Chem. Phys., 2000, 112(3), 1344–1352, DOI:10.1063/1.480688.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- L. Pauling, The Diamagnetic Anisotropy of Aromatic Molecules, J. Chem. Phys., 1936, 4(10), 673–677, DOI:10.1063/1.1749766.
- P. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe, J. Am. Chem. Soc., 1996, 118(26), 6317–6318, DOI:10.1021/ja960582d.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, The Gauge Including Magnetically Induced Current Method, Phys. Chem. Chem. Phys., 2011, 13(46), 20500, 10.1039/c1cp21812c.
- R. Herges and D. Geuenich, Delocalization of Electrons in Molecules, J. Phys. Chem. A, 2001, 105(13), 3214–3220, DOI:10.1021/jp0034426.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Calculations of Magnetically Induced Current Densities: Theory and Applications, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2016, 6(6), 639–678, DOI:10.1002/wcms.1270.
- A. D. A. Becke, New Mixing of Hartree–Fock and Local Density-functional Theories, J. Chem. Phys., 1993, 98(2), 1372–1377, DOI:10.1063/1.464304.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623–11627, DOI:10.1021/j100096a001.
- M. Mitoraj and A. Michalak, Natural Orbitals for Chemical Valence as Descriptors of Chemical Bonding in Transition Metal Complexes, J. Mol. Model., 2007, 13(2), 347–355, DOI:10.1007/s00894-006-0149-4.
- J. X. Zhang, F. K. Sheong and Z. Lin, Unravelling Chemical Interactions with Principal Interacting Orbital Analysis, Chem.–A Eur. J., 2018, 24(38), 9639–9650, DOI:10.1002/chem.201801220.
- D. Y. Zubarev and A. I. Boldyrev, Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning, Phys. Chem. Chem. Phys., 2008, 10(34), 5207–5217, 10.1039/b804083d.
- T. Lu and F. M. Chen, A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33(5), 580–592, DOI:10.1002/jcc.22885.
- I. Mayer, Bond Order and Valence Indices: A Personal Account, J. Comput. Chem., 2007, 28(1), 204–221, DOI:10.1002/jcc.20494.
- M. S. Gopinathan and K. Jug, Valency. I. A Quantum Chemical Definition and Properties, Theor. Chim. Acta, 1983, 63(6), 497–509, DOI:10.1007/BF02394809.
- A. Michalak, R. L. Dekock and T. Ziegler, Bond Multiplicity in Transition-Metal Complexes: Applications of Two-Electron Valence Indices, J. Phys. Chem. A, 2008, 112(31), 7256–7263, DOI:10.1021/jp800139g.
- R. F. Nalewajski, J. Mrozek and A. Michalak, Two-Electron Valence Indices from the Kohn-Sham Orbitals, Int. J. Quantum Chem., 1997, 61(3), 589–601, DOI:10.1002/(SICI)1097-461X(1997)61:3<589::AID-QUA28>3.0.CO;2-2.
- R. O. Jones and O. Gunnarsson, The Density Functional Formalism, Its Applications and Prospects, Rev. Mod. Phys., 1989, 61(3), 689–746, DOI:10.1103/RevModPhys.61.689.
- J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Au20 : A Tetrahedral Cluster, Science, 2003, 299(5608), 864–867, DOI:10.1126/science.1079879.
- W. L. Li, J. Su, T. Jian, G. V. Lopez, H. S. Hu, G. J. Cao, J. Li and L. S. Wang, Strong Electron Correlation in UO2-: A Photoelectron Spectroscopy and Relativistic Quantum Chemistry Study, J. Chem. Phys., 2014, 140(9) DOI:10.1063/1.4867278.
- J. Su, W. L. Li, G. V. Lopez, T. Jian, G. J. Cao, W. L. Li, W. H. E. Schwarz, L. S. Wang and J. Li, Probing the Electronic Structure and Chemical Bonding of Mono-Uranium Oxides with Different Oxidation States: UOx− and UOx (x = 3-5), J. Phys. Chem. A, 2016, 120(7), 1084–1096, DOI:10.1021/acs.jpca.5b11354.
- Z. L. Wang, H. S. Hu, L. von Szentpály, H. Stoll, S. Fritzsche, P. Pyykkö, W. H. E. Schwarz and J. Li, Understanding the Uniqueness of 2p Elements in Periodic Tables, Chem.–A Eur. J., 2020, 26(67), 15558–15564, DOI:10.1002/chem.202003920.
- D. R. Lonsdale and L. Goerigk, The One-Electron Self-Interaction Error in 74 Density Functional Approximations: A Case Study on Hydrogenic Mono- And Dinuclear Systems, Phys. Chem. Chem. Phys., 2020, 22(28), 15805–15830, 10.1039/d0cp01275k.
- R. G. Pearson, The Second-Order Jahn-Teller Effect, J. Mol. Struct.: THEOCHEM, 1983, 103, 25–34, DOI:10.1016/0166-1280(83)85006-4.
- J. C. Santos, W. Tiznado, R. Contreas and P. Fuentealba, Sigma-Pi Separation of the Electron Localization Function and Aromaticity, J. Chem. Phys., 2004, 120(4), 1670–1672, DOI:10.1063/1.1635799.
- Z.-J. Lv, Z. Huang, J. Shen, W.-X. Zhang and Z. Xi, Well-Defined Scandacyclopropenes: Synthesis, Structure, and Reactivity, J. Am. Chem. Soc., 2019, 141(51), 20547–20555, DOI:10.1021/jacs.9b11631.
- B. J. R. Cuyacot and C. Foroutan-Nejad, [{Th(C8H8)Cl2}3]2− Is Stable but Not Aromatic, Nature, 2022, 603(7902), E18–E20, DOI:10.1038/s41586-021-04319-z.
- Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, All-Metal Aromaticity: Revisiting the Ring Current Model among Transition Metal Clusters, J. Chem. Theory Comput., 2013, 9(11), 4789–4796, DOI:10.1021/ct4007184.
- C. Foroutan-Nejad, J. Vícha and A. Ghosh, Relativity or Aromaticity? A First-Principles Perspective of Chemical Shifts in Osmabenzene and Osmapentalene Derivatives, Phys. Chem. Chem. Phys., 2020, 22(19), 10863–10869, 10.1039/D0CP01481H.
- C. Foroutan-Nejad, Is NICS a Reliable Aromaticity Index for Transition Metal Clusters?, Theor. Chem. Acc., 2015, 134(2), 8, DOI:10.1007/s00214-015-1617-7.
- M. Orozco-Ic, N. D. Charistos, A. Muñoz-Castro, R. Islas, D. Sundholm and G. Merino, Core-Electron Contributions to the Molecular Magnetic Response, Phys. Chem. Chem. Phys., 2022, 24(20), 12158–12166, 10.1039/D1CP05713H.
- C. Foroutan-Nejad, S. Shahbazian and P. Rashidi-Ranjbar, The Electron Density vs. NICS Scan: A New Approach to Assess Aromaticity in Molecules with Different Ring Sizes, Phys. Chem. Chem. Phys., 2010, 12(39), 12630, 10.1039/c004254d.
- C. Foroutan-Nejad, Z. Badri, S. Shahbazian and P. Rashidi-Ranjbar, The Laplacian of Electron Density versus NICSzz Scan: Measuring Magnetic Aromaticity among Molecules with Different Atom Types, J. Phys. Chem. A, 2011, 115(45), 12708–12714, DOI:10.1021/jp203681x.
- A. C. Castro, E. Osorio, J. O. C. Jiménez-Halla, E. Matito, W. Tiznado and G. Merino, Scalar and Spin−Orbit Relativistic Corrections to the NICS and the Induced Magnetic Field: The Case of the E122− Spherenes (E = Ge, Sn, Pb), J. Chem. Theory Comput., 2010, 6(9), 2701–2705, DOI:10.1021/ct100304c.
- M. Orozco-Ic, J. Barroso, R. Islas and G. Merino, Delocalization in Substituted Benzene Dications: A Magnetic Point of View, ChemistryOpen, 2020, 9(6), 657–661, DOI:10.1002/open.202000105.
- J. Vícha, M. Straka, M. L. Munzarová and R. Marek, Mechanism of Spin–Orbit Effects on the Ligand NMR Chemical Shift in Transition-Metal Complexes: Linking NMR to EPR, J. Chem. Theory Comput., 2014, 10(4), 1489–1499, DOI:10.1021/ct400726y.
- L. Alvarez-Thon and W. Caimanque-Aguilar, Spin-Orbit Effects on Magnetically Induced Current Densities in the M42- (M = B, Al, Ga, In, Tl) Clusters, Chem. Phys. Lett., 2017, 671, 118–123, DOI:10.1016/j.cplett.2017.01.027.
- A. E. Kuznetsov and A. I. Boldyrev, Theoretical Evidence of Aromaticity in X3- (X = B, Al, Ga) Species, Struct. Chem., 2002, 13(2), 141–148, DOI:10.1023/A:1015704515336.
- X. Chen, T. T. Chen, W. L. Li, J. B. Lu, L. J. Zhao, T. Jian, H. S. Hu, L. S. Wang and J. Li, Lanthanides with Unusually Low Oxidation States in the PrB3− and PrB4− Boride Clusters, Inorg. Chem., 2019, 58(1), 411–418, DOI:10.1021/acs.inorgchem.8b02572.
- M. Zhou, L. Andrews, J. Li and B. E. Bursten, Reaction of Laser-Ablated Uranium Atoms with CO: Infrared Spectra of the CUO, CUO− , OUCCO, (η2−C2)UO2, and U(CO)x (x = 1−6) Molecules in Solid Neon, J. Am. Chem. Soc., 1999, 121(41), 9712–9721, DOI:10.1021/ja9921322.
- J. Su, S. Hu, W. Huang, M. Zhou and J. Li, On the Oxidation States of Metal Elements in MO3− (M=V, Nb, Ta, Db, Pr, Gd, Pa) Anions, Sci. China Chem., 2016, 59(4), 442–451, DOI:10.1007/s11426-015-5481-z.
- Y. Zheng, C.-S. Cao, W. Ma, T. Chen, B. Wu, C. Yu, Z. Huang, J. Yin, H.-S. Hu, J. Li, W.-X. Zhang and Z. Xi, 2-Butene Tetraanion Bridged Dinuclear Samarium(III) Complexes via Sm(II)-Mediated Reduction of Electron-Rich Olefins, J. Am. Chem. Soc., 2020, 142(24), 10705–10714, DOI:10.1021/jacs.0c01690.
- Y. Xiao, X.-K. Zhao, T. Wu, J. T. Miller, H.-S. Hu, J. Li, W. Huang and P. L. Diaconescu, Distinct Electronic Structures and Bonding Interactions in Inverse-Sandwich Samarium and Ytterbium Biphenyl Complexes, Chem. Sci., 2021, 12(1), 227–238, 10.1039/D0SC03555F.
Footnotes |
| † Dedicated to Professor Dr W. H. E. Schwarz on his 85th birthday. |
| ‡ Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02852b |
| § These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: