Dielectric properties of ice VII under the influence of time-alternating external electric fields
Zdenek
Futera
 *a and
Niall J.
English
*a and
Niall J.
English
 *b
*b
aFaculty of Science, University of South Bohemia, Branisovska 1760, 370 05 Ceske Budejovice, Czech Republic. E-mail: zfutera@prf.jcu.cz
bSchool of Chemical and Bioprocess Engineering, University College Dublin, Belfield, Dublin 4, Ireland. E-mail: niall.english@ucd.ie; Fax: +353-1-7161177; Tel: +353-1-7161646
First published on 26th October 2021
Abstract
The high-pressure solid phase of water known as ice VII has recently attracted a lot of attention when its presence was detected in large exoplanets, their icy satellites, and even in Earth's mantle. Moreover, a transition of ice VII to the superionic phase can be triggered by external electric fields. Here, we investigate the dielectric responses of ice VII to applied oscillating electric fields of various frequencies employing non-equilibrium ab initio molecular dynamics. We focus on the dynamical properties of a dipole-ordered ice VII structure, for which we explored external-field-induced electronic polarisation and the vibrational spectral density of states (VDOS). These analyses are important for the understanding of collective motions in the ice-VII lattice and the electronic properties of this exotic water phase.
Introduction
Ice VII is one of the 18 currently-known phases of water, which, in contrast to everyday hexagonal ice Ih, crystalises to a cubic body-centered lattice under high pressure, above 2 GPa at room temperature.1–3 Although such conditions might seem to be extreme, ice VII plays an important role in the geophysics of solar-system planets. For example, the conditions in mantles of large planets like Uranus and Neptune allow not only for ice-VII formation but also its transition to a conductive superionic phase.4–7 High-pressure ice phases could be present on the icy moons of Saturn and Jupiter too.8,9 Recently, even the ice VII presence deep in the Earth's mantle has been discovered by its detection in the natural diamond crystal.10A good deal of well-warranted attention has been paid to superionic ice phases when water molecules's intact-molecular structure is lost by rapid dissociation of covalent O–H bonds, and the hydrogen protons diffuse freely amongst the crystallographically-placed oxygen atoms, which retain the Wyckhoff lattice positions. The transition of ice VII to a superionic phase is usually initiated by increasing the pressure to critical values where the potential barrier for proton transfer between two neighboring oxygen atoms is low enough to allow symmetric proton exchange to become possible,11–13 enhanced by significant nuclear quantum effects.14–17 Finally, the protons themselves become fully diffusive upon a further pressure increase as the double-welled O–H⋯O potential transforms to a symmetric O⋯H⋯O profile, where the individual protons cannot be assigned to particular oxygen atoms anymore.18–21 This phenomenon is intimately connected with changes in proton diffusivity and conductivity.22–24
The above-mentioned transitions occur at extreme >50 GPa pressures and relatively high temperatures. Nevertheless, proton diffusion could be also initiated by externally-applied static electric fields – allowing to lower the critical “proton-hopping-onset” pressure to 10–15 GPa range, as we recently demonstrated by non-equilibrium ab initio molecular dynamics (NE-AIMD) simulations.25 Static electric fields are known to align water dipoles, and, eventually, facilitate the breaking of O–H bonds when their intensities reach the electro-dissociation threshold. Saitta et al.26 studied these effects on liquid water by DFT-based non-deterministic simulations, establishing this field-threshold intensity of ∼0.35 V Å−1, whilst Casone et al.27 showed that in ice Ih and ice XI these limits are considerably lower – slightly above above 0.25 V Å−1 and 0.22 V Å−1, respectively. These external-field intensities, although strong enough to induce molecular-dipole alignment and the consequent covalent-bond breaking, are of the order of ∼15% of the intrinsic electric-field strengths in these condensed-matter states of solid/liquid water, which are within the range of 1.5 to 2.5 V Å−1 in these condensed water phases.28 Recently, as mentioned in passing above, we investigated the static-field effect on dipole-ordered ice VII structure under a pressure of 10 GPa and temperature 410 K.25 Under these conditions, the lower boundary of field intensity required to initiate collective proton-hopping processes was found to be 0.33 V Å−1.
In contrast to external static electric fields, where structural and energetic reaarangement typically occurs more rapidly, the investigation of the effects of time-varying external fields requires significantly longer simulation times, as one needs to simulate at least several periodic field oscillations to gain enough data for meaningful statistical analyses.28–31 This is usually a limiting factor for first-principles studies where the potential-energy and wavefunction evaluation of reasonably large systems is computationally demanding. However, by leveraging the so-called second-generation CPMD method,32,33 which speeds up the computations by lowering convergence thresholds of the energy and forces calculation in Born–Oppenheimer-type dynamics whilst utilising canny extrapolation techniques and Langevin stochastic thermostatting, the propagation of relatively large system to sub-nanosecond times become possible. Using rigorous Berry-phase treatment of electric-field effects on systems within periodic boundary conditions, we have demonstrated good performance of this procedure for non-equilibrium ab initio molecular dynamics (NE-AIMD) simulation of both static and oscillating electric fields on liquid water,28 clathrate hydrates,34 ice VII,25,35 and, very recently, also on fully-solvated interfaces of hematite,36 where we were able to study external-field responses on 0.1-ns time scales.
Here, bearing in mind open questions of the effect of oscillating electric fields, as opposed to static ones,25,35 on the behaviour of ice VII, notably vibrational behaviour,35 we study the effects of oscillating fields on ice-VII structure to compare their influence on this hydrogen-bonded, pressurised, condensed phase of water with previously explored static-electric-field responses.25,35 A root-mean-square (r.m.s.) field intensity 0.2 V Å−1 was chosen – well below the intramolecular-dissociation limit of static fields (0.33 V Å−1),25 to focus on the dynamical dielectric responses of structural motions and electronic density. In this way, we investigate by means of autocorrelation functions and by computing and analyzing the vibrational densities of states, the system response to oscillating electric fields, as we discuss further in the text.
Computational details
Density-Functional Theory (DFT) calculations performed within this study were based on the accurate van der Waals density functional (vdW-DF) with the opt-B88 exchange–correlation part37,38 and DRSSL nonlocal correlation correction describing the dispersion interactions.39,40 This functional was demonstrated to capture well the properties of water, hexagonal ice Ih, weakly-bonded networks of clathrate hydrates as well as the high-pressure structure of ice VII,25,28,34,35,41–46 and we have highlighted before the importance of choosing appropriate functionals in condensed-phase systems.47 We applied Goedecker–Teter–Hutter (GTH) pseudopotentials,48 triple-zeta polarised basis set (TZV2P), and plane-wave cutoff 350 Ry to describe the system potential within the CP2K software,49 as justified by our previous calculations of water-based systems.25,28,34–36The system was propagated by ab initio molecular dynamics (AIMD) using the second-generation CPMD technique.32,33 This method allows us to use relatively long integration time steps – 1 fs in our case – and obtain long enough trajectories (100 ps) needed for reliable statistical analyses, bearing in mind the applied-field periods – 50, 150, 250, and 500 GHz frequencies for the NE-AIMD case, with r.m.s. magnitude of 0.2 V Å−1. A zero-field, equilibrium run was also carried out. Numerical stability of these simulations is ensured by application of ASPC corrector50 and Langevin thermostat with stochastic parameter γ set to 0.005. The model was studied in canonical (NVT) ensemble at temperature 410 K and fixed cubic cell dimensions with side length 12.62 Å accomodating 128 water molecules in 2 × 2 × 2 supercell shown in Fig. 1. This setup corresponds to a pressure of 10 GPa. Although the ice-VII water phase is characterised by hydrogen disorder, the ordered structure with water dipoles aligned to the x-direction of the cell was used as an initial structure for the simulations to bring the system into the ferroelectric state that would be induced by applied electric fields, an this was used in our previous NE-AIMD studies of electric-field effects on ice VII.25,35
Results and discussion
Dielectric materials, like water and its ice phases, interact with external electric fields primarily through their constituent molecular dipoles, which tend to align with local electric fields. Macroscopically, this effect is manifested by the polarisation of the system, and the response, within the linear regime, is generally described by the frequency dependent dielectric constant also known as permittivity. At the microscopic level, the dipoles not only rearrange their oritentation, at least in part, with the field direction by molecular rotation (so-called orientational polarisation), but their magnitude can also be enhanced due to underlying structural changes (e.g., bond stretches, angle bending, or intra-molecular rotations) and the connected charge-density redistributions (i.e., electronic polarisation). These electronic changes are, in general, much faster than the orientational effects. In the present study, we focus on the electronic-polarisation contributions to ice VII's dielectric response by investigating the effects of homogeneous, time-alternating, harmonic electric fields acting along the direction where the water molecular dipoles have been pre-oriented by electric-field effects.25,35First, we explored the molecular O–H bond stretching field response by calculating normalised autocorrelation functions (ACFs) of the ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) OH vectors oriented along with these bonds as
OH vectors oriented along with these bonds as
c(t) = 〈![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) OH(t0)· OH(t0)·![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) OH(t0 + t)〉/〈 OH(t0 + t)〉/〈![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) OH(t0)· OH(t0)·![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) OH(t0)〉. OH(t0)〉. | (1) |
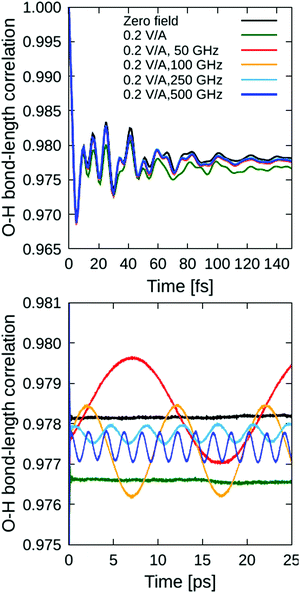
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time origins t0 along the computed (NE-)AIMD trajectories, are shown in Fig. 2. Because there is no reorientation effect, the water molecules are only allowed to liberate (or “wiggle”) in their equilibrium positions, and even these motions are considerably hindered by a strong hydrogen-bond network typical for this high-pressure ice phase; unsurprisingly, the correlation functions are close to unity, indicating strong correlations.
000 time origins t0 along the computed (NE-)AIMD trajectories, are shown in Fig. 2. Because there is no reorientation effect, the water molecules are only allowed to liberate (or “wiggle”) in their equilibrium positions, and even these motions are considerably hindered by a strong hydrogen-bond network typical for this high-pressure ice phase; unsurprisingly, the correlation functions are close to unity, indicating strong correlations.
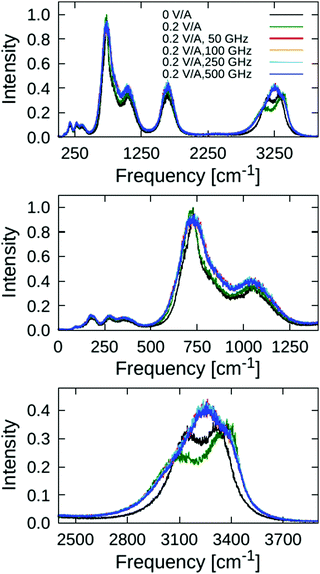
The fast variations at short times (within 140 ps) that can be seen in the upper panel of Fig. 2 correspond to O–H vibrations, which form the stretching band in the vibrational spectrum spanning approximately 2600 to 3700 cm−1 range, as we discuss further below. The fast vibrations are only slightly affected by 0.2 V ÅRMS−1 oscillating fields with 50, 150, 250, and 500 GHz frequencies, and the corresponding bond ACFs are very similar to the one obtained from zero-field reference simulation. For comparison, we also analysed the effect of a static electric field to the same magnitude (0.2 V Å−1), which, in stark contrast to the oscillating fields, affects the bond ACF considerably (cf. green curve in Fig. 2). This is natural, because static electric fields tend to “stretch” the bonds (with the water oxygen atom carrying a negative partial charge due to electron-density localisation thereat, whilst the hydrogen atoms are electron-deficient and positively charged); this suppresses anti-symmetric vibrations. However, oscillating fields change their polarisation in time, ipso facto, and their average effect is small – in particular at higher frequencies when the system has less time to respond. To witness these time-varying effects more clearly, we magnify the long-time tail of the bond ACFs in the lower panel of Fig. 2.
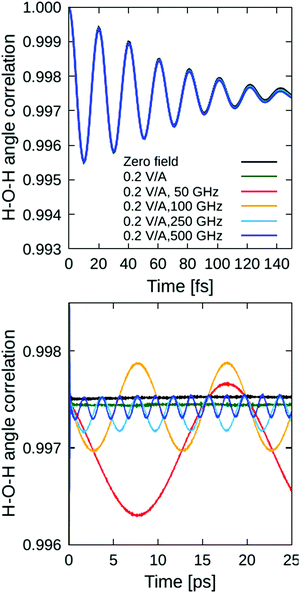
Besides bond stretching per se, the applied electric fields affect also the bending motions of the water-valence angles. To detect these effects, we computed the angle autocorrelation function analogous to eqn (1), where, instead of the ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) OH vector, the valence H–O–H angle ϑHOH was correlated. The calculated ACFs are shown in Fig. 3. Obviously, the external-field effects on the bending motions are much weaker than on the previously-discussed bond stretching. The fast variations in the short-time region (cf. upper panel of Fig. 3) are manifested by the vibrational spectral band between circa 1300 and 2000 cm−1, and are practically not affected at all by the applied fields of 0.2 V Å−1 in intensity. The field-induced perturbations are detectable only in the long-time tail of the ACFs (lower panel of Fig. 3), where it can be clearly seen that higher frequencies lead to smaller effects on average, as the system does not have enough time to adapt to rapidly-varying field periods; note that 50 GHz corresponds to a field period of 20 ps, whilst the 500 GHz field has a period of only 2 ps.
OH vector, the valence H–O–H angle ϑHOH was correlated. The calculated ACFs are shown in Fig. 3. Obviously, the external-field effects on the bending motions are much weaker than on the previously-discussed bond stretching. The fast variations in the short-time region (cf. upper panel of Fig. 3) are manifested by the vibrational spectral band between circa 1300 and 2000 cm−1, and are practically not affected at all by the applied fields of 0.2 V Å−1 in intensity. The field-induced perturbations are detectable only in the long-time tail of the ACFs (lower panel of Fig. 3), where it can be clearly seen that higher frequencies lead to smaller effects on average, as the system does not have enough time to adapt to rapidly-varying field periods; note that 50 GHz corresponds to a field period of 20 ps, whilst the 500 GHz field has a period of only 2 ps.
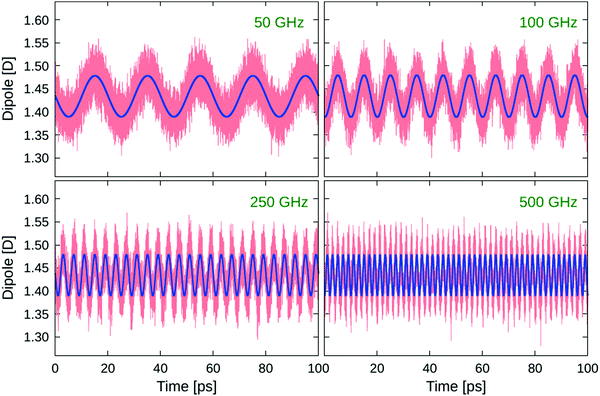
Although the changes in bond lengths and valence angles are small and their mean values (ROH = 1.00 Å, ϑHOH = 105.20 deg) are not affected by the applied oscillating fields, there is a considerable field response of the collective dipole moment 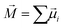 , which is the sum of the individual molecular dipoles
, which is the sum of the individual molecular dipoles ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i. The dipoles were calculated semiclassically using Hirshfeld point charges derived from the charge density obtained by DFT. The collective dipole, normalised on the number of water molecules in the studied systems, is tracked in Fig. 4 for all four frequencies of the oscillating electric fields studied here. The response is clearly harmonic, following the applied E0
i. The dipoles were calculated semiclassically using Hirshfeld point charges derived from the charge density obtained by DFT. The collective dipole, normalised on the number of water molecules in the studied systems, is tracked in Fig. 4 for all four frequencies of the oscillating electric fields studied here. The response is clearly harmonic, following the applied E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) field. For clarity, we fitted the collective-dipole time series by harmonic functions
cos(ωt) field. For clarity, we fitted the collective-dipole time series by harmonic functions
f(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) + B cos(ωt) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) sin(ωt) | (2) |
Finally, we analysed the field effects on the vibrational spectra, which characterise collective motions of the water molecules in the ice VII structure. We computed the vibrational density of states (VDOS) by Fourier-transforming the velocity autocorrelation function of the hydrogen atoms
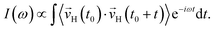 | (3) |
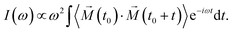 | (4) |
Conclusions
We employed non-equilibrium ab initio MD based on an accurate correlation-corrected DFT potential and the second-generation CPMD procedure to investigate the dielectric response of dipole-oriented ice VII under pressure 10 GPa and temperature 410 K to oscillating external electric fields of 0.2 V Å−1 RMS intensity and frequencies 50, 100, 250, and 500 GHz. The dynamical responses were analysed by tracking of the collective dipole of the system, computing of autocorrelation functions for H–O bond stretching and H–O–H angle bending, and total VDOS. In contrast to a static electric field of the same intensity, the effects of the time-alternating fields are relatively weak, although nevertheless detectable. Although static fields in general lead to electro-freezing when they have large enough intensities to restrain the water dipoles, and they can even initiate the ice VII transition to the superionic phase by promoting the H–O dissociation, as we showed in ref. 25, the impact of oscillating fields is quite different. The harmonic time variations of the field vector in a given direction promote librational motions and smear the contrasts between the symmetric and anti-symmetric stretching vibrations. There is relatively little difference in response to fields of the presently-explored frequency range, and their effects are clearly distinctive from those induced by the static field of the same intensity, meaning that the 50 GHz can be already characterised as a high-frequency field for ice VII, at least for the presently-gauges properties in terms of system response. Investigation of lower-frequency-field effects towards the lower-frequency end of the microwave spectrum (e.g., 10 GHz and lower) at the DFT level is unfortunately hampered by the need to compute correspondingly longer MD trajectories, close to, and beyond, nanosecond durations. Still, advances in computer hardware mean that deterministic second-generation CPMD will be accessible in the short- to medium-term for such NE-AIMD explorations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Science Foundation Ireland for funding with grants 17/NSFC/5229 and 15/ERC/-I3142. Z. F. is grateful for computational resources provided by The Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development and Innovations projects “e-Infrastructure CZ – LM2018140”. Both authors thanks Annraoi de Paor for very interesting conversations about the electric-field response of ice VII.References
- A. N. Dunaeva, D. V. Antsyshkin and O. L. Kuskov, Phase Diagram of H2O: Thermodynamic Functions of the Phase Transitions of High-Pressure Ices, Sol. Syst. Res., 2010, 44, 222–243 CrossRef.
- C. G. Salzmann, Advances in the Experimental Exploration of Water's Phase Diagram, J. Chem. Phys., 2019, 150, 060901 CrossRef PubMed.
- A. J. Amaya, H. Pathak, V. P. Modak, H. Laksmomo, N. D. Loh, J. A. Sellberg, R. G. Sierra, T. A. McQueen, M. J. Hayes, G. J. Williams, M. Messerschmidt, S. Boutet, M. J. Bogan, A. Nilsson, C. A. Stan and G. J. Wyslozil, How Cubic Can Ice Be?, J. Phys. Chem. Lett., 2017, 8, 3216–3322 CrossRef CAS.
- C. Cavazzoni, G. L. Chiarotti, S. Scandolo, E. Tosatti, M. Bernasconi and M. Parrinello, Superionic and Metallic States of Water and Ammonia at Giant Planet Conditions, Science, 1999, 283, 44–46 CrossRef CAS PubMed.
- N. Nettlemann, R. Helled, J. J. Fortney and R. Redmer, New Indication for a Dichotomy in the Interior Structure of Uranus and Neptune from the Application of Modified Shape and Rotation Data, Planet. Space Sci., 2013, 77, 143–151 CrossRef.
- M. Millot, S. Hamel, J. R. Rygg, P. M. Cellier, G. W. Collins, F. Coppari, D. E. Fratanduono, R. Jeanloz, D. C. Swift and J. H. Eggert, Experimental Evidence for Superionic Water Ice Using Shock Compression, Nat. Phys., 2018, 14, 297–302 Search PubMed.
- M. Millot, F. Coppari, J. R. Rygg, A. C. Barrios, S. Hamel, D. C. Swift and J. H. Eggert, Nanosecond X-Ray Diffraction of Shock-Compressed Superionic Water Ice, Nature, 2019, 569, 251–255 CrossRef CAS.
- F. Nimmo and R. T. Pappalardo, Ocean Worlds in the Outer Solar System, J. Geophys. Res. Planets, 2016, 121, 1378–1399 Search PubMed.
- M. K. Dougherty and L. J. Spilker, Review of Saturn's Icy Moons Following the Cassini Mission, Rep. Prog. Phys., 2018, 81, 065901 CrossRef PubMed.
- O. Tschauner, S. Huang, E. Greenberg, V. B. Prakapenka, C. Ma, G. R. Rossman, A. H. Shen, D. Zhang, M. Newville, A. Lanzirotti and K. Tait, Ice-VII Inclusions in Diamonds: Evidence for Aqueous Fluid in Earth's Deep Mantle, Science, 2018, 359, 1136–1139 CrossRef CAS.
- W. B. Holtzapfel, On the Symmetry of the Hydrogen Bonds in Ice VII, J. Chem. Phys., 1972, 56, 712–715 CrossRef.
- R. J. Hemley, A. P. Jephcoat, H. K. Mao, C. S. Zha, L. W. Finger and D. E. Cox, Static Compression of H2O-Ice to 128 GPa (1.28 Mbar), Nature, 1987, 330, 737–740 CrossRef CAS.
- K. Aoki, H. Yamawaki, M. Sakashita and H. Fujihisa, Infrared Absorption Study of the Hydrogen-Bond Symmetrization in Ice to 110 GPa, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 15673–15677 CrossRef CAS PubMed.
- M. Benoit, D. Marx and M. Parrinello, Tunnelling and Zero-Point Motion in High-Pressure Ice, Nature, 1998, 392, 258–261 CrossRef CAS.
- M. Benoit, D. Marx and M. Parrinello, Quantum Effects on Phase Transitions in High-Pressure Ice, Comput. Mater. Sci., 1998, 10, 88–93 CrossRef.
- Y. Bronstein, P. Depondt, F. Finocchi and A. M. Saitta, Quantum-Driven Phase Transition in Ice via an Efficient Langevin Approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214101 CrossRef.
- T. Meier, S. Petitgirard, S. Khandarkhaeva and L. Dubrovinski, Observation of Nuclear Quantum Effects and Hydrogen Bond Symmetrisation in High Pressure Ice, Nat. Commun., 2018, 9, 2766 CrossRef.
- N. Goldman, L. E. Fried, I.-F. W. Kuo and C. J. Mundy, Bonding in the Superionic Phase of Water, Phys. Rev. Lett., 2005, 94, 217801 CrossRef.
- J. Sun, B. K. Clark, S. Torquato and R. Car, The Phase Diagram of High-Pressure Superionic Ice, Nat. Commun., 2015, 6, 8156 CrossRef CAS.
- J.-A. Hernandez and R. Caracas, Superionic-Superionic Phase Transition in Body-Centered Cubic H2O Ice, Phys. Rev. Lett., 2016, 117, 135503 CrossRef.
- F. Trybel, M. Cosacchi, T. Meier, V. M. Axt and G. Steinle-Neumann, Proton Dynamics in High-Pressure Ice-VII from Density Functional Theory, Phys. Rev. B, 2020, 102, 184310 CrossRef CAS.
- E. Katoh, H. Yamawaki, H. Fujihisa, M. Sakashita and K. Aoki, Protonic Diffusion in High-Pressure Ice VII, Science, 2002, 295, 1264–1266 CrossRef CAS.
- E. Sugimura, T. Komabayashi, K. Ohta, K. Hirose, Y. Ohishi and L. S. Dubrovinsky, Experimental Evidence of Superionic Conduction in H2O Ice, J. Chem. Phys., 2012, 137, 194505 CrossRef.
- T. Okada, T. Iitaka, T. Yagi and K. Aoki, Electrical Conductivities of Ice VII, Sci. Rep., 2014, 4, 5778 CrossRef CAS.
- Z. Futera, J. S. Tse and N. J. English, Possibility of Realizing Superionic Ice VII in External Electric Fields of Planetary Bodies, Sci. Adv., 2020, 6, eaaz2915 CrossRef CAS PubMed.
- A. M. Saitta, F. Saija and P. V. Giaquinta, Ab Initio Molecular Dynamics Study of Dissociation of Water Under an Electric Field, Phys. Rev. Lett., 2012, 108, 207801 CrossRef PubMed.
- G. Cassone, P. V. Giaquinta, F. Saija and A. M. Saitta, Effect of Electric Field Orientation on the Mechanical and Electrica Properties of Water Ices: An Ab Initio Study, J. Phys. Chem. B, 2014, 118, 12717–12724 CrossRef CAS.
- Z. Futera and N. J. English, Influence of External Static and Alternating Electric Fields on Water from Long-Time Non-Equilibrium Ab Initio Molecular Dynamics, J. Chem. Phys., 2017, 147, 031102 CrossRef.
- J. Baker-Jarvis and S. Kim, The Interaction of Radio-Frequency Fields with Dielectric Materials at Macroscopic to Mesoscopic Scales, J. Res. Natl. Inst. Stand. Technol., 2012, 117, 1–60 CrossRef.
- R. Reale, N. J. English, P. Marracino, M. Liberti and F. Apollonio, Dipolar Response and Hydrogen-Bond Kinetics in Liquid Water in Square-Wave Time-Varying Electric Fields, Mol. Phys., 2013, 112, 1870–1878 CrossRef.
- N. J. English and C. J. Waldron, Perspectives on External Electric Fields in Molecular Simulation: Progress, Prospects and Challenges, Phys. Chem. Chem. Phys., 2015, 17, 12407–12440 RSC.
- T. D. Kuhne, M. Krack, F. R. Mohamed and M. Parrinello, Efficient and Accurate Car-Parrinello-like Approach to Born-Oppenheimer Molecular Dynamics, Phys. Rev. Lett., 2007, 98, 066401 CrossRef PubMed.
- T. D. Kuhne, M. Krack and M. Parrinello, Static and Dynamical Properties of Liquid Water from First Principles by a Novel Car-Parrinello-like Approach, J. Chem. Theory Comput., 2009, 5, 235–241 CrossRef CAS PubMed.
- Z. Futera, M. Celli, L. del Rosso, C. J. Burnham, L. Ulivi and N. J. English, Vibrational Modes of Hydrogen Hydrates: A First-Principles Molecular Dynamics and Raman Spectra Study, J. Phys. Chem. C, 2017, 121, 3690–3696 CrossRef CAS.
- Z. Futera and N. J. English, Pressure Dependence of Structural Properties of Ice VII: An Ab Initio Molecular-Dynamics Study, J. Phys. Chem., 2018, 148, 204505 CrossRef.
- Z. Futera and N. J. English, Water Breakup at Fe2O3 - Hematite/Water Interfaces: Influence of External Electric Fields from Nonequilibrium Ab Initio Molecular Dynamics, J. Phys. Chem. Lett., 2021, 12, 6818–6826 CrossRef CAS PubMed.
- A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. Klimes, D. R. Bowler and A. Michaelides, Chemical Accuracy for the van der Waals Density Functional, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef.
- M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- G. Roman-Perez and J. M. Soler, Efficient Implementation of a van der Waals Density Functional: Application to Double-Wall Carbon Nanotubes, Phys. Rev. Lett., 2009, 103, 096102 CrossRef.
- J. Wang, G. Roman-Perez, J. M. Soler, E. Artacho and M.-V. Fernandez-Serra, Density, Structure, and Dynamics of Water: The Effect of van der Waals Interactions, J. Chem. Phys., 2011, 134, 024516 CrossRef.
- C. Zhang, J. Wu, G. Galli and F. Gygi, Structural and Vibrational Properties of Liquid Water from van der Waals Density Functionals, J. Chem. Theory Comput., 2011, 7, 3054–3061 CrossRef CAS.
- F. Corsetti, E. Artacho, J. M. Soler, S. S. Alexandre and M. V. Fernandez-Serra, Room Temperature Compressibility and Diffusivity of Liquid Water from First Principles, J. Chem. Phys., 2013, 139, 194502 CrossRef.
- A. Bankura, A. Kamakar, V. Carnevale, A. Chandra and M. L. Klein, Structure, Dynamics, and Spectral Diffusion of Water from First-Principles Molecular Dynamics, J. Phys. Chem. C, 2014, 118, 29401–29411 CrossRef CAS.
- N. J. English, Structural Properties of Liquid Water and Ice Ih from Ab-Initio Molecular Dynamics with a Non-Local Correlation Functional, Energies, 2015, 8, 9383–9391 CrossRef.
- M. J. Gillan, D. Alfe and A. Michaelides, Perspective: How Good is DFT for Water?, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- P. Dev, S. Agrawal and N. J. English, Functional assessment for predicting charge-transfer excitations of dyes in complexed state: A study of triphenylamine-donor dyes on titania for dye-sensitized solar cells, J. Phys. Chem. A, 2013, 117, 2114–2124 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, CP2K: Atomistic Simulations of Condensed Matter Systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. Kolafa, Time-Reversible Always Stable Predictor-Corrector Method for Molecular Dynamics of Polarizable Molecules, J. Comput. Chem., 2004, 25, 335–342 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |