 Open Access Article
Open Access ArticleEngineering first-order spin–orbit coupling in a pentagonal bipyramidal Fe(II) complex and subsequent SMM behavior†
Kateryna
Bretosh
 a,
Virginie
Béreau
a,
Virginie
Béreau
 ab,
Flaurent
Heully-Alary
c,
Nicolas
Suaud
*c,
Carine
Duhayon
a,
Elen
Duverger-Nédellec
de,
Nathalie
Guihéry
*c and
Jean-Pascal
Sutter
ab,
Flaurent
Heully-Alary
c,
Nicolas
Suaud
*c,
Carine
Duhayon
a,
Elen
Duverger-Nédellec
de,
Nathalie
Guihéry
*c and
Jean-Pascal
Sutter
 *a
*a
aLaboratoire de Chimie de Coordination du CNRS (LCC-CNRS), Université de Toulouse, CNRS, 205 route de Narbonne, F-31077 Toulouse, France. E-mail: jean-pascal.sutter@lcc-toulouse.fr
bUniversité de Toulouse, Institut Universitaire de Technologie-Département de Chimie, Av. Georges Pompidou, F-81104 Castres, France
cLaboratoire de Chimie et Physique Quantiques (LCPQ), Université de Toulouse, CNRS, F-31062 Toulouse, France. E-mail: suaud@irsamc.ups-tlse.fr; nathalie.guihery@irsamc.ups-tlse.fr
dDepartment of Condensed Matter Physics, Faculty of Mathematics and Physics, Charles University, Ke Karlovu 5, 121 16 Praha 2, Czech Republic
eUniv. Bordeaux, CNRS, Bordeaux INP, ICMCB, UMR 5026, F-33600 Pessac, France
First published on 18th March 2025
Abstract
Pentagonal bipyramidal (PBP) complexes with a first-order spin–orbit coupling contribution can be readily obtained, mainly through chemical design optimization ensuring minimum structural distortion and a more symmetrical ligand field. This conclusion follows from the investigation of a series of five Fe(II) complexes: [FeLN5(H2O)Cl]Cl·4.5H2O, 1; [FeLN5Cl2]·3H2O, 2; [FeLN5Br2], 3; [FeLN5I2], 4; and [Fe0.12Zn0.88LN5I2], 5 (LN5 stands for the pentadentate macrocyclic ligand formed by the condensation of 2,6-diacetylpyridine and 2,9-di(α-methylhydrazino)-1,10-phenanthroline). Theoretical calculations revealed quasi-degeneracy of the dxz and dyz orbitals for the complexes with halide ligands at the apical positions (ΔE = 91, 134, and 142 cm−1, respectively, for 2–4). This small energy gap leads to SO states with very strong mixing of the ground and first excited quintet states. Therefore, the ZFS Hamiltonian is not suitable for modelling the magnetic properties of complexes 2–5. This does not apply for 1 with ΔE = 412 cm−1. The recorded magnetic behaviors indicated strong magnetic anisotropy; for 1D = −24 cm−1 was obtained. The Br and I derivatives were found to behave as SMMs (with a U/kB of about 90 K), the latter even in the absence of a static field.
10th anniversary statementInorganic Chemistry Frontiers is undoubtedly the benchmark journal for inorganic chemistry. From the beginning, it has been the policy of the journal that quality should prevail over quantity, and this policy has enabled it to quickly make a difference. I know that I am going to find in the journal the latest remarkable developments in my field. This is important to me, not only as a reader, but also as an author. |
Introduction
The paradigm of single-molecule and single-chain magnets (i.e. SMM and SCM)1,2 has triggered efforts to achieve large magnetic anisotropy in molecular compounds.3–8 One way of achieving this is to be close to the first-order spin–orbit regime. However, while the orbital angular momentum, L, plays a dominant role in lanthanide ions, it is generally quenched by the ligand field in transition metal ions.9,10 In 3d ion complexes, the coordination sphere leads to an energy distribution of the d orbitals with differences of a few hundreds to a few thousands cm−1 between them. The magnetic anisotropy exhibited by the metal center stems from the interaction between the fundamental and excited levels resulting from the promotion of an electron to a higher-energy orbital, a process known as second-order spin–orbit coupling (SOC). This magnetic anisotropy is described by the zero-field splitting (ZFS) model,11 and quantified by the axial parameter, D, and the rhombic term, E. The sign of D, which is positive for in-plane anisotropy and negative for axial anisotropy, is regulated by the coordination polyhedron and the electronic configuration of the metal center,12 and its strength is inversely proportional to the energy difference of the ground and excited states. However, under certain conditions, the splitting of the orbital levels can lead to quasi-degenerate orbitals giving rise to a certain amount of first-order spin–orbit contribution. This results in much larger anisotropy and, in the case of an axial-symmetry ligand field, axial (i.e. Ising-type) anisotropy is observed. The use of low coordination number complexes is an effective approach to generate first-order SOC. This has been illustrated for Fe derivatives with two-coordinate linear13–16 or trigonal-pyramid17,18 coordination spheres, most exhibiting slow relaxation of magnetization (i.e. SMM behavior). Similar results have been reported for Co(II)19,20 and Ni(I/II)21–23 derivatives. However, the slightest deformation of the coordination sphere or the symmetry of the ligand field leads to an increase in the energy difference between the d orbitals of the metal ion and lifts the quasi-degeneracy of the spin–orbit free states, resulting in the suppression of first-order SOC.15,24–26While the contribution of the first-order SOC is clearly essential for enhancing the magnetic anisotropy in 3d ions, achieving this objective by chemical design remains highly challenging. And this becomes even more difficult if such complexes are to form the building blocks of polynuclear systems such as SCMs; a crucial requirement will be that the suitable geometry of the coordination polyhedron is structurally robust.
Energy diagrams with degenerate orbitals are also observed for geometries with higher coordination numbers.12 This is the case for heptacoordinated species with pentagonal bipyramidal (PBP) arrangements for which two sets of two orbitals with the same energy levels are expected in the ideal geometry (Scheme 1). In real compounds, structural distortions and low symmetry of the ligand field lead to the lifting of degeneracies of the energy levels of these orbitals (from a few hundreds to thousands cm−1). However, a significant ZFS effect has been demonstrated for such complexes, with D parameters of the order of 30 cm−1 for Co(II) to −30 cm−1 for Fe(II) and Ni(II).27 For a given metal ion, the value of D depends on the actual energy difference between these orbitals.28 For instance, in Fe(II) derivatives, the main contribution to the negative D value arises from the transfer of an electron between dxz and dyz orbitals; therefore their energy separation significantly affects the overall value of D. Theoretical calculations have revealed that D will not exceed −10 cm−1 for an energy difference above 400 cm−1, but that D value may reach −20 to −30 cm−1 when the energy difference is reduced to about 200 cm−1.29–32 The same applies to Ni(II) in PBP coordination, but for the d8 configuration it is the dxy and dx2−y2 orbitals that are relevant.28 Thus, to achieve large magnetic anisotropy, it is essential to minimize the energy gap between d orbitals. The optimum situation would be to achieve quasi-degeneracy, which would de facto induce a substantial contribution from first-order SOC.
 | ||
| Scheme 1 Relative energy diagram of the d orbitals in an ideal pentagonal bipyramidal geometry (D5h), the electron filling is for high-spin Fe(II), and sketch of the molecular complexes 1–5. | ||
We show here that PBP complexes with a first-order SOC contribution can be readily obtained, mainly through chemical design optimization ensuring minimum structural distortion and a more symmetrical ligand field.
The PBP coordination polyhedron is typically induced by a pentadentate ligand, which occupies the equatorial positions of the complex and confers remarkable structural robustness. The phenanthroline-based macrocyclic ligand LN5 (Scheme 1) gained our preference because it is planar, obviously stiff, and symmetrical with five coordinating sp2-N atoms. A suitable metal ion is Fe(II). Its high-spin d6 electronic configuration in the PBP geometry leads to three electrons occupying the two dxz and dyz orbitals. As these orbitals are ideally degenerate and are linear combinations of ml = ±1 spherical harmonics, 1st order SOC can take place. However, to maintain the (quasi-)degeneracy of these orbitals, the apical ligands of the complex must have the same interaction with each of these orbitals, and any dissymmetry would induce an energy difference between them.29 Halides (Cl−, Br−, and I−) seemed best suited for this purpose. The corresponding complexes are reported here. Theoretical calculations revealed quasi-degeneracy of the dxz and dyz orbitals (ΔE < 200 cm−1) for all those with halide ligands in the apical positions. Their magnetic behavior indicated strong magnetic anisotropy, and the bromide and iodide derivatives were found to behave as SMMs, the latter even in the absence of a static field.
Results and discussion
Syntheses
The PBP complexes [FeLN5(H2O)Cl]Cl·4.5H2O, 1; [FeLN5Cl2]·3H2O, 2; [FeLN5Br2], 3; [FeLN5I2], 4; and [Fe0.12Zn0.88LN5I2], 5, were obtained by adapting a reported procedure.33 The Fe(II) complex [FeLN5(H2O)Cl]Cl·4.5H2O, 1, was prepared by reacting FeCl2·4H2O, 2,6-diacetylpyridine, and 2,9-di(α-methylhydrazino)-1,10-phenanthroline in H2O in the presence of HCl. When excess NaCl was added to the reaction mixture, co-crystallization of 1 and [FeLN5Cl2]·5H2O, 2 occurred. However, the complexes [FeLN5Br2], 3 and [FeLN5I2], 4 were isolated as single products by the same procedure (i.e. in the presence of an excess amount of either NaBr or NaI, and the corresponding HX acid). The reactions were performed under strictly oxygen-free conditions, although the addition of ascorbic acid was required to avoid traces of oxidation. This was systematically confirmed by Mössbauer spectroscopy (see below). All the complexes were isolated as crystallized solids and the same batch was used for the characterization studies.In order to investigate these Fe complexes diluted in a diamagnetic matrix, the corresponding Zn(II) complexes were synthesized to verify structural concordance. Only the iodide derivative [ZnLN5I2] proved isostructural to the Fe homologue. With Br−, a pentagonal pyramidal complex, [ZnLN5Br]Br·0.5H2O, with a single axial ligand was obtained (Fig. S6†), and the Cl derivative could not be crystallized. Thus, only mixed-metal derivative [Fe0.12Zn0.88LN5I2], 5, was prepared. Information on these Zn complexes are provided in the ESI.†
Crystal structures
The crystal structures for all the complexes have been determined by single-crystal X-ray diffraction analyses; the crystallographic data are given in Table S1 (ESI).† The metal–ligand bond lengths and axial bond angles for the first coordination sphere of 1–4 are gathered in Table 1, and additional information can be found in the ESI (Fig. S1–S6†).| 1 | 2 | 3 | 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fe1–N1 | 2.1112(2) | Fe1–N3 | 2.13(1) | Fe2–N6 | 2.07(1) | Fe1–N1 | 2.128(5) | Fe1–N1 | (2.1053) |
| Fe1–N2 | 2.273(2) | Fe1–N4 | 2.248(7) | Fe2–N5 | 2.252(9) | Fe1–N2 | 2.304(3) | Fe1–N2 | 2.280(2) |
| Fe1–N7 | 2.270(2) | Fe1–N7 | 2.117(9) | Fe2–N2 | 2.124(9) | Fe1–N4 | 2.114(3) | Fe1–N4 | 2.123(2) |
| Fe1–N4 | 2.137(2) | Fe1–Cl1 | 2.575(6) | Fe2–Cl1 | 2.544(2) | Fe1–Br1 | 2.7106(5) | Fe1–I1 | 2.9231(2) |
| Fe1–N5 | 2.134(2) | Fe1–Cl2 | 2.555(6) | Fe2–Cl2 | 2.591(6) | Br–Fe–Br | 171.08(4) | I–Fe–I | 170.556(4) |
| Fe1–Cl | 2.2549(7) | Cl–Fe1–Cl | 171.5(1) | Cl–Fe2–Cl | 170.0(1) | ||||
| Fe1–O1 | 2.193(2) | ||||||||
| Cl–Fe–O | 174.26(5) | ||||||||
Complexes 1–4 and [ZnLN5I2] are mononuclear and have a chemical organization similar to known PBP complexes of 3d metal ions with ligand LN5.33–38 The crystal arrangement of 2 was found to be incommensurable and composed of two superimposed inversed configurations, more information can be found in the ESI.† For each molecular complex, the M(II) center is heptacoordinated and sits in a slightly distorted pentagonal bipyramid environment (Fig. 1 and ESI†). The equatorial plane is formed by five N atoms from pentadentate ligand LN5, while axial positions are occupied by different donor groups: H2O and Cl− for 1, Cl− for 2, Br− for 3, and I− for 4 and [ZnLN5I2]. The Fe–N bond distances in the equatorial sites are found between 2.07 and 2.28 Å, the shortest is with the N of the pyridyl moiety and the longer with the imine groups (Table 1). These bond distances are very similar to those reported for [FeLN5(H2O)2]2+.33 The bonds between the metal center and the halogen atoms in the apical sites are longer, extending from 2.25 to 2.92 Å for Cl− to I−, in line with the increasing van der Waals radii of these atoms. The equatorial coordination arrangement is perfectly planar, the five nitrogen atoms and the iron atom (as well as Zn in [ZnLN5I2]) lie in the same plane (defined by the 5 N, see Fig. S1–S5†), and only for 1 the Fe atom is very marginally outside the plane by 0.022 Å. The apical arrangement very slightly deviates from normal to the equatorial plane, and the X–Fe–X links form an angle of around 170° (Table 1) in all the complexes. Thus, the coordination polyhedron of all these complexes is best described by a pentagonal bipyramidal geometry.
To evaluate the degree of deviation from the ideal PBP geometry, continuous shape measures analysis of the coordination polyhedron was performed with SHAPE software.39,40 The CShM parameter values related to the deviation of the actual shape from ideal PBP for 1–4 are 0.499, 1.060, 1.326, and 2.214, respectively. The divergence, which increases from 1 to 4, can be ascribed to the increasing size of the halogen atoms. Indeed, the distortion of the equatorial plane from the pentagonal geometry is quite small and similar for all complexes (Table S2†). The increasing deviation from the ideal PBP geometry is therefore mainly due to the lengthening of the Fe–Xaxial bonds from 1 to 4 (Table 1) due to the larger size of the halogen atoms which results in an elongated pentagonal bipyramidal environment.
For [ZnLN5Br]Br, the molecular complex exhibits a pentagonal pyramidal coordination sphere with the five N atoms of LN5 bonded to Zn forming the pentagonal base and a coordinated Br located on the apex of the pyramid (Fig. S6†). Zn(II) is located approximately 0.441 Å above the basal plane with N–Zn bond distances ranging from 2.134 Å to 2.350 Å (Fig. S6†), which are slightly longer than those in [ZnLN5I2]. The charge of this cationic complex is compensated by a bromide anion. Although unusual, the formation of a pentagonal pyramidal complex between LN5 and a 3d metal ion is not unprecedented, and it was reported for an Mn(II) derivative with Cl as the apical ligand.41
For all the compounds the crystal packing shows that the complexes are stacked in parallel (Fig. S1–S4†). For 1 and 2 the complexes are organized in layers, with uncoordinated Cl and/or H2O solvates in between (Fig. S1 and S2†), whereas the packing is more compact for the solvent-free 3 and 4. The closest distances between the Fe centers are similar, with values of 8.352(1) to 8.7229(3) Å from 1 to 4. For the Br- and I-derivatives, some rather close separations between the halogen atoms and the hydrogen of adjacent complexes, especially with phenanthroline and pyridyl moieties, become evident when the van der Waals radii of the halogens are considered (about 1.85 and 2.0 Å, respectively). These weak hydrogen bonds (H⋯X: 2.8062(4)–2.9585(4) Å in 3 and 3.0592(2)–3.1730(2) in 4) are likely to inter-connect all the molecules in the solid (Fig. S4†) and propagate magnetic interactions (vide infra).
With the exception of compound 2, the phase concordance of the bulk samples with the crystal structures was confirmed by powder X-ray diffraction (Fig. S7†).
Mössbauer spectroscopy
57Fe Mössbauer spectroscopy was carried out to confirm the oxidation state of the Fe centers and the purity of samples 1, 3, and 4 for magnetic studies. The spectra recorded at 80 K show a unique doublet (Fig. S8†) with a chemical shift near δ = 1.1 mm s−1 and a quadrupole splitting of about Δ = 2.1 mm s−1 (Table 2). These characteristics are comparable to those reported (i.e. 1.1 and 2.74 mm s−1, respectively) for a homologous high-spin Fe(II) complex with H2O as ligands in the apical positions.33 Moreover, Mössbauer data have been reported for several other Fe(II) complexes in the PPB surrounding featuring either a macrocyclic ligand42–44 or an open pentadentate ligand29,45–49 in their equatorial coordination sphere. In all cases the chemical shift is found between 1.0 and 1.2 mm s−1 while their quadrupole splitting is more versatile as it varies with the ligands located in the apical positions.29 Interestingly, Fe(III) in the same PBP environment exhibits a decrease in the chemical shift to about δ = 0.5 mm s−1 with smaller splitting,50,51 which makes it very distinguishable and easy to identify in the Mössbauer spectrum of a Fe(II) derivative. The spectra obtained for 1, 3 and 4 are typical of high spin PBP Fe(II) complexes with no detectable traces of oxidation products.| 1 | 3 | 4 | 5 | |
|---|---|---|---|---|
| Mössbauer doublet (80 K) | ||||
| δ (mm s−1) | 1.10 | 1.09 | 1.05 | — |
| Δ (mm s−1) | 2.12 | 2.14 | 2.03 | — |
| Magnetic characteristics | ||||
| χ M T at 300/2 K (cm3 mol−1 K) | 3.16/2.21 | 3.90/2.11 | 3.27/0.58 | — |
| M (μB) for 50 kOe at 2 K | 2.52 | 2.73 | 2.14 | 2.28 |
| U/kB (K) | — | 89 ± 5 | 99 ± 8 | 88 ± 9 |
| τ 0 (s) | — | 7 × 10−12 | 3 × 10−11 | 2 × 10−10 |
Theoretical calculations
Wavefunction based calculations (SO-CAS(6/5)SCF + NEVPT2) (see the Experimental section for computational information) have been performed on complexes 1 to 4 followed by the procedure of anisotropic parameter extraction proposed by Maurice et al.52 The atom coordinates from the X-ray structures were considered except for the positions of the H atoms that were optimized using DFT calculations.The NEVPT2 energy differences between the spin–orbit free quintuplet ground state and the first excited quintuplet state resulting from d–d transitions are given in Table 3, together with the energies of the AILFT 3d MOs. It should be specified that the lowest Q1 and Q2 states essentially have a mono-configurational wavefunction with a double occupancy either in the dxz or the dyz orbital (depending on the complex).
| Complex | Q2 | Q3 | Q4 | Q5 | dyz | dxz | dx2−y2 | dxy | dz2 |
|---|---|---|---|---|---|---|---|---|---|
| The x, y, and z axes are those presented in Fig. S15.† | |||||||||
| 1 (Cl H2O) | 450 | 6661 | 7951 | 9228 | 0 | 412 | 5275 | 6278 | 7197 |
| 2 (Cl) | 92 | 6804 | 7756 | 9060 | 0 | 91 | 5323 | 6122 | 7048 |
| 3 (Br) | 42 | 5734 | 7999 | 8070 | 134 | 0 | 4597 | 6415 | 6470 |
| 4 (I) | 37 | 6314 | 7962 | 8739 | 142 | 0 | 5020 | 6570 | 7035 |
Atanasov et al.26 have studied a family of trigonal pyramidal iron(II) complexes that exhibit very similar spectra to those calculated here with almost degenerate dxz and dyz orbitals. They proposed a model that accounts for the first-order SOC and the lift of degeneracy arising from geometrical distortions from the ideal C3 symmetry. A related approach has also been developed to characterize a Ni(II) complex.21 This model is applicable to the complexes studied here, for which the ideal symmetry would contain a C5 symmetry axis. In the case of strictly degenerate dxz and dyz orbitals, the ground state is degenerate and consists of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of two quintuplet states (Q1 and Q2) in which either the dxz or the dyz orbital contains a single electron. Distortions of the ideal C5 symmetry will lead to a lift of the degeneracy (2δ1) of these orbitals and to their mixing (δ2) so that the ligand field Hamiltonian matrix can be written as:
1 mixture of two quintuplet states (Q1 and Q2) in which either the dxz or the dyz orbital contains a single electron. Distortions of the ideal C5 symmetry will lead to a lift of the degeneracy (2δ1) of these orbitals and to their mixing (δ2) so that the ligand field Hamiltonian matrix can be written as:
 | (1) |
In the complexes studied here, the states Q1 and Q2 are almost mono-configurational, hence the δ2 parameter is close to zero. As the dxz and dyz orbitals are linear combinations of the Ml = ±1 spherical harmonics, the two spin–orbit free quintuplet states Q1 and Q2 can only be coupled through the ζIzsz part of the spin–orbit Hamiltonian:
 | (2) |
SOCs will generate 10 spin–orbit states, which are the eigenfunctions of the spin–orbit and ligand field Hamiltonian, the representative matrix of which is provided in the ESI (Table S6†). In the absence of SOC with the other excited states, the analytical expressions of the energy of the SO states resulting from this first-order SOC would be:
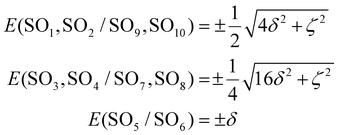 | (3) |
 .
.
The ab initio energy of these SO states is given in Table 4 as well as their wavefunction decomposition on the basis of the two spin–orbit free quintuplet states Q1 and Q2. Of course, the SOC with other excited states is non-zero and is treated ab initio, indicating that the reported energies do not strictly follow these spacings.
| Complex | SO1 | SO2 | SO3 | SO4 | SO5 | SO6 | SO7 | SO8 | SO9 | SO10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Weights (in %) are given for Q1/Q2. SO states SO1, SO2, SO9 and SO10 are based on the Ms = ±2 of Q1 and Q2 respectively, SO3, SO4, SO7 and SO8 on the Ms = ±1 components, and SO5 and SO6 on the Ms = 0 components. | |||||||||||
| 1 | Energies | 0.0 | 1.0 | 34 | 48 | 58 | 507 | 521 | 548 | 601 | 603 |
| Weights | 86/12 | 87/12 | 96/3 | 95/5 | 98/0 | 0/96 | 3/95 | 5/94 | 12/87 | 12/85 | |
| 2 | Energies | 0.0 | 0.0 | 81 | 82 | 141 | 228 | 280 | 320 | 408 | 410 |
| Weights | 61/39 | 61/39 | 71/28 | 69/31 | 99/0 | 0/99 | 28/71 | 31/69 | 39/60 | 39/60 | |
| 3 | Energies | 0.0 | 0.0 | 84 | 86 | 161 | 207 | 275 | 315 | 411 | 411 |
| Weights | 55/44 | 55/44 | 62/38 | 59/40 | 99/0 | 0/99 | 37/62 | 41/59 | 44/55 | 44/55 | |
| 4 | Energies | 0.0 | 0.0 | 87 | 88 | 169 | 208 | 284 | 320 | 421 | 421 |
| Weights | 54/45 | 54/45 | 60/40 | 58/42 | 99/0 | 0/99 | 40/60 | 42/58 | 45/54 | 45/54 | |
In complex 1, the ground state is mainly based on a configuration with a doubly occupied dyz MO (and a single occupation of all other MOs), while Q2, Q3, Q4, and Q5 exhibit double occupancy of the dxz, dx2−y2, dxy and dz2 MOs, respectively. The spectrum presents an energy gap of 450 cm−1 between the ground and first excited states originating from the energy gap between the dyz and dxz MOs. Therefore, the 5 lowest SO states SO1–SO5 are mainly based on the Ms components of Q1 (more than 86%) and are low in energy compared to SO6–SO10 that are mainly based on Q2 components. In this case, the anisotropic ZFS spin Hamiltonian applies (eqn (4)); it is extended with a fourth-order tensor operator represented by B40, as recommended.26
 | (4) |
Parameters B40, D and E, reported in Table 5, have been extracted for complex 1 using the following formulas which result from the diagonalization of the Hamiltonian  matrix (given in Table S7†):
matrix (given in Table S7†):
 | (5) |
| Complex | D (eqn (5)) | D (ORCA) | D (exp) | E (eqn (5)) | E (ORCA) | E (Exp) | B 40 | δ | ζ (ORCA) |
|---|---|---|---|---|---|---|---|---|---|
| Axes are those of the D tensor for complex 1 (Fig. S15†). z is almost aligned with the bond between the metal and the apical ligands and x and y are in the plane of the pentadentate ligand. x is almost along the Fe–N(pyridine) direction in 1 (N1). | |||||||||
| 1 | −14.00 | −13.64 | −24.9 ± 0.4 | 2.33 | 2.24 | 4.06 ± 0.04 | 0.09 | 225 | 411 |
| 2 | — | — | — | — | — | — | — | 43 | 409 |
| 3 | — | — | — | — | — | — | — | 23 | 404 |
| 4 | — | — | — | — | — | — | — | 20 | 396 |
In eqn (5), En±2, En±1 and En0 are the mean energy values of the SO states essentially carried by the Ms = ±2, Ms = ±1, and Ms = 0 spin components, respectively. E is 1/6 of the splitting between the two SO states essentially carried by the Ms = ±1 spin components. The values of the ZFS parameters D and E, and of the spin–orbit constant calculated in ORCA are also reported (Table 5). The decrease of the spin–orbit constant in complexes (in comparison with the free metal ion) is due to the covalent interaction between the metal ion and the ligand and is called the relativistic nephelauxetic effect. As expected, the obtained values follow the spectrochemical series, and therefore, they decrease as the nephelauxetic effect increases, i.e. H2O ≪ Cl− < Br− < I−. This effect is well documented in the literature.54–58 As expected from the nature of the excitation from Q1 to Q2–Q5, the contribution of Q2 to D is negative (−18.9 cm−1) while those of Q3 and Q4 are positive and of much smaller amplitude (+1.97 and 0.72 cm−1, respectively) since these states are much higher in energy, and the contribution of Q5 is almost zero.
The case of complexes 2, 3 and 4 is more complex since the energy gap between Q1 and Q2 is much smaller than in 1, as dyz and dxz are almost degenerate. This small energy gap leads to SO states with a very strong mixing of Q1 and Q2 spin–orbit free states (except for Ms = 0 components that do not interact through SOC) and no clear gap is observed between the 5 lowest and 5 highest energy states. Therefore, the ZFS Hamiltonian is not suited to model magnetic properties of complexes 2–4,60 and only their δ and ζ parameters have been reported in Table 5. Note that parameters D and E are provided by the ORCA code and can be calculated using the formulas given above, but the magnetic moment, which now contains a non-negligible contribution from the angular momentum, can no longer be equated with spin momentum alone. For this reason, an evaluation of the D and E parameters from the magnetic data using spin S = 2 is irrelevant for these complexes.
The calculated g-factors show the anticipated trend with gx ≈ gy ≪ gz, values are tabulated in Table S8.† In addition, the magnetization versus field has been calculated at various temperatures and will be compared below to the measured magnetizations.
Compared with previous works on PBP Fe(II) complexes,29,48 the first order SOC contribution in complexes 2 to 4 is much more important. Indeed, it should be noted that the energy differences between the ground state Q1 spin–orbit free quintuplet and the first excited state (Q2) are particularly small here. For instance, in the earlier reports these values vary between 170 and 410 cm−1, compared to the 37–92 cm−1 found for 2–4 (Table 3). Complex 1, with H2O in the apical position, has an energy difference of 450 cm−1 between Q1 and Q2, and can therefore be described using a ZFS model. In 1, this energy difference is governed by the energy difference between the dyz and dxz orbitals, which in turn is governed by the difference of interactions in the x and y axes. In this respect, the orientation of the π-doublets in the apical positions plays a crucial role in these complexes.48 In 1, the π doublet of H2O is oriented along the x axis (Fig. S15†) and therefore introduces a dissymmetry between x and y axes, which is responsible for the lift of degeneracy between the two orbitals. On the other hand, for halogen atoms as in 2–4, 2 π doublets are involved with identical interactions with dyz and dxz, leading to quasi-degeneracy of the orbitals.
Magnetic properties
The temperature dependence of the molar magnetic susceptibility, χM, in the 2 to 300 K range, and the field dependence of the magnetization at different temperatures between 2 and 8 K were recorded for complexes 1, 3, and 4 (Fig. 2 and S10†).All the derivatives exhibit a paramagnetic behavior characterized by a constant χMT value between 300 and 100 K, followed by an increasingly steep decline as T approaches 2 K. The characteristic values found at 300 and 2 K are listed in Table 2. As can be seen in Fig. 2, the decline is clearly more pronounced for 4. For this compound the M versus H at 2 K also exhibits an S-shape behavior (Fig. 2b). These behaviors indicate antiferromagnetic interactions between the complexes in the solid state.61 This was anticipated from the crystal lattice arrangement of 4, which shows short contacts existing between the Fe complexes by means of I atoms and phenanthroline moieties (vide supra). The M versus H behavior for 5 confirms this hypothesis (Fig. 2b), as such intermolecular magnetic interactions no longer occur for the diluted derivative.
The field dependences of the magnetizations for 1, 3, and 4 between 2 and 8 K are depicted in Fig. S10.† For all complexes, the magnetization achieved for a field of 50 kOe at 2 K is around 2.5μB (Table 2), a value lower than the expected contribution of spin alone for a center with S = 2, confirming the existence of substantial magnetic anisotropy. The theoretical calculations revealed that only derivative 1 shows no mixing between ground and excited states, and so its magnetic behaviors were likely to be analyzed with a ZFS-based model. Indeed, a good adjustment of the experimental M versus H behaviors was obtained with a model for an S = 2 with magnetic anisotropy accounted by ZFS, yielding D = −24.9 ± 0.4 cm−1 and E = 4.06 ± 0.04 cm−1 for g = 2.34 (Fig. S10a†). The negative value for D is in agreement with the anticipated axial magnetic anisotropy for a high-spin d6 ion in PBP geometry,27 and with the calculated value. A similar analysis proved impossible for 3 (let alone 4), which is in line with the conclusion of the theoretical studies. However, for these complexes the experimental M versus H behaviors are well reproduced by the calculated behaviors as described above (Fig. S10†).
The existence of a slow magnetization relaxation phenomenon was examined by AC-mode magnetic susceptibility measurements in zero field and in the presence of an applied magnetic field. For 1, just the onset of an out-of-phase component of the susceptibility,  , is observed in the applied field (Fig. S11†), a behavior indicative of fast relaxation above 2 K. For 3, a slow relaxation is revealed when a small field is applied to cancel the QTM (quantum tunneling of the magnetization), while the
, is observed in the applied field (Fig. S11†), a behavior indicative of fast relaxation above 2 K. For 3, a slow relaxation is revealed when a small field is applied to cancel the QTM (quantum tunneling of the magnetization), while the  versus T for 4 in zero field shows a frequency dependent peak (Fig. S12a and S13a,† respectively).
versus T for 4 in zero field shows a frequency dependent peak (Fig. S12a and S13a,† respectively).
For 3, the optimum applied DC field, i.e. for which the peak signal of  is the largest and at the lowest frequency, turned out to be 5 kOe (Fig. S12b†). Detailed AC studies were carried out with this applied field to reveal frequency and temperature dependencies of the
is the largest and at the lowest frequency, turned out to be 5 kOe (Fig. S12b†). Detailed AC studies were carried out with this applied field to reveal frequency and temperature dependencies of the  characteristic for an SMM (Fig. 3 and S12†). The relaxation times, τ, between 2 and 5.6 K were obtained from the analyses of
characteristic for an SMM (Fig. 3 and S12†). The relaxation times, τ, between 2 and 5.6 K were obtained from the analyses of  versus ν behaviors using a generalized Debye model.62 The temperature dependency of τ is well modeled by an expression combining an Orbach process (Arrhenius law) and a direct mechanism to account for the lower temperature behavior (eqn (6), respectively first and second term).1,5 The best fit gave U/kB = 89 ± 5 K, τ0 = 7 × 10−12 s, DHn = 14.6 ± 0.1 K−1 s−1.
versus ν behaviors using a generalized Debye model.62 The temperature dependency of τ is well modeled by an expression combining an Orbach process (Arrhenius law) and a direct mechanism to account for the lower temperature behavior (eqn (6), respectively first and second term).1,5 The best fit gave U/kB = 89 ± 5 K, τ0 = 7 × 10−12 s, DHn = 14.6 ± 0.1 K−1 s−1.
τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−U/kBT) + DH2T + QTM−1 exp(−U/kBT) + DH2T + QTM−1 | (6) |
 | ||
Fig. 3 [FeLN5Br2], 3: (left panel)  versus ν, in the 2–6 K temperature range with HDC = 5 kOe; (right panel) experimental (O) and calculated (—) relaxation time, τ, versus 1/T with best-fit associated with eqn (6) (see the main text). versus ν, in the 2–6 K temperature range with HDC = 5 kOe; (right panel) experimental (O) and calculated (—) relaxation time, τ, versus 1/T with best-fit associated with eqn (6) (see the main text). | ||
For 4, the temperature dependency of  in the absence of a static applied magnetic field exhibits a well-defined peak shape with the maximum shifts from about 6 K to lower T with decreasing AC frequencies from 1500 to 1 Hz (Fig. S13b†). However,
in the absence of a static applied magnetic field exhibits a well-defined peak shape with the maximum shifts from about 6 K to lower T with decreasing AC frequencies from 1500 to 1 Hz (Fig. S13b†). However,  does not tend to return to zero after reaching the peak when the temperature is lowered. The behavior at lower temperatures (<3 K) is characteristic of QTM, but a second, smaller peak is also observed at around 3.5 K. This second component could be the signature of magnetic ordering, which is also suggested by the meta-magnetic behavior shown by 4 (Fig. 2b). Indeed, the second (T-independent) signal is no longer found for 5 (vide infra). Moreover, the signal at 3.5 K is dampened by the application of a DC field (Fig. S13e and f†). In the field, the maximum of
does not tend to return to zero after reaching the peak when the temperature is lowered. The behavior at lower temperatures (<3 K) is characteristic of QTM, but a second, smaller peak is also observed at around 3.5 K. This second component could be the signature of magnetic ordering, which is also suggested by the meta-magnetic behavior shown by 4 (Fig. 2b). Indeed, the second (T-independent) signal is no longer found for 5 (vide infra). Moreover, the signal at 3.5 K is dampened by the application of a DC field (Fig. S13e and f†). In the field, the maximum of  at 2 K steadily shifts to a lower frequency until about 5 kOe, suggesting QTM cancellation, but it also continuously increases in intensity with DC fields up to 10 kOe (Fig. S13e†). The latter trend can be attributed to a gradual decoupling of intermolecular interactions by the applied field.
at 2 K steadily shifts to a lower frequency until about 5 kOe, suggesting QTM cancellation, but it also continuously increases in intensity with DC fields up to 10 kOe (Fig. S13e†). The latter trend can be attributed to a gradual decoupling of intermolecular interactions by the applied field.
The relaxation times, τ, for 4 in the absence of an applied field could be obtained between 2 and 6.4 K from the analyses of  versus ν behaviors by a generalized Debye model (Fig. S13c and Table S4†). The plot of τ versus 1/T (Fig. S13d†) shows three domains characteristic of temperature activated relaxation (6.4–5.8 K), T-independent relaxation (5.6 to about 3.5 K), and for lower T a steady increase of the relation time likely due to the intermolecular interactions taking place at these temperatures. The temperature dependence of τ between 6.4 and 3.0 K is well modeled by an expression combining an Orbach process and QTM (first and third terms in eqn (6)). Best fit gave U/kB = 76 ± 6 K, τ0 = 8 × 10−10 s, and QTM = 3.41 × 10−4 s (Fig. S13d†), confirming the SMM behavior in zero-field for 4.
versus ν behaviors by a generalized Debye model (Fig. S13c and Table S4†). The plot of τ versus 1/T (Fig. S13d†) shows three domains characteristic of temperature activated relaxation (6.4–5.8 K), T-independent relaxation (5.6 to about 3.5 K), and for lower T a steady increase of the relation time likely due to the intermolecular interactions taking place at these temperatures. The temperature dependence of τ between 6.4 and 3.0 K is well modeled by an expression combining an Orbach process and QTM (first and third terms in eqn (6)). Best fit gave U/kB = 76 ± 6 K, τ0 = 8 × 10−10 s, and QTM = 3.41 × 10−4 s (Fig. S13d†), confirming the SMM behavior in zero-field for 4.
In order to avoid the contribution of the QTM, an investigation of the SMM characteristics was performed with an applied field of 5 kOe (Fig. S13g–l†). Under these conditions, the temperature dependence of the relaxation of the relaxation time follows an Orbach behavior in the higher T-domain and a Direct process below 5 K, characterized by U/kB = 99 ± 8 K, τ0 = 3 × 10−11 s, and DHn = 11.47 ± 0.09 K−1 s−1. It can be noticed that these parameters are very similar to those of the Br-derivative, 3.
For the solid solution of [FeLN5I2] in [ZnLN5I2], 5, AC magnetic susceptibility recorded in the absence of an applied static magnetic field confirms the emergence of a  signal below 9 K for a test frequency of 997 Hz (Fig. S14a†). However, the profile of the behavior, with a poorly resolved peak and a continuously increasing contribution with decreasing temperature, is a characteristic of rapid relaxation processes such as QTM. The latter is quenched when a static field is applied; for 5, 1 kOe was found to be optimal (Fig. S14b†) and was applied for detailed AC studies. The
signal below 9 K for a test frequency of 997 Hz (Fig. S14a†). However, the profile of the behavior, with a poorly resolved peak and a continuously increasing contribution with decreasing temperature, is a characteristic of rapid relaxation processes such as QTM. The latter is quenched when a static field is applied; for 5, 1 kOe was found to be optimal (Fig. S14b†) and was applied for detailed AC studies. The  versus ν behavior at different temperatures between 2 and 7 K and the related temperature dependence of τ are depicted in Fig. 4 (additional plots are shown in Fig. S14†). And here again, τ versus 1/T of [FeLN5I2] in 5 is perfectly modeled using an Orbach and a Direct process (eqn (6)) with U/kB = 88 ± 9 K, τ0 = 2 × 10−10 s, and DHn = 4.13 ± 0.04 K−1 s−1. The energy barrier for magnetization reversal is very similar to that obtained for the bulk [FeLN5I2], confirming the molecular origin of the low T magnetization freezing. No evidence for magnetic hysteresis was found in the M versus H behaviors recorded at 2 and 5 K (Fig. S10†).
versus ν behavior at different temperatures between 2 and 7 K and the related temperature dependence of τ are depicted in Fig. 4 (additional plots are shown in Fig. S14†). And here again, τ versus 1/T of [FeLN5I2] in 5 is perfectly modeled using an Orbach and a Direct process (eqn (6)) with U/kB = 88 ± 9 K, τ0 = 2 × 10−10 s, and DHn = 4.13 ± 0.04 K−1 s−1. The energy barrier for magnetization reversal is very similar to that obtained for the bulk [FeLN5I2], confirming the molecular origin of the low T magnetization freezing. No evidence for magnetic hysteresis was found in the M versus H behaviors recorded at 2 and 5 K (Fig. S10†).
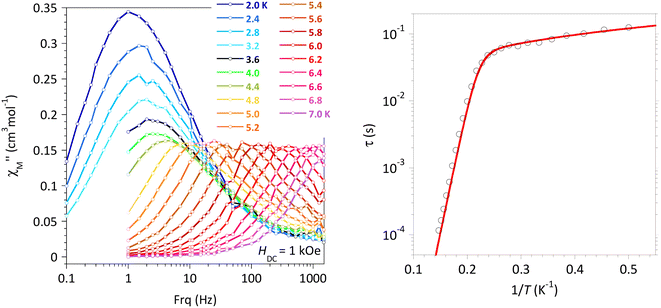 | ||
Fig. 4 [Fe0.12Zn0.88LN5I2], 5: (left panel)  versus ν with HDC = 1 kOe, in the 2–7 K temperature range; (right panel) experimental (O) and calculated (—) relaxation time τ versus 1/T with best-fit associated with eqn (6) (see the main text). versus ν with HDC = 1 kOe, in the 2–7 K temperature range; (right panel) experimental (O) and calculated (—) relaxation time τ versus 1/T with best-fit associated with eqn (6) (see the main text). | ||
An SMM-type behavior with a magnetization reversal regulated mainly by a thermal activation is clearly evidenced for 2–5. For the I-derivative, slow magnetization relaxation is even observed in zero-field, a behavior hardly found in mononuclear 3d ion SMMs. For all, the effective energy barriers, U/kB, are much larger than those usually reported for PBP complexes of Fe(II),27 and reach that described for linear two-coordinated Fe(II) with first-order SOC.15
Concluding remarks
Unlike lanthanide ions, 1st-order spin–orbit coupling is cancelled by the ligand field for transition metal ions, and achieving high magnetic anisotropy is generally considered the Holy Grail for these ions. The results gathered herein show that the contribution from first-order SOC is not confined to low-coordination number complexes but can be implemented in a pentagonal bipyramidal Fe(II) complex by appropriate chemical design.The rigid pentadentate ligand, LN5, imposes an effective equatorial coordination sphere close to a pentagonal and symmetrical ligand field, and apical ligands (halogens in the present case), which exhibit a very similar overlap with the dxz and dyz orbitals, lead to a quasi-degenerate state for these orbitals sharing 3 electrons. The mixing of the Ms levels, revealed by the theoretical calculations, confirms the existence of the 1st-order SOC and rules out the possibility of describing the magnetic behavior within the ZFS formalism.
Further evidence is provided by the experimental behavior, which is consistent with the existence of large magnetic anisotropy, the most salient feature being the SMM behavior with large energy barriers for magnetization reversal. The observation of such a behavior without an applied static magnetic field is quite unique for a mononuclear 3d complex.
Finally, such complexes with quasi-degenerated magnetic orbitals are also desirable building units for the design of exchange-coupled polynuclear compounds. Some recent studies have shown that close to a first-order SOC regime, anisotropic interactions such as the Dzyaloshinskii–Moriya63,64 or the symmetric exchange tensor of anisotropy may also reach high values.65,66
Experimental section
Materials and methods
All the chemicals used were commercially available and were employed without further purification. 2,9-Di(α-methylhydrazino)-1,10-phenanthroline·2HCl, denoted as PhenMeNH2·2HCl, was synthesized from methylhydrazine and 2,9-dichloro-1,10-phenanthroline67 according to a literature procedure.68 All the syntheses of FeII complexes were carried out under N2 using Schlenk techniques and degassed solvents (diethyl ether was purified using an Innovative Technology Solvent Purification® system while the alcohol and water solvents were distilled under N2 prior to use). The solid samples for the characterization of the FeII complexes were prepared in a glovebox. Technical information can be found in the ESI.†Synthetic procedures
Single-crystal X-ray diffraction
Intensity data were collected at low temperature on an Apex2 Bruker diffractometer equipped with a 30 W air-cooled microfocus source (λ = 0.71073 Å). Structures for 1, 3, 4, [ZnLN5Br]·Br and ZnLN5I2 were solved using SUPERFLIP69 or ShelxT70 and refined by means of least squares procedures using the PC version of the CRYSTALS program.71 Atomic scattering factors were taken from the international tables for X-ray crystallography.72 All non-hydrogen atoms were refined anisotropically. Structure for 2 was found to be modulated with a modulation vector of 0.6754a + 0.1052c. The structure was solved by charge flipping methods using the SUPERFLIP program69 using the super-space group C2/m(a0g)0s and refined using Jana2006.73 The structure is composed of two superimposed inversed configurations of the complex. The incommensurately modulated structure of this complex was successfully solved and refined in (3 + 1) dimensions, evidencing an ordered-disorder along the fourth dimension as well as a significant atomic displacement from the average positions. Additional information can be found in the ESI.†Computational information
CASSCF and NEVPT2 calculations were performed with Orca5.0 package59 considering 6 active electrons and 5 active MOs, i.e. those with a major Fe 3d character. Extended DKH-def2 atomic basis sets were used for all atoms except I: QZVPP for Fe atoms (14s10p5d4f2 g), TZVP for C (6s3p2d1f), N (6s3p2d1f), O (6s3p2d1f), Cl (8s4p2d1f), Br (10s8p4d1f), SVP for H atoms (2s1p) and a 15s11p5d1f basis set for I atoms. Optimization of the positions of the H atoms was performed by DFT calculations using def2-SVP atomic basis sets and the PBE functional.Data availability
Crystallographic data have been deposited at the CCDC under 2352840 (1), 2352845 (2), 2352841 (3), 2352842 (4), 2352843 ([ZnLN5Br]·Br), and 2352844 (ZnLN5I2) and can be obtained from https://www.ccdc.cam.ac.uk/structures/.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to M. J.-F. Meunier (LCC) and M. V. Collière (LCC) for technical assistance in magnetic, Mössbauer, and EDX data collection.References
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed.
- C. Coulon, H. Miyasaka and R. Clérac, in Single-Molecule Magnets and Related Phenomena, ed. R. Winpenny, Springer, Berlin, 2006, vol. 122, pp. 163–206 Search PubMed.
- J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078 Search PubMed.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef CAS PubMed.
- S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- J. M. Frost, K. L. M. Harriman and M. Murugesu, The rise of 3-d single-ion magnets in molecular magnetism: towards materials from molecules?, Chem. Sci., 2016, 7, 2470–2491 RSC.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- P. Kumar Sahu, R. Kharel, S. Shome, S. Goswami and S. Konar, Understanding the unceasing evolution of Co(II) based single-ion magnets, Coord. Chem. Rev., 2023, 475, 214871 CrossRef CAS.
- E. A. Boudreaux and L. N. Mulay, Theory and applications of molecular paramagnetism, Wiley-Interscience Publication, 1976 Search PubMed.
- L. Sorace, C. Benelli and D. Gatteschi, Lanthanides in molecular magnetism: old tools in a new field, Chem. Soc. Rev., 2011, 40, 3092 RSC.
- R. Boca, Zero-field splitting in metal complexes, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef CAS.
- A. K. Bar, C. Pichon and J.-P. Sutter, Magnetic anisotropy in two- to eight-coordinated transition–metal complexes: Recent developments in molecular magnetism, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS.
- W. M. Reiff, A. M. LaPointe and E. H. Witten, Virtual Free Ion Magnetism and the Absence of Jahn-Teller Distortion in a Linear Two-Coordinate Complex of High-Spin Iron(II), J. Am. Chem. Soc., 2004, 126, 10206–10207 CrossRef CAS PubMed.
- W. M. Reiff, C. E. Schulz, M.-H. Whangbo, J. I. Seo, Y. S. Lee, G. R. Potratz, C. W. Spicer and G. S. Girolami, Consequences of a Linear Two-Coordinate Geometry for the Orbital Magnetism and Jahn-Teller Distortion Behavior of the High Spin Iron(II) Complex Fe[N(t-Bu)2]2, J. Am. Chem. Soc., 2009, 131, 404–405 CrossRef CAS PubMed.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Slow magnetization dynamics in a series of two-coordinate iron(II) complexes, Chem. Sci., 2013, 4, 125–138 RSC.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Magnetic blocking in a linear iron(I) complex, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, Slow Magnetic Relaxation in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes, J. Am. Chem. Soc., 2010, 132, 18115 CrossRef CAS PubMed.
- A. V. Palii, J. M. Clemente-Juan, E. Coronado, S. I. Klokishner, S. M. Ostrovsky and O. S. Reu, Role of Orbital Degeneracy in the Single Molecule Magnet Behavior of a Mononuclear High-Spin Fe(II) Complex, Inorg. Chem., 2010, 49, 8073–8077 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state, Science, 2018, 362, 7319 CrossRef PubMed.
- X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS PubMed.
- R. Ruamps, R. Maurice, L. Batchelor, M. Boggio-Pasqua, R. Guillot, A. L. Barra, J. Liu, E.-E. Bendeif, S. Pillet, S. Hill, T. Mallah and N. Guihéry, Giant Ising-Type Magnetic Anisotropy in Trigonal Bipyramidal Ni(II) Complexes: Experiment and Theory, J. Am. Chem. Soc., 2013, 135, 3017–3026 CrossRef CAS PubMed.
- S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, Huge Magnetic Anisotropy in a Trigonal-Pyramidal Nickel(II) Complex, Inorg. Chem., 2013, 53, 676–678 CrossRef PubMed.
- R. C. Poulten, M. J. Page, A. G. Algarra, J. J. Le Roy, I. López, E. Carter, A. Llobet, S. A. Macgregor, M. F. Mahon, D. M. Murphy, M. Murugesu and M. K. Whittlesey, Synthesis, Electronic Structure, and Magnetism of [Ni(6-Mes)2]+: A Two-Coordinate Nickel(I) Complex Stabilized by Bulky N-Heterocyclic Carbenes, J. Am. Chem. Soc., 2013, 135, 13640–13643 CrossRef CAS PubMed.
- W. A. Merrill, T. A. Stich, M. Brynda, G. J. Yeagle, J. C. Fettinger, R. De Hont, W. M. Reiff, C. E. Schulz, R. D. Britt and P. P. Power, Direct Spectroscopic Observation of Large Quenching of First-Order Orbital Angular Momentum with Bending in Monomeric, Two-Coordinate Fe(II) Primary Amido Complexes and the Profound Magnetic Effects of the Absence of Jahn− and Renner−Teller Distortions in Rigorously Linear Coordination, J. Am. Chem. Soc., 2009, 131, 12693–12702 CrossRef PubMed.
- M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, A theoretical analysis of chemical bonding, vibronic coupling, and magnetic anisotropy in linear iron(II) complexes with single-molecule magnet behavior, Chem. Sci., 2013, 4, 139–156 RSC.
- M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Detailed Ab Initio First-Principles Study of the Magnetic Anisotropy in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes, Inorg. Chem., 2011, 50, 7460–7477 CrossRef CAS PubMed.
- J.-P. Sutter, V. Béreau, V. Jubault, K. Bretosh, C. Pichon and C. Duhayon, Magnetic anisotropy of transition metal and lanthanide ions in pentagonal bipyramidal geometry, Chem. Soc. Rev., 2022, 51, 3280–3313 RSC.
- R. Ruamps, L. J. J. Batchelor, R. Maurice, N. Gogoi, P. Jiménez-Lozano, N. Guihéry, C. de Graaf, A.-L. Barra, J.-P. Sutter and T. Mallah, Origin of the Magnetic Anisotropy in Ni(II) and Co(II) Heptacoordinate Complexes, Chem. – Eur. J., 2013, 19, 950–957 CrossRef CAS PubMed.
- A. K. Bar, N. Gogoi, C. Pichon, V. M. L. D. P. Goli, M. Thlijeni, C. Duhayon, N. Suaud, N. Guihéry, A.-L. Barra, S. Ramasesha and J.-P. Sutter, Pentagonal Bipyramid FeII Complexes: Robust Ising-Spin Units towards Heteropolynuclear Nanomagnets, Chem. – Eur. J., 2017, 23, 4380–4396 CrossRef CAS PubMed.
- P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Structure and Magnetism of Seven–Coordinate FeIII, FeII, CoII and NiII Complexes Containing a Heptadentate 15–Membered Pyridine–Based Macrocyclic Ligand, Eur. J. Inorg. Chem., 2018, 4286–4297 CrossRef CAS.
- A. Mondal, S.-Q. Wu, O. Sato and S. Konar, Effect of Axial Ligands on Easy-Axis Anisotropy and Field-Induced Slow Magnetic Relaxation in Heptacoordinated FeII Complexes, Chem. – Eur. J., 2020, 26, 4780–4789 CrossRef CAS PubMed.
- V. Jubault, B. Pradines, C. Pichon, N. Suaud, C. Duhayon, N. Guihéry and J.-P. Sutter, Homochiral SCM Built of Tetrahedral and Pentagonal Bipyramidal Fe(II) Units Bridged by Chlorine, Cryst. Growth Des., 2023, 23, 1229–1237 CrossRef CAS.
- M. M. Bishop, J. Lewis, T. D. O'Donoghue, P. R. Raithby and J. N. Ramsden, Chemistry of polydentate ligands. Part 8. Preparation and properties of iron(II) complexes with quinquedentate macrocyclic ligands. Crystal and molecular structure of a compound where high-spin Fe sits in the ligand cavity. Electrochemistry of a series of complexes with the macrocycles, Dalton Trans., 1980, 1390–1396 RSC.
- M. M. Bishop, J. Lewis, T. D. O'Donoghue, P. R. Raithby and J. N. Ramsden, X-Ray crystal structure of a planar, high-spin iron(II) complex of a pentadentate unsaturated macrocycle formed by reaction of 2,9-di(1-methylhydrazino)1,10-phenanthroline monohydrochloride with 2,6-diacetylpyridine, J. Chem. Soc., Chem. Commun., 1978, 828–829 RSC.
- L. R. Hanton and P. R. Raithby, Diaqua(7,l5-dihydro-7,9,13,15-tetramethylpyrido[2′,1′,6′:12,13,14][1,2,4,7,9,10,13]heptaazacyclopentadeca[3,4,5,6,7,8-aklmn][1,10]phenanthroline)cobalt(II) bis(tetrafluoroborate) [Co(H2O)2(tdmmb)][BF4]2, Acta Crystallogr., Sect. B, 1980, 36, 1489–1491 CrossRef.
- C. W. G. Ansell, J. Lewis, P. R. Raithby, J. N. Ramsden and M. Schroder, X-Ray crystal structure of the pentagonal bipyramidal nickel(II) complex [Ni(L)(H2O)2](BF4)2 and the selective stabilisation of the nickel(I) oxidation state by a quinquedentate macrocyclic ligand, J. Chem. Soc., Chem. Commun., 1982, 546–547 RSC.
- D. Shao, S.-L. Zhang, L. Shi, Y.-Q. Zhang and X.-Y. Wang, Probing the Effect of Axial Ligands on Easy-Plane Anisotropy of Pentagonal-Bipyramidal Cobalt(II) Single-Ion Magnets, Inorg. Chem., 2016, 55, 10859–10869 CrossRef CAS PubMed.
- K. Bretosh, V. Béreau, C. Duhayon, C. Pichon and J.-P. Sutter, A ferromagnetic Ni(II)–Cr(III) single-chain magnet based on pentagonal bipyramidal building units, Inorg. Chem. Front., 2020, 7, 1503–1511 RSC.
- D. Casanova, P. Alemany, J. M. Bofill and S. Alvarez, Shape and symmetry of heptacoordinated transition-metal complexes: structural trends, Chem. – Eur. J., 2003, 9, 1281–1295 CrossRef CAS PubMed.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE: Program for the stereochemical analysis of molecular fragments by means of continuous shape measures and associated tools, University of Barcelona, Barcelona, 2013 Search PubMed.
- J. Lewis, T. D. O'Donoghue and P. R. Raithby, Chemistry of polydentate ligands. Part 7. Synthesis, characterisation, and properties of some manganese(II) complexes of quinquedentate macrocyclic ligands based on 1,10-phenanthroline. Crystal and molecular structure of a complex with pentagonal-pyramidal coordination geometry about the Mn, Dalton Trans., 1980, 1383–1389 RSC.
- M. G. Drew, A. Hamid Bin Othman, W. Hill, P. McIlroy and S. M. Nelson, Seven-coordinate complexes of iron(II) with pentadentate macrocyclic ligands, Inorg. Chim. Acta, 1975, 12, L25–L26 CrossRef.
- T. S. Venkatakrishnan, S. Sahoo, N. Bréfuel, C. Duhayon, C. Paulsen, A.-L. Barra, S. Ramasesha and J.-P. Sutter, Enhanced Ion Anisotropy by Nonconventional Coordination Geometry: Single-Chain Magnet Behavior for a [{FeIIL}2{NbIV(CN)8}] Helical Chain Compound Designed with Heptacoordinate FeII, J. Am. Chem. Soc., 2010, 132, 6047–6056 CrossRef CAS PubMed.
- B. Drahoš, R. Herchel and Z. Trávníček, Single-Chain Magnet Based on 1D Polymeric Azido-Bridged Seven-Coordinate Fe(II) Complex with a Pyridine-Based Macrocyclic Ligand, Inorg. Chem., 2018, 57, 12718–12726 Search PubMed.
- A. S. M. Al-Shihri, J. R. Dilworth, S. D. Howe, J. Silver, R. M. Thompson, J. Davies and D. C. Povey, Synthesis and characterization of some novel pentagonal bipyramidal 2,6-diacetylpyridine bis(benzoylhydrazone) (DAPBH2) complexes of Rhenium(III) and molybdenum crystal and molecular structure of [ReCl(DAPB)(PPh3)]. An investigation of the Mössbauer spectroscopy of [FeIICl2(DAPBH2)]·H2O and [FeIIICl(DAP-Me-B)(H2O)], Polyhedron, 1993, 12, 2297–2305 CrossRef CAS.
- H. S. Soo, M. T. Sougrati, F. Grandjean, G. J. Long and C. J. Chang, A seven-coordinate iron platform and its oxo and nitrene reactivity, Inorg. Chim. Acta, 2011, 369, 82–91 CrossRef CAS.
- A. K. Bar, C. Pichon, N. Gogoi, C. Duhayon, S. Ramasesha and J.-P. Sutter, Single-ion magnet behaviour of heptacoordinated Fe(II) complexes: on the importance of supramolecular organization, Chem. Commun., 2015, 51, 3616–3619 Search PubMed.
- C. Pichon, N. Suaud, V. Jubault, C. Duhayon, N. Guihéry and J.-P. Sutter, Trinuclear Cyanido-Bridged [Cr2Fe] Complexes: To Be or not to Be a Single-Molecule Magnet, a Matter of Straightness, Chem. – Eur. J., 2021, 27, 15484–15495 CrossRef CAS PubMed.
- Y. P. Tupolova, D. V. Korchagin, A. S. Andreeva, V. V. Tkachev, G. V. Shilov, V. A. Lazarenko, L. D. Popov, K. A. Babeshkin, N. N. Efimov, R. B. Morgunov, A. V. Palii, S. P. Kubrin, I. N. Shcherbakov and S. M. Aldoshin, Mononuclear Heptacoordinated 3d-Metal Helicates as a New Family of Single Ion Magnets, Magnetochemistry, 2022, 8, 153 CrossRef CAS.
- F. A. Deeney and S. M. Nelson, Relaxation effects in the mössbauer spectra of some seven-coordinate iron(III) complexes, J. Phys. Chem. Solids, 1973, 34, 277–282 CrossRef CAS.
- D. Darmanović, I. N. Shcherbakov, C. Duboc, V. Spasojević, D. Hanžel, K. Anđelković, D. Radanović, I. Turel, M. Milenković, M. Gruden, B. Čobeljić and M. Zlatar, Combined Experimental and Theoretical Investigation of the Origin of Magnetic Anisotropy in Pentagonal Bipyramidal Isothiocyanato Co(II), Ni(II), and Fe(III) Complexes with Quaternary-Ammonium-Functionalized 2,6-Diacetylpyridine Bisacylhydrazone, J. Phys. Chem. C, 2019, 123, 31142–31155 CrossRef.
- R. Maurice, R. Bastardis, C. D. Graaf, N. Suaud, T. Mallah and N. Guihéry, Universal Theoretical Approach to Extract Anisotropic Spin Hamiltonians, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
- R. S. Fishman and F. A. Reboredo, Magnetic anisotropy in the Fe(II)Fe(III) bimetallic oxalates, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 144421 CrossRef.
- C. K. Jorgensen, Orbitals in atoms and molecules, Academic Press, London, 1962 Search PubMed.
- C. K. Jørgensen, in Advances in Chemical Physics, ed. I. Prigogine, 1963, vol. 5, pp. 33–146 Search PubMed.
- C. K. Jørgensen, in Structure and Bonding, ed. C. K. Jørgensen, J. B. Neilands, R. S. Nyholm, D. Reinen and R. J. P. Williams, Springer Berlin Heidelberg, Berlin, Heidelberg, 1969, pp. 94–115 Search PubMed.
- A. Bencini, C. Benelli and D. Gatteschi, The angular overlap model for the description of the paramagnetic properties of transition metal complexes, Coord. Chem. Rev., 1984, 60, 131–169 CrossRef CAS.
- F. Neese and E. I. Solomon, Calculation of Zero-Field Splittings, g-Values, and the Relativistic Nephelauxetic Effect in Transition Metal Complexes. Application to High-Spin Ferric Complexes, Inorg. Chem., 1998, 37, 6568–6582 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- B. R. McGarvey and J. Telser, Simple Ligand-Field Theory of d4 and d6 Transition Metal Complexes with a C3 Symmetry Axis, Inorg. Chem., 2012, 51, 6000–6010 CrossRef CAS PubMed.
- Y. Hosokoshi, M. Tamura, D. Shiomi, N. Iwasawa, K. Nozawa, M. Kinoshita, H. Aruga Katori and T. Goto, Organic radical crystals, α-nitronyl nitroxide family: High-field magnetization study, Phys. B, 1994, 201, 497–499 CrossRef CAS.
- C. Dekker, A. F. M. Arts, H. W. de Wijn, A. J. van Duyneveldt and J. A. Mydosh, Activated dynamics in a two-dimensional Ising spin glass: Rb_{2}Cu_{1-x}Co_{x}F_{4}, Phys. Rev. B:Condens. Matter Mater. Phys., 1989, 40, 11243 CrossRef CAS PubMed.
- I. Dzyaloshinsky, A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics, J. Phys. Chem. Solids, 1958, 4, 241–255 CrossRef CAS.
- T. Moriya, Anisotropic Superexchange Interaction and Weak Ferromagnetism, Phys. Rev., 1960, 120, 91–98 CrossRef CAS.
- M.-A. Bouammali, N. Suaud, R. Maurice and N. Guihéry, Extraction of giant Dzyaloshinskii–Moriya interaction from ab initio calculations: First-order spin–orbit coupling model and methodological study, J. Chem. Phys., 2021, 155, 164305 CrossRef CAS PubMed.
- M.-A. Bouammali, N. Suaud, C. Martins, R. Maurice and N. Guihéry, How to create giant Dzyaloshinskii–Moriya interactions? Analytical derivation and ab initio calculations on model dicopper(II) complexes, J. Chem. Phys., 2021, 154, 134301 CrossRef CAS PubMed.
- H. C. Guo, R. H. Zheng and H. J. Jiang, Improved Synthesis of 2,9-Dichloro-1,10-phenanthroline, Org. Prep. Proced. Int., 2012, 44, 392–396 CrossRef CAS.
- J. Lewis and T. D. O'Donoghue, Chemistry of polydentate ligands. Part 5. Complexes of 2,9-di-hydrazino-derivatives of 1,10-phenanthroline. Dependence of co-ordination number of a ligand on the anion present, Dalton Trans., 1980, 736–742 RSC.
- L. Palatinus and G. Chapuis, Superflip, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- S.-P. V5.4, Bruker Analytical X-ray Systems, Madison, WI., 1999 Search PubMed.
- P. W. Betteridge, J. R. Carruthers, R. I. Cooper, K. Prout and D. J. Watkin, CRYSTALS, J. Appl. Crystallogr., 2003, 36, 1487–1487 CrossRef CAS.
- International Tables for X-ray Crystallography, ed. A. J. C. Wilson, Kluwer Academic, Dordrecht, 1992 Search PubMed.
- M. Dusek, V. Petricek and L. Palatinus, Introduction to JANA2006, Acta Crystallogr., Sect. A:Found. Crystallogr., 2006, 62, s46 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental information; crystal structure solution for 2, crystallographic information, related plots, and bond lengths and angles for all the compounds, PXRD, Mössbauer spectra, EDX analysis of 5, additional magnetic behaviors, and data from theoretical calculations. CCDC 2352840–2352845. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi03255a |
| This journal is © the Partner Organisations 2025 |


