Open Access Article
Open Access ArticleMass transport effects in gas-phase selective hydrogenation of 1,3-butadiene over supported Pd†
Oscar E.
Brandt Corstius
 a,
M.
Kikkert
a,
S. T.
Roberts
a,
M.
Kikkert
a,
S. T.
Roberts
 b,
E. J.
Doskocil
c,
J. E. S.
van der Hoeven
b,
E. J.
Doskocil
c,
J. E. S.
van der Hoeven
 a and
P. E.
de Jongh
a and
P. E.
de Jongh
 *a
*a
aMaterials Chemistry and Catalysis, Debye Institute for Nanomaterials Science, Utrecht University, Universiteitsweg 99, 3584 CG Utrecht, The Netherlands. E-mail: P.E.deJongh@uu.nl
bApplied Sciences, bp Innovation and Engineering, BP plc, Saltend, Hull, HU12 8DS, UK
cApplied Sciences, bp Innovation and Engineering, BP plc, Chicago, IL 60606, USA
First published on 26th March 2024
Abstract
Selective hydrogenation reactions are essential in the purification of light olefins by removal of polyunsaturated hydrocarbon impurities (alkynes/alkadienes). Pd-based catalysts are typically used because of their high activity at ambient temperatures. Unfortunately, retaining high selectivity at high conversion using a Pd catalyst is challenging, resulting in more undesired alkane formation, which is often ascribed to intrinsic properties of the Pd metal. However, in this work we show that heat and mass transport effects strongly impact the catalytic activity and selectivity of Pd nanoparticles on carbon catalysts (Pd/C) in the selective hydrogenation of butadiene. By systematically varying the Pd loading and catalyst grain size, we show that higher loadings and larger grains strongly decrease the butene selectivity. This is ascribed to an effect of internal diffusion limitations, arising from butadiene depletion in the core of the catalyst grains, and not by intrinsic properties of Pd. The comprehensive assessment of heat and mass transport phenomena is essential to reliably relate experimental observations to catalyst properties such as Pd particle size, support or promoter effects. It contributes to the understanding and rational design of catalysts for selective hydrogenation of butadiene and can be extended to other reactions and/or supported metal catalysts.
1. Introduction
Selective hydrogenation is of great interest both for academic research as well as for industrial applications.1–4 Examples of selective hydrogenation reactions are (i) the semi-hydrogenation of alkynes or alkadienes to alkenes, (ii) the partial hydrogenation of α,β-unsaturated ketones or aldehydes to unsaturated alcohols and (iii) the selective hydrogenation of substituted nitro-arenes.1 These reactions are essential for the industrial production of fine chemicals,2 food additives, flavours, fragrances and pharmaceuticals.3 A large-scale industrial application of selective hydrogenation is the semi-hydrogenation of polyunsaturated hydrocarbons (e.g., alkynes or alkadienes) for the purification of alkenes, such as ethylene, propylene and butenes.4 These alkenes (light olefins) are chemical building blocks for the production of polymers (plastics) with varying applications. It is essential to reduce these alkyne or alkadiene impurities from the %-level down to parts per million (ppm) to prevent deactivation of the polymerisation catalyst and minimise uncontrolled crosslinking in the polymer product.1,4,5Typical industrial catalysts for selective hydrogenation reactions are supported Pd-based nanoparticles, because of their superior activity at moderate temperatures.5–7 Of the platinum group metals (Rh, Pd, Pt), Pd shows the highest selectivity to alkenes.8 The high activity of Pd, however, also induces challenges in retaining good selectivity, as Pd often leads to unwanted alkane production, which decreases the total yield of the desired alkenes. The poor performance of monometallic Pd is ascribed to properties such as strong heat of adsorption of the reactant9 and/or the formation of Pd-hydride.6 Therefore, commercially available Pd-based catalysts for selective hydrogenation are typically modified with secondary metals such as Ag (ref. 10) or Pb (ref. 11) and/or molecular adsorbates.11,12 Proposed explanations for the increased selectivity of modified Pd include geometric13–15 and/or electronic9,15–19 effects. Such modifications increase the selectivity but often come at the expense of the conversion. The surface- or mass-normalised activity roughly decreases by 1 to 2 orders of magnitude compared to monometallic Pd, which is undesirable considering the scarcity and costs of Pd metal.13,18–21 This raises the question of how improved selectivity can be disentangled from the effects of reduced activity. Hence, a fundamental understanding of Pd-based catalyst intrinsic performance is valuable.
In addition to the chemical properties of a catalyst, a considerable influence on the catalytic performance is related to its physical and structural properties in combination with the reaction conditions. For example, the heat generation in exothermic reactions can induce local temperature effects on or near the active metal nanoparticle surface if the overall heat conductivity of the system is not sufficient. Early attempts by Luss to model the heat generated by an exothermic reaction over platinum nanoparticles predicted a temperature increase with an upper bound as high as 200 to 500 °C.22 Sharma et al. spectroscopically showed that the surface temperature of a 1% Pt/SiO2 catalyst increased by 119 °C, from 98 to 217 °C, upon continuous exposure to a CO/O2 mixture.23 Similarly, a temperature difference of 130 °C between the metal nanoparticle and the reaction gas was found during steady-state oxidation of 2% CO over a Pt/Al2O3 monolith.24 Geitenbeek et al. showed by luminescence thermometry that a sharp increase in temperature is induced during methanol-to-hydrocarbons (MTH) reactions.25 Upon exposure of the reaction gas (18% methanol in He) over H-ZSM-5 zeolite catalyst, a temperature increase of 100 °C was observed, from 500 to 600 °C, which took up to 2 hours to stabilise to steady-state conversion. This illustrates that exothermic reactions can cause local heating effects that can be deliberately applied to induce higher catalytic activity,26 but should be avoided when determining the intrinsic structure–performance relationships of a catalyst.
In heterogeneous catalysis, the activity scales with the concentration of the reactants and the reaction order. Hence, the reactant concentration at the catalyst active site is highly relevant. In typical reactors (e.g. plug flow), unless operating in differential conversion mode, a significant concentration gradient over the catalytic bed exists due to the difference in reactant concentration at the beginning (inlet) and end of the catalytic bed (outlet). This concentration gradient increases with the increasing conversion. If a catalyst reaction rate surpasses the reactant diffusion rate, a concentration gradient is generated in the vicinity of the catalyst, which is referred to as mass transport or diffusion limitations. With external mass transport limitations, the reaction rate is limited by the reactant supply from the bulk gas or liquid phase to the catalyst grains. Internal mass transport limitations describe the limitations of diffusion within a catalyst grain, as a gradient is induced from the surface to its interior. A framework for assessing the effect of these mass transport limitations has been developed by Thiele, Weisz and Prater.27,28 For selective hydrogenation reactions, the presence of diffusion limitations can negatively influence not only the activity but also the selectivity.29,30 This is aggravated by the presence of micropores,31 larger catalyst grain sizes,32 and/or coke build-up.33–36 The Barreto group studied the kinetics of selective hydrogenation of butyne- and butadiene–butene mixtures in trickle bed reactors.37,38 They demonstrated that the local concentration of polyunsaturated molecules sharply dropped inside the catalyst grains due to internal mass transfer limitations. These results gave valuable insights into some parameters determining selectivity during selective hydrogenation reactions. However, the literature has been focused on liquid-phase hydrogenation in batch operation, whereas academic selective hydrogenation of alkynes and alkadienes mostly occurs in the gas phase during continuous operation.1 Liquid-phase and gas-phase hydrogenation differ from a kinetic viewpoint, as the effective diffusion of gasses is orders of magnitude faster than in the condensed phase.39 Moreover, in liquid-phase hydrogenation reactions, the reaction kinetics depend on the solubility of molecular hydrogen, which complicates the comparison of literature with gas–solid heterogeneous catalysis.
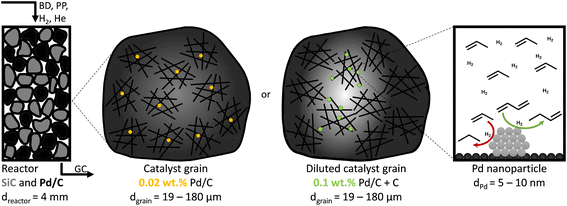
Therefore, the objectives of this work were to assess the influence of local temperature and reactant concentration gradients for selective hydrogenation of hydrocarbons using Pd-catalysts. As a model system, we tested the catalytic removal of 1,3-butadiene (butadiene hereafter) traces from a propylene-rich gas mixture. We describe the influence of heat and mass transport on the catalytic performance during the gas-phase selective hydrogenation, over a wide range of Pd weight loadings (from 2.5% to 0.02%, decreases in catalyst activity) and average catalyst grain sizes (from 180 to 19 μm, increases in reactant diffusion). We demonstrate that diffusion limitations, induced by high metal loading and large grain sizes, strongly affect the catalytic performance of Pd/C catalysts and explain how these effects are identified and avoided.
2. Methodology
2.1 Chemicals and gasses
For the preparation of Pd/C catalysts, 10 wt% tetraamine palladium(II) nitrate solution (99.99%, Sigma Aldrich) and graphene nanoplatelets (GNP, xGNP®C-500, 500 m2 g−1, 1–20 nm average thickness, 0.5–1.0 μm average width, XG Sciences) were used.For the heat treatments and catalytic testing, 1,3-butadiene (>99.5% purity, Air Liquide Benelux, 0.21% cis-2-butene impurity), propylene (>99.5% purity, The Linde Group, 0.04% propane impurity), hydrogen (>99.9990% purity), helium (>99.9990% purity) and nitrogen (>99.9990% purity) were used.
2.2 Catalyst preparation and characterisation
Carbon-supported Pd-catalysts were prepared by incipient wetness impregnation of Pd-precursor onto graphene nanoplatelets (GNP) support. It was shown before that this carbon material is effective in (selective) oxidation and hydrogenation reactions.21,40–43 In short, 2 g of carbon was dried under a dynamic vacuum at 180 °C for 1 hour. Subsequently, a Pd-precursor solution with a volume equal to support pore volume (0.8 cm3 g−1) was added dropwise to the dried carbon material. The desired metal weight loading (2.5 wt%) of the Pd/C catalyst was achieved by dilution of the 10 wt% tetraamine palladium(II) nitrate with purified water (18.2 MΩ cm resistivity at 25 °C, Direct-Q® 3 UV), while the lower weight loadings (0.5 wt%, 0.1 wt% and 0.02 wt%) were prepared by successive further dilution of the impregnation solution of the 2.5%_Pd/C catalyst with purified water. The range of Pd loadings was chosen in line with typical selective hydrogenation catalysts (e.g., 5% Pd/CaCO3 with Pb- and quinoline-modifiers and 0.01% Pd/Al2O3 with Ag additive).10,11 After incipient wetness impregnation, the solids were homogenised by gentle stirring for 1 hour. The impregnated support was dried under a dynamic vacuum overnight at room temperature. Subsequently, the material was heat treated in N2 at 250 °C (1 °C min−1, 1 hour isothermal, 100 mL min−1 flow) and cooled to room temperature. Pd nanoparticles were grown to the desired size using a high-temperature reduction step at 500 °C in 10% H2 (1 °C min−1, 1 hour hold, 10 and 90 mL min−1 H2 and N2 flow).21,44Transmission Electron Microscopy (TEM) of the as-synthesised Pd/C catalysts was performed on a Talos L120C (Thermo Scientific) electron microscope operated in bright field mode at 120 kV. Images of the post-catalysis samples were acquired by scanning TEM (STEM) on a Talos F200X (Thermo Scientific) electron microscope operated in dark field mode at 200 kV. Pd/C catalysts were loaded into Cu-grids (300-micron mesh, Holey Carbon Film, Agar Scientific) by dry-dipping the grid into the catalyst powder. Nanoparticle sizes were determined by manually measuring the diameters of 100–400 Pd particles in different regions of the sample using ImageJ software. The number-averaged particle diameter (dTEM), as derived from TEM, is defined as:
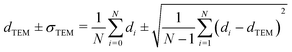 | (1) |
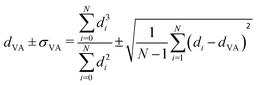 | (2) |
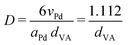 | (3) |
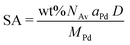 | (4) |
X-ray diffraction (XRD) measurements were performed on a Bruker D2 Phaser equipped with a Co,Kα radiation source (λ = 0.179 nm). Diffractograms were obtained by measuring 0.2 g of undiluted catalyst in Bruker powder specimen holder from 20 to 70° 2θ, with 0.05° step size and 1 second time step under 15 rpm rotation. Scans were continuously accumulated for at least 60 hours to improve the signal-to-noise ratio. Pd crystallite sizes (dXRD) were determined from the width of the Pd(111) diffraction signal using the Scherrer equation:47
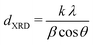 | (5) |
2.3 Catalytic testing
The catalytic performance was assessed in a custom-built gas-phase hydrogenation set-up using a glass U-shaped fixed-bed reactor of 4.0 mm internal diameter, as previously described by Masoud et al.50 A thermocouple was pressed into a glass notch directly after the catalytic bed to measure the temperature of the catalytic bed as accurately as possible without interacting with the reactant gasses. During the selective hydrogenation, a gas flow of 50 mL min−1 was used, consisting of 0.3% butadiene, 30% propylene, 20% hydrogen and helium as a balance, to mimic typical industrial front-end concentrations.51The as-prepared catalysts of 2.5%, 0.5% and 0.1% Pd/C (by weight) were diluted in bare carbon (GNP), so the final weight loading of all Pd/C–C mixtures was 0.02% Pd (Fig. 1). Of the (diluted) catalysts, 1.0 g was pressed into a pellet (74 MPa), which was then gently crushed over a set of sieves to obtain sieve fractions of 1–37 μm, 38–74 μm, 75–149 μm and 150–211 μm. The chosen sieve fractions resulted in broad range of catalyst grain sizes, from very fine particles to more coarse grains, in line with typical catalysts in academic studies.53 For each catalytic test, 2.50 mg of (diluted) catalyst was mixed with 0.30 g of SiC (212–400 μm), which resulted in a constant metal loading of 0.50 μg Pd in the reactor. Prior to the introduction of the reaction gas, the reactor was flushed for 30 minutes with N2, to remove traces of air. Simultaneously the reaction gas composition was analysed on bypass by an on-line GC (Thermo Scientific TRACE 1300, FID detector, hydrocarbons detected: C1 to C5). During the catalytic test, the product and reactant concentrations were measured every 15 minutes, calibrated using a known mixture of 1,3-butadiene, 1-butene, trans-2-butene, cis-2-butene, n-butane, hydrogen, helium, propylene and propane (The Linde Group).
From the GC injections, the conversion (Xi) was calculated as:
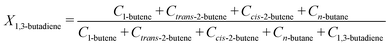 | (6) |
The selectivity (Si) of the reaction to butenes is defined as:
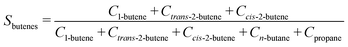 | (7) |
| Qbutenes = X1,3-butadieneSbutene | (8) |
2.4 Calculations of transport phenomena
Estimations of heat and mass transfer effects in catalytic fixed-bed reactions were calculated using the Eurokin web-tool52 and the references therewithin. As criteria for mass and heat transport limitations, a deviation of more than 5% from the non-limited activity is considered as a transport-limited reaction.27,28,52,53 A detailed description of the calculations is provided in the supporting information. The calculations are based on the diffusion and thermal properties of the gasses as obtained from the literature (Table S1†). Temperature-dependent values are determined at the relevant reaction temperature during the catalysis. The density of the gas mixture is based on the ideal gas law, assuming constant pressure (1 atm). The properties of the reactor and the catalyst materials are listed in Table 1. The pellet density was calculated by measuring the thickness of a 13 mm catalyst pellet with known mass prior to sieving, pressed at 74 MPa. The porosity was calculated by adding a known amount of material to catalytic reactor and measuring the height of a catalyst bed.| a Average grain size from 1–37, 38–74, 75–149 and 150–211 μm sieve fractions. | |||||
|---|---|---|---|---|---|
| Pressure | 1.01325 | ×105 Pa | Pellet porosity (εp) | 0.82 | m3 mcat−3 |
| Molar inlet flow (F) | 3.44 | ×10−5 mol s−1 | Pellet density (ρp) | 657 | kg mcat−3 |
| Internal diameter | 4.0 | ×10−3 m | Catalyst density (ρcat) | 1045 | kg mbed−3 |
| Bed porosity (ε) | 0.37 | m3 mbed−3 | Mass catalyst (mcat) | 2.5 | ×10−6 kg |
| Tortuosity (τ) | 1.64 | — | Catalyst grain size (dp) | 19, 56,112, 180a | ×10−6 m |
| Reaction-order (n) | −0.2521 | — | Catalyst surface area | 500 | ×103 m2 kg−1 |
For the diffusion criteria, butadiene is taken as the limiting reactant (0.3 mol%) in the gas mixture. The calculated bulk diffusivity (DBD,Bulk, eqn (S1)–(S3)†) of butadiene in the mixture was 1.5–2.5 × 10−6 m2 s−1 between 25 and 100 °C (Table S1†). Taking in consideration Knudsen diffusion, the effective diffusivity (DBD,eff, eqn (S4)–(S6)) was estimated to be between 3.5 × 10−7 and 3.9 × 10−7 m2 s−1 (see ESI† for details), in line with other estimations on gas-phase diffusion in porous solids.39 In this calculation, cylindrical pores were assumed for the support, for which the pore diameter was estimated from the catalyst density and the surface area of the carbon (Table 1). This geometrical assumption overestimated the microporosity of the carbon, which had a relatively open catalyst structure (vide infra, section 3.1). For the carbon support, porosity arises from the stacking of graphitic plate-like sheets and not from channel-like micropores. Hence the provided values for Deff should be considered as a lower limit for butadiene diffusion rates.
External and internal heat transfer phenomena were calculated based on the rate and exothermicity of the reactions and the thermal properties of the gas mixture (Table S1†) or the solid catalyst. The heat of the reaction was determined from the hydrogenation reaction enthalpy of each reactant (butadiene, butene, propylene). In the butadiene hydrogenation reaction, the different butene products have slightly different reaction enthalpies (−110, −120 and −116 kJ mol−1 for 1-butene, trans-2-butene and cis-2-butene, respectively). An average value of −113.8 kJ mol−1 is obtained for the typical product distribution of Pd-catalysed butadiene hydrogenation (60% 1-butene, 37% trans-2-butene and 3% cis-2-butene).8,21 For the hydrogenation of propylene −124 kJ mol−1 is used, and −125 kJ mol−1 for the over-hydrogenation of 1-butene to n-butane. External temperature gradients were calculated as the temperature difference over the gas film that surrounds the catalyst grain (eqn (S16)–(S20)). The difference between the average temperature of the catalyst grain and the external surface temperature of the grain was calculated as the internal temperature gradient (eqn (S21)). The temperature differences were compared to the dimensionless activation energy of butadiene hydrogenation to check the activity criterion (<5% deviation) as a result of heat transfer limitations.
External and internal mass transfer limitations were assessed by comparison of the effective diffusion of butadiene and the observed rate of consumption of butadiene molecules. The volumetric reaction rate of the catalyst grains, RObsvol. (mol m−3 s−1), is defined as:
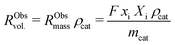 | (9) |
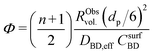 | (10) |
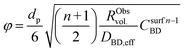 | (11) |
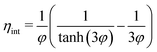 | (12) |
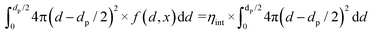 | (13) |
| f(d, x) = e−dx | (14) |
| f(d, x) = 1 − dx | (15) |
| f(d, x) = 1 − edx | (16) |
3. Results and discussion
3.1 Structural properties of supported Pd catalysts
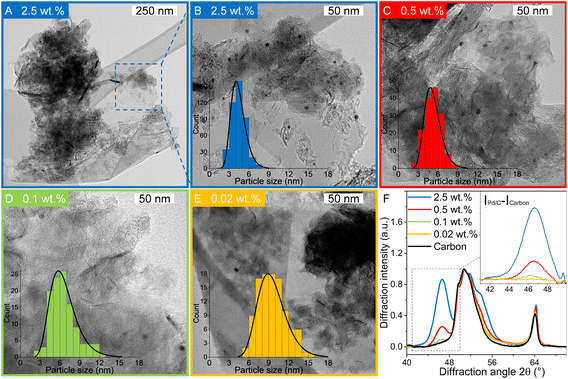
Pd-catalysts of different weight loadings were prepared by incipient wetness impregnation followed by a reduction treatment at 500 °C to induce Pd particle growth.21,44Fig. 2A shows the Transmission Electron Microscopy (TEM) image of a typical Pd/C catalyst grain of roughly 1 micron. Fig. 2B–E depict higher magnification images of the supported Pd nanoparticles of four selected catalysts. The images show Pd particles of similar size dispersed over the carbon support. The number of visible particles per image decreased with decreasing weight loading, showing just a single Pd particle in the TEM image with the lowest Pd loading (Fig. 2E, 0.02 wt%). Average Pd particle sizes between 4.4 and 9.6 nm in diameter were found for the different catalysts, resulting in a specific Pd surface area between 0.01 and 2.6 m2 g−1 (Table 2). An increasing trend in size was observed with decreasing weight loading, contrary to expected loading-size correlations, where higher metal loadings typically result in more agglomeration and thus larger particles.57–60 The observed trend in particle size might be attributed to a slight instability of the diluted Pd-precursor, as the catalysts were prepared from high to low weight loading in successive order (see section 2.2), although more a more detailed study into the catalyst synthesis mechanism would be required to confirm this interpretation. Regardless of the slight trend, the nanoparticles in the different catalysts were of a suitable size (>4 nm), so minimal effects due to size-dependent catalytic performance are present.21 For the catalytic results, the catalysts will be referred to according to their specific Pd surface area (SA) as X_Pd/C, where X is the exposed surface of the Pd nanoparticles, in mPd2 gcatalyst−1.| Catalyst | Pda wt% | d TEM (nm) | d VA (nm) | Dispersionb | SA (mPd2 gcat−1) | d XRD (nm) |
|---|---|---|---|---|---|---|
| a Determined from precursor amount in incipient wetness impregnation. b Determined by Dispersion = 1.112/dVA (eqn (3)). c Not determined due too low weight loading. | ||||||
| 2.6_Pd/C | 2.51 | 4.4 ± 1.1 | 4.9 ± 1.2 | 22.6% | 2.55 | 3.8 |
| 0.4_Pd/C | 0.49 | 5.3 ± 1.2 | 5.8 ± 1.3 | 19.3% | 0.42 | 4.3 |
| 0.06_Pd/C | 0.10 | 6.6 ± 2.0 | 7.8 ± 2.5 | 14.2% | 0.064 | 5.8 |
| 0.01_Pd/C | 0.019 | 9.6 ± 2.1 | 10.4 ± 2.3 | 10.6% | 0.0091 | n.d.c |
X-ray diffraction (XRD, Fig. S1†) showed diffraction peaks of graphite (support) and metallic palladium nanoparticles and no indication of other crystalline phases, such as Pd-oxide, between 20 and 70° 2θ. Fig. 2F shows the Pd(111) diffraction at 46.6° 2θ, which increased in intensity for higher Pd weight loading. The carbon-subtracted spectra in the inset of the figure gives the isolated Pd(111) peak. The crystallite size of Pd particles was determined from the full width at half maximum (FWHM) of the carbon-subtracted Pd(111) diffraction peak, according to the Scherrer equation.47–49 Average crystallite sizes between 3.8 and 5.8 nm were found for the catalyst between 2.5 and 0.1 wt% Pd, respectively (Table 1). For the 0.02 wt% catalyst, the diffraction signal was too weak to observe any Pd diffraction. The trends in crystallite size from XRD corroborate the particle sizes obtained by TEM (Table 2), suggesting that the Pd particles are single crystalline.
3.2 Conversion and catalyst activity
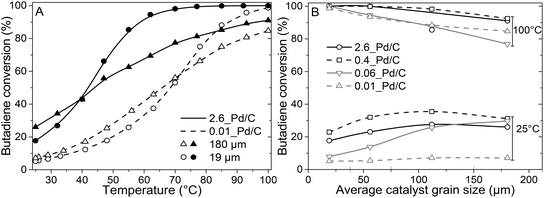
The catalytic activity was tested in the selective hydrogenation of 0.3% butadiene in a 100-fold excess of propylene and 20% H2 (He balance). Fig. 3A depicts the conversion of butadiene as a function of temperature for 0.01_Pd/C and 2.6_Pd/C for the smallest (19 μm) and largest (180 μm) average grain size. The conversion increased with temperature and showed an S-shaped curve. This shape reflects an initial exponential increase followed by saturation when approaching full conversion. A complete overview of all combinations of Pd loadings and grain sizes is provided in Fig. S2.†Surprisingly, the observed activity at 25 °C was different for the different catalyst grain sizes within the same catalyst sample (comparing triangles to circles), even though an identical amount of Pd metal was loaded in each reactor (0.50 μg Pd). For example, the activity of the 180 μm grains was 1.4–1.5 times higher than the 19 μm grains at 25 °C. A local heating effect can explain this phenomenon. With the larger grains, the same amount of catalyst is concentrated in fewer grains. For example, decreasing the radius of one spherical grain by a factor of 2, results in 23 = 8 times smaller grains with a combined volume equal to the single larger grain. Therefore, with larger grain size, the generated heat from the exothermic hydrogenation reactions was retained in fewer particles, in a smaller fraction of the catalyst bed. The generated heat within the vicinity of the catalyst grains resulted in a higher local temperature, which induced higher apparent activity. The 1.4–1.5 times increase corresponds to a temperature increase of 5–6 °C assuming Arrhenius behaviour and 50 kJ mol−1 activation energy (eqn (S14)†), which is less than 9.1 °C adiabatic temperature increase estimated at 100% butadiene conversion (eqn (S15)†).5,21
Fig. 3A also shows that at 25 °C, the activity for 2.6_Pd/C was roughly 3.5 times higher than for 0.01_Pd/C with an equal amount of metal loaded in the reactor. The activity ratio between these two catalysts (3.5) was larger than their corresponding metal dispersion ratio (2.1, Table 2). Therefore, the particle size difference cannot explain the activity increase of 2.6_Pd/C. The trends in higher activity with higher Pd loading were ascribed to more local heating of the catalysts with higher Pd loading. In the undiluted 0.01_Pd/C (Fig. 1), the distribution of Pd is uniform over the catalyst grain. In contrast, for 0.06_Pd/C, the specific Pd area is 7 times more concentrated and more heterogeneously distributed throughout the catalyst grain since it is mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 ratio with bare carbon (Fig. 1). Such local concentration effects also contributed to local heating in the 0.4_Pd/C and 2.6_ Pd/C catalysts, with 25 and 125 more concentrated Pd in parts of the catalyst grain.
4 ratio with bare carbon (Fig. 1). Such local concentration effects also contributed to local heating in the 0.4_Pd/C and 2.6_ Pd/C catalysts, with 25 and 125 more concentrated Pd in parts of the catalyst grain.
From the initial exponential increase with temperature, the apparent activation energies (Eact) were derived between 25 and 47 °C. The Arrhenius plots (Fig. S3†) yield Eact of 45.9 ± 0.4 and 43.4 ± 0.3 kJ mol−1 for 2.6_Pd/C and 0.01_Pd/C with 19 μm grain size, respectively, in line with previous studies on Pd-catalysed butadiene hydrogenation.5,21 For the 0.01_Pd/C catalyst with 180 μm grains, a similar Eact (43.3 ± 0.7 kJ mol−1) was found, whereas for 2.6_Pd/C, the obtained value is only 25.8 ± 2 kJ mol−1. The lower apparent activation energies for higher loadings and larger grains suggested the occurrence of mass transport limitations already below 47 °C and 40% conversion.
At higher conversion, the 19 μm grains were more active than the 180 μm grains, and an inverted trend was observed compared to at 25 °C (Fig. 3A and B). The decrease in activity for the larger grains originated from mass transfer limitations becoming more prominent, as evidenced by the decreasing slope in the Arrhenius plot (Fig. S3†). Because of the increasing activity of Pd/C at elevated temperatures, the diffusion rate of butadiene became limiting. Hence, a part of the volume of the catalyst grains was deficient in butadiene concentration, resulting in a lower average activity. As a result, none of the tested catalysts with 180 μm grains showed 100% conversion at 100 °C, whereas for the smaller grains, full conversion was obtained (Fig. 3B).
In short, reactors with equal Pd mass loading showed variable catalytic activity, which cannot be explained by an effect of particle size.21 Local heating effects induced higher activity over Pd/C catalysts with higher Pd loading and/or larger grain size, especially at low conversion. At higher conversion, the activity trend as a function of grain size was inverted due to increasing mass transfer limitations. Here, smaller grains outperformed the larger grains, as depicted by the cross-over point of the catalysts in Fig. 3A and S2.† Local concentration gradients as a result of diffusion limitations, have a large influence in obtaining active catalysts.26 However, this only describes the activity of the catalyst, whereas selectivity is of essential importance, especially in selective hydrogenation applications.
3.3 Selectivity to butenes
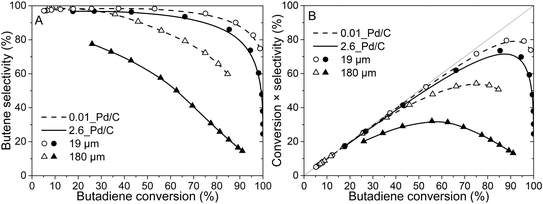
Fig. 4A shows the selectivity to butenes as of function over butadiene conversion of 2.6_Pd/C and 0.01_Pd/C catalysts for the smallest (19 μm) and largest (180 μm) tested average grain size. The complete overview of tested catalysts is shown in Fig. S4.† In Fig. 4A, the 19 μm grains show a selectivity close to 100% at low (e.g. <25%) butadiene conversion levels. The high butene selectivity is explained by the strong adsorption of butadiene, in comparison to butenes or propylene (adsorption energy of −1.7 eV for butadiene, between −0.7 and −0.9 eV for propylene and butenes on Pd(111)).61,62 Therefore, as a result of strong competitive adsorption, the Pd nanoparticle surface is covered by butadiene, which effectively blocks propylene adsorption and limits the residence time of the butene that is formed. Only at higher butadiene conversion levels (e.g., >85%), the selectivity decreased due to a decreasing concentration of butadiene at the nanoparticle surface.The 0.01_Pd/C catalyst with larger grains (180 μm) also showed a high selectivity at low conversion levels (e.g., >90% selectivity below 50% conversion), whereas, for 2.6_Pd/C, the selectivity was below 80% at 26% conversion. For the butane selectivity, similar trends were observed as a function of Pd loading and grain size (Fig. S5A†). The combination of high loading and large grains resulted in a poor selectivity, which is ascribed to internal mass transfer limitations as a result of high activity (increases with higher loading) and lower butadiene diffusion rate (decreases with larger grain size). This combination induced an intraparticle butadiene concentration gradient, which decreases from the edge of the grain toward the interior. As a result, near the edge of the grain, butadiene is converted selectively, whereas further inside the grain, butane and propane formation occur due to the lower butadiene concentration and hence higher coverage with alkenes. A more detailed discussion of internal mass transfer limitations is provided in section 3.4. For the combination of the tested highest Pd loading and grain size, this selectivity was already limited at low temperatures (25 °C, 26% conversion), where smaller grain and lower loading retained their selectivity up to higher conversion. For example, the 19 μm grains retained a selectivity above 90% up to 75% conversion.
Fig. 4B depicts the butene yield as a function of butadiene conversion, where yield was calculated by multiplication of conversion and selectivity (eqn (8)). At low conversions, the yield increased linearly, following the diagonally (i.e., 100% selectivity) dotted lines because the total reaction selectivity is constant and near 100% (Fig. 4A). The yield slowly deviated from the diagonal line upon increasing temperature and hence conversion as selectivity declines. Eventually, the yield even decreases with increasing conversion. Thus, the interplay between increasing butadiene conversion and decreasing butene selectivity induced an optimum butene concentration in the gas mixture. This optimum was close to 80% butene yield (95% conversion) for the 0.01_Pd/C with 19 μm grains, whereas lower values for the optimum yield and conversion were found for the larger grains (Fig. 4B). For example, over the 2.6_Pd/C catalyst with 180 μm grains, a maximum yield of only 32% was obtained at 58% butadiene conversion.
Thus, the selectivity of the reaction strongly depended on the Pd loading and catalyst grain size, especially at higher conversion levels. All tested catalysts showed a decrease in selectivity with increasing conversion. The smallest tested grains (19 μm) showed good butene selectivity up to ∼100% butadiene conversion, in line with the requirements for selective hydrogenation.1,4,5 On the contrary, the largest tested catalyst grains (180 μm) showed a steep decrease in selectivity already at moderate conversion levels (<50%), as was also observed in liquid-phase selective hydrogenation reactions.29 The strong dependence of the selectivity on catalyst grain size showed that internal mass transfer limitations can greatly influence catalyst selectivity.
3.4 The influence of heat and mass transport
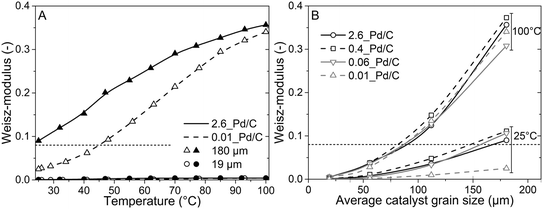
To better understand the experimental observations in sections 3.2 and 3.3, potential heat and mass transport limitations were assessed. First, the catalyst of which the performance was most affected by transport limitations (180 μm grain size, 2.6_Pd/C) was studied in more detail. An overview of all the heat and mass transport calculations is presented in Table S2.† In short, heat transport limitations were negligible, as the estimated temperature gradients (external and internal) were less than 0.7 °C (eqn (S16) and (S21)†). This low value is related to the high thermal conductivity of the reaction mixture (50% He and 20% H2, >150 mW mK−1 (ref. 63)) and the solid catalyst material (Pd and C, >70 and >400 W mK−1, respectively).64,65External mass transfer limitations, resulting in a butadiene concentration gradient from the bulk gas phase to the outer surface of the catalyst grain, had little to no influence on catalysis. Even at 100 °C, a Carberry number of 0.03 (Table S2†) was calculated, well below the 0.2 criterion for a 5% activity deviation (eqn (S22)†). However, internal mass transfer limitations were present already at 25 °C, as a Weisz-modulus (Φ) of 0.09 was calculated, just above the Weisz-Prater criterion of 0.08 (eqn (10), dashed horizontal line). At higher temperatures, the increased activity led to more diffusion limitations of the reactants (Φ = 0.3), resulting in an effectiveness factor of 87% at 100 °C.
Since internal diffusion limitations were the main contributor to transport-limitations, they were examined in more detail. Fig. 5A shows the calculated Weisz-modulus of 0.01_Pd/C and 2.6_Pd/C catalysts, with either 19 μm or 180 μm average grain size. The 19 μm grains showed a small Weisz-modulus (Φ < 0.005 at 100 °C) and internal mass transfer limitations can be neglected. More severe limitations were observed over the larger grains, with Φ = 0.02 or 0.09 at 25 °C for 2.6_Pd/C or 0.01_Pd/C, respectively. With increasing temperature, the Weisz-moduli increased to values above 0.3 at 100 °C, indicating strong internal diffusion limitations. Fig. 5B provides an overview of the derived Weisz-moduli of tested Pd loadings and grain sizes, at the lowest (25 °C) and highest (100 °C) tested temperature. For the 180 μm grains at 25 °C, only the 0.01_Pd/C catalyst showed a sufficiently low Weisz-modulus below the Weisz–Prater criterion (Φ < 0.08, dashed horizontal line). At 100 °C, catalysts with 56 μm or smaller grains were needed to satisfy this criterion. The internal effectiveness factors (eqn (12)) are depicted in Fig. S6.† The calculated values of Φ for the catalysts in Fig. 5A clearly indicate the importance of internal mass transfer limitations for both the experimentally observed activity (Fig. 3A) and selectivity (Fig. 4A), which both decrease with increasing Weisz-modulus.
The internal effectiveness factor, ηint, can be used to estimate the butadiene concentration gradient within the catalyst grain (eqn 13). Fig. 6 shows the calculated butadiene concentration in a spherical 180 μm grain of the 0.01_Pd/C catalyst. The values for ηint were taken at the lowest (25 °C) and highest (100 °C) catalysis testing temperatures (Fig. S6†), and the Pd loading was assumed to be uniformly distributed throughout a spherical grain. At 25 °C, an effectiveness factor of 98% was obtained, resulting in a relatively flat concentration profile (black lines in Fig. 6). This means the average butadiene concentration in the grain equalled 98% of the concentration at the surface of the grain (d = 0, eqn (13)). At 100 °C, the bulk concentration was slightly lower, following the ideal gas law. Moreover, a lower effectiveness factor of 84% was obtained. Accordingly, a steeper decrease of the butadiene concentration gradient was calculated (red lines in Fig. 6). For a linear concentration gradient (assuming zero-order reaction, n = 0), the butadiene concentration in the middle of the grain was calculated to be less than 37% of the surface concentration. When a negative reaction order (n < 0) is assumed (as observed for strongly adsorbing butadiene5,21), the reaction rate increases with decreasing reactant concentration, resulting in a faster declining gradient towards the middle of the catalyst grain.66 As a result, in this example, part of the grain (31% of the diameter, 3.0% of the volume) is completely free of butadiene, which enables alkane formation in the interior. Although near the external surface of the grain, hydrogenation is selective due to the high concentration of butadiene,67 the unselective alkane formation in the interior of the grain will strongly decrease the overall selectivity. Note that this concentration profile is a one-dimensional representation of the grain, and for a spherical shape, half of the volume is located in the outer 21% radial distance. Moreover, this analysis assumed uniformly distributed Pd throughout the catalyst grain, which in practice is only valid for the undiluted 0.01_Pd/C catalyst. For the higher weight loadings, the Pd/C catalyst was mixed with inert carbon (see Fig. 1), resulting in locally higher Pd concentration and steeper local butadiene concentration gradients.
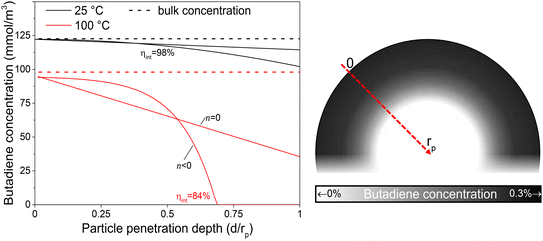 | ||
| Fig. 6 Schematic intraparticle concentration gradient. Estimated butadiene concentration as function of penetration depth into an exemplary catalyst grain. Calculated by eqn (15) (n = 0) or eqn (16) (n < 0). Bulk concentration calculated from the ideal gas law at 1 atm. Surface concentration estimated from Carberry number for 180 μm grains (eqn (S23)†). The grayscale in the inset illustrates the radial concentration inside a spherical catalyst grain with ηint = 84% (n < 0). | ||
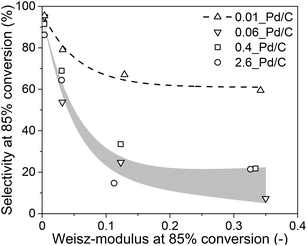
From the experimental data in sections 3.2 and 3.3 and the calculations in section 3.4, it is evident that internal mass transfer limitations strongly affect the performance in selective butadiene hydrogenation. Fig. 7 depicts the dependence of the butene selectivity (taken at 85% butadiene conversion) as a function of the calculated Weisz-modulus for different Pd loading and grain size combinations. All catalysts showed a steep decrease in selectivity with increasing Φ, already at Φ < 0.05, well below the generally accepted criterion of Φ < 0.08,27,28,52,53 indicating that the selectivity was more strongly affected than the activity by internal diffusion limitations. The 0.01_Pd/C showed higher selectivity than the catalyst with higher Pd loading, even at similar estimated diffusion limitations. This is ascribed to the preparation of the catalyst grains, where the catalysts 0.1%, 0.5% and 2.5% Pd/C were diluted with inert carbon powder (5, 25 and 125 times, respectively) to obtain a final weight loading of 0.02 wt% Pd (Fig. 1). Therefore, within these catalyst grains, there is a heterogeneity of Pd-rich and purely inert (carbon) regions at the scale of the support sheets (0.5–1.0 μm, Fig. 2A). The calculations of the Weisz-modulus do not take into account these local Pd concentrations. As a result, the Pd-rich regions of the grain will have a steeper butadiene concentration gradient at the same conversion and internal effectiveness factor, which is associated with lower selectivities, especially at high conversion levels. This analysis provides a qualitative understanding of the selectivity trend, which depends on meso- and microscopic properties such as Pd loading and catalyst grain size. More sophisticated kinetic modelling could offer a more precise quantification of the impact on selectivity.68
Lastly, these findings can be extended to different catalysts (such as supported coinage metal nanoparticles) for the selective hydrogenation of butadiene, or to other reactions (such as acetylene semihydrogenation). From the previous section, some insights into the selectivity trends were determined for metal catalysts other than Pd. If a metal turnover frequency (TOF) is measured or estimated, the volumetric reaction rate of the catalyst (Restvol.) can be calculated from eqn (S7†). Analogous to section 2.4, the Weisz-modulus can be calculated (eqn (10)) and compared to the effective diffusion rate required for good selectivity. Fig. 7 indicates that a Weisz-modulus smaller than 0.03 is necessary for retaining higher selectivity above 70% at 85% butadiene conversion. Table 3 provides an overview of various metal catalysts for the selective hydrogenation of butadiene in large excess of propylene that are reported in the literature.21,41,50,69,70 For Pd/C, a maximum grain size of ca. 50 μm is required, in line with the experimental results from Fig. 7. The coinage metals (Cu, Ag, Au) show orders of magnitude lower intrinsic metal activity (TOF), even at the higher reaction temperature. Therefore, the critical grain sizes for internal diffusion limitations are 5 to 34 times larger than for Pd catalysts, even at higher weight loading and smaller nanoparticle (NP) size.
| Catalyst | NP size (nm) | Wt% | TOF (s−1) | T (°C) | n | d p (μm) |
|---|---|---|---|---|---|---|
| a Calculated so that Φ < 0.03. Catalyst properties, intrinsic activity (TOF) and reaction order in butadiene (n) taken from the literature. Calculations based on selective butadiene hydrogenation (20% conversion, 0.3 mol% inlet). | ||||||
| Pd/C (ref. 21), this work | 5.0 | 0.1% | 20 | 25 | −0.25 | 53 |
| Cu/C (ref. 41) | 7.3 | 6.3% | 6 × 10−3 | 125 | 0.25 | 268 |
| Cu/SiO2 (ref. 41) | 7.3 | 5.7% | 5 × 10−3 | 125 | 0.25 | 309 |
| Ag/SiO2 (ref. 50) | 2.9 | 1.8% | 0.2 × 10−3 | 120 | 0.75 (ref. 69) | 1807 |
| Au/SiO2 (ref. 50) | 2.6 | 3.7% | 4 × 10−3 | 120 | 0.2 (ref. 70) | 437 |
Our findings emphasise the need to assess internal mass transfer limitations during selective hydrogenation of trace amounts (e.g. 0.3%) of butadiene over highly active Pd, and show the importance of carefully evaluating if experimental trends are not partially due to heat or mass transfer effects. The same supported Pd nanoparticles showed a broad range of catalytic performances, which could wrongfully be ascribed to intrinsic catalyst properties rather than due to diffusion limitations. Therefore, for academic research, the occurrence of any of these effects should be carefully discarded before ascribing trends to various catalyst properties such as metal nanoparticle size, weight loading and/or promoters. Diffusion-related effects also rely on catalyst geometry, accessibility, meso- and/or microporosity, grain size and/or gas–solid interaction with the support. The impact of a variation of the thermal properties should also be carefully assessed, for example, when comparing conductive to insulating catalyst supports or when varying inert dilute gasses such as Ar and He, which have a tenfold difference in thermal conductivity.71
More generally, this manuscript its experimental observations and calculations can be extended to any heterogeneous catalysis system. One can estimate the associated transport phenomena by adapting some of the properties of Table 3 for the desired application, as typical industrial catalysts operate at very different reaction conditions than those discussed for selective hydrogenation. For example, in Cu-catalysed hydrogenation of CO/CO2 to methanol, metal weight loadings up to 60 wt% Cu and temperatures around 230 °C are used, greatly increasing the catalyst volumetric activity.72 The effective diffusion, however, is also much higher due to 20% CO/CO2 reactant feed and 50–100 atm operation pressure. However, reactants might condense inside the catalyst pores, which greatly lowers diffusion rates. In short, the mass transport limitations have a strong influence on the catalytic performance, especially for the combination of highly active metals, such as Pd, and trace amounts of reactants. Metals with lower activity, such as Cu, are less affected by this, especially when the inlet reactant concentrations are higher.
4. Conclusions
The influence of heat and mass transport limitations was investigated for the gas-phase selective hydrogenation of butadiene in a large excess of propylene with Pd/C catalysts. At low temperatures and conversions, higher Pd loading and larger catalyst grains led to enhanced activity due to local heating by the exothermic reactions. However, at high conversions, the activity of larger grains was lowered due to mass transfer limitations. The selectivity towards butenes strongly depended on internal diffusion limitations and strongly decreased with increasing Pd loading and catalyst grain size. The combination of catalytic results and calculations highlighted the importance of diffusion-induced concentration gradients inside catalyst grains. The impact on selectivity was much more severe than the impact on activity according to the Weisz–Prater criterion. Our insights provide guidelines for the understanding of the influence of catalyst structure for Pd-catalysed hydrogenation reactions and can be extended to other catalysts and reactions to better understand catalytic materials and design reliable catalytic testing conditions.Author contributions
O. E. B. C.: conceptualization, methodology, validation, formal analysis, investigation, resources, writing – original draft, writing – review & editing, visualization, project administration. M. K.: methodology, formal analysis, investigation, visualization. S. T. R.: supervision, writing – review & editing. E. J. D.: supervision, writing – review & editing. J. E. S. v d H.: writing – original draft, writing – review & editing, supervision. P. E. d J.: conceptualization, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
BP plc is ackowlegded for financial support of this work. Giorgio Totarella, Krijn de Jong and Glenn Sunley are thanked for their contributions to the scientific discussion.References
- L. Zhang, M. Zhou, A. Wang and T. Zhang, Chem. Rev., 2020, 120, 683–733 CrossRef CAS PubMed.
- H.-U. Blaser, C. Malan, B. Pugin, F. Spindler, H. Steiner and M. Studer, Adv. Synth. Catal., 2003, 345, 103–151 CrossRef CAS.
- B. Chen, U. Dingerdissen, J. G. E. Krauter, H. G. J. Lansink Rotgerink, K. Möbus, D. J. Ostgard, P. Panster, T. H. Riermeier, S. Seebald, T. Tacke and H. Trauthwein, Appl. Catal., A, 2005, 280, 17–46 CrossRef CAS.
- M. L. Derrien, Stud. Surf. Sci. Catal., 1986, 27, 613–666 CrossRef CAS.
- G. C. Bond, in Metal-Catalysed Reactions of Hydrocarbons, Springer US, 2005, pp. 357–394 Search PubMed.
- A. Borodziński and G. C. Bond, Catal. Rev.: Sci. Eng., 2006, 48, 91–144 CrossRef.
- A. Borodziński and G. C. Bond, Catal. Rev.: Sci. Eng., 2008, 50, 379–469 CrossRef.
- G. C. Bond, G. Webb, P. B. Wells and J. M. Winterbottom, J. Chem. Soc., 1965, 3218 RSC.
- F. Studt, F. Abild-Pedersen, T. Bligaard, R. Z. Sorensen, C. H. Christensen and J. K. Norskov, Science, 2008, 320, 1320–1322 CrossRef CAS PubMed.
- M. M. Johnson, D. W. Walker and G. P. Nowack, US Pat., US4404124, 1983 Search PubMed.
- H. Lindlar, Helv. Chim. Acta, 1952, 35, 446–450 CrossRef CAS.
- P. T. Witte, P. H. Berben, S. Boland, E. H. Boymans, D. Vogt, J. W. Geus and J. G. Donkervoort, Top. Catal., 2012, 55, 505–511 CrossRef CAS.
- H. Yan, H. Cheng, H. Yi, Y. Lin, T. Yao, C. Wang, J. Li, S. Wei and J. Lu, J. Am. Chem. Soc., 2015, 137, 10484–10487 CrossRef CAS PubMed.
- H. Yan, H. Lv, H. Yi, W. Liu, Y. Xia, X. Huang, W. Huang, S. Wei, X. Wu and J. Lu, J. Catal., 2018, 366, 70–79 CrossRef CAS.
- H. Ibrahim, T. Weckman, D. Murzin and H. Karoliina, Understanding Selective Hydrogenation of Phenylacetylene on PdAg Single Atom Alloy: DFT Insights on Molecule Size and Surface Ensemble Effects, ChemRxiv, Cambridge Open Engage, Cambridge, 2024, This content is a preprint and has not been peer-reviewed, DOI:10.26434/chemrxiv-2024-7mq3w.
- A. V. Rassolov, I. S. Mashkovsky, G. N. Baeva, G. O. Bragina, N. S. Smirnova, P. V. Markov, A. V. Bukhtiyarov, J. Wärnå, A. Y. Stakheev and D. Y. Murzin, Nanomaterials, 2021, 11, 3286 CrossRef CAS PubMed.
- G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1212 CrossRef CAS PubMed.
- M. B. Boucher, B. Zugic, G. Cladaras, J. Kammert, M. D. Marcinkowski, T. J. Lawton, E. C. H. Sykes and M. Flytzani-Stephanopoulos, Phys. Chem. Chem. Phys., 2013, 15, 12187–12196 RSC.
- R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088 CrossRef CAS PubMed.
- P. Aich, H. Wei, B. Basan, A. J. Kropf, N. M. Schweitzer, C. L. Marshall, J. T. Miller and R. Meyer, J. Phys. Chem. C, 2015, 119, 18140–18148 CrossRef CAS.
- O. E. Brandt Corstius, J. E. S. van der Hoeven, G. J. Sunley and P. E. de Jongh, J. Catal., 2023, 427, 115103 CrossRef CAS.
- D. Luss, Chem. Eng. J., 1970, 1, 311–317 CrossRef CAS.
- S. Sharma, D. Boecker, G. J. Maclay and R. D. Gonzalez, J. Catal., 1988, 110, 103–116 CrossRef CAS.
- J. Theis and E. Gulari, Appl. Catal., B, 2007, 75, 39–51 CrossRef CAS.
- R. G. Geitenbeek, A.-E. Nieuwelink, T. S. Jacobs, B. B. V. Salzmann, J. Goetze, A. Meijerink and B. M. Weckhuysen, ACS Catal., 2018, 8, 2397–2401 CrossRef CAS PubMed.
- K. Arnby, A. Törncrona, B. Andersson and M. Skoglundh, J. Catal., 2004, 221, 252–261 CrossRef CAS.
- E. W. Thiele, Ind. Eng. Chem., 1939, 31, 916–920 CrossRef CAS.
- P. B. Weisz and C. D. Prater, Adv. Catal., 1954, 6, 143–196 CAS.
- J. Zhu, F. Wu, M. Li, J. Zhu, J. G. Van Ommen and L. Lefferts, Appl. Catal., A, 2015, 498, 222–229 CrossRef CAS.
- H. Harju, G. Pipitone and L. Lefferts, Front. Chem., 2020, 8, 17 CrossRef CAS PubMed.
- J. Zhu, M. Li, M. Lu and J. Zhu, Catal. Sci. Technol., 2013, 3, 737–744 RSC.
- T. Nijhuis, G. van Koten, F. Kapteijn and J. Moulijn, Catal. Today, 2003, 79–80, 315–321 CrossRef CAS.
- S. Asplund, J. Catal., 1996, 158, 267–278 CrossRef CAS.
- A. Sarkany, Appl. Catal., A, 1997, 165, 87–101 CrossRef CAS.
- A. Sarkany, Appl. Catal., A, 1998, 175, 245–253 CrossRef CAS.
- A. Sarkany, J. Catal., 1998, 180, 149–152 CrossRef CAS.
- S. P. Bressa, J. A. Alves, O. M. Martínez and G. F. Barreto, Chem. Eng. Technol., 2003, 26, 783–789 CrossRef CAS.
- J. A. Alves, G. García Colli, O. M. Martínez and G. F. Barreto, Int. J. Chem. React. Eng., 2023, 21, 1073–1090 CrossRef CAS.
- R. R. Ratnakar and B. Dindoruk, Processes, 2022, 10, 1194 CrossRef CAS.
- B. Donoeva, N. Masoud and P. E. De Jongh, ACS Catal., 2017, 7, 4581–4591 CrossRef CAS PubMed.
- G. Totarella, R. Beerthuis, N. Masoud, C. Louis, L. Delannoy and P. E. de Jongh, J. Phys. Chem. C, 2021, 125, 366–375 CrossRef CAS PubMed.
- F. Mattarozzi, M. Tapia Rosales, R. C. J. van de Poll, E. J. M. Hensen, P. Ngene and P. E. de Jongh, Eur. J. Inorg. Chem., 2023, 26, e202300152 CrossRef CAS.
- N. L. Visser, J. C. Verschoor, L. C. J. Smulders, F. Mattarozzi, D. J. Morgan, J. D. Meeldijk, J. E. S. van der Hoeven, J. A. Stewart, B. D. Vandegehuchte and P. E. de Jongh, Catal. Today, 2023, 418, 114071 CrossRef CAS.
- R. W. P. Wagemans, Chapter 6: Particle Size Effects in the Palladium-Carbon-Hydrogen System, PhD Thesis, Utrecht University, ISBN:90-393-4321-7, 2006 Search PubMed.
- J. Sauter, Die Grössenbestimmung der im Gemischnebel von Verbrennungskraftmaschinen vorhandenen Brennstoffteilchen, 1926 Search PubMed.
- K. S. W. Singh, J. Rouquerol, G. Bergeret, P. Gallezot, M. Vaarkamp, D. C. Koningsberger, A. K. Datye, J. W. Niemantsverdriet, T. Butz, G. Engelhardt, G. Mestl, H. Knözinger and H. Jobic, in Handbook of Heterogeneous Catalysis, Wiley, Weinheim, Germany, 1997, vol. 1–5, pp. 427–582 Search PubMed.
- P. Scherrer, in Kolloidchemie Ein Lehrbuch, Springer, Berlin, Heidelberg, 1912, pp. 387–409 Search PubMed.
- A. L. Patterson, Phys. Rev., 1939, 56, 978–982 CrossRef CAS.
- C. Weidenthaler, Nanoscale, 2011, 3, 792–810 RSC.
- N. Masoud, L. Delannoy, C. Calers, J. J. Gallet, F. Bournel, K. P. de Jong, C. Louis and P. E. de Jongh, ChemCatChem, 2017, 9, 2418–2425 CrossRef CAS PubMed.
- A. J. McCue and J. A. Anderson, Front. Chem. Sci. Eng., 2015, 9, 142–153 CrossRef CAS.
- EUROKIN spreadsheet on requirements for measurement of intrinsic kinetics in the gas-solid fixed-bed reactor, EUROKIN_fixedbed_html, http://www.eurokin.org/wp-content/uploads/webtool/EUROKIN_fixed-bed_html.htm.
- R. H. Perry and D. W. Green, Perry's Chemical Engineers' Handbook, McGraw-Hill Education, 8th edn, 2008 Search PubMed.
- J. R. Anderson and K. C. Pratt, Introduction to Characterization and Testing of Catalysts, Academic Press, 1985 Search PubMed.
- S. Li, Chemical Reaction Engineering, Elsevier, 2017, pp. 265–310 Search PubMed.
- H. S. Fogler, Essentials of Chemical Reaction Engineering,Pearson Prentice Hall, 2nd edn, 2017 Search PubMed.
- R. Beerthuis, J. W. de Rijk, J. M. S. Deeley, G. J. Sunley, K. P. de Jong and P. E. de Jongh, J. Catal., 2020, 388, 30–37 CrossRef CAS.
- G. Totarella, J. W. de Rijk, L. Delannoy and P. E. de Jongh, ChemCatChem, 2022, 14, e202200348 CrossRef CAS.
- N. L. Visser, O. Daoura, P. N. Plessow, L. C. J. Smulders, J. W. de Rijk, J. A. Stewart, B. D. Vandegehuchte, F. Studt, J. E. S. van der Hoeven and P. E. de Jongh, ChemCatChem, 2022, 14, 1–11 CrossRef.
- L. Barberis, A. H. Hakimioun, P. N. Plessow, N. L. Visser, J. A. Stewart, B. D. Vandegehuchte, F. Studt and P. E. de Jongh, Nanoscale, 2022, 14, 13551–13560 RSC.
- A. Valcárcel, A. Clotet, J. M. Ricart, F. Delbecq and P. Sautet, Surf. Sci., 2004, 549, 121–133 CrossRef.
- J. E. S. van der Hoeven, J. Jelic, L. A. Olthof, G. Totarella, R. J. A. van Dijk-Moes, J.-M. Krafft, C. Louis, F. Studt, A. van Blaaderen and P. E. de Jongh, Nat. Mater., 2021, 20, 1216–1220 CrossRef CAS PubMed.
- P. Mukhopadhyay and A. K. Barua, Br. J. Appl. Phys., 1967, 18, 635–640 CrossRef CAS.
- A. W. Smith, Phys. Rev., 1954, 95, 1095–1096 CrossRef CAS.
- M. J. Laubitz and T. Matsumura, Can. J. Phys., 1972, 50, 196–205 CrossRef CAS.
- L. J. Zhao and Q. Sun, Int. J. Low-Carbon Technol., 2013, 10, 288–293 CrossRef.
- B. A. Johnson and S. Ott, Chem. Sci., 2020, 11, 7468–7478 RSC.
- W. Chen, G. Qian, Y. Wan, D. Chen, X. Zhou, W. Yuan and X. Duan, Acc. Chem. Res., 2022, 55, 3230–3241 CrossRef CAS PubMed.
- A. Sárkány and Z. Révay, Appl. Catal., A, 2003, 243, 347–355 CrossRef.
- A. Hugon, L. Delannoy and C. Louis, Gold Bull., 2009, 42, 310–320 CrossRef CAS.
- E. Thornton and W. A. D. Baker, Proc. Phys. Soc., London, 1962, 80, 1171–1175 CrossRef CAS.
- K. C. Waugh, Catal. Lett., 2012, 142, 1153–1166 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: http://doi.org/10.1039/d4re00039k |
| This journal is © The Royal Society of Chemistry 2024 |