A minor difference in the hydrogen-bonding group structure has a major impact on the mechanical properties of polymers

Abstract

The toughness of polymer materials can be enhanced by the incorporation of reversible interchain interactions such as hydrogen bonds (H-bonds), which are weaker than typical covalent bonds. Diverse interacting motifs have been designed and implemented to significantly alter the properties of polymers. Herein, we report that even a subtle difference in the placement of H-bonding groups within a repeat unit leads to distinct mechanical properties of a polymer. We synthesized two types of polynorbornene-based random copolymers which differed only in the relative position of two hydroxymethyl side groups: one in the vicinal arrangement ((2,3)Diol) and the other in the geminal arrangement ((2,2)Diol). When compared with each other, the polymer with the (2,3)Diol structure showed higher stiffness and superior recoverability, while the one with the (2,2)Diol structure exhibited higher stretchability. The combination of viscoelastic characterization of the polymers and quantum chemical calculations of model compounds revealed that the difference in the structural flexibility of the H-bonded (2,3)Diol and (2,2)Diol structures was the key to the distinct mechanical properties of the two copolymers. Our findings open up a new pathway to flexibly and largely tune the mechanical properties of polymeric materials without the need for considerable changes to the molecular design.

---

Introduction

There is an inherent trade-off between stiffness and stretchability in materials in general: stiffer materials tend to be more brittle, and high stretchability is often realized at the cost of stiffness. Various design principles have been devised to break this trade-off, that is, to achieve both high stiffness and high stretchability. One of the effective strategies is to introduce weak and reversible interactions between polymer chains. The interactions bridge between chains and ensure stiffness on small deformations, while they can dissociate and reassociate in response to further deformation of the material, thereby dissipating mechanical energy and preventing failure. A variety of non-covalent interactions^1–16 as well as some dynamic covalent bonds^17–23 have been used as the weak intermolecular interactions for tough polymer materials.

Among various weak interactions, hydrogen bonds (H-bonds) are extensively studied and employed because their characteristics can be widely tuned through molecular design.²⁴ As a single H-bond is weak, H-bonding groups are often designed so that multiple H-bond donors and acceptors are placed on a rigid planar molecule. This type of “rigid” multidentate H-bonding motif plays an important role in nature, as exemplified by nucleotide base pairs. Rigid H-bonding motifs such as ureidopyrimidinone (UPy) have been created and employed as robust interaction sites for supramolecular polymers.¹ Recently, “flexible” H-bonding motifs that can form a wide variety of H-bonds have been gaining much attention. Yanagisawa et al. developed a self-healable polymer glass consisting of low molecular weight polymers with densely introduced thiourea groups.⁵ Disordered arrays of H-bonds between thiourea groups prevented crystallization and contributed to mechanical robustness while allowing for the slipping motion of the polymer chains for self-healing. Wang et al. developed a self-healable glassy hyperbranched polymer densely functionalized with various H-bonding groups.⁶ The random hyperbranched structure had many chain-ends with high mobility and prevented ordered packing of H-bonding groups, resulting in good self-healing ability. We previously reported a tough and self-healable elastomer based on a structurally simple aliphatic vicinal diol as the flexible H-bonding motif.⁷ Vicinal diols could form multiple stable H-bonded dimers due to their high conformational freedom. The H-bonded dimer could dynamically change its conformation, thereby prolonging its lifetime. Moreover, the omni-directional nature of the dimer contributed to the reassociation probability of dissociated vicinal diols and facilitated the self-healing.

Thus, it is possible to tune the dynamic properties of polymeric materials through the structure of H-bonding groups. The molecular design of H-bonding motifs usually needs a significant modification of the elements, chemical composition, and entire shape, in order to realize distinct mechanical performances.^4,5,8 In this study, we report that a subtle difference in the arrangement of two hydroxy groups within the repeat unit can significantly alter the H-bonding properties and thus the mechanical properties of polymers. We synthesized polynorbornene-based random copolymers containing either one of two monomers, each having two hydroxy groups. The two monomers were structural isomers, differing only in the arrangement of the two hydroxy groups. We observed a significant difference in the mechanical properties between the two types of copolymers, clearly indicating the impact of a seemingly minor structural modification on H-bonding groups. Our findings open up a new opportunity to rationally design the properties of polymeric materials just by a minor structural modification in the H-bonding group, without changing the chemical composition at all.

Results and discussion

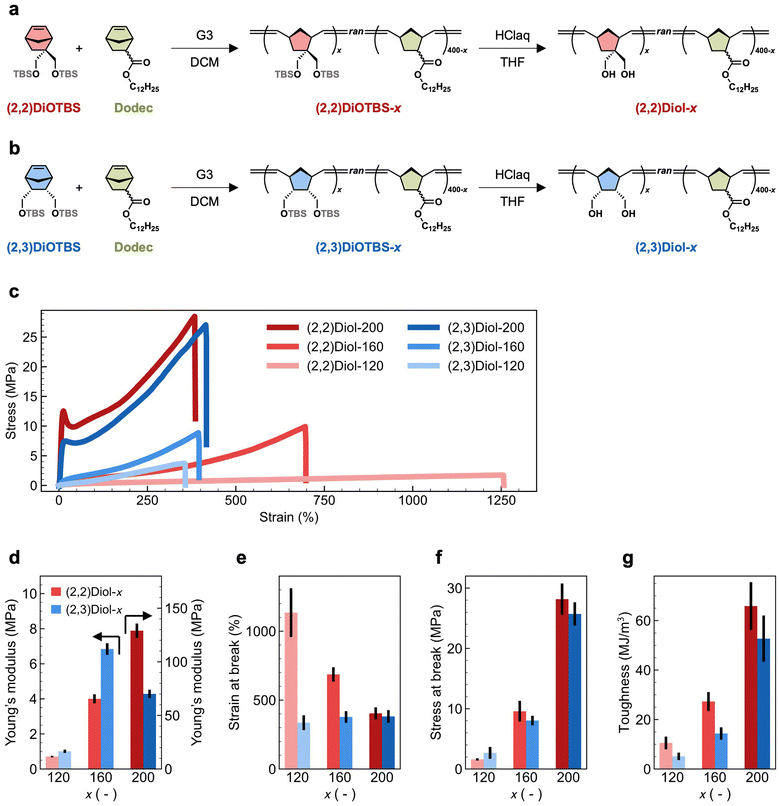
Preparation and mechanical properties of the copolymers

The chemical structure and synthetic route of the copolymers are shown in Fig. 1a and b. We used two protected diol monomers: 2,2-di((tert-butyldimethylsilyloxy)methyl)-5-norbornene ((2,2)DiOTBS) and 2-endo,3-endo-di((tert-butyldimethylsilyloxy)methyl)-5-norbornene ((2,3)DiOTBS). These monomers were structural isomers differing only in the position of one of the two hydroxymethyl groups. Either (2,2)DiOTBS or (2,3)DiOTBS was copolymerized with dodecyl 5-norbornene-2-carboxylate (a mixture of endo and exo isomers, Dodec) via ring-opening metathesis polymerization (ROMP) using the Grubbs third-generation catalyst (G3). Due to the difference in monomer reactivity, simple copolymerization starting from a mixture of all monomers would lead to an inhomogeneous comonomer sequence distribution along the chain.²⁵ Therefore, we added the comonomers to the reaction mixture gradually according to a predetermined time schedule, which was obtained by a computational method developed by us.²⁶ This ensured that the protected diol monomers were randomly and evenly distributed along the chain in the resultant copolymer. The feed ratio of all monomers against G3 was fixed at 400, while the ratio of (2,2)DiOTBS or (2,3)DiOTBS against G3, denoted as x, was varied from 120 to 200. The copolymers containing (2,2)DiOTBS or (2,3)DiOTBS are denoted as (2,2)DiOTBS-x and (2,3)DiOTBS-x, respectively. The synthetic details of (2,2)DiOTBS-x are described in the ESI† and those of (2,3)DiOTBS-x can be found elsewhere.²⁶ Finally, the hydroxy groups were deprotected under acidic conditions to obtain the diol-functionalized copolymers, denoted as (2,2)Diol-x and (2,3)Diol-x. The deprotection of (2,2)DiOTBS-x was confirmed by ¹H NMR and infrared (IR) spectroscopy (Fig. S10–S18†). The signals from the tert-butyldimethylsilyl ether (OTBS) group completely disappeared in the ¹H NMR spectrum, indicating full deprotection. In the IR spectrum, the bands at 1250 cm⁻¹ and 750–850 cm⁻¹ vanished: combined with the ¹H NMR results, these bands could be attributed to the characteristic bands of the OTBS group. For (2,3)DiOTBS-x, only IR spectroscopy could be used to confirm the deprotection due to the poor solubility of the product (Fig. S19–S24†). Similar to the cases of (2,2)DiOTBS-x, the bands at 1250 cm⁻¹ and 750–850 cm⁻¹ were completely absent in (2,3)Diol-x, from which we confirmed the full conversion of OTBS groups into hydroxy groups.

Fig. 1 Synthetic route of (a) (2,2)Diol-x and (b) (2,3)Diol-x (x = 120, 160, and 200). (c) Stress–strain curves of (2,2)Diol-x and (2,3)Diol-x. The tensile properties of (d) Young's modulus, (e) stress at break, (f) strain at break, and (g) toughness. Vertical black lines represent error bars indicating the standard deviation.

The mechanical properties of (2,2)Diol-x and (2,3)Diol-x were evaluated by tensile tests. The obtained stress–strain curves are shown in Fig. 1c. The tensile properties, including Young's modulus, maximum stress, maximum strain, and toughness, are summarized in Fig. 1d–g and Table 1. The mechanical properties of (2,2)Diol-x and (2,3)Diol-x are significantly different. When x is 120 or 160, (2,2)Diol-x shows a lower Young's modulus and larger strain at break than (2,3)Diol-x. At x = 200, however, the Young's modulus of (2,2)Diol-200 is higher than (2,3)Diol-200. Interestingly, though, there is no significant difference in the maximum stress between (2,2)Diol-x and (2,3)Diol-x at the same x value. As to the toughness, (2,2)Diol-x consistently exhibits higher values compared to (2,3)Diol-x for all x values. The x-dependence of the mechanical properties is also distinct between the two series. The strain at break of (2,2)Diol-x decreases with increasing x, whereas that of (2,3)Diol-x barely depends on x. For other properties (Young's modulus, stress at break, and toughness), the two series share the same trend: the values increase with increasing x, reflecting the increasing reinforcement effect of H-bonds. These results show that a small modification in the microscopic arrangement of hydroxy groups can lead to marked differences in macroscopic mechanical properties.

Table 1 Tensile properties of the copolymer

Sample	Young's modulus (MPa)	Strain at break (%)	Stress at break (MPa)	Toughness (MJ m^−3)
(2,2)Diol-120	0.710 ± 0.043	1134 ± 336	1.6 ± 0.2	10.5 ± 2.6
(2,2)Diol-160	4.00 ± 0.26	686 ± 52	9.6 ± 1.7	27.3 ± 3.8
(2,2)Diol-200	129 ± 7	404 ± 43	28.2 ± 2.6	65.9 ± 9.7
(2,3)Diol-120	1.01 ± 0.09	336 ± 54	2.7 ± 0.1	5.1 ± 1.5
(2,3)Diol-160	6.84 ± 0.33	377 ± 42	8.0 ± 0.8	14.4 ± 2.5
(2,3)Diol-200	70.1 ± 3.9	381 ± 46	25.7 ± 1.9	52.7 ± 9.4

---

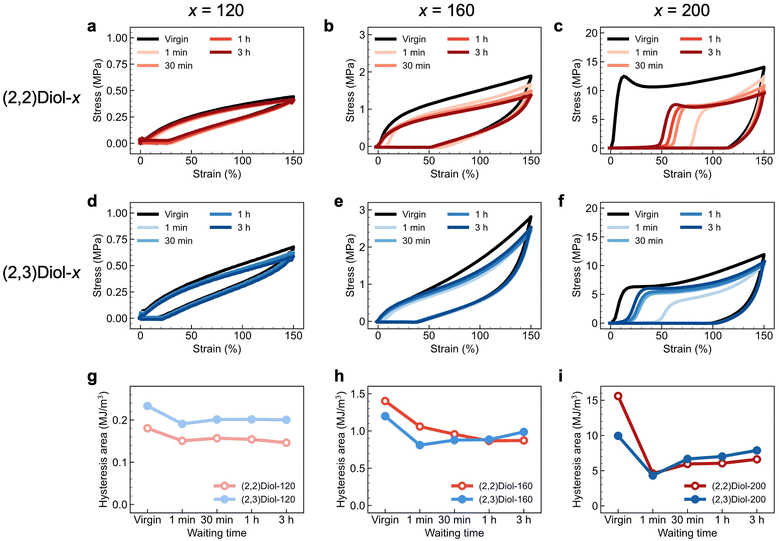
Energy dissipation and self-recovery abilities of (2,2)Diol-x and (2,3)Diol-x were demonstrated by cyclic tensile tests. The samples were stretched to 150% strain at a constant speed and unloaded to zero strain at the same speed. This cycle was repeated five times with a different waiting time before each cycle. The loading and unloading stress–strain curves of each copolymer are shown in Fig. 2. All samples show large hysteresis in the first cycle, which is a sign of energy dissipation by dissociation of H-bonds. In the second cycle, residual strain is observed as a delayed onset of the stress increase, and the hysteresis area is smaller than that in the first cycle, reflecting fatigue due to the first cycle. As the waiting time before loading is increased in the subsequent cycles, the residual strain decreases and the hysteresis area recovers. The polymers can recover from fatigue due to mechanical loading, despite the absence of covalent crosslinks. The degree and trend of recovery differ significantly between (2,2)Diol-x and (2,3)Diol-x. Fig. 2g–i compare the hysteresis area at each cycle for (2,2)Diol-x and (2,3)Diol-x at the same x value. At x = 120 (Fig. 2g), both (2,2)Diol-120 and (2,3)Diol-120 show rapid recovery within ∼30 min. The recovery efficiency, defined as the ratio of the hysteresis area in the nth cycle against that in the first cycle, reached 87% and 86%, respectively, for (2,2)Diol-120 and (2,3)Diol-120 in the third cycle. However, at x = 160 (Fig. 2h), the hysteresis area of (2,2)Diol-160 keeps decreasing with the cycle number, while for (2,3)Diol-160, it keeps increasing from the second cycle. Consequently, there is a marked difference in the recovery efficiency at the fifth cycle: 62% and 82% for (2,2)Diol-160 and (2,3)Diol-160, respectively. The difference is even more obvious at x = 200 (Fig. 2i). (2,2)Diol-200 shows a lower hysteresis area compared to (2,3)Diol-200 from the third cycle onward. The recovery efficiency in the fifth cycle was 42% for (2,2)Diol-200, while it was 79% for (2,3)Diol-200. The superior recoverability of (2,3)Diol-200 is also evident from the residual strain in Fig. 2c and f, which is seen as the onset of stress increase in the loading process. The residual strain in the fifth cycle is ∼20% for (2,3)Diol-200, which is much lower than that of (2,2)Diol-200 (∼50%).

Fig. 2 Cyclic stress–strain curves of (a) (2,2)Diol-120, (b) (2,2)Diol-160, (c) (2,2)Diol-200, (d) (2,3)Diol-120, (e) (2,3)Diol-160, and (f) (2,3)Diol-200. (g–i) Hysteresis area at each cycle. (g) (2,2)Diol-120 and (2,3)Diol-120. (h) (2,2)Diol-160 and (2,3)Diol-160. (i) (2,2)Diol-200 and (2,3)Diol-200.

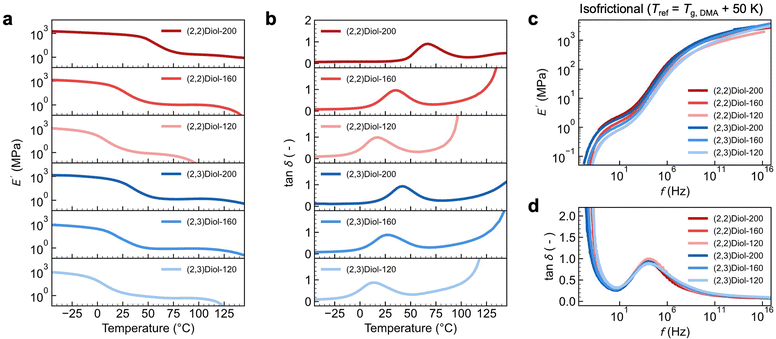
Viscoelastic relaxation

To gain further insight into the difference between (2,2)Diol-x and (2,3)Diol-x, the linear viscoelastic properties were examined by dynamic mechanical analysis (DMA). Fig. 3a and b show the temperature dependence of the storage modulus E′ and the loss tangent tan δ of the copolymers at a strain frequency of 1.0 Hz. All samples show sharp decreases in E′ in two steps, which are separated by a rubbery plateau region. This indicates the presence of two distinct relaxation processes. The first relaxation at a lower temperature appears as a peak in tan δ. The onset temperature of the tan δ peak coincides with the glass transition temperature T_g observed by differential scanning calorimetry (DSC) (T_g,DSC, Fig. S27b†). Therefore, the first relaxation is assigned to be a glass transition due to the segmental relaxation of the polymer. We denote the peak temperature of tan δ as T_g,DMA. We could readily confirm that these two temperatures are very well correlated by plotting T_g,DMA against T_g,DSC (Fig. S27c†). The second relaxation at higher temperatures involves a rapid drop of E′ and diverging tan δ. These are characteristic of the terminal flow relaxation of the polymer chains. We note here that (2,2)Diol-200 does not show a clear terminal flow relaxation because of the undesired irreversible chemical crosslinking of the polynorbornene backbone that occurs at elevated temperatures (typically above ∼160 °C).³ Another point to note is the relationship between the Young's modulus in the tensile tests and E′ in DMA. Fig. 3a and b indicate that (2,2)Diol-200 behaves as a glass at room temperature, showing E′ close to 1 GPa. However, the Young's modulus observed in the tensile test at room temperature was only 129 ± 7 MPa (Table 1). This discrepancy can be ascribed to the difference in the observation time scale of the two techniques. The deformation frequency for the DMA data in Fig. 3a is 1.0 s⁻¹, the time scale of which is much shorter than that of the tensile test performed at a strain rate of 0.1 s⁻¹. While (2,2)Diol-200 behaves mostly as a glass on the time scale of the DMA measurement at room temperature, it would be only partly glassy on the time scale of the tensile tests.

Fig. 3 Linear viscoelastic spectra of the copolymers. (a) Storage modulus E′ at f = 1.0 Hz as a function of temperature. (b) Loss tangent tan δ as a function of temperature. (c) Isofrictional master curves of E′ as a function of frequency f constructed at T_ref = T_g,DMA + 50 K. (d) Loss tangent tan δ as a function of f.

Next, we analyzed the frequency dependence of the dynamic moduli. We constructed master curves in the frequency domain by using the time–temperature superposition principle. Fig. S28† shows the master curves constructed by setting the reference temperature T_ref to 25 °C. As expected from the temperature dependence data, the two relaxation processes were readily discernible. We define two relaxation times to quantify the dynamics at 25 °C: the inverse of the frequency at the tan δ peak as τ_g and the inverse of the frequency at the point where tan δ = 1 as τ_flow. Fig. S29† shows the relaxation times, τ_g and τ_flow, for (2,2)Diol-x and (2,3)Diol-x at T_ref = 25 °C plotted against x. When compared at the same x, both the τ_g and τ_flow are longer for (2,2)Diol-x than for (2,3)Diol-x. The dynamics of (2,2)Diol is slower than that of (2,3)Diol in both the segmental and terminal relaxation regimes.

We also constructed “isofrictional” master curves by setting T_ref = T_g,DMA + 50 K using T_g,DMA of each sample, as shown in Fig. 3c and d. This allows cancelling the effect of different T_gs, i.e., of different segmental mobilities. Surprisingly, the curves of all samples overlap with each other across the entire frequency range, except for minor vertical discrepancies in E′. The overlapping of E′ curves could be further improved by applying vertical shifts (Fig. S30†). The difference in the relaxation behavior among the samples in isothermal master curves (Fig. S28†) turns out to be solely due to the difference in T_g or equivalently the segmental relaxation rate. Notably, the width of the rubbery plateau region is almost the same for all samples. We emphasized here that all samples have the same polynorbornene main chain structure and the same degree of polymerization (i.e., chain length): they differ only in the structure and number of diol units. Therefore, the similarity of the isofrictional master curves of all samples suggests that the linear viscoelastic behavior is independent of the structure and number of diol units. Chain entanglement should be the main viscoelastic mechanism governing the isofrictional master curves. The H-bonds between the diols control the elementary segmental mobility, leading to variations in the viscoelastic relaxation time of the entangled polymer chains under isothermal conditions (Fig. S29†).

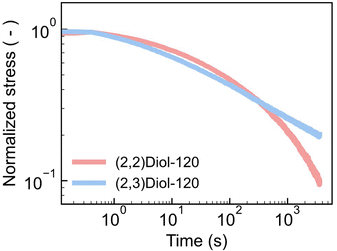
We have shown so far that the difference in linear viscoelasticity is mostly due to the difference in T_g. In fact, the master curves of the samples with similar T_g values such as (2,2)Diol-120 and (2,3)Diol-120 were similar to each other (Fig. S27b†). However, the stress–strain curves of (2,2)Diol-120 and (2,3)Diol-120 are quite different (Fig. 1c). (2,2)Diol-x shows lower stress and larger strain at break. To investigate the reason for this difference in behavior in the large strain region, we carried out stress relaxation tests with a large step strain (Fig. 4 and S31†). A strain of 100% was applied rapidly to the sample at time zero and maintained. Although the stress decays similarly for the two polymers in the beginning, the decay of (2,2)Diol-120 is clearly faster in the longer time scale (>100 s). This is in sharp contrast to the linear viscoelastic relaxation time: (2,2)Diol-120 showed longer τ_flow than (2,3)Diol-120. These observations indicate that segmental mobility depends on the applied strain, and the strain dependence is different in (2,2)Diol-x and (2,3)Diol-x. The segments in (2,2)Diol-x become more mobile under large strains compared to those in (2,3)Diol-x. As a result, (2,2)Diol-120 showed faster relaxation under a large strain (Fig. 4). The lower stress and higher stretchability of (2,2)Diol-x (x = 120 and 160) in the tensile test (Fig. 2c) are also attributable to the increased mobility under large strains. The distinct strain dependence is solely due to the small structural difference between (2,2)Diol-x and (2,3)Diol-x, i.e., the difference in the arrangement of hydroxy groups. We hypothesize that the interaction between (2,2)Diol structures via H-bonds becomes easier to dissociate and more difficult to reform under large strains, compared to that between (2,3)Diol structures. We conducted DFT calculations to examine this hypothesis, which will be discussed in the next section.

Fig. 4 Stress relaxation curves of (2,2)Diol-120 and (2,3)Diol-120 at 100% initial strain.

H-bonding structure

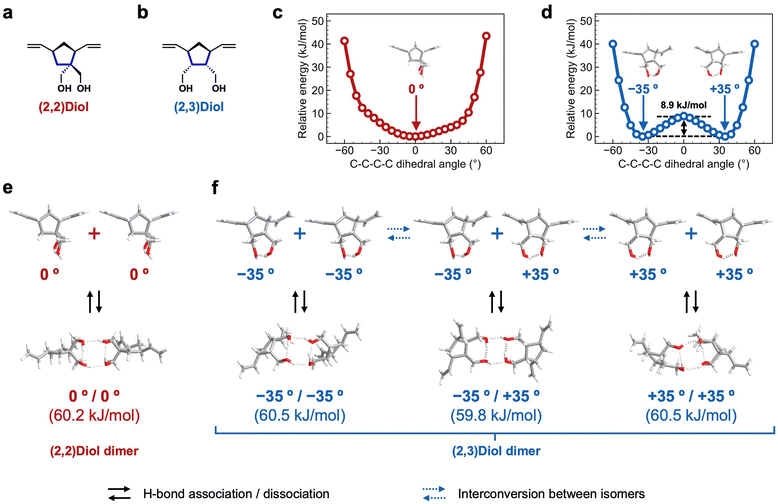
We characterized the H-bonding structure in (2,2)Diol-x and (2,3)Diol-x by DFT calculations to understand the molecular origin of the macroscopic mechanical properties. The structure of one unit of diol in the polymer chain was extracted from (2,2)Diol-x and (2,3)Diol-x as the model compounds, as shown in Fig. 5a and b. All calculations were carried out at the B3LYP/6-311G(d,p) level of theory. Structural optimization of the model compounds was performed to obtain the initial structure. To examine the flexibility of each structure, the C–C–C–C dihedral angle related to the orientation of hydroxy groups (shown in blue lines in Fig. 5a and b) was varied from −60° to +60° every 5° and the energy was calculated at each angle. The relative energy is plotted as a function of the C–C–C–C dihedral angle in Fig. 5c and d. While the (2,2)Diol structure has only one energy minimum at 0° (Fig. 5c), the (2,3)Diol structure exhibits two stable conformers at −35° and +35° (Fig. 5d). The energy barrier between the two stable conformers is 8.9 kJ mol⁻¹, which can be easily overcome at ambient temperature: the conformers can easily be interconverted. Thus, the (2,3)Diol structure is more flexible than the (2,2)Diol structure.

Fig. 5 Model compounds for (a) the (2,2)Diol structure and (b) the (2,3)Diol structure. The bonds in blue denote the position of the C–C–C–C dihedral angle that is varied in panels c and d. Relative energy profile for the rotation of the C–C–C–C dihedral angle in (c) the (2,2)Diol model compound and (d) the (2,3)Diol model compound. Diagram of various possible routes for the association/dissociation and interconversion between the isomers of (e) (2,2)Diol and (f) (2,3)Diol.

We then constructed H-bonded dimers from the stable conformers in Fig. 5c and d. The stable dimers found are shown in Fig. 5e and f along with the dimerization energies. Both (2,2)Diol and (2,3)Diol structures have four hydrogen bonds in the dimerized state, two intramolecular and two intermolecular. The calculated dimerization energies are almost the same for all dimer modes, ranging from 59.8 to 60.5 kJ mol⁻¹. The obvious difference between (2,2)Diol and (2,3)Diol structures is the diversity of dimer modes: the (2,2)Diol compound has only one stable dimer structure while there are three for (2,3)Diol (including a pair of enantiomers). The diverse H-bonding structures of (2,3)Diol would contribute to the stability and dynamic nature of intermolecular interactions. From a thermodynamic point of view, the large number of dimer modes increases the entropy of the dimerized state, i.e., it stabilizes the dimer entropically in addition to the enthalpic contributions from the individual H-bonds.^7,13,19 From a kinetic point of view, a dimer may change its conformation flexibly via interconversion between isomers while maintaining the dimerized state, delaying the dissociation event. Moreover, it would be easy for free diol moieties to form a dimer due to the high degree of freedom of the dimer structure.

It is interesting to compare the properties of the corresponding monomers to examine the predicted differences between (2,2)Diol and (2.3)Diol structures. The melting point of the (2,3)Diol monomer (85–86 °C)²⁷ is significantly lower than that of the (2,2)Diol monomer (111–113 °C),²⁸ suggesting that the packing of (2,3)Diol in the crystal is looser than that of (2,2)Diol. This is consistent with the predictions of the DFT calculations, i.e., (2,3)Diol was structurally more flexible and had more diverse H-bonding structures than (2,2)Diol.

Origin of the differences in the mechanical behavior

We propose the origin of the differences in the viscoelastic properties between (2,2)Diol-x and (2,3)Diol-x (Fig. 6). The (2,2)Diol structure had only one stable dimer mode according to the DFT calculations. When the polymer chains are not strained, the single stable dimer mode leads to low segmental mobility and high T_g (Fig. 6a). The (2,3)Diol structure had multiple modes, allowing for more diverse H-bonding patterns and higher mobility at the segment level (Fig. 6d), leading to low T_g. Consequently, (2,3)Diol-x relaxed faster than (2,2)Diol-x under small strains. In the large strain region, the rigidity of the (2,2)Diol structure makes it difficult for the once-dissociated diol to form an H-bonded dimer again (Fig. 6b) while the (2,3)Diol structure with its diverse dimer modes can easily find a partner and form a dimer frequently (Fig. 6e). As a result, (2,2)Diol-x relaxed faster in the large strain region compared to (2,3)Diol-x. The faster relaxation caused lower stress for (2,2)Diol-x compared to (2,3)Diol-x in the tensile test (x = 120 and 160). For x = 200, however, the stress–strain curves of (2,2)Diol-200 and (2,3)Diol-200 were somewhat similar. This may be attributed to the glassy nature of these polymers. The T_g values of (2,2)Diol-200 and (2,3)Diol-200 were 47 °C and 16 °C, respectively (Fig. S27†), which were close to or higher than room temperature. As polymers approach the glassy state, they become much stiffer and the difference among different polymers usually become less significant. Despite the similarity, (2,2)Diol-200 showed a higher Young's modulus than (2,3)Diol-200. We speculate that the higher T_g of the former, which was due to the rigidity of the H-bonded structure, contributed to its higher stiffness. During the stretching process, the entanglements that sustain the network gradually dismiss due to the sliding motion of the chains. Because the (2,3)Diol structure retards the chain motion more than the (2,2)Diol structure does, the entanglements and hence the network in (2,3)Diol-x are better retained than (2,2)Diol-x (Fig. 6c and f). This was the reason for the better recoverability of (2,3)Diol-x in the cyclic tensile tests.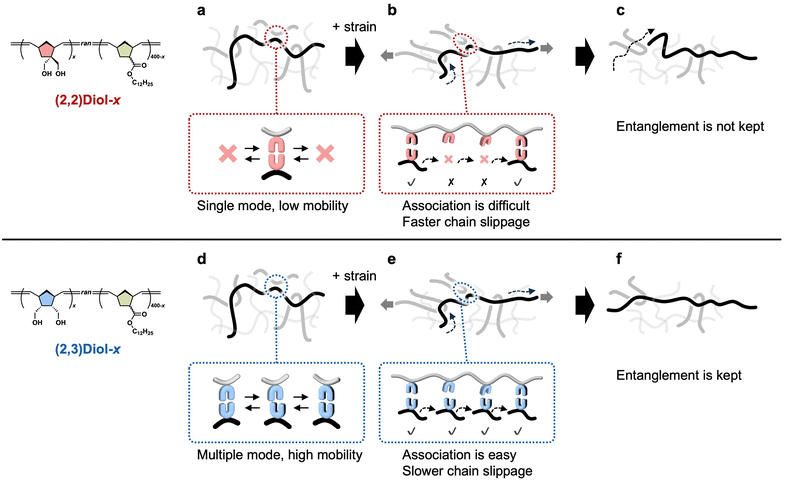

Fig. 6 Schematic illustrations of the structure and dynamics of (a–c) (2,2)Diol-x and (d and e) (2,3)Diol-x. (a and d) In the equilibrium state without strain. (b, c, e and f) Under a large strain.

In summary, we have shown that the dynamic properties of the polymer were drastically altered by a subtle structural difference between the (2,2)Diol and (2,3)Diol structures. The key factor was the structural flexibility of the diol structure: the (2,2)Diol structure was relatively rigid, while the (2,3)Diol structure was able to form H-bonds in a relatively flexible manner. This study paves the way to a novel design strategy for H-bonded polymers, in which the dynamic properties can be tuned just by tweaking the structure a little bit, without a significant change.

Conclusion

We synthesized two types of random copolymers, (2,2)Diol-x and (2,3)Diol-x, which differ only in the arrangement of two hydroxy groups in the repeat unit, and their mechanical properties were compared. A slight difference in the arrangement of the hydroxy groups resulted in a marked difference in the mechanical properties. At a lower content of diol units (x = 120 and 160), (2,2)Diol-x was softer and more stretchable than (2,3)Diol-x, while (2,2)Diol-200 was more rigid than (2,3)Diol-200 at the highest diol content investigated (x = 200). Cyclic tensile tests revealed that (2,3)Diol-x was more recoverable than (2,2)Diol-x. Linear viscoelastic behavior was found to be governed by segmental mobility and chain entanglement. Because all polymers shared the same degree of polymerization, the degree of entanglement was also the same, whereas the segmental mobility, characterized by T_g, varied significantly depending on the number and types of diol units. (2,3)Diol-x generally showed higher segmental mobility and hence faster relaxation compared to (2,2)Diol-x. Interestingly, this tendency changed in the nonlinear, large-deformation regime: (2,2)Diol-120 relaxed faster than (2,3)Diol-120. DFT calculations suggested that the (2,2)Diol structure was less flexible than the (2,3)Diol structure. As a result, the (2,2)Diol structure had only one stable H-bonded dimer mode, whereas at least three stable H-bonded dimer modes were found for the (2,3)Diol structure. It should be emphasized that the distinct dimerization behavior resulted only from the way a single hydroxymethyl group was placed in the repeat unit of the polymer. The flexibility of the (2,3)Diol structure contributed to faster relaxation in the equilibrium state (in the linear regime). However, under a large deformation where the polymer chains were strained, multiple dimer modes of the (2,3)Diol structure facilitated the reassociation/reformation of H-bonded dimers after dissociation, which effectively retarded the chain motion and delayed the relaxation. The delayed relaxation also helped preserve the entanglement when a large strain was applied to the sample, leading to good fatigue recoverability. Thus, we have shown that the mechanical properties of polymeric materials were affected by only a subtle difference in the arrangement of H-bonding groups. The present findings open the possibility of rationally designing high-performance polymeric materials through a minor structural modification on the H-bonding moiety.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This project was funded and commissioned by the New Energy and Industrial Technology Development Organization (proposal no. JPNP18016). The SAXS measurements were performed with the approval of the Photon Factory Advisory Committee (proposal no. 2019G160 and 2021G096).

References

1. R. P. Sijbesma, F. H. Beijer, L. Brunsveld, B. J. B. Folmer, J. H. K. K. Hirschberg, R. F. M. Lange, J. K. L. Lowe and E. W. Meijer, Reversible Polymers Formed from Self-Complementary Monomers Using Quadruple Hydrogen Bonding, Science, 1997, 278(5343), 1601–1604,  DOI:10.1126/science.278.5343.1601.
2. P. Cordier, F. Tournilhac, C. Soulié-Ziakovic and L. Leibler, Self-Healing and Thermoreversible Rubber from Supramolecular Assembly, Nature, 2008, 451(7181), 977–980,  DOI:10.1038/nature06669.
3. S. Yoshida, H. Ejima and N. Yoshie, Tough Elastomers with Superior Self-Recoverability Induced by Bioinspired Multiphase Design, Adv. Funct. Mater., 2017, 27(30), 1701670,  DOI:10.1002/adfm.201701670.
4. J. Tellers, S. Canossa, R. Pinalli, M. Soliman, J. Vachon and E. Dalcanale, Dynamic Cross-Linking of Polyethylene via Sextuple Hydrogen Bonding Array, Macromolecules, 2018, 51(19), 7680–7691,  DOI:10.1021/acs.macromol.8b01715.
5. Y. Yanagisawa, Y. Nan, K. Okuro and T. Aida, Mechanically Robust, Readily Repairable Polymers via Tailored Noncovalent Cross-Linking, Science, 2018, 359(6371), 72–76,  DOI:10.1126/science.aam7588.
6. H. Wang, H. Liu, Z. Cao, W. Li, X. Huang, Y. Zhu, F. Ling, H. Xu, Q. Wu, Y. Peng, B. Yang, R. Zhang, O. Kessler, G. Huang and J. Wu, Room-Temperature Autonomous Self-Healing Glassy Polymers with Hyperbranched Structure, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(21), 11299–11305,  DOI:10.1073/pnas.2000001117.
7. C. Kim, S. Nakagawa, M. Seshimo, H. Ejima, H. Houjou and N. Yoshie, Tough Supramolecular Elastomer via Entropy-Driven Hydrogen Bonds between Vicinal Diols, Macromolecules, 2020, 53(10), 4121–4125,  DOI:10.1021/acs.macromol.9b02639.
8. S. Mondal, J. J. Lessard, C. L. Meena, G. J. Sanjayan and B. S. Sumerlin, Janus Cross-Links in Supramolecular Networks, J. Am. Chem. Soc., 2022, 144(2), 845–853,  DOI:10.1021/jacs.1c10606.
9. T. Bai, P. Zhang, Y. Han, Y. Liu, W. Liu, X. Zhao and W. Lu, Construction of an Ultrahigh Strength Hydrogel with Excellent Fatigue Resistance Based on Strong Dipole–Dipole Interaction, Soft Matter, 2011, 7(6), 2825–2831,  10.1039/C0SM01108H.
10. Y. Zhang, Y. Li and W. Liu, Dipole–Dipole and H-Bonding Interactions Significantly Enhance the Multifaceted Mechanical Properties of Thermoresponsive Shape Memory Hydrogels, Adv. Funct. Mater., 2015, 25(3), 471–480,  DOI:10.1002/adfm.201401989.
11. Y. Miwa, J. Kurachi, Y. Kohbara and S. Kutsumizu, Dynamic Ionic Crosslinks Enable High Strength and Ultrastretchability in a Single Elastomer, Commun. Chem., 2018, 1(1), 1–8,  DOI:10.1038/s42004-017-0004-9.
12. T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. A. Haque, T. Nakajima and J. P. Gong, Physical Hydrogels Composed of Polyampholytes Demonstrate High Toughness and Viscoelasticity, Nat. Mater., 2013, 12(10), 932–937,  DOI:10.1038/nmat3713.
13. J.-C. Lai, X.-Y. Jia, D.-P. Wang, Y.-B. Deng, P. Zheng, C.-H. Li, J.-L. Zuo and Z. Bao, Thermodynamically Stable Whilst Kinetically Labile Coordination Bonds Lead to Strong and Tough Self-Healing Polymers, Nat. Commun., 2019, 10(1), 1164,  DOI:10.1038/s41467-019-09130-z.
14. X. Guo, S. Nakagawa and N. Yoshie, Tunable Mechanical Properties in Microphase-Separated Thermoplastic Elastomers via Metal–Ligand Coordination, Macromolecules, 2024, 57(5), 2351–2362,  DOI:10.1021/acs.macromol.4c00178.
15. S. Nomimura, M. Osaki, J. Park, R. Ikura, Y. Takashima, H. Yamaguchi and A. Harada, Self-Healing Alkyl Acrylate-Based Supramolecular Elastomers Cross-Linked via Host–Guest Interactions, Macromolecules, 2019, 52(7), 2659–2668,  DOI:10.1021/acs.macromol.9b00471.
16. J. Liu, C. S. Y. Tan, Z. Yu, Y. Lan, C. Abell and O. A. Scherman, Biomimetic Supramolecular Polymer Networks Exhibiting Both Toughness and Self-Recovery, Adv. Mater., 2017, 29(10), 1604951,  DOI:10.1002/adma.201604951.
17. M. Nadgorny, Z. Xiao and L. A. Connal, 2D and 3D-Printing of Self-Healing Gels: Design and Extrusion of Self-Rolling Objects, Mol. Syst. Des. Eng., 2017, 2(3), 283–292,  10.1039/C7ME00023E.
18. C. Kim, H. Ejima and N. Yoshie, Polymers with Autonomous Self-Healing Ability and Remarkable Reprocessability under Ambient Humidity Conditions, J. Mater. Chem. A, 2018, 6(40), 19643–19652,  10.1039/C8TA04769C.
19. Z.-H. Zhao, D.-P. Wang, J.-L. Zuo and C.-H. Li, A Tough and Self-Healing Polymer Enabled by Promoting Bond Exchange in Boronic Esters with Neighboring Hydroxyl Groups, ACS Mater. Lett., 2021, 3(9), 1328–1338,  DOI:10.1021/acsmaterialslett.1c00314.
20. O. Doat, S. Nakagawa, Y. Yanaba, H. Inoue and N. Yoshie, Controlling the Marine Biodegradation Profile and Mechanical Properties of Poly(ε-Caprolactone) with Hydrophobic Water-Responsive Linkages, ACS Appl. Polym. Mater., 2024, 6(1), 244–252,  DOI:10.1021/acsapm.3c01843.
21. E. Kolomiets and J.-M. Lehn, Double Dynamers: Molecular and Supramolecular Double Dynamic Polymers, Chem. Commun., 2005, 12, 1519–1521,  10.1039/B418899C.
22. P. Reutenauer, E. Buhler, P. J. Boul, S. J. Candau and J.-M. Lehn, Room Temperature Dynamic Polymers Based on Diels–Alder Chemistry, Chem. – Eur. J., 2009, 15(8), 1893–1900,  DOI:10.1002/chem.200802145.
23. S.-M. Kim, H. Jeon, S.-H. Shin, S.-A. Park, J. Jegal, S. Y. Hwang, D. X. Oh and J. Park, Superior Toughness and Fast Self-Healing at Room Temperature Engineered by Transparent Elastomers, Adv. Mater., 2018, 30(1), 1705145,  DOI:10.1002/adma.201705145.
24. Z. Xie, B.-L. Hu, R.-W. Li and Q. Zhang, Hydrogen Bonding in Self-Healing Elastomers, ACS Omega, 2021, 6(14), 9319–9333,  DOI:10.1021/acsomega.1c00462.
25. S. Ishizaka, S. Nakagawa, K. Matsuoka and N. Yoshie, Tough Polymer with a Gradual Spatial Change in the Hydrogen Bond Density Controlled by Simple One-Pot Copolymerization, Polymer, 2022, 246, 124748,  DOI:10.1016/j.polymer.2022.124748.
26. S. Ishizaka, S. Nakagawa and N. Yoshie, Computer-Aided Design of Copolymers with Controlled Comonomer Distributions, Macromolecules, 2023, 56(18), 7312–7319,  DOI:10.1021/acs.macromol.3c00409.
27. C. F. Culberson, J. H. Seward and P. Wilder, 2-Oxa-1,2-Dihydrodicyclopentadiene ¹, J. Am. Chem. Soc., 1960, 82(10), 2541–2547,  DOI:10.1021/ja01495a037.
28. T. Hino, N. Inoue and T. Endo, Cationic Copolymerization Behavior of Cyclic Ether Monomers with Norbornene-Containing Cyclic Carbonate or Spiro–Orthoether Structure, J. Polym. Sci., Part A: Polym. Chem., 2004, 42(20), 5113–5120,  DOI:10.1002/pola.20341.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed experimental procedures and other characterization data. See DOI: https://doi.org/10.1039/d4py00580e

---