Recent progress in solid-state NMR of spin-½ low-γ nuclei applied to inorganic materials

Abstract

Significant technological and methodological advances in solid-state NMR techniques in recent years have increased the accessibility of nuclei with small magnetic moments (hereafter termed low-γ) underpinning an increased range of applications of such nuclei. These methodological advances are briefly summarised, including improvements in hardware and pulse sequences, as well as important developments in associated computational methods (e.g. first principles calculations, spectral simulation). Here spin-½ nuclei are the focus, with this Perspective complementing a very recent review that looked at half-integer spin low-γ quadrupolar nuclei. Reference is made to some of the original reports of such spin-½ nuclei, but recent progress in the relevant methodology and applications to inorganic materials (most within the last 10 years) of these nuclei are the focus. An overview of the current state-of-the-art of studying these nuclei is thereby provided for both NMR spectroscopists and materials researchers.

---

1. Introduction

In adopting a fully multinuclear approach to NMR there are many NMR-active nuclei to potentially observe across the Periodic Table. However the NMR characteristics of nuclei vary greatly, with one of the most important factors determining the observability of a particular isotope being the magnitude of the signal.² For a given isotope the combination of external factors (i.e. the applied magnetic field, temperature) and intrinsic nuclear properties (i.e. gyromagnetic ratio (γ), nuclear spin (I) and natural abundance (NA, a percentage)) influence the magnitude of the magnetisation and hence the observed signal (see eqn. (2.19)–(2.22) in ref. 2) which provide a factor at fixed field and temperature of γ²(NA)I(I + 1). The size of the NMR signal also depends on the rate of precession of this magnetisation introducing a further factor of γ.² The IUPAC recommended standardised comparison of the observability of a nucleus is provided by a combination of these factors termed the receptivity (RC) (eqn (1)),³

RC = γ³(NA)I(I + 1). (1)

RC is an absolute quantity, but comparison to a commonly studied nucleus, the relative receptivity is usually quoted to give a practical feel for the ease of observation of little studied nuclear isotopes. Additionally for a particular sample the concentration of that particular element therein is a further consideration. Given key early applications of NMR were in solution-state organic chemistry it is common to make the comparison to the very widely studied spin-½ nuclei ¹H or ¹³C. For inorganic materials as probably the most often studied spin-½ nuclei is ²⁹Si this is used as a reference here (Table 1). The utility of NMR spectroscopy as a structural probe technique to understand molecules and materials comes from the fact that within the spectral resolution available the range of local interactions present experienced by the nucleus can provide a lot of information about the local surroundings (i.e. the immediate coordination up to intermediate length scales). These interactions include the through-space dipolar coupling, indirect through-bond spin–spin coupling and chemical shielding, the latter which provides the small changes in the resonance frequency between different environments. The physical background to these interactions has been previously described in detail.^2,4

Table 1 Some of the NMR properties of the nuclei considered in this review, with RC determined from eqn (1) given relative to ²⁹Si to three significant figures using parameters taken from ref. 1 and references therein

Isotope	ν o (MHz) @ 14.1 T	Natural abundance (NA)	Receptivity (RC)	Commonly used chemical shift referencing
^89Y	29.502	100	0.322	IUPAC reference^9 Y(NO3)3 H2O/D2O
				Secondary references 1 M YCl3 in H2O at 0 ppm and solid Y2Ti2O7 at 65 ppm^10
^103Rh	19.032	100	0.0856	IUPAC reference^9 Rh(acac)3, CDCl3, satd.
				0.5 M solution of the Rh(H2O)6^3+ ion 9915.8 ppm^11
				It has also been suggested to reference directly against ^1H^12
^107Ag	24.282	51.82	0.0943	As for ^109Ag
^109Ag	27.138	48.18	0.133	IUPAC reference^9 AgNO3 D2O (sat.)
				9.1 M AgNO3 (0.54 M Fe(NO3)3) −47.3 ppm
^183W	24.966	14.40	0.0287	IUPAC reference^9 1 M Na2WO4 D2O
				H3PW12O40 in water −99 ppm^13

---

In examining categories of nuclei across the Periodic Table one of the classes is made up of those nuclei with smaller gyromagnetic ratios. A convenient definition for such nuclei is those possessing smaller magnetic moment than ¹⁵N, since in the early days of commercial magic angle spinning (MAS) probes (i.e. up to the mid-1990s) there were no standard probes equipped on the so-called X-channel to tune to such low frequencies and were very much the preserve of the specialist, resulting in very few studies of such nuclei at that time. A useful shorthand for the nuclei with magnetic moments smaller than ¹⁵N is ‘low-γ’ which is now commonly used in the literature.⁵ It is convenient to split this group further into spin-½ and those with higher spin. The latter group experience the same interactions as for spin-½, but with the significant additional complication of the quadrupolar interaction.^2,4,6,7 Low-γ non-integer spin quadrupolar nuclei were recently comprehensively reviewed.¹

There are a range of other factors which complicate the observation of low-γ nuclei since the Larmor frequency (ν₀ = γB₀, B₀ is the main static magnetic field applied) will be lower at given applied magnetic fields than for nuclei with higher magnetic moments. Lower frequencies tend to result in more acoustic ringing, longer longitudinal relaxation times (T₁) and weaker internuclear interactions.² Acoustic ringing can have a number of sources which have been described in detail,⁸ but tends to be worse at lower Larmor frequencies. Also given the elements in this category (Table 1) tend to be heavier, they can also exhibit quite large shift ranges and often have significant associated anisotropies which can make the lines cover a wide frequency range. This adds to the challenges of detection and sensitivity, with recent methods of tackling these issues discussed below. The last time low-γ spin-½ nuclei were collectively reviewed was around 20 years ago.^2,5 There have been updates on particular aspects of these nuclei individually which are referenced below. This Perspective will therefore examine the methodological and technical advances that have enhanced the ability to observe and interpret the spectra from low-γ spin-½ nuclei. Their applications to probe inorganic materials problems are illustrated by recent examples taken from the last decade. To be completely comprehensive low-γ spin-½ nuclei would also include ⁵⁷Fe and ¹⁶⁹Tm. However the magnetic nature of both these isotopes means NMR reports from them are usually from internal field observation or heavily paramagnetically perturbed spectra which are quite different from conventional NMR approaches so are not discussed further here.

2. Recent advances in solid-state NMR methodology

The physical background and technological advances underpinning NMR since 2001/2 have been the subject of previous reviews^14–17 and are briefly recapped here. The intrinsic sensitivity of any spectroscopic approach such as NMR depends on population differences determined by the Boltzmann factor which provide the signal. The local interactions provide information about the environment a nucleus is in, but in powder samples the anisotropy of these interactions causes line broadening which both diminishes sensitivity by spreading the signal over a greater frequency range and degrades the spectral resolution by increasing the linewidth of the individual components. Magic angle spinning (MAS) is the most common approach for solid-state NMR as it can average anisotropic line broadening, greatly increasing the spectral resolution.^2,4 This is particularly effective for spin-½ nuclei in highly crystalline and ordered solids as there is no broadening from dispersion or the quadrupolar interaction.^2,4,6

As commercial spectrometers with MAS probes first became available for solid-state NMR these were typically equipped with wide-bore (89 mm) magnets of 4.7–9.4 T. Low-γ nuclei therefore resonated at low frequencies and there were no commercial probes available for such frequencies and the modest (by today's standards) magnetic field did not help observe the intrinsically weak signals. The low observation frequencies also introduced additional experimental complexities such as probe ringing.^2,8 In the mid-1990s more wide-bore 11.7 and 14.1 T instruments became available meaning that observation of low-γ nuclei became much more feasible, which one starts to see in the reviews of around 2001/2.^2,5 Fields have continued to rise as persistent magnetic fields of 18.8–20.0 T have become much more widely available, with the current more common state-of-the-art corresponding to wide-bore 20/21.1 T commercial instruments with now some extension to ≥21 T with persistent standard bore (57 mm) magnets and first reports of commercial 28.4 T instruments being installed. It should be noted that the advantages of the very high magnetic fields are less pronounced for spin-½ systems than for non-integer spin quadrupolar nuclei.^1,2 The other major experimental advance is the increase in the MAS rate, but this is less important for smaller magnetic moment spin-½ nuclei. Choosing the optimal combination of applied magnetic field and MAS rate depends on a range of factors such as the nature of the sample (e.g. highly crystalline vs. glassy) and the local interactions experienced determining the extent of the line broadening. For low-γ spin-½ nuclei in samples without a high density of high-γ nuclei modest MAS rates can usually narrow the lines. This is borne out by looking at the literature on low-γ spin-½ nuclei since although some work using faster MAS certainly exists the use of relatively modest MAS rates by using larger rotors (e.g. ≥7 mm) to boost the sample volume and hence the signal size is still quite widely used. Higher applied magnetic fields will also give larger signals, but given chemical shift anisotropy (CSA) is the likely dominant line broadening mechanism² in these heavy spin-½ nuclei then at higher magnetic fields the signal will be spread over a wider frequency range. Faster spinning will produce fewer spinning sidebands, but if that means using a smaller rotor this gain in signal could be offset by the smaller sample. The intrinsic linewidth under MAS also plays a role in determining the optimum conditions, with it being very low for highly crystalline materials, but can be very significant for glassy/amorphous materials. Hence compared to low-γ spin-½ quadrupolar nuclei where the highest field with fast spinning is often the best choice, a more nuanced compromise of the choice of applied magnetic field and spinning speed is necessary for the nuclei considered here. In the last 20 years there has been much progress in approaches to boost the signal. These have included using echo trains, hyperpolarisation methods, such as dynamic nuclear polarisation (DNP), where there can be some very impressive gains in signal observed and indirect detection which are described in more detail below. There are other very recent review articles that also provide useful background to recent methodological advances.^1,18,19

Once a signal is observed then the spectrum itself or approaches which manipulate the spin provide information about the environment of the observed nucleus which in turn is providing information about the structure. Key is the translation of the experimentally measured data on the nucleus to the structural detail. The initial approach which is still used is effectively the fingerprinting approach of direct comparison of the spectral parameters with those resonances from a known structure. With real developments in the understanding of the theoretical underpinnings, first principles density functional theory (DFT) calculations of both the structure and the NMR interaction parameters, combined with the availability of significant computational power, new computational approaches for extracting structural information have become much more widely applied and added a new dimension to the NMR methodology. The reader is referred to several very helpful reviews for more details of how such computational work is being applied.^20–22 The approaches are most directly applicable to extended crystalline solids. There are also examples of the computational approaches being adapted to calculation of the parameters with some atomic disorder (e.g. from solid solutions, see below examples from ⁸⁹Y) and even from glasses. Combining simulation of the observed NMR spectra and calculation of the NMR interaction parameters from the structure has led to the powerful new approach termed ‘NMR crystallography’ which has already provided real new understanding of materials.²³

2.1 Techniques for sensitivity enhancement

The sensitivity issues for low-γ, spin-½ nuclei start with the intrinsically small magnetic moments. However on top of this several other factors exacerbate accumulating a good signal-to-noise. There can be low natural abundance, although this is not much of a problem for the nuclei listed in Table 1. The nuclide of interest can be diluted in the sample. Also in the samples of interest there could be significant line broadening, which for heavier spin-½ nuclei is likely from chemical shift anisotropy. Low-γ, spin-½ nuclei can also suffer from long longitudinal (T₁) relaxation times, which must be carefully accounted for. When MAS is applied to a highly crystalline sample with inhomogeneous anisotropic line broadening, for these nuclei the static powder pattern breaks up into a series of sharp signals – the isotropic resonance plus a set of spinning sidebands. This effectively concentrates the signal into these much sharper features and hence improves the signal-to-noise. In 2.1.1 other echo trains for increasing the sensitivity are examined. However given that inherent low signal sensitivity is one of the key weaknesses for NMR there has always been an impetus to enhance the signal by the transfer of signal from a stronger source or to use a strong signal to indirectly detect a weaker signal. For example this could be transfer of magnetisation from stronger sources as in cross-polarisation (CP) from nuclei with larger nuclear moments (2.1.2) or from the magnetisation of unpaired electrons in dynamic nuclear polarisation (DNP, 2.1.3), where under favourable conditions spectacular gains in signal are possible. Given low sensitivity is even more of an issue for low-γ nuclei there is an added premium in gaining signal from other sources. There is also the possibility of detecting the nuclei indirectly (2.1.4) or some combination of these techniques might be used.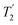

2.1.1 Echo trains. The concept of concentrating the signal from a broad line into a series of sharper signals is the same physical principle as for other echo-based approaches that refocus the magnetisation, thereby extending the lifetime of the magnetisation and increasing the sensitivity. A Carr–Purcell–Meiboom–Gill (CPMG) sequence consists of a single π/2 pulse followed by a train of alternating π pulses forming a series of spin-echoes (Fig. 1(a)). A train of time-domain spin echoes is collected. The Fourier transformation of the echo train results in a spectrum consisting of narrow ‘spikelets’, whose widths are determined by the (the spin–spin relaxation time) and whose separation in the frequency domain is (2τ)⁻¹. The peaks of the spikelets quite closely map out the lineshape that would be obtained by Fourier transformation of one half-echo. The gain in S/N comes from the concentration of the signal intensity into these narrow spikelets. The maximum possible enhancement will depend on the value of 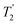and it has been shown²⁴ that the gain in S/N ratio is 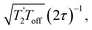where T_off is the time for the free induction decay of the individual echo to become comparable to the noise level of the standard echo. This was first demonstrated for non-integer spin quadrupolar nuclei,²⁵ with it being realised that the gain in sensitivity could help with the observation in particular of low-γ nuclei including spin-½ nuclei if they are experiencing a significant anisotropy.²⁶ This approach works if the effective spin–spin relaxation time (i.e. the decay of the echo envelope, 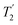) is much longer than the decay of the magnetisation caused by the local interactions. The ideal conditions for the CPMG sequence to work are when there is a large difference between the inhomogeneous and homogeneous broadening. Applications to spin-½ nuclei to enhance the sensitivity^27,28 include reports on ¹⁰⁹Ag with significant increases in sensitivity observed.²⁸

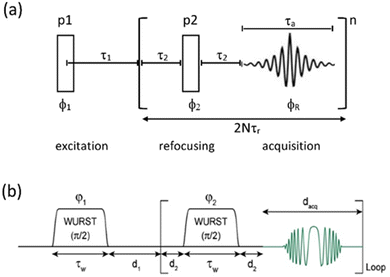Fig. 1 (a) CPMG echo sequence, with the two pulses (p1, p2) a combination that will create an echo (usually 90°, 180°) with the echo train repeated n times. In combination with MAS the repeat period is synchronised to an integer multiple of the MAS rotation period (τ_r). (b) The Wurst CPMG pulse sequence with the two WURST pulses identical and two-step phase cycling (φ₁ = φ_receiver = 0, π and φ₂ = π/2) resulting in echo formation.³⁴ (b) Reproduced from the ref. 34 with permission from Elsevier copyright 2013.

Two other points to make here are that although this CPMG approach was initially applied to static samples it can be readily coupled with MAS, as long as the two echo processes are aligned. Second, if the static line covers a very wide frequency range such that the excitation bandwidth by the pulses causes an issue, the full spectrum can be collected piecewise by stepping the rf carrier frequency, which is referred to as Variable-Offset Cumulative Spectroscopy (VOCS).^29,30 If one uses a VOCS experiment with different frequency offsets this can be combined with the CPMG sequence, with then the VOCS frequency steps set at an exact multiple of the spikelet separation. There are various considerations about the optimal pulses for such echo trains and typical practical conditions used can be found in the literature.^26–28 In the classical configuration rectangular 90° and 180° pulses are used. However with modern digital spectrometers shaped and modulated pulses often result in better echoes, such as for example using chirp pulses.³¹ These concepts are the basis for broader more uniform excitation through for example WURST (wideband uniform-rate smooth truncation) pulses that can be used for such echoes and have been applied to spin-½ nuclei (Fig. 1(b)).³² The pulses are shaped with usually modulation of both the amplitude and phase, with the latter the more complex which results in the pulse creating an effective frequency sweep and the much broader excitation.^33,34 Echoes can be formed through using different pulse lengths and/or sweep rates. Optimisation of such approaches has been considered in detail.^33–35 No matter which approach is applied if the spectrum is split up into spikelets these points selectively sample the static envelop of the spectrum which is a less complete data set than the full static spectrum. Also if several distinct sites are present their apparent relative intensity will depend on the relative 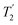for each site.

2.1.2 Cross-polarisation. Cross-polarisation (CP) is a very widely used approach for sensitivity enhancement in solid-state NMR experiments for samples containing high-sensitivity nuclei such as ¹H or ¹⁹F in close contact with nuclei with much weaker signals. This approach gave much impetus to ¹³C of polymers in the early days of solid-state NMR. Signal enhancement by CP is driven by magnetisation transfer from a higher-γ, more abundant nucleus (I, and typically ¹H), to a more dilute spin (S) via through-space dipolar coupling.² The magnetisation transfer occurs through two rf-fields applied simultaneously to the I and S spins such that their respective nutation frequencies are matched (Fig. 2(a)). As a first approximation the gain in sensitivity can be ∼(γ_I/γ_S). Although the potential enhancement increases as γ_S decreases, given the CP process is driven by dipolar coupling, its dynamics will slow as γ_S produces weaker dipole-dipole couplings. Straightforward Hartmann–Hahn matching² is usually much more challenging for a low-γ nucleus than for carbon as (i) for a given proton field to achieve the match requires a much higher B₁ field (the rf-field applied to particular nucleus) as γ_S decreases, and (ii) the much weaker dipolar interactions increase the optimum contact time, potentially up to several tens of milliseconds (as opposed to a few ms which would be typical for ¹³C) greatly increasing the power strain on the probe. The use of conventional CP to enhance the signal has been demonstrated in all the nuclei being discussed here, with pioneering examples for each of ⁸⁹Y,³⁶¹⁰³Rh,³⁷¹⁰⁹Ag^38,39 and ¹⁸³W.⁴⁰

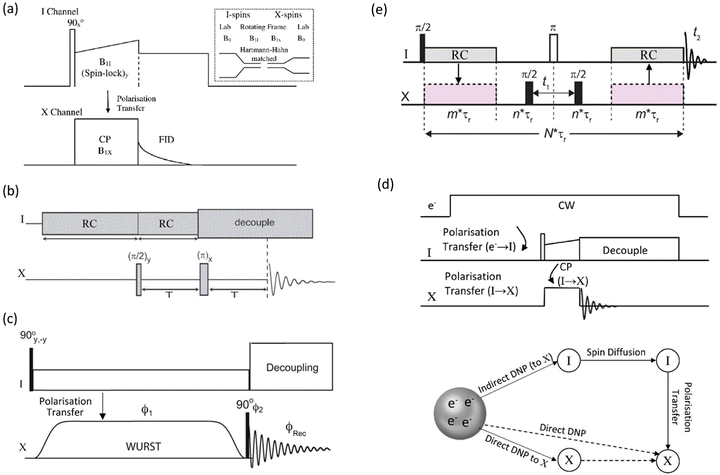Fig. 2 (a) Conventional cross-polarisation (CP) sequence between an abundant spin (I) and dilute spin (X), with the inset showing schematically the change in the energy level spacing from the applied magnetic field (B₀) to the spinlock fields (B₁s) to create the Hartmann–Hahn condition. (b) A PRESTO sequence creating polarisation transfer by recoupling (RC).⁴¹ (c) CP created using a WURST pulse in the BRAIN sequence.⁴² (d) The pulse sequence for dynamic nuclear polarisation (DNP) for indirect detection (i.e. via I) and a schematic showing the magnetisation pathways for both indirect and direct pathways. (e) An HMQC-type sequence that provides enhancement via indirect detection of the abundant spin I.

As digital spectrometer technology has evolved more sophisticated pulse sequences and shapes have been implemented ameliorating the power issues on the hardware. An interesting approach is the PRESTO (phase-shifted recoupling effects a smooth transfer of order) sequence.⁴¹ PRESTO is effective at recoupling spins and thereby transferring magnetisation (Fig. 2(b)). As it does not require the conventional spinlock for polarisation transfer it greatly reduces the radiofrequency power requirements on the probe. The paper that initially demonstrated the PRESTO approach noted ‘The method is particularly attractive for nuclei with low gyromagnetic ratios or for those experiencing strong anisotropic spin interactions…’, with one of the examples chosen to illustrate the approach ¹⁹F–¹⁰⁹Ag in AgSbF₆.⁴¹ More recently developments for polarisation transfer have included pulse sequences that allow broader excitation at lower powers on both channels. BRoadband Adiabatic INversion (BRAIN) CP uses an adiabatic inversion pulse (i.e. like WURST) applied to the rare spin nuclide and a conventional spin-locking pulse on the abundant nucleus channel (Fig. 2(c)); both static⁴² and in combination with MAS have been reported.⁴³ Under the frequency sweep created by the WURST pulse on the dilute spin there will be points where the Hartmann–Hahn matching condition is fulfilled with the conventional spin-locking pulse applied to the abundant spin for each frequency element of the powder pattern. This has the advantages that there is a much lower power requirement on the X-spin side and the transfer efficiency is far less frequency offset dependent than for the conventional hard pulse CP experiment.⁴² Another recent CP concept to boost the signal from dilute, weaker signals is based on the idea of solution and chemical exchange saturation transfer, but modified for dilute heteronuclei in solids. Although chemical exchange cannot occur as in a solution there is a group of highly abundant, more distant protons that are used to replenish the magnetisation of the more local protons that are in stronger dipolar coupling with the X nucleus and are undergoing the CP action. This has been termed PROgressive Saturation of the Proton Reservoir (PROSPR) and has been demonstrated on some low-γ quadrupolar nuclei.⁴⁴

2.1.3 Dynamic nuclear polarisation. The progress that different approaches have made can be gauged by the rate at which they appear in the literature and how their referencing in reviews change. For example dynamic nuclear polarisation (DNP) was not mentioned in a 2010 review looking at recent progress in solid-state NMR.¹⁴ DNP remains a relatively specialist technique, but is increasingly used as it develops rapidly, with commercial instruments now available.^15,45–51 There can be spectacular gains in sensitivity as the theoretical gain in signal is γ_e/γ_N where e and N correspond to electron and nucleus respectively. The key experimental points are that there needs to be a source of the electron polarisation via the right type of electron spins which are often added as a free radical in some form. There then needs to be a suitable microwave source to saturate the electron spins. Often indirect mechanisms are used where an abundant spin (e.g.¹H) has its magnetisation enhanced via DNP and then equilibrium between the protons occurs via spin diffusion. Then a mechanism for polarisation transfer between the abundant and less abundant spins is needed such as CP (Fig. 2(d)). There are cases where the DNP can be direct to the dilute (X) nuclei. There are a range radical polarisation sources that can be added and the underlying transfer mechanism (e.g. thermal mixing, cross effect, solid effect or Overhauser effect) will depend on the system and radical combination being studied. Some of the radicals used with the nuclei reviewed here are given below and the attributed mechanisms are discussed in those papers.

The application of DNP to enhance the signal from challenging nuclei has been summarised, including for ⁸⁹Y.⁴⁷ For ⁸⁹Y there are several examples in the recent literature with a range of approaches to the polarisation. The common approach is indirect polarisation using an exogeneous free radical which polarises ¹H with subsequent CP to ⁸⁹Y. The ‘model’ sample used was a frozen solution of 0.5 M Y(NO₃)₃ with the 12 mM AMUPol biradical added. Very significant signal enhancement was observed with the frozen solution added and the different peaks to different local coordinations.⁵² The same experimental approach was then applied to understanding hydrated yttrium-doped barium zirconate. Two samples were examined with 20 and 30% yttrium and water contents of ∼7 and ∼9%. Without DNP only very weak signals were observed, whereas with microwave irradiation applied two ⁸⁹Y signals are observed. Rather than via a biradical addition some samples can have intrinsic paramagnetic ions to act as the electron polarisation source effectively meaning the bulk sample is observed. Mixed samples of ceria with yttria and doped with gadolinia (general formula Ce_1−x−yY_xGd_yO_{2−x/2−y/2} with x = 0.1, 0.25, and 0.4 and y = 0.001 and 0.005) have been examined with DNP. The nature of the field sweep used indicated that polarisation transfer occurs via the solid-effect mechanism and produced very significant gains in the signal and experimental time savings of four orders of magnitude (Fig. 3).⁵³ In a different DNP study of Y₂O₃ in a frozen solution of Y(NO₃)₃ signal enhancements of >80 were observed using the trityl OX063 monoradical with polarisation transfer under MAS occurring via the cross-effect mechanism. In Gd₂O₃-doped Y₂O₃ (for T₁ relaxation reduction) spectra could be obtained quickly (∼30 min).⁵⁴

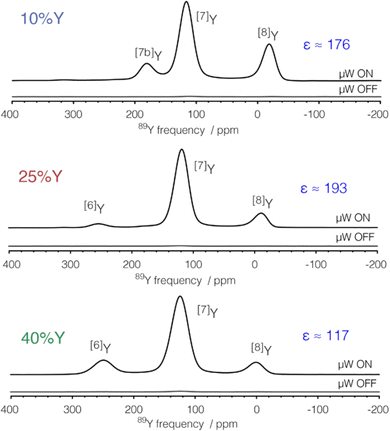Fig. 3 ⁸⁹Y MAS NMR Hahn-echo spectra from co-precipitated ceria samples with various levels (10, 25 and 40%) of Y₂O₃ substitution and 0.1% Gd₂O₃ showing the signal enhancement (ε) via DNP when microwaves (μW) are applied, with the different yttrium coordinations ^[x]Y observed.⁵³ Reproduced from ref. 53 with permission from the American Chemical Society, copyright 2021.

2.1.4 Indirect detection. In systems containing a nucleus with a much higher magnetic moment (e.g.¹H) then indirect detection is possible. A general approach that has been taken in the case of indirect detection when one of the nuclei has low sensitivity is based on dipolar recoupling within a heteronuclear correlation (HETCOR) experiment.⁵⁵ One of the most straight forward versions of such an approach is the dipolar-heteronuclear multiple-quantum coherence experiment, which has been applied to spin-½ nuclei where the signal is broad and weak.⁵⁶ A comparison was made for the theoretical enhancement for a signal obtained from a conventional approach of polarisation of the proton spins followed by CP then direct detection of the low-γ (X) nucleus to when a signal is collected by initial excitation of the X-nucleus and then detection of proton spins. It was shown this gain could be ∼(γ_1H/γ_X)^3/2 × (Δ_X/Δ_1H)^1/2, where Δ is the respective full width at half-maximum.⁵⁵ In ref. 55 this approach was applied to all of the nuclei being examined here. Efficient proton detection requires narrow ¹H signals which is most straightforwardly obtained with fast MAS. Indirect detection with protons is typically reported with MAS rates 10–50 kHz. A detailed study using 1.3 or 4 mm MAS probes compared various approaches such as the coherence transfer between ¹H and low-γ nuclei (Fig. 2(e)) being via low-power double quantum (DQ) or zero quantum (ZQ) cross-polarisation (CP) or dipolar-refocused insensitive nuclei enhanced by polarisation transfer (D-RINEPT) approaches. The limitations and advantages of these different methods are demonstrated experimentally and with numerical simulations. Examples of the gains produced by the different approaches are shown in Fig. 4 for ¹⁰⁹Ag and ⁸⁹Y. Across the series of nuclei, sensitivity gains in the range 5–165 were observed.⁵⁵ Indirect detection of ⁸⁹Y using D-HMQC was recently reported for the metal organic framework phase Y-MOF-76, which compared approaches to refocus CSA effects and reduce t₁-noise.⁵⁷

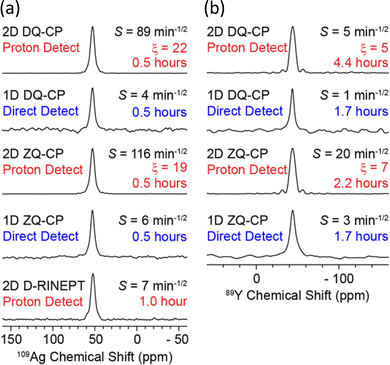Fig. 4 Demonstration of the signal enhancements produced by proton-detected compared to directly-detected solid-state NMR signals for (a) ¹⁰⁹Ag in AgSO₃CH₃ and (b) ⁸⁹Y in Y(NO₃)₃·6H₂O. The CP condition/pulse sequence used for acquisition, sensitivity (S), total experiment time and gain in sensitivity from proton detection (ξ) are indicated – see ref. 55 for the definitions. The proton-detected NMR spectra were obtained from the positive projections of the corresponding 2D HETCOR spectrum.⁵⁵ Reproduced from ref. 55 with permission from the American Chemical Society, copyright 2018.

To gain even more in signal DNP has recently been combined with indirect detection, which has become possible with the availability of low-temperature fast MAS probes. A detailed theoretical and experimental study with DNP-enhanced 2D indirectly detected HETCOR (idHETCOR) experiments on four spin-½ nuclei (¹³C, ¹⁵N, ¹¹³Cd, ⁸⁹Y), with 1.3 and 3.2 mm probes used.⁵⁸ For the experiments on yttria nanoparticles (50 nm) impregnated with a 16 mM solution of TEKPol in TCE-d₂, Fig. 5 shows the signals obtained with the two probes used. Two prominent yttrium signals are observed with differing numbers of hydroxyl nearest neighbours. The faster spinning and higher rf fields shows much better sensitivity in the 1.3 mm probe (Fig. 5(a) and (b), note the respective acquisition times (AT) of 1.5 minutes vs. 2.7 hours). Then with indirect detection for an idHETCOR a very significant gain in sensitivity was observed compared to a direct HETCOR of 42 (Fig. 5(c) and (d)).⁵⁸

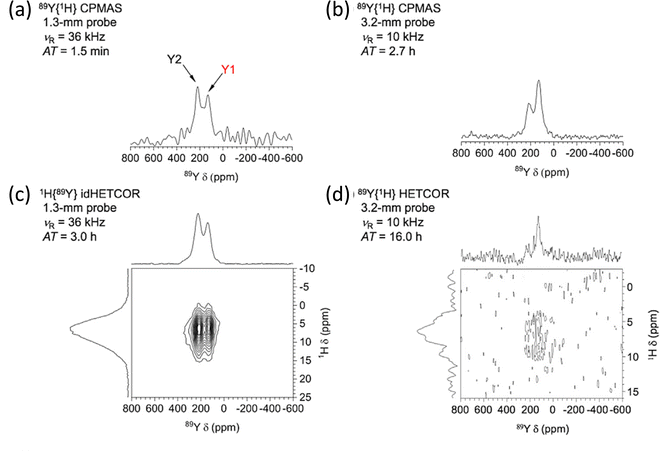Fig. 5 The effect of signal enhancement for various NMR experiments on yttria nanoparticles (50 nm) impregnated with a 16 mM solution of TEKPol in TCE-d₂, with a comparison of the signals obtained with two different NMR probes. The faster spinning and higher rf fields in the 1.3 mm probe show much better sensitivity (cf. (a) and (b)), noting the respective acquisition times (ATs). With indirect detection (idHETCOR) a very significant gain in sensitivity was observed compared to a direct HETCOR of 42 ((c) and (d)). A full list of experimental parameters can be found in Table S1 in ESI of ref. 58. Reproduced from ref. 58 with permission from Elsevier, copyright 2020.

2.2 Computational approaches – structure, NMR parameters and lineshape calculations

In parallel with experimental advances, the role of complementary computational work in overall NMR methodologies for understanding materials has developed rapidly in recent years. Progress has been driven by the greater availability of the necessary compute power with better, more sophisticated code. This was recently described in a review of non-integer spin quadrupolar low-γ nuclei¹ and is briefly recapitulated here. There are two distinct aspects of the computational work, i.e. (i) direct extraction of the NMR interaction parameters from the experimental data, and (ii) the use of first-principles calculations of both the structure and the NMR interaction parameters. To simulate spectra one can calculate the full evolution of the Hamiltonian, with SIMPSON being a widely used approach⁵⁹ although others exist. Given they are full calculations of the Hamiltonian considerable computing resource is often necessary. The much more commonly adopted approach to extracting parameters from spectra is to use a simulation program based on formulae for frequencies derived directly from the Hamiltonian and a whole range of programmes are available.^60–64 In using such programs they will be making some different approximations, for example perhaps the relevance of the high field limit (i.e. the Zeeman interaction dominates), ideal excitation, etc., which are likely to be highly valid for most cases, especially for the spin-½ nuclei being described here, but needs to always be considered.

First principles calculations of structure and the resulting NMR interaction parameters from that structure have become much more straightforward as the theoretical underpinnings have allowed the development of more readily used and efficient code. Several relatively recent comprehensive reviews provide the reader with the detailed background and development of these approaches.^20–22 A cluster is usually taken as an approximation for the extended solid or periodic boundary conditions are applied, being a good approximation for extended crystalline solids. Although these approaches were initially aimed at periodic systems there have been adaptations that allow parameters to be calculated when there is some atomic disorder (e.g. from solid solutions). A discrepancy between the calculated and observed NMR parameters suggests that the structural detail is not correct and the structure can be refined. Hence spectral simulation and NMR interaction parameters extracted from the calculated structure can be considered interactively. As a result the measured NMR parameters can more intimately and directly constrain the structure in what has become termed ‘NMR crystallography’.^23,65,66 The literature clearly shows that such an approach is being increasingly used to give new structural insight, strengthening the role of NMR in understanding structure-function relations in materials.

3. Applications to inorganic materials

The nuclei examined here were first reviewed as a group in 1994 as part of an article looking at NMR of less commonly studied spin-½ nuclei.⁶⁷ Their application collectively to inorganic materials was comprehensively reviewed around 2001.^2,5 These works^2,5 contained compilations of the NMR interaction parameters known at that time. There have been some subsequent updates on observations of individual nuclei, with some of the illustrative examples including inorganic materials. These are referenced below. Several of the advances described in Section 2 can be combined for example DNP and NMR crystallography. Some of the reviews of the developments of NMR techniques also make some reference to low-γ spin-½ nuclei.¹⁴ Some brief reference to low-γ spin-½ nuclei has been made in recent reviews of solid-state NMR applied to glasses⁶⁸ and to oxide-based materials.⁶⁹ Most of the illustrations of the application of the nuclei reported on here are taken from examples of the last few years, although to give some context for the reader who is not a long-standing afficionado of the solid-state NMR of these nuclei reference to some of the key early publications in the observation of these nuclei is provided. The present review updates of NMR parameters already collected in previous literature reviews.

3.1. Yttrium-89

With 100% natural abundance yttrium is potentially highly attractive, with two of the pioneering studies^70,71 showing from crystalline materials narrow resonances could be observed under MAS and despite the relatively few data points then available suggesting an extensive shift range in diamagnetic materials. Y₂O₃ provides a good illustration showing two sharp ⁸⁹Y resonances with a shift difference of ca. 40 ppm corresponding to the two octahedral YO₆ environments in the crystal structure. The intensity ratio of these two peaks at 3 : 1 is as expected from the known site occupancies. The high purity oxide and low-γ nature of ⁸⁹Y result in the T₁ values for both of these sites being just under four hours.⁷² This early work indicated that the ⁸⁹Y chemical shift becomes more negative with an increasing number of nearest neighbour oxygen atoms, and to become less paramagnetic as the electronegativity of the coordinating group increases. In oxide-based materials yttrium shows typical coordinations YO₅–YO₉. The influence of different effects means that direct structural assignment to such a coordination based solely on the isotropic chemical shift is often ambiguous. The data below shows that δ_iso for ⁸⁹Y moves to lower frequencies as the coordination number and/or with decreasing field strengths of the next-nearest neighbour cations, with these effects causing quite considerable overlap of the shifts associated with particular local coordinations. However in a given compound/solid solution the appearance of different peaks and their trend with composition gives good insight into changes of siting and structure. Now coupled with calculations greatly aid this situation of identification of the sites present. The applications reviewed below include direct phase identification in crystalline samples and structural siting within glasses since 2002. A particularly powerful application of ⁸⁹Y has been to probe ordering within a wide range of solid solutions given its relatively large chemical shift range.^22,73 This builds on the original application of ⁸⁹Y NMR to solid solutions in a range of lanthanide-doped variants of a pyrochlore Y₂(Sn/Ti)₂O₇.¹⁰ Recently a very helpful tutorial review has been published introducing from first principles the application of ⁸⁹Y to such ordering problems along with a good overview of the systems studied to date by such an approach, complementing well what is presented here.⁷⁴ A recent computational chemistry approach modelled the chemical shift in a wide range of molecular compounds and showed how δ_iso readily distinguishes the different ligands based on electronegativity arguments. This work is important in enabling ⁸⁹Y NMR to probe surface-formed species on for example oxides and that the CSA can often be more discriminating than δ_iso.⁷⁵

3.1.1 Yttria, its addition to other binary oxides and hydroxides. The spatial dependence of DNP means it is an approach that can be used to examine the surface of a material, particularly if an exogeneous radical source is used. In Gd₂O₃-doped Y₂O₃ DNP at varying polarisation times shows how the signal builds up (Fig. 6). Four signals are observed, with the expected ⁸⁹Y signals from bulk Y₂O₃ at 330 and 287 ppm. In addition there are two broader resonances centred around ∼200 and 100 ppm and covering a range of ∼300 ppm are observed, which are ascribed to the surface. The DNP build-up is significantly faster for the surface-related sites which is likely due to the closer proximity to the paramagnetic sources or better relaxation through dipolar effects (e.g. in Y–OH). The surface of such particles are hydroxylated and the assignment of the broad lines are to yttrium centres attached to one (∼200 ppm) or two hydroxyl groups (∼100 ppm).⁵⁴ Layered yttrium hydroxides Y₂(OH)₅X·nH₂O (X = monovalent anions, n ∼ 1.5) can incorporate ions between the layers, with NMR experiments and calculations being combined to probe the structural features that enhance such properties. Interestingly it was the chemical shift anisotropy (CSA) of ⁸⁹Y that was much more sensitive than the isotropic shift to the differences in structure and the structural changes. Each compound contained several sites, but they could each be well resolved such that the CSA could be calculated for each site. The DFT calculations allowed the sites to be assigned to different coordinations.⁷⁶

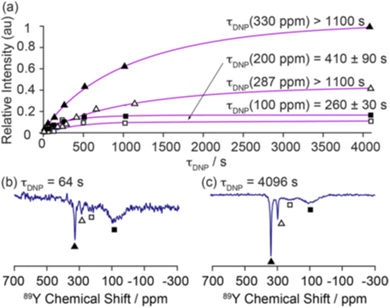Fig. 6 Demonstration of the magnetisation build up for ⁸⁹Y under DNP for 0.1% Gd₂O₃-doped Y₂O₃ with a trityl polarising agent with (a) fitted build-up curves of the bulk (330 ppm, filled triangles; 287 ppm, hollow triangles) and surface sites (∼200 ppm, hollow squares; ∼100 ppm, filled squares). The ⁸⁹Y MAS NMR spectra recorded at τ = (b) 64 and (c) 4096 s are shown to demonstrate the surface selectivity of the approach.⁵⁴ Reproduced from ref. 54 with permission from the American Chemical Society, copyright 2019.

Some other oxides to which Y₂O₃ is added are of real technological significance. ZrO₂ and CeO₂ occur in fluorite-structured forms with the metal in MO₈ coordination. As the differently valent yttrium is added this creates oxygen vacancies. Some of the properties of these materials depend on the creation of these vacancies so that understanding their distribution can be very important. Yttria-stabilised zirconia is an important engineering ceramic with high toughness, is an important material for solid oxide fuel cells (SOFC) and as an oxygen sensor. As the yttrium-content was varied from 5.9 to 42.9 mol% three peaks of varying intensity were observed in the ⁸⁹Y MAS NMR spectra at 80–90, 190–195 and 290–315 ppm which are attributed to YO₈, YO₇ and YO₆ respectively, the latter two sites being associated with one and two oxygen vacancies respectively.⁷⁷ The integrated intensity of these peaks could be extracted and compared to models of the vacancy distribution. The data shows a clear preference for vacancies associating with the zirconium site.⁷⁷ An equivalent study has been carried out for yttria-doped ceria and again three peaks are observed, with a shift offset showing peaks occurring at 0, 120 and 250 ppm reflecting the different relative electronegativity of the elements in the system. In this case the changing intensity showed that there is a preference for the vacancies to be associated with yttrium. The intensity data along with observations of ¹⁷O suggest some pairing of yttrium centres occurs.⁷⁸ A further study made a direct comparison of yttria-doped ZrO₂ and CeO₂, as well as looking at micro- and nanocrystalline variants. The vacancy preference differences between ZrO₂ and CeO₂ on doping with yttria were confirmed. When the samples were made nanocrystalline there was a marked tendency for the vacancy distribution to become much more random which was attributed to the energetics changing due to the changing balance of electrostatic and strain terms.⁷⁹ Very recently DNP has been applied to examine yttria-doped ceria. Polarisation was driven from Gd³⁺ dopants giving large sensitivity enhancements homogeneously throughout the sample approaching 200. The data confirms that the vacancies in this system have a preference for the cerium. The much greater sensitivity allowed ⁸⁹Y–⁸⁹Y homonuclear dipolar correlation experiments to be undertaken and is the first such observation for ⁸⁹Y. The experiments provide insight into the local distribution of yttrium and indicate there is no spatial clustering of the yttrium into domains.⁵³ It is also possible to then have mixtures of ZrO₂ and CeO₂ as the underlying system and/or to dope with other oxides (e.g. Sc₂O₃, CaO), which then leads to multiple doping and the effect of these changes on the structural chemistry can likewise be investigated. For yttria-doped CeO₂–ZrO₂ the vacancy preference for the metal centres follows what is observed in the binary systems.⁸⁰ Small additions of CaO, Sc₂O₃ and Y₂O₃ to a base 8 mol% yttria-stabilised composition showed CaO created more oxygen vacancies around the yttrium site, whereas they were decreased when Sc₂O₃ was added, which was explained as the larger Ca²⁺ preferring to remain as CaO₈ whilst the smaller Sc³⁺ ion prefers to be ScO₇.⁸¹

3.1.2 Pyrochlores. The general formula for pyrochlores is A₂B₂O₇ where the A cation is coordinated as a distorted AO₈ and the B cation as BO₆. Pyrochlores are closely related to some of the structures discussed above with some having a fluorite-like superstructure with an ordered removal of one eighth of the anions. There can also be a phase change to a defect-fluorite structure. These phases have a range of practically interesting properties such as ionic conductivity, relative chemical inertness and good resistance to radiation damage. There are a number of systems of real interest where yttrium is the dominant element on the A site, with solid solutions playing an important role. The structure provides a rich structural playground as many substitutions can occur. There can be differing degrees of ordering and changes between the pyrochlore and defect-fluorite structures, with a range of local environments that are of interest. A key here is that not only is there sufficient spectral resolution in ⁸⁹Y NMR to pick out the different nearest neighbour (NN) coordinations as seen above in yttrium-containing ZrO₂ and CeO₂, but different peaks can be distinguished for the different combinations of next nearest neighbour (NNN) coordinations as well. Given the quantitative nature of NMR the intensity of the peaks assigned with different NNN combinations has been the key to determining local ordering. The body of NMR work that has been built up for pyrochlores acts as a good model for showing what can be achieved in arriving at a really detailed understanding of atomic ordering on a crystalline lattice using the resolution from differences in the isotropic chemical shift, the directly quantitative nature of the NMR signal and the combination with computational work in an NMR crystallography approach.

The early NMR work looking at atomic ordering in these pyrochlores used ¹¹⁹Sn MAS NMR of rare-earth (RE) doped Y_2−xRE_xSn₂O₇ since ¹¹⁹Sn is a relatively high-γ spin-½ nucleus. Distinct paramagnetically shifted peaks could be seen, attributed to differing numbers of NNN REs.⁸² This was soon followed up by using ⁸⁹Y MAS NMR to complement the ¹¹⁹Sn NMR in the stannates, but also opened up Y₂Ti₂O₇ for investigation¹⁰ since the other two nuclei are even more challenging than ⁸⁹Y at natural abundance. An early extension of ⁸⁹Y NMR of Y₂Ti₂O₇ was to examine low levels of calcium doping on the yttrium site at 5 and 10% to create ionic conduction pathways. On doping a shoulder on the main resonance to high frequency is observed.⁸³ The most likely cause of the shoulder, given a shift in the direction of a lower coordination suggests that the yttrium coordination is lower and hence is associated with vacancies. Although there was not resolution of these separate peaks the estimated intensity suggests the vacancies are more likely forming near yttrium. Ashbrook and co-workers have built up an extensive body of work that has defined what NMR can do in examining ordering in inorganic solid solutions in crystals. For yttrium-containing pyrochlore systems there have been various dimensions of the ordering investigated with one case of A-site ordering in (Y,La)₂Ti₂O₇,⁸⁴ the majority of the work on Y₂(Sn,Ti)₂O₇,^85–88 with further reports on Y₂(Zr,Sn)₂O₇⁸⁹ and Y₂(Hf,Sn)₂O₇.⁹⁰ The series of papers on Y₂(Sn,Ti)₂O₇^85–88 shows nicely the evolution in the sophistication of the methodology.

For (Y_1−xLa_x)₂Ti₂O₇⁸⁹Y MAS NMR data complemented neutron and X-ray diffraction as well as scanning electron microscopy and electron probe microanalysis. As lanthanum substitutes for yttrium a pyrochlore solid solution exists at x = 0 to 0.134, followed by a phase mixture of the pyrochlore with a monoclinic La₂Ti₂O₇-type phase in the range x = 0.134 to 0.807, after which a solid solution in the monoclinic phase forms. The key is different peaks could be observed attributed to different combinations of NNN. In Y₂Ti₂O₇ the data suggested that lanthanum substitutes randomly, whereas at high x in the monoclinic structure yttrium showed a preference for two of the sites.⁸⁴ When substitution on the B site is examined in Y₂Ti_2−xSn_xO₇ a single phase pyrochlore solid solution exists for all x. There is a ∼15 ppm change in the chemical shift of ⁸⁹Y observed per tin NNN substitution. The evolution of the intensity of each of these peaks closely follows that expected for the tin and titanium randomly occupying the B site.⁸⁵ The use of first-principles DFT calculations allowed the assumptions of assignment of resonances to particular NNN configurations to be directly confirmed. The data also showed when the equilibrium atomic distribution had occurred.⁸⁶ The understanding of the local environments in this solid solution was extended by applying to ⁸⁹Y for the first time the two-dimensional (2D) CSA-amplified phase adjusted spinning sideband (PASS) experiments extracting CSA for ⁸⁹Y which was compared to DFT calculations. The span Ω can be more reliably extracted than the skew κ and is shown to be a sensitive probe of the NNN environment.⁸⁷ The most recent addition to work on this system takes the modelling a step further by examining a more comprehensive ensemble of configurations of the distribution of NNN. For example with say two Sn and four Ti NNN that corresponds to a single high level NNN combination, but there are three distinct configurations (Fig. 7). The NMR parameters will be largely determined by being 2 Sn and 4 Ti, but with subtle variations arising from the next level of configuration and by taking these into account spectral details were even more closely reproduced (Fig. 7).⁸⁸

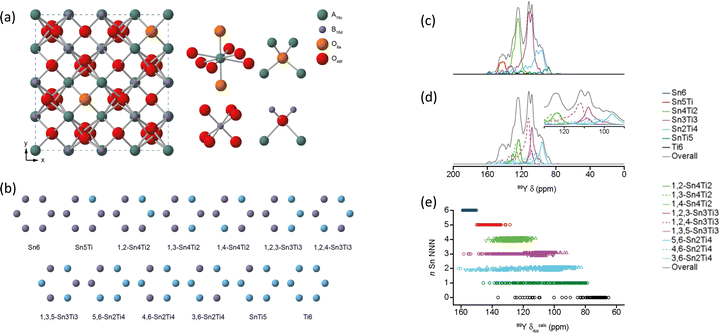Fig. 7 (a) Structure of a typical A₂B₂O₇ pyrochlore, with expansions of the local environments of the Wyckoff 16c (A), 16d (B), and 8a and 48f(O) sites. (b) Possible arrangements on the six NNN B sites that surround the pyrochlore A and B sites for Y₂(Sn,Ti)₂O₇. (c) ⁸⁹Y MAS NMR spectra of Y₂SnTiO₇ showing the breakdown into different components assuming full tin/titanium disorder, with the isotropic chemical shift decreasing as the number of NNN tins decreases. (d) The fine detail is produced when the different ordering of the tin/titanium for a given number of NNN tin is also considered. (e) The DFT calculated shift ranges show significant overlaps of different NNN tins across the structural models generated.⁸⁸ Reproduced from ref. 88 with permission from the American Chemical Society, copyright 2019.

For Y₂Zr_2−xSn_xO₇ as the zirconium content increases the equilibrium phase changes from pyrochlore to defect fluorite. However for much of the compositional range two phases co-exist. The NMR data was able to provide clear quantitative evidence as to the phases present and details of the coordinations and NNN ordering. A more complex picture of the phase variation emerged and the distribution of zirconium between the two phases. Interestingly it was shown that the vacancies have a definite preference of associating with zirconium as opposed to tin.⁸⁹ Similarly complex phase behaviour is observed in Y₂Hf_2−xSn_xO₇ with again pyrochlore (tin-rich) and defect-fluorite (hafnium-rich) structures present. Key to a real understanding was the full use of the NMR crystallography approach.⁹⁰

3.1.3 Perovskites. Perovskites (ABX₃) form another group of widely studied materials that have found a very wide range of technological applications, a result of properties such as ferroelectricity and ionic conductivity. Underlying structural features drive such properties with many related to local structure. The parent perovskite structure is cubic, but there are a whole range of variations that distort the structure away from cubic e.g. tilting of the BX₆ units and/or displacements of the A- and B-site cations from the centres of their units. A flux grown single crystal of the perovskite-structured YScO₃ doped with 1% ytterbium showed a single ⁸⁹Y resonance at 265 ppm.⁹¹ A rationalisation of the observed shift at the high end of the YO₆ range was provided in terms of the relative electronegativity of scandium. Later this system provided an example of where ⁸⁹Y MAS NMR has been applied as part of a fully multinuclear study in the solid solution La_1−xY_xScO₃.⁹² The experimental data was complemented by DFT calculations and diffraction, with the latter showing an orthorhombic structure. For the end-member YScO₃ a conventional slow spinning ⁸⁹Y MAS NMR spectrum allowed the chemical shift tensor parameters to be extracted (Table 2). In the solid solution all ⁸⁹Y spectra showed a single resonance, with the local structural variation manifest in the spectrum as a broadening compared to the end member. Across the series there was a small change of isotropic shift of ∼120 ppm, suggesting a relatively small variation in the yttrium environment across the solid solution. The changes in the relative degree of disorder can be directly understood for a spin-½ system from the linewidth. The linewidth data indicated the maximum level of disorder occurs at x ∼ 0.4 in agreement with the diffraction data which indicates that the maximum disorder occurs at x ∼ 0.5. This suggests that yttrium is distributed randomly across the A-site. The comparison with the scandium on the B-site is interesting as there are more profound effects at this point which is probably to be expected as the B-site is closer to the effects of the A-site substitution than is the next nearest A sites.

Table 2 Experimentally determined NMR shifts of ⁸⁹Y from inorganic compounds with local coordinations YO_x since previous summaries.^2,5 The accuracy of the data is found in the original publication

Compound	δ iso (ppm)	Local coordination and other comments	Ref.
YScO3	265	YO8	91
	263.1	YO8, Ω = −221 ppm, κ = 0.33	92
YVO4	−66	YO8	98
y-Y2Si2O7	170.8	YO8	99
	132.9	YO8
	95.1	YO8
	37.7	YO8
β-Y2Si2O7	207.3	YO6	99
	207.2	YO6	100
γ-Y2Si2O7	198.9	YO7	99
δ-Y2Si2O7	121.1	YO7	99
X1-Y2SiO5	215.1	YO7	99
	73.9	YO9
X2-Y2SiO5	237.1	YO6	99
	149.5	YO7
G-(La,Y)2Si2O7	88–128	YO8	101
	95–101	YO8
YBO3	117.6, 113.8	2 × YO8	108
	121.5, 118.1	2 × YO8	109
Y3BO6	15 peaks 297–168	YO7, YO8	108
YAl3(BO3)4	135	YO6	111
Y(OH)3	68	YO9	112

---

Yttrium-doped BaZrO₃ has been studied for several potential technological applications and there are several reports of ⁸⁹Y NMR from such systems. The local yttrium environments have been probed (Ba_x(Zr_0.8Y_0.2)O_3−δ) for four different values of x.⁹³ Two signals are seen in the ⁸⁹Y NMR data. One narrower peak at 420 ppm and the other much broader line in the range 100–300 ppm ascribed to YO₅ and YO₆ respectively. The much greater linewidth of the YO₆ site is down to higher disorder around this site, although no definitive reason for this is suggested. Within the signal-to-noise recorded there is no evidence of any substitution on the A-site. The YO₅ is associated with oxygen vacancies, with the intensity of this line correlated with the barium-content and indicates that maximising the barium-content is important. A study using DNP to enhance the ⁸⁹Y signal in hydrated yttrium-substituted barium zirconate samples containing 20 and 30% yttrium and water contents of ∼7 and ∼9% respectively showed very significant gains in sensitivity, although using the indirect approach i.e. via the protons required long CP contact times as the ¹H–⁸⁹Y dipolar coupling is quite weak.⁵² It was noted⁵² that the low temperature of the DNP experiment (105 K) helps enable long contact times to be used and reduces the mobility and hence averaging of dipolar interactions. The increase in sensitivity allowed a 2D ¹H–⁸⁹Y CP MAS Frequency Switched Lee-Goldburg HETCOR spectrum to be collected. Two ⁸⁹Y signals could be seen at ∼415 and 350 ppm, both assigned to octahedral coordination. The correlation experiment showed these two peaks were correlated to proton signals at 5.4 and 6.1 ppm respectively. Calculating possible local structural configurations and the resulting NMR parameters using DFT and GIPAW approaches gave direct evidence that the structural feature corresponding to the (415, 5.4) correlation is a proton bound to a yttrium – a ‘trapped’ site. The other correlation corresponds to a further distinct trapped proton site. This a very good example of how a leading-edge methodology is providing real insight into the local features that drive the properties that are of technological interest in such materials.

A further perovskite that has been studied using an approach that included ¹¹⁹Sn, ¹⁷O and ⁸⁹Y NMR is BaSn_1−xY_xO_3−x/2, with the ⁸⁹Y NMR data collected for only x = 0.1, 0.3, and 0.5. As seen for the zirconate above two yttrium signals are resolved.⁹⁴ One which shifts with composition from 300 to 343 ppm. As the first B-sublattice is known to be all tins, this effect is ascribed to changing Y cations in the second B-shell. A second site is seen, most clearly at high yttrium concentration and given it is a higher shift (∼450 ppm), as for the study by Lee et al. in a zirconate is thought to be a YO₅ site.⁹³ This latter peak disappears on hydration as the oxygen vacancy sites are occupied by hydroxyls. The experimental work was combined with computational outputs. There was some broad agreement with the trends e.g. relative shifts and changes with composition, but there were larger discrepancies between computed and observed values compared to the agreement in some other yttrium-containing systems which were not fully understood. Proton mobility remains high even at high yttrium doping which suggests there is quite strong order that prevents Y–O–Y formation as this more basic configuration would likely trap protons. The presence of magnetic ions complicated the spectrum through direct magnetic and relaxation effects, but ⁸⁹Y MAS NMR has been reported from two double perovskites, Ba₂YRuO₆⁹⁵ and Ba₂YReO₆,⁹⁶ which are geometrically frustrated antiferromagnets. ⁸⁹Y MAS NMR showed a major peak at −5860 ppm for Ba₂YRuO₆, with the large shift a result of the direct magnetic interaction from the ruthenium, along with a second much smaller peak observed at −5100 ppm which are attributed to YO₆ units with six and five ruthenium NNN respectively. The relative intensity suggests that there is strong yttrium/ruthenium ordering with only a few % disorder.⁹⁵ For Ba₂YReO₆ only a single peak at −23 290 ppm is observed suggesting almost perfect yttrium/rhenium ordering.⁹⁶

3.1.4 Crystalline silicates, garnet and zircon. Yttrium aluminium garnet (Y₃Al₅O₁₂, YAG) is a technologically widely used material, especially as a laser host and in other optical applications when doped with REs. An NMR study using the same approach as on the RE-doped pyrochlores examined ²⁷Al and ⁸⁹Y, with the majority of the data reported from ²⁷Al.⁹⁷ Several peaks could be observed and the general conclusion from changes in intensity is that there is a random distribution of the dopants. In observing ⁸⁹Y comparison between very long and short recycling times was able to separate spectra from the main (unshifted) peak at 222 ppm and those fast relaxing species that are associated with the dopant. The shifts could qualitatively be rationalised in terms of the anticipated interaction between with yttrium site in the likely configuration in the case of some dopants, but were not able to explain all the spectra.⁹⁷⁸⁹Y MAS NMR has been reported from 1% erbium-doped YVO₄ which adopts a zircon structure.⁹⁸ A single peak is observed with an isotropic chemical shift of 66 ppm, and a full-width at half-height (FWHH) of about 120 Hz. Yttrium occurs in YO₈ units in this structure which is consistent with the shift. At the 1% doping in the second coordination sphere there was no observable perturbation of the yttrium sites.

Yttrium silicates are of technological interest as yttria is often used as a sintering aid in non-oxide ceramics (e.g. Si₃N₄, SiC), which then often results in yttrium-containing silicates or oxynitrides occurring as grain boundary phases. A study using ⁸⁹Y MAS NMR reported data from the known polymorphs of Y₂Si₂O₇ (y, α, β, γ, δ) and Y₂SiO₅ (X1, X2).⁹⁹ This data expanded on the range of polymorphs and in some cases provided significantly better resolution than had previously been reported.⁷¹ The narrower lines obtained in this study allowed a fuller reconciliation with the crystal structures and in the case y-Y₂Si₂O₇ indicated only a single yttrium resonance suggesting that the crystal structure determination needs re-examining. In α-Y₂Si₂O₇ four yttrium sites were completely resolved in agreement with the structure. The two competing structures in the literature for δ-Y₂Si₂O₇ could be distinguished as only one of these structures has a single crystallographic site for yttrium. As this data updates that appearing in the previous summary in the literature² it is included in Table 2. There is a clear correlation with the mean Y–O distance across most of the dataset. The data for α-Y₂Si₂O₇ clearly illustrates this with all four sites being YO₈ coordinated, but a shift difference of >130 ppm across the sites resulting from the changing average Y–O bond length. There is also a trend of decreasing δ_iso with increasing coordination number of the yttrium, although there is quite strong overlap between the shift ranges, re-emphasising any assignment based on the shift alone has to be approached carefully (Table 2 and Fig. 8).

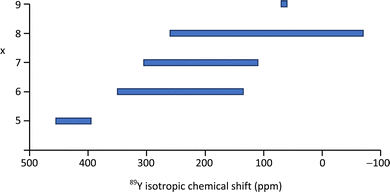Fig. 8 ⁸⁹Y isotropic chemical shift ranges associated with YO_x local coordinations based on the values reported in the literature as given in Table 2 or summarised previously.^2,5

The application of ⁸⁹Y to crystalline silicates has been extended to examine solid solutions, in analogy to the work described above on pyrochlores and perovskites. An example is the solid solution Sc₂Si₂O₇–β-Y₂Si₂O₇.¹⁰⁰ The data was collected using the CPMG approach for x = 0.5, 1.0, 1.5 and 2.0 in Y_xSc_2−xSi₂O₇. The pure yttrium end member shows a single very sharp resonance (Fig. 9). The other spectra are much broader, with some asymmetry. Given that Sc³⁺ and Y³⁺ have very different ionic radii, as scandium enters the structure there must be some local distortion which results in the significant broadening observed from chemical shift dispersion. The asymmetry observed as scandium is added cannot be explained by the effect on the yttrium site of a random distribution of NNN substitution as the intensity does not vary as expected. It was suggested that it is more likely that the symmetry is being lowered with there being two crystallographically distinct sites. Small resonances are also observed from impurity X2-(Sc,Y)₂SiO₅. The CPMG sequence has been applied to ⁸⁹Y in the solid solution (La,Y)₂Si₂O₇.¹⁰¹ The phase diagram shows that different phases can co-exist and at 99% yttrium two signals are seen at 199 and 121 ppm, corresponding to γ- and δ-(La,Y)₂Si₂O₇ polymorphs respectively. At 5% yttrium the γ has disappeared and the δ has become broader. This broadening results from the increasing range of NNN configurations possible. This system contains a further crystallographic phase G-(La,Y)₂Si₂O₇, which as two distinct lanthanum/yttrium sites. Some of the spectra where G-(La,Y)₂Si₂O₇ is present could be assigned to a single yttrium resonance showing that there is a strong preference for yttrium for one of the sites (RE2).¹⁰¹

Fig. 9 ⁸⁹Y CPMG MAS NMR spectra of Y_xSc_2−xSi₂O₇ with (a) x = 0.5, (b) 1.0, (c) 1.5 and (d) 2.0. As scandium is added the appearance of more lines suggests inequivalent sites result from differing NNN yttrium and scandium.¹⁰⁰ Reproduced from ref. 100 with permission from the International Union of Crystallography, copyright 2011.

3.1.5 Glasses. As for several of the crystalline phases discussed yttrium-based glasses are also of significant technological interest, acting as RE hosts for example in lasing and scintillation applications. ⁸⁹Y NMR data from such glasses has been reported for aluminoborates,^102–105 aluminates¹⁰⁶ and aluminosilicates.¹⁰⁷ For the aluminoborates Deters et al. carried out two paired studies looking at the base glasses and then the effect of heat treatment to form glass-ceramics for the compositions (Y₂O₃)_x(Al₂O₃)_0.4−x(B₂O₃)_0.6 (0.1 ≤ x ≤ 0.25)^102,103 and (Y₂O₃)_0.2(Al₂O₃)_x(B₂O₃)_0.8−x (0.15 ≤ x ≤ 0.4).^104,105 The work on these glasses built on work looking at crystalline solid solutions (e.g. (1 − x)RE₂O₃–xB₂O₃) for similar applications where yttrium was used as a close analogue to RE of interest such as gadolinium. A study reported ⁸⁹Y from both YBO₃ and Y₃BO₆.¹⁰⁸ For YBO₃ two resonances were observed (Table 2) which were ascribed to three possible sites although the detailed assignment is not clear. A very recent study has revisited YBO₃ including single crystal work of the pseudowollatonite structure with a monoclinic space group determined. 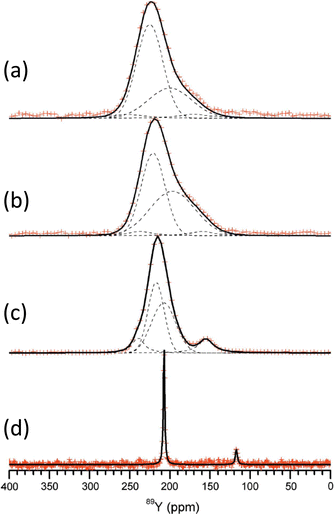The observed ⁸⁹Y MAS NMR spectrum is consistent with this structure with two yttrium sites in the ratio 2 : 1.¹⁰⁹ Y₃BO₆ is a nominal composition, better represented by Y_17.33(BO₃)₄(B₂O₅)₂O₁₆ with nine yttrium sites (YO₈,YO₇) in the structure¹¹⁰ and a complex ⁸⁹Y MAS NMR spectrum was obtained with several peaks spanning the range 297–168 ppm.¹⁰⁸ No assignment was given and this could usefully be revisited using NMR crystallography techniques. A further closely related phase YAl₃(BO₃)₄ that crystallises in the huntite structure, containing YO₆ showed a single ⁸⁹Y MAS NMR resonance (Table 2).¹¹¹ Applying ⁸⁹Y MAS NMR to (Y₂O₃)_x(Al₂O₃)_0.4−x(B₂O₃)_0.6 collected by a CPMG approach is probably the first such data reported from a glass showed quite broad resonances ∼100 ppm due to chemical shift dispersion. The addition of low levels of paramagnetic doping did not degrade the effectiveness of the CPMG approach, but considerably shortened the T₁ allowing a good signal-to-noise to be collected relatively quickly, with an optimum level of doping suggested.¹⁰² With increasing yttria content the peak position changes monotonically from ∼70 ppm up to 120 ppm. By comparison with the model crystalline compounds the shifts are in much better agreement with the borates than those in the oxides or aluminates suggesting that yttrium bonding is dominated by borate-like environments. The crystallisation of this series of glasses was followed using ¹¹B, ²⁷Al and ⁸⁹Y MAS NMR, with the yttrium showing the expected borate/aluminoborate phases formed.¹⁰³ The second series of (Y₂O₃)_0.2(Al₂O₃)_x(B₂O₃)_0.8−x (0.15 ≤ x ≤ 0.4) glasses was also studied by a combination of ¹¹B, ²⁷Al and ⁸⁹Y MAS NMR. Across this series with increasing x, δ_iso for ⁸⁹Y increases from 102 to 133 ppm. Comparison with the model crystalline compounds shows yttrium is becoming more associated with aluminium.¹⁰⁴ As glasses from this series are crystallised the NMR very nicely shows how YBO₃ and YAl₃(BO₃)₄ form as the yttrium-containing phases (Fig. 10) and a model that has four (five with the unknown phase ‘X’) phases, with the equilibrium phases changing at around x = 0.3.¹⁰⁵

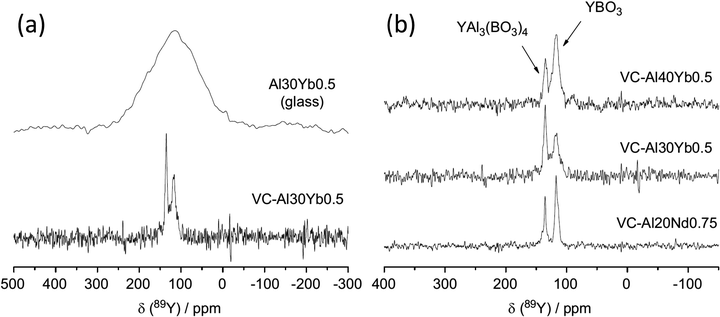Fig. 10 Application of ⁸⁹Y MAS NMR to probe glass to ceramic transitions, with an example given for (a) (Y₂O₃)_0.1(Al₂O₃)_0.3(B₂O₃)_0.6 (Al30) Yb-doped sample and (b) comparison of the major yttrium phases that form for different aluminium levels as well as a comparison of ytterbium to neodymium.¹⁰⁵ Reproduced from ref. 105 with permission from Elsevier, copyright 2012.

The concept of polyamorphism has been examined in Y₂O₃–Al₂O₃ glasses through three glasses in the compositional range 24 to 41 mol% Y₂O₃ using ²⁷Al and ⁸⁹Y MAS NMR in combination with microscopy and calorimetry.¹⁰⁶ Polyamorphism is an interesting concept where there is a density driven ‘glass-in-glass’ phase separation. The ⁸⁹Y MAS NMR data showed two resonances, a broader resonance covering the range 110–300 ppm and a narrower one at ∼75 ppm, with the relative integrated intensity and centre of gravity of the broader peak changing with composition. By comparison with the shift trends in crystalline yttrium aluminates the peak ∼220 ppm corresponds predominantly to YO₈. Peaks at lower shift are most likely due to higher coordinations. Although the exact assignment was not possible the data showed distinct regions exist within the sample with differing average yttrium coordinations.¹⁰⁶ In aluminosilicate glasses the structural incorporation of REs was investigated using ⁸⁹Y as a proxy. A comprehensive study combined experimental data with DFT GIPAW calculations of the NMR parameters based on MD simulations of the glass structure.¹⁰⁷ A comparison of direct ⁸⁹Y MAS NMR and ²⁷Al-⁸⁹Y RAPT-CP-MAS NMR data showed relatively little difference in the spectra suggesting that aluminium is close to yttrium throughout the composition range. The computational work showed that yttrium exists in all coordinations five to eight, with six and seven dominant. It also showed that the CSA tends to be larger than in crystalline compounds. The chemical shift increases as silicon replaces aluminium and/or yttrium as the NNN.¹⁰⁷

3.1.6 Fluorides. RE fluorides also have several technological applications and examining the structures of solid fluorides has been used to understand the dynamics that occur in melts. NMR can be combined with diffraction, X-ray absorption and thermal measurements, with ¹⁹F combined with ⁸⁹Y.¹¹³ Model crystalline compounds provided a range of coordinations YF₆ to YF₉ (Table 3). A comparison of the ⁸⁹Y NMR shifts between solids and melts suggested that unlike the previous non-NMR data which suggested that yttrium is present as YF₆, the shift indicated it was more likely present as YF₇/YF₈.¹¹³ A much more recent study including several of the same compounds as in the original study used ¹⁹F–⁸⁹Y variable amplitude CP (VACP) and DFT calculations to understand the shift trends with structure. The new data also revealed a significant discrepancy with some of the previously reported shifts (Table 3).¹¹⁴ A good correlation was observed between the measured δ_iso and calculated shielding. Although the coordination number and average Y–F bondlength are a helpful indicator of the expected shift (Fig. 11), other factors such as the number and type of NNN cation also have a significant influence on the shift.

Table 3 Experimentally determined NMR shift of ⁸⁹Y from inorganic compounds with local coordinations YF_x (apart from the mixed environment on r-YOF) reported since the previous reviews.^2,5 The accuracy of the data is found in the original publication

Compound	δ iso (ppm)	Local coordination and other comments	Ref.
YF3	−112	YF9	113
	−107.0	YF9	114
	−109.6, −108.7	YF9	116 and 117
β-NaYF4	−78, −80	YF9	113
α-KY3F10	−55	YF8	113
	−50.8	YF8	114
LiYF4	−54	YF8	113
α-NaYF4	−44	YF8	113
β-K2Y2F7	−47.9, −49.9	YF8 peaks in ratio 1 : 3	114
KYF4	−25, −32	YF7 peaks in ratio 1 : 1	113
	−28.5, 2.1	YF7	114
K2YF5	−25	YF7	113
	29.7	YF7	114
γ-K3YF6	20.9	YF6	113
r-YOF	125.6	YO4F4	116

---

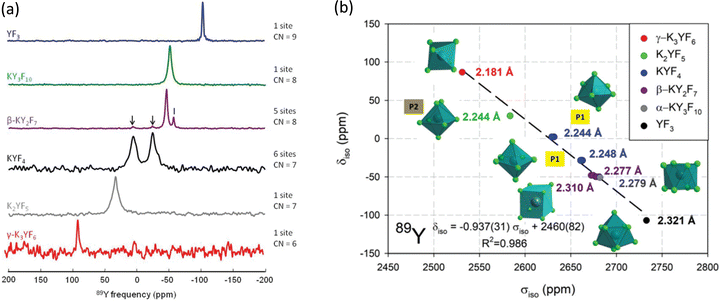Fig. 11 (a) ⁸⁹Y VACP MAS (3 kHz) NMR spectra from various KF-YF₃ binary compounds with the yttrium coordination number (CN) given. In β-KY₂F₇ known KYF₄ impurities with I indicating an unidentified impurity. (b) Experimental ⁸⁹Y δ_isoversus calculated ⁸⁹Y σ_iso with the line showing the linear regression calculated on these values corresponding to the equation given.¹¹⁴ Reproduced from ref. 114 with permission from the Royal Society of Chemistry, copyright 2019.

For yttrium fluoride nanoparticles of composition (H₃O)YF₁₀·xH₂O ¹⁹F and ⁸⁹Y showed that the nanoparticles did not consist of bulk YF₃. Static and MAS NMR data was collected using VACP and showed two ⁸⁹Y species with resonances at ∼55 and −36 ppm, with the intensity of the latter increasing with decreasing particle size suggesting it was a surface related species.¹¹⁵ Fluorolytic sol–gel formation of nanoscale yttrium fluorides/oxyfluorides from acetate precursors was followed by a combination of ¹⁹F and ⁸⁹Y which included data from the crystalline oxyfluoride r-YOF.¹¹⁶ Yttrium was added to CaF₂via a sol–gel route to form Ca_1−xY_xF_2+x.¹¹⁷ To enhance the yttrium NMR signal ¹⁹F–⁸⁹Y CP was used. At low yttrium contents a single resonance was observed at −33 ppm (which then shifts to more negative values with increasing yttrium content) attributed to yttrium occupying the YF₈ cubic site in the host structure. At higher concentrations fluorine clustering occurs and a second signal at −50 to −60 ppm is observed, but associated with YF₈ in a square antiprism. The trends in intensity qualitatively agree the expected changes in structure. Yttrium was also introduced into the closely related SrF₂ to form a solid solution Sr_1−xY_xF_2+x using mechanochemical and sol–gel approaches.¹¹⁸ The two synthetic approaches show very similar spectra and the same two yttrium species as for the calcium system, but with slightly different shift and opposite trends in the shift with changing composition which is related to the opposite trends in the lattice parameter as yttrium is added. However the two species and underlying structural explanations are the same for both systems.

3.1.7 Hydrides, intermetallics and related compounds. The great majority of NMR applied to materials follows the pattern of the cases described above which are electronic insulators and have no electron-based magnetism. Although relatively niche there are examples of the application of NMR to materials where the resonance is influenced by other effects such as via the presence of conduction electrons. In such systems in addition to chemical shift effects the delocalised conduction electrons cause an additional shift, termed the Knight shift, which can often be much larger than chemical shift effects.²⁸⁹Y has been reported in a number of such systems. For Y₅Si₂B₈ a single asymmetric peak ∼800 ppm was observed in the MAS NMR spectrum which was believed to cover inequivalent yttrium sites in the structure.¹¹⁹ A subsequent study of the closely related phase YB₄ showed a single yttrium resonance, consistent with the single site in the structure at a shift of 294.6 ppm,¹²⁰ which is substantially different from Y₅Si₂B₈ highlighting how much greater the scale of Knight shifts can be. The MAS data also allowed the Knight Shift Anisotropy (KSA) to be extracted which results from a combination of the lower than cubic symmetry at the yttrium site and the contribution of electrons (e.g. p, d) in addition to s to the density of states.¹²⁰

More recently a collaboration between Eckert and Pöttgen has produced an extensive set of ⁸⁹Y NMR data from intermetallics. Their first ⁸⁹Y MAS NMR study examined YPd₂Sn and YPdSn, also reporting 18 other related compounds for comparison. The shift range covered by the 20 compounds was ∼3000 ppm.¹²¹ There was only very modest sideband intensity for both YPdSn and YPd₂Sn indicating a relatively small KSA. YPdSn has a much smaller linewidth than YPd₂Sn which was possibly caused by local variations around the yttrium due Pd/Sn disorder.¹²¹ In the wider set of compounds reported three yttrium sites could be resolved in YPdSi. In the group of 20 compounds studied there was no obvious correlation to parameters that would normally be expected (e.g. electronegativity) since the density of states in the conduction band is generally not a reflection of the local environment given the band structure is delocalised. Full electronic structure calculations provide better insight. ⁸⁹Y NMR has also been applied to the series YNiX and YIrX (X = Si, Ge, Sn, Pb), compounds which crystallise in an orthorhombic TiNiSi-type structure.¹²² There were some attempts to rationalise the shift changes observed with the s-electron density of states and additional quantum mechanical calculations. Although there was a general increase in the shift with the s density of states other structural factors must be complicating things. For YIrSi and YIrGe a sizeable KSA was observed which was related to the reverse T/X site occupancy in these two compounds.¹²² For the compounds Y₂RuB₆, Y₂ReB₆, Y₂RhSi₃, YRh₂Si, and YPdSi, the first four have two and the last one three yttrium sites. ⁸⁹Y MAS NMR was able to readily resolve these sites with shift differences >1500 ppm.¹²³ A further report concerned the ThCr₂Si₂-structured silicides YT₂Si₂ (T = Co, Ni, Cu, Ru, Rh, Pd).¹²⁴ Again a large range of shifts was observed and in one case, YRu₂Si₂ a large KSA was found which could be attributed to local structural distortion.¹²⁴ The Pauli paramagnet YIrSb showed a single ⁸⁹Y resonance that was shifted by ∼600 ppm from the isotypic YIrSn which is a result of the increased electron withdrawing power of antimony compared to tin reducing the s-electron spin density at the yttrium site.¹²⁵ In the YCrB₄-structured borides YTB₄ (T = Mo, W, Re) the ⁸⁹Y MAS NMR data shows very much smaller Knight shifts than for the compounds above. For YMoB₄ and YWB₄ the shifts are in the range for non-magnetic, insulating materials whereas YReB₄ is a metal and therefore the Knight shift makes an important contribution.¹²⁶ Recently a computational study has drawn together many of these experimental observations applying an ab initio DFT approach to calculating the ⁸⁹Y shielding parameters. The calculated shift variation of ∼2500 ppm matches well with the experimentally observed shift variation, with some outliers. The calculations show that although the spin-contact (s-electron) term dominates other terms cannot be neglected including the chemical shift.¹²⁷

Metal hydrides have several potential technological applications, such as for hydrogen storage and thin films can display varying optical properties. For yttrium hydride as hydrogen is added to yttrium metal the stoichiometry strongly influences the metallic character of the system. Addition of oxygen to form YH_xO_y can create photochromic materials.¹¹²¹H–⁸⁹Y CP-MAS showed a relatively broad peak 372–190 ppm, which was made up of at least 7 separate components. There are interesting changes in the spectrum on illumination, such as the increase of the Knight-shifted peak. A 2D ⁸⁹Y–¹H HETCOR spectrum confirmed the presence of the numerous local yttrium coordinations.¹¹²

3.2 Rhodium-103

¹⁰³Rh is 100% naturally abundant like ⁸⁹Y, but its smaller γ typically leads to lower sensitivity and longer relaxation times than ⁸⁹Y meaning it is typically more difficult to observe. Its NMR was extensively reviewed by Carlton in 2008.¹² Rhodium also possesses a very large chemical shift range of ∼12 000 ppm largely determined from solution-state studies. Solid-state NMR reports made up only a very small fraction of those in the review by Carlton. The examples included rhodium nanoparticles.¹²⁸ From insulating solids ¹H–¹⁰³Rh CP on two crystalline salts of polynuclear Rh(III) clusters were reported. One was a mesitylate salt of a dimer and the other the perchlorate salt of a trimer. To boost the signal-to-noise a 7.5 ppm MAS probe was used coupled with relatively long contact times (>10 ms) for the CP. For the mesitylate sample δ_iso = 10 131 ppm, with slow spinning (∼1 kHz) showing a set of spinning sidebands (Fig. 12) allowing the CSA components to be extracted, with a span (Ω) of 758 ppm and skew of −0.33. For the perchlorate salt two sets of spinning sidebands were clearly resolved with an approximate intensity ratio of 1 : 2, with careful inspection of the more intense set of sidebands showing evidence of two partially resolved peaks, consistent with the presence of three inequivalent rhodium positions, with the δ_iso of 9401, 9359, and 9354 ppm. The first line has a span of 1720 ppm and skew of −0.64 and the latter two have a single set of parameters reported with a span of 1620 ppm and skew of −0.58.³⁷ Despite these elegant results there has been no data building on this work. This is most likely due to the very large shift range observed making the CSA sizeable for everything apart from the most symmetric sites, as well as driving a significant intrinsic linewidth from chemical shift dispersion in samples with disorder/imperfections. These factors coupled with the low intrinsic sensitivity result in the low number of ¹⁰³Rh NMR observations from solids. The recent successful development of indirect proton-detected ¹⁰³Rh NMR data was reported from a solid rhodium complex, where two distinct peaks at chemical shifts of −8300 and −8375 ppm were observed.⁵⁵ The shift difference is much larger than any expected scalar or residual dipolar coupling and was therefore attributed to different solid forms.

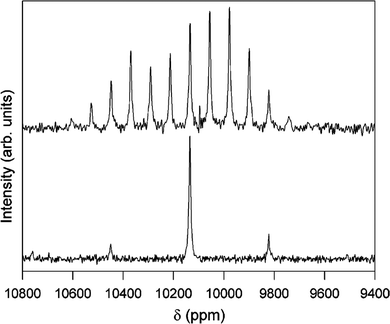Fig. 12 ¹H–¹⁰³Rh CP-MAS NMR spectra of [[(H₂O)₄Rh(μ₂-OH)₂Rh(H₂O)₄]‚(dmtos)₄]·8H₂O comparing spinning rates of 1.0 (top) and 4.0 kHz (bottom). Both spectra acquired with 8 ms contact time, 5 s relaxation delay for 12 000 (top) and 15 800 (bottom) acquisitions.³⁷ Reproduced from the ref. 37 with permission from the American Chemical Society, copyright 2006.

3.3 Silver-109

Silver had two isotopes suitable for NMR spectroscopy, ¹⁰⁷Ag and ¹⁰⁹Ag, with almost equal natural abundance. However ¹⁰⁹Ag has a 41% greater receptivity and forms the vast majority of NMR reports on silver.² Early work covered fast-ion conducting glasses (where static lines were observed due to silver ion motion) and complexes of biological significance. As expected for a relatively heavy metal a sizable chemical shift range is observed and often spectra show very significant CSA. Merwin and Sebald³⁸ showed that ¹H–¹⁰⁹Ag CP could significantly improve the sensitivity, but relatively long contact times (>10 ms) were necessary and that silver lactate was a good set-up compound. A body of work 2003–2007 by Penner and co-workers added a significant amount of new ¹⁰⁹Ag NMR data from model compounds and extensively reviewed^129,130 the development of it as a nucleus up to that point. An alternative set-up compound for CP was suggested in AgSO₃CH₃ which could also act as secondary chemical shift reference at 87.2 ppm.³⁹ The literature up to around 2006 is very well covered through the four articles,^2,5,129,130 with the data given here from studies since then. The key themes that have become more common for studies using ¹⁰⁹Ag NMR are the state of silver in microporous materials, with some sporadic reports on other systems e.g. chromatographic media, quantum dots, silver cluster formation and some continuing work on fast-ion conducting glasses.

The ¹⁰⁹Ag MAS NMR spectrum reported from Ag₂PO₃F showed three resonances at 190, 38, and −10 ppm with an approximate intensity ratio of 2 : 1 : 1. There are three crystallographically distinct sites with significantly different local coordinations. The relative intensities allow the 190 ppm peak to be assigned to the Ag1 site which is also consistent with this site having the lowest coordination number. The differences in the local structures around the other two sites did not allow an assignment to the Ag2 and Ag3 sites on the basis of the information available.¹³¹ For the samples AgOP(OR)₂ (R = CH₃, C₂H₅, C₄H₉) using CP-MAS NMR allowed all the parameters of the CSA to be collected. With two peaks in the isotropic position J(¹⁰⁹Ag,³¹P) couplings of ∼1300 Hz could be seen, with this magnitude indicating that the silver and phosphorus are directly bonded.¹³² The contribution that computational work now plays in NMR is illustrated by a study applying a full-potential linearised augmented plane wave (FP-LAPW) approach to calculate a range of properties including the NMR response for the compounds AgXC₇H₁₀N₂ (X = Cl, Br, I).¹³³ The approach was tested by calculating δ_iso (via the shielding) for AgNO₃ which gave −72.13 ppm, compared to the experimental value of −76.0 ppm.¹²⁹ The full CSA tensor was calculated for each of the three compounds, with the shift trends showing that as the electronegativity of the attached halogen decreases leads to a larger chemical shift.¹³³

3.3.1 Silver in microporous and mesoporous materials. Zeolites have long been a class of compounds that have been a rich source of NMR studies because of the intricate structural detail that ²⁹Si and ²⁷Al MAS NMR have been able to provide that was very difficult to determine by other characterisation techniques.² These microporous materials are typically tetrahedral frameworks where the aluminium carries a nett negative lattice charge that is compensated for by a cation, e.g. Ag⁺. An early study using ¹⁰⁹Ag collected static NMR data with a spin-echo to look at changes in the local environment and the dynamics of silver as the samples change their hydration state.¹³⁴ Different zeolites (A, X and Rho) were studied and showed significant colour changes as the hydration state changes. In Ag-Rho a distinct Knight shifted peak is seen as metallic silver nanoparticles formed. For Ag–X the colour change is related to a stronger interaction of the Ag⁺ with the framework whereas in Ag–A it was the change of coordination of the cation with the loss of water that was the dominant effect.¹³⁴ In chabazite containing silver on heat treatment the silver can migrate through the structure and ¹⁰⁹Ag NMR showed the formation of metallic silver or partially reduced silver clusters and that the size of the nanoparticles formed depended on the atmosphere used.¹³⁵ A similar study was carried out on silver-containing ETS-10 and mordenite.¹³⁶ In ETS-10 most treatments showed two peaks at 78 and 26 ppm which are associated with different sites in the channels. These peaks change intensity with heat treatment and atmosphere, with 400 °C under hydrogen showing the formation of metallic silver. For mordenite there is a single site at 30 ppm, with silver forming under the same conditions as for ETS-10, but with a wider line and poorer signal-to-noise suggesting either less formation or smaller particles.

A study of 3–6 wt% silver-containing BEA zeolites after different treatments used a range of different probe techniques, but included ¹⁰⁹Ag MAS NMR. For a 3% silver-containing sample ¹⁰⁹Ag MAS NMR showed a single silver site at 21.5 ppm, but at 6% the single peak had shifted to −33.2 ppm, with the shift explained as changes in the paramagnetic character of small silver clusters. On reduction of the 6% sample a large shift to the Knight-shifted position of a silver nanoparticle at 5272 ppm is observed.¹³⁷ For two small pore zeolites (Cha, Rho) silver loadings were varied between 14 and 26 wt% silver. On reduction extensive formation of metallic silver was observed. The differences in lineshape suggested those particles formed in Cha(2) are quite similar to that of silver metal whereas in Rho(4) the significantly narrower resonance observed suggests a lower aggregation of silver, which was corroborated by UV-Vis spectra.¹³⁸ For silver-exchanged sodium zeolite Y, the as-prepared sample showed a single peak 42 ppm corresponding to Ag⁺ associated with the lattice. On reduction all the silver is transformed to the metal at 5570 ppm. As it is used for catalytic oxidation of ammonia the spectrum then shows a mixture of the two species.¹³⁹ The mesoporous framework material silver 4,4′-bipyridine nitrate can capture perchlorate to form silver 4,4′-bipyridine perchlorate and the structural transformation can be followed by ¹⁰⁹Ag NMR. For the initial compound ¹⁰⁹Ag CP MAS NMR shows a single isotropic resonance at 438.5 ppm and a significant CSA. J-coupling to two equivalent ¹⁴N (I = 1) nuclei shows the expected quintet fine structure. As chlorate is added a second signal that increases in intensity with chlorate concentration is formed at 341 ppm with different CSA.¹⁴⁰

3.3.2 Other silver-containing materials. The above section has shown that within porous materials silver nanoparticles can often be formed. The importance of noble metal nanoparticles to a whole range of technologies means there are other methods of preparation and NMR has been used to characterise them.¹⁴¹ The formation of complexes such as Ag₇(H)[E₂P(OR)]₆ (E = Se, S) can be the precursors for the fabrication silver nanoparticles.¹⁴² At the centre of this complex are seven equivalent silver atoms with a ¹⁰⁹Ag peak at slightly different shifts ∼1120 ppm split into a doublet because of the J-coupling of ∼20 Hz to the hydride. Small mixed-valence silver clusters were formed in a porous ionic crystal based on dodecamolybdophosphate. Again ¹⁰⁹Ag MAS NMR was used to show the state of the silver at different reaction points. For one sample a peak at ∼240 ppm was observed confirming the existence of Ag⁺, whereas in other samples no signal was observed attributed to real nanosized silver clusters.¹⁴³ A study examined two differently sized (average diameter 20 and 80 nm) silver nanoparticles capped with a 1 nm layer of polyvinylpyrrolidone to prevent aggregation and oxidation. For both particles the shift and T₁ relaxation time were very close to the values of bulk silver. This static data showed a size-dependent and somewhat unexpected strongly temperature-dependent ¹⁰⁹Ag linewidth, with an explanation advanced in terms of the oscillatory spin-density and “even-and-odd-electron particle” models.¹⁴⁴

Silver-ion chromatography can separate unsaturated compounds such as light olefin/paraffin mixtures. Tuning the selectivity of the stationary phase towards olefins occurs by varying the ratio of silver ion : mixed ligands. ¹⁰⁹Ag NMR was carried out using indirect detection based around the ¹H–¹⁰⁹Ag dipolar couplings for proton-detected HETCOR spectra. For other samples as the silver coordination changed strong shift differences of ∼370 ppm were observed.¹⁴⁵ Fast-ion conducting glasses in the series 40AgI–(60 − x)AgPO₃–xAg₂WO₄ (0 ≤ x ≤ 25 mol%) with interesting optical properties which strongly depend on composition have been studied with a range of techniques including ³¹P and ¹⁰⁹Ag NMR. For ¹⁰⁹Ag both static and MAS NMR data was collected, with the MAS NMR spectra showing a single sharp peak ∼490 ppm, which did not change position with composition. This indicates that the silver is present as Ag⁺, the location of which is independent of composition consistent with the fact that it depends on the O/I ratio, which in constant across this series.¹⁴⁶

3.4 Tungsten-183

With tungsten having the lowest receptivity and being the heaviest of the nuclei reported here, these facts combine to make this the most difficult of them to observe. This is reflected in the continuing scarcity of solid-state NMR observations of ¹⁸³W, which is well illustrated by the paucity of citations to the pioneering observations of this nucleus by MAS¹⁴⁷ and ¹H CP.⁴⁰ There has been a recent addition to the literature of ¹⁸³W via the report of NMR data from some polyoxometallates which have a range of potential technological applications.¹³ High field (18.8 T) was applied along with MAS at 10 kHz and CPMG with SPINAL-64 ¹H decoupling for most samples. ¹⁸³W MAS NMR spectra were reported for K₃₃H₇P₈W₄₈O₁₈₄ (crown-type), K₈γ-SiW₁₀O₃₆ and NaK₆PW₁₁O₃₉ (Keggin-type), K₆P₂W₁₈O₆₂ (Dawson-type) and (TBA)₄SiW₁₂O₄₀. In all of these polyoxometalate units the tungsten is present as WO₆, with these units clustered in various ways to form the complex. The isotropic chemical shifts were reported (Table 4). Despite the relatively poor signal-to-noise two distinct tungsten sites are observable in K₃₃H₇P₈W₄₈O₁₈₄ in the ratio 2 : 1 and three equally populated sites for K₈γ-SiW₁₀O₃₆ (Fig. 13). Similarly for K₆P₂W₁₈O₆₂, the two anticipated signals are seen, whereas although six are expected for NaK₆PW₁₁O₃₉ only two could be seen. The CSA for ¹⁸³W in these complexes ranges up to ∼1500 ppm.¹³ The proton-detected approach has also been applied to ¹⁸³W, demonstrated on (NH₄)₂WS₄,⁵⁵ with the observed shift at 3648 ppm agreeing with the original CP observation.⁴⁰

Table 4 Experimentally determined NMR shifts of ¹⁸³W from inorganic polyoxometalate cluster compounds with the tungsten present as WO₆¹³

Compound	δ iso (ppm) (±1)
K33H7P8W48O184	−170, −202
K8γ-SiW10O36	−95, −125, −164
NaK6PW11O39	−136, −183
K6P2W18O62	−118, −168
(TBA)4SiW12O40	−145

---

Fig. 13 ¹⁸³W NMR spectra of (i) K₃₃H₇P₈W₄₈O₁₈₄, (ii) K₈SiW₁₀O₃₆, (iii) K₆P₂W₁₈O₆₂, (iv) NaK₆PW₁₁O₃₉ and (v) (TBA)₄SiW₁₂O₄₀. collected static (left) and MAS (right).¹³ For details of the collection conditions see the ESI of ref. 13. Reproduced from the ref. 13 with permission from the John Wiley and Sons Ltd, copyright 2017.

4. Summary and outlook

A summary is presented of the progress made over the last 20 years in the application of solid-state NMR of spin-½ low-γ nuclei to the study of inorganic materials up to approximately spring 2022. Progress is illustrated in the period since the last overview of this set of nuclei collectively was provided around 20 years ago,^2,5 as well as using more recent summaries of individual nuclei. Key differences that have emerged in the period are the better sensitivity available now and the complementary computational work. For sensitivity the much higher magnetic fields now typically available start things off in a much better place. It should be noted though that for nuclei where chemical shift-based mechanisms are important there can be a downside of higher magnetic fields with the CSA spreading the intensity over a greater frequency range and if disorder is present the intrinsic width under MAS will be greater. A range of other signal enhancement techniques have been successfully applied such as CPMG echo sequences, DNP and indirect detection. All show advantage and should help further develop these nuclei. DFT calculations of both structure and then the corresponding NMR parameters are widely impacting on solid-state NMR which is no different for this group of nuclei. The development of these four nuclei over the last 20 years has proceeded at significantly different rates. It is clear that ⁸⁹Y has made the most progress with a significant body of work building on the foundations of the literature in early 2001. Between 2000–2006 a substantial database of ¹⁰⁹Ag shifts was reported by Penner.^129,130 Up to this point static work on fast-ion silver based materials had been the most common solid-state NMR application of ¹⁰⁹Ag. Since then the use of ¹⁰⁹Ag has been dominated by using the large shift difference between silver in Ag⁰ and Ag⁺ states to identify the nature of the silver present and the formation of silver nanoparticles in a range of settings. For ¹⁰³Rh and ¹⁸³W there still are very few solid-state NMR reports probably largely as a result of sensitivity limitations. As the methods for signal enhancement become more routine there will be increasing impact on the observation of such nuclei. Also as the leading-edge of individual techniques (e.g. ultrafast MAS, ultrahigh field, higher temperature DNP) develop so will their combinations which will open up new applications to such nuclei. This Perspective clearly illustrates that NMR continues to make real strides with a multinuclear approach becoming more fully realised.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author gratefully acknowledges the support of the Universities of Southampton, Lancaster and Warwick of his research over the last decade. Copyright holders who gave permission for the use of figures from their publications are thanked. NMR infrastructure at Warwick funded through a variety of sources including EPSRC, the HEFCE and the University of Warwick, as well as through the Science City Advanced Materials project supported by Advantage West Midlands (AWM) and part funded by the European Regional Development Fund (ERDF) has been important in making low-γ nuclei more accessible. Current support from EPSRC is acknowledged via EP/T014911/1 for the provision of ultrahigh solid-state NMR infrastructure.

References

1. M. E. Smith, Magn. Reson. Chem., 2021, 59, 864–907.
2. K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State NMR of Inorganic Materials, Pergamon, 2002.
3. R. K. Harris, E. D. Becker, S. M. C. De Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795–1818.
4. M. J. Duer, Solid-State NMR Spectroscopy Principles and Applications, Blackwell Science, 2002.
5. M. E. Smith, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, 2001, vol. 43, pp. 121–175.
6. M. E. Smith and E. R. H. van Eck, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 159–201.
7. R. E. Wasylishen, S. E. Ashbrook and S. Wimperis, NMR of Quadrupolar Nuclei in Solid Materials, John Wiley & Sons, 2012.
8. I. P. Gerothanassis, Prog. Nucl. Magn. Reson. Spectrosc., 1987, 19, 267–329.
9. R. K. Harris, E. D. Becker, S. M. C. De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59–84.
10. C. P. Grey, M. E. Smith, A. K. Cheetham, C. M. Dobson and R. Dupree, J. Am. Chem. Soc., 1990, 112, 4670–4675.
11. M. C. Read, J. Glaser, M. Sandstrom and I. Toth, Inorg. Chem., 1992, 31, 4155–4159.
12. L. Carlton, in Annual Reports on Nmr Spectroscopy, ed. G. A. Webb, Elsevier Academic Press Inc, San Diego, 2008, vol. 63, pp. 49–178.
13. M. Haouas, J. Trebosc, C. Roch-Marchal, E. Cadot, F. Taulelle and C. Martineau-Corcos, Magn. Reson. Chem., 2017, 55, 902–908.
14. J. V. Hanna and M. E. Smith, Solid State Nucl. Magn. Reson., 2010, 38, 1–18.
15. C. Leroy and D. L. Bryce, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 109, 160–199.
16. B. F. Chmelka, J. Magn. Reson., 2019, 306, 91–97.
17. S. E. Ashbrook, J. M. Griffin and K. E. Johnston, in Annual Review of Analytical Chemistry, ed. P. W. Bohn and J. E. Pemberton, Annual Reviews, Palo Alto, 2018, vol. 11, pp. 485–508.
18. D. L. Bryce, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, Elsevier, 2022, ch. 1, vol. 107, pp. 1–46.
19. F. A. Perras and A. L. Paterson, in Comprehensive Inorganic Chemistry III, ed. J. Reedijk and K. R. Poeppelmeier, Elsevier, 2021 DOI:10.1016/B978-0-12-823144-9.00015-7.
20. T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20.
21. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779.
22. S. E. Ashbrook and D. M. Dawson, Acc. Chem. Res., 2013, 46, 1964–1974.
23. R. K. Harris, R. E. Wasylishen and M. J. Duer, NMR Crystallography, John Wiley & Sons, 2012.
24. R. Lefort, J. W. Wiench, M. Pruski and J. P. Amoureux, J. Chem. Phys., 2002, 116, 2493–2501.
25. F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, J. Phys. Chem. A, 1997, 101, 8597–8606.
26. F. H. Larsen, J. Skibsted, H. J. Jakobsen and N. C. Nielsen, J. Am. Chem. Soc., 2000, 122, 7080–7086.
27. R. Siegel, T. T. Nakashima and R. E. Wasylishen, J. Phys. Chem. B, 2004, 108, 2218–2226.
28. I. Hung, A. J. Rossini and R. W. Schurko, J. Phys. Chem. A, 2004, 108, 7112–7120.
29. D. Massiot, I. Farnan, N. Gautier, D. Trumeau, A. Trokiner and J. P. Coutures, Solid State Nucl. Magn. Reson., 1995, 4, 241–248.
30. A. J. Pell, R. J. Clement, C. P. Grey, L. Emsley and G. Pintacuda, J. Chem. Phys., 2013, 138, 114201.
31. E. Kupce and R. Freeman, J. Magn. Reson., Ser. A, 1995, 115, 273–276.
32. A. W. MacGregor, L. A. O'Dell and R. W. Schurko, J. Magn. Reson., 2011, 208, 103–113.
33. R. W. Schurko, Acc. Chem. Res., 2013, 46, 1985–1995.
34. L. A. O'Dell, Solid State Nucl. Magn. Reson., 2013, 55–56, 28–41.
35. I. Hung and Z. H. Gan, J. Magn. Reson., 2010, 204, 256–265.
36. L. H. Merwin and A. Sebald, J. Magn. Reson., 1990, 88, 167–171.
37. B. L. Phillips, J. R. Houston, J. Feng and W. H. Casey, J. Am. Chem. Soc., 2006, 128, 3912–3913.
38. L. H. Merwin and A. Sebald, J. Magn. Reson., 1992, 97, 628–631.
39. G. H. Penner and W. L. Li, Solid State Nucl. Magn. Reson., 2003, 23, 168–173.
40. L. H. Merwin and A. Sebald, Solid State Nucl. Magn. Reson., 1992, 1, 45–47.
41. X. Zhao, W. Hoffbauer, J. Gunne and M. H. Levitt, Solid State Nucl. Magn. Reson., 2004, 26, 57–64.
42. K. J. Harris, A. Lupulescu, B. E. G. Lucier, L. Frydman and R. W. Schurko, J. Magn. Reson., 2012, 224, 38–47.
43. S. Wi, R. W. Schurko and L. Frydman, Solid State Nucl. Magn. Reson., 2018, 94, 31–53.
44. M. J. Jaroszewicz, A. R. Altenhof, R. W. Schurko and L. Frydman, J. Am. Chem. Soc., 2021, 143, 19778–19784.
45. A. G. M. Rankin, J. Trebosc, F. Pourpoint, J. P. Amoureux and O. Lafon, Solid State Nucl. Magn. Reson., 2019, 101, 116–143.
46. P. Berruyer, L. Emsley and A. Lesage, Emagres, 2018, 7, 93–104.
47. F. A. Perras, T. Kobayashi and M. Pruski, Emagres, 2018, 7, 35–50.
48. A. J. Rossini, J. Phys. Chem. Lett., 2018, 9, 5150–5159.
49. M. Rosay, L. Tometich, S. Pawsey, R. Bader, R. Schauwecker, M. Blank, P. M. Borchard, S. R. Cauffman, K. L. Felch, R. T. Weber, R. J. Temkin, R. G. Griffin and W. E. Maas, Phys. Chem. Chem. Phys., 2010, 12, 5850–5860.
50. M. Ha and V. K. Michaelis, in Modern Magnetic Resonance, ed. G. A. Webb, Springer, 2018, pp. 1183–1206.
51. Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941.
52. F. Blanc, L. Sperrin, D. Lee, R. Dervisoglu, Y. Yamazaki, S. M. Haile, G. De Paepe and C. P. Grey, J. Phys. Chem. Lett., 2014, 5, 2431–2436.
53. D. Jardon-Alvarez, N. Kahn, L. Houben and M. Leskes, J. Phys. Chem. Lett., 2021, 12, 2964–2969.
54. N. J. Brownbill, D. Lee, G. De Paepe and F. Blanc, J. Phys. Chem. Lett., 2019, 10, 3501–3508.
55. A. Venkatesh, M. J. Ryan, A. Biswas, K. C. Boteju, A. D. Sadow and A. J. Rossini, J. Phys. Chem. A, 2018, 122, 5635–5643.
56. A. Venkatesh, D. Gioffre, B. A. Atterberry, L. Rochlitz, S. L. Carnahan, Z. R. Wang, G. Menzildjian, A. Lesage, C. Coperet and A. J. Rossini, J. Am. Chem. Soc., 2022, 144, 13511–13525.
57. F. A. Perras, T. W. Goh and W. Y. Huang, Solid State Nucl. Magn. Reson., 2022, 120, 101807.
58. Z. R. Wang, M. P. Hanrahan, T. Kobayashi, F. A. Perras, Y. H. Chen, F. Engelke, C. Reiter, A. Purea, A. J. Rossini and M. Pruski, Solid State Nucl. Magn. Reson., 2020, 109, 101685.
59. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.
60. D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calve, B. Alonso, J. O. Durand, B. Bujoli, Z. H. Gan and G. Hoatson, Magn. Reson. Chem., 2002, 40, 70–76.
61. K. Eichele, WSolids1, version 1.21.3, Universität Tübingen, 2015.
62. T. F. Kemp and M. E. Smith, Solid State Nucl. Magn. Reson., 2009, 35, 243–252.
63. F. A. Perras, C. M. Widdifield and D. L. Bryce, Solid State Nucl. Magn. Reson., 2012, 45–46, 36–44.
64. S. G. J. van Meerten, W. M. J. Franssen and A. P. M. Kentgens, J. Magn. Reson., 2019, 301, 56–66.
65. C. Martineau, J. Senker and F. Taulelle, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, 2014, vol. 82, pp. 1–57.
66. S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204.
67. A. Sebald, NMR Basic Principles and Progress, 1994, 31, 91–131.
68. R. Youngman, Materials, 2018, 11, 476–499.
69. O. B. Lapina, A. A. Shubin and V. V. Terskikh, in Modern Magnetic Resonance, ed. G. A. Webb, Springer, 2018, pp. 1125–1160.
70. A. R. Thompson and E. Oldfield, J. Chem. Soc., Chem. Commun., 1987, 27–29.
71. R. Dupree and M. E. Smith, Chem. Phys. Lett., 1988, 148, 41–44.
72. T. Harazono and T. Watanabe, Bull. Chem. Soc. Jpn., 1997, 70, 2383–2388.
73. M. E. Smith, in NMR Crystallography, ed. R. K. Harris, R. E. Wasylishen and M. J. Duer, J. Wiley and Sons Ltd, 2009, ch. 23, pp. 341–353.
74. J. Xu, S. J. Jiang and Y. P. Du, ChemPhysChem, 2020, 21, 825–836.
75. L. Latsch, E. Lam and C. Coperet, Chem. Sci., 2020, 11, 6724–6735.
76. Z. M. Liu, L. X. Liang, D. Xiao, Y. Ji, Z. C. Zhao, J. Xu and G. J. Hou, Phys. Chem. Chem. Phys., 2021, 23, 27244–27252.
77. K. Kawata, H. Maekawa, T. Nemoto and T. Yamamura, Solid State Ion., 2006, 177, 1687–1690.
78. N. J. Kim and J. F. Stebbins, Chem. Mater., 2007, 19, 5742–5747.
79. P. Jain, H. J. Avila-Paredes, C. Gapuz, S. Sen and S. Kim, J. Phys. Chem. C, 2009, 113, 6553–6560.
80. H. Maekawa, K. Kawata, Y. P. Xiong, N. Sakai and H. Yokokawa, Solid State Ion., 2009, 180, 314–319.
81. R. J. Darby, I. Farnan and R. V. Kumar, Ionics, 2009, 15, 183–190.
82. C. P. Grey, C. M. Dobson, A. K. Cheetham and R. J. B. Jakeman, J. Am. Chem. Soc., 1989, 111, 505–511.
83. N. Kim and C. P. Grey, Dalton Trans., 2004, 3048–3052.
84. E. J. Harvey, S. E. Ashbrook, R. L. Gregory and S. A. T. Redfern, J. Mater. Chem., 2006, 16, 4665–4674.
85. S. E. Ashbrook, K. R. Whittle, G. R. Lumpkin and I. Farnan, J. Phys. Chem. B, 2006, 110, 10358–10364.
86. S. W. Reader, M. R. Mitchell, K. E. Johnston, C. J. Pickard, K. R. Whittle and S. E. Ashbrook, J. Phys. Chem. C, 2009, 113, 18874–18883.
87. M. R. Mitchell, D. Carnevale, R. Orr, K. R. Whittle and S. E. Ashbrook, J. Phys. Chem. C, 2012, 116, 4273–4286.
88. R. F. Moran, D. McKay, P. C. Tornstrom, A. Aziz, A. Fernandes, R. Grau-Crespo and S. E. Ashbrook, J. Am. Chem. Soc., 2019, 141, 17838–17846.
89. S. E. Ashbrook, M. R. Mitchell, S. Sneddon, R. F. Moran, M. de los Reyes, G. R. Lumpkin and K. R. Whittle, Phys. Chem. Chem. Phys., 2015, 17, 9049–9059.
90. R. F. Moran, A. Fernandes, D. M. Dawson, S. Sneddon, A. S. Gandy, N. Reeves-McLaren, K. R. Whittle and S. E. Ashbrook, J. Phys. Chem. C, 2020, 124, 17073–17084.
91. S. Balamurugan, U. C. Rodewald, T. Harmening, L. van Wullen, D. Mohr, H. Deters, H. Eckert and R. Pottgen, Z. Naturforsch., B: J. Chem. Sci., 2010, 65, 1199–1205.
92. K. E. Johnston, M. R. Mitchell, F. Blanc, P. Lightfoot and S. E. Ashbrook, J. Phys. Chem. C, 2013, 117, 2252–2265.
93. J. H. Lee, Z. H. Gan and O. H. Han, J. Am. Ceram. Soc., 2014, 97, 3749–3754.
94. L. Buannic, F. Blanc, D. S. Middlemiss and C. P. Grey, J. Am. Chem. Soc., 2012, 134, 14483–14498.
95. T. Aharen, J. E. Greedan, F. Ning, T. Imai, V. Michaelis, S. Kroeker, H. D. Zhou, C. R. Wiebe and L. M. D. Cranswick, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 134423.
96. T. Aharen, J. E. Greedan, C. A. Bridges, A. A. Aczel, J. Rodriguez, G. MacDougall, G. M. Luke, V. K. Michaelis, S. Kroeker, C. R. Wiebe, H. D. Zhou and L. M. D. Cranswick, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 064436.
97. R. J. McCarty and J. F. Stebbins, Solid State Nucl. Magn. Reson., 2016, 79, 11–22.
98. R. Amantea, P. Ghigna, P. Mustarelli and V. Tartara, J. Solid State Chem., 2005, 178, 1692–1696.
99. A. I. Becerro, A. Escudero, P. Florian, D. Massiot and M. D. Alba, J. Solid State Chem., 2004, 177, 2783–2789.
100. M. Allix, M. D. Alba, P. Florian, A. J. Fernandez-Carrion, M. R. Suchomel, A. Escudero, E. Suard and A. I. Becerro, J. Appl. Crystallogr., 2011, 44, 846–852.
101. A. J. Fernandez-Carrion, M. Allix, P. Florian, M. R. Suchomel and A. I. Becerro, J. Phys. Chem. C, 2012, 116, 21523–21535.
102. H. Deters, A. S. S. de Camargo, C. N. Santos, C. R. Ferrari, A. C. Hernandes, A. Ibanez, M. T. Rinke and H. Eckert, J. Phys. Chem. C, 2009, 113, 16216–16225.
103. H. Deters, A. S. S. de Camargo, C. N. Santos and H. Eckert, J. Phys. Chem. C, 2010, 114, 14618–14626.
104. H. Deters, J. F. de Lima, C. J. Magon, A. S. S. de Camargo and H. Eckert, Phys. Chem. Chem. Phys., 2011, 13, 16071–16083.
105. H. Deters and H. Eckert, Solid State Nucl. Magn. Reson., 2012, 41, 48–59.
106. N. K. Nasikas, S. Sen and G. N. Papatheodorou, Chem. Mater., 2011, 23, 2860–2868.
107. A. Jaworski, T. Charpentier, B. Stevensson and M. Eden, J. Phys. Chem. C, 2017, 121, 18815–18829.
108. M. T. Cohen-Adad, O. Aloui-Lebbou, C. Goutaudier, G. Panczer, C. Dujardin, C. Pedrini, P. Florian, D. Massiot, F. Gerard and C. Kappenstein, J. Solid State Chem., 2000, 154, 204–213.
109. B. Fuchs, F. Schroder, G. Heymann, R. Siegel, J. Senker, T. Justel and H. Huppertz, Z. Anorg. Allg. Chem., 2021, 647, 2035–2046.
110. J. H. Lin, S. Zhou, L. Q. Yang, G. Q. Yao, M. Z. Su and L. P. You, J. Solid State Chem., 1997, 134, 158–163.
111. O. Aloui-Lebbou, C. Goutaudier, S. Kubota, C. Dujardin, M. T. Cohen-Adad, C. Pedrini, P. Florian and D. Massiot, Opt. Mater., 2001, 16, 77–86.
112. C. V. Chandran, H. Schreuders, B. Dam, J. W. G. Janssen, J. Bart, A. P. M. Kentgens and P. J. M. van Bentum, J. Phys. Chem. C, 2014, 118, 22935–22942.
113. C. Bessada, A. Rakhmatullin, A. L. Rollet and D. Zanghi, J. Fluor. Chem., 2009, 130, 45–52.
114. J. Dabachi, M. Body, J. Dittmer, A. Rakhmatullin, F. Fayon and C. Legein, Dalton Trans., 2019, 48, 587–601.
115. B. E. G. Lucier, K. E. Johnston, D. C. Arnold, J. L. Lemyre, A. Beaupre, M. Blanchette, A. M. Ritcey and R. W. Schurko, J. Phys. Chem. C, 2014, 118, 1213–1228.
116. G. Scholz, M. Dreger, R. Bertram and E. Kemnitz, Dalton Trans., 2015, 44, 13522–13529.
117. T. Krahl, G. Scholz and E. Kemnitz, J. Phys. Chem. C, 2014, 118, 21066–21074.
118. B. Ritter, T. Krahl, G. Scholz and E. Kemnitz, J. Phys. Chem. C, 2016, 120, 8992–8999.
119. J. Roger, V. Babizhetskyy, S. Cordier, J. Bauer, K. Hiebl, L. Le Polles, S. E. Ashbrook, J. F. Halet and R. Guerin, J. Solid State Chem., 2005, 178, 1851–1863.
120. O. J. Zogal, P. Florian, D. Massiot, S. Paluch, N. Shitsevalova and D. F. Borshchevsky, Solid State Commun., 2009, 149, 693–696.
121. C. Hoting, H. Eckert, T. Langer, I. Schellenberg and R. Pottgen, J. Solid State Chem., 2012, 190, 216–220.
122. C. Hoting, H. Eckert, F. Haarmann, F. Winter and R. Pottgen, Dalton Trans., 2014, 43, 7860–7867.
123. C. Hoting, H. Eckert, F. Haarmann and R. Pottgen, Z. Anorg. Allg. Chem., 2014, 640, 1303–1308.
124. C. Hoting, H. Eckert, S. F. Matar, U. C. Rodewald and R. Pottgen, Z. Naturforsch., B: J. Chem. Sci., 2014, 69, 305–312.
125. C. Benndorf, L. Heletta, T. Block, H. Eckert and R. Pottgen, Z. Anorg. Allg. Chem., 2017, 643, 294–298.
126. C. Benndorf, M. de Oliveira, C. Doerenkamp, F. Haarmann, T. Fickenscher, J. Kosters, H. Eckert and R. Pottgen, Dalton Trans., 2019, 48, 1118–1128.
127. L. Kalantari, P. Blaha, K. H. Khoo and R. Laskowski, J. Phys. Chem. C, 2017, 121, 28454–28461.
128. P. A. Vuissoz, T. Yonezawa, D. L. Yang, J. Kiwi and J. J. vanderKlink, Chem. Phys. Lett., 1997, 264, 366–370.
129. G. H. Penner and W. L. Li, Inorg. Chem., 2004, 43, 5588–5597.
130. G. H. Penner and X. L. Liu, Prog. Nucl. Magn. Reson. Spectrosc., 2006, 49, 151–167.
131. M. Weil, M. Puchberger, E. Fuglein, E. J. Baran, J. Vannahme, H. J. Jakobsen and J. Skibsted, Inorg. Chem., 2007, 46, 801–808.
132. F. Chen and R. E. Wasylishen, Magn. Reson. Chem., 2010, 48, 270–275.
133. M. Samsami, B. Azadegan, H. A. R. Aliabad and F. Amiri-Shookoh, J. Mol. Model., 2022, 28, 136.
134. G. E. Pavlovskaya, C. F. Horton-Garcia, C. Dybowski, D. R. Corbin and T. Meersmann, J. Phys. Chem. B, 2004, 108, 1584–1589.
135. Y. Liu, F. Chen, S. M. Kuznicki, R. E. Wasylishen and Z. H. Xu, J. Nanosci. Nanotechnol., 2009, 9, 2768–2771.
136. Y. Liu, F. Chen, R. E. Wasylishen, Z. H. Xu, J. Sawada and S. M. Kuznicki, J. Nanosci. Nanotechnol., 2012, 12, 6420–6427.
137. N. Popovych, P. Kyriienko, S. Soloviev, R. Baran, Y. Millot and S. Dzwigaj, Phys. Chem. Chem. Phys., 2016, 18, 29458–29465.
138. C. W. Lopes, J. Martinez-Ortigosa, K. Gora-Marek, K. Tarach, J. A. Vidal-Moya, A. E. Palomares, G. Agostini, T. Blasco and F. Rey, J. Mater. Chem. A, 2021, 9, 27448–27458.
139. J. Martinez-Ortigosa, C. W. Lopes, G. Agostini, A. E. Palomares, T. Blasco and F. Rey, Microporous Mesoporous Mater., 2021, 323, 111230.
140. I. R. Colinas, K. K. Inglis, F. Blanc and S. R. J. Oliver, Dalton Trans., 2017, 46, 5320–5325.
141. L. E. Marbella and J. E. Millstone, Chem. Mater., 2015, 27, 2721–2739.
142. C. W. Liu, Y. R. Lin, C. S. Fang, C. Latouche, S. Kahlal and J. Y. Saillard, Inorg. Chem., 2013, 52, 2070–2077.
143. S. Uchida, T. Okunaga, Y. Harada, S. Magira, Y. Noda, T. Mizuno and T. Tachikawa, Nanoscale, 2019, 11, 5460–5466.
144. K. Son and Z. Jang, J. Korean Phys. Soc., 2013, 62, 292–296.
145. H. Nan, C. Zhang, A. Venkatesh, A. J. Rossini and J. L. Anderson, J. Chromatogr. A, 2017, 1523, 316–320.
146. M. Blais-Roberge, S. H. Santagneli, S. H. Messaddeq, M. Rioux, Y. Ledemi, H. Eckert and Y. Messaddeq, J. Phys. Chem. C, 2017, 121, 13823–13832.
147. C. T. G. Knight, G. L. Turner, R. J. Kirkpatrick and E. Oldfield, J. Am. Chem. Soc., 1986, 108, 7426–7427.

---