Electrochromic response and control of plasmonic metal nanoparticles
Yoonhee
Kim†
 a,
Seungsang
Cha†
a,
Seungsang
Cha†
 a,
Jae-Ho
Kim
a,
Jae-Ho
Kim
 a,
Jeong-Wook
Oh
a,
Jeong-Wook
Oh
 b and
Jwa-Min
Nam
b and
Jwa-Min
Nam
 *a
*a
aDepartment of Chemistry, Seoul National University, Seoul 151-747, South Korea. E-mail: jmnam@snu.ac.kr
bDepartment of Chemistry, Hankuk University of Foreign Studies, Yongin 17035, South Korea
First published on 21st May 2021
Abstract
Plasmonic electrochromism, the dependence of the colour of plasmonic materials on the applied electrical potential, has been under the spotlight recently as a key element for the development of optoelectronic devices and spectroscopic tools. In this review, we focus on the electrochromic behaviour and underlying mechanistic principles of plasmonic metal nanoparticles, whose localised surface plasmon resonance occurs in the visible part of the electromagnetic spectrum, and present a comprehensive review on the recent progress in understanding and controlling plasmonic electrochromism. The mechanisms underlying the electrochromism of plasmonic metal nanoparticles could be divided into four categories, based on the origin of the LSPR shift: (1) capacitive charging model accompanying variation in the Fermi level, (2) faradaic reactions, (3) non-faradaic reactions, and (4) electrochemically active functional molecule-mediated mechanism. We also review recent attempts to synchronise the simulation with the experimental results and the strategies to overcome the intrinsically diminutive LSPR change of the plasmonic metal nanoparticles. A better understanding and controllability of plasmonic electrochromism provides new insights into and means of the connection between photoelectrochemistry and plasmonics as well as future directions for producing advanced optoelectronic materials and devices.
Introduction
Plasmonic nanostructures have drawn extensive interest over the past few decades owing to their ability to manipulate exceptionally strong light–matter interactions on a sub-diffraction scale. In nanostructures, such interactions are mainly responsible for the localised surface plasmon resonance (LSPR), that is, the collective oscillation of the conduction electrons along the incident electromagnetic waves within the physical boundaries of the nanostructures. Since LSPR has numerous potential applications, including sensing,1 therapeutics,2 nonlinear optics,3 and catalysis,4,5 it is highly desirable to precisely control LSPR and related properties. Accordingly, various ways to regulate the LSPR have been extensively reported both theoretically and experimentally, for example, by changing the size and geometry of the nanostructure as well as the dielectric function of the constituent material and surrounding medium. Another strategy to tune LSPR by applying an electric potential across the nanostructure through electrical or chemical means, referred to as plasmonic electrochromism, has received attention due to its reversible and prompt response. Such susceptible colouring behaviours of plasmonic nanoparticles showed great potential for facilitating various applications, especially in display applications such as electrically tuned colour filters, low-power display or smart windows encompassing a broad spectral range.6 However, most studies on the electrochromic behaviour of plasmonic materials have been limited to semiconducting nanocrystals whose LSPRs are positioned beyond the visible range.7,8 Therefore, the use of plasmonic metals is inevitable to study electrochromic responses in the visible range, which is necessary for developing functional optoelectronic devices, such as adaptive displays and energy-efficient smart windows.8–10In 1991, the electrochemical LSPR shift of Ag nanoparticles was first reported, stating that the electronic properties of Ag nanoparticles should be considered to fully understand the plasmon absorption band along with chemical reactions and changes in the refractive index of the surroundings.11 Subsequently, one of the authors of this paper, Paul Mulvaney, developed this field of plasmonic electrochromism as engrafting spectroelectrochemistry to investigate the electrochromic behaviour of Ag nanoparticles. The optical response, however, was diminutive to be practically utilised.12 Hereafter, several pioneers began to study the exact principle causing the electrochromic LSPR shift in tandem along with investigating various ways to improve the minute change (Fig. 1). The electrochromic behaviour of plasmonic nanoparticles is classically explainable by the Drude model and Mie theory, with the concept that the individual nanoparticles are viewed as nanoscale capacitors. Under the applied electric potential, the additional conduction electrons are charged or discharged on the nanoparticle surface, which acts as a capacitor, in response to changes in the Fermi level.13 Then, the dielectric function and plasma resonance frequency of the constituent metal are changed as per the Drude model.12,14–17 However, it is not sufficient to describe the plasmonic electrochromic phenomena, which draws researchers to propose more exquisite models and perform simulations that take real situations into account. However, it is not practically possible to perfectly synchronise the simulation results with the experimental data, and naturally in this process, some discrepancy exists.18–21 In this review paper, we compare and discuss the classically designed models with more recently developed models, including quantum mechanical insights into capacitance related to the density of states (DOS), and introduce a number of conceptual designs for high-performance optoelectronic displays and sensors.
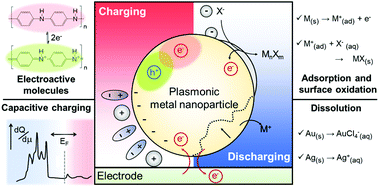
As another aspect of research in this field, strategies to enlarge the small LSPR shift have been developed. A number of research groups have employed electrochemically active functional molecules, such as, polyaniline (PANI),22–26 methylene blue (MB),27 and graphene,28 onto the plasmonic metal nanoparticle surface to control the electrochromic responses through the functionalities of the additional electrochemically active layers rather than the plasmonic material itself.22–28 In addition, methods inducing chemical reactions of plasmonic nanoparticles, such as metal oxide21,29 and metal halide formation,30 and dissolution31–33 have been developed. We also review the operational principles, performances of these methods, and key applications with electrochromic principles and materials.
Operational principles of electrochromic behaviours of plasmonic nanoparticles
Devices to investigate the electrochromic actuation of metal nanoparticles are basically two or three electrode electrochemical cells, mainly composed of two transparent conducting oxide (TCO) thin films, usually indium tin oxide (ITO), on glass substrates facing each other, an electrolyte filled between them, and sometimes with a Pt quasi-reference electrode (Fig. 2a).15–17,21,29–33 One of the TCO films is used as the working electrode and the other as the counter electrode. Further, the metal nanoparticles are loaded on the working electrode. Transparent electrodes are necessary to monitor the optical response of the nanoparticles by using in situ dark-field spectroscopy at both the single particle level and ensemble level while applying an external bias. The electrolytes should be selected appropriately depending on the investigation purpose. Electrochemically active electrolytes, including chloride and bromide ions in water, are used if electrolytes are involved in the electrochromic mechanism. On the other hand, it is better to choose electrochemically inert molecules, for example, NaF in water21 and TBAPF6 in acetonitrile, to guarantee uniform and consistent charging throughout a wide range of voltage window, especially to avoid unexpected faradaic reactions.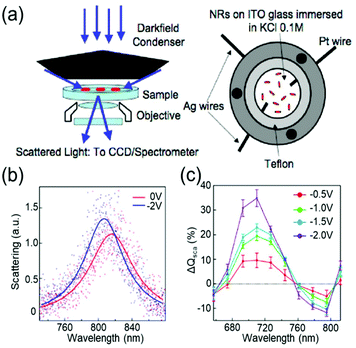 | ||
| Fig. 2 General set-up of plasmonic electrochromic devices and typical trends in their spectral change. (a) Scattering spectra of individual nanoparticles, as observed using a dark-field microscope connected to a spectrometer (left). The plasmonic electrochromic devices are electrochemical cells with 2 or 3 electrodes and electrolytes. Two faced ITO glasses and a Pt wire are playing the role of the working, counter, and quasi-reference electrodes, respectively. Reprinted with permission.15 Copyright 2009 American Chemistry Society. (b) Electrochromic behaviour of a gold nanorod. Its LSPR blue shifts under cathodic bias. (c) Percentage change in the scattering cross-section at the wavelength of the longitudinal LSPR mode. The scattering intensity gradually increases as negative voltages are applied. Reprinted with permission 6. Copyright 2016 American Chemistry Society. | ||
Change in intrinsic free carrier density by capacitive (dis)charging
The electrochromic behaviours of plasmonic metal nanoparticles are typically based on the assumption that the nanostructure can be considered as a capacitor. This is mainly because charges cannot cross the metal nanoparticle–solution interface, even though the electric potential across it is changed, apart from the case where the faradaic reaction occurs. Instead, the charges in the metal are accumulated just below the interface, while the counterions in the solution are piled up on the opposite side of the interface to compensate the applied potential, which highly resembles the behaviour of a capacitor.34 Therefore, as a capacitor, the nanoparticles with electrolytes can be capacitively charged or discharged in response to the applied voltages.The electrochromic behaviour of the metal nanoparticles is based on the density of free electrons on the metal nanoparticle surface, which changes depending on the capacitive charging or discharging. The simplest model for understanding this system is the Drude model in which the free electron density is directly related to the plasma frequency and dielectric function according to the equation:
| ε(ω) = ε∞ − ωp2/ω2+iγω) | (1) |
Here, γ is the damping constant, plasma frequency is ωp = (Ne2/mε0)1/2, ε∞ is the dielectric constant of the bulk metal at a very high frequency, N is the free electron density, e is the elementary charge, and m is the effective mass of the free electrons. LSPR features, such as the resonance frequency, full width at half maximum (FWHM), and intensity, are changed in response to the altered dielectric function. For example, in a quasi-static approach35 of spherical nanoparticles, the resonance frequency is easily quantified at which the polarisability, αsph, of the nanoparticles of radius a reaches a maximum using the following equation:
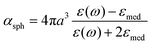 | (2) |
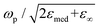 , which shows that the resonance frequency is proportional to N1/2.14,15,35,36 Consequently, this relation indicates that capacitive charging induces a blueshift of the LSPR peak by increasing the free electron density, while discharging results in a redshift. Due to the intrinsically large free electron density of metals, the shifts are so small that they seem to vary linearly.
, which shows that the resonance frequency is proportional to N1/2.14,15,35,36 Consequently, this relation indicates that capacitive charging induces a blueshift of the LSPR peak by increasing the free electron density, while discharging results in a redshift. Due to the intrinsically large free electron density of metals, the shifts are so small that they seem to vary linearly.
The classical capacitive charging model for electrochromism is matched qualitatively with experimental observations. The anodic potential typically causes a redshift in the LSPR peak, whereas under the cathodic potential, the peak shows a blueshift. Fig. 2b shows the single-particle scattering spectra of a gold (Au) nanorod that follow the general trend.15 The scattering intensity increases as the FWHM decreases in the cathodic potential range and vice versa (Fig. 2c). These trends are universally interpreted using the capacitive charging (or discharging) model discussed above.
The anisotropic nanostructures have different expressions of polarizability as compared to eqn (2), and the peak shifting rate appears to vary. However, they still produce monotonic and slow variations in the LSPR.14,15,36 For instance, the Chang group experimentally showed the morphology effects in the electrochromic behaviour of gold nanorods according to their size and aspect ratio. The capacitively changed resonance frequency moved faster when the nanoparticles were smaller in size and had a larger aspect ratio.21 In addition, the Abajo group reported theoretical results that single-monolayer gold disks have potential for the dramatic modulation of the LSPR shift using the Drude model with doping charges.19 The authors claimed that the rapid LSPR change is due to the small thickness of the disk that makes all the doping charges accumulate in the outermost atomic layer, while the doping charges in the spherical Au nanoparticles are homogeneously distributed over the entire volume. Beyond this monotonic change, however, the trend of the LSPR shift could drastically change with a high cathodic bias, and this anomaly will be discussed in detail in the next section.
In addition to the shift in the resonance frequency, the FWHM exhibits various tendencies depending on the experimental conditions, while the Drude model predicts it to decrease as the charge density increases. Consequently, simple classical models are insufficient to explain this inconsistent change in the FWHM, which makes people devise a more elaborate model to properly emulate the reality. It is exceptionally important to consider the surface chemistry of the system because the FWHM is determined by the damping constant of the system. Furthermore, surface chemistry is directly associated with surface damping or chemical interface damping.37 The general chemistry near the nanoparticle surface in electrochromic devices is explained below.
Excess charges are pushed in or out of the conductor through capacitive charging or discharging, and they have to be distributed on the surface and continuously screened beneath the surface within the ionic diameter or Fermi screening length. This charge-depleted layer has a different dielectric function compared to that inside the metal nanoparticle.12,16,18 Simultaneously, under the applied electric potential, electrolytes in the solution form an electric double layer on the nanoparticle surface, which consists of a Stern layer and a diffusion layer. The counterions forming the Stern layer not only affect the dielectric constant of the surrounding medium but also the quantity of surface damping while interacting with the metal surface in the vicinity.16,18,29,31 Therefore, the electrolyte species and their concentrations are major factors determining the damping constant and, sequentially, the FWHM change. Furthermore, the Stern layer of the ions can be transformed into lossy layers or absorbing layers that possess larger damping and dielectric constants, for example, a metal halide or metal oxide layer, which will be discussed more deeply in the third section.
To describe the FWHM shift of the electrochromic actuation, one of the electromagnetic simulation strategies to include this complicated surface chemistry is based on the construction of a core–shell nanostructure. The modified shell has an altered dielectric function due to capacitive charging or discharging while the dielectric function of the core remains unchanged.18,21 The modified shell structure includes effects of the Stern layer formation, electron depletion layer, and counterion absorbing layer. For instance, the Atwater group introduced such modified shells to match the experimental extinction spectra with the full-wave finite-difference time-domain (FDTD) simulation (Fig. 3a). The dielectric function of the modified shell was calculated using the Lorentz–Drude model with a Brendel and Bormann (BB) oscillator model. The optical response of the metal nanoparticles was successfully fitted and interpreted by several independent parameters, including charge density, refractive index of the surrounding medium, damping parameters, and thickness of the modified shell.18Fig. 3b presents the changes in the parameters and shows that the surface damping constants and charge density changes have more influence on the spectral features than the other parameters. Moreover, the Borisov20,38 and Chang21 groups used more advanced models that reflect quantum mechanical effects causing non-uniform electron distribution close to the surface. The metal surface with inhomogeneous electron distribution, generated by electron spill-out and Friedel oscillations, is regarded as several thin shells having diversified dielectric functions (Fig. 3c). The individual thin shells create side bands and thus, eventually broaden the absorption spectra. They assert that a steeper electron-drop across the boundary of negatively charged nanoparticles leads to fewer side bands and narrower FWHM (Fig. 3d).
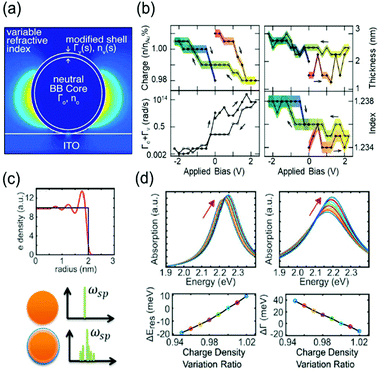 | ||
| Fig. 3 Advanced theoretical models with the modified shell structures. (a) Introduction of modified dielectric shell on the nanoparticle surface for full-wave FDTD simulation and parameter fitting. (b) Simulation parameters for the best match with the experimental data. Charge density (top left), thickness (top right), total damping constants of the modified shell (bottom Left), and refractive index of the surrounding medium (bottom right). Reprinted with permission.18 Copyright 2015 American Chemistry Society. (c) Electron density distribution drops abruptly at the boundary (top). Spectral side bands broadening the width produced by several shells of nonuniform electron density (bottom). (d) Change in absorption spectra and their spectral width calculated by classical TDLDA (time-dependent local density approximation) which cannot predict damping of the plasmon (left) and by the semi-classical approach (right). Reprinted with permission.21 Copyright 2017 American Chemistry Society. | ||
Despite the theoretical understanding of electrochromic responses, the limited LSPR shift upon applying a bias is still an unsolved issue in this field. To achieve a dramatic change in the plasmon resonance spectrum, several research groups have suggested numerous methods, such as pushing electronic structures of the plasmonic metal to the non-classical limit, facilitating electrochemical reactions, and using functional molecules, which will be reviewed in the following sections.
Beyond the electrochromic view, particularly in the perspective of plasmoelectronics, the reverse effect of the electrical colour manipulation could be expected: the light-coupled charge density in plasmonic nanoparticles might drive the charge flow for optimum charge density at the resonance and induce a current.39,40 Thus, a better understanding of optical responses related to the charge density and the electric potential of plasmonic systems is needed.
Non-linear responses from quantum capacitance
The capacitive charging or discharging models are fundamentally based on the classical assumption that the capacitance is constant, regardless of the electric potential applied across the interface, and is determined only by the geometry of the capacitor. This basic assumption may not be valid in low-dimensional materials, such as graphene41 and carbon nanotubes (CNTs).42,43 These materials have a nonuniform DOS that has several sharp rises called van-Hove singularity and a lingering slow decrease of the DOS (Fig. 4a). Owing to the nonconstant DOS, the rate of electron charging or discharging is continuously changing as the Fermi level increases or decreases according to the applied bias. We can expect another term to affect the charge of a capacitor under the chemical potential change. This variance of capacitance is defined as quantum capacitance and is ascribed to another capacitor that is connected in series to the geometric capacitor (Fig. 4b).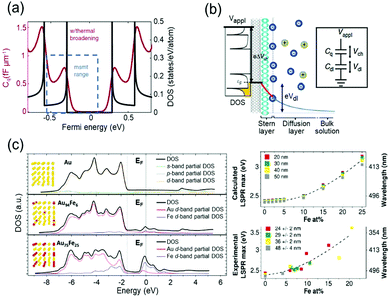 | ||
| Fig. 4 DOS mediated anomalous electrochromic behaviour of plasmonic nanoparticles. (a) Theoretical DOS of single-walled carbon nanotubes having several van-Hove singularities with following a slow decrease of DOS (black) and the corresponding quantum capacitance (red) at room temperature. (b) The concept of the electrical double layer at the nanotube-electrolyte interface and the quantum capacitance. The total capacitance of the system is explained by the capacitors connected in series. Reprinted with permission.43 Copyright 2019 Nature Research. (c) DOS of Au and Au–Fe alloys calculated by DFT and LSPR maxima of the corresponding DOS. Reprinted with permission.46 Copyright 2019 American Chemistry Society. | ||
Normal metal electrodes are, hitherto, considered to have a uniquely defined capacitance depending on electrolytes because the DOS of a metal electrode is almost fixed in a voltage window of electrochemical systems and also in general electrochromic devices.34 In other words, by moving away from the classical viewpoint of electrochemistry, the capacitance of the normal metal electrodes can be inconsistent under dramatic potential variations and happens to have a nature of quantum capacitance similar to that of graphene and CNT.
Therefore, it is reasonable to investigate the electrochromic behaviours of the capacitive nanoparticles composed of plasmonic metals such as Au44 or silver (Ag)45 by taking their electronic structures into consideration, and several groups studied the relationship between electronic structures and charge-dependent plasmonic properties.19,46 A quantum mechanical model considering d-band screening anticipated the deviation from the classical monotonic LSPR shift in the single-monolayer Au disk.19 The authors did not refer to how the d-band screening results in an abrupt change in the rate of the LSPR shift; however, they emphasised the importance of quantum mechanical aspects of the metal nanoparticles for their optical responses. The Amendola group reported that the LSPR of alloy nanoparticles can be modulated by controlling the composition of the alloy and consequently manipulating the DOS, especially near the Fermi level (Fig. 4c).46 They used Au–Fe nanoalloys as a model system and matched experimental observations with the DFT calculation results based on Au–Fe intermetallic lattices. These studies have shown the possibility that the intrinsically diminutive responses of metal nanoparticles can be surmounted by controlling the DOS of the surface materials and ensure the stability of the system in such a high-voltage range. In electrochromic devices, containing metal nanoparticles, this subtle DOS change might be tracked by their scattering spectra because the DOS may change the charging rate of the free electrons.
Electrochemical reactions of plasmonic nanoparticles
Although the free carrier density tuning mechanism provides fundamental insights into the electrochromic phenomenon, it is challenging to explain the unexpected resonance shift and its damping using this mechanism. As an electrochromic device can be considered as an electrochemical cell, investigating electrochemical processes, which are non-faradaic and faradaic processes, is helpful for a better understanding of the unpredicted LSPR modulations. Electrolytes and other chemical species in electrochromic devices have different chemical affinities to metal surfaces and show different kinetics under an electrochemical potential.29,31,32,47,48 In many electrochromic studies of plasmonic metal nanoparticles, these chemical and electrochemical effects are attributed to unexpected nonlinear shifts at their respective onset potentials. To address this issue, we divide the chemical and electrochemical tuning mechanism into two categories: (1) non-faradaic and (2) faradaic.Non-faradaic processes on metal nanoparticles, such as adsorption and desorption of chemicals, play an important role in capacitive charging or discharging at the metal-solution interface because from the view point of electrochemistry, the amount of capacitive charging or discharging electrons residing at the metal surface is determined by the electrical double layer.34 In the electrostatic model, called the Gouy–Chapman–Stern (GCS) model, the electrical double layer is affected by the electrode geometry, physical properties of ions, and distance between the metal surface and Stern layer, where the Stern layer is the closest adsorbed counter ion layer to the metal surface.33 However, theoretical explanations for the electrochromic properties using the GCS model have not been explored yet, even though this model could precisely explain the particle-shape and ion-size effects on the electric double layer capacitance, which depicts the capability of capacitive charging or discharging.
The chemical affinity between molecules of the Stern layer and metal surfaces also has a profound influence on the number of capacitive charging or discharging electrons and electrochromic behaviour of nanoparticles. The electrochromic responses combined with conventional cyclic voltammetry support this mechanism, that is, the potential-dependent spectral changes of plasmonic nanoparticles are associated with electrolyte adsorption and desorption.29 For example, peaks for the differential scattering intensity of Au nanoparticle dimers in surface electrolyte solutions correspond to the onset potentials of non-faradaic processes in conventional cyclic voltammetry. Particularly in anodic potential, the LSPR shift is highly affected by the strength of the metal–anion interaction at the individual onset potential of the anion adsorption. The strength effect of the metal–anion interaction is clearly observed in a study on the chemical affinity effect of the halide anion. Greater changes in the LSPR energy and damping at a less positive potential are observed in the scattering spectrum for Au nanorods in a NaBr electrolyte solution as compared to NaF and NaCl electrolytes (Fig. 5).31 Due to a strong adsorption of the bromide anion onto the Au surface, the adsorption of the bromide anion occurs at a less positive potential. This adsorption unexpectedly increases the capacitive discharging electrons and decreases the LSPR radiative dephasing time, referred to as the chemical interface damping.37,49,50
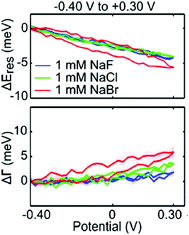 | ||
| Fig. 5 Halide anion effect on adsorption from −0.4 V to +0.3 V. Change in resonance energy (up) and line width (down) as a function of potential for a single Au nanorod in 1 mM NaF (blue), 1 mM NaCl (green), and 1 mM NaBr (red). Reprinted with permission.31 Copyright 2016 American Chemical Society. | ||
Another mechanism for the electrochemical modulation of LSPR is the faradaic processes, such as reduction or oxidation reactions that are governed by Faraday's law of electrolysis. In this section, we limit the term of faradaic processes to the reduction or oxidation reactions of the metal nanoparticle, rather than the typical electrocatalytic reactions in which electrodes, the nanoparticles in plasmonic electrochromic devices, are not involved. The redox reactions of metal nanoparticles in electrochromic devices are not only important considerations for reversibility of LSPR modulation, including spectral shifts, its intensity variation, and damping, but also provide a new opportunity for optical applications by improving the minute LSPR changes with respect to only capacitive charging.
Depending on the chemical reactivity of the electrolyte with plasmonic metals, when the applied potential exceeds a particular value, adsorbates can mediate chemisorption and metal dissolution.29,31–33,47,48 The dissolution of metal nanoparticles induces irreversible changes in intensity, line width, and resonance energy by transforming the morphology of the metal nanoparticles.31 Thus, it is crucial to investigate the role of electrolyte chemical reactivity with metal nanoparticles in electrochromic modulation. The importance of the choice of electrolytes has been recognised in a comparison between the electrochromic behaviours of plasmonic nanoparticles with halide anions and oxoanions. Fig. 6a shows an example of the difference in the chemical reactivity of a chloride anion and nitrate anion with the metal surface, which influences the reversibility of LSPR tuning.47 As chloride anions were used as the electrolyte, they were adsorbed on the metal surface, and an Au–chloride complex was formed on the surface of the Au nanorods at the onset potential. The Au–chloride complex is of two types as follows47
| Au + 2Cl−(aq) ↔ [AuCl2]−(ad) + e− | (3) |
| Au + 4Cl−(aq) ↔ [AuCl4]−(ad) + 3e− | (4) |
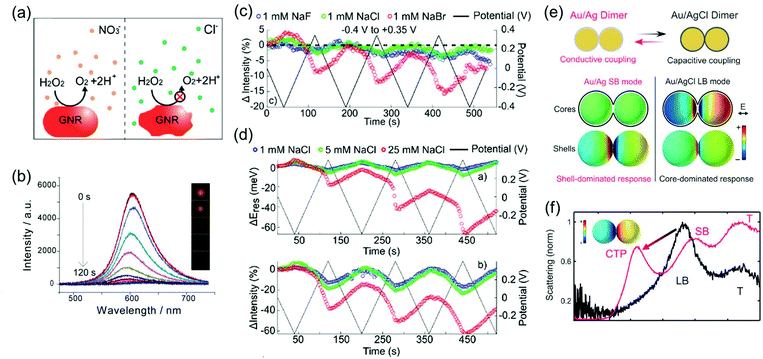 | ||
| Fig. 6 (a) Schematic view of the dissolution of metal nanoparticle in KNO3 and KCl electrolyte solution. (b) Time-dependent scattering spectra and (inset) time-dependent dark field images of a single gold nanorod under +1.0 V potential in KCl electrolyte solution. Reprinted with permission.47 Copyright 2014 American Chemical Society. (c) Comparison of reversibility of changes in scattering intensity was investigated in 1 mM NaF (blue), 1 mM NaCl (green), and 1 mM NaBr (red) electrolyte solution under applied potential (black). (d) Concentration effect of the electrolyte was observed by investigating changes and reversibility in resonance energy (up) and intensity (down) in 1 mM NaCl (blue), 5 mM NaCl (green), and 25 mM NaCl (red) under applied potential (black). Reprinted with permission.31 Copyright 2016 American Chemical Society. (e) Illustration of the switching capacitive coupling mode and conductive coupling mode for an Ag bridged Au dimer and surface charge density plots of the representative capacitive and conductive plasmon mode. (f) Electrochemical conversion from the core-dominated mode (LB mode) to shell-dominated mode (CTP mode and SB mode) occurred at −0.22 V due to the increase of the conductive pathway. Reprinted with permission.30 Copyright 2015 American Association for the Advancement of Science. | ||
The complex gradually dissolved, and in the process, it induced irreversible changes in the optical properties of the Au nanorods (Fig. 6b).47 Conversely, nitrate anions having less reactivity than chloride anions allowed reversible modulations of the intensity, linewidth, and resonance energy, under the same conditions as those for the chloride ions.
In addition to the differences between the halide anion and oxoanion, a reactivity effect was observed among the three halide electrolytes, F−, Cl−, and Br−. LSPR band modulation in resonance energy and its damping indicated the reactivity with Au as: F− < Cl− < Br−.31 The irreversible change in intensity from −0.4 to +0.35 V also followed the trend of halide anion reactivity with Au (Fig. 6c).31 Interestingly, increasing the chloride electrolyte concentration also yielded irreversible changes due to chloride-mediated electrochemical dissolution of Au nanoparticles (Fig. 6d).31 These studies indicate that halide ion electrolytes, which are commonly used in electrochromic devices and electrochemical cells, would not be feasible for improving electrochromic modulations, depending on the halide concentration. Although a recent study reported that the electrochemical dissolution in aqueous chloride ion solution at high voltage was inhibited by adding oxoanions as additives,32 improving the stability of nanoparticle morphology for reversible and dramatic electrochromic modulations is still challenging in halide electrolyte solutions.33
On the other hand, reversible optical modulations under an electrochemical potential can be generated even through faradaic processes. Such a redox reaction is the formation of a dielectric layer on the metal surface; for instance, Ag–AgCl redox chemistry on Ag-coated Au nanospheres and Ag-bridged Au dimers, studied by Landes and co-workers (Fig. 6e).30 This study highlighted that the Ag–AgCl redox chemistry on the dimer system provided reversible switching between the initial plasmon modes and new plasmon modes. An increase in the conductive pathway with increasing Ag content converted the longitudinal bonding dipolar plasmon mode (LB mode), as the initial core-dominated mode, into the longitudinal screened bonding dipolar plasmon mode (SB mode) and charge transfer plasmon mode (CTP mode), as the shell-dominated mode, by the conductive coupling mode (Fig. 6f).30 This novel plasmon mode switching system opens up the field of plasmonic electrochromism having the ability of fully reversible, controllable, and relatively remarkable colour tuning, which is highly desirable to overcome the fatal disadvantage of plasmonic nanoparticles for optoelectronic applications. Moreover, metal deposition and dissolution on plasmonic nanoparticles can induce reversible colour changes.51
Electrochemically active dielectric environments
The other operational principle is based on the optical properties of the electrochemically active shell surrounding the plasmonic metal nanoparticle.22–24,26–28,52,53 When stimulated by an electric field, the electrochemically active materials exhibit charge doping or changes in the redox states, which results in the electrochromic behaviour of the system. It is well known that the refractive index of the surrounding medium modulates the position of the plasmon resonance energy peak.54 Thus, coating an electrochemically active material on the metal nanoparticles is an indispensable tool in electrochromism.LSPR band modulation by voltage-induced charge doping of the electrochemically active shell was demonstrated in a top electrolyte gating device with an ionic liquid. For example, graphene, as an electrochemically active shell, was placed on top of the Au nanorods, and a top electrolyte gate controlled the doped charges and Fermi energy (Fig. 7a).28 As shown in Fig. 7b, an unusual shift in the LSPR band position and decreased damping was observed in this system.28 These results were demonstrated by the voltage-dependent complex dielectric constant and interband transition of graphene by plasmon resonance energy of the Au nanorods. Furthermore, the voltage-dependent complex dielectric constant of graphene has been studied55–57 and can influence the plasmon resonance energy. In addition to changes in the dielectric constant, switching off of the interband transition is also attributed to the LSPR band shift and its damping. As hole doping decreases the Fermi energy, the initial states for optical transition by plasmon resonance energy are empty and interband optical transitions can be blocked. This study indicates that the voltage-induced charge doping of electrochemically active materials would govern the plasmon resonance band in electrochromic devices.
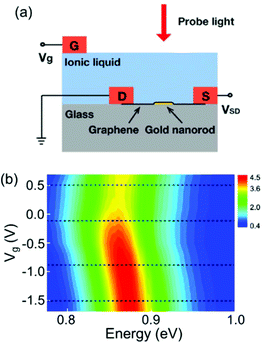 | ||
| Fig. 7 (a) Schematic illustration of a device configuration with graphene placed on top of the Au nanorod. Doping charge was controlled by a top electrolyte gate with ionic liquid. (b) Experimental scattering spectra of a graphene-Au hybrid nanorod as a function of the gate voltage. Reprinted with permission.28 Copyright 2012 American Chemical Society. | ||
Another approach is to switch the redox states of the electrochemically active shell.22–24,26,27,53 In a recent study, Au nanoparticles encapsulated by an electrochemically active polymer shell, polyaniline (PANI), placed on the Au film, resulted in spectral shifts greater than 100 nm in the visible range. This system, called electrochromic nanoparticle-on-mirror (eNPoM), gives rise to strong optical field coupling in a gap, known as a hot spot, and generates hot carriers near the hot spot (Fig. 8a).26 Polarisability of the polymers and their refractive indices are altered while hot carriers switch the redox states (PANI0 ↔ PANI+1 ↔ PANI+2) of the responsive polymer shell. Depending on the redox states, the variation of optical characteristics58 in the gap can generate reversible, dramatic, and fast colour switching of ∼100 nm in response to less than 1 V applied potential (Fig. 8b).26 Although the eNPoM system showed remarkable electrochromic capability for display prospects, this system still has a relatively large chemical damping. Therefore, a new model system with a narrow line-width for colour purity needs to be developed for practical applications.
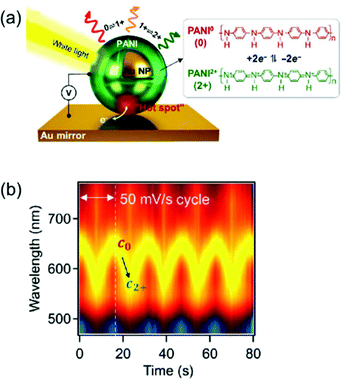 | ||
| Fig. 8 (a) Schematic representation of eNPoM geometry, which changes the redox states of PANI in hot spot under electrochemical potential. (b) Time-dependent normalized DF scattering spectra of a single spot in eNPoM showed dramatic and reversible tuning by the redox states of PANI. Reprinted with permission.26 Copyright 2019 American Association for the Advancement of Science. | ||
Applications
Based on the capability of colour tuning, which depends on the induced voltages, the representative application is the development of optoelectronic devices including smart windows and adaptive displays. Owing to their fast and reversible responses and easy controllability, it is a highly promising approach for electrically actuating the versicolour plasmonic systems. It is used for collecting other information by detecting the colour change. For example, single-particle electrochemistry occurring near the nanoelectrodes, which might be inaccessible to investigation by other techniques, could be tracked by detecting the colour modulation of a single particle. In the following subsections, we will show the potential of the plasmonic electrochromic field and suggest future perspectives in this field.Plasmonic nanopixels and displays
The representative applications of conventional semi-conductor electrochromic devices are energy-efficient smart windows. In particular, plasmonic metal oxide nanocrystals, whose resonance frequencies lie in the near-infrared region, have been widely studied owing to their fast switching speed and long-term reproducibility for repetitive cycles. The LSPR of metal oxides is generally regulated by introducing defects and dopants or by controlling their morphologies and materials. It is also possible to actively modify LSPR through external electrical, chemical, and photo-stimuli, which leads to smart window applications.7,59 For example, the Milliron group designed an electrochromic device with ITO nanocrystals and Li+-containing electrolytes and showed fast colouration and bleaching processes, which are the pivotal abilities of energy-efficient smart windows.8,9 Although smart windows containing semiconducting nanocrystals can have simple on–off systems, a more advanced display technique should possess the ability of a diversified colouring process. Therefore, electrochromic devices should include materials with the LSPR in the visible range to express adequate RGB colour, which leads researchers to explore the field of plasmonic electrochromism.Among the numerous ways to tune the LSPR introduced so far, faradaic reaction-based devices have lesser long-term durability and slower switching speed. In addition, the electrochromic responses of the plasmonic nanoparticles by capacitive charging or discharging still show subtle changes. Furthermore, the stability of electrolytes cannot be guaranteed yet over a large range of potentials to securely enter the electric potential regime of DOS-mediated dramatic changes. On the other hand, functional molecule-induced electrochromic devices are receiving attention as the most successful means to realise advanced display devices. The Baumberg group has proposed the fabrication of eNPoM nanopixels with nanoparticles encapsulated in the PANI shell (Fig. 9a).26 They manufactured centimetre-scale plasmonic functional metasurfaces of eNPoM through the meniscus-guided nanoparticle assembly method, and these metasurfaces were functional for more than 3 months (Fig. 9b). Furthermore, pixels of the metasurfaces are the individual eNPoMs and their ultra-small pixel size in large colour dynamics (Fig. 9c) is anticipated to reduce the display device thickness.
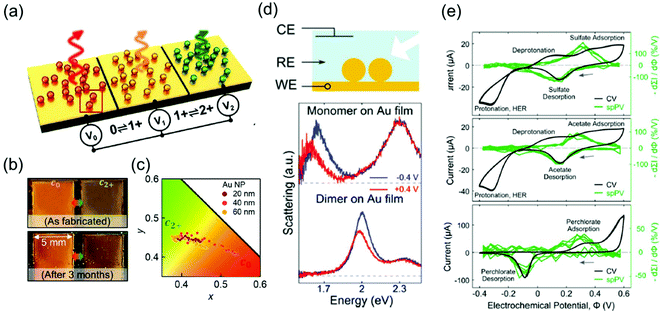 | ||
| Fig. 9 Applications of plasmonic electrochromic devices. (a) Schematic illustration of eNPoM metasurfaces. (b) Durability of the eNPoM metasurface under normal light, before and after 3 months. (c) Colour gamut (CIE 1931 chromaticity) of the fabricated nanopixels. Reprinted with permission.26 Copyright 2019 American Association for the Advancement of Science. (d) Scheme of the spectroelectrochemical cell (top). Single-particle scattering spectrum of a gold nanoparticle monomer (middle) and dimer (bottom) on the gold film. (e) Conventional cyclic voltammetry and single-particle plasmon voltammetry in 0.1 M electrolyte solution. Na2SO4 (top), NaC2H3O2 (middle), and NaClO4 (bottom) are used. Reprinted with permission.48 Copyright 2016 American Chemistry Society. | ||
Single-particle electrochemical surface plasmon resonance spectroscopy
Another tool based on the electrochromic response of plasmonic nanoparticles is associated with electrochemistry around the nanoparticle surface. As discussed in the previous sections, chemical events occurring around the nanoparticle surface induce changes in the capacitance, dielectric function of the surrounding, compositions of the metal and even morphologies of the nanoparticles. Electrolyte adsorption, metal oxide and metal–halide complex formation, or self-oxidation of the particle are involved in these processes. As a result, the corresponding LSPR peaks are immediately shifted, FWHM broadens or sharpens, and intensity is enhanced or reduced. Therefore, these instant changes inherently represent microscopic phenomena, and one can investigate the electrochemical reactions, whether faradaic or not, by simply tracking the features of the LSPR peaks of the nanoparticles. This is because the common ensemble-level methods, such as cyclic voltammetry or electrochemical impedance spectroscopy cannot detect changes in the microscopic system.As a representative example, the Landes group first employed single-particle plasmon voltammetry (spPV) to measure the spectral response, according to anion adsorption and desorption.48 They used Au nanoparticle dimers on a thin Au film that showed more sensitive response to the non-faradaic reactions than monomers (Fig. 9d). By tracking the two-point differential of the peak scattering intensity for the applied potentials as a criterion, the onset potentials of several anion adsorption and desorption were successfully identified. Even conventional cyclic voltammetry hardly distinguished the non-faradaic current buried under other large peaks (Fig. 9e). In the same year, the Long group imaged the electrocatalytic oxidation of hydrogen peroxide that takes place on an Au nanorod surface.60 This study visualised the dark-field images and scattering spectra of a number of nanoparticles together and demonstrated that the performance of the catalytic activity of the nanoparticles can be evaluated by the heterogeneity of the individual spectrum.
Conclusions and remarks
In this review, we presented four electrochromic mechanisms for plasmonic nanoparticles–capacitive charging model accompanying variation in the Fermi level, faradaic reactions, non-faradaic reactions, and electrochemically active functional molecule-mediated mechanism. First of all, when an electric potential is applied across the nanoparticle, the electrons are capacitively charged or discharged on the nanoparticle surfaces, while the counterions are accumulated on the opposite side of the nanoparticle-electrolyte interface, forming an electric double layer. This capacitive behaviour leads to a change in the plasma frequency of the plasmonic metal and hence, the resonance frequency of the nanoparticles. In spite of a consensus on the mechanism of plasmonic electrochromism based on the Drude model, which explains that the change in the free carrier concentration causes a shift in the LSPR frequency, more advanced theoretical models considering quantum mechanical effects have been proposed. Furthermore, this capacitive charging model becomes invalid when the metallic nanoparticles do not belong to the classical regime any longer, i.e. at high negative voltages. The DOS deviates from flatness as the Fermi level reaches a 6sp band plateau, and this transition would cause anomalous blueshift rates in the LSPR. Such consideration of the band structure of the plasmonic metals not only gives insight for the engagement with the capacitive materials but also provides a breakthrough for measurable plasmonic electrochromic responses without any chemical modifications. Also, a device to quantitatively measure the quantum capacitance of metal nanoparticles should be devised to appropriately select surface materials and control their band structures.On top of that, electrochemical reactions, both faradaic and non-faradaic reactions, also induce the LSPR shift. When electrolytes or ions in the solution are adsorbed or desorbed upon applying bias, the dielectric functions of both the surrounding and outermost layers of the surface are changed. In particular at highly positive potentials, the constituent metal could be dissolved into the solution in the form of ions, and the electrochemical dissolution causes irreversible changes in their morphology and LSPR. By tracking the electrochromic behaviour of the plasmonic nanoparticles, we can figure out the microscopic electrochemical events occurring very near the surface of the nanometre-sized electrodes.
Finally, electrochemically active functional molecules, such as PANI and graphene, can change the colour of the nanosystems. The colour of PANI is directly changed by an external bias, and this functionality has garnered considerable attention because of its potential applications in adaptive displays or advanced smart windows. The graphene encapsulated nanoparticles, on the other hand, change the dielectric constants of the surrounding medium and LSPR of the nanoparticles, which is similar to the electrochemical reaction-mediated LSPR changes. These four mechanisms are not completely independent in a system. It is obvious that two or more operational mechanisms should be considered simultaneously for an appropriate description of complicated systems. However, clarifying the quantitative contribution of each mechanism in the colour modulation is a challenging task. Therefore, more quantitative studies are needed for understanding synergetic effects of two or more operational mechanisms of electrochromic behaviours with analysis of the quantitative contribution of each mechanism in the colour modulation.
The field of plasmonic electrochromism is in the period of transition toward interdisciplinary convergence, especially among fundamental plasmonics, electrochemistry, and electronics. By combining with plasmonics, electrochromic behaviours originating from coupling between individual plasmon modes or array-based optical responses need to be explored more systematically and deeply. In addition, it is better to note that the kinetics of electrolytes or chemicals in the electrochromic devices can be important, which depicts the influence of the diffusion layer because kinetics is expressed in terms of the speeds of the capacitive charging or discharging. These sorts of studies can be performed by investigating the effects of scan rates or with the assistance of electrochemical instruments like electrochemical impedance spectrometer, and further extended to all-solid-state devices. Also, investigations on light-induced surface potential change with spatially resolved electrochemistry and single-particle spectroscopy could allow for understanding hot-carrier-related charge transfer or chemical reactions on the surface, and this understanding can give us insights for developing better sensors, batteries, supercapacitors, and catalysts. From the viewpoint of plasmonics and plasmoelectronics, by further exploiting the electrically stimulated instantaneous tuning of plasmon resonance frequency, newly emerging applications including smart windows, ultrahigh-resolution displays by nanopixels, low-power always-on displays, ultrafast information processors, or all-optical computing nanophotonic devices can be realized to go beyond the Si-based electronics.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea Government (MSIT) (NRF-2017R1A5A1015365 and NRF-2021R1A2C3010083) and BioNano Health-Guard Research Center funded by the Ministry of Science and ICT (MSIT) of Korea as Global Frontier Project (HGUARD_2013M3A6B2078947). J.-W. Oh was supported by Hankuk University of Foreign Studies Research Fund of 2020 and by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2019R1I1A1A01059985).Notes and references
- K. Saha, S. S. Agasti, C. Kim, X. Li and V. M. Rotello, Chem. Rev., 2012, 112, 2739–2779 CrossRef CAS PubMed.
- A. Kumar, S. Kim and J. M. Nam, J. Am. Chem. Soc., 2016, 138, 14509–14525 CrossRef CAS PubMed.
- M. Kauranen and A. V. Zayats, Nat. Photonics, 2012, 6, 737–748 CrossRef CAS.
- S. Mukherjee, F. Libisch, N. Large, O. Neumann, L. V. Brown, J. Cheng, J. B. Lassiter, E. A. Carter, P. Nordlander and N. J. Halas, Nano Lett., 2013, 13, 240–247 CrossRef CAS PubMed.
- M. Kim, M. Lin, J. Son, H. Xu and J.-M. Nam, Adv. Opt. Mater., 2017, 5, 170004 Search PubMed.
- S. S. E. Collins, X. Wei, T. G. McKenzie, A. M. Funston and P. Mulvaney, Nano Lett., 2016, 16, 6863–6869 CrossRef CAS PubMed.
- A. Agrawal, R. W. Johns and D. J. Milliron, Annu. Rev. Mater. Res., 2017, 47, 1–31 CrossRef CAS.
- G. Garcia, R. Buonsanti, E. L. Runnerstrom, R. J. Mendelsberg, A. Llordes, A. Anders, T. J. Richardson and D. J. Milliron, Nano Lett., 2011, 11, 4415–4420 CrossRef CAS PubMed.
- E. L. Runnerstrom, A. Llordes, S. D. Lounis and D. J. Milliron, Chem. Commun., 2014, 50, 10555–10572 RSC.
- E. Hopmann and A. Y. Elezzabi, Nano Lett., 2020, 20, 1876–1882 CrossRef CAS PubMed.
- A. Henglein, P. Mulvaney and T. Linnert, Faraday Discuss., 1991, 92, 31–44 RSC.
- T. Ung, M. Giersig, D. Dunstan and P. Mulvaney, Langmuir, 1997, 13, 1773–1782 CrossRef CAS.
- M. D. Scanlon, P. Peljo, M. A. Mendez, E. Smirnov and H. H. Girault, Chem. Sci., 2015, 6, 2705–2720 RSC.
- Y. Huang, M. C. Pitter and M. G. Somekh, Langmuir, 2011, 27, 13950–13961 CrossRef CAS PubMed.
- C. Novo, A. M. Funston, A. K. Gooding and P. Mulvaney, J. Am. Chem. Soc., 2009, 131, 14664–14666 CrossRef CAS PubMed.
- T. Sannomiya, H. Dermutz, C. Hafner, J. Vörös and A. B. Dahlin, Langmuir, 2010, 26, 7619–7626 CrossRef CAS PubMed.
- C. P. Byers, B. S. Hoener, W. S. Chang, M. Yorulmaz, S. Link and C. F. Landes, J. Phys. Chem. B, 2014, 118, 14047–14055 CrossRef CAS PubMed.
- A. M. Brown, M. T. Sheldon and H. A. Atwater, ACS Photonics, 2015, 2, 459–464 CrossRef CAS.
- A. Manjavacas and F. Javier García de Abajo, Nat. Commun., 2014, 5, 3548 CrossRef CAS PubMed.
- M. Z. Herrera, J. Aizpurua, A. K. Kazansky and A. G. Borisov, Langmuir, 2016, 32, 2829–2840 CrossRef PubMed.
- B. S. Hoener, H. Zhang, T. S. Heiderscheit, S. R. Kirchner, A. S. De Silva Indrasekara, R. Baiyasi, Y. Cai, P. Nordlander, S. Link, C. F. Landes and W. S. Chang, J. Phys. Chem. Lett., 2017, 8, 2681–2688 CrossRef CAS PubMed.
- N. Jiang, L. Shao and J. Wang, Adv. Mater., 2014, 26, 3282–3289 CrossRef CAS PubMed.
- T. Xu, E. C. Walter, A. Agrawal, C. Bohn, J. Velmurugan, W. Zhu, H. J. Lezec and A. A. Talin, Nat. Commun., 2016, 7, 10479 CrossRef CAS PubMed.
- J.-W. Jeon, P. A. Ledin, J. A. Geldmeier, J. F. Ponder, M. A. Mahmoud, M. El-Sayed, J. R. Reynolds and V. V. Tsukruk, Chem. Mater., 2016, 28, 2868–2881 CrossRef CAS.
- W. Lu, N. Jiang and J. Wang, Adv. Mater., 2017, 29, 1604862 CrossRef PubMed.
- J. Peng, H.-H. Jeong, Q. Lin, S. Cormier, H.-L. Liang, M. F. L. De Volder, S. Vignolini and J. J. Baumberg, Sci. Adv., 2019, 5, eaaw2205 CrossRef CAS PubMed.
- C. Jing, Z. Gu, T. Xie and Y. T. Long, Chem. Sci., 2016, 7, 5347–5351 RSC.
- J. Kim, H. Son, D. J. Cho, B. Geng, W. Regan, S. Shi, K. Kim, A. Zettl, Y. R. Shen and F. Wang, Nano Lett., 2012, 12, 5598–5602 CrossRef CAS PubMed.
- S. K. Dondapati, M. Ludemann, R. Muller, S. Schwieger, A. Schwemer, B. Handel, D. Kwiatkowski, M. Djiango, E. Runge and T. A. Klar, Nano Lett., 2012, 12, 1247–1252 CrossRef CAS PubMed.
- C. P. Byers, H. Zhang, D. F. Swearer, M. Yorulmaz, B. S. Hoener, D. Huang, A. Hoggard, W.-S. Chang, P. Mulvaney, E. Ringe, N. J. Halas, P. Nordlander, S. Link and C. F. Landes, Sci. Adv., 2015, 1, e1500988 CrossRef PubMed.
- B. S. Hoener, C. P. Byers, T. S. Heiderscheit, A. S. De Silva Indrasekara, A. Hoggard, W.-S. Chang, S. Link and C. F. Landes, J. Phys. Chem. C, 2016, 120, 20604–20612 CrossRef CAS.
- C. Flatebo, S. S. E. Collins, B. S. Hoener, Y.-y. Cai, S. Link and C. F. Landes, J. Phys. Chem. C, 2019, 123, 13983–13992 CrossRef CAS.
- A. Al-Zubeidi, B. S. Hoener, S. S. E. Collins, W. Wang, S. R. Kirchner, S. A. Hosseini Jebeli, A. Joplin, W. S. Chang, S. Link and C. F. Landes, Nano Lett., 2019, 19, 1301–1306 CrossRef PubMed.
- J. B. Allen and R. F. Larry, Electrochemical methods fundamentals and applications, John Wiley & Sons, 2001 Search PubMed.
- S. A. Maier, Plasmonics: fundamentals and applications, Springer Science & Business Media, 2007 Search PubMed.
- B. K. Juluri, Y. B. Zheng, D. Ahmed, L. Jensen and T. J. Huang, J. Phys. Chem. C, 2008, 112, 7309–7317 CrossRef CAS.
- B. Foerster, A. Joplin, K. Kaefer, S. Celiksoy, S. Link and C. Sönnichsen, ACS Nano, 2017, 11, 2886–2893 CrossRef CAS PubMed.
- M. Z. Herrera, A. K. Kazansky, J. Aizpurua and A. G. Borisov, Phys. Rev. B, 2017, 95, 245413 CrossRef.
- M. T. Sheldon, J. van de Groep, A. M. Brown, A. Polman and H. A. Atwater, Science, 2014, 346, 828 CrossRef CAS PubMed.
- S. C. Warren, D. A. Walker and B. A. Grzybowski, Langmuir, 2012, 28, 9093–9102 CrossRef CAS PubMed.
- J. Xia, F. Chen, J. Li and N. Tao, Nat. Nanotechnol., 2009, 4, 505–509 CrossRef CAS PubMed.
- S. Ilani, L. A. K. Donev, M. Kindermann and P. L. McEuen, Nat. Phys., 2006, 2, 687–691 Search PubMed.
- J. Li and P. J. Burke, Nat. Commun., 2019, 10, 3598 Search PubMed.
- N. E. Christensen, J. Phys. F: Met. Phys., 1978, 8, L51–L55 CrossRef CAS.
- N. E. Christensen, Phys. Status Solidi B, 1972, 54, 551–563 CrossRef.
- D. T. L. Alexander, D. Forrer, E. Rossi, E. Lidorikis, S. Agnoli, G. D. Bernasconi, J. Butet, O. J. F. Martin and V. Amendola, Nano Lett., 2019, 19, 5754–5761 CrossRef CAS PubMed.
- C. Jing, F. J. Rawson, H. Zhou, X. Shi, W. H. Li, D. W. Li and Y. T. Long, Anal. Chem., 2014, 86, 5513–5518 CrossRef CAS PubMed.
- C. P. Byers, B. S. Hoener, W. S. Chang, S. Link and C. F. Landes, Nano Lett., 2016, 16, 2314–2321 CrossRef CAS PubMed.
- H. Hövel, S. Fritz, A. Hilger, U. Kreibig and M. Vollmer, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 18178–18188 CrossRef PubMed.
- B. Foerster, V. A. Spata, E. A. Carter, C. Sönnichsen and S. Link, Sci. Adv., 2019, 5, eaav0704 CrossRef CAS PubMed.
- N. Li, P. Wei, L. Yu, J. Ji, J. Zhao, C. Gao, Y. Li and Y. Yin, Small, 2019, 15, 1804974 CrossRef PubMed.
- P. A. Ledin, J. W. Jeon, J. A. Geldmeier, J. F. Ponder Jr., M. A. Mahmoud, M. El-Sayed, J. R. Reynolds and V. V. Tsukruk, ACS Appl. Mater. Interfaces, 2016, 8, 13064–13075 CrossRef CAS PubMed.
- A. Yin, Q. He, Z. Lin, L. Luo, Y. Liu, S. Yang, H. Wu, M. Ding, Y. Huang and X. Duan, Angew. Chem., Int. Ed., 2016, 55, 583–587 CrossRef CAS PubMed.
- P. Mulvaney, Langmuir, 1996, 12, 788–800 CrossRef CAS.
- V. P. Gusynin, S. G. Sharapov and J. P. Carbotte, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165407 CrossRef.
- J. M. Dawlaty, S. Shivaraman, J. Strait, P. George, M. Chandrashekhar, F. Rana, M. G. Spencer, D. Veksler and Y. Chen, Appl. Phys. Lett., 2008, 93, 131905 CrossRef.
- K. F. Mak, M. Y. Sfeir, Y. Wu, C. H. Lui, J. A. Misewich and T. F. Heinz, Phys. Rev. Lett., 2008, 101, 196405 CrossRef PubMed.
- C. Barbero and R. Kötz, J. Electrochem. Soc., 1994, 141, 859–865 CrossRef CAS.
- V. G. Deonikar, J. M. C. Puguan and H. Kim, Acta Mater., 2021, 207, 116693 CrossRef CAS.
- C. Jing, Z. Gu and Y.-T. Long, Faraday Discuss., 2016, 193, 371–385 RSC.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |