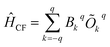Modulating magnetic anisotropy in Ln(III) single-ion magnets using an external electric field

Abstract

Single-molecule magnets have potential uses in several nanotechnology applications, including high-density information storage devices, the realisation of which lies in enhancing the barrier height for magnetisation reversal (U_eff). However, Ln(III) single-ion magnets (SIMs) that have been reported recently reveal that the maximum value of U_eff values that can be obtained by modulating the ligand fields has already been achieved. Here, we have explored, using a combination of DFT and ab initio CASSCF calculations, a unique way to enhance the magnetisation reversal barrier using an oriented external electric field in three well-known Ln(III) single-ion magnets: [Dy(Py)₅(O^tBu)₂]⁺ (1), [Er{N(SiMe₃)₂}₃Cl]⁻ (2) and [Dy(Cp^Me3)Cl] (3). Our study reveals that, for apt molecules, if the appropriate direction and values of the electric fields are chosen, the barrier height can be enhanced by twice that of the limit set by the ligand field. The application of an electric field along the equatorial direction was found to be suitable for oblate shaped Dy(III) complexes and an electric field along the axial direction was found to enhance the barrier height for a prolate Er(III) complex. For complexes 2 and 3, the external electric field was able to magnify the barrier height to 2–3 times that of the original complexes. However, a moderate enhancement was noticed after application of the external electric field in the case of complex 1. This novel non-chemical fine-tuning approach to modulate magnetic anisotropy is expected to yield a new generation of SIMs.

---

Introduction

There is great interest in the area of single-molecule magnets (SMMs), as they are reported to have potential applications in information storage devices, cryogenic refrigeration, quantum computing and spintronic devices etc.¹ SMMs containing lanthanide(III) ions have gained interest in recent years, as they possess a huge barrier height for magnetisation reversal (U_eff) and, at the same time, possess record high blocking temperatures (T_B). While there are various classes of molecules that exhibit blocking temperatures in the range of 4–15 K,² higher blocking temperatures can be found for organometallic Dy(III) single-ion magnets (SIMs) containing substituted cyclopentadienyl ligands (T_B in the range of 48 K to 80 K).³ It is well-known that the shape of the electron density of the ground state m_J levels of the lanthanide ion is critical in dictating the magnetic properties. The Ln(III) ions can be classified as follows: (i) those possessing oblate density require strong axial ligands with no/weak equatorial ligation, and (ii) those with prolate density demand strong equatorial ligands with weak/no axial ligation. Synthetic chemists have utilised these ideas to develop novel molecules with attractive U_eff and T_B values.⁴ While most of the molecules that possess very high-blocking temperatures also possess substantial U_eff values, often the T_B value is only a fraction of the reported U_eff value. While establishing the relationship between the U_eff and T_B values and the mechanism beyond the single-ion relaxation has gained attention,⁵ it is also equally important to realise large U_eff values in order to move forward.

Various chemical fine-tuning methods, such as (i) using designer ligands that control the ligand field around the Ln(III) ion in an anticipated fashion,⁶ (ii) maintaining the symmetry around the metal centre,^2,7 (iii) incorporating diamagnetic elements in the cluster aggregation to enhance the axiality⁸ or (iv) incorporating a transition metal or radicals to induce an exchange interaction as a way to suppress tunnelling, have been explored to obtain larger U_eff values.^4a,9 With numerous Dy(III) mononuclear complexes reported in the literature, it has been stated that the axial limit that controls the overall U_eff value has been reached.^2a While increasing the T_B value has been the focus for the present, other avenues to enhance the U_eff values have not been explored. As chemical fine-tuning of the ligand field has already reached its potential, we aim to search for an alternative route to enhance the U_eff values in Ln(III) SIMs. In this context, using various computational tools, here we set out to explore the role of an applied electric field in the magnetisation reversal of Ln(III) SIMs. Recent examples in this area where an electric field has been utilised to modulate the magnetic properties offered strong motivation for this work.¹⁰ To enumerate the effect of an oriented external electric field (OEEF) on lanthanide SIMs, we chose three example complexes, [Dy(Py)₅(O^tBu)₂][BPh₄]^2a (1), Li(THF)₄[Er{N(SiMe₃)₂}₃Cl]¹¹ (2), and [Dy(Cp^Me3)₂Cl]^3c (3). All three complexes were characterized well and are among the best-known SIMs in their family. In particular, complex 1 was found to exhibit an U_eff value of 1815 K with a blocking temperature of 14 K, while complex 2 was found to have an U_eff value of 63 K with a T_B of 3 K. Complex 3, on the other hand, did not exhibit any out-of-phase signals and, therefore, is not a single-ion magnet.^3c

Results and discussion

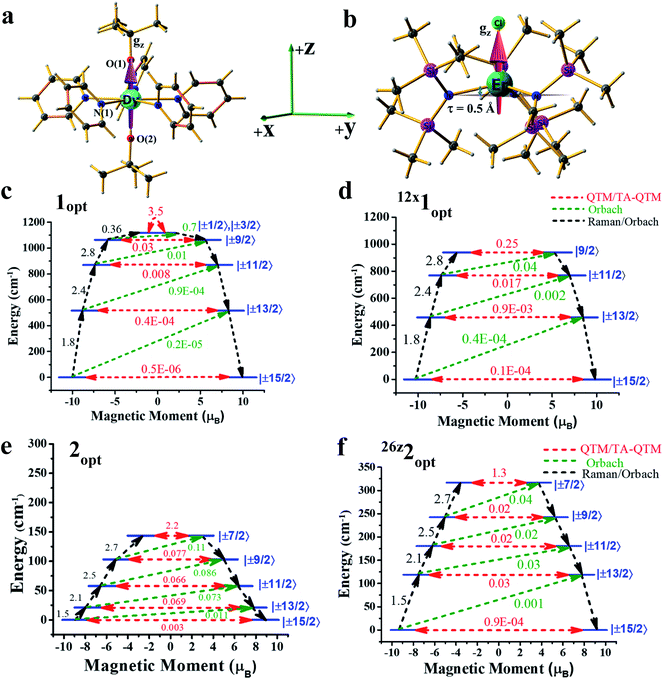
Computing the magnetic anisotropy of Ln(III) SIMs in the presence of an electric field has not been attempted before, and multiple challenges are present to account for such effects. The application of oriented electric fields is expected to distort the geometry, and capturing this effect is crucial in understanding the magnetic anisotropy. As Ln(III) SIMs are known to be extremely sensitive to small structural changes, static OEEFs on an X-ray structure are unlikely to reveal the real scenario. As structure optimisation with ab initio CASSCF calculations is not practical at the present time, here, we have chosen a combination of methodologies, wherein DFT calculations in the presence of an electric field were utilized to obtain reasonable structures.

These structures were then subject to ab initio CASSCF/RASSI-SO/SINGLE_ANISO calculations in the presence of the same electric field, in order to capture both the structural distortion and also the electric field effect on the magnetic anisotropy (see computational details for more information). Ab initio calculations were performed on the crystal structures of the complexes (or models derived from the X-ray structures) of 1-3 in the absence of any external perturbation (see Tables S1–S3 in the ESI†). Complexes 1 and 2 are well-known examples, and exhibited strong axiality in the estimated g_z values with computed barrier heights of 1183 cm⁻¹ and 181 cm⁻¹, respectively (relaxation via 4^th excited Kramers doublet).^2a,12

As the geometries of 1 and 2 are relaxed in the presence of an electric field, it is imperative to understand how the optimised geometry in the gas phase correlates to the X-ray structure. The optimised geometries of the complexes (1_opt and 2_opt) reveal elongation of all the bonds within the molecules, as intermolecular interactions in the crystal lattices are removed. The axial Dy–O(1) bond length increases from 2.110 Å in the X-ray structure to 2.142 Å in 1_opt, and the average equatorial Dy–N bond length also increases by ∼0.05 Å in the geometry of 1_opt (see Table 1). A similar elongation was seen in the Er–N/Cl bond lengths in complex 2. The CASSCF calculations of 1_opt and 2_opt yield U_cal values of 1118 cm⁻¹ and 144 cm⁻¹, respectively, assuming relaxation via the 4^th excited state (see Fig. 1). These computed values are slightly smaller than the values obtained from the X-ray structures, and this is due to relatively weaker axial ligand fields (LFs) in the optimised geometries (see Tables S4 and S5†).

Table 1 Selected structural parameters of complexes 1 and 2 in the presence of an electric field. Bond lengths and τ in Å, angles are in (°) and the U_cal values are in cm⁻¹

	X-ray	1opt	^4z1opt	^8z1opt	^12z1opt	^4x1opt	^8x1opt	^12x1opt
Dy–O1	2.114	2.141	2.170	2.203	2.244	2.138	2.138	2.139
Dy–O2	2.110	2.142	2.118	2.098	2.081	2.140	2.139	2.139
Dy–N1	2.534	2.616	2.604	2.605	2.604	2.649	2.710	2.798
Dy–N2	2.556	2.610	2.616	2.616	2.619	2.604	2.574	2.554
Dy–N3	2.563	2.618	2.626	2.625	2.628	2.604	2.582	2.559
Dy–N4	2.572	2.618	2.606	2.608	2.607	2.615	2.642	2.674
Dy–N5	2.580	2.612	2.629	2.627	2.626	2.617	2.630	2.649
∠O1–Dy–O2	178.9	178.3	178.5	178.3	178.0	171.2	164.6	157.2
U cal	1183	1118	1108	1083	1040	1111	1070	939

---

	X-ray	2opt	^4z2opt	^8z2opt	^12z2opt	^16z2opt	^20z2opt	^26z2opt
Er–Cl	2.528	2.586	2.614	2.647	2.686	2.736	2.803	3.042
Er–N1	2.231	2.308	2.304	2.301	2.298	2.295	2.293	2.285
Er–N2	2.251	2.308	2.304	2.301	2.298	2.295	2.292	2.284
Er–N3	2.246	2.309	2.306	2.303	2.302	2.300	2.300	2.296
τ	0.454	0.508	0.488	0.468	0.446	0.419	0.385	0.293
U cal	181	144	163	178	200	223	250	317

---

Fig. 1 Optimised geometries and ab initio blocking barriers at different external electric fields: structures of (a) 1_opt and (b) 2_opt, along with the computed g_z-axis. Colour code: Dy – cyan, Er – dark cyan, N – blue, Cl – green, Si – pink, C – grey, and H – light grey. Ab initio blocking barriers and relaxation mechanisms of complexes (c) 1_opt, (d) ^12x1_opt, (e) 2_opt and (f) ^26z2_opt. For figures c-f, the red arrows indicate the QTM or TA-QTM via ground or excited KDs, respectively. The blue characters indicate the major components of m_J of a KD. The green dotted arrows show the mechanisms of the Orbach processes. The black arrows indicate the pathways of magnetic relaxation.

In the next step, we attempted to optimise the geometry in the presence of an oriented external electric field (OEEF) starting from 0.004 au (atomic unit, equivalent to 0.2 V Å⁻¹).^10c,13 The electric field applied here varied from 0.004 au to 0.026 au and lies within the limits of ionisation energies and bond dissociation energies, and is accessible for most of the STM tips.^13,14 While the electric field-induced spectroscopic techniques use a smaller field, organic reactions that are performed using an OEFF are comparable to the electric field utilised here.^13,14 Applying the electric field along the +z-axis (which is co-linear with the g_z axis for complex 1) in 1_opt (see Fig. 1a, b and S1 in the ESI†) elongates the Dy–O(1) bond and, at the same time, shortens the Dy–O(2) bond, and therefore breaks the pseudo-D_5h symmetry of the molecule. We performed ab initio CASSCF calculations on this optimised geometry for ^4z1_opt (here, the superscript denotes the amount of OEEF applied × 10⁻³ au along the +z direction) in the presence of an electric field (EF), wherein a reduction in the barrier height was witnessed. This is due to the fact that Dy–O(1) bond elongation causes weakening of the axial LF and hence reduces the axial anisotropy for the oblate Dy(III) ion. Although a simultaneous shortening of the Dy–O(2) bond is seen, the ^4z1_opt geometry reveals that elongation is larger than the shortening (see Fig. S1†). This asymmetric distortion leads to a smaller U_cal value of 1108 cm⁻¹ for ^4z1_opt. In the next step, we increased the OEEF value in a stepwise manner to 0.012 au, and could clearly see that an increase in the electric field increases the Dy–O(1) bond further and, at the same time, shortens the Dy–O(2) bond, albeit asymmetrically. This led to a further reduction in the barrier height, with a value of 1040 cm⁻¹ noted for the ^12z1_opt structure (see Tables S6 and S9–S11 in the ESI†). This reduction in the barrier height can be rationalised by analysing the LoProp charges at the spin-free ground state. By increasing OEEF, the LoProp charge on O(1) gradually decreases, while it is increased on O(2) (see Tables S8 and S16†). Perceiving this effect, we switched the OEEF along the x/y direction for complex 1_opt (see Fig. S1 in the ESI†), and this yields structure of ^4x1_opt (here, the superscript denotes the amount of OEEF applied × 10⁻³ au along the +x direction). Here, the Dy–N(1) bond length was found to increase sharply from 2.62 Å to 2.80 Å, vis-à-vis, the geometries of 1_optvs.^12x1_opt (see Table 1) and, at the same time, two of the Dy–N bonds (along the −x-direction) were found to shorten asymmetrically. Also, the effect of applying an OEEF along the Dy–N(1) direction could be seen by a substantial decrease in the LoProp charge of the N(1) atom, while the charges on the oxygen atoms remained unaltered (see Table S8 in the ESI†). As three Dy–N bonds were significantly elongated in the geometry of the ^12x1_opt complex, it could be expected to possess a large barrier height. However, ab initio calculations revealed the contrary, with the barrier height diminishing with an increase in OEEF value, yielding a U_cal value of 939 cm⁻¹ for ^12x1_opt, and this relaxes via 3^rd excited KDs (see Tables S7 and S12–S14 in the ESI†). This is due to the fact that an alteration of the Dy–N distances is accompanied by a variation in the ∠O–Dy–O angle, which is reduced to 157° in ^12x1_opt from 178° in the geometry of 1_opt (see Table 1). Thus, the application of the electric field along the perpendicular or g_x-direction decreases the barrier height in complex 1. In addition, in both directions (x or z), the ground state as well as the excited state, the QTM (quantum tunnelling of magnetisation) values increase for complex 1, further supporting the reduction in the U_cal values. To prove that the reduction is solely due to the ∠O–Dy–O angle bending, we performed one additional set of calculations on the geometry of ^12x1_opt, where the ∠O–Dy–O angle was fictitiously set at 178° and this structure yielded a barrier height of 1162 cm⁻¹ (see Fig. S2 and Table S15 in the ESI†). This estimated value is ∼50 cm⁻¹ higher, compared to the optimised geometry, offering a possibility, however small, of enhancing the U_cal value in 1 using an applied electric field. Furthermore, increasing the OEEF to 0.016 au resulted in dissociation of the Dy–N bond, and this sets the electric field limit in the x/y direction of the molecule.

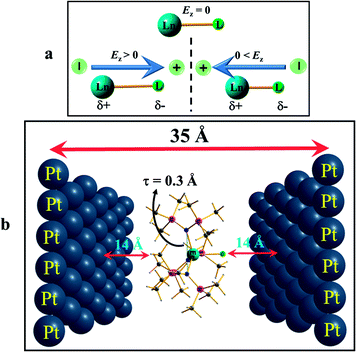
To further understand how the alteration of the structure occurs due to the applied OEEF, it is important to understand the nature of dipoles and their behaviour in the applied electric field conditions. The application of an OEEF is expected to polarise a non-polar bond and enhance the ionic character of a polar bond.¹³ For a Ln–L bond, the application of an OEEF will stretch it further if the dipolar field creates an opposite dipole with respect to the Ln–L dipole, and will shorten it if the dipolar field is in the same direction as the Ln–L dipole (see Fig. 2a). Therefore, the molecule has to be chosen in such a way that an increase in the Ln–L bond length will enhance the magnetic anisotropy and will subsequently increase the barrier height (U_eff).

Fig. 2 Arrangement of the application of an external electric field. (a) Result of applying an OEEF on a polar Ln–L bond axis. (b) Arrangement of applying an external electric field by placing point charges on two opposite Pt (111) layers that are 35 Å apart, and the molecule is at the centre, during ab initio calculations (the distance between the molecule to the Pt layers is not to scale). For more information see the computational details.

Applying an OEEF along an equatorial Ln–L bond in oblate ions, such as Dy(III), or along an axial Ln–L bond in prolate ions, such as Er(III), is thus likely to increase the U_eff value beyond the reported values from the X-ray structures. However, if the OEEF is applied along the opposite directions, it is expected to further decrease the U_eff values.

Based on the knowledge gained, we intuitively expanded the study to a prolate Er(III) ion using complex 2. We narrowed it down to this example for two reasons: (i) to choose a well-studied prolate Er(III) SIM with a significant barrier height, and (ii) to choose an Er(III) SIM with a strong equatorial ligand and a weak axial ligand along only one direction, as this would be expected to facilitate the enhancement of the U_cal value upon application of an OEEF. Upon application of the OEEF along the Er–Cl direction (g_z axis, see Fig. 2b), with the same step-size as before, the Er–Cl bond length was found to increase significantly (see Fig. S3 in the ESI† and Table 1), reaching a value of 2.91 Å at 0.024 au E_Z (^24z2_Opt). To determine the tolerance limit, we further increased the electric field to 0.026 au E_Z (^26z2_Opt) and found that the Er–Cl bond length elongated further to 3.04 Å. The application of an OEEF beyond this value was found to cleave the Er–Cl bond, suggesting a possible ionisation/decomposition limit.

Additionally, the {N₃Er} out-of-plane pyramidal shift (parameter τ, see Fig. 2 and S3 in the ESI†) was also found to change upon application of the OEEF. As the OEEF was applied along the Er–Cl bond, this bond elongates and pushes the Er(III) ion down, and therefore decreases the τ value. The τ value decreased from 0.5 Å in the 2_opt complex to 0.3 Å at ^26z2_opt. If the OEEF was applied along the −z-direction (Cl–Er direction), this tended to enhance the pyramidalisation (see Fig. S3 in the ESI†) and, thus, the τ value increased to 0.62 Å at ^26-z2_opt. Theoretical studies performed earlier on complex 2 revealed that this is an important parameter that enhances the barrier height.¹⁵

The application of an OEEF along the g_z axis in 2 (i.e. along the Er–Cl bond) enhanced the value of U_cal from 163 cm⁻¹ at ^4z2_opt to a remarkable 317 cm⁻¹ at ^26z2_opt. This estimate is one of the highest obtained for any Er(III) SIMs.¹⁶ Computed QTM (and TA-QTM) values revealed a smooth decrease of these values from 2.2 μ_B at ^4z2_opt to 1.3 μ_B at ^26z2_opt (see Tables S17–S24 in the ESI†). In addition, a smooth linear increase of the negative B₂⁰ parameter was observed for complex 2 under the applied electric field range along the +z direction (see Fig. S4 and Table S27 in the ESI†). If an OEEF was applied in the reverse direction on complex 2, i.e. along the −z-direction, a reverse trend was visible, with a gradual decrease in the U_cal value. As expected, here the Er(III)–Cl bond length decreased and a decrease in the τ value was noticed upon application of an electric field in the −z-direction. The U_cal value decreased from 131 cm⁻¹ for ^4-z2_opt to the much smaller value of 52 cm⁻¹ (via the 3^rd excited state) for the ^24-z2_opt structure (see Tables S25–S27 in the ESI†). Furthermore, the U_cal value diminishes to zero for ^26-z2_opt, with a notable ground state QTM. We also plotted the β-electron density of Er(III) under the applied electric field conditions, and this reflects well with the observed changes (see Fig. S5† for a plot corresponding to ^26-z2_opt, 2_opt and ^26z2_opt).

After achieving such a large U_cal value for complex 2, we extended the study further to another Dy(III) example, namely [Dy(Cp^Me3)₂Cl] (complex 3) (Cp^Me3 = trimethylcyclopentadienyl) (see Fig. 3a), which is a model complex derived from the X-ray structure of the famous precursor, [Dy(Cp^ttt)₂Cl].^3a The calculations on the optimised structure (3_opt) revealed a very small U_cal value of 144 cm⁻¹ relaxing via the first excited state due to high QTM being in operation due to the coordination of –Cl along the equatorial direction (see Tables S28 and S29 in the ESI†). In order to quench this QTM, we applied the OEEF along the Dy–Cl bond direction (perpendicular to the g_z axis), and this led to the weakening of the Dy–Cl bond and a gradual increase in the U_cal value from 160 cm⁻¹ at ^4z3_opt (here the +z direction indicates application of OEEF along the Dy–Cl bond axis) to 519 cm⁻¹ in the ^22z3_opt structure (see Table S29† and Fig. 3a–d). The Dy–Cl bond length increased from 2.59 Å for ^4z3_opt to 2.94 Å for ^22z3_opt. As the Dy–Cl bond distance increases with the applied electric field, two other important structural parameters were also found to have been altered. Firstly, the distance between the two Cp rings was found to decrease and, secondly, the Cp–Dy–Cp angle was found to increase (see Table S28 in the ESI†). The application of an electric field beyond 0.022 au resulted in the rupture of the Dy–Cl bond. At the ^22z3_opt geometry, the U_cal value estimated is found to be three times larger than the optimized structure obtained in the absence of OEEF (3_opt).

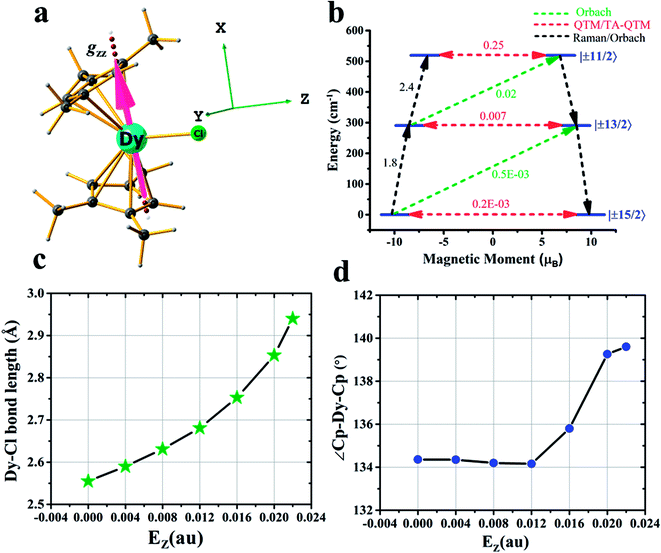Fig. 3 Details of the application of an external electric field in complex 3. (a) DFT optimised geometry of complex 3, along with the g_zz axis and the three cartesian axes directions. (b) An ab initio computed magnetization blocking barrier diagram of ^22z3_opt. See Fig. 1 caption for further details. (c) Variations in the Dy–Cl bond length and (d) Cp–Dy–Cp angle with respect to the oriented external electric field.

While the QTM (or TA-QTM) probabilities have been found to alter upon the application of an electric field, the challenge of controlling the blocking temperature still remains. As the electric field modifies the geometry, this in turn alters the corresponding molecular vibrations and hence offers a way to control the molecular vibrations that are responsible for magnetisation relaxation. This idea can be utilised to modulate the prominent vibrations that are responsible for the reduction in the blocking temperature, and work in this direction is currently underway in our laboratory.

Conclusions

As chemical fine-tuning of the ligand field has already reached its potential, here we set out to search for an alternative route to enhance the U_eff values in Ln(III) SIMs. In this context, we explored the role of an applied external electric field in the magnetisation reversal in [Dy(Py)₅(O^tBu)₂]⁺ (1), [Er{N(SiMe₃)₂}₃Cl]⁻ (2), and [Dy(Cp^Me3)₂Cl] (3) single-ion magnets. Our calculations revealed a moderate improvement in the U_cal value of 1 if the electric field was applied along the g_x direction. Learning from this example, we studied the [Dy(Cp^Me3)₂Cl] complex, where the application of an electric field along the Dy–Cl direction was found to weaken the Dy–Cl bond, leading to an enhancement of the barrier height by three times (it was increased from 144 cm⁻¹ at a 0.004 au electric field to a remarkable 519 cm⁻¹ at a 0.022 au electric field), compared to the original molecule. Based on these understandings, we intuitively studied [Er{N(SiMe₃)₂}₃Cl]⁻, where the application of an electric field along the Er–Cl g_z-direction was found to boost the barrier height twice that of the reported U_eff values. The enhancement in the U_cal value was much larger than that of the X-ray structures, offering a viable non-chemical method to enhance the barrier height beyond the limits set by the ligand fields. This novel approach is expected to generate substantial interest in obtaining new generation SIMs, unveiling its potential applications.

Computational details

DFT calculations

All the geometry optimisations were performed with DFT (Density Functional Theory) calculations using the Gaussian 09 package (revision D.01).¹⁷ During geometry optimisations, we replaced the central Dy(III) and Er(III) ions with a diamagnetic Y(III) ion, as this ion has a similar ionic radius. The hybrid B3LYP functional, along with the SDD basis set¹⁸ and corresponding ECP basis set for Y and the Ahlrichs split-valence polarisation (SVP)¹⁹ for the rest of the atoms were used during the optimisation steps. In addition, the diffused 6-31+G(d,p) basis set was tested and used for the non-metals and compared with the SVP results. The geometrical parameters were found not to change upon changing the basis set from SVP to 6-31+G(d,p). An oriented external electric field (OEEF) was applied during the optimisation in a particular direction using the Field keyword available in G09 suite. The OEEF was increased with a step-size of a 0.004 au electric field, which is equivalent to 0.2 V Å⁻¹ (1 au = 51.4 V Å⁻¹).

Ab initio calculations

After the geometry optimisation at different electric fields, the optimised complexes were inserted between the Platinum (Pt) layers for single point CASSCF calculations. Here, in the ab initio setup, the central metal ion was placed back into the original lanthanide centres to perform anisotropy calculations in the presence of the external electric field. Since the OEEF was applied along a particular direction during the DFT calculations, a similar orientation was fixed during the ab initio setup as well. All the ab initio single point calculations were performed using the MOLCAS 8.0 program package.²⁰ Here, a multi-configurational CASSCF (complete active space self-consistent field) method was chosen to compute the spin-Hamiltonian parameters. We employed relativistic contracted atomic natural orbital type basis sets: [ANO-RCC-VTZP…8s7p5d3f2g1h] for Ln(III) {Ln = Dy, Er}, ANO-RCC-VDZP (ANO-RCC…6s5p3d1f) for Si and Cl, ANO-RCC-VDZP (ANO-RCC…3s2p1d) for N and O, ANO-RCC-VDZ (ANO-RCC…3s2p) and ANO-RCC-VDZP (in the case of complex 3) for C, and ANO-RCC-VDZ (ANO-RCC…2s) for H, throughout our calculations. First, we performed a simple low-level SCF to generate the starting estimated orbitals in the Guessorb step. The Pt(111) layer was introduced as point charges to generate the external static electric field using the XFIELD keyword available in MOLCAS suite. In order to generate the external electric field for the ab initio calculations in MOLCAS, we placed two oppositely charged single Pt(111) layers, each containing 39 Pt atoms of dimension 14 × 14 (Å),² on each side and at 35 Å apart (see Fig. 2b in the main manuscript). Point charges of the different signs were imposed on the opposite Pt(111) layers to generate the electric field, mimicking the electrode setup. Then, in this arrangement, the optimised Dy^III/Er^III complex was placed exactly at the centre of the two Pt(111) layers. It was assumed that no chemical interaction was possible between the two layers and the molecule, as the distance is too high (∼15 Å). More precisely, the electric field was directed perpendicular to the Pt layers. The direction of the electric field could be switched by altering the sign of the charges on the Pt(111) layers. The charges were chosen in a trial and error method, so that the generated electric field matched exactly with the oriented electric field used earlier during optimisation in DFT. The imposed point charges and the corresponding generated electric fields at the origin or centre of the Pt layer were calculated and are listed in Tables S6 and S7.†

The AMFI (atomic mean field integral) spin–orbit operator was introduced to account for the spin–orbit effects. The scalar relativistic effect was considered using the DKH Hamiltonian. The Cholesky decomposition method was adopted to accelerate the two-electron integral calculation. In the configuration interaction (CI) step (CASSCF), an active space of 9 electrons in seven 4f orbitals, i.e. CAS(9,7) for Dy; 11 electrons in seven 4f orbitals, i.e. CAS(11,7) for Er(III) were considered throughout the calculations. This active space was optimised with 21 sextets for Dy(III), and 35 quartets and 112 doublets for Er(III). The spin–orbit coupling was taken into account using the RASSI-SO (Restricted Active Space State Interaction Spin–Orbit) module, which acts on all the spin-free states generated from the CASSCF wavefunctions. Finally, eight lower energy ground state Kramer doublets (KDs) for Dy(III) and Er(III) were used for the calculation of the spin-Hamiltonian properties, such as the g tensor values, using a specially designed routine SINGLE-ANISO module.

Crystal field description

The crystal field Hamiltonian for lanthanide coordination complexes has been defined as follows,
where B_k^q and O_k^q are the extended crystal field (CF) operator and the Stevens operator, respectively. Here, if the value of k is 2, then B_k^q is the tensor quantity, and k = 2 (higher-order indices like 4, 6,… are also possible), where q = 0 denotes an axial crystal field and a non-zero value of q denotes a non-axial crystal field.²¹ Therefore, a large negative B_k=2,4…^q=0 value with a very small B_k=2,4…^q≠0 value indicates axial anisotropy and the reverse situation indicates transverse magnetic anisotropy.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AS thanks CSIR for the senior research fellowship (SRF) and GR would like to thank DST (DST/SJF/CSA-03/2018-10) and SERB (CRG/2018/000430; SB/SJF/2019-20/12) for funding.

References

1. (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. Novak, Nature, 1993, 365, 141–143; (b) M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793; (c) S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355; (d) E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513.
2. (a) Y. S. Ding, N. F. Chilton, R. E. Winpenny and Y. Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074; (b) S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191; (c) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer and S. Gao, J. Am. Chem. Soc., 2016, 138, 5441–5450.
3. (a) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442; (b) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403; (c) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449; (d) K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503; (e) P. Evans, D. Reta, G. F. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2019, 141, 19935–19940; (f) C. A. Gould, K. R. McClain, J. M. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, J. Am. Chem. Soc., 2019, 141, 12967–12973.
4. (a) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542; (b) S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. Walsh and F. Tuna, Coord. Chem. Rev., 2017, 346, 216–239.
5. (a) Y.-Z. Zheng, Y.-S. Ding, T. Han, Y.-Q. Zhai, D. Reta, N. F. Chilton and R. E. Winpenny, Chem.–Eur. J., 2020, 26, 5893–5902; (b) K.-X. Yu, J. G. C. Kragskow, Y.-S. Ding, Y.-Q. Zhai, D. Reta, N. F. Chilton and Y.-Z. Zheng, Chem, 2020, 6, 1777–1793; (c) A. Castro-Alvarez, Y. Gil, L. Llanos and D. Aravena, Inorg. Chem. Front., 2020, 7, 2478–2486; (d) B. Yin and C. C. Li, Phys. Chem. Chem. Phys., 2020, 22, 9923–9933; (e) A. Chiesa, F. Cugini, R. Hussain, E. Macaluso, G. Allodi, E. Garlatti, M. Giansiracusa, C. A. P. Goodwin, F. Ortu, D. Reta, J. M. Skelton, T. Guidi, P. Santini, M. Solzi, R. De Renzi, D. P. Mills, N. F. Chilton and S. Carretta, Phys. Rev. B, 2020, 101, 174402.
6. D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
7. A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Angew. Chem., 2019, 131, 14284–14289.
8. A. Upadhyay, S. K. Singh, C. Das, R. Mondol, S. K. Langley, K. S. Murray, G. Rajaraman and M. Shanmugam, Chem. Commun., 2014, 50, 8838–8841.
9. M. K. Singh, N. Yadav and G. Rajaraman, Chem. Commun., 2015, 51, 17732–17735.
10. (a) A. S. Zyazin, J. W. van den Berg, E. A. Osorio, H. S. van der Zant, N. P. Konstantinidis, M. Leijnse, M. R. Wegewijs, F. May, W. Hofstetter, C. Danieli and A. Cornia, Nano Lett., 2010, 10, 3307–3311; (b) T. Goswami and A. Misra, Chem.–Eur. J., 2014, 20, 13951–13956; (c) A. Palii, S. Aldoshin and B. Tsukerblat, J. Phys. Chem. C, 2017, 121, 27218–27224; (d) M. Fittipaldi, A. Cini, G. Annino, A. Vindigni, A. Caneschi and R. Sessoli, Nat. Mater., 2019, 18, 329–334; (e) J. Liu, J. Mrozek, W. K. Myers, G. A. Timco, R. E. P. Winpenny, B. Kintzel, W. Plass and A. Ardavan, Phys. Rev. Lett., 2019, 122, 037202; (f) A. K. Boudalis, J. Robert and P. Turek, Chem.–Eur. J., 2018, 24, 14896–14900; (g) M. Weisheit, S. Fähler, A. Marty, Y. Souche, C. Poinsignon and D. Givord, Science, 2007, 315, 349–351.
11. A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, Angew. Chem., Int. Ed., 2015, 54, 5864–5868.
12. S. K. Singh, B. Pandey, G. Velmurugan and G. Rajaraman, Dalton Trans., 2017, 46, 11913–11924.
13. S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145.
14. (a) C. Wang, D. Danovich, H. Chen and S. Shaik, J. Am. Chem. Soc., 2019, 141, 7122–7136; (b) X. Huang, C. Tang, J. Li, L.-C. Chen, J. Zheng, P. Zhang, J. Le, R. Li, X. Li and J. Liu, Sci. Adv., 2019, 5, eaaw3072; (c) A. B. Zakharov, V. V. Ivanov and L. Adamowicz, Int. J. Quantum Chem., 2020, e26260.
15. S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Chem. Commun., 2014, 50, 15513–15516.
16. (a) M. J. Heras Ojea, L. C. Maddock and R. A. Layfield, Organometallic Magnets, 2019, pp. 253–280; (b) T. Gupta, M. K. Singh and G. Rajaraman, in Organometallic Magnets, Springer, 2018, pp. 281–354; (c) A. Swain, A. Sarkar and G. Rajaraman, Chem.–Asian J., 2019, 14, 4056–4073.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision D.01, Wallingford CT, 2013.
18. T. H. Dunning and P. J. Hay, in Modern theoretical chemistry, Plenum Press, New York, 1977, vol. 3, p. 1.
19. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
20. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, N. Ferré, L. M. Frutos, L. Gagliardi and M. Garavelli, J. Comput. Chem., 2016, 37, 506–541.
21. C. Rudowicz, J. Phys. C: Solid State Phys., 1985, 18, 1415.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc03982a

---