Open Access Article
Open Access ArticleSpatio-temporal dynamics in graphene
Roland
Jago
 ,
Raül
Perea-Causin
,
Raül
Perea-Causin
 ,
Samuel
Brem
,
Samuel
Brem
 and
Ermin
Malic
*
and
Ermin
Malic
*
Chalmers University of Technology, Department of Physics, SE-412 96 Gothenburg, Sweden. E-mail: ermin.malic@chalmers.se
First published on 13th May 2019
Abstract
Temporally and spectrally resolved dynamics of optically excited carriers in graphene has been intensively studied theoretically and experimentally, whereas carrier diffusion in space has attracted much less attention. Understanding the spatio-temporal carrier dynamics is of key importance for optoelectronic applications, where carrier transport phenomena play an important role. In this work, we provide a microscopic access to the time-, momentum-, and space-resolved dynamics of carriers in graphene. We determine the diffusion coefficient to be D ≈ 360 cm2 s−1 and reveal the impact of carrier–phonon and carrier–carrier scattering on the diffusion process. In particular, we show that phonon-induced scattering across the Dirac cone gives rise to back-diffusion counteracting the spatial broadening of the carrier distribution.
The time- and momentum-resolved carrier dynamics in graphene is meanwhile well understood,1–7 but there have been only a few studies on spatio-temporal dynamics and diffusion in graphene8–10 and other low dimensional materials, such as carbon nanotubes11 and transition metal dichalcogenides.12–15 Kulig et al. studied15 the exciton diffusion in WS2 and determined that the diffusion coefficient varies over two orders of magnitude with respect to the pump fluence. In graphene, pump–probe experiments performed at relatively high pump fluences16,17 demonstrated a diffusion coefficient of D = 250 ± 140 cm2 s−1 on a picosecond timescale after optical excitation. The diffusion of photoexcited carriers has been studied theoretically18 with an effective Boltzmann approach, where many-particle scattering has been only considered with relaxation rates.
However, a full microscopic view on the spatio-temporal dynamics revealing the interplay between diffusion and momentum- and time-dependent scattering processes is still missing.
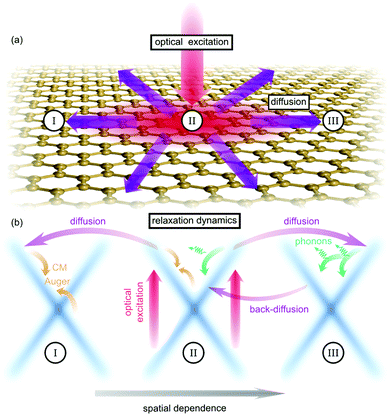
Exploiting the density matrix formalism19,20 and the Wigner representation,21 we provide microscopic insights into the temporally, spectrally, and spatially resolved dynamics of optically excited carriers in graphene including carrier diffusion, carrier–light, carrier–phonon, and carrier–carrier scattering processes on the same microscopic footing, cf. Fig. 1. In particular, we determine the diffusion coefficient and show that the diffusion process can be tuned with experimentally accessible knobs, such as pump fluence, substrate and temperature. Furthermore, we reveal how carrier–phonon scattering counteracts the diffusion through efficient scattering across the Dirac cone resulting in an efficient back-diffusion, cf. Fig. 1(b).
Theoretical approach
We consider a graphene sheet under local optical excitation (red arrows in Fig. 1). The optically excited carriers relax to lower energies via Coulomb- (orange arrows) and phonon-induced scattering (green arrows). The inhomogeneous optical excitation creates spatial gradients in the carrier density, giving rise to diffusion of carriers (purple arrows). To obtain microscopic access to the spatio-temporal dynamics, we derive a set of coupled equations of motion for the electron occupation probability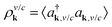 , the microscopic polarization
, the microscopic polarization 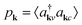 , and the phonon number
, and the phonon number 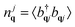 . Here, the creation and annihilation operators
. Here, the creation and annihilation operators 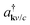 and akv/c with momentum k are used for electrons in the valence or conduction band (v,c), while the hole occupation probability is given by ρhk = 1 − ρvk. The corresponding phonon operators are
and akv/c with momentum k are used for electrons in the valence or conduction band (v,c), while the hole occupation probability is given by ρhk = 1 − ρvk. The corresponding phonon operators are 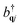 , bqj with the phonon mode j and the phonon momentum q.
, bqj with the phonon mode j and the phonon momentum q.
To introduce spatial effects, we transform the occupation probability into the Wigner formalism.22,23 Here, we consider fluctuations of the occupation probability 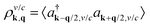 and perform the Fourier transformation with respect to the momentum difference q resulting in the Wigner function
and perform the Fourier transformation with respect to the momentum difference q resulting in the Wigner function
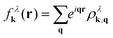 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λk(r) is a quasi-probability function, i.e. f
λk(r) is a quasi-probability function, i.e. f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λk(r) can be negative. Nevertheless, integration over r or k gives the actual distribution in momentum space or the carrier density in real space, i.e.
λk(r) can be negative. Nevertheless, integration over r or k gives the actual distribution in momentum space or the carrier density in real space, i.e.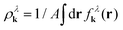 or
or 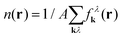 with A as the area of the graphene sheet.
with A as the area of the graphene sheet.
The carrier dynamics is determined by a many-particle Hamilton operator H, where we take into account the free carrier and phonon contribution H0, the carrier–carrier Hc–c and the carrier–phonon Hc–ph interaction accounting for Coulomb- (orange arrows) and phonon-induced scattering (green arrows), and the carrier–light coupling Hc–l (red arrows) that is treated on a semi-classical level. Details on the contributions of the many-particle Hamilton operator including the calculation of the matrix elements can be found in ref. 1 and 5.
Exploiting the Heisenberg equation of motion, we derive the equation of motion for the carrier fluctuation ρλk,q. Taking into account the free-particle Hamilton operator H0 leads to 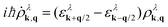 with the electronic dispersion ελk. To determine an equation for the Wigner function we perform a Fourier transformation resulting in
with the electronic dispersion ελk. To determine an equation for the Wigner function we perform a Fourier transformation resulting in 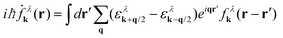 . To simplify this integro-differential equation we expand the Wigner function to the first order
. To simplify this integro-differential equation we expand the Wigner function to the first order 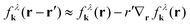 . By using r'eiqr‘ = −i∇qeiqr‘ and shifting the q-derivative to the electron dispersion via partial integration, the r′-integral depends only on the exponential function resulting in δk,q, whereby the zeroth order of the expansion of the Wigner function vanishes. Finally, the equation of motion for the Wigner function for the free Hamilton operator reads
. By using r'eiqr‘ = −i∇qeiqr‘ and shifting the q-derivative to the electron dispersion via partial integration, the r′-integral depends only on the exponential function resulting in δk,q, whereby the zeroth order of the expansion of the Wigner function vanishes. Finally, the equation of motion for the Wigner function for the free Hamilton operator reads
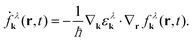 | (2) |
To derive the equations of motion for the Wigner function, the polarization and the phonon number with the full Hamilton operator we make the following assumptions: (i) we consider diffusion processes in the polarization to be small, since the latter quickly decays in momentum space and vanishes directly after the optical excitation.5 In contrast, the relaxation of carriers occurs on a picosecond timescale which is comparable to diffusion processes, and therefore the diffusion term can not be neglected in the equation for the Wigner function. (ii) We also neglect the phonon diffusion, since it is expected to be much slower than the electronic diffusion due to the flat phonon dispersion. (iii) We expect scattering processes between different spatial positions to be small compared to the diffusion. Now, using the Heisenberg equation of motion, we derive the full spatio-temporal graphene Bloch equations in second-order Born-Markov approximation
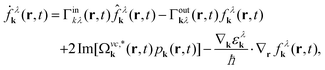 | (3) |
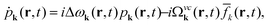 | (4) |
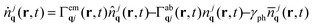 | (5) |
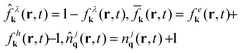 , and
, and 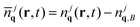 with the initial Bose-distribution for phonons njq,B. The equations describe the time-, momentum- and space-resolved coupled dynamics of electrons/holes, phonons, and the microscopic polarization. The dynamics of electrons in the conduction band and holes in the valence band is symmetric, but has different initial conditions for doped graphene samples. The appearing Rabi frequency is defined as
with the initial Bose-distribution for phonons njq,B. The equations describe the time-, momentum- and space-resolved coupled dynamics of electrons/holes, phonons, and the microscopic polarization. The dynamics of electrons in the conduction band and holes in the valence band is symmetric, but has different initial conditions for doped graphene samples. The appearing Rabi frequency is defined as 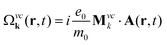 with the free electron mass m0, the vector potential A(r,t), and the optical matrix element Mvck = 〈kv|∇k|kc〉. Since we study the carrier dynamics close to the Dirac point, renormalization effects can be neglected. Furthermore, we have introduced
with the free electron mass m0, the vector potential A(r,t), and the optical matrix element Mvck = 〈kv|∇k|kc〉. Since we study the carrier dynamics close to the Dirac point, renormalization effects can be neglected. Furthermore, we have introduced 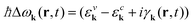 with the electronic dispersion ελk and the dephasing rate γk(r,t). The time-, momentum- and spatial dependent dephasing γk(r,t) and in- and out-scattering rates Γin/outkλ(r,t) include carrier–carrier and carrier–phonon scattering channels. The dynamics of the phonon number n
with the electronic dispersion ελk and the dephasing rate γk(r,t). The time-, momentum- and spatial dependent dephasing γk(r,t) and in- and out-scattering rates Γin/outkλ(r,t) include carrier–carrier and carrier–phonon scattering channels. The dynamics of the phonon number n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) jq(t) is driven by the emission and absorption rates1,5 Γem/absqj(r,t). The constant γph is the experimentally determined phonon decay rate.24 More details on the appearing many-particle scattering and dephasing rates can be found in ref. 1 and 5. In this work, we assume that graphene lies on a SiC-substrate and is surrounded by air on the other side. This is taken into account by introducing an averaged dielectric background constant25
jq(t) is driven by the emission and absorption rates1,5 Γem/absqj(r,t). The constant γph is the experimentally determined phonon decay rate.24 More details on the appearing many-particle scattering and dephasing rates can be found in ref. 1 and 5. In this work, we assume that graphene lies on a SiC-substrate and is surrounded by air on the other side. This is taken into account by introducing an averaged dielectric background constant25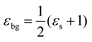 , where εs = 9.66 is the static screening constant of the substrate, while 1 describes the dielectric constant of air. Furthermore, the internal many-particle screening is taken into account by calculating the static limit of the Lindhard equation,19,26 which screens the Coulomb matrix elements.
, where εs = 9.66 is the static screening constant of the substrate, while 1 describes the dielectric constant of air. Furthermore, the internal many-particle screening is taken into account by calculating the static limit of the Lindhard equation,19,26 which screens the Coulomb matrix elements.
The derived set of equations resemble the semiconductor Bloch equations for spatial homogeneous systems (cf.ref. 1 and 5) up to the additional term 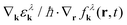 , which describes the diffusion of carriers in the direction ∇kελk ∝ ek = k/|k|. As a result, carriers with different sign in momentum move in opposite directions generating locally asymmetric carrier distributions in momentum space and resulting in a local current
, which describes the diffusion of carriers in the direction ∇kελk ∝ ek = k/|k|. As a result, carriers with different sign in momentum move in opposite directions generating locally asymmetric carrier distributions in momentum space and resulting in a local current 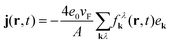 with the Fermi velocity vF. The sum contains both electrons in the conduction band and holes in the valence band and in a spatially homogeneous system, the mean current vanishes.
with the Fermi velocity vF. The sum contains both electrons in the conduction band and holes in the valence band and in a spatially homogeneous system, the mean current vanishes.
Spatio-temporal dynamics
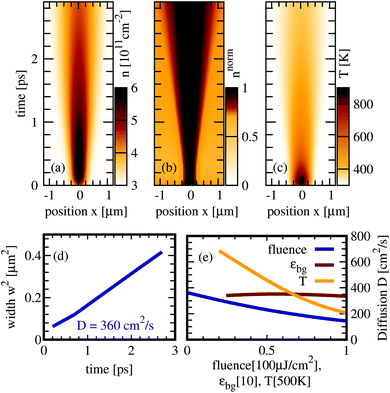
Now, we numerically evaluate the spatio-temporal graphene Bloch equations and investigate the interplay of diffusion and relaxation processes after optical excitation. We excite carriers with an optical pulse with a Gaussian profile both in time and space. We chose typical values for pulse characteristics including a temporal FWHM of 115 fs, a spatial FWHM of 265 nm, an excitation energy of 1 eV and a pump fluence of 1 μJ cm−2. The temporally and spatially dependent carrier density n(x,t) is shown in Fig. 2(a). The diffusion of carrriers is reflected in the broadening of the carrier density in space. Normalizing the density for each time step, the broadening becomes more visible (Fig. 2(b)), since phonon- and Auger-driven interband processes give rise to a reduction of carriers with increasing time. Fig. 2(c) shows the temporal and spatial distribution of the electronic temperature. The latter has been determined via the average kinetic energy per particle. Assuming a Fermi distribution, one obtains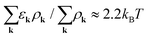 . Note that shortly after the pulse the carrier distribution deviates from an equilibrium Fermi distribution and therefore the temperature is there not well defined.
. Note that shortly after the pulse the carrier distribution deviates from an equilibrium Fermi distribution and therefore the temperature is there not well defined.
To quantify the diffusion and to estimate the diffusion coefficient for graphene, we fit the carrier density with a Gaussian exp(−x2/w2(t)) for every time step. The temporal evolution of the width w(t) is depicted in Fig. 2(d). It is connected to an effective diffusion coefficient D via27w2(t) = w02+ 4Dt resulting in D ≈ 360 cm2 s−1 for the investigated graphene sample on a SiC substrate. Our results fit well to the experimentally obtained values17 for the diffusion coefficient of D = 250 ± 140 cm2 s−1. In Fig. 2(e) we show the influence of pump fluence, substrate and temperature on the diffusion coefficient. We find that the temperature has the largest impact. The underlying processes will be discussed later.
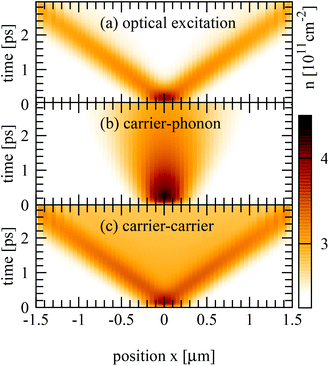
So far we have investigated the diffusion behaviour by taking into account the full carrier dynamics. Now, to understand the fundamental interplay of many-particle scattering and diffusion processes we study separately the impact of different scattering mechanisms on the diffusion process, cf. Fig. 3. We start with the case without any scattering channels just considering the electron–light interaction. After the optical excitation, carriers with positive/negative momenta diffuse in opposite spatial directions according to the diffusion term in eqn (3). After approximately 100 fs the carrier separation becomes visible, as the intial carrier density distribution splits into two pronounced peaks of the same width but with half of the amplitude, cf. Fig. 3(a). Including the carrier–phonon scattering, we observe a strongly reduced spatial broadening of the carrier density and no splitting appears (Fig. 3(a)). Phonon-induced relaxation processes counteract the diffusion via back-scattering across the Dirac cone and the following back-diffusion (cf.Fig. 1). The impact of carrier–phonon scattering will be further microscopically resolved in the next section. Including only the carrier–carrier scattering, the density diffuses with the same speed as in the case without any scattering channels (cf.Fig. 3(c)). This is a consequence of the symmetry of Coulomb matrix elements, which favor parallel scattering.28,29 Scattering across the Dirac cone is relatively inefficient and back-scattering is even forbidden. In contrast to the case without scattering, the spatial region between the two peaks contains a non-zero density. This reflects the weak but not vanishing Coulomb scattering processes bringing carriers from one to the other side of the Dirac cone.
Carrier–phonon dynamics
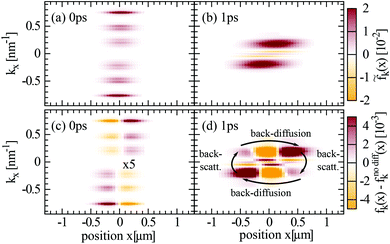
To get a thorough understanding of the microscopic processes governing the spatio-temporal carrier dynamics, we investigate the spectral and spatial behaviour of the Wigner function for different times. We start with the interplay of diffusion and carrier–phonon scattering processes. The optically excited carriers scatter via optical phonons to lower energies and form enhanced carrier occupations separated by the energy of optical phonons (red regions in Fig. 4(a)). Diffusion processes lead to a spatial broadening of the carrier distribution and after approx. 1 ps the carriers have relaxed to lower energies close to the Dirac point (Fig. 4(b)).To investigate the impact of diffusion in more detail we performed the same calculation twice, but in the second computation we excluded diffusion processes. Illustrating the difference of both calculations, i.e. fk(x) − fk(x)nodiff, we can directly observe the impact of diffusion on carrier–phonon scattering (Fig. 4(c) and (d)). As already discussed in the theory section carriers with positive/negative momentum diffuse in opposite spatial direction. This behaviour is illustrated in Fig. 4(c), where carriers with positive momentum diffuse from x < 0 positions (orange spots) to x > 0 positions (red spots). After 1 ps the carriers have already relaxed to energies close to the Dirac cone and below the optical phonon energy. Consequently, the scattering with acoustic phonons becomes dominant. Due to the flat dispersion of acoustic phonons with respect to the Dirac cones back-scattering across the Dirac cone is preferred, such that carriers with positive momenta are scattered to negative momenta and vice versa (Fig. 1). The inversion of momenta results in a back-diffusion, such that the overall carrier distribution stays bunched in space, cf. Fig. 3(b). The back-diffusion is shown in Fig. 4(d) by the the multiple sign change in the colored regions (red to orange to red).
Carrier–carrier dynamics
Now, we investigate the impact of carrier–carrier scattering on diffusion of optically excited carriers. An important aspect here is that Auger scattering is efficient giving rise to a carrier multiplication30–34 that increases the overall carrier density (note the scale of the color map in Fig. 5 compared to Fig. 4(a)). This also results in a quick increase of the carrier distribution close to the Dirac cone already during the optical excitation (Fig. 5(a)). Since electrons and holes diffuse in the same direction, the conditions for carrier multiplication are still satisfied after the diffusion. The directional dependence (in momentum space) for intraband carrier–carrier scattering is determined by the Coulomb matrix element that includes a form factor proportial to1 1 + eiϕ with the scattering angle ϕ. This means that parallel scattering (ϕ = 0) is the preferable scattering channel, and that for the back-scattering (ϕ = π) the amplitude of the Coulomb matrix element completely vanishes. As a result, scattering processes across the Dirac cone that change the sign of the carrier momentum (and lead to a back-diffusion) are inefficient. As a result, carriers with positive/negative momenta remain separated with respect to their spatial position – similarly to the case without any scattering (Fig. 3(a)). Fig. 5(b) illustrates that carriers with positive/negative momenta are mainly distributed towards positive/negative spatial positions.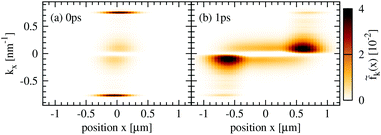 | ||
| Fig. 5 Impact of carrier–carrier scattering. The same as Fig. 4, but now only including the carrier–carrier instead of carrier–phonon scattering. Coulomb interaction is most efficient for parallel scattering along the Dirac cone in the momentum space. As a result, carrier–carrier scattering does not efficiently counteract the diffusion of carriers in opposite direction as clearly observed in (b). | ||
Tuning the diffusion
Now, we can explain the dependence of the diffusion coefficient on pump fluence, substrate and temperature shown in Fig. 2(e). We find that the diffusion becomes less efficient with the increasing pump fluence (blue curve). Here, more carriers are excited resulting also in an increased number of emitted phonons. Thus, hot-phonon effects become important, i.e. an increasing number of phonons can be reabsorbed in back-scattering processes giving rise to additional channels for back-diffusion. Furthermore, we find that the diffusion coefficient is nearly independent of the substrate (red curve) entering in our calculations through the screening of the Coulomb potential. This is not surprising, since Coulomb-induced scattering processes have been shown to only play a minor role for the diffusion of carriers, cf. Fig. 3. Finally, we observe that the diffusion can be most efficiently tuned by varying the temperatures (orange curve). The lower the temperature, the weaker the carrier–phonon scattering, the less efficient is back-scattering and back-diffusion resulting in a considerably increased diffusion coefficient.In summary, we provide a microscopic view on the spatio-temporal carrier dynamics in graphene based on the density matrix formalism in Wigner representation. We investigate the interplay of diffusion and many-particle scattering processes after a local optical excitation. In particular, we determine a diffusion coefficient of D ≈ 360 cm2 s−1 that agrees well with recent experimental values. Furthermore, we reveal that carrier–phonon scattering across the Dirac cone and the resulting back-diffusion are crucial ingredients to understand the spatial broadening of the carrier distribution. The gained insights are important e.g. for graphene-based photodetectors,35–39 that are governed by the thermoelectric effect, which relies on spatial temperature gradients.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No. 785219 (Graphene Flagship). Furthermore, we acknowledge support from the Swedish Research Council (VR). The computations were performed on resources at Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC).References
- E. Malic and A. Knorr, Graphene and Carbon Nanotubes: Ultrafast Optics and Relaxation Dynamics, Wiley-VCH, 2013 Search PubMed.
- S. Butscher, F. Milde, M. Hirtschulz, E. Malic and A. Knorr, Appl. Phys. Lett., 2007, 91, 203103 CrossRef.
- J. M. Dawlaty, S. Shivaraman, M. Chandrashekhar, F. Rana and M. G. Spencer, Appl. Phys. Lett., 2008, 92, 042116 CrossRef.
- P. Plochocka, P. Kossacki, A. Golnik, T. Kazimierczuk, C. Berger, W. A. de Heer and M. Potemski, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245415 CrossRef.
- E. Malic, T. Winzer, E. Bobkin and A. Knorr, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205406 CrossRef.
- D. Sun, C. Divin, M. Mihnev, T. Winzer, E. Malic, A. Knorr, J. E. Sipe, C. Berger, W. A. de Heer, P. N. First and T. B. Norris, New J. Phys., 2012, 14, 105012 CrossRef.
- E. Malic, T. Winzer, F. Wendler, S. Brem, R. Jago, A. Knorr, M. Mittendorff, J. C. König-Otto, T. Plötzing, D. Neumaier, H. Schneider, M. Helm and S. Winnerl, Ann. Phys., 2018, 1700038 Search PubMed.
- L. Huang, G. V. Hartland, L.-Q. Chu, Luxmi, R. M. Feenstra, C. Lian, K. Tahy and H. Xing, Nano Lett., 2010, 10, 1308 CrossRef CAS PubMed.
- R. Rengel, E. Pascual and M. J. Martin, Appl. Phys. Lett., 2014, 104, 233107 CrossRef.
- Y. Ishida, H. Masuda, H. Sakai, S. Ishiwata and S. Shin, Phys. Rev. B, 2016, 93, 100302 CrossRef.
- J. H. Grönqvist, M. Hirtschulz, A. Knorr and M. Lindberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035414 CrossRef.
- T. Kato and T. Kaneko, ACS Nano, 2016, 10, 9687 CrossRef CAS PubMed.
- L. Yuan, T. Wang, T. Zhu, M. Zhou and L. Huang, J. Phys. Chem. Lett., 2017, 8, 3371 CrossRef CAS.
- R. Rosati, F. Lengers, D. E. Reiter and T. Kuhn, Phys. Rev. B, 2018, 98, 195411 CrossRef CAS.
- M. Kulig, J. Zipfel, P. Nagler, S. Blanter, C. Schüller, T. Korn, N. Paradiso, M. M. Glazov and A. Chernikov, Phys. Rev. Lett., 2018, 120, 207401 CrossRef CAS PubMed.
- B. A. Ruzicka, S. Wang, L. K. Werake, B. Weintrub, K. P. Loh and H. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195414 CrossRef.
- B. A. Ruzicka, S. Wang, J. Liu, K.-P. Loh, J. Z. Wu and H. Zhao, Opt. Mater. Express, 2012, 2, 708 CrossRef CAS.
- F. T. Vasko and V. V. Mitin, Appl. Phys. Lett., 2012, 101, 151115 CrossRef.
- H. Haug and S. W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors, World Scientific, 2009 Search PubMed.
- M. Kira, F. Jahnke, W. Hoyer and S. Koch, Prog. Quantum Electron., 1999, 23, 189 CrossRef CAS.
- E. Wigner, Phys. Rev., 1932, 40, 749 CrossRef CAS.
- O. Hess and T. Kuhn, Phys. Rev. A, 1996, 54, 3347 CrossRef CAS.
- F. Rossi and T. Kuhn, Rev. Mod. Phys., 2002, 74, 895 CrossRef CAS.
- K. Kang, D. Abdula, D. G. Cahill and M. Shim, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165405 CrossRef.
- L. Patrick and W. J. Choyke, Phys. Rev. B: Solid State, 1970, 2, 2255 CrossRef.
- M. Kira and S. Koch, Prog. Quantum Electron., 2006, 30, 155 CrossRef.
- R. Pathria and P. Beale, in Statistical Mechanics, Academic Press, Boston, 3rd edn, 2011, pp. 583–635 Search PubMed.
- E. Malic, T. Winzer and A. Knorr, Appl. Phys. Lett., 2012, 101, 213110 CrossRef.
- M. Mittendorff, T. Winzer, E. Malic, A. Knorr, C. Berger, W. A. de Heer, H. Schneider, M. Helm and S. Winnerl, Nano Lett., 2014, 14, 1504 CrossRef CAS PubMed.
- T. Winzer, A. Knorr and E. Malic, Nano Lett., 2010, 10, 4839 CrossRef CAS PubMed.
- D. Brida, A. Tomadin, C. Manzoni, Y. J. Kim, A. Lombardo, S. Milana, R. R. Nair, K. S. Novoselov, A. C. Ferrari, G. Cerullo and M. Polini, Nat. Commun., 2013, 4, 1987 CrossRef CAS.
- T. Plötzing, T. Winzer, E. Malic, D. Neumaier, A. Knorr and H. Kurz, Nano Lett., 2014, 14, 5371 CrossRef.
- M. Mittendorff, F. Wendler, E. Malic, A. Knorr, M. Orlita, M. Potemski, C. Berger, W. A. de Heer, H. Schneider, M. Helm and S. Winnerl, Nat. Phys., 2015, 11, 75 Search PubMed.
- I. Gierz, M. Mitrano, J. C. Petersen, C. Cacho, I. C. E. Turcu, E. Springate, A. Stöhr, A. Köhler, U. Starke and A. Cavalleri, J. Phys.: Condens. Matter, 2015, 27, 164204 CrossRef.
- F. H. L. Koppens, T. Mueller, P. Avouris, A. C. Ferrari, M. S. Vitiello and M. Polini, Nat. Nanotechnol., 2014, 9, 780 CrossRef CAS PubMed.
- Z. Sun and H. Chang, ACS Nano, 2014, 8, 4133 CrossRef CAS.
- M. Buscema, J. O. Island, D. J. Groenendijk, S. I. Blanter, G. A. Steele, H. S. J. van der Zant and A. Castellanos-Gomez, Chem. Soc. Rev., 2015, 44, 3691 RSC.
- S. Schuler, D. Schall, D. Neumaier, L. Dobusch, O. Bethge, B. Schwarz, M. Krall and T. Mueller, Nano Lett., 2016, 16, 7107 CrossRef CAS PubMed.
- J. C. W. Song, M. S. Rudner, C. M. Marcus and L. S. Levitov, Nano Lett., 2011, 11, 4688 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |