Open Access Article
Open Access ArticleDumbbells, chains, and ribbons: anisotropic self-assembly of isotropic nanoparticles†
Enrico
Lavagna
,
Sebastian
Salassi
,
Davide
Bochicchio
 and
Giulia
Rossi
and
Giulia
Rossi
 *
*
Physics Department, University of Genoa, Via Dodecaneso 33, 16146 Genoa, Italy. E-mail: giulia.rossi@unige.it
First published on 17th August 2023
Abstract
Functionalizing the surface of metal nanoparticles can assure their stability in solution or mediate their self-assembly into aggregates with controlled shapes. Here we present a computational study of the colloidal aggregation of gold nanoparticles (Au NPs) isotropically functionalized by a mixture of charged and hydrophobic ligands. We show that, by varying the relative proportion of the two ligands, the NPs form anisotropic aggregates with markedly different topologies: dumbbells, chains, or ribbons. In all cases, two kinds of connections keep the aggregates together: hydrophobic bonds and ion bridges. We show that the anisotropy of the aggregates derives from the NP shell reshaping due to the formation of the hydrophobic links, while ion bridges are accountable for the “secondary structure” of the aggregates. Our findings provide a general physical principle that can also be exploited in different self-assembled systems: anisotropic/directional aggregation can be achieved starting from isotropic objects with a soft, deformable surface.
Nanoparticle (NP) synthesis and engineering techniques have progressed significantly during the last thirty years,1–6 serving a wide range of applications that includes nanofluidics7 and biomedicine,6,8–10 electronic devices,11 and catalysis.12 In every field, it is crucial to control the extent of NP self-assembly,13–15 both during the synthesis stage and in the target application environment.15–17 The interaction forces that drive NP self-assembly can originate from geometric, electric, or magnetic properties of the NP core.18–22 For instance, the shape of the NPs is a feature that can be used to obtain assemblies with specific structures.17,22–25 In the simplest case, the shape determines the packing geometry of a NP cluster, which can help drive the formation of specific materials, in particular 2D or 3D superlattices.25,26
The importance of specific surface interactions increases as the NPs get smaller, and the forces originating at the NP–solvent interface are often dominant and intrinsically short-range.14 In the <50 nm regime, the classic DLVO theory27 is often insufficient to explain the NP self-assembly since the interactions become non-additive14 and highly dependent on the NP surface structure and chemical specificity. Indeed, a feature that can lead to directional interactions between NPs is their surface patchiness.17,25,26 The complexity of the aggregate can be controlled by having a finite number of adhesive patches corresponding to the maximum number of possible junctions. For instance, Janus NPs, whose surface is divided into two well-distinct domains, can be the building blocks of colloidal polymers.18,23,28,29
Functionalization with a shell of covalently bound molecules is a common strategy for designing the surface features of colloidal nanomaterials. The functionalizing shell can assure colloidal stability or mediate the self-assembly behavior to form aggregates with controlled shapes.18,19,30,31 The ligands on the NP surface can mediate NP–NP and NP–environment interactions by different means depending on fine details of their chemical structure:32,33 simple Coulomb forces for charged ligands,34–38 hydrogen bonds,14,18 dipole–dipole interactions,14,18,35 DNA base pairing interactions,14,18 and hydrophobic interactions.39,40 The broad freedom of choice of functionalizing agents, and the possibility to vary their density and heterogeneity, imply that the NP assembly processes30 can be very diverse. If a single ligand type functionalizes the surface of the NP, it can mediate NP–NP interactions, while the resulting superlattice structure will be mainly driven by the NP shape.41
Using two or more functionalizing molecules can provide the NP with Janus patchiness,42 tetravalent directional bonding that can lead to colloidal crystal assembly,43 and facet-specific functionalities that can drive the assembly into rods or planar aggregates.44 In the regime of sparse grafting, also nanoparticles grafted with (usually hydrophobic) polymer tethers can effectively show some patchiness, due to the irregular and incomplete covering of the (usually hydrophilic) nanoparticle surface.45,46 Throughout this vast corpus of literature, the growth of anisotropic NP assemblies results from either anisotropic core shape or surface patchiness, or both. An interesting exception to this general trend was represented by silica nanoparticles functionalized by a thick, soft and hydrophobic polystyrene (PS) shell47,48 that, despite the random surface arrangement of the PS chains, were found to aggregate anisotropically, forming different structures depending on the PS surface grafting density. Anisotropy was shown to emerge from the entropy–enthalpy balance resulting from the deformation of the soft shell of neighbor NPs within the aggregates. Another example of emergent surface patchiness leading to directional interaction is provided by dendrimer nanofibers,49 disordered soft nanoclusters in which patches are generated upon exposition to asymmetric negative ions.
Here we show that Au NPs with an isotropic, amphiphilic surface functionalization can spontaneously form anisotropic NP aggregates, whose topology can be finely tuned by the ratio between hydrophobic and charged ligands on the NP surface. Using coarse-grained molecular dynamics (MD), we observe these NPs self-assembling into highly anisotropic supra-molecular structures such as dumbbells, chains, and ribbons, depending on the charged-to-hydrophobic ligand ratio. We further show that NP–NP connections can either be stable, hydrophobic interactions or weak, ion-mediated electrostatic interactions. The former interactions determine the topology of the primary structure of the aggregates, while the latter drive the folding of the primary structure into a secondary structure, which has a more dynamic and reversible nature.
Amphiphilic Au NPs: competing driving forces to dimerization
Gold nanoparticles functionalized with anionic 11-mercapto-undecane-sulphonate (MUS) and hydrophobic octane-thiol (OT) ligands are promising theranostic platforms, as they have spontaneous, stable interactions with biological membranes.4,50 The amphiphilic shell serves, by design, two purposes. The presence of the hydrophobic OT ligand provides hydrophobicity to the NPs, allowing them to penetrate their biological target (the lipid bilayer) spontaneously.50–52 The negatively charged MUS ligands instead provide colloidal stability to the NPs in solution. However, recent experimental and theoretical works39,40 have shown that MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT nanoparticles can aggregate, in aqueous solution, into oligomers or larger (tens of nm) aggregates. As expected, the aggregation is promoted by increasing salt concentrations.40 Which are the main driving forces controlling the extent and shape of the aggregates?
OT nanoparticles can aggregate, in aqueous solution, into oligomers or larger (tens of nm) aggregates. As expected, the aggregation is promoted by increasing salt concentrations.40 Which are the main driving forces controlling the extent and shape of the aggregates?
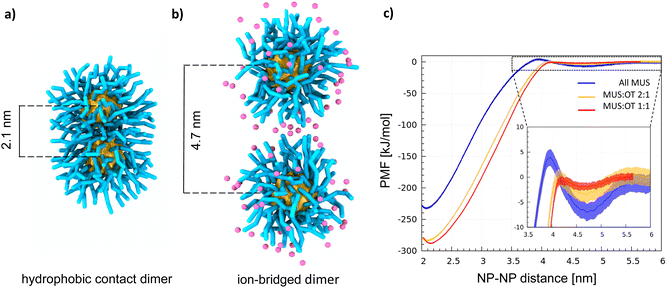
With atomistic and coarse-grained molecular dynamics simulations, our group and the group of S. Vanni observed that the NP–NP dimer has two stable configurations: the hydrophobic contact state, corresponding to the lowest free energy state (shown in Fig. 1a), in which the ligand shells interpenetrate leading to cores in direct contact, and the ion-bridged state, a metastable state in which positive counterions39,40 mediate the interaction between the negatively charged terminals of the MUS ligands (shown in Fig. 1b).
Here we modeled NPs, ions, and water using the standard Martini force field.53,54 The NP model was already used and characterized in previous works.55–59
In the ESI† we recall the main features of the NP model and the Martini force field in general, as well as its potential limitations, with particular attention to the treatment of electrostatic interactions. In our simulations we used a physiological concentration of salt (150 mM NaCl), and verified that salt concentration does not affect the NP aggregation behavior (see the ESI† for the details). Within this coarse-grained description, Fig. 1c shows how the competition between hydrophobic bonds and ion-bridged contacts depends on the anionic![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hydrophobic (MUS
hydrophobic (MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT) ligand ratio. The Au NPs have a core size of 2 nm and are functionalized with three different MUS
OT) ligand ratio. The Au NPs have a core size of 2 nm and are functionalized with three different MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT ratios: 100% MUS (all MUS), 66% MUS (MUS
OT ratios: 100% MUS (all MUS), 66% MUS (MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), 50% MUS (MUS
1), 50% MUS (MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).
1).
Two minima characterize all profiles (Fig. 1c), coherently with the dimerization Potential of Mean Force (PMF) profile of the NPs described in ref. 40 and with the same PMF profile obtained for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT NPs with a diameter of 4 nm, shown in Fig. S1.† The deepest minimum, at a NP–NP distance of 2.1 nm, corresponds to the hydrophobic contact configuration;40 the metastable minimum at a NP–NP distance of ∼4.7 nm corresponds to the ion-bridged dimer configuration. A discussion on the origin of the size-dependence of the dimerization behavior is included in the ESI.† In addition to core size, the stability of the ion-bridged minimum depends on the NP shell composition, as highlighted by the insert in Fig. 1c. The most stable ion-bridged configuration is obtained for all-MUS NPs, where the minimum has a depth of −7 kJ mol−1 and is separated from the hydrophobic contact state by an 11 kJ mol−1 barrier. Coherently with these free energy profiles, our unbiased MD simulations show that 2 NPs, initially located far from each other in the simulation box, always form a dimer stabilized by a hydrophobic bond in less than a microsecond. MUS
OT NPs with a diameter of 4 nm, shown in Fig. S1.† The deepest minimum, at a NP–NP distance of 2.1 nm, corresponds to the hydrophobic contact configuration;40 the metastable minimum at a NP–NP distance of ∼4.7 nm corresponds to the ion-bridged dimer configuration. A discussion on the origin of the size-dependence of the dimerization behavior is included in the ESI.† In addition to core size, the stability of the ion-bridged minimum depends on the NP shell composition, as highlighted by the insert in Fig. 1c. The most stable ion-bridged configuration is obtained for all-MUS NPs, where the minimum has a depth of −7 kJ mol−1 and is separated from the hydrophobic contact state by an 11 kJ mol−1 barrier. Coherently with these free energy profiles, our unbiased MD simulations show that 2 NPs, initially located far from each other in the simulation box, always form a dimer stabilized by a hydrophobic bond in less than a microsecond. MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complete the transition from the isolated to the hydrophobic contact state, through the intermediate ion-bridged configuration, within tens of ns. All MUS NPs are the only ones that may indulge in the ion-bridged configuration for a few hundred nanoseconds, as shown in Fig. S2.† This stabilization of the secondary minimum induced by the ions in all-MUS NPs can be rationalized based on their higher surface charge density.
1 complete the transition from the isolated to the hydrophobic contact state, through the intermediate ion-bridged configuration, within tens of ns. All MUS NPs are the only ones that may indulge in the ion-bridged configuration for a few hundred nanoseconds, as shown in Fig. S2.† This stabilization of the secondary minimum induced by the ions in all-MUS NPs can be rationalized based on their higher surface charge density.
The topology of large NP aggregates depends on the ligand ratio
To investigate the aggregation process beyond dimerization, we ran 5 unbiased simulations for each composition (all-MUS, MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and MUS
1, and MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), starting with 27 NPs in a 3 × 3 × 3 grid at a non-interacting distance (9 nm between the first neighbor NPs), solvated in water with Na+ counterions in a cubic simulation box of 27 nm lateral size.
1), starting with 27 NPs in a 3 × 3 × 3 grid at a non-interacting distance (9 nm between the first neighbor NPs), solvated in water with Na+ counterions in a cubic simulation box of 27 nm lateral size.
In each case, the NPs form a single cluster within the first few microseconds. All the final aggregates appear to be stable but relatively flexible in shape. Interestingly, the aggregate topology strongly depends on the composition of the ligand shell, as detailed in the following paragraphs. In order to exclude subtle dependencies of the resulting aggregate structures on the details of the random ligand arrangement, we also performed control runs with alternative, yet random, ligand arrangements at each MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT composition.
OT composition.
All-MUS NPs aggregate as clusters of dumbbells
Fig. 2a shows two representative aggregates obtained from the simulations of all-MUS NPs. Snapshots of all the aggregates can be found in Fig. S3.† The aggregates appear quite spherical, but at closer inspection, they are composed of dimers loosely bound to each other. We thus analyzed the structure of the all-MUS aggregates in more detail, as shown in Fig. 3a. We calculated the NP–NP radial distribution function g(r) in the last 3 μs of the simulations (when the aggregates were formed and stable). The g(r) presented in Fig. 3a, obtained as an average over the 5 independent simulations, shows two main peaks, one at 2.1 nm, which corresponds to the hydrophobic bond, and one at about 4.7 nm, which corresponds to the ion-bridged contact.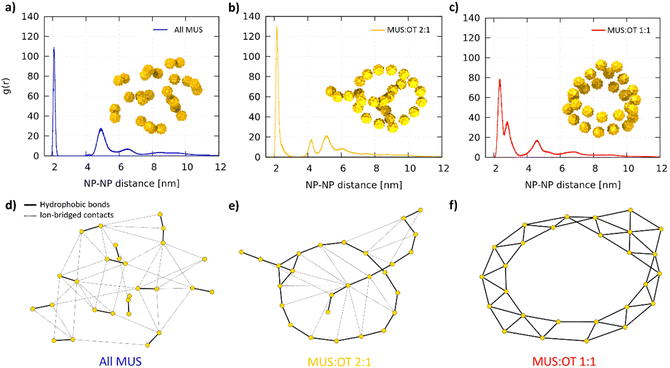 | ||
Fig. 3 Final aggregate analysis. NP–NP radial distribution functions g(r) for (a) All MUS, (b) MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2 OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (c) MUS 1, (c) MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1 OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Each g(r) is computed as an average over 5 independent simulations with the same NP composition. The snapshot of a corresponding aggregate is included as an example. In (d), (e) and (f) the graphs obtained from the network analysis are presented for the snapshots in (a), (b) and (c), respectively. The gold nodes represent the NPs, which are connected by solid black edges (hydrophobic bonds, responsible for the primary structure of the aggregates) and dashed black edges (ion-bridged contacts, responsible for the secondary structure). The positions of the nodes are not representative of the physical position of the NPs, and are generated by the Kamada–Kawai algorithm.60 1. Each g(r) is computed as an average over 5 independent simulations with the same NP composition. The snapshot of a corresponding aggregate is included as an example. In (d), (e) and (f) the graphs obtained from the network analysis are presented for the snapshots in (a), (b) and (c), respectively. The gold nodes represent the NPs, which are connected by solid black edges (hydrophobic bonds, responsible for the primary structure of the aggregates) and dashed black edges (ion-bridged contacts, responsible for the secondary structure). The positions of the nodes are not representative of the physical position of the NPs, and are generated by the Kamada–Kawai algorithm.60 | ||
We designed a tailored analysis of the aggregates to appreciate the network of NP–NP connections and obtain the precise aggregate topology. We assigned each NP to the node of an undirected graph, in which the edges represent the hydrophobic bonds or ion-bridged contacts. The operational definition of these two different connections is described in the ESI.†Fig. 3d shows, as a representative example, the network graph we obtained for the aggregate shown in Fig. 3a. The connection between the NPs within the dimers is hydrophobic, while the connection among different dimers is ion-bridged.
MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 NPs form linear aggregates
1 NPs form linear aggregates
The MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs aggregate in a radically different way. The NPs form the linear chains shown in Fig. 2b. These chains can close into ring structures, like in the second configuration of Fig. 2b. The longer chains can fold on themselves, while the rings can be stuck together or to a linear chain. A single long chain can adopt a knot-like structure in other final configurations. More examples are shown in Fig. S4,† where all the final MUS
1 NPs aggregate in a radically different way. The NPs form the linear chains shown in Fig. 2b. These chains can close into ring structures, like in the second configuration of Fig. 2b. The longer chains can fold on themselves, while the rings can be stuck together or to a linear chain. A single long chain can adopt a knot-like structure in other final configurations. More examples are shown in Fig. S4,† where all the final MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NP aggregates are shown. In the MUS
1 NP aggregates are shown. In the MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 average g(r) (Fig. 3b), we still observe the two peaks, corresponding to the hydrophobic bonds and ion-bridged contacts, but also a third one at about 4 nm, which is the second neighbor distance of the NPs along the chains. The graph shows that hydrophobic bonds are responsible of first-neighbor connections along the chain, while many ion-bridged contacts can establish weaker links between segments of the linear aggregates.
1 average g(r) (Fig. 3b), we still observe the two peaks, corresponding to the hydrophobic bonds and ion-bridged contacts, but also a third one at about 4 nm, which is the second neighbor distance of the NPs along the chains. The graph shows that hydrophobic bonds are responsible of first-neighbor connections along the chain, while many ion-bridged contacts can establish weaker links between segments of the linear aggregates.
MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 NPs form ribbon-like aggregates
1 NPs form ribbon-like aggregates
Lastly, the MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs assume a third different configuration. The aggregates, as shown in Fig. 2c and Fig. S5,† present a ribbon-like structure, composed of two lines of NPs in a parallel configuration. The aggregates can also present a hexagonal arrangement of 7 NPs. The ribbons can form planar or cylindrical rings, as shown in the left and right configurations in Fig. 2c. In some cases, like in the aggregate of Fig. S5b,† the ribbons fold on themselves. In the average g(r) of MUS
1 NPs assume a third different configuration. The aggregates, as shown in Fig. 2c and Fig. S5,† present a ribbon-like structure, composed of two lines of NPs in a parallel configuration. The aggregates can also present a hexagonal arrangement of 7 NPs. The ribbons can form planar or cylindrical rings, as shown in the left and right configurations in Fig. 2c. In some cases, like in the aggregate of Fig. S5b,† the ribbons fold on themselves. In the average g(r) of MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs, shown in Fig. 3c, the hydrophobic connection region is broader and has two peaks: the second, smaller one represent the second neighbors; the third peak accounts for both third neighbors and ion-bridged contacts, which are less relevant in this case. The graph in Fig. 3f shows an example in which all NP–NP connections are hydrophobic contacts.
1 NPs, shown in Fig. 3c, the hydrophobic connection region is broader and has two peaks: the second, smaller one represent the second neighbors; the third peak accounts for both third neighbors and ion-bridged contacts, which are less relevant in this case. The graph in Fig. 3f shows an example in which all NP–NP connections are hydrophobic contacts.
Using a language inspired by protein biology, we will refer to the structure imposed by the hydrophobic contact bonds as primary structure and to the one imposed by ion-bridging as secondary structure. Summarizing, changing the hydrophobic ligand concentration affects the primary structure, which is dimers for All MUS, chains for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and ribbons for MUS
1, and ribbons for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Ion-bridging causes the dimers to cluster in the case of All MUS, while for MUS
1. Ion-bridging causes the dimers to cluster in the case of All MUS, while for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and MUS
1 and MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 it causes the folding of the primary aggregate, originating the secondary structure.
1 it causes the folding of the primary aggregate, originating the secondary structure.
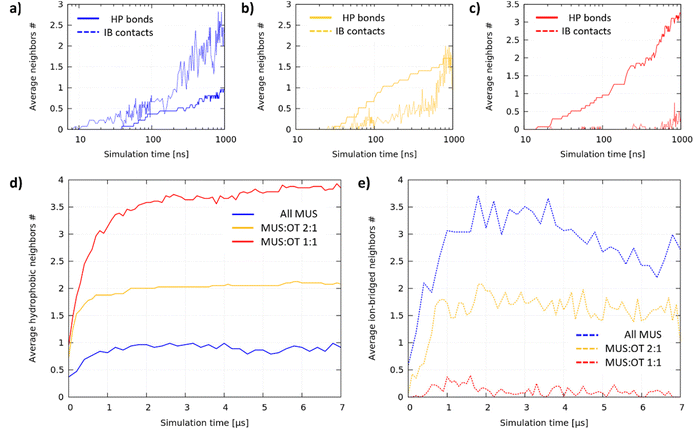
The aggregation dynamics depends on the ligand ratio
We analyzed the aggregation dynamics by monitoring the time evolution of the average node coordination (see the ESI† for further details), distinguishing between hydrophobic bonds and ion-bridged contacts (see Fig. 4a–c for the first microsecond of 1 representative simulation for each composition). All MUS NPs (Fig. 4a) start forming ion-bridged contacts right away, while hydrophobic bonds increase at a slower rate. The trend is inverted for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs (Fig. 4b), in which linear hydrophobic bonds form first, followed by inter-chain ion-bridged contacts. The same trend is even more pronounced for MUS
1 NPs (Fig. 4b), in which linear hydrophobic bonds form first, followed by inter-chain ion-bridged contacts. The same trend is even more pronounced for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs (Fig. 1c), where only hydrophobic bonds increase initially, while ion-bridged contacts form once the ribbon aggregates are almost completed. We performed an additional analysis investigating the formation of triplets (3 NPs connected by at least 2 hydrophobic bonds), which is reported in Fig. S6 of the ESI.†
1 NPs (Fig. 1c), where only hydrophobic bonds increase initially, while ion-bridged contacts form once the ribbon aggregates are almost completed. We performed an additional analysis investigating the formation of triplets (3 NPs connected by at least 2 hydrophobic bonds), which is reported in Fig. S6 of the ESI.†
Fig. 4d and e show how the average hydrophobic and ion-bridged node coordination progressed during the whole simulation. In each system, after an initial phase of about 1 microsecond, hydrophobic bonds saturate at a different value, indicating that the primary structure is complete and stable: 1 hydrophobic neighbor for All MUS is the signature of dumbbells, 2 neighbors for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reveals chain formation, and 3–4 neighbors for MUS
1 reveals chain formation, and 3–4 neighbors for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reveals ribbon formation. On the other hand, the ion-bridged aggregation is more fluid-like, coherently with the shallow energy minimum that we observe for the NP dimer. All MUS NPs saturate at the largest number of ion-bridged contacts, followed by MUS
1 reveals ribbon formation. On the other hand, the ion-bridged aggregation is more fluid-like, coherently with the shallow energy minimum that we observe for the NP dimer. All MUS NPs saturate at the largest number of ion-bridged contacts, followed by MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs and finally MUS
1 NPs and finally MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs, for which the ion-bridged contacts are vanishingly few.
1 NPs, for which the ion-bridged contacts are vanishingly few.
The ligand shell reshaping drives the anisotropic aggregation
The ligand shell composition, particularly the MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT ratio, drastically influences the growth of aggregates of otherwise identical NP. While a larger fraction of OT is expected to enhance hydrophobic aggregation, it is less obvious why the aggregates can have such different topologies, considering that the NP surface is homogeneous with ligands randomly bound to the NP.
OT ratio, drastically influences the growth of aggregates of otherwise identical NP. While a larger fraction of OT is expected to enhance hydrophobic aggregation, it is less obvious why the aggregates can have such different topologies, considering that the NP surface is homogeneous with ligands randomly bound to the NP.
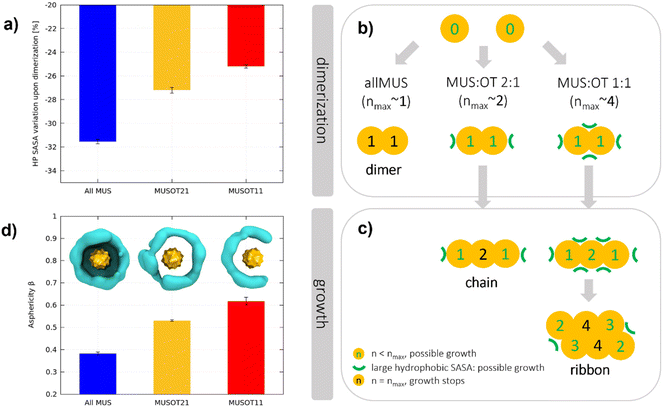
The formation of a hydrophobic bond implies that the interfacial ligands bend and open to expose their hydrophobic stretches. As a result of dimerization, the terminal groups of the MUS ligands are pushed away from the NP–NP interface and compacted in non-contact regions. Consequently, a lower net volume is available to the ligands around the NPs, and a higher surface charge density is present in non-contact regions. To quantify this effect, we calculated the hydrophobic area exposed by the surface of the NPs, before and after dimerization. In analogy with the solvent-accessible-surface-area (SASA), we will refer to this hydrophobic area as the hydrophobic SASA (see ESI† for further details). In the unbiased runs comprising 2 NPs, the hydrophobic SASA changes abruptly upon dimerization (see Fig. S7†). Fig. 5a shows the percentage decrease of the hydrophobic SASA upon dimerization for all MUS, MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs. There is a clear trend: the more OT in the shell, the less the hydrophobic SASA reduction upon dimerization.
1 NPs. There is a clear trend: the more OT in the shell, the less the hydrophobic SASA reduction upon dimerization.
The different availability of hydrophobic area at the different MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT ratios determines the aggregate growth, as exemplified in Fig. 5b and c. For all-MUS NPs, the reduction of the hydrophobic SASA upon dimerization (almost 32%) is such that it becomes almost impossible to establish more hydrophobic bonds, and the growth stops (Fig. 5b). On the contrary, the growth can proceed for MUS
OT ratios determines the aggregate growth, as exemplified in Fig. 5b and c. For all-MUS NPs, the reduction of the hydrophobic SASA upon dimerization (almost 32%) is such that it becomes almost impossible to establish more hydrophobic bonds, and the growth stops (Fig. 5b). On the contrary, the growth can proceed for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as shown in Fig. 5c. The equatorial region of a dimer, around the NP–NP interface, has the highest MUS (and thus charge) density. Therefore, a third NP will attach more easily at the Poles, where the ligands have more conformational freedom than in the equatorial region. Once the linear triplet is formed, the central NP has two neighbors. In the MUS
1, as shown in Fig. 5c. The equatorial region of a dimer, around the NP–NP interface, has the highest MUS (and thus charge) density. Therefore, a third NP will attach more easily at the Poles, where the ligands have more conformational freedom than in the equatorial region. Once the linear triplet is formed, the central NP has two neighbors. In the MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case, two is already the maximum possible number of neighbors, and the aggregate can only grow as a linear chain (Fig. 2 and S4†). In the MUS
1 case, two is already the maximum possible number of neighbors, and the aggregate can only grow as a linear chain (Fig. 2 and S4†). In the MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case, the ligand density at the surface of the linear triplets is not yet large enough to prevent further hydrophobic bonds, and 2D growth is possible until the NPs achieve their maximum number of possible hydrophobic bonds, namely four. The aggregates do not develop as isotropic planar lattices since they are more likely to grow from the NPs with the lowest coordination, thus forming ribbons.
1 case, the ligand density at the surface of the linear triplets is not yet large enough to prevent further hydrophobic bonds, and 2D growth is possible until the NPs achieve their maximum number of possible hydrophobic bonds, namely four. The aggregates do not develop as isotropic planar lattices since they are more likely to grow from the NPs with the lowest coordination, thus forming ribbons.
It is worth remarking that this mechanism, illustrated above as a step-by-step kinetic process, also reflects the thermodynamic stability of the final aggregate topology. To prove this concept, we designed 6 additional simulations in which the starting configuration of each system has been set to a different, “non native” topology (chains and ribbons for all MUS, dumbbells and ribbons for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, dumbbells and chains for MUS
1, dumbbells and chains for MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). As better detailed in the ESI (Fig. S8†), in each of this artificial systems the starting topology was not stable and evolved towards the “native” one.
1). As better detailed in the ESI (Fig. S8†), in each of this artificial systems the starting topology was not stable and evolved towards the “native” one.
As detailed in the ESI,† the NP reshaping upon aggregation can be quantified by its asphericity in the final aggregate. When NPs are isolated, the NP–water interface is roughly a sphere, and the average asphericity is 0 for any ligand composition. When NPs aggregate, instead, their shell is deformed, and the asphericity increases. In Fig. 5d, we report the NP asphericity β obtained in each system from the final aggregate of 27 NPs and measured as an average over each NP and trajectory. The asphericity β, proportional to the maximum deformation a NP can afford, increases significantly with the OT fraction. All MUS NPs have a relatively low asphericity in the final aggregate since they are only deformed on one side. MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 2
OT 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs are deformed on two sides, assuming a disc-like structure, and MUS
1 NPs are deformed on two sides, assuming a disc-like structure, and MUS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OT 1
OT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NPs are typically deformed on 3 or 4 sides, assuming a semi-disc shape.
1 NPs are typically deformed on 3 or 4 sides, assuming a semi-disc shape.
Eventually we remark that the anisotropic structures observed in this computational study are coherent with experimental observations in similar systems.40,61 In a past work,61 different aggregate topologies (characterized by a different coordination numbers) have been experimentally obtained and interpreted in terms of ligand migration and rearrangement on the surface of the gold nanoparticles. However, the evolution of the shell morphology at room temperature, in absence of exchange reactions with ligands in solution, has been later reported to be very slow.62 Here we have shown that both the limited coordination number and the directionality of the interactions can originate from the soft NP shell reshaping due to aggregation, without any need for ligand migration.
Conclusions
In conclusion, we have shown that directionality and complex topologies, with a primary and secondary structure architecture, can arise from the aggregation of NPs with a soft isotropic ligand shell. Hydrophobic bond saturation dictates the primary structure (dumbbells, chains, or ribbons) of the aggregates, while ion-bridged reversible contacts are responsible for their secondary structure. It is worth noting that, in the revealed mechanism, the soft shell deformation is reversible: if a NP detaches from an aggregate, it returns to its isotropic condition. Moreover, controlling the topology of the final aggregate can be achieved at the synthesis stage. Increasing the hydrophobic ligand fraction, NPs shift from the dumbbell regime to the linear and, finally, planar, ribbon-like regime. The choice of different hydrophobic ligands, characterized by different length, steric interactions, or specific affinities, as well as the choice of the sign and pKa of the charged ligand, could be optimized to control the thermodynamic stability, or thermo-reversibility, of the aggregates. Moreover, both salt concentration in solution, specific ion affinity and selectivity may be exploited to further control the aggregates’ secondary structure, achieving a dynamic control on the NPs’ self-assembly behavior.This physical principle is general, as it could apply to any colloidal system in which dimerization reshapes the soft colloid interface, breaking the spherical symmetry of their interaction potential, and thus could be exploited in several self-assembled systems involving moldable monomers.
Author contributions
Enrico Lavagna: investigation, methodology, software, writing – first draft. Sebastian Salassi: investigation. Davide Bochicchio: methodology, supervision, writing – review & editing. Giulia Rossi: conceptualization, methodology, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
GR acknowledges funding from the H2020 ERC Starting Grant BioMNP – 677513. GR, EL and DB acknowledge funding by MIUR – DIFI Dipartimento di Eccellenza 2018-2022 for computational resources. The authors thank Riccardo Ferrando for a critical reading of the manuscript, and Francesco Stellacci, Stefano Vanni, and Emanuele Petretto for many useful discussions and insights.References
- M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas and R. Langer, Nat. Rev. Drug Discovery, 2020, 20, 101–124 CrossRef PubMed
.
- A. Selmani, D. Kovačević and K. Bohinc, Adv. Colloid Interface Sci., 2022, 303, 102640 CrossRef CAS PubMed
.
- J. E. Ortiz-Castillo, R. C. Gallo-Villanueva, M. J. Madou and V. H. Perez-Gonzalez, Coord. Chem. Rev., 2020, 425, 213489 CrossRef CAS
.
- A. Verma and F. Stellacci, Small, 2010, 6, 12–21 CrossRef CAS PubMed
.
- L. Yildirimer, N. T. K. Thanh, M. Loizidou and A. M. Seifalian, Nano Today, 2011, 6, 585–607 CrossRef CAS PubMed
.
- J. H. Ryu, S. Lee, S. Son, S. H. Kim, J. F. Leary, K. Choi and I. C. Kwon, J. Controlled Release, 2014, 190, 477–484 CrossRef CAS PubMed
.
- G. McHale and M. I. Newton, Soft Matter, 2011, 7, 5473–5481 RSC
.
- S. Dasgupta, T. Auth and G. Gompper, J. Phys.: Condens. Matter, 2017, 29, 373003 CrossRef CAS PubMed
.
- B. Fadeel and A. E. Garcia-Bennett, Adv. Drug Delivery Rev., 2010, 62, 362–374 CrossRef CAS PubMed
.
- C. J. Murphy, A. M. Vartanian, F. M. Geiger, R. J. Hamers, J. Pedersen, Q. Cui, C. L. Haynes, E. E. Carlson, R. Hernandez, R. D. Klaper, G. Orr and Z. Rosenzweig, ACS Cent. Sci., 2015, 1, 117–123 CrossRef CAS PubMed
.
- D. v. Talapin and J. Steckel, MRS Bull., 2013, 38, 685–691 CrossRef CAS
.
- M. Turner, V. B. Golovko, O. P. H. Vaughan, P. Abdulkin, A. Berenguer-Murcia, M. S. Tikhov, B. F. G. Johnson and R. M. Lambert, Nature, 2008, 454, 981–983 CrossRef CAS PubMed
.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed
.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS PubMed
.
- M. Niederberger, Adv. Funct. Mater., 2017, 27, 1703647 CrossRef
.
-
S. Jungblut and A. Eychmüller, in Chemical Modelling, Royal Society of Chemistry, 2020, vol. 15, pp. 1–27 Search PubMed
.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed
.
- Z. Li, Q. Fan and Y. Yin, Chem. Rev., 2022, 122, 4976–5067 CrossRef CAS PubMed
.
- N. R. Anderson, J. Davidson, D. R. Louie, D. Serantes and K. L. Livesey, Nanomaterials, 2021, 11, 2870 CrossRef CAS PubMed
.
- A. Y. Sinyagin, A. Belov, Z. Tang and N. A. Kotov, J. Phys. Chem. B, 2006, 110, 7500–7507 CrossRef CAS PubMed
.
- Z. Tang, N. A. Kotov and M. Giersig, Science, 2002, 297, 237–240 CrossRef CAS PubMed
.
- B. W. Kwaadgras, R. van Roij and M. Dijkstra, J. Chem. Phys., 2014, 140, 154901 CrossRef
.
- W. Xu, Z. Li, Y. Yin, W. Xu, Z. Li and Y. Yin, Small, 2018, 14, 1801083 CrossRef PubMed
.
- Y. Zhou, R. L. Marson, G. van Anders, J. Zhu, G. Ma, P. Ercius, K. Sun, B. Yeom, S. C. Glotzer and N. A. Kotov, ACS Nano, 2016, 10, 3248–3256 CrossRef CAS PubMed
.
- X. Ye, J. Chen, M. Engel, J. A. Millan, W. Li, L. Qi, G. Xing, J. E. Collins, C. R. Kagan, J. Li, S. C. Glotzer and C. B. Murray, Nat. Chem., 2013, 5, 466–473 CrossRef CAS PubMed
.
- L. Cademartiri, K. J. M. Bishop, P. W. Snyder and G. A. Ozin, Philos. Trans. R. Soc., A, 2012, 370, 2824–2847 CrossRef CAS PubMed
.
-
J. Israelachvili, Intermolecular and Surface Forces, 2011 Search PubMed
.
- A. Walther and A. H. E. Müller, Chem. Rev., 2013, 113, 5194–5261 CrossRef CAS PubMed
.
- F. Sciortino, C. de Michele and J. F. Douglas, J. Phys.: Condens. Matter, 2008, 20, 155101 CrossRef
.
- J. C. Wang, P. Neogi and D. Forciniti, J. Chem. Phys., 2006, 125, 194717 CrossRef PubMed
.
- L. Cheng and D. Cao, J. Chem. Phys., 2011, 135, 124703 CrossRef PubMed
.
- E. Pellizzoni, M. Şologan, M. Daka, P. Pengo, D. Marson, Z. Posel, S. Franchi, L. Bignardi, P. Franchi, M. Lucarini, P. Posocco and L. Pasquato, J. Colloid Interface Sci., 2022, 607, 1373–1381 CrossRef CAS PubMed
.
- C. Gabellini, M. Şologan, E. Pellizzoni, D. Marson, M. Daka, P. Franchi, L. Bignardi, S. Franchi, Z. Posel, A. Baraldi, P. Pengo, M. Lucarini, L. Pasquato and P. Posocco, ACS Nano, 2022, 16, 20902–20914 CrossRef CAS PubMed
.
- O. Uzun, Y. Hu, A. Verma, S. Chen, A. Centrone and F. Stellacci, Chem. Commun., 2008, 196–198 RSC
.
- H. Zhang and D. Wang, Angew. Chem., Int. Ed., 2008, 47, 3984–3987 CrossRef CAS PubMed
.
- D. A. Walker, C. E. Wilmer, B. Kowalczyk, K. J. M. Bishop and B. A. Grzybowski, Nano Lett., 2010, 10, 2275–2280 CrossRef CAS PubMed
.
- M. E. Leunissen, C. G. Christova, A. P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Nature, 2005, 437, 235–240 CrossRef CAS PubMed
.
- J. Kolny, A. Kornowski and H. Weller, Nano Lett., 2002, 2, 361–364 CrossRef CAS
.
- E. Lavagna, D. Bochicchio, A. L. De Marco, Z. P. Güven, F. Stellacci and G. Rossi, Nanoscale, 2022, 14, 6912–6921 RSC
.
- E. Petretto, Q. K. Ong, F. Olgiati, T. Mao, P. Campomanes, F. Stellacci and S. Vanni, Nanoscale, 2022, 14, 15181–15192 RSC
.
- M. A. Boles, M. Engel and D. v Talapin, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS PubMed
.
- V. Montes-García and P. Samorì, Chem. Sci., 2022, 13, 315–328 RSC
.
- F. Li, W. C. Yoo, M. B. Beernink and A. Stein, J. Am. Chem. Soc., 2009, 131, 18548–18555 CrossRef CAS PubMed
.
- W. Ren, S. Wen, S. A. Tawfik, Q. P. Su, G. Lin, L. A. Ju, M. J. Ford, H. Ghodke, A. M. van Oijen and D. Jin, Chem. Sci., 2018, 9, 4352–4358 RSC
.
- B. Bozorgui, D. Meng, S. K. Kumar, C. Chakravarty and A. Cacciuto, Nano Lett., 2013, 13, 2732–2737 CrossRef CAS PubMed
.
- M. Asai, A. Cacciuto and S. K. Kumar, Soft Matter, 2015, 11, 793–797 RSC
.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos, V. Pryamitsyn, V. Ganesan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed
.
- J. A. Luiken and P. G. Bolhuis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012303 CrossRef PubMed
.
- M. Garzoni, N. Cheval, A. Fahmi, A. Danani and G. M. Pavan, J. Am. Chem. Soc., 2012, 134, 3349–3357 CrossRef CAS PubMed
.
- A. Verma, O. Uzun, Y. Hu, Y. Hu, H. S. Han, N. Watson, S. Chen, D. J. Irvine and F. Stellacci, Nat. Mater., 2008, 7, 588–595 CrossRef CAS PubMed
.
- P. U. Atukorale, Z. P. Guven, A. Bekdemir, R. P. Carney, R. C. van Lehn, D. S. Yun, P. H. Jacob Silva, D. Demurtas, Y. S. Yang, A. Alexander-Katz, F. Stellacci and D. J. Irvine, Bioconjugate Chem., 2018, 29, 1131–1140 CrossRef CAS PubMed
.
- R. P. Carney, T. M. Carney, M. Mueller and F. Stellacci, Biointerphases, 2012, 7, 17 CrossRef CAS PubMed
.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed
.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC
.
- F. Simonelli, G. Rossi and L. Monticelli, J. Phys. Chem. B, 2019, 123, 1764–1769 CrossRef CAS PubMed
.
- F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. Lett., 2015, 6, 3175–3179 CrossRef CAS
.
- A. Torchi, F. Simonelli, R. Ferrando and G. Rossi, ACS Nano, 2017, 11, 12553–12561 CrossRef CAS PubMed
.
- S. Salassi, F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. C, 2017, 121, 10927–10935 CrossRef CAS
.
- S. Salassi, E. Canepa, R. Ferrando and G. Rossi, RSC Adv., 2019, 9, 13992–13997 RSC
.
- T. Kamada and S. Kawai, Inf. Process. Lett., 1989, 31, 7–15 CrossRef
.
- H. Y. Lee, S. H. R. Shin, A. M. Drews, A. M. Chirsan, S. A. Lewis and K. J. M. Bishop, ACS Nano, 2014, 8, 9979–9987 CrossRef CAS PubMed
.
- Z. Luo, J. Hou, L. Menin, Q. K. Ong and F. Stellacci, Angew. Chem., Int. Ed., 2017, 56, 13521–13525 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr02384b |
| This journal is © The Royal Society of Chemistry 2023 |