A nickel-catalysed radical mechanism by three-component dimensionality reduction strategies: a theoretical study

Abstract

Three-component coupling reactions represent a potent approach for synthesizing complex products. Radical-initiated three-component coupling reactions hold significant promise in synthetic chemistry but are often challenged by the high reactivity of radical species and the complex coordination environment of transition metal catalysts. Herein, we employed density functional theory (DFT) and ab initio molecular dynamics (AIMD) simulations to investigate the mechanism of three-component olefin difunctionalization. Our study reveals that the dimensionality reduction in multi-component coupling reactions is fundamentally governed by a metal-free radical–radical cycle mechanism. A concentration-driven coordination mode shift modulates the reactivity of the Ni(0) centre, thereby enabling the multi-component reaction to proceed with high selectivity. Pauli repulsion plays a decisive role in determining enantiomeric isomerism in the radical capture step during two-component cross-coupling. This work provides a theoretical comprehension for the rational design of efficient radical-mediated multi-component coupling reactions.

---

1 Introduction

The incorporation of diverse functional groups and intricate spatial configurations into compounds not only augments their novelty but also substantially amplifies their application value in a wide range of fields, such as pharmaceuticals and materials science.^1,2 In this context, a multi-component reaction (MCR), which involves the in situ synthesis of three or more compounds and effectively constructs rich molecular skeletons, holds great research significance.^3,4 The MCR offers the advantage of functionalization or the construction of different chemical bonds^5,6 and chiral centres^7,8 within a single reaction vessel. This not only heightens the coupling efficiency but also complies with the principles of green synthetic chemistry.^9–11 As depicted in Scheme 1I, a three-component coupling product A–C–B could potentially be achieved via a single transition metal (TM) catalysis in the presence of multiple substrates (A, B or C). However, this approach for constructing complex molecules presents formidable challenges. Generally, when molecules possess multiple reactive sites, controlling the substrate selectivity is an extremely arduous task.^12,13 It encompasses not only the anticipated three-component coupling but also competitive two-component cross-coupling (A–C, B–C…) and (or) homo-coupling (A–A, B–B…).^14,15 Additionally, stereo-chemical complexity demands precise control over reactions to attain the desired 3D orientations, which is often a difficult feat. Moreover, the stability of functional groups can be compromised during multi-step syntheses, with some groups degrading under specific conditions, leading to unwanted reactions.

Scheme 1 Typical patterns (I), common strategies in three-component coupling (II), and the focus in this work (III).

To more effectively surmount these challenges, numerous research groups have devised efficacious design strategies in recent years.¹⁶ Since various competitive pathways result in different coupling products, pre-designing substrates or ligands to direct the reaction is undeniably an effective approach, as illustrated in Scheme 1IIa. A typical example is a nickel-catalysed syn-selective 1,2-carbosulfenylation reaction of simple unactivated alkenes reported by Engle and colleagues.¹⁷ A significant breakthrough entailed the identification of N-sulfenyl-N-alkyl sulfonamides as N–S electrophiles. This discovery exploits the tunable characteristics of the sulfonamide leaving group to control reactions both spatially and electronically, thereby enhancing selectivity and augmenting yields in three-component coupling reactions. Yin and co-workers demonstrated that nickel-catalysed regio-selective silylalkylation of alkenes could be steered towards different coupling products through strategic ligand design.¹⁸ Although remarkable progress has been made, the multi-component couplings achieved via the pre-design of substrates or ligands frequently necessitate harsh reaction conditions.^19,20

In recent years, radical-mediated reactions have emerged as a research focus due to their capacity to perform complex transformations under mild conditions, broad functional group compatibility, and potential for innovation.^21–23 Their congruence with green chemistry principles and the ascendancy of photoredox catalysis have further stoked interest, rendering them central to modern organic chemistry.^24–27 Consequently, such radical-mediated reactions have become prominent subjects in multi-component coupling reactions, especially their potential to enhance multi-component activation through a radical relay mechanism.^28–31 Specifically, as shown in Scheme 1IIb, a highly reactive radical (C·) selectively reacts with one of the substrates (A) to generate a new radical species (A–C·). Then, the species A–C· can further react with another substrate B (such as radical capture, oxidative addition, or reductive elimination) to generate A–C–B. Here, the A–C· is not a stable intermediate, but a free radical transfer node that guides the reaction sequence rather than reduces the substrate dimension. For instance, Jiang and co-workers utilized inorganic bases to regulate radical activity, guiding the reaction and producing diverse three component intermediates.³² Importantly, by simplifying the reaction to two components through photo-induced radical relays, the problem of uncontrollable selectivity among multiple substrates is mitigated. This method is also efficacious in five-component systems,³³ where Chen and colleagues developed a high-yield, high-selectivity five-component reaction driven by visible light.³ Evidently, the coupling of multiple substrates and the selective initiation of radicals are of paramount importance for the efficient execution of such reactions. On one hand, it is essential to precisely control the selectivity of the three-component target products and comprehensively understand the competitive mechanism of by-products in order to effectively circumvent them.

On the other hand, although highly reactive radicals can potentially reduce the complexity of the reaction system through radical relay processes, they also introduce significant mechanistic challenges, due to the transient and elusive nature of radical intermediates. Overall, the methods for minimizing unnecessary side reactions while effectively generating free radicals and streamlining the reaction scale remain elusive. This underscores the necessity of achieving better control over radical reactivity. The dearth of detailed knowledge significantly impedes the precision of multi-component reactions, restricting their broader applications and future development. A profound understanding of the underlying reaction mechanisms is crucial for propelling this field forward. Owing to the limitations of experimental conditions and equipment, experimentally revealing the mechanism is highly costly and challenging. Therefore, a comprehensive and detailed theoretical exploration of such a radical-mediated multi-component reaction mechanism is urgently required.

Recently, Chu and co-workers reported a highly enantioselective three-component reaction involving allyl ester, perfluoroalkyl iodide (C₄F₉I) and aryl bromide (ArBr) catalysed by L*Ni^IICl₂ (L* = (R,R)-4 heptyl-BiO_X) in the presence of manganese powder. This method efficiently produces 1,2-fluoroalkylarylation products with excellent ee values, which inspired our work (Scheme 1III and Scheme S1†).³⁴ Interestingly, a two-component intermediate alkyl iodide was identified during the reaction, as shown in Scheme 1III. However, the precise pathway leading to its formation remains unclear, posing a key mechanistic question. As the reaction progresses, changes in substrate and intermediate concentrations trigger a shift in the nickel catalyst's coordination mode from 1 to 2, enabling the final three-component coupling. The new coordination mode will result in different reactivity of the metal centre. Unlike classical radical relay mechanisms, this process involves a dimensionality reduction from three-component to two-component coupling, the origin of which remains to be elucidated.

This offers an outstanding platform to explore potential dimensionality reduction mechanisms and the origins of selectivity for multi-component coupling. Based on our previous work, the presence of heterogeneous manganese metal powder in the system may partially activate high-valent nickel species. This leads to another open question: how does the manganese powder modulate the valence state of inert high-valent nickel, and what are the particulars of the charge transfer process involved? Moreover, how is the two-component intermediate generated, and are there catalytic mechanisms involved that differ from those previously proposed?

Herein, to address the aforementioned open questions, density functional theory (DFT) combined with ab initio molecular dynamics (AIMD) has been utilized to investigate the mechanisms of three-component alkene difunctionalization facilitated by both homogeneous catalysis and heterogeneous reduction. This study would enhance our comprehension of the complex selectivity inherent in radical-mediated multi-component coupling, thereby contributing to the progress of chemical synthesis methods.

2 Calculation methods

Understanding the active valence states of transition metals is essential for unraveling catalytic mechanisms. However, the inherently variable oxidation states of transition metals—especially under heterogeneous reduction conditions—pose significant challenges to mechanistic interpretation. Recognizing the limitations of traditional DFT or AIMD when used independently, this study integrates both into a unified framework to better capture the complexity of valence state evolution at heterogeneous interfaces. This dual approach is critical for simultaneously capturing the dynamic behavior of the catalytic system and providing detailed electronic structure insights at key mechanistic steps. AIMD enables the exploration of real-time fluctuations and interactions at the metal interface, while QM offers high-resolution snapshots of the electronic and structural features that govern reactivity. The complementary strengths of AIMD and QM make this strategy particularly well-suited for investigating the Ni-catalysed transformation facilitated by heterogeneous Mn powder. A detailed description of this integrated computational methodology is presented in Scheme 2.

Scheme 2 The computational strategy of a nickel-catalysed radical mechanism by three-component dimensionality reduction.

2.1 Quantum chemistry calculations

2.1.1 Homogeneous catalytic process by L*Ni^IICl₂. All the calculations pertaining to the homogeneous catalytic process by L*Ni^IICl₂ were executed using the Gaussian 16 C01 program.³⁵ Geometry optimizations were carried out in the gas phase, employing the exchange–correction (U)M06 functional³⁶ in conjunction with the all-electron basis def2SVP.³⁷ The vibrational frequency was computed at the identical computational level to acquire the Gibbs energy under ambient pressure and temperature (P = 1 bar, T = 298.15 K). Moreover, each transition state possesses only one imaginary frequency, and the intermediates were guaranteed to be minimum energy points devoid of imaginary frequency. Intrinsic reaction coordinates (IRC)³⁸ ascertain that the transition state could precisely connect a corresponding reactant and a product. Single-point energy calculations were conducted using a more refined basis set, def2TZVP, to ensure the accuracy of the energy with a high degree of precision. The solvent effect of 1,2-dimethoxyethane (DME) was taken into account by utilizing the SMD solvation model.³⁹ The steric map was obtained via the SambVca 2.1 web application.⁴⁰ Energy decomposition analysis was performed using the XEDA program.⁴¹ The Multiwfn program was employed to analyse orbital interactions between fragments. IBO analysis was carried out using the IboView program.^42,43 The optimized structure was three-dimensionally rendered using the CYLview 2.0 program.⁴⁴

2.1.2 The reductive process of L*Ni^IICl₂ by Mn and Zn dust. Spin-polarized DFT calculations were conducted using the Vienna Ab initio Simulation Package (VASP) software^45,46 at the generalized gradient approximation (GGA) level. The models of Mn with a (4 × 3 × 1) super-cell and a perfect (110) surface, and Zn with a (2 × 3 × 1) super-cell and a perfect (100) surface, presented by a two-layer slab, were applied for the spin-polarized DFT calculation (Fig. S2†). To preclude the inter-layer interaction, a vacuum space of 15 Å was established along the z direction. The Perdew–Burke–Ernzerhof (PBE) functional⁴⁷ was utilized in these calculations. Plane wave basis sets were employed for valence electrons with an energy cutoff of 400 eV, and projector-augmented-wave (PAW) pseudopotentials⁴⁸ were used for the core electrons. A 3 × 3 × 1 Monkhorst–Pack k-point grid was employed to integrate the Brillouin region of the structure. The convergence criterion for electron iteration was set at 10⁻⁴ eV. The atomic structure was optimized until the force was below 0.1 eV Å⁻¹.

2.2 Ab initio molecular dynamics simulation

The AIMD simulations were performed at the PBE theory level, making use of the QUICKSTEP module of the CP2K software package.⁴⁹ Dispersion interactions were accounted for by employing the Grimme's ‘D3’ dispersion correction,⁵⁰ and DZVP-MOLOPT-SR-GTH was chosen as the basis set with a plane-wave cutoff of 300 Ry. A 6 × 5 × 1 Mn (110) surface slab consisting of four layers was utilized as the heterogeneous reduction interface (Fig. S3†). The constrained MD simulations were applied to restrain the bottom two layers of the Mn (110) slab. The total simulation time was 1.2 ps with a time step of 2 fs under the NPT ensemble, and the pressure could be independently controlled in different directions. The CSVR thermostat⁵¹ was employed to maintain the temperature at 298.15 K.

3 Results and discussion

3.1 Generation of the active catalyst facilitated by manganese powder

To commence, the configurations of the initial Ni(II) catalyst complex, including its coordination modes and spin multiplicities, are scrutinized. The complex (DME)Ni^IICl₂ is determined to possess a stable triplet state (IC-1^T, Fig. S1I†), where the superscripts S, D, and T denote singlet, doublet, and triplet states, respectively. Moreover, taking into account the existence of the L* ligand (L* = (R,R)-4-heptyl-BiOX), the coordination exchange with the DME ligand in IC-1^T is probed. This process is ascertained to be exothermic, liberating 11.8 kcal mol⁻¹ and yielding a new Ni(II) species, L*Ni^IICl₂ (IC-2^T, Fig. S1I†I). Additionally, the singlet state of L*Ni^IICl₂ (IC-2, Fig. S1III†) is found to be less stable than the triplet state by 12.2 kcal mol⁻¹. Thus, IC-2^T is likely to serve as the initial catalyst and participate in the subsequent heterogeneous reduction, considering the reducing potency of manganese powder and the flexible oxidation state of the inert divalent nickel species.^52,53 As illustrated in Fig. 1I, the reduction of the IC-2^T complex on the Mn(110) surface to form monovalent nickel, L*Ni^ICl, is an exothermic process with an energy release of 39.7 kcal mol⁻¹. A subsequent single-electron reduction of L*Ni^ICl on the Mn(110) surface leads to the formation of a zero-valent nickel complex L*Ni⁰, accompanied by an additional energy release of 22.7 kcal mol⁻¹. It is also worthy of note that the two-step single-electron reduction process involves the migration of chloride ions and their delocalization across the heterogeneous manganese surface. Consequently, the Ni(0) complex is thermodynamically the most favourable product.

Fig. 1 Thermodynamic evaluation (I), potential energy landscape of heterogeneous reduction of Ni^IICl₂ by the Mn(110) surface (II), and charge density difference between two phases during the reduction process (III) (isovalue = 0.002 e Bohr⁻³).

Nevertheless, the intricate details of the dynamic reduction and electron transfer processes on heterogeneous surfaces remain elusive. In this regard, AIMD simulations present a promising avenue for precisely reproducing the dynamic reduction phenomena of L*Ni^IICl₂ by Mn(110). Given the computational cost of AIMD, we initially utilize the xtb method to conduct MD simulations (Fig. S4†). Subsequently, one structure among them is selected as the starting point (A in Fig. 1II) for AIMD. Therefore, the stable conformation can be more expeditiously searched for via the semi-empirical approach, while the accuracy can be enhanced to simulate the reduction process. Based on the AIMD results, as depicted in Fig. 1II, at a specific time scale, several local minima of the potential energy are chosen as snapshots (B–E) to represent the dynamic evolution process from L*Ni^IICl₂ to L*Ni⁰, corresponding to the red dots on the curve.

The potential energy outcomes suggest that the reduction process from L*Ni^IICl₂ to L*Ni⁰ is exothermic, attaining dynamic stability after approximately 800 fs. Hence, it can be concluded that the reduction of L*Ni^IICl₂ to L*Ni⁰ by Mn(110) is thermodynamically feasible. The temperature evolution during AIMD simulations for the reduction model is also portrayed in Fig. S5,† revealing that as the reduction advances, the temperature varies dynamically before gradually stabilizing.

The charge density difference across all snapshot structures in Fig. 1II, where the blue isosurface signifies electron depletion and the yellow isosurface represents electron accumulation, is depicted in Fig. 1III. The transition from the blue isosurface on the manganese surface to the yellow isosurface on the nickel complex distinctly indicates electron transfer from the manganese surface to the metal centre, driving the reduction process. This electron transfer becomes increasingly conspicuous as the catalyst approaches, visually demonstrating the charge transfer from manganese powder to the Ni^IICl₂ complex.

In summary, these discoveries corroborate that the Ni^IICl₂ complex is reduced by manganese powder, giving rise to the formation of the Ni(0) complex, which is regarded as the active catalyst implicated in the subsequent catalytic cycles.

3.2 Initiation of the radical C₄F₉·

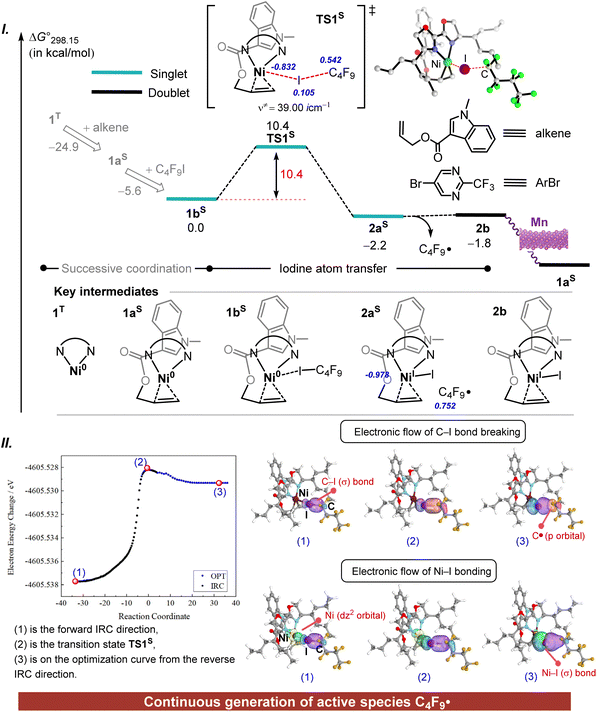
The exposed Ni(0) centre will initially encounter different coordination modes from multiple substrates (including C₄F₉I, ArBr, and alkene). Hence, a further concern is to identify the coordination state of the Ni(0) catalyst. Fig. S6† presents the thermodynamic assessment of the multiple coordination modes of the Ni(0) complex, where various spin multiplicities with distinct structures are taken into account. The bare Ni(0) complex is most stable in its triplet state (1^T); however, upon substrate coordination, the singlet-state complex becomes thermodynamically preferred. Notably, although both the alkene and ArBr coordinate through double bonds, the alkene exhibits significantly greater stabilization. This preferential coordination can impact the selectivity of subsequent reaction pathways. To understand the factors contributing to the differences in stabilization between the two substrates, an energy decomposition analysis of complexes 1a^S and 1c^S is carried out using the XEDA program (Fig. S7†). The results disclose that, in addition to occupying a coordination site with its carbon–carbon double bond, the alkene's heterocyclic moiety engages in π–π interactions, which remarkably enhance the stability of complex 1a^S compared to that of the aryl bromide complex 1c^S. Thus, the design of this bulky heterocyclic alkene substrate is particularly ingenious as it promotes selective substrate coordination. Furthermore, the Ni(0) complex 1a^S can coordinate with C₄F₉I to form the saturated complex 1b^S. The singlet-state complex 1b^S is stable at 13.3 kcal mol⁻¹ relative to the triplet-state 1b^T, with the entire coordination process releasing an energy of 30.5 kcal mol⁻¹.

Subsequently, the Ni(0) intermediate 1b^S may undergo various competitive processes in the presence of C₄F₉I or ArBr. Firstly, the C–I bond activation of C₄F₉I is considered. As illustrated in Fig. 2I, compared with the stable complex 1b^S, the transition state TS1^S with a Gibbs activation energy barrier (ΔG°^‡) value of 10.4 kcal mol⁻¹ and a Gibbs free energy (ΔG°) value of −2.2 kcal mol⁻¹ leads to the formation of the open-shell 2a^S, which includes a Ni(I)–I complex and a perfluoride alkyl radical (C₄F₉·). In TS1^S, the spin density is mainly concentrated on the Ni, I, and C atomic centres. The C and I atoms have spin density values of 0.542 and 0.105, respectively, while the Ni centre shows a density of −0.832. These opposing spin orientations suggest that this step proceeds via an open-shell singlet transition state. Thus, the C–I bond activation is regarded as an iodine atom transfer process. The above understanding is supported by intrinsic bond orbital (IBO) analysis.^40,41 Two points (1 and 2) are selected on the intrinsic reaction coordinates of TS1^S and shown in Fig. 2II. An additional point (3) was selected from the curve obtained by further optimization of the IRC path to ensure comprehensive sampling. The IBOs clearly demonstrate that the head-to-head p–p hybrid orbitals of the C–I bond shift towards the carbon and iodine atoms, respectively, as the reaction progresses. Meanwhile, the dz² orbital of the nickel centre gradually approaches the p orbital of the iodine atom, leading to the hybridization of atomic orbitals. Consequently, the diagram on the left illustrates the electron flow involved in the breaking of the C–I bond, resulting in the formation of a carbon radical and the Ni–I bond. In other words, the activation of the C–I bond occurs through carbon–iodine bond homolysis.

Fig. 2 Gibbs energy profile (in kcal mol⁻¹) of radical initiation by the Ni⁰ catalyst (I). IBO analysis of the open-shell singlet process in iodine atom transfer (II). Blue bold italic text represents spin density values, and red numbers indicate Gibbs activation energies for the corresponding steps.

The Ni(I) species 2b, formed in the process, can be reduced to the Ni(0) species using manganese powder, with an associated exothermic energy release of 109.7 kcal mol⁻¹ (Fig. S8†). Additionally, the Gibbs energy profile for iodine atom transfer, based on the triplet state of Ni(0), has been considered, showing a ΔG°^‡ value of 11.4 kcal mol⁻¹ (Fig. S9†). It is worth noting that the activation of C–I and C–Br bonds in C₄F₉I and ArBr through two-electron oxidative addition requires Gibbs activation energies of 20.3 and 39.5 kcal mol⁻¹, respectively (Fig. S10†). The larger ΔG°^‡ value for the C–Br bond indicates that the C–I bond in C₄F₉I is more favourable for activation via iodine atom transfer.

3.3 Metal-free radical–radical cycle in multi-component dimensional reduction

Subsequently, the C₄F₉· radical encounters a high concentration of alkene in the homogeneous environment (Fig. S11†). A low-barrier polymerization process between C₄F₉· and the alkene proceeds, leading to the two-component coupling radical intermediate C2 with the values of ΔG°^‡ and ΔG° being 5.8 and −23.7 kcal mol⁻¹, respectively.

In the presence of C₄F₉I, alkene, and complex 1b^S, the highly reactive C2 radical can undergo several competing mechanisms, including radical relay, radical capture and radical conversion. Radical relay is the addition of the C2 radical to alkene. The values of ΔG°^‡ and the overall ΔG° are 11.7 kcal mol⁻¹ and −38.1 kcal mol⁻¹, respectively, to generate the C5 radical (C2 → TS6 → C5). Additionally, complex 1b^S captures radical C2, and proceeds through the transition state TS7 by forming intermediate 7b, which is the most thermodynamically stable at −40.8 kcal mol⁻¹. However, the ΔG°^‡ for this capture by 1b^S is 13.6 kcal mol⁻¹, significantly higher than that of transition state TS5. This is essential for preserving the catalyst's high activity, see Fig. S12 and 13 and detailed discussions below them in the ESI.†

Among these, a particularly noteworthy pathway is the radical conversion viaTS5, in which C2 reacts with C₄F₉I to regenerate the C₄F₉· radical while forming the coupled intermediate C4, with a moderate ΔG°^‡ value of 8.3 kcal mol⁻¹. Therefore, compared to the termination of the C2 radical by C₄F₉I, this polymerization by alkene and the radical termination by 1b^S are more kinetically disadvantageous. In general, in this critical step, the 1 : 1 participation of C₄F₉I and alkene in a rapid reaction is achieved, and a large number of two-component coupling intermediates C4 are obtained. This transformation serves as a key dimensionality-reduction step in the multi-component reaction: by converging two substrates (alkene and C₄F₉I) into a single intermediate C4. In a word, an efficient radical–radical cycle mechanism that sustains the propagation of reactive species has been established (see the inset in Fig. 3).

Fig. 3 Gibbs energy profile (in kcal mol⁻¹) of polymerization and termination of radicals to form a two-component coupled intermediate C4. Red numbers indicate Gibbs activation energies for the corresponding steps, and the fluorescent yellow line marks the most favorable pathway.

3.4 Ligand-directed selective activation by the Ni(0) catalyst

Different from the original high concentrations of alkene and C₄F₉I in the homogeneous environment, with the advancement of the reaction process, the new concentration conditions will inevitably guide the coordination environment that determines the transition metal, which we call the “concentration-oriented new coordination mode” in the multi-component dimensionality reduction system. As depicted in Fig. 4 left, the radical–radical cycle leads to the continuous accumulation of the two-component coupling product C4, as well as the consumption of C₄F₉I and alkene. Therefore, the coordination mode of the Ni(0) catalyst undergoes a concentration-oriented transition from 1b^S to the complex 1e^S, coordinated with C4 and ArBr. This shift in the coordination environment alters the subsequent reactivity of the nickel centre, switching from radical initiation to a distinct reaction pathway.

Fig. 4 Gibbs energy profile (in kcal mol⁻¹) of the metal-free radical–radical cycle in multi-component dimensional reduction. The fluorescent yellow line marks the most favourable pathway.

Commencing from 1e^S, C4 undergoes iodine atom transfer via the transition state TS8^S, leading to the formation of Ni^I–I and a carbon-centred radical 8^S, with a ΔG°^‡ value of 12.7 kcal mol⁻¹ (Fig. 4, right-hand side). Alternatively, ArBr can undergo oxidative addition to 1d^S through TS2^S, resulting in a tetrahedral aryl bromide Ni(II) complex 3^T. This pathway has ΔG°^‡ and ΔG° values of 7.1 and −32.3 kcal mol⁻¹, respectively. These results suggest that the C–Br bond in ArBr is preferentially activated over the C–I bond in C4. Fig. S14† further presents the Gibbs energy profile for the triplet state, which also favours C–Br bond activation.

The resulting Ni(II) species 3^T can then be reduced by manganese powder to yield the aryl nickel(I) complex 4, with a favourable ΔG° value of −48.5 kcal mol⁻¹ (Fig. S15I†). Notably, zinc powder fails to achieve this reduction effectively, as the reduction of 3^T by zinc is endothermic (Fig. S15II†), consistent with experimental observations where reactions using zinc powder proceed with difficulty. This underlines the essential role of manganese powder as a potent reducing agent. Importantly, maintaining a concentration balance is crucial in designing successful multi-component coupling experiments.

3.5 Ni-catalysed enantioselective two-component cross-coupling

Upon generation of the Ni(I)–Ar intermediate 4, it coordinates with C4 to form intermediate 4a, as illustrated in Fig. 5. Subsequently, the two-component coupling intermediate C4 can be further activated via two possible pathways: C–I concerted oxidative addition or outer-sphere activation through single-electron transfer (SET) followed by radical capture. The former pathway proceeds via transition state TS9-1 (grey line) with a remarkably high energy barrier of 28.4 kcal mol⁻¹, rendering it less favourable. In contrast, the latter pathway occurs through the transition state TS9, where iodine transfer from carbon to nickel proceeds with a much lower ΔG°^‡ value of 14.8 kcal mol⁻¹. A spin-polarized doublet transition state, TS9^U, is also considered but excluded due to its considerably lower stability compared to TS9.

Fig. 5 Gibbs energy profile (in kcal mol⁻¹) of the generation of enantiomeric three-component coupling products. Blue bold italic text represents spin density values, red numbers indicate Gibbs activation energies for the corresponding steps, and the fluorescent yellow line marks the most favorable pathway.

This transformation yields an ArNi(II)I complex and a carbon-centred radical (9), each possessing distinct geometries, planar for the nickel complex and tetrahedral for the radical, which lead to different modes of radical attack in the subsequent capture step (Fig. S16†). This step allows for two possible orientations of radical attack, resulting in the formation of chiral centres and producing either the R or S configuration at the carbon atom.

A detailed mechanistic analysis focuses on the R-conformation, where the transition state ^RTS10 facilitates radical capture on the nickel plane, with a ΔG°‡ value of 18.5 kcal mol⁻¹, leading to the formation of the trivalent nickel intermediate ^R10a. Following an isomerization from ^R10a to ^R10, the intermediate ^R10 proceeds through a three-membered Ni–C–C transition state (^RTS11), ultimately generating the target product ^RPro with a ΔG°^‡ value of 5.6 kcal mol⁻¹ and an overall ΔG° value of −55.3 kcal mol⁻¹. Notably, the radical capture step introduces a chiral center, identified as the key step in the formation of enantiomeric isomers.

To investigate this further, an alternative chiral pathway is considered, proceeding through the transition state ^STS10 to form the S-configured chiral centre. This pathway has a small energy barrier difference (ΔΔG°^‡) of 2.7 kcal mol⁻¹ compared to ^RTS10, causing the reaction to preferentially progress along the R-conformation due to kinetic favourability.

Finally, the Ni^I–I complex is rapidly reduced back to Ni(0) (1^T) by manganese powder, thereby completing the catalytic cycle. This analysis highlights the radical capture step as the rate-determining and enantioselectivity-determining steps in the overall process, emphasizing the crucial role of geometric and energetic factors in achieving enantioselective product formation.

3.6 Exploration of the origin of enantioselectivity

To further clarify the origin of enantioselectivity, activation strain-distortion/interaction analyses^54,55 relative to intermediate 5 are carried out for the transition states ^RTS10 and ^STS10 during the radical capture step (Table S1†). The 3D geometries of these transition states are presented in detail in Fig. 6, left panel. The deformation energies of the metal component (ΔE_dist-1) are 8.14 and 8.31 kcal mol⁻¹, while those of the radical component (ΔE_dist-2) are 7.47 and 7.34 kcal mol⁻¹, respectively. Thus, the deformation of the metal and radical components in ^RTS10 and ^STS10 does not vary significantly. Conversely, the interaction energies (ΔE_int) between the transition metal and the radical are −17.19 and −14.04 kcal mol⁻¹, with the interaction energy difference (ΔΔE_int) between the R and S configurations calculated as −3.15 kcal mol⁻¹ in Fig. 6, suggesting that interaction energy plays a dominant role in enantioselectivity. Firstly, buried volume analysis is also conducted to investigate the steric environment around the transition states ^RTS10 and ^STS10, exploring whether steric hindrance affects the kinetic differences contributing to enantioselectivity (Fig. S17†). Considering a 4.0 Å radius around the nickel centre, the %V buried values for both conformations are found to be almost identical, indicating minimal steric hindrance differences.

Fig. 6 The origin of enantioselectivity. Relative activation energies are given in kcal mol⁻¹.

Then, the energy decomposition analysis offers additional understanding of the interaction energies between the metal and radical fragments in the two enantiomers (Fig. S18†). As shown in the right panel of Fig. 6, Pauli repulsion energy between the fragments emerges as the main factor, with a ΔΔE_rep of −8.8 kcal mol⁻¹ favouring ^RTS10. Additionally, the degree of orbital overlap (|δ_(R−S)|) in occupied orbitals was calculated to evaluate enantioselectivity influenced by Pauli repulsion, revealing a significant difference of 1.56%. Notably, while the radical's orbitals exhibited minimal change, the orbital distribution within the nickel complex fragments was dominant, especially through strong orbital repulsion between the p orbitals of the carbon atoms in the radicals and both the π orbitals of the Ar-substituents and the occupied orbitals on the nickel ligand. This repulsion disfavours the S-configuration, contributing to the preference for the R-configuration.

Finally, the mechanism of the entire catalytic cycle is depicted in Fig. S19.† The precise coupling of multiple components occurs through the sequential progression of three catalytic cycles, leading to highly enantioselective products.

4 Conclusions

This study systematically elucidates the mechanism of radical-mediated multi-component functionalization, identifying the metal valence modulation and the core strategy for dimensionality reduction in multi-component reactions. A combination of DFT and AIMD simulations was employed to investigate the critical interfacial effects in heterogeneous reduction processes, revealing the mechanism by which L*Ni^IICl₂ is effectively reduced to the Ni(0) complex through interaction with the Mn(110) surface. We elucidate that the dimensionality reduction in multi-component coupling reactions is fundamentally governed by a metal-free radical–radical cycle mechanism. In this process, the C₄F₉· radical undergoes a relay with the alkene to form a secondary radical (C2), which then engages in a metal-free radical–radical cycle mechanism, ultimately generating the two-component C-I intermediate (C4), achieving the dimensionality reduction. Subsequently, the coordination mode of the Ni(0) catalyst undergoes a concentration-driven transition from complex 1b^S to 1e^S. This shift in the coordination environment fundamentally alters the reactivity of the nickel centre, enabling selective activation in the final coupling step. The subsequent cross-coupling forms the desired enantiomeric product, wherein Pauli repulsion plays a decisive role in determining the preferred isomer. These theoretical insights would be expected to deepen the understanding and advance the development of radical-mediated three-component alkene difunctionalization by cooperative homogeneous catalysis and heterogeneous reduction.

Data availability

The data underlying this study are available in the published article and its ESI.†

Author contributions

Lin-Yan Bao and Rong-Wan Gao have contributed equally to this work, and are responsible for the original draft, conceptualization, investigation, visualization, formal analysis, data curation, and validation. Zhong-Min Su, Bo Zhu and Wei Guan are jointly responsible for writing – review & editing, conceptualization, supervision, funding acquisition, resources, and project management.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the research Project of Jilin Provincial Department of Education (JJKH20241415KJ) and National Natural Science Foundation of China (22173016, 22203014 and 22271023).

References

1. B. C. Lee, C.-F. Liu, L. Q. H. Lin, K. Z. Yap, N. Song, C. H. M. Ko, P. H. Chan and M. J. Koh, Chem. Soc. Rev., 2023, 52, 2946–2991.
2. S. Bhadra and H. Yamamoto, Chem. Rev., 2018, 118, 3391–3446.
3. Y. Hayashi, Chem. Sci., 2016, 7, 866–880.
4. H. Y. Cho and J. P. Morken, Chem. Soc. Rev., 2014, 43, 4368–4380.
5. S. N. Gockel, S. Lee, B. L. Gay and K. L. Hull, ACS Catal., 2021, 11, 5166–5171.
6. Y. Ping, K. Wang, Q. Pan, Z. Ding, Z. Zhou, Y. Guo and W. Kong, ACS Catal., 2019, 9, 7335–7342.
7. J. A. Boerth, S. Maity, S. K. Williams, B. Q. Mercado and J. A. Ellman, Nat. Catal., 2018, 1, 673–679.
8. L.-F. Fan, R. Liu, X.-Y. Ruan, P.-S. Wang and L.-Z. Gong, Nat. Synth., 2022, 1, 946–955.
9. L. P. Zorba and G. C. Vougioukalakis, Coord. Chem. Rev., 2021, 429, 213603.
10. N. R. Agrawal, S. P. Bahekar, P. B. Sarode, S. S. Zade and H. S. Chandak, RSC Adv., 2015, 5, 47053–47059.
11. J. Montgomery, Acc. Chem. Res., 2000, 33, 467–473.
12. C. Sambiagio, D. Schönbauer, R. Blieck, T. Dao-Huy, G. Pototschnig, P. Schaaf, T. Wiesinger, M. F. Zia, J. Wencel-Delord, T. Besset, B. U. W. Maes and M. Schnürch, Chem. Soc. Rev., 2018, 47, 6603–6743.
13. S. H. Cho, S. J. Hwang and S. Chang, J. Am. Chem. Soc., 2008, 130, 9254–9256.
14. W. Wang, C. Ding, Y. Li, Z. Li, Y. Li, L. Peng and G. Yin, Angew. Chem., Int. Ed., 2019, 58, 4612–4616.
15. B. M. Trost, M. T. Sorum, C. Chan and G. Rühter, J. Am. Chem. Soc., 1997, 119, 698–708.
16. D. M. D'Souza and T. J. J. Müller, Chem. Soc. Rev., 2007, 36, 1095–1108.
17. Z.-Q. Li, Y. Cao, T. Kang and K. M. Engle, J. Am. Chem. Soc., 2022, 144, 7189–7197.
18. C. Ding, Y. Ren, Y. Yu and G. Yin, Nat. Commun., 2023, 14, 1–9.
19. B. M. Trost, Chem. Rev., 1996, 96, 395–422.
20. E. Negishi, Acc. Chem. Res., 1982, 15, 340–348.
21. H. Bonin, M. Sauthier and F. X. Felpin, Adv. Synth. Catal., 2014, 356, 645–671.
22. S. Murarka, Adv. Synth. Catal., 2018, 360, 1735–1753.
23. X.-Y. Yu, J.-R. Chen and W.-J. Xiao, Chem. Rev., 2021, 121, 506–561.
24. D. A. Nicewicz and D. W. C. MacMillan, Science, 2008, 322, 77–80.
25. G. A. Molander and C. R. Harris, Chem. Rev., 1996, 96, 307–338.
26. G. A. Coppola, S. Pillitteri, E. V. Van der Eycken, S.-L. You and U. K. Sharma, Chem. Soc. Rev., 2022, 51, 2313–2382.
27. C. Hervieu, M. S. Kirillova, T. Suárez, M. Müller, E. Merino and C. Nevado, Nat. Chem., 2021, 13, 327–334.
28. L. Lei, M. C. Aguilera, W. Lee, C. R. Youshaw, M. L. Neidig and O. Gutierrez, Science, 2021, 374, 432–439.
29. Y.-L. Su, G.-X. Liu, L. De Angelis, R. He, A. Al-Sayyed, K. S. Schanze, W.-H. Hu, H. Qiu and M. P. Doyle, ACS Catal., 2022, 12, 1357–1363.
30. C. Ma, J. Shen, C. Qu, T. Shao, S. Cao, Y. Yin, X. Zhao and Z. Jiang, J. Am. Chem. Soc., 2023, 145, 20141–20148.
31. M. E. Greaves, T. O. Ronson, G. C. Lloyd-Jones, F. Maseras, S. Sproules and D. J. Nelson, ACS Catal., 2020, 10, 10717–10725.
32. B. Li, H.-H. Zhang, Y. Luo, S. Yu, W. A. Goddard III and Y. Dang, J. Am. Chem. Soc., 2024, 146, 6377–6387.
33. B. Lu, Z. Zhang, M. Jiang, D. Liang, Z.-W. He, F.-S. Bao, W.-J. Xiao and J.-R. Chen, Angew. Chem., Int. Ed., 2023, 62, e202309460.
34. H.-Y. Tu, F. Wang, L. Huo, Y. Li, S. Zhu, X. Zhao, H. Li, F.-L. Qing and L. Chu, J. Am. Chem. Soc., 2020, 142, 9604–9611.
35. G. W. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision C.01), Gaussian Inc., Wallingford CT, 2016.
36. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
37. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
38. K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163.
39. C. J. C. Aleksandr, V and D. G. Marenich, J. Phys. Chem. B, 2009, 113, 6378–6396.
40. X. Luan, R. Mariz, M. Gatti, C. Costabile, A. Poater and L. Cavallo, J. Am. Chem. Soc., 2008, 130, 6848–6858.
41. Z. Tang, Y. Song, S. Zhang, W. Wang, Y. Xu, D. Wu, W. Wu and P. Su, J. Comput. Chem., 2021, 42, 2341–2351.
42. G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518–5522.
43. G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843.
44. C. Y. Legault, CYLview, 2.0b, Université de Sherbrooke, 2020, http://www.cylview.org.
45. G. Kresse and J. Furthmuller, Phys. Rev. B, 1996, 54, 11169–11186.
46. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. B, 1996, 77, 3865–3868.
48. M. Marsman and G. Kresse, J. Chem. Phys., 2006, 125, 104101.
49. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
50. S. Grimme, W. Hujo and B. Kirchner, Phys. Chem. Chem. Phys., 2012, 14, 4875–4883.
51. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
52. C.-F. Meng, B.-B. Zhang, Q. Liu, K.-Q. Chen, Z.-X. Wang and X.-Y. Chen, J. Am. Chem. Soc., 2024, 146, 7210–7215.
53. C. X. Zhan, D. Dong, J. Chang, S. Zhou, P. Sun, Y. Li and L.-A. Chen, ACS Catal., 2024, 14, 4369–5480.
54. Y. Xu and Y. Dang, J. Org. Chem., 2023, 88, 6126–6131.
55. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647.

---

Footnotes

† Electronic supplementary information (ESI) available: Calculation models, competition mechanism, geometric configurations, and coordinates of all intermediates and transition states. See DOI: https://doi.org/10.1039/d5sc03563e

‡ These authors contributed equally to this work.

---