Insights for controlling plutonium behavior in hydrochloric acid solutions

Abstract

Advancing understanding of aqueous chemistry for plutonium is important because it impacts energy production, environmental management, and national security. Unfortunately, plutonium's aqueous chemistry remains poorly characterized. We addressed this problem by characterizing Pu(IV) redox and coordination chemistry in aqueous solutions as a function of hydrochloric acid concentration using X-ray absorption spectroscopy, ultraviolet-visible near-infrared spectroscopy, and electrochemistry. The impact of Pu–Cl vs. Pu–O_H2O bonding was correlated with the stability of different plutonium oxidation states. We discovered that anionic Cl¹⁻ ligands stabilized electron-deficient Pu(IV) over Pu(III) and neutral H₂O ligands stabilized Pu(III) over Pu(IV). These findings offer a way to control plutonium electron transfer chemistry and imply that selective stabilization of Pu(IV) or Pu(III) may be achieved through tuning the electron donating ability of the ligand. Overall, this work advances predictive capabilities for aqueous plutonium chemistry, particularly within nuclear application spaces.

---

Introduction

Controlling the aqueous chemistry of plutonium (Pu) is critical for solving technical problems that are important for energy production, environmental management, and national security. On the energy front, there are aqueous processing challenges facing the advancement of nuclear power for clean energy production.^1,2 In terms of the environment, the aqueous chemistry of plutonium impacts safely storing nuclear waste,³ reprocessing of spent nuclear fuel,^2,3 and remediating sites contaminated by historic activities at nuclear facilities.⁴ For national security, large-scale aqueous processing and small-scale aqueous radioanalytical separations of plutonium are important for two main reasons: firstly, to ensure the safety, security, and effectiveness of nuclear weapon stockpiles,^5,6 and secondly to provide a technical basis for mounting calculated responses to domestic and international nuclear emergencies.⁷ These needs have inspired researchers to study aqueous plutonium chemistry and substantial advances have been made since the discovery of plutonium in the 1940s.^8–13 Unfortunately, many fundamental aspects associated with plutonium chemistry in aqueous matrixes are still poorly defined. This lack of understanding makes plutonium's aqueous chemistry seem unruly, especially in comparison to transition metals,^14–17 lanthanides,^18–21 and other actinides (uranium^22–27 and thorium^26–28) that have been studied to a larger extent. Researchers, engineers, and technical staff working in the nuclear sector would be better suited to solve plutonium challenges if this knowledge gap was reduced, predictive capabilities were improved, and the ability to control plutonium reactivity in aqueous solutions was advanced.

One aqueous matrix ubiquitously used in the nuclear industry is hydrochloric acid, HCl_(aq). Surprisingly, many fundamental aspects about plutonium in this matrix are not well characterized. It is known that plutonium's coordination chemistry in HCl_(aq) is defined by the plutonium oxidation state. However, plutonium can adopt four different oxidation states in aqueous media at the same time: Pu(III), Pu(IV), Pu(V) and Pu(VI).^13,29 It is also unclear what chemical factors influence plutonium oxidation state stability within HCl_(aq) solutions. These attributes engender plutonium with diverse reaction chemistry in HCl_(aq) solutions that can be difficult to control and predict, e.g., disproportionation reactions, comproportionation reactions, hydrolysis, colloid formation, to name a few. As a result, there is dogma associated with HCl_(aq) solutions that contain plutonium. When things go awry, many variables get blamed blindly (such as temperature, the concentration of plutonium in solution, radiolysis, photolysis, etc.). Better correlating chemical attributes with plutonium electron transfer chemistry would provide clarity and enable avoidance of deleterious side reactions accessible to plutonium in HCl_(aq) solutions.

Motivated by the need to reduce the aforementioned knowledge gap, we set out to better define how Pu(IV) coordination chemistry and electron transfer reactivity varied in HCl_(aq) solutions as a function of one important chemical factor, ionic strength [H¹⁺_(aq) and Cl¹⁻_(aq) concentrations]. The complexity of this system was outlined in Scheme 1. The Pu⁴⁺_(aq) cation can undergo reduction to generate Pu³⁺_(aq). Oxidation and Pu–O bond formation reactions can also occur to generate PuO₂ⁿ⁺_(aq) (n = 1, 2). In HCl_(aq) solutions, plutonium can undergo complexation by neutral H₂O and anionic Cl¹⁻ ligands. There are also numerous coordination numbers and geometries accessible to Pu⁴⁺_(aq), Pu³⁺_(aq), and PuO₂ⁿ⁺_(aq) in HCl_(aq).^30,31 To provide insight on this topic, we turned to four complimentary analytical methods that are exceptionally suited for speciation studies in aqueous media, namely cyclic voltammetry, X-ray absorption near edge spectroscopy (XANES), extended X-ray absorption fine structure (EXAFS), and Ultraviolet–Visible-Near Infrared (UV-Vis-NIR) spectroscopy. This technique quartet enabled electron transfer reactions, metal oxidation states, ligand identities, coordination numbers, and bond distances accessible to plutonium in HCl_(aq) solutions to be rigorously defined.

Scheme 1 Overview of some reactions that impact plutonium speciation in HCl_(aq).

Our results suggested that Pu(IV)–aquo ions [Pu(H₂O)_x⁴⁺] dominated the speciation profile in dilute HCl_(aq) concentrations (≤3 M). The data also showed that plutonium speciation shifted to anionic chloride complexes (PuCl_y^4−y) when HCl_(aq) concentrations were high (>8 M). It was surprising to discover that conversion of the homoleptic Pu(H₂O)_x⁴⁺ aquo complex to the homoleptic PuCl_y^4−y chloride complex occurred rather abruptly and over a relatively small HCl_(aq) concentration range (∼4.5 to 8 M). Heteroleptic Pu(IV)-aquochloride complexes [PuCl_y(H₂O)_x^4−y] were the dominant species present in solution over this HCl_(aq) concentration regime. Evaluating the X-ray absorption speciation results alongside the electrochemical data provided additional insight regarding the Cl¹⁻ for H₂O ligand substitution reaction. This analysis suggested that the plutonium speciation profile shifted suddenly from being dominated by Cl¹⁻ to dominated by H₂O when the HCl_(aq) content crossed the 5.5 M concentration value. Changing the plutonium ligand environment from being homoleptic in Cl¹⁻ to homoleptic in H₂O also impacted the half-wave potential (E_½) for the reversible Pu(IV) + e¹⁻ ⇌ Pu(III) (Pu^4+/3+) one-electron transfer reaction. For example, the E_½ potential was 0.572(2) V for PuCl_y^4−y, 0.744(2) V for Pu(H₂O)_x⁴⁺, and at intermediate values for heteroleptic PuCl_y(H₂O)_x^4−y species. No additional redox events, e.g., oxidation to PuO₂ⁿ⁺_(aq) or reduction of Pu²⁺_(aq), were observed electrochemically over the surveyed potential window (ca. 0.4 to 1 V). We interpreted these data as suggesting that anionic Cl¹⁻ ligands stabilized more electron-deficient Pu⁴⁺_(aq) over Pu³⁺_(aq) and neutral H₂O ligands stabilized more electron-rich Pu³⁺_(aq) over Pu⁴⁺_(aq). The data indicated that Pu⁴⁺_(aq) was a reasonably strong oxidant and able to generate Pu³⁺_(aq) in solutions over the sampled HCl_(aq) concentration range. It also highlighted Pu⁴⁺_(aq) stability toward losing electrons and generating PuO₂ⁿ⁺_(aq). These observations have general implications on plutonium behavior within aqueous solutions and may help explain unexpected plutonium fractionation that occurs during industrial-scale processing (e.g., using solvent extraction or ion exchange chromatography), while conducting small-scale radioanalytical separations, and in regard to the fate and transport of plutonium through the environment.

Results and discussion

Sample preparation

A series of aqueous solutions were prepared to study how the plutonium speciation varied as a function of HCl_(aq) concentration. Toward this end, we first prepared a chemically pure and oxidation state pure stock solution of Pu⁴⁺_(aq) in HCl_(aq) (5.5 or 6 M). Aliquots from this stock solution were gently heated on a hot block until the solution evaporated. The resulting residues were subsequently dissolved in aqueous solutions whose HCl_(aq) content systematically varied. For X-ray absorption (XANES and EXAFS) and UV-Vis-NIR measurements the HCl_(aq) concentrations were 1, 3, 5.5, 8, and 11 M. For electrochemical measurements the HCl_(aq) concentrations were 1, 3, 4.5, 6, 8, and 11 M. The HCl content in the commercially available source of HCl_(aq) used to make the more dilute HCl_(aq) samples varied from batch-to-batch and ranged 10.8 to 11.1 M. Hence, we estimated the HCl content in the concentrated HCl_(aq) solutions as being 11 M and used this value to calculate the HCl_(aq) content in all subsequently made serial dilutions. No attempt was made to rigorously characterize the HCl_(aq) content in the solutions for our experiments because the HCl_(aq) concentration variations were small in comparison to the experimentally observed plutonium speciation changes.

Pu L₃-edge X-ray absorption near edge spectroscopy (XANES)

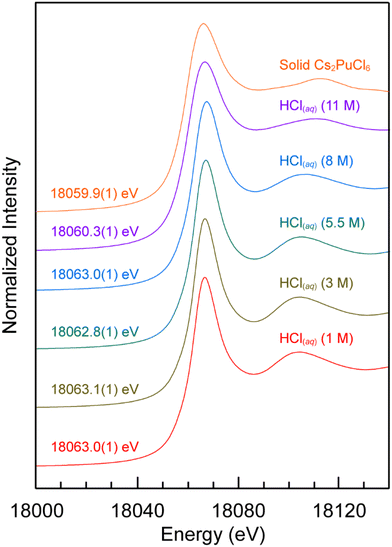
The dependence of Pu(IV) oxidation state stability on HCl_(aq) concentration (1, 3, 5.5, 8, 11 M) in aqueous solutions was evaluated using Pu L₃-edge XANES. Background subtracted and normalized Pu L₃-edge XANES data from Pu⁴⁺_(aq) (∼0.02 M) dissolved in aqueous solutions were compared in Fig. 1 as a function of HCl_(aq) concentration. The spectra were dominated by an absorption peak that was superimposed on a step-like absorption threshold. This main absorption peak is often attributed to the electric dipole allowed 2p → 6d transition,^32–35 and the inflection point for the rising absorption edge (near 18 063 eV) is routinely correlated with formal plutonium oxidation state values.³³ Inflection point energies were determined graphically as the point at which the second derivative of these data equaled zero and these data were used to characterize the oxidation state of plutonium in these samples (Fig. 1). Those energy values ranged from 18 060.3 to 18 063.1 eV (calibrated to the Zr K-edge from zirconium metal; 17 998 eV) with an estimated uncertainty of ±0.1 eV (at 1σ), based on our ability to reproduce XANES spectra on other actinide samples. The inflection energy values were consistent with those determined for other Pu(IV) samples that had Cl¹⁻ and/or H₂O ligands. For example, the plutonium inflection point energy in dilute HCl_(aq) (1 M) was 18 063.0(1) eV and similar to that reported previously for the plutonium aquo ion (18 063.2 eV).³² Increasing the HCl_(aq) concentration to 8 M had essentially no detectable impact on the inflection point energies and the resulting values were equivalent within the estimated uncertainty of our measurement. Pushing the HCl_(aq) content even higher, to 11 M, caused the inflection point energy to drop by ca. 3 eV. This 18 060.3(1) eV value was slightly higher than the inflection point energy from our Pu(IV) standard Cs₂PuCl₆ [18 059.9(1) eV] and slightly lower than that reported previously for Pu⁴⁺_(aq) dissolved in 10.8 M HCl (18 061.7 eV).³³ Hence, we concluded that the dominant plutonium species present in all of these plutonium samples had an oxidation state of +4. Overall, these data indicated that Pu⁴⁺_(aq) was stable in concentrated and dilute HCl_(aq) solutions under conditions associated with shipping the samples to the synchrotron and making the X-ray absorption measurements.

Fig. 1 Room temperature, background-subtracted, and normalized Pu L₃-edge XANES spectra from Pu⁴⁺_(aq) in HCl_(aq) solutions (1–11 M from top to bottom). The orange trace is the low temperature (77 K) background-subtracted and normalized Pu L₃-edge XANES spectrum from the solid Pu(IV) standard (Cs₂PuCl₆).⁶⁰ Inflection point energies are included.

Pu Ultraviolet–Visible-near infrared spectroscopy (UV-Vis-NIR)

Conclusions regarding the dependence of plutonium oxidation states on HCl_(aq) concentrations derived from the Pu L₃-edge XANES data were validated by analogous UV-Vis-NIR measurements. Optical spectroscopy samples were prepared in the same way as the XANES samples. Spectra were measured at room temperature and collected every few days over the course of one week. This period was equivalent to the time required to package, ship (from LANL to SSRL), and analyze samples using Pu L₃-edge XANES. Because no change in the optical data was observed over the course of one week, we concluded that the plutonium oxidation states were stable in HCl_(aq) (1 to 11 M) solutions for the duration of the XANES experiments. This conclusion alleviated concerns of spontaneous redox events that could occur during the shipping process to the synchrotron, which was of concern. Representative spectra have been provided in Fig. 2 (see ESI† also).

Fig. 2 Room temperature UV-Vis-NIR spectra from Pu⁴⁺_(aq) after dissolution in HCl_(aq) solutions (1–11 M from bottom to top) collected immediately after sample preparation. Relevant peaks were labeled with their associated plutonium oxidation states.

The UV-Vis-NIR spectrum collected in dilute HCl_(aq) (1 M) was consistent with other spectra from Pu(IV) collected in dilute acid and reported previously.^36,37 Most notable were the intense cluster of peaks centered at 15 385 cm⁻¹ (650 nm) and the sharp absorbance peak at 21 277 cm⁻¹ (470 nm). Our interpretation of these data agreed with the aforementioned Pu L₃-edge XANES spectrum and we concluded that Pu(IV) was the major species present in solution. In addition to these Pu(IV) absorption peaks were small features at 12 048 cm⁻¹ (830 nm) and 16 639 cm⁻¹ (601 nm) that indicated PuO₂²⁺ and Pu(III) were also present in small quantities. Reproducing the sample preparation procedure repeatedly generated PuO₂²⁺_(aq) and Pu³⁺_(aq) in the dilute HCl_(aq) matrix. We estimated the amount of PuO₂²⁺ and Pu(III) to be at 5% and 10% of the total plutonium in the samples, respectively. Note, there was a high uncertainty associated with these estimates because the extinction coefficients (ε) used to quantify the relative plutonium concentrations were matrix mismatched, meaning that ε values were determined in HClO_4(aq) (2 M)⁸ and the measurements were made in HCl_(aq) (1 M). It was unclear what caused PuO₂²⁺_(aq) and Pu³⁺_(aq) to form in the dilute HCl_(aq) (1 M) solution. We speculated that the redox reaction occurred during sample preparation and assume that the combination of heating the parent Pu⁴⁺_(aq) stock solution to dryness for 12 hours, followed by dissolution in dilute HCl_(aq) (1 M), forced disproportionation of Pu⁴⁺_(aq) to make PuO₂²⁺_(aq) and Pu³⁺_(aq).

Increasing the HCl_(aq) concentration to be >1 M had marked impact on the plutonium spectra. Most importantly, features associated with PuO₂²⁺ and Pu(III) were not detected. We also observed evidence for Cl¹⁻ complexation of Pu(IV) when the HCl_(aq) was ≥5.5 M in three notable ways. The first change was that increasing the HCl_(aq) concentration beyond 3 M caused the cluster of peaks centered at 15 385 cm⁻¹ (650 nm) to spread out. Their intensities also changed, such that the low energy absorbance peaks gained intensity relative to the high energy peaks. The second notable change was that a shoulder emerged near 14 500 cm⁻¹ (670 nm); see the 5.5 M HCl_(aq) spectrum. This feature gained intensity and shifted bathochromically (red) with increasing HCl_(aq) content. The third notable observation was that the sharp peak at 21 277 cm⁻¹ (470 nm) decreased in intensity and was swallowed by a broad absorption feature. This absorption band commenced near 19 000 cm⁻¹ (526 nm) and gained intensity with increased HCl_(aq) concentration. Our observations align well with previously reported UV-Vis data in HCl_(aq) matrices.^37–40

Taken as a whole, the optical and XANES measurements complemented one another. Both characterization techniques confirmed Pu(IV) was the dominant species present in each sample. The UV-Vis-NIR experiments enabled identification of PuO₂ⁿ⁺_(aq) (n = 1, 2) and Pu³⁺_(aq) contaminants present in solution at quantities below the XANES detection limit (typically estimated at <10% of the total plutonium content in the sample). The Pu L₃-edge XANES studies enabled us to conclude that the UV-Vis-NIR spectra obtained in 5.5, 8, and 11 M were characteristic of Pu(IV) dissolved in these higher concentration HCl_(aq) solutions. It can be difficult to assign plutonium oxidation states based on UV-Vis-NIR data in concentrated HCl_(aq) solutions because Cl¹⁻ ligands bind Pu⁴⁺_(aq), displace neutral H₂O, and alter the UV-Vis-NIR spectra. In this regard, the optical data in Fig. 2 provide Pu⁴⁺_(aq) UV-Vis-NIR reference spectra paired with precise speciation profiles that can be used by those manipulating plutonium in HCl_(aq) solutions in the future. This X-ray absorption and UV-Vis-NIR spectroscopy combination is absent from the literature at this time, to the best of our knowledge.

Pu L₃-edge extended X-ray absorption fine structure (EXAFS) data

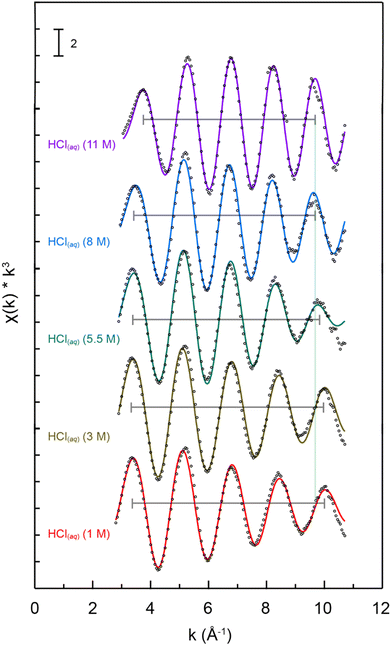
Changes in Pu⁴⁺_(aq) speciation in aqueous solution were evaluated as a function of HCl_(aq) concentration (1, 3, 5.5, 8, 11 M) using Pu L₃-edge EXAFS spectroscopy. These room temperature and solution phase k³-weighted Pu L₃-edge EXAFS spectra were compared in Fig. 3. The data were best described as having a single wave with five resolved crests that oscillated in intensity from 3 to 11 Å⁻¹. The amplitude for the wave observed in dilute HCl_(aq) (1 M) decreased in intensity with increasing energy. Increasing the HCl_(aq) concentration from 1 to 11 M did not impact the wave amplitudes, which remained qualitatively constant across the surveyed energy space. However, changing the HCl_(aq) concentration caused the wavelength to increase and frequency to become longer in Å⁻¹. We indicated this change in Fig. 3 using black brackets and a green vertical line.

Fig. 3 The k³-weighted room temperature Pu L₃-edge EXAFS spectra displaying the χ(k) function (points) with non-linear curve fitting (lines) from aqueous Pu⁴⁺_(aq) solutions in HCl_(aq) solutions (1–11 M). The gray bracket and the vertical green line were included to help visualize that the wavelength changed with changing HCl_(aq) concentration.

The impact of increasing the HCl_(aq) concentration (1 to 11 M) on the Pu L₃-edge EXAFS data was also evident in the Fourier transforms for the k³-weighted spectra (Fig. 4). In dilute HCl_(aq), there was a single symmetric feature just below 2 Å. Increasing the HCl_(aq) concentration to 5.5 M caused the feature to change: it broadened, became asymmetric, and its intensity decreased. In 11 M HCl_(aq), the feature gained intensity, sharpened, and became symmetric again. Crossing the entire series from 1 to 11 M shifted the peak maximum to longer distances and increased R + δ from ca. 1.9 Å in 1 M HCl_(aq) to 2.2 Å in 11 M HCl_(aq) (R is the scattering pathway distance and δ is the phase-shift).

Fig. 4 Fourier transforms of room temperature k³-EXAFS spectra for aqueous Pu⁴⁺_(aq) solutions in HCl_(aq) at varied concentrations (1 to 11 M; black circles). Fits for the data are shown as pink traces. The Pu → Cl and Pu → O scattering pathways used to generate the fits are shown as yellow and blue traces, respectively.

Qualitatively, we interpreted these data as follows. Plutonium speciation was dominated by homoleptic aquo tetracations, Pu(H₂O)_x⁴⁺, at low HCl_(aq) concentrations (e.g., 1 M). The resulting single shell of H₂O ligands manifested as a single scattering peak in the Fourier transform for the k³-weighted spectrum. Heteroleptic aquochloride species, PuCl_y(H₂O)_x^4−y, existed at intermediate HCl_(aq) concentrations (e.g., 5.5 M). Here, the plutonium primary coordination sphere contained H₂O ligands with short Pu–O_H2O distances and Cl¹⁻ ligands with longer Pu–Cl bond distances. The presence of these two coordination environments enabled two distinct scattering pathways (Pu → O_H2O and Pu → Cl) that manifested as a broad asymmetric feature in the Fourier transform for the k³-weighted spectra. Moving to concentrated HCl_(aq) (11 M) solutions increased the Cl¹⁻_(aq) content to the point that Cl¹⁻_(aq) outcompeted H₂O for Pu⁴⁺_(aq) complexation. Hence, under these conditions, homoleptic Cl¹⁻_(aq) coordination compounds of the general formula PuCl_y^4−y dominated the Pu⁴⁺_(aq) speciation profile. Having only Cl¹⁻_(aq) ligands in the primary coordination sphere manifested as a sharp single peak in the Fourier transform of the k³-weighted spectra that was reminiscent of the Pu(H₂O)_x⁴⁺ spectrum obtained at low HCl_(aq) concentrations (e.g., 1 M). The major difference between the spectra obtained from Pu(H₂O)_x⁴⁺ vs. PuCl_y^4−y was associated with the intensity (peak area) and R + δ value. The spectrum from PuCl_y^4−y had a smaller intensity and larger R + δ value. This difference suggested that (1) the overall coordination number for PuCl_y^4−y was smaller than that of Pu(H₂O)_x⁴⁺ – fewer Cl¹⁻ ligands bound to PuCl_y^4−y than H₂O ligands bound to Pu(H₂O)_x⁴⁺ – and (2) the bond distance between Pu(IV) and anionic Cl¹⁻ was longer than Pu(IV) bound to neutral H₂O.

A more quantitative evaluation of the Pu L₃-edge Fourier transforms of the k³-weighted spectra employed conventional shell-by-shell fitting methods.^41–43 Those models were consistent with the qualitative interpretation described above. The energy ranges over which usable data were obtained spanned from ca. 3 to 11 Å⁻¹, which limited the resolution in R-space to 0.2 Å (resolution = π/2Δk). Care was taken to constrain our models so that a reasonable number of variables were used, which protected against overparameterizing the fit (typically 75% of the maximum number of free variables allowed for the fitted region). Atomic coordinates from Pu(H₂O)₉³⁺ and PuCl₆²⁻ were used to calculate scattering pathways using FEFF8.^44–46

The dilute HCl_(aq) (1 M) data were fitted using a single scattering pathway associated with a shell of H₂O ligands bound by Pu(IV). The obtained model returned 9(1) H₂O ligands in the Pu(IV) inner coordination sphere at a Pu–O_H2O distance of 2.37(11) Å. The parameters associated with this fit converged to reasonable values with acceptable error bars (Table 1). The measured Pu–O bond distance was consistent with our interpretation of the Pu L₃-edge XANES data and suggested that the plutonium oxidation state was +4. For example, subtracting the 8-coordinate Pu(IV) ionic radius (0.96 Å)⁴⁷ from our Pu–O_H2O distance gave a value of 1.41 Å. This value was bracketed by the calculated (1.67 Å) and crystallographically measured H₂O ionic radii (1.38 Å).⁴⁸ The Pu–O_H2O distance was shorter than the 2.476(2) and 2.574(3) Å bond distances determined for trivalent Pu(H₂O)₉³⁺ aquo ion using single crystal X-ray diffraction, which was consistent with the 0.14 Å difference in Pu(IV) vs. Pu(III) ionic radii.⁴⁵ Including a Pu → Cl¹⁻ scattering pathway did not significantly improve our model; hence, it was not included in our final fit. Our coordination numbers – and interpretation that Pu(H₂O)_9±1⁴⁺ was the dominant species in solution – were in good agreement with other EXAFS analyses conducted in dilute HCl_(aq) solutions. For example, Conradson and coworkers used EXAFS to determine that in dilute HCl_(aq) (1.4 M) solutions Pu⁴⁺_(aq) had a small number of Cl¹⁻ ligands (0.9) and that the rest of the coordination sphere was occupied by H₂O ligands [Pu–O_H2O = 2.39 Å].³³

Table 1 Fitting parameters used to model Pu L₃-edge EXAFS spectra from variable HCl_(aq) concentration (1 to 11 M). Bond lengths are reported in angstroms (Å). Numbers that contain uncertainty values (indicated by parenthesis) were free variables in the fitted model and numbers that do not contain uncertainty values were fixed variables

	Pu HCl(aq) Solutions
	1 M HCl(aq)	3 M HCl(aq)	5.5 M HCl(aq)	8 M HCl(aq)	11 M HCl(aq)
O coordination number	9(1)	10(1)	6(1)	3(1)	—
σ^2 (O)	0.009(2)	0.007(2)	0.007	0.007	—
An–O	2.37(11)	2.37(10)	2.33(14)	2.30(18)	—
Cl coordination number	—	—	3(1)	5(1)	6(1)
σ^2 (Cl)	—	—	0.006	0.006	0.006(1)
An–Cl	—	—	2.598(6)	2.588(4)	2.594(3)
Pu coordination number	—	—	—	—	—
σ^2 (Pu)	—	—	—	—	—
S0^2	0.9	0.9	0.9	0.9	0.9
E°	0.21 ± 0.97	0.3 ± 1.0	−2.73	−3.5	2.9 ± 0.9
Total variables used	4	4	4	4	4
Independent variables available for the fitting range	7.97	7.42	7.72	8.04	8.81
Reduced χ^2	6049.24	5626.01	2418.60	2228.83	637.6129
R-Factor	0.012	0.0092	0.0072	0.011	0.010

---

Our data from 3 M HCl_(aq) solutions were also best modeled as having only H₂O ligands in the inner Pu(IV) coordination sphere. The fit showed 10(1) H₂O ligands with a Pu–O_H2O distance of 2.37(10) Å. Incorporating a Pu → Cl scattering pathway did not provide a suitable model. The H₂O coordination number and Pu–O_H2O bond distance were statistically equivalent to that observed in 1 M HCl_(aq) and discussed above. We interpreted these data as suggesting that the dominant Pu⁴⁺_(aq) species present in dilute HCl_(aq) (3 M) had an average stoichiometry of Pu(H₂O)_10±1⁴⁺ and that the Pu(IV) aquo ion persisted in solution when HCl_(aq) concentrations were between 1 and 3 M.

The Pu L₃-edge EXAFS data from concentrated HCl_(aq) (11 M) solutions were modeled using a Pu → Cl single scattering pathway. The obtained model returned 6(1) chlorides and a 2.594(3) Å Pu–Cl distance. Attempts to include a Pu → H₂O scattering pathway into the model failed to converge. This Pu–Cl distance matched the average bond distance determined for PuCl₆²⁻ using single crystal X-ray diffractometry (2.59 Å).⁴⁶ Both of these distances were slightly shorter than the sum (2.67 Å) of the Pu(IV) 6-coordinate (0.86 Å) and the Cl¹⁻ (1.81 Å) ionic radii. Our Pu–Cl distance in HCl_(aq) (11 M) was also in good agreement with other Pu–Cl bond distances determined in the solution phase by EXAFS, e.g., solution phase Pu–Cl distances of 2.63 Å and 2.61 Å have been reported previously.³³ Hence, we concluded the dominant Pu⁴⁺_(aq) species present in concentrated HCl_(aq) (11 M) had an average stoichiometry of PuCl_6±1^(2±1)−.

Fitting the Pu L₃-edge EXAFS from plutonium samples dissolved in intermediate concentrations of HCl_(aq) (5.5 and 8 M) suggested both Cl¹⁻ and H₂O ligands were bound to Pu(IV). Modeling data obtained from the 5.5 M HCl_(aq) solution showed Pu(IV) was complexed by 6(1) H₂O ligands [Pu–O_H2O = 2.33(14) Å] and 3(1) Cl¹⁻ ligands [Pu–Cl = 2.598(6) Å]. Increasing the HCl_(aq) concentration to 8 M decreased the H₂O coordination number and increased the Cl¹⁻ coordination number: 3(1) H₂O ligands [Pu–O_H2O = 2.30(18) Å] and 5(1) Cl¹⁻ ligands [Pu–Cl = 2.588(4) Å]. We interpreted these data as showing that the dominant species present in 5.5 M HCl_(aq) had an average chemical formula of PuCl_3±1(H₂O)_6±1^(1±1)+ and a charge that ranged from being neutral to dicationic, based on the uncertainty associated with the Cl¹⁻ coordination number. In 8 M HCl_(aq), the dominant species in solution had an average chemical formula of PuCl_5±1(H₂O)_3±1^(1±1)− and a charge that ranged from being neutral to anionic.

In summary, the Pu L₃-edge EXAFS experiments demonstrated that complexation of Pu⁴⁺_(aq) in aqueous solutions could be controlled by altering the HCl_(aq) concentration. The Pu⁴⁺_(aq) speciation was dominated by the Pu⁴⁺-aquo ion in dilute HCl_(aq) (between 1 and 3 M). Heteroleptic aquochloride species, PuCl_y(H₂O)_x^4−y, were detected at intermediate HCl_(aq) concentrations (between 4.5 and 8 M). Homoleptic Pu(IV)-chloride complexes, corresponding to PuCl_6±1^(2±1)−, were observed in concentrated HCl_(aq) solutions (11 M). All recorded XANES, UV-Vis-NIR, and EXAFS data were self-consistent with the reduction potentials and Cl¹⁻ coordination numbers determined using electrochemical methods (vide infra).

Aqueous cyclic voltammetry

Plutonium redox chemistry was investigated in aqueous media as a function of HCl_(aq) (1–11 M) concentration using cyclic voltammetry (Fig. 5). These studies provided additional insight and validation for the conclusions drawn from the X-ray absorption and UV-Vis-NIR measurements described above. In general, the cyclic voltammograms were similar across the sampled HCl_(aq) concentrations. They contained a reversible single wave that we attributed to the Pu^4+/3+_(aq) one-electron transfer reaction (eqn (1)).³⁰

Pu⁴⁺_(aq) + e¹⁻ ⇌ Pu³⁺_(aq) (1)

Fig. 5 Cyclic voltammograms from Pu(IV) (16.7 mM) dissolved in HCl_(aq) (1–11 M) at a scan rate of 0.01 V s⁻¹ for the Pu^4+/3+_(aq) redox reaction. Data from HCl_(aq) solutions at 1 to 11 M are represented by red, brown, green, orange, blue, and purple traces, respectively. The arrows represent the direction of the potential sweep. The dot with the dashed line indicates the half-wave potential (E_½), which are also provided and referenced to Ag/AgCl. Errors are the standard deviation from three replicates.

Closer inspection of the voltammograms obtained in HCl_(aq) revealed how peak current (i_p), anodic and cathodic peak separation (ΔE_p), and the half-wave potentials (E_½) varied as a function of scan rate and HCl_(aq) concentration. These variations, in turn, informed on how changing the HCl_(aq) concentration impacted plutonium speciation.

The influence of scan rate on peak currents (i_p) was depicted in Fig. 6. This figure showed that i_p varied with scan rate and ranged from ∼0.03 mA at a scan rate of 0.01 V s⁻¹ to 0.6 mA at a scan rate of 10 V s⁻¹. Current passed for the anodic wave (i_pa) was nearly equivalent in magnitude to that for the cathodic wave (i_pc) for a given HCl_(aq) concentration and scan rate, i.e., the ratio of i_pa/i_pc was near one (see ESI†). We interpreted these data as indicating reversibility of the anodic, Pu(III) → e¹⁻ + Pu(IV), and cathodic, Pu(IV) + e¹⁻ → Pu(III), electron transfer events. This suggested that the number of electrons associated with the Pu⁴⁺_(aq) reduction was equivalent to that of the Pu³⁺_(aq) oxidation under all examined experimental conditions and that the primary coordination environment for Pu(IV) was similar to Pu(III) on the electrochemical time scale in HCl_(aq).

Fig. 6 Peak current (i_p) from cyclic voltametric measurements made on plutonium (16.7 mM) in HCl_(aq) (1–11 M) solutions plotted as a function of scan rate (0.01–1 V s⁻¹). Error bars are the standard deviation from three replicates.

Electrochemical reversibility suggested that the Pu(III) coordination environment was equivalent to that of Pu(IV) on the cyclicvoltammographic timescale in all HCl_(aq) solutions tested. This observation was anticipated in dilute HCl_(aq) solutions, where Pu(IV)-aquo and Pu(III)-aquo ions were both expected to exist. Reversibility was unexpected – however – in more concentrated HCl_(aq) for the following reasons. Our Pu L₃-edge EXAFS data showed that homoleptic PuCl_y^4−y chlorides exist for Pu(IV) when HCl_(aq) concentrations were high. It is also well established that Pu³⁺_(aq) prefers binding H₂O over Cl¹⁻ in aqueous media when the Cl¹⁻_(aq) concentration are similarly high.³⁰ Hence, we expected electrochemical irreversibility for the Pu⁴⁺_(aq) to Pu³⁺_(aq) redox couple at high HCl_(aq) concentrations because of the anticipated H₂O for Cl¹⁻ ligand substitution reaction: e.g., Pu(III)-homoleptic chloride to Pu(III) heteroletpic aquochloride. Surprisingly, this was not observed. The ensuing electrochemical reversibility showed that the Cl¹⁻ for H₂O ligand exchange was slow on the cyclicvoltammographic timescale and that electrochemical methods can be effectively used to probe species that contain Pu(III)–Cl bonds in aqueous media, even the illusive Pu^IIICl₆³⁻ trianion.

The impact of scan rate on the anodic and cathodic peak separations (ΔE_p) was depicted in Fig. 7A. The plot showed ΔE_p was weakly dependent on the scan rate when the scan rate was relatively slow, ca. 0.06–0.08 V between 0.01 and 0.2 V s⁻¹. We interpreted this near-independence on scan rate as indicating that a reversible and diffusion-controlled electron transfer processes occurred on the time scale of the experiment, a designation that was consistent with convention⁴⁹ despite being slightly larger than the theoretical value for a reversible process: 0.057 V at 25 °C.⁵⁰ At higher scan rates (>0.2 V s⁻¹), more extreme potentials (increased ΔE_p values) were needed to drive the Pu^4+/3+_(aq) redox reactions. This result indicated that the redox process became kinetically controlled, meaning that electron transfer to plutonium was faster than diffusion of plutonium away from the electrode.

Fig. 7 (A) Cathodic and anodic peak separation potential (ΔE_p) and (B) half-wave potential (E_1/2) as a function of the scan rate from plutonium (16.7 mM) dissolved in HCl_(aq) (1–11 M) solutions. Error bars are the standard deviation from three replicates.

Fig. 7A also documented impact of scan rate on ΔE_p as a function of HCl_(aq) concentration. The anodic and cathodic peak separations were essentially independent of the HCl_(aq) content. For example, the ΔE_p values were equivalent within measurement uncertainty for each given HCl_(aq) concentration. However, we acknowledge that the ΔE_p uncertainty increased with the scan rate and the error bars were large (as high as ±0.067 V) at fast scan rates (>1 V s⁻¹).

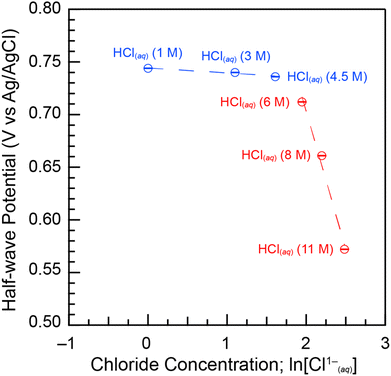
Fig. 5 showed that the half-wave potentials between the cathodic and anodic peaks (E_½) were positive, ranging from 0.57(1) V to 0.74(1) V as the HCl_(aq) concentration decreased from 11 to 1 M. The E_½ values were also independent of scan rate at each HCl_(aq) concentration (Fig. 7b). Utilizing the E_½ values in Fig. 5 as estimates for formal Pu^4+/3+_(aq) potential,⁵¹ we estimated Gibbs free energy values (ΔG_est) for the reversible Pu^4+/3+_(aq) electron transfer reaction as a function of HCl_(aq) concentration using Eq. 2. These calculations showed that decreasing the HCl_(aq) concentration from 11 to 1 M decreased the ΔG_est values from −55.2 to −71.8 kJ mol⁻¹, respectively. Uncertainty was estimated to be ±0.1 kJ mol⁻¹ at 1σ. We proposed that the major contributor for the E_½ dependence on HCl_(aq) was associated with a plutonium speciation change from Pu(H₂O)_x⁴⁺ to PuCl_y(H₂O)_x^4−y to PuCl_y^4−y that accompanied decreasing the Cl¹⁻ content in solution. These calculations also indicated that the Pu(H₂O)_x⁴⁺ aquo cation was more strongly oxidizing than the PuCl_y^4−y anion and that Cl¹⁻ complexation stabilized substantially the plutonium +4 oxidation state over the plutonium +3 oxidation state.

ΔG_est = −nFE_½ (2)

Variables: ΔG_est = estimate of Gibbs free energy; E_½ = halfway potential; n = number of electrons, one for Pu^4+/3+_(aq); F = Faraday's constant.

Using half-wave potential (E_½) to evaluate Pu⁴⁺_(aq) coordination number

Electrochemical methods were used to further evaluate how plutonium speciation varied as a function of HCl_(aq) concentration. These experiments validated the conclusions described above that were based on the Pu L₃-edge EXAFS studies. As an introduction to these experiments, we remind the reader that it is difficult to use EXAFS as a standalone technique for identifying speciation changes. This issue was rooted in the high uncertainties associated with the EXAFS coordination number measurements. A more robust understanding of chemical speciation changes can be obtained if interpretation of the EXAFS data is informed by a complimentary physical method. In this case, we selected electrochemical measurements for two reasons. First, cyclic voltammetry measurements are quite sensitive to chemical speciation changes. Second, it is well established that half-wave potentials (E_½) can be used to determine the number of ligands (in this case Cl¹⁻) bound to a redox active metal (in this case plutonium), provided that the measured electron transfer process and the metal–ligand complexation process are both reversible. As stated above, both conditions were met for plutonium dissolved in HCl_(aq) (eqn (1) and Scheme 1): the Pu^4+/3+_(aq) redox reaction was electrochemically reversible and plutonium underwent chemically reversible complexation reactions with Cl¹⁻ and H₂O ligands (Scheme 1).

The mathematical expression that relates the number of Cl¹⁻ ligands bound by plutonium to the E_½ for the Pu^4+/3+_(aq) redox reaction is shown in eqn (3).

Variables: E°′ = formal potential n = number of electrons, one for Pu^4+/3+_(aq); x = Cl¹⁻ coordination number [Cl¹⁻] = Cl¹⁻ bulk concentration, M; R = ideal gas constant; 8.314 J mol⁻¹ K⁻¹; K = equilibrium constant for the Pu(IV) and Cl¹⁻ complexation reaction; T = temperature, K; k_{c for Pu(III)} = mass transfer coefficient for Pu³⁺_(aq); F = Faraday constant; 96 485 C mol⁻¹; k_{c for Pu(IV)} = mass transfer coefficient for Pu⁴⁺_(aq).

The derivation of this equation is based on the Nernst equation, the steady-state mass transport equation, and the reaction equilibrium equation. For more details, we direct interested readers to the ESI† and the textbook “Electrochemical Methods: Fundamentals and Applications, second edition”, by Bard and Faulkner (pages 36–37 and 186–188) where this relationship was derived.⁵⁰ Included here is a high-level description that shows how to relate E_½ to coordination number within the context of Pu^4+/3+_(aq) redox reaction and Pu–Cl complexation reactions.

For this scenario, the Cl¹⁻ coordination number can be determined by plotting E_½ vs. the natural logarithm of the chloride concentration, ln[Cl¹⁻_(aq)]. The E_½ values should be linearly dependent on ln[Cl¹⁻_(aq)] and the slope of that relationship equal to x(RT/nF) when a single species is present as the Cl¹⁻_(aq) concentration changes (variables defined in eqn (2)). Fig. 8 showed two linear regimes when E_½ and ln[Cl¹⁻] were plotted accordingly. The first linear regime occurred at low HCl_(aq) concentrations. Here, E_½ was highest for the Pu^4+/3+_(aq) redox reaction in dilute HCl_(aq) (1 M) at 0.744(3) V. This value dropped slightly and monotonically to 0.736(1) V when the HCl_(aq) concentration was raised to 4.5 M, such that a near horizontal relationship existed between E_½ and ln[Cl¹⁻] as the HCl_(aq) concentration was increased from 1 to 4.5 M. The slight decrease in E_½ suggested that increasing the HCl_(aq) concentration to 4.5 M slightly increased the propensity of Cl¹⁻_(aq) to complex Pu⁴⁺_(aq); however, the speciation profile strongly favored Pu(H₂O)_x⁴⁺ over PuCl_y(H₂O)_x^4−y. Consistent with that notion, we calculated the average Cl¹⁻ coordination number for Pu⁴⁺_(aq) over this HCl_(aq) concentration range using eqn (4) (variables defined in eqn (3)). Slope analysis returned a value of −0.0046(9) V, which corresponded to an average Cl¹⁻ coordination number of 0.18(3). This result was consistent with the Pu L₃-edge X-ray absorption data (vide supra), which showed Cl¹⁻_(aq) was not bound by Pu(IV) in dilute HCl_(aq). Instead, the homoleptic Pu⁴⁺-aquo ion, Pu(H₂O)_x⁴⁺, existed when HCl_(aq) concentrations were ≤3(1).

Fig. 8 Half-wave potentials (E_1/2) from cyclic voltammetry measurements made on plutonium dissolved in HCl_(aq) (1–11 M) solutions plotted as a function of the natural log of the HCl_(aq) concentration. Error bars are the standard deviation of E_½ measured at eight scan rates from 0.01 to 10 V s⁻¹.

Linearity also occurred when HCl_(aq) concentrations were high (4.5 to 11 M). Here, E_½ dropped from 0.736(1) [4.5 M HCl_(aq)] to 0.572(3) [11 M HCl_(aq)]. Slope analysis of the concentrated HCl_(aq) regime returned a value of −0.19(3) V, which corresponded to an average Cl¹⁻ coordination number of 7(1) (eqn (3)) over the 4.5 to 11 M HCl_(aq) concentration range. This result was consistent with the Pu L₃-edge X-ray absorption data (vide supra), which showed Cl¹⁻ coordination numbers ≥5(1) when HCl_(aq) concentrations were high (≥8 M) and Cl¹⁻ coordination numbers ≤3(1) when HCl_(aq) concentrations decreased to ≤5.5 M. Other important information extracted from Fig. 8 was related to the domain over which heteroleptic PuCl_y(H₂O)_x^4−y complexes existed. The graph highlighted a clear and abrupt Pu⁴⁺_(aq) speciation change when the HCl_(aq) concentration was between 4.5 and 6 M.

Evaluating Pu⁴⁺_(aq) and Pu³⁺_(aq) diffusion coefficients and hydrodynamic radii via peak current (i_p)

The diffusion coefficients and hydrodynamic radii for Pu⁴⁺_(aq) and Pu³⁺_(aq) were determined from the cyclic voltammetry measurements. This was possible because the cyclic voltammetry mass transfer was purely diffusion-limited. Hence, the Randles–Ševčík equation (eqn (5)) could be readily employed to obtain the diffusion coefficient.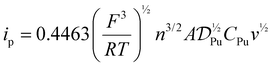Variables: i_p = peak potential; ; n = number of electrons, one for Pu^4+/3+_(aq); T = temperature, 25 K; A = Electrode surface area, cm²; C_Pu = bulk Pu concentration, M; R = ideal gas constant, 8.314 J mol⁻¹ K⁻¹; F = Faraday constant, 96 485 C mol⁻¹; v = scan rate, V s⁻¹.

In Fig. 6, the peak current (i_p) was plotted against the scan rate (v^½) for each HCl_(aq) concentration value. In all cases, there was a linear relationship between i_p and v^½ for both anodic Pu(III) → e¹⁻ + Pu(IV) and cathodic Pu(IV) + e¹⁻ → Pu(III) electron transfer events at scan rates < 1 V s⁻¹. Hence, diffusion coefficients for Pu⁴⁺_(aq) and Pu³⁺_(aq) could be extracted from the slope analyses in this regime using least squares fitting. The goodness of fit was assessed by the coefficient of determination, R², which ranged from 0.987 to 0.998 for plutonium in HCl_(aq) solutions (1–11 M) (see ESI†).

The diffusion coefficients were plotted as a function of HCl_(aq) concentration in Fig. 9A. All diffusion coefficients were similar in magnitude and subtly varied from 3.5(2) × 10⁻⁶ to 5.5(1) × 10⁻⁶ cm² s⁻¹. These values agreed well with estimates we calculated using the Nernst–Haskell equation (eqn (6)). We note that the values determined from eqn (5) should be taken as a rough estimation, as this equation is only valid for ion-pair analytes dissolved in infinitely dilute solutions.

Fig. 9 (A) Dependence of the diffusion coefficients of Pu⁴⁺_(aq) (blue) and Pu³⁺_(aq) (red), calculated by both the Randles–Ševčík and Nernst–Haskell equations, on the concentration of the HCl_(aq) (1–11 M) solution. (B) Dependence of the hydrodynamic radii of Pu⁴⁺_(aq) (blue) and Pu³⁺_(aq) (red), calculated from Stokes–Einstein equation and the group contribution method, on the concentration of the HCl_(aq) (1–11 M) solutions.

The mathematical expression in eqn (6) related the diffusion coefficient 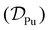for both Pu⁴⁺_(aq) and Pu³⁺_(aq) to the oxidation states of plutonium (m′ = +4 or +3) and chloride (m′′ = –1) and the limiting molar ionic conductivities of plutonium and chloride : such that and 66.6 S·cm² mol⁻¹ for Pu⁴⁺_(aq) and Pu³⁺_(aq), respectively⁵² and .⁴⁶ The R, T, and F variables were defined above in eqn (5). This expression enabled the Pu⁴⁺_(aq) and Pu³⁺_(aq) diffusion coefficients to be estimated based on oxidation state and limiting molar ionic conductivity.

As the HCl_(aq) concentration was increased from 1 to 11 M, plutonium species transitioned from Pu(H₂O)_xⁿ⁺ (n = 4 or 3), to PuCl_y(H₂O)_x^4−y, and PuCl_y^4−y. Accompanying this speciation change was a slight decrease in the plutonium diffusion coefficients, such that PuCl_y^4−y moved through the aqueous solution slower than Pu(H₂O)_x⁴⁺. The marginal decrease was attributed to the increased molecular weight of the plutonium species and the increased viscosity of the solution matrixes. Only minor differences between the diffusion coefficients for Pu³⁺_(aq) vs. Pu⁴⁺_(aq) species were observed.

The diffusion coefficients were used to calculate how the hydrodynamic radii of the Pu⁴⁺_(aq) and Pu³⁺_(aq) species varied as a function of increasing HCl_(aq) concentrations (1 to 11 M) using the Stokes–Einstein equation (eqn (7)).

Variables: r = hydrodynamic radius, m; μ = dynamic viscosity, Pa s; k_B = Boltzmann constant, 1.3806 × 10⁻²³ J K⁻¹; ; T = temperature, K.

This analysis assumed the plutonium species were rigid spheres and the experimentally determined hydrodynamic radii for the Pu⁴⁺_(aq) and Pu³⁺_(aq) species were plotted as a function of HCl_(aq) concentration in Fig. 9B. Our experimentally determined hydrodynamic radii tended toward slightly smaller radii [5.1(2) to 2.6(1) Å] as the HCl_(aq) concentration increased from 1 to 11 M. These values agreed well with the 3.7 Å theoretical hydrodynamic radius calculated by the group contribution method,⁵³ which summed the atomic volume of each element (Pu and Cl¹⁻). The experimental and theoretical radii were also consistent with the reported hydrodynamic radius of 4.6 Å for Pu(IV) in nitric acid solutions.^54,55

These results did not follow the expected inverse relationship between hydrodynamic radii and diffusion coefficients. We suspected the origin of this deviation was related to significant changes in viscosity of the aqueous solutions that occurred when the HCl_(aq) concentrations were increased from 1 to 11 M.⁵⁶ Regarding the size difference between the Pu³⁺_(aq) and Pu⁴⁺_(aq) species at the same HCl_(aq) concentration, there was no significant difference in hydrodynamic radius (t test, two-tailed p > 0.05), indicating the Pu(IV) chloride and aquo complexes were similar in size in solution.

Outlook

Herein, we utilized a combination of XANES and EXAFS, UV-Vis-NIR, and electrochemical methods to advance understanding of how plutonium speciation in aqueous solutions varied as a function of HCl_(aq) concentration. Collectively, the data showed how changing the HCl_(aq) content from concentrated (11 M) to dilute (1 M) provided control over the electron transfer processes accessible to plutonium. The plutonium speciation profile was dominated by anionic PuCl_y^4−y complexes at high HCl_(aq) concentrations (>8 M) and cationic Pu(H₂O)_x⁴⁺ complexes at low HCl_(aq) concentrations (≤3 M). Heteroleptic aquochloride complexes, PuCl_y(H₂O)_x^4−y, dominated the speciation profile over a relatively small HCl_(aq) concentration range (∼4.5 to 8 M). Evaluating the X-ray absorption data alongside the electrochemical results provided additional fidelity in terms of the Cl¹⁻ for H₂O ligand substitution reaction. This analysis showed that an abrupt speciation change occurred when the HCl_(aq) content passed over the 5.5 M concentration value, suggesting the plutonium coordination environment was dominated by Cl¹⁻ ligands when HCl_(aq) concentration was >5.5 M and dominated by H₂O ligands when the HCl_(aq) concentration was <5.5 M. Despite Cl¹⁻ and H₂O both being relatively weak field ligands (on the spectrochemical series),⁵⁷ the ligand environment substantially impacted the half-wave potential (E_½) for the reversible Pu^4+/3+_(aq) one-electron transfer reaction. For instance, the E_½ potential was 0.572(2) V for the homoleptic PuCl_y^4−y complex and 0.744(2) V for the homoleptic Pu(H₂O)_x⁴⁺ complex. We interpreted the E_½ difference (∼170 mV) as suggesting that anionic Cl¹⁻ ligands stabilized electron-deficient Pu⁴⁺_(aq) over Pu³⁺_(aq) and neutral H₂O ligands stabilized electron-rich Pu³⁺_(aq) over Pu⁴⁺_(aq). These data also showcased the stability of Pu⁴⁺_(aq) over Pu³⁺_(aq) and the unlikeliness of Pu⁴⁺_(aq) and Pu³⁺_(aq) to generate PuO₂ⁿ⁺_(aq) (n = 1, 2) within the surveyed potential window (ca. 0.4 to 1 V).

Overall, these findings offer a simple way to control the electron transfer chemistry of plutonium in aqueous solutions. Changing the HCl_(aq) concentration altered the coordination chemistry accessible to plutonium, which in turn changed potentials required to access the one-electron Pu(IV) + e¹⁻ ⇌ Pu(III) redox reaction. Based on these results, it seemed likely that increasing the electron donating ability of the complexing agent (stronger field than Cl¹⁻) would shift E_½ more negative and stabilize electron-deficient Pu⁴⁺_(aq) further. Conversely, increasing the electron withdrawing properties of the complexing agent should shift E_½ more positive and stabilize electron-rich Pu³⁺_(aq) further. It is our hope that these results will help scientists working with plutonium in aqueous solutions by demystifying some of the unexpected electron transfer chemistry plutonium experiences under those conditions. This insight may also aid researchers in better controlling plutonium when conducteing separations for energy-related systems, evaluating the fate and transport of plutonium through aqueous solutions in the environment, and processing aqueous plutonium solutions relevant to national nuclear security missions.

Materials and methods

General consideration

¡Caution! The ²³⁸Pu [half-life (t_½) = 87.7(1) years], ²³⁹Pu [t_½ = 24 110(30) years], ²⁴⁰Pu [t_½ = 6561(7) years], ²⁴¹Pu [t_½ = 14.325(6) years], and ²⁴²Pu [t_½ = 3.75(2) × 10⁵ years] isotopes – and their radioactive progeny products – present serious health threats because of their α-, β-, and γ-emission.⁵⁸ Hence, all studies with plutonium were conducted in a laboratory dedicated to studies on radioactive elements. This laboratory is equipped with HEPA-filtered hoods, continuous air monitors, negative pressure gloveboxes, and radiation monitoring equipment. All experiments were carried out with approved safety operating procedures. All free-flowing plutonium solids were handled in negative-pressure gloveboxes equipped with HEPA filters.

Plutonium (a mixture of ²³⁸Pu, 0.02 wt%; ²³⁹Pu, 93.7 wt%; ²⁴⁰Pu, 6.1 wt%; ²⁴¹Pu, 0.22 wt%; and ²⁴²Pu, 0.03 wt%) used in this study was obtained as either residues from previous experiments, plutonium oxide, or in metallic form dissolved as previously described.⁵⁹ The NaClO_2(s) reagent was obtained commercially (Sigma Aldrich) as a mixture of NaClO₂ (80%) and NaCl (20%) and used as received. All water used in these experiments was deionized and passed through a Thermoscientific Barnstead Micropure water purification system until a resistivity of 18.2 MΩ cm was achieved.

The experiments described in this study relied on making aqueous solutions that contained varied amounts of hydrochloric acid, HCl_(aq). These solutions were made from serial dilutions of commercially available concentrated HCl_(aq) (OPTIMA Grade; Fisher Scientific). The HCl concentration for the concentrated HCl_(aq) varied from batch-to-batch, ranging 10.8 to 11.1 M. Hence, we assigned the HCl content in the concentrated solutions as being 11 M and used this value to calculate the HCl_(aq) content in all subsequently made serial dilutions.

UV-Vis-NIR absorption measurements of plutonium samples dissolved in HCl_(aq)

A Cary 6000i UV-Vis-NIR spectrophotometer was used for all measurements. Data were collected from 10 000 cm⁻¹ (1000 nm) to 25 000 cm⁻¹ (400 nm). An aliquot (464 μL, 2.1 mg) of the Pu⁴⁺_(aq) reagent stock solution in HCl_(aq) (6 M) was added to a Falcon cone (50 mL). The cone was gently heated on a hot plate (∼70 °C) overnight. The resulting residue was dissolved in a small amount of HCl_(aq) (945 μL; 11 M). The solution was loaded into a quartz cuvette equipped with a screw top lid. The lid was closed and sealed with electrical tape. This procedure was used to prepare four additional samples in HCl_(aq) at varied concentrations by substituting the HCl_(aq) (11 M) used to dissolve the Pu⁴⁺_(aq) residue for 8, 5.5, 3, and 1 M HCl_(aq) solutions. The more concentrated HCl_(aq) solutions (11, 8, and 5.5 M) were orange in color, while the more dilute HCl_(aq) solutions (3 and 1 M) were peach in color. After data collection was finished, the cuvettes were stored in a room-temperature, dark place. Measurements were taken immediately after sample preparation: 24 hours later, 5 days later, and 7 days later. No colloidal precipitate, solution loss, or color change was observed during this time.

Cyclic voltammetry from Pu⁴⁺_(aq) dissolved in aqueous solutions

A CH Instruments 620C potentiostat was used for all voltammetric measurements. Experiments were carried out within a HEPA-filtered fume hood using a standard three-electrode cell. An aliquot of a Pu⁴⁺_(aq) stock solution (16 mg Pu, 1 mL, 67 mM) in HCl_(aq) (5.5 M) was transferred to a plastic Falcon cone (50 mL). The solution was heated (near 80 °C) on a hot plate under a stream of filtered air until a soft dryness was achieved. The term “soft dryness” is used to caution against overheating, which can complicate subsequent dissolution efforts. The resulting residue was dissolved in concentrated HCl_(aq) (4 mL, 11 M), which generated a solution that was 4 mg L⁻¹ (16.7 mM) in Pu⁴⁺_(aq). This orange solution was transferred in its entirety (4 mL) to an electrochemical cell. Three electrodes were then submerged into the solution: a platinum disk (2.0 mm diameter) working electrode that had been polished with an alumina (0.05 μm) aqueous slurry on a felt polishing pad, a platinum wire (1.3 mm diameter and 92.4 mm length) counter electrode, and fritted Ag/AgCl reference electrode in a saturated KCl_(aq) solution (CH Instruments, Inc.). Voltammograms were collected as a function of scan rates (0.01–10 V s⁻¹) and iR compensation was applied when the scan rate was >1 V s⁻¹ using the CHI630E Electrochemical Analyzer software.

The solutions used for the electrochemical assay in concentrated HCl_(aq) (11 M) was recovered into a plastic Falcon cone (50 mL). The cone was heated (near 80 °C) on a hot plate under a stream of filtered air to evaporate the solution. The resulting residue was dissolved in HCl_(aq) (4 mL; 8 M) and the electrochemical measurements were repeated in analogy to that described above in 11 M HCl_(aq). This process was repeated with a series of HCl_(aq) solutions: 6, 4.5, 3, and 1 M. Voltammetric measurements were collected in triplicate. This was achieved on three separate days by evaporating a Pu_(aq) solution to dryness, dissolving the residue in fresh HCl_(aq), and then recovering the Pu_(aq) samples. The obtained voltammograms were corrected for the Ag/AgCl drift at non-standard conditions across different chloride concentrations using the Nernst equation.

Preparing plutonium samples dissolved in HCl_(aq) for X-ray absorption measurements

An aliquot (29 μL, 2 mg) of the Pu⁴⁺_(aq) reagent stock solution in HCl_(aq) (6 M) was added to a Falcon cone (50 mL). The cone was gently heated on a hot plate (∼65 °C) overnight. The resulting residue was dissolved in a small amount of HCl_(aq) (900 μL; 11 M). An aliquot (450 μL, ∼1 mg Pu, ∼0.02 M in Pu) of that solution was loaded into the X-ray absorption sample holder. This procedure was used to prepare four additional samples in HCl_(aq) at varied concentrations by substituting the HCl_(aq) (11 M) used to dissolve the Pu⁴⁺_(aq) residue for 8, 5.5, 3, and 1 M HCl_(aq) solutions.

The X-ray absorption sample holder was custom-made and designed for assaying solutions that contained radiological samples. These holders – and the associated handling procedures – provided adequate containment (three layers) for radiological samples. We additionally deployed appropriate administrative and engineering controls that guarded against the release of radiological material during shipment and data acquisition. The holder consisted of a Teflon body with a 5 mm well. It was equipped with a set of Teflon windows (1 mil thickness) and an additional Kapton window (1 mil thickness). These windows were secured by stainless-steel brackets. Solutions were introduced into the holder through an injection hole that was sealed with a Teflon plug. The plug was secured with an aluminum plate. This primary holder was held within a secondary container, which in turn was nested within the tertiary container. The secondary and tertiary containers were best described as a set of aluminum holders equipped with Kapton windows (2 mil thickness) and rubber gaskets. The assembly was shipped to the Stanford Synchrotron Radiation Lightsource (SSRL). Upon arrival, the samples were surveyed for contamination at the beamline within a radiological tent, placed in a cryostat (which provided tertiary containment), and attached to the SSRL Beamline's 11-2 rail.

Preparing dicesium hexachloroplutonate, Cs₂PuCl₆, for X-ray absorption measurements

The Cs₂PuCl₆ compound was made using a modified procedure from the original synthesis.⁶⁰ In a negative-pressure, air-filled glovebox, a plutonium sample (4.0 g; 16.7 mmol) was suspended in water (11.4 mL). Concentrated HCl_(aq) (70.7 mL; 11 M) was then added to the mixture, forming a solution whose total volume was 82.1 mL and that was 0.2 M in plutonium. Analysis by UV-Vis-NIR spectroscopy showed a mixture of Pu(IV) and Pu(III) were present. Separately, NaClO_2(s) reagent (80% NaClO₂/20% NaCl by weight, 2.24 g; 19.8 mmol) was dissolved in water (3 mL) to make a solution that was 6.6 M in NaClO_2(aq). This NaClO_2(aq) solution was slowly added to the plutonium solution. After mixing for 20 min, an aliquot (3 mL) was taken from the solution for characterization. Analysis by UV-Vis-NIR spectroscopy showed that the oxidation state for plutonium was +4 and that Pu(III) contaminants had oxidized (see ESI†). The radiochemical analyses (described previously⁶¹) confirmed the plutonium concentration was 1.97(1) × 10⁻⁴ M. Acid–base titration with a Thermo Scientific Orion Star A121 pH meter using a NaOH solution (0.1 M) showed the HCl_(aq) concentration was 9.3 M, and this value was confirmed using a Metrohm chloride ion-selective electrode.

Approximately 1 hour after oxidation, a solution of CsCl_(aq) [30.1 mL; 3 M in 9.3 M HCl_(aq)] was added to the Pu⁴⁺_(aq) solution [82.1 mL; 1.97(1) × 10⁻⁴ M in 9.3 M HCl_(aq)] described above. Upon combining these two solutions, a pale-yellow powder immediately precipitated. The slurry was mixed (30 min) and the precipitate was allowed to settle for 12 hours. This powder was isolated by vacuum filtration, washed with HCl_(aq) (100 mL, 11 M), and dried in an oven (∼120 °C, 8 hours). Analysis of the filtrate by UV-Vis-NIR absorption spectroscopy showed no detectible plutonium dissolved in solution (see ESI†). Radiochemical analyses showed a precipitation yield of 99.9%. The compound was analyzed by powder X-ray diffraction (see ESI†), and its identity was confirmed as Cs₂PuCl_6(s) by comparison with previously published data.⁶²

The Cs₂PuCl_6(s) sample was transferred to a negative-pressure, argon-filled glovebox. A small portion of the sample (3.7 mg, 5.3 μmol) was mixed with boron nitride powder (170.0 mg) in a polystyrene canister (0.5 × 1 inch) that contained a Teflon ball (1/8-inch diameter). The mixture was ground (5 min) using a Wig-L-Bug grinder. The resulting homogeneous powder contained 0.7 wt% Pu(IV), which was calculated to have a plutonium edge jump of 0.15 absorption length in transmission 500 eV above the Pu L₃-edge. The fine white powder was loaded into a Teflon NMR tube liner that had been cut to a length of ∼1 inch. This powder was quite flocculant and the potential for spreading unwanted contamination throughout the glovebox was high. The dispersion hazard was mitigated by using a small funnel made from an automated pipette tip (5 mL) to aid in the sample transfer. Additionally, disposable Latex gloves were worn over the glovebox gloves (inside the box) during the solid transfer, and the glovebox floor was covered with aluminum foil to catch any straggling plutonium powder. The powder was packed with a stainless-steel shaft into the Teflon NMR tube liner to generate a tight cylindrical plug (ca. height = 20 mm; diameter = 3 mm). A Teflon stopper was inserted into the tube until it pressed against the plug, which in turn sealed the tube. The tube was transferred to a HEPA-filtered hood and loaded into a slotted aluminum plate. This plate was equipped with two windows made from Kapton tape (1 mil). This primary holder was nested within an additional aluminum sample holder that was equipped with Kapton windows (2 mil). These windows were sealed with indium wire and held in place by stainless-steel brackets and bolts. Care was taken to ensure that the outside of the primary and secondary holders was not contaminated. The sample holder was shipped to SSRL. Upon arrival, the samples were unpackaged at the beamline within a tented workstation and attached to the cold finger of a liquid N_2(liq) cryostat, which served as a third layer of containment during the measurements. The cryostat was attached to the SSRL's Beamline 11-2 rail, such that the samples were held at 45° to the incident radiation. The cryostat was attached to a turbo pump and then placed under vacuum (10⁻⁶ torr) and cooled with N_2(liq) prior to X-ray measurement.

Pu L₃-edge X-ray absorption data acquisition

The room-temperature solution-phase Pu L₃-edge X-ray measurements were collected under dedicated operating conditions (3.0 GeV, 5%, 500 mA using continuous top-off injections) on end station 11-2. At the time of these measurements, this beamline was equipped with a 26-pole and a 2.0 tesla wiggler. Using a liquid nitrogen-cooled double-crystal Si[220] (ϕ = 90°) monochromator that employed collimating and mirrors, a single energy was selected from the incident white beam. Vertical acceptance was controlled by slits positioned before the monochromator. All measurements were conducted with the monochromator crystals fully tuned. High-energy harmonics were rejected using a 370 mm Rh-coated harmonic rejection mirror. The Rh coating was 50 nm with 20 nm seed coating and the substrate was Zerodur. The harmonic rejection cut-off was set by the mirror angle to 23.5 keV to control which photons experience total external reflection.

Beamline 11-2 XAS rail (SSRL) was equipped with three ionization chambers, through which nitrogen gas continually flowed. One chamber was positioned before the sample (10 cm) to monitor the incident radiation (I₀). A second chamber was positioned after the sample (30 cm) so that sample transmission (I₁) could be evaluated against I₀ and so that the absorption coefficient (μ) could be calculated as ln(I₀/I₁). A third chamber (I₂; 30 cm) was positioned downstream from I₁ so that the XANES of a calibration foil could be measured against I₁. A potential of 1600 V was applied in series to the ionization chambers. The samples were positioned 45° to the incident radiation. Samples were measured in fluorescence. A Lytle detector was used for the HCl_(aq) that had concentrations of 1, 3, 5.5, and 8 M. A 100-element Ge detector was used for the 11 M HCl_(aq)-containing samples. A Sr (3 mm) filter mounted to Soller slits that were positioned in front of the detector to help remove unwanted X-ray scattering from the samples. All data were collected with vertical slits set at 0.5 mm and horizontal slits set between 7 to 9 mm. A zirconium foil (Zr) was placed between the I₁ and I₂ ion chambers so that plutonium samples could be calibrated in situ to the energy of the first inflection point of the Zr K-edge (17 998 eV).

Pu L₃-edge X-ray absorption data analyses

To correct the HCl (11 M) Pu L₃-edge data for detector dead time, nonlinear response curves were defined from 0 to ∼70% dead (windowed counts of the emission line versus the total incoming counts into the detector) using a Sr 3 mm filter (300 eV above the Sr K-edge). Each channel was manually surveyed for outliers, which were omitted. The deadtime correction was applied before averaging the individual channels. Then, the six individual scans for each HCl_(aq) concentration were calibrated in energy to the first inflection point of the Zr K-edge from a metallic foil (17 998 eV), measured in situ. The individual scans were then averaged using IFEFFIT³⁸ within the Athena software package. Within the same program, the data were analyzed by fitting a line to the pre-edge region, which removed the experimental background from the data. Then, a third-order polynomial fit was chosen for the post-edge region of the spectra. The difference between pre- and post-edge functions were set to unity at the first inflection point of the X-ray absorption data. This normalized the absorption jump to 1.0. This normalization procedure gave spectra that were normalized to a single Pu atom. The EXAFS data were analyzed by shell-by-shell fitting methods using the Artemis program and FEFF8.³⁸ The spectra were k³-weighted and Fourier transformed prior to nonlinear least squares curve fitting. The amplitude reduction factor (S₀²) was set to 0.9 in all solutions. The actinides coordination number (N), scattering path length (R), and mean-squared displacements (σ²) were used as variables and refined as free unless otherwise noted. The FEFF8 calculations were obtained from published SC-XRD data from Pu(H₂O)₉³⁺, and [PuCl₆]²⁻.^39,40

Author contributions

All authors contributed to writing, reviewing, and editing the document. Yufei Wang, Natalie T. Rice, Julia G. Knapp, Stosh A. Kozimor, and Molly M. MacInnes conceived the study and wrote the original draft of the paper. Yufei Wang, Molly M. MacInnes, and Jan Klouda contributed to the cyclic voltammetry measurements. Julia G. Knapp, Natalie T. Rice, and Manuel L. Besmer contributed to the UV-Vis-NIR measurements. Yufei Wang, Molly M. MacInnes, Sara L. Adelman, and Stosh A. Kozimor analyzed the cyclic voltammetry data. Natalie T. Rice, J. Connor Gilhula, Ida D. Piedmonte, Stosh A. Kozimor, Travis Marshall-Roth, and Alexandra L. Nagelski contributed to XAS sample preparation and measurements. Natalie T. Rice and Stosh A. Kozimor analyzed the XAS data. Stosh A. Kozimor and Brian N. Long collected the PXRD measurements. All samples were prepared by Natalie T. Rice, Yufei Wang, Molly M. MacInnes, Julia G. Knapp, Christopher J. Godt, Kelly E. Aldrich, and Brian T. Arko. All authors contributed to writing the manuscript.

Data availability

Data associated with this study are available from the corresponding author upon request.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We thank the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Heavy Element Chemistry program (2020LANLE372) for funding the majority of this work. Additional support came from LANL's LDRD projects (20220054DR), the US Department of Energy, National Nuclear Security Association (NNSA), Plutonium Modernization Program (NA-191), the Los Alamos National Laboratory Directors (Rice) and Harold Agnew National Security (Piedmonte) fellowships, and the Glenn T. Seaborg Institute (Gilhula, Klouda, Marshall-Roth). LANL is an affirmative action/equal opportunity employer managed by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. DOE. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, was supported by the US DOE, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515.

References

1. F. N. von Hippel, Plutonium and Reprocessing of Spent Nuclear Fuel, Science, 2001, 293(5539), 2397–2398,  DOI:10.1126/science.1064667%U.
2. Y. Wang, Application of a hydroxypyridinone chelator to f-element separations for aqueous reprocessing of used nuclear fuel, University of California, Berkeley, 2021.
3. A. B. Kersting, Plutonium Transport in the Environment, Inorg. Chem., 2013, 52(7), 3533–3546,  DOI:10.1021/ic3018908.
4. T. E. Payne, J. J. Harrison, C. E. Hughes, M. P. Johansen, S. Thiruvoth, K. L. Wilsher, D. I. Cendón, S. I. Hankin, B. Rowling and A. Zawadzki, Trench ‘Bathtubbing’ and Surface Plutonium Contamination at a Legacy Radioactive Waste Site, Environ. Sci. Technol., 2013, 47(23), 13284–13293,  DOI:10.1021/es403278r.
5. G. S. Jones, Reactor-Grade Plutonium and Nuclear Weapons: Ending the Debate, Nonproliferation Rev., 2019, 26(1–2), 61–81,  DOI:10.1080/10736700.2019.1603497.
6. M. Bunn and E. P. Maslin, All Stocks of Weapons-Usable Nuclear Materials Worldwide Must be Protected Against Global Terrorist Threats, J. Nucl. Mater. Manage., 2011, 39, 21–27.
7. S. F. Ashley, G. J. Vaughan, W. J. Nuttall and P. J. Thomas, Considerations in relation to off-site emergency procedures and response for nuclear accidents, Process Saf. Environ. Prot., 2017, 112, 77–95,  DOI:10.1016/j.psep.2017.08.031.
8. D. L. Clark, S. S. Hecker, G. D. Jarvinen and M. P. Neu, Plutonium, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer Netherlands, 2006, pp. 813–1264.
9. C. F. Metz, Analytical Chemistry of Plutonium, Anal. Chem., 1957, 29(12), 1748–1756,  DOI:10.1021/ac60132a023.
10. B. G. Harvey, H. G. Heal, A. G. Maddock and E. L. Rowley, 188. The chemistry of plutonium, J. Chem. Soc. (Resumed), 1947,(0), 1010–1021,  10.1039/JR9470001010.
11. B. Allard, H. Kipatsi and J. O. Liljenzin, Expected species of uranium, neptunium and plutonium in neutral aqueous solutions, J. Inorg. Nucl. Chem., 1980, 42(7), 1015–1027,  DOI:10.1016/0022-1902(80)80394-0.
12. R. J. Lemire and P. R. Tremaine, Uranium and plutonium equilibriums in aqueous solutions to 200.degree.C, J. Chem. Eng. Data, 1980, 25(4), 361–370,  DOI:10.1021/je60087a026.
13. G. R. Choppin, A. H. Bond and P. M. Hromadka, Redox speciation of plutonium, J. Radioanal. Nucl. Chem., 1997, 219(2), 203–210,  DOI:10.1007/BF02038501.
14. I. Zilbermann, E. Maimon, H. Cohen and D. Meyerstein, Redox Chemistry of Nickel Complexes in Aqueous Solutions, Chem. Rev., 2005, 105(6), 2609–2626,  DOI:10.1021/cr030717f.
15. M. Uudsemaa and T. Tamm, Density-Functional Theory Calculations of Aqueous Redox Potentials of Fourth-Period Transition Metals, J. Phys. Chem. A, 2003, 107(46), 9997–10003,  DOI:10.1021/jp0362741.
16. K. J. Takeuchi, M. S. Thompson, D. W. Pipes and T. J. Meyer, Redox and spectral properties of monooxo polypyridyl complexes of ruthenium and osmium in aqueous media, Inorg. Chem., 1984, 23(13), 1845–1851,  DOI:10.1021/ic00181a014.
17. S. J. Slattery, J. K. Blaho, J. Lehnes and K. A. Goldsby, pH-Dependent metal-based redox couples as models for proton-coupled electron transfer reactions, Coord. Chem. Rev., 1998, 174(1), 391–416,  DOI:10.1016/S0010-8545(98)00143-X.
18. K. L. Nash and J. C. Sullivan, Chapter 102 Kinetics of complexation and redox reactions of the lanthanides in aqueous solutions, in Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 1991, vol. 15, pp. 347–391.
19. D. Parker, R. S. Dickins, H. Puschmann, C. Crossland and J. A. K. Howard, Being Excited by Lanthanide Coordination Complexes: Aqua Species, Chirality, Excited-State Chemistry, and Exchange Dynamics, Chem. Rev., 2002, 102(6), 1977–2010,  DOI:10.1021/cr010452+.
20. L. G. Nielsen and T. J. Sørensen, Including and Declaring Structural Fluctuations in the Study of Lanthanide(III) Coordination Chemistry in Solution, Inorg. Chem., 2020, 59(1), 94–105,  DOI:10.1021/acs.inorgchem.9b01571.
21. J. A. Rard, Chemistry and thermodynamics of europium and some of its simpler inorganic compounds and aqueous species, Chem. Rev., 1985, 85(6), 555–582,  DOI:10.1021/cr00070a003.
22. D. E. Morris, Redox Energetics and Kinetics of Uranyl Coordination Complexes in Aqueous Solution, Inorg. Chem., 2002, 41(13), 3542–3547,  DOI:10.1021/ic0201708.
23. A. Ikeda, C. Hennig, S. Tsushima, K. Takao, Y. Ikeda, A. C. Scheinost and G. Bernhard, Comparative Study of Uranyl(VI) and -(V) Carbonato Complexes in an Aqueous Solution, Inorg. Chem., 2007, 46(10), 4212–4219,  DOI:10.1021/ic070051y.
24. H. Moll, A. Rossberg, R. Steudtner, B. Drobot, K. Müller and S. Tsushima, Uranium(VI) Chemistry in Strong Alkaline Solution: Speciation and Oxygen Exchange Mechanism, Inorg. Chem., 2014, 53(3), 1585–1593,  DOI:10.1021/ic402664n.
25. J. P. Austin, M. Sundararajan, M. A. Vincent and I. H. Hillier, The geometric structures, vibrational frequencies and redox properties of the actinyl coordination complexes ([AnO2(L)n]m; An = U, Pu, Np; L = H₂O, Cl−, CO32−, CH₃CO2−, OH−) in aqueous solution, studied by density functional theory methods, Dalton Trans., 2009,(30), 5902–5909,  10.1039/B901724K.
26. Z. Szabó, T. Toraishi, V. Vallet and I. Grenthe, Solution coordination chemistry of actinides: Thermodynamics, structure and reaction mechanisms, Coord. Chem. Rev., 2006, 250(7), 784–815,  DOI:10.1016/j.ccr.2005.10.005.
27. A. Dash, R. Agarwal and S. K. Mukerjee, Electrochemical behaviour of uranium and thorium aqueous solutions at different temperatures, J. Radioanal. Nucl. Chem., 2017, 311(1), 733–747,  DOI:10.1007/s10967-016-5088-7.
28. S. Skanthakumar, G. B. Jin, J. Lin, V. Vallet and L. Soderholm, Linking Solution Structures and Energetics: Thorium Nitrate Complexes, J. Phys. Chem. B, 2017, 121(36), 8577–8584,  DOI:10.1021/acs.jpcb.7b06567.
29. J. M. Cleveland, Aqueous coordination complexes of plutonium, Coord. Chem. Rev., 1970, 5(1), 101–137,  DOI:10.1016/S0010-8545(00)80076-4.
30. B. W. Stein, S. A. Kozimor and V. Mocko, The Plutonium Handbook, American Nuclear Society, 2019.
31. P. G. Allen, J. J. Bucher, D. K. Shuh, N. M. Edelstein and T. Reich, Investigation of Aquo and Chloro Complexes of UO22+, NpO2+, Np4+, and Pu3 + by X-ray Absorption Fine Structure Spectroscopy, Inorg. Chem., 1997, 36(21), 4676–4683,  DOI:10.1021/ic970502m.
32. C. H. Booth, S. A. Medling, Y. Jiang, E. D. Bauer, P. H. Tobash, J. N. Mitchell, D. K. Veirs, M. A. Wall, P. G. Allen and J. J. Kas, et al. Delocalization and occupancy effects of 5f orbitals in plutonium intermetallics using L3-edge resonant X-ray emission spectroscopy, J. Electron Spectrosc. Relat. Phenom., 2014, 194, 57–65,  DOI:10.1016/j.elspec.2014.03.004.
33. S. D. Conradson, K. D. Abney, B. D. Begg, E. D. Brady, D. L. Clark, C. den Auwer, M. Ding, P. K. Dorhout, F. J. Espinosa-Faller and P. L. Gordon, et al. Higher Order Speciation Effects on Plutonium L3 X-ray Absorption Near Edge Spectra, Inorg. Chem., 2004, 43(1), 116–131,  DOI:10.1021/ic0346477.
34. S. D. Conradson, I. Al Mahamid, D. L. Clark, N. J. Hess, E. A. Hudson, M. P. Neu, P. D. Palmer, W. H. Runde and C. Drew Tait, Oxidation state determination of plutonium aquo ions using X-ray absorption spectroscopy, Polyhedron, 1998, 17(4), 599–602,  DOI:10.1016/S0277-5387(97)00287-8.
35. K. O. Kvashnina, A. Y. Romanchuk, I. Pidchenko, L. Amidani, E. Gerber, A. Trigub, A. Rossberg, S. Weiss, K. Popa and O. Walter, et al., A Novel Metastable Pentavalent Plutonium Solid Phase on the Pathway from Aqueous Plutonium(VI) to PuO2 Nanoparticles, Angew. Chem., Int. Ed., 2019, 58(49), 17558–17562,  DOI:10.1002/anie.201911637 , (acccessed 2024/12/18).
36. C. Walther, H. R. Cho, C. M. Marquardt, V. Neck, A. Seibert, J. I. Yun and T. Fanghänel, Hydrolysis of plutonium(IV) in acidic solutions: no effect of hydrolysis on absorption-spectra of mononuclear hydroxide complexes, Radiochim. Acta, 2007, 95(1), 7–16,  DOI:10.1524/ract.2007.95.1.7 , (acccessed 2024-12-19).
37. M. H. Lee, Y. J. Park and W. H. Kim, Absorption spectroscopic properties for Pu(III, IV and VI) in nitric and hydrochloric acid media, J. Radioanal. Nucl. Chem., 2007, 273(2), 375–382,  DOI:10.1007/s10967-007-6848-1.
38. J. L. Ryan, Actinide(IV) Chloride Species Absorbed by Anion Exchange Resins from Chloride Solutions1, J. Phys. Chem., 1961, 65(10), 1856–1859,  DOI:10.1021/j100827a040.
39. G. Bailly, D. Maloubier and G. Legay, Plutonium(IV) quantification in acidic process solutions using partial least-squares regression applied to UV–Vis spectrophotometry, J. Radioanal. Nucl. Chem., 2022, 331(3), 1267–1273,  DOI:10.1007/s10967-022-08205-4.
40. M. H. Lee, M. Y. Suh, K. K. Park, Y. J. Park and W. H. Kim, Determination of Pu Oxidation states in the HCl Media Using with UV-Visible Absorption Spectroscopic Techniques, J. Nucl. Fuel Cycle Waste Technol., 2006, 4, 1–7.
41. E. Gerber, A. Y. Romanchuk, I. Pidchenko, L. Amidani, A. Rossberg, C. Hennig, G. B. M. Vaughan, A. Trigub, T. Egorova and S. Bauters, et al., The missing pieces of the PuO2 nanoparticle puzzle, Nanoscale, 2020, 12(35), 18039–18048,  10.1039/D0NR03767B.
42. C. Ekberg, K. Larsson, G. Skarnemark, A. Ödegaard-Jensen and I. Persson, The structure of plutonium(IV) oxide as hydrolysed clusters in aqueous suspensions, Dalton Trans., 2013, 42(6), 2035–2040,  10.1039/C2DT32185H.
43. P. Estevenon, T. Dumas, P. L. Solari, E. Welcomme, S. Szenknect, A. Mesbah, K. O. Kvashnina, P. Moisy, C. Poinssot and N. Dacheux, Formation of plutonium(IV) silicate species in very alkaline reactive media, Dalton Trans., 2021, 50(36), 12528–12536,  10.1039/D1DT02248B.
44. A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Real-space multiple-scattering calculation and interpretation of X-ray-absorption near-edge structure, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58(12), 7565–7576,  DOI:10.1103/PhysRevB.58.7565.
45. J. H. Matonic, B. L. Scott and M. P. Neu, High-Yield Synthesis and Single-Crystal X-ray Structure of a Plutonium(III) Aquo Complex: [Pu(H₂O)9][CF3SO3]3, Inorg. Chem., 2001, 40(12), 2638–2639,  DOI:10.1021/ic015509p.
46. S. D. Reilly, B. L. Scott and A. J. Gaunt, [N(n-Bu)4]2[Pu(NO3)6] and [N(n-Bu)4]2[PuCl6]: Starting Materials To Facilitate Nonaqueous Plutonium(IV) Chemistry, Inorg. Chem., 2012, 51(17), 9165–9167,  DOI:10.1021/ic301518g.
47. R. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767,  DOI:10.1107/S0567739476001551.
48. C. W. Kammeyer and D. R. Whitman, Quantum Mechanical Calculation of Molecular Radii. I. Hydrides of Elements of Periodic Groups IV through VII, J. Chem. Phys., 1972, 56(9), 4419–4421.
49. C. Batchelor-McAuley, M. Yang, E. M. Hall and R. G. Compton, Correction factors for the analysis of voltammetric peak currents measured using staircase voltammetry, J. Electroanal. Chem., 2015, 758, 1–6,  DOI:10.1016/j.jelechem.2015.10.004.
50. A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, 2022.
51. N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, A Practical Beginner's Guide to Cyclic Voltammetry, J. Chem. Educ., 2018, 95(2), 197–206,  DOI:10.1021/acs.jchemed.7b00361.
52. F. H. David and V. Vokhmin, Thermodynamic properties of some tri- and tetravalent actinide aquo ions, New J. Chem., 2003, 27(11), 1627–1632,  10.1039/B301272G.
53. J. R. Welty, G. L. Rorrer and D. G. Foster, Fundamentals of Momentum, Heat, and Mass Transfer, John Wiley & Sons, 2015.
54. A. Fallet, N. Larabi-Gruet, S. Jakab-Costenoble and P. Moisy, Electrochemical behavior of plutonium in nitric acid media, J. Radioanal. Nucl. Chem., 2016, 308(2), 587–598,  DOI:10.1007/s10967-015-4423-8.
55. F. H. David, Structure of trivalent lanthanide and actinide aquo ions, New J. Chem., 1997, 21(2), 167–176.
56. E. Nishikata, T. Ishii and T. Ohta, Viscosities of aqueous hydrochloric acid solutions, and densities and viscosities of aqueous hydroiodic acid solutions, J. Chem. Eng. Data, 1981, 26(3), 254–256,  DOI:10.1021/je00025a008.
57. J. E. Huheey, E. A. Keiter, R. L. Keiter and O. K. Medhi, Inorganic Chemistry: Principles of Structure and Reactivity, Pearson Education, 2006.
58. National Nuclear Data Center, https://www.nndc.bnl.gov/nudat2/(accessed 2024 December 18).
59. S. K. Cary, K. S. Boland, J. N. Cross, S. A. Kozimor and B. L. Scott, Advances in containment methods and plutonium recovery strategies that led to the structural characterization of plutonium(IV) tetrachloride tris-diphenylsulfoxide, PuCl4(OSPh2)3, Polyhedron, 2017, 126, 220–226,  DOI:10.1016/j.poly.2017.01.013.
60. F. J. Miner, R. P. DeGrazio and J. T. Byrne, Dicesium Plutonium Hexachloride, a Proposed Primary Standard for Plutonium, Anal. Chem., 1963, 35(9), 1218–1223,  DOI:10.1021/ac60202a003.
61. J. M. Blackader, A. S. Wong, N. D. Stalnaker and J. R. Willerton, Radiochemistry Calculations of Plutonium and 241Am Using the Rad Calc III Program, Los Alamos National Laboratory, Los Alamos, NM, 2001.
62. W. Zachariasen, Crystal chemical studies of the 5f-series of elements. II. The crystal structure of Cs2PuCl6, Acta Crystallogr., 1948, 1(5), 268–269,  DOI:10.1107/S0365110X48000715.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional UV-Vis spectra, PXRD pattern, and equation derivation. See DOI: https://doi.org/10.1039/d5qi00409h

‡ These are co-first authors because they contributed equally to this manuscript.

---