Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Resonance-induced anomalies in temperature-dependent Raman scattering of PdSe2†
Omar
Abdul-Aziz
 a,
Daniel
Wolverson
b,
Charles J.
Sayers
a,
Daniel
Wolverson
b,
Charles J.
Sayers
 c,
Ettore
Carpene
d,
Fulvio
Parmigiani
e,
Hamoon
Hedayat
c,
Ettore
Carpene
d,
Fulvio
Parmigiani
e,
Hamoon
Hedayat
 *a and
Paul H. M.
van Loosdrecht
*a and
Paul H. M.
van Loosdrecht
 *a
*a
aUniversität zu Köln, II. Physikalisches Institut, Zülpicher Straße 77, Köln D-50937, Germany. E-mail: hedayat@ph2.uni-koeln.de; pvl@ph2.uni-koeln.de
bCentre for Nanoscience and Nanotechnology, Department of Physics, University of Bath, BA2 7AY Bath, UK
cDipartimento di Fisica, Politecnico di Milano, 20133 Milan, Italy
dCNR-IFN, Dipartimento di Fisica, Politecnico di Milano, 20133 Milan, Italy
eDipartimento di Fisica, Università di Trieste, via A. Valerio 2, 34127 Trieste, Italy
First published on 24th June 2024
Abstract
We report a comprehensive Raman study of the phonon behavior in PdSe2 in the temperature range of 5 K to 300 K. A remarkable change in the Raman spectrum is observed at 120 K: a significant enhancement of the out-of-plane phonon A1g mode, accompanied by a suppression of the in-plane A2g and B21g modes. This intriguing behavior is attributed to a temperature-dependent resonant excitation effect. The results are supported by density functional theory (DFT) calculations, which demonstrate that the electron–phonon coupling for the phonon modes varies and is strongly associated with the relevant electronic states. Furthermore, nonlinear frequency shifts are identified in all modes, indicating the decay of an optical phonon into multiple acoustic phonons. The study of Raman emission reported here, complemented by linear optical spectroscopy, reveals an unexpected scenario for the vibrational properties of PdSe2 that holds substantial promise for future applications in PdSe2-based optoelectronics.
1. Introduction
Transition metal dichalcogenides (TMDs) are a prominent category of van der Waals layered materials with outstanding optical and electronic properties and diverse correlated phases.1–4 Among them, PdSe2 has emerged as a material of particular interest due to its unique low-symmetry puckered atomic structure which in the literature is sometimes referred to as pentagonal5 and is characterized by an orthorhombic lattice of Pbca space-group symmetry and D2h point-group symmetry.6 The distinctive bond arrangement within PdSe2 leads to substantial interlayer interactions, resulting in significant layer-dependent electronic properties and anisotropic features.5,7 Compared to conventional TMDs, PdSe2 exhibits excellent stability in air, a unique linear dichroism conversion phenomenon, a high carrier mobility of ∼150 cm2 V−1 s−1, and an exceptional long-wavelength infrared photoresponsivity.8–11 PdSe2 is a semiconductor with a bandgap in the infrared (IR) spectral region that is tunable from 0 to 1.3 eV when transitioning from its bulk to monolayer form.8,12 Additionally, a sign change occurs in magnetoresistance at approximately 100 K, attributed to electronic anisotropy, despite PdSe2 being a non-magnetic material.13 These unique features make PdSe2 a promising candidate for advanced polarization-sensitive photodetectors and other optoelectronic applications.8,14–17Raman spectroscopy has been recently used to characterize the basic vibrational properties of PdSe2,8,10,18 however, a deeper understanding of the intricate electron–phonon interactions remains an area that deserves further exploration. For example, limited attention has been paid to the temperature-dependent behavior of Raman spectra in PdSe2, with previous studies focusing primarily on temperatures above 300 K.19,20 Despite demonstrating the anisotropy of lattice vibrations in PdSe2,21–23 its connection to electronic states requires further clarification. Electron–phonon interactions within TMDs similar to other anisotropic-layered materials, such as black phosphorus,24–26 give a strong Raman response. Therefore, Raman scattering is used as a powerful probe to gain insight into phonons and the way they interact with interband electronic transitions, uncovering the symmetry-dependent electron–phonon coupling of materials with anisotropic properties.27–31 In these cases, the intensities of the phonon modes exhibit energy-dependent variations. A prototypical example is MoS2, where the Ag mode shows an enhancement when the excitation energy coincides with the exciton states A and B.32,33 This enhancement has been attributed to resonance-induced symmetry breaking, as strongly localized exciton wave functions effectively break the symmetry of the system, thereby activating normally Raman-inactive modes. This selective increase in the intensity of phonon modes has been linked to symmetry-dependent electron–phonon coupling, as demonstrated in resonance Raman studies of MoS2 using different excitation energies.32 Similar to other TMDs, PdSe2 also exhibits a selective response to different excitation energies as recently shown by Luo et al.34
In this study, we present the Raman spectra of PdSe2 using different polarization configurations. Furthermore, we offer a comprehensive analysis of the evolution of the Raman spectrum in the temperature range of 5 K to 300 K. We find that the Raman intensity of the A1g out-of-plane phonon modes experiences a significant enhancement at 120 K when excited with 2.33 eV, while the in-plane A2g and B21g phonon modes are suppressed under the same conditions. This intriguing phenomenon can be understood as a result of resonance effects combined with diverse electron–phonon coupling of different modes, which were further confirmed by optical spectroscopy experiments. To gain a deeper understanding of the electron–phonon interactions responsible for these observations, we employed density functional theory (DFT) calculations. The calculations reveal details of how each phonon mode is coupled to the specific electronic orbitals. The results elucidate the intricate interplay between electronic states and phonons in PdSe2, unveiling distinct electron–photon interactions associated with specific electronic states and phonon modes. Additionally, the study highlights phonon–phonon interactions spanning a wide temperature range that can be explained by a physical model that includes anharmonic contributions and offers an in-depth analysis of the nonlinear temperature-dependent Raman shifts of prominent optical phonon modes in PdSe2. Such insights lay the groundwork for future developments in PdSe2-based thermo-optoelectronic applications.
2. Results and discussions
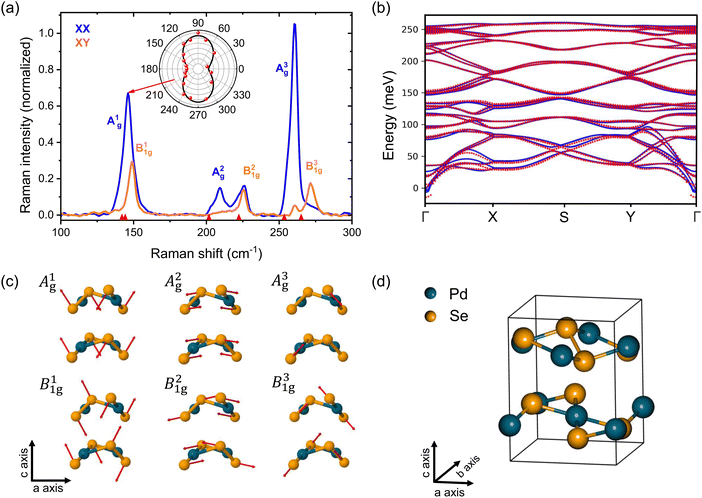
Fig. 1(a) shows room temperature Raman spectra of bulk PdSe2 using 532 nm (2.33 eV) laser excitation. The spectra were acquired in backscattering geometry with parallel (xx) and cross (xy) polarization configurations. We observe six characteristic Raman peaks corresponding to Ag-symmetry modes at 146.7, 209.4, and 260.6 cm−1, and B1g-symmetry modes found at at 148.7, 225.9, and 271.5 cm−1. To validate the understanding of phonons in bulk PdSe2, we performed calculations using density functional perturbation theory (DFPT).35 The phonon dispersion curves of bulk PdSe2 along the high-symmetry crystallographic axes are presented in Fig. 1(b), while Fig. 1(c) presents the calculated atomic displacements corresponding to the observed Raman modes. Fig. 1(b) also demonstrates that the phonon dispersion used in calculating the electron–phonon coupling via EPW36 (discussed in the ESI†) is consistent with the DFPT results. We find that the modes A1g, A3g, B11g, and B31g arise primarily from nearly out-of-plane vibrations of Se atoms along the c-axis, while the modes A2g and B21g predominantly stem from in-plane vibrations along the b- and a-axes, respectively. Note that the Ag and B1g modes exhibit distinctive responses to laser polarization as a result of their different symmetry. B1g modes are detected mainly in the cross-configuration, whereas the Ag modes are predominantly visible in the parallel configuration, allowing for their clear differentiation. Furthermore, our experimental resolution enables us to discern between the A1g and B11g modes, thus clarifying what was reported in previous Raman studies in which a mixed mode was detected.1,2,8 To understand the anisotropic optical properties, we investigated the dependence of the Raman scattering versus the polarization angle and crystal orientation. The results are reported in the inset of Fig. 1(a). Under parallel conditions, the A1g mode intensity has maxima at 90° and 270°, with a periodicity of 180°. The Raman intensity at a given angle θ can be fitted using curves of the form δ(θ) = δa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θ + ϕ) + δb
cos2(θ + ϕ) + δb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(θ + ϕ), where δa or δb represents the Raman intensity along the a and b crystal axes, and ϕ is the fitting parameter.10 This reveals that the Ag modes exhibit two-fold symmetry, aligning with the inherent in-plane anisotropy of the structure of PdSe2, where the a- and b-axes correspond to high and low Raman intensity of the Ag modes, respectively. The symmetry of the Raman modes is analyzed and the results are provided in the ESI.†Fig. 2(a) presents the Raman spectra of bulk PdSe2 measured in parallel configuration, where the polarization of the incident light is taken along the a-axis of the crystal, as a function of temperature. Temperature variations induce noticeable alterations in the frequency and intensity of the three Raman-active phonon modes. All observed Raman peaks experience a blue shift, attributed to lattice thermal anharmonicity, which contains contributions from phonon–phonon scattering and volume thermal expansion effects. Interestingly, as the temperature decreases from 300 to 5 K, a prominent feature emerges, the clear visibility of the B11g mode on the high-frequency side of the A1g which is highlighted in Fig. 2(b). At 120 K, further changes become evident, with the peak A1g reaching its maximum intensity, while modes A2g and B21g are suppressed. In this temperature range, the intensity of the Raman mode with a higher frequency A3g remains relatively constant. Additionally, a marked transformation in the Raman spectrum is observed at higher frequencies when the temperature decreases from 250 to 5 K. In particular, the Raman mode at 273 cm−1, associated with the B31g mode, appears in the parallel configuration similar to the B11g mode, which is not normally allowed. This suggests either a subtle change in the symmetry or a resonant Raman scattering process as observed in the breakdown of polarization Raman selection rules in few-layer TMDs by resonant Raman spectroscopy.29
sin2(θ + ϕ), where δa or δb represents the Raman intensity along the a and b crystal axes, and ϕ is the fitting parameter.10 This reveals that the Ag modes exhibit two-fold symmetry, aligning with the inherent in-plane anisotropy of the structure of PdSe2, where the a- and b-axes correspond to high and low Raman intensity of the Ag modes, respectively. The symmetry of the Raman modes is analyzed and the results are provided in the ESI.†Fig. 2(a) presents the Raman spectra of bulk PdSe2 measured in parallel configuration, where the polarization of the incident light is taken along the a-axis of the crystal, as a function of temperature. Temperature variations induce noticeable alterations in the frequency and intensity of the three Raman-active phonon modes. All observed Raman peaks experience a blue shift, attributed to lattice thermal anharmonicity, which contains contributions from phonon–phonon scattering and volume thermal expansion effects. Interestingly, as the temperature decreases from 300 to 5 K, a prominent feature emerges, the clear visibility of the B11g mode on the high-frequency side of the A1g which is highlighted in Fig. 2(b). At 120 K, further changes become evident, with the peak A1g reaching its maximum intensity, while modes A2g and B21g are suppressed. In this temperature range, the intensity of the Raman mode with a higher frequency A3g remains relatively constant. Additionally, a marked transformation in the Raman spectrum is observed at higher frequencies when the temperature decreases from 250 to 5 K. In particular, the Raman mode at 273 cm−1, associated with the B31g mode, appears in the parallel configuration similar to the B11g mode, which is not normally allowed. This suggests either a subtle change in the symmetry or a resonant Raman scattering process as observed in the breakdown of polarization Raman selection rules in few-layer TMDs by resonant Raman spectroscopy.29
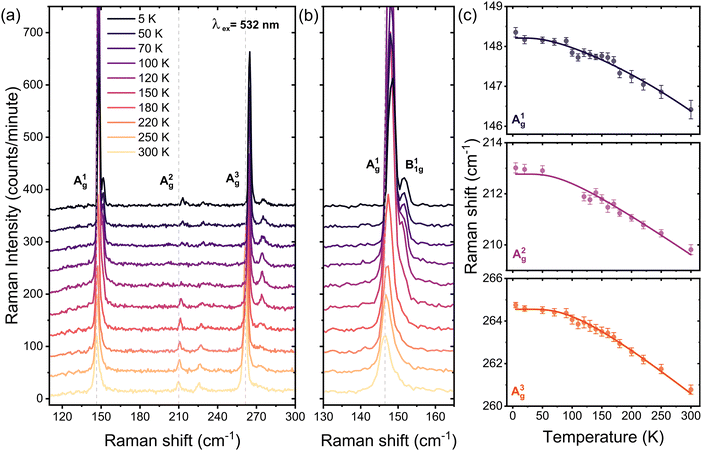 | ||
| Fig. 2 (a) and (b) Temperature-dependent Raman spectra of bulk PdSe2 under parallel configuration (xx), with an excitation energy of 2.33 eV (532 nm). (c) Raman frequencies as a function of temperature for the A1g, A2g, and A3g phonon modes. In each panel, we fit the data to the anharmonic model characterized by the processes of optical phonon decay (solid lines) using eqn (1) over the entire temperature range 5 to 300 K. | ||
To gain deeper insight into the anomalous phonon response of the A1g, A2g, A3g, B11g and B31g modes, we performed a Lorentzian lineshape fitting of the Raman spectra. In the following, we present the temperature dependence of Raman frequency, and full width at half maximum (FWHM) of each mode, while later we discuss the scattering strength obtained by the fittings. As shown in Fig. 2(c), for T > 100 K, a decrease of temperature results in a linear blueshift of all Raman frequencies. Conversely, in the low temperature range, all Raman mode frequencies tend to reach constant values. The pronounced nonlinearity of the mode frequencies originates from the anharmonic phonon interactions.37 Taking three- and four-phonon scattering processes into account, corresponding to cubic and quartic anharmonicities, the temperature dependence of the Raman mode frequencies can be described by the following relation:
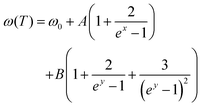 | (1) |
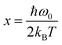 ,
, 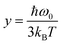 , while A and B are the anharmonic constants for the three- and four-phonon processes, respectively.37
, while A and B are the anharmonic constants for the three- and four-phonon processes, respectively.37
At high temperatures, when considering only the first terms of a Taylor expansion, eqn (1) tends toward a linear dependence. The fit of eqn (1) to the Raman frequencies is presented in Fig. 2(c) (solid lines). The behavior of the B1g phonon modes is taken from the close-to-cross configuration where all phonon modes are observed simultaneously and is presented in the ESI.† We also performed temperature-dependent Raman measurements on a trilayer PdSe2 for comparison (see ESI†). The fitted values of the anharmonic constants are presented in Table 1. These coefficients are lower than those observed in bulk PdSe2.
| Mode | ω 0 (cm−1) | A (cm−1) | B (cm−1) |
|---|---|---|---|
| Bulk | |||
| A1g | 148.6392 | −0.3853 | −0.0443 |
| A2g | 215.2802 | −2.3291 | −0.2067 |
| A3g | 267.1185 | −2.3042 | −0.2727 |
| B11g | 153.4026 | −1.1921 | −0.0245 |
| B21g | 231.5289 | −2.4889 | −0.0762 |
| B31g | 277.1462 | −2.0256 | −0.5453 |
| Trilayer | |||
| A1g | 152.7897 | −0.5447 | −0.00134 |
| B21g | 233.6546 | −1.2792 | −0.00509 |
The ratio A/B is high for phonons Ag and B1g modes, due to the higher probability of decay process of optical phonons into two acoustic phonons than the three acoustic phonons. Additionally, the value of the A coefficient for A1g is the smallest among all the modes. A similar non-linear temperature dependence of the Raman mode frequencies was also observed for other materials such as black phosphorus, MoS2, and SnSe2 nanosheets.38–42
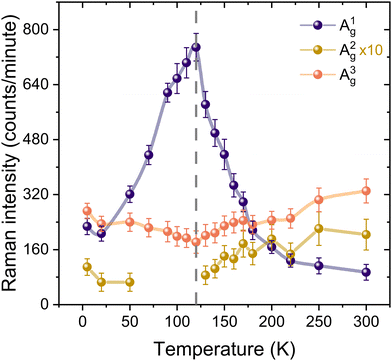
The behavior of Raman modes widths mirrors that of their frequencies as the temperature decreases: they decrease initially and then tend to saturate at temperatures below 100 K (see the ESI†). Concerning the scattering strength of the phonon modes, Fig. 3 shows the temperature-dependent spectral intensity of the A1g, A2g, and A3g modes. Specifically, A1g reaches its maximum intensity at 120 K, while A2g exhibits a zero intensity at the same temperature, followed by partial recovery. We note that this behavior was also observed for the B1g modes in the close-to-cross-polarization configuration (see the ESI†).
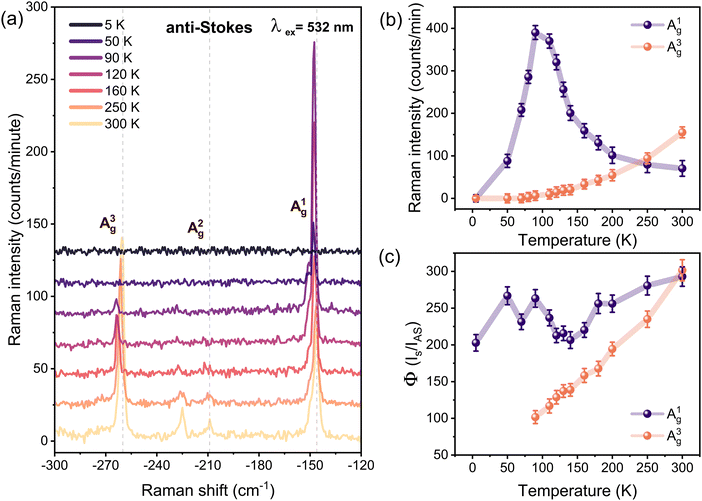
To further explore the anomalous behavior of the A1g mode, we performed temperature-dependent anti-Stokes Raman measurements, as reported in Fig. 4(a). We find that the A1g mode exhibits a gradual increase in intensity, reaching its maximum at about 90 K, mirroring the behavior observed in the Stokes measurements. In contrast, the A3g modes showed a consistent reduction in intensity with decreasing temperature, following the typical temperature-dependent behavior and ultimately becoming undetectable at 5 K, as shown in Fig. 4(b). The anti-Stokes to Stokes scattering ratio is a useful quantity for determining the effective phonon temperature, as discussed in ref. 43. In the absence of resonant conditions, the function ϕ can give an indication of the phonon temperature 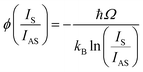 , where Ω is the phonon frequency. Fig. 4(c) presents the values of
, where Ω is the phonon frequency. Fig. 4(c) presents the values of 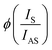 determined for the A1g and A3g phonon modes at different temperatures.
determined for the A1g and A3g phonon modes at different temperatures. 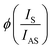 can be used to extract the temperature of the A3g phonon, as it demonstrates a linear behavior when the sample temperature is reduced. However, for A1g, this relationship does not exhibit the expected linear behavior, suggesting a possible resonant excitation effect linked to A1g.
can be used to extract the temperature of the A3g phonon, as it demonstrates a linear behavior when the sample temperature is reduced. However, for A1g, this relationship does not exhibit the expected linear behavior, suggesting a possible resonant excitation effect linked to A1g.
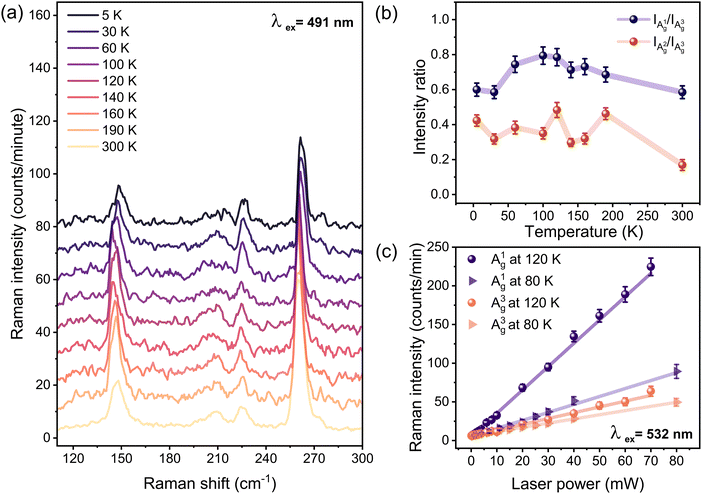
To clarify the effect of resonance enhancement of the A1g mode at 120 K, we measured the temperature-dependent Raman spectra of bulk PdSe2 employing alternative excitation energy. If the anomalous increase of A1g mode is due to resonance with 532 nm excitation, we anticipate that it will not be visible when using other laser lines. Fig. 5(a) shows the results of Raman measurements detected using 491 nm (2.52 eV) excitation in parallel configuration. As the temperature decreases from 300 K to 5 K, all phonon modes exhibit a blue shift, consistent with the observations from the 2.33 eV excitation laser measurements. However, the Raman spectrum is relatively unchanged, and the subtle change in symmetry observed using 2.33 eV excitation is entirely absent. The absence of phonon-selective resonant enhancement is discernible through the negligible change observed in the intensity ratios between A1g to A3g and A2g to A3g as shown in Fig. 5(b).
By altering the excitation energy, we observed that the peculiar temperature-dependent amplitude behaviour was absent. We then investigated whether changing the energy of the electronic states had a similar effect on the anomaly. The thickness of PdSe2 has a major influence on its electronic band structure and optical resonances. To further explore this effect and understand the dependence of this behaviour on the flake thickness, we studied the temperature-dependent Raman spectra of a mechanically exfoliated thin sample (trilayer). The electronic band gap of PdSe2 has been reported to increase significantly with the transition from the bulk to the thin-layer regime, causing a substantial modification of the entire electronic landscape.8 We observe significant frequency shifts of several Raman modes, ranging from 5 to 9 cm−1, as we move from the bulk to the trilayer system, which is in excellent agreement with the other reports8,44 (see the ESI†). This large blueshift from bulk to trilayer is attributed to the strong interlayer coupling and the change of the in-plane lattice constants. Temperature-dependent measurements revealed that the resonance effect is not as strong in the trilayer system, and the significant increase of A1g that was seen in the bulk is completely absent, which is in agreement with our interpretation.
Using 2.33 eV excitation, we investigated the power dependent behavior of the A1g and A3g modes at selected temperatures of 120 K and 80 K aiming to assess the influence of optical excitation on these modes under resonant (120 K) and non-resonant (80 K) conditions. As shown in Fig. 5(c), we clearly see that the A3g mode exhibits a similar power-dependent behavior at both temperatures, i.e. there is no significant resonance effect, which is almost identical to the behavior of A1g at 80 K. In contrast, at 120 K, A1g exhibits a remarkable sensitivity to increasing laser power, indicating a resonant effect at this temperature. This effect can be attributed to an enhancement of the prefactor in the Raman response associated with resonant optical properties at 120 K. Consequently, all experimental observations consistently point towards a resonant Raman effect. The non-resonant components within the Raman spectrum may neutralize the resonant Raman component, resulting in the suppression of the Raman signal, as explained in ref. 45. This phenomenon accounts for the observed extinction of the in-plane A2g and B2g modes at 120 K.
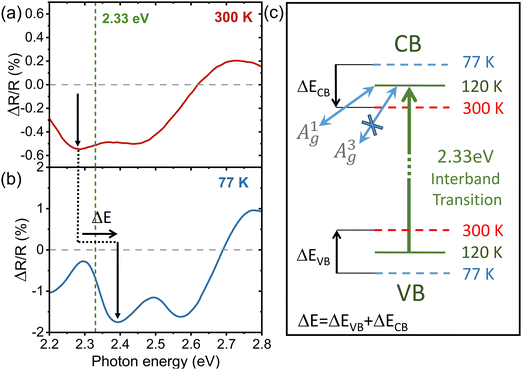
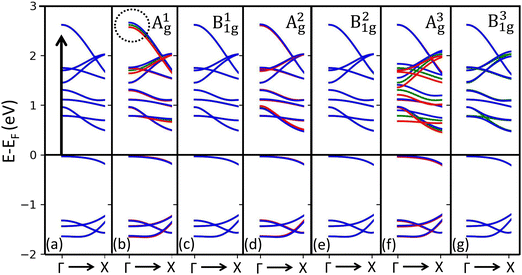
To gain experimental insights into the resonance phenomena in the Raman response of bulk PdSe2 and to explore its dependence on temperature, we employed optical spectroscopy within the range of Raman excitation energy. We used broadband transient reflectivity experiments that involved photoexciting the sample with an optical pump pulse centered at approximately 2.30 eV and subsequently measuring the differential reflectivity, ΔR/R, after a 1 picosecond time delay. Fig. 6(a) shows the 1 ps optical response at room temperature where a negative feature of ΔR/R approximately at 2.28 eV (indicated by arrows) is identified. Upon reducing the temperature to 77 K, we observed a discernible shift of the reflectivity peak towards higher energies (about 2.39 eV), as shown in Fig. 6(b). Notably, this transition crosses the 2.33 eV energy (dashed green line, the Raman excitation energy) as the temperature was lowered from 300 K to 77 K. Analogous behavior was also observed in other materials such as WSe2 and MoSe2.46,47Fig. 6(c) illustrates this transition and energy shift, resembling a resonance at 2.33 eV, possibly at 120 K. This observation supports the conjecture of a significant change in Raman modes on the basis of electronic transitions. A recent study has revealed that the transient absorption spectrum of an 8-layer PdSe2 displays coherent oscillations at a frequency of 143 cm−1, identified as the only optical phonon in the transient optical response, suggesting the strong interaction between the A1g mode and the electronic states.17 Given that the excitonic characteristics of the 2.31 eV optical transition are discussed in ref. 17, it is reasonable to attribute the observed Raman resonance to strong exciton–phonon interactions, similar to those seen in resonant excitation in monolayers of WS2 and WSe2.28,48 To investigate the electron–phonon interactions, we conducted theoretical calculations based on DFT. We calculated the band structure of bulk PdSe2 perturbed by small displacements (both positive and negative) of the atoms according to each of the Γ point phonon eigenvectors. This highlights in a simple way which optical transitions should give rise to strong phonon scattering via the deformation potential. The results are presented in Fig. 7(a)–(g), revealing not only that the electron–phonon coupling is different for the A1g and A3g modes, but that they also couple to different electronic states. Specifically, the bands located approximately around 2.5 eV above the Fermi level display strong coupling with A1g, although the overall electron–phonon coupling is more pronounced for A3g (we show the calculated strengths of the electron–phonon coupling for all the Raman modes active in backscattering in the ESI†). Hence, through resonant optical excitation, the phonon behavior of PdSe2 can be manipulated due to the strong and diverse electron–phonon interactions specific to each phonon mode and electronic state. These results illustrate the significant potential of resonance Raman scattering in examining layered TMDs, particularly in highly anisotropic PdSe2.
3. Conclusion
We examined phonon behavior in bulk PdSe2 using Raman spectroscopy over a temperature range of 5 to 300 K. We found that there is a temperature-dependent enhancement of specific Raman modes linked to resonance effects with particular optical transitions. For 2.33 eV excitation, we observed an opposite response: a significant increase in the intensity of the out-of-plane A1g mode, which peaks at 120 K, while there was a corresponding decrease in the in-plane A2g and B2g modes, while the out-of-plane A3g mode remains almost unchanged. The interpretation of the experimental results is supported by density functional theory (DFT) calculations, which confirm an enhanced electron–phonon coupling strength related to relevant optical transition energies. The anomalous behavior at 120 K can be explained by electron–phonon coupling and resonance effect in PdSe2. Additionally, we observed nonlinear frequency shifts in all phonon modes, originating from multiple phonon scattering decay channels. This work provides essential insights into the low-temperature electronic and vibrational properties of this anisotropic material, offering valuable information for further applications of the thermal characteristics of PdSe2 in optoelectronic devices. Our study serves to inspire further experimental and theoretical advancements in understanding the physics of two-dimensional materials.4. Methods
4.1 Sample preparation and characterization
The bulk PdSe2 crystals were purchased from HQ Graphene.49 PdSe2 thin flakes were mechanically exfoliated from the bulk crystals using Nitto SPV 224R tape and then transferred to a substrate of 280 nm SiO2/Si substrate. An optical microscope was used to determine and identify the thinner flakes based on their optical contrast. Using a Veeco Dimension 3000 atomic force microscope (AFM) the thickness of the trilayer was determined.4.2 Experimental procedures and measurement technique
The Raman spectra of bulk and trilayer PdSe2 samples were measured, using a micro-Raman system in backscattering geometry. To prevent any significant local temperature increase in the sample, an appropriate laser power was employed during the experiment. Two lasers with excitation energies of 2.33 eV (532 nm) and 2.52 eV (491 nm) were used. All measurements were performed in a vacuum using an optical coldfinger cryostat (Janis ST500) with a working distance (about 2 mm). The laser beam was focused to a spot size of 1 μm onto the sample by a 50× microscope objective lens and a long working distance of 12 mm. The laser power was set to a maximum of 100 μW. The backscattered light, collected by the same objective lens, was transmitted and directed onto the spectrometer's entrance slit. Following this path, the scattered signal underwent dispersion within the spectrometer and was subsequently detected using a liquid nitrogen-cooled back-illuminated charge-coupled-device (CCD) detector, specifically a low-etaloning PyLoN:1000BR_eXcelon, featuring a 1340 × 100 pixels CCD.Polarization-resolved Raman measurements incorporated an analyzer into the light path detection to determine the scattered light's polarization direction. Throughout the measurements, the PdSe2 samples remained fixed on the sample stage, while the polarization directions of the incident and scattered light were manipulated using a halfwave plate and analyser in steps of 15 degrees. The Raman spectra were obtained under both parallel and cross configurations. In the parallel configuration (xx), the scattered light's polarization aligned parallel to the incident light, while in the cross configuration (xy), the polarization was perpendicular. This distinction was achieved using the same analyzer.
4.3 Phonon displacements and DFT calculations
Phonon displacements and eigenmodes were computed using VASP50,51 by evaluating force constants for a 2 × 2 × 2 supercell through the frozen phonon approach implemented in phonopy. The structures were relaxed in VASP to achieve forces below 10−6 eV Å−1, with a kinetic energy cutoff of 300 eV and a Monkhorst–Pack k-point density of 8 × 8 × 6 for the primitive unit cell.52 In the DFT calculations, we employed the regularized SCAN meta-GGA exchange–correlation functional,53 along with the rVV10 kernel for the inclusion of van der Waals forces between layers54 (more details can be found in the ESI†).Author contributions
O. A. conducted the Raman measurements and analyzed the data. The study was supervised by H. H. and P. v. L. D. W. developed the theoretical support in discussions with E. C. and conducted the calculations. C. S. performed the optical spectroscopy experiments. O. A. wrote the manuscript with the support of H. H. The results were discussed and the paper was reviewed by O. A., D. W., C. S., E. C., F. P., H. H., and P. v. L.Data availability
The experimental data are accessible through: https://doi.org/10.5281/zenodo.10424154. Inputs to the computational codes are available free of charge at https://doi.org/10.15125/BATH-01356.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
The authors acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG) through project German Research Foundation via project No. 277146847 – CRC 1238: Control and Dynamics of quantum Materials. Computational work was performed on the University of Bath's High Performance Computing Facility and was supported by the EU Horizon 2020 OCRE/GEANT project “Cloud funding for research”. We acknowledge the financial support from the Italian Ministry of University and Research (Grant No. PRIN 2017BZPKSZ).References
- S. Sugai and T. Ueda, High-pressure Raman spectroscopy in the layered materials 2H-MoS2, 2H-MoSe2, and 2H-MoTe2, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 6554–6558 CrossRef CAS.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Electronics and optoelectronics of two-dimensional transition metal dichalcogenides, Nat. Nanotechnol., 2012, 7(11), 699–712 CrossRef CAS PubMed.
- O. Lopez-Sanchez, D. Lembke, M. Kayci, A. Radenovic and A. Kis, Ultrasensitive photodetectors based on monolayer MoS2, Nat. Nanotechnol., 2013, 8(7), 497–501 CrossRef CAS.
- J. A. Wilson and A. Yoffe, The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties, Adv. Phys., 1969, 18(73), 193–335 CrossRef CAS.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Penta-Graphene: A new carbon allotrope, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(8), 2372–2377 CrossRef CAS.
- F. Grønvold and E. Røst, The crystal structure of PdSe2 and PdS2, Acta Crystallogr., 1957, 10(4), 329–331 CrossRef.
- S. Deng, L. Li and Y. Zhang, Strain modulated electronic, mechanical, and optical properties of the monolayer PdS2, PdSe2, and PtSe2 for tunable devices, ACS Appl. Nano Mater., 2018, 1(4), 1932–1939 CrossRef CAS.
- A. D. Oyedele, S. Yang, L. Liang, A. A. Puretzky, K. Wang and J. Zhang, et al., PdSe2: pentagonal two-dimensional layers with high air stability for electronics, J. Am. Chem. Soc., 2017, 139(40), 14090–14097 CrossRef CAS PubMed.
- M. Long, Y. Wang, P. Wang, X. Zhou, H. Xia and C. Luo, et al., Palladium diselenide long-wavelength infrared photodetector with high sensitivity and stability, ACS Nano, 2019, 13(2), 2511–2519 CAS.
- J. Yu, X. Kuang, Y. Gao, Y. Wang, K. Chen and Z. Ding, et al., Direct observation of the linear dichroism transition in two-dimensional palladium diselenide, Nano Lett., 2020, 20(2), 1172–1182 CrossRef CAS PubMed.
- Y. Gu, H. Cai, J. Dong, Y. Yu, A. N. Hoffman and C. Liu, et al., Two-dimensional palladium diselenide with strong in-plane optical anisotropy and high mobility grown by chemical vapor deposition, Adv. Mater., 2020, 32(19), 1906238 CrossRef CAS PubMed.
- M. Wei, J. Lian, Y. Zhang, C. Wang, Y. Wang and Z. Xu, Layer-dependent optical and dielectric properties of centimeter-scale PdSe2 films grown by chemical vapor deposition, npj 2D Mater. Appl., 2022, 6(1), 1 CrossRef CAS.
- R. Zhu, Z. Gao, Q. Liang, J. Hu, J. S. Wang and C. W. Qiu, et al., Observation of anisotropic magnetoresistance in layered nonmagnetic semiconducting PdSe2, ACS Appl. Mater. Interfaces, 2021, 13(31), 37527–37534 CrossRef CAS PubMed.
- Y. Wang, J. Pang, Q. Cheng, L. Han, Y. Li and X. Meng, et al., Applications of 2D-layered palladium diselenide and its van der Waals heterostructures in electronics and optoelectronics, Nano-Micro Lett., 2021, 13(1), 143 CrossRef CAS PubMed.
- L. H. Zeng, Q. M. Chen, Z. X. Zhang, D. Wu, H. Yuan and Y. Y. Li, et al., Multilayered PdSe2/perovskite Schottky junction for fast, self-powered, polarization-sensitive, broadband photodetectors, and image sensor application, Adv. Sci., 2019, 6(19), 1901134 CrossRef CAS PubMed.
- Z. Wang, P. Wang, F. Wang, J. Ye, T. He and F. Wu, et al., A noble metal dichalcogenide for high-performance field-effect transistors and broadband photodetectors, Adv. Funct. Mater., 2020, 30(5), 1907945 CrossRef CAS.
- Z. Li, B. Peng, M. L. Lin, Y. C. Leng, B. Zhang and C. Pang, et al., Phonon-assisted electronic states modulation of few-layer PdSe2 at terahertz frequencies, npj 2D Mater. Appl., 2021, 5(1), 87 CrossRef CAS.
- D. Li, J. Fu, P. Suo, W. Zhang, B. Lu and X. Lin, et al., Layer dependent interlayer coherent phonon dynamics in PdSe2 films, Appl. Phys. Lett., 2021, 118(19), 191105 CrossRef CAS.
- L. Pi, C. Hu, W. Shen, L. Li, P. Luo and X. Hu, et al., Highly in-plane anisotropic 2D PdSe2 for polarized photodetection with orientation selectivity, Adv. Funct. Mater., 2021, 31(3), 2006774 CrossRef CAS.
- G. Li, S. Yin, C. Tan, L. Chen, M. Yu and L. Li, et al., Fast Photothermoelectric Response in CVD-Grown PdSe2 Photodetectors with In-Plane Anisotropy, Adv. Funct. Mater., 2021, 31(40), 2104787 CrossRef CAS.
- A. A. Puretzky, A. D. Oyedele, K. Xiao, A. V. Haglund, B. G. Sumpter and D. Mandrus, et al., Anomalous interlayer vibrations in strongly coupled layered PdSe2, 2D Mater., 2018, 5(3), 035016 CrossRef.
- W. Luo, A. D. Oyedele, Y. Gu, T. Li, X. Wang and A. V. Haglund, et al., Anisotropic phonon response of few-layer PdSe2 under uniaxial strain, Adv. Funct. Mater., 2020, 30(35), 2003215 CrossRef CAS.
- B. Wei, J. Liu, Q. Cai, A. Alatas, M. Hu and C. Li, et al., Giant anisotropic in-plane thermal conduction induced by Anomalous phonons in pentagonal PdSe2, Mater. Today Phys., 2022, 22, 100599 CrossRef CAS.
- Q. Zhong, Intrinsic and engineered properties of black phosphorus, Mater. Today Phys., 2022, 100895 CrossRef CAS.
- J. Wu, N. Mao, L. Xie, H. Xu and J. Zhang, Identifying the crystalline orientation of black phosphorus using angle-resolved polarized Raman spectroscopy, Angew. Chem., Int. Ed., 2015, 54(8), 2366–2369 CrossRef CAS.
- H. B. Ribeiro, M. A. Pimenta and C. J. de Matos, Raman spectroscopy in black phosphorus, J. Raman Spectrosc., 2018, 49(1), 76–90 CrossRef CAS.
- J. Zhao, H. Zeng and G. Yao, Computational design of a polymorph for 2D III-V orthorhombic monolayers by first principles calculations: excellent anisotropic, electronic and optical properties, Phys. Chem. Chem. Phys., 2021, 23(6), 3771–3778 RSC.
- E. del Corro, A. Botello-Méndez, Y. Gillet, A. L. Elias, H. Terrones and S. Feng, et al., Atypical exciton-phonon interactions in WS2 and WSe2 monolayers revealed by resonance Raman spectroscopy, Nano Lett., 2016, 16(4), 2363–2368 CrossRef CAS PubMed.
- Q. H. Tan, Y. J. Sun, X. L. Liu, K. X. Xu, Y. F. Gao and S. L. Ren, et al., Breakdown of Raman selection rules by Fröhlich interaction in few-layer WS2, Nano Res., 2021, 14, 239–244 CrossRef CAS.
- J. M. Lai, Y. R. Xie and J. Zhang, Detection of electron–phonon coupling in two-dimensional materials by light scattering, Nano Res., 2021, 14, 1711–1733 CrossRef.
- E. Del Corro, H. Terrones, A. Elias, C. Fantini, S. Feng and M. A. Nguyen, et al., Excited excitonic states in 1L, 2L, 3L, and bulk WSe2 observed by resonant Raman spectroscopy, ACS Nano., 2014, 8(9), 9629–9635 CrossRef CAS PubMed.
- B. R. Carvalho, L. M. Malard, J. M. Alves, C. Fantini and M. A. Pimenta, Symmetry-dependent exciton-phonon coupling in 2D and bulk MoS2 observed by resonance Raman scattering, Phys. Rev. Lett., 2015, 114(13), 136403 CrossRef PubMed.
- D. Nam, J. U. Lee and H. Cheong, Excitation energy dependent Raman spectrum of MoSe2, Sci. Rep., 2015, 5(1), 17113 CrossRef CAS.
- W. Luo, A. D. Oyedele, N. Mao, A. Puretzky, K. Xiao and L. Liang, et al., Excitation-Dependent Anisotropic Raman Response of Atomically Thin Pentagonal PdSe2, ACS Phys. Chem. Au, 2022, 2(6), 482–489 CrossRef CAS PubMed.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS . Available from:.
- J. Noffsinger, F. Giustino, B. D. Malone, C. H. Park, S. G. Louie and M. L. Cohen, EPW: A program for calculating the electron–phonon coupling using maximally localized Wannier functions, Comput. Phys. Commun., 2010, 181(12), 2140–2148 CrossRef CAS.
- M. Balkanski, R. Wallis and E. Haro, Anharmonic effects in light scattering due to optical phonons in silicon, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28(4), 1928 CrossRef CAS.
- A. Łapińska, A. Taube, J. Judek and M. Zdrojek, Temperature evolution of phonon properties in few-layer black phosphorus, J. Phys. Chem. C, 2016, 120(9), 5265–5270 CrossRef.
- A. Taube, J. Judek, C. Jastrzebski, A. Duzynska, K. Świtkowski and M. Zdrojek, Temperature-dependent nonlinear phonon shifts in a supported MoS2 monolayer, ACS Appl. Mater. Interfaces, 2014, 6(12), 8959–8963 CrossRef CAS PubMed.
- A. Taube, A. Łapińska, J. Judek and M. Zdrojek, Temperature dependence of Raman shifts in layered ReSe2 and SnSe2 semiconductor nanosheets, Appl. Phys. Lett., 2015, 107(1), 013105 CrossRef.
- W. D. Kong, S. F. Wu, P. Richard, C. S. Lian, J. T. Wang and C. L. Yang, et al., Raman scattering investigation of large positive magnetoresistance material WTe2, Appl. Phys. Lett., 2015, 106(8), 081906 CrossRef.
- A. Taube, A. Łapińska, J. Judek, N. Wochtman and M. Zdrojek, Temperature induced phonon behaviour in germanium selenide thin films probed by Raman spectroscopy, J. Phys. D: Appl. Phys., 2016, 49(31), 315301 CrossRef.
- A. Compaan and H. Trodahl, Resonance Raman scattering in Si at elevated temperatures, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29(2), 793 CrossRef CAS.
- J. Yu, X. Kuang, J. Li, J. Zhong, C. Zeng and L. Cao, et al., Giant nonlinear optical activity in two-dimensional palladium diselenide, Nat. Commun., 2021, 12(1), 1083 CrossRef CAS PubMed.
- J. Ralston, R. Wadsack and R. Chang, Resonant cancelation of Raman scattering from CdS and Si, Phys. Rev. Lett., 1970, 25(12), 814 CrossRef CAS.
- T. Yan, X. Qiao, X. Liu, P. Tan and X. Zhang, Photoluminescence properties and exciton dynamics in monolayer WSe2, Appl. Phys. Lett., 2014, 105(10), 101901 CrossRef.
- J. Ye, T. Yan, B. Niu, Y. Li and X. Zhang, Nonlinear dynamics of trions under strong optical excitation in monolayer MoSe2, Sci. Rep., 2018, 8(1), 2389 CrossRef PubMed.
- L. P. McDonnell, C. C. Huang, Q. Cui, D. W. Hewak and D. C. Smith, Probing excitons, trions, and dark excitons in monolayer WS2 using resonance Raman spectroscopy, Nano Lett., 2018, 18(2), 1428–1434 CrossRef CAS PubMed.
- HQ Graphene, https://www.hqgraphene.com/PdSe2.php, 2022.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758 CrossRef CAS.
- J. Hafner, Ab-initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29(13), 2044–2078 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- A. P. Bartók and J. R. Yates, Regularized SCAN functional, J. Chem. Phys., 2019, 150(16), 161101 CrossRef PubMed.
- R. Sabatini, T. Gorni and S. De Gironcoli, Nonlocal van der Waals density functional made simple and efficient, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(4), 041108 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc02012j |
| This journal is © The Royal Society of Chemistry 2024 |