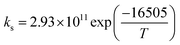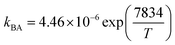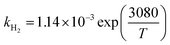Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Catalytic hydrodeoxygenation of benzoic acid as a bio-oil model compound: reaction and kinetics using nickel-supported catalysts†
Mustapha
Yusuf
 ab,
Gary A.
Leeke
a and
Joseph
Wood
ab,
Gary A.
Leeke
a and
Joseph
Wood
 *a
*a
aSchool of Chemical Engineering, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK. E-mail: j.wood@bham.ac.uk; Tel: +44 (0)121 414 5295
bDepartment of Chemical Engineering, Ahmadu Bello University, Zaria, 810261, Nigeria
First published on 19th June 2024
Abstract
The development of technologies for the bio-oil upgrading process is a crucial step towards achieving sustainable energy production. This study investigates the effects of support properties during the hydrodeoxygenation (HDO) of benzoic acid as a bio-oil model compound with the aim to produce a catalyst of superior activity and selectivity. Three Ni-based catalysts were prepared: microporous m-Ni/ZSM-5, mesoporous h-Ni/ZSM-5, and Ni/SiO2. The h-Ni/ZSM-5 exhibited the highest concentration of acid sites, strongest metal-support interaction and best metal dispersion. The highest conversion of benzoic acid was recorded over the h-Ni/ZSM-5 catalyst (97%). Ni/SiO2 catalysts produced toluene, while others produced benzene and cyclohexane in addition. This was linked to a synergy between support acidity and metal sites. The catalyst from the nearly neutral support, Ni/SiO2, showed higher activity (91% conversion) compared to m-Ni/ZSM-5 (84%), which was attributed to the mesoporous nature of Ni/SiO2, allowing more access to active sites for bulk benzoic acid molecules. A kinetic model was developed using the Langmuir–Hinshelwood–Hougen–Watson (LHHW) approach. A mechanism assuming dual-site adsorption of dissociatively adsorbed hydrogen was shown to be the most accurate representation of the three-phase benzoic acid HDO. The observed activation energy from the model was 137.2 kJ mol−1.
1 Introduction
Fossil fuels remain the major global energy source, accounting for about 88% of the total world's energy supply.1–4 Petroleum reserves, which are thought to have peaked and are currently declining, provide a significant share of the world's liquid transportation fuels.5 In addition to the depletion of fossil fuel reserves, carbon dioxide is one of the principal greenhouse gases produced primarily by the combustion of the fuels.6,7 This poses a great environmental concern.8 To meet up with future energy demands as well as to avert global warming and other forms of environmental deterioration caused by the use of fossil fuels, there is a need for alternative, sustainable, and green energy sources.9,10 Consequently, research on biomass and biomass-based fuels and chemicals has drawn a lot of interest.A proposal by the European Commission entitled “The Energy Strategy 2020” strongly recommended the utilisation of plant and animal-derived resources (biomass) as alternative sources of energy. Similarly, the International Renewable Energy Agency (IRENA) introduced a programme called “Renewable Energy Roadmap (REmap 2030)” to strategize and boost the developmental capacities of biomass energy.11 In addition, a UK legislation known as the Renewable Transport Fuels Obligation (RTFO) is designed to reduce greenhouse gas emissions from fuel used for transportation. This is to be realised by promoting the provision of renewable fuels, which, by extension, would support the government's ultimate goal of attaining net zero by 2050. It is predicted that bioenergy will make up 25–33% of the world's energy supply by 2050.12
Bio-oil, a dark brown liquid commonly referred to as biomass oil or biocrude, has been recognised as a promising renewable energy source that can be used in various applications in energy and industries.13 It is derived from the pyrolysis of various biomass resources, such as agricultural waste, wood chips, and algae. Bio-oil is a complex mixture of organic compounds containing molecules such as phenol, ketones, aldehydes, furans, sugars, and carboxylic acids. This property makes bio-oil a suitable feedstock to produce fuels and chemicals.14 However, one of the challenges in the utilization of bio-oil is its high oxygenates content. These compounds confer on bio-oil high viscosity, low heating value, thermal instability, and acidity, which limit its use as a direct substitute for petroleum-based fuels and chemical feedstocks.6,15,16 Hence, the need for upgrading.17–19 Upgrading processes such as hydrotreating or hydrocracking can convert bio-oil into more stable products with lower acidity and a higher calorific value, making it suitable for use in diesel and petrol engines. Of the various hydrotreating processes, catalytic hydrodeoxygenation (HDO) has been identified as the most promising approach for upgrading bio-oil. In this method, oxygen-containing functional groups are removed through hydrogenation reactions in the presence of a solid catalyst, and subsequently, valuable products such as gasoline are produced. Different catalysts have been investigated for bio-oil HDO, including traditional hydrodesulphurization and hydrogeneration catalysts.20 In addition, the noble and transition metal catalysts were also reported.21 Nonetheless, these catalysts are extremely prone to the coke formation and quick deactivation.22 Since the catalyst pore structures and acidity are shown to be very important in the HDO reaction,23–25 the focus of recent research works has been to identify better solid-support candidates.26,27
Organic acids such as carboxylic acid, acetic acid, and formic acid found in bio-oil are principally responsible for bio-oil acidity.28,29 The presence of these molecules in bio-oil poses a serious challenge in the field of renewable energy, leading to the deterioration of structural materials within the processing settings. This could further result in a total failure of the equipment or a high maintenance cost.30 Several solutions have been proposed to tackle this issue, including using catalysts to reduce the formation of acids during the biomass pyrolysis process.31,32 Kumar et al.33 investigated the catalytic pyrolysis of pine wood biomass over Cu and Ni-based zeolite catalysts via in situ and a combination of in situ and ex situ catalytic pyrolysis. While the former promoted acid formation in the product, the latter has two reaction stages, each requiring a substantial amount of heat and catalyst, making it capital-intensive. As a result, researchers are currently exploring hydrogenation and hydrodeoxygenation (HDO) as efficient methods for removing acidic functionalities from bio-oils.
Many researchers studied catalytic hydrogenation and HDO mechanisms using model compounds rather than bio-oils because of the complexity of bio-oil components. Among the acidic model compounds studied are the HDO of acetic acid and palmitic acid.18,34–36 The simple aliphatic hydrocarbon chains of both compounds and the carboxylic acid substitutes are much simpler than their more complex benzene-ring counterparts found in benzoic acid. In our previous study the HDO of anisole was investigated.9 Anisole is a simple aromatic ether, consisting of a phenyl ring attached to a methoxy group (–OCH3). In terms of molecular size, benzoic acid molecules are generally larger (0.8–1.2 nm) than anisole molecules (0.5–1.0 nm) due to the additional atoms in the carboxyl group.37,38 Thus, in order to better understand the diffusion effects across different catalyst support materials, it is imperative to consider the bulky compound. This will also highlight how the aromatic acid molecule interacts within the catalyst pores. Therefore, the aim of this paper is to investigate the HDO of benzoic acid over different nickel-supported catalysts. Zeolite supports enable the pore structure to be modified to increase access and diffusion rate to the catalyst active site. Zeolite ZSM-5, in particular, is a microporous aluminosilicate material that can be modified to form a new version of mesoporous material. This material combines the synergetic effect of large pores, large surface area and amorphous wall saturated with hydroxyl groups readily available for the generation of active sites needed for catalytic reaction.39 Hence, ZSM-5 was used. A mesoporous silica support (SiO2) combines a high surface area, thermal stability, tunable surface properties, ease of synthesis, and cost-effectiveness. The chemical inertness of SiO2 will elaborate on the role of acidic support when compared to ZSM-5. Nickel metal, on the other hand, eliminates the need for scarce and precious group metals such as platinum. The objective of the study is to development a robust catalyst for bio-oil upgrading, and in addition, to gain insight into the reaction mechanism and kinetics of benzoic acid HDO. The study could be an important step towards further developing effective methods to upgrade real bio-oil.
2 Materials and methods
2.1 Materials
These include microporous ZSM-5 (m-ZSM-5, SiO2/Al2O3 = 30, Alfa Aesar), mesoporous ZSM-5 (h-ZSM-5, SiO2/Al2O3 = 28, obtained via NaOH desilication of the m-ZSM-5), mesoporous silica (90%, Alfa Aesar), ammonium (II) nitrate (99%, Sigma-Aldrich), benzene (99.5%, Sigma-Aldrich), cyclohexane (99.8%, Sigma-Aldrich), decahydronaphthalene (98%, Alfa Aesar), cyclohexane (99%, Sigma-Aldrich), formic acid (96%, Sigma-Aldrich), n-decane (98%, Sigma-Aldrich), nickel(II) nitrate hexahydrate (99.9%, Sigma-Aldrich), sodium hydroxide (98%, Sigma-Aldrich), toluene (99.5%, Sigma-Aldrich), 1,2,3,4-tetrahydronaphthalene (98+%, Thermo Scientific), benzoic acid (99%, Thermo Scientific), benzaldehyde (99+%, Alfa Aesar), benzyl alcohol (99%, Alfa Aesar).2.2 Catalyst preparation
The m-ZSM-5 which is microporous in nature, was used as parent support. The h-ZSM-5 was obtained via 0.2 M NaOH treatment of the m-ZSM-5 to improve diffusion properties and enhance metal–support interaction. While the zeolite supports are acidic, the mesoporous and neutral support, SiO2, was also chosen. This will highlight the combined effect of acidity and mesoporosity. The three supports were impregnated with 5 wt% nickel, as reported previously.9 The obtained catalysts were dried over night at 80 °C and calcined at 500 °C under the flow of nitrogen for 3 hours. The resulting catalysts were designated m-Ni/ZSM-5, h-Ni/ZSM-5, Ni/SiO2.2.3 Catalyst characterisation
Using an X-ray diffraction (XRD) Bruker D8 Advance machine equipped with Cu-K radiation (1.5406 Å), the crystallographic nature of both the supports and the prepared nickel-based catalysts was determined. Diffraction patterns were recorded for a 2-theta angle range of 5° to 80° with a 0.05 step increase. Nitrogen adsorption–desorption analyses were performed on a Micromeritics 3-Flex analytical instrument at 77 K. Morphologies and chemical compositions of the catalysts were analysed using a Hitachi TM3030 SEM-EDX machine. Transmission electron microscopy (TEM) images were recorded using the Tecnai F20 instrument. The acidity of the catalysts was determined by ammonia temperature-programmed desorption (NH3-TPD) on a ChemBET machine. The hydrogen temperature programmed reduction (H2-TPR) data was collected on a Hiden Analytical CatLab instrument.2.4 HDO of benzoic acid
Reactions were carried out in a 100 mL high-pressure batch reactor, model 4590 supplied by the Parr Instrument Company, US. The reactor was equipped with a vessel of 33 mm internal diameter, 20 mm impeller diameter, and 117 mm depth. Prior to the reaction, the catalyst was reduced ex situ in a furnace at 500 °C for 3 hours under a continuous flow of hydrogen (5% H2/N2) at a heating rate of 5 °C min−1. Tetralin (1,2,3,4-tetrahydronaphthalene) was used as the solvent. In a typical run, a 50 mL mixture containing 1–9 wt% of benzoic acid in tetralin and 100 mg of the catalyst was charged into the reactor. The reactor was flushed three times with nitrogen, then pressurised to 20 bar and heated to the desired reaction temperature (300–340 °C). Stirring speed was maintained at 100 rpm during the heating-up period. Thereafter, the nitrogen was replaced with 20 to 60 bar hydrogen. Subsequently, the reactor was maintained at 800 rpm stirring rate for 1–6 hours. The liquid product was recovered from the solid catalyst by filtration.In a preliminary experiment, five different solvents were tested in order to identify the one with best dissolution of the benzoic acid and conversion during HDO. The solubility of 3 wt% benzoic acid at 20 °C in the following solvents were obtained in mass basis; decalin (1.3%), acetone (3.0%), n-decane (0.8%), ethyl acetate (2.6%), and tetralin (1.5%), respectively. Although, a total dissolution was obtained in all the solvents at 70 °C except for the n-decane. In addition, HDO reactions were carried out at temperatures of 200, 250, and 300 °C, and a pressure of 60 bar. A reasonable conversion of benzoic acid was noticed at 300 °C. These were 7% (decalin), <1% (acetone), <1% (n-decane), <2% (ethyl acetate), and about 10% (tetralin) respectively. Hence the tetralin was selected. Since the maximum operating temperature for the batch reactor is 350 °C, a temperature range of 310 °C to 340 °C with a step increase of 10 °C was chosen.
2.5 Product analysis
Liquid products from the HDO reaction were analysed using an Agilent GC (model 6890N) equipped with a flame ionisation detector (FID) and a Zebron ZB-Wax capillary column (30 m × 0.25 mm × 0.25 μm). Before the analysis, the GC was calibrated with the chemical standard of the expected liquid products. These include methyl-cyclohexane, cyclohexane, cyclohexanol, cyclohexanone, benzene, toluene, benzaldehyde, benzyl alcohol, and cyclohexane carboxylic acid for identification and quantification. To evaluate the extent of conversion, yield, and selectivity of products, the following expressions were used;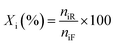 | (1) |
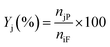 | (2) |
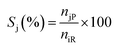 | (3) |
2.6 Kinetic study of benzoic acid HDO
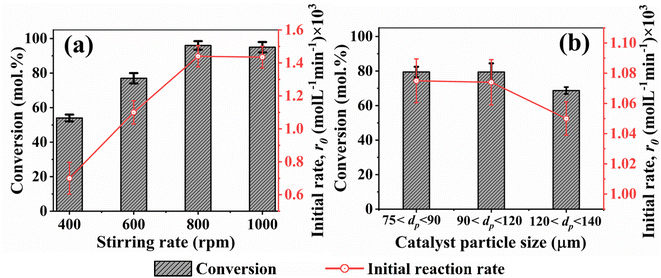
A kinetic study was performed to evaluate the influence of some reaction variables and provide a model that could be used to simulate reaction rates for process design and scale-up studies. Important parameters such as activation energy, reaction rates, and rate constants were estimated. To achieve this, it is a prerequisite to ensure the effect of mass transfer limitation is eliminated and that reaction is kinetically controlled. Hence, a study was carried out on the effect of stirring rate and catalyst particle size on the initial rate of reaction and conversion. At constant pressure and temperature, the stirring speed was varied from 400 to 1000 rpm. Prior to that, a critical impeller speed, Njs, at which no particles are stationary at the bottom of the vessel for more than a second or two, as defined by Zwietering,40 was determined (using eqn (4)).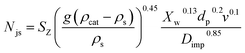 | (4) |
For the internal mass transfer and intraparticle diffusion, the influence of the catalyst particle size was investigated. The catalyst was sieved into different sizes ranging from <75, 75–90, 90–120, and >120 μm, respectively. These various sizes of the catalyst were employed for the HDO reaction under the same temperature and pressure. Subsequently, the combined effects of the stirring speed and the catalyst particle size were used to establish the kinetically controlled region, which were then applied for the remaining kinetic studies.
To estimate the kinetic parameters, some proposed correlations were adopted. Fogg and Gerrard correlations were employed to determine the value of hydrogen concentration in the reactor.42–44 The measure of the ability of reactants and the solvent to diffuse through one another at a given temperature T, also known as diffusivity or diffusion coefficient (Dei)T, was calculated using Díaz correlations.45,46 For accuracy, this correlation considered diffusivity at both 25 °C and the actual reaction temperature.
To further confirm the absence of intraparticle diffusion, a criterion suggested by Weisz and Prater47 was deployed (eqn (5)). This states that if the value of the observable modulus (nφ2), a dimensionless quantity, is less than 0.3 for a reaction order of less than or equal to 2, effect of internal diffusion is eliminated. Then the experimental observations are appropriate for kinetic study;
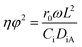 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k against the inverse of temperature T was generated according to the Arrhenius equation (eqn (6)) and the activation energy was determined. In addition, the thermodynamic parameters for the adsorption of the reactant i were evaluated using the Van't Hoff equation;43,48
k against the inverse of temperature T was generated according to the Arrhenius equation (eqn (6)) and the activation energy was determined. In addition, the thermodynamic parameters for the adsorption of the reactant i were evaluated using the Van't Hoff equation;43,48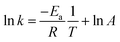 | (6) |
3 Results and discussion
3.1 Catalyst characterization
Detailed characterization results of both the supports and the prepared catalysts were described in a previous work.9 In summarising the earlier characterisations, distinctive diffraction peaks for ZSM-5, SiO2 and NiO were observed from the XRD result. The BET analysis, shown in Table S1,† confirmed the mesoporosity in the support in a decreasing order; SiO2 > h-ZSM-5 > m-ZSM-5. Elemental analysis revealed the presence of Si, Al, O, C and Ni in the respective catalysts. While there was no evidence of nickel in all the supports. Nickel was found in all the impregnated samples corresponding to a metal loading of 5 wt% ± 0.4. SEM analysis shows agglomerates of fine particles in all the samples. However, the ZSM-5-based catalysts exhibited less agglomeration and more defined crystal shapes compared to Ni/SiO2. The NH3-TPD analysis revealed low-temperature peaks at 204 °C and a high-temperature desorption peak at 460 °C in both m-ZSM-5 and h-ZSM-5 supports. This implies the presence of weak and strong acid sites. A very low intensity and broad NH3-TPD peak was found for SiO2, indicating a nearly neutral nature of the support. It can be seen from Table S1† that nickel impregnation caused an increase in the acid site concentration in all the catalysts in the order; SiO2 < m-ZSM-5 < h-ZSM-5. The H2-TPR result shows the highest metal–support interaction in h-Ni/ZSM-5 compared to the other catalysts. This is related to the combined effects of acidity and mesoporosity of the support. Acidic supports create a favourable environment for active metal species by stabilizing them via coordination interactions.49 Acid sites provide strong interaction between metal ions or complexes and the support. This improves metal dispersion and prevents leaching during catalytic reactions, resulting in long-term stability and activity.50New TEM images were captured to display finer detail and shown in Fig. 1a–f. It is clear that there is a high degree of metal dispersion, particularly in m-Ni/ZSM-5 and h-Ni/ZSM-5. The nickel particles there are smaller than those on Ni/SiO2 catalysts. The particle sizes range from 2 to 8 nm (m-Ni/ZSM-5), 2 to 7 nm (h-Ni/ZSM-5), and 5 to 22 nm (Ni/SiO2) respectively. The degree of metal dispersion on the respective catalysts was evaluated using Anderson51 equation (eqn S(1)†) as 20% for m-Ni/ZSM-5, 29% for h-Ni/ZSM-5, and 11% for Ni/SiO2. Fig. 1d–f shows the dark field TEM images of the Ni-based catalysts, which revealed bright spots indicative of nickel particles due to their higher electron scattering contrast. The bright spots are spread throughout the image, suggesting that nickel particles are well-dispersed. The spots are more pronounced on the m-Ni/ZSM-5 and Ni/SiO2 catalysts than on the h-Ni/ZSM-5 catalysts. This can be attributed to the microporous nature of the m-ZSM-5 and the highly mesoporous nature of SiO2, which make the nickel particles more visible on and within the pores of the supports. The low bright spot visibility on the h-Ni/ZSM-5 suggests high dispersion of nickel within the mesopores of the most acidic support. This agrees with the BET result, where a significant decrease in the total pore volume was seen in h-ZSM-5 after nickel impregnation. In addition, acidic support such as ZSM-5 allows for strong bonding with metal ions. This enhances metal dispersion and ensures long-term stability and activity.50
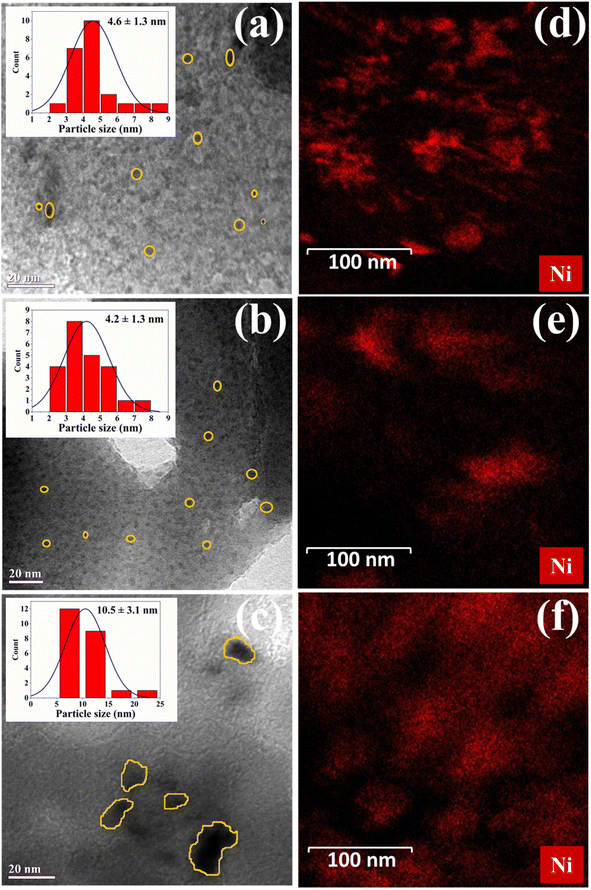 | ||
| Fig. 1 TEM image of the prepared catalysts; (a) m-Ni/ZSM-5, (b) h-Ni/ZSM-5, and (c) and Ni/SiO2. Elemental mapping by dark-field scanning TEM; (d) m-Ni/ZSM-5, (e) h-Ni/ZSM-5, and (f) Ni/SiO2. | ||
3.2 Activity test
| Conversion (%) | |||
|---|---|---|---|
| h-Ni/ZSM-5 | m-Ni/ZSM-5 | Ni/SiO2 | |
| Temp. change (°C) at 60 bar H 2 | |||
| 310 | 64.1 ± 4.3 | 57.3 ± 2.1 | 63.8 ± 4.8 |
| 320 | 76.7 ± 2.8 | 74.2 ± 3.3 | 74.5 ± 3.8 |
| 330 | 82.3 ± 5.2 | 79.7 ± 1.5 | 82.7 ± 2.6 |
| 340 | 97.9 ± 4.0 | 84.3 ± 2.8 | 91.5 ± 3.5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Change in H 2 press (bar) at 330 °C | |||
| 20 | 64.3 ± 5.0 | 61.0 ± 2.5 | 55.7 ± 6.1 |
| 40 | 71.5 ± 6.1 | 65.3 ± 1.8 | 70.2 ± 3.3 |
| 60 | 82.3 ± 5.2 | 79.7 ± 1.5 | 82.7 ± 2.6 |
From the BET result, the h-Ni/ZSM-5 has higher mesopore volume (0.169 m3 g−1) compared to the m-Ni/ZSM-5 (0.109 m3 g−1). In addition, the TEM results revealed better nickel dispersion of 29% on h-Ni/ZSM-5 against 20% recorded over the m-Ni/ZSM-5. Hence, the m-Ni/ZSM-5 is more likely to be mass transport limited than the h-Ni/ZSM-5 catalyst. Interestingly, a relatively higher activity than what was observed on the m-Ni/ZSM-5 at all the examined temperatures was achieved over the mesoporous Ni/SiO2 catalyst. HDO reaction over the mesoporous Ni/SiO2 catalyst for the respective temperatures studied achieved benzoic acid conversions of 63.8% (310 °C), 74.5% (320 °C), 82.7% (330 °C), and 91.5% (340 °C). The Ni/SiO2 catalyst has a lower concentration of acid sites compared to the m-Ni/ZSM-5 catalyst as seen from the NH3-TPD analysis result in the previous work.9 These are metal sites normally acting as weak acid sites, producing an increase in the polarisation of the reactive bonds of reactants.54 So, it is expected that the Ni/SiO2 catalyst will show low activity compared to the m-Ni/ZSM-5 catalyst that has higher density of acid sites from both the support and the active metal. However, the former outperformed the latter at all temperatures studied. This might be linked to the mesoporous nature of the SiO2 support, which will possibly allow the bulk aromatic carboxylic acid group to diffuse and access most of the available active site presence on the catalyst. From the BET results (Table S1†), the average pore width for the m-Ni/ZSM-5 and Ni/SiO2 are 3.68 nm and 10.31 nm. Relating these to the molecular geometry of benzoic acid, which is 0.55 ± 0.5 nm by 0.52 ± 0.5 nm by 2.20 ± 0.20 nm, it is expected to experience less diffusion resistance over the Ni/SiO2.55 On the other hand, the HDO reaction is more sensitive to the active metal dispersed on the carrier than to the acidity of the catalyst support. This was noticed during the catalytic HDO of anisole over the m-ZSM-5 and h-ZSM-5 supports.9 At 200 °C, 50 bar H2, 100 mg of catalyst loading, and decalin as a solvent, an anisole conversion of around 2 to 4% was recorded in 140 minutes. However, while light ends (C1–C4) were generated owing to the cracking reaction, no product was detected in the liquid sample. A similar result was obtained by Kim et al.56 when HDO of vanillin was carried out over HZSM-5 (Si/Al = 23). The same pressure (50 bar), temperature (200 °C), and catalyst loading (100 mg) as that of anisole were used. This made it apparent that successful HDO requires a catalyst with a combined effect of mesoporosity, acid, and metal sites. Acid and metal sites were shown to promote the following reactions during the HDO of phenol; formation of cyclohexanol by the metal sites; dehydration to cyclohexene by the acid site; hydrogenation to cyclohexane by the metal sites; and isomerisation to methylcyclopentane by the acid sites.57
Contrary to what is recorded here for benzoic acid, when the same set of catalysts were tested in the HDO of anisole, the m-Ni/ZSM-5 outperformed the Ni/SiO2 catalyst.9 Anisole conversion was 82.6% (m-Ni/ZSM-5) and 48.9% (Ni/SiO2) respectively, in 2 h at 200 °C and 100 mg catalyst loading. The simple reason is the higher concentration of active sites on m-Ni/ZSM-5. In addition, the smaller size of anisole eliminates mass transport limitations over the two catalysts. However, benzoic acid could not access some of the active sites on the microporous m-Ni/ZSM-5 due to its larger size compared to anisole. Hence, a lower conversion was seen over m-Ni/ZSM-5 compared to the mesoporous Ni/SiO2 catalyst during benzoic acid HDO. On the other hand, at the same catalyst loading (100 mg h-Ni/ZSM-5) and pressure (60 bar H2), a longer reaction time was seen for the benzoic acid conversion of 97.9% (6 h at 340 °C) than the anisole conversion of 100% (2 h at 200 °C). This clearly demonstrates how the carboxylic acid functional group can make bio-oil upgrading more challenging. This further illustrates how different functional groups have distinct chemical properties that influence their interaction with the catalyst surface.58
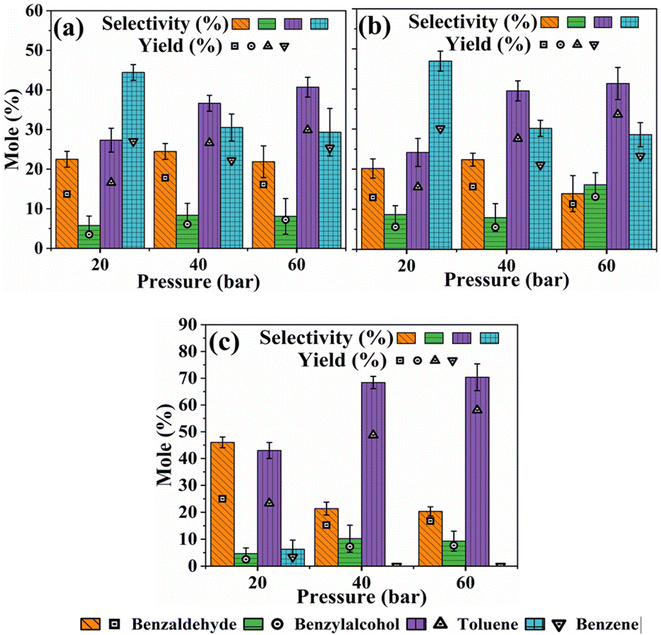
The effect of change in reaction pressure was investigated at a constant temperature of 330 °C (Table 1). There were changes in benzoic acid conversion as the hydrogen partial pressure increased. Conversion reached 79.7% (60 bar) from 61.0% (20 bar) over m-Ni/ZSM-5 catalyst, 82.3% (60 bar) from 64.3% (20 bar) when h-Ni/ZSM-5 catalyst was used, and 82.7% (60 bar) from 55.7% (20 bar) over Ni/SiO2 catalyst, respectively. This increase could be related to an increase in the number of moles of hydrogen present in the reaction medium as hydrogen pressure increases (Table S2†), thus making it more readily available for reaction at the catalyst surface. This is due to an increase in the solubility of hydrogen in tetralin (reaction solvent) as the partial pressure of hydrogen in the reactor increased.
| m-Ni/ZSM-5 temp. (°C) | Selectivity (%) | Total yield (%) | |||
|---|---|---|---|---|---|
| Benzaldehyde | Benzylalcohol | Toluene | Benzene | ||
| 310 | 16.2 ± 3.5 | 8.5 ± 4.0 | 56.6 ± 2.5 | 18.7 ± 5.0 | 54.0 ± 2.1 |
| 320 | 19.0 ± 2.4 | 9.1 ± 2.6 | 47.6 ± 2.1 | 24.3 ± 6.2 | 72.9 ± 3.5 |
| 330 | 21.9 ± 4.2 | 8.1 ± 3.5 | 40.7 ± 1.6 | 29.3 ± 2.1 | 78.6 ± 2.9 |
| 340 | 16.3 ± 6.2 | 11.6 ± 5.2 | 36.0 ± 3.4 | 36.1 ± 2.6 | 83.7 ± 5.8 |
| h-Ni/ZSM-5 temp. (°C) | Selectivity (%) | Total yield (%) | |||
|---|---|---|---|---|---|
| Benzaldehyde | Benzylalcohol | Toluene | Benzene | ||
| 310 | 8.5 ± 3.4 | 23.6 ± 5.6 | 49.5 ± 3.8 | 18.4 ± 4.3 | 59.7 ± 5.6 |
| 320 | 13.6 ± 6.1 | 17.3 ± 7.2 | 42.6 ± 2.6 | 26.6 ± 1.7 | 73.9 ± 4.2 |
| 330 | 13.9 ± 3.7 | 16.1 ± 3.5 | 37.4 ± 3.4 | 32.6 ± 5.6 | 81.3 ± 2.3 |
| 340 | 12.8 ± 5.6 | 20.1 ± 4.8 | 25.0 ± 5.7 | 42.1 ± 3.8 | 94.7 ± 6.2 |
| Ni/SiO2 temp. (°C) | Selectivity (%) | Total yield (%) | |||
|---|---|---|---|---|---|
| Benzaldehyde | Benzylalcohol | Toluene | Benzene | ||
| 310 | 15.7 ± 6.2 | 2.3 ± 6.4 | 82.1 ± 3.5 | 0.0 ± 0.0 | 63.5 ± 3.5 |
| 320 | 14.5 ± 5.4 | 7.6 ± 4.2 | 77.9 ± 2.6 | 0.0 ± 0.0 | 78.3 ± 4.1 |
| 330 | 20.3 ± 3.8 | 9.3 ± 3.5 | 70.4 ± 2.4 | 0.0 ± 0.0 | 82.5 ± 5.2 |
| 340 | 23.0 ± 5.8 | 11.0 ± 4.5 | 66.0 ± 1.7 | 0.0 ± 0.0 | 89.3 ± 1.3 |
On the other hand, the highest selectivity for toluene was 56.6% at 310 °C. A similar pattern was observed from the h-Ni/ZSM-5 catalyst. However, the selectivity towards benzene was higher over h-Ni/ZSM-5 compared to m-Ni/ZSM-5. Another key product identified is the benzaldehyde formed from the deoxygenation of the functional group –COOH to –COH. The effect of catalyst porous structure on the selectivity towards benzaldehyde was evaluated by comparing the results obtained when m-Ni/ZSM-5 and h-Ni/ZSM-5 catalysts were used. At all temperatures investigated, the selectivity towards benzaldehyde is higher with m-Ni/ZSM-5 catalyst than h-Ni/ZSM-5. Since higher benzoic acid conversion was recorded over h-Ni/ZSM-5 compared to m-Ni/ZSM-5, it can be concluded that there is a high rate of transformation to benzyl alcohol from benzaldehyde on h-Ni/ZSM-5. This implies high activity, which can be attributed to the concentration of catalytic active sites, extent of metal dispersion, and pore size distribution. In the literature, the production of benzaldehyde from benzoic acid studied over ZnO2 and ZrO2 catalysts generated benzyl alcohol, benzophenone, and traces of toluene and benzene as by-products.59,63,64 However, selective hydrogenation over the following catalysts: Pt/C, RuPd–C, Pd–C, Pt/TiO2 and Ir-based catalyst showed cyclohexane carboxylic acid and benzyl alcohol as the two major products.63,65 Herein, both benzaldehyde, benzyl alcohol, toluene, benzene, and cyclohexane were observed during the HDO of benzoic acid over the m-Ni/ZSM-5, h-Ni/ZSM-5, and Ni/SiO2 catalysts at different reaction temperatures and pressures. But since the main objective of HDO is to maximise the removal of oxygenates, toluene, benzene, and cyclohexane are considered the most desired products.
Notably, over the course of the experiment, the total yield of liquid product steadily increased with increasing reaction temperature. The yield was 83.7% over the m-Ni/ZSM-5, and 94.7% over the h-Ni/ZSM-5 at 340 °C. The proportionality relation observed between the reaction temperature and selectivity to benzene could be explained based on the findings of de Lange60 that when there is high adsorption of benzoic acid onto the catalyst active surface, it decomposes at high temperature to produce benzene or benzophenone. Unlike the m-Ni/ZSM-5 and h-Ni/ZSM-5 catalysts, the Ni/SiO2 catalyst shows zero selectivity towards benzene at all the reaction temperatures studied under 60 bar hydrogen partial pressure. The reason for this is that unlike ZSM-5 support, which has higher acid sites, SiO2 support is nearly neutral. This explains why C–C bond cleavage during the process of conversion of toluene to benzene could not take place with the Ni/SiO2 catalyst. This also agrees with the observation reported by Yusuf et al.9 during the HDO of anisole over the same catalysts. However, a high selectivity of 82.1% for toluene was recorded at 310 °C, which decreased to 66.0% at 340 °C. This can be ascribed to the HDO and hydrogenation of the –COOH functional groups that are induced by the Ni nanoparticles impregnated on the SiO2 support. However, the first-degree HDO of benzoic acid over the Ni/SiO2 catalyst yielded intermediate benzaldehyde, resulting in benzyl alcohol upon further hydrogenation. The selectivity of benzaldehyde and benzyl alcohol increased with temperature, but their conversion to the desired product decreased as the selectivity to toluene decreased. Likewise, the total yield of liquid product increased from 63.5% (310 °C) to 89.3% (340 °C).
Based on the products identified over the three prepared catalysts, m-Ni/ZSM-5, h-Ni/ZSM-5, and Ni/SiO2, the reaction pathways can be summarised using the scheme presented in Fig. 2. In brief, at a high reaction temperature and hydrogen partial pressure, there will be a high concentration of oxygen vacancies, making a favourable condition for surface reaction. At this point, benzoic acid is deoxygenated to benzaldehyde and subsequently to benzyl alcohol via hydrogenation. The benzyl alcohol is further deoxygenated into toluene. The formation of benzene requires that the toluene produced from the benzyl alcohol undergo demethylation. This was only recorded over the highly acidic Ni/ZSM-5 catalyst, herein. The possibilities of benzoic acid reacting directly through to toluene or benzene was reported in the literature.20,61 Although it is apparent that decarboxylation of benzoic acid is a much slower process than deoxygenation to benzaldehyde or toluene.60 Decarboxylation of methyl-benzoate to benzene proceeds through a radical mechanism reaction, whereby a benzyloxy-radical is formed via a homolytic cleavage of the carboxylic acid (R–COO–Ni). Thereafter, the benzyloxy-radical rapidly decarboxylates to a benzyl radical. Finally, the hydrogen atom reacts with the benzyl radical chain to terminate the reaction.64
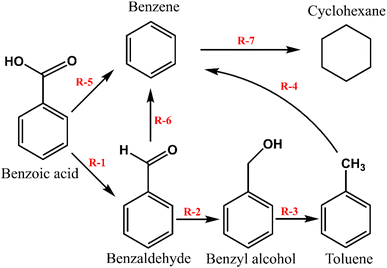 | ||
| Fig. 2 Simplified reaction pathway for the benzoic acid transformation over m-Ni/ZSM-5, h-Ni/ZSM-5, and Ni/SiO2 catalysts. (R-1; Deoxygenation, R-2; hydrogenation, R-3; deoxygenation, R-4; demethylation, R-5; decarboxylation, R-6; decarbonylation, R-7; hydrogenation).60,77 | ||
Remarkably, the current work exhibits a higher degree of benzoic acid deoxygenation than previously reported. Catalytic hydrogenation of benzoic acid over Pt/TiO2 to cyclohexane carboxylic acid was described by Guo et al.63 The conversion and selectivity at 80 °C, 50 bar H2, and 6 h of reaction were 99% and 99% in hexane as the solvent, 84% and 99% in water, and 68% and 96% in acetic acid, respectively. In a related work, the reaction was conducted at 85 °C and 1 bar H2 for 24 h using the lead-supported carbon catalyst, Pb/CN. Conversion and selectivity were 100% both in water, 10% and 100% in ethanol, and 0% both in dioxane.66 The deoxygenation of benzoic acid to benzaldehyde over a ZnO catalyst was reported.60 Complete conversion was achieved at 360 °C with a higher yield of 99% than what was seen at 420 °C, where 64% of the yield was toluene. Hydrogenation of benzoic acid using mono- and bimetallic catalysts of Ru and Pd yielded different products.67 It was observed that 5% Ru/C was an active catalyst for hydrogenation of both the aromatic ring and carboxylic group yielding cyclohexane carboxylic acid (70%) and cyclohexyl methanol (30%). The Pd/C catalyst hydrogenated only the aromatic ring to yield 60% cyclohexane carboxylic acid. Whereas, Ru–Sn/Al2O3 catalyst chemo-selectively hydrogenates the –COOH group of benzoic acid to produce benzyl alcohol.
Fig. 3a–c shows the results of the impact of H2 pressure on product distribution during the HDO of benzoic acid over m-Ni/ZSM-5 (a), h-Ni/ZSM-5 (b), and Ni/SiO2 (c) catalysts. With an increase in hydrogen pressure, both m-Ni/ZSM-5 and h-Ni/ZSM-5 catalysts show increased selectivity towards toluene but decreased selectivity towards benzene. Thus, HDO and hydrogenation reactions increase as more hydrogen molecules become available, leading to more toluene being produced as hydrogen pressure increases from 20 bar to 60 bar (Table S2†). Low hydrogen partial pressure was shown to favour benzene selectivity during the catalytic hydrogenation of benzoic acid to benzaldehyde.64 Toluene selectivity increased from 43.0% (20 bar) to 70.4% (60 bar) over Ni/SiO2 as hydrogen pressure increased. Except at a lower hydrogen pressure of 20 bar, where the liquid product was 6.3% selective to benzene, there is no benzene observed with the Ni/SiO2 catalyst at 40 and 60 bar hydrogen partial pressure. This may be linked to the neutral nature of the SiO2 support, leading to a lack of C–C bond cleavage functionality at the acid sites. This observation implies that, as the hydrogen partial pressure increased, the concentration of oxygen vacancies also increased. With more neighbouring oxygen vacancies available, benzaldehyde can be re-adsorbed on the catalyst's active sites. This leads to further transformation and generation of more toluene.64 Hence, the selectivity of benzaldehyde decreased with an increase in hydrogen pressure, while that of benzyl alcohol increased (Fig. 3c). However, the selectivity of both benzaldehyde and benzyl alcohol followed a similar trend for both m-Ni/ZSM-5 and h-Ni/ZSM-5 catalysts, except at the hydrogen pressure of 60 bar (Fig. 3a and b). As recorded with temperature, there was an increase in the yield of liquid products as the reaction pressure increased for all the catalysts studied.
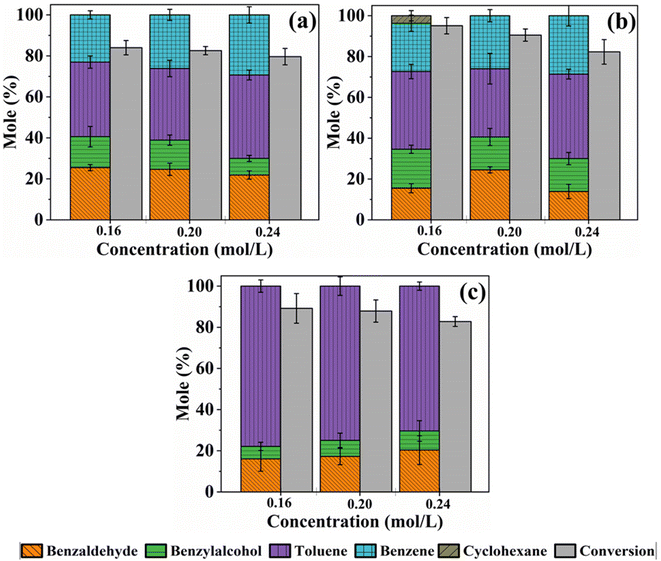
It can be observed that in all the three catalysts, the benzoic acid conversion decreases as its initial concentration increases from 0.16 M to 0.24 M. This observed trend could be explained by increasing competition between the reactants to occupy a limited number of active sites on the catalyst as initial concentrations rise.68 As the ratio of the concentration of the catalyst active sites to benzoic acid in the reaction mixture decreases, conversion also decreases. Hence, a decrease in benzoic acid conversion from 84.0 to 79.6% on m-Ni/ZSM-5, 95.0 to 82.3% on h-Ni/ZSM-5, and 89.2, to 82.8% over Ni/SiO2 was observed as the initial concentration increased from 0.16 to 0.24 M, respectively. The amount of benzene produced increased slightly, from 23.0% to 29.3% and from 23.7% to 28.6% over m-Ni/ZSM-5 and h-Ni/ZSM-5 catalysts. Similarly, toluene selectivity increased from 36.4 to 40.7% and 38.1% to 41.3% for initial benzoic acid concentrations of 0.16 M and 0.24 M. When the Ni/SiO2 catalyst was used, the amount of toluene produced decreased as the initial concentration of benzoic acid increased, while both benzaldehyde and benzyl alcohol increased slightly (Fig. 4c). Notably, about 3.7% cyclohexane was formed when the h-Ni/ZSM-5 catalyst was used on a 0.16 M benzoic acid initial concentration (Fig. 4b). For the same concentration (0.16 M), cyclohexane was seen at reaction temperatures of 320, 330, and 340 °C respectively, over the h-Ni/ZSM-5 catalyst (Table S3†). The formation of cyclohexane was possible via hydrogenation of benzoic acid to cyclohexane carboxylic acid, which decarboxylates to cyclohexane.20,67 However, as the cyclohexane carboxylic acid was not detected at any point during the reaction while the samples were being withdrawn from the reactor for analysis, and that decarboxylation is a much slower process than deoxygenation,60 cyclohexane may possibly emerge from the hydrogenation of benzene.
3.3 Kinetic study of benzoic acid HDO
The study was carried out to evaluate the effect of reaction variables and determine some important kinetic parameters. These parameters, such as activation energy (EA), rate constants (k), enthalpy (ΔH), and entropy (ΔS) changes, provide valuable information about the mechanism of a reaction and useful data for the design, optimization, and scale-up of chemical processes. The parameters can only be estimated accurately if mass transfer limitations are eliminated within the heterogeneous reaction system.35,69,70 This can be done by changing variables such as stirring speed and catalyst particle size while observing their effects on conversion.67,71 The sole aim is to remove both external and internal mass transfer constraints so that reaction rates are determined within a kinetic control regime.34,72 The differential method of rate analysis was used to evaluate the experimental rates due to the complex nature of the reaction. A second order polynomial was employed to fit the concertation-time data (Fig. S1†) generated from the 6 h HDO. The reaction temperature was varied between 310 and 340 °C at 10 °C step increase while benzoic acid concentrations were 0.24, 0.20, and 0.16 M. The LHHW model was used because most of the reaction mechanisms proposed for the HDO reaction of bio-oil are based on this model.68 Although other kinetic models, such as power-law and Eley-Rideal might be suitable for certain reactions, they did not capture the full complexity of surface reactions addressed by the LHHW model. Among the catalysts prepared and tested herein, h-Ni/ZSM-5 shows the best activity and is therefore selected for the kinetic study.To further confirm the absence of intraparticle diffusion, a criterion suggested by Weisz and Prater47 was deployed. This states that if the value of the observable modulus (ηφ2), as defined in eqn (5), is less than 0.3 for a reaction order of less than or equal to 2, the effect of internal diffusion is eliminated. Then the experimental data are appropriate for kinetic model development. Table 3 displays the Weisz-Prater values for both hydrogen and benzoic acid reactants at the different reaction temperatures investigated. The results show that the values are significantly lower than 0.3, which agrees with the results presented in Fig. 5, implying that at 800 rpm and catalyst particles with a diameter of less than or equal to 120 μm both external and internal mass transport limitations are eliminated.
| Temperature (°C) | 310 | 320 | 330 | 340 |
|---|---|---|---|---|
| C H2 (mM) | 49 | 54 | 60 | 66 |
| r 0 × 10−6 (kmol kgcat−1 s−1) | 5.77 | 7.03 | 8.92 | 12.00 |
| D eH2 × 10−7 (m2 s−1) | 1.72 | 1.85 | 1.98 | 2.12 |
| D eBA × 10−8 (m2 s−1) | 8.13 | 8.75 | 9.39 | 10.06 |
| ηφ H2 2 × 10−7 | 3.60 | 3.71 | 3.98 | 4.54 |
| ηφ BA 2 × 10−7 | 1.56 | 1.77 | 2.09 | 2.63 |
| Constants | ω = 2 (kg m−3), CBA = 240 mM, L = 1.625 × 10−5 m | |||
(A) Single site adsorption of dissociatively chemisorbed H2;
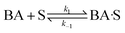 | (7) |
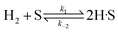 | (8) |
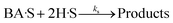 | (9) |
(B) Dual site adsorption of dissociatively chemisorbed H2;
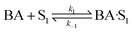 | (10) |
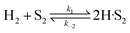 | (11) |
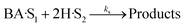 | (12) |
(C) Single site adsorption of non-dissociatively chemisorbed H2;
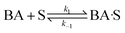 | (13) |
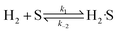 | (14) |
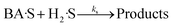 | (15) |
(D) Dual site adsorption of non-dissociatively chemisorbed H2;
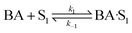 | (16) |
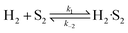 | (17) |
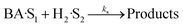 | (18) |
For all the proposed models, the surface reaction step (eqn (9), (12), (15) and (18)) was assumed to be the rate-limiting step. This is because more than 75% of all heterogeneous reactions that are not diffusion-limited are surface reaction-limited.73 For instance, the HDO of acetic acid over a supported platinum catalyst was modeled based on the LHHW kinetics.34 A model assuming dual-site adsorption of dissociative H2 and acetic acid, with surface reaction step as the rate-determining, fitted the experimental data. Similarly, the LHHW kinetic model was successfully employed to investigate the HDO of m-cresol over Pt/SiO2 catalyst. Surface reaction was assumed the rate-determining step.74 In addition, the deoxygenation step was identified as the rate-determining step in the HDO of oxygen-containing components such as phenolics.75
Four LHHW-type kinetic models were developed to describe the overall rate expression of benzoic acid consumption during the HDO reaction and the corresponding mechanism involved. To identify the best LHHW kinetic model, the different developed models were linearised and fitted to the experimental data. A linearised method is used to check if a model, accurately, predicts the behaviour of the experimental data.73 When the coefficient of determination (R2) is greater than or equal to 0.99, the experimental data is well fitted by the kinetic model. Table 4 shows the two best fitted proposed kinetic models and their linearised forms. In addition, Fig. 6 shows the linearised model fit to the experimental data at the different temperatures investigated. Since both models I and II have the same values on x (CBA) and y (CBA/r) axes, then the two models produced same plot. The R2 values from the plot were greater than 0.99 at all temperatures. This implies that the experimental data is in accordance with a LHHW dual-site adsorption isotherm.
| Model | Mechanism | Rate expression | Linearised expression |
|---|---|---|---|
a Where 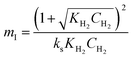 , , 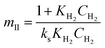 , , 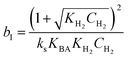 and and 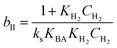 . .
|
|||
| I | Dual sites adsorption of dissociatively adsorbed H2 |
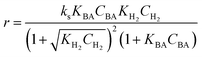
|
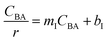
|
| II | Dual sites adsorption of non-dissociatively adsorbed H2 |
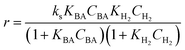
|
|
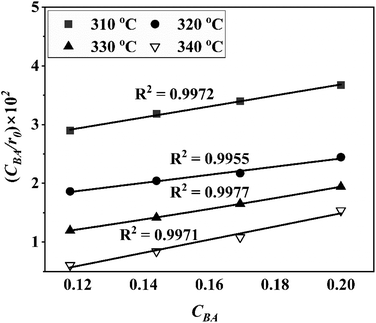 | ||
| Fig. 6 Plot of the linearised form of the best fitted kinetic models (I) dual sites adsorption of dissociatively adsorbed H2 and (II) dual sites adsorption of non-dissociatively adsorbed H2. | ||
Furthermore, to determine which of the two best fitted models is more appropriate to use in evaluating the kinetics parameters, the kinetic data was further analysed with Excel's solver optimizer. Eqn (19) and (20) define the objective functions to be minimised (RSS) and maximised (R2) to solve the model and determine its parameters;
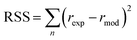 | (19) |
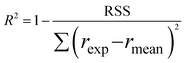 | (20) |
The significance of the R2 value determines how applicable a model is. Model II with low values of R2 compared to the model I (Table 5) was regarded as not adequately describing the experimental data and therefore rejected. Based on model I (dual-sites adsorption of dissociatively adsorbed H2), kinetic parameters such as the surface reaction rate constant (ks), hydrogen equilibrium constant (KH2), and benzoic acid equilibrium constant (KBA) were estimated using a non-linear solver in Microsoft Excel. Table 5 presents the results. The upper and the lower values of equilibrium constants determined at 310 °C and 340 °C were 3.09 and 1.64 m3 mol−1 (KBA), and 0.23 and 0.18 m3 mol−1 (KH2) respectively. These parameters are key indicators of the nature of the bond between the h-Ni/ZSM-5 catalyst and reactants. According to the result obtained here, the species has a moderately strong binding to the catalyst surface. Balanced adsorption and desorption are thus provided, which is frequently necessary for effective catalytic activity.76 In a similar study, 2.53 m3 mol−1 was reported as the adsorption equilibrium constant for benzoic acid, and 0.78 m3 mol−1 for hydrogen over a Ru–Sn/Al2O3 catalyst during chemo-selective hydrogenation of benzoic acid at 240 °C.67 Furthermore, the Arrhenius and Van't Hoff isochore equations were used to estimate the activation energy, enthalpies and entropies of adsorption, shown in Table 6. The estimated activation energy is 137.2 kJ mol−1, while 2.9 × 1011 kmol kgcat−1 min−1 is the frequency factor. This value is higher than the 81.6 kJ mol−1 reported for the hydrogenation of benzoic acid to benzyl alcohol over a bimetallic Ru–Sn/Al2O3 catalyst.64 Similarly, an activation energy of 96.6 kJ mol−1 was reported for the hydrogenation of benzoic acid over Pt–Sn/Al2O3 catalyst.77 Herein, the enthalpy change (ΔH) for benzoic acid and hydrogen were −65.1 kJ mol−1 and −25.6 kJ mol−1 K−1, and the entropy change (ΔS) were −0.102 and −0.056 kJ mol−1 K−1 respectively. The negative values of the enthalpies and entropies recorded indicate the process is exothermic and spontaneous.
| Kinetic parameters | 310 °C | 320 °C | 330 °C | 340 °C |
|---|---|---|---|---|
| k s (kmol kgcat−1 mim−1) | 0.145 ± 0.001 | 0.249 ± 0.001 | 0.378 ± 0.001 | 0.587 ± 0.016 |
| K BA (m3 kmol−1) | 3.090 ± 0.007 | 2.455 ± 0.013 | 1.850 ± 0.005 | 1.637 ± 0.016 |
| K H2 (m3 kmol−1) | 0.225 ± 0.001 | 0.204 ± 0.004 | 0.184 ± 0.001 | 0.175 ± 0.006 |
| RSS | 6.131 × 10−10 | 1.129 × 10−8 | 2.289 × 10−8 | 2.584 × 10−8 |
| Variance | 1.004 × 10−8 | 4.485 × 10−8 | 1.153 × 10−7 | 2.071 × 10−7 |
| R model-I 2 | 0.991 | 0.968 | 0.974 | 0.978 |
| R model-II 2 | 0.969 | 0.942 | 0.930 | 0.950 |
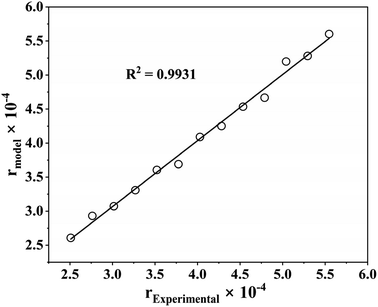
With an R2 value greater than 99%, Fig. 7 shows the parity plot for model I and the experimental data, which supports the claim that experimental and predicted reaction rates are highly correlated. Therefore, model I can also predict the benzoic acid concentration at various reaction temperatures, which agrees with experimental results. Consequently, it can be concluded that model I, which includes a dual-site adsorption and hydrogen is dissociatively adsorbed, is accurately representative of the kinetics of the three-phase benzoic acid HDO reaction conducted in a batch reactor with 5% h-Ni/ZSM-5 catalyst.
4 Conclusion
The influence of support properties during the HDO of benzoic acid as a typical bio-oil model compound was successfully investigated. Three catalysts; m-Ni/ZSM-5, h-Ni/ZSM-5 and Ni/SiO2, were prepared, characterised, and tested in a 100 mL high-pressure batch reactor. The highest conversion of benzoic acid, 97.9%, was recorded from the h-Ni/ZSM-5 catalyst. This superior catalytic activity was attributed to the improved acid sites concentration and very good metal dispersion. The mesoporous Ni/SiO2 which is nearly neutral compared to the ZSM-5-based catalysts, shows a higher benzoic acid conversion (91.5%) than the microporous nickel-zeolite catalyst, m-Ni/ZSM-5 (84.3%). While the reaction pathways were similar over the three catalysts, the ZSM-5 based catalysts promoted demethylation of toluene to produce benzene. Subsequently, the hydrogenation of benzene to cyclohexane over the h-Ni/ZSM-5. It is obvious from the outcome of this study that both the support acidity, the porosity, and the active metal site are crucial in the design of HDO catalysts. Similarly, the LHHW kinetic model was successfully employed to investigate the HDO of benzoic acid over the h-Ni/ZSM-5 catalyst. A model assuming dual-site adsorption of dissociative H2, with surface reaction step as the rate-determining, fitted the experimental data. The observed activation energy from the model was 137.2 kJ mol−1.Conflicts of interest
The authors declare no competing financial interests related to this research.Acknowledgements
This research was financially supported by the Petroleum Technology Development Fund (PTDF) Abuja-Nigeria under the Overseas Scholarship Scheme (OSS) grant, PTDF/ED/OSS/PHD/MY/1554/19.References
- P. R. Bhoi, A. S. Ouedraogo, V. Soloiu and R. Quirino, Renew. Sustain. Energy Rev., 2020, 121, 109676 CrossRef CAS.
- S. Cheng, L. Wei, X. Zhao and J. Julson, Catalysts, 2016, 6, 195 CrossRef.
- M. K. G. Deshmukh, M. Sameeroddin, D. Abdul and M. Abdul Sattar, Mater. Today Proc., 2023, 80, 1756–1759 CrossRef CAS.
- J. M. Neto, A. Komesu, L. H. d S. Martins, V. O. O. Gonçalves, J. A. R. de Oliveira and M. Rai, J. Sustain. Bioenergy, 2019, 283–298 Search PubMed.
- A. M. Lawal, A. Hart, H. Daly, C. Hardacre and J. Wood, Ind. Eng. Chem. Res., 2019, 58, 7998–8008 CrossRef CAS.
- U. Lawan Muhammad, J. Pet. Sci. Eng., 2018, 2, 44 CrossRef.
- X. Xu, E. Jiang, R. W. S. Lima, T. L. R. Hewer, M. Schmal, X. Lan, E. J. M. Hensen, T. Weber, M. Hellinger, S. Baier, P. Mortensen, W. Kleist, A. Jensen, J.-D. Grunwaldt, K. Liu, K. Liu, J. E. Peters, J. R. Carpenter, D. C. Dayton, P. Sirous-Rezaei, J. Jae, J. M. Ha, C. H. Ko, J. M. Kim, J. K. Jeon, Y. K. Park and W. Song, Energy Fuel., 2015, 550, 1472–1483 Search PubMed.
- Y. Q. Zhang, L. Li, M. Sadiq and F. S. Chien, Energy Environ., 2024, 35, 2248–2269 CrossRef.
- M. Yusuf, G. Leeke and J. Wood, Energy Fuel., 2023, 37, 1225–1237 CrossRef CAS.
- Y. Zhou and C. Hu, Catalysts, 2020, 10, 1–25 CrossRef CAS.
- W. Jin, L. Pastor-Pérez, D. K. Shen, A. Sepúlveda-Escribano, S. Gu and T. Ramirez Reina, ChemCatChem, 2019, 11, 924–960 CrossRef CAS.
- H. M. Salmi, MSc dessertation, Haaga-Helia University, 2023 Search PubMed.
- M. Haghighat, N. Majidian, A. Hallajisani and M. Samipourgiri, Sustain. Energy Technol. Assessments, 2020, 42, 100870 CrossRef.
- X. Li, G. Chen, C. Liu, W. Ma, B. Yan and J. Zhang, Renew. Sustain. Energy Rev., 2017, 71, 296–308 CrossRef CAS.
- Y. Dahman, K. Syed, S. Begum, P. Roy and B. Mohtasebi, Biofuels: Their Characteristics and Analysis, Elsevier Ltd, 2019 Search PubMed.
- I. Mudi, A. Hart, A. Ingram and J. Wood, Catalysts, 2023, 13, 171 CrossRef CAS.
- S. Hansen, A. Mirkouei and L. A. Diaz, Renew. Sustain. Energy Rev., 2020, 118, 109548 CrossRef CAS.
- M. Song, Z. Zhong and J. Dai, J. Anal. Appl. Pyrolysis, 2010, 89, 166–170 CrossRef CAS.
- A. Witsuthammakul and T. Sooknoi, Catal. Sci. Technol., 2015, 5, 3639–3648 RSC.
- M. Chen, C. Li, G. R. Li, Y. L. Chen and C. G. Zhou, Pet. Sci., 2019, 16, 439–446 CrossRef CAS.
- S. Gutiérrez-Rubio, I. Moreno, D. P. Serrano and J. M. Coronado, ACS Omega, 2019, 4, 21516–21528 CrossRef PubMed.
- S. Keav, A. Martin, J. Barbier and D. Duprez, Catal. Today, 2010, 151, 143–147 CrossRef CAS.
- N. S. Nesterov, A. A. Smirnov, V. P. Pakharukova, V. A. Yakovlev and O. N. Martyanov, Catal. Today, 2021, 379, 262–271 CrossRef CAS.
- M. Saidi and M. Safaripour, Sustain. Energy Technol. Assessments, 2022, 49, 101770 CrossRef.
- P. Szczyglewska, A. Feliczak-Guzik and I. Nowak, Microporous Mesoporous Mater., 2020, 293, 109771 CrossRef CAS.
- M. Zhang, H. Wang, X. Han, Y. Zeng and C. C. Xu, Biomass Bioenergy, 2023, 174, 106814 CrossRef CAS.
- Y. Zhang, S. Wu, X. Xu and H. Jiang, Catal. Sci. Technol., 2020, 10, 835–843 RSC.
- L. Qu, X. Jiang, Z. Zhang, X. G. Zhang, G. Y. Song, H. L. Wang, Y. P. Yuan and Y. L. Chang, Green Chem., 2021, 23, 9348–9376 RSC.
- D. Sulejmanovic, J. R. Keiser, Y. F. Su, M. D. Kass, J. R. Ferrell, M. V. Olarte, J. E. Wade and J. Jun, Sustainability, 2022, 14, 11743 CrossRef CAS.
- A. Oasmaa, D. C. Elliott and J. Korhonen, Energy Fuel., 2010, 24, 6548–6554 CrossRef CAS.
- D. Chen, K. Cen, X. Jing, J. Gao, C. Li and Z. Ma, Bioresour. Technol., 2017, 233, 150–158 CrossRef CAS PubMed.
- M. Sharifzadeh, M. Sadeqzadeh, M. Guo, T. N. Borhani, N. V. S. N. Murthy Konda, M. C. Garcia, L. Wang, J. Hallett and N. Shah, Prog. Energy Combust. Sci., 2019, 71, 1–80 CrossRef.
- R. Kumar, V. Strezov, E. Lovell, T. Kan, H. Weldekidan, J. He, S. Jahan, B. Dastjerdi and J. Scott, J. Anal. Appl. Pyrolysis, 2019, 140, 148–160 CrossRef CAS.
- A. M. Lawal, A. Hart, H. Daly, C. Hardacre and J. Wood, Energy Fuel., 2019, 33, 5551–5560 CrossRef.
- X. Liu, M. Yang, Z. Deng, A. Dasgupta and Y. Guo, Chem. Eng. J., 2021, 407, 126332 CrossRef CAS.
- A. Wang, D. Austin, A. Karmakar, G. M. Bernard, V. K. Michaelis, M. M. Yung, H. Zeng and H. Song, ACS Catal., 2017, 7, 3681–3692 CrossRef CAS.
- D. C. Spellmeyer, P. D. J. Grootenhuis, M. D. Miller, L. F. Kuyper and P. A. Kollman, J. Phys. Chem., 1990, 94, 4483–4491 CrossRef CAS.
- S. L. Tan and E. R. T. Tiekink, Acta Crystallogr., 2019, 75, 1–7 CrossRef CAS PubMed.
- J. Ćejka and A. Vinu, Ordered Porous Solids, 2009, pp. 669–692 Search PubMed.
- P. M. Armenante, E. U. Nagamine and J. Susanto, Can. J. Chem. Eng., 1998, 76, 413–419 CrossRef CAS.
- C. Devarajulu and M. Loganathan, J. Appl. Fluid Mech., 2016, 9, 2753–2761 CrossRef.
- A. Pintar, G. Berčič and J. Levec, AIChE J., 1998, 44, 2280–2292 CrossRef CAS.
- S. Srivastava, G. C. Jadeja and J. K. Parikh, Int. J. Chem. React. Eng., 2018, 16, 20170197 CrossRef CAS.
- P. Chang and C. R. Wilke, AIChE J., 1955, 264–270 Search PubMed.
- M. N. Siddiquee, A. De Klerk and N. Nazemifard, React. Chem. Eng., 2016, 1, 418–435 RSC.
- M. Díaz, A. Vega and J. Coca, Chem. Eng. Comm., 1987, 52, 271–281 CrossRef.
- P. B. Weisz, C. D. Prater, W. G. Frankenburg, V. I. Komarewsky and E. K. Rideal, Advances in Catalysis, 1954, vol. 6, pp. 143–196 Search PubMed.
- H. S. Fogler, Elements of Chemical Reaction Engineering, 2019 Search PubMed.
- L. Ezeonu, Z. Tang, Y. Qi, F. Huo, Y. Zheng, B. E. Koel and S. G. Podkolzin, J. Catal., 2023, 418, 190–202 CrossRef CAS.
- R. Kumar, V. Strezov, E. Lovell, T. Kan, H. Weldekidan, J. He, B. Dastjerdi and J. Scott, Bioresour. Technol., 2019, 279, 404–409 CrossRef CAS PubMed.
- J. R. Anderson, Sci. Prog., 1985, 69, 461–484 CAS.
- M. Hosseinpour, M. Akizuki, A. Yoko, Y. Oshima and M. Soltani, Microporous Mesoporous Mater., 2020, 292, 109708 CrossRef CAS.
- J. A. Hunns, M. Arroyo, A. F. Lee, J. M. Escola, D. Serrano and K. Wilson, Catal. Sci. Technol., 2016, 6, 2560–2564 RSC.
- J. Albero and H. García, Metal Organic Frameworks as Catalysts for Organic Reactions, Elsevier B.V., 2016 Search PubMed.
- R. Feld, M. S. Lehmann, K. W. Muir and J. C. Speakman, Z. für Kristallogr.–Cryst. Mater., 1981, 157, 215–232 CrossRef CAS.
- H. Kim, S. Yang, Y. H. Lim, J. M. Ha and D. H. Kim, J. Hazard. Mater., 2022, 423, 126525 CrossRef CAS PubMed.
- A. Berenguer, S. Gutiérrez-Rubio, M. Linares, C. Ochoa-Hernández, I. Moreno, J. L. García-Fierro, J. M. Coronado, D. P. Serrano and P. Pizarro, Energy Technol., 2019, 7, 1–13 CrossRef.
- W. Wang, J. Lin, S. Shao, H. Chen, J. Dai and Y. Yang, J. Environ. Chem. Eng., 2023, 11, 109002 CrossRef CAS.
- X. Q. Hu, Z. K. Liu, Y. X. Hou and Y. Gao, iScience, 2020, 23, 101266 CrossRef CAS PubMed.
- M. W. De Lange, J. G. Van Ommen and L. Lefferts, Appl. Catal., 2002, 231, 17–26 CrossRef CAS.
- M. Tang, S. Mao, X. Li, C. Chen, M. Li and Y. Wang, Green Chem., 2017, 19, 1766–1774 RSC.
- Z. Chen, Y. Hou, W. Song, D. Cai, Y. Yang, Y. Cui and W. Qian, Chem. Eng. J., 2019, 371, 639–646 CrossRef CAS.
- M. Guo, X. Kong, C. Li and Q. Yang, Commun. Chem., 2021, 4, 1–10 CrossRef PubMed.
- S. B. Shinde and R. M. Deshpande, Asian J. Chem., 2022, 34, 2538–2544 CAS.
- A. Kong, M. Liu, H. Zhang, Z. Cao, J. Zhang, W. Li, Y. Han and Y. Fu, Chem. Eng. J., 2022, 445, 136719 CrossRef CAS.
- X. Xu, M. Tang, M. Li, H. Li and Y. Wang, ACS Catal., 2014, 4, 3132–3135 CrossRef CAS.
- S. B. Shinde and R. M. Deshpande, Asian J. Chem., 2022, 34, 2538–2544 CAS.
- E. Aliu, A. Hart and J. Wood, Ind. Eng. Chem. Res., 2019, 58, 15162–15172 CrossRef CAS.
- A. Coker, Modeling of Chemical Kinetics and Reactor Design, 2001 Search PubMed.
- J. G. Wang, L. Y. Yang, H. Liu and C. Y. Li, J. Beijing Univ. Chem. Technol. (Nat. Sci. Ed.), 2005, 32, 10–15 CAS.
- C. Perego and S. Peratello, Catal. Today, 1999, 52, 133–145 CrossRef CAS.
- H. S. Fogler, Chemical Reaction Engineering, 2004 Search PubMed.
- H. S. Fogler, Elements of Chenzicn 1 Reaction Engineering, 2006 Search PubMed.
- L. Nie and D. E. Resasco, J. Catal., 2014, 317, 22–29 CrossRef CAS.
- Z. Yu, K. Yao, Y. Wang, Y. Yao, Z. Sun, Y. Liu, C. Shi, W. Wang and A. Wang, Catal. Today, 2021, 371, 179–188 CrossRef CAS.
- A. Corma and F. J. Ortega, J. Catal., 2005, 233, 257–265 CrossRef CAS.
- X. Chen, PhD Thesis, University of Manchester, 2019 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4se00589a |
| This journal is © The Royal Society of Chemistry 2024 |