Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Adaptive mixed variable Bayesian self-optimisation of catalytic reactions†
Naser
Aldulaijan
,
Joe A.
Marsden
,
Jamie A.
Manson
 and
Adam D.
Clayton
and
Adam D.
Clayton
 *
*
Institute of Process Research and Development, Schools of Chemistry & Chemical and Process Engineering, University of Leeds, LS2 9JT, UK. E-mail: A.D.Clayton@leeds.ac.uk
First published on 17th October 2023
Abstract
Catalytic reactions play a central role in many industrial processes, owing to their ability to enhance efficiency and sustainability. However, complex interactions between the categorical and continuous variables leads to non-smooth response surfaces, which traditional optimisation methods struggle to navigate. Herein, we report the development and benchmarking of a new adaptive latent Bayesian optimiser (ALaBO) algorithm for mixed variable chemical reactions. ALaBO was found to outperform other open-source Bayesian optimisation toolboxes, when applied to a series of test problems based on simulated kinetic data of catalytic reactions. Furthermore, through integration of ALaBO with a continuous flow reactor, we achieved the rapid self-optimisation of an exemplar Suzuki–Miyaura cross-coupling reaction involving six distinct ligands, identifying a 93% yield within a budget of just 25 experiments.
Introduction
The optimisation of chemical reactions plays a pivotal role in addressing critical global challenges, such as reducing the environmental impact of waste generated during manufacturing processes.1 Significant steps towards achieving a more sustainable future can be taken by maximising resource efficiency and minimising the formation of hazardous by-products.2 Moreover, within the pharmaceutical industry, process optimisation can reduce the production costs of essential medicines, enabling greater accessibility for vulnerable populations in low-income countries.3Reaction optimisation involves systematically fine-tuning the various parameters of a chemical reaction to achieve the desired product outcomes. One-variable-at-a-time (OVAT) is a traditional optimisation approach, whereby individual variables are altered while keeping others constant to observe the effect on the reaction. Although simple to perform, this method often fails to capture interactions between variables, and is susceptible to bias from chemists' intuition.4 In contrast, high-throughput screening (HTS) approaches typically involve exhaustively exploring combinations of reaction conditions to identify the global optimum. However, chemical reactions are examples of expensive-to-evaluate functions, as conducting experiments to evaluate performance requires significant time and costly reagents. Therefore, ongoing research is focused on the development of more efficient optimisation strategies that reduce the number of required experiments.5
Recently, there has been an increase in the development and application of machine learning methods for optimisation of chemical reactions.6–15 Self-optimising platforms leverage automation and robotics to rapidly conduct experiments suggested by optimisation algorithms, thus accelerating process development.16,17 For example, Taylor et al. explored the use of multi-task Bayesian optimisation (MTBO) to efficiently optimise previously unseen C–H activation reactions.18 Data from previous optimisation campaigns of similar reactions was used to inform and accelerate the optimisation of reactions with differing substrates. However, this method becomes less effective as the difference in reactivity of the substrates increases, highlighting a need for efficient single task optimisers when there is no suitable a priori information available.19
Most examples of self-optimisation have focused on continuous variables due to their ease of handling in traditional mathematical formulae and algorithms. However, this reveals a major limitation as categorical variables can have a significant effect on the performance of a chemical reaction. One approach to overcome this challenge is to convert categorical variables into continuous representations. For example, Lapkin et al. demonstrated optimum solvent selection for an asymmetric hydrogenation reaction, where the solvents were input as a set of molecular descriptors.20 Although this method can provide a model which describes the relationship between categorical variables, it relies on the selection of appropriate molecular descriptors which can require extensive preliminary data collection to deduce.
To remove this necessity, Bourne et al. reported the development of a mixed variable multiobjective optimisation (MVMOO) algorithm, where categorical variables were retained in the optimisation domain by using novel distance metrics based on Gower similarity.21 However, the target of multiobjective optimisation techniques is the identification of the trade-off curve between conflicting performance criteria, which typically require up to four times the number of experiments compared to their single objective counterparts.22 Whilst this provides useful information in late-stage process development, the additional expense required can be undesirable in early-stage discovery where yield is often the primary objective. Although Bayesian optimisation toolboxes have been applied for single objective mixed variable self-optimisation,7–9,13,14 the absence of a systematic and chemically-motivated comparison of these techniques makes algorithm selection a challenging task.23–26
Herein, we describe the development of a new single objective adaptive latent Bayesian optimiser (ALaBO) for reactions involving continuous and categorical variables. The performance of the algorithm is benchmarked against current state-of-the-art open-source Bayesian optimisation packages, using five different case studies based on simulated kinetic data of catalytic reactions. The self-optimisation of a Pd-catalysed Suzuki–Miyaura cross-coupling reaction is demonstrated by integration of ALaBO with an automated continuous flow reactor platform.
Results and discussion
Adaptive latent Bayesian optimiser (ALaBO)
Bayesian optimisation is a probabilistic approach for efficiently optimising complex and costly problems. By leveraging Bayesian inference and constructing a surrogate model, samples are taken to iteratively guide the search towards promising regions. This is achieved through optimisation of an acquisition function, which balances the exploration of areas of uncertainty with the exploitation of available information. Traditional approaches require the user to predefine the hyperparameter, ε, which controls the trade-off between exploration and exploitation. In cases where a priori information is inadequate, this often leads to insufficient or excessive local searching.For optimisations requiring physical experimentation, the consequences of selecting a poor value for ε can be significant. For example, this can result in the need to run multiple optimisation campaigns which are time-consuming, costly, and infeasible in cases where reagent supplies are limited. Adaptive expected improvement (AEI) attempts to overcome this limitation by dynamically controlling the explore-exploit trade-off throughout the optimisation. This disconnects the quality of the results from the setting of ε, creating a ‘one shot’ technique.27 Indeed, AEI was found to outperform most static ε models for the camelback minimisation problem,27 and we have successfully applied it to the Bayesian self-optimisation of continuous variables in a telescoped flow process.10
To enable optimisation of systems with mixtures of continuous and categorical variables, we have combined AEI with latent variable Gaussian process modelling (LVGP) to create ALaBo.28 In this approach, a 2D latent variable representation of the space is created by mapping the levels of each categorical variable to a set of numerical values. This requires the estimation of 2mj − 3 parameters, where m is the number of levels of each categorical variable, j. Optimisation of these parameters is performed using maximum likelihood estimation. Notably, this approach mimics the behaviour of real physical systems, where the effect of categorical variables on the response can be described by a set of underlying quantitative variables. An advantage of LVGP is that the different level combinations of categorical variables are described by a single continuous response surface, enabling them to be handled using standard numerical Gaussian process (GP) modelling techniques with unmodified covariance functions.
Mathematical details of the algorithm are provided in the ESI,† and an open-source implementation of the algorithm is available on GitHub (https://github.com/adamc1994/ALaBO).
Benchmarking performance
Traditionally, the performances of optimisation algorithms are compared using test set libraries containing synthetic functions with artificial landscapes of varying complexity.29 However, this performance does not always translate well to real-world applications. For chemical reaction optimisation, it would be more informative to test algorithm performance on chemically-motivated virtual benchmarks.23–26 Therefore, the performance of ALaBO for optimising mixed variable catalytic reactions was evaluated using five in silico case studies proposed by Jensen et al.30The parameter space was equivalent for all case studies (Scheme 1), consisting of three continuous variables (residence time, catalyst mol%, temperature) and one categorical variable (catalyst) with eight levels [eqn (1)]. Each case study was designed to represent a catalytic reaction with different characteristics, thus providing a diverse test set (Table 1). This was achieved by varying the catalyst-specific activation energies of a bimolecular reaction [eqn (2)], and the introduction of a potential side reaction ([eqn (3)], case 3), product decomposition ([eqn (4)], case 4) and temperature dependent catalyst deactivation (case 5). Values for the kinetic parameters are provided in the ESI.†
| Reaction Properties | Optimum | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case | Catalyst effect | k S 1 | k S 2 | t res | T | C cat | Cat. | Yield | TON | f(x) |
| — | — | — | — | (min) | (°C) | (mol%) | — | (%) | — | — |
| 1 | E a1 > Ea2–8 | =0 | =0 | 10.0 | 110.0 | 0.500 | 1 | 90.4 | 180.8 | 4.6775 |
| 2 | E a1 = Ea2 > Ea3–8 | =0 | =0 | 10.0 | 110.0 | 0.500 | 1, 2 | 90.4 | 180.8 | 4.6775 |
| 3 | E a1 > Ea2–8 | >0 | =0 | 10.0 | 81.9 | 1.522 | 1 | 54.9 | 36.1 | 3.9012 |
| 4 | E a1 > Ea2–8 | =0 | >0 | 2.2 | 110.0 | 1.380 | 1 | 36.8 | 26.6 | 3.5243 |
| 5 | E a1 > Ea2–8 if T < 80 °C | =0 | =0 | 10.0 | 80.0 | 0.500 | 1 | 93.8 | 187.5 | 4.7141 |
In contrast to the original paper, the definition of the optimisation objective was modified to remove the nonlinear constraint on the product yield, as self-optimisations are seldom performed in this fashion. Rather, a scalarised objective function balancing the product yield with catalyst turnover number (TON) was formulated [eqn (5)], where TON was defined as the ratio between the desired product and catalyst concentrations. The yield and TON with respect to the desired product, R, were determined on each iteration by solving the corresponding rate equations. The relative weightings for yield and TON were selected to provide similar response surfaces to the original case studies.30 This was validated by performing separate global optimisations for each catalyst across all five case studies (see ESI† for details).
The algorithm's performance was compared against two Bayesian optimisation toolboxes: Dragonfly31 and ProcessOptimizer.32 Under their default settings, both Dragonfly and ProcessOptimizer use GPs as surrogate models. ProcessOptimizer utilises expected improvement (EI) as the acquisition function, which is optimised by computing the function at randomly sampled points. In contrast, Dragonfly uses an adaptive sampling strategy to choose between different acquisition functions (UCB, EI, TS, TTEI) on each iteration. The GP hyperparameters are then tuned in a similar fashion, where either maximum likelihood or posterior sampling is chosen at every iteration.
These algorithms were selected as they are open source and can be operated in ask-tell mode, which enables straightforward integration with automated experimental platforms. Furthermore, both have recently been applied to the self-optimisation of chemical reactions.6,7,9,11,13 Tuning of the algorithm settings on a case-by-case basis is impractical, and minimising the number of optimisation campaigns required is highly desirable. Therefore, these algorithms were operated under their recommended default settings for the purpose of this comparison. In addition, as catalysts cannot be ordered without knowing the relative importance of their molecular descriptors, they were treated as nominal categorical variables rather than discrete integers.
The starting point chosen for an optimisation can have a profound effect on algorithm performance. In this case, Latin hypercube (LHC) sampling was used to generate three data points with respect to the continuous variables, which were then evaluated for each of the eight catalysts for a total of 24 samples. Given the relatively low number of categorical variable levels in these cases, initial samples were collected for each level to prevent potential bias towards or against specific levels arising from unbalanced data. However, it should be noted that this can lead to a large initial cost when there are multiple categorical variables with many levels in the optimisation problem.21 To capture the effect of variation in LHC sampling, a different LHC was generated for each run. However, to ensure fair benchmarking, the same set of LHCs were stored outside of the testing process and used for all algorithms and case studies.29
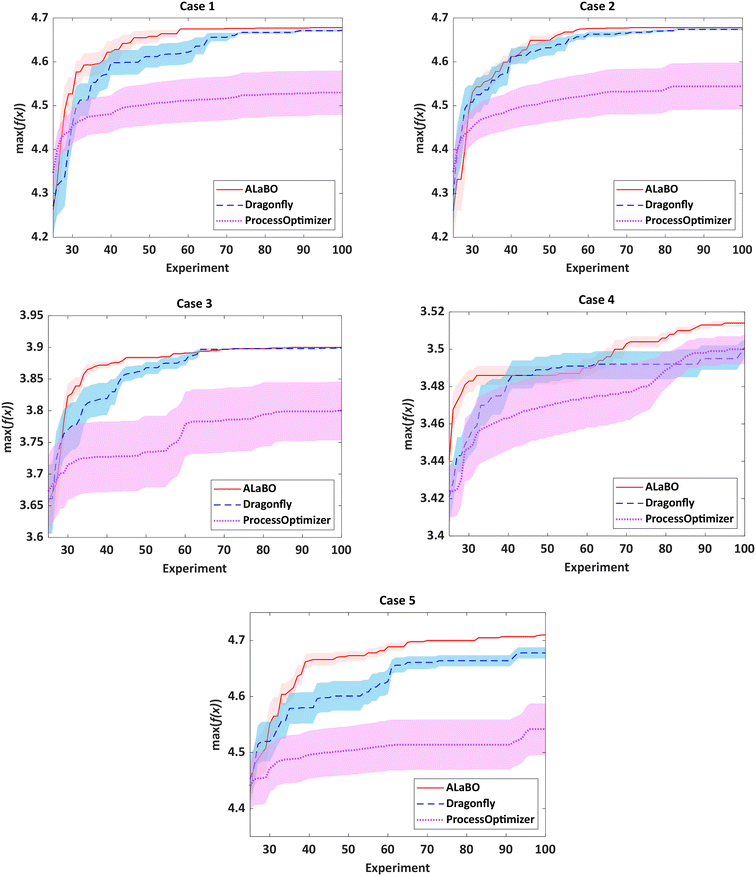
For chemical reaction optimisation, there are two key performance measures: (i) speed of convergence – the number of experiments required to find the optimum; (ii) robustness – the variance between repeat searches. To assess these criteria, each algorithm was run 10 times per case study with an experiment budget of 100, including initialisation. The performance of each algorithm could then be visualised and compared using optimisation progress plots, displaying the average of the running maxima and 95% confidence intervals across all runs (Fig. 1).
Notably, both ALaBO and Dragonfly were able to consistently identify solutions within 1% of the true optima across all five case studies. In contrast, ProcessOptimiser was only able to achieve this for one out of the five test problems (case 4) within the same experimental budget. This was due to a significantly slower rate of improvement, which often did not improve for many iterations. Scrutiny of the reaction conditions explored revealed that ProcessOptimiser was performing excessive local searches around the current best point. Hence, only minor adjustments to the variables were made on each iteration, rather than exploring the design space to find the global optimum. As this algorithm utilises an EI acquisition function, this suggests that the default value of the ε hyperparameter was set to strongly favour exploitation. Indeed, this setting was found to be unfavourable for reaction optimisation and highlights the limitations of using acquisition functions which require predefined hyperparameters.
Previous approaches using EI have suggested incorporation of an ε changeover, where the algorithm switches from an exploratory to an exploitative state after a predefined number of experiments.9 In contrast, we generally observed ALaBO to initially conduct a focused search over the continuous design space using the best catalyst identified from the LHC, followed by a more exploratory search over the remaining levels of the categorical variable (see Fig. S2,† for example). The advantage of this is the ability to rapidly identify solutions which would be satisfactory for most applications, without having to collect extensive amounts of preliminary data. Additional experiments can then be conducted to further improve or validate the current best point if required.
With the exception of case 4, ALaBO had a faster convergence speed compared to Dragonfly, and is on average 1.4 times faster at identifying a solution within 1% of the true optima. This observation could be explained by the adaptive sampling strategy used by Dragonfly to choose between different acquisition functions. This strategy initially samples all acquisitions with equal probability, and progressively favours those that are better performing.31 However, as the performance of each acquisition is problem dependent, this selection process will often result in slower progress during the initial iterations.
The relative robustness of the approaches was determined by comparing the magnitude of the 95% confidence intervals across all runs (Fig. S3†). Ideally, only one optimisation campaign would be required for a chemical reaction, therefore smaller values are desirable. Based on this, ALaBO was found to have the greatest reliability over multiple runs for all case studies. This can be further illustrated by the results from case 5, where selection of the optimum catalyst is significantly more challenging, due to its temperature-dependent deactivation. In this case, ALaBO and Dragonfly had 100% and 70% success rates for optimum catalyst identification respectively.
It should be noted that there are likely other algorithmic contributions beyond the acquisition functions which will affect performance (e.g., covariance functions). Nevertheless, the results of this study clearly indicate that ALaBO has superior accuracy, convergence speed and reliability compared to other open-source Bayesian algorithms currently used for mixed variable chemical reaction optimisation. As a result, we conducted further simulations using ALaBO to investigate its performance using different initialisation strategies and batch sizes.
Choosing initialisation strategies for Bayesian optimisation is a non-trivial task, as it requires a balance between efficiently using resources while gathering sufficient data to create a robust model. To identify the most resource-efficient strategy, we compared the use of different LHC sizes (three or five sampling points per catalyst) against a single centre-point (CP) per catalyst (Fig. S4†).33 Remarkably, the size of the initial dataset had only a small effect on the subsequent speed of convergence towards the optimum in most cases. As a result, optimisations using CP initialisation required on average 21 and 28 fewer total experiments compared to LHC sizes of three and five respectively.
The batch size refers to the number of experiments evaluated in each iteration. In the context of self-optimisation, experimental efficiency can be improved by increasing the batch size, which enables reactions to be performed in parallel with analysis of the previous run. However, larger batch sizes rely on less well-informed predictions, as models are updated less frequently. Therefore, batch size must be selected to strike a balance between convergence speed and experimental efficiency. To assess the effect of batch size on reaction optimisation, we compared batch sizes ranging from one to four for each case study using the CP initialisation strategy (Fig. S5†). When a batch size of greater than one is used, the algorithm iteratively generates single suggestions by updating the model with the predicted responses, and then combines them to create the batch. The batch of experiments are then evaluated, and the actual values used to refit the model. For cases 1 and 2, the expected trend was observed, where convergence speed reduced with increasing batch size. However, for cases 3 to 5, where the optima are not located at a boundary of the design space, the effect of batch size on convergence speed was much less significant, with no clearly observable trend.
As a batch size of one had either comparable or superior convergence speed, this clearly represents the most reliable method for identifying the optimum, particularly in cases where the number of experiments is limited by reagent availability. Furthermore, the higher convergence speed often outweighed the theoretical increase in experimental efficiency with respect to overall optimisation time. For example, for case 1, batch sizes of one and four required 27 and 39 experiments respectively to locate a solution within 1% of the true optimum. Assuming an average reaction time of 5 min and an analysis time of 10 min, this corresponds to total optimisation times of 405 min and 439 min for batch sizes of one and four.
Self-optimisation of a Suzuki–Miyaura cross-coupling
To demonstrate the application of ALaBO to real-world problems, we integrated the algorithm with a continuous flow reactor platform and performed an automated self-optimisation of an exemplar catalytic reaction. Optimisation in continuous flow has numerous benefits, including greater control of reaction conditions, and access to an extended operating window (e.g., higher temperatures) which enables faster rates of reactions.34 We selected the Pd-catalysed Suzuki–Miyaura cross-coupling as a case study, due to its extensive use in the synthesis of pharmaceutical compounds, agrochemicals, and various functional materials.35The coupling of bromobenzene 1 and 4-methylphenylboronic acid 2 was chosen to allow the desired cross-coupling and undesired homocoupling pathways to be distinguished. The yield and TON with respect to 4-methylbiphenyl 3 were optimised using the same weighted objective function as the simulations [eqn (5)], and a similar design space consisting of three continuous variables (time, Pd mol%, temperature) and one categorical variable (ligand) with six levels (Scheme 2). A variety of dialkylbiaryl phosphine ligands (DavePhos, XPhos, SPhos, CyJohnPhos) and bidentate phosphine ligands (dppp, dppf) were selected to enable a comparison between different classes of ligand. All other reaction parameters, including the solvent mixture, base, and reagent stoichiometries, were selected and fixed according to previous studies of Suzuki–Miyaura cross-couplings in flow.36
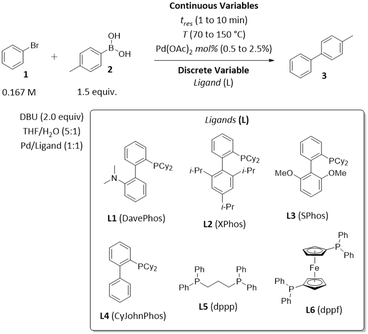 | ||
| Scheme 2 Optimisation parameters for the exemplar Suzuki–Miyaura cross-coupling reaction between bromobenzene 1 and 4-methylphenylboronic acid 2. | ||
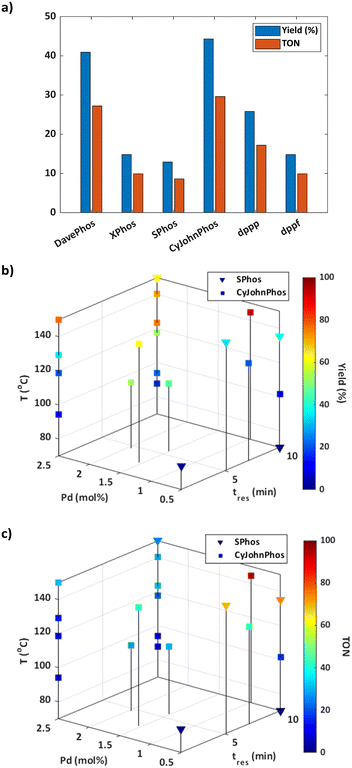
Informed by the results of the simulations, the optimisation was initialised using the CP strategy and set to a batch size of one. The budget for the optimisation was predefined as 25 experiments to strike a balance between optimisation time, resource utilisation, and achieving a satisfactory solution. As the catalyst mol% was the same for each ligand tested during initialisation, the response for these experiments was solely dependent on the yield of 3 (Fig. 2a). The results suggest that dialkylbiaryl phosphine ligands with minimal substitution, such as CyJohnPhos and DavePhos, are the most effective for promoting this reaction.
The optimisation pathway taken by ALaBO resembled a similar pattern to that observed in the simulations (Fig. S9†), which started by testing different combinations of continuous variables, using the best identified ligand (CyJohnPhos) from the initial data. This approach identified the optimum solution after just four iterations of the algorithm, which corresponded to a yield of 93% (Fig. 2b) and a TON of 95 (Fig. 2c). Longer residence times and higher temperatures were used to enhance the yield, and a catalyst mol% of 0.97 was identified to achieve a high TON without compromise. The algorithm then primarily explored the effect of different temperatures at the upper and lower bounds of residence time and catalyst mol%, and identified local optima at 1 and 10 min using 2.5 Pd mol%. For example, a 77% yield could be obtained with a residence time of just 1 min, highlighting a significant potential increase in productivity.
Despite SPhos giving the worst performance during initialisation, this was the only other ligand except for CyJohnPhos that was explored by the algorithm. Our understanding is that SPhos was first selected for the purpose of exploration on experiment 12, where it outperformed all initial data points, making it the second most viable option for subsequent exploitation. In general, there was an inverse relationship between yield and TON for both ligands i.e., increasing TON by reducing catalyst mol% was outweighed by a significant reduction in yield. This applied across the entire design space except for at high temperatures using CyJohnPhos where, in contrast to SPhos, high yields could be achieved at a lower mol% of catalyst. It should also be noted that no protodeboronation or homocoupling of 4-methylboronic acid 2 was observed at the conditions explored during this optimisation.
Based on the previous simulations, we predict that the algorithm would have continued to explore the remaining ligands if given a larger experimental budget. Nevertheless, given that ALaBO successfully identified a solution within 1% of the true optima in an average of just 23 experiments across the five simulated case studies (when using CP initialisation and a batch size of one), we are confident that a near-optimal solution has been found. In this study, our experimental budget was set partly based on reagent availability, as continuous flow operation requires significant quantities of material to reach steady state. In the future, we envisage that integration of ALaBO with recently reported droplet flow reactors will result in a significant increase in experimental efficiency,7,37,38 as well as the capability to rapidly optimise design spaces with multiple categorical variables.
Conclusion
In conclusion, we have introduced a new optimisation strategy for the autonomous development of mixed variable catalytic reactions. Our approach combines latent variable Gaussian process modelling with an adaptive expected improvement acquisition function. This provides a robust ‘one shot’ technique for the concurrent optimisation of categorical and continuous variables without any a priori information. Simulations on several chemically-motivated test problems (each with eight discrete catalysts and three continuous variables) demonstrated the superior convergence speed of ALaBO compared to other open-source Bayesian optimisers. On average across five different case studies, ALaBO successfully identified a close-to-optimal solution 1.4 times faster than the next best algorithm.Different initialisation strategies and batch sizes were also evaluated, which informed the subsequent self-optimisation of a Suzuki–Miyaura cross-coupling reaction in continuous flow (with six discrete ligands and three continuous variables). In agreement with our simulations, ALaBO required an experimental budget of only 25 experiments, and located an optimal solution with a yield greater than 90% in just 10 experiments. We envisage that this increase in efficiency will enable automated optimisation to be used for reactions with limited material availability in the future, such as late-stage functionalisation of high-value precursors.
Experimental
General information
All of the following chemicals were purchased from commercial sources and used as received: bromobenzene (98.0%, Fluorochem); 4-methylphenylboronic acid (>97%, Apollo Scientific); DBU (98.0%, Fluorochem); palladium(II) acetate (≥99.9%, Sigma-Aldrich); DavePhos (98.0%, Fluorochem); XPhos (98.0%, Fluorochem); SPhos (98.0%, Fluorochem); CyJohnPhos (99.0%, Fluorochem); dppp (95.0%, Fluorochem); dppf (97%, Sigma-Aldrich); 4-methylbiphenyl (98.0%, Fluorochem); 4,4′-dimethylbiphenyl (98%, Activate Scientific); toluene (≥99.8%, Fisher Scientific); biphenyl (99.5%, Sigma-Aldrich); tetrahydrofuran (≥99.8%, Fisher Scientific); acetonitrile (≥99.9%, Sigma-Aldrich). HPLC method development and analytical calibrations were performed using the products from commercial sources and biphenyl as internal standard.Computational study
The five catalytic case studies described by Jensen et al. were formulated in MATLAB R2023a, where the differential rate equations (see ESI†) were solved using ordinary differential equation (ODE) solver ODE45. The performance of different optimisation settings and algorithms for each case study was determined by comparing the running max average and 95% confidence intervals across 10 runs with 100 function evaluations each. All algorithms were used with their recommended default settings, with catalysts expressed as nominal categorical variables. The ALaBO algorithm was written in MATLAB and therefore applied directly. Dragonfly and ProcessOptimizer are open access Bayesian optimisation toolboxes available on GitHub and written in Python. Hence, these algorithms were installed using Python 3.10 and operated in ask-tell mode, where MATLAB would call the algorithm in Python, and provide the past results of the optimisation to generate the next recommendation for evaluation. Simulations were run using a Stone desktop PC with a Microsoft Windows 11 operating system, 12th Gen Intel 6-Core i5-12400 processor and 16.0 GB of RAM.Self-optimising reactor set-up
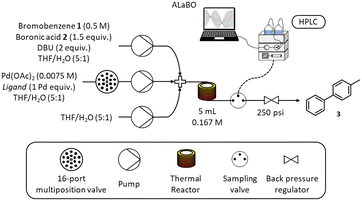
A schematic of the self-optimising reactor is shown in Scheme 3. Ligand selection was achieved using a Knauer Azura 16-port multiposition valve connected to a pre-prepared array of catalyst/ligand stock solutions stored under nitrogen. Reagents were pumped using a combination of JASCO (PU-4580) and Knauer Azura (P 4.1S) HPLC pumps and mixed using Swagelok SS-100-3 tee pieces. A 5 mL reactor was made from stainless steel tubing (1/16′′ OD, 1/32′′ ID), which was fitted to an aluminium cylinder and heated with a Eurotherm 3200 temperature controller. The reactor was maintained under 250 psi using an Upchurch Scientific back pressure regulator. Online HPLC sampling was achieved using a VICI Valco EUHA-CI4W sample loop (4-port) with 0.1 μL direct injection volume. Quantitative analysis was performed on an Agilent 1100 series HPLC instrument fitted with a Supelco Ascentis Express C18 reverse phase column (5 cm length, 4.6 mm ID and 2.7 μm particle size) and an Agilent EC-C18 (4.6 × 5 mm, 2.7 μm) guard column. The platform was controlled and automated using a custom written MATLAB program.Automated flow experiments
Reservoir solutions were prepared by dissolving the desired reagents in solvent under nitrogen, and were replenished as required throughout the optimisation. Reagent pump (150 mL): bromobenzene 1 (7.85 mL, 0.075 mol, 0.50 M), 4-methylphenylboronic acid 2 (15.30 g, 0.113 mol, 0.75 M), DBU (22.43 mL, 0.150 mol, 1.00 M) and biphenyl (1.39 g, 0.009 mol, 0.06 M) in THF/H2O (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Catalyst pump (25 mL): Pd(OAc)2 (42.1 mg, 0.0002 mol, 0.0075 M) and ligand (0.0002 mol, 0.0075 M) in THF/H2O (5
1). Catalyst pump (25 mL): Pd(OAc)2 (42.1 mg, 0.0002 mol, 0.0075 M) and ligand (0.0002 mol, 0.0075 M) in THF/H2O (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Solvent pump: THF/H2O (5
1). Solvent pump: THF/H2O (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The catalyst pump was connected to a multiposition valve, enabling selection of six different ligands (DavePhos, XPhos, SPhos, CyJohnPhos, dppp, dppf) from separate reservoir solutions. The solvent pump was necessary to enable residence time and catalyst mol% to be varied independently whilst holding the concentration of the limiting reactant (bromobenzene 1) fixed at 0.167 M within the reactor.
1). The catalyst pump was connected to a multiposition valve, enabling selection of six different ligands (DavePhos, XPhos, SPhos, CyJohnPhos, dppp, dppf) from separate reservoir solutions. The solvent pump was necessary to enable residence time and catalyst mol% to be varied independently whilst holding the concentration of the limiting reactant (bromobenzene 1) fixed at 0.167 M within the reactor.
A custom written MATLAB program controlled the pump flow rates, valve positions, reactor temperature and sampling. Each iteration adhered to the following sequence: (i) multiposition valve was set to the corresponding ligand; (ii) reactor was allowed to stabilise at the desired operating temperature (iii) pumps were set to the required flow rates and left for three reactor volumes to reach steady state; (iv) sampling valve was triggered alongside HPLC analysis. The response was calculated from the HPLC chromatograms at the end of each iteration, and the results used to update the surrogate models and generate the next recommended reaction conditions. The optimisation was performed using the same weighted objective function for yield and TON as the computational benchmarking study.
The ALaBO algorithm was initialised using one centre point experiment with respect to the quantitative variables per ligand, equalling six total experiments. The optimisation was performed with a batch size of one, therefore the reactor was set to minimum conditions for the duration of the analytical method to reduce material consumption. This process was repeated iteratively with a total experimental budget (including initialisation) of 25, after which point the optimisation was terminated.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
ADC thanks the Royal Academy of Engineering for support under the Research Fellowships scheme.References
- R. A. Sheldon, M. L. Bode and S. G. Akakios, Curr. Opin. Green Sustainable Chem., 2022, 33, 100569 CrossRef CAS.
- Z. Wang and S. Hellweg, ACS Sustainable Chem. Eng., 2021, 9, 6939 CrossRef CAS.
- H. Gao, C. W. Coley, T. J. Struble, L. Li, Y. Qian, W. H. Green and K. F. Jensen, React. Chem. Eng., 2020, 5, 367 RSC.
- D. W. Lendrem, B. C. Lendrem, D. Woods, R. Rowland-Jones, M. Burke, M. Chatfield, J. D. Isaacs and M. R. Owen, Drug Discovery Today, 2015, 20, 1365 CrossRef PubMed.
- C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089 CrossRef CAS PubMed.
- A. Slattery, Z. Wen, P. Tenblad, D. Pintossi, J. Sanjosé-Orduna, T. den Hartog and T. Noël, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-r0drg.
- N. S. Eyke, T. N. Schneider, B. Jin, T. Hart, S. Monfette, J. M. Hawkins, P. D. Morse, R. M. Howard, D. M. Pfisterer, K. Y. Nandiwale and K. F. Jensen, Chem. Sci., 2023, 14, 8798 RSC.
- E. Braconi and E. Godineau, ACS Sustainable Chem. Eng., 2023, 11, 10545 CrossRef CAS.
- N. V. Faurschou, R. H. Taaning and C. M. Pedersen, Chem. Sci., 2023, 14, 6319 RSC.
- A. D. Clayton, E. O. Pyzer-Knapp, M. Purdie, M. F. Jones, A. Barthelme, J. Pavey, N. Kapur, T. W. Chamberlain, A. J. Blacker and R. A. Bourne, Angew. Chem., Int. Ed., 2023, 62, e202214511 CrossRef CAS PubMed.
- A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, ACS Cent. Sci., 2022, 8, 825 CrossRef CAS PubMed.
- P. Sagmeister, F. F. Ort, C. E. Jusner, D. Hebrault, T. Tampone, F. G. Buono, J. D. Williams and C. O. Kappe, Adv. Sci., 2022, 9, 2105547 CrossRef.
- K. Y. Nandiwale, T. Hart, A. F. Zahrt, A. M. K. Nambiar, P. T. Mahesh, Y. Mo, M. J. Nieves-Remacha, M. D. Johnson, P. García-Losada, C. Mateos, J. A. Rincón and K. F. Jensen, React. Chem. Eng., 2022, 7, 1315 RSC.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89 CrossRef CAS.
- A. D. Clayton, A. M. Schweidtmann, G. Clemens, J. A. Manson, C. J. Taylor, C. G. Niño, T. W. Chamberlain, N. Kapur, A. J. Blacker, A. A. Lapkin and R. A. Bourne, Chem. Eng. J., 2020, 384, 123340 CrossRef CAS.
- A. D. Clayton, J. A. Manson, C. J. Taylor, T. W. Chamberlain, B. A. Taylor, G. Clemens and R. A. Bourne, React. Chem. Eng., 2019, 4, 1545 RSC.
- A. D. Clayton, Chem.: Methods, 2023, e202300021 Search PubMed.
- C. J. Taylor, K. C. Felton, D. Wigh, M. I. Jeraal, R. Grainger, G. Chessari, C. N. Johnson and A. A. Lapkin, ACS Cent. Sci., 2023, 9, 957 CrossRef CAS.
- P. Mueller, A. Vriza, A. D. Clayton, O. S. May, N. Govan, S. Notman, S. V. Ley, T. W. Chamberlain and R. A. Bourne, React. Chem. Eng., 2023, 8, 538 RSC.
- Y. Amar, A. M. Schweidtmann, P. Deutsch, L. Cao and A. A. Lapkin, Chem. Sci., 2019, 10, 6697 RSC.
- J. A. Manson, T. W. Chamberlain and R. A. Bourne, J. Glob. Optim., 2021, 80, 865 CrossRef.
- O. J. Kershaw, A. D. Clayton, J. A. Manson, A. Barthelme, J. Pavey, P. Peach, J. Mustakis, R. M. Howard, T. W. Chamberlain, N. J. Warren and R. A. Bourne, Chem. Eng. J., 2023, 451, 138443 CrossRef CAS.
- K. C. Felton, J. G. Rittig and A. A. Lapkin, Chem.: Methods, 2021, 1, 116 CAS.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch, M. Christensen, E. Liles, J. E. Hein and A. Aspuru-Guzik, Mach. Learn.: Sci. Technol., 2021, 2, 035021 Search PubMed.
- P. Müller, A. D. Clayton, J. Manson, S. Riley, O. S. May, N. Govan, S. Notman, S. V. Ley, T. W. Chamberlain and R. A. Bourne, React. Chem. Eng., 2022, 7, 987 RSC.
- Z. Crandall, K. Basemann, L. Qi and T. L. Windus, React. Chem. Eng., 2022, 7, 416 RSC.
- D. Jasrasaria and E. O. Pyzer-Knapp, arXiv, 2018, preprint, arXiv:1807.01279, DOI:10.48550/arXiv.1807.01279.
- Y. Zhang, S. Tao, W. Chen and D. W. Apley, Technometrics, 2020, 62, 291 CrossRef.
- V. Beiranvand, W. Hare and Y. Lucet, Optim. Eng., 2017, 18, 815 CrossRef.
- L. M. Baumgartner, C. W. Coley, B. J. Reizman, K. W. Gao and K. F. Jensen, React. Chem. Eng., 2018, 3, 301 RSC.
- K. Kandasamy, K. R. Vysyaraju, W. Neiswanger, B. Paria, C. R. Collins, J. Schneider, B. Póczos and E. P. Xing, J. Mach. Learn. Res., 2020, 21, 3098 Search PubMed.
- A. Obdrup, B. E. Nielsen, R. H. Taaning, S. Carlsen and S. Bertelsen, ProcessOptimizer, v0.8.1, 2023, DOI:10.5281/zenodo.8068270.
- J. H. Dunlap, J. G. Ethier, A. A. Putnam-Neeb, S. Iyer, S.-X. L. Luo, H. Feng, J. A. G. Torres, A. G. Doyle, T. M. Swager, R. A. Vaia, P. Mirau, C. A. Crouse and L. A. Baldwin, Chem. Sci., 2023, 14, 8061 RSC.
- L. Capaldo, Z. Wen and T. Noël, Chem. Sci., 2023, 14, 4230 RSC.
- S. E. Hooshmand, B. Heidari, R. Sedghi and R. S. Varma, Green Chem., 2019, 21, 381 RSC.
- B. J. Reizman, Y.-M. Wang, S. L. Buchwald and K. F. Jensen, React. Chem. Eng., 2016, 1, 658 RSC.
- F. Wagner, P. Sagmeister, C. E. Jusner, T. G. Tampone, V. Manee, F. G. Buono, J. D. Williams and C. O. Kappe, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-gb117.
- C. Avila, C. Cassani, T. Kogej, J. Mazuela, S. Sarda, A. D. Clayton, M. Kossenjans, C. P. Green and R. A. Bourne, Chem. Sci., 2022, 13, 12087 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00476g |
| This journal is © The Royal Society of Chemistry 2024 |