Discovery of Rb-based auric–aurous halide perovskites as promising narrow bandgap semiconductors for energy conversion applications†
Xuteng
Yu
acg,
Chang
Liu
abcd,
Xifeng
Fu
bdf,
Zi-Ang
Nan
f,
Yuheng
Li
abcd,
Zilong
Zhang
ac,
Qiu
Xiong
c,
Yingyao
Zhang
c,
Lingyi
Meng
 abdf,
Shui-yang
Lien
abdf,
Shui-yang
Lien
 e and
Peng
Gao
e and
Peng
Gao
 *abcd
*abcd
aCAS Key Laboratory of Design and Assembly of Functional Nanostructures, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, China. E-mail: peng.gao@fjirsm.ac.cn
bFujian Normal University, Fuzhou 350007, China
cLaboratory for Advanced Functional Materials, Xiamen Key Laboratory of Rare Earth Photoelectric Functional Materials, Xiamen Institute of Rare Earth Materials, Haixi Institute, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, P.R. China
dFujian College, University of Chinese Academy of Sciences, Fuzhou, 350002, China
eXiamen University of Technology, Xiamen 361024, China
fFujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, P.R. China
gUniversity of Chinese Academy of Sciences, Beijing 100049, China
First published on 28th June 2024
Abstract
Inorganic gold halide perovskites, owing to their excellent stability and tunable bandgaps, are poised to serve as environmentally benign alternatives to lead halide perovskites in the field of photovoltaics. In this study, we successfully synthesized two inorganic auric–aurous halide perovskites, Rb2Au2I6 and RbAuCl4, using a straightforward and efficient hydrothermal method, achieving millimeter-sized single crystals. Single-crystal structural analysis revealed that Rb2Au2I6 exhibits a three-dimensional (3D) double perovskite structure, whereas RbAuCl4 shows a two-dimensional (2D) Dion–Jacobson (DJ)-type perovskite structure. We further analyzed their crystallographic information and elucidated the reasons behind the structural differences between them. Moreover, first-principles calculations ascertained their high optical absorption coefficients within the visible light spectrum and indirect bandgap properties. Utilizing theoretical models, we discovered that Rb2Au2I6 and RbAuCl4 exhibit spectroscopic limited maximum efficiency (SLME) of 30.12% and 22.30%, respectively, in films of 500 nm thickness, signifying their potential candidacy as solar cell absorbers. Theoretical calculations related to thermoelectric properties illustrate high ZT (thermoelectric figure of merit) values of about 1.4 and 1.2 at 500 K for Rb2Au2I6 and RbAuCl4, respectively. Based on the significantly shortened synthesis of Rb2Au2I6 and RbAuCl4, our study demonstrated their potential in the field of optoelectronics and thermoelectric materials, which could lay a solid foundation for future applications in energy-conversion devices.
Introduction
Over the past two decades, lead halide perovskite (LHP) materials have emerged as a focal point for next-generation energy-conversion semiconductor materials due to their advantageous economic characteristics, high quantum efficiencies, defect tolerance, high absorption coefficients, facile solution processability, and adjustable band gaps.1–3 Furthermore, LHPs offer extensive application prospects spanning photon detectors,4 light-emitting diodes,5 memristors,6 solar cells,7,8 and semiconductor lasers,9 garnering considerable research attention in recent years.10,11 However, their promising performance as semiconductor materials is hindered by two significant challenges: stability and toxicity.12,13 Toxicity concerns primarily stem from the environmental and health risks associated with lead.14 Long-term instability arises from the susceptibility of ionic LHPs to degradation upon exposure to light, oxygen, moisture, or heat.15Gold elements exhibit diverse oxidation states, enabling the synthesis of a wide range of auric–aurous halide perovskites (AAHPs) and derivatives through the manipulation of A-site cations and X-site halide anions16,17 Moreover, the significant light absorption coefficients and relatively narrow bandgaps manifest AAHPs as potential candidates for photovoltaic applications. Notably, recent advancements made by Fan et al. significantly improved the synthesis of hybrid AAHPs using a highly efficient hydrothermal method,18 in contrast to the tedious volatilization protocol.16 In the realm of inorganic AAHPs, researchers have primarily focused on Cs-based double perovskites: Cs2AuIAuIIIX6 (X = Cl−, Br−, I−),19 Cs4AuIIAuIIICl12,20 and Cs8AuIII4M8X23 (M = In3+, Sb3+, Bi3+, X = Cl−, Br−, I−),21 focusing on their crystal structure, chemical properties, and formation mechanisms. Theoretical calculations by Debbichi et al. suggest that Cs2AuIAuIIII6 possesses an optimal band gap close to the Shockley–Queisser limit, potentially achieving over 20% photo-conversion efficiency (PCE).22 Additionally, Li et al. predicted three novel Cs2AuSbCl6, Cs2AuInCl6, and Cs2AuBiCl6 double perovskites as promising solar cell absorbers, exhibiting a spectroscopic limited maximum efficiency (SLME) of approximately 30% in a 500 nm thick film.23
Another significant series of all-inorganic AAHPs, featuring Rb as the A-site cation, has been reported since the previous century.24 However, research on these materials has remained scarce, mainly due to the interminable preparation process. In this study, two inorganic AAHPs, Rb2Au2I6 and RbAuCl4, were successfully obtained as millimeter-scale single crystals via an elegantly simple yet highly efficient hydrothermal approach. Based on the single crystals of two AAHPs, we conducted structural analysis and, for the first time, elucidated the mechanisms underlying their dimensional variances. The optical band gaps of Rb2Au2I6 and RbAuCl4 determined through UV-Vis absorption spectroscopy were found to be 1.11 eV and 2.37 eV, respectively. Leveraging first-principles calculations, we explored the optical properties of these perovskites, revealing the robust light absorption coefficients of two perovskites within the visible spectrum. Notably, these materials exhibit exceptionally high SLME values of 30.12% and 22.30%, respectively, within 500 nm thick films. Additionally, based on theoretical modeling, both perovskites hold promise for thermoelectric applications. Specifically, at a temperature of 500 K, we anticipate achieving high thermoelectric figure of merit (ZT) values of 1.4 and 1.2 for Rb2Au2I6 and RbAuCl4, respectively. Our findings significantly improved the synthesis of Rb2Au2I6 and RbAuCl4 while providing predictions for their outstanding performance in photoelectric and thermoelectric devices. We believe that our research could shed light on the future applications of inorganic AAHP materials.
Experimental
Materials and methods
All initial precursor materials and solvents were obtained from commercial sources and employed without subsequent purification processes. Rubidium iodide (RbI, 99.0%), rubidium chloride (RbCl, 99.0%), and gold(III) chloride hydrate (HAuCl4·XH2O, 98.0%) were purchased from Innochem. HI (57 wt% in H2O) solution was purchased from Aladdin.Preparation process of single crystals
637 mg (3 mmol) of rubidium iodide (RbI) and 412 mg (1 mmol) of gold(III) chloride hydrate (HAuCl4·XH2O) were mixed in 10 ml of deionized water and stirred for 5 minutes. After that, 0.5 ml of hydroiodic acid (48%) was added to the mixed solution and then transferred into a Teflon-lined hydrothermal reactor. After the hydrothermal reaction at 80 °C for 24 h with a cooling rate of 2 °C h−1, black, shiny, and cuboid-shaped square crystals were successfully obtained. Afterwards, we kept the obtained single crystals and the reaction residue in a refrigerator for further crystallization at 5 °C to increase the single-crystal production rate.The process of preparing RbAuCl4 is similar to that used for Rb2Au2I6, except that the reactants are replaced with 726 mg (6 mmol) of rubidium chloride (RbCl) and 412 mg (1 mmol) of gold(III) chloride hydrate (HAuCl4·XH2O). It is noteworthy that the reaction was able to proceed without the addition of hydrochloric acid, as enough chloride ions were already present in the solution. With the same hydrothermal reaction conditions, we can get yellow, shiny, and cuboid-shaped square crystals.
Photovoltaic property calculations
First-principles density functional theory (DFT) simulations were performed with the Vienna ab initio simulation package (VASP) to study the geometric and electronic structures of the Au-based perovskites. We adopted the Perdew–Burke–Ernzerhof (PBE) functional in the generalized gradient approximation (GGA) to optimize their geometrical structures.The spin–orbit coupling (SOC) effect is taken into account in the electronic structure calculations. The electronic constituents are 5d 6s 6p for Au, 5s 5p 6s for I, 5s 5p for Cl, and 3p 3d for Rb. For geometric optimization, the Monkhorst–Pack k-point grid was set as 2 × 9 × 3, while for self-consistent calculations, it was adjusted to 4 × 6 × 7. We adopted the PBE + SOC (spin–orbit coupling) function to calculate the band structures in our investigations. Projector augmented wave pseudopotentials with a cut-off energy of 520 eV were employed.
Thermoelectric property calculations
All the calculations based on density functional theory (DFT) and the Projector Augmented Wave (PAW) potential were performed using the Device Studio,25 which provides a number of functions for performing visualization, modeling, and simulation. Structural optimization was performed using DS-PAW code26 integrated into the Device Studio program. The generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE) format was used to compute exchange and correlation energies, and a plane wave basis set cut-off energy of 600 eV was adopted. Grimme's DFT-D3 was used for dispersion correction. To avoid imaginary frequency, a mesh of 16 × 16 × 14 gamma-centered k-points was used for Brillouin-zone integration. The criterion of electron self-consistent iteration was set as 1.0 × 10−9 eV, and the maximum force was relaxed down to 1.0 × 10−4 eV Å−1.Thermoelectric properties were simulated using Nanodcal code7, which is based on non-equilibrium Green's function density functional theory (NEGF-DFT). We used 2 × 2 × 2 supercells to calculate the phonon part. LDA-PZ81 was employed as the exchange–correlation functional, and the cut-off energy was set to 80 Hartee. The criterion of electron self-consistent iteration was set as 1.0 × 10−12 eV.
Results and discussion
Crystal structure analysis
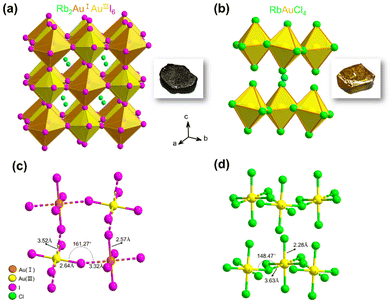
We successfully prepared millimeter-scale single crystals of 3D Rb2Au2I6 and 2D DJ RbAuCl4 using a straightforward and efficient hydrothermal reaction. After cooling at 5 °C for 24 hours, black cuboid-shaped crystals of Rb2Au2I6 and yellow cuboid-shaped crystals of RbAuCl4 were obtained, as depicted in the insets of Fig. 1a and b. To further determine the microstructure of the crystals, scanning electron microscopy (SEM) images were obtained from these samples, revealing a regular polyhedron morphology at a magnification of 2500× (Fig. S1, ESI†). It is worth noting that the single crystals are prone to humidity and should be stored in a vacuum environment.The crystal structures of Rb2Au2I6 and RbAuCl4 were determined and refined through single-crystal X-ray diffraction at 200 K, as presented in Fig. 1a and b. Analysis of the two single-crystal structures revealed that Rb2Au2I6 and RbAuCl4 adopt perovskite structures composed of corner-sharing octahedra. Besides different halogen atoms at the X position, the primary distinction between them lies in that Rb2Au2I6 crystallizes into a 3D double perovskite structure, while RbAuCl4 adopts a 2D layered perovskite configuration. Details of the crystal structure can be found in Table S1 of the ESI.†
Fig. 1a illustrates the structure of Rb2Au2I6, which, at room temperature, crystallizes in a distorted tetragonal mixed-valence perovskite structure with a monoclinic phase (space group C2/m (12)), consistent with the previous reports.27 During the formation of the double perovskite, the AuIII ions were reduced by iodides, leading to the formation of elemental iodine and monovalent gold ions (Au3+ + 2I− → I2 + Au+), resulting in the dual-valent (I and III) B-site auric–aurous cations. Both AuI and AuIII are coordinated by six iodide ions, with AuIII directly linked to four iodide ions forming a square plane [AuIIII4]−, while AuI is connected to two I− anions to form linear [AuII2]−. Therefore, in the structure of Rb2Au2I6, square-planar [AuIIII4]− and linear [AuII2]− alternate in three dimensions, forming a 3D corner-shared octahedron network, with Rb+ ions occupying the octahedral voids within the framework. Upon further analyzing the crystal structure, we observed significant distortion of the octahedra within Rb2Au2I6.
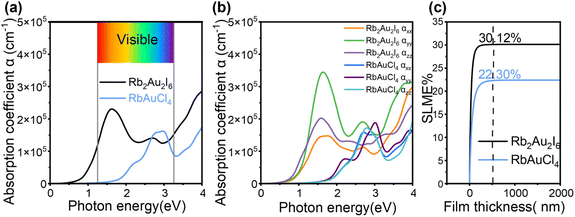
According to Corrêa et al., the tolerance factor of the double perovskite can be expressed as:
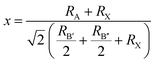 | (1) |
Based on a previous study, we assumed that the underlying cause of such twisted perovskite structures could be elucidated through the Jahn–Teller effect.29 This phenomenon, also observed in other AAHPs, involves the distortion of octahedra by stretching or compressing.30 Due to the splitting of Au-5d orbitals, lattice distortion occurs spontaneously when Au atoms with differing degenerate energy levels are present in the lattice, aiming to reduce degeneracy. This reduction in degeneracy leads to symmetry and energy reduction within the system, facilitating the spontaneous progression of the Jahn–Teller effect during the formation of the crystal structure.31,32
The single-crystal structure of 2D DJ AAHP RbAuCl4 is illustrated in Fig. 1b, exhibiting an ABX4-type perovskite structure with a monoclinic space group of C2/c (15).33,34 Within the RbAuCl4 structure, the B-site cations comprise only trivalent gold ions arranged in a continuous square-planar [AuIIICl4]− orientation along the horizontal direction. The [AuCl6]3− octahedra are connected by neighboring Cl− anions, forming continuous octahedron layers horizontally. Furthermore, these octahedron layers extend uniformly in the vertical (001) direction, with Rb+ cations occupying the interlayer spaces, serving to balance the charge. A schematic representation of the 2 × 2 × 2 single-crystal structure of RbAuCl4 is presented in Fig. S2† to enhance our comprehension of its layered structure.
In RbAuCl4, there are two types of chemical bonds within the [AuCl6]3− octahedron centered around Au3+: vertical AuIII–Cl (2.28 Å) and horizontal AuIII⋯Cl (3.63 Å) (Fig. 1b). The bond length along the vertical direction of the [AuCl6]3− octahedron (2.28 Å) is shorter than that along the horizontal axis (3.63 Å), resulting in a compressed octahedral structure. The substitution of halide ions from I− to Cl− leads to reduced anion radii in the [AuCl6]3− octahedron, resulting in decreased lattice constants and volumes compared to those of [AuI6]3−. Consequently, significant gaps between different octahedral layers are created due to the reduced octahedral volume, causing increased inter-layer distances. Unlike the arrangement in Rb2Au2I6, the B-site elements in RbAuCl4 exclusively consist of Au3+ instead of alternating Au+ and Au3+ configurations. This deviation is believed to be attributed to the limited reducibility of Cl−, preventing the reduction of Au3+ to Au+ during hydrothermal reactions.
Furthermore, in the RbAuCl4 structure, the [AuCl6]3− octahedron within different layers is unable to connect through shared Cl− ions along the (001) direction, such as between linear [AuII2]− and square planar [AuIIII4]− units. These factors ultimately contribute to the distinctive 2D DJ-type perovskite structure of RbAuCl4, in contrast to the 3D double perovskite structure of Rb2Au2I6. It is worth noting that, according to eqn (1), the double perovskite structure of Rb2Au2Cl6 is theoretically stable (t = 0.875). However, experimental synthesis has so far been unable to produce single crystals of Rb2Au2Cl6, possibly due to the absence of stable Au+ ions in the reaction system.
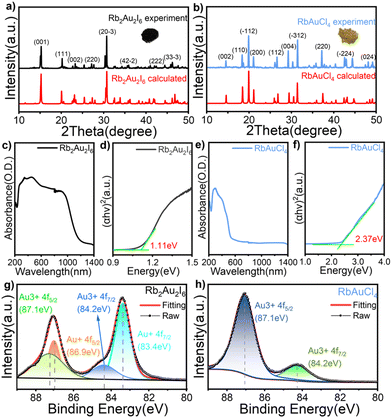
Phase identification and optical bandgaps
Fig. 2a and b show the powder X-ray diffraction (PXRD) patterns of Rb2Au2I6 and RbAuCl4 along with the calculated XRD patterns of single crystals. The excellent agreement between all diffraction peaks and the calculated patterns confirms the phase purity of Rb2Au2I6 and RbAuCl4 powders. Subsequent characterization studies were conducted based on the synthesized pure-phase single crystals or powders. The UV–vis absorption spectra of both compounds are presented in Fig. 2c and e. Rb2Au2I6 demonstrates extensive absorption ranging from approximately 200 to 1200 nm, which is characteristic of 3D narrow bandgap perovskites. In contrast, RbAuCl4 exhibits a narrow absorption peak at 300–550 nm. The optical bandgaps of the two compounds, calculated precisely from Tauc plots, are 1.11 and 2.37 eV, as shown in Fig. 2d and f. The 3D double perovskite Rb2Au2I6 shows red-shifted absorption edges and reduced bandgaps compared to the 2D DJ perovskite RbAuCl4, consistent with the trend observed in ABX3-type perovskites, where the bandgap decreases with increasing dimensionality. Previous studies have shown that the bandgap of halide perovskites decreases as the X-site halide radius increases (from Cl− to I−), a trend mirrored in our experimental results.Upon a comprehensive literature review, we attribute the remarkably low bandgap of Rb2Au2I6 to the metal–ligand intervalence charge transfer (MLIVCT) between the linear [AuII2]− and square [AuIIII4]− units.35 This narrow bandgap characteristic has also been observed in hybrid AAHPs ((CH3NH3)2Au2X6, X = Br, I), with bandgaps of 1.38 and 1.22 eV, respectively.19 Through crystal structure analysis, we observed a metal–halide–metal bond angle of 161.27° (AuIII–I⋯AuI) in Rb2Au2I6 compared to 148.47° (AuIII–Cl⋯AuIII) in RbAuCl4, as illustrated in Fig. 1c and d. The smaller bond angles in RbAuCl4 result in more pronounced octahedral distortion, leading to a larger bandgap (2.37 eV). This trend aligns with prior research, suggesting that reductions in the metal–halide–metal bond angles may lead to an increase in the bandgap.36 The bandgap of RbAuCl4 closely resembles that of (CH3NH3)AuCl4, a compound with analogous structural features, exhibiting a bandgap of 2.50 eV.37 It is noteworthy that the bandgap of RbAuCl4 is significantly lower than those of lead chloride-based 2D perovskites with similar structures, with a difference exceeding 1 eV; the latter typically exhibit bandgaps exceeding 3.5 eV.38 The significantly lower bandgap of Rb2Au2I6 than those of conventional halide perovskites indicates that Rb2Au2I6 can function effectively as a light absorber layer, facilitating the generation of electron–hole pairs throughout the entire visible spectrum, demonstrating its potential application in single-junction solar cells.39,40 Conversely, the wider bandgap of RbAuCl4 (approximately 2.4 eV) indicates its potential use as a semi-transparent upper absorber in tandem solar cells.41–43
X-ray photoelectron spectroscopy (XPS), known for its high surface sensitivity, is widely employed to determine the chemical composition and valence states of compounds. We conducted a qualitative analysis via XPS on slice samples prepared from single-crystal powder to confirm the elemental composition of the two perovskites. The full scan results of the XPS spectra in Fig. S2† illustrate characteristic peaks of Rb, Au, Cl, and I, validating the composition of perovskites under investigation. Fig. 2g and h present the valence state of the Au element. XPS analysis of the two compounds, Rb2Au2I6 and RbAuCl4, revealed the binding energies of the Au 4f regions fitted using Voigt functions. In Fig. 2g, the Au 4f core level displays four components at 83.4, 84.2, 86.9, and 87.1 eV, indicating two distinct chemical environments for the gold ions in the compound, corresponding to Au+ and Au3+ states. Fig. 2h shows XPS spectra for 4f5/2 and 4f7/2 with single peaks, positioning the 4f5/2 peak at 87.1 eV and the 4f7/2 peak at 84.2 eV, confirming the exclusive Au3+ oxidation state of gold in RbAuCl4.
Thermal stability is crucial for viable applications in optoelectronics, and TGA/DTG (thermogravimetric analysis/derivative thermogravimetry) analysis was conducted on two perovskite powders to understand their thermal decomposition pathways. In Fig. S4a,† Rb2Au2I6 exhibits a single-step degradation behavior (P1) in its TGA curve. The DTG curve shows this decomposition process more intuitively, with the decomposition initiated at 110 °C (T1) and concluding at 260 °C (T2). Following the decomposition stage, Rb2Au2I6 experiences a 37% mass loss, attributed to the release of I2, with metal Au and RbI being identified as the primary decomposition products. In Fig. S4b,† the TGA curve of RbAuCl4 reveals a two-stage thermal decomposition process: phase 1 (P1) and phase 2 (P2). Similarly, the accurate temperature of the enthalpy change peak was obtained by analyzing the DTG curve. Phase 1 commences at an onset temperature (TA) of 280 °C, resulting in a gradual weight loss, with a 10% mass reduction at TB = 360 °C, corresponding to the weight of Cl2. Subsequently, as the temperature rises to TC = 470 °C, a further 25% mass loss occurs, completing Phase 2, with the remaining mass corresponding to Au and RbCl. Our analysis indicates that Rb2Au2I6 exhibits comparable thermal stability (above 100 °C) with MAPbX3 (X = Cl/Br/I), while RbAuCl4 shows superior thermal resistance, initiating decomposition at 280 °C. Previous studies have shown that Ruddlesden–Popper perovskites containing Cl− as the halide component tend to exhibit enhanced thermal stability, potentially explaining the different thermal behaviors of Rb2Au2I6 and RbAuCl4.44,45
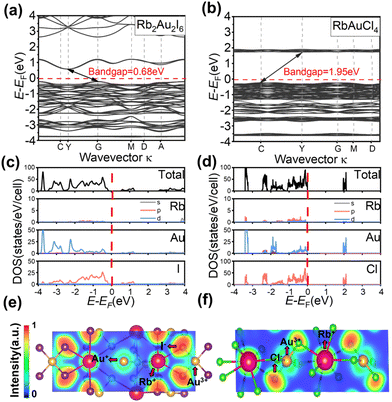
For elucidating the electronic structures and semiconductor properties of Rb2Au2I6 and RbAuCl4, we employed the Vienna Ab initio Simulation Package (VASP) with the Perdew–Burke–Ernzerhof (PBE) functional incorporating spin–orbit coupling (SOC) to compute the band structures and density of states (DOS).46,47Fig. 3a illustrates the electronic band structure of Rb2Au2I6 across high-symmetry points, revealing an electronic bandgap of 0.68 eV. Similarly, the bandgap of RbAuCl4 was determined to be 1.95 eV (Fig. 3b). The calculated bandgaps, though slightly smaller by 0.43 eV and 0.42 eV for the 3D and 2D perovskites, respectively, than the experimental values, are consistent with DFT calculations usually underestimating results due to artificial self-interaction and the exchange–correlation potential discontinuity from the valence to conduction bands. This trend has been observed in the bandgap calculations of other AAHPs,18,19,22 confirming the reliability of our computational results. Despite prior reports48 suggesting a direct bandgap for Rb2Au2I6, our single-crystal-based calculations demonstrate an indirect bandgap for this compound with the conduction band minimum (CBM) at G and the valence band maximum (VBM) at Y (Fig. 3a). Similarly, RbAuCl4 also exhibits an indirect bandgap nature.
To qualitatively comprehend the bonding characteristics and identify the different atomic orbital contributions, the normalized total and projected density of states (TDOS and PDOS) for the perovskites are depicted in Fig. 3c and d, providing insights into their semiconductor properties. In the PDOS of Rb2Au2I6, the VBM originates from Au-d and Cl-p orbitals (Fig. 3(c)). The difference in angular momentum between the Au+-d and Au3+-d orbitals, caused by Au-d orbital splitting, leads to asymmetry in these double perovskites. Consequently, the VBM shifts from the G point to the Y point, rendering Rb2Au2I6 an indirect bandgap material.19 In addition, the CBM in Rb2Au2I6 consists mainly of I-p orbitals, with a minor contribution from Au-d orbitals. The analysis of the PDOS reveals that the Rb+ cation does not significantly contribute to near band edges, indicating its role primarily as a charge donor to stabilize the perovskite structure, aligning with observations from traditional halide perovskite compounds.
As illustrated in Fig. 3(d), the VBM and CBM of RbAuCl4 are formed by the hybridization of Au-d orbitals and Cl-p orbitals, with Cl-p orbitals exerting a more substantial influence on both the CBM and VBM. Similar to the findings in Fig. 3(c), the Rb+ cation does not contribute significantly to near band edges. Subsequent analysis of the electronic band structure reveals a significantly larger bandgap for RbAuCl4 compared to that for Rb2Au2I6. This augmentation is attributed to the halogen atom substitution from I to Cl at the X position, leading to a reduction in the energy levels of the halogen's outermost orbitals. This transition elevates the CBM, resulting in a pronounced expansion of the bandgap.36,49 With a 2D perovskite structure, RbAuCl4 experiences quantum confinement effects, such as the Rashba and Dresselhaus effects.50 These effects restrict the movement of electrons and holes in specific dimensions, leading to increased effective mass and decreased carrier mobility. Additionally, quantum confinement in 2D perovskites causes the effective mass of electrons and holes to increase relative to their momentum space distribution, resulting in indirect bandgap characteristics.51 In summary, the 2D structure and quantum effects of RbAuCl4 contribute to its behavior characteristic of an indirect bandgap.
To further study the interatomic bonding and charge transfer, we performed the electron localization function (ELF) analysis of the (1, 1, −1) lattice planes of Rb2Au2I6 and RbAuCl4 (see Fig. 3(e and f)). Based on a second-order Taylor expansion of sphere average pair density,52 the ELF can be used to visualize atomic shell structures and the distribution of bond pairs, thus monitoring the electron distribution change during the formation and breaking of the bonds.53 The smaller ELF value (approaching 0) implies that the electron has an ultra-low density between two atoms with a typical ionic bond character. Conversely, while the ELF approaches 1, electrons are highly localized between two atoms, indicating the presence of an ideal covalent bond.54,55
The ELF calculations clearly show the bonding properties between the metal cations (e.g., Au+ and Rb+) and the X-site halide ions (I− and Cl−). As shown in Fig. 3(e and f), the electron sharing behavior between Au+, Au3+, and the X-site halide anions indicates a stronger covalent bond. The lower ELF values between Rb+ and other ions represent the interactions between Rb+ and [AuX]− (X = Cl or I) units, corresponding to ionic bonds. This convinced us that there is a strong charge transfer between the ionic units in the perovskite structure, enhancing the stability of the structure.
Optical and photovoltaic properties
Following a comprehensive analysis of the bandgap properties of both materials, we proceeded with further investigation of their band structures. The calculated carrier masses of Rb2Au2I6 and RbAuCl4 were determined to be 0.58m0 and 3.03m0, respectively (Table S2†). The effective mass, derived from fitting the CBM and VBM of the materials, is inversely related to the curvature of the band edge: a steeper (flatter) curvature signifies a smaller (larger) effective mass and a faster (slower) carrier mobility. Consequently, the significant difference in CBM and VBM configurations between Rb2Au2I6 and RbAuCl4 engenders a notable contrast in their effective carrier masses. It is worth noting that Rb2Au2I6 exhibits a relatively lighter carrier mass (|meff| < 1), a characteristic that extends the carrier lifetime and enhances photovoltaic performance.To delve deeper into the potential applications of the two materials in photovoltaics, we employed the PBE + SOC method to calculate their dielectric constants (e) and exciton binding energies (Eb). The dielectric constants were found to be 6.83 and 3.21 for Rb2Au2I6 and RbAuCl4, respectively, with Eb values of 67 meV and 620 meV, as shown in Table S2.† Notably, the exciton binding energy of Rb2Au2I6 (67 meV) closely approximates that of the classic light-absorbing material MAPbI3 (48 meV).56 This relatively low Eb signifies a significant energy difference between electrons and holes, thereby reducing the likelihood of recombination.57 Consequently, excitons generated in Rb2Au2I6 can readily dissociate into free charge carriers, thereby achieving high photovoltaic conversion efficiency. Combining suitable bandgaps, light carrier masses, and modest exciton binding energies, Rb2Au2I6 shows promise as a solar cell absorption layer.
On the other hand, in RbAuCl4, the presence of Rb+ ion spacing layers induces a low dielectric constant region between the [AuCl6]3−octahedron layers, resulting in quantum confinement and dielectric confinement effects that increase the Eb. However, higher Eb values typically hinder charge carrier transport.58 Therefore, for the practical implementation of RbAuCl4 in photovoltaic cells, achieving a high-quality perovskite film with vertical orientation to the substrate is crucial.59,60 It is noteworthy that semiconductors with high exciton binding energies are more favorable in light-emitting applications since the radiative recombination that occurs through excitons can reach high quantum yields at relatively lower carrier densities.61 As RbAuCl4 exhibits a high Eb, it is advantageous for achieving a higher photoluminescence quantum yield (PLQY) and holds potential for applications in the field of light-emitting devices.62
The PBE method was then utilized to calculate the optical absorption coefficients of the two compounds, aimed at evaluating their potential as absorber layers in solar cells. A sharp increase in the optical absorption coefficient is observed near the bandgap edge for both Rb2Au2I6 and RbAuCl4, with absorption coefficients in the visible light region near the bandgap reaching values as high as 105 cm−1, as depicted in Fig. 4a. The significant optical absorption coefficient is attributed to the flat and dense bands near the band edges (see Fig. 3a and b), resulting in a well-defined joint density of states (JDOS).22 This elevated density implies that more electrons and holes can participate in transitions, thus increasing the optical absorption coefficient even through an indirect transition mechanism. Furthermore, in materials with indirect bandgaps, the relaxation of excited electron–hole pairs to the VBM and CBM is influenced by the mismatch in crystal momentum. This relaxation mechanism suppresses radiative recombination, enhancing long-carrier diffusion. The prolonged diffusion length of charge carriers means that the generated electrons and holes can migrate longer distances within the material, allowing for charge separation and collection over a larger range, further enhancing the collection efficiency of photogenerated charge carriers and improving device performance. Comparatively, the light absorption coefficient of RbAuCl4 is lower than that of Rb2Au2I6, attributed to its unique 2D structure. Within the crystal structure of RbAuCl4, the octahedral layers are separated by Rb cations along the c-axis (001) direction, impeding carrier transfer along this axis and consequently resulting in a reduced absorption coefficient. Overall, our calculations suggest that both perovskites demonstrate high absorption efficiency.
 | ||
| Fig. 4 Optical properties of Rb2Au2I6 and RbAuCl4. (a) Calculated absorption spectra of average optical directions and (b) different optical polarizations. (c) SLME as a function of film thickness. | ||
We then calculated the absorption coefficients of the two compounds in various light polarization directions, as illustrated in Fig. 4b. By comparing the optical absorption intensities in different directions, we observed significant optical anisotropy stemming from the distortion in their cubic crystal structures. Further examination revealed that the absorption coefficient strength (αzz) perpendicular to the ab plane in the (001) direction is approximately equal to that in the (100) direction (αxx), with both values lower than the absorption coefficient (αyy) in the (010) direction. This disparity is more pronounced in the absorption spectrum of Rb2Au2I6 than in that of RbAuCl4, possibly due to transitions between different oxidation states of Au atoms.23 Optical anisotropy plays an indispensable role in diverse optical components and can be leveraged by aligning crystal growth orientation in thin films to maximize light absorption, thereby enhancing the photovoltaic performance of devices.59
Furthermore, the anisotropic light absorption of perovskite materials can also be exploited in photodetector fabrication.63 By capitalizing on absorption direction variations, efficient detection of light signals with specific orientations and polarization states can be achieved, thereby heightening sensitivity and enhancing the performance of photodetectors.64,65 Additionally, we evaluated the potential efficacy of the two compounds as solar cell absorbers using the SLME metric, which influences the optical absorption spectrum, the thickness of the thin-film absorber, and the magnitude of bandgaps.66 In Fig. 4c, it is evident that with an absorber layer thickness of 500 nm, Rb2Au2I6 and RbAuCl4 show predicted SLMEs of 30.12% and 22.30%, respectively. The significant SLME of Rb2Au2I6 is attributed to its superior light absorption capability and appropriate bandgap. Moreover, the SLME of the 2D DJ perovskite RbAuCl4 slightly surpasses that of Cs2Au2I6 (21.50%), indicating that it is a promising lead-free alternative.22 Despite the usual variations between theoretical predictions and actual solar cell efficiencies due to various factors like interfacial effects, surface defects, and incomplete light absorption, the SLME metric remains valuable. Therefore, considering the outstanding theoretical performance and actual bandgap values of Rb2Au2I6, it more effectively fulfills the criteria of a single-junction solar absorber. Meanwhile, the marginally larger optical bandgap of RbAuCl4 renders it better suited for application in tandem solar cells.
Thermoelectric properties
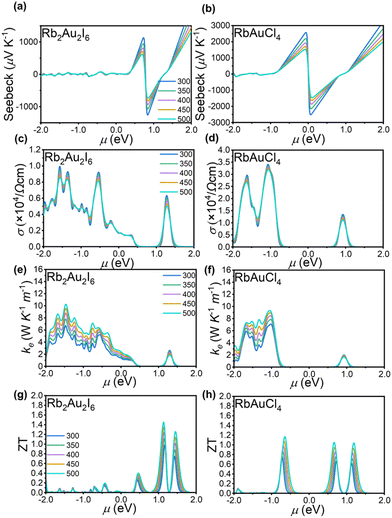
Semiconductive perovskites are considered suitable thermoelectric materials because they efficiently convert heat differentials into electrical energy.10 A narrow bandgap allows for a higher density of states near the Fermi level, leading to an increased electrical conductivity and Seebeck coefficient, resulting in a higher power factor. Based on the crystal structures of the two perovskites, we employed the linear combination atomic orbital basis set (LCAO) method within the framework of Density Functional Theory (DFT) to calculate their thermoelectric properties.Initially, the phonon spectra of the two perovskites were computed, as shown in Fig. S5(a and b),† revealing the absence of imaginary frequencies, thus confirming the thermodynamic stability of the crystal structures. The thermoelectric performance of a material can be assessed using the figure of merit (ZT = S2σT/κ), where S represents the Seebeck coefficient, σ denotes the electrical conductivity, T signifies the absolute temperature, and κ encompasses both electronic (κe) and lattice (κl) thermal conductivity. From the figure of merit calculation formula, it is evident that enhancing thermoelectric efficiency requires simultaneous improvement of the material's Seebeck coefficient and electrical conductivity while simultaneously reducing thermal conductivity.
The thermoelectric parameters were evaluated as a function of the chemical potential m at temperatures of 300, 350, 400, 450, and 500 K for Rb2Au2I6 and RbAuCl4. When the chemical potential m > 0, S exhibits an n-type character, while with m < 0, it demonstrates a p-type character. Fig. 5(a and b) presents the correlation between the S and the chemical potential, m, for Rb2Au2I6 and RbAuCl4. First, it was observed that S decreased with increasing temperature. By comparing S values at the same temperature corresponding to identical chemical potentials, the magnitude of S for RbAuCl4 was found to be greater than that of Rb2Au2I6. Taking 300 K as an example, under identical chemical potential conditions, the S of RbAuCl4 surpassed that of Rb2Au2I6. Specifically, RbAuCl4 demonstrated a maximum S of 2584.3 mV K−1, corresponding to m = −0.05 eV, whereas Rb2Au2I6 exhibited a maximum S of 1136.0 mV K−1, corresponding to m = 0.73 eV. Moreover, S underwent rapid changes as m increased or decreased, as shown in Fig. 5(a and b). When the band structures and scattering mechanism remain unchanged, the S of a semiconductor material can be described using the following equation:
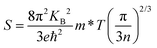 | (2) |
Fig. 5(e and f) illustrates the electronic thermal conductivity (κe) of the two perovskites. A noticeable increase in the electronic thermal conductivity is observed for both perovskite materials with escalating temperatures. Specifically, the peak thermal conductivities of Rb2Au2I6 and RbAuCl4 were observed at m = −1.46 eV and m = 1.04 eV, respectively, yielding values of 9.31 W K−1 m−1 and 10.19 W K−1 m−1. Then, the ZT values of both perovskites were calculated based on the outcomes of S, σ, and κe. Fig. 5(g and h) delineates the trend of ZT concerning temperature and m. Notably, to mitigate the influence of lattice thermal conductivity (κl), Density Functional Perturbation Theory (DFPT) was employed for the computation, as depicted in Fig. S5 (c and d). Relative to κe, the κl of both perovskites undergoes a reduction by an order of magnitude, aligning with the characteristic ultra-low lattice thermal conductivity inherent in perovskite materials.67,68 Consequently, the impact of lattice thermal conductivity on the thermoelectric performance of the investigated materials is deemed negligible. Both perovskites exhibit sharp peaks in the figure of merit. For Rb2Au2I6, the ZT peak is observed at m = 1.13 eV, reaching approximately 1.44 at 500 K. The corresponding values for S and electrical conductivity σ are −218.75 mV K−1 and 800 S cm−1, respectively. On the other hand, RbAuCl4 shows the highest ZT of 1.16 at 500 K, located at m = −0.65 eV. The corresponding S and σ values are 440 mV K−1 and 580 S cm−1, respectively.
Subsequently, we proceed to elucidate the high thermoelectric performance of two AAHPs from an electronic perspective. It is well-established that the shape of the electronic band structure and DOS play a crucial role in influencing the thermoelectric properties of semiconductor materials. As depicted in Fig. 4(a and b), compared to Rb2Au2I6, RbAuCl4 exhibits a flatter band structure, implying a higher carrier mobility. Notably, both Rb2Au2I6 and RbAuCl4 display significant asymmetry in the DOS near the Fermi level, characterized primarily by the resonant peaks in close proximity. These DOS peaks near the Fermi level lead to a significant increase in electron density at relevant energy levels, potentially boosting the carrier concentration and thereby enhancing the electron mobility and conductivity.69 Consequently, the increased carrier mobility augments the thermoelectric effect near the Fermi level, manifested by larger Seebeck coefficients, ultimately reinforcing the thermoelectric performance of the AAHPs.70
Conclusion
In summary, we have successfully synthesized AAHPs, Rb2Au2I6 and RbAuCl4, through a modified efficient hydrothermal method, yielding millimeter-scale single crystals. Compared to previous synthesis approaches, the significantly improved synthetic procedure could accelerate the practical application of these materials. Subsequent analysis of their crystal structures revealed that Rb2Au2I6 features interconnected octahedra in 3D space, constituting a 3D double perovskite, while the octahedron layers of RbAuCl4 are separated by Rb ions, forming a 2D DJ-type perovskite. Furthermore, by integrating experimental characterization with theoretical calculations, both materials were found to have optical bandgaps of 1.11 eV and 2.37 eV, respectively, along with high absorption coefficients. Notably, with a film thickness of 500 nm, Rb2Au2I6 and RbAuCl4 showed high SLMEs of 30.12% and 22.30%, respectively, as absorber layers in thin-film solar cells, rendering them promising light-absorbing materials. Moreover, given the high exciton binding energy and inherent optical anisotropy of RbAuCl4, we posit significant potential for luminescence applications. Our theoretical predictions indicate that both perovskites are excellent medium-temperature thermoelectric materials, with ZT values reaching approximately 1.4 and 1.2 at 500 K for Rb2Au2I6 and RbAuCl4. Currently, the exploration of film fabrication techniques for these two materials is progressing steadily in our laboratory, with the anticipation of their imminent application in actual photovoltaic or thermoelectric devices. This study lays a solid foundation for the practical application of inorganic AAHP materials in the field of energy conversion.Data availability
• The data supporting this article have been included as part of the ESI.†• The crystallographic data for Rb2Au2I6 and RbAuCl4 have been deposited at the CCDC under 2341967 and 2363017† and can be obtained from https://www.ccdc.cam.ac.uk/structures/.
Author contributions
X.Y., C. L. and P. G. conceived and designed the project. X.Y., C. L., Z. Z., Z. N., Q. X, Y. Z., and S. L. prepared the samples and characterized their properties. X. F., Y. L., and L. M. assisted in the first-principles calculation. All authors discussed the results and contributed to the writing of this paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. G. acknowledges the financial support from the National Natural Science Foundation of China (Grant No. 22175180 and 52311530673). The authors thank HZWTECH for allowing the use of the DS-PAW and BDF code in Device Studio. The authors also gratefully acknowledge HZWTECH for supporting the computational resources.References
- A. R. B. Mohd Yusoff, P. Gao and M. K. Nazeeruddin, Coord. Chem. Rev., 2018, 373, 258–294 CrossRef.
- P. Gao, M. Grätzel and M. K. Nazeeruddin, Energy Environ. Sci., 2014, 7, 2448–2463 RSC.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- L. Dou, Y. Yang, J. You, Z. Hong, W.-H. Chang, G. Li and Y. Yang, Nat. Commun., 2014, 5, 5404 CrossRef CAS PubMed.
- H. Cho, S.-H. Jeong, M.-H. Park, Y.-H. Kim, C. Wolf, C.-L. Lee, J. H. Heo, A. Sadhanala, N. Myoung, S. Yoo, S. H. Im, R. H. Friend and T.-W. Lee, Science, 2015, 350, 1222–1225 CrossRef CAS PubMed.
- Y. Park, S. H. Kim, D. Lee and J.-S. Lee, Nat. Commun., 2021, 12, 3527 CrossRef CAS PubMed.
- P. Gao, A. R. Bin Mohd Yusoff and M. K. Nazeeruddin, Nat. Commun., 2018, 9, 5028 CrossRef PubMed.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS PubMed.
- H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X.-Y. Zhu, Nat. Mater., 2015, 14, 636–642 CrossRef CAS PubMed.
- T. Wu and P. Gao, Materials, 2018, 11, 999 CrossRef PubMed.
- T. Wu, W. Pisula, M. Y. A. Rashid and P. Gao, Adv. Electron. Mater., 2019, 5, 1900444 CrossRef CAS.
- H. Zhu, S. Teale, M. N. Lintangpradipto, S. Mahesh, B. Chen, M. D. McGehee, E. H. Sargent and O. M. Bakr, Nat. Rev. Mater., 2023, 8, 569–586 CrossRef.
- G. Li, Y. Liu, F. Yang, M. Li, Z. Zhang, J. Pascual, Z. Wang, S. Wei, X. Zhao, H. Liu, J. Zhao, C. Lin, J. Li, Z. Li, A. Abate and I. Cantone, Adv. Mater., 2024, 36, 2306860 CrossRef CAS PubMed.
- L. Liang and P. Gao, Adv. Sci., 2018, 5, 1700331 CrossRef PubMed.
- E. L. Lim, A. Hagfeldt and D. Bi, Energy Environ. Sci., 2021, 14, 3256–3300 RSC.
- N. Matsushita, A. Tanaka and N. Kojima, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, i201–i203 CrossRef CAS.
- H. A. Evans, E. C. Schueller, S. R. Smock, G. Wu, R. Seshadri and F. Wudl, Inorg. Chim. Acta, 2017, 468, 280–284 CrossRef CAS.
- Y. Fan, Q. Liu, Z. Zhang, S.-Y. Lien, Y. Xie, W. Liang and P. Gao, Chem. Mater., 2022, 34, 1544–1553 CrossRef CAS.
- B. Ghosh, B. Febriansyah, P. C. Harikesh, T. M. Koh, S. Hadke, L. H. Wong, J. England, S. G. Mhaisalkar and N. Mathews, Chem. Mater., 2020, 32, 6318–6325 CrossRef CAS.
- K. P. Lindquist and K. P. Eghdami, et al. , Nat. Chem., 2023, 12, 1780–1786 CrossRef PubMed.
- K. P. Lindquist, M. A. Boles, S. A. Mack, J. B. Neaton and H. I. Karunadasa, J. Am. Chem. Soc., 2021, 143, 7440–7448 CrossRef CAS PubMed.
- L. Debbichi, S. Lee, H. Cho, A. M. Rappe, K. Hong, M. S. Jang and H. Kim, Adv. Mater., 2018, 30, 1707001 CrossRef PubMed.
- W. Li, Y. Li, Z. Zhang and P. Gao, J. Energy Chem., 2023, 84, 347–353 CrossRef CAS.
- J. Strähle, J. Gelinek and M. Kälmel, Z. Anorg. Allg. Chem., 1979, 456, 241–260 CrossRef.
- Hongzhiwei Technology, Available online: https://iresearch.net.cn/cloudSoftware.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- N. Matsushita, A. Tanaka and N. Kojima, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, i201–i203 CrossRef CAS.
- H. P. S. Corrêa, I. P. Cavalcante, D. O. Souza, E. Z. Santos, M. T. D. Orlando, H. Belich, F. J. Silva, E. F. Medeiro, J. M. Pires, J. L. Passamai, L. G. Martinez and J. L. Rossi, Cerâmica, 2010, 56, 193–200 CrossRef.
- P. Novak, J. Phys. Chem. Solids, 1970, 31, 125–130 CrossRef CAS.
- X. J. Liu, K. Matsuda, Y. Moritomo, A. Nakamura and N. Kojima, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7925–7930 CrossRef CAS.
- A. V. Ushakov, S. V. Streltsov and D. I. Khomskii, J. Phys.: Condens. Matter, 2011, 23, 445601 CrossRef CAS PubMed.
- T. Mizokawa, J. Phys.: Conf. Ser., 2013, 428, 012020 CrossRef CAS.
- I. P. Swainson, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 616–626 CrossRef PubMed.
- Z.-Z. Zhang, T.-M. Guo, Z.-G. Li, F.-F. Gao, W. Li, F. Wei and X.-H. Bu, Acta Mater., 2023, 245, 118638 CrossRef CAS.
- N. Kojima, S. H. H. Kitagawa and T. Kikegawa, J. Am. Chem. Soc., 1994, 116, 11368–11374 CrossRef CAS.
- R. Prasanna, A. Gold-Parker, T. Leijtens, B. Conings, A. Babayigit, H.-G. Boyen, M. F. Toney and M. D. McGehee, J. Am. Chem. Soc., 2017, 139, 11117–11124 CrossRef CAS PubMed.
- C. Worley, A. Yangui, R. Roccanova, M. Du and B. Saparov, Chem. – Eur. J., 2019, 25, 9875–9884 CrossRef CAS PubMed.
- H. Barkaoui, H. Abid, A. Yangui, S. Triki, K. Boukheddaden and Y. Abid, J. Phys. Chem. C, 2018, 122, 24253–24261 CrossRef CAS.
- Z. Zhang, Q. Sun, Y. Lu, F. Lu, X. Mu, S.-H. Wei and M. Sui, Nat. Commun., 2022, 13, 3397 CrossRef CAS PubMed.
- F. Ji, G. Boschloo, F. Wang and F. Gao, Sol. RRL, 2023, 7, 2201112 CrossRef CAS.
- F. Xu, E. Aydin, J. Liu, E. Ugur, G. T. Harrison, L. Xu, B. Vishal, B. K. Yildirim, M. Wang, R. Ali, A. S. Subbiah, A. Yazmaciyan, S. Zhumagali, W. Yan, Y. Gao, Z. Song, C. Li, S. Fu, B. Chen, A. Ur Rehman, M. Babics, A. Razzaq, M. De Bastiani, T. G. Allen, U. Schwingenschlögl, Y. Yan, F. Laquai, E. H. Sargent and S. De Wolf, Joule, 2024, 8, 224–240 CrossRef CAS.
- J. Wang, L. Zeng, D. Zhang, A. Maxwell, H. Chen, K. Datta, A. Caiazzo, W. H. M. Remmerswaal, N. R. M. Schipper, Z. Chen, K. Ho, A. Dasgupta, G. Kusch, R. Ollearo, L. Bellini, S. Hu, Z. Wang, C. Li, S. Teale, L. Grater, B. Chen, M. M. Wienk, R. A. Oliver, H. J. Snaith, R. A. J. Janssen and E. H. Sargent, Nat. Energy, 2023, 9, 70–80 CrossRef.
- R. He, W. Wang, Z. Yi, F. Lang, C. Chen, J. Luo, J. Zhu, J. Thiesbrummel, S. Shah, K. Wei, Y. Luo, C. Wang, H. Lai, H. Huang, J. Zhou, B. Zou, X. Yin, S. Ren, X. Hao, L. Wu, J. Zhang, J. Zhang, M. Stolterfoht, F. Fu, W. Tang and D. Zhao, Nature, 2023, 618, 80–86 CrossRef CAS PubMed.
- H. Ren, S. Yu, L. Chao, Y. Xia, Y. Sun, S. Zuo, F. Li, T. Niu, Y. Yang, H. Ju, B. Li, H. Du, X. Gao, J. Zhang, J. Wang, L. Zhang, Y. Chen and W. Huang, Nat. Photonics, 2020, 14, 154–163 CrossRef CAS.
- E. S. Vasileiadou, B. Wang, I. Spanopoulos, I. Hadar, A. Navrotsky and M. G. Kanatzidis, J. Am. Chem. Soc., 2021, 143, 2523–2536 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. Liu, H. Zeng, H. Peng and R. Sa, Phys. Chem. Chem. Phys., 2023, 25, 28974–28981 RSC.
- V. D'Innocenzo, A. R. Srimath Kandada, M. De Bastiani, M. Gandini and A. Petrozza, J. Am. Chem. Soc., 2014, 136, 17730–17733 CrossRef PubMed.
- D. B. Straus and C. R. Kagan, J. Phys. Chem. Lett., 2018, 9, 1434–1447 CrossRef CAS PubMed.
- X. Li, J. M. Hoffman and M. G. Kanatzidis, Chem. Rev., 2021, 121, 2230–2291 CrossRef CAS PubMed.
- W. Shi, T. Cai, Z. Wang and O. Chen, J. Chem. Phys., 2020, 153, 141101 CrossRef CAS PubMed.
- J. Navas, A. Sánchez-Coronilla, J. J. Gallardo, J. C. Piñero, D. De Los Santos, E. I. Martín, N. C. Hernández, R. Alcántara, C. Fernández-Lorenzo and J. Martín-Calleja, Nano Energy, 2017, 34, 141–154 CrossRef CAS.
- K. Wang, Y. He, M. Zhang, J. Shi and W. Cai, J. Phys. Chem. C, 2021, 125, 21160–21168 CrossRef CAS.
- R.-K. Pan, J.-G. Yao, R.-L. Ji, W.-W. Liu and D.-F. Yin, Int. J. Hydrogen Energy, 2018, 43, 3862–3870 CrossRef CAS.
- E. Menéndez-Proupin, P. Palacios, P. Wahnón and J. C. Conesa, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045207 CrossRef.
- Y. Jiang, X. Wang and A. Pan, Adv. Mater., 2019, 31, 1806671 CrossRef CAS PubMed.
- Q. Fu, M. Chen, Q. Li, H. Liu, R. Wang and Y. Liu, J. Am. Chem. Soc., 2023, 145, 21687–21695 CrossRef CAS PubMed.
- L. Yan, J. Ma, P. Li, S. Zang, L. Han, Y. Zhang and Y. Song, Adv. Mater., 2022, 34, 2106822 CrossRef CAS PubMed.
- P. Liu, N. Han, W. Wang, R. Ran, W. Zhou and Z. Shao, Adv. Mater., 2021, 33, 2002582 CrossRef CAS PubMed.
- J. Xing, F. Yan, Y. Zhao, S. Chen, H. Yu, Q. Zhang, R. Zeng, H. V. Demir, X. Sun, A. Huan and Q. Xiong, ACS Nano, 2016, 10, 6623–6630 CrossRef CAS PubMed.
- N. Li, Y. Jia, Y. Guo and N. Zhao, Adv. Mater., 2022, 34, 2108102 CrossRef CAS PubMed.
- C. Xie, C. Liu, H. Loi and F. Yan, Adv. Funct. Mater., 2020, 30, 1903907 CrossRef CAS.
- Z. Chen, Z. Shi, W. Zhang, Z. Li and Z.-K. Zhou, Nanophotonics, 2022, 11, 1379–1387 CrossRef CAS.
- C. Lin, C. Kang, T. Wu, C. Tsai, C. Sher, X. Guan, P. Lee, T. Wu, C. Ho, H. Kuo and J. He, Adv. Funct. Mater., 2020, 30, 1909275 CrossRef CAS.
- L. Yu and A. Zunger, Phys. Rev. Lett., 2012, 108, 068701 CrossRef PubMed.
- M. A. Haque, S. Kee, D. R. Villalva, W. Ong and D. Baran, Adv. Sci., 2020, 7, 1903389 CrossRef CAS PubMed.
- A. Bhui, T. Ghosh, K. Pal, K. Singh Rana, K. Kundu, A. Soni and K. Biswas, Chem. Mater., 2022, 34, 3301–3310 CrossRef CAS.
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616–8639 CrossRef CAS PubMed.
- J. He and T. M. Tritt, Science, 2017, 357, eaak9997 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: SEM mapping, schematic spectra of single crystals, XPS spectra, TGA curves, phonon spectra, and lattice electrical conductivity. CCDC 2341967 and 2363017. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi00816b |
| This journal is © the Partner Organisations 2024 |