 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Minimal numerical ingredients describe chemical microswimmers’ 3-D motion†
Maximilian R.
Bailey
 ab,
C. Miguel
Barriuso Gutiérrez
ab,
C. Miguel
Barriuso Gutiérrez
 b,
José
Martín-Roca
bc,
Vincent
Niggel
a,
Virginia
Carrasco-Fadanelli
d,
Ivo
Buttinoni
b,
José
Martín-Roca
bc,
Vincent
Niggel
a,
Virginia
Carrasco-Fadanelli
d,
Ivo
Buttinoni
 d,
Ignacio
Pagonabarraga
d,
Ignacio
Pagonabarraga
 ef,
Lucio
Isa
ef,
Lucio
Isa
 a and
Chantal
Valeriani
a and
Chantal
Valeriani
 *bg
*bg
aLaboratory for Soft Materials and Interfaces, Department of Materials, ETH Zürich, Zürich, Switzerland
bDepartamento de Estructura de la Materia, Física Térmica y Electrónica, Universidad Complutense de Madrid, Madrid, Spain. E-mail: cvaleriani@ucm.es
cDepartamento de Química Física, Facultad de Química, Universidad Complutense de Madrid, Madrid, Spain
dDepartment of Physics, Institute of Experimental Colloidal Physics, Heinrich-Heine University, Düsseldorf, Germany
eDepartament de Física de la Matèria Condensada, Universitat de Barcelona, Barcelona, Spain
fUniversitat de Barcelona Institute of Complex Systems (UBICS), Universitat de Barcelona, Barcelona, Spain
gGISC - Grupo Interdiplinar de Sistemas Complejos, Madrid, Spain
First published on 29th December 2023
Abstract
The underlying mechanisms and physics of catalytic Janus microswimmers is highly complex, requiring details of the associated phoretic fields and the physiochemical properties of catalyst, particle, boundaries, and the fuel used. Therefore, developing a minimal (and more general) model capable of capturing the overall dynamics of these autonomous particles is highly desirable. In the presented work, we demonstrate that a coarse-grained dissipative particle-hydrodynamics model is capable of describing the behaviour of various chemical microswimmer systems. Specifically, we show how a competing balance between hydrodynamic interactions experienced by a squirmer in the presence of a substrate, gravity, and mass and shape asymmetries can reproduce a range of dynamics seen in different experimental systems. We hope that our general model will inspire further synthetic work where various modes of swimmer motion can be encoded via shape and mass during fabrication, helping to realise the still outstanding goal of microswimmers capable of complex 3-D behaviour.
1. Introduction
In the last two decades, potential applications for directed transport at length scales where thermal fluctuations are important have prompted the development of a range of synthetic microswimmers, each with its intricacies.1–3 Amongst the various synthetic active materials, Janus catalytic microswimmers remain one of the most popular due to their straightforward fabrication protocols, simple experimental set-ups, and good reproducibility between experiments.4,5 Typically, these are spherical particles asymmetrically modified with a catalytic material leading to the production of asymmetric local chemical gradients in the presence of a “fuel”, causing propulsion via self-phoresis.6–9 Such microswimmers generally move in 2-D (xy) due to their density mismatch with the surrounding fluid and attractive interactions with the underlying substrate.10 However, controlling the motion of microswimmers in 3-D is appealing from an applications perspective, and there is a growing body of work on active materials capable of motion in all dimensions.11–22The rational design of chemical microswimmers displaying tailored motion in 3-D would greatly profit from models which can capture empirical observations.16 However, their experimental simplicity masks a complex system of chemical and mass transfer relationships, the underlying mechanisms and physics of which are still the subject of ongoing debate.23,24 It is generally accepted that a more complete description of such “chemically active colloids” requires the full solution of their phoretic fields, including details of the colloids, the substrate, and the solution composition.25–27 Unfortunately, such detailed descriptions call for a high level of technical expertise, are system-specific due to phoretic mobility parameters, have only been solved for spherical and ellipsoidal structures, and do not easily allow the inclusion of thermal fluctuations, which are critical when describing the dynamics of micron-scale objects.
To avoid the consideration of chemical phoretic fields and only account for hydrodynamic flows, the “squirmer” model is frequently invoked.28 This model was first proposed for microorganisms such as Paramecia and Volvox,29,30 and is now used as a generic description for various active systems. Squirmers swim due to a self-generated, usually stationary31 and axi-symmetric velocity field which is typically evaluated as tangential across its surface. Considered as a spherical rigid body, the squirmer can be defined using two modes describing its swimming velocity and force-dipole (B1 and B2 respectively32). Promisingly, it has been shown that a bottom-up model of Janus self-diffusiophoretic microswimmers – accounting for the unique interaction potentials of the different chemical species with the separate hemispheres of a Janus particle – will produce flow fields characteristic of spherical squirmers.33 Recent experimental studies investigating tracer flows around chemical microswimmers34 and their directed motion under flow (“rheotaxis”)35,36 have also indicated that the flow fields generated by such active agents are characteristic of squirmer-type systems. Therefore, “coarse-graining” Janus chemical microswimmers as squirmers provides a viable approach to model their behaviour despite neglecting the (albeit important) contributions arising from chemical fields26,27 and an asymmetric surface.33
A number of numerical strategies have been implemented to simulate the coarse-grained dynamics of (chemical) microswimmers, amongst which a multi-particle-collision dynamics (MPCD) description of the solvent is perhaps the most frequently invoked due to its ability to include thermal fluctuations at a lower computational cost than e.g. the Lattice Boltzmann (LB) method.32,37–46 Nevertheless, we note particularly relevant studies where LB approaches were utilised to study the behaviour of raspberry-type and other shape anisotropic microswimmers.47,48 Like MPCD, dissipative particle dynamics (DPD)49 coarse-grains the solvent as point-like fluid particles (packets of fluid molecules), and thus inherently includes the effects of thermal noise while solving the Navier–Stokes equations.50 By utilising a particle-based approach to model the solvent, the computational cost is significantly reduced, allowing the simulation of hydrodynamic interactions in systems where advection dominates over diffusion (high Péclet number, Pe).51 In DPD, the solvent particles themselves act as local thermostats due to their competing stochastic and dissipative pair-wise terms, conserving momentum and thus accounting for hydrodynamics and thermal fluctuations.52 Additionally, DPD makes use of softer inter-particle potentials, allowing greater timesteps compared to MPCD, thereby enabling simulations of larger systems at longer timescales.53,54 Therefore, DPD emerges as a suitable candidate to model microswimmers as squirmers, as it can handle hydrodynamics in high Pe systems (where directed motion dominates over diffusion) with (relatively) large time-steps, while properly dealing with thermal fluctuations. For these reasons, a DPD framework capturing the hydrodynamic interactions of microswimmers in the presence of confining boundaries – by applying tangential solvent forces around the swimmer – was recently developed by some of the authors.55 As DPD is already implemented in the open-access molecular dynamics program Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS),56 this provides the opportunity to exploit a range of in-built functions to extend previous studies, with the goal of mimicking the behaviour of chemical microswimmers above a substrate.
Here, we further develop this model to consider the influence of mass and shape asymmetries on the dynamics of spherical microswimmers in the presence of a bounding substrate, mirroring common experimental conditions for chemical active colloids.55,57–59 The strength of our approach lies in its modularity, which allows the simple inclusion of these asymmetries that may have otherwise presented significant complications when considering other numerical schemes. We find that the interplay between hydrodynamic interactions, gravity, bottom-heaviness, and shape is sufficient to qualitatively capture the 2- and 3-D physics of a range of catalytic (and photo-catalytic) Janus microswimmer systems,17,18,20i.e. while neglecting contributions from chemical59 and light60,61 gradients. Specifically, there is a competition between the hydrodynamic attraction to the substrate that grows with the swimming speed and the active force required to overcome gravity, which determines the ability of the microswimmer to enter the bulk. This balance can be furthermore adjusted by introducing mass or shape asymmetry to the particles. Our coarse-grained approach thus opens the door to the informed design of chemical microswimmers whose dynamics can be encoded via shape or mass during fabrication, helping to realise the still outstanding goal of active colloids capable of truly 3-D dynamics.
2. Numerical method
Following the approach outlined in ref. 55, we use an in-house extension of the open source LAMMPS package56 to simulate the motion of squirmer-like microswimmers, modelled as rigid-body raspberry structures constructed from DPD “filler” spheres using the LAMMPS fix-rigid module (see Fig. 1). The thermal energy of the solvent particles kBT is set to 1, the solvent density ρ = 5.9 (where ρ = NpVp/Vsystem, for Np solvent particles with volume Vp, in a simulation volume Vsystem), and the dissipative force γ = 1. The simulation length-scales are as described in Fig. 1a, normalised with respect to the radius of 1 DPD filler particle, while the masses of DPD particles are set to 1 unless introducing mass asymmetry (see below). Solvent DPD spheres (purple particles, see Fig. 1) interact with the microswimmer's constituent “filler” particles with a DPD cutoff of Rfs = 2 while between them we set Rss = 0.58 to achieve a lower Reynolds number.49 The simulation time-scale τ is set according to these parameters, and numerically integrated at 0.01τ time-steps. When present, substrates are modelled as overlapping DPD particles (see Fig. 1b (ref. 55)), properly aligned along the x- and y-axes to ensure a flat repulsive potential interacting with both the solvent and colloid particles via the DPD soft conservative force with a large amplitude Fc = 100.49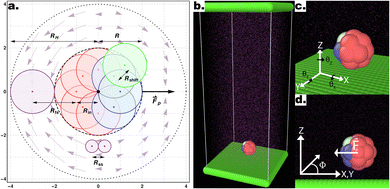 | ||
| Fig. 1 (a) Schematic representation of a 2D section of the colloid using a raspberry model with cap-front (CF) mass imbalance and shape asymmetry. The colloid is built from 18 DPD filler particles (red and blue), distributed on the surface of a sphere radius Rin = 1, each with a DPD cut-off for interactions with other DPD particles (e.g. solvent particles), resulting in an overall effective microswimmer radius of R = 2. Shape asymmetry is implemented by introducing an additional particle Pshape (green) displaced a distance Rshift from an off-axis filler particle. Here, the equatorial 2D slice containing the shape asymmetry is shown, thus only depicting the 8 filler particles within this section. The thruster particle (not visible) generates the force field (light purple arrows), here consistent with a pusher-type squirmer, emanating from the center of mass of the colloid and fixed with its internal frame of reference. (b–d) Snapshot of the full simulation box (b), as well as the definition of the angles θx,y,z (c) and the azimuthal angle Φ (d) Graphics presented here and elsewhere were generated in part using the visualisation software Ovito.63 | ||
The microswimmers motility originates from one central “thruster” particle, which generates the squirmer-type force field experienced by the solvent particles in the spherical shell between the outer surface of the microswimmer (dashed black circle) and RH=4 (dashed black circle and dotted black circle respectively, see Fig. 1a). These solvent particles in turn apply an equal and opposite reaction force to their nearest colloid “filler” particle (18–20 DPD particles, depending on whether or not shape asymmetry is introduced to the microswimmer, see Fig. 1a), resulting in the net self-propulsion force of the microswimmer 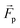 . The mass of specific filler particles can be adjusted, allowing us to introduce mass asymmetry, and thus model microswimmers equipped with heavy “caps” (e.g. Pt-coated catalytic microparticles). We define mass asymmetry as
. The mass of specific filler particles can be adjusted, allowing us to introduce mass asymmetry, and thus model microswimmers equipped with heavy “caps” (e.g. Pt-coated catalytic microparticles). We define mass asymmetry as 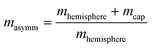 (where mhemisphere and mcap are the mass of a particle hemisphere and the heavy cap respectively), noting that the motion can thus be defined with the heavier cap at the back (CB) or at the front (CF) of the swimmer with respect to the swimming direction. Mass imbalance is thus introduced by increasing the mass of the particles constituting the cap (blue particles, see Fig. 1). In all cases, we use a squirmer active stress parameter β = B2/B1 = −2.5, i.e. a weak pusher, based on qualitative matching of simulated trajectories to the behaviour described in.20 We note that this squirmer parameter corresponds to that experimentally determined by Campbell et al.34 for a similar Pt catalytic system as that studied in ref. 20, which provides further evidence for the suitability of our selection. Solvent conditions are selected to ensure that all microswimmers with radius R studied remain in the low Reynolds (Re) number regime (
(where mhemisphere and mcap are the mass of a particle hemisphere and the heavy cap respectively), noting that the motion can thus be defined with the heavier cap at the back (CB) or at the front (CF) of the swimmer with respect to the swimming direction. Mass imbalance is thus introduced by increasing the mass of the particles constituting the cap (blue particles, see Fig. 1). In all cases, we use a squirmer active stress parameter β = B2/B1 = −2.5, i.e. a weak pusher, based on qualitative matching of simulated trajectories to the behaviour described in.20 We note that this squirmer parameter corresponds to that experimentally determined by Campbell et al.34 for a similar Pt catalytic system as that studied in ref. 20, which provides further evidence for the suitability of our selection. Solvent conditions are selected to ensure that all microswimmers with radius R studied remain in the low Reynolds (Re) number regime (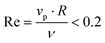 ,62 also see ESI, Fig. S1†), where vp is the particle speed, and specifically by controlling for the kinematic viscosity ν via the solvent parameters.49 To map different simulations to experiments, we modulate the ratio of swimming velocity Vswim to sedimentation velocity Vgravity. A minimum of 2000 time steps are used for equilibrating solvent conditions in all simulations, as were periodic boundary conditions. The number of solvent DPD particles depends on the simulation dimensions, ranging from 47
,62 also see ESI, Fig. S1†), where vp is the particle speed, and specifically by controlling for the kinematic viscosity ν via the solvent parameters.49 To map different simulations to experiments, we modulate the ratio of swimming velocity Vswim to sedimentation velocity Vgravity. A minimum of 2000 time steps are used for equilibrating solvent conditions in all simulations, as were periodic boundary conditions. The number of solvent DPD particles depends on the simulation dimensions, ranging from 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002 for a (20 × 20 × 20, xyz) box, to 57
002 for a (20 × 20 × 20, xyz) box, to 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 solvent DPD particles for a (16 × 16 × 40) box.
197 solvent DPD particles for a (16 × 16 × 40) box.
3. Results & discussion
3.1. Role of mass asymmetry and hydrodynamic interactions in microswimmer motion
To begin, we consider colloids characterised by hydrodynamic interactions with a surface and bottom-heaviness, and study their dynamics with or without activity. Specifically, we reproduce the ‘classic’ Pt-SiO2 Janus chemical microswimmers to determine whether our DPD raspberry particle model captures their dynamics. We investigate the chemical microswimmers studied by Niggel et al.,64 as the 3-D rotations of the Janus particles with fluorescent surface asperities can be tracked via correlation-based image analysis. To reproduce their experimental findings, we simulate the microswimmers with CB motion and masymm = 1.081. Fitting the short-time mean-square-displacement (MSD) of those chemical microswimmers (MSD = 4DTΔt + vp2Δt2, while acknowledging its shortcomings65), we obtain a Péclet number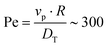 (where vp, DT are the fitted swimming speed and translational diffusion coefficient from the MSD, respectively, and R is the particle radius), which we set to ∼100 in simulations of our active microswimmers to ensure that they remain in the low Reynolds regime as described above. Likewise, we set the gravitational force such that Vgravity ∼ Vswim, for Vswim = 〈v0〉, where v0 is the microswimmer's instantaneous velocity over time. As we have access to the structural coordinates of our DPD raspberries, we are able to follow their rotational dynamics via singular value decomposition (SVD) and calculate the cumulative mean-squared-angular-displacement (MSAD) (see Fig. 2 (ref. 66)). By doing so, we are able to reproduce the findings presented in.64 Specifically, we find that for passive particles, the presence of a heavy cap and a substrate reduces the rotation “out-of-plane” (θx,y) compared to in plane (θz) rotations (see Fig. 1c and d) due to bottom-heaviness (see Fig. 2a (ref. 67)), while the introduction of activity saturates the out-of-plane rotation at much lower values (Fig. 2b). We attribute the confinement of possible rotations to the hydrodynamic attraction between the microswimmer and the substrate due to its generated flow fields,68 mirrored by later theoretical investigations into the role of the produced phoretic fields.10 Therefore, we see that the rotational dynamics of chemical microswimmers near confining boundaries are qualitatively well captured when only considering hydrodynamic interactions (and bottom-heaviness).
(where vp, DT are the fitted swimming speed and translational diffusion coefficient from the MSD, respectively, and R is the particle radius), which we set to ∼100 in simulations of our active microswimmers to ensure that they remain in the low Reynolds regime as described above. Likewise, we set the gravitational force such that Vgravity ∼ Vswim, for Vswim = 〈v0〉, where v0 is the microswimmer's instantaneous velocity over time. As we have access to the structural coordinates of our DPD raspberries, we are able to follow their rotational dynamics via singular value decomposition (SVD) and calculate the cumulative mean-squared-angular-displacement (MSAD) (see Fig. 2 (ref. 66)). By doing so, we are able to reproduce the findings presented in.64 Specifically, we find that for passive particles, the presence of a heavy cap and a substrate reduces the rotation “out-of-plane” (θx,y) compared to in plane (θz) rotations (see Fig. 1c and d) due to bottom-heaviness (see Fig. 2a (ref. 67)), while the introduction of activity saturates the out-of-plane rotation at much lower values (Fig. 2b). We attribute the confinement of possible rotations to the hydrodynamic attraction between the microswimmer and the substrate due to its generated flow fields,68 mirrored by later theoretical investigations into the role of the produced phoretic fields.10 Therefore, we see that the rotational dynamics of chemical microswimmers near confining boundaries are qualitatively well captured when only considering hydrodynamic interactions (and bottom-heaviness).
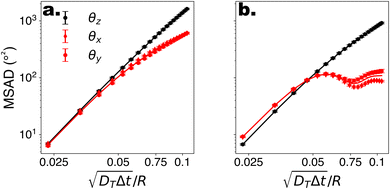 | ||
Fig. 2 Rotational dynamics of CB microswimmers as a function of scaled time, simulated to reproduce the properties of the chemical active colloids studied in ref. 64. (a) Mean-squared-angular-displacement (MSAD) of the passive colloid (no activity). (b) Introducing activity to the microswimmer dampens its rotational diffusivity, particularly about the x- and y-axes, which saturate due to the hydrodynamic coupling to the substrate. We note the scaling of the MSAD with time here is with 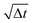 , and is therefore quadratic. Error bars depict the standard error of the mean from 2401 frames (sub-sampled from 50 , and is therefore quadratic. Error bars depict the standard error of the mean from 2401 frames (sub-sampled from 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation steps). 000 simulation steps). | ||
We then map our squirmer-inspired DPD model to the experimental findings presented by Carrasco-Fadanelli and Buttinoni.20 Specifically, we adjust Vswim![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vgravity to reproduce the different conditions studied in their work, while using the same value for mass asymmetry of their Janus polystyrene spheres coated with a Pt thin film (2.8 μm with a coating of 4 nm, masymm = 1.22) with CB motion. When Vswim < Vgravity, the gravitational torque from the heavier cap aligns the particle's internal orientation axis away from the substrate (see Fig. 3b), however the particle is unable to leave the substrate due to the force of gravity (see Fig. 3a and c). As Vswim is increased and becomes larger than Vgravity, the particle is able to leave the substrate when its internal orientation axis is directed upwards (see Fig. 3d–f, and ESI, Fig. S2†), assisted by its bottom-heaviness.59 Notably, we find that we can reproduce the structure of the microswimmer dynamics previously seen experimentally17–19 (see ESI, Fig. S3†), without requiring the previously hypothesised self-shadowing effects.60,61 The two scenarios qualitatively capture the behaviour described in ref. 20, where the gravitational torque due to the mass asymmetry introduced by the denser Pt cap favours an anti-parallel orientation of the microswimmer with gravity, competing with hydrodynamic interactions and thermal fluctuations. Interestingly, by further increasing Vswim, the simulated microswimmer is once again confined to 2-D motion in the xy plane (see Fig. 3g–i). However, here the confinement arises due to the internal orientation of the microswimmer, rather than its inability to overcome the applied gravitational force. For fast swimmers, the flow fields created by the microswimmer lead to a strong hydrodynamic attraction to the substrate, effectively “trapping” the particle in 2-D (compare insets in Fig. 3a and g). This is similar to the “sliding-state" behaviour proposed by Uspal and coworkers as a result of hydrodynamic flows from self-generated phoretic gradients,10 and mirrors the experimental observations of many chemical microswimmer systems, including that discussed in Fig. 2.
Vgravity to reproduce the different conditions studied in their work, while using the same value for mass asymmetry of their Janus polystyrene spheres coated with a Pt thin film (2.8 μm with a coating of 4 nm, masymm = 1.22) with CB motion. When Vswim < Vgravity, the gravitational torque from the heavier cap aligns the particle's internal orientation axis away from the substrate (see Fig. 3b), however the particle is unable to leave the substrate due to the force of gravity (see Fig. 3a and c). As Vswim is increased and becomes larger than Vgravity, the particle is able to leave the substrate when its internal orientation axis is directed upwards (see Fig. 3d–f, and ESI, Fig. S2†), assisted by its bottom-heaviness.59 Notably, we find that we can reproduce the structure of the microswimmer dynamics previously seen experimentally17–19 (see ESI, Fig. S3†), without requiring the previously hypothesised self-shadowing effects.60,61 The two scenarios qualitatively capture the behaviour described in ref. 20, where the gravitational torque due to the mass asymmetry introduced by the denser Pt cap favours an anti-parallel orientation of the microswimmer with gravity, competing with hydrodynamic interactions and thermal fluctuations. Interestingly, by further increasing Vswim, the simulated microswimmer is once again confined to 2-D motion in the xy plane (see Fig. 3g–i). However, here the confinement arises due to the internal orientation of the microswimmer, rather than its inability to overcome the applied gravitational force. For fast swimmers, the flow fields created by the microswimmer lead to a strong hydrodynamic attraction to the substrate, effectively “trapping” the particle in 2-D (compare insets in Fig. 3a and g). This is similar to the “sliding-state" behaviour proposed by Uspal and coworkers as a result of hydrodynamic flows from self-generated phoretic gradients,10 and mirrors the experimental observations of many chemical microswimmer systems, including that discussed in Fig. 2.
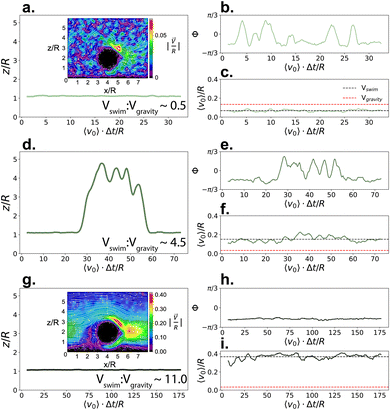 | ||
Fig. 3 Dynamics of CB microswimmers, simulated to reproduce the properties of the chemical active colloids studied in.20z/R refers to the height that a microswimmer reaches above the substrate with respect to its radius R (a, d, and g). Φ is the azimuthal angle of the microswimmer (b, e, and h) as defined in Fig. 1, and v0 is the time-series of the microswimmer's instantaneous velocity (c, f, and i, with Vswim = 〈v0〉/R). The insets in (a) and (g) show the solvent velocity flow fields around the (fixed) microswimmer at the different self-propulsion forces. Here, we progressively increase the swimming to sedimentation velocity (Vswim![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vgravity) from top to bottom to qualitatively map onto the different systems studied by Carrasco-Fadanelli and Buttinoni. The first two cases (a–c and d–f) are in good agreement with the findings presented in ref. 20, while the final case (g–i) recaptures the typical dynamics observed for chemical active colloids, where phoretic particles are essentially confined to 2-D (also see Fig. 2b). Vgravity) from top to bottom to qualitatively map onto the different systems studied by Carrasco-Fadanelli and Buttinoni. The first two cases (a–c and d–f) are in good agreement with the findings presented in ref. 20, while the final case (g–i) recaptures the typical dynamics observed for chemical active colloids, where phoretic particles are essentially confined to 2-D (also see Fig. 2b). | ||
To summarise, we find that hydrodynamic interactions and gravitational forces on a mass-asymmetric spherical microswimmer are sufficient to qualitatively capture the physics of chemical microswimmers above a substrate under different conditions. We also confirm the importance of gravity on both the translational and rotational dynamics of active colloids suspended just above a planar surface.
3.2. Influence of shape asymmetry on microswimmer 3-D dynamics
Motivated by the ability of the reported DPD squirmer-like microswimmers to qualitatively reproduce the behaviour of different chemical microswimmers, we then investigate strategies to promote the “lift-off” of particles from the substrate, and thus observe 3-D motion. Recently, photocatalytic microswimmers synthesised using functional nanoparticles via “Toposelective Nanoparticle Attachment” were shown to display quasi 3-D behaviour,17–19 characterised by 2-D motioninterdispersed with “rollercoaster”-like looping behaviour. This happens in spite of their high speeds with respect to their sedimentation speed, putting them in a regime closer to the third case highlighted in Fig. 3(g–i), as well as their CF motion which should in fact promote orientation into the wall due to top-heaviness. We note the use of surface-bound functional nanoparticles incorporates rough asperities to the microswimmers, which in turn introduce asymmetry in the drag acting on the surface of the microswimmers. In fact, explicitly considering non-axisymmetric flow fields in spherical squirmers was very recently shown to induce body rotations and thus complex patterns of motion.69 To investigate the potential effect of such shape-asymmetries on the motion of microswimmers, we simulate the motion of our DPD raspberries with introduced shape asymmetry in the absence of gravity or bounding substrates, this time with CF swimming (see Fig. 4). Specifically, we introduce weightless “shape” particles (Pshape) along the axis of the existing “filler” particles, shifted by different distances (normalised by the DPD particle radius – Rshift) to control the extent of its protrusion (see Fig. 1a). The filler particle axis along which the shape particle is introduced can be changed to modify the extent of asymmetry, i.e. with respect to the swimming direction (see ESI S5†). We focus on the case where Pshape is introduced so as to maximise the shape-asymmetry possible using this approach (see Fig. 1a, ESI Fig. S5,† “1 Edge” case).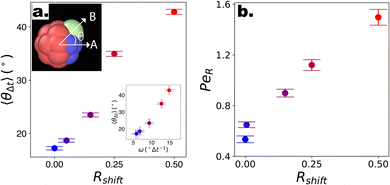 | ||
Fig. 4 Swimming dynamics of CF microswimmers with respect to their cap orientation, in the absence gravity and bounding substrates, as a function of introduced shape asymmetry Rshift (colour coded from blue to red with increasing Rshift). (a) Increasing divergence 〈θ〉 in the internal body axis and the observed swimming direction is measured with increasing Rshift. We note that the values of 〈θ〉 are a function of the time-step evaluated (here, 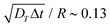 , where DT is the constant obtained for a passive sphere with Rshift = 0). Inset: linear growth in 〈θ〉 with ω values fitted from the microswimmers’ MSAD (see ESI, Fig. S6†). Graphical inset: angle θ between the swimming direction and internal body axis, as defined in the text. The particle depicted has Rshift = 0.5. (b) Rotational Pèclet number as a function of Rshift for Δt = 1. Error bars either indicate the standard error of the mean, or for the fits of ω and DR are obtained from the co-variance matrix, accounting for error propagation where relevant, from 1001 frames (sub-sampled from 50 , where DT is the constant obtained for a passive sphere with Rshift = 0). Inset: linear growth in 〈θ〉 with ω values fitted from the microswimmers’ MSAD (see ESI, Fig. S6†). Graphical inset: angle θ between the swimming direction and internal body axis, as defined in the text. The particle depicted has Rshift = 0.5. (b) Rotational Pèclet number as a function of Rshift for Δt = 1. Error bars either indicate the standard error of the mean, or for the fits of ω and DR are obtained from the co-variance matrix, accounting for error propagation where relevant, from 1001 frames (sub-sampled from 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation steps). 000 simulation steps). | ||
To quantify the effect that increasing Rshift has on the dynamics of our bulk microswimmers, we calculate the angle, θ, between the vectors describing the particle's internal orientation axis, A, (governing the direction of the self-propulsion force, see Fig. 1a), and the particles displacement vector, B, (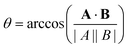 ), where A is defined by 3 particles along the microswimmers body axis at time t and B = [xt+Δt − xt, yt+Δt − yt, zt+Δt − zt]. We note that the value of 〈θ〉 is dependent on the Δt over which the displacement vector is evaluated. We find a positive correlation between Rshift and 〈θ〉 (coefficient of determination = 0.953, see Fig. 4a), which we attribute to the increasing torque experienced by the microswimmer due to the solvent forces applied to Rshape at the distance Rshift. We hypothesise that the non-zero value for 〈θ〉 at Rshift = 0 arises due to the presence of thermal fluctuations from the solvent and their effect on microswimmer motion (see ESI, Fig. S4† for further discussion). The source of the growing divergence between the internal orientation of the particles and their swimming velocity can also be observed in the MSAD of the microswimmers as the trends become increasingly ballistic with larger Rshift (see ESI, Fig. S6†). Notably, the fitted angular velocity ω (ballistic component of the MSAD, MSAD = 2DRΔt + ω2Δt2, where DR is the rotational diffusion coefficient) grows with shape asymmetry, and we determine a strong linear relationship between ω and 〈θ〉 (see Fig. 4a, bottom inset – coefficient of determination = 0.981). We furthermore note a linear growth of the “rotational” Péclet (
), where A is defined by 3 particles along the microswimmers body axis at time t and B = [xt+Δt − xt, yt+Δt − yt, zt+Δt − zt]. We note that the value of 〈θ〉 is dependent on the Δt over which the displacement vector is evaluated. We find a positive correlation between Rshift and 〈θ〉 (coefficient of determination = 0.953, see Fig. 4a), which we attribute to the increasing torque experienced by the microswimmer due to the solvent forces applied to Rshape at the distance Rshift. We hypothesise that the non-zero value for 〈θ〉 at Rshift = 0 arises due to the presence of thermal fluctuations from the solvent and their effect on microswimmer motion (see ESI, Fig. S4† for further discussion). The source of the growing divergence between the internal orientation of the particles and their swimming velocity can also be observed in the MSAD of the microswimmers as the trends become increasingly ballistic with larger Rshift (see ESI, Fig. S6†). Notably, the fitted angular velocity ω (ballistic component of the MSAD, MSAD = 2DRΔt + ω2Δt2, where DR is the rotational diffusion coefficient) grows with shape asymmetry, and we determine a strong linear relationship between ω and 〈θ〉 (see Fig. 4a, bottom inset – coefficient of determination = 0.981). We furthermore note a linear growth of the “rotational” Péclet (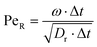 ) with Rshift (see Fig. 4b, coefficient of determination = 0.982), demonstrating the increasingly deterministic orientational motion of the microswimmer as shape asymmetry becomes more pronounced. Finally, we note that introducing Pshape along axes resulting in a reduced shape asymmetry with respect to A have a negligible effect on θ, indicating the importance of appropriate shape selection (see ESI; Fig. S5, S7, and S8†).
) with Rshift (see Fig. 4b, coefficient of determination = 0.982), demonstrating the increasingly deterministic orientational motion of the microswimmer as shape asymmetry becomes more pronounced. Finally, we note that introducing Pshape along axes resulting in a reduced shape asymmetry with respect to A have a negligible effect on θ, indicating the importance of appropriate shape selection (see ESI; Fig. S5, S7, and S8†).
After establishing the effect of shape asymmetry on microswimmer motion in the absence of external fields and confining boundaries, we then introduce gravity and a substrate to simulate the experimental conditions in ref. 17 and 18 using masymm = 1.25. We define Vswim![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vsediment ∼ 1.5 to prevent the microswimmers from escaping too far into the bulk. Under these conditions, microswimmers with no or low shape asymmetry are unable to leave the bottom substrate due to the joint forces of gravity and hydrodynamic attraction (see Fig. 5a). However, beyond a threshold value of Rshift > 0.25, the microswimmers display 3-D motion and begin to loop into the bulk, demonstrated by the emerging tail in P(z/R). This ability to leave the substrate is reflected in the angles which the internal orientation of the microswimmer makes with the substrate, Φ. Specifically, with increasing shape asymmetry, we observe an increase in positive values in the distribution P(Φ) (see Fig. 5b), which indicates that the particle points upwards and away into the bulk, thus overcoming gravity.
Vsediment ∼ 1.5 to prevent the microswimmers from escaping too far into the bulk. Under these conditions, microswimmers with no or low shape asymmetry are unable to leave the bottom substrate due to the joint forces of gravity and hydrodynamic attraction (see Fig. 5a). However, beyond a threshold value of Rshift > 0.25, the microswimmers display 3-D motion and begin to loop into the bulk, demonstrated by the emerging tail in P(z/R). This ability to leave the substrate is reflected in the angles which the internal orientation of the microswimmer makes with the substrate, Φ. Specifically, with increasing shape asymmetry, we observe an increase in positive values in the distribution P(Φ) (see Fig. 5b), which indicates that the particle points upwards and away into the bulk, thus overcoming gravity.
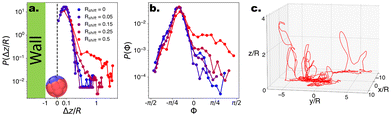 | ||
| Fig. 5 Probability distributions for CF microswimmers describing their out-of-plane motion P(Δz/R) and orientation P(Φ), as a function of their introduced shape asymmetry Rshift, indicated by the colour code in the legend. (a) Above a threshold (Rshift > 0.25), the microswimmers are able to leave the substrate and enter the bulk. For visualisation, Δz where Δz/R < 0.05 is set to 0, and the presence of the wall is indicated. The particle depicted at the wall has an orientation Φ ∼ −π/8. (b) The ability to leave the substrate is reflected in the emergence of a shoulder in P(Φ) for Φ > 0, as Vswim > Vgravity and therefore the microswimmer can overcome its sedimentation velocity and enter the bulk. (c) Example quasi-3D trajectory of a microswimmer with Rshift = 0.5. Note that the motion is predominantly in the xy plane, with looping out-of-plane (z) segments as described in ref. 17–19. | ||
We thus propose that the angular velocity ω, introduced by the shape asymmetry of the microswimmers, drives its internal swimming orientation away from the substrate, competing with the effects of gravity and hydrodynamic wall interactions (as well as thermal fluctuations). Above a certain threshold shape asymmetry – governed by the dynamics of the system – the microswimmer is able to escape the substrate and move out-of-plane.
In summary, we demonstrated that shape asymmetry is an important design parameter to control the dynamics of chemical microswimmers, in particular to promote 3-D motion. Specifically, the presence of these introduced asperities explains the unconventional swimming patterns observed in some experimental systems.17,18
4. Conclusions
By extending the DPD numerical framework described in55 to include the effects of mass and shape asymmetries, we have demonstrated that hydrodynamic interactions, gravity, and thermal fluctuations are sufficient to capture the dynamics of a range of experimental chemically active colloidal systems.17,18,20,64 Promisingly, the use of DPD particles to build the overall structure of the microswimmer enables us to access to a range of more complex shapes than those described here, whose formulation would otherwise be either intractable or highly challenging when using other numerical modelling frameworks, or explicitly including chemical fields. We believe that our numerical simulations could be used in the design of new chemical colloidal swimmers, e.g. via sequential-capillarity-particle-assembly (sCAPA)70 or two-photon polymerization direct laser writing (2PP-DLW),71 with the goal of realising chemical microswimmers capable of 3-D motion. Furthermore, this modular approach to generating complex structures enables the study of microswimmer physics considering arbitrary geometries, e.g. swimming above rough surfaces20 or along inclined walls,22 informing experiments into the interactions of active materials with confining boundaries commonplace in applied settings. To conclude, we foresee DPD based approaches to microswimmer modelling to provide opportunities in the development and application of chemically active colloids.Author contributions
Author contributions are defined based on the CRediT (contributor roles taxonomy). Conceptualization: M. R. B., C. M. B. G., L. I., C. V. Discussions: M. R. B., C. M. B. G., J. M. R., V. N., V. C., I. B., I. P., L. I., C. V. Formal analysis: M. R. B., C. M. B. G. Funding acquisition: M. R. B., L. I. Investigation: M. R. B. Methodology: M. R. B., C. M. B. G., J. M. R. Software: M. R. B., C. M. B. G., J. M. R. Supervision: L. I., C. V. Validation: M. R. B. Visualization: M. R. B., C. M. B. G., L. I. Writing – original draft: M. R. B., C. M. B. G., L. I. Writing – review and editing: M. R. B., C. M. B. G., J. M. R., V. N., I. B., I. P., L. I., C. V.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. R. B. acknowledges financial support from the ETH Zurich Doc.Mobility Fellowship scheme. I. P. acknowledges support from Ministerio de Ciencia MCIN/AEI/FEDER for financial support under grant agreement PID2021-126570NB-100 AEI/FEDER-EU, and from Generalitat de Catalunya under Program Icrea Academia and project 2021SGR-673. C. V. acknowledges financial support from MINECO under grant agreements EUR2021-122001, PID2019-105343GB-I00, IHRC22/00002, and PID2022-140407NB-C21.References
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- G. Gompper, R. G. Winkler, T. Speck, A. Solon, C. Nardini, F. Peruani, H. Löwen, R. Golestanian, U. B. Kaupp and L. Alvarez, et al. , J. Phys.: Condens. Matter, 2020, 32, 193001 CrossRef CAS PubMed.
- J. R. Howse, R. A. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 8–11 CrossRef PubMed.
- W. Wang, X. Lv, J. L. Moran, S. Duan and C. Zhou, Soft Matter, 2020, 16, 3846–3868 RSC.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 1–4 CrossRef PubMed.
- M. N. Popescu, S. Dietrich, M. Tasinkevych and J. Ralston, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 351–367 CrossRef CAS PubMed.
- K. K. Dey, F. Wong, A. Altemose and A. Sen, Curr. Opin. Colloid Interface Sci., 2016, 21, 4–13 CrossRef CAS.
- M. R. Bailey, N. Reichholf, A. Flechsig, F. Grillo and L. Isa, Part. Part. Syst. Charact., 2022, 39, 2100200 CrossRef CAS.
- W. E. Uspal, M. N. Popescu, S. Dietrich and M. Tasinkevych, Soft Matter, 2015, 11, 434–438 RSC.
- A. I. Campbell and S. J. Ebbens, Langmuir, 2013, 29, 14066–14073 CrossRef CAS PubMed.
- A. I. Campbell, R. Wittkowski, B. Ten Hagen, H. Löwen and S. J. Ebbens, J. Chem. Phys., 2017, 147, 084905 CrossRef PubMed.
- D. P. Singh, W. E. Uspal, M. N. Popescu, L. G. Wilson and P. Fischer, Adv. Funct. Mater., 2018, 28, 1706660 CrossRef.
- O. Yasa, P. Erkoc, Y. Alapan and M. Sitti, Adv. Mater., 2018, 30, 1804130 CrossRef PubMed.
- J. G. Lee, A. M. Brooks, W. A. Shelton, K. J. Bishop and B. Bharti, Nat. Commun., 2019, 10, 2575 CrossRef PubMed.
- A. M. Brooks, S. Sabrina and K. J. Bishop, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E1090–E1099 CAS.
- M. R. Bailey, T. A. Gmür, F. Grillo and L. Isa, Chem. Mater., 2023, 35, 3731–3741 CrossRef CAS PubMed.
- M. R. Bailey, F. Grillo, N. D. Spencer and L. Isa, Adv. Funct. Mater., 2022, 32, 2109175 CrossRef CAS.
- M. R. Bailey, F. Grillo and L. Isa, Soft Matter, 2022, 18, 7291–7300 RSC.
- V. Carrasco-Fadanelli and I. Buttinoni, Phys. Rev. Res., 2023, 5, L012018 CrossRef CAS.
- O. Chepizhko and T. Franosch, Phys. Rev. Lett., 2022, 129, 228003 CrossRef CAS PubMed.
- Q. Brosseau, F. B. Usabiaga, E. Lushi, Y. Wu, L. Ristroph, M. D. Ward, M. J. Shelley and J. Zhang, Soft Matter, 2021, 17, 6597–6602 RSC.
- X. Lyu, X. Liu, C. Zhou, S. Duan, P. Xu, J. Dai, X. Chen, Y. Peng, D. Cui, J. Tang, X. Ma and W. Wang, J. Am. Chem. Soc., 2021, 143, 12154–12164 CrossRef CAS PubMed.
- A. Domínguez and M. N. Popescu, Curr. Opin. Colloid Interface Sci., 2022, 61, 101610 CrossRef.
- M. N. Popescu, W. E. Uspal, Z. Eskandari, M. Tasinkevych and S. Dietrich, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 1–24 CrossRef CAS PubMed.
- J. Katuri, W. E. Uspal, M. N. Popescu and S. Sánchez, Sci. Adv., 2021, 7, eabd0719 CrossRef CAS PubMed.
- J. D. Torrenegra-Rico, A. Arango-Restrepo and J. M. Rubí, J. Chem. Phys., 2022, 157, 104103 CrossRef CAS PubMed.
- A. Zöttl and H. Stark, Annu. Rev. Condens. Matter Phys., 2023, 14, 109–127 CrossRef.
- M. J. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef.
- J. R. Blake, Math. Proc. Cambridge Philos. Soc., 1971, 70, 303–310 CrossRef.
- V. Magar, T. J. Pedley and T. Goto, Q. J. Mech. Appl. Math., 2003, 56, 65–91 CrossRef.
- M. Theers, E. Westphal, G. Gompper and R. G. Winkler, Soft Matter, 2016, 12, 7372–7385 RSC.
- M. Yang, A. Wysocki and M. Ripoll, Soft Matter, 2014, 10, 6208–6218 RSC.
- A. I. Campbell, S. J. Ebbens, P. Illien and R. Golestanian, Nat. Commun., 2019, 10, 3952 CrossRef PubMed.
- J. Katuri, W. E. Uspal, J. Simmchen, A. Miguel-López and S. Sánchez, Sci. Adv., 2018, 4, eaao1755 CrossRef PubMed.
- P. Sharan, Z. Xiao, V. Mancuso, W. E. Uspal and J. Simmchen, ACS Nano, 2022, 16, 4599–4608 CrossRef CAS PubMed.
- A. Malevanets, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- A. Malevanets and R. Kapral, J. Chem. Phys., 2000, 112, 7260–7269 CrossRef CAS.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef PubMed.
- S. Thakur and R. Kapral, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 026121 CrossRef PubMed.
- P. De Buyl and R. Kapral, Nanoscale, 2013, 5, 1337–1344 RSC.
- I. Llopis and I. Pagonabarraga, J. Non-Newtonian Fluid Mech., 2010, 165, 946–952 CrossRef CAS.
- I. Pagonabarraga and I. Llopis, Soft Matter, 2013, 9, 7174 RSC.
- F. Alarcon, E. Navarro-Argemí, C. Valeriani and I. Pagonabarraga, Phys. Rev. E, 2019, 99, 062602 CrossRef CAS PubMed.
- A. Scagliarini and I. Pagonabarraga, Soft Matter, 2022, 18, 2407–2413 RSC.
- A. Zöttl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 1–11 CrossRef PubMed.
- L. P. Fischer, T. Peter, C. Holm and J. de Graaf, J. Chem. Phys., 2015, 143, 084107 CrossRef PubMed.
- J. de Graaf, H. Menke, A. J. Mathijssen, M. Fabritius, C. Holm and T. N. Shendruk, J. Chem. Phys., 2016, 144, 134106 CrossRef PubMed.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- P. J. Hoogerbrugge and J. M. Koelman, EPL, 1992, 19, 155–160 CrossRef.
- J. M. Koelman and P. J. Hoogerbrugge, EPL, 1993, 21, 363–368 CrossRef CAS.
- P. Espanol and P. Warren, EPL, 1995, 30, 191–196 CrossRef CAS.
- T. Soddemann, B. Dünweg and K. Kremer, Phys. Rev. E, 2003, 68, 046702 CrossRef PubMed.
- F. Lugli, E. Brini and F. Zerbetto, J. Phys. Chem. C, 2012, 116, 592–598 CrossRef CAS.
- C. M. Barriuso Gutiérrez, J. Martín-Roca, V. Bianco, I. Pagonabarraga and C. Valeriani, Front. Phys., 2022, 10, 926609 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- B. ten Hagen, F. Kümmel, R. Wittkowski, D. Takagi, H. Löwen and C. Bechinger, Nat. Commun., 2014, 5, 4829 CrossRef CAS PubMed.
- J. Simmchen, J. Katuri, W. E. Uspal, M. N. Popescu, M. Tasinkevych and S. Sánchez, Nat. Commun., 2016, 7, 10598 CrossRef CAS PubMed.
- S. Das, Z. Jalilvand, M. N. Popescu, W. E. Uspal, S. Dietrich and I. Kretzschmar, Langmuir, 2020, 36, 7133–7147 CrossRef CAS PubMed.
- D. P. Singh, W. E. Uspal, M. N. Popescu, L. G. Wilson and P. Fischer, Adv. Funct. Mater., 2018, 28, 1706660 CrossRef.
- W. E. Uspal, J. Chem. Phys., 2019, 150, 114903 CrossRef CAS PubMed.
- J. T. Padding and A. A. Louis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 1–29 CrossRef PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- V. Niggel, M. R. Bailey, C. van Baalen, N. Zosso and L. Isa, Soft Matter, 2023, 19, 3069–3079 RSC.
- M. Bailey, A. Sprenger, F. Grillo, H. Löwen and L. Isa, Phys. Rev. E, 2022, 106, L052602 CrossRef CAS PubMed.
- B. Ilhan, J. J. Schoppink, F. Mugele and M. H. Duits, J. Colloid Interface Sci., 2020, 576, 322–329 CrossRef CAS PubMed.
- A. Rashidi, S. Razavi and C. L. Wirth, Phys. Rev. E, 2020, 101, 042606 CrossRef CAS PubMed.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- P. S. Burada, R. Maity and F. Jülicher, Phys. Rev. E, 2022, 105, 1–8 CrossRef PubMed.
- S. Ni, E. Marini, I. Buttinoni, H. Wolf and L. Isa, Soft Matter, 2017, 13, 4252–4259 RSC.
- R. P. Doherty, T. Varkevisser, M. Teunisse, J. Hoecht, S. Ketzetzi, S. Ouhajji and D. J. Kraft, Soft Matter, 2020, 16, 10463–10469 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Further details of numerical results and extracted parameters. See DOI: https://doi.org/10.1039/d3nr03695b |
| This journal is © The Royal Society of Chemistry 2024 |
