Open Access Article
Open Access ArticleBest practices of modeling complex materials in electrocatalysis, exemplified by oxygen evolution reaction on pentlandites†
Maksim
Sokolov
ab,
Katharina
Doblhoff-Dier
 *c and
Kai S.
Exner
*c and
Kai S.
Exner
 *abd
*abd
aFaculty of Chemistry, Theoretical Inorganic Chemistry, University Duisburg-Essen, Universitätsstraße 5, 45141 Essen, Germany. E-mail: kai.exner@uni-due.de; k.doblhoff-dier@lic.leidenuniv.nl
bCluster of Excellence RESOLV, 44801 Bochum, Germany
cLeiden Institute of Chemistry, Leiden University, P.O. Box 9502, Leiden 2300, RA, The Netherlands
dCenter for Nanointegration (CENIDE) Duisburg-Essen, 47057 Duisburg, Germany
First published on 19th August 2024
Abstract
Pentlandites are natural ores with structural properties comparable to that of [FeNi] hydrogenases. While this class of transition–metal sulfide materials – (Fe,Ni)9S8 – with a variable Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni ratio has been proven to be an active electrode material for the hydrogen evolution reaction, it is also discussed as electrocatalyst for the alkaline oxygen evolution reaction (OER), corresponding to the bottleneck of anion exchange membrane electrolyzers for green hydrogen production. Despite the experimental evidence for the use of (Fe,Ni)9S8 as an OER catalyst, a detailed investigation of the elementary reaction steps, including consideration of adsorbate coverages and limiting steps under anodic polarizing conditions, is still missing. We address this gap in the present manuscript by gaining atomistic insights into the OER on an Fe4.5Ni4.5S8(111) surface through density functional theory calculations combined with a descriptor-based analysis. We use this system to introduce best practices for modeling this rather complex material by pointing out hidden pitfalls that can arise when using the popular computational hydrogen electrode approach to describe electrocatalytic processes at the electrified solid/liquid interface for energy conversion and storage.
Ni ratio has been proven to be an active electrode material for the hydrogen evolution reaction, it is also discussed as electrocatalyst for the alkaline oxygen evolution reaction (OER), corresponding to the bottleneck of anion exchange membrane electrolyzers for green hydrogen production. Despite the experimental evidence for the use of (Fe,Ni)9S8 as an OER catalyst, a detailed investigation of the elementary reaction steps, including consideration of adsorbate coverages and limiting steps under anodic polarizing conditions, is still missing. We address this gap in the present manuscript by gaining atomistic insights into the OER on an Fe4.5Ni4.5S8(111) surface through density functional theory calculations combined with a descriptor-based analysis. We use this system to introduce best practices for modeling this rather complex material by pointing out hidden pitfalls that can arise when using the popular computational hydrogen electrode approach to describe electrocatalytic processes at the electrified solid/liquid interface for energy conversion and storage.
1. Introduction
An in-depth understanding of the oxygen evolution reaction (OER) is central to the development of advanced electrolyzers and metal–air batteries for energy conversion and storage, respectively.1,2 In an aqueous medium, the OER can either take place in acid, 2H2O → O2 + 4H+ + 4 e− or in base, 4OH− → O2 + 2H2O + 4e− (U0OER = 1.23 V vs. reversible hydrogen electrode (RHE)). While a change in the electrolyte pH affects the reactants, another important role of pH stems from the distinct electrode materials used as the electrocatalyst for the kinetically sluggish OER3–5 in acidic and alkaline environments. To date, only IrO2-based electrodes can cope with the harsh anodic reaction conditions in acid electrolytes, whereas the use of oxide-based catalysts consisting of less scarce elements such as Ni, Fe, or Co offers a significant cost reduction under alkaline conditions.6–10Besides transition–metal oxides, there are also reports on transition–metal sulfides as electrocatalysts for the alkaline OER.11,12 A promising material is pentlandite, i.e., iron–nickel sulfides with the chemical formula (Fe,Ni)9S8.13–16 While the nickel-to-iron ratios in the chemical composition of pentlandite can vary, its composition in nature is close to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, although dedicated synthetic procedures in the lab can adjust the nickel-to-iron ratios to any desired ratio.17
1 ratio, although dedicated synthetic procedures in the lab can adjust the nickel-to-iron ratios to any desired ratio.17
So far, there are only a few works available that have studied pentlandites by the application of electronic structure calculations. While Lu and Yu presented a thorough study of the pentlandite bulk structure resulting from the variety of possible configurations,18 Waterson et al. followed this train of thought and discussed pentlandite surface models.19 Theoretical modeling of the hydrogen evolution reaction (HER) and OER on a trimetallic Fe–Ni–Co pentlandite was performed by Lu et al. and Hegazy et al., respectively.16,20 However, for a seemingly simple bimetallic pentlandite surface, a detailed study of the elementary reaction steps, including a contemplation of adsorbate coverages and limiting steps under OER conditions, is missing so far. The reason for this is threefold: first, the variety in nickel-to-iron ratio that can be achieved in the lab leads to a large parameter space to investigate. Second, the surface structure of this three-component material will generally be unknown (in particular under operando conditions), and, third, the correct inclusion of adsorbates can be challenging.
In the present work, we focus on the last point and investigate the OER over a Fe4.5Ni4.5S8(111) surface as a model electrode by density functional theory (DFT) calculations. Thanks to the computational hydrogen electrode (CHE) approach introduced by Nørskov and coworkers about 20 years ago,21 the modeling of charge-transfer processes at electrified solid/liquid interfaces has received major attention in recent years. In fact, due to the current energy transition from fossil fuels to environmentally friendly processes, this topic is of increasing interest, and it is believed that electronic structure theory can contribute to the identification of material candidates22–25 for energy conversion and storage. However, despite the simplifications made in the CHE approach to describe electrocatalytic processes, in silico materials modeling remains a challenge. In this paper, we present good practices for materials modeling on the example of pentlandite as OER catalyst by discussing the importance of considering a suitable cell size, by investigating the influence of adsorbate coverage on the computational description of the reaction under reaction conditions, and by examining the best way to include the aqueous environment during the calculations.
2. Computational details
We performed electronic structure calculations in the DFT approximation with the software VASP,26–28 using the RPBE functional including Grimme's D3 correction.29,30 The choice of the exchange–correlation functional for calculations in an electrochemical environment is extremely important.31,32 In the present contribution, it is justified by recent works indicating that RPBE+D3 leads to relatively small errors for adsorption free energies when compared to other (dispersion corrected) general gradient approximated exchange–correlation functionals.33,34 While it is a common practice to include the Hubbard U correction to account for the self-interaction terms in the exchange–correlation functional, to predict the band gap correctly for materials that contain transition metals,35,36 and to improve the description of single-atom catalysts (SAC's),31,37 we do not apply it in our calculations because pentlandite shows conductive properties.16 In addition, the available benchmarks33,34 contained mainly data on the RPBE-D3 description without the U correction. For a complete overview of the computational details, we refer the reader to Table S1 of the ESI,† Section S1.In this paper, we consider the (111) surface termination of a pentlandite with the chemical formula Fe4.5Ni4.5S8 as a model. The iron-to-nickel ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
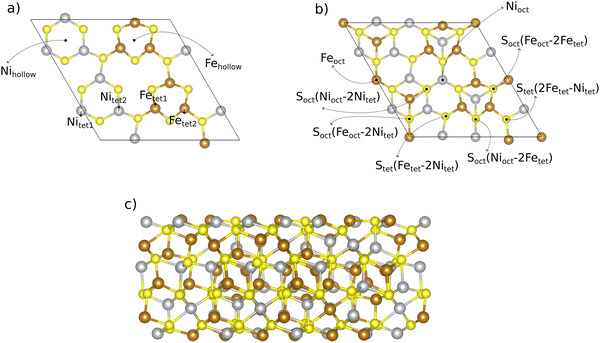
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is inspired by the natural form of pentlandites.15 We created the (111) slab model (cf.Fig. 1) from the energetically most favorable pentlandite (Pn) bulk structure found in ref. 19. Bulk structures are shown in Fig. S1 of the ESI† (Section S1). When cutting the bulk structure along the (111) direction, 7 different surfaces can be derived. We chose the cut indicated in Fig. 1 to obtain a stoichiometric slab with a similar termination on the other side of the slab,19 thus aiming to avoid artificial dipole effects for the investigated Fe4.5Ni4.5S8 composition.
1 is inspired by the natural form of pentlandites.15 We created the (111) slab model (cf.Fig. 1) from the energetically most favorable pentlandite (Pn) bulk structure found in ref. 19. Bulk structures are shown in Fig. S1 of the ESI† (Section S1). When cutting the bulk structure along the (111) direction, 7 different surfaces can be derived. We chose the cut indicated in Fig. 1 to obtain a stoichiometric slab with a similar termination on the other side of the slab,19 thus aiming to avoid artificial dipole effects for the investigated Fe4.5Ni4.5S8 composition.
Our slab model consists of 10 metal layers. While the bottom layer of the slab is kept frozen to simulate bulk effects and to facilitate geometry relaxation, the upper 9 layers including adsorbates are allowed to relax freely. To avoid cell size effects, we performed DFT calculations for a 2 × 1 superslab. In Section 3.2, we compare the results of the 2 × 1 superslab with those obtained by a simple 1 × 1 surface slab and show the significant influence of the super-cell size on the quantitative results.
The 2 × 1 superslab contains a total of 14 unique adsorption sites if one counts both metal (6 unique sites) and sulfur (8 unique sites) atoms on the (111) surface. All these 14 adsorption sites, which are potential active sites for the OER, are displayed in Fig. 1. Note that there are some sites which have the same coordination (e.g., tetrahedral), but a different chemical environment. To differentiate between those sites, we use numbers as indices (e.g., tet1 or tet2).
OER is a complex four proton–electron transfer reaction. While we are aware of the mechanistic diversity in that various pathways may be operative under reaction conditions,38,39 we choose a single mechanism as a representative example to discuss best practices in materials modeling of pentlandites as OER catalysts. This pathway is denoted as the mononuclear mechanism,40,41 and its description is provided in eqn (1)–(4). A * indicates an active surface site (cf.Fig. 1), and the ΔGj (j = 1, 2, 3, 4) values refer to the (potential-dependent) free energy changes of the elementary steps. In the free energy expressions, e denotes the elementary charge, and the applied electrode potential, U, is given on the RHE (reversible hydrogen electrode) scale.
| * + H2O → *OH + H+ + e− ΔG1 = ΔG01 − eU | (1) |
| *OH → *O + H+ + e− ΔG2 = ΔG02 − eU | (2) |
| *O + H2O → *OOH + H+ + e− ΔG3 = ΔG03 − eU | (3) |
| *OOH → * + O2(g) + H+ + e− ΔG4 = 4.92 − Σ3i=1ΔGi − 4eU | (4) |
Another important aspect in the modeling of an electrocatalytic reaction refers to the description of the electrolyte. While gas-phase DFT calculations treat the volume above the slab as a vacuum, it could also be described as a dielectric medium (in our case water) at low computational cost. Such schemes are collectively referred to as “implicit solvation” approaches, and it is suggested that their inclusion into the analysis brings the simulations closer to reality. For this purpose, we utilize the VASPsol code.49,50 However, it is debated51 if such an approach truly improves the precision of the model and the calculated free energy changes. Therefore, we also apply another scheme, namely micro-solvation, which involves the inclusion of a few explicit but static water molecules in the calculations. We performed calculations with one and two explicit water molecules in the vicinity of the active site as this quantity of water molecules had been shown to be sufficient to capture local solvation effects,52 and compare the results with those obtained from implicit solvation and in the gas phase.
While the electrocatalytic activity of complex proton–electron transfer processes such as the OER is governed by the transition-state free energies (kinetics) of the elementary steps, it is a common practice to analyze the ΔGj (j = 1, 2, 3, 4) values to render activity predictions.53,54 This is justified by considering that the Brønsted–Evans–Polanyi (BEP) relation55,56 connects the thermodynamic and kinetic pictures, thus allowing the usage of free energy changes for activity estimations. While only the calculation of the barriers of the elementary steps offers kinetic insight beyond the common assumption of the BEP relation,57 theoretical frameworks for the determination of transition-state free energies under constant potential are computationally demanding, and even state-of-the-art methods reveal error bars on the order of about 0.15 eV for solid/liquid interfaces.58,59 This is the reason why we rely on the thermodynamic evaluation, where two central frameworks are available in the electrocatalysis community: the most popular activity measure is the thermodynamic overpotential, ηTD, which is based on the analysis of a single free energy change at the OER equilibrium potential.21,60,61 Another activity descriptor refers to the free energy span model of Gmax(U),62,63 which enables potential-dependent analysis of activity trends by incorporating overpotential and kinetic effects in the evaluation of adsorption free energies across different material compositions. For a more detailed discussion, we refer the reader to Section S2 of the ESI,† where the two descriptors are compared on the example of the mononuclear OER mechanism. We note that the descriptor Gmax(U) was benchmarked based on a comparison with experimental transition states of single-crystalline model electrodes and its sensitivity is on the order of 0.20 eV.62 Therefore, we make use of Gmax(U) at an applied electrode potential of U = 1.53 V vs. RHE, which is equivalent to an OER overpotential of 0.30 V, to gain insight into the electrocatalytic activity; this applied electrode potential refers to typical experimental conditions to reach a current density on the order of about 10 mA cm−2.15,64
3. Results and discussion
3.1 Stability diagram
The first step in the modeling of an electrocatalytic reaction refers to a dedicated understanding of the surface composition under reaction conditions.65 Due to the presence of the aqueous electrolyte and the application of an electrode potential, it is evident that, under OER conditions, any surface may not be pristine, but rather different intermediate species can be adsorbed to the electrocatalyst surface. As we are going to discuss in a later section (cf. Section 3.2), the omission of initial adsorbate coverage of the surface can lead to erroneous conclusions relating to activity predictions or the catalytically active site. Adsorbate coverage thus adds to (and may even be more important than) the complexity induced by various surface terminations and the possibility of surface restructuring.OER is an anodic process with an equilibrium potential of 1.23 V vs. RHE. Under these harsh oxidizing reaction conditions, it can be assumed that the surface is oxygenated to some extent.16 This supposition is supported when calculating the adsorption free energies of single OER intermediates (*OH, *O, and *OOH) on different surface sites (cf.Fig. 1), summarized in Tables S2–S4 of the ESI† (cf. Section S3). When comparing the relative stability of these three intermediates at U = 1.53 V vs. RHE, it turns out that the *O adsorbate is energetically preferred over the *OH and *OOH adsorbates and the pristine surface.
To understand the level of oxygen saturation on the Pn surface, we construct a surface Pourbaix diagram.66–70 The concept of Pourbaix diagrams aims to resolve the surface structure of an electrode material, in dependence of the applied electrode potential, by minimizing the free energy of all possible configurations that can be observed during the surface reaction. Note that this type of approach belongs to the category of ‘constrained thermodynamics’71 in that the actual surface reaction (formation of O2 in eqn (4)) is suppressed, and only the formation of the *OH, *O, and *OOH intermediates (cf.eqn (1)–(3)) is allowed to proceed. It is also relevant to point out that Pourbaix diagrams rely on the tacit assumption that the thermodynamically stable surface structure, as obtained by the Pourbaix approach, does not change as degradation processes or defects are not considered. Regrettably, this presumption might not always be fulfilled,72 as the elementary steps in the OER can be accompanied by catalyst decomposition under the harsh anodic reaction conditions. Despite these caveats, Pourbaix diagrams are still the method of choice to gain insight into the surface composition of electrode materials under applied bias. We note that recently, approaches beyond Pourbaix diagrams have been reported in the literature,69 which, however, are beyond the scope of the present contribution.
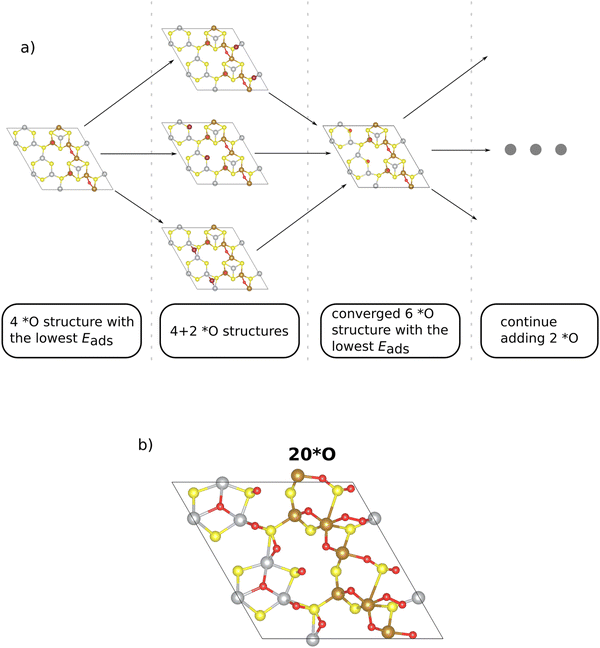
The construction of a Pourbaix diagram for the 2 × 1 Pn(111) surface is not trivial due to the following reasons: (a) there are fourteen different surface sites (cf.Fig. 1); (b) there are four different intermediate species (*, *OH, *O, and *OOH) to be considered in the analysis. Let us assume that each of the 12 metal sites of the superslab is occupied by one of the four intermediate species. This gives rise to a combinatorial problem as altogether, 412 ∼ 1.7 × 107 structures are conceivable, and this structural diversity cannot be solved by DFT. To this end, we simplify the analysis by referring to the *O adsorbate only, and we developed an iterative procedure to determine which surface sites are capped by surface oxygen under OER conditions (cf.Fig. 2a). Note that the choice of the *O adsorbate as the dominant species under OER conditions (U = 1.53 V vs. RHE) is corroborated by the calculated adsorption free energies on the Pn(111) surface (cf. Tables S2–S4 in Section S3, ESI†).
In the initial step, we commence from the 4*O surface, as further discussed in the ESI,† Section S4 (ESI†). Due to the symmetric nature of the 2 × 1 superslab, we choose n options to gradually add two oxygen atoms symmetrically to the corresponding equal sites (cf.Fig. 2a). Note that the n sites, to which two *O adsorbates are added, are primarily determined based on the adsorption energy of a single *O intermediate (cf. Table S3 in Section S3, ESI†). From the n structures considered, we select the structure with the lowest adsorption energy, thus arriving at the energetically preferred 6*O surface. This phase serves as the starting point for the addition of two additional *O adsorbates, and the other (n − 1) investigated phases provide insight into a more precise location of the subsequent *O. The process culminates in finally identifying stable surface structures with higher *O coverage (cf.Fig. 2a).
The main advantage of our iterative procedure is that it simplifies the search for stable configurations at higher *O coverages as the most stable sites are identified at every coverage. This point is best illustrated by comparing surface structures for the case of 12*O (100% coverage if only the metal atoms are counted; cf.Fig. 1). In Fig. S3 of the ESI† (Section S4), we compare the energetics and adsorption sites of the structures obtained by our iterative procedure or by a naïve guess, placing all oxygen atoms directly on top of the 12 metal atoms. While the surface structures are chemically different relating to the position of the *O adsorbates, we point out that the structure obtained by our iterative procedure is by 2.76 eV more stable than the naïve guess, thus corroborating the suggested procedure.
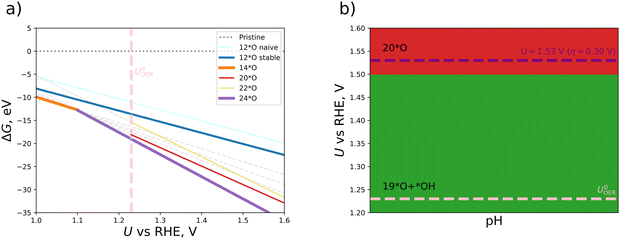
We continue this procedure to higher coverages of up to 24*O (that is, 200% coverage when referring to the metal atoms). For all the derived oxygen phases (4*O, 6*O, 8*O, …, 24*O), we construct a stability diagram to determine the energetically most favorable surface structure under OER conditions. For clarity, surfaces with less than 12*O are not shown in Fig. 3a. It turns out that at the OER equilibrium potential, the 24*O structure is reconciled with the thermodynamically preferred phase. However, as discussed in Section S5 of the ESI,† the 24*O structure is prone to reconstruction due to observable sulfur desorption from the surface in the form of sulfur dioxide (cf. Fig. S4, ESI†). Although this may be a physical effect and may actually occur under reaction conditions, we consider such reconstruction15 of the surface to be a separate effect, and modeling these processes is out of scope of the present contribution, where we focus on non-reconstructed Pn(111) surfaces. To avoid a possible surface reconstruction, we do not use the 24*O surface and adopt the second most stable surface phase at the OER equilibrium potential; that is, the 20*O phase as displayed in Fig. 2b.
Based on the 20*O phase, we qualitatively address the question of whether some of the oxygen atoms could still be hydrogenated under OER conditions. To this end, we investigate mixed *O/*OH coverages, namely, 19*O + 1*OH and 18*O + 2*OH. While adding a single *OH atop Fe enhances the stability in terms of a smaller free energy at U = 1.23 V vs. RHE, adding another *OH to the equivalent position in the 2 × 1 cell at maximum distance from the first one results in surface structures with a larger free energy compared to the 20*O phase. We add the thermodynamically stable 19*O + 1*OH and 18*O + 2*OH to our set of oxygenated non-reconstructed surfaces (4*O, 6*O, 8*O, …, 22*O) and construct a Pourbaix diagram, which is depicted in Fig. 3b. Due to the fact that the 20*O surface is thermodynamically preferred at U = 1.53 V vs. RHE, we choose this phase as the active configuration to identify the active site and the limiting step of the OER, which is discussed in the following section.
3.2 Determination of the active site and the limiting reaction step
In the following, we discuss the active site and the limiting reaction step of the OER over the Pn(111) model electrode by the construction of free-energy diagrams (FED). To this end, we compare three different scenarios: (a) a pristine Pn(111) surface without any adsorbates (cf.Fig. 1); (b) the 20*O surface as determined by the Pourbaix approach for the 2 × 1 superslab (cf.Fig. 3b); and (c) an oxygenated surface for a 1 × 1 slab (10*O surface), which refers to a halved 2 × 1 slab shown in Fig. 1.As evident from eqn (1)–(4), the OER requires the formation of three different intermediate species. Our DFT calculations for a single adsorbate on the pristine surface indicate that the formation of the *OOH intermediate refers to the main bottleneck in the catalytic cycle. In fact, in most of the structures investigated, the initial *OOH adsorbate converges to a chemically different final state where the two oxygen atoms are separated (cf. Table S4 in Section S3, ESI†), i.e., effectively oxygenating the surface. The most stable surface sites for the *OOH intermediate on the pristine (111) surface are encountered at the Fetet1 and Nitet2 sites (cf.Fig. 1). We therefore model the OER pathway of eqn (1)–(4) over these two sites and discuss the electrocatalytic activity based on the descriptor Gmax(1.53 V).
Fig. 4a and b illustrate that, within the structures sampled, Gmax(1.53 V) for the OER over the Fetet1 and Nitet2 sites of the pristine surface amounts to 1.75 eV and 1.14 eV, respectively, suggesting Nitet2 to be the catalytically more active site. For both, the Nitet2 and the Fetet1 site, we find the *OOH intermediate to be a limiting factor: for the Fetet1 site, the limiting free-energy span is governed by the transition of *O → *OOH → * + O2; for the Nitet2 site, it is governed by *O → *OOH. Finally, a free-energy span of 1.14 eV as found here for the Nitet2 site would suggest that pentlandites are inactive materials for the OER. Using the Butler–Volmer formalism73,74 and the framework of Gmax(U),62 one would obtain a current density j at U = 1.53 V vs. RHE of only j ≈ 2 × 10−15 mA cm−2 (cf. eqn (S13) at the end of Section S2 of the ESI†). Although our sampling may not be complete leading to intermediates that are energetically too high, we will show in the following that significantly larger OER currents can be found using the same sampling strategies, but taking an oxygenated surface into account. This strongly suggests that the energetics of the intermediates is sensitively influenced by the presence of surface adsorbates.
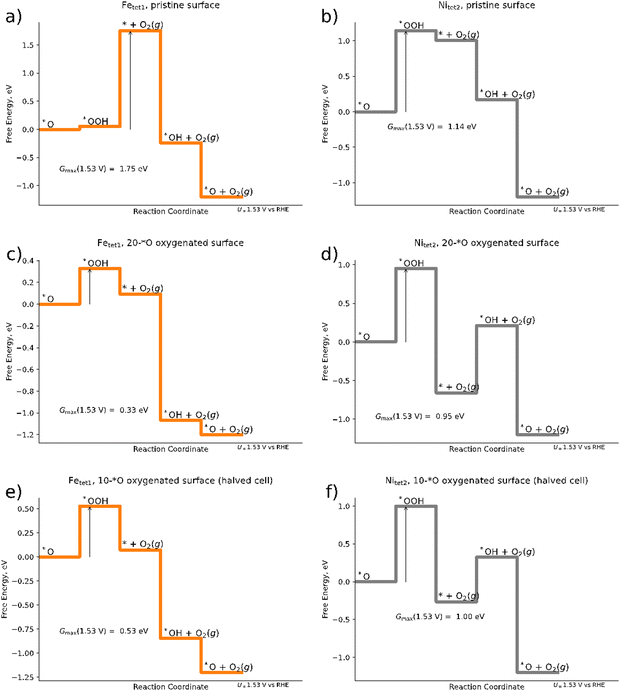 | ||
| Fig. 4 Free energy diagrams of the mononuclear OER mechanism for (a) pristine Pn surface with Fetet1 as the catalytically active site; (b) pristine surface with Nitet2 as the catalytically active site; (c) 20*O surface for a 2 × 1 superslab (cf.Fig. 2b) with Fetet1 as the catalytically active site; (d) 20*O surface for a 2 × 1 superslab with Nitet2 as the catalytically active site; (e) 10*O surface (1 × 1 slab) with Fetet1 as the catalytically active site; (f) 10*O surface (1 × 1 slab) with Nitet2 as the catalytically active site. Arrows denote the activity descriptor Gmax(U = 1.53 V). | ||
When modeling the OER over the 20*O surface based on the 2 × 1 superslab (cf.Fig. 4e and f) Gmax(1.53 V) is suddenly reduced to 0.33 eV and 0.95 eV for the Fetet1 and Nitet2 sites, respectively, suggesting the Fe sites to become catalytically much more active than in the pristine surface. The free energy span of 0.33 eV corresponds to a current density of about 0.2 mA cm−2 at U = 1.53 V vs. RHE, now suggesting pentlandites to be reasonably active OER materials – in agreement with experiments.15,16 Fe sites as the catalytically active center are also in line with a recent study on trimetallic pentlandites.16 In fact, the agreement we find here is even semi-quantitative: when estimating the catalytic activity of the Fetet1 site of the 20*O surface at an applied overpotential of 401 mV, the calculated Gmax(1.63 V) is equal to 0.23 eV, corresponding to a current density is j ≈ 6 mA cm−2. This is in close agreement with the 10 mA cm−2 found experimentally under the same applied potential for the pentlandite Fe5Ni4S8. Although the agreement between theory and experiment agreement should not be overinterpreted, as surface reconstructions and the stability of various surface terminations are not investigated or considered here and sampling is limited, the large change in reaction energetics observed when considering surface adsorbate highlights the importance of the inclusion of adsorbates in the simulations when aiming at a physically correct description of the OER reaction (mechanism) on pentlandite.
When computationally screening different surface terminations including various amounts of different adsorbates and their corresponding activity, it is interesting to ask the question of whether the same conclusions could have been obtained in a smaller supercell. To this end, we halve the cells that we obtained for the oxygenated 2 × 1 slab and reoptimize the geometries for the resulting 1 × 1 slab. Although the free energy diagram doesn’t differ qualitatively from that obtained for the 2 × 1 surface (compare Fig. 4c–f), there are clear quantitative differences: the Gmax(1.53 V) descriptor over the Fetet1 site increases from 0.33 eV for the 2 × 1 slab to 0.53 eV for the smaller 1 × 1 slab, which would reduce the predicted current density by three orders of magnitude to j ≈ 3 × 10−3 mA cm−2 at an applied overpotential of 401 mV. Considering that the 1 × 1 structure was obtained from the preoptimized 2 × 1 structure (and should thus be structurally as similar as possible), the difference in energy suggests that large cells are needed to allow for the relatively large structural changes observed in the subsurface when adsorbing various intermediates (see Table S5 in the ESI†) and to diminish other finite-size effects.75–77
Taken together, we have shown that a correct inclusion of pre-adsorbed oxygen species and relatively large supercells are needed to obtain qualitatively (inclusion of adsorbed oxygen) and quantitatively (both inclusion of adsorbed oxygen and super-cell size) correct predictions compared to less computationally demanding approaches.
3.3 Impact of solvation
Electrocatalytic processes such as the OER take place at electrified solid/liquid interfaces. This indicates that the aqueous environment may also have a non-negligible impact on the catalytic surface processes culminating in product formation. Despite this, there is no unifying framework yet of how to account for the aqueous environment in static DFT calculations. Three different approaches can be conceived: (a) gas-phase DFT calculations where the surface slab is surrounded by vacuum; (b) implicit solvation by using continuum solvation approaches such as VASPsol;49,50 (c) explicit solvation, also termed microsolvation,78,79 by adding additional water molecules above the adsorbed intermediate species.From a computational perspective, it is evident that the scenarios (a) and (b) require the least resources compared to the consideration of the liquid phase by explicit approaches. In this section we examine the impact of the three different methodologies on the OER over the catalytically active 20*O Pn(111) surface on the mononuclear mechanism (cf.eqn (1)–(4)) over the Fetet1 site as identified above for the oxygen-covered surface (cf. Section 3.2).
DFT calculations with implicit solvation are performed by using the VASPsol extension. For the explicit approach we place one or two water molecules close to the respective OER intermediate. The water molecules in each initial configuration are oriented such that hydrogen bonds are allowed to form or remain during the relaxation process. For the case of explicit water molecules, we also include the chemical step of water adsorption in the analysis of the FED. Fig. 5 depicts the FED at 1.53 V vs. RHE, the free energy changes at 1.53 V vs. RHE, and the activity descriptor Gmax(1.53 V) for the three different scenarios. All results are also compiled in Table S6 of the ESI† (cf. Section S6).
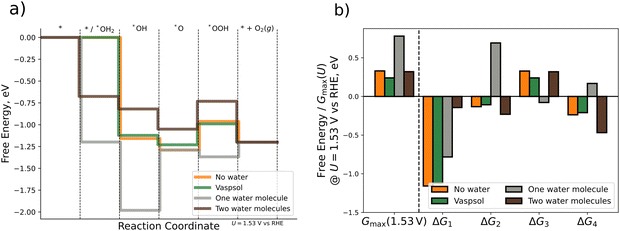 | ||
| Fig. 5 Comparison of different computational methodologies for the consideration of solvation effects. (a) Free energy diagram for gas-phase DFT calculations (orange), implicit solvation by VASPsol (green), and explicit solvation by one (grey) or two (brown) water molecules. (b) Bar plot displaying Gmax(1.53 V) and the ΔGj (j = 1, 2, 3, 4) values (cf.eqn (1)–(4)) at U = 1.53 V vs. RHE for the different scenarios. | ||
First, we analyze the impact of implicit solvation on the free energies. As shown in Fig. 5, the energetic changes caused by implicit solvation are relatively small. Quantitatively speaking, the descriptor Gmax(1.53 V) decreases by 0.09 eV when using implicit solvation instead of gas phase calculations. Much larger changes in the FED are, however, observed when using micro-solvation. When using one water molecule only, Gmax(1.53 V) increases by 0.46 eV if one explicit water molecule is added to the system. This difference is mainly traced to the dissimilar ΔG2 value (cf.Fig. 5b), which is uphill rather than downhill in free energy at 1.53 V vs. RHE. Consequently, this results in a change in the limiting free energy span from *O → *OOH to *OH → *O, thus indicating a switch of the RDS if the Tafel slope remains constant. The FED obtained when modeling solvation via one water molecule is thus qualitatively different from that obtained in gas phase and for implicit solvation. Interestingly, for the case of two explicit water molecules, the energetics are rather similar again to the gas-phase and the implicit solvation case: the free energy changes are the same among all three cases (uphill or downhill), and only the individual ΔGj values are quantitatively different. The activity descriptor Gmax(1.53 V) is kept virtually constant (0.32 eV) compared to the gas-phase value (0.33 eV) and the limiting free energy-span corresponds to the transition *O → *OOH as in gas phase and for implicit solvation.
Based on the comparison of the three different approaches, we conclude that solvation effects are of minor importance for the OER over Pn(111) as gas-phase DFT calculations, implicit solvation by means of VASPsol, and explicit solvation by two water molecules yield the same qualitative results and differ quantitatively by less than 0.1 eV. If included, the correct modeling of solvation by explicit approaches requires, however, at least two water molecules due to the significant difference between the data for one explicit water molecule and all other approaches. The source of this deviation can be linked to the orientation of the water molecule/-s around the *O intermediate (cf. Fig. S6, Section S6 of the ESI†). A single water molecule in its energetically most favorable configuration is oriented with both hydrogen atoms pointing toward the surface adsorbate, thus overstabilizing the *O intermediate due to the occurrence of up to two hydrogen bonds. In contrast, two water molecules form a chain by intermolecular hydrogen bonding (even when only adding a second water molecule to the geometry obtained for one water molecule). Consequently, the stabilization of the *O intermediate by hydrogen bonding is reduced for two explicit water molecules. As such, at least two water molecules are needed to avoid artificial overstabilization effects of intermediates, which are not in line with the interfacial water structure.80,81 Our findings are in agreement with previous studies, indicating that two water molecules are sufficient for the estimation of solvation effects of adsorbates.52
We close this section by comparing our results to the study of Heenen et al.,51 who reported, based on a comparison of ab initio molecular dynamics simulations and static DFT calculations, that the consideration of implicit solvation techniques does not necessarily result in an improved description of adsorption free energies. Therefore, we purport that, while it is beneficial to countercheck the impact of solvation on the adsorption free energies, gas-phase DFT calculations are likely sufficient for most electrocatalytic processes over solid-state electrodes to render reliable conclusions on the electrocatalytic activity, catalytically active surface sites, and limiting steps (cf. Section 3.2) if the respective conditions of a suitable cell size and consideration of the adsorbate coverage under reaction conditions (cf. Section 3.1) are taken into account.
4. Conclusions
In this manuscript, we present density functional theory calculations for the oxygen evolution reaction (OER) over a pentlandite (Pn) Fe4.5Ni4.5S8(111) model electrode. While future work should address the exact surface termination and surface stability under operando conditions as well as further sampling, it is interesting to see that the investigated model system does actually predict Pn to be active for the OER with Fe being the active site, in agreement with experiment – at lease if oxygen pre-coverage of the surface is taken into account.To come to this conclusion, we introduce an iterative procedure (cf.Fig. 2a) to construct stability and Pourbaix diagrams for the Pn electrode (cf.Fig. 3), indicating that the Pn surface considered here is capped by oxygen adsorbates (20*O surface, cf.Fig. 2b) under OER conditions.
Based on a comparison of three different calculation protocols including omitting adsorbate coverage or using a 1 × 1 slab (cf.Fig. 4), we demonstrate that the inclusion of oxygen pre-coverage on the surface leads to important energetic changes and – within our model – even to a change of active site. Use of a large enough supercell is important at least on the quantitative level as energetic changes of up to 0.2 eV were observed in the limiting reaction steps when reducing the cell size.
Finally, we discuss the impact of solvation on the elementary steps for the catalytically active tetrahedral Fe site of the Pn electrode. Three different approaches are used (cf.Fig. 5), ranging from implicit solvation to explicit solvation with one or two water molecules adjacent to the intermediate adsorbed to the active site. While it is shown that solvation effects are relatively small for the Pn electrode, we demonstrate that modeling the solvent through explicit approaches requires at least two water molecules per adsorbate to avoid artificial overstabilization effects of intermediates by a single water molecule.
Author contributions
Maksim Sokolov: software, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization. Katharina Doblhoff-Dier: methodology, writing – original draft, writing – review & editing, supervision. Kai S. Exner: methodology, conceptualization, resources, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
MS and KSE acknowledge funding from the RESOLV Cluster of Excellence, funded by the Deutsche Forschungsgemeinschaft under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV. MS and KSE are thankful for fruitful discussions with Prof. Dr Ulf-Peter Apfel (RU Bochum) on experimental investigations of pentlandite electrodes and with Dr Ebrahim Tayyebi (University of Duisburg-Essen) and Prof. Dr Ian T. McCrum (Clarkson University) for the provided insight into solvation modeling. KSE thanks the Ministry of Culture and Science of the Federal State of North Rhine-Westphalia (NRW Return Grant) and the CRC/TRR247: “Heterogeneous Oxidation Catalysis in the Liquid Phase” (Project No. 388390466-TRR 247) for financial support. This article is based upon the work from COST Action 18234, supported by COST (European Cooperation in Science and Technology).References
- J. Jayabharathi, B. Karthikeyan, B. Vishnu and S. Sriram, Research on Engineered Electrocatalysts for Efficient Water Splitting: A Comprehensive Review, Phys. Chem. Chem. Phys., 2023, 25(13), 89–9019, 10.1039/D2CP05522H.
- A. Vazhayil, L. Vazhayal, J. Thomas, S. Ashok C and N. Thomas, A Comprehensive Review on the Recent Developments in Transition Metal-Based Electrocatalysts for Oxygen Evolution Reaction, Appl. Surf. Sci. Adv., 2021, 6, 100184, DOI:10.1016/j.apsadv.2021.100184.
- D. Friebel, M. Bajdich, B. S. Yeo, M. W. Louie, D. J. Miller, H. Sanchez Casalongue, F. Mbuga, T.-C. Weng, D. Nordlund, D. Sokaras, R. Alonso-Mori, A. T. Bell and A. Nilsson, On the Chemical State of Co Oxide Electrocatalysts during Alkaline Water Splitting, Phys. Chem. Chem. Phys., 2013, 15(40), 17460, 10.1039/c3cp52981a.
- Q. Dang, H. Lin, Z. Fan, L. Ma, Q. Shao, Y. Ji, F. Zheng, S. Geng, S.-Z. Yang, N. Kong, W. Zhu, Y. Li, F. Liao, X. Huang and M. Shao, Iridium Metallene Oxide for Acidic Oxygen Evolution Catalysis, Nat. Commun., 2021, 12(1), 6007, DOI:10.1038/s41467-021-26336-2.
- Y. Xiong and P. He, A Review on Electrocatalysis for Alkaline Oxygen Evolution Reaction (OER) by Fe-Based Catalysts, J. Mater. Sci., 2023, 9(31), 26134–26142, DOI:10.1007/s10853-023-08176-1.
- M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling, I. Staffell, P. Balcombe, Y. Shao-Horn and H. Schäfer, Water Electrolysis: From Textbook Knowledge to the Latest Scientific Strategies and Industrial Developments, Chem. Soc. Rev., 2022, 51(11), 4583–4762, 10.1039/D0CS01079K.
- H. Over, Fundamental Studies of Planar Single-Crystalline Oxide Model Electrodes (RuO2, IrO2) for Acidic Water Splitting, ACS Catal., 2021, 11(14), 8848–8871, DOI:10.1021/acscatal.1c01973.
- L. Vasić, N. Tričković, Z. Bošković, A. Jovanović, N. Skorodumova, S. Mentus and I. Pasti, Electrocatalysis of Hydrogen and Oxygen Electrode Reactions in Alkaline Media by Rh-Modified Polycrystalline Ni Electrode, ChemRxiv, 2023, preprint DOI:10.26434/chemrxiv-2023-0p036.
- P. Liao, J. A. Keith and E. A. Carter, Water Oxidation on Pure and Doped Hematite (0001) Surfaces: Prediction of Co and Ni as Effective Dopants for Electrocatalysis, J. Am. Chem. Soc., 2012, 134(32), 13296–13309, DOI:10.1021/ja301567f.
- B. Nedić Vasiljević, A. Z. Jovanović, S. V. Mentus, N. V. Skorodumova and I. A. Pašti, Galvanic Displacement of Co with Rh Boosts Hydrogen and Oxygen Evolution Reactions in Alkaline Media, J. Solid State Electrochem., 2023, 27(7), 1877–1887, DOI:10.1007/s10008-023-05374-4.
- M. Wang, L. Zhang, Y. He and H. Zhu, Recent Advances in Transition–Metal–Sulfide-Based Bifunctional Electrocatalysts for Overall Water Splitting, J. Mater. Chem. A, 2021, 9(9), 5320–5363, 10.1039/D0TA12152E.
- N. Karmodak, L. Bursi and O. Andreussi, Oxygen Evolution and Reduction on Two-Dimensional Transition Metal Dichalcogenides, J. Phys. Chem. Lett., 2022, 13(1), 58–65, DOI:10.1021/acs.jpclett.1c03431.
- B. Konkena, K. Junge Puring, I. Sinev, S. Piontek, O. Khavryuchenko, J. P. Dürholt, R. Schmid, H. Tüysüz, M. Muhler, W. Schuhmann and U.-P. Apfel, Pentlandite Rocks as Sustainable and Stable Efficient Electrocatalysts for Hydrogen Generation, Nat. Commun., 2016, 7(1), 12269, DOI:10.1038/ncomms12269.
- S. Piontek, C. Andronescu, A. Zaichenko, B. Konkena, K. Junge Puring, B. Marler, H. Antoni, I. Sinev, M. Muhler, D. Mollenhauer, B. Roldan Cuenya, W. Schuhmann and U.-P. Apfel, Influence of the Fe:Ni Ratio and Reaction Temperature on the Efficiency of (FexNi1−x)9S8 Electrocatalysts Applied in the Hydrogen Evolution Reaction, ACS Catal., 2018, 8(2), 987–996, DOI:10.1021/acscatal.7b02617.
- H. M. A. Amin, M. Attia, D. Tetzlaff and U. Apfel, Tailoring the Electrocatalytic Activity of Pentlandite FexNi9−xS8 Nanoparticles via Variation of the Fe:Ni Ratio for Enhanced Water Oxidation, ChemElectroChem, 2021, 8(20), 3863–3874, DOI:10.1002/celc.202100713.
- M. B. Z. Hegazy, K. Harrath, D. Tetzlaff, M. Smialkowski, D. Siegmund, J. Li, R. Cao and U.-P. Apfel, Boosting the Overall Electrochemical Water Splitting Performance of Pentlandites through Non-Metallic Heteroatom Incorporation, iScience, 2022, 25(10), 105148, DOI:10.1016/j.isci.2022.105148.
- D. Tetzlaff, K. Pellumbi, D. M. Baier, L. Hoof, H. Shastry Barkur, M. Smialkowski, H. M. A. Amin, S. Grätz, D. Siegmund, L. Borchardt and U.-P. Apfel, Sustainable and Rapid Preparation of Nanosized Fe/Ni-Pentlandite Particles by Mechanochemistry, Chem. Sci., 2020, 11(47), 12835–12842, 10.1039/D0SC04525J.
- L. Lu and S. Yu, Metal Distribution in Iron-Nickel Sulfide Mineral Pentlandite: First-Principles Study, Chem. Phys. Lett., 2019, 736, 136786, DOI:10.1016/j.cplett.2019.136786.
- C. N. Waterson, J. O. Sindt, J. Cheng, P. A. Tasker and C. A. Morrison, First-Principles Study on Ligand Binding and Positional Disorder in Pentlandite, J. Phys. Chem. C, 2015, 119(45), 25457–25468, DOI:10.1021/acs.jpcc.5b08649.
- L. Lu, S. Yu and H. Tian, Theoretical Insight into Surface Structures of Pentlandite toward Hydrogen Evolution, J. Colloid Interface Sci., 2022, 607, 645–654, DOI:10.1016/j.jcis.2021.09.020.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892, DOI:10.1021/jp047349j.
- J. D. Benck, T. R. Hellstern, J. Kibsgaard, P. Chakthranont and T. F. Jaramillo, Catalyzing the Hydrogen Evolution Reaction (HER) with Molybdenum Sulfide Nanomaterials, ACS Catal., 2014, 4(11), 3957–3971, DOI:10.1021/cs500923c.
- C. D. Griego, A. M. Maldonado, L. Zhao, B. Zulueta, B. M. Gentry, E. Lipsman, T. H. Choi and J. A. Keith, Computationally Guided Searches for Efficient Catalysts through Chemical/Materials Space: Progress and Outlook, J. Phys. Chem. C, 2021, 125(12), 6495–6507, DOI:10.1021/acs.jpcc.0c11345.
- C. Guo, X. Tian, X. Fu, G. Qin, J. Long, H. Li, H. Jing, Y. Zhou and J. Xiao, Computational Design of Spinel Oxides through Coverage-Dependent Screening on the Reaction Phase Diagram, ACS Catal., 2022, 12(11), 6781–6793, DOI:10.1021/acscatal.2c00237.
- C. Guo, J. Chen and J. Xiao, High-Throughput Computational Design of Novel Catalytic Materials, in Heterogeneous Catalysts, ed. W. Y. Teoh, A. Urakawa, Y. H. Ng and P. Sit, Wiley, 2021, pp. 497–524 DOI:10.1002/9783527813599.ch28.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561, DOI:10.1103/PhysRevB.47.558.
- G. Kresse and J. Furthmüller, Efficiency of Ab Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465, DOI:10.1002/jcc.21759.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, Modeling Hydrogen and Oxygen Evolution Reactions on Single Atom Catalysts with Density Functional Theory: Role of the Functional, Adv. Theory Simul., 2023, 6(10), 2200513, DOI:10.1002/adts.202200513.
- D. Misra, G. Di Liberto and G. Pacchioni, CO2 Electroreduction on Single Atom Catalysts: The Role of the DFT Functional, Phys. Chem. Chem. Phys., 2024, 26(14), 10746–10756, 10.1039/D4CP00175C.
- F. Göltl, E. A. Murray, S. A. Tacey, S. Rangarajan and M. Mavrikakis, Comparing the Performance of Density Functionals in Describing the Adsorption of Atoms and Small Molecules on Ni(111), Surf. Sci., 2020, 700, 121675, DOI:10.1016/j.susc.2020.121675.
- D. Mahlberg, S. Sakong, K. Forster-Tonigold and A. Groß, Improved DFT Adsorption Energies with Semiempirical Dispersion Corrections, J. Chem. Theory Comput., 2019, 15(5), 3250–3259, DOI:10.1021/acs.jctc.9b00035.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band Theory and Mott Insulators: Hubbard U Instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943–954, DOI:10.1103/PhysRevB.44.943.
- B. Himmetoglu, A. Floris, S. De Gironcoli and M. Cococcioni, Hubbard-Corrected DFT Energy Functionals: The LDA+U Description of Correlated Systems, Int. J. Quantum Chem., 2014, 114(1), 14–49, DOI:10.1002/qua.24521.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Revisiting the Universal Principle for the Rational Design of Single-Atom Electrocatalysts, Nat. Catal., 2024, 7(2), 207–218, DOI:10.1038/s41929-023-01106-z.
- K. S. Exner, On the Mechanistic Complexity of Oxygen Evolution: Potential-Dependent Switching of the Mechanism at the Volcano Apex, Mater. Horiz., 2023, 10(6), 2086–2095, 10.1039/D3MH00047H.
- K. S. Exner, Importance of the Walden Inversion for the Activity Volcano Plot of Oxygen Evolution, Adv. Sci., 2023, 10(36), 2305505, DOI:10.1002/advs.202305505.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Electrolysis of Water on (Oxidized) Metal Surfaces, Chem. Phys., 2005, 319(1–3), 178–184, DOI:10.1016/j.chemphys.2005.05.038.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, Electrolysis of Water on Oxide Surfaces, J. Electroanal. Chem., 2007, 607(1–2), 83–89, DOI:10.1016/j.jelechem.2006.11.008.
- Q. Liang, G. Brocks and A. Bieberle-Hütter, Oxygen Evolution Reaction (OER) Mechanism under Alkaline and Acidic Conditions, JPhys Energy, 2021, 3(2), 026001, DOI:10.1088/2515-7655/abdc85.
- T. J. Shaldehi, L. Meng, S. Rowshanzamir, M. J. Parnian, K. Exner, F. Viñes and F. Illas, Computationally Screening Non-Precious Single Atom Catalysts for Oxygen Reduction in Alkaline Media, Catal. Today, 2024, 431, 114560, DOI:10.1016/j.cattod.2024.114560.
- N. G. Hörmann, N. Marzari and K. Reuter, Electrosorption at Metal Surfaces from First Principles, npj Comput. Mater., 2020, 6(1), 136, DOI:10.1038/s41524-020-00394-4.
- D. Kim, J. Shi and Y. Liu, Substantial Impact of Charge on Electrochemical Reactions of Two-Dimensional Materials, J. Am. Chem. Soc., 2018, 140(29), 9127–9131, DOI:10.1021/jacs.8b03002.
- S. Yu, Z. Levell, Z. Jiang, X. Zhao and Y. Liu, What Is the Rate-Limiting Step of Oxygen Reduction Reaction on Fe–N–C Catalysts?, J. Am. Chem. Soc., 2023, 145(46), 25352–25356, DOI:10.1021/jacs.3c09193.
- N. G. Hörmann and K. Reuter, Thermodynamic Cyclic Voltammograms Based on Ab Initio Calculations: Ag(111) in Halide-Containing Solutions, J. Chem. Theory Comput., 2021, 17(3), 1782–1794, DOI:10.1021/acs.jctc.0c01166.
- G. Kastlunger, L. Wang, N. Govindarajan, H. H. Heenen, S. Ringe, T. Jaramillo, C. Hahn and K. Chan, Using pH Dependence to Understand Mechanisms in Electrochemical CO Reduction, ACS Catal., 2022, 12(8), 4344–4357, DOI:10.1021/acscatal.1c05520.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit Solvation Model for Density-Functional Study of Nanocrystal Surfaces and Reaction Pathways, J. Chem. Phys., 2014, 140(8), 084106, DOI:10.1063/1.4865107.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit Self-Consistent Electrolyte Model in Plane-Wave Density-Functional Theory, J. Chem. Phys., 2019, 151(23), 234101, DOI:10.1063/1.5132354.
- H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, Solvation at Metal/Water Interfaces: An Ab Initio Molecular Dynamics Benchmark of Common Computational Approaches, J. Chem. Phys., 2020, 152(14), 144703, DOI:10.1063/1.5144912.
- S. Siahrostami and A. Vojvodic, Influence of Adsorbed Water on the Oxygen Evolution Reaction on Oxides, J. Phys. Chem. C, 2015, 119(2), 1032–1037, DOI:10.1021/jp508932x.
- M. T. M. Koper, Theory of Multiple Proton–Electron Transfer Reactions and Its Implications for Electrocatalysis, Chem. Sci., 2013, 4(7), 2710, 10.1039/c3sc50205h.
- M. T. M. Koper, Analysis of Electrocatalytic Reaction Schemes: Distinction between Rate-Determining and Potential-Determining Steps, J. Solid State Electrochem., 2013, 17(2), 339–344, DOI:10.1007/s10008-012-1918-x.
- R. A. Van Santen, M. Neurock and S. G. Shetty, Reactivity Theory of Transition-Metal Surfaces: A Brønsted−Evans−Polanyi Linear Activation Energy−Free-Energy Analysis, Chem. Rev., 2010, 110(4), 2005–2048, DOI:10.1021/cr9001808.
- H. Ooka, J. Huang and K. S. Exner, The Sabatier Principle in Electrocatalysis: Basics, Limitations, and Extensions, Front. Energy Res., 2021, 9, 654460, DOI:10.3389/fenrg.2021.654460.
- C. F. Dickens, C. Kirk and J. K. Nørskov, Insights into the Electrochemical Oxygen Evolution Reaction with Ab Initio Calculations and Microkinetic Modeling: Beyond the Limiting Potential Volcano, J. Phys. Chem. C, 2019, 123(31), 18960–18977, DOI:10.1021/acs.jpcc.9b03830.
- N. Govindarajan, G. Kastlunger, H. H. Heenen and K. Chan, Improving the Intrinsic Activity of Electrocatalysts for Sustainable Energy Conversion: Where Are We and Where Can We Go?, Chem. Sci., 2022, 13(1), 14–26, 10.1039/D1SC04775B.
- T. Tchakoua, N. Gerrits, E. W. F. Smeets and G.-J. Kroes, SBH17: Benchmark Database of Barrier Heights for Dissociative Chemisorption on Transition Metal Surfaces, J. Chem. Theory Comput., 2023, 19, 245–270 CrossRef CAS PubMed.
- A. Valdes, Z. W. Qu, G. J. Kroes, J. Rossmeisl and J. K. Nørskov, Oxidation and Photo-Oxidation of Water on TiO2 Surface, J. Phys. Chem. C, 2008, 112(110), 9872–9879 CrossRef CAS.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, How Copper Catalyzes the Electroreduction of Carbon Dioxide into Hydrocarbon Fuels, Energy Environ. Sci., 2010, 3(9), 1311, 10.1039/c0ee00071j.
- K. S. Exner, A Universal Descriptor for the Screening of Electrode Materials for Multiple-Electron Processes: Beyond the Thermodynamic Overpotential, ACS Catal., 2020, 10(21), 12607–12617, DOI:10.1021/acscatal.0c03865.
- S. Razzaq and K. S. Exner, Materials Screening by the Descriptor Gmax(η): The Free-Energy Span Model in Electrocatalysis, ACS Catal., 2023, 13(3), 1740–1758, DOI:10.1021/acscatal.2c03997.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, Benchmarking Heterogeneous Electrocatalysts for the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2013, 135(45), 16977–16987, DOI:10.1021/ja407115p.
- A. Groß, Reversible vs. Standard Hydrogen Electrode Scale in Interfacial Electrochemistry from a Theoretician's Atomistic Point of View, J. Phys. Chem. C, 2022, 126(28), 11439–11446, DOI:10.1021/acs.jpcc.2c02734.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Surface Pourbaix Diagrams and Oxygen Reduction Activity of Pt, Ag and Ni(111) Surfaces Studied by DFT, Phys. Chem. Chem. Phys., 2008, 10(25), 3722, 10.1039/b803956a.
- M. J. Eslamibidgoli, J. Huang, P. M. Kowalski, M. H. Eikerling and A. Groß, Deprotonation and Cation Adsorption on the NiOOH/Water Interface: A Grand-Canonical First-Principles Investigation, Electrochim. Acta, 2021, 398, 139253, DOI:10.1016/j.electacta.2021.139253.
- K. S. Exner, J. Anton, T. Jacob and H. Over, Chlorine Evolution Reaction on RuO2(110): Ab Initio Atomistic Thermodynamics Study – Pourbaix Diagrams, Electrochim. Acta, 2014, 120, 460–466, DOI:10.1016/j.electacta.2013.11.027.
- A. Zagalskaya, P. Chaudhary and V. Alexandrov, Corrosion of Electrochemical Energy Materials: Stability Analyses Beyond Pourbaix Diagrams, J. Phys. Chem. C, 2023, 127(30), 14587–14598, DOI:10.1021/acs.jpcc.3c01727.
- M. López, K. S. Exner, F. Viñes and F. Illas, Computational Pourbaix Diagrams for MXenes: A Key Ingredient toward Proper Theoretical Electrocatalytic Studies, Adv. Theory Simul., 2022, 2200217, DOI:10.1002/adts.202200217.
- K. Reuter and M. Scheffler, Composition, Structure, and Stability of RuO2(110) as a Function of Oxygen Pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65(3), 035406, DOI:10.1103/PhysRevB.65.035406.
- T. E. Madey, W. Chen, H. Wang, P. Kaghazchi and T. Jacob, Nanoscale Surface Chemistry over Faceted Substrates: Structure, Reactivity and Nanotemplates, Chem. Soc. Rev., 2008, 37(10), 2310, 10.1039/b719551f.
- K. S. Exner, I. Sohrabnejad-Eskan and H. Over, A Universal Approach to Determine the Free Energy Diagram of an Electrocatalytic Reaction, ACS Catal., 2018, 8(3), 1864–1879, DOI:10.1021/ACSCATAL.7B03142/SUPPL_FILE/CS7B03142_SI_001.PDF.
- J. O. Bockris and A. K. N. Reddy, Modern Electrochemistry, Springer US, Boston, MA, 1973, vol. 2 DOI:10.1007/978-1-4613-4560-2.
- C. W. M. Castleton, A. Höglund and S. Mirbt, Density Functional Theory Calculations of Defect Energies Using Supercells, Modell. Simul. Mater. Sci. Eng., 2009, 17(8), 084003, DOI:10.1088/0965-0393/17/8/084003.
- D. F. Tracey, B. Delley, D. R. McKenzie and O. Warschkow, Molecular Adsorption on Silicon (001): A Systematic Evaluation of Size Effects in Slab and Cluster Models, AIP Adv., 2013, 3(4), 042117, DOI:10.1063/1.4802837.
- C. Zhang, G. Chen, Y. Si and M. Liu, Surface Modeling of Photocatalytic Materials for Water Splitting, Phys. Chem. Chem. Phys., 2022, 24(3), 1237–1261, 10.1039/D1CP04352H.
- F. Calle-Vallejo, R. F. De Morais, F. Illas, D. Loffreda and P. Sautet, Affordable Estimation of Solvation Contributions to the Adsorption Energies of Oxygenates on Metal Nanoparticles, J. Phys. Chem. C, 2019, 123(9), 5578–5582, DOI:10.1021/acs.jpcc.9b01211.
- A. Rendón-Calle, S. Builes and F. Calle-Vallejo, Substantial Improvement of Electrocatalytic Predictions by Systematic Assessment of Solvent Effects on Adsorption Energies, Appl. Catal., B, 2020, 276, 119147, DOI:10.1016/j.apcatb.2020.119147.
- A. Groß and S. Sakong, Ab Initio Simulations of Water/Metal Interfaces, Chem. Rev., 2022, 122(12), 10746–10776, DOI:10.1021/acs.chemrev.1c00679.
- S. Sakong, J. Huang, M. Eikerling and A. Groß, The Structure of the Electric Double Layer: Atomistic versus Continuum Approaches, Curr. Opin. Electrochem., 2022, 33, 100953, DOI:10.1016/j.coelec.2022.100953.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01792g |
| This journal is © the Owner Societies 2024 |