Delayed photodissociation of the tin cluster Sn22−
Alexander
Jankowski
 *a,
Paul
Fischer
*a,
Paul
Fischer
 a,
Klavs
Hansen
a,
Klavs
Hansen
 b and
Lutz
Schweikhard
a
b and
Lutz
Schweikhard
a
aInstitute for Physics, University of Greifswald, Felix-Hausdorff-Straße 6, 17498 Greifswald, Germany. E-mail: alexander.jankowski@uni-greifswald.de
bCenter for Joint Quantum Studies and Department of Physics, School of Science, Tianjin University, 92 Weijin Road, Tianjin 300072, China
First published on 15th December 2023
Abstract
Millisecond-delayed photodissociation of gas-phase Sn22− clusters stored in a Penning trap is investigated as a function of excitation energy. Sn15− is the only significant charged fragment, indicative of the break-off of neutral heptamers. Fits of the time-resolved fragmentation require a distribution of decay constants, caused by the finite width of the internal energy distribution of the cluster ensemble prior to photoexcitation. A lower limit for the dissociation energy for the loss of Sn7 is determined to be 2.1(1) eV, a factor of two above literature quantum chemical calculations.
1 Introduction
The reactivity of isolated molecules and clusters is of prime importance for the quantitative understanding of a number of questions ranging from stabilities in molecular beams to abundances in the interstellar medium. The characteristics of thermal decays is one of these questions. Most metal clusters decay by emission of monomers or dimers.1–3 However, elements close to the bulk metal-nonmetal boundary behave differently. Prominent examples are clusters of group-14 elements—carbon, silicon, germanium, tin, and lead. The interatomic bonds of small clusters formed from these elements are more directional and less metallic than those of, e.g., alkali or coinage metals. This is observed, for example, in ion-mobility measurements, where deviations from spherical structures can be matched to less metallic bonding.4 The non-metallic nature of the bonds is also reflected in the more complex fragmentation patterns of such clusters. In particular, the break-off of polyatomic fragments has been observed for singly-charged carbon5–8 as well as silicon9–13 and germanium clusters,11,12 highlighting their covalent nature. This matches the elements' bulk classification as nonmetal (C) and metalloids (Si, Ge).The structures of clusters formed from tin, which is characterized as a metal in the bulk, are of great interest, both theoretical and experimental. Neutral tin clusters Snn have been probed by combined electric beam deflection and photodissociation spectroscopy to reveal their geometric structures and optical absorption properties,14 as well as by photo-induced ionization to determine ionization thresholds.15 For the anionic species Snn−, photoelectron spectroscopy (PES) has been performed to find the electron affinities16–19 as well as the HOMO–LUMO gaps of those clusters.18,19 Collision-induced dissociation and trapped-ion electron diffraction has been applied to both anionic Snn− and cationic Snn+ clusters, alongside density-functional theory (DFT) calculations as probes of the dissociation pathways and their energy thresholds.20–22 Furthermore, ion-mobility measurements have been performed to investigate the structure of Snn+ clusters, as well as their melting point,23,24 and surface-induced dissociation was performed to investigate their dissociation pathways.25 DFT calculations have been performed for neutral and singly-charged cations and anions20–22,26–31 to determine geometric and electronic properties. Similar to Pbn2−, doubly-charged Snn2− clusters have been found experimentally to decay by fission into two singly-charged smaller clusters at size ranges up to n ≃ 50,32,33 further highlighting the exceptional characteristics of these two elements. Tin also has potential applications as feedstock for the highly-charged atomic tin ions that can provide the XUV light needed for the increasingly smaller sizes aimed for in nanodevice lithography.34
Here, the decay of the photoexcited singly-charged cluster Sn22− is investigated in the gas phase. The cluster is found to decay by break-off of a neutral tin heptamer:
| Sn22− → Sn15− + Sn7. | (1) |
Following the procedure of previous experiments35,36 the decay is monitored as a function of time after photoexcitation with various photon energies. The observed shifts in the time-depended decay, and thus the decay-constant distribution, are used to derive the energy distribution of the cluster ensemble and the dissociation energy of Sn22−. Such activation energies are notoriously difficult to determine experimentally. The result we will find here is a lower limit which is a factor of two higher than the value calculated by quantum chemical methods. It therefore provides a possibility to calibrate the theoretical methods for the fairly large electron number system (Sn22− has 1101 electrons).
An important and directly observable phenomenon in the experiments is the width of the distribution of rate constants. This width in turn reflects the width of the thermal energy distribution of the clusters prior to the pulsed laser excitation. The energy distribution will be shown to be slightly above the thermal distribution defined by the trap temperature. The increase is due to the hyperthermal motion of the charged particles in the trap. The finding is important given the widespread use of traps as collection and thermalization devices for which much still remains to be understood. The present results will contribute with fitted effective temperatures to the future model building of the topic.
2 Experimental procedure
The experiments were performed at the ClusterTrap setup,37,38 where delayed reactions after photoexcitation of clusters have previously been studied for gold,39,51 silver,40 vanadium,41,42 and lead.36 The gas-phase reactions were performed in a 12-Tesla Penning trap, where a pulsed laser beam was axially guided through the trap for photoexcitation. The details of the specific experimental procedure used here are described in the following.Anionic tin clusters were produced in a pulsed laser-ablation source43 (pulse rate of 10 Hz) with cluster condensation in helium, producing singly-charged anionic tin clusters. These were captured in a linear Paul trap with argon buffer gas at a pressure of around 10−3 mbar. After accumulation of typically ten cluster pulses, the ion ensemble was transferred into the Penning trap. Here, the cluster ions were exposed to argon gas pulsed into the trap volume through a piezoelectric valve, to a peak pressure of 10−6 mbar, as measured outside of the magnet. The collisions with the gas atoms dampened the axial oscillations along the magnetic field lines and their perpendicular cyclotron motion.
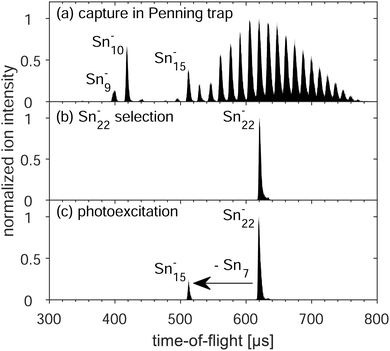
To record the distribution of ion species stored in the trap at a given time, all ions were ejected towards a multichannel-plate ion detector and a time-of-flight (ToF) spectrum was recorded. Such a spectrum is shown in Fig. 1(a). The distribution of cluster sizes observed between n ≈ 14 and n ≈ 32 is determined by the parameters chosen for the source, the Paul trap acceptance, the timing for the transfer section, and the Penning-trap capture process. In addition, some smaller clusters resulted from collision-induced dissociation during capture and cooling of the cluster ions. Note that, already in this spectrum, in addition to the smaller clusters Sn9− and Sn10−, Sn15− was present with a prominent intensity.
For photoexcitation studies, a mass-selective process needs to be employed to ensure that only a single species of interest is present in the trap. To that end, all ions were excited with respect to their magnetron motion, resulting in an increased magnetron radius.44 Quadrupolar excitation at the frequency of the cyclotron motion of the cluster species to be retained was applied for mass-to-charge selective conversion of magnetron into cyclotron motion.45 In combination with the buffer-gas collisions, this led to the axialization of the Sn22− clusters46,47 (Fig. 1(b)). This mass-selection procedure took about two seconds.
After the Sn22− precursor selection, the argon gas was pumped from the trap for half a second before the clusters were irradiated by a pulsed nanosecond laser and ejected for time-of-flight analysis (Fig. 1(c)). The delay time between photoexcitation and ion ejection was varied between 25 microseconds and a second with a logarithmic spacing between the 24 measuring points. The finite time it takes to accelerate the ions out of the trap limits the accessible times to longer than 25 microseconds. On the other hand, at delay times above a second, additional cooling effects, e.g. radiative or buffer-gas cooling, have to be considered. For the photoexcitation, a nanosecond pulse from an OPO laser system (EKSPLA NT342B) was used with pulse energies between 5 and 10 millijoules at wavelengths λ = 410, 430, 450, 475, 500, 525, 550 and 595 nm, i.e. photon energies Eph ranging from 3.0 eV to 2.1 eV. This range leads to delayed fragmentation processes observable within the time frame mentioned above. The laser-beam diameter was d = 1.7 cm at the center of the Penning trap, fully irradiating the stored cluster ensemble. A uniform photon-density distribution is assumed for the laser beam profile as an approximation to the higher order Laguerre–Gaussian mode at which the laser operates.
The number of Sn22− precursors per experimental cycle was between 100 and 200. For a given wavelength and delay, the cycle was repeated 20 to 30 times to increase statistics. Additionally, a reference ToF spectrum without application of the laser pulse (similar to the spectrum in Fig. 1(b)) was recorded interleaved for subtraction of a small amount of background counts, not visible in the linear vertical scaling of Fig. 1.
3 Experimental results
In the following, spectra such as the one of Fig. 1(c) are analysed with respect to the fragmentation yield of Sn15− as a function of the excitation pulse energy in Section 3.1 and as a function of time and photon energy in Section 3.2.3.1 Yield as a function of excitation pulse energy
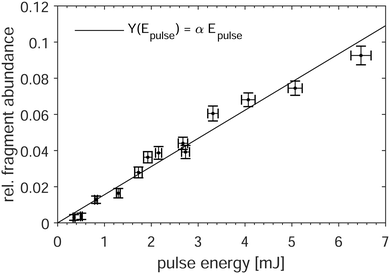
For best reliability of the time- and wavelength-resolved measurements in the present study, restriction to regimes of predominantly single-photon absorption is crucial. To ensure this, measurements were first performed at different excitation-laser pulse energies Epulse, from 0.35 to 6.5 mJ, for a fixed photon energy of Eph = 2.33 eV and fixed delay time of a second. The resulting data (Fig. 2) are well described by a linear function through the origin, which indicates that fragmentation occurs after absorption of a single photon in this pulse-energy regime. In particular, there is no indication of the positive curvature one expects from higher-order processes. Fitting the yield Y(Epulse) = αEpulse to the data results in a slope of α = 15.6(6) J−1. Thus, the photoabsorption cross section σph at this wavelength of 532 nm is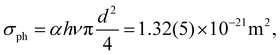 | (2) |
3.2 Yield as a function of delay time after photo-excitation
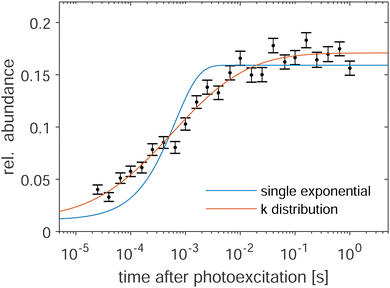
Fig. 3 shows the fragment yields Y of Sn15−, i.e. the observed product of the Sn22− decay, normalized to all detected ions (i.e. the sum of Sn22− and Sn15− ions) as a function of the delay time between photoexcitation and extraction into the time-of-flight mass spectrometer for the photon wavelength of λ = 500 nm (2.48 eV).The yields represent the integral of Sn15− fragments produced from the time of photoexcitation up to ion ejection. Note that the ToF section is linear and clusters that fragment in flight are detected as unfragmented.
The Sn15− yield rises with increasing delay time, reaching a plateau at the longest times. The blue line in Fig. 3 results from fitting the yield with a single-exponential function of the form
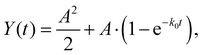 | (3) |
In past investigations, this model function was used to describe the delayed photo-decay of various cluster species at the present setup.35,36 However, in the present case the fragmentation yield is not well represented by eqn (3), as it is obvious from the fit in Fig. 3 (blue line), where the fitted curve systematically underestimates the yield for short delay times while overestimating it for intermediate delay times. For a better description of the fragment yield, a superposition of exponential decays is required. Denoting the decay-constant distribution as ρ(k), the fragment yield becomes
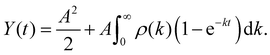 | (4) |
The distribution is parameterized with a log-normal form
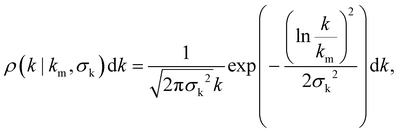 | (5) |
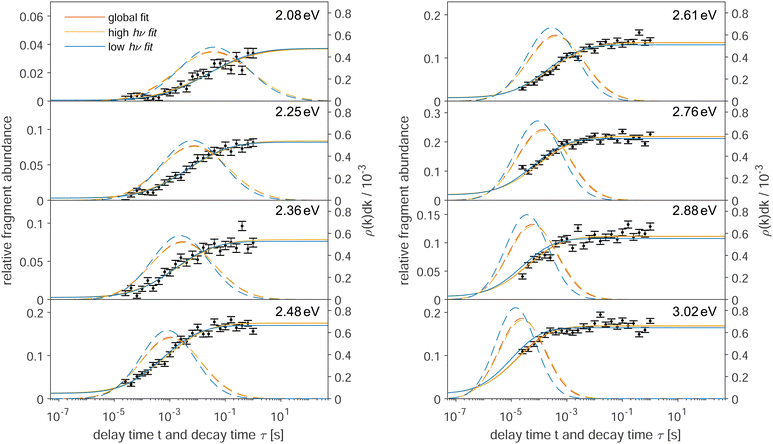
Data as in Fig. 3 recorded for other photon energies are shown in Fig. 4. As the precursor preparation is the same for all measurements, the k-distributions, while being different, are connected via their identical initial energy distributions prior to the photoabsorption. Therefore, this energy distribution is fitted to the data of all photon energies resulting in a “global” fit and the red lines in Fig. 4. This energy distribution is defined by a single parameter T, the temperature of the initial cluster ensemble, which, together with the clusters’ heat capacity, defines the mean internal energy and width of the distribution.
The parameters km and σk of the distribution function (5) are expressed as
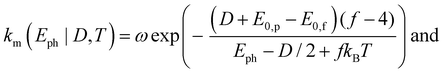 | (6) |
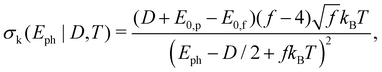 | (7) |
Note that—for the chosen photon energies and delay times—there is no observable yield decrease of the Sn15− cluster signal which would indicate a sequential decay. This suggests that the energy remaining in the clusters after the first fragmentation is not high enough to lead to another decay within the time frame probed in the present study. The observability of such decays has been demonstrated in another study.36
4 Discussion
The parameters f = 60, E0,p − E0,f = 39 meV, and ω = 2.1 × 1016 s−1, approximated as energy independent, are determined as described in the appendix. Thus, only D and T are fitted to the data, together with the individual amplitude values A for the different photon energies. This results in a temperature T = 460(20) K prior to the photoexcitation as well as a dissociation energy D = 2.1(1) eV of Sn22−. As described in the appendix, the frequency factor ω includes an empirically determined factor of 100 on the bulk Debye frequency. To provide an uncertainty estimation for this parameter, the fits are performed without this correction. The resulting dissociation energy is lowered by ΔDω = − 0.3 eV, while the temperature stays within the uncertainty of the initial fit, i.e. ΔTω < 20 K. The disregard of the effect of the rotational degrees of freedom for the products in the decay has an unknown effect. It is clear, however, that the effect on D would be positive and that the value quoted is therefore a lower limit.For the lower photon energies, the fragment yields do not reach the plateau at long delay times, while for the higher photon energies the yields start at times well into the rise of the curve. Thus, in order to check the robustness of the fit, it is also performed using only the data of the four lowest and highest photon energies, i.e. 2.08 eV to 2.48 eV (yellow lines) and 2.61 eV to 3.02 eV (blue lines), respectively. On the one hand, the resulting fit values for the lower energies are lower than those from the global fit, namely differing by ΔTlow = −70 K and ΔDlow = −0.2 eV. The fit values from the higher energies, on the other hand, stay within the uncertainties of the global fit (ΔThigh < 20 K and ΔDhigh < 0.1 eV). The small deviations indicate a very robust fitting procedure.
While the low- and high-energy fits are performed using only half of the available data, respectively, curves for both of these fits are drawn for all photon energies in Fig. 4 for easier comparison. For these additional curves, the k-distributions are calculated by using the fit results for temperature T and dissociation energy D of the high-energy and low-energy fit, respectively, while only the amplitudes are fitted to the data.
As an additional parameter for goodness-of-fit evaluation, the χr2 values are compared. The global fit produces a reduced-chi-squared value of χr2 = 2.2. The high-energy fit is nearly identical with a small increase of Δχr,high2 < 0.01, while the low-energy fit deviates slightly with an increase of Δχr,low2 = 0.4. This is also visible in Fig. 4, where the curves from the low-energy fits deviate somewhat from those of the highest energies. Nevertheless, the fits are in good agreement, suggesting a reliable overall result.
The width of the k-distributions σk decreases with increasing photon energy, as seen in Fig. 4. This suggests that for increasingly higher photon energies with respect to the dissociation energy, the fragment yields can eventually be approximated by a single exponential function, if the experimental observation window of the delay time allows it. Indeed, this was the case in the early days of the ClusterTrap measurements more than two decades ago.3,40–42,51 In contrast, as demonstrated by Fig. 2, the present case is more complex and calls for a more detailed approach such as the one presented here.
Note that, in general, the experiment-specific observation-time window limits the photon energies that can be probed. For broad k-distributions this limit can be a severe problem, as data points from an extended delay-time range are needed to fully describe the time-dependent fragment yield. The obvious solution to this problem would be to adjust, specifically to lower, the initial temperature of the cluster ensemble. This is not possible at the present setup. However, it should also be noted that the dissociation energy can be determined without extended modeling as well, namely in cases where sequential decays can be characterized by a photon-energy dependent parameter. This can be, e.g., competing decay pathways,52 but also delayed decays.53 For the latter, the particular parameter characterizing the decay curve is not essential, as long as the determination is performed consistently. In the present case, the intensity of the excitation laser pulse was, however, not high enough to observe the sequential decay of Sn22−via Sn15− to smaller clusters, which prevented the application of this method.
Density-Functional-Theory (DFT) calculations by Wiesel et al.22 found a dissociation energy for Sn22− of DDFT = 1.0 eV, i.e. considerably lower than the present result. In the same work, collision-induced-dissociation measurements have shown several different decay channels with Sn15− being the most prominent. In the present work, the comparatively low photon energies of the photodissociation yielded the observation of only Sn15− fragments, which confirms it as the lowest-energy decay channel for this cluster size.
In other investigations, the electron affinity EA(n) of Sn7 and Sn15 have been measured by Negishi et al.18 and Cui et al.19 by photo-electron-spectroscopy. Both report considerably higher electron affinities for Sn15 than Sn7 at EANegishi(7) = 1.87(7) eV and EANegishi(15) = 2.66(4) eV, and EACui(7) = 2.10(7) eV and EACui(15) = 2.97(5) eV, respectively. This aligns with the finding in the present work, as the charged Sn7− fragment is not observed, indicating a very strong statistical preference of the excess electron to stay attached to the Sn15− fragment.
5 Summary and conclusion
The delayed decay of the tin cluster Sn22− after photoexcitation has been measured. The abundance of the product fragment Sn15− is monitored with respect to the delay time and photon energy. In contrast to previous experiments with the same apparatus, the data analysis requires that distributions of decay constants are considered. One reason for the importance of the spread in rate constants in the present work can be traced to the small dissociation energy, which increases the impact of the thermal energy contribution and its width compared to more stable species. A simultaneous fit of the delayed fragment yields for multiple photon energies has been applied. The resulting estimations for the internal energy of the cluster ensemble prior to the photoexcitation pulse is somewhat higher than room temperature, but still reasonably possible given that the charged clusters are exposed to buffer-gas collisions and radial excitation fields during their axialization in the Penning trap prior to the photoexcitation. The dissociation threshold resulting from the fits is the first report of this value for a small tin cluster derived from experimental data. The experimental value is a factor of two higher than the one from quantum chemical calculations.Conflicts of interest
There are no conflicts to declare.Appendix
The decay-constant distribution
Calculating the distributions of decay constants ρ(k)dk requires the underlying energy distribution of the cluster ensemble and an expression for the energy dependence of the cluster decay constant. In the present study the tin cluster Sn22− is described as a collection of f harmonic oscillators, where| f = 3n − 6 = 60, | (8) |
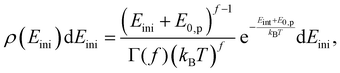 | (9) |
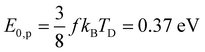 | (10) |
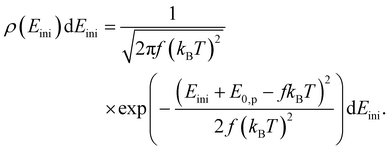 | (11) |
We do not distinguish between a canonical ensemble (fkBT) and a micro-canonical ensemble ((f − 1)kBT) in the two denominators. To convert the energy distribution to a decay constant distribution, an Arrhenius-like expression is applied.56,57 The detailed balance expression involves the ratio of the product and the precursor level densities. It can be approximated by an exponential. The value of the argument is calculated in detail in.56 The leading order approximation, with the modifications required for the loss of a polyatomic fragment with its own vibrational degrees of freedom, is
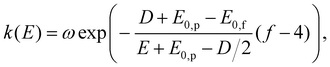 | (12) |
| ω = ωD × 100 × n2/3, | (13) |
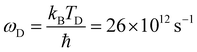 | (14) |
| E = Eph + fkBT − E0,p. | (15) |
To convert the energy distribution into a k-distribution, the Gaussian approximation for the initial thermal source distribution is used. With the previously given expressions and definitions of the constants and a saddle point expansion the decay-constant distribution becomes
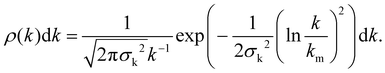 | (16) |
Here,
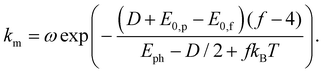 | (17) |
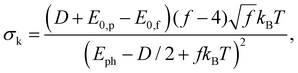 | (18) |
References
- C. Bréchignac, P. Cahuzac, F. Carlier, M. de Frutos and J. Leygnier, Alkali-metal clusters as prototypes of metal clusters, J. Chem. Soc., Faraday Trans., 1990, 86(13), 2525–2531 RSC.
- S. Nonose, H. Tanaka, T. Mizuno, J. Hirokawa and T. Kondow, Role of electron pairing in collisional dissociation of Na9+ by a rare-gas atom, J. Chem. Phys., 1996, 104, 5869–5874 CrossRef CAS.
- M. Vogel, A. Herlert and L. Schweikhard, Photodissociation of Small Group-11 Metal Cluster Ions: Fragmentation Pathways and Photoabsorption Cross Sections, J. Am. Soc. Mass Spectrom., 2003, 14, 614–621 CrossRef CAS PubMed.
- A. A. Shvartsburg and M. F. Jarrold, Transition from covalent to metallic behavior in group-14 clusters, Chem. Phys. Lett., 2000, 317, 615–618 CrossRef CAS.
- M. E. Geusic, M. F. Jarrold, T. J. McIlrath, R. R. Freeman and W. L. Brown, Photodissociation of carbon cluster cations, J. Chem. Phys., 1987, 86, 3862–3869 CrossRef CAS.
- M. J. Deluca and M. A. Johnson, Photofragmentation of Cn−, 4 ≤ n ≤ 20: Loss of neutral C3, Chem. Phys. Lett., 1988, 152, 67–70 CrossRef CAS.
- B. Pozniak and R. C. Dunbar, Photodissociation and photodetachment of small carbon cluster anions, Int. J. Mass Spectrom. Ion Processes, 1994, 133, 97–110 CrossRef CAS.
- B. P. Pozniak and R. C. Dunbar, Photodissociation studies of Cn+ at 193 nm (n = 5–19), Int. J. Mass Spectrom. Ion Processes, 1997, 165–166, 299–313 CrossRef.
- L. A. Bloomfield, R. R. Freeman and W. L. Brown, Photofragmentation of Mass-Resolved Si2-12+ Clusters, Phys. Rev. Lett., 1985, 54, 2246–2249 CrossRef CAS PubMed.
- M. F. Jarrold and J. E. Bower, Collision-induced dissociation of silicon cluster ions, J. Phys. Chem., 1988, 92, 5702–5705 CrossRef CAS.
- Y. Liu, Q.-L. Zhang, F. K. Tittel, R. F. Curl and R. E. Smalley, Photodetachment and photofragmentation studies of semiconductor cluster anions, J. Chem. Phys., 1986, 85, 7434–7441 CrossRef CAS.
- Q.-L. Zhang, Y. Liu, R. F. Curl, F. K. Tittel and R. E. Smalley, Photodissociation of semiconductor positive cluster ions, J. Chem. Phys., 1988, 88, 1670–1677 CrossRef CAS.
- P. Ferrari, E. Janssens, P. Lievens and K. Hansen, Thermal radiation and fragmentation pathways of photo-excited silicon clusters, J. Chem. Phys., 2015, 143, 224313 CrossRef PubMed.
- A. Lehr, F. Rivic, M. Jäger, M. Gleditzsch and R. Schäfer, Optical absorption and shape transition in neutral SnN clusters with N ≤ 40: a photodissociation spectroscopy and electric beam deflection study, Phys. Chem. Chem. Phys., 2022, 24(19), 11616–11635 RSC.
- S. Yoshida and K. Fuke, Photoionization studies of germanium and tin clusters in the energy region of 5.0–8.8 eV: Ionization potentials for Gen (n = 2–57) and Snn (n = 2–41), J. Chem. Phys., 1999, 111, 3880–3890 CrossRef CAS.
- G. Ganteför, M. Gausa, K. H. Meiwes-Broer and H. O. Lutz, Photoemission from tin and lead cluster anions, Z. Phys. D: At., Mol. Clusters, 1989, 12, 405–409 CrossRef.
- V. D. Moravec, S. A. Klopcic and C. C. Jarrold, Anion photoelectron spectroscopy of small tin clusters, J. Chem. Phys., 1999, 110, 5079–5088 CrossRef CAS.
- Y. Negishi, H. Kawamata, A. Nakajima and K. Kaya, Photoelectron spectroscopy of tin and lead cluster anions: application of halogen-doping method, J. Electron Spectrosc. Relat. Phenom., 2000, 106, 117–125 CrossRef CAS.
- L.-F. Cui, L.-M. Wang and L.-S. Wang, Evolution of the electronic properties of Snn− clusters (n = 4–45) and the semiconductor-to-metal transition, J. Chem. Phys., 2007, 126, 064505 CrossRef PubMed.
- E. Oger, R. Kelting, P. Weis, A. Lechtken, D. Schooss, N. R. M. Crawford, R. Ahlrichs and M. M. Kappes, Small tin cluster anions: Transition from quasispherical to prolate structures, J. Chem. Phys., 2009, 130, 124305 CrossRef PubMed.
- N. Drebov, E. Oger, T. Rapps, R. Kelting, D. Schooss, P. Weis, M. M. Kappes and R. Ahlrichs, Structures of tin cluster cations Sn3+ to Sn15+, J. Chem. Phys., 2010, 133, 224302 CrossRef PubMed.
- A. Wiesel, N. Drebov, T. Rapps, R. Ahlrichs, U. Schwarz, R. Kelting, P. Weis, M. M. Kappes and D. Schooss, Structures of medium sized tin cluster anions, Phys. Chem. Chem. Phys., 2012, 14(1), 234–245 RSC.
- A. A. Shvartsburg and M. F. Jarrold, Tin clusters adopt prolate geometries, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 1235–1239 CrossRef CAS.
- A. A. Shvartsburg and M. F. Jarrold, Solid Clusters above the Bulk Melting Point, Phys. Rev. Lett., 2000, 85, 2530–2532 CrossRef CAS PubMed.
- Y. Tai, J. Murakami, C. Majumder, V. Kumar, H. Mizuseki and Y. Kawazoe, Fragmentation of small tin cluster ions (Snx+: x = 4–20) in the low-energy collisions with a highly oriented pyrolytic graphite surface, J. Chem. Phys., 2002, 117, 4317–4322 CrossRef CAS.
- H. Li, H. Du, W. Chen, Q. Q. Shan, Q. Sun, Z. X. Guo and Y. Jia, Threadlike Tin Clusters with High Thermal Stability Based on Fundamental Units, J. Phys. Chem. C, 2011, 116, 231–236 CrossRef.
- H. Li, W. Chen, F. Wang, Q. Sun, Z. X. Guo and Y. Jia, Tin clusters formed by fundamental units: a potential way to assemble tin nanowires, Phys. Chem. Chem. Phys., 2013, 15(6), 1831–1836 RSC.
- D. Wu, Q. Du, X. Wu, R. Shi, L. Sai, X. Liang, X. Huang and J. Zhao, Evolution of atomic structures of SnN, SnN−, and SnNCl− clusters (N = 4–20): Insight from ab initio calculations, J. Chem. Phys., 2019, 150, 174304 CrossRef PubMed.
- C. Majumder, V. Kumar, H. Mizuseki and Y. Kawazoe, Small clusters of tin: Atomic structures, energetics, and fragmentation behavior, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 233405 CrossRef.
- P. Jackson, I. G. Dance, K. J. Fisher, G. D. Willett and G. E. Gadd, Mass spectrometry and density functional studies of neutral and anionic tin clusters, Int. J. Mass Spectrom. Ion Processes, 1996, 157–158, 329–343 CrossRef.
- K. Joshi, D. G. Kanhere and S. A. Blundell, Thermodynamics of tin clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 235413 CrossRef.
- S. König, A. Jankowski, G. Marx, L. Schweikhard and M. Wolfram, Fission of Polyanionic Metal Clusters, Phys. Rev. Lett., 2018, 120, 163001 CrossRef PubMed.
- M. Wolfram, S. Bandelow, A. Jankowski, S. König, G. Marx and L. Schweikhard, Photodissociation of mono- and di-anionic tin clusters, Eur. Phys. J. D, 2020, 74, 135 CrossRef CAS.
- Y. Tao, H. Nishimura, T. Okuno, S. Fujioka, N. Ueda, M. Nakai, K. Nagai, T. Norimatsu, N. Miyanaga, K. Nishihara and Y. Izawa, Dynamic imaging of 13.5 nm extreme ultraviolet emission from laser-produced Sn plasmas, Appl. Phys. Lett., 2005, 87, 241502 CrossRef.
- A. Herlert and L. Schweikhard, Delayed neutral-atom evaporation of photoexcited anionic gold clusters, Int. J. Mass Spectrom., 2006, 249–250, 215–221 CrossRef.
- M. Wolfram, S. König, S. Bandelow, P. Fischer, A. Jankowski, G. Marx and L. Schweikhard, Disentangling the photodissociation pathways of small lead clusters by time-resolved monitoring of their delayed decays: the case of Pb31+, J. Phys. B, 2018, 51, 044005 CrossRef.
- L. Schweikhard, S. Krückeberg, K. Lützenkirchen and C. Walther, The Mainz cluster trap, Eur. Phys. J. D, 1999, 9, 15–20 CrossRef CAS.
- F. Martinez, S. Bandelow, C. Breitenfeldt, G. Marx, L. Schweikhard, A. Vass and F. Wienholtz, Upgrades at ClusterTrap and Latest Results, Int. J. Mass Spectrom., 2014, 365–366, 266–274 CrossRef CAS.
- M. Vogel, K. Hansen, A. Herlert and L. Schweikhard, Decay pathways of small gold clusters, Eur. Phys. J. D, 2001, 16, 73–76 CrossRef CAS.
- U. Hild, G. Dietrich, S. Krückeberg, M. Lindinger, K. Lützenkirchen, L. Schweikhard, C. Walther and J. Ziegler, Time-resolved photofragmentation of stored silver clusters Agn+ (n = 8–21), Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 2786–2793 CrossRef CAS.
- C. Walther, G. Dietrich, W. Dostal, K. Hansen, S. Krückeberg, K. Lützenkirchen and L. Schweikhard, Radiative Cooling of a Small Metal Cluster: The Case of V13+, Phys. Rev. Lett., 1999, 83, 3816–3819 CrossRef CAS.
- K. Hansen, A. Herlert, L. Schweikhard, M. Vogel and C. Walther, The dissociation energy of V13+ and the consequences for radiative cooling, Eur. Phys. J. D, 2005, 34, 67–71 CrossRef CAS.
- H. Weidele, U. Frenzel, T. Leisner and D. Kreisle, Production of Cold/Hot Metal Cluster Ions: a Modified Laser Vaporization Source, Z. Phys. D: At. Mol. Clusters, 1991, 20, 411–412 CrossRef CAS.
- L. Schweikhard and A. G. Marshall, Excitation modes for Fourier transform-ion cyclotron resonance mass spectrometry, J. Am. Soc. Mass Spectrom., 1993, 4, 433–452 CrossRef CAS PubMed.
- G. Bollen, R. B. Moore, G. Savard and H. Stolzenberg, The accuracy of heavy-ion mass measurements using time of flight-ion cyclotron resonance in a Penning trap, J. Appl. Phys., 1990, 68, 4355–4374 CrossRef CAS.
- G. Savard, S. Becker, G. Bollen, H.-J. Kluge, R. B. Moore, T. Otto, L. Schweikhard, H. Stolzenberg and U. Wiess, A new cooling technique for heavy ions in a Penning trap, Phys. Lett. A, 1991, 158, 247–252 CrossRef CAS.
- L. Schweikhard, S. Guan and A. G. Marshall, Quadrupolar excitation and collisional cooling for axialization and high pressure trapping of ions in Fourier transform ion cyclotron resonance mass spectrometry, Int. J. Mass Spectrom. Ion Processes, 1992, 120, 71–83 CrossRef CAS.
- V. V. Kresin, Collective resonances and response properties of electrons in metal clusters, Phys. Rep., 1992, 220, 1–52 CrossRef CAS.
- C. Brechignac and J. P. Connerade, Giant resonances in free atoms and in clusters, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 3795–3828 CrossRef CAS.
- I. Vasiliev, S. Öğüt and J. R. Chelikowsky, Ab Initio Excitation Spectra and Collective Electronic Response in Atoms and Clusters, Phys. Rev. Lett., 1999, 82, 1919–1922 CrossRef CAS.
- (a) C. Walther, G. Dietrich, M. Lindinger, K. Lützenkirchen, L. Schweikhard and J. Ziegler, Time resolved photofrag-mentation of Au15+ clusters, Chem. Phys. Lett., 1996, 256(1–2), 77–82 CrossRef CAS; (b) C. Walther, G. Dietrich, M. Lindinger, K. Lützenkirchen, L. Schweikhard and J. Zieglers, Erratum: Time resolved photofragmentation of Au15+ clusters, Chem. Phys. Lett., 1996, 262(5), 668 CrossRef CAS.
- M. Vogel, K. Hansen, A. Herlert and L. Schweikhard, Model-independent determination of dissociation energies: method and applications, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 1073–1083 CrossRef CAS.
- M. Vogel, K. Hansen, A. Herlert and L. Schweikhard, Model-Free Determination of Dissociation Energies of Polyatomic Systems, Phys. Rev. Lett., 2001, 87, 013401 CrossRef CAS PubMed.
- P. Fischer and L. Schweikhard, Decay-rate power-law exponent as a link between dissociation energy and temperature, Phys. Rev. Res., 2020, 2, 043177 CrossRef CAS.
- C. Kittel, Introduction to solid state physics. John Wiley and Sons, 2018 Search PubMed.
- K. Hansen, Decay dynamics in molecular beams, Mass Spectrom. Rev., 2020, 40, 725–740 CrossRef PubMed.
- K. Hansen, Statistical Physics of Nanoparticles in the Gas Phase, Springer International Publishing, 2018 Search PubMed.
| This journal is © the Owner Societies 2024 |