Open Access Article
Open Access ArticleFundamental and higher eigenmodes of qPlus sensors with a long probe for vertical-lateral bimodal atomic force microscopy†
Yuya
Yamada
 a,
Takashi
Ichii
a,
Takashi
Ichii
 *a,
Toru
Utsunomiya
*a,
Toru
Utsunomiya
 a,
Kuniko
Kimura
b,
Kei
Kobayashi
a,
Kuniko
Kimura
b,
Kei
Kobayashi
 b,
Hirofumi
Yamada
b and
Hiroyuki
Sugimura
a
b,
Hirofumi
Yamada
b and
Hiroyuki
Sugimura
a
aDepartment of Materials Science and Engineering, Kyoto University, Yoshida Honmachi, Sakyo, Kyoto 606-8501, Japan. E-mail: ichii.takashi.2m@kyoto-u.ac.jp
bDepartment of Electronic Science and Engineering, Kyoto University, Katsura, Nishikyo, Kyoto 615-8510, Japan
First published on 26th December 2022
Abstract
The detection of vertical and lateral forces at the nanoscale by atomic force microscopy (AFM) reveals various mechanical properties on surfaces. The qPlus sensor is a widely used force sensor, which is built from a quartz tuning fork (QTF) and a sharpened metal probe, capable of high-resolution imaging in viscous liquids such as lubricant oils. Although a simultaneous detection technique of vertical and lateral forces by using a qPlus sensor is required in the field of nanotribology, it has still been difficult because the torsional oscillations of QTFs cannot be detected. In this paper, we propose a method to simultaneously detect vertical and lateral force components by using a qPlus sensor with a long probe. The first three eigenmodes of the qPlus sensor with a long probe are theoretically studied by solving a set of equations of motion for the QTF prong and probe. The calculation results were in good agreement with the experimental results. It was found that the tip oscillates laterally in the second and third modes. Finally, we performed friction anisotropy measurements on a polymer film by using a bimodal AFM utilizing the qPlus sensor with a long probe to confirm the lateral force detection.
1 Introduction
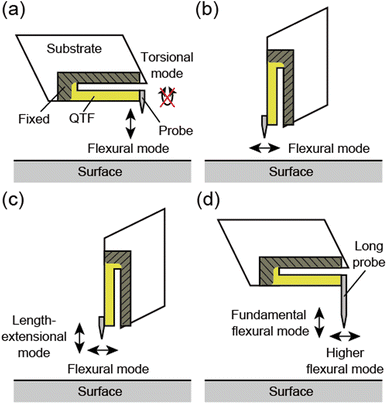
Friction, wear, and lubrication are fundamental physical phenomena on solid surfaces and at solid/liquid interfaces, which are crucial in both science and industry. Detecting vertical and lateral forces at the nanometer scale by atomic force microscopy (AFM) can provide essential knowledge on such tribological issues.1 In recent years, dynamic AFM was adopted to investigate friction with higher spatial resolution and force sensitivity.2,3 In dynamic AFM, the force sensor is vibrated at or near its eigenfrequency, and the tip–sample interaction is detected via the changes in its oscillation state. To access the vertical and lateral interactions simultaneously, it is required that the tip oscillates in the vertical and lateral directions separately in independent modes, the so-called bimodal AFM. In the case of silicon cantilevers, it is realized by utilizing its flexural and torsional modes detected by an optical beam deflection detector with a quadrant photodiode4–7 or by an optical interferometer system.8 Atomic-scale friction analysis was demonstrated in ultra-high vacuum (UHV) environments4,6 and recently in water.7 However, it is difficult to apply dynamic AFM with silicon cantilevers to viscous liquid environments such as lubricant oil/solid interfaces because the quality factor of the silicon cantilever decreases, and the force sensitivity is seriously suppressed. Another technique for detecting vertical and lateral forces at the lubricated interfaces is required to investigate lubrication mechanisms at the atomic and molecular scales.The qPlus sensor is another force sensor built from a quartz tuning fork (QTF) and a sharp tip.9,10 One prong of a QTF is fixed to a substrate, and a probe with a sharp tip is attached to the other prong, in the so-called “qPlus” configuration. Atomic-resolution imaging has been achieved by qPlus sensors in various environments, UHV,11 ambient conditions,12–16 and liquid environments,17–22 including lubricant oils.22 In these reports, the vertical tip–sample interaction was detected for regulating the tip–sample distance. The probe was attached perpendicularly to the QTF prong, and its tip oscillated vertically to the surface in its fundamental flexural mode (Fig. 1a). However, torsional oscillations cannot be detected because commercially available QTFs are generally manufactured for detecting flexural oscillations.
By attaching the probe parallel to the QTF prong and rotating the sensor by 90°, the tip oscillates parallel to the surface (Fig. 1b). The lateral tip–sample interaction can also be detected with atomic resolution by lateral force microscopy (LFM) utilizing this qPlus sensor.23–26 Namely, vertical and lateral forces can be individually detected by qPlus sensors with different arrangements. However, simultaneous detection of both vertical and lateral forces with a single qPlus sensor had not been reported until recent years.
Kirpal et al. recently presented a method to simultaneously excite the fundamental flexural and length-extensional modes of a qPlus sensor, where the probe was attached parallel to the QTF prong (biaxial excitation).27 By setting the QTF prong perpendicular to the surface, the vertical and lateral movements of the tip were provided by the length-extensional and flexural modes, respectively (Fig. 1c). They achieved atomic resolution in both modes under UHV and ambient conditions. However, the electrode arrangement of the QTF they used, which is required for detecting the length-extensional mode, differs from that of conventional QTFs.
There is another way to oscillate the probe apex laterally, which uses the higher eigenmodes of the QTF sensor with a long probe.20,28–32 Higuchi et al. analyzed the eigenmodes of the QTF sensor with an angled-attached long probe by the finite element method (FEM).28 They revealed the lateral tip oscillation in the second mode and demonstrated topographic imaging with the sensor. Afterward, Chen et al. also reported a FEM study on QTF sensors with an angled-attached long probe with various probe lengths and diameters.30 In contrast, we found lateral tip oscillation in the higher flexural mode of a qPlus sensor, where a long probe was attached perpendicularly to the QTF prong (Fig. 1d).20 In these methods, commercially available QTFs can be used without any modification, which is advantageous over the method using the length-extensional mode.
To apply a QTF sensor with lateral tip oscillation for dynamic lateral force detection, additional issues remain to be solved. First, the determination of the spring constant and oscillation amplitude is necessary for the quantitative analysis of tip–sample interaction. The effective spring constant of the qPlus sensor with a long probe was already analyzed by FEM.28,30,31 Some methods to calibrate the amplitude of the higher mode of the qPlus sensor with a long probe were proposed, such as scanning electron microscopy28,30 and laser Doppler vibrometry.31,32 Furthermore, the analysis of piezoelectric sensitivity, which is the ratio of the output voltage signals to the tip oscillation amplitude, is crucial because it determines the deflection noise density, which dominates the minimum detectable force gradient in AFM.33 Although several research groups have analyzed the piezoelectric current,30 to the best of our knowledge, there have been no studies analyzing piezoelectric sensitivity.
In general, FEM is a powerful method for sensor vibration mode analysis. However, it can only analyze individual sensors. Mathematical analysis based on equations of motion is more effective for sensor optimization and is also crucial in the scientific context. In previous mathematical studies on the dynamic properties of qPlus sensors,34–36 the probe was treated as rigid in the mathematical models. The higher eigenmodes of a qPlus sensor with a long probe, which are the coupled oscillations of the QTF prong and probe, cannot be described in these models.20 In this paper, we show a mathematical study on the first three eigenmodes of the qPlus sensor with a long probe considering the deformation of the probe. The eigenfrequencies, the tip oscillation angles, the effective spring constants, and the piezoelectric sensitivities of these modes were obtained by solving a set of equations of motion for the QTF prong and the probe. We optimized the probe length for lateral force detection and found that the third mode is more suitable than the second mode in terms of piezoelectric sensitivity. The calculated eigenfrequencies and piezoelectric sensitivities agreed with the experimental results, and we proved the validity of the mathematical model we constructed.
Finally, it is of utmost importance to experimentally verify whether the lateral force can be detected by the lateral oscillation mode. Although several groups have revealed that the probe apex of the QTF sensor oscillates laterally, there have been few studies that show experimental evidence of lateral force detection. To achieve this goal, we investigated a poly(vinylidenefluoride-trifluoroethylene) (P(VDF-TrFE)) film by bimodal AFM utilizing a qPlus sensor with a long probe. The friction anisotropy depending on the polymer crystal direction was successfully imaged by the third mode, and we experimentally demonstrated that dynamic lateral forces can be detected by this technique.
2 Analysis of the eigenmodes
2.1 Equations of motion
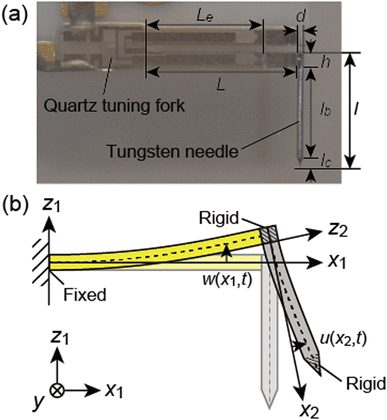
Referring to the discussion in ref. 34, we analyze the eigenmodes of the qPlus sensor by adding considerations for the probe deformation. First, we derive the equations of motion for the bending motion of qPlus sensors. A photograph and a schematic illustration of a qPlus sensor are shown in Fig. 2. One prong and the base of a QTF are fixed to a substrate, and a long probe is attached to the end of the other prong perpendicularly. In this study, an electrochemically etched tungsten needle was used as the probe. L and h are the length and thickness of the QTF prong, l and d are the length and diameter of the needle, lc is the length of the etched part of the needle, lb is the length of the free cylindrical part of the needle, lb = l − h − lc, and Le is the length of the electrode on the QTF prong. The physical parameters of the QTF prong and the tungsten needle are tabulated in Table 1. We model the QTF prong and tungsten needle as Euler–Bernoulli beams to analyze their coupled oscillation. The bonded part and etched part of the tungsten needle are modeled as a rigid cylinder and a rigid cone, respectively. Though the tungsten needle was attached to the QTF prong using epoxy glue, they are modeled as rigidly bonded.| QTF prong | Tungsten needle | ||
|---|---|---|---|
| a ρ q and Eq are the mass density and Young's modulus of quartz, L, h, and b are the length, thickness, and width of the QTF prong, Le is the length of the electrode on the QTF prong, ρw and Ew are the mass density and Young's modulus of tungsten, d is the diameter of the tungsten needle, and lc is the length of the etched part of the tungsten needle. | |||
| ρ q | 2650 kg m−3 | ρ w | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 kg m−3 300 kg m−3 |
| E q | 80 GPa | E w | 345 GPa |
| L | 2.357 mm | d | 0.10 mm |
| h | 0.2134 mm | l c | 0.15 mm |
| b | 0.127 mm | ||
| L e | 1.74 mm | ||
The bending displacements of the QTF prong and tungsten needle are described in the (x1, z1) and (x2, z2) coordinate systems, respectively. The bending displacement of the QTF prong at x1 in the z1 direction as a function of time is represented as w(x1, t), and that of the tungsten needle at x2 in the z2 direction is represented as u(x2, t). To simplify the expression, the point, x2 = 0, is set to the lower end of the QTF prong (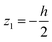 without displacements). The axial displacements and rotational inertia of two beams are assumed to be negligibly small. The total kinetic energy T and potential energy U of a qPlus sensor are given by
without displacements). The axial displacements and rotational inertia of two beams are assumed to be negligibly small. The total kinetic energy T and potential energy U of a qPlus sensor are given by
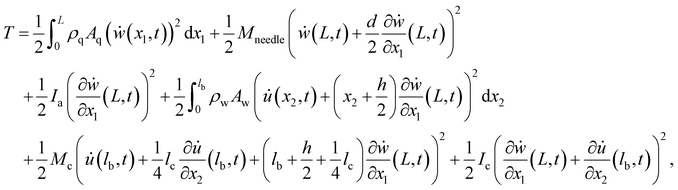 | (1a) |
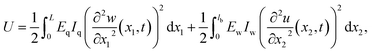 | (1b) |
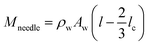 , Mc is the mass of the etched part of the needle,
, Mc is the mass of the etched part of the needle, 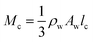 , Ia is the rotational inertia of the bonded part of the needle about the y direction calculated about its center of gravity,
, Ia is the rotational inertia of the bonded part of the needle about the y direction calculated about its center of gravity, 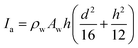 , and Ic is the rotational inertia of the etched part about the y direction calculated about its center of gravity,
, and Ic is the rotational inertia of the etched part about the y direction calculated about its center of gravity, 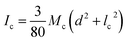 . Over dots represent derivatives with respect to time. Using eqn (1) along with Hamilton's principle, we obtain the equations of motion for free undamped oscillations and the relevant boundary conditions (shown in the ESI S1†). As the global displacement of the tungsten needle,
. Over dots represent derivatives with respect to time. Using eqn (1) along with Hamilton's principle, we obtain the equations of motion for free undamped oscillations and the relevant boundary conditions (shown in the ESI S1†). As the global displacement of the tungsten needle, 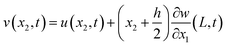 , is induced under an assumption that the bending displacements of the beams and the gradient at the end of the QTF prong are small
, is induced under an assumption that the bending displacements of the beams and the gradient at the end of the QTF prong are small 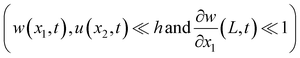 , the equations of motion are obtained in the form of
, the equations of motion are obtained in the form of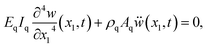 | (2a) |
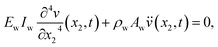 | (2b) |
| w(0,t) = 0, | (3a) |
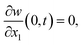 | (3b) |
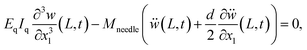 | (3c) |
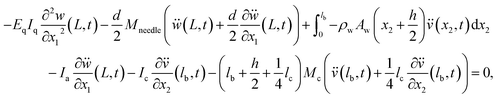 | (3d) |
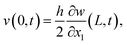 | (4a) |
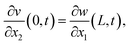 | (4b) |
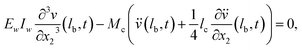 | (4c) |
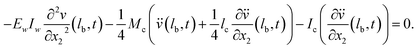 | (4d) |
Using the method of separation of variables, the solutions of the displacements of the QTF prong and tungsten needle are assumed as w(x1,t) = exp(iωt)Φ(x1) and v(x2,t) = exp(iωt)Ψ(x2), where exp(iωt) is the temporal component of the solution with an angular frequency ω, and Φ(x1) and Ψ(x2) are the spatial components of the solution. By substituting the solutions of the displacements in eqn (2)–(4) and solving the equations, we can obtain the eigenfrequencies of the qPlus sensor, fi = ωi/2π(i = 1,2,3…) and the corresponding mode shapes, Φi(x1) and Ψi(x2) (details shown in ESI S1†). In the following sections, the characteristics of the eigenmodes obtained by this theory are discussed.
2.2 Eigenfrequencies and eigenmodes
In this section, we analyze the probe-length dependence on eigenfrequencies and eigenmodes of qPlus sensors based on the theory described in the previous section. The first, second, and third eigenfrequencies are obtained with the help of mathematical software (Maple™), varying the probe length (1.36 mm ≤ l ≤ 2.0 mm) with the physical parameters shown in Table 1. We calculated for the probe length longer than 1.36 mm because eqn (2b) holds for the condition that the length of the cylindrical part of the needle lb is enough longer than the diameter d (lb/d ≥ 10). Fig. 3 shows the calculated first three eigenfrequencies. As the probe length increases from 1.36 mm to 2.0 mm, the first, second, and third eigenfrequencies (f1, f2, and f3) monotonically decrease from 13 kHz to 10 kHz, from 45 kHz to 20 kHz, and from 160 kHz to 100 kHz, respectively. In this calculation, f2 and f3 are 2–3 times and 10–13 times higher than f1, respectively.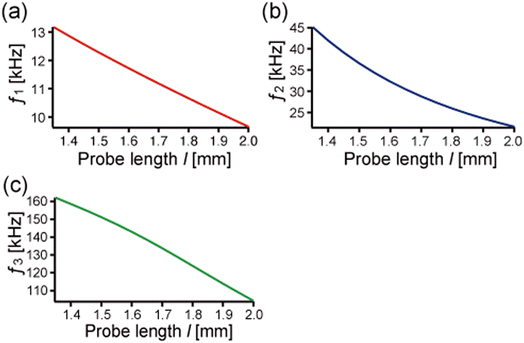 | ||
| Fig. 3 The first three eigenfrequencies calculated by using the properties listed in Table 1 while varying the probe length. (a) The first eigenfrequency, f1. (b) The second eigenfrequency, f2. (c) The third eigenfrequency, f3. | ||
Fig. 4 shows the displacement of the center lines of the QTF prong and tungsten needle of the qPlus sensors at the first, second, and third eigenfrequencies with the probe lengths of 1.4, 1.7, and 2.0 mm, and those of the QTF prong without the needle (no probe) for comparison. The first eigenmodes are normalized with the vertical displacement of the tip (the apex of the tungsten needle), 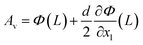 . The second and third eigenmodes are normalized with the lateral displacement of the tip,
. The second and third eigenmodes are normalized with the lateral displacement of the tip, 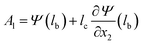 . To clarify the shape of the eigenmodes, the displacements of the QTF prong and tungsten needle are exaggerated in Fig. 4 on the order of 0.1 mm (typically 0.1–1.0 nm in dynamic AFM). The calculated eigenmode shapes agreed with the FEM results shown in Fig. S1.† It is clear from Fig. 4a that the displacement of the QTF prong in the first eigenmode is barely affected by the probe length. In addition, the tungsten needle scarcely deforms in the first eigenmode shown in Fig. 4a, which explains why the first eigenmode can be calculated accurately by using previously reported theories treating the probe as rigid.34–36Fig. 4b and c show that the second and third modes are greatly affected by the probe length. The tungsten needle deforms in these modes, corresponding to previous reports with FEM20,31 and laser Doppler vibrometer experiments.31Fig. 4d shows the third eigenmode expanded around its node in the QTF prong. The node shifts toward the end of the QTF prong (+x direction) as the probe length increases from 1.4 mm to 2.0 mm. These results agree with a previous report that the node in the higher eigenmode of the qPlus sensor shifts toward the end of the QTF prong as the probe length increases.34 As the node approaches the end of the QTF prong, the tip oscillation amplitude in the vertical direction decreases.
. To clarify the shape of the eigenmodes, the displacements of the QTF prong and tungsten needle are exaggerated in Fig. 4 on the order of 0.1 mm (typically 0.1–1.0 nm in dynamic AFM). The calculated eigenmode shapes agreed with the FEM results shown in Fig. S1.† It is clear from Fig. 4a that the displacement of the QTF prong in the first eigenmode is barely affected by the probe length. In addition, the tungsten needle scarcely deforms in the first eigenmode shown in Fig. 4a, which explains why the first eigenmode can be calculated accurately by using previously reported theories treating the probe as rigid.34–36Fig. 4b and c show that the second and third modes are greatly affected by the probe length. The tungsten needle deforms in these modes, corresponding to previous reports with FEM20,31 and laser Doppler vibrometer experiments.31Fig. 4d shows the third eigenmode expanded around its node in the QTF prong. The node shifts toward the end of the QTF prong (+x direction) as the probe length increases from 1.4 mm to 2.0 mm. These results agree with a previous report that the node in the higher eigenmode of the qPlus sensor shifts toward the end of the QTF prong as the probe length increases.34 As the node approaches the end of the QTF prong, the tip oscillation amplitude in the vertical direction decreases.
 | ||
| Fig. 4 The shapes of the first three eigenmodes of the qPlus sensors, corresponding to Φi and Ψi, calculated by using the properties listed in Table 1 for varying the probe length (l = 1.4 mm (red lines), 1.7 mm (blue lines), and 2.0 mm (green lines)). The black lines show the eigenmodes of the QTF prong without the probe (no probe) for comparison. (a) The first eigenmode. (b) The second eigenmode. (c) The third eigenmode. (d) The third eigenmode expanded around its node in the QTF prong. The node shifts toward the end of the QTF prong as the probe length increases. | ||
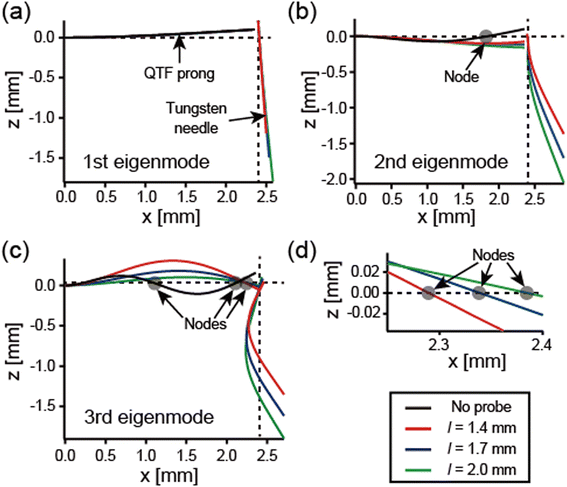
Fig. 5 shows the tip oscillation angle from the lateral direction of the first three eigenmodes calculated from the vertical and lateral displacements of the tip, θi = arctan |Av/Al|. Note that although the trajectory of the tip oscillation is in an arc shape, it can be regarded as linear when the amplitude is sufficiently small. The tip oscillation angle of the first mode θ1 is relatively close to 90° (normal to the surface) and decreases as the probe length increases. In the first eigenmode, the displacement of the QTF prong is barely affected by the probe lengths, and the tungsten needle barely deforms (see Fig. 4a). Therefore, Al increases and θ1 decreases as the probe length increases. The tip oscillation angles of the second and third modes, θ2 and θ3, are relatively close to 0° (parallel to the surface). As the probe length increases, θ2 increases and θ3 decreases. That is because of the variation of those modes of qPlus sensors, especially the position of the node of the QTF prong described above (also see Fig. 4b–d).
 | ||
| Fig. 5 The tip oscillation angle of the first (red), second (blue), and third (green) eigenmodes, θi = arctan |Av/Al|, for the properties listed in Table 1 while varying the probe length. θ1 is relatively close to 90° (normal to the surface). θ2 and θ3 are relatively close to 0° (parallel to the surface). | ||
2.3 Effective spring constants
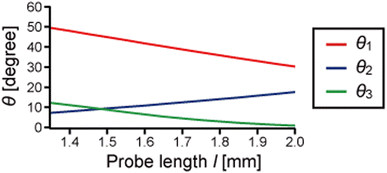
Next, we derive the effective spring constant of the eigenmodes. The tip motion in dynamic AFM can be described with a point-mass oscillator model.37,38 We calculated the effective spring constant of the ith eigenmode ki by equating the strain energy stored in the sensor, , to the potential energy of a point-mass oscillator,
, to the potential energy of a point-mass oscillator, 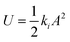 , where A is the maximum displacement of the tip,
, where A is the maximum displacement of the tip, 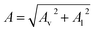 . The effective spring constant in the vertical and lateral directions can be described as ki,v = ki
. The effective spring constant in the vertical and lateral directions can be described as ki,v = ki![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin−2θi and ki,l = ki
sin−2θi and ki,l = ki![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos−2θi, respectively.36Fig. 6 shows the probe-length dependence of k1,v, k2,l, and k3,l, which are the effective spring constants in its main oscillation direction. k1,v varies little with the probe length at 1.9 kN m−1, which agrees with previous theoretical studies.34,35k2,l and k3,l decrease as the probe length increases. k2,l is in the same order of magnitude as k1,v, and k3,l is 10–100 times higher than k1,v.
cos−2θi, respectively.36Fig. 6 shows the probe-length dependence of k1,v, k2,l, and k3,l, which are the effective spring constants in its main oscillation direction. k1,v varies little with the probe length at 1.9 kN m−1, which agrees with previous theoretical studies.34,35k2,l and k3,l decrease as the probe length increases. k2,l is in the same order of magnitude as k1,v, and k3,l is 10–100 times higher than k1,v.
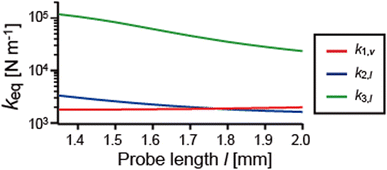 | ||
| Fig. 6 Effective spring constants calculated by equating the strain energy stored in the sensor to the potential energy of a point-mass oscillator for the properties listed in Table 1 while varying the probe length. The effective spring constant in the vertical direction of the first mode, k1,v (red line). The effective spring constant in the lateral direction of the second mode, k2,l (blue line). The effective spring constant in the lateral direction of the third mode, k3,l (green line). | ||
2.4 Piezoelectric sensitivities
qPlus sensors utilize the piezoelectric effect to convert the tip oscillation to electric signals. The piezoelectric sensitivity of qPlus sensors is dramatically affected by the shape of the eigenmode.34 Piezoelectric charge, Q = Q0T(t), is generated on the top and bottom electrodes by tip oscillation, where Q0 is the maximum charge in one oscillation cycle, and T(t) is the temporal component. Q0 is given by34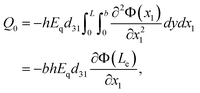 | (5) |
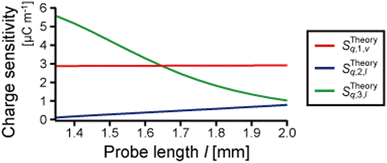 | ||
| Fig. 7 Piezoelectric charge sensitivities, the relationship between the oscillation amplitude and the generated charge Sq = Q/A, calculated for the properties listed in Table 1 while varying the probe length. The calculated charge sensitivity of the vertical oscillation of the first mode, STheoryq,1,v (red line). The calculated charge sensitivity of the lateral oscillation of the second mode, STheoryq,2,l (blue line). The calculated charge sensitivity of the lateral oscillation of the third mode, STheoryq,3,l (green line). | ||
2.5 Discussion
In this section, we analyzed the characteristics of the eigenmodes of the qPlus sensor, considering the deformation of the probe. The probe barely deforms in the first mode, and the mode shape of the QTF prong is less affected by the probe length. The second and third modes are coupled oscillations of the QTF prong and tungsten needle, and the mode shapes are greatly affected by the probe length. The spring constant of the QTF prong and the cylindrical part of the tungsten needle, calculated by using 3EqIq/L3 and 3EwIw/l3b, are 1.9 kN m−1 and 1.2–5.1 kN m−1, respectively. The fundamental eigenfrequencies of the QTF prong and the cylindrical part of the tungsten needle calculated from their shapes and physical parameters are 34 kHz and 22–59 kHz, respectively. Thus, the qPlus sensor with the long tungsten needle can be regarded as two cantilevers with similar spring constants and eigenfrequencies, perpendicularly connected at the one's free and the other's fixed ends. The first mode of the coupled oscillation system is the first mode of the QTF prong, whose eigenfrequency is decreased by the mass and rotational inertia of the tungsten needle. In the second mode, the first mode of the tungsten needle is coupled with the fundamental mode of the QTF prong, in which the free end is weakly constrained. The third mode is considered to be the coupled oscillation of the second modes of the QTF prong and tungsten needle. Although the tip apex oscillates laterally in the second mode, the deflection of the QTF prong is small, and the gradient of the QTF prong at the end of the electrode is almost 0. Thus, the piezoelectric sensitivity of the second mode is low. In contrast, in the third mode, the QTF prong deforms, and the gradient of the QTF prong at the end of the electrode is large. Thus, the piezoelectric sensitivity of the third mode is high.The third mode is more suitable for lateral force detection because the sensitivity of the third mode is expected to be much higher than that of the second mode. In dynamic LFM, the tip oscillation angle should be parallel to the surface to suppress the crosstalk of the vertical force components. However, as the probe length is increased, θ3 approaches 0°, and STheoryq,3,l decreases. That is, there is a trade-off between the piezoelectric sensitivity and the crosstalk of the vertical force component in the third mode. We chose a probe length of 1.6–1.7 mm for the vertical and lateral force detection to obtain STheoryq,3,l with the same magnitude as STheoryq,1,v. The crosstalk of the vertical force component in the third mode is less than 2 percent.
3 Experiments
3.1 Tip length dependencies on eigenfrequencies and sensitivities
In this section, the eigenfrequencies and piezoelectric sensitivities of several qPlus sensors with various probe lengths were experimentally obtained and compared with the theoretical values. Experimentally, the piezoelectric signal of a qPlus sensor is measured with a current-to-voltage conversion amplifier. The voltage sensitivity of the qPlus sensor is given by Sv = V0/A, where V0 is the maximum voltage output of the amplifier in one oscillation cycle. In this study, we use a differential current preamplifier,39 whose output signal is twice as large as a single transimpedance system. The frequency response of this differential amplifier has not been thoroughly examined. However, assuming that it is similar to that of a single transimpedance amplifier, the gain of the amplifier is inversely proportional to the frequency f for frequencies higher than the corner frequency fc = 1/(2πRC), where R is the resistance of the feedback resistor and C is its parasitic capacitance.33 In this study, the corner frequency is given by fc ∼ 40 Hz for R = 20 GΩ and C ∼ 0.2 pF. The gain of the amplifier G is assumed to be inversely proportional to the frequency f in the frequency range of the first three eigenfrequencies of the sensor (10–200 kHz), G = V/I = G0/f, where G0 is a constant of proportionality. Sinusoidally varying charge Q = Q0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(2πift) corresponds to a current I = Q˙ = 2πifQ0
exp(2πift) corresponds to a current I = Q˙ = 2πifQ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(2πift). Thus, we obtain Sv = V0/A = 2πQ0G0/A = 2πG0Sq. That means the voltage sensitivity of the qPlus sensor Sv in this experimental system should be linear with the calculated charge sensitivity Sq.
exp(2πift). Thus, we obtain Sv = V0/A = 2πQ0G0/A = 2πG0Sq. That means the voltage sensitivity of the qPlus sensor Sv in this experimental system should be linear with the calculated charge sensitivity Sq.
The qPlus sensors were made for measuring their eigenfrequencies and piezoelectric sensitivities experimentally. One prong and the base of the QTF (STATEK Co., TFW 1165, the geometry and physical parameters corresponding to the values listed in Table 1) were glued to an alumina substrate. A tungsten wire (Nilaco Co., diameter: 0.10 mm) was electrochemically etched in potassium hydroxide (1.2 mol L−1) and was cut to various probe lengths (l = 1.53 mm, 1.60 mm, 1.61 mm, 1.68 mm, 1.69 mm, and 1.75 mm), and then was glued to the end of the free QTF prong by using epoxy glue (EPO-TEK H70E, Epoxy Technology, Inc). The thermal oscillation of the qPlus sensor can be used to calibrate its sensitivity.11,40 The thermal noise spectra of the qPlus sensors were recorded by using a spectrum analyzer (Agilent Technologies Inc., N9000A) under ambient conditions at T = 25 °C (spectra are not shown).
Fig. 8a–c show the first three eigenfrequencies of the qPlus sensors, which correspond to the peak frequencies of the thermal spectra. The calculated eigenfrequencies are also shown in these figures for comparison (solid lines, the same data shown in Fig. 3). The eigenfrequencies experimentally obtained from the thermal spectra are in excellent agreement with the theoretical values (the deviation is less than 2 percent). The thermal peaks of the second mode of three sensors (l = 1.53 mm, 1.60 mm, and 1.61 mm) were not detected, which would be due to the low piezoelectric sensitivity of the second mode. This result corresponds well to the theoretical prediction described in Section. 2.4.
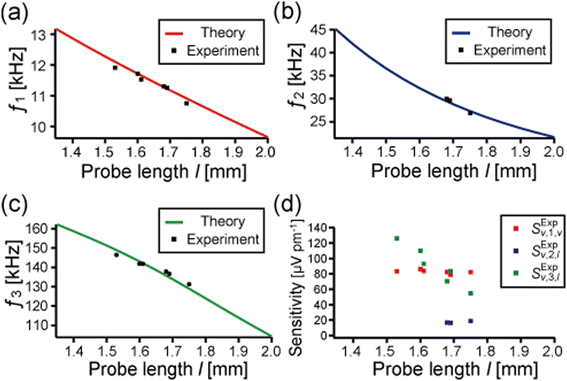 | ||
| Fig. 8 (a)–(c) Experimentally obtained first (a), second (c), and third (c) eigenfrequencies of the qPlus sensors with various probe lengths (1.53 mm, 1.60 mm, 1.61 mm, 1.68 mm, 1.69 mm, and 1.75 mm). The calculated eigenfrequencies (already shown in Fig. 3) are also shown for comparison (solid lines). Experimentally obtained eigenfrequencies are in good agreement with the theory. (d) Piezoelectric voltage sensitivities, Sv = V0/A, derived from the thermal spectrum of the qPlus sensors. The sensitivity of the vertical oscillation of the first mode, SExpv,1,v (red points). The sensitivity of the lateral oscillation of the second mode, SExpv,2,l (blue points). The sensitivity of the lateral oscillation of the third mode, SExpv,3,l (green points). | ||
Fig. 8d shows the piezoelectric sensitivities of the first three eigenmodes of the qPlus sensors derived from the thermal noise spectra using the calculated effective spring constants. The sensitivities of the vertical oscillation of the first mode SExpv,1,v of all tested sensors were 83 ± 4 μV pm−1. This result is 28 percent lower than previously reported by Huber and Giessibl (115 μV pm−1).39 This is probably due to the different resistance values of the feedback resistor used in the preamplifier and the different QTFs used for qPlus sensors in this study. The sensitivities of the lateral oscillation of the second mode SExpv,2,l for three sensors (l = 1.53 mm, 1.60 mm, and 1.61 mm) were too low to be detected. Though it increased as the probe length increased, it was still much lower than SExpv,1,v. The sensitivity of the lateral oscillation of the third mode SExpv,3,l decreased as the probe length increases. It is higher than SExpv,1,v for three sensors (l = 1.53 mm, 1.60 mm, and 1.61 mm) and lower than SExpv,1,v for two sensors (l = 1.68 mm and 1.75 mm). For the sensor with the probe length of 1.69 mm, SExpv,1,v and SExpv,3,l have similar values. This length-dependent sensitivity for the first three eigenmodes was similar to the theoretically obtained charge sensitivity STheoryq. Thus, we experimentally and theoretically confirmed that the piezoelectric sensitivity depends on the probe length, which changes the shape of the eigenmode.
3.2 Confirmation of lateral force detection
Finally, we confirmed that the lateral force can be detected using the third mode of a qPlus sensor with a long probe. Previous LFM studies have indicated that the main chain orientation of polymer crystals causes friction anisotropy.41,42 In conventional LFM experiments, the tip is in contact with the sample surface, and the lateral force (friction force) is detected via the torsional deflection of the cantilever. Friction anisotropy caused by atomic- or molecular-scale surface structures was also detected by dynamic LFM without static contact, where the tip–sample distance was regulated by tunneling current24 or amplitude modulation of lateral tip oscillation.43 Therefore, friction anisotropy detection in our experimental setup will reveal the capability of detecting lateral (in-plane) tip–sample interactions. In this experiment, we used poly(vinylidenefluoride-trifluoroethylene) (P(VDF-TrFE)), which is a copolymer of vinylidenefluoride (VDF) and trifluoroethylene (TrFE). Friction anisotropy on a well-crystalized P(VDF-TrFE) thin film was detected by lateral-modulation LFM (LM-LFM).44P(VDF-TrFE) with a VDF/TrFE molar content ratio of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 was provided by Daikin Industries Ltd and used as received. The melting point (Tm) and the ferroelectric-to-paraelectric phase transition temperature during the heating process (Tc−heat) of the copolymer with this content ratio are 147 °C and 123 °C, respectively.45 A P(VDF-TrFE) film was obtained by spin-coating 2 wt% P(VDF-TrFE)-methylethylketone solution on freshly cleaved, highly oriented pyrolytic graphite. The film was annealed for 2 h to improve its crystallinity at 145 °C and cooled naturally to room temperature under ambient conditions. After crystallization, the film surface was investigated by bimodal AFM using a qPlus sensor. The P(VDF-TrFE) crystal shows highly regulated molecular orientation above Tc−heat (paraelectric phase), whose friction force was detected uniformly inside each crystal.44 The sample temperature during the AFM measurement was kept at 125 °C to clarify the friction difference between differently oriented crystals. The sample was heated by using a ceramic heater equipped on a sample holder with a direct current to avoid the noise increase in the signal of the qPlus sensor.
25 was provided by Daikin Industries Ltd and used as received. The melting point (Tm) and the ferroelectric-to-paraelectric phase transition temperature during the heating process (Tc−heat) of the copolymer with this content ratio are 147 °C and 123 °C, respectively.45 A P(VDF-TrFE) film was obtained by spin-coating 2 wt% P(VDF-TrFE)-methylethylketone solution on freshly cleaved, highly oriented pyrolytic graphite. The film was annealed for 2 h to improve its crystallinity at 145 °C and cooled naturally to room temperature under ambient conditions. After crystallization, the film surface was investigated by bimodal AFM using a qPlus sensor. The P(VDF-TrFE) crystal shows highly regulated molecular orientation above Tc−heat (paraelectric phase), whose friction force was detected uniformly inside each crystal.44 The sample temperature during the AFM measurement was kept at 125 °C to clarify the friction difference between differently oriented crystals. The sample was heated by using a ceramic heater equipped on a sample holder with a direct current to avoid the noise increase in the signal of the qPlus sensor.
The qPlus sensor used in this study was made in the same way described in Section 3.1. The probe length l and the etched part length lc were 1.61 mm and 0.17 mm, respectively. The first three eigenfrequencies confirmed by mechanically forced excitation at 25 °C were 11.6 kHz (f1), 32.9 kHz (f2), and 142.8 kHz (f3). They are in good agreement with eigenfrequencies calculated from the theory described in Section 2, of 11.7 kHz, 32.4 kHz, and 143.2 kHz. The calculated tip oscillation angles were 41.7°, 10.8°, and 6.3° for f1, f2, and f3, respectively. The first and third modes were used to detect vertical and lateral forces in the bimodal AFM experiment. The thermal spectra and transfer functions around f1 and f3 of the sensor were measured to analyze the sensor characteristics (data shown in Fig. S2†). The voltage sensitivities, Sv,1,v and Sv,3,l, obtained from the thermal noise spectra were 84.4 μV pm−1 and 110 μV pm−1, respectively. There is no “forest of peaks” in the amplitude components of the transfer functions (Fig. S2c and d†), which can cause instrumental artifacts in the detected signals.
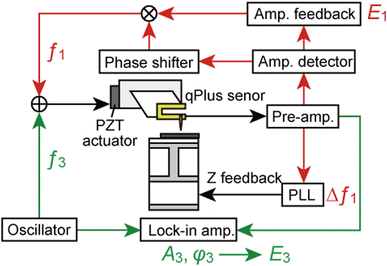
The details of the bimodal AFM setup were already described elsewhere.20 The experiments are carried out by using a system based on a commercial AFM (JEOL, JSPM-5200) with a home-built AFM head made for a qPlus sensor.17Fig. 9 shows a block diagram of the bimodal AFM. The first and third eigenmodes of the sensor were simultaneously excited by using a lead zirconate titanate (PZT) piezoelectric actuator. The frequency shift of the first eigenmode Δf1 was detected by using a commercial FM demodulator (Kyoto Instruments, KI-2001) with some modifications. The oscillation amplitude of the first mode A1 was kept constant with an automatic gain controller, and the energy dissipation in the first mode E1 was measured via the driving amplitude. The third eigenmode was excited at a constant frequency equal to f3 with a constant driving amplitude. The amplitude and phase of the third eigenmode, A3 and ϕ3, were detected by using a lock-in amplifier (NF Electronic Instruments, LI 5640). Such bimodal AFM operation is called frequency modulation–amplitude modulation, “FM–AM”. Topographic images were obtained by scanning the tip on the surface while Δf1 was kept constant. E1, A3, and ϕ3 images were obtained simultaneously with the topographic image. The energy dissipation in the third mode E3 was calculated from A3 and ϕ3 (details shown in ESI S4†). AFM images were processed by using WSxM software.46
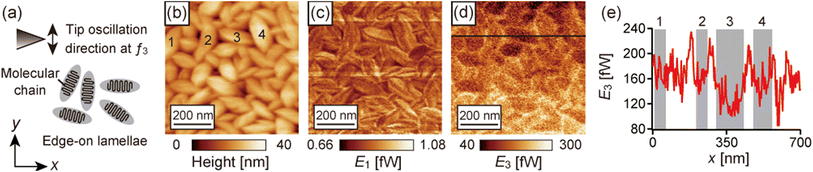
The bimodal AFM images obtained on the P(VDF-TrFE) film at a sample temperature of 125 °C are shown in Fig. 10. The probe oscillated laterally in the y direction at f3 as indicated by the arrow in Fig. 10a. In the topographic image shown in Fig. 10b, randomly oriented rodlike grains are recognized. This feature indicates that they were the edge-on lamellae of P(VDF-TrFE).44 In the edge-on lamellae, the molecular chains align parallel to the film surface and perpendicular to the lamellar plane, the direction of the short axis of the grains, with folds as illustrated in Fig. 10a. Fig. 10c and d show E1 and E3 images simultaneously obtained with the topographic image shown in Fig. 10b. E1 did not depend on the direction of the grains. In contrast, E3 changed depending on the grain directions. Fig. 10e shows the line profile of E3 on the black lines in Fig. 10d. Fig. 10d and e show that E3 increased between the grains, which is because of the topographic effects, that the tip strongly interacts with the surface at the grain edge where the topographic slope is large, and that the tip interacts with two grains when the tip is between the grains. Next, we discuss E3 in the grains considering the relationship between the tip oscillation direction and the molecular orientation in the grains. The short axis of the grains 1–4 indicated in the topographic image (Fig. 10b) tilted 66°, 84°, −12°, and −81° from the +y direction, respectively. The gray-colored zones in the line profiles (Fig. 10e) correspond to the numbered grains. Fig. 10e shows Egrain1(66°)3 ≃ Egrain2(84°)3 ≃ Egrain4(−81°)3 > Egrain3(−12°)3. Thus, E3 decreased when the shorter axis of the grain was parallel to the tip oscillation direction at f3. Namely, the dissipative tip–sample interactions detected in the third mode decreased when the tip oscillated parallel to the molecular chain orientation of P(VDF-TrFE). The interaction stiffness in the third mode shows a similar fashion corresponding to the molecular chain orientation (shown in Fig. S4†). In a previous LM-LFM study,44 the friction force on the P(VDF-TrFE) film was smaller when the molecular chain orientation was parallel to the lateral modulation direction. These results indicate that the friction anisotropy on P(VDF-TrFE) was detected by this bimodal AFM and that lateral force was detected by the third mode of the qPlus sensor with a long probe.
We should note that E3 gradually drifted in the slow scan direction (y direction) because A3 and ϕ3 drifted (shown in Fig. S3†). It is assumed that the sensor was being heated during the imaging, which caused the shift of the eigenfrequencies and the variation of the quality factors. It reproducibly occurs even after heating 1 h before approaching and keeping under the imaging conditions over 1 h. Thus, we compared E3 at the same y position in the above discussions.
4 Conclusions
In this paper, we showed a method to simultaneously detect vertical and lateral force components by using a qPlus sensor with a long probe. The dynamics of the qPlus sensor with a long probe were theoretically studied by solving the equations of motion of the coupled oscillation of a QTF prong and probe. The eigenfrequencies, eigenmode shapes, tip oscillation angles, effective spring constants, and piezoelectric sensitivities of the first three eigenmodes were analyzed. The calculated first eigenmode indicates that the probe barely deforms, which supports previously reported theories with rigid probe approximation.34–36 The probe length greatly influences the second and third modes. In these modes, the probe deforms, and the lateral tip oscillation is dominant, corresponding to previous reports with FEM20,31 and vibrometer experiments.31 The calculated eigenfrequencies were in excellent agreement with the experimentally obtained values, which indicated the validity of our mathematical method. The probe-length dependence of the calculated piezoelectric sensitivities agreed with that of the sensitivities derived from thermal spectra. It was theoretically and experimentally revealed that the piezoelectric sensitivity of the third mode is much greater than that of the second mode due to the eigenmode shape. These calculation results indicated that the eigenmodes of the qPlus sensor are affected by not only the mass and rotational inertia of the probe but also its stiffness and deformation. Eigenmode analysis taking into consideration the probe deformation, as shown in this study, is also important for the force sensor built from multiple components except for qPlus sensors, such as length-extension resonator sensors47 and cantilevers with a carbon nanotube probe.48Also, we experimentally revealed that the developed bimodal AFM can detect lateral tip–sample interactions. The friction anisotropy on P(VDF-TrFE) was investigated in the third mode, and the energy dissipation in the third mode corresponded well to the molecular chain orientation in the lamellae grains. Since the qPlus sensor can be applied to various liquid environments, including lubricant oils,22 this method would be useful for studying various phenomena at solid/liquid interfaces, such as lubrication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Daikin Industries Ltd. for providing P(VDF-TrFE). This work was supported by a Grant-in-Aid for Challenging Research (Exploratory) (No. JP20K21143) and a Grant-in-Aid for JSPS Research Fellow (No. JP21J10543) from the Japan Society for Promotion of Science (JSPS).Notes and references
- B. Bhushan, J. N. Israelachvili and U. Landman, Nature, 1995, 374, 607–616 CrossRef CAS.
- A. J. Weymouth, J. Phys.: Condens. Matter, 2017, 29, 323001 CrossRef CAS PubMed.
- A. Vanossi, D. Dietzel, A. Schirmeisen, E. Meyer, R. Pawlak, T. Glatzel, M. Kisiel, S. Kawai and N. Manini, Beilstein J. Nanotechnol., 2018, 9, 1995–2014 CrossRef CAS PubMed.
- S. Kawai, T. Glatzel, S. Koch, B. Such, A. Baratoff and E. Meyer, Phys. Rev. B, 2010, 81, 085420 CrossRef.
- S. Kawai, F. F. Canova, T. Glatzel, T. Hynninen, E. Meyer and A. S. Foster, Phys. Rev. Lett., 2012, 109, 146101 CrossRef PubMed.
- F. Federici Canova, S. Kawai, C. de Capitani, K.-i. Kan’no, T. Glatzel, B. Such, A. S. Foster and E. Meyer, Phys. Rev. Lett., 2013, 110, 203203 CrossRef PubMed.
- M. Umemoto, R. Kawamura, H. Y. Yoshikawa, S. Nakabayashi and N. Kobayashi, Jpn. J. Appl. Phys., 2020, 59, SIII01 CrossRef CAS.
- Y. Naitoh, R. Turanský, J. Brndiar, Y. J. Li, I. Štich and Y. Sugawara, Nat. Phys., 2017, 13, 663–667 Search PubMed.
- F. J. Giessibl, Appl. Phys. Lett., 1998, 73, 3956–3958 CrossRef CAS.
- F. J. Giessibl, Rev. Sci. Instrum., 2019, 90, 011101 CrossRef PubMed.
- F. J. Giessibl, Appl. Phys. Lett., 2000, 76, 1470–1472 CrossRef CAS.
- D. S. Wastl, A. J. Weymouth and F. J. Giessibl, Phys. Rev. B, 2013, 87, 245415 CrossRef.
- D. S. Wastl, A. J. Weymouth and F. J. Giessibl, ACS Nano, 2014, 8, 5233–5239 CrossRef CAS PubMed.
- H. Ooe, D. Kirpal, D. S. Wastl, A. J. Weymouth, T. Arai and F. J. Giessibl, Appl. Phys. Lett., 2016, 109, 141603 CrossRef.
- H. Ooe and T. Arai, Appl. Phys. Express, 2019, 12, 115002 CrossRef CAS.
- K. Pürckhauer, D. Kirpal, A. J. Weymouth and F. J. Giessibl, ACS Appl. Nano Mater., 2019, 2, 2593–2598 CrossRef.
- T. Ichii, M. Fujimura, M. Negami, K. Murase and H. Sugimura, Jpn. J. Appl. Phys., 2012, 51, 08KB08 CrossRef.
- T. Ichii, M. Negami and H. Sugimura, J. Phys. Chem. C, 2014, 118, 26803–26807 CrossRef CAS.
- K. Pürckhauer, A. J. Weymouth, K. Pfeffer, L. Kullmann, E. Mulvihill, M. P. Krahn, D. J. Müller and F. J. Giessibl, Sci. Rep., 2018, 8, 1–9 Search PubMed.
- Y. Yamada, T. Ichii, T. Utsunomiya and H. Sugimura, Jpn. J. Appl. Phys., 2019, 58, 095003 CrossRef CAS.
- T. Ichii, S. Ichikawa, Y. Yamada, M. Murata, T. Utsunomiya and H. Sugimura, Jpn. J. Appl. Phys., 2020, 59, SN1003 CrossRef CAS.
- Y. Yamada, T. Ichii, T. Utsunomiya and H. Sugimura, Jpn. J. Appl. Phys., 2020, 59, SN1009 CrossRef CAS.
- F. J. Giessibl, M. Herz and J. Mannhart, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12006–12010 CrossRef CAS PubMed.
- A. J. Weymouth, D. Meuer, P. Mutombo, T. Wutscher, M. Ondracek, P. Jelinek and F. J. Giessibl, Phys. Rev. Lett., 2013, 111, 126103 CrossRef CAS PubMed.
- A. J. Weymouth, T. Hofmann and F. J. Giessibl, Science, 2014, 343, 1120–1122 CrossRef CAS PubMed.
- A. J. Weymouth, E. Riegel, O. Gretz and F. J. Giessibl, Phys. Rev. Lett., 2020, 124, 196101 CrossRef CAS PubMed.
- D. Kirpal, J. Qiu, K. Pürckhauer, A. J. Weymouth, M. Metz and F. J. Giessibl, Rev. Sci. Instrum., 2021, 92, 043703 CrossRef CAS PubMed.
- S. Higuchi, H. Kuramochi, O. Kubo, S. Masuda, Y. Shingaya, M. Aono and T. Nakayama, Rev. Sci. Instrum., 2011, 82, 043701 CrossRef PubMed.
- T. Nakayama, O. Kubo, Y. Shingaya, S. Higuchi, T. Hasegawa, C.-S. Jiang, T. Okuda, Y. Kuwahara, K. Takami and M. Aono, Adv. Mater., 2012, 24, 1675–1692 CrossRef CAS PubMed.
- K. Chen, Z. Liu, Y. Xie, C. Zhang, G. Xu, W. Song and K. Xu, Beilstein J. Nanotechnol., 2021, 12, 82–92 CrossRef CAS PubMed.
- M. G. Ruppert, D. Martin-Jimenez, Y. K. Yong, A. Ihle, A. Schirmeisen, A. J. Fleming and D. Ebeling, Nanotechnology, 2022, 33, 185503 CrossRef PubMed.
- D. Martin-Jimenez, M. G. Ruppert, A. Ihle, S. Ahles, H. A. Wegner, A. Schirmeisen and D. Ebeling, Nanoscale, 2022, 14, 5329–5339 RSC.
- F. J. Giessibl, F. Pielmeier, T. Eguchi, T. An and Y. Hasegawa, Phys. Rev. B, 2011, 84, 125409 CrossRef.
- R. C. Tung, T. Wutscher, D. Martinez-Martin, R. G. Reifenberger, F. Giessibl and A. Raman, J. Appl. Phys., 2010, 107, 104508 CrossRef.
- J. Stirling and G. A. Shaw, Beilstein J. Nanotechnol., 2013, 4, 10–19 CrossRef PubMed.
- J. Melcher, J. Stirling and G. A. Shaw, Beilstein J. Nanotechnol., 2015, 6, 1733–1742 CrossRef CAS PubMed.
- T. R. Rodriguez and R. Garcia, Appl. Phys. Lett., 2002, 80, 1646–1648 CrossRef CAS.
- J. Melcher, S. Hu and A. Raman, Appl. Phys. Lett., 2007, 91, 053101 CrossRef.
- F. Huber and F. J. Giessibl, Rev. Sci. Instrum., 2017, 88, 073702 CrossRef PubMed.
- J. Welker, F. de Faria Elsner and F. J. Giessibl, Appl. Phys. Lett., 2011, 99, 084102 CrossRef.
- H. Schönherr and G. J. Vancso, Macromolecules, 1997, 30, 6391–6394 CrossRef.
- Y. Ryousho, S. Sasaki, T. Nagamura, A. Takahara and T. Kajiyama, Macromolecules, 2004, 37, 5115–5117 CrossRef CAS.
- L. Huang and C. Su, Ultramicroscopy, 2004, 100, 277–285 CrossRef CAS PubMed.
- K. Kimura, K. Kobayashi, H. Yamada and K. Matsushige, Langmuir, 2007, 23, 4740–4745 CrossRef CAS PubMed.
- K. Koga and H. Ohigashi, J. Appl. Phys., 1986, 59, 2142–2150 CrossRef CAS.
- I. Horcas, R. Fernandez, J. M. Gomez-Rodriguez, J. Colchero, J. Gomez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 13705 CrossRef CAS PubMed.
- S. Heike and T. Hashizume, Appl. Phys. Lett., 2003, 83, 3620–3622 CrossRef CAS.
- V. Barwich, M. Bammerlin, A. Baratoff, R. Bennewitz, M. Guggisberg, C. Loppacher, O. Pfeiffer, E. Meyer, H.-J. Güntherodt, J.-P. Salvetat, J.-M. Bonard and L. Forró, Appl. Surf. Sci., 2000, 157, 269–273 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2na00686c |
| This journal is © The Royal Society of Chemistry 2023 |