Tuning catalytic activity with steric and electron-withdrawing effects of a porphyrin substituent

Abstract

Tuning of the electron-withdrawing effect of a ligand is an essential process to develop an efficient metal-complex catalyst. We studied here the steric and electron-withdrawing effects on the catalytic activity of an iron(III) porphyrin catalyst for the hydroxylation reaction of a nonactivated alkane. Although previous studies reported that the catalytic activity increases with an increase in the electron-withdrawing effect of the porphyrin substituent, this study shows that an excessive electron-withdrawing effect of the porphyrin substituent leads to a decrease of the catalytic activity. Kinetic analysis of the catalytic reaction reveals that the decrease in the catalytic activity can be rationalized with the change of the rate limiting step, which is controlled by the formation and reaction rates of a reactive intermediate: compound I. The increase in the electron-withdrawing effect increases the reaction rate, but decreases the formation rate, shifting the rate limiting step from the reaction step to the formation step. Because of the low formation rate, compound I having an excessive electron-withdrawing effect is hardly generated in the catalytic reaction, resulting in a decrease in the catalytic activity. This study also shows that the steric effect of the o-position of the meso-aryl group of the iron porphyrin is an essential factor for it to be an efficient catalyst. The results presented in this study provide us insight on how to tune the catalytic activity of a metal-catalyst with the electron-withdrawing and steric effect of the ligand.

---

Introduction

Heme enzymes contain iron porphyrin complexes in their active sites and utilize them as catalysts to achieve their own catalytic reactions.^1–4 For example, the iron porphyrin complex in cytochrome P450 (P450) catalyses various hydroxylation reactions of nonactivated C–H bonds of substrates under mild conditions.^1–3,5,6 In P450, the iron porphyrin is changed to a reactive intermediate called compound I in the catalytic cycle by electrons donated from the reductase and the aid of the proton from solvent (water).^2,3,6,7 Compound I of P450 has been characterized as an oxoiron(IV) porphyrin π-cation radical species, which is in a two-electron more oxidized state than the resting state.^7,8 The hydroxylation reaction of P450 has been believed to proceed in accordance with the rebound mechanism, in which compound I initially abstracts a hydrogen atom from the substrate, and the formed substrate-radical rebounds with the hydroxyl group generated by the hydrogen abstraction of compound I.⁹

The reactions of P450 have attracted many catalytic chemists because of their extremely high efficiency and high selectivity. For example, P450 from Priestia megaterium can catalyse the hydroxylation reaction of a long chain fatty acid more than 10 000 times per minute.¹⁰ To mimic the reactions of P450, there have been studies on catalytic reactions with synthetic metalloporphyrin complexes.^9,11–24 Groves et al. first reported that the iron(III) chloride complex of meso-tetraphenylporphyrin (1 in Fig. 1) catalyzes the hydroxylation and epoxidation reactions of hydrocarbons with iodosylbenzene as an oxygen source.^11,25 Later, they showed that these hydroxylation and epoxidation reactions are catalyzed by the oxoiron(IV) porphyrin π-cation radical complex, which is an analogue of compound I of P450, using iron(III) meso-tetramesitylporphyrin (2 in Fig. 1) and m-chloroperoxybenzoic acid (mCPBA).²⁰ After the pioneering studies by Groves et al., there have been studies on various catalytic oxidation reactions using various metalloporphyrin complexes and terminal oxidants. Manganese, chromium, ruthenium, and osmium porphyrins have been shown to be powerful catalysts comparable to iron porphyrin.^9,11–24

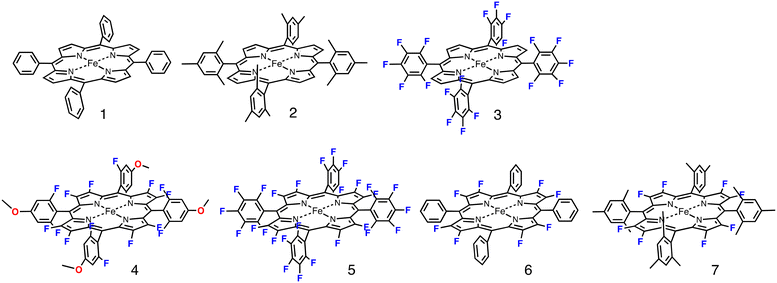Fig. 1 Structures of iron porphyrin complexes 1–7 used in this study. The anionic axial ligands (chloride or TFA) were deleted for clarity.

While 1 and 2 could catalyze the hydroxylation and epoxidation reactions, the yields of the products were relatively low, especially for the hydroxylation reactions. Although there have been studies on many metalloporphyrin catalysts, the reactivity of these complexes is not so high as to oxidize gaseous alkanes, such as methane, ethene, and propane. To increase the reactivity, an electron-withdrawing substituent was introduced as the porphyrin substituent. Traylor et al. reported that the introduction of an electron-withdrawing group at the meso-position such as the pentafluorophenyl group (3 in Fig. 1) drastically increases the yields of the hydroxylation reactions.² Later, we showed that the reactive intermediate of the hydroxylation reactions of 3 is an oxoiron(IV) porphyrin π-cation radical complex as in the cases of P450 and 1.²⁷ Moreover, we showed that the reactivity of the oxoiron(IV) porphyrin π-cation radical complex increases with an increase in the electron-withdrawing effect of the meso-aryl substituent.^28–31

These studies imply us an idea that iron perfluorotetraphenylporphyrin (5 in Fig. 1), in which all protons in 1 are substituted with fluorine atom, would be a much more powerful catalyst than 3. However, the catalytic activity of the pyrrole-β-fluorinated iron porphyrin complex for hydroxylation reactions has not been studied well although it was reported for manganese and ruthenium porphyrin complexes.^32,33 To comprehensively investigate the electron-withdrawing effect of the porphyrin ligand on the catalytic hydroxylation of an alkane, we prepared various iron porphyrin complexes having different numbers of fluorine atoms, as shown in Fig. 1. We examined the catalytic hydroxylation reactions of cyclohexane using these iron porphyrin complexes. The results of the catalytic reactions clearly indicate that the catalytic activity does not simply increase with an increase in the electron-withdrawing effect of the porphyrin ligand. The kinetic study on the formation, reaction, and decomposition reactions of compound I in the catalytic reaction showed that the catalytic activity is determined by the balance of the rates of formation, reaction, and decomposition reactions in the catalytic reaction.

Results and discussion

Steric and electron-withdrawing effects on the catalytic activity of iron(III) porphyrins

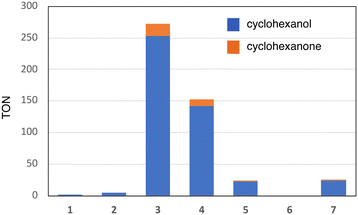
Fig. 1 shows the structures of iron(III) porphyrin complexes, 1–7, prepared to study the effect of the porphyrin substituent. Syntheses of these porphyrin complexes are described in the Experimental section. To confirm the electron-withdrawing effect, we measured the redox potentials of these complexes and the results are summarized in Table 1. We examined the catalytic oxygenation reactions of cyclohexane with chloride complexes of 1–7 (1-Cl–7-Cl) as catalysts and iodosylbenzene as the terminal oxidant at room temperature. The reaction solutions were initially brown in colour resulting from 1-Cl–7-Cl, but the brown colour gradually faded in the reactions. The product analysis with gas chromatography-mass spectrometry (GC-MS) showed that cyclohexane was oxidized to cyclohexanol and cyclohexanone in the catalytic reactions. The turn-over numbers (TONs) of these catalytic reactions are summarized in Fig. 2 and Table 2. 1-Cl, which has a phenyl group at the meso-position, hardly produces oxygenated products, but 2-Cl, which has a sterically hindered meso-substituent (mesityl group) at the meso-position, afforded more cyclohexanol than 1-Cl. The same trend can be seen in the reactions of 6-Cl and 7-Cl. The catalytic reaction of 6-Cl having a meso-phenyl group like 1-Cl does not afford the oxygenated product, but the catalytic reaction of 7-Cl having a meso-mesityl group like 2-Cl produces cyclohexanol and cyclohexanone more than that of 6-Cl. The structural difference between 1-Cl and 2-Cl, and 6-Cl and 7-Cl, is the presence of methyl groups at the o- and p-positions of the meso-aryl groups. These results can be explained by the steric effect of the o-methyl group in the meso-phenyl group. Previous studies showed that the steric effect of the o-substituent in the meso-phenyl group is important to stabilize compound I.^20,34 The increase in the stability of compound I increases the chance to react with cyclohexane. The catalytic activity of 7-Cl is higher than that of 2-Cl. This is due to the electron-withdrawing effect of the fluorine atoms at the pyrrole-β-position, because the redox potential of 7-Cl is much higher than that of 2-Cl. This is consistent with previous studies, in which the catalytic activity of a porphyrin complex increases with an increase in the electron-withdrawing effect of the porphyrin ligand.^26,28 A more important result was obtained in the reactions of 2-Cl–5-Cl. The TON of the catalytic reaction increases in the order of 2-Cl and 3-Cl, but it decreases in the order of 3-Cl, 4-Cl, and 5-Cl. Since the redox potentials of these porphyrin complexes increase in the order of 2-Cl, 3-Cl, 4-Cl, and 5-Cl,^32,33 the electron-withdrawing effect of the porphyrin increases in the order of 2-Cl, 3-Cl, 4-Cl, and 5-Cl. Although the total number of fluorine atoms in 4-Cl is less than that in 3-Cl, the direct substitution of the fluorine atom at the pyrrole-β position induces a more drastic effect on the porphyrin ligand than that at the meso-phenyl position. Therefore, these results clearly indicate that the catalytic activity does not simply increases with an increase in the electron-withdrawing effect of the porphyrin as reported previously, but an excessive electron-withdrawing effect decreases the catalytic activity.

Table 1 Redox potentials (E_1/2vs. SCE in dichloromethane) of iron porphyrins of 1–7

Catalyst	E 1/2/V vs. SCE			Ref.
	Fe(III)/Fe(II)	P ^+˙/P	Cpd-I/Cpd-II
Details are described in the Experimental section. tw: this work.a The redox process was irreversible and afforded only the Epc peak at −0.57 V.b The numbers in parentheses are the E1/2 values for perchlorate complexes.
1-Cl	−0.32	1.18		35
2-Cl	n.d.^a	1.10	0.97 (0.88)^b	tw, 36
3-Cl	−0.03	1.48	(1.39)^b	36
4-Cl	0.18	1.61		tw
5-Cl	0.37	n.d.		37
6-Cl	0.04	1.41		tw
7-Cl	0.01	1.47		tw

---

Fig. 2 Catalytic activities (TON) of iron porphyrins (1–7) for the oxidation reaction of cyclohexane with iodosylbenzene at 20 °C. Blue bar: TON of cyclohexanol and orange bar: TON of cyclohexanone. Details of the catalytic conditions are described in the Experimental section.

Table 2 Catalytic oxygenation reactions of cyclohexane with iron porphyrins 1-Cl–7-Cl at room temperature

Catalyst	TON		Ratio A/(A + K)
	Cyclohexanol	Cyclohexanone
Details of the reaction conditions are described in the Experimental section.
1-Cl	1	<1
2-Cl	5	<1
3-Cl	253	20	0.93
4-Cl	142	10	0.93
5-Cl	22	2	0.92
6-Cl	<1	<1
7-Cl	24	1	0.96

---

Absorption spectral change in the catalytic reactions at 20 °C.

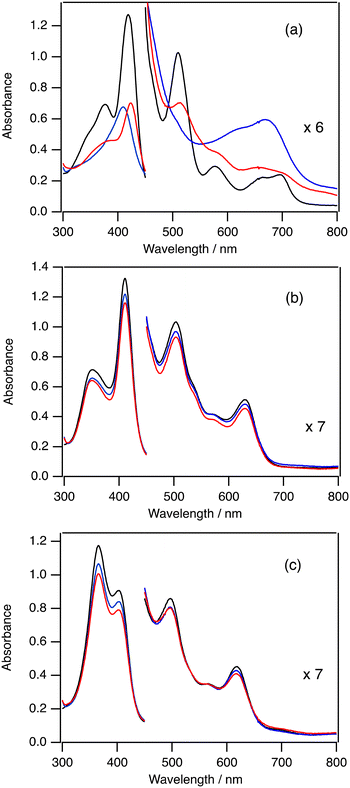
To investigate the mechanism of the change of TON by the electron-withdrawing effect of the porphyrin ligand, we measured the absorption spectra in the catalytic oxygenation reactions of 2-Cl, 3-Cl, and 5-Cl. Since iodosylbenzene is hardly soluble in dichloromethane, we used mCPBA and 1-(t-butylsulfonyl)-2-iodosylbenzene (^sPh-IO) as a terminal oxidant for the spectroscopic study. Fig. 3(a) shows the absorption spectral change in the catalytic oxygenation reaction of cyclohexane with 2-Cl at 20 °C. The absorption spectrum of 2-Cl gradually changes to a new one immediately after the addition of mCPBA (see the blue one in Fig. 3a). The absorption spectrum of the new species shows peaks at 407 and 668 nm, which is almost identical to the spectrum of compound I of 2 (2-Cpd I).^20,282-Cpd I has been reported as an reactive intermediate of the catalytic oxygenation reactions of 2.¹⁹ After the formation of 2-Cpd I, the intensity of the spectrum of 2-Cpd I slowly decreases. After 5 min, the spectrum of 2-Cpd I changes to the spectrum close to the initial 2-Cl and the intensities of peaks become about half of the initial ones. These results suggest that the reactive intermediate (2-Cpd I) is rapidly generated in the catalytic reaction of 2-Cl and the rate limiting step of the catalytic reaction of 2-Cl is the reaction of 2-Cpd I with cyclohexane.

Fig. 3 Absorption spectral changes in the catalytic cyclohexane oxidation reactions of 2-Cl (a), 3-Cl (b), and 5-Cl (c) with mCPBA at 20 °C. Black line: before addition of mCPBA, blue line: immediately after the addition of mCPBA, red line: after 300 s.

Fig. 3(b) shows the absorption spectral change in the catalytic oxygenation reaction of cyclohexane with 3-Cl at 20 °C. In contrast to the reaction of 2, the absorption spectrum of 3-Cl hardly changes even when mCPBA is added to the solution of 3-Cl and cyclohexane at 20 °C. The intensity of the absorption for 3-Cl slightly decreases after 5 min. These results suggest that that the rate limiting step of the catalytic reaction is the reaction of 3-Cl with mCPBA. Previously, we showed that compound I of 3 (3-Cpd I) having chloride as the axial ligand was very unstable. Moreover, we also showed that, due to the electron-withdrawing effect of the porphyrin substituent, the formation of compound I from iron(III) porphyrin with a terminal oxidant became slower and the reaction of compound I with a substrate became faster.³⁰ These changes would result in the shift of the rate limiting step from the reaction step of compound I to the formation step of compound I.

Fig. 3(c) shows the absorption spectral change in the catalytic oxygenation reaction of cyclohexane with 5-Cl at 20 °C. As the reaction of 3-Cl, the absorption spectral feature of 5-Cl hardly changes even when mCPBA is added to the solution of 5-Cl and cyclohexane at 20 °C. The intensity of the absorption for 5-Cl is slightly decreased after 5 min. Compound I of 5 (5-Cpd I) has not been characterized in previous studies. However, we show that cyclohexane is oxidized to cyclohexanol in the present catalytic reaction of 5-Cl with iodosylbenzene. These results indicate that, as in the case of 3-Cl, the rate limiting step of the catalytic reactions of 5-Cl is the formation of compound I.

We carried out the catalytic reactions with iodosylbenzene, which is hardly soluble in dichloromethane. Therefore, we also measured the absorption spectra in the catalytic reactions of 2-Cl, 3-Cl, and 5-Cl with ^sPh-IO, which is an iodosylbenzene-analogue and soluble in dichloromethane, at 20 °C (Fig. S1†). The spectral changes for the reactions of 2-Cl and 3-Cl with ^sPh-IO were almost the same as those with mCPBA. The absorption spectrum of 5-Cl changed to a new one with the addition of ^sPh-IO. However, the absorption spectral feature was different from the spectrum of compound I, but close to that of ferric porphyrin species, probably due to the coordination of ^sPh-IO. The intensity of the peaks for the complex slightly decreased for 5 min, like the reaction of 3-Cl with ^sPh-IO.

We further monitored the catalytic reaction of cyclohexane with the trifluoroacetate (TFA) complex of 2, 3, and 5 (2-TFA, 3-TFA, and 5-TFA) at 20 °C to investigate the axial ligand effect (Fig. S2†). Since the binding of TFA is weaker than that of chloride, the binding of mCPBA to the TFA complex is faster than that of the chloride complex.³⁸ This is confirmed in the later kinetic section. The absorption spectral changes for the TFA complexes are similar to those for the chloride complexes. 2-Cpd I is observed in the catalytic reaction of 2-TFA, but the peaks corresponding to 3-Cpd I and 5-Cpd I are not detected in their catalytic reactions. It is also clear that the decomposition reactions for 3-TFA and 5-TFA are faster than those for 3-Cl and 5-Cl, probably due to the fast binding of mCPBA.

Absorption spectral change in the catalytic reactions at −80 °C

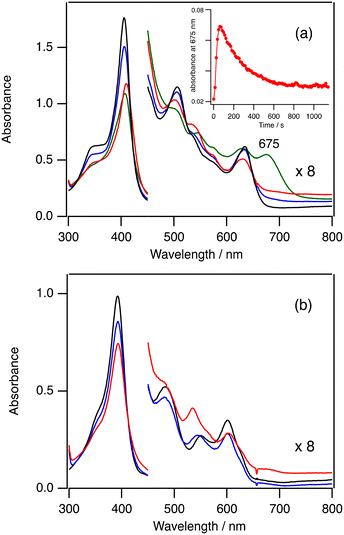
In order to confirm the formation of 3-Cpd I and 5-Cpd I, we measured the absorption spectra in the catalytic reactions at −80 °C. As observed at 20 °C, the absorption spectra in the catalytic reaction of 3-Cl are also very close to the spectrum of 3-Cl and the absorbance resulting from 3-Cpd I cannot be detected even at −80 °C (Fig. S3†). However, the absorption spectrum in the catalytic reaction of 3-TFA at −80 °C shows a new peak at 675 nm (the green line in Fig. 4a). The peak intensity at 675 nm increases for 1 min, but it slowly decreases for 10 min (inset in Fig. 4a). The peak at 675 nm can be assigned to 3-Cpd I because 3-Cpd I can be observed when 3-TFA is reacted with 10 equiv. of mCPBA in the absence of cyclohexane at −80 °C (Fig. S4†). These results indicate that 3-Cpd I is generated in the catalytic conditions of 3-TFA. The detection of 3-Cpd I from 3-TFA, but not from 3-Cl, can be explained by the difference in the formation and reaction rates of 3-Cpd I between 3-Cl and 3-TFA. The binding of TFA to the ferric iron center of 3 is weaker than that of chloride.³⁸ The weaker binding of TFA would hasten the formation rate of 3-Cpd I from 3-TFA. This is confirmed by stopped-flow experiments of 2-Cl and 2-TFA with mCPBA described in the next kinetic section (Fig. 5). In addition, previous studies showed that the reaction and decomposition rates of 3-Cpd I generated from 3-TFA are slower than those from 3-Cl.^38–41 The increase of the formation rate and the decrease of the reaction and decomposition rates of 3-Cpd I would allow the detection of 3-Cpd I in the catalytic reaction of 3-TFA at −80 °C. It is worth noting that the rate limiting step of the catalytic reaction of 3-TFA at 20 °C is the same as that of 3-Cl: the formation step of 3-Cpd I under the present catalytic conditions, because the absorption spectrum in the catalytic reaction of 3-TFA is almost identical to the spectrum of 3-TFA (Fig. S2†).

Fig. 4 Absorption spectral changes in the catalytic reactions of 3-TFA (a) and 5-TFA (b) at −80 °C. (a) Black line: before addition of mCPBA, blue line: immediately after the addition of mCPBA, green line: after 60 s, red line: after 800 s. (b) Black line: before the addition of 10 equiv. of mCPBA, blue line: immediately after the addition of 10 equiv. of mCPBA, red line: after 600 s. inset of (a): time course of the absorbance at 675 nm.

Fig. 5 (a) Absorption spectral change for the formation of 2-Cpd I from the rapid mixing of 2-Cl with 10 equiv. of mCPBA with a stopped-flow technique at 20 °C. Black line: immediately after the mixing of 2-Cl with mCPBA, red line: after 1 s, grey line: after 2 s, 4 s, and 6 s, green line: after 8 s. (b) Time courses of the absorbances at 665 nm, the peak of 2-Cpd I, in the reactions of 2-Cl with 10 equiv. of mCPBA (red line) and 2-TFA with 10 equiv. of mCPBA at 20 °C.

Fig. 4b shows the absorption spectral change in the catalytic reaction of 5-TFA at −80 °C. The absorption spectrum of 5-TFA hardly changes in the catalytic reaction at −80 °C. A small absorption peak is observed at 535 nm after 10 min. Although 3-Cpd I can be detected in the catalytic reaction of 3-TFA, 5-Cpd I cannot be detected in the catalytic reactions of 5-Cl and 5-TFA even at −80 °C. Because of an increase in the electron-withdrawing effect of the porphyrin ligand, the formation step of 5-Cpd I becomes slower than that of 3-Cpd I,^30,37 and the reaction and decomposition of 5-Cpd I become faster than those of 3-Cpd I. The slow formation and the fast reaction and decomposition of 5-Cpd I make the detection of 5-Cpd I difficult in the catalytic reaction even at −80 °C.

Kinetic analysis of formation, reaction, and decomposition reactions of 2-Cpd I

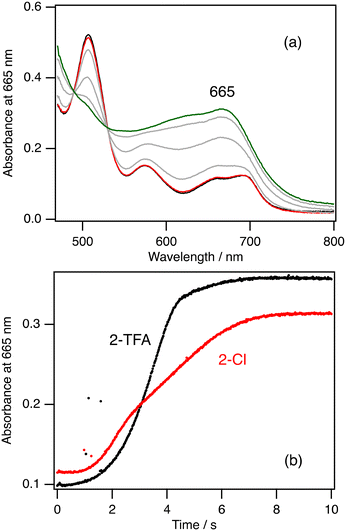
To further investigate the rate limiting step of the catalytic reaction, we conducted kinetic analysis of the formation, reaction, and decomposition steps of 2-Cpd I at 20 °C. Fig. 5a shows the absorption spectral change after mixing of 2-Cl with 10 equiv. of mCPBA and Fig. 5b shows the time course at 665 nm, the peak position of 2-Cpd I, after the mixing. It is clear from these data that the absorption spectrum of 2-Cl hardly changes for about 1 s after the mixing. After the 1 s delay, the spectrum of 2-Cl changes to that of 2-Cpd I with isosbestic points for 8 s. The presence of the delay time in the reaction was reported previously.⁴² When 2-TFA is mixed with 10 equiv. of mCPBA, a similar spectral change was observed, but 2-Cpd I was produced for 4 s from 2-TFA, about half the time of 2-Cl (Fig. 5b). These results confirm the discussion in the previous section that the formation of compound I for the trifluoroacetate complex is faster than that for the chloride complex. We could not obtain the formation rate from these measurements because the time courses for the formation of 2-Cpd I are not so simple as to simulate with a single or double exponential function.

We further estimated the reaction and decomposition rates of 2-Cpd I at 20 °C to confirm the rate limiting step. The absorption spectrum of 2-Cpd I changed to that of 2-Cl in the presence of cyclohexane at 20 °C. Although excess mCPBA is present in the solution, we estimated the rate constant from the time courses (Fig. S5†). To reduce the influence on the reformation of 2-Cpd I with excess mCPBA, we estimated the rate constant from the last parts of the time courses. The estimated rate constant linearly increases with an increase in the concentration of cyclohexane (Fig. S5†). The second-order rate constant for the reaction of 2-Cpd I with cyclohexane at 20 °C was estimated to be 1.8 × 10⁻² M⁻¹ s⁻¹ and the decomposition rate constant was estimated to be 4.1 × 10⁻² s⁻¹. These kinetic analyses clearly confirm that the rate limiting step of the catalytic reaction of 2-Cl is the reaction step of 2-Cpd I with cyclohexane because the reaction of 2-Cpd I with cyclohexane under the catalytic conditions takes about 120 s, while the formation of 2-Cpd I takes about 8 s. The reaction rate under the catalytic conditions can be calculated to be 3.6 × 10⁻³ s⁻¹ from the present kinetic analysis. This rate is much smaller than the decomposition rate (4.1 × 10⁻² s⁻¹). This means that most of 2-Cpd I generated in the catalytic reaction of 2-Cl leads to the decomposition of the catalyst without the production of cyclohexanol, explaining the low TON and the decrease in the absorption peaks in the catalytic reaction of 2-Cl.

Electron-withdrawing effect of the porphyrin ligand on catalytic reaction

The catalytic reaction with an iron porphyrin catalyst has been thought to proceed via the mechanism shown in Fig. 6. The catalytic reaction is initiated by the coordination of a terminal oxidant (O–X) to the iron center of the iron porphyrin catalyst, generating a terminal oxidant adduct. Then, the O–X bond of the metal-bound terminal oxidant is cleaved to generate compound I. Compound I is usually a reactive intermediate of the catalytic reaction to induce the oxidation reaction of a substrate. The oxidation reaction of compound I with the substrate reproduces the initial iron porphyrin catalyst. Since compound I is not a stable compound, the oxidation reaction of compound I with the substrate always competes with the self-decomposition reaction of compound I in the catalytic reaction. The efficiency of the catalytic reaction should be determined by the balance of these reaction steps. This scheme is also applicable to the catalytic reactions of other metal-catalysts.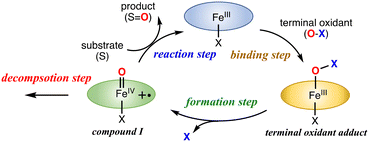

Fig. 6 Proposed reaction mechanism for the catalytic oxidation reaction of the iron(III) porphyrin catalyst with a terminal oxidant.

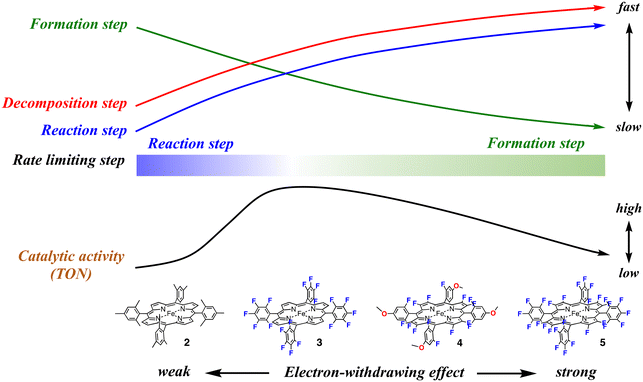
This study shows that, as shown in Fig. 2 and Table 2, the catalytic activity (TON) increases in the order of 1, 2, 5, 4, and 3. In spite of the stronger electron-withdrawing effect than 3, the catalytic activities of 4 and 5 are lower than that of 3. The catalytic activity does not simply increase with an increase in the electron-withdrawing effect of the porphyrin ligand and the excessive electron-withdrawing effect decreases the catalytic activity. How does the electron-withdrawing effect of the porphyrin substituent tune the catalytic activity? The mechanism on how to tune the catalytic activity can be explained by using Fig. 7.

Fig. 7 Electron-withdrawing effect of the porphyrin substituent on the rates of the formation (green arrow), reaction (blue arrow), and decomposition (red arrow) steps, and on the overall catalytic activity (TON) for the cyclohexane oxidation reaction (black arrow). The bar of the rate limiting step indicates the change of the rate limiting step with an increase in the electron-withdrawing effect.

We previously reported the electron-withdrawing effect of the porphyrin substituent on each step of the catalytic reaction.^{28,30,37,43,44} As the electron-withdrawing effect of the porphyrin substituent gets stronger, the formation step of compound I becomes slower because of the decrease of the electron density at the iron center (the green arrow in Fig. 7). However, as the electron-withdrawing effect gets stronger, compound I becomes more reactive and thus the reaction and decomposition steps of compound I become faster (the blue and red arrows in Fig. 7). Therefore, when the electron-withdrawing effect is weak like that in 2, compound I is rapidly generated from the reaction with a terminal oxidant, but the reactivity of compound I is too low to oxidize cyclohexane efficiently. After all, the rate limiting step of the catalytic reaction results in the reaction step of compound I with a substrate. Since compound I cannot oxidize cyclohexane, compound I is decomposed to the initial iron porphyrin by the reaction with solvent (dichloromethane). The decomposition step generates a radical species, which destroys the iron porphyrin catalyst. Although the terminal oxidant is consumed in the catalytic reaction, it does not lead to product formation, but the decomposition of the iron porphyrin catalyst. This scheme is consistent with the present experimental results for 2. The detection of 2-Cpd I and the rates for the formation and reaction steps clearly indicate that the rate limiting step in the catalytic reaction of 2-Cl is the reaction step of compound I. The decrease in the peak intensities also indicates the decomposition of the iron porphyrin catalyst in the catalytic reaction.

With an increase in the electron-withdrawing effect of the porphyrin substituent, the formation step of compound I becomes slower and the reaction step of compound I becomes faster.³⁰ As a result, the formation rate of compound I becomes comparable to the reaction rate. Although compound I becomes hard to generate, the generated compound I becomes reactive enough to oxidize a nonactivated C–H bond and the catalytic reaction changes to produce the product efficiently. This is the case of the catalytic reaction of 3-Cl. Previous studies showed that the redox potential of 3-Cl is about 400 mV higher than that of 2-Cl.^28,44 The formation rate of 3-Cpd I would be comparable to the reaction and decomposition rates. This is confirmed by the present results showing that 3-Cpd I can be detected in the catalytic reaction of 3-TFA at −80 °C, but it cannot be detected at 20 °C. Since the rates of the formation and reaction steps of compound I are close, the rate-limiting step of the catalytic reaction is changed by the reaction temperature, as well as the concentration of the substrate and terminal oxidant. The relatively fast formation and reaction rates make 3 the most effective catalyst among the catalysts (the right side of the black arrow in Fig. 7).

With a further increase in the electron-withdrawing effect, the formation rate of compound I becomes slower than the reaction rate of compound I. This means that the rate limiting step of the catalytic reaction changes to the formation step of compound I. Although compound I becomes very reactive, the generation of compound I becomes difficult in the catalytic reaction. Moreover, the increase in the reactivity of compound I increases the decomposition rate of compound I. As a result, the catalytic reaction becomes less efficient in spite of the further increase in the electron-withdrawing effect (the left side of the black arrow in Fig. 7). This is the case of the catalytic reaction of 5-Cl. The TON decreases in the order of 3, 4, and 5. The detection of 5-TFA in the catalytic reaction of 5-TFA at 20 °C and −80 °C indicates that the rate limiting step in the catalytic reaction is the formation step of compound I. We recently reported the reaction of 5-Cl with hypochlorite as a terminal oxidant.³⁷5-Cl reacted with hypochlorite to form the bis-hypochlorite adduct of 5, but the O–Cl bond of the iron bound hypochlorite was not cleaved at −20 °C. Similarly, in the present catalytic reaction, iodosylbenzene binds to the iron center of 5-Cl, but the bond cleavage step of the O–I bond of the iron bound iodosylbenzene, the formation step of compound I, is very slow, leading to the low catalytic activity.

While the electron-withdrawing effect of the meso-substituent has been studied well (2-Cl and 3-Cl), the electron-withdrawing effect of the pyrrole-β-fluorine atom has not been studied well (4-Cl–7-Cl). The electron-withdrawing effect of 4–7 can be seen in their redox potentials (Table 1). The comparison of the redox potentials among 1-Cl, 2-Cl, 6-Cl, and 7-Cl clearly shows that the electron-withdrawing effect of the pyrrole-β-fluorine atom is fairly strong and it is comparable to that of the meso-pentafluorophenyl group. The electron-withdrawing effect increases in the order of 1 ≈ 2 < 3 ≈ 6 ≈ 7 < 4 < 5. The catalytic activities of 4–7 (the pyrrole-β-fluorinated iron porphyrins) have not also been studied well in previous studies. A similar trend can be seen in the catalytic activity of the pyrrole-β-fluorinated iron porphyrins, 4–7. The catalytic activity increases in the order of 6, 5, 7, and 4. It is also true for the pyrrole-β-fluorinated iron porphyrin that the catalytic activity increases with an increase in the electron-withdrawing effect, but an excessive electron-withdrawing effect decreases the catalytic activity. Furthermore, it is worth noting that the catalytic activity of 7-Cl is much lower than that of 3-Cl although the redox potential of 7-Cl is close to that of 3-Cl. This means that the electron-withdrawing effect of the pyrrole-β-fluorine atom increases the catalytic activity, but the effect is less effective than that of the meso-aryl group.

This study shows that the electron-withdrawing effect of the porphyrin substituent changes the rate limiting step of the catalytic reaction. With an increase in the electron-withdrawing effect, the rate limiting step shifts from the reaction step of compound I with a substrate to the formation step of compound I. The catalytic efficiency (TON) is determined by the balance among the formation, reaction, and decomposition rates in the catalytic reaction. In this study, the most efficient catalyst can be obtained when the rate of the formation step of compound I is comparable to that of the reaction step of compound I with a substrate.

Steric effect of the porphyrin substituent on catalytic activity

The comparison of TONs between 1-Cl and 2-Cl, and 6-Cl and 7-Cl allows us to discuss the steric effect of the porphyrin substituent on the catalytic activity. It is clear from Fig. 2 and Table 2 that the catalysts having a bulky substituent at the o-position of the meso-aryl group are efficient catalysts. This is explained by the decomposition rate of compound I because the electron-withdrawing effect of the porphyrins of 1-Cl and 6-Cl is the same as that of 2-Cl and 7-Cl, respectively. Previous studies showed that the presence of the bulky substituent at the o-position of the meso-aryl group is essential to stabilize compound I.^20,34 In fact, all of the previously characterized compounds I have the substituent at the o-position.^8,15 Therefore, the decompositions of compound I generated in the catalytic reactions of 1 and 6 are much faster than those of 2-Cl and 7-Cl, resulting in low TON.

Conclusions

We studied here the steric and electron-withdrawing effects on the catalytic activity of an iron(III) porphyrin catalyst for the hydroxylation reaction of cyclohexane using iron(III) porphyrin catalysts of 1–7. The TON of the catalytic reaction indicates that an excessive electron-withdrawing effect of the porphyrin substituent leads to a decrease of the catalytic activity although previous studies reported that the reactivity of compound I increases with an increase in the electron-withdrawing effect of the porphyrin substituent. Kinetic analysis of the catalytic reaction reveals that the decrease in the catalytic activity can be explained by the change of the rate limiting step, which is determined by the formation and reaction rates of compound I. The increase in the electron-withdrawing effect increases the reaction rate of compound I, but decreases the formation rate of compound I, shifting the rate limiting step from the reaction step to the formation step. Although compound I having an excessive electron-withdrawing effect is very reactive, it is hardly generated in the catalytic reaction, resulting in a decrease in the catalytic activity. The most efficient catalytic reaction can be obtained when the rate of the formation step of compound I is comparable to that of the reaction step of compound I with a substrate. This study also shows that the steric effect of the o-position of the meso-aryl group of the iron porphyrin is an essential factor for it to be an efficient catalyst. The steric effect can be rationalized by the decomposition rate of compound I. The results in this study provide us insight on how to tune the catalytic activity of a metal-catalyst with the electron-withdrawing effect of the ligand.

Experimental

Instrumentation

UV-visible absorption spectra at 20 °C were recorded on an Agilent 8453 spectrometer equipped with an Agilent 89090A temperature control unit (Agilent Technologies). Low-temperature absorption spectra were recorded on an Agilent 8453 spectrometer equipped with a USP-203 low-temperature chamber (UNISOKU). ¹H NMR spectra were measured on a Lambda-400 spectrometer (JEOL). The chemical shifts were referenced to the residual proton peaks in deuterated dichloromethane (5.32 ppm) and chloroform (7.24 ppm). The concentrations of the NMR samples were 1 mM. The stopped-flow experiments and kinetic analyses were performed on a stopped-flow rapid mixing system USP-R100 (UNISOKU) with a low-temperature double mixer USP-SFM-CRD10 (UNISOKU). Gas chromatography–mass spectrometry (GC–MS) analysis was performed on a GC-MS QP-2010 SE system (Shimadzu) equipped with a capillary gas chromatograph (CBP5-M25-025 capillary column). The cyclic voltammograms and differential pulse voltammograms were measured with an ALS612A electrochemical analyzer (BAS) in degassed acetonitrile containing 0.1 M tetra-n-butylammonium perchlorate (TBAP) as a supporting electrolyte. A platinum electrode was used as the working electrode and a platinum-wire electrode was employed as the counter-electrode. The potentials were recorded with respect to a saturated calomel electrode (SCE) as the reference electrode.

Materials

Anhydrous organic solvents were obtained commercially and stored in a glove box. Dichloromethane was purified by passing through an alumina column just before use in the glove box. Iodosylbenzene was obtained from TCI (Tokyo). mCPBA was purchased from Wako (Japan) and used without further purification. Other chemicals were purchased commercially and used without further purification. 3,4-Difluoropyrrole was prepared from 3,3,4,4-tetrafluoropyrrolidine hydrochloride in accordance with a published method.⁴⁵

meso-Tetraarylporphyrins (1–7). meso-Tetraphenylporphyrin (1) was obtained from Aldrich and purified with silica gel chromatography. meso-Tetraarylporphyrins (2–7) were prepared by the condensation of corresponding pyrroles and benzaldehydes with BF₃ etherate as previously published.⁴⁶ Crude porphyrins were purified by a silica gel column with dichloromethane as an eluent.

Ferric chloride complexes (1-Cl–7-Cl). Ferric chloride complexes of 1–7 were prepared by insertion of iron into the corresponding free base porphyrins of 1–7 with FeCl₂ and sodium acetate in acetic acid, respectively. After purification of crude iron porphyrins, the iron porphyrins are reacted with 1 M sodium hydroxide solution, then HCl solution to exchange the axial ligand with chloride.

Ferric trifluoroacetate complexes (2-TFA, 3-TFA and 5-TFA). 2-TFA and 3-TFA was prepared by the reactions of hydroxy iron(III) porphyrin complexes of 2 and 3 with trifluoroacetic acid, respectively.^38,472-Cl or 3-Cl in dichloromethane was vigorously mixed with 1 M sodium hydroxide solution with a separation funnel. The dichloromethane layer was separated and a few drops of trifluoroacetic acid were added to the solution. After stirring the mixture for 1 h, the mixture was evaporated. The residue was recrystallized with dichloromethane and hexane. 5-TFA was prepared from the reaction of 5-Cl with silver trifluoroacetate.⁴⁷5-Cl dissolved in anhydrous dichloromethane was added to silver trifluoroacetate and the mixture was stirred for 3 h. The mixture was filtered with a membrane filter and the filtrate was evaporated. The residue was used immediately without further purification to avoid ligand exchange in the purification processes.

Catalytic reactions of 1-Cl–7-Cl with cyclohexane

The iron(III) porphyrin chloride complex (1-Cl–7-Cl) was added into dichloromethane (1 mL) and cyclohexane was added to the solution. The catalytic reaction was initiated by addition of iodosylbenzene. The initial concentrations of iron porphyrin, cyclohexane, and iodosylbenzene were 40 μM, 0.2 M, and 20 mM, respectively. The reaction mixture was stirred for 5 min. The reaction was terminated by addition of tetra-n-butylammonium iodide (50 mM). After addition of the internal standard sample (n-undecane or n-tetradecane) to the reaction mixture, the products and their yields were analyzed by GC-MS. The assignments of the peaks were carried out by comparisons of the retention times and MS spectra of the authentic samples. The yields of the products were determined with calibration curves prepared with the authentic samples.

Absorption spectra in catalytic reactions

Typical procedure: iron(III) porphyrin complex (0.10 mM) in dichloromethane was placed in a 0.1 cm quartz cuvette and the sample cell was set on a UV-visible absorption spectrometer. After stabilization of solution temperature at 20 °C or −80 °C, the dichloromethane solution of mCPBA (1.0 mM: 10 equiv.) was then added to the solution. After the solution was mixed with argon gas bubbles, the reaction was monitored at constant time intervals.

Kinetic analysis

Kinetic analysis for the reaction rate of 2-Cpd I with cyclohexane was carried out using a UV-vis absorption spectrometer. General procedure: 2-Cl (40 μM) in dichloromethane was placed in a 0.1 cm quartz cuvette and the sample cell was set on a UV-visible absorption spectrometer. After stabilization of solution temperature at 20 °C, the dichloromethane solution of mCPBA (400 μM: 10 equiv.) was then added to the solution. After the solution was mixed with argon gas bubbles, the reaction was monitored using a UV-vis absorption spectrometer. After confirming the formation of 2-Cpd I, cyclohexane was added to the solution. The reaction was monitored at constant time intervals. The reaction rate was estimated from the time course of the absorbance at 665 nm, the peak of 2-Cpd I, with a commercial program, Igor 7 (WaveMetrics, USA). The time course was simulated well with a single exponential function. The second-order rate constant was estimated from the dependence of the rate constant with the concentration of cyclohexane with a linear function.

Kinetic analysis for the formation rate of 2-Cpd I with mCPBA was carried out using a rapid-mixing stopped-flow technique. General procedure: the solutions of 2-Cl or 2-TFA (80 μM) and mCPBA (800 μM) were placed in sample holders of the mixer of the stopped-flow system. After setting the samples, the temperature of the mixer was set at 20 °C. After stabilization of the temperature, the sample solutions of 2-Cl or 2-TFA and mCPBA were rapidly mixed. The final concentration of the iron porphyrin complex after the mixing is 40 μM. The reactions were monitored by the absorption spectral change at constant time intervals. The reaction rate constants were determined by simulation of the time course of the absorbance of the peaks around 665 nm with the commercial program Igor 7 (WaveMetrics, USA). The time courses of the absorbance did not follow the first-order kinetics.

Author contributions

Lulu Jiang: investigation; data curation; formal analysis. Yosuke Imanaka: investigation; data curation; formal analysis. Hiroshi Fujii: conceptualization; visualization; funding acquisition; project administration; writing-original draft; writing-review and editing.

Conflicts of interest

“There are no conflicts to declare”.

Acknowledgements

This work was supported by grants from JSPS (Grant 22H02096) and CREST from JST.

References

1. T. L. Poulos, Chem. Rev., 2014, 114, 3919–3962.
2. M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841–2888.
3. P. R. O. D. Montellano, Chem. Rev., 2010, 110, 932–948.
4. H. Fujii, in Heme Peroxidases, ed. E. Raven and B. Dunford, The Royal Society of Chemistry, London, 2016, pp. 183–217.
5. I. G. Denisov, T. M. Makris, S. G. Sligar and I. Schlichting, Chem. Rev., 2005, 105, 2253–2277.
6. F. P. Guengerich, Chem. Res. Toxicol., 2001, 14, 611–650.
7. J. Rittle and M. T. Green, Science, 2010, 330, 933–937.
8. H. Fujii, Coord. Chem. Rev., 2002, 226, 51–60.
9. J. T. Groves and G. A. McClusky, J. Am. Chem. Soc., 1976, 98, 859–861.
10. F. Bruhlmann, L. Fourage, C. Ullmann, O. P. Haefliger, N. Jeckelmann, C. Dubois and D. Wahler, J. Biotechnol., 2014, 184, 17–26.
11. J. T. Groves, T. E. Nemo and R. S. Myers, J. Am. Chem. Soc., 1979, 101, 1032–1033.
12. J. T. Groves and T. E. Nemo, J. Am. Chem. Soc., 1983, 105, 5786–5791.
13. T. G. Taylor and F. Xu, J. Am. Chem. Soc., 1988, 110, 1953–1958.
14. J. P. Collman, T. Kodadek and J. I. Brauman, J. Am. Chem. Soc., 1986, 108, 2588–2594.
15. R. A. Baglia, J. P. T. Zaragoza and D. P. Goldberg, Chem. Rev., 2017, 117, 13320–13352.
16. W. Liu and J. T. Groves, Acc. Chem. Res., 2015, 48, 1727–1735.
17. C. Wang, K. V. Shalyaev, M. Bonchio, T. Carofiglio and J. T. Groves, Inorg. Chem., 2006, 45, 4769–4782.
18. C.-J. Liu, W.-Y. Yu, S.-M. Peng, T. C. W. Mak and C.-M. Che, J. Chem. Soc., Dalton Trans., 1988, 1805–1812.
19. J. T. Groves and W. J. Kruper, J. Am. Chem. Soc., 1979, 101, 7613–7615.
20. J. T. Groves, R. C. Haushalter, M. Nakamura, T. E. Nemo and B. J. Evans, J. Am. Chem. Soc., 1981, 103, 2884–2886.
21. P. Battioni, J. P. Renaud, J. F. Bartoli, M. Reina-Artiles, M. Fort and D. Mansuy, J. Am. Chem. Soc., 1988, 110, 8462–8470.
22. A. R. Sandro Campestrini and B. Meunier, J. Org. Chem., 1991, 56, 3725–3727.
23. A. Sorokin, A. Robert and B. Meunier, J. Am. Chem. Soc., 1993, 115, 7293–7299.
24. E. V. Kudrik, P. Afanasiev, L. X. Alvarez, P. Dubourdeaux, M. Clémancey, J.-M. Latour, G. Blondin, D. Bouchu, F. Albrieux, S. E. Nefedov and A. B. Sorokin, Nat. Chem., 2012, 4, 1024–1029.
25. J. T. Groves and D. V. Subramanian, J. Am. Chem. Soc., 1984, 106, 2177–2181.
26. P. S. Traylor, D. Dolphin and T. G. Traylor, J. Chem. Soc., Chem. Commun., 1984, 279–280.
27. H. Fujii, Chem. Lett., 1994, 1491–1494.
28. H. Fujii, J. Am. Chem. Soc., 1993, 115, 4641–4648.
29. Y. Ishimizu, Z. Ma, M. Hada and H. Fujii, J. Biol. Inorg. Chem., 2019, 24, 483–494.
30. S. Yokota and H. Fujii, J. Am. Chem. Soc., 2018, 140, 5127–5137.
31. H. Fujii, T. Yoshimura and H. Kamada, Inorg. Chem., 1996, 35, 2373–2377.
32. C. M. Che, J. L. Zhang, R. Zhang, J. S. Huang, T. S. Lai, W. M. Tsui, X. G. Zhou, Z. Y. Zhou, N. Zhu and C. K. Chang, Chem. – Eur. J., 2005, 11, 7040–7053.
33. E. Porhiel, A. Bondon and J. Leroy, Eur. J. Inorg. Chem., 2000, 1097–1105.
34. H. Fujii and K. Ichikawa, Inorg. Chem., 2002, 31, 1110–1112.
35. A. Wolberg and J. Manassen, J. Am. Chem. Soc., 1970, 92, 2982–2991.
36. A. Takahashi, T. Kurahashi and H. Fujii, Inorg. Chem., 2011, 50, 6922–6928.
37. S. Yokota, Y. Suzuki, S. Yanagisawa, T. Ogura, S. Nozawa, M. Hada and H. Fujii, ACS Catal., 2022, 12, 10857–10871.
38. A. Takahashi, D. Yamaki, K. Ikemura, T. Kurahashi, T. Ogura, M. Hada and H. Fujii, Inorg. Chem., 2012, 51, 7296–7305.
39. Z. Cong, T. Kurahashi and H. Fujii, Angew. Chem., Int. Ed., 2011, 50, 9935–9939.
40. M. Asaka and H. Fujii, J. Am. Chem. Soc., 2016, 138, 8048–8051.
41. Y. Ishimizu, Z. Ma, M. Hada and H. Fujii, Inorg. Chem., 2021, 60, 17687–17698.
42. J. T. Groves and Y. Watanabe, J. Am. Chem. Soc., 1986, 108, 7834–7836.
43. Y. Ishimizu, Z. Ma, M. Hada and H. Fujii, Inorg. Chem., 2021, 60, 17687–17698.
44. M. Asaka and H. Fujii, J. Am. Chem. Soc., 2016, 138, 8048–8051.
45. E. K. Woller, V. V. Smirnov and S. G. DiMagno, J. Org. Chem., 1998, 63, 5706–5707.
46. J. S. Lindsey, Acc. Chem. Res., 2010, 43, 300–311.
47. E. W. H. Ogoshi, Z. Yoshida, J. Kincaid and K. Nakamoto, J. Am. Chem. Soc., 1973, 95, 2845–2849.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy00758h

---