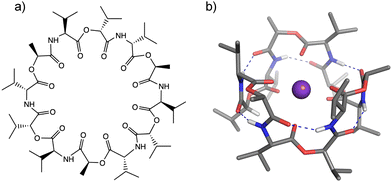
Cation-responsive cavity expansion of valinomycin revealed by cryogenic ion trap infrared spectroscopy†
Keisuke
Hirata
 ab,
Eiko
Sato
ac,
James M.
Lisy
ab,
Eiko
Sato
ac,
James M.
Lisy
 *de,
Shun-Ichi
Ishiuchi
*de,
Shun-Ichi
Ishiuchi
 *ab and
Masaaki
Fujii
*ab and
Masaaki
Fujii
 *abd
*abd
aLaboratory for Chemistry and Life Science, Institute of Innovative Research, Tokyo Institute of Technology, 4259 Nagatsuta-cho, Midori-ku, Yokohama, 226-8503, Japan. E-mail: ishiuchi.s.aa@m.titech.ac.jp; mfujii@res.titech.ac.j
bDepartment of Chemistry, School of Science, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo, 152-8550, Japan
cSchool of Life Science and Technology, Tokyo Institute of Technology, 4259 Nagatsuta-cho, Midori-ku, Yokohama, Kanagawa 226-8503, Japan
dInternational Research Frontiers Initiative (IRFI), Institute of Innovative Research, Tokyo Institute of Technology, 4259, Nagatsuta-cho, Midori-ku, Yokohama, 226-8503, Japan
eDepartment of Chemistry, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA. E-mail: j-lisy@illinois.edu
First published on 6th December 2022
Abstract
Valinomycin (VM) is a natural K+-selective ionophore that transports K+ through the cell membrane. VM captures K+ in its central cavity with a C3-symmetric β-turn-like backbone. Although the binding affinity is drastically decreased for the VM-sodium (Na+VM) complex with respect to K+VM, VM holds relatively high affinity to Rb+ and Cs+. The high affinity for larger ions irrespective of ionic size seems to conflict with the expected optimal size matching model and raises questions on what factors determine ion selectivity. A combination of infrared spectroscopy with supporting computational calculations reveals that VM can accommodate larger Rb+ and Cs+ by flexibly changing its cavity size with the elongation of its folded β-turn-like backbone. The high affinity to Rb+ and Cs+ can be ascribed to a size-dependent cavity expansion. These findings provide a new perspective on molecular recognition and selectivity beyond the conventional size matching model.
Introduction
Ionophores provide one mechanism for transporting ions in biological systems and in many cases with size-specificity. The transport of biologically active ions via the cell membrane disrupts the membrane potential, leading to cell apoptosis. This makes ionophores promising candidates as antimicrobial, antibacterial, anticancer, and antifungal agents.1–3 Valinomycin (VM) (Fig. 1) is a natural K+-selective ionophore (∼104 higher than Na+)4,5 consisting of six alternating ester and amide COs, and has displayed antibacterial6 and antiviral7 activities. The mechanism of the K+ selectivity has been extensively studied by numerous experimental methods.8–10 These studies all agree that when binding to a K+ ion, VM forms the C3-symmetric structure, called a “bracelet”, in which K+ has near octahedral coordination by six ester carbonyls (see Fig. 1b). The main chain is folded in a β-turn-like manner, in which six equivalent intramolecular hydrogen bonds are formed between the amide NH group in the i-th residue and the amide CO group in the (i + 3)-th residue. All the hydrophobic side chains point outwardly, suggesting that the structure is adopted inside hydrophobic lipid membranes when carrying an ion.The ion selectivity of ionophores has been traditionally described by the optimal size matching model.11,12 In this model, an ionophore strongly binds to a metal when the cavity size of the ionophore is a close match to the ionic size of the metal. A representative example is a well-known K+-selective ionophore, 18-crown-6 ether,11,13,14 though the ion selectivity mechanism of crown ether has not been perfectly clarified and some arguments have been raised in terms of microscopic solvation.15–17 This crown ether has specific bonding to K+ (Table S1, ESI†) and this is ascribed to an optimal cavity size, matching the ionic radius for K+, and thus allowing K+ to be secured inside the cavity.11,18 The larger ions Rb+ and Cs+ cannot fit inside and reside above the cavity, in contrast to the conformation of the K+(18-crown-6) complex.11,16,17 This suboptimal binding of Rb+ and Cs+ leads to 5–10 times lower binding affinity in comparison to K+.11,16,17 A notable characteristic of VM is relatively high affinity to Rb+ and Cs+, the equilibrium binding constant for these two ions closely brackets the value for K+, as shown in Table S1 (ESI†).4 Infrared (IR) and nuclear magnetic resonance spectroscopy indicate similar values for vibrational frequencies, chemical shifts, and coupling constants among K+, Rb+, and Cs+, suggesting the same structural motif (bracelet structure) for these three ions.8,10 In this respect, the size matching model does not appear to work for VM because of the ionic size-independent affinity for larger alkali metal ions (ionic radius: K+ = 1.33 Å, Rb+ = 1.48 Å, Cs+ = 1.69 Å). It would be interesting to characterize the mechanism of ion capture by VM for different-sized metal ions, which appears to be at variance to the conventional understanding of ion selectivity.
Cryogenic ion trap IR spectroscopy19–26 is an essential tool in determining gas-phase molecular structures of ion–ionophore complexes. This technique employs a combination of electrospray mass spectrometry and laser spectroscopy. Mass spectrometry allows the isolation of a specific ion–ionophore target molecule and eliminates contaminants such as uncomplexed VM, complexes with other ions, or higher complexes (M+(VM)2, (M+)2(VM)3, ⋯ etc.). In solution-phase measurements, spectroscopic signatures of the target molecule are often perturbed by solvent molecules or contaminated by the above-mentioned undesired molecules. Cryogenic ion trap IR spectroscopy enables clear-cut spectroscopic assignments by eliminating such interference from solvents and contaminants. In fact, the gas-phase conformation of VM-potassium (hereafter denoted K+VM) has been unambiguously assigned to the “bracelet” structure by cryogenic ion trap IR spectroscopy,27 which resembles the crystal structure of K+VM and the conformation in polar solvents. In the present study, this approach is applied to the other alkali metal ions to understand the mechanism of efficient capture of large ions (Rb+ and Cs+) by VM.
Experimental and theoretical methods
IR photodissociation (IRPD) spectra of M+VM were measured in a cryogenic ion trap setup (Fig. S1, ESI†).26,27 In short, methanol solutions of VM (Wako, 10−5 M) and the desired alkali metal chloride (Wako, 2 × 10−5 M) were electrosprayed via a glass capillary heated to 60 °C (where the solvent is driven off), and the ion–neutral complexes were allowed to enter the vacuum apparatus. The specific ions of interest were mass-selected by a quadrupole mass spectrometer, deflected by a quadrupole bender, and then guided into a cryogenic quadrupole ion trap (QIT). The QIT was cooled to 4 K by a closed cycle He refrigerator. A mixture of hydrogen (20%) and helium buffer gas was introduced to the QIT via a pulsed nozzle and cooled down by collisions with the QIT's gold-coated copper electrodes. The complex ions were trapped and cooled to ∼10 K by collisions with helium gas. Hydrogen molecules were condensed onto the cold ions, forming a variety of weakly-bound hydrogen-attached cluster ions. The cluster ions were then irradiated with a tunable IR laser. Absorption of a photon triggers the dissociation of the weakly-bound hydrogen molecules from the cluster ions, yielding the parent M+VM complex ion as a photofragment. The IRPD spectrum of the trapped ions, which is negligibly affected by the attached hydrogen, was measured by monitoring the fragment yield, recorded by a time-of-flight mass spectrometer as a function of the wavenumber of the IR laser, thus providing the IR absorption spectrum of the M+VM complex.Calculated vibrational frequencies presented in this study were obtained from density functional theory (DFT) calculations using the dispersion-corrected B3LYP-D3BJ functional and the lanl2dz (Rb, Cs)/6-31G(d,p) (C, N, O, H) basis sets.27 The DFT calculations were performed using the Gaussian 16 package.28 Initial structures were prepared, based on the geometry data of the crystal structures of K+VM (bracelet-type conformation9) and bare VM (twisted bracelet- and propeller-type conformations29,30), and are shown in Fig. S2 (ESI†). All the optimized structures were confirmed to be local minima with no imaginary vibrational frequencies. All of the calculated frequencies have been corrected for anharmonicity with a scaling factor of 0.961, identical to the previous report on the K+VM complex.27 This value was a good compromise between the fingerprint region (slightly underestimated) and the NH stretch regions (slightly overestimated) in K+VM.27 The calculated IR spectra were convoluted with a Lorentz lineshape function with a half width of 3 cm−1. The binding energy (EBE) between metal and VM was calculated at the B3LYP-D3BJ/def2-SVP level using eqn (1).
| EBE = (GM + GVM) − (GMVM + BSSE) | (1) |
The BSSE value corresponds to the correction term of basis set superposition error (BSSE). This value was calculated by the counterpoise method. GM, GVM, and GMVM represent Gibbs free energy for a metal ion, VM, and the complex of the metal and VM at 298 K, respectively.
Results and discussion
Fig. 2 and Fig. S3 (ESI†) display IRPD spectra of bare VM-alkali metal ion complexes. The observed bands were assigned based on previous studies27 of K+VM and its monohydrated complexes: NH bends at 1520–1560 cm−1, amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches (amide I) at 1630–1690 cm−1, ester C
O stretches (amide I) at 1630–1690 cm−1, ester C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches at 1700–1780 cm−1, CH stretches at 2800–3100 cm−1, and amide NH stretches (amide A) at 3200–3400 cm−1 (frequencies are given in Table S2, ESI†). The spectral features in the Li+VM complex are clearly distinct from the other four complexes and are discussed below. The spectral features in the IRPD spectra of Na+VM, Rb+VM and Cs+VM are very similar to that of K+VM (see Fig. S3 in ESI†). Specifically, the NH stretches and ester C
O stretches at 1700–1780 cm−1, CH stretches at 2800–3100 cm−1, and amide NH stretches (amide A) at 3200–3400 cm−1 (frequencies are given in Table S2, ESI†). The spectral features in the Li+VM complex are clearly distinct from the other four complexes and are discussed below. The spectral features in the IRPD spectra of Na+VM, Rb+VM and Cs+VM are very similar to that of K+VM (see Fig. S3 in ESI†). Specifically, the NH stretches and ester C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches appear as a single peak and the amide C
O stretches appear as a single peak and the amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bands have a main peak and a shoulder. This is in light of the presence of six NH/amide CO/ester CO bonds for each complex. This strongly suggests that M+VM (M+ = Na+, Rb+, Cs+) has a similar molecular structure to K+VM, in which VM forms a C3 symmetric bracelet structure with intramolecular H-bonds. To confirm this, we performed structural optimizations and harmonic frequency calculations for M+VM at the B3LYP-D3BJ/6-31G(d,p) level. The computation level was of sufficient accuracy to reproduce the experimental results in the IRPD spectrum of K+VM.27 For the larger ions such as Rb+ and Cs+, all the initial structures converged to the same bracelet structure as K+VM (Fig. 2). The features of the single band for NH stretch, ester CO stretch, amide CO stretches (peak and shoulder) and NH bend are well reproduced by the calculated IR spectrum of the bracelet conformer (Fig. 2). The reason why only the amide CO stretches are split into two bands is discussed later. For the smaller Na+, the C3-symmetric bracelet-type conformer (Conf. A) was energetically most stable at 298 K, while a few metastable conformers (Conf. B–D) were obtained (Fig. 3). Conf. B resembles Conf. A, but one of the distances between Na+ and ester (C
O bands have a main peak and a shoulder. This is in light of the presence of six NH/amide CO/ester CO bonds for each complex. This strongly suggests that M+VM (M+ = Na+, Rb+, Cs+) has a similar molecular structure to K+VM, in which VM forms a C3 symmetric bracelet structure with intramolecular H-bonds. To confirm this, we performed structural optimizations and harmonic frequency calculations for M+VM at the B3LYP-D3BJ/6-31G(d,p) level. The computation level was of sufficient accuracy to reproduce the experimental results in the IRPD spectrum of K+VM.27 For the larger ions such as Rb+ and Cs+, all the initial structures converged to the same bracelet structure as K+VM (Fig. 2). The features of the single band for NH stretch, ester CO stretch, amide CO stretches (peak and shoulder) and NH bend are well reproduced by the calculated IR spectrum of the bracelet conformer (Fig. 2). The reason why only the amide CO stretches are split into two bands is discussed later. For the smaller Na+, the C3-symmetric bracelet-type conformer (Conf. A) was energetically most stable at 298 K, while a few metastable conformers (Conf. B–D) were obtained (Fig. 3). Conf. B resembles Conf. A, but one of the distances between Na+ and ester (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) is elongated by ∼0.3 Å (Table S3, ESI†) and the C3-symmetry is slightly broken. The simplicities of the NH and CO bands of Conf. A are in good agreement with the experimental ones. Conf. B has a splitting of the NH stretch bands, which is inconsistent with the experimental IRPD spectrum. The other two conformers Conf. C and D also give several bands of the NH stretches, CO stretches and NH bends, deviating from the obtained IRPD spectrum. The relatively high free energies (>30 kJ mol−1) of Conf. C and D make their presence in the cluster ion ensemble unlikely. In the previous ion mobility measurements on Na+VM,31 the gas-phase conformation was ascribed not to the C3-symmetric bracelet structure (like Conf. A) but to an asymmetric one with five coordination of the ester CO to Na+, structurally similar to Conf. B. However, the collision cross sections for the symmetric and asymmetric conformers were the same, and the structural assignment to the asymmetric conformer was based on the conformational sampling using molecular dynamics simulations with a classical force field. This apparent inconsistency with our findings could arise from the use of the classical force field. In this study, the gas-phase conformation of Na+VM can be unambiguously assigned to Conf. A from the vibrational signature in the IRPD spectrum. In conclusion, VM can adopt the symmetrical “bracelet” structure regardless of ionic size from Na+ (0.95 Å) to Cs+ (1.69 Å).
O) is elongated by ∼0.3 Å (Table S3, ESI†) and the C3-symmetry is slightly broken. The simplicities of the NH and CO bands of Conf. A are in good agreement with the experimental ones. Conf. B has a splitting of the NH stretch bands, which is inconsistent with the experimental IRPD spectrum. The other two conformers Conf. C and D also give several bands of the NH stretches, CO stretches and NH bends, deviating from the obtained IRPD spectrum. The relatively high free energies (>30 kJ mol−1) of Conf. C and D make their presence in the cluster ion ensemble unlikely. In the previous ion mobility measurements on Na+VM,31 the gas-phase conformation was ascribed not to the C3-symmetric bracelet structure (like Conf. A) but to an asymmetric one with five coordination of the ester CO to Na+, structurally similar to Conf. B. However, the collision cross sections for the symmetric and asymmetric conformers were the same, and the structural assignment to the asymmetric conformer was based on the conformational sampling using molecular dynamics simulations with a classical force field. This apparent inconsistency with our findings could arise from the use of the classical force field. In this study, the gas-phase conformation of Na+VM can be unambiguously assigned to Conf. A from the vibrational signature in the IRPD spectrum. In conclusion, VM can adopt the symmetrical “bracelet” structure regardless of ionic size from Na+ (0.95 Å) to Cs+ (1.69 Å).
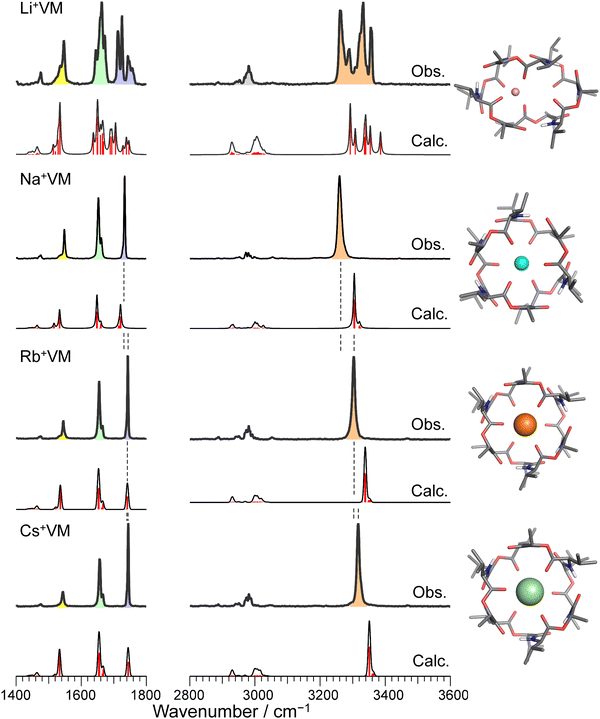 | ||
| Fig. 2 IRPD spectra of Li+, Na+, Rb+, and Cs+VM complexes. The calculated IR spectrum of the most stable conformer at 298 K is shown with its molecular structure for each IRPD spectrum. The black solid curves in the calculated spectra are made by convolution of stick red lines. Color codes: gray = C, blue = N, red = O, white = H, pink = Li, cyan = Na, orange = Rb, light green = Cs. The IRPD spectrum of K+ complex is shown in Fig. S3 in ESI.† | ||
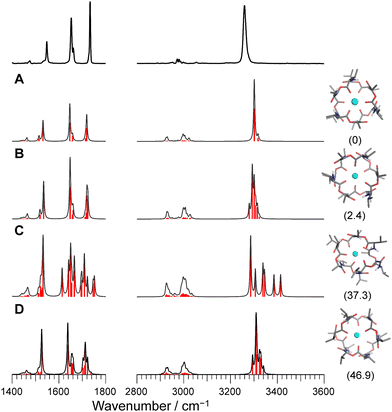 | ||
| Fig. 3 Calculated IR spectra of conformers A–D for Na+VM with the experimental IRPD spectrum. Parentheses indicate the relative Gibbs free energy for each conformer at 298 K. | ||
A close look at the IRPD spectra reveals significant blueshifts in the NH stretches with increasing ionic size. Because the NH stretches involve the intramolecular H-bonds in the bracelet structure, the blueshift indicates a weakening of the H-bonds between amide COs and NHs, as the ionic radius increases. Another important finding is that ester CO stretches display a similar blue-shift. Because ester COs directly coordinate with the alkali metal ion, the blueshift strongly suggests weaker binding to larger ions. In fact, the calculated binding energy between VM and the metal ion also decreases for larger ions (Table S4, ESI†). The observed blueshifts in the NH stretch and ester CO stretch are well reproduced by the calculated IR spectra. In the calculated bracelet-type structures, both the distances of the ester metal–O(C) and H-bonding distances of amide (N)H–O(C) are elongated with increasing ionic radius (Tables S3 and S4, ESI†). These results indicate that the cavity of valinomycin is expanded with the accommodation of larger ions. In other words, VM possesses some degrees of flexibility to bind ions with a wide range of size, due to its β-turn-like folded structure constructed by non-covalent H-bonds (Fig. 1).
The complete structural assignment has led us to consider the reason for the split bands of amide CO stretches despite the single bands of amide NH and ester CO stretches. The vibrational modes of these stretches are coupled (Fig. S4–S7, ESI†). We take the example of K+VM because the others have the same vibrational modes. The amide NHs are almost aligned on a plane and can be classified as D6h symmetry (Fig. S4, ESI†). The six vibrational modes of amide NH stretches are assigned to IR-inactive a1g, e2g, and b1u and IR-active e1u modes, which is consistent with the observed single band of amide NH stretches (Fig. S5, ESI†). This is in parallel with the fact that only v20 with e1u symmetry is the IR-active CH stretch in benzene.32 On the other hand, the amide COs no longer reside on a plane and its symmetry is degraded to D3d (Fig. S4, ESI†). The vibrational modes of amide COs are assigned to IR-active eu, a2u and IR-inactive eg, a1g modes, which well accounts for the split bands of amide CO stretches (Fig. S6, ESI†). The symmetry in the configuration of the ester COs can be grouped to D3d as well (Fig. S4, ESI†) and the vibrational modes are assigned to IR-active (eu, a2u) and IR-inactive (eg, a1g) modes (Fig. S7, ESI†). Different from the amide CO stretches, the IR-active eu modes of ester CO stretches are much more intense than the a2u mode, which is the plausible reason for the single band of ester COs. The IR intensities depend on the magnitude of the vibrational transition dipole moment (VTM), which is due to the displacement of vibrating C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O as well as the polarization of C
O as well as the polarization of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O caused by the electric field (E) by a charged alkali metal ion. The latter effect becomes prominent when VTM is parallel to E, as evident in the OH stretches of Cs+(H2O)1.33 The VTMs in the eu modes are closely parallel to E generated by K+ (Fig. S7, ESI†), which well accounts for the enhancement of the eu modes.
O caused by the electric field (E) by a charged alkali metal ion. The latter effect becomes prominent when VTM is parallel to E, as evident in the OH stretches of Cs+(H2O)1.33 The VTMs in the eu modes are closely parallel to E generated by K+ (Fig. S7, ESI†), which well accounts for the enhancement of the eu modes.
For the case of Li+VM, the amide NH and ester/amide CO bands split into several bands, indicating the breakdown of the C3 symmetry. The conformational search of Li+VM provided an energetically stable conformer A in which Li+ is coordinated by four ester COs, losing the C3 symmetry. Other conformers are obtained as metastable species though they have high energy gaps (>20 kJ mol−1) to the most stable Conf. A (Fig. 4 and Fig. S8, ESI†). The calculated IR spectra for the conformers with ΔG < 30 kJ mol−1 are shown in Fig. 4. The spectral pattern in the Li+VM matches closely to the calculated IR spectrum of Conf. A. The calculated IR spectra of the other conformers do not match as well; Conf. B does not match the split of amide CO stretches; Conf. C does not match the intensity pattern of the NH stretches; the NH stretches in Conf. D are considerably blue-shifted compared to the experimental spectrum. The conformation of the gas-phase Li+VM is thus ascribed to Conf. A. The fact that Li+VM does not adopt the C3-symmetric bracelet structure, but a distorted structure (Conf. A), is consistent with the low affinity of VM to Li+ (Table S1, ESI†).
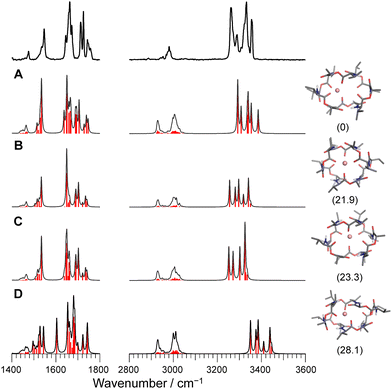 | ||
| Fig. 4 Calculated IR spectra of conformers A–D for Li+VM with the experimental IRPD spectrum. Parentheses indicate the relative Gibbs free energy for each conformer at 298 K. | ||
Conclusion
In summary, we have measured IRPD spectra of M+VM (M = Li, Na, Rb, Cs) and found that VM can capture Na+, Rb+, and Cs+ with the six ester COs forming the C3-symmetric “bracelet” structure. This symmetric structure was also observed in K+VM.27 The ability to capture different-sized metals with the same structural motif relies on the structural flexibility of VM. VM forms an intramolecular H-bond within its folded β-turn-like backbone. This affords flexibility to VM and enables VM to have the same bracelet motif regardless of ionic size (Na+–Cs+). This bracelet structure is the same as the proposed structure of the Rb+VM and Cs+VM complexes in polar solvents.8,10 The conformational resemblance suggests minimal perturbations to the conformations of Rb+VM and Cs+VM gas-phase structures when placed in the solvent environment. The relatively high affinity of VM to Rb+ and Cs+ in polar solvents can be explained by the cation-size dependent cavity expansion of VM. On the other hand, the proposed conformation for Na+VM in polar solvents indicates less than six-fold coordination to Na+,10 deviating from the gas-phase structure. This strongly suggests that the low affinity of VM to Na+ (Table S1, ESI†) arises from the solvation effect on the conformation of Na+VM. This will be addressed in the near future by the structural analysis for the solvated clusters of Na+VM, which will be performed by incorporating a second ion trap for the generation of solvated clusters.27,34 For the smallest Li+, VM no longer holds C3 symmetry with less than six-fold coordination of the ester COs. This also explains the low affinity between VM and Li+. Conventionally, the selectivity in molecular recognition has been described by optimal size matching, in which a guest molecule strongly binds to a host molecule when the size of the guest pairs with the size of the host. In contrast, VM can flexibly change its cavity size to fit to the various sizes of metal ions. These findings shed new light on the molecular recognition in host–guest chemistry and demonstrate the potential of cryogenic ion trap IR spectroscopy to clarify unique properties of molecular recognition in host–guest supramolecules.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported in part by KAKENHI (JP19K23624, JP20K20446, JP20H00372, JP21H04674, and JP21K14585), the Core-to-Core program (JPJSCCA20210004) from Japan Society for the Promotion of Science, a research grant from World Research Hub Initiative (WRHI) of Tokyo Institute of Technology, the Cooperative Research Program of the “Network Joint Research Center for Materials and Devices” from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, and the RIKEN Pioneering Project, “Fundamental Principles Underlying the Hierarchy of Matter: A Comprehensive Experimental Study”. The computations were performed at the Research Center for Computational Science, Okazaki, Japan (21-IMS-C109, 22-IMS-C110).References
- B. C. Pressman, Annu. Rev. Biochem., 1976, 45, 501–530 CrossRef CAS PubMed.
- V. Kaushik, J. S. Yakisich, A. Kumar, N. Azad and A. K. V. Iyer, Cancers, 2018, 10, 360 CrossRef CAS PubMed.
- Q. Wu, J. Patocka and K. Kuca, Mini-Rev. Med. Chem., 2019, 19, 206–214 CrossRef CAS PubMed.
- R. M. Izatt, J. S. Bradshaw, S. A. Nielsen, J. D. Lamb, J. J. Christensen and D. Sen, Chem. Rev., 1985, 85, 271–339 CrossRef CAS.
- A. Casnati, A. Pochini, R. Ungaro, C. Bocchi, F. Ugozzoli, R. J. M. Egberink, H. Struijk, R. Lugtenberg, F. De Jong and D. N. Reinhoudt, Chem. – Eur. J., 1996, 2, 436–445 CrossRef CAS.
- S. Huang, Y. Liu, W. Q. Liu, P. Neubauer and J. Li, Microorganisms, 2021, 9, 780 CrossRef CAS PubMed.
- D. Zhang, Z. Ma, H. Chen, Y. Lu and X. Chen, Biomed. J., 2020, 43, 414–423 CrossRef.
- D. J. Patel, Biochemistry, 1973, 12, 496–501 CrossRef CAS.
- K. Neupert-Laves and M. Dobler, Helv. Chim. Acta, 1975, 58, 432–442 CrossRef CAS PubMed.
- F. Wang, C. Zhao and P. L. Polavarapu, Biopolymers, 2004, 75, 85–93 CrossRef CAS PubMed.
- C. J. Pedersen and H. K. Frensdorff, Angew. Chem., Int. Ed. Engl., 1972, 11, 16–25 CrossRef CAS PubMed.
- S. Varma, D. Sabo and S. B. Rempe, J. Mol. Biol., 2008, 376, 13–22 CrossRef CAS PubMed.
- C. J. Pedersen, J. Am. Chem. Soc., 1967, 89, 2495–2496 CrossRef CAS.
- C. J. Pedersen, J. Am. Chem. Soc., 1967, 89, 7017–7036 CrossRef CAS.
- J. D. Rodriguez, T. D. Vaden and J. M. Lisy, J. Am. Chem. Soc., 2009, 131, 17277–17285 CrossRef CAS.
- J. D. Rodriguez and J. M. Lisy, J. Am. Chem. Soc., 2011, 133, 11136–11146 CrossRef CAS PubMed.
- Y. Inokuchi, T. Ebata, T. R. Rizzo and O. V. Boyarkin, J. Am. Chem. Soc., 2014, 136, 1815–1824 CrossRef CAS PubMed.
- R. M. Izatt, R. E. Terry, D. P. Nelson, Y. Chan, D. J. Eatough, J. S. Bradshaw, L. D. Hansen and J. J. Christensen, J. Am. Chem. Soc., 1976, 98, 7626–7630 CrossRef CAS.
- O. V. Boyarkin, S. R. Mercier, A. Kamariotis and T. R. Rizzo, J. Am. Chem. Soc., 2006, 128, 2816–2817 CrossRef CAS PubMed.
- N. S. Nagornova, T. R. Rizzo and O. V. Boyarkin, Science, 2012, 336, 320–323 CrossRef CAS PubMed.
- E. Garand, M. Z. Kamrath, P. A. Jordan, A. B. Wolk, C. M. Leavitt, A. B. McCoy, S. J. Miller and M. A. Johnson, Science, 2012, 335, 694–698 CrossRef CAS.
- J. Jašík, J. Žabka, J. Roithová and D. Gerlich, Int. J. Mass Spectrom., 2013, 354–355, 204–210 CrossRef.
- J. G. Redwine, Z. A. Davis, N. L. Burke, R. A. Oglesbee, S. A. McLuckey and T. S. Zwier, Int. J. Mass Spectrom., 2013, 348, 9–14 CrossRef CAS.
- M. Broquier, S. Soorkia and G. Grégoire, Phys. Chem. Chem. Phys., 2015, 17, 25854–25862 RSC.
- Y. Inokuchi, K. Soga, K. Hirai, M. Kida, F. Morishima and T. Ebata, J. Phys. Chem. A, 2015, 119, 8512–8518 CrossRef CAS PubMed.
- S. Ishiuchi, H. Wako, D. Kato and M. Fujii, J. Mol. Spectrosc., 2017, 332, 45–51 CrossRef CAS.
- E. Sato, K. Hirata, J. M. Lisy, S. Ishiuchi and M. Fujii, J. Phys. Chem. Lett., 2021, 12, 1754–1758 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16, Gaussian, Inc.; Wallingford, CT, 2016 Search PubMed.
- I. L. Karle, J. Am. Chem. Soc., 1975, 97, 4379–4386 CrossRef CAS.
- I. L. Karle and J. L. Flippen-Anderson, J. Am. Chem. Soc., 1988, 110, 3253–3257 CrossRef CAS.
- T. Wyttenbach, J. J. Batka, J. Gidden and M. T. Bowers, Int. J. Mass Spectrom., 1999, 193, 143–152 CrossRef CAS.
- R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 5362–5376 CrossRef CAS.
- J. M. Lisy, Int. Rev. Phys. Chem., 1997, 16, 267–289 Search PubMed.
- B. M. Marsh, J. M. Voss and E. Garand, J. Chem. Phys., 2015, 143, 204201 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04570b |
| This journal is © the Owner Societies 2023 |