Selective adsorption of sulphur dioxide and hydrogen sulphide by metal–organic frameworks†
S.
Grubišić
 *a,
R.
Dahmani‡
*a,
R.
Dahmani‡
 bc,
I.
Djordjević
bc,
I.
Djordjević
 a,
M.
Sentić
a,
M.
Sentić
 a and
M.
Hochlaf
a and
M.
Hochlaf
 *b
*b
aUniversity of Belgrade, Institute of Chemistry, Technology and Metallurgy, National Institute of Republic of Serbia, Njegoševa 12, Belgrade, 11000, Serbia. E-mail: sonja.grubisic@ihtm.bg.ac.rs
bUniversité Gustave Eiffel, COSYS/IMSE, 5 Bd Descartes 77454, Champs sur Marne, France. E-mail: majdi.hochlaf@univ-eiffel.fr
cUniversity of Tunis El Manar, Department of Chemistry, Laboratory of Characterizations, Applications and Modeling of Materials (LCAMM), LR18ES08, Tunis, Tunisia
First published on 23rd November 2022
Abstract
The removal of highly toxic gasses such as SO2 and H2S is important in various industrial and environmental applications. Metal organic frameworks (MOFs) are promising candidates for the capture of toxic gases owing to their favorable properties such as high selectivity, moisture stability, thermostability, acid gas resistance, high sorption capacity, and low-cost regenerability. In this study, we perform first principles density functional theory (DFT) and grand-canonical Monte Carlo (GCMC) simulations to investigate the capture of highly toxic gases, SO2 and H2S, by the recently designed ZTF and MAF-66 MOFs. Our results indicate that ZTF and MAF-66 show good adsorption performances for SO2 and H2S capture. The nature of the interactions between H2S or SO2 and the pore surface cavities was examined at the microscopic level. SO2 is adsorbed on the pore surface through two types of hydrogen bonds, either between O of SO2 with the closest H of the triazole 5-membred ring or between O of SO2 with the hydrogen of the amino group. For H2S inside the pores, the principal interactions between H2S and surface pores are due to a relatively strong hydrogen bonds established between the nitrogens of the organic part of MOFs and H2S. Also, we found that these interactions depend on the orientation of SO2/H2S inside the pores. Moreover, we have studied the influence of the presence of water and CO2 on H2S and SO2 capture by the ZTF MOF. The present GCMC simulations reveal that the addition of H2O molecules at low pressure leads to an enhancement of the H2S adsorption, in agreement with experimental findings. However, the presence of water molecules decreases the adsorption of SO2 irrespective of the pressure used. Besides, SO2 adsorption is increased in the presence of a small number of CO2 molecules, whereas the presence of carbon dioxide in ZTF pores has an unfavorable effect on the capture of H2S.
I. Introduction
Sulphur is an essential element of living systems, and the sulphur cycle plays a prominent role in environmental and climate changes. Sulphur bearing acid gases such as hydrogen sulphide (H2S) and sulphur dioxide (SO2) are naturally released into the environment through volcanic eruptions, hot springs, gas streams, breakdown of organic matter, and anaerobic bacterial reduction.1,2 The anthropogenic sources significantly increase their atmospheric concentrations,1,2 which have a major impact on the natural sulphur cycle.3,4 Both gases are highly toxic to humans and the environment. Indeed, they have a detrimental effect on human and animal health and represent precursors for acid rains, causing an increase in soil acidity and the availability of heavy metals.5,6 Also, recent studies revealed that high concentrations of SO2 and NOx strongly contribute to the PM2,5 particle formation.7 In fact, CO, CO2, O3, SOx, H2S, NOx, NH3 and fine particle matter (PM10 and PM2.5) are pollutants and among the major environmental threats to human health. Prevention and control of air pollution still represent the main challenges for modern society. At the same time, these pollutants cause climate change and negatively affect the natural biogeochemical cycles of many elements.7Realizing the gravity of the problems, researchers have developed several techniques to remove SO2 and H2S from gaseous emissions and mixtures. Previous studies have considered alkaline aqueous solutions and alkylamine solutions to capture sulphur gases.8,9 The more efficient procedures for capturing sulphur bearing gases included ozone injection10 and organic superbases of a tertiary amine.11 Some recent approaches successfully implemented liquid-based adsorbents for SO2 and H2S removal. Liquid-based adsorbers containing ammonium or imidazolium salts influence the conversion of SO2, higher than 95% at a relatively low working temperature of 40 °C and with good recycling.12,13 The need for using water or organic solvents in these procedures is a drawback due to increased liquid waste. Therefore, scientific attention has shifted towards dry adsorption procedures of removing sulphur gases with porous materials such as zeolites14–16 and metal–organic framework materials (MOFs).7,17,18 Besides, metal oxides,19–22 porous materials, activated carbons,23–25 and carbon nanotubes26 have shown efficient capture ability for acids and other gases. In particular, MOFs have been recognized as promising materials for gas capturing due to their cavity dimension, the diversity of their chemical composition, the possibility of ligand functionalization, and the relatively low-cost reactivation.27,28
In the literature, only a few theoretical and experimental studies on the H2S and SO2 removal by MOFs have been published.29–34 Most of them are recent. Indeed, experimental and computational efforts have been made recently to explore the use of MOFs35 or natural or synthetic zeolites36 for the effective removal of SO2 and H2S gases. For instance, Xu et al.31 conducted an experimental study on ZIF8 functionalized with aminoterazole ATZ (i.e., ZIF8-A), confirming that the introduction of amino groups enhances the SO2 adsorption capacity due to the formation of hydrogen bonds between SO2 and these amino groups. They also established a SO2 saturation capacity of 498 mg g−1 and 336 mg g−1 for ZIF8-A and ZIF8, respectively. Furthermore, the SO2 saturation capacity of ZIF8-A/n-heptanol (589 mg g−1) was 18.3% higher than that of ZIF8-A under the same experimental conditions. Very recently, Wang et al.32 reported a combined theoretical and experimental study of reversible SO2 adsorption by ZIF8 modified with 5-aminotetrazole (i.e., Zn(5-ATZ)1.5). They showed that the SO2 adsorption capacity of Zn(5-ATZ)1.5 at a concentration of 1.6% vol can reach 122 mg g−1 under optimal conditions. Within the Zn(5-ATZ)1.5 pores, SO2 interacts via hydrogen bonds between its oxygens and the amino hydrogen of the Zn(5-ATZ)1.5 or with the nitrogen of 5-amino tetrazole forming a non-covalent charge transfer complex. Moreover, theoretical study by Zhou et al.33 explored the selectivity and adsorption capacity of various zeolitic imidazolate frameworks towards H2S and SO2 gases. In particular, they showed that UiO-66, ZIF-71, ZIF-69, and ZIF-97 exhibit good performances for H2S separation from air, with selectivity and adsorption capacities higher than 300 mg g−1 and 0.01 mmol g−1 at room temperature and atmospheric pressure, respectively. Besides, Beheshti et al.34 synthesized a set of four new sulphur coordination polymers (e.g. [ZnCl2(Ls)2]n polymer where the ligands Ls = 1,1′-(pentane-1,5-diyl)bis(-3-methyl-1H-imidazole-2-thione)). They pointed out the high adsorption capacity of these polymers, which is due to the hydrogen bonding interactions between the H2S molecules and the neighboring flexible sulphur donor linker, chloride, thiocyanate, and uncoordinated perchlorate anions. Furthermore, Song et al.37 reported through computational study with grand canonical Monte Carlo (GCMC) simulation combined with DFT that SO2 interacts with MOF IRMOF10 (M = transition metal = Zn) first, through Zn atoms since they are more energetically favorable as adsorption sites, then through H bonds of organic unit i.e. C–H groups. As a general outcome, the studies confirmed that MOFs containing N-heterocycles improved SO2 adsorption and emphasized the importance of modulating the host–guest binding interaction between gases (H2S and SO2) and MOFs to achieve a reversible process.7 In sum, these previous works showed that zeolites, as adsorbents, interact with acid gases through chemosorption (covalent bonds), which generate an irreversible structure transformation, whereas MOFs interact with guest molecules through physical or weak chemical adsorption which requires a lower energy cost regeneration without transforming the adsorbent structure.35
Molecular simulation techniques have been proven to be more cost-efficient alternatives to experimental investigations of the influence of different factors such as the diameter and surface of the pores, pressure, temperature, and nature of the MOF–gases interactions. However, the capture of acidic gases such as H2S and SO2 by MOFs has been demonstrated to be a difficult and challenging task, mainly due to the formation of a strong and sometimes irreversible bond (e.g., a metal–sulphur bond in the case of H2S), causing structural degradation of MOFs.38,39 Consequently, the type of interaction between the host and guest plays a key role in order to achieve a good adsorption capacity with low cost regeneration of adsorbents. Accordingly, we need to regulate (or to adjust) the type of binding interaction through several types of adsorbents. Indeed, the determination of appropriate host–guest binding interactions between MOFs and H2S or SO2, such as non-covalent interactions, hydrogen bonds, or donor-acceptor bonds, is a decisive factor for successful reversible sulphur gas capture.
Recently, we have presented an in silico method to design a new MOF, named ZTF (for the zinc triazolate based framework), exhibiting good adsorption properties for CO2 capture.40 The newly designed ZTF MOF was generated by replacing the NH2 group of the triazolate ring of the MAF-66 MOF40 with a hydrogen atom. Our initial DFT investigations of the stable structures of the non-reactive and reactive clusters formed between Zn2+-triazole ([Zn2+-Tz]) and CO2 and/or H2O, where [Zn2+-Tz] is the subunits of triazolate based MOFs, showing the presence of covalent or weak interactions (hydrogen bonds, van der Waals type) between the [Zn2+-Tz] subunits and CO2 and/or H2O molecules.41,42 We have further studied the carbon dioxide and water adsorption in both ZTF and MAF-66 zinc triazolate based frameworks by using force field based GCMC simulations. GCMC simulations indicated that the ZTF MOF has a higher CO2 adsorption capacity than MAF-66 at high pressure under dry conditions, at 273 K. This sequestration is associated with the formation of several types of interactions such as electron acceptor–electron donor interactions between the carbon of CO2 and the nitrogen of triazole (Tz) of ZTF, π stacking interactions between CO2 and aromatic rings of Tz and hydrogen bonds. In addition, the results showed that strong hydrogen bonds between water molecules and N atoms of Tz rings are responsible for water adsorption in MAF-66 and ZTF structures. Furthermore, adsorption is favored by Lewis acid–Lewis base interactions, and hydrogen bonds, along with electrostatic interactions. The good performances of our MOF model (ZTF) for CO2 uptake inspired us to further investigate toxic or corrosive gases that must be removed from the atmosphere such as SO2 and H2S.
In the search for new alternatives for capturing SO2 and H2S pollutants, here we have investigated the adsorption of SO2 and H2S, with and without the presence of H2O/CO2 molecules by both MAF-66, a well-established high gas capture MOF, and ZTF MOF using the GCMC and first principles approaches. Through comparison of the ZTF and MAF-66, we target testing the adsorption properties of our recently proposed ZTF porous material to enhance the adsorption capacity of MOFs and to predict new alternatives of these materials for H2S and SO2 capture under dry and humid conditions. At the microscopic level, we found several binding sites between ZTF/MAF-66 and pollutant guest molecules through weak interactions (hydrogen bonds, van der Waals). In addition, metal–organic frameworks such as those considered in this work are a class of materials consisting of zinc metal ions that remain joined together through organic linkers, leading to the formation of three dimensional structures. Hence, their properties and applications are closely related to those of zinc cluster subunits themselves, and more generally, zinc metal clusters. In this way, our GCMC simulations were carried out using 3 × 3 × 3 supercell models including more than 200 Zn atoms inside.
II. Computational details
Our computations started with periodic density functional theory (DFT) calculations using the SIESTA43,44 software package, with the generalized gradient approximation (GGA) of the PBE functional.45 Double zeta polarized basis sets (DZP) and norm conserving pseudo potentials have been used for these computations.46 DFT calculations consist of optimizing the structures of MAF-66 and ZTF positions, together with H2S and SO2 molecules inside the pores. Real space integrals are performed on a mesh with a 200 Ry cut-off. Geometry optimizations were performed in such a way to allow full atomic and cell relaxation without geometrical constraints up to a force threshold of 0.05 eV Å−1. The Brillouin zone was sampled by the 4 × 4 × 4 Γ-centered Monkhorst–Pack k-point.Adsorption energies (ΔEads) for SO2 and H2S molecules are calculated using the following equations:
| ΔEads = EZc − (EMOF + EX) | (1) |
The interaction energy between the atoms was computed through Lennard–Jones (LJ) potentials. This LJ potential is a simple pair potential, representing the London dispersion forces that can accurately model weak van der Waals bonds and has the following form:
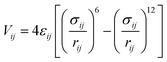 | (2) |
In this work, the standard combining rules of Lorentz–Berthelot were considered to estimate the cross terms of the LJ parameters. LJ parameters for all atoms of frameworks were taken from the DREIDING47 force field supplemented with zinc parameters from the Universal Force Field.48 These parameters are listed in Table 1 together with the partial charges, which are deduced from DFT calculations. The listed DFT partial atomic charges of ZTF and MAF-66 were validated in our previous work.40 For those of SO2 and H2S, we used a similar calculation scheme. Moreover, CO2, SO2 and H2S were modelled as three-site rigid molecules with charges on each site. Partial charges and LJ parameters for CO2, SO2 and H2S were taken from the TraPPE49–52 force field and are listed in Table 1 as well. The parameters used to model SO2 and H2S are able to reproduce the bulk phase properties of these species.51,52 They have been widely used to investigate adsorption in porous carbons, zeolites and MOFs.52,53 For the studies of the water adsorption in ZTF, the TIP3P54 model was selected for H2O molecules. Lorentz-Berthelot mixing rules were employed to calculate cross-LJ interactions.
Monte Carlo simulations were used to compute the single adsorption isotherms of SO2 and H2S in MAF-66 and ZTF. Besides, we have examined the adsorption of SO2 and H2S in the presence of H2O or CO2 molecules. All simulations were performed with the Monte Carlo55 suite of the RASPA code.56 A cut-off distance of 12 Å was used for LJ interactions. The Ewald sum technique was used to complete the electrostatic interactions. Simulations were performed using 3 × 3 × 3 supercells and included random insertion, abstraction and translation motions of molecules with equal probabilities. The simulations consisted of 3 × 105 equilibrations and 6 × 105 production cycles.
The void fraction of each MOF structure was determined in the GCMC simulations using spherical probes that were representative of He atoms. These GCMC simulations were carried out on PARADOX-IV supercomputing facility.
III. Results and discussion
A. Structural and adsorption energy calculations
First principles DFT calculations were used to optimize the structures of SO2 and H2S inside the pores of MAF-66 and ZTF MOFs and to evaluate the energetics associated with the adsorption of SO2 and H2S molecules at the surface of the pores of MAF-66 and ZTF frameworks. Optimized structures of MAF-66 and ZTF with SO2 and H2S molecules inside cavities are presented in Fig. 1. In the case of ZTF we performed calculations for 2 initial positions of SO2 and H2S. Optimized structures of ZTF with SO2 and H2S molecules inside cavities are shown in Fig. 2 and 3, respectively. We give in Table 2 the structural parameters of optimized MOFs (MAF-66 and ZTF) with H2S or SO2 inside the pores. The results are similar to those discussed in ref. 40 as well as the experimental geometrical parameters for the MAF-66 crystal structure given by Lin et al.57 The calculated volumes inside the MOFs available for adsorption are 1329 Å3 for MAF-66 and 1383 Å3 for ZTF. The computed pore sizes are 0.45 and 0.50 nm for MAF-66 and ZTF. The helium void fraction and the surface area were computed with RASPA and they are the same as those given in ref. 40. The structural parameters of these empty MOFs did not change upon insertion of H2S/SO2 gases inside their pores due to the formation of reversible non-bonded weak interactions between such guest molecules and the respective surface pores.| MOF | a | b | c | α | β | γ | Vol | SO2 | H2S | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔEads | Bond | Angle | ΔEads | Bond | Angle | ||||||||
| MAF-66 | 9.939 | 10.076 | 13.287 | 91.6 | 88.5 | 88.8 | 1329 | −11.41 | 1.485 | 118 | −11.56 | 1.361 | 91 |
| ZTF | 10.25 | 10.22 | 13.20 | 90.7 | 89.9 | 89.6 | 1383 | −7.48 | 1.548 | 113 | −13.50 | 1.485 | 95 |
| (10.25) | (10.23) | (13.21) | (90.7) | (89.9) | (89.6) | (−9.00) | (1.517) | (116) | (−7.41) | (1.388) | (90.4) | ||
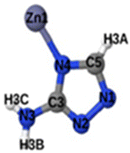
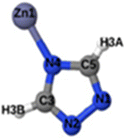
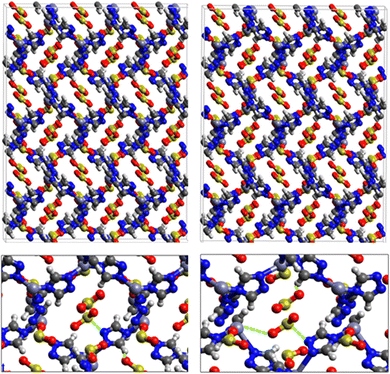
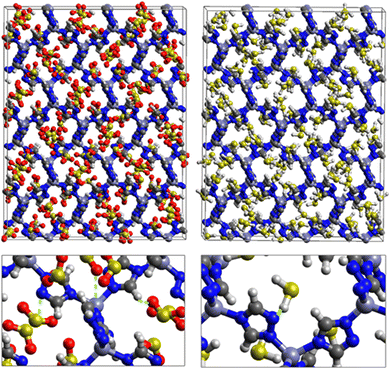
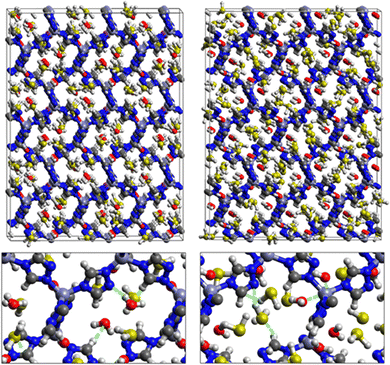
Fig. 1 shows that SO2 molecules are adsorbed in MAF-66 through H-bonds between O atom of SO2 and H atom of amino group (NH2), whereas inside ZTF the main interactions that contribute to the adsorption mechanism are between the positively charged S atom of SO2 and the uncoordinated N atom or between the O atom of SO2 and zinc of ZTF pore classified as electrostatic interactions (Fig. 2). For H2S inside MAF-66 and ZTF MOF pores, the present DFT calculations showed that the principal interactions between H2S and surface pores involves the nitrogens of this nanomaterial through a relatively strong hydrogen bonds (Fig. 1 and 3) and between sulfur of H2S bonded to H–C of Tz (Fig. 3).
We have calculated adsorption energies (ΔEads) of one SO2/H2S molecule inside MAF-66 or ZTF pores and for 2 different positions of sulfur gases inside MOFs using the procedures described above. Table 2 shows that the calculated adsorption energies of SO2 inside MAF-66 and ZTF are −11.41 and −7.48/−9.0 kcal mol−1, respectively. Adsorption energies of H2S inside MAF-66 and ZTF are slightly larger. Indeed, they amount to −11.56 and −13.50/−7.41 kcal mol−1. The binding energies are in the range of physical adsorption. When hydrogen sulfide is adsorbed only via hydrogen atom of H2S, the binding energy of this configuration is slightly lower than the configuration when sulfur atom of H2S is included in adsorption (Fig. 3). Similar mechanism of adsorption of H2S inside MAF-199 was already noticed.58 Therefore, both MAF-66 and ZTF nanoporous materials favor the adsorption of sulfur dioxide and hydrogen sulfide molecules, mainly due to the interactions between these guest molecules and the functional groups available at the surface of the corresponding pores. Besides, the adsorption of H2S is slightly stronger than that of SO2 because of the H-bonding interactions described above. They are indeed the main driving forces for the high adsorption capacities of ZTF and MAF-66. This is in line with our previous investigation of water inside a ZTF MOF, where we concluded that the H bonding interactions of water molecule guests with N atoms of ZTF dominate their adsorption properties and therefore enhance their performances, in particular at low pressures.40
B. GCMC simulations
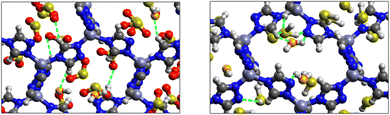
Fig. 5 shows the adsorption positions of SO2 and H2S molecules inside the pores of MAF-66 after GCMC computations, together with non-bonded interactions between adsorbed hosted molecules and pores. SO2 is adsorbed on the surface of the MAF-66 pore by two types of hydrogen bonds, either between one oxygen of SO2 with the closest hydrogen of the triazole 5-membred ring or between one oxygen of SO2 with the hydrogens of the amino group. These interactions depend on the orientation of SO2 inside the pore. In the case of H2S, GCMC simulations reveal that H2S interacts with MAF-66 mainly through hydrogen bonds between the nitrogens of the MOF organic subunit and the hydrogens of H2S. The same interactions between sulfur containing gases and MAF-66 are found at first and middle snapshots extracted during GCMC simulations (see Fig. S1 and S2, ESI†).
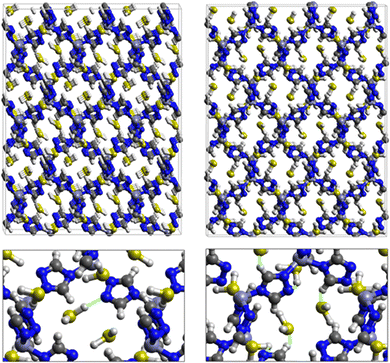
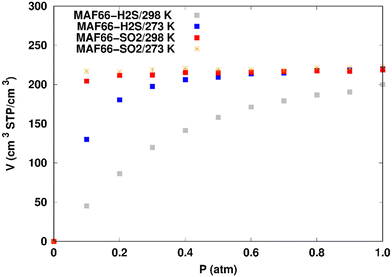
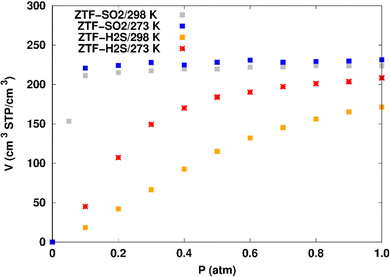
Fig. 7 displays the adsorption positions of SO2 and H2S molecules inside the pores of ZTF after GCMC simulations, together with non-bonding interactions between adsorbed hosted molecules and pores. The GCMC snapshots of initial and middle frames are also presented in Fig. S3 and S4 (ESI†). The SO2 molecules are stabilized in the pores of ZTF by several types of interactions: either by the hydrogen bonds between one oxygen of SO2 and the hydrogen of the C–H of the triazole organic subunit or by the electrostatic interactions between the nitrogens of the MOF subunit and the sulphur of SO2 or by the electrostatic interaction between metal zinc of these MOFs and oxygens of SO2. It has been found that the SO2 molecule electrostatically orients to the unsaturated coordination sites (which act as M⋯O(SO2) acid–base Lewis interactions), and hence SO2 is physisorbed rather than chemisorbed. Thus, the collapse of the MOF structure is avoided. Similar interactions were already observed.7,37 For example, in IRMOF-10 MOFs, Song et al.37 suggested that the SO2 molecules initially occupy the zinc corner regions through Zn⋯O(SO2) electrostatic interactions, as the most favorable energetic adsorption sites. These authors also found weak hydrogen bonds between the aromatic C–H group and O of SO2. In the case of H2S, we identified the presence of hydrogen bonds between the hydrogens of H2S and the nitrogens of Tz subunits. It was also observed that increasing temperature had an adverse effect on H2S adsorption as can be seen in Fig. 4 and 6, suggesting that physical adsorption is predominant. In addition to this, as already pointed out in ref. 35 and 37, pore sizes greater than 0.4 nm have high SO2/H2S gas adsorption capacity and the volume/surface area are still important characteristics for evaluating gas adsorption potential.
In the case of carbon dioxide, we considered the adsorption of SO2 and H2S with NCO2 preloaded CO2 molecules (SO2–CO2 and H2S–CO2 mixtures). While the number of SO2 and H2S molecules varied in the course of simulations, the number of CO2 molecules was kept fixed to NCO2. Also, CO2 molecules were allowed to move within the cavities of these MOFs until reaching equilibrium.
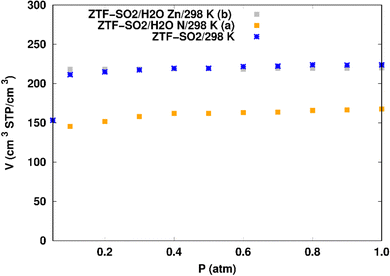
SO2 adsorption in ZTF with active sites occupied by H2O molecules. We performed GCMC simulations to evaluate the SO2 adsorption isotherms for the hydrated ZTF MOF at 298 K. Here, we report the GCMC results of the influence of the H2O molecules on SO2 adsorption where water molecules occupy either the coordinately unsaturated Zn atoms or the uncoordinated N atom of the triazolate ring active sites. The corresponding simulated adsorption isotherms of SO2 at 298 K in ZTF with and without the presence of H2O molecules in two different positions are shown in Fig. 8. This figure reveals that SO2 uptake significantly decreases when H2O molecules are located in the vicinity of the nitrogen of the triazole subunit. Indeed, when going from dry to hydrated conditions at higher pressures (P ∼ 1 atm) the average absolute adsorption values of SO2 significantly decreased from ∼223 cm3 (STP) cm−3 to ∼168 cm3 (STP) cm−3 when H2O interacts with nitrogen through N⋯H(OH) hydrogen bond. Whereas, when H2O molecules are placed near the Zn atom, the situation is different, where the presence of water molecules slightly changes the adsorption of SO2 from 220 cm3 (STP) cm−3 to 219 cm3 (STP) cm−3. In fact, humidity in MOF materials with open metal sites has unfavorable effects on the capture of SO2 due to the competition between this molecule and water molecules towards the interactions with the nitrogens or open metal sites which are possible sites for SO2 adsorption through electrostatic SO2⋯N and M⋯O (SO2) interactions (Fig. 9). Similar behavior of an unfavorable effect of humidity on the capture of SO2 while using Mg-MOF-747 as the MOF is also observed as well in our previous work with CO2 as guest molecule inside ZTF.40
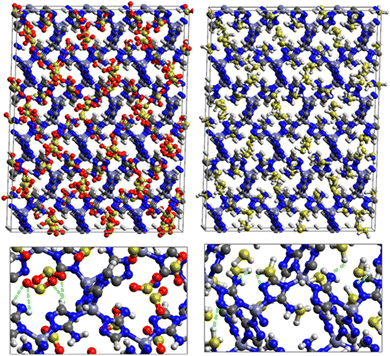
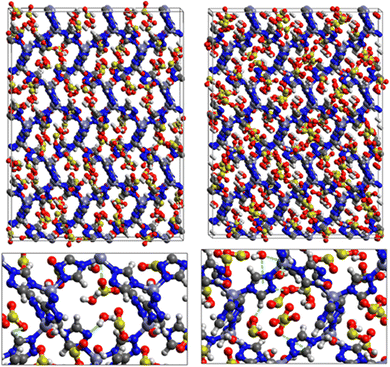
Fig. 9 shows the GCMC adsorption sites of SO2 molecules inside the pores of ZTF in the presence of H2O molecules near the zinc or nitrogen atoms of the [Zn-triazole] subunits. Close examination of this figure reveals the occurrence of several types of interactions that contribute to the SO2 capture by the MOF. Again, when water is near the nitrogens several types of interactions were found: (i) hydrogen bonds between one oxygen of SO2 and the hydrogen of triazole subunit (i.e. C–H–O(SO2)), with d{OSO2–HC} distances in the [2.8–3.0] Å range. (ii) Electrostatic interactions between one oxygen of SO2 and the zinc atom of the [Zn-triazole] subunit with d{OSO2–ZnTz] in the ∼[3.09 – 3.3] Å range. (iii) Hydrogen bonds between the hydrogen of H2O and the unprotonated nitrogen of Tz, N–H(H2O), with d{HH2O–N} distances in the [1.8–2.2] Å range.
When H2O is placed near the zinc of the [Zn-triazole] subunit, the electrostatic interaction is present between the oxygen of water and the zinc of Tz with intermolecular distances of ∼[2.3–2.4] Å. Also, we found π stacking interactions between the SO2 molecule and the aromatic ring of the triazole subunits, as well as electrostatic interactions between one oxygen of SO2 and the unprotonated nitrogen of triazole with d{OSO2–NTz} in the ∼[2.75–3.1] Å range. In addition, we characterized hydrogen bonds between the oxygen of SO2 and the hydrogen of triazole, C–H–O(CO2), with d{OSO2–HC} distances in the [2.65–3.3] Å range. These types of interactions (H-bonds and electrostatic) were also identified between CO2 and the surface pore atoms of ZTF.40 Consequently, the selectivity of MOFs towards adsorbents for the CO2/SO2 gas mixture should be challenging. Nevertheless, ZTF exhibits a better binding affinity to SO2 compared to CO2 due to the polar character of SO2, which induces the stabilizing electrostatic interactions highlighted above. For instance, the average absolute adsorption value of CO2 in ZTF at 273 K and 1 atm, is equal to ∼174 cm3 (STP) g−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and of SO2 is equal to ∼180 cm3 (STP) g−1 under the same P and T conditions.
40 and of SO2 is equal to ∼180 cm3 (STP) g−1 under the same P and T conditions.
H2S adsorption in ZTF with active sites occupied by H2O molecules. GCMC simulations were performed to investigate the H2S adsorption isotherms for a hydrated ZTF MOF at 298 K. The corresponding simulated adsorption isotherms with and without the presence of water molecules are shown in Fig. 10. This figure allows us to identify two regimes:
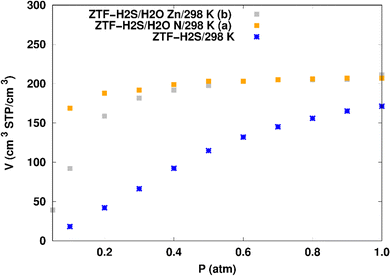 | ||
| Fig. 10 Simulated adsorption isotherms of H2S at 298 K in ZTF with and without the presence of water molecules, where H2O is located near nitrogen (in (a)) or in the vicinity of the Zn atom (in (b)). | ||
(i) “very low pressure” regime for P < 0.3 atm: dry ZTF presents lower capacities for H2S uptake than the hydrated case. The enhancement of adsorption is better when water is placed near nitrogen. For instance, H2S uptake significantly increases from 42.08 cm3 (STP) cm−3 at P = 0.2 atm and T = 298 K under dry conditions to 188.0/158.78 cm3 (STP) cm−3 in the presence of water. Thus the presence of H2O molecules attached to both adsorption sites (around Zn and at N of triazole) enhances the H2S adsorption.
(ii) “high pressure” regime for P > 0.3 atm: we observe an identical increase in H2S adsorption for both positions of water inside pores. The position of water seems not to have any difference on the H2S uptake. Indeed, a plateau is observed at around 211.0 cm3 (STP) cm−3. This is the signature of a saturation of the H2S adsorption available sites. Fig. 10 also shows that the H2S uptake slightly increases when H2O molecules are present for higher pressures. For instance, H2S uptake slightly increases from 170.1 cm3 (STP) cm−3 at P = 1 atm and T = 298 K under dry conditions to around 211 cm3 (STP) cm−3 in the presence of water. Such water induced enhancement of H2S adsorption on nanomaterials was already experimentally observed.7
Nonbonded interactions between H2S and ZTF pore are presented in Fig. 11. In this case, we observe hydrogen bonds between the hydrogen of C–H with sulfur of H2S for both positions of water. We also characterized interaction between the hydrogen of triazole and sulfur of H2S C–H–S(H2S), with d{SSO2–HC} distances in the [2.7–3.5] Å range.
SO2/H2S adsorption with a fixed number of preloaded H2O molecules inside the ZTF pore. We performed several simulations where we varied the number of preloaded H2O molecules (Nwater) inside the ZTF cavity. Table 3 gives the results of the SO2 and H2S adsorption in the ZTF model MOF by varying Nwater from 0 to 100. All simulations were performed at a temperature of 273 K and at very low (0.1 atm) and high pressures (1 atm). Table 3 shows that, at both pressures, increasing the number of H2O molecules up to 10 slightly increases the amount of adsorbed SO2 (at 0.1 atm from ∼221 to ∼224 cm3 (STP) cm−3). Beyond this preloaded amount of H2O, the SO2 uptake starts to decrease. This behavior is due to the interaction between the quadrupole moment of SO2 and the electric dipoles of H2O molecules, which increases the SO2 uptake. At higher number of water molecules, water and sulfur dioxide compete for the adsorption sites. For example, at 1 atm, calculations show that increasing the number of H2O molecules acts to decrease the adsorption of SO2 in ZTF from ∼231 cm3 (STP) cm−3 (without H2O molecules) to ∼150 cm3 (STP) cm−3 (with 100 H2O molecules). The reduction of SO2 adsorption at lower pressure in the presence of adsorbed water can be attributed to the stronger binding interactions for H2O@[Zn2+-Tz] complexes compared to the SO2@[Zn2+-Tz] ones, whereas at higher pressure the free volume of MOF ZTF contributes to the adsorption capacity as well. Non-bonded interactions between H2O and ZTF pore are shown in Fig. 12. The H2O molecules are stabilized in the pores of ZTF with SO2 molecules by hydrogen bonds between the oxygen of H2O and the hydrogen of C-(Tz). In the case of H2S, the presence of H2O decreases the amount of adsorbed H2S at 1 atm, whereas at lower pressure, the presence of water molecules slightly increases the adsorption of H2S similar to the results presented in Fig. 10. This is due to the increased polarity of H2S in the presence of water at lower pressure. Non-bonded interactions between H2O/H2S and the ZTF pore at 1 atm are presented in Fig. 12. We identified the presence of two types of hydrogen bonds: either between the oxygen of H2O and the hydrogen of C-(Tz) or between the nitrogen of the MOF subunit and the hydrogen of H2O.
| NH2O | 0 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|
| SO2 (1 atm) | 231 | 233 | 213 | 190 | 150 |
| SO2 (0.1 atm) | 221 | 224 | 220 | 205 | 173 |
| H2S (1 atm) | 208 | 200 | 193 | 173 | 140 |
| H2S (0.1 atm) | 45 | 46 | 47 | 52 | 58 |
SO2/H2S adsorption with a fixed number of preloaded CO2 molecules inside the ZTF pore. We performed several simulations where we varied the number of the preloaded CO2 molecules (NCO2) inside the ZTF cavity. Table 4 gives the results of the SO2 and H2S adsorptions in the ZTF model MOF by varying the number of CO2 molecules from 0 to 100. All simulations were performed at T = 273 K and P = 1 atm. Table 4 shows that increasing the number of CO2 molecules to up to 10 slightly increases the amount of adsorbed SO2 (from ∼231 to ∼233 cm3 (STP) cm−3). Polarity of SO2 compared to that of CO2 plays a key role at low pressure and enhances the adsorption uptake of these molecules in ZTF. Beyond this preloaded amount of CO2, the SO2 uptake starts to decrease since at higher number of preloaded CO2, carbon dioxide and sulfur dioxide compete for the adsorption sites. We can explain this behavior by the stronger interaction between SO2 and pore surface atoms than in the case of CO2, which is due to the presence of one strong interaction between one oxygen of SO2 and zinc of the ZTF pore as discussed above. This behavior was also observed by Ding and Yazaydin.29 In the case of hydrogen sulfide, the presence of CO2 in the pore, irrespective of the number of CO2 molecules, decreases the H2S adsorption. Indeed, calculations show that increasing the number of CO2 molecules acts to decrease the adsorption of H2S in ZTF from ∼208 cm3 (STP) cm−3 (without CO2 molecules) to ∼130 cm3 (STP) cm−3 (with 100 CO2 molecules). The reduction of H2S adsorption at higher pressures in the presence of adsorbed CO2 can be attributed to the strong nonbonding interactions40 of the CO2@[Zn2+-triazole] ZTF subunit through several types of interactions like electron acceptor–electron donor interactions between the carbon of CO2 and the nitrogen of Tz of ZTF, π stacking interactions between CO2 and aromatic rings of Tz and hydrogen bonds. Whereas H2S is unable to adsorb into the same adsorption positions of the cell as CO2.
| NCO2 | 0 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|
| SO2 | 231 | 233 | 213 | 190 | 150 |
| H2S | 208 | 200 | 192 | 169 | 130 |
IV. Conclusions
In this work, we used first principles density functional theory calculations and grand canonical Monte Carlo simulations to explore the adsorption properties of SO2 and H2S gases with and without the presence of water and carbon dioxide in MAF-66 and ZTF zinc triazolate based frameworks. We have shown here, by using GCMC simulations, that the recently designed ZTF MOF composed of triazolate as the organic ligand and Zn(II) as the metal linker, as well as MAF-66 have good SO2 and H2S adsorption capacities at high pressure under dry conditions, at 273 K and 298 K. This sequestration is associated with several types of interactions like hydrogen bonds or electron acceptor–electron donor interactions with the uncoordinated metal sites within these MOFs. Also, we observed that one oxygen of the SO2 molecule (which acts as the Lewis base) electrostatically interacts with zinc, and therefore SO2 is physiosorbed rather than chemisorbed avoiding irreversible structural modifications of MOFs and possible drawbacks for recycling these nanomaterials and their subsequent industrial uses. Molecular simulations reveal that the amount of adsorbed gases is closely correlated with the free volume and the accessible surface area, suggesting that the free volume/surface area are important parameters in evaluating SO2/H2S gas adsorption capacities.In general, we established that sulfur dioxide/hydrogen sulphide/carbon dioxide/water compete for adsorption sites. For instance, GCMC simulations of the influence of water on SO2 adsorption in ZTF, show that water has an unfavorable effect on the capture of SO2 due to the competition among water molecules to occupy the nitrogens of the triazole ring. In the case of H2S, the presence of water, however, enhances the adsorption of H2S for both positions of water inside pores, in agreement with experimental observations. This behavior is confirmed by pre-adsorbing higher amounts of H2O molecules at a low pressure. At higher pressure and under hydrated conditions, the CO2 uptake slightly decreases while increasing the number of H2O molecules. Moreover, our work shows that pre-adsorbing small amount of CO2 molecules at low pressure increases the capacity of the ZTF for SO2 uptake, because of the favorable electrostatic interactions between zinc and one oxygen of SO2. At higher pressure and in the presence of CO2, the SO2 uptake slightly decreases while increasing the number of CO2 molecules. However, the adsorption of H2S in ZTF in the presence of carbon dioxide is reduced even with a small amount of pre-adsorbed CO2 molecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. G., I. D. J. and M. S. acknowledge support from the Serbian Ministry of Education and Science (Grant no. 451-03-68/2022-14/200026). Numerical simulations were run on the PARADOX-IV supercomputing facility at the Scientific Computing Laboratory, National Center of Excellence for the Study of Complex Systems, Institute of Physics Belgrade, supported in part by the Ministry of Education, Science, and Technological Development of the Republic of Serbia. We thank the COST Action CA21101 – Confined Molecular Systems: from a new generation of materials to the stars (COSY) of the European Community for support.References
- P. J. Baxter, J.-C. Baubron and R. Coutinho, J. Volcanol. Geotherm. Res., 1999, 92, 95–106 CrossRef CAS.
- M. S. Shah, M. Tsapatsis and J. I. Siepmann, Chem. Rev., 2017, 117, 9755–9803 CrossRef CAS PubMed.
- M. O. Andreae, Mar. Chem., 1990, 30, 1–29 CrossRef CAS.
- T. F. Berglen, T. K. Berntsen, I. S. A. Isaksen and J. K. Sundet, J. Geophys. Res., 2004, 109, D19310 CrossRef.
- F. C. Menz and H. M. Seip, Environ. Sci. Policy, 2004, 7, 253–265 CrossRef CAS.
- B. Liao, Z. Guo, A. Probst and J.-L. Probst, Geoderma, 2005, 127, 91–103 CrossRef CAS.
- E. Martínez-Ahumada, A. López-Olvera, V. Jancik, J. E. Sánchez-Bautista, E. González-Zamora, V. Martis, D. R. Williams and I. A. Ibarra, Organometallics, 2020, 39(7), 883–915 CrossRef.
- H. Hikita, S. Asai and T. Tsuji, AIChE J., 1977, 23, 538–544 CrossRef CAS.
- R. N. Maddox, G. J. Mains and M. A. Rahman, Ind. Eng. Chem. Res., 1987, 26, 27–31 CrossRef CAS.
- Y. S. Mok and H.-J. Lee, Fuel Process. Technol., 2006, 87, 591–597 CrossRef CAS.
- S. G. Khokarale and J.-P. Mikkola, RSC Adv., 2018, 8, 18531–18541 RSC.
- K. Huang, X. Feng, X.-M. Zhang, Y.-T. Wu and X.-B. Hu, Green Chem., 2016, 18, 1859–1863 RSC.
- Q. Zhang, Y. Hou, S. Ren, K. Zhang and W. Wu, ACS Sustainable Chem. Eng., 2019, 7, 10931–10936 CrossRef CAS.
- M. D. Dolan, A. Y. Ilyushechkin, K. G. McLennan and S. D. Sharma, Asia-Pac. J. Chem. Eng., 2012, 7, 1–13 CrossRef CAS.
- M. Khabazipour and M. Anbia, Ind. Eng. Chem. Res., 2019, 58, 22133–22164 CrossRef CAS.
- P. Cosoli, M. Ferrone, S. Pricl and M. Fermeglia, Chem. Eng. J., 2008, 145, 86–92 CrossRef CAS.
- L. Hamon, C. Serre, T. Devic, T. Loiseau, F. Millange, G. Férey and G. D. Weireld, J. Am. Chem. Soc., 2009, 131, 8775–8777 CrossRef CAS PubMed.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781 CrossRef CAS PubMed.
- T. Baird, K. C. Campbell, P. J. Holliman, R. W. Hoyle, M. Huxam, D. Stirling, B. P. Williams and M. Morris, J. Mater. Chem., 1999, 9, 599–605 RSC.
- P. R. Westmoreland and D. P. Harrison, Environ. Sci. Technol., 1976, 10, 659–661 CrossRef CAS.
- M. Xue, R. Chitrakar, K. Sakane and K. Ooi, Green Chem., 2003, 5, 529–534 RSC.
- N. E. R. Zimmermann and M. Haranczyk, Cryst. Growth Des., 2016, 16, 3043–3048 CrossRef CAS.
- S. Tian, H. Mo, R. Zhang, P. Ning and T. Zhou, Adsorption, 2009, 15, 477–488 CrossRef CAS.
- J. Guo and A. C. Lua, J. Colloid Interface Sci., 2002, 251, 242–247 CrossRef CAS PubMed.
- A. Wang, R. Fan, X. Pi, Y. Zhou, G. Chen, W. Chen and Y. Yang, ACS Appl. Mater. Interfaces, 2018, 10, 37407–37416 CrossRef CAS PubMed.
- J. Zhao, A. Buldum, J. Han and J. P. Lu, Nanotechnology, 2002, 13, 195–200 CrossRef CAS.
- N. S. Bobbitt, M. L. Mendonca, A. J. Howarth, T. Islamoglu, J. T. Hupp, O. K. Farha and R. Q. Snurr, Chem. Soc. Rev., 2017, 46, 3357–3385 RSC.
- N. C. Burtch and K. S. Walton, Acc. Chem. Res., 2015, 48, 2850–2857 CrossRef CAS PubMed.
- L. Ding and A. O. Yazaydin, Phys. Chem. Chem. Phys., 2013, 15, 11856–11861 RSC.
- E. Chen, L. Jia, X. Jia, Q. Wei and L. Zhang, Chem. Phys. Lett., 2021, 778, 138788–138794 CrossRef CAS.
- X. Xu, P. Wu, C. Li, K. Zhao, C. Wang, R. Deng and J. Zhang, Energy Fuels, 2021, 35, 5110–5121 CrossRef CAS.
- C. Wang, H. Xu, P. Huang, X. Xu, H. Wang, Y. Zhang and R. Deng, Atmosphere, 2022, 13, 462–475 CrossRef CAS.
- X. Zhou, Y. Yu, H. Chen, L. Yang, Y. Qin, T. Wang, W. Sun and C. Wang, Langmuir, 2020, 36, 2775–2785 CrossRef CAS PubMed.
- A. Beheshti, M. Bahrani-Pour, T. Sedaghat, B. Salahshournia, H. Arefi-Nasab, P. Mayer, R. Centore and E. Parisi, Cryst. Growth Des., 2022, 22, 4343–4356 CrossRef CAS.
- A. G. Georgiadis, N. Charisiou, I. V. Yentekakis and M. A. Goula, Materials, 2020, 13, 3640 CrossRef CAS PubMed.
- A. Pudi, M. Rezaei, V. Signorini, M. P. Andersson, M. G. Baschetti and S. S. Mansouri, Sep. Purif. Technol., 2022, 298, 121448-1–1211448-51 CrossRef.
- X.-D. Song, S. Wang, C. Hao and J.-S. Qiu, Inorg. Chem. Commun., 2014, 46, 277–281 CrossRef CAS.
- K. Vellingiri, A. Deep and K.-H. Kim, ACS Appl. Mater. Interfaces, 2016, 8, 29835–29857 CrossRef CAS PubMed.
- S. Bhattacharyya, S. H. Pang, M. R. Dutzer, R. P. Lively, K. S. Walton, D. S. Sholl and S. Nair, J. Phys. Chem. C, 2016, 120, 27221–27229 CrossRef CAS.
- R. Dahmani, S. Grubišić, I. Djordjević, S. Ben Yaghlane, S. Boughdiri, G. Chambaud and M. Hochlaf, J. Chem. Phys., 2021, 154(2), 024303 CrossRef CAS PubMed.
- R. Dahmani, S. Grubišić, S. Ben Yaghlane, S. Boughdiri and M. Hochlaf, J. Phys. Chem. A, 2019, 123, 5555–5565 CrossRef CAS PubMed.
- R. Dahmani, S. Ben Yaghlane, S. Boughdiri, M. Mogren Al-Mogren, M. Prakash and M. Hochlaf, Spectrochim. Acta, Part A, 2018, 193, 375–384 CrossRef CAS PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- A. Garcia, et al. , J. Chem. Phys., 2020, 152, 204108-1–204108-31 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- W. E. Pickett, Comput. Phys. Rep., 1989, 9, 115–197 CrossRef.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114(25), 10024–10035 CrossRef CAS.
- J. J. Potoff and J. I. Siepmann, AlChE J., 2001, 47, 1676–1682 CrossRef CAS.
- F. Sokolic, Y. Guissani and B. Guillot, Mol. Phys., 1985, 56, 239–253 CrossRef CAS.
- M. C. C. Ribeiro, J. Phys. Chem. B, 2006, 110, 8789–8797 CrossRef CAS PubMed.
- K. N. Shyamal, J. Phys. Chem. B, 2003, 107, 9498–9504 CrossRef.
- X. Peng and D. Cao, AIChE J., 2013, 59, 2928–2942 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- D. Dubbeldam, A. Torres-Knoop and K. S. Walton, Mol. Simulat., 2013, 39, 1253–1292 CrossRef CAS.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simulat., 2016, 42, 81–101 CrossRef CAS.
- R. B. Lin, D. Chen, Y. Y. Lin, J. P. Zhang and X. M. Chen, Inorg. Chem., 2012, 51, 9950–9955 CrossRef CAS PubMed.
- H. Y. Zhang, Z. R. Zhang, C. Yang, L. X. Ling, B. J. Wang and H. L. Fan, J. Inorg. Organomet. Polym. Mater., 2018, 28, 694–701 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04295a |
| ‡ Present address: Université Paul Sabatier Toulouse [UT3], Laboratoire de Chimie Physique Quantiques (LCPQ), Fédération Fermi, UMR 5626, CNRS, 118 Route de Narbonne, 31062 Toulouse, France. |
| This journal is © the Owner Societies 2023 |