Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Compartmentalizing and sculpting nanovesicles by phase-separated aqueous nanodroplets†
Fatemeh Kazemi Sabet a,
Arash Bahrami
a,
Arash Bahrami a and
Amir H. Bahrami
a and
Amir H. Bahrami *bc
*bc
aSchool of Mechanical Engineering, College of Engineering, University of Tehran, North Kargar St., 14399-57131, Tehran, Iran
bUNAM-National Nanotechnology Research Center and Institute of Materials Science & Nanotechnology, Bilkent University, Ankara, Turkey. E-mail: bahrami@unam.bilkent.edu.tr
cLiving Matter Physics, Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
First published on 8th November 2022
Abstract
Phase-separated liquid droplets inside giant vesicles have been intensely studied as biomimetic model systems to understand cellular microcompartmentation and molecular crowding and sorting. On the nanoscale, however, how aqueous nanodroplets interact with and shape nanovesicles is poorly understood. We perform coarse-grained molecular simulations to explore the architecture of compartmentalized nanovesicles by phase-separated aqueous nanodroplets, and their morphological evolution under osmotic deflation. We show that phase separation of a biphasic liquid mixture can form both stable two-compartment and meta-stable multi-compartment nanovesicles. We identify morphological transitions of stable two-compartment nanovesicles between tube, sheet and cup morphologies, characterized by membrane asymmetry and phase-separation propensity between the aqueous phases. We demonstrate that the formation of local sheets and in turn cup-shaped nanovesicles is promoted by negative line tensions resulting from large separation propensities, an exclusive nanoscale phenomenon which is not expected for larger vesicles where energetic contributions of the line tensions are dominated by those of the membrane tensions. Despite their instability, we observe long-lived multi-compartment nanovesicles, such as nanotubules and branched tubules, whose prolonged lifetime is attributed to interfacial tensions and membrane asymmetry. Aqueous nanodroplets can thus form novel membrane nanostructures, crucial for cellular processes and forming cellular organelles on the nanoscale.
Introduction
Lipid vesicles, loaded with aqueous droplets, serve as model systems to explore several biological processes in living cells. These processes include cellular compartmentation by phase-separated biomolecular condensates,1–3 vesicle budding,4–6 membrane tube formation,7 and clustering of synaptic vesicles by synapsin droplets.8–10 Molecular signalling,11 formation of cellular tight junctions,12 and cellular transport13 are other prime examples. These biomimetic setups are also used to understand active regulation of cellular processes by phase-separated liquid droplets. Examples include shaping vesicles by various types of active particles,14,15 and remodelling of biomimetic cells, synthetic vesicles,5,16–20 nucleoli, and germinal vesicles.21Vesicle membranes are formed by the self-assembly of lipid molecules in aqueous solution, thereby separating an interior compartment from the surrounding bulk medium. These vesicles have a size that varies over a wide range from a few tens of nanometers, like synaptic and secretory vesicles, to hundreds of nanometers such as cellular organelles. Besides cellular vesicles, they also represent synthetic vesicles prepared from synthetic molecules such as block copolymers. Interior aqueous droplets have been found capable of modulating morphological transformations of vesicles.4,6,7,22 Conversely, lipid membranes can regulate the phase separation of biomolecular condensates.23 The experimental use of vesicles as model cells has mostly focused on giant vesicles on the micron scale to mimic the cell and cellular organelles.
Recent findings have highlighted the significant role of aqueous droplets in shaping biomembranes on the nanoscale, thereby regulating nano-sized cellular processes and structures. Formation of membrane nanotubes by phase separation of aqueous phases7 and autophagosome biogenesis in autophagy24–26 exemplify membrane remodeling by liquid nanodroplets. Membrane wetting by liquid droplets has been found to play a key role in forming the pre autophagosomal structure (PAS) as a precursor for autophagosome biogenesis in autophagy.24–26 The PAS is hypothesized to have formed via fusion of a few, reportedly three, Atg9 vesicles with a diameter within the range 30–60 nm resulting in a larger vesicle, 50 to 100 nm in diameter.27 How aqueous droplets regulate biological processes and shape cellular organelles, in particular on the nanoscale where experimental imaging becomes fragile, can be understood by simulating a nanovesicle with internal aqueous nanodroplets.
Based on theories of wetting and elastocapillary,28,29 vesicle remodelling by internal aqueous droplets depends on the interplay between four factors: the curvature elasticity of the vesicle; membrane tensions within membrane segments; interfacial tensions at liquid–liquid interfaces; and mostly-negative line tensions acting along the contact line of the vesicle and the droplets. Within the theoretical framework of curvature elasticity,30–32 membrane elastic energy depends on local or non-local spontaneous curvature. For simplified uniform membranes considered here, membrane shape is modulated by non-local spontaneous curvature or membrane asymmetry which is the difference in the lipid numbers between the two leaflets.33–37 It results from lipid exchange between the membrane leaflets, from non-uniform membrane growth by lipid synthesis, and from vesicle fusion. Interfacial surface and line tensions depend on the interfacial forces between the two aqueous phases i.e. liquid–liquid interactions represented in our model by the phase-separation propensity (referred to as separation propensity hereafter). The vesicle-droplet system, composed of a vesicle with two internal liquid phases of fixed concentration, is thus characterized by two properties: membrane asymmetry; and separation propensity between the liquid phases.
On the micron scale, the free energy contributions of membrane and interfacial tensions dominate those of the line tensions.6,38,39 Therefore, compared to membrane asymmetry and membrane and interfacial tensions, the line tensions are hypothesized to play a negligible role on the morphological transformations of giant vesicles wetted by large liquid droplets. By contrast, morphological behaviour of nanovesicles is expected to be significantly affected by the mostly-negative line tensions.38
Due to the small size of the nanovesicles and the dynamic nature of their shape transformations it is not easy to study their morphological behavior experimentally. Molecular dynamics simulation of coarse-grained models provides an alternative approach to explore both equilibrium and dynamic vesicle remodelling. We used DPD (Dissipative Particle Dynamics) simulations40 of a coarse-grained membrane model which has been successfully applied to study vesicle dynamics. Prime examples include the evolution of lipid vesicles and polymersomes under osmotic deflation,41,42 vesicle deformation by lipid flippase,37,43,44 vesicle fission by membrane phase separation,45,46 and vesicles in contact with aqueous droplets.38 Coarse-grained DPD simulations allow us to perform relatively long simulations of about 100 μs of rather large nanovesicles.
Our first goal is to explore vesicle compartmentation by non-equilibrium phase separation of two initially-mixed liquid phases inside an initial spherical vesicle. Then, we propose to investigate morphological behaviour of the resulting stable two-compartment and meta-stable multi-compartment vesicles under osmotic deflation to understand how membrane asymmetry and separation propensity determine the vesicle architecture. In our model the lipid membrane and the aqueous liquids were presented by coarse-grained beads and the phase-separation of liquids occurs due to steric repulsive interactions between them,15 where stronger repulsion corresponds to a larger separation propensity. See Methods for more details about our coarse-grained simulations.
We started by simulating non-equilibrium phase separation of two initially-mixed liquid phases forming both stable two-compartment and meta-stable multi-compartment nanovesicles. When we reduced the vesicle volume, meta-stable vesicles exhibited complex morphologies, such as branched tubules, with long lifetimes presumably due to the stabilizing role of the interfacial tensions. To understand complex polymorphism of mostly multi-compartment nanovesicles, we then focused on stable two-compartment vesicles as the building blocks of meta-stable multi-compartment nanovesicles. Upon volume reduction, mimicking the osmotic deflation and vesicle fusion in autophagy, these vesicles underwent different morphological transitions between stable tube, sheet and cup shapes, identified by membrane asymmetry and separation propensity. We demonstrated that lower membrane asymmetry, i.e. smaller non-local spontaneous curvature, and larger separation propensity promote formation of the sheet-like structures thereby transforming the vesicles from tubes to sheets and in turn toward cups.
Methods
DPD simulation
We used LAMMPS simulator47 to perform DPD simulations. The vesicles were built from lipid molecules composed of three hydrophilic head groups H and two hydrophobic chains of six tail groups C surrounded by an external liquid phase γ composed of beads of type D.37 All vesicles enclosed two internal liquid phases α and β corresponding to bead types A and B. All beads had a diameter of d = 0.8 nm which defined the length scale of our simulations.The interaction force parameter fij between the liquid bead types A (α), B (β), and D (γ), and lipid head H and tail C groups. The interfacial force parameter fAB varies in the range fAB ∈ [35, 50]kBT/d to adjust p, see Table 2.
Interfacial force parameter fAB between the two liquid phases with the corresponding separation propensity p.
Pairwise interactions between different pairs of DPD beads are distinguished by the interaction force parameter fij of the conservative DPD force.
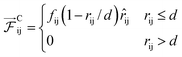 | (1) |
The unit vector ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ij points from bead i to bead j with a distance rij. The remaining random and dissipative terms of the DPD pairwise force are identical for all bead pairs.
ij points from bead i to bead j with a distance rij. The remaining random and dissipative terms of the DPD pairwise force are identical for all bead pairs.
The two liquid phases were taken to equally wet the membrane for interfacial force parameters fAi = fBi (i = H and C) between the liquid beads A and B, and the lipid head H and hydrocarbon tail C groups. The external liquid phase γ, composed of bead type D, is also an aqueous phase with the same properties of the tow phases α and β.
The thermal energy kBT, obtained from Boltzmann constant kB and absolute temperature T, defines the energy scale. All simulations were performed in an NVT ensemble in cubic simulation boxes with volume (80 d)3 under periodic boundary conditions. The DPD bead density 3/d3, together with an interaction force parameter fAA = fBB = 25 kBT/d leads to aqueous liquid phases that approximate water compressibility at room temperature. DPD equations were integrated with a time step 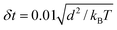 where the time scale
where the time scale 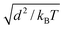 of the system is about 1 ns for beads of unit mass. Except for interfacial force parameter fAB which was varied to control the phase separation between the liquid phases α and β, the same interaction parameters, listed in Table 1, were used for all simulations throughout this article.
of the system is about 1 ns for beads of unit mass. Except for interfacial force parameter fAB which was varied to control the phase separation between the liquid phases α and β, the same interaction parameters, listed in Table 1, were used for all simulations throughout this article.
| j = H | j = C | j = D | j = A | j = B | |
|---|---|---|---|---|---|
| i = H | 30 | 50 | 30 | 30 | 30 |
| i = C | 50 | 10 | 75 | 75 | 75 |
| i = D | 30 | 75 | 25 | 25 | 25 |
| i = A | 30 | 75 | 25 | 25 | fAB |
| i = B | 30 | 75 | 25 | fAB | 25 |
Interfacial surface tension and phase separation propensity
To find the interfacial surface tensions, a slab of liquid phase β was placed in the middle of a periodic simulation box surrounded with liquid phase α at both sides, see Fig. S1A.† The interfacial tension depends on the repulsive interactions between the two liquid phases i.e. their tendency to phase separate. Liquid phase separation between the liquid phases α and β is defined by the rescaled separation propensity p = fAB/fAA as the ratio of the interfacial force parameter fAB and the internal force parameter fAA = fBB = 25 kBT within each liquid phase. The separation propensity p = 1.48, corresponding to the interfacial force parameter fAB = 37 kBT, was obtained as the particular interfacial force for which the density of each liquid phase was above 95% of the total DPD bead density 3/d3, see Fig. S1C.† Below this separation propensity, the two liquids completely mixed including the smallest propensity p = 1.4, which we used for two miscible liquid phases. In this article, we used five different interaction force parameters fAB with their corresponding separations propensities as listed in Table 2.| fAB [kBT/d] | p |
|---|---|
| 35 | 1.4 |
| 37 | 1.48 |
| 40 | 1.6 |
| 45 | 1.8 |
| 50 | 2 |
The interfacial tension Σαβ was computed by integrating the Cartesian stress profile
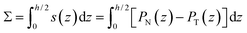 | (2) |
perpendicular to the interfacial surface of the two liquids.38,48,49 Here, PN(z) and PT(z) are the normal and tangential pressure components and h is the height of the simulation box, see Fig. S1A.† The smallest separation propensity p = 1.4 corresponds to two miscible liquid phases that do not phase-separate based on the criterion we used here. Larger separation propensities 1.48 < p ≤ 2 corresponding to larger interfacial tensions Σαβ, lead to stronger more active liquid phase separation, see Fig. S1B† and Table 3. We thus found that the interfacial tensions depend on the separation propensity p an are independent of Δ.
| p | Σαβ [kBT/d2] | λ [kBT/d] |
|---|---|---|
| 1.48 | 0.45 ± 0.09 | − 0.21 ± 0.43 |
| 1.6 | 0.87 ± 0.13 | − 0.77 ± 0.39 |
| 1.8 | 1.4 ± 0.13 | − 1.81 ± 0.38 |
| 2 | 1.88 ± 0.13 | − 2.63 ± 0.37 |
Assembling initial spherical vesicles
We first assembled spherical vesicles with a fixed total number Nlip = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 of lipids by placing Ni = 5220 and No = Nlip − Ni = 6780 lipids with their heads on two concentric spheres of radii Ri = 19d and Ro = 25d, corresponding to inner and outer leaflets respectively. The length scale d ≃ 0.8 nm denotes a single bead diameter. These vesicles, nearly 32 nm in diameter, initially enclose Niliq = NiA + NiB = 126
000 of lipids by placing Ni = 5220 and No = Nlip − Ni = 6780 lipids with their heads on two concentric spheres of radii Ri = 19d and Ro = 25d, corresponding to inner and outer leaflets respectively. The length scale d ≃ 0.8 nm denotes a single bead diameter. These vesicles, nearly 32 nm in diameter, initially enclose Niliq = NiA + NiB = 126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 liquid beads of types A and B corresponding to liquid phases α and β with relative concentration ϕ = NiA/Niliq which defined the initial vesicle volume. The two liquid phases are either initially separated, see Fig. 1A and B, or are randomly mixed as seen in the left panel of Fig. 1C. The surrounding liquid phase γ is an inert spectator phase, see Fig. 1A. Upon volume reduction, a vesicle with reduced volume v = Nliq/Niliq ≤ 1 contains less number Nliq < Niliq of liquid beads for a constant relative concentration ϕ = NA/Nliq = NiA/Niliq.
000 liquid beads of types A and B corresponding to liquid phases α and β with relative concentration ϕ = NiA/Niliq which defined the initial vesicle volume. The two liquid phases are either initially separated, see Fig. 1A and B, or are randomly mixed as seen in the left panel of Fig. 1C. The surrounding liquid phase γ is an inert spectator phase, see Fig. 1A. Upon volume reduction, a vesicle with reduced volume v = Nliq/Niliq ≤ 1 contains less number Nliq < Niliq of liquid beads for a constant relative concentration ϕ = NA/Nliq = NiA/Niliq.
For the given total number Nlip = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 of lipids, we redistributed the lipids between the two leaflets to produce five vesicles with different membrane asymmetries Δ = (No − Ni)/Nlip = 0.13, 0.17, 0.21, 0.25, and 0.27, representing the relative difference in lipid numbers of the two vesicle leaflets. These vesicles were then equilibrated with the two internal nanodroplets of relative concentration ϕ = 0.5 and different separation propensities. Vesicle parameters of the resulting vesicles are listed in Tables S1 to S3.†
000 of lipids, we redistributed the lipids between the two leaflets to produce five vesicles with different membrane asymmetries Δ = (No − Ni)/Nlip = 0.13, 0.17, 0.21, 0.25, and 0.27, representing the relative difference in lipid numbers of the two vesicle leaflets. These vesicles were then equilibrated with the two internal nanodroplets of relative concentration ϕ = 0.5 and different separation propensities. Vesicle parameters of the resulting vesicles are listed in Tables S1 to S3.†
To determine the reference state of membrane asymmetry, we simulated the vesicle with a single internal liquid phase α, see Fig. S2A.† For the vesicle with Nlip = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, a unique combination of Ni = 5023 and No = 6977 leads to a reference vesicle, with Δr = 0.16, for which both leaflets experience equal surface tensions,37 shown to vanish upon a small reduction in the vesicle volume as shown in Fig. S2B.† The reference vesicle is characterized by its negligible non-local spontaneous curvature. Lipid chains were taken long enough to suppress lipid exchange between the leaflets, resulting in a constant membrane asymmetry Δ for each individual vesicle. Fig. S2C† shows the leaflet tensions of this vesicle as well as other initial vesicles with different membrane asymmetries whose leaflets have different tensions and are thus expected to show different morphological behaviour under volume reduction. Vesicles with membrane asymmetries different from that of the reference vesicle Δ ≠ Δr = 0.16 have their outer and inner leaflets stretched or compressed depending on larger or smaller asymmetries relative to the reference state Δr = 0.16.
000, a unique combination of Ni = 5023 and No = 6977 leads to a reference vesicle, with Δr = 0.16, for which both leaflets experience equal surface tensions,37 shown to vanish upon a small reduction in the vesicle volume as shown in Fig. S2B.† The reference vesicle is characterized by its negligible non-local spontaneous curvature. Lipid chains were taken long enough to suppress lipid exchange between the leaflets, resulting in a constant membrane asymmetry Δ for each individual vesicle. Fig. S2C† shows the leaflet tensions of this vesicle as well as other initial vesicles with different membrane asymmetries whose leaflets have different tensions and are thus expected to show different morphological behaviour under volume reduction. Vesicles with membrane asymmetries different from that of the reference vesicle Δ ≠ Δr = 0.16 have their outer and inner leaflets stretched or compressed depending on larger or smaller asymmetries relative to the reference state Δr = 0.16.
Membrane tensions
The two liquid phases were taken to equally wet the membrane with identical molecular interactions between liquid beads A and B and both lipid head H and hydrocarbon tail C groups resulting in identical affinities of both liquid phases for the vesicle bilayer. The vesicle bilayer thus experiences a uniform membrane tension Σ = Σαγ = Σβγ across its surface.Line and interfacial tensions as a function of p for a stable vesicle with two compartments according to the computational method presented in Fig. 1. Both line and interfacial tensions depend on p.
Membrane tension within different membrane segments was computed by finding the first moment of the stress profile across the membrane interface. For initial spherical vesicles of unit volume v = 1 with a single internal liquid phase and different membrane asymmetries Δ, the stress or pressure profile has spherical symmetry. The normal and tangential pressure components PN(r) and PT(r) are thus functions of the radial coordinate r. For these vesicles, the bilayer tension Σ was obtained by integrating the stress profile s(r) = PN(r) − PT(r) across the membrane.
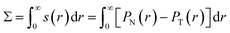 | (3) |
The two leaflet tensions were also obtained by splitting the same integral at the bilayer midplane r = Rm as
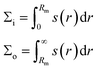 | (4) |
The free energy of the vesicles and the line tension
To compute the line tensions, we started from two initially-separated liquid nanodroplets inside the vesicle with Δ = 0.17, known to have a negligible non-local spontaneous curvature.The free energy.
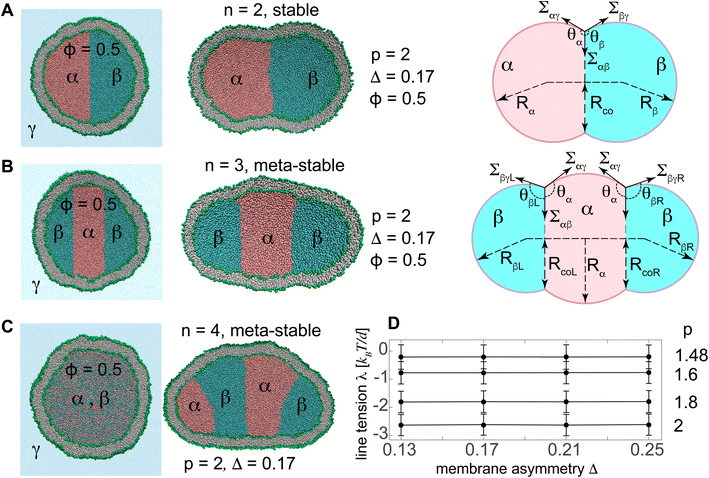
Two and three initially-separated liquid droplets inside an initially-spherical reference vesicle, Fig. 1A and B left panels, rapidly transformed into stable and meta-stable vesicles with n = 2 and 3 droplets respectively, Fig. 1A and B middle panels. The free energies F2 and F3 of these vesicles are
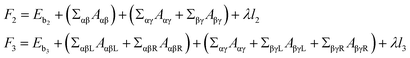 | (5) |
The line tension.
The two internal liquid phases α and β are separated from the external aqueous phase γ through membrane interface. The intersection of the interfacial surface αβ and the membrane defines a triple phase line along which the line tension acts. Initially-spherical vesicles were shortly equilibrated with a single internal liquid phase which was subsequently divided into two separate phases with relative concentration ϕ = 0.5, see the left panel in Fig. 1A. Two initially-separated liquids with different separation propensities p, and corresponding interfacial tension Σαβ, rapidly equilibrated into a stable two-compartment vesicle, with minimum free energy as seen in the right panel of Fig. 1A. Knowing the interfacial and membrane tensions for the given separation propensity p, we computed the line tension as described in more details in the ESI S1.† We then varied the separation propensity p inside different vesicles with various membrane asymmetries and found the corresponding line tensions. Like interfacial tensions, line tensions were found to depend on the separation propensity p and not on Δ, see Fig. 1D and Table 3.
Results and discussion
We first assembled initial vesicles with different membrane asymmetries enclosing two liquid phases with various separation propensities that were either initially separated or mixed. In this way, each stable vesicle was characterized by two independent parameters: the separation propensity p which exclusively determines the pair of interrelated line tension λ and interfacial tension Σαβ; and the membrane asymmetry Δ. These vesicles are subsequently used to simulate vesicle compartmentation and morphological transition of compartmetalized vesicles under osmotic deflation.Vesicle compartmentation by liquid phase separation
To explore the polymorphism of both stable and meta-stable vesicles, we started with non-equilibrium phase separation of two initially-mixed liquids by steric interactions.15 The initial mixture was assembled by random distribution of liquid beads α and β with relative concentration ϕ inside an initially-spherical vesicle with v = 1, see the left panel of Fig. 1C.For each set of ϕ and p, thirty simulations were performed from different initial random arrangements of liquid beads A and B (see the left panel in Fig. 1C) for a short time, t = 5 μs, and the statistical distribution of number of compartments were obtained.
Despite the entropic forces that tend to retain the mixture, the two liquids rapidly phase-separated due to steric forces between them. The non-equilibrium phase separation of the internal liquids thus transformed the vesicle shape by exerting active forces from liquid droplets on the vesicle membrane. Steric interactions between the two liquid phases were controlled by separation propensity p which determines the compartmentation activity level. These active forces compartmentalized the vesicle by forming various multi-droplet structures inside the nanovesicles with n compartments some of which are displayed in Fig. 2 and Video SV4.†
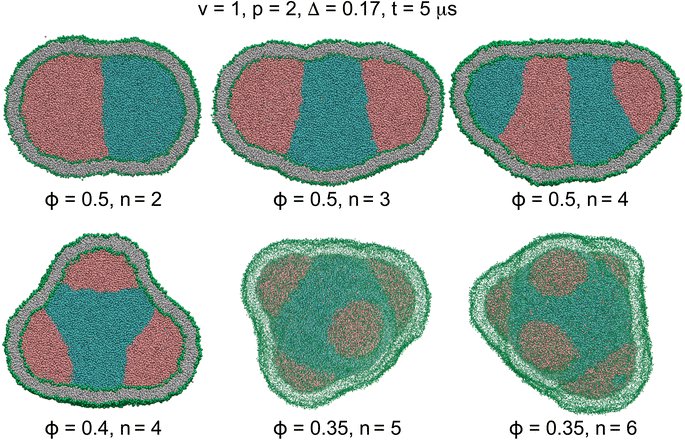 | ||
| Fig. 2 Cross sections (n = 2–4) and 3D views (n = 5 and 6) of actively-compartmentalized stable two-compartment (n = 2) and meta-stable multi-compartment vesicles (n > 2) with Δ = 0.17, having a negligible non-local spontaneous curvature, obtained from phase separation of initial random mixtures of the two liquids with p = 2 and different values of ϕ inside initially-equilibrated vesicles with v = 1 as seen in Fig. 1C. Number of compartments n decreases with ϕ and increases with p as shown in Table 4. The snapshots show the vesicles after a rather short simulation time of t = 5 μs when the two liquids have separated. | ||
For each pair of relative concentration ϕ ∈ {0.4, 0.5} and separation propensity 1.6 ≤ p ≤ 2, we performed thirty simulations starting from different initial random assembly of liquid beads. For two liquids equally wetting the membrane, the liquid phase with smaller concentration rapidly nucleated into multiple nanodroplets, in about 5 μs, on the periphery of a single droplet of the liquid phase with larger concentration. Both stable two-compartment, n = 2, and meta-stable multi-compartment vesicles, n > 2, resulted from vesicle compartmentation, as listed in Table 4 and shown in Fig. 2. The number of nanodroplets, and thus the vesicle compartments n, increased with the separation propensity p and decreased with the relative concentration ϕ. More active compartmentation with larger separation propensity p led to nanovesicles with more compartments giving rise to an enriched polymorphism of the resulting membrane structures.
| ϕ | p | n = 2 | n = 3 | n ≥ 4 |
|---|---|---|---|---|
| 0.5 | 1.6 | 77% | 23% | — |
| 0.5 | 2 | 66% | 30% | 4% |
| 0.4 | 1.6 | 16% | 68% | 16% |
| 0.4 | 2 | 10% | 47% | 43% |
For n > 2, the small nanodroplets are expected to coalesce to form two large droplets of the two liquid phases to reduce the free energy contributions of the interfacial tensions, membrane tensions, and membrane bending, as reflected in eqn (6). Interestingly, however, as seen in Video SV5,† we did not observe droplet coalescence in our extended simulation, for about 100 μs, of a meta-stable nanovesicle with three separated nanodroplets, with membrane asymmetry Δ = 0.17 and line and interfacial tensions λ = −2.6 kBT/d, Σαβ = 1.88 kBT/d2.
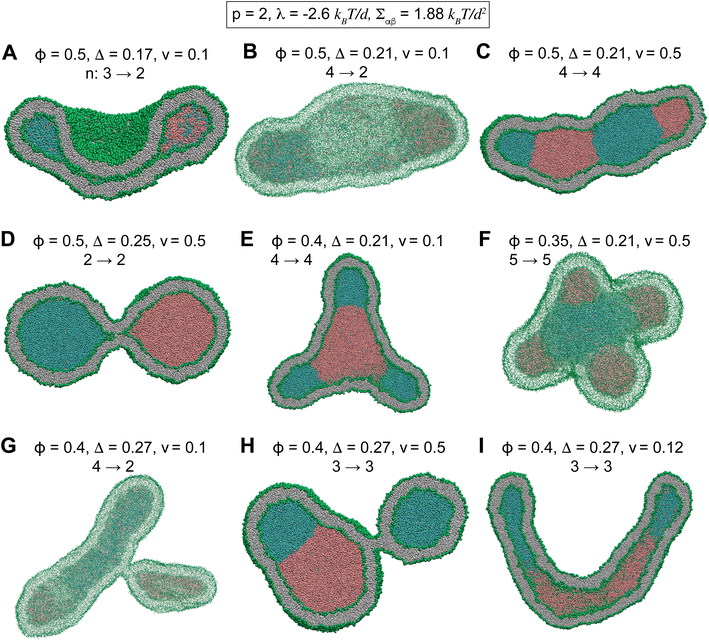
Starting from a nanovesicle with interior phase-separated multi-droplets, we slowly reduced the vesicle volume from v = 1 to v = 0.1 in about 90 μs. In all the following simulations, the vesicle volume is reduced by a fixed rate of 0.01 per micro second which is sufficiently small to ensure equilibrium intermediate vesicles.37 Fig. 3 and S4† show some of intermediate vesicle structures with various values of ϕ and v. Morphological evolution of some of these vesicles through intermediate morphologies is shown in Videos SV6 to SV8.† Vesicles were observed to undergo shape transitions consisting a rich variety of both stable two-compartment and meta-stable multi-compartment conformations such as branched tubules (Fig. 3E, G and S4F†), dumbbells (Fig. 3D), tubes (Fig. 3I), sheets (Fig. 3B), cups (Fig. 3A), and pearled vesicles (Fig. 3C and H) with up to n = 5 (Fig. 3F and S4C†) and n = 6 (Fig. S4E†) compartments. Whereas some of the internal droplets of multi-compartment vesicles coalesced to form larger droplets upon vesicle deflation, many others persisted over long 90 μs simulations.
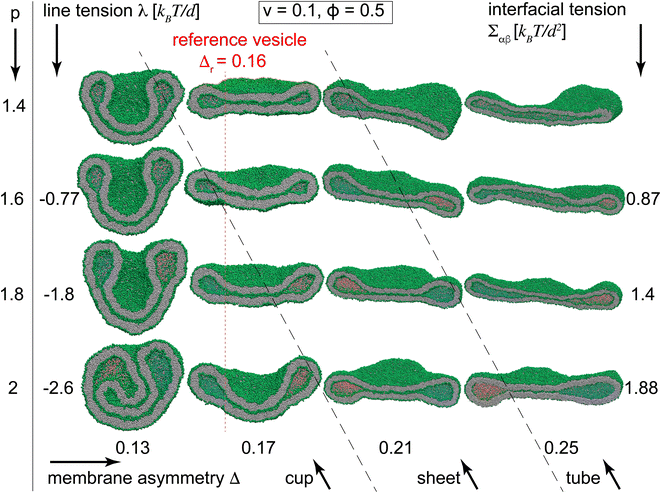
Stable two-compartment vesicles
To better understand the novel membrane nanostructures of meta-stable multi-compartment nanovesicles, we concentrated on two-compartment nanovesicles as the building blocks of the more general multi-compartment vesicles. Starting from equilibrated vesicles with various membrane asymmetries 0.13 ≤ Δ ≤ 0.25 and two initially-separated liquid droplets, we slowly decreased the vesicle volume to v = 0.1, thereby constructing the morphological diagram of stable two-compartment vesicles. Simulations were performed for vesicles with internal liquid phases with ϕ = 0.5 and different separation propensities 1.48 ≤ p ≤ 2, corresponding to −3 kBT/d < λ < 0 and Σαβ ∈ (0.4, 2)kBT/d2. We also simulated particular vesicles with miscible internal liquids with p = 1.4, for which the line and interfacial tensions are not defined. We observe morphological transitions between tubules, sheets, and cup vesicles for different values of Δ and p, see Fig. 4 and Videos SV1 to SV3.†Inspecting columns of Fig. 4, we observe transitions from mostly tubular structures for large membrane asymmetries Δ = 0.25, into sheets for intermediate asymmetries Δ = 0.17 and 0.21, and toward cups for Δ = 0.13 at the leftmost column. For any individual column with a fixed Δ, more negative line tensions and larger interfacial tensions, corresponding to larger p, transform the vesicle from mostly tubular to mostly sheet-like structures as seen for Δ = 0.21 and 0.25. For smaller membrane asymmetries Δ = 0.13 and 0.17, a similar transition from sheet-like to cup-shaped vesicles takes place upon decreasing line tensions to more negative values. Similar behaviour is observed for the special case of p = 1.4, corresponding to two fully miscible liquids without energetic contributions from line and interfacial tensions, see first row in Fig. 4. As seen in the bottom left snapshot of Fig. 4, larger separation propensity p = 2 corresponding to a larger Σαβ = 1.88 kBT/d2 and a more negative λ = −2.6 kBT/d at sufficiently low Δ = 0.13 are even capable of forming a double-cup morphology.
The key step in forming membrane stacks and cup membranes, critical for many biological processes and ubiquitous in cellular membranes, is the formation of intermediate sheet morphology. For stable vesicles with constant vesicle volume, the positive interfacial tension tends to reduce the area of the interfacial surface while the negative line tension acts to increase its perimeter i.e. the length of the contact line. The two effects cooperate to form lipped-like structure, a characteristic feature of sheet membranes, that helps transform tubular structures toward sheet membranes which in turn bend toward the cup shape for more negative line tensions or lower membrane asymmetries.
Fig. 5 displays how a stable dumbbell vesicle with two compartments (Fig. 5A and B) adopts sheet-like structure at the interfacial surface for a more negative λ and a larger Σαβ (Fig. 5D) at fixed Δ = 0.17. A similar sheet-like cross section is observed in Fig. 5C for smaller Δ = 0.17 at constant λ = −2.6 kBT/d and Σαβ = 1.88 kBT/d2, compared to the circular cross section for Δ = 0.25.
The instability of multi-compartment vesicles
Multi-compartment giant vesicles are known to be meta-stable as energetic penalties of membrane tensions make vesicles with two coalesced droplets more favorable than vesicles with multi-droplets. We need, however, to examine the stability of nanovesicles in presence of negative line tensions we have already found to contribute to the shapes of the nanovesicle. To explore the stability of multi-compartment vesicles, we focused on two vesicles with Δ = 0.17, close to the reference vesicle Δr = 0.16, and thus negligible non-local spontaneous curvature. The liquid phases were taken to strongly phase separate with p = 2 corresponding to Σαβ = 1.88 kBT/d2 and λ = −2.6 kBT/d. For the two vesicles with n = 2 and 3 compartments, see Fig. 1A,B middle panels, the free energies are given by
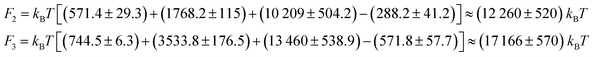 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 kBT of the stable two-compartment vesicle with n = 2 is much less than that of the meta-stable three-compartment vesicle F3 = 17
260 kBT of the stable two-compartment vesicle with n = 2 is much less than that of the meta-stable three-compartment vesicle F3 = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166 kBT. Membrane and interfacial tensions favor the two-compartment vesicle, increasing from F2 to F3 by (3533.8 − 1768.2) kBT = 1766 kBT and (13
166 kBT. Membrane and interfacial tensions favor the two-compartment vesicle, increasing from F2 to F3 by (3533.8 − 1768.2) kBT = 1766 kBT and (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 − 10
460 − 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209) kBT = 3251 kBT respectively, while negative line tension tends to stabilize the meta-stable three-compartment vesicle, decreasing by [ −288.2 − (−571.8)] kBT = 283.6 kBT from F2 to F3. As expected, the vesicle bending energy also tends to stabilize the two-compartment vesicle with a slight energy deference Eb3 − Eb2 = 173.1 kBT, which is due to the reduced area of the highly-curved spherical membrane segments formed for n = 3 droplets.
209) kBT = 3251 kBT respectively, while negative line tension tends to stabilize the meta-stable three-compartment vesicle, decreasing by [ −288.2 − (−571.8)] kBT = 283.6 kBT from F2 to F3. As expected, the vesicle bending energy also tends to stabilize the two-compartment vesicle with a slight energy deference Eb3 − Eb2 = 173.1 kBT, which is due to the reduced area of the highly-curved spherical membrane segments formed for n = 3 droplets.
More strongly separating liquids with a larger p have larger interfacial tensions and more negative line tensions. While larger interfacial tensions stabilize two-compartment vesicles, more negative line tensions favor meta-stable three-compartment vesicles. The interfacial surface area 4πRco2, however, grows faster than the line 2πRco, with Rco being the radius of almost circular interfacial surface, see right panel in Fig. 1A. Negative line tensions are thus more likely to stabilize nanovesicles for which the contribution of these tensions becomes more comparable to those of the interfacial tensions as opposed to larger vesicles where surface tensions are dominant.
Conclusion
Using extensive molecular dynamics simulations, we explored compartmentation of nanovesicles by liquid phase-separation and vesicle remodelling by the resulting aqueous droplets under osmotic deflation. We showed that the phase-separation propensity of the two liquid phases determines the line and interfacial tensions as well as the activity level of the vesicle compartmentation. The vesicles are thus parametrized by two independent parameters: membrane asymmetry — or its non-local spontaneous curvature — and the separation propensity. We identified morphological transitions of stable two-compartment vesicles between tubules, sheets, and cups, induced by liquid droplets and regulated by membrane asymmetry and separation propensity.Our results elucidate how tubules, sheets, and cups, as the building blocks of cellular membranes can be induced and maintained by phase-separated aqueous nanodroplets. These structures, exclusive to nanovesicles, have important implications for shaping cellular membrane nanostructures. We find that typical negative line tensions, resulting from larger separation propensities, play a key role in sculpting nanovesicles. At fixed vesicle volumes, these negative tensions, together with positive interfacial tensions, lead to the formation of lipped-like cross sections, thereby transforming tubular shapes into sheet-like structures on stable vesicles with two compartments.38 Larger interfacial tensions and more negative line tensions can bend the sheet-like biconcave nanovesicle into concave-convex sheet, thereby forming the cup-shaped vesicles that even turn to double cups for larger separation propensities. For a fixed line tension, similar behaviour is observed by decreasing membrane asymmetries, or non-local spontaneous curvatures, where vesicles transform from tubules to sheets and eventually cup morphologies for smaller membrane asymmetries.
Quantifying the free energies of two stable and meta-stable nanovesicles with two and three compartments we demonstrated the instability of long-lived multi-compartment nanovesicles. We thus indicate the important role of internal nanodroplets in conferring meta-stable nanovesicles their prolonged lifetime. Phase-separated nanodroplets can thus contribute to creating and maintaining meta-stable membrane nanostructures such as branched tubules which serve as building blocks of many cellular organelles such as endoplasmic reticulum and mitochondria.
We also show how phase separation of liquids, with smaller relative concentrations and larger separation propensities, generates more compartments which subsequently lead to a more diverse polymorphism of nanovesicles upon osmotic deflation. For meta-stable multi-compartment vesicles with more than two compartments subject to volume reduction, more negative line tensions and higher asymmetries promote formation of meta-stable complex morphologies such as tubular branches. Some of these long-lived structures are also experimentally observed, for instance in nucleoli.21
Our results on forming cup-shaped vesicles have immediate implication for the recently-found impact of liquid phase separation in autophagosome biogenesis.24–26 Our findings also reveal that stable dumbbell vesicles with two aqueous compartments can be formed by adjusting appropriate combinations of separation propensities and membrane asymmetries. This suggests a novel mechanism that can be used to divide a vesicle into two smaller vesicles by internal liquid droplets, mimicking cell division, and may have particular applications in synthetic biology.5
Several structures, observed here for small vesicles, were previously reported for larger vesicles with liquid droplets including shape transformation of nucleoli,3,21 Fig. 3C and H and S4A and D,† and division and budding of model cells and giant vesicles,5,6,16,50 Fig. 5A, B and 3D.
Conflicts of interest
There are no conflicts to declare.Author contributions
Fatemeh Kazemi Sabet: data curation, formal analysis, investigation, software, validation, visualization, writing – review &editing; Arash Bahrami: supervision, project administration, writing – review & editing; Amir H. Bahrami: conceptualization, formal analysis, investigation, methodology, project administration, resources, supervision, validation, visualization, writing – original draft preparation, writing – review & editing.Acknowledgements
A. H. B. acknowledges support from the Max Planck Society within the framework of Max Planck Partner Group, and from the European Molecular Biology Organization, grant EMBO IG 5032.References
- Y. Shin and C. P. Brangwynne, Science, 2017, 357 DOI:10.1146/annurev-cellbio-100913-013325.
- A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58 CrossRef CAS PubMed.
- J. Berry, C. P. Brangwynne and M. Haataja, Rep. Prog. Phys., 2018, 81, 046601 CrossRef PubMed.
- H. Kusumaatmaja and R. Lipowsky, Soft Matter, 2011, 7, 6914–6919 RSC.
- M. Andes-Koback and C. D. Keating, J. Am. Chem. Soc., 2011, 133, 9545–9555 CrossRef CAS PubMed.
- M. S. Long, A.-S. Cans and C. D. Keating, J. Am. Chem. Soc., 2008, 130, 756–762 CrossRef CAS PubMed.
- Y. Li, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci., 2011, 108, 4731–4736 CrossRef CAS PubMed.
- D. Milovanovic, Y. Wu, X. Bian and P. De Camilli, Science, 2018, 361, 604–607 CrossRef CAS PubMed.
- X. Wu, M. Ganzella, J. Zhou, S. Zhu, R. Jahn and M. Zhang, Mol. Cell, 2021, 81, 13–24 CrossRef CAS PubMed.
- N. A. McDonald, R. D. Fetter and K. Shen, Nature, 2020, 588, 454–458 CrossRef CAS PubMed.
- X. Su, J. A. Ditlev, E. Hui, W. Xing, S. Banjade, J. Okrut, D. S. King, J. Taunton, M. K. Rosen and R. D. Vale, Science, 2016, 352, 595–599 CrossRef CAS PubMed.
- O. Beutel, R. Maraspini, K. Pombo-Garcia, C. Martin-Lemaitre and A. Honigmann, Cell, 2019, 179, 923–936 CrossRef CAS PubMed.
- Y.-C. Liao, M. S. Fernandopulle, G. Wang, H. Choi, L. Hao, C. M. Drerup, R. Patel, S. Qamar, J. Nixon-Abell and Y. Shen, et al., Cell, 2019, 179, 147–164 CrossRef CAS PubMed.
- M. Spellings, M. Engel, D. Klotsa, S. Sabrina, A. M. Drews, N. H. Nguyen, K. J. Bishop and S. C. Glotzer, Proc. Natl. Acad. Sci., 2015, 112, E4642–E4650 CrossRef CAS PubMed.
- M. Paoluzzi, R. Di Leonardo, M. C. Marchetti and L. Angelani, Sci. Rep., 2016, 6, 34146 CrossRef CAS PubMed.
- C. D. Crowe and C. D. Keating, Interface Focus, 2018, 8, 20180032 CrossRef PubMed.
- T. Trantidou, M. Friddin, Y. Elani, N. J. Brooks, R. V. Law, J. M. Seddon and O. Ces, ACS Nano, 2017, 11, 6549–6565 CrossRef CAS PubMed.
- D. Bracha, M. T. Walls and C. P. Brangwynne, Nat. Biotechnol., 2019, 1–11 Search PubMed.
- M. S. Long, C. D. Jones, M. R. Helfrich, L. K. Mangeney-Slavin and C. D. Keating, Proc. Natl. Acad. Sci., 2005, 102, 5920–5925 CrossRef CAS PubMed.
- A. Ianiro, H. Wu, M. M. van Rijt, M. P. Vena, A. D. Keizer, A. C. C. Esteves, R. Tuinier, H. Friedrich, N. A. Sommerdijk and J. P. Patterson, Nat. Chem., 2019, 11, 320–328 CrossRef CAS PubMed.
- C. P. Brangwynne, T. J. Mitchison and A. A. Hyman, Proc. Natl. Acad. Sci., 2011, 108, 4334–4339 CrossRef CAS PubMed.
- M. R. Helfrich, L. K. Mangeney-Slavin, M. S. Long, K. Y. Djoko and C. D. Keating, J. Am. Chem. Soc., 2002, 124, 13374–13375 CrossRef CAS PubMed.
- W. T. Snead and A. S. Gladfelter, Mol. Cell, 2019, 76, 295–305 CrossRef CAS PubMed.
- Y. Fujioka, J. M. Alam, D. Noshiro, K. Mouri, T. Ando, Y. Okada, A. I. May, R. L. Knorr, K. Suzuki and Y. Ohsumi, et al., Nature, 2020, 578, 301–305 CrossRef CAS PubMed.
- J. Agudo-Canalejo, S. W. Schultz, H. Chino, S. M. Migliano, C. Saito, I. Koyama-Honda, H. Stenmark, A. Brech, A. I. May and N. Mizushima, et al., Nature, 2021, 591, 142–146 CrossRef CAS PubMed.
- N. N. Noda, Z. Wang and H. Zhang, J. Cell Biol., 2020, 219 DOI:10.1016/j.devcel.2016.06.015.
- H. Yamamoto, Y. Fujioka, S. W. Suzuki, D. Noshiro, H. Suzuki, C. Kondo-Kakuta, Y. Kimura, H. Hirano, T. Ando and N. N. Noda, et al., Dev. Cell, 2016, 38, 86–99 CrossRef CAS PubMed.
- P.-G. De Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- J. Bico, É. Reyssat and B. Roman, Annu. Rev. Fluid Mech., 2018, 50, 629–659 CrossRef.
- W. Helfrich, Z. Naturforsch., C: Biosci., 1973, 28, 693–703 CrossRef CAS PubMed.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A, 1991, 44, 1182 CrossRef CAS PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- A. Hossein and M. Deserno, Biophys. J., 2020, 118, 624–642 CrossRef CAS PubMed.
- M. S. Bretscher, Nature, New Biol., 1972, 236, 11–12 CrossRef CAS PubMed.
- B. Różycki and R. Lipowsky, J. Chem. Phys., 2015, 142, 02B6011 CrossRef PubMed.
- A. H. Bahrami and G. Hummer, ACS Nano, 2017, 11, 9558–9565 CrossRef CAS PubMed.
- R. Ghosh, V. Satarifard, A. Grafmueller and R. Lipowsky, Nano Lett., 2019, 19, 7703–7711 CrossRef CAS PubMed.
- V. Satarifard, A. Grafmueller and R. Lipowsky, ACS Nano, 2018, 12, 12424–12435 CrossRef CAS PubMed.
- R. Lipowsky, J. Phys. Chem. B, 2018, 122, 3572–3586 CrossRef CAS PubMed.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- A. Markvoort, P. Spijker, A. Smeijers, K. Pieterse, R. Van Santen and P. Hilbers, J. Phys. Chem. B, 2009, 113, 8731–8737 CrossRef CAS PubMed.
- K. Chakraborty, W. Shinoda and S. M. Loverde, Soft Matter, 2020, 16, 3234–3244 RSC.
- A. J. Markvoort, N. Pfleger, R. Staffhorst, P. A. Hilbers, R. A. Van Santen, J. A. Killian and B. De Kruijff, Biophys. J., 2010, 99, 1520–1528 CrossRef CAS PubMed.
- N. Urakami, Y. Sakuma, T. Chiba and M. Imai, Soft Matter, 2021, 17, 8434–8445 RSC.
- K. Yang, X. Shao and Y.-q. Ma, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051924 CrossRef PubMed.
- X. Li, Y. Liu, L. Wang, M. Deng and H. Liang, Phys. Chem. Chem. Phys., 2009, 11, 4051–4059 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- J. S. Rowlinson and B. Widom, Molecular theory of capillarity, Courier Corporation, 2013 Search PubMed.
- T. Nakamura, S. Kawamoto and W. Shinoda, Comput. Phys. Commun., 2015, 190, 120–128 CrossRef CAS.
- R. Dimova and R. Lipowsky, Adv. Mater. Interfaces, 2017, 4, 1600451 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary information includes two supplementary texts, four supplementary figures, five supplementary tables, and eight supplementary videos. See DOI: https://doi.org/10.1039/d2ra05855c |
| This journal is © The Royal Society of Chemistry 2022 |