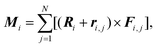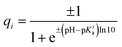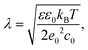Open Access Article
Open Access ArticlePacking and trimer-to-dimer protein reconstruction in icosahedral viral shells with a single type of symmetrical structural unit
Sergei B.
Rochal†
*a,
Olga V.
Konevtsova†
a,
Daria S.
Roshal
 a,
Anže
Božič
a,
Anže
Božič
 b,
Ivan Yu.
Golushko
a and
Rudolf
Podgornik
b,
Ivan Yu.
Golushko
a and
Rudolf
Podgornik
 *bcdef
*bcdef
aPhysics Faculty, Southern Federal University, Rostov-on-Don, Russia. E-mail: rochal_s@yahoo.fr
bDepartment of Theoretical Physics, Jožef Stefan Institute, SI-1000 Ljubljana, Slovenia
cDepartment of Physics, Faculty of Mathematics and Physics, University of Ljubljana, SI-1000 Ljubljana, Slovenia
dSchool of Physical Sciences and Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China. E-mail: podgornikrudolf@ucas.ac.cn
eCAS Key Laboratory of Soft Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
fWenzhou Institute of the University of Chinese Academy of Sciences, Wenzhou, Zhejiang 325000, China
First published on 21st September 2022
Abstract
Understanding the principles of protein packing and the mechanisms driving morphological transformations in virus shells (capsids) during their maturation can be pivotal for the development of new antiviral strategies. Here, we study how these principles and mechanisms manifest themselves in icosahedral viral capsids assembled from identical symmetric structural units (capsomeres). To rationalize such shells, we model capsomers as symmetrical groups of identical particles interacting with a short-range potential typical of the classic Tammes problem. The capsomere particles are assumed to retain their relative positions on the vertices of planar polygons placed on the spherical shell and to interact only with the particles from other capsomeres. Minimization of the interaction energy enforces equal distances between the nearest particles belonging to neighboring capsomeres and minimizes the number of different local environments. Thus, our model implements the Caspar and Klug quasi-equivalence principle and leads to packings strikingly similar to real capsids. We then study a reconstruction of protein trimers into dimers in a Flavivirus shell during its maturation, connecting the relevant structural changes with the modifications of the electrostatic charges of proteins, wrought by the oxidative switch in the bathing solution that is essential for the process. We highlight the key role of pr peptides in the shell reconstruction and show that the highly ordered arrangement of these subunits in the dimeric state is energetically favored at a low pH level. We also discuss the electrostatic mechanisms controlling the release of pr peptides in the last irreversible step of the maturation process.
1. Introduction
Viruses span an intermediate region between living and non-living matter, requiring at certain stages of their life cycle a host cell to replicate their genome and produce the genome-enclosing protein shell (capsid).1 Self-assembly of new viruses is a multi-stage process requiring many steps controlled exclusively by physical forces and chemical equilibria.2 For many viruses, the final stage of the assembly process, referred to as maturation, involves structural transformations of the proteinaceous capsid that convert a noninfectious precursor particle into an infectious virion, able to proliferate in host cells.3 Studying the principles of self-assembly and the structural transformations involved in the capsid maturation process is therefore crucial for the understanding of virus infectivity as well as developing appropriate antiviral strategies.Being encoded by a relatively simple and by necessity, relatively short viral genome,4 the capsid proteins cannot be too complex and can be characterized by a small number of conformational states and types of bond with their nearest neighbors. While an unlimited number of crystallographically equivalent positions would exist in an ideal periodic protein lattice, any closed discrete shell such as the proteinaceous capsid, by necessity, supports only a limited number of crystallographically equivalent positions. For identical asymmetric proteins in the case of capsids with icosahedral symmetry, this number equals 60, which is also the order of the capsid symmetry group I, implying furthermore that when the number of proteins exceeds 60, their environments cannot be strictly identical. Therefore, most proteinaceous capsids exhibit a hidden, i.e., approximate symmetry5–8 characterized by a local periodic order, allowing the proteins to occupy quasi-equivalent positions, as the next best thing to the geometrically forbidden strictly equivalent crystallographic positions. This principle of quasi-equivalence, introduced by Caspar and Klug (CK), permits the description of the structure of icosahedral capsids as consisting of pentamers and hexamers within their well-known viral shell model.9
While the CK model seems to be applicable to a plethora of viral capsids, it is not universal, and anomalous viral shells that cannot be rationalized within it, consisting of identical symmetric capsomeres, namely, dimers,10–14 trimers,13,15,16 or more rarely pentamers17,18 and decamers,10,11,14 abound in nature. These symmetrical structural units pre-assemble in a solution from identical proteins or symmetrically arranged protein domains before the capsid assembly, with intra-capsomere protein bonds clearly differing from the bonds between proteins of neighboring capsomers. This situation begs the question of how do the viral proteins minimize the number of their local environments in this type of capsid. Some large viral shells assembled from trimers exhibit a locally periodic order of SU environments similar to the CK model, while some small anomalous viral capsids exhibit a hidden locally periodic order of SU environments, quite unlike the CK model.5 In order to get a clearer grasp of the nature of local environments and packings of symmetrical structural units in these anomalous proteinaceous shells, we will show in what follows how their tendency to form dense packings on spherical shells also minimizes the number of different local environments.
The simplest dense particle packing on a spherical surface can be formed by disks, and the well-known Tammes problem is devoted to finding the densest packings for N identical disks embedded on a spherical surface.19 The equilibrium dense packing of disks can be obtained by minimizing the sum of the pair interaction energies of equivalent point particles located at the disk centers. If all disks are identical and touch each other, then the short-range potential of such pair interaction decreases with increasing distance l between their centers as l−n, where n → ∞.20,21 Going beyond the disk-like structural units, we now generalize the Tammes problem and consider equilibrium configurations of identical symmetrical groups of particles distributed on the spherical surface. In the proposed model, within the SU that corresponds to a capsomere, the distances between particles are kept fixed while particles from different SUs interact with each other in the same way as in the Tammes problem. As we show, the resulting equilibrium packings on a spherical surface turn out to be similar to the structures of certain actually existing viral shells. An analysis of the structural data22 for such shells reveals that the separations between nearest proteins belonging to neighboring symmetrical structural units are similar. This allows us to use the short-rang potential to reproduce the general features of the considered dense protein packings and clarify how the CK quasi-equivalence principle works in the considered case.
As part of the generalization of the Tammes problem and as an illuminating illustration of our theory, along with other examples of capsid self-assembly from a single type of symmetrical SU, we consider specifically the packaging of proteins in the immature and mature outer shells of the Dengue virus and similar viruses from the Flavivirus genus in the family Flaviviridae. In viruses of this genus, the immature viral shell first self-assembles from trimers and then reorganizes itself into a shell composed of dimers during the maturation process. This structural change occurs with an increase in the acidity of the bathing environment,23 and we show how the change in the electrostatic energy of the system induced by a change in the pH level controls this intriguing dimer-to-trimer transformation. Moreover, we also show that the pH change finally assists in the subsequent irreversible stage of the capsid maturation yielding the final form of the virion.
2. Results and discussion
2.1. Modelling dense packing of identical structural units
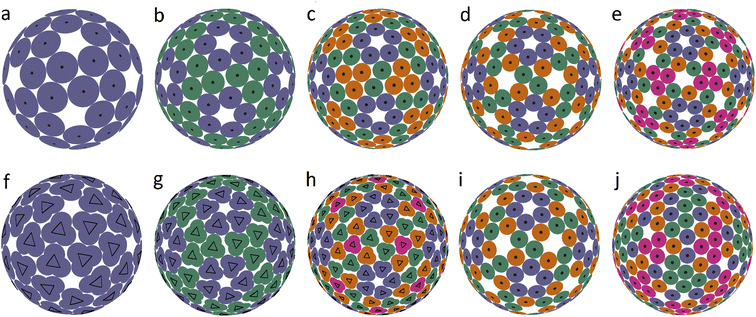
To construct the model energy function that would describe the capsomer packing, we consider regular identical rigid polygons placed on the spherical shell, with interactions operating only between their vertices. We assume that these polygons can change the position and orientation, while their centers remain confined to the spherical surface, and their plane is constrained to coincide with the tangential plane to the surface. Because the polygons are rigid, only the interactions between different polygons need to be taken into account, and we therefore postulate that the interaction energy is of the form: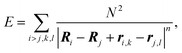 | (1) |
Note that the interaction energy (1) contains only terms corresponding to repulsive interactions. While at first glance it may seem that a model disregarding the attractive interaction between distant particles is an oversimplification, in actuality when self-assembly is modeled on the surface of a finite manifold, the confinement on the surface is equivalent to an effective attraction of SUs, and energy minimization leads to a relatively uniform distribution of SUs over the surface.
Eqn (1) can be expanded into a series in terms of the ratios r/Rij (where Rij is the distance between the centers of i-th and j-th polygons) by using the standard theory of multipole decomposition, but the ensuing representation of the pair interaction energy involving convolutions of various multipole tensors is quite cumbersome and will not be pursued further. It is easier to use the symmetry of the problem from the very beginning, in particular the fact that the pair interaction energy in (1) is invariant under the 2π/N-rotation of the regular polygon with N sides. Consequently, the interaction energy must be expanded in a series of cos(2πmϕ/N) and sin(2πmϕ/N) terms, where m is an integer, and ϕ is a rotation of the polygon around its N-fold axis. It is then possible to expand the interaction energy of two polygons to the lowest order in terms of the dependence on ϕ. In particular, for two dimers (N = 2) of radius r, whose centers are separated by a distance R, the expansion up to order O((r/R)4) yields:
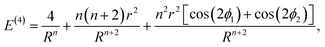 | (2) |
The features of the multipole expansions can be very fruitful for constructing various model interaction potentials for different nano-objects,23 including interactions between capsomeres in viruses, that are sufficiently far apart. However, when considering specifically the problem of dense (contact) packing of capsomers, one should stick with the complete expression of the interaction energy (1). Comparison of the spherical packings of viral shell capsomers based on the interaction energy (1) is carried out in the next section.
2.2. Model structures of viral capsids
Equilibrium packings arising from energy minimization by the rotation method (see the Methods), as in other similar methods such as the gradient descent method, generally depend on initial coordinates and orientations of the SUs. We used PDB data to define the initial state of the system before minimization. First, we defined centers of mass (CoMs) of individual proteins. Then, these coordinates were used to calculate coordinates of the centers and orientations of symmetrical SUs. Since CoMs only approximately characterize positions of the proteins in the structure, we performed multiple minimizations of the energy (1) by slightly varying the initial conditions to make sure that a model structure similar to a real capsid would not be accidently missed.
In an icosahedral capsid, the dimer centers can lie on the twofold axis and/or occupy general positions, so that such a capsid can be assembled from 30T dimers, where T is an integer equal to the number of crystallographic orbits of proteins in the capsid. Fig. 1 shows examples of capsids self-assembling from dimers with T = 2, 3 and models of these shells obtained by minimization of energy (1). Since the capsids can significantly change their shape and rearrange themselves during viral maturation, we explicitly indicate the PDB identifiers of the structures under consideration. In this work, all images of viral capsids were taken directly from the PDB website or obtained with UCSF Chimera.25
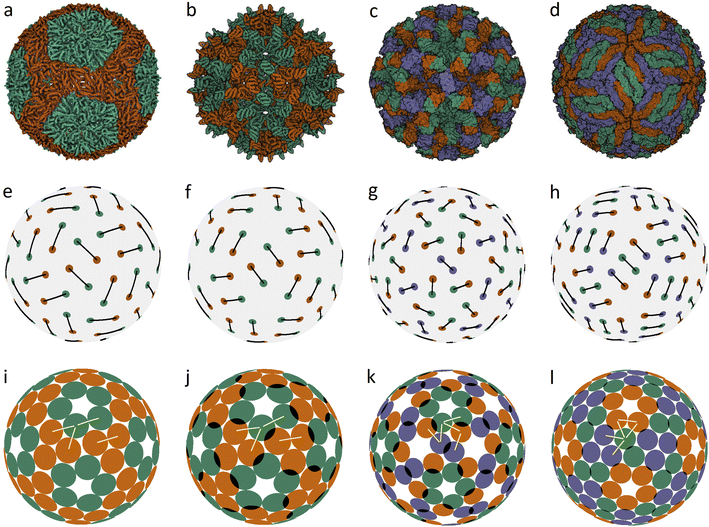 | ||
| Fig. 1 Capsid structures from PDB: (a) bacteriophage ϕ6 (4BTQ) (Cystoviridae) (T = 2); (b) penicillium stoloniferum virus S (3IYM) (Partitiviridae) (T = 2); (c) Norwalk virus (1IHM) (Caliciviridae) (T = 3); (d) dengue virus (3J05) (Flaviridae) (T = 3); (e–h): position of the CoMs according to PDB with the corresponding arrangement of dimers. The ratio of the dimer length to the sphere radius r/R for cases (a–d) is: 0.172, 0.1355, 0.104, and 0.13; (i–l) optimized icosahedral model structures with the same r/R ratio. In each structure, all disks are identical in size, and a pair of overlapping disks corresponds to a dimer. In (a), distances between the disks in a dimer and disks between neighboring dimers practically coincide. The yellow segments correspond to quasi-equivalent bonds that are not symmetry equivalent. The lengths of these segments in the limit n → ∞ become exactly equal. The corresponding distances between the protein CoMs in real structures (see (e–h)) are close, but not equal. | ||
Fig. 1a shows the mature capsid of bacteriophage ϕ6, which acquires an approximately spherical shape after genome packaging. In the mature state, the mass centers of proteins, despite their grouping into dimers, correspond to a conventional packing of disks on a sphere: the distance between the mass centers of proteins in a dimer and that between the proteins from neighboring dimers practically coincide.
To assess the stability of the model structures, we randomly shifted the centers of the dimers as well as randomly rotated them. Under this perturbation, the displacement of the dimer center and the shift of the dimer vertices (mass centers of individual proteins), due to dimer rotation in the local coordinate system, were both limited by a certain value V. After this perturbation, we minimized the energy (1) again and observed that the model structure shown in Fig. 1i is stable within V/R ≈ 0.05. Importantly, we could not find any structures with lower energies and thus assumed that probably this packing of dimers corresponds to the global minimum of energy (1). The structure shown in Fig. 1j is stable at slightly larger random distortions V/R ≲ 0.06; however, we found an asymmetric packing with a slightly lower energy. The model structure from the 3rd column (unlike the other structures presented in this figure) is stable only if the icosahedral symmetry is imposed during the energy minimization. Otherwise, the packing loses its symmetry after small perturbations, turning into a more energetically favorable structure with slightly shifted dimers, as in the case of the icosahedral packing of non-overlapping disks (Fig. 2d) that undergoes a similar transformation into a more energetically favorable structure (Fig. 2i).
The mature shell of Dengue virus from the Flaviridae family consists of dimers (see the last column of Fig. 1). The immature shell initially self-assembles from trimers and then radically rearranges its structure, the situation which is considered in more detail in the next sections. The structural model of the virus (Fig. 1l) is stable for V/R ≈ 0.04 and probably corresponds to the global minimum of energy (1).
Concluding the discussion of dimer shells, we note that minimization of energy (1) of an arbitrary initial arrangement of dimers with imposed icosahedral symmetry always leads to the model structures shown in the lower line of Fig. 1. Naturally, the obtained packings depend on the ratio r/R and the number of dimers (60 or 90).
It is interesting that the model structures presented in the last line of Fig. 1 can be additionally symmetrized if all particles interact identically with a pair potential l−200, i.e., particles are no longer grouped into dimers. The resulting packings are shown in Fig. 2b–d. This figure shows the first 5 spherical structures (panels a–e) with the icosahedral symmetry and location of SUs in general crystallographic positions. Since proteins cannot occupy positions with nontrivial symmetry, such icosahedral dense packings are not exhibited in Fig. 2. The dense packing makes the local environment of symmetry-nonequivalent disks quasi-equivalent, and therefore in the structure (b), both types of disk (blue and green) have 5 nearest neighbors, while in the structures (c–e), the blue disks that form pentamers around the 5-fold axes have 5 nearest neighbors, and the others have 4 nearest neighbors.
Structures 2(a–c) are stable for V/R ≲ 0.12, 0.1, 0.09 and, according to our calculations, (b and c) are potential solutions to the Tammes problem for 120 and 180 disks. Recall that so far, only solutions to the Tammes problem for 100 or fewer disks have been found.26,27 Packings (d and e) are stable only for such distortions of the SU positions that preserve icosahedral symmetry, while small random distortions force these structures to lose their icosahedral symmetry. Packing (d) is transformed into a slightly distorted, more energetically favorable packing (k), and packing (e) is converted into various strongly distorted structures like (l). With stronger perturbations, the packing (k) subsequently rearranges itself into a more energetically favorable structure. A complete analysis of the energy landscape of the proposed model is computationally cumbersome, as is well known from the studies on other similar systems28 and clearly goes beyond the goals of this work.
While packings 2a–e are a somewhat rougher approximation to the structures of the relevant capsids, they are nevertheless still useful, since they can be helpful in rationalizing other types of spherical viral shell. It is straightforward to see that the close-packed structures shown in Fig. 2a–e are based on so-called icosahedral spherical lattices (SLs), in which the nodes lying on the symmetry axes of the icosahedron are excluded. The relationship between these SLs and the arrangement of proteins in small spherical viruses was analyzed in ref. 5. Recall that regular SLs (without exclusion of positions) are the basis of the CK model of viral capsids,9 in which twelve 5-valent nodes of SLs are occupied by pentamers, and the remaining nodes with 6 neighbors are occupied by hexamers. SLs can be constructed as the mapping of the nodes of a simple hexagonal lattice onto the surface of the icosahedron. Due to geometric constraints, the edge of the icosahedron must be a translation of the hexagonal lattice, and translation indices are used to characterize the resulting SL.
We also found several examples of small icosahedral shells assembled from 60 and 80 trimers. Two of them are shown in Fig. 3. They are those of the immature Zika virus (6LNU) (Flaviridae) and Hepatitis B virus (6W0K). The corresponding model structures are stable under random distortions within V/R ≈ 0.03 and 0.01, respectively. While the first structure probably corresponds to the global minimum of energy (1), it is strongly reconstructed during the maturation of Zika virus. The self-assembly of Hepatitis B virus is also very interesting. After the initial stage of self-assembly, where dimers are formed in solution, they are subsequently reassembled into trimers, and the resulting structure is often treated as consisting of pseudo-hexamers.
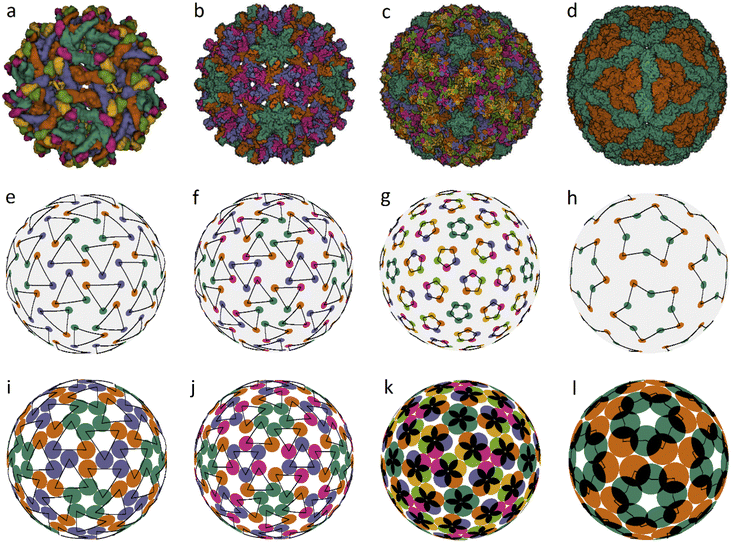 | ||
| Fig. 3 Viral capsids self-assembled from trimers and pentamers, as well as their corresponding model structures. Capsid structures according to PDB: (a) immature Zika virus (6LNU), (b) Hepatitis B virus (6W0K), (c) Human Papillomavirus (5KEP). (d) Leishmania RNA virus (6H83), (e–h) positions of the CoMs of individual proteins. The location of trimers, pentamers and decamers is shown with triangles, pentagons and five-pointed stars, respectively, drawn with black lines. The ratios of the capsomere radius to the sphere radius r/R for cases (e–g) are: 0.254, 0.187, and 0.12; the decamer in (h) is given by two pentagons rotated relative to each other at ∼30° with r/R = 0.32 and 0.48, respectively. (i–l) Optimized model structures with the same ratio r/R. | ||
Assembly of some viruses also involves formation of intermediate complex SUs from dimers. For example, a trimer of dimers is the basic building block of HIV39 and some other large viruses (from families Phycodnaviridae and Iridoviridae).33,35,36 Self-assembly of T = 2 capsids of dsRNA viruses from the Reoviridae14 and Totiviridae40 families starts with the formation of pentamers of dimers in the bathing solution. These transient SUs are also called pseudo-decamers,10 and an example of such a capsid is shown in Fig. 3d. Our analysis of PDB structural data on Reoviridae and Totiviridae reveals that CoMs of individual proteins in viruses from these two families practically coincide. The CoM positions, shown in Fig. 3h, make individual decamers clearly distinguishable. For comparison, this is not the case in the T = 2 structures shown in Fig. 1e and f. Indeed, during self-assembly of T = 2 capsids from the families Partitiviridae and Cystoviridae, no decamers are formed.14 The arrangement of CoMs of proteins in the decamer (Fig. 3h) has C5 symmetry, and the CoMs form two regular pentagons rotated relative to each other. Within the framework of energy (1), the packing of decamers into an icosahedral capsid corresponds to the global energy minimum. Note that in the considered case, the system energy has only two minima.
Fig. 3c shows another very interesting example of Human Papillomavirus capsid (panel c) and similar capsids assembled from 72 pentamers and belonging to the same family Papillomaviridae. In such capsids, the pentamer centers are localized at all SL (2, 1) nodes. Fig. 3g and k show positions of protein CoMs and the model structure corresponding to the global energy minimum at the considered ratio r/R = 0.12.
An analysis of the real structures shown in Fig. 1 and 3, as well as other similar structures self-assembling from a single type of capsomere, reveals that the number of different distances between CoMs of the neighboring proteins and, accordingly, the number of corresponding bond types, are minimal. Bonds of the first type connect CoMs of nearest proteins within symmetrical SUs, whereas bonds of the second type connect CoMs of nearest proteins belonging to neighboring SUs. Bonds of the second type are similar in length, which is, however, not determined by the symmetry of the system.
In the proposed model, minimization of the total energy for short-range interaction potential with n = 200 furthermore equalizes the second-type bond lengths up to a spread of ±0.25%. In the case n → ∞, all these symmetry-nonequivalent lengths become exactly the same. It is easy to determine the total number of such lengths for an arbitrary packing of the considered type. In the general case, in order to uniquely specify the position of the capsomere on the sphere, all three coordinates must be determined. Two of them determine the position of its center, and the third one describes the capsomere orientation. If the capsomere position coincides with a symmetry axis of the icosahedron, then only one coordinate remains, specifying the rotation of the capsomere. To determine M coordinates, it is necessary to solve the system of equations stemming from the condition that M + 1 symmetry-nonequivalent distances are identical. Thus, there should be 4 such distances (see the corresponding yellow lines in Fig. 1) for structures (k and l) and 5 for structures (m and n). However, finding actual solutions of the corresponding system of equations leads to coordinate corrections, which are so small that they are indistinguishable on the scale of Fig. 1–3. It is also interesting to note that our model compares favorably with real structures not only in the case of distances just discussed (that become exactly equal in the n → ∞ limit), but also for other structural properties. For example, in the vicinity of the 3-fold axis (see Fig. 1l), the distance between the centers of SUs in the model structure turns out to be somewhat larger than the minimal one, resulting in a small gap between the disks, which tallies with the situation in real capsids (see Fig. 1d), where the corresponding distances between protein CoMs (see Fig. 1h) are also similar in length. In all cases presented in Fig. 1 and 3, it is easy to notice other similar examples by paying attention to the corresponding model structure and finding disks separated by a small gap. Thus, both real structures and model packings are in good agreement with the CK principle of quasi-equivalence of symmetry-nonequivalent bonds between nearest proteins.
2.3. Morphological changes in Flavivirus viral shells during their maturation
In the previous sections, we proposed a simple packing model for immature and mature viral shells of Flaviviruses. Recall that the immature shell self-assembles from trimers, and then during the maturation process, the trimers reorganize into dimers. Let us discuss this intriguing transformation that has two intermediate stages23 in more detail using the PDB structural data on the dengue virus shell. The radical reconstruction occurs at the first maturation stage when the trimeric structure 3C6D turns into the dimeric one 3C6R (see Fig. 4a and b). Both states consist of 180 complex proteins, referred to as the heterodimers.41 Each heterodimer includes the main M–E part and the pr peptide. The main part is the largest and has the shape of a short, bent rod that is thicker at one end (head). The small pr peptide is connected to the thinner end (tail) of the main SU.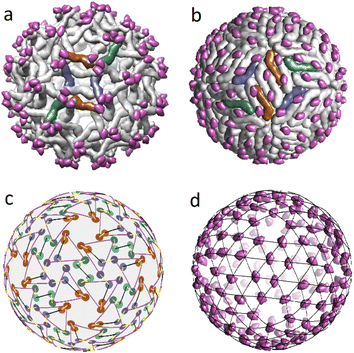 | ||
| Fig. 4 Structural transformation occurring during the Dengue virus shell maturation. (a) Trimeric structure of the viral shell 3C6D. M–E subunits of six heterodimers forming two neighbouring trimers are colored in dark orange, blue and green. (b) Dimeric structure of the viral shell 3C6R. The same subunits M–E as in panel (a) are shown in color to demonstrate correspondence between two structures. (c) Superimposed mass centers of heterodimers in trimeric and dimeric structures. CoM positions in the dimeric structure are represented by lighter circles. The displacement field of the mass centers that defines 3C6D ↔ 3C6R correspondence is shown with yellow lines. (d) Positions of the pr peptides in 3C6R with superimposed icosahedral SL (3, 2). In (a, b, d), pr peptides are shown in magenta. | ||
In the 3C6D state, the immature shell consists of 60 trimers, each of which is formed by three heterodimers connected close to their heads. In Fig. 3e, such a structural organization is represented by a motif of triangles with vertices being CoMs of individual heterodimers belonging to the same trimer. In Fig. 4a a pair of such trimers, that is symmetric with respect to the 2-fold axis of the immature shell, is highlighted in color. Like their heads, the tails of heterodimers are also connected in triplets located above the centers of neighboring trimers. So, in Fig. 3e, one can see that the triangle vertices also form the vertices of a weakly deformed hexagon, which allows classifying the 3C6D structure as a pseudo-hexagonal one.
By establishing the correspondence between protein positions in trimeric state 3C6D and dimeric state 3C6R states, one can fully define the structural mechanism of the transition. For this aim, we superimpose the heterodimer CoMs and assume that the CoM displacements are small (see Fig. 4c). Then, considering these reasonable displacements of CoMs in the vicinity of 3-fold axes, one can see that there are two possible rearrangements of this heterodimer orbit as the corresponding CoM displacements are close in lengths. Fig. 4a and b show the rearrangement in which heterodimers rotate less. Let us note that details of the considered 3C6D → 3C6R transition are still unclear. For example, rearrangement that leads to a larger rotation of heterodimers has been recently considered in ref. 41. In contrast, earlier work42 focused on a different type of rearrangement characterized by smaller rotations of heterodimers, but involving longer shifts of their CoM positions.
Independent of the rearrangement mechanism, formation of the first intermediate dimeric state 3C6R requires that heterodimer tails cease to combine into triplets. In this context, it is interesting to note that in the dimeric state, the pr peptides (attached to heterodimer tails) occupy almost equidistant positions and form a relatively regular structure (see Fig. 4d). Note also that the second intermediate state 3YIA involves irreversible changes, as the connection between the pr peptide and the M part of the heterodimer is terminated. Nevertheless, in this state, cleaved pr peptides remain associated with the shell. Finally, at the end of the maturation process, when the shell is reintroduced into the neutral environment, pr peptides are released from the viral surface.
Unlike the 3C6R → 3IYA transition, the first intermediate stage of the maturation, transforming the trimeric structure 3C6D into the dimeric one 3C6R, is reversible and can be activated in vitro by decreasing the pH of the solution to 5.5.23 This experimental finding, combined with the fact that generally the net charge of a protein is controlled by the pH of the buffer solution, suggests that the electrostatic interactions between shell proteins could play a significant role in the 3C6D → 3C6R transition. To test this hypothesis, we examined how electrostatic energies (see the Methods for details) of the two shell states depend on the acidity of the solution.
First, we calculated the degree of dissociation and partial charge of each amino acid in the heterodimer at different pH values within the framework of ref. 24 and 43 using the Henderson–Hasselbalch equation (see the Methods). Total charges of the whole heterodimer and its pr and M–E subunits, as a function of the pH value, are shown in Fig. 5a. All three plots increase monotonously with the decrease of the bathing solution pH. Both subunits are negatively charged at neutral pH. With the decrease of pH, the pr subunit remains negatively charged, whereas the charge of the M–E subunit changes its sign. Accordingly, the heterodimer as a whole has an isoelectric point at around pH = 6.
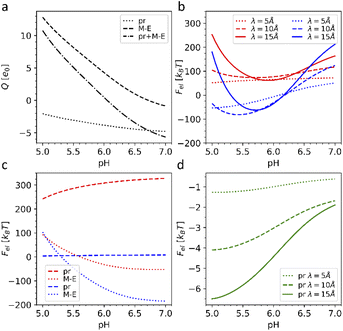 | ||
| Fig. 5 Electrostatic effects associated with dengue shell maturation. (a) Charges of the single heterodimer and its M–E and pr parts separately, expressed in the elementary charge units e0 as a function of the pH level. (b) Effective electrostatic energies of the trimeric 3C6D (shown in red) and dimeric 3C6R (shown in blue) states expressed in kBT units as a function of pH for three different screening constant values. (c) Energy of the effective electrostatic interaction between M–E (dashed line) and pr (dotted line) subunits separately (interactions between pr and M–E subunits are ignored) as a function of pH for three different electrostatic screening constant values λ. The plots corresponding to the trimeric and dimeric sates are color-coded as in (b). (d) Effective energy of attractive electrostatic interaction between a single pr peptide and the rest of the 3IYA shell as a function of pH for three different electrostatic screening lengths λ. The value λ = 10 Å corresponds to the physiological salt concentration and temperature T = 300 K. | ||
Let us note that generally speaking, amino acids can be ionized only when they are in contact with the solvent. 3C6D → 3C6R transition should modify contacts between heterodimers changing the solvent accessibility as quantified by the solvent accessible surfaces (SASs).44,45 Because of the low resolution of structural data provided in PDB (positions of amino acids are defined by a single carbon atom), we were unable to consider the effects associated with the variation of SASs, so that in our model, the charges of SUs have the same pH dependencies in both structures.
To our knowledge, after ref. 46, structures of the intermediate states in viral shells of the Flaviviruses have not been experimentally studied; however, as we show later, our simplified model is sufficient for obtaining results that are in good agreement with experimental data and provides valuable insight into the maturation process itself.
A typical average value of the electrostatic screening length λ at the physiological salt concentration can be estimated to be λ = 9.74 Å; however, since the local salt concentration can vary, we calculated energies (3) for the three typical screening lengths, namely: 5, 10 and 15 Å (see more details in the Methods). Fig. 5b shows that the electrostatic energy behaves qualitatively the same for all three λ values considered. For pH < 6.6, the electrostatic energy of the dimeric state becomes lower than that of the trimeric one, and the energy gap between the two states increases up to pH ∼ 5.7–6.0, which are also the pH values reported for the maturation transformation.23,46 Importantly, the 3C6R structure was studied experimentally at pH ∼ 5.5,46 where, according to our calculations, the energy of the dimeric structure is substantially lower. The screening of electrostatic interactions implied by the energy (3) is an essential ingredient of the model, since, when λ exceeds the characteristic size of the capsid, the gain in the electrostatic energy of the dimeric state disappears.
To better understand why the transition from the trimeric to the dimeric structure lowers the electrostatic energy of the shell, we also considered the interaction energies of all M–E subunits and all pr subunits separately. In Fig. 5c, one can see that the energy associated with electrostatic interactions between pr peptides (dotted line) drops after the 3C6D → 3C6R maturation transition, strongly decreasing the total electrostatic energy of the whole shell. The pr subunits in the trimeric structure repel each other at all considered pH levels, substantially increasing electrostatic energy of the trimeric state. Even though this contribution slightly decreases with the decrease of pH, it is the structural transition that drastically reduces the electrostatic energy by forcing pr peptides into the positions corresponding to the icosahedral SL (3, 2) (Fig. 4d), and since the asymmetric pr peptides cannot occupy positions corresponding to the 5-fold axes, they are left vacant. Such a quasi-equidistant arrangement combined with the screening of the electrostatic interactions by the solution ions leads to the interaction energy between pr peptides that is close to zero. Thus, pr subunits play a key role in the considered reversible structural transition.
The details of the above scenario can be developed further by noting that the trimeric to dimeric structure transition could be engendered by another likely driving force. In fact, the proteinaceous outer shell self-assembles on a lipid membrane,47 and it is well known that an important fraction of biological membrane lipids in general are anionic.48,49 In our opinion, the membrane charge can play a role in virus surface protein rearrangement during Dengue maturation, where the membrane composition contains about 10% of anionic lipids.50Fig. 5a shows that at pH < 6, heterodimers as a whole are positively charged, and therefore, they are highly likely attracted to the negatively charged lipid membrane. Since the positive charge of heterodimers increases with the oxidation of the bathing solution, the attraction should also increase. Considering that in the dimeric state, heterodimers are located closer to the lipid membrane, we conclude that the membrane-to-shell electrostatic attraction can probably also contribute to the trimeric to dimeric structure transformation. We will analyze more details of this phenomenology in our future work.
Obviously, the proposed framework considers only electrostatic interactions between fixed protein units of outer shells and does not allow to take into account specific chemical changes during the irreversible transition to the second intermediate state 3C6R → 3IYA. Nevertheless, 3YIA structural data can be used to study the release of the pr peptides, which completes the maturation process and occurs when the viral shell returns to the neutral (pH = 7) environment. To explain this phenomenon, we analyzed how the energy of the electrostatic interaction between a single pr peptide and the rest of the 3YIA shell depends on the pH. Fig. 5d shows that with increasing pH, the attraction of the pr subunits to the viral surface significantly decreases, and an increase in the screening length leads to a steeper dependence. On a qualitative level, such behavior agrees with the way the subunit charges depend on pH (see Fig. 5a).
Our electrostatic model is based on several simplifications: we disregarded possible effects associated with the contribution of other long-range interactions,51 such as van der Waals interactions, and we did not include the effects of various short-range solvent mediated and contact couplings, which certainly affect the packing of trimers and dimers and thus also the properties of the maturation transitions. Nonetheless, our analysis highlights the crucial role of the electrostatic interactions between the viral shell subunits and their connection with the variation in the pH bathing environment in both irreversible and reversible morphological transitions during the Flavivirus maturation process, rationalizing the existing experimental data.
3. Conclusions
Here, we studied the principles controlling the structural organization of capsids assembled from identical structural units (capsomers), which can contain two, three, five, or ten proteins. We demonstrated that the main morphological features of such viral shells are well reproduced by our new model, related to the Tammes problem,19 that considers the densest spherical packings of identical discs. As was shown before,20,21 these packings correspond to the global minimum of the short-range pair interaction energy scaling as l−n, where l is the distance between disc centers, and n → ∞. In our approach, interacting particles (located at the protein mass centers) are divided into identical SUs (which can be dimers, trimers, pentamers, or decamers), and the analogous short-range potential describes the interactions between the particles from different SUs. Within each SU, the relative coordinates of particles remain unchanged, forming a regular polygon with a fixed radius. Note also that an explicit attractive component of the interaction potential between SUs is not considered directly since an effective attraction is indirectly provided by the SU confinement on a spherical surface.Thus, our approach takes explicitly into account only the effective size r/R and the n-fold symmetry of proteinaceous capsomers, which we believe are the two crucial properties characterizing the packing of identical capsomers on the spherical surface. The interaction model proposed in this work appears to be the simplest meaningful implementation of the finite size and symmetry of interacting SUs confined to a spherical surface. While point-like models or models with point-like symmetry of interactions between capsomeres are certainly well known in the literature,52–57 our model proposes a minimal generalization of these approaches that retains some features of the point-like interaction models but also takes into account the effective size r/R and the n-fold symmetry of the interacting SUs.
The short-range potential used in our model evens out the distances between nearest interacting particles and minimizes the number of local environments in the resulting packings, conforming fully with the Caspar and Klug quasi-equivalence principle. By comparing our results with PDB structural data, we have demonstrated that the proposed model is universal and suitably describes a large number of viral shells.
Understanding of principles controlling spherical dense packings of symmetrical capsomers and corresponding contact interactions is essential for rationalizing structures and functions of virus shells. Concurrently, electrostatic interactions, being important in protein physics in general,58 are also seen to play a key role in the virus life cycle. Proteins have electrical charge that can reach tens of elementary charges e0 per molecule depending on the pH level.59 During their life cycle, viruses often travel through areas of the cell with varying pH and sometimes can even control it.60,61 The electrostatic forces are therefore essential at practically all stages of virus development including capsid self-assembly,62–65 genome packing,66,67 and capsid modification during virus maturation.68 The model describing contact interactions between identical symmetrical capsomers, which has been developed in this paper, can be readily modified in the future to study electrostatic interactions between identical symmetrical groups of electrostatic charges corresponding to such capsomers. To our knowledge, this problem has not been considered before, even though interactions of neutral multipoles in different systems including capsids are actively studied.2
In this work, we considered the role of electrostatic interactions in the pH controlled morphological changes of the proteinaceous outer shells of the Flavivirus genus. These changes are observed at the maturation and start from reversible transition from the trimeric to dimeric arrangement of proteins. As we have shown, the phenomenon can be explained by the changes in the charges of heterodimer subunits induced by the pH decrease and the tendency of the system to minimize its electrostatic energy via structural rearrangement. Pr peptides play a key role in this process, and the highly ordered arrangement of these subunits in the dimeric state makes this packing more energetically favorable than the initial trimeric one. We have also considered the irreversible transition of the outer virus shell that finalizes the maturation process and demonstrated that prior to the release of the pr peptides, the energy of their attractive electrostatic interaction with the viral shell significantly decreases due to the increase in the pH of the bathing solution. These results might be useful for the development of new immunogens, as some human antibodies (EDE2 A11, EDE2 B7, EDE1 C8 and EDE1 C10), neutralizing dengue virus serotypes of Flaviridae, bind to E proteins specifically in the former positions of pr peptide attachment.69 Thus, similar to pr peptides in the immature shell, arrangement of these antibodies on the surface of the mature capsid could be highly ordered, and their binding could be also controlled by the acidity of the surrounding medium, which we plan to examine in our future work.
4. Methods
4.1. Energy minimization
To minimize energy (1), we developed the method of finite rotations, that is a modification of the ordinary gradient descent. An arbitrary polygon motion (including a local rotation) over the sphere surface can be considered as a rotation of the polygon around a certain axis that passes through the sphere center. This approach to the considered constrain minimization problem ensures that the polygon remains embedded on the sphere surface. At each minimization step, first, we calculate moments of forces Mi applied to the i-th polygon:where Fi,j is the force, applied to the j-th vertex of i-th polygon. The latter force is calculated directly by differentiating eqn (1). Then, we perform the corresponding small rotation of the i-th polygon through an angle αi that is proportional to the absolute value |Mi| around the normal ni‖Mi. The coefficient of proportionality between αi and |Mi| is chosen so that the rotation decreases energy (4.1). The minimization of energy (1) is stopped when all moments Mi vanish. In general, vectors Mi and Ri are non-collinear, which means that the rotation of the polygon around ni also involves its movement over the sphere surface. Let us recall that a rotation through angle α around n relates initial vector A and rotated one A′ as
A′ =Acos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α + (1 − cos α + (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)(n·A)n + (n × A)sin α)(n·A)n + (n × A)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α. α. |
Minimization of energy (1) with an accuracy of 10–15 digits may require about 104–105 steps of the algorithm.
4.2. Calculating amino acid charges and debye screening length
To calculate partial charges of the amino acids, total charges of heterodimer subunits, and energies of their electrostatic interactions, we first extracted data on all ionizable amino acids from PDB structure files 3CHD, 3CHR, and 3IYA corresponding to the immature Zika virion, the first and the second intermediate states accordingly. In these files, each amino acid is represented by a single carbon atom. According to ref. 70, only six amino acids can carry electric charge. To calculate their charges at a given pH value, we used the Henderson–Hasselbach equation:where the plus sign is used when calculating charges of basic amino acids (arginine, histidine, and lysine), and the minus sign corresponds to acidic amino acids (aspartic acid, glutamic acid, and tyrosine). Values of the acid-based dissociation constant pKa for these amino acids were taken from ref. 71. They are 3.71, 4.15, 10.10, 12.10, 6.04, and 10.67 for aspartic acid, glutamic acid, tyrosine, arginine, histidine, and lysine accordingly. When calculating electrostatic energy (3), we assume that the coordinates of amino acid charges are equal to those of the abovementioned carbon atoms and use the following expression for the screening length:
where kB is the Boltzmann constant, ε0 is the electric constant, and e0 is the elementary charge. The parameters we used to estimate λ are: temperature T = 300 K, dielectric constant of water ε = 80 and monovalent salt concentration c0 = 100 mM, which are typical of experimental settings. These parameters correspond to the value of λ ≈ 9.74 Å.
4.3. Calculating the electrostatic energy
Knowing the charges qi of the amino acids within each structural unit, we then calculated the normalized electrostatic energy of interactions between heterodimers forming the shell using the basic Debye–Huckel approximation:43,72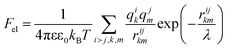 | (3) |
Author contributions
S. R. and R. P. proposed main approaches. O. K. found examples of appropriate viral shells and drew the figures. I. G., O. K., and D. R., with the help of A. B. carried out numerical simulations. S. R. with the essential help of R. P. wrote the manuscript. All authors reviewed and edited the text. S. R. managed the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. P. would like to acknowledge funding from the Key Project No. 12034019 of the Natural Science Foundation of China. S. R., I. G., O. K., and D. R. acknowledge financial support from the Russian Science Foundation, grant no. 22-12-00105.References
- S. J. Flint, L. W. Enquist, V. R. Racaniello and A. M. Skalka, Principles of Virology: Molecular Biology, Pathogenesis, and Control, ASM, Washington, 2000 Search PubMed.
- R. Zandi, B. Dragnea, A. Travesset and R. Podgornik, Phys. Rep., 2020, 847, 1–102 CrossRef CAS.
- A. C. Steven, J. B. Heymann, N. Cheng, B. L. Trus and J. F. Conway, Curr. Opin. Struct. Biol., 2005, 15, 227–236 CrossRef CAS PubMed.
- F. H. Crick and J. D. Watson, Nature, 1956, 177, 473–475 CrossRef CAS PubMed.
- S. B. Rochal, O. V. Konevtsova, A. E. Myasnikova and V. L. Lorman, Nanoscale, 2016, 8, 16976–16988 RSC.
- S. B. Rochal, O. V. Konevtsova and V. L. Lorman, Nanoscale, 2017, 9, 12449–12460 RSC.
- V. V. Pimonov, O. V. Konevtsova and S. B. Rochal, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 135–141 CrossRef CAS PubMed.
- O. V. Konevtsova, D. Roshal, A. L. Božič, R. Podgornik and S. Rochal, Soft Matter, 2019, 15, 7663–7671 RSC.
- D. L. D. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS PubMed.
- D. Luque, J. M. González, D. Garriga, S. A. Ghabrial, W. M. Havens, B. Trus, N. Verdaguer, J. L. Carrascosa and J. R. Castón, J. Virol., 2010, 84, 7256–7266 CrossRef CAS PubMed.
- H. S. Savithri and M. R. N. Murthy, Curr. Sci., 2010, 98, 346–351 CAS.
- G. K. Shoemaker, E. van Duijn, S. E. Crawford, C. Uetrecht, M. Baclayon, W. H. Roos, G. J. L. Wuite, M. K Estes, B. V. Prasad and A. J. R. Heck, Mol. Cell. Proteomics, 2010, 9, 1742–1751 CrossRef CAS PubMed.
- K. Holmes, D. A. Shepherd, A. E. Ashcroft, M. Whelan, D. J. Rowlands and N. J. Stonehouse, J. Biol. Chem., 2015, 290, 16238–16245 CrossRef CAS PubMed.
- M. M. Poranen and D. H. Bamford, Viral Molecular Machines, Advances in Experimental Medicine and Biology, ed. M. G. Rossmann and V. B. Rao, Springer, 2012th edn, 2012, vol. 726, pp. 379–402 Search PubMed.
- C. Helgstrand, S. Munshi, J. E. Johnson and L. Liljas, Virology, 2004, 318, 192–203 CrossRef CAS PubMed.
- Z. Gao, H. Pu, J. Liu, X. Wang, C. Zhong, N. Yue, Z. Zhang, X.-B. Wang, C. Han, J. Yu, D. Li and Y. Zhang, Mol. Plant-Microbe Interact., 2021, 34, 49–61 CrossRef CAS PubMed.
- R. C. Liddington, Y. Yan, J. Moulai, R. Sahli, T. L. Benjamin and S. C. Harrison, Nature, 1991, 354, 278–284 CrossRef CAS PubMed.
- M. Wolf, R. L. Garcea, N. Grigorieff and S. C. Harrison, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6298–6303 CrossRef CAS PubMed.
- P. M. L. Tammes, Recl. Trav. Bot. Neerl., 1930, 27, 1–84 Search PubMed.
- J. H. Conway and N. J. A. Sloane, Sphere Packings, Lattices and Groups, Springer Science & Business Media, 2013, vol. 290 Search PubMed.
- M. J. Bowick and L. Giomi, Adv. Phys., 2009, 58, 449–563 CrossRef CAS.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- D. Sirohi and R. J. Kuhn, J. Infect. Dis., 2017, 216, S935–S944 CrossRef CAS PubMed.
- A. L. Božič and R. Podgornik, J. Chem. Phys., 2013, 138, 074902 CrossRef PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- L. Hars, Numerical Solutions of the Tammes Problem for up to 60 Points, https://www.hars.us/Papers/Numerical_Tammes.pdf, accessed July 2022 Search PubMed.
- L. Hars, Numerical Solutions of Midsize Tammes Problems: N = 61,…, 100, https://www.hars.us/Papers/MidsizeNumerical_Tammes.pdf, accessed July 2022 Search PubMed.
- D. J. Wales, Energy Landscapes, Cambridge University Press, Cambridge, UK, 2003 Search PubMed.
- L. M. Iyer, L. Aravind and E. V. Koonin, J. Virol., 2001, 75, 11720–11734 CrossRef CAS PubMed.
- L. M. Iyer, S. Balaji, E. V. Koonin and L. Aravind, Virus Res., 2006, 117, 156–184 CrossRef CAS PubMed.
- N. Yutin, Y. I. Wolf, D. Raoult and E. V. Koonin, Virol. J., 2009, 6, 223 CrossRef PubMed.
- P. Colson, X. De Lamballerie, N. Yutin, S. Asgari, Y. Bigot, D. K. Bideshi, X.-W. Cheng, B. A. Federici, J. L. Van Etten, E. V. Koonin, B. La Scola and D. Raoult, Arch. Virol., 2013, 158, 2517–2521 CrossRef PubMed.
- C. Xiao and M. G. Rossmann, Curr. Opin. Virol., 2011, 1, 101–109 CrossRef CAS PubMed.
- N. G. Wrigley, J. Gen. Virol., 1969, 5, 123–134 CrossRef CAS PubMed.
- X. Yan, P. R. Chipman, T. Castberg, G. Bratbak and T. S. Baker, J. Virol., 2005, 79, 9236–9243 CrossRef CAS PubMed.
- M. V. Cherrier, V. A. Kostyuchenko, C. Xiao, V. D. Bowman, A. J. Battisti, X. Yan, P. R. Chipman, T. S. Baker, J. L. Van Etten and M. G. Rossmann, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11085–11089 CrossRef CAS PubMed.
- X. Yan, Z. Yu, P. Zhang, A. J. Battisti, H. A. Holdaway, P. R. Chipman, C. Bajaj, M. Bergoin, M. G. Rossmann and T. S. Baker, J. Mol. Biol., 2009, 385, 1287–1299 CrossRef CAS PubMed.
- A. A. Simpson, N. Nandhagopal, J. L. Van Etten and M. G. Rossmann, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59, 2053–2059 CrossRef PubMed.
- O. Pornillos, B. K. Ganser-Pornillos, B. N. Kelly, Y. Hua, F. G. Whitby, C. D. Stout, W. I. Sundquist, C. P. Hill and M. Yeager, Cell, 2009, 137, 1282–1292 CrossRef PubMed.
- C. P. Mata, J. M. Rodrígueza, N. Suzukic and J. R. Castón, Adv. Virus Res., 2020, 108, 213–247 CAS.
- T. Y. Tan, G. Fibriansah, V. A. Kostyuchenko, T.-S. Ng, X.-X. Lim, S. Zhang, X.-N. Lim, J. Wang, J. Shi, M. C. Morais, D. Corti and S.-M. Lok, Nat. Commun., 2020, 11, 895 CrossRef CAS PubMed.
- L. Li, S. M. Lok, I. M. Yu, Y. Zhang, R. J. Kuhn, J. Chen and M. G. Rossmann, Science, 2008, 319, 1830–1834 CrossRef CAS PubMed.
- A. L. Božič and R. Podgornik, J. Phys.: Condens. Matter, 2018, 30, 024001 CrossRef PubMed.
- T. J. Richmond, J. Mol. Biol., 1984, 178, 63–89 CrossRef CAS PubMed.
- A. L. Božič and R. Podgornik, Biophys. J., 2017, 113, 1454–1465 CrossRef PubMed.
- I.-M. Yu, W. Zhang, H. A. Holdaway, L. Li, V. A. Kostyuchenko, P. R. Chipman, R. Kuhn, M. G. Rossmann and J. Chen, Science, 2008, 319, 1834–1837 CrossRef CAS PubMed.
- B. D. Lindenbach, H. J. Thiel and C. M. Rice, Fields Virology, ed. D. M. Knipe and O. M. Howley, Lippincott Williams & Wilkins, Philadelphia, 5th edn, 2011, pp. 1101–1151 Search PubMed.
- V. V. Galassi and N. Wilke, Membranes, 2021, 11, 478 CrossRef CAS PubMed.
- P. Khunpetch, A. Majee and R. Podgornik, Soft Matter, 2022, 18, 2597–2610 RSC.
- Q. Zhang, C. Hunke, Y. H. Yau, V. Seow, S. Lee, L. B. Tanner, X. L. Guan, M. R. Wenk, G. Fibriansah, P. L. Chew, P. Kukkaro, G. Biuković, P. Y. Shi, S. G. Shochat, G. Grüber and S. M. Lok, J. Biol. Chem., 2012, 287, 40525–40534 CrossRef CAS PubMed.
- R. H. French, V. A. Parsegian, R. Podgornik, R. F. Rajter, A. Jagota, J. Luo, D. Asthagiri, M. K. Chaudhury, Y.-M. Chiang, S. Granick, S. Kalinin, M. Kardar, R. Kjellander, D. C. Langreth, J. Lewis, S. Lustig, D. Wesolowski, J. S. Wettlaufer, W.-Y. Ching, M. Finnis, F. Houlihan, O. A. von Lilienfeld, C. J. van Oss and T. Zemb, Rev. Mod. Phys., 2010, 82, 1887–1944 CrossRef.
- R. F. Bruinsma, W. M. Gelbart, D. Reguera, J. Rudnick and R. Zandi, Phys. Rev. Lett., 2003, 90, 248101 CrossRef PubMed.
- R. Zandi, D. Reguera, R. F. Bruinsma, M. Gelbart and J. Rudnick, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15556–15560 CrossRef CAS PubMed.
- R. Zandi and D. Reguera, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021917 CrossRef PubMed.
- T. Chen, Z. Zhang and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 717–722 CrossRef CAS PubMed.
- T. Chen and S. C. Glotzer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051504 CrossRef PubMed.
- A. Luque, R. Zandi and D. Reguera, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5323–5328 CrossRef CAS PubMed.
- A. Finkelstein and O. Ptitsyn, Protein Physics: A Course of Lecture, Academic Press, 2nd edn, 2016 Search PubMed.
- D. J. Winzor, Anal. Biochem., 2004, 325, 1–20 CrossRef CAS PubMed.
- T. Y. Tan, G. Fibriansah and S.-M. Lok, PLoS Pathog., 2020, 16, e1008542 CrossRef CAS PubMed.
- H. Liu, H. Maruyama, T. Masuda, A. Honda and F. Arai, Front. Microbiol., 2016, 7, 1127 Search PubMed.
- L. Li, Z. Jia, Y. Peng, S. Godar, I. Getov, S. Teng, J. Alper and E. Alexov, Sci. Rep., 2017, 7, 8237 CrossRef PubMed.
- A. Siber and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061906 CrossRef PubMed.
- P. van der Schoot and R. Bruinsma, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061928 CrossRef PubMed.
- L. Li, L. Wang and E. Alexov, Front. Mol. Biosci., 2015, 2, 5 Search PubMed.
- V. A. Belyi and M. Muthukumar, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17174–17178 CrossRef CAS PubMed.
- S. Karlin and V. Brendel, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 9396–9400 CrossRef CAS PubMed.
- D. Roshal, O. Konevtsova, A. L. Božič, R. Podgornik and S. Rochal, Sci. Rep., 2019, 9, 5341 CrossRef CAS PubMed.
- A. Rouvinski, P. Guardado-Calvo, G. Barba-Spaeth, S. Duquerroy, M.-C. Vaney, C. M. Kikuti, M. E. Navarro Sanchez, W. Dejnirattisai, W. Wongwiwat, A. Haouz, C. Girard-Blanc, S. Petres, W. E. Shepard, P. Desprès, F. Arenzana-Seisdedos, P. Dussart, J. Mongkolsapaya, G. R. Screaton and F. A. Rey, Nature, 2015, 520, 109–113 CrossRef CAS PubMed.
- M. J. Betts and R. B. Russell, Bioinformatics for Geneticists, ed. M. R. Barnes and I. C. Gray, 2003, vol. 14, pp. 289–316 Search PubMed.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, Boston, MA, 97th edn, 2016 Search PubMed.
- D. Roshal, O. Konevtsova, A. L. Božič, R. Podgornik and S. Rochal, Sci. Rep., 2019, 9, 5341 CrossRef CAS PubMed.
Footnote |
| † Equally contributed to this work. |
| This journal is © The Royal Society of Chemistry 2022 |